引言
界面的几何特征主要包括界面的高度分布、沿垂向间歇因子分布及界面的分形维度等.Corrsin和Kisteler[8]指出, 间歇因子分布的导数就是界面高度的概率密度分布,因此这两个分布密切相关. Borrell和Jiménez[3]的研究指出,界面高度的分布受到识别界面时阈值选取的影响.由于越靠近壁面无论是涡量还是湍动能都会增大,因此常用的涡量阈值或是湍动能阈值方法, 所得界面平均位置都会随阈值增大而降低.De Silva等[1]研究了界面的分形维度,发现在高雷诺数的情况下分形维度$D_{f}\approx 2.3$,且受雷诺数、界面识别的阈值选取影响较小. Wu等[4]得到$D_{f} = 2.22$比DeSilva的结果略小. 张爽和时钟[9]的研究也表明随着湍流强度的减弱,界面形状会更加平滑, 分形维度也相应地减小.
相对于光滑平板湍流边界层湍流/非湍流界面特性的研究,对非光滑壁面、特别是具有重要应用前景的减阻沟槽表面湍流边界层湍流/非湍流界面特性的研究工作相对较少,对其界面湍流扩散的影响亦缺乏了解. 众所周知,顺流向的沟槽表面在适当的条件下通过改变近壁面流动结构降低了壁面摩擦阻力[10-17].Bechert等[18]研究发现在沟槽内尺度无量纲间距$s^{+}$为15 $\sim$ 20, 深宽比$h$/$s$为0.5 $\sim$ 0.8时最大减阻率可达10%左右.杨绍琼等[19]及袁一平等[20]也在相近的尺度范围内得到了最佳的沟槽减阻效果.Koeltzsch等[21]发现发散-汇聚型沟槽在特定情况下也能够减小阻力的现象引发了很多关注.崔光耀等[22]通过研究发现发散型沟槽能够减阻的原因主要是沟槽引起局部顺向涡的减少.Kevin等[23]在汇聚-发散型沟槽壁面上流动的研究中发现壁面加强了湍流/非湍流的掺混程度,发散型沟槽表面上湍流区域中的非湍流块出现的概率是光滑壁面和汇聚型沟槽壁面的两倍.Wu等[4]指出汇聚型和发散型沟槽分别具有增阻和减阻的作用,而对应的湍流/非湍流界面高度概率密度分布相对于正态分布分别存在正的和负的偏度.
本实验主要采用时间解析的二维粒子图像测速技术(PIV)对光滑和顺流向沟槽平板湍流边界层流场进行测量,研究低雷诺数沟槽表面对湍流边界层湍流/非湍流界面的影响. 本文第1节为实验仪器设备、实验模型、实验参数的介绍,第2节对测量所得流场进行分析, 主要包括湍流边界层摩擦速度的确定、湍流/非湍流界面识别、界面的几何特征和动力学特征,第3节为论文的结论.
1 实验设置
本实验在北京航空航天大学的低速回流式水槽中进行,水槽实验段的侧壁和底壁均由光滑的有机玻璃制成. 实验段几何尺寸为3 m $\times$ 60 cm $\times$ 70 cm (长 $\times$ 宽 $\times$ 深), 实验采用的模型为光滑平板、精细的顺流向沟槽平板, 模型尺寸均为长2.4 m, 宽60 cm,平铺在水槽实验段中.
图1给出了沟槽模型的示意图, 沟槽截面形状为锯齿形,其齿间距为$s$, 沟槽深度为$h$, 顶角为$\alpha $. 由于数据来自两次实验,具体参数稍有不同, 详情可见表1. 齿根部位以小圆弧过度, 以便给铣刀加工留够空间.实验模型前端加装坡度比1:10的与平板宽度、厚度相同的斜劈, 用以避免来流在模型的钝体前缘发生分离.模型平板前端还放置了直径3 mm的拌线用来加速流动转捩, 以保证下游实验数据采集区域处于充分发展的湍流状态.本文中实验坐标系的$x$, $y$, $z$轴分别对应流向、垂向和展向方向, 对应的流速分别用$u$, $v$, $w$表示. 对于光滑壁面和沟槽壁面的模型, 坐标$y$轴的原点分别建立在光滑壁面的表平面和沟槽壁面齿顶所在平面上.
图1
表1 各组实验模型参数及流场条件设置
Table 1
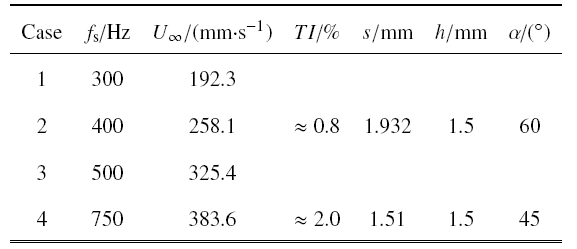 |
注: T I 为湍流度(turbulent intensity).
本实验采用PIV技术对不同雷诺数下光滑、沟槽平板湍流边界层进行测量, 通过改变来流速度$U_{\infty } $来使得雷诺数$Re_{\tau } $在400 $\sim$ 1000范围变化. 实验中采用连续激光照亮示踪粒子, 激光片光厚度约为1 mm.示踪粒子采用的是直径为5 $\sim$ 20 $\mu$m的空心玻璃珠,密度为1.05 g/cm$^{3}$. 拍摄视野的中心位于从斜劈前端算起的下游2 m处,激光平面垂直于模型表面并平行于来流方向, 即位于$Oxy$平面内.激光平面位于水槽的中心对称面上, 距离水槽侧壁有足够的距离(30 cm),因此可以忽略侧壁边界的影响[4]. 采用CMOS相机采集粒子图像,相机的像素为2048 $\times$ 2048, 测量视野的大小为120 mm $\times$ 120 mm, 因此空间分辨率约为每像素0.059 mm. 实验中根据来流速度的变化,采用了不同的采样频率$f_{s}$ (表1), 以尽量保证相邻两幅粒子图像中最大的粒子位移约为8 $\sim$ 12个像素.由于CMOS相机内存的限制, 单次采样连续采样时间受限, 因此每个工况重复采样5次,以保证统计数据收敛. 速度场计算采用了MILK算法[24-25],查询窗口大小为32 $\times$ 32像素, 重叠率为75%.
2 实验结果与分析
2.1 摩擦速度
本实验中无法直接测量模型壁面某处的摩擦阻力,因此采用Clauser[26]的方法拟合摩擦速度$u_{\tau } $,以此衡量模型表面阻力大小. 然而对于沟槽表面来说,一般认为其理论零点会低于沟槽齿顶平面, 传统的Clauser拟合方法失效了.针对这一问题人们常采用修正的Clauser方法: 对于沟槽表面的速度型在对数区满足
式中, $\hat{{y}}$为理论法向高度, 可以看作测量点物理坐标与由沟槽引起的零点偏移量$y_{v}$之和, 即$\hat{{y}}=y + y_{v}$. $\kappa $为卡门常数, 本文中取$\kappa =0.41$, $B$为对数律截距,本文中取$B = 5.0$, $\Delta U^{+}$为沟槽表面对数速度分布相对于光滑表面的偏移量.将式(1)等号两边对$y$进行微分可得
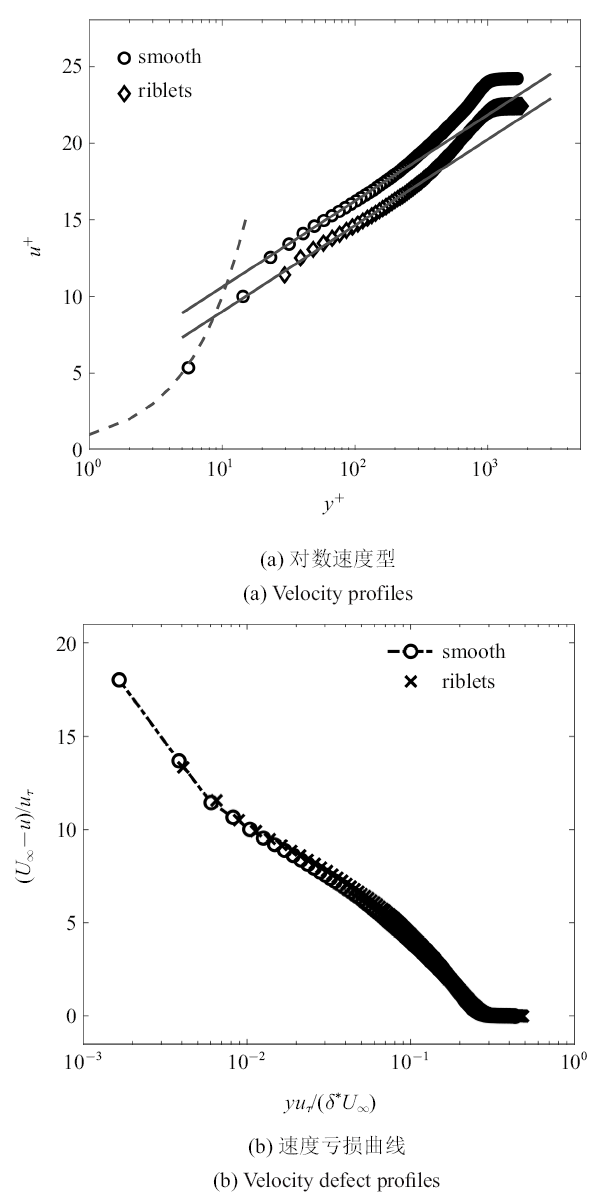
通过迭代计算可以同时得到摩擦速度$u_{\tau } $和理论零点$y_{v}$的值.本文也采用了Choi[27]研究中采用的方法,他认为无论平板表面是何种类型的粗糙, 以${{yu_{\tau } }/{\delta^{\ast}}}U_{\infty } $来表示的无量纲高度在0.002 $\sim$ 0.15范围时,无量纲速度亏损${{(U_{\infty } -u)}/{u_{\tau }}}$在粗糙表面上的分布应与其在光滑表面上的分布相吻合.根据实验数据得出$Re_{\tau } \approx 1000$的拟合结果如图2(b)所示,其中$y_{v}= 0.8$ mm, $u_{\tau } = 16.0$ mm/s. 这两种方法本质上都假设沟槽表面上的速度同样服从对数分布,修正的Clauser方法在低雷诺数下使用时常遇到多解的问题,此时可与Choi方法结合使用, 相互印证, 提高结果准确性. 本文中为表述方便,图片及下文中均直接用符号$y$来表示理论法向高度$\hat{{y}}$.
图2
图2
$Re_{\tau } \approx 1000$组对数速度型及速度亏损曲线
Fig. 2
Velocity profiles and Velocity defect profiles for $Re_{\tau } \approx 1000$
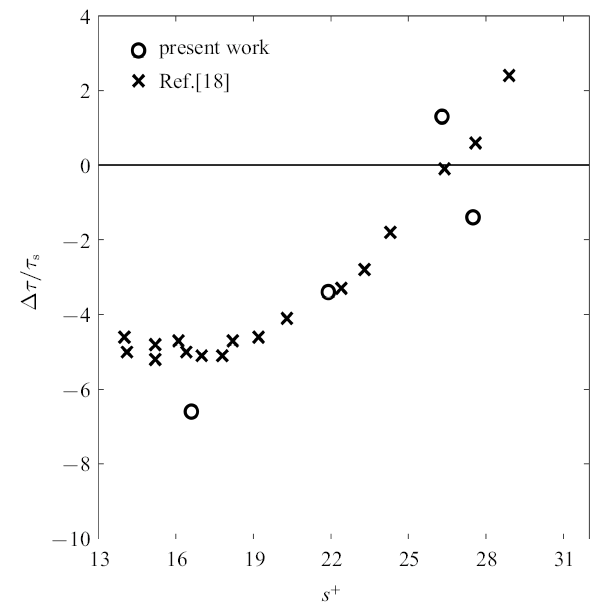
通过与Bechert等[18]研究中沟槽减阻效果比较, 可以确定摩擦速度$u_{\tau }$结果的合理性, 如图3所示. 其中, $\Delta \tau$是沟槽表面和光滑表面摩阻应力之差, 负值表示沟槽表面相对于光滑表面有减阻效果,正值则表示阻力增大的情况. $\tau_{s}$是光滑表面上的摩阻应力,由于$\tau =\rho u_{\tau }^{2} $, 因此在得到$u_{\tau } $后就可以算出.本实验中改变雷诺数进而影响了无量纲间距$s^{+}$, 使得沟槽表面分别出现了阻力增大、减小的情况. 从图3可以看出,本文的实验结果与Bechert等[18]直接改变沟槽几何尺寸得到结果的变化规律相吻合.
图3
图3
不同无量纲齿距下的增减阻情况
Fig. 3
Drag reduction at difference dimensionless distances of riblets
2.2 界面识别
湍流/非湍流界面通常采用流场中某个物理量的大小作为一个阈值来提取其等值面作为界面,例如采用速度大小、涡量大小, 或者PIV中粒子浓度的等值面等方法.在直接数值模拟中,由于可以采用空间分辨率较高的网格且湍流度可以控制得非常低, 以及没有背景噪声,涡量的计算相对准确, 人们常采用涡量阈值判则识别湍流/非湍流界面. 在实验研究中,往往很难到达精确计算涡量场的空间分辨率及消除背景噪声,因此Chauhan等[2]提出的湍动能阈值判则更为实用. 他们把局部湍动能定义为
式中, $u$, $v$分别为流向、垂向速度分量, 并将所求点周围3 $\times$ 3网格点上湍流能的平均值作为该点的湍动能值, 最后以$U_{\infty }^{2}$来无量纲化并乘以100, 这样, 当测量点位于湍流/非湍流界面以外时,$\tilde{k}$的值会非常接近当地的湍流度, 而随着测量点逐渐靠近壁面, $\tilde{k}$的值总体上会逐渐增大.取一个$\tilde{{k}}$值的作为阈值$\tilde{{k}}_{th} $,湍动能场中这个阈值对应的等值线就是要找的湍流/非湍流界面.
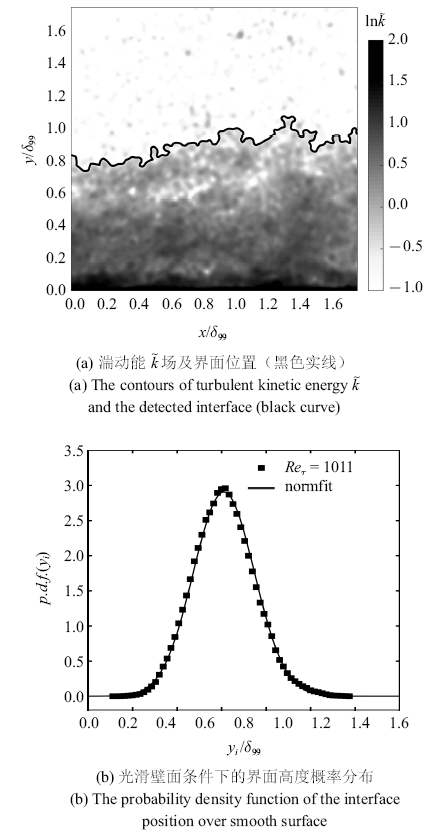
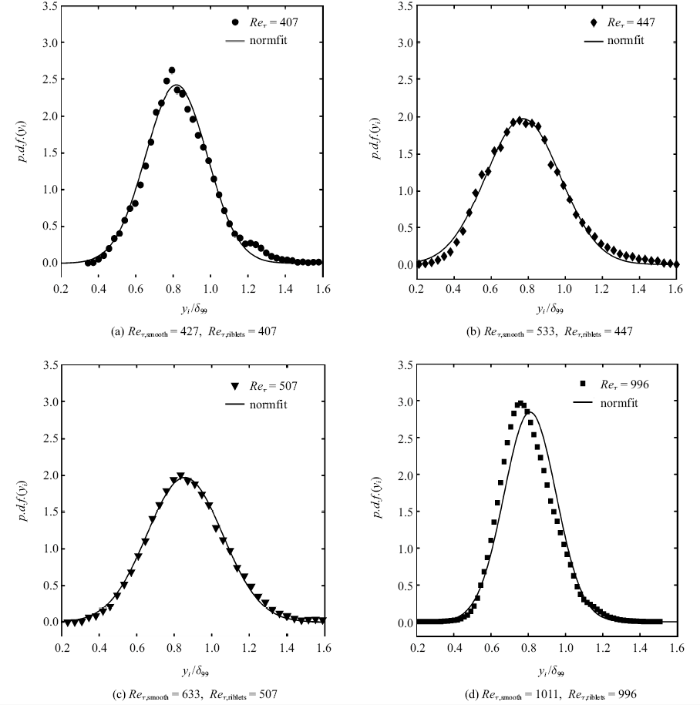
Chauhan等[2]给出了阈值选取的条件:(1)湍流边界层间歇因子的分布应该服从高斯误差函数,(2)界面高度$y_{i}$的均值$Y_{i}$和标准差$\sigma_{i} $满足$Y_{i}+3\sigma_{i} \approx \delta $, 其中$\delta $是边界层厚度.这两个条件一般也可等价为界面高度的概率密度($p.d.f.)$服从正态分布, 一般而言,这里的界面高度仅统计主界面, 即最长的连续界面曲线. 图4给出了本实验中$Re_{\tau} = 1011$、湍动能阈值$\tilde{{k}}_{th} = 0.21$所得结果, 其中图4(a)黑色实线即为湍流/非湍流主界面位置轮廓线, 图4(b)所示为界面高度概率密度分布, 可见其满足正态分布,符合Chauhan等[2]给出的阈值选取条件.
图4
图4
湍流/非湍流界面识别结果($Re_{\tau } = 1011$)
Fig. 4
Example of detection results of the turbulent/non-turbulent interface for $Re_{\tau } = 1011$
2.3 界面几何特性
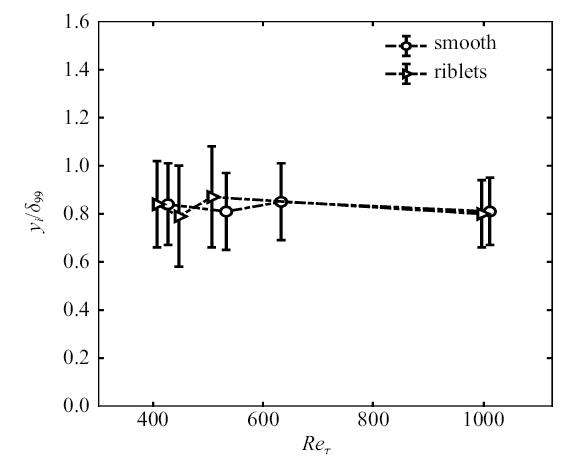
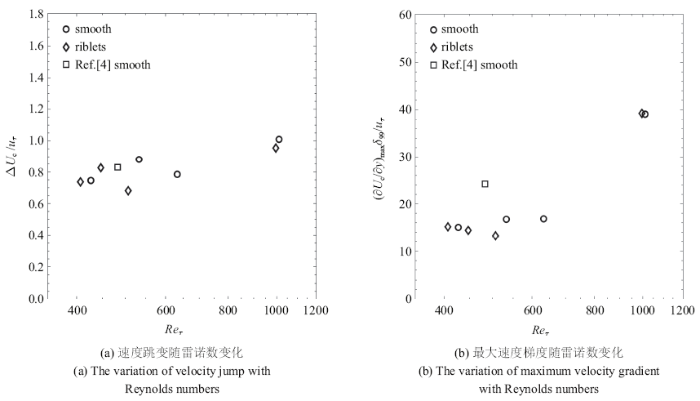
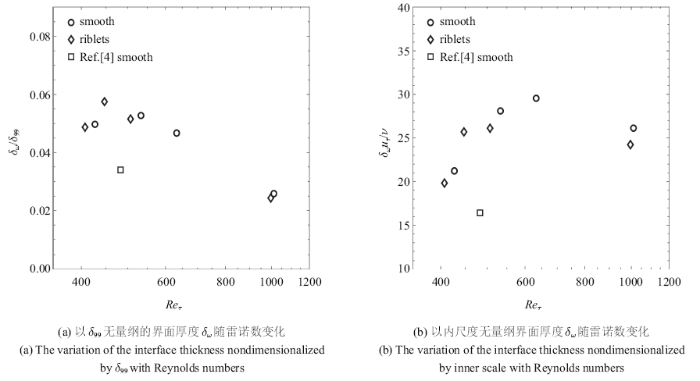
本实验中所得界面分布的统计平均高度${{Y_{i} }/{\delta_{99}}}$如图5所示, 其中数据点上竖线的长度表示了该雷诺数下界面高度标准差${{\sigma_{i} }/{\delta_{99} }}$的大小. 与Wu等[4]、Corrsin和Kistler[8]及Eisma等[28]的结果相比,界面的无量纲平均高度与标准差是相近的. 可以看到, 界面高度$Y_{i}$约为(0.8 $\sim$ 0.9)$\delta_{99}$且受雷诺数及壁面条件的影响均不大,沟槽壁面使得界面高度的标准差大于光滑壁面的情况, 而$Y_{i} +\sigma_{i} $基本保持在$\delta_{99}$附近.图6中将沟槽壁面湍流边界层湍流/非湍流界面高度的概率密度分布与同来流速度光滑壁面上界面高度服从的正态分布(黑色虚线)进行了对比.可以明显看到, 在本实验条件下, 在$Re_{\tau,riblets} = 996$时, 界面高度分布呈现正的偏度, 对应的壁面摩阻增大了1.3%,这与Wu等[4]得到的汇聚型沟槽壁面造成摩擦阻力增大的情况下, 湍流/非湍流界面会相应地呈现出正偏度的结果是一致的.
图5
图5
界面平均高度与标准差随雷诺数的变化
Fig. 5
Mean height and standard deviation of the interface under different Reynolds numbers
图6
图6
各雷诺数下沟槽壁面条件下的界面高度概率分布
Fig. 6
Probability density functions of the interface position over riblets surface under different Reynolds numbers compared with the ones over smooth surface
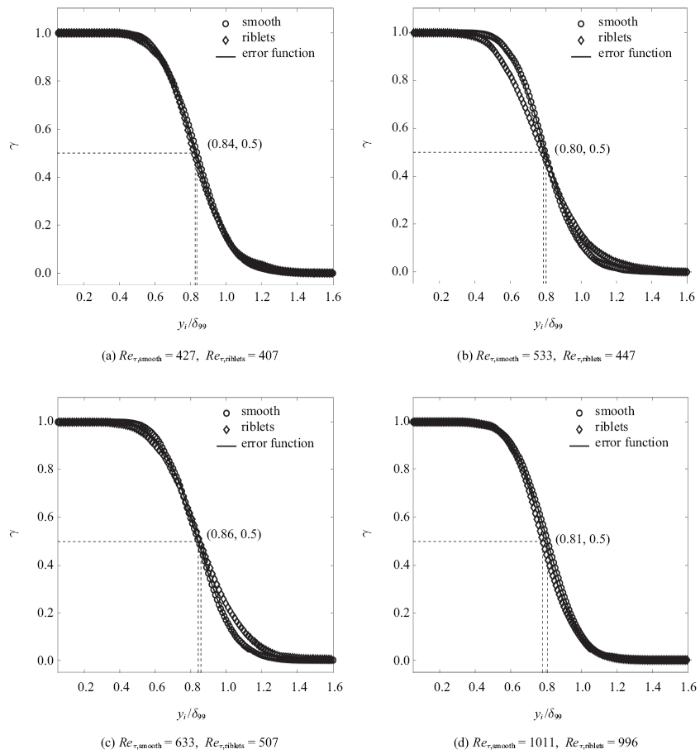
在识别出湍流/非湍流界面所在位置之后, 可以把流场以界面为界进行二值化,界面及界面以下的区域置为1, 界面以上的区域置为0,这样对流场在同一垂向高度进行系综平均,就能够得到任意流向位置的沿垂向分布的间歇因子$\gamma $, 如图7所示. 可以看到,光滑壁面条件下的间歇因子分布很好地服从误差函数,也印证前面提到的其界面高度分布服从正态分布的结果,即实质上对间歇因子分布的微分即可求得界面高度的概率密度分布.当沟槽壁面上界面高度分布的标准差相比光滑壁面上的大得多时,其间歇因子变化也相对更加平缓(图7(b)和图7(c)). $\gamma =0.5$的位置表示湍流和非湍流出现概率相等的位置,对于界面高度服从正态分布的光滑壁面流动来说$\gamma =0.5$的高度理论上就是界面平均高度, 因此这里插值得到的$\gamma =0.5$的高度与直接对界面高度求得的平均值相当接近.
图7
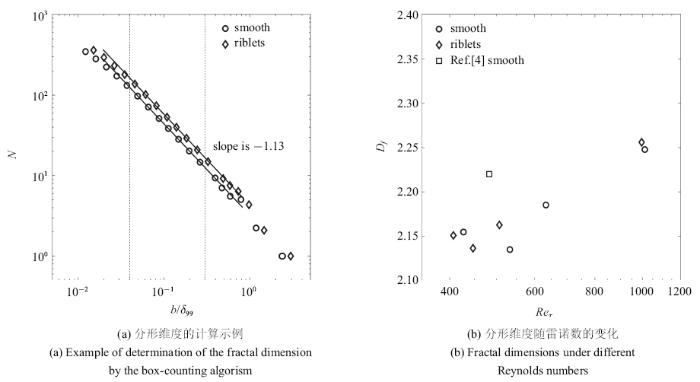
Mandelbrot[29]首次猜测在高雷诺数下湍流中应该存在分形特征,而随后被Sreenivasan等[30]首次在湍流/非湍流界面中发现.Prasad和Sreenivasan[31]采取了一种盒计数算法来衡量湍流/非湍流界面的分形维度:将二维流场分割为边长为${b/\delta }$的方形格子,并记录将界面曲线完全包纳进去的所需的最少格子数量$N(b)$,改变方格边长$b$并重复上述操作, 最后将不同帧所得结果求平均,就得到了包纳最少格数$N$与方格边长$b$的关系, 在一定的范围内,格子边长$b$和最少格数$N$应该满足$N\propto ({b/\delta })^{-D}$,根据Mandelbrot和Wheeler[32]提出的共维准则(the co-dimension rule),三维分形维度$D_{f}= D + 1$.
图8(a)中在对数坐标下绘制了$Re_{\tau ,{smooth}} = 533$ ($Re_{\tau,{riblets}} = 447$)时的${b/\delta }_{99} $ $\sim$ $N$的关系曲线, 由于其满足指数型正相关, 因此在虚线之间的范围内(${b/\delta }_{99}= 0.04$ $\sim$ 0.3)其关系近似一条直线, 直线的斜率就是指数的幂,即$-D$. 图8(b)绘制了不同壁面下湍流/非湍流界面分形维度随雷诺数的变化, 图中还包括了Wu等[4]的结果.按照雷诺相似性假设和小尺度结构为Kolmogorov尺度来预测可得分形维度$D_{f} = 2+ 1/3$. Breda和Buxton[34]认为界面分形维度与小尺度结构相关, 当小尺度结构不为Kolmogorov尺度时分形维度不一定为2.3左右. 可以看出, 在$Re_{\tau } $小于1000范围内, $D_{f}$呈增长趋势, 界面的多尺度结构还没有充分发展. 结合De Silva等[1]的结果, 可以推断湍流/非湍流界面分形维度约在$Re_{\tau } $大于2000以后趋于$D_{f}=2.3$.
图8
2.4 界面动力学特性
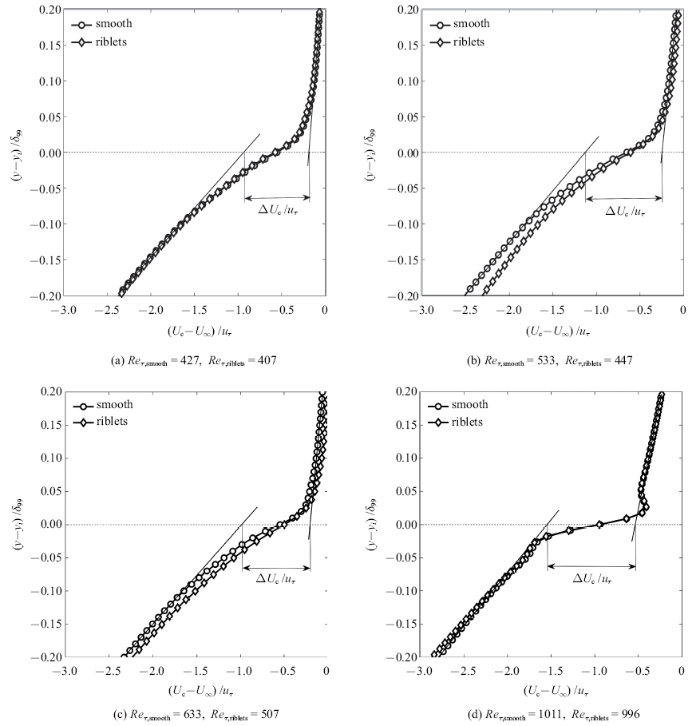
为了明显地显示发生在湍流/非湍流界面附近的速度、涡量跳变,人们常常采用条件平均的方法进行分析: 在某一时刻某一流向位置上,在界面所在高度位置建立一个新的坐标系, 其原点落在界面曲线上,坐标轴与$x$, $y$轴分别平行, 然后采集新坐标系下原点附近沿着$y$轴分布的速度矢量,作为一组速度样本. 遍历每个时刻每个流向位置, 将所得的所有速度样本整合在一起求系综平均, 就得到了条件平均速度$U_{c} $.由于界面具有分形特征, 界面曲线在流场中蜿蜒伸展,在同一时刻同一流向位置下可能会出现多个界面高度(参见图4(a)), 针对这种情况,采用了仅取最低的界面位置建立新坐标系的方式, 以保证在新的坐标中,垂向坐标的负半轴区域始终表示的是湍流区域[2,4].图9给出了不同条件下的条件平均流向速度型, 在${{(y-y_{i} )}/{\delta_{99} }}=\pm 0.1$以外的区域, 流向速度梯度基本已经趋近于近似线性分布,湍流/非湍流界面以外接近势流区(${{(y-y_{i} )}/{\delta_{99} }}>0.1)$,流向速度梯度非常小, 界面以内处于湍流区(${{(y-y_{i} )}/{\delta_{99}}}<-0.1)$, 流向速度梯度相对大一些, 并且在界面附近位置, 流向速度梯度最大,即速度发生跳变. 沟槽壁面使得界面处条件平均流向速度会有所不同,顺流向沟槽壁面的影响主要集中在界面附近及界面以内而很难影响到界面以外的区域.
采用Chauhan等[2]的方法来估量名义界面厚度:先以远离界面位置近似线性的速度型的线性拟合与${{(y-y_{i} )}/{\delta_{99} }}=0$轴的交点之距离作为速度跳变量$\Delta U_{c} $,然后以速度跳变$\Delta U_{c}$与速度最大梯度之比作为名义界面厚度$\delta_{\omega } $, 即
图9
图9
界面附近的条件平均流向速度
Fig. 9
Conditional averaged streamwise velocity profiles across the interface
图10
图10
条件平均速度在界面附近跳变
Fig. 10
The conditional averaged velocity jump across the interface
图11
图11
无量纲界面厚度随$Re_{\tau } $变化
Fig. 11
The variation of the dimensionless interface thickness with Reynolds numbers
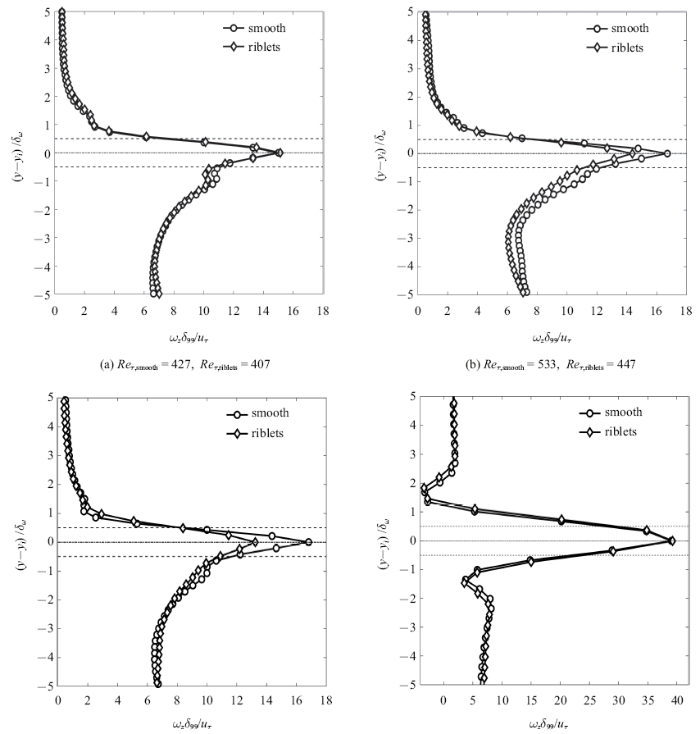
图12绘制了条件平均的展向涡量分布,这里采用了简化的近似计算[2], 由于垂向速度的梯度${{\partial v}/{\partial x}}$相对于流向速度的梯度${{\partial u}/{\partial y}}$小很多,在计算涡量时可以忽略不计, 因此这里条件平均展向涡量$\omega_{z} ={{\partial U_{c} }/{\partial y}}$,因此图12中无量纲涡量的峰值与图10(b)中条件平均流向速度最大梯度相应, 从图12也可以看出, 当雷诺数较小时, 其条件平均展向涡量分布是相似的.图中${{(y-y_{i} )}/{\delta_{\omega }}}=0$处的点画线对应条件平均坐标系下的界面位置,上下两条虚线分别位于${{(y-y_{i} )}/{\delta_{\omega } }}=\pm0.5$的位置, 虚线包含的区域则是1倍的界面厚度范围.无论是何种壁面条件、何种雷诺数,条件平均展向涡量的跳变基本都发生在1倍界面厚度$\delta_{\omega } $之内.远离界面位置向外, 涡量逐渐减少并趋近于0, 与外区流动基本为势流相适应,远离界面位置向内, 涡量先减少后增加, 越靠近壁面流动剪切越强, 展向涡量也越大.
图12
3 结论
本实验采用二维粒子图像测速技术技术对光滑、顺流向锯齿形沟槽表面湍流边界层流动在不同雷诺数下进行了测量,并着重研究和分析了雷诺数$Re_{\tau } $约为400 $\sim$ 1000时通过湍动能方法识别的湍流/非湍流界面的几何特性和动力学特性,主要的结论如下:
(1)湍流/非湍流界面的平均高度基本在(0.8 $\sim$ 0.9)$\delta_{99}$附近.截面为锯齿状的顺流向沟槽壁面在影响摩阻特性的同时影响了界面高度的概率密度分布,阻力增大的条件下界面高度的概率密度分布存在正的偏度,而在减阻情况范围时则基本呈正态分布. 在雷诺数$Re_{\tau } $小于1000的情况下,湍流/非湍流界面的分形维度会随着雷诺数的增大而增大, 而壁面条件影响不明显.
(2)跨越湍流/非湍流界面的无量纲速度跳变随雷诺数增大而增大的趋势,但壁面形状的影响不明显. 在本实验雷诺数条件下,无量纲界面厚度随雷诺数的变化存在一个极大值, 沟槽影响有降低该极值的趋势.此外, 界面附近条件平均涡量分布具有相似性, 受壁面形状和雷诺数影响很小.顺流向沟槽的壁面对于跨界面的速度跳变, 条件平均涡量没有显著的影响.
参考文献
Multiscale geometry and scaling of the turbulent-nonturbulent interface in high Reynolds number boundary layers
The scaling and surface area properties of the wrinkled surface separating turbulent from nonturbulent regions in open shear flows are important to our understanding of entrainment mechanisms at the boundaries of turbulent flows. Particle image velocimetry data from high Reynolds number turbulent boundary layers covering three decades in scale are used to resolve the turbulent-nonturbulent interface experimentally and, for the first time, determine unambiguously whether such surfaces exhibit fractal scaling. Box counting of the interface intersection with the measurement plane exhibits power-law scaling, with an exponent between -1.3 and -1.4. A complementary analysis based on spatial filtering of the velocity fields also shows power-law behavior of the coarse-grained interface length as a function of filter width, with an exponent between -0.3 and -0.4. These results establish that the interface is fractal-like with a multiscale geometry and fractal dimension of Df approximately 2.3-2.4.
The turbulent/non-turbulent interface and entrainment in a boundary layer
Nature shuns homogeneity. In turbulent clouds, industrial reactors and geophysical flows, discrete particles arrange in clusters, posing difficult challenges to theory. A persistent question is whether clusters can be modelled with continuum equations. Recent evidence presented by Mitrano et al. (J. Fluid Mech., vol. 738, 2014, R2) indicates that suitable equations can predict the formation of clusters in granular flows, despite violating the simplifying assumptions upon which they are based.
Properties of the turbulent/non-turbulent interface in boundary layers
Effects of surface shapes on properties of turbulent/non-turbulent interface in turbulent boundary layers
The turbulent/non-turbulent interface bounding a far wake
Mechanics of the turbulent-nonturbulent interface of a jet
Scaling of the turbulent/non-turbulent interface in boundary layers
Scaling of the interface that demarcates a turbulent boundary layer from the non-turbulent free stream is sought using theoretical reasoning and experimental evidence in a zero-pressure-gradient boundary layer. The data-analysis, utilising particle image velocimetry (PIV) measurements at four different Reynolds numbers (delta u(tau)/v = 1200-14 500), indicates the presence of a viscosity dominated interface at all Reynolds numbers. It is found that the mean normal velocity across the interface and the tangential velocity jump scale with the skin-friction velocity u(tau) and are approximately u(tau)/10 and u(tau), respectively. The width of the superlayer is characterised by the local vorticity thickness delta(omega) and scales with the viscous length scale v/u(tau). An order of magnitude analysis of the tangential momentum balance within the superlayer suggests that the turbulent motions also scale with inner velocity and length scales u(tau) and v/u(tau), respectively. The influence of the wall on the dynamics in the superlayer is considered via Townsend's similarity hypothesis, which can be extended to account for the viscous influence at the turbulent/non-turbulent interface. Similar to a turbulent far-wake the turbulent motions in the superlayer are of the same order as the mean velocity deficit, which lends to a physical explanation for the emergence of the wake profile in the outer part of the boundary layer.
Free-stream boundaries of turbulent flows. Technical Report
稳定分层流密度界面处湍流混合与分形结构
h);(2) 淡、盐水层的密度(ρ0,ρ), (3) 淡、盐水密度界面. 其中, 淡、盐水密度界面通过照片、录像进行记录. 观测结果用于计算:(1) 盐水层密度;(2) 卷挟速度, (3) 整体理查孙数(Rio), (4) 二维、三维密度界面, (5) 二维、三维密度界面的分形维度. 结果分析发现:(1) 湍流卷挟率随Rio 增大而减小, 并且满足Rio的-3=2 或-7=4 幂律;表明随着湍流强度的减弱, 混合的速度也越来越缓慢;(2) 二维密度界面分形维度大于1, 三维密度界面分形维度大于2;表明二维、三维密度界面存在分形结构;(3) 分形维度随Rio的增大而减小;表明随着湍流强度的减弱, 密度界面也越来越趋于光滑.]]>
Turbulent mixing and fractal structure at a density interface in a stably stratified fluid
Ri0); and (3) the fractal dimension of the two-dimensional and three-dimensional density interfaces. The entrainment rate decreases with an increasing overall Richardson number. It can be expressed as Rio to the -3/2 or -7/4 power. This indicates that the rate of mixing deceases with decreasing turbulence intensity. Fractal dimension of the two-dimensional density interface is larger than 1, while that of the three-dimensional density interface is larger than 2. Fractal structures are present on the two-dimensional and three-dimensional density interfaces. Fractal dimension decreases with an increasing overall Richardson number. This suggests that the density interfaces become smoother with decreasing turbulence intensity.]]>
A combined visualization-anemometry study of the turbulent drag reducing mechanisms of triangular micro-groove surface modifications
沟槽面湍流减阻研究综述
对近20年来沟槽面湍流边界层特性、湍流拟序结构、湍流减阻及其机理的研究进展进行了综述.内容涉及沟槽面平板、旋成体、机翼等在压、跨、超音速流动情况下的实验研究成果;压力梯度、攻角、侧滑角等的影响;湍流猝发特性、紊动特性、近壁区带条结构的特征及减阻机理等方面的工作.为更有效地减少表面摩阻,必须深入开展对沟槽面湍流边界层特性、湍流拟序结构及湍流减阻机理等方面的研究.
Review and prospects in turbulent drag reduction over riblets surface
The experimental investigations of turbulent boundary layer flow,turbulent coherent structures,turbulent drag reduction and its mechanism have been reviewed.The experimental velocities cover subsonic,transonic and supersonic flows,and the content includes: (1) flow over flat plate,revolution body and wing with riblets surface at zero angle of attack;(2) the effect of pressure gradient,angle of attack and slide angle;(3) the burst characteristics,characteristics of turbulence,the streak structure in the near wall region and the drag reduction mechanism.In order to reduce the skin friction efficiently,more research works should be done on the characteristics of turbulent boundary layer,turbulent coherent structures and the mechanism of turbulent drag reduction for flow over riblets surfaces.
沟槽面湍流边界层减阻特性研究
Drag-reduction characteristics of turbulent boundary layer flow over riblets surfaces
沟槽对湍流边界层中展向涡影响的实验研究
An experimental study on riblet-induced spanwise vortices in turbulent boundary layers
沟槽张角对流体减阻机理的数值模拟研究
Numerical simulation research of groove angle on the mechanism of flow drag reduction
Two-point statistics of coherent structures in turbulent flow over riblet-mounted surfaces
超疏水沟槽表面通气减阻实验研究
Experimental study on drag reduction characteristics of superhydrophobic groove surfaces with ventilation
Experiments on drag-reducing surfaces and their optimization with an adjustable geometry
纵向沟槽壁面湍流边界层内类开尔文-亥姆霍兹涡结构的流动显示
s+ 在一定范围内,与光滑壁面湍流边界层相比,具有减阻效应;并在s+ 约为17 个黏性长度单位时减阻效果达到最优,之后其减阻趋弱,直至增阻;其原因可能是沟槽壁面湍流边界层由于“开尔文-亥姆霍兹” 不稳定性而产生的一种“类开尔文-亥姆霍兹”展向涡结构. 实验采用烟雾流动显示技术,首次在风洞中显示了这种“类开尔文-亥姆霍兹” 展向涡结构,确认了其存在性,并在概念上简单勾勒了其结构模型.]]>
Flow visualizations on kelvin-helmholtz-like roller structures in turbulent boundary layer over riblets
s+. However, the drag reduction produced by the riblets breaks down after s+ increasing beyond its optimum value, and eventually the drag reduction becomes an increase case. García-Mayoral and Jiménez (2011) believed that the breakdown is due to the onset of a Kelvin-Helmholtz instability in the TBL over riblets, which introduces a kind of Kelvin-Helmholtz-like roller structures. In the present study, these spanwise rollers, for the first time in experiments, were clearly observed by the smoke flow visualization technique. And their conceptual model was outlined lastly as well.]]>
风力机专用翼型表面微沟槽减阻特性研究
Study on drag reduction characteristics of airfoil for wing turbine with microgrooves on surface
Flow over convergent and divergent wall riblets
沟槽方向对湍流边界层流动结构影响的实验研究
Flow structure in the turbulent boundary layer over directional riblets surfaces
Cross-stream stereoscopic particle image velocimetry of a modified turbulent boundary layer over directional surface pattern
Fast and accurate PIV computation using highly parallel iterative correlation maximization
Our contribution deals with fast computation of dense two-component (2C) PIV vector fields using Graphics Processing Units (GPUs). We show that iterative gradient-based cross-correlation optimization is an accurate and efficient alternative to multi-pass processing with FFT-based cross-correlation. Density is meant here from the sampling point of view (we obtain one vector per pixel), since the presented algorithm, folki, naturally performs fast correlation optimization over interrogation windows with maximal overlap. The processing of 5 image pairs (1,376 x 1,040 each) is achieved in less than a second on a NVIDIA Tesla C1060 GPU. Various tests on synthetic and experimental images, including a dataset of the 2nd PIV challenge, show that the accuracy of folki is found comparable to that of state-of-the-art FFT-based commercial softwares, while being 50 times faster.
Evaluating the accuracy performance of lucas-kanade algorithm in the circumstance of piv application
Turbulent boundary layers in adverse pressure gradients
Near wall structure of turbulent boundary layer with riblets
Interfaces and internal layers in a turbulent boundary layer
On the geometry of homogeneous turbulence, with stress on the fractal dimension of the iso-surfaces of scalars
Mixing, entrainment and fractal dimensions of surfaces in turbulent flows
Scalar interfaces in digital images of turbulent flows
The multi-scale geometry of the near field in an axisymmetric jet