引言
随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域.
航天器单脉冲轨道机动可达域是指航天器在某一位置施加机动冲量后,未来时间所有可能到达位置的集合[11 ] . 其中机动冲量满足一定约束条件[12 ] ,一般用速度机动球或速度机动椭球来描述,用以限制脉冲机动的大小和方向.
航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法.
针对现有研究不足,本文基于近心点坐标系建立了针对未来可达位置矢量极值求解的可达域求解模型. 首先基于边界速度双曲线推导可达性判断条件;其次在待求位置指向可达前提下,构建可达矢径极值求解算法,求解基于单一参变量的非线性方程,获得可达域包络位置坐标;最后采用 Monte Carlo 打靶仿真方法验证所提方法的正确性.
1 可达域求解模型
1.1 坐标系定义
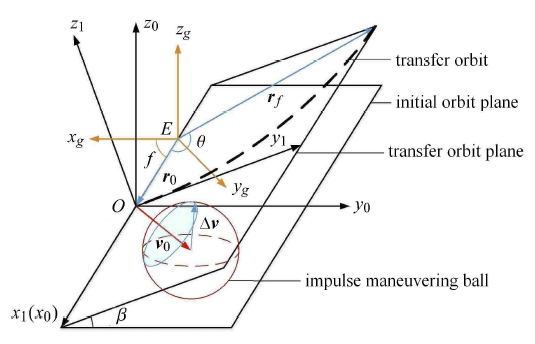
令 ${\pmb r}_{0}$ 表示航天器初始位置矢量,${\pmb r}_{f}$ 表示航天器终端位置矢量,如图1 所示,航天器在 ${\pmb r}_{0}$ 处执行一次机动,经转移轨道到达 ${\pmb r}_{f}$. 由 ${\pmb r}_{0}$,${\pmb r}_{f}$ 可确定 转移轨 道平面 $M$,设该平面与初始轨道平面夹角为 $\beta $.
图1
图1
坐标系位置关系
Fig. 1
Illustration of the defined coordinates
定义近心点坐标系 $S_{g}$:原点 $E$ 位于地心,$x_{g}$ 轴指向初始轨道近地点,$z_{g}$ 轴指向初始轨道角动量方向,$y_{g}$ 轴位于初始轨道平面内,并与 $x_{g}$,$z_{g}$ 轴构成右手直角坐标系.设初始轨道航天器机动位置的真近角为 $f$,则 ${\pmb r}_{0}$ 在 $S_{g}$ 坐标系下表达式
(1) ${\pmb r}_0 = \left[ \!\! \begin{array}{ccc} {r_0 \cos f} & {r_0 \sin f} & 0 \end{array} \!\! \right]^{T}$
其中 $r_{0}$ 表示初始位置矢量 ${\pmb r}_{0}$ 的长度.
定义坐标系 $S_{0}$:原点 $O$ 位于航天器质心,$x_{0}$ 轴与 ${\pmb r}_{0}$ 重合,$z_{0}$ 轴指向初始轨道角动量方向,$y_{0}$ 轴与 $x_{0}$ 轴、$z_{0}$ 轴构成右手直角坐标系. 航天器初始轨道速度 ${\pmb v}_{0}$ 在 $S_{0}$ 坐标系下可表示为[11 ]
(2) $ \left( { {\pmb v}_0 } \right)_0 = \sqrt {\dfrac{\mu }{p_0 }} \left[ \!\! \begin{array}{c} {e_0 \sin f} \\ {1 + e_0 \cos f} \\ 0 \end{array} \!\! \right]$
定义轨道坐标系 $S_{1}$:$x_{1}$ 轴与 $x_{0}$ 轴重合,$z_{1}$ 垂直于平面 $M$ 并指向转移轨道角动量,$y_{1}$ 位于 $M$ 面内,与 $x_{1}$,$z_{1}$ 构成右手直角坐标系. 航天器初始轨道速度 ${\pmb v}_{0}$ 在 $S_{1}$ 坐标系下可表式为
(3) $ \left( { {\pmb v}_0 } \right)_1 = {\pmb R}_0^1 \left( { {\pmb v}_0 } \right)_0 = \sqrt {\dfrac{\mu }{p_0 }} \left[\!\! \begin{array}{c} {e_0 \sin f} \\ {\left( {1 + e_0 \cos f} \right)\cos \beta } \\ { - \left( {1 + e_0 \cos f} \right)\sin \beta } \end{array} \!\! \right]$
(4) $ {\pmb R}_0^1 = \left[ \!\! \begin{array}{ccc} 1 & 0 & 0 \\ 0 & {\cos \beta } & {\sin \beta } \\ 0 & { - \sin \beta } & {\cos \beta } \end{array} \!\! \right]$
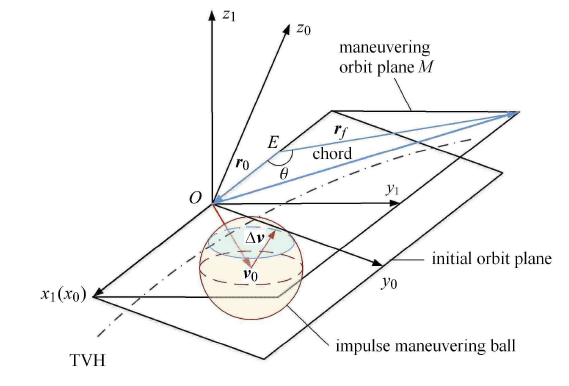
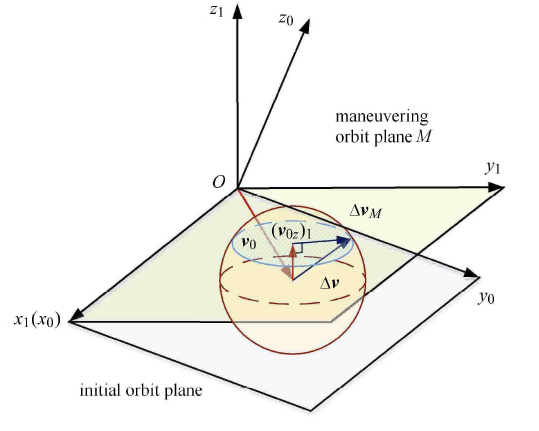
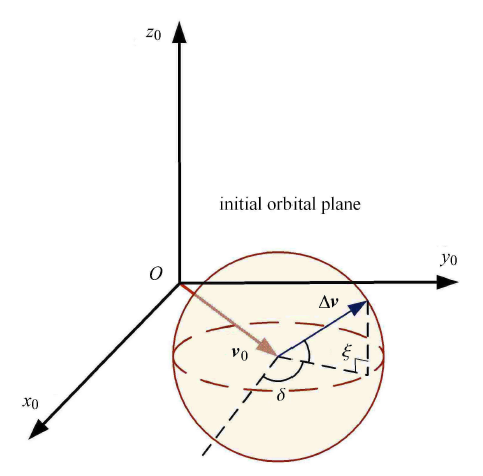
一般而言,航天器携带的推进剂有限,其最大机动能力亦有限,可以转化为总速度增量 $\Delta {\pmb v}$ 表示. 假设航天器最大机动能力为 $\Delta {\pmb v}$,机动方向任意,即可将航天器的机动能力建模为速度机动球. 如图2 所示,在速度机动球内,航天器执行某一可能的机动后,将进入 $M$ 平面内的某一对应转移轨道,到达 ${\pmb r}_{f}$ 位置. 定义 $\Delta{\pmb v}_{M}$ 为 $\Delta {\pmb v}$ 在转移轨道面内的投影,用角度 $\alpha $ 表示 $\Delta {\pmb v}_{M}$ 相对于参考方向 $\hat {r}_0 = {r_0 } / {r_0 }$ 的夹角,即转移轨道面机动方位角.
图2
图2
速度脉冲方位角
Fig. 2
Azimuth of the maneuvering impulse
记航天器机动后的速度为 ${\pmb v}_{1}={\pmb v}_{0}+\Delta {\pmb v}$,根据$S_{1}$ 坐标系定义,${\pmb v}_{1}$ 在 $S_{1}$ 中可表示为
(5) $\left( { {\pmb v}_1 } \right)_1 = \left\{ \!\! \begin{array}{l} {\left( {{\pmb v}_{1x} } \right)_1 = \left( {{\pmb v}_{0x} } \right)_1 + \Delta {\pmb v}_M \cos \alpha } \\ {\left( {{\pmb v}_{1y} } \right)_1 = \left( {{\pmb v}_{0y} } \right)_1 + \Delta {\pmb v}_M \sin \alpha } \\ 0 \end{array} \!\! \right.$
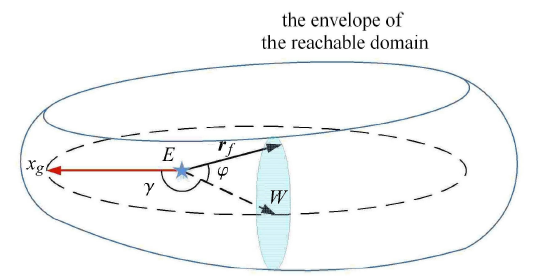
在近心点坐标系 $S_{g}$ 中,定义角度 $\gamma $ 与 ${\pmb\varphi}$,用来描述机动后未来可达位置矢量 ${\pmb r}_{f}$ 的 空间指向,如图3 所示. 图中 $\varphi$ 表示 ${\pmb r}_{f}$ 与初始轨道面的夹角. ${\pmb r}_{f}$ 在初始轨道面内的投影用线段 ${EW}$ 表示,$E$ 为引力中心,$W$ 为初始轨道上某点, $\gamma$ 表示 ${\pmb r}_{f}$ 在初始轨道面投影 ${EW}$ 与 $x_{g}$ 轴之间的角距,即近心点角距. 显然,$\gamma $ 与 $\varphi $ 取值变化可使 ${\pmb r}_{f}$ 指向空间任一方向,而该指向在给定速度机动约束条件下是否可达,需要进一步验证并给出可达性判据.
图3
图3
$\gamma $ 和 $\varphi $ 角度示意图
Fig. 3
Illustration of angle $\gamma $ and $\varphi $
1.2 轨道机动可达性判据
以轨道机动位置 ${\pmb r}_{0}$ 为起点,终端位置 ${\pmb r}_{f}$ 为终点,二点之间的转移过程可以看做是两点边值问题,Battin[15 ] 证明轨道两点边值问题满足如下等式
(6) $ P = {\pmb v}_c {\pmb v}_\rho = \left( {\dfrac{1}{2r_0 } - \dfrac{1}{{ r}_0 + { r}_f + c}} \right) \dfrac{\mu }{\cos ^2\left( {\psi / 2} \right)} = {const}$
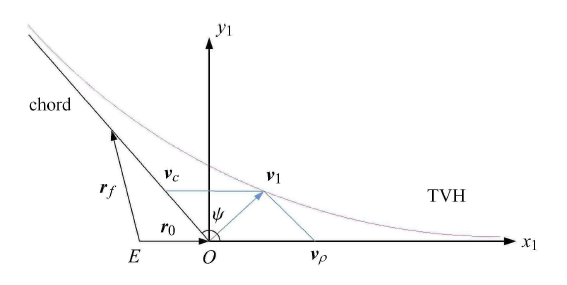
定义从机动位置到目标位置的弦为 ${\pmb c} = {\pmb r}_f - {\pmb r}_0 $,式 (6) 中 ${\pmb v}_{c}$, ${\pmb v}_{\rho }$ 分别 表示 $S_{1}$ 中坐标系下转移轨道初始速度矢量 ${\pmb v}_{1}$ 在弦长方向和 ${\pmb r}_{0}$ 方向的速度分量,$c = \left\| {\pmb c} \right\|$ 为连接 ${\pmb r}_{0}$ 和 ${\pmb r}_{f}$ 的弦长, $\psi $ 表示 ${\pmb v}_{c}$ 与 ${\pmb v}_{\rho }$ 之间的夹角,如图4 所示.
图4
图4
边界速度双曲线示意图
Fig. 4
Illustration of terminal velocity hyperbola
由等式 (6) 可得轨道两点边值问题的重要结论[15 ] :能到达给定目标位置矢量的所有可能转移轨道,其初始速度矢量的轨迹是一条边界速度双曲线 (terminal velocity hyperbola,TVH),该双曲线两条渐近线分别为弦和初始位置矢量 ${\pmb r}_{0}$ 所在的直线. 因此,为使得 ${\pmb r}_{f}$ 目标方向可达,需保证机动后的速度始端能够落在边界速度双曲线上,如图5 所示.
图5
图5
边界速度双曲线与速度机动球关系
Fig. 5
Relationship of TVH and impulsive maneuvering ball
当 $[ \gamma , \varphi ]$ 确定后,${\pmb r}_{f}$ 的指向随之确定,随着 ${\pmb r}_{f}$ 矢径长度 变化,TVH 渐近线走势也随之变化,从而可以得到一簇边界速度双曲线,该双曲线簇随 ${\pmb r}_{f}$ 长度变化可覆盖整个转移轨道平面$M$,如图6 所示.因此,只需保证转移轨道面与速度机动球相交,即可保证机动后速度矢端落在边界速度双曲线上,从而使得 ${\pmb r}_{f}$ 目标方向可达.
图6
图6
边界速度双曲线在 $M$ 平面内分布
Fig. 6
Distribution of TVH in the plane $M$
若要使得转移轨道面与速度机动球相交,只需保证速度脉冲 $\Delta {\pmb v}$ 在转移轨道面内存在分量 $\Delta {\pmb v}_{M}$,由图7 可知 $\Delta {\pmb v}_{M}$ 可由下式求解
(7) $ \Delta v_M = \sqrt {\Delta v^2 - \left( {v_{0z} } \right)_1^2 } = \sqrt {\Delta v^2 - \dfrac{\mu }{p_0 }\left( {1 + e_0 \cos f} \right)^2\sin ^2\beta }$
图7
图7
$\Delta {\pmb v}_{M}$ 位置关系
Fig. 7
Location of $\Delta {\pmb v}_{M}$
为使式 (7) 可解,需保证式中根号下表达式非负. 式 (7) 中角度 $f$, $\gamma $, $\varphi $, $\beta$ 的几何关 系如图8 所示,由空间几何公式可知
(8) $\tan \varphi = \sin \left( {\gamma - f} \right)\tan \beta$
图8
图8
角度几何关系
Fig. 8
Geometry of the defined angles
将式 (8) 代入式 (7),令式 (7) 中根号下表达式非负得到
(9) $\Delta v^2\sin ^2\left( {\gamma - f} \right) + \left[ {\Delta v^2 - \dfrac{\mu }{p_0 }\left( {1 + e_0 \cos f} \right)^2} \right]\tan ^2\varphi \geqslant 0$
进一步整理式 (9) 得到可达性判据, $\varphi $ 应满足
(10) $0 \leqslant \tan ^2\varphi \leqslant \dfrac{\sin ^2\left( {\gamma - f} \right)}{\dfrac{\mu }{p_0 \Delta v^2}\left( {1 + e_0 \cos f} \right)^2 - 1}$
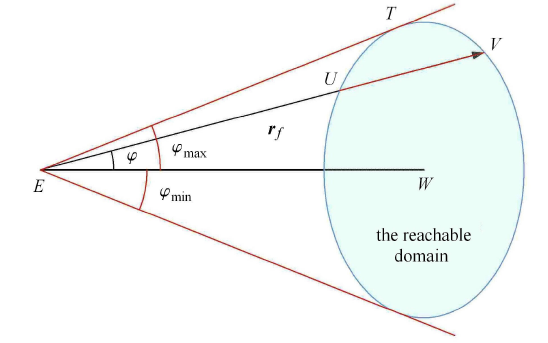
当 ${\pmb r}_{f}$ 与 ${\pmb r}_{0}$ 共线时,此时 $\gamma -f = 0$ 或 $\gamma -f = \pi $, $\varphi_{\max} = \varphi_{\min} =0$. 对 ${\pmb r}_{f}$ 与 ${\pmb r}_{0}$ 不共线的一般 情况,当 ${\pmb r}_{f}$ 方向可达时,取纵向切面如图9 所示,根据可达性判据, $\varphi $ 存在取值范围 $[\varphi_{\min}$,$\varphi_{\max} ]$,极值 $\varphi_{\min}$, $\varphi _{\max}$ 分别对应 ${\pmb r}_{f}$ 与可达域上下两端相切的情况. 一般情况下,${\pmb r}_{f}$ 会穿过可达域得到一条可达线段 ${UV}$.${EU}$ 对应 ${\pmb r}_{f}$ 方向可达矢径的极小值,${EV}$ 对应 ${\pmb r}_{f}$ 方向可达矢径的极大值.因此,获得轨道机动可达性判据后,求解轨道机动可达域包络的核心问题是如何计算所有可达方向的矢径极值,本文将在 2.1 节给出求解算法.
图9
图9
可达线段 ${UV}$
Fig. 9
The reachable line ${UV}$
1.3 可达域包络的几何特性
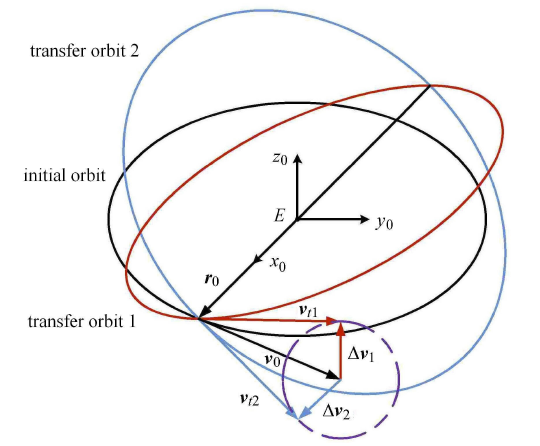
如图10 所示,在 $S_{0}$ 坐标系下,速度机动球关于初始轨道平面 对称,令 $\Delta {\pmb v}_{1}$,$\Delta{\pmb v}_{2}$ 为两个对称的速度机动冲量,显然机动后速度矢量 ${\pmb v}_{t1}$,${\pmb v}_{t2}$ 也关于初始轨道平面对称,有
(11) $ \left.\begin{array}{l} v_{t1x} = v_{t2x} \\ v_{t1y} = v_{t2y} \\ v_{t1z} = - v_{t2z} \end{array}\right\}$
图10
图10
转移轨道对称性
Fig. 10
Symmetry of transfer orbits
在二体轨道初值问题中,设经过一段时间后,两条轨道的位置相对于初始位置的真近角差均为 $\Delta f$,则该时刻轨道位置可以表示为[30 ]
(12) $\left.\begin{array}{l} {\pmb r}_1 = F{\pmb r}_0 + G{\pmb v}_{t1} \\ {\pmb r}_2 = F{\pmb r}_0 + G{\pmb v}_{t2} \end{array}\right\}$
其中,$F$ 与 $G$ 为拉格朗日系数,仅与 $\Delta f$ 取值相关[30 ] ,当 $\Delta f$ 相同时,可作为常系数处理.
若不采取任何机动,航天器自由运行到距离初始位置真近角差 $\Delta f$ 处的轨道位置可以表示为
(13) ${\pmb r}_t = F{\pmb r}_0 + G{\pmb v}_0$
如图10 所示,在 $S_{0}$ 坐标系中,$x_{0} O y_{0}$ 平面是基于初始轨道面建立的,因此 ${\pmb r}_{0z}=0$;${\pmb v}_{0z} =0$,从而式 (13) 中
(14) ${\pmb r}_{tz} = F{\pmb r}_{0z} + G{\pmb v}_{0z} = {\bf 0}$
(15) ${\pmb r}_{1z} + {\pmb r}_{2z} = {\bf 0}$
根据上述结论可知,${\pmb r}_{1}$ 和 ${\pmb r}_{2}$ 始终关于初始轨道面 $(z _{0} =0)$ 上下对称.由于单脉冲 机动可达域是上述对称轨道分布的区域,因此也是关于初始轨道面对称的.
因此,在二体轨道假设下,求解轨道机动可达域,只需计算位于初始轨道平面一侧的可达域包络,可达域的另一半可由对称性快速获得,如图11 所示.
图11
图11
可达域包络对称性
Fig. 11
Symmetry of reachable domain
2 可达域求解算法
由第 1 节可达域求解模型可知,求解航天器单脉冲轨道机动可达域的核心是按照一定顺序求解航天器在 $[\gamma , \varphi ]$ 方向上可达矢径的极值. 本节介绍可达方向矢径极值求解算法,给出完整求解流程,并与两种已有算法流程对比,说明本算法改进之处.
2.1 可达方向矢径极值求解算法
基于二体轨道动力学模型可得目标位置矢量 ${\pmb r}_{f}$ 可表示为[25 ]
(16) $r_f = \left\| { {\pmb r}_f } \right\| = \dfrac{h^2}{\mu \left( {1 - \cos \theta } \right) + hv_{1y} \cos \theta - hv_{1x} \sin \theta }$
式中, $\theta $ 表示 ${\pmb r}_{0}$ 与 ${\pmb r}_{f}$ 的夹角;$h = \left\|{\pmb h}\right\|$,其中 ${\pmb h}$ 表示转移轨道角动量
(17) ${\pmb h} = {\pmb r}_0 {\pmb v}_{1y}$
(18) $\cos \theta = \cos \left( {\gamma - f} \right)\cos \varphi$
根据 $\gamma $ 和 $f$ 的位置关系,进一步确定 $\theta $ 的取值范围如下
(19) $ \theta = \left\{ \!\! \begin{array}{l} \arccos \left[ {\cos \left( {\gamma - f} \right)\cos \varphi } \right] \\ \quad \text{if} \ - 2\pi \leqslant \gamma - f < - \pi , \ {or} , \ 0 \leqslant \gamma - f < \pi \\ 2\pi - \arccos \left[ {\cos \left( {\gamma - f} \right)\cos \varphi } \right] \\ \quad\text{if} \ - \pi \leqslant \gamma - f < 0 , \ {or} , \ \pi \leqslant \gamma - f < 2\pi \end{array} \!\! \right.$
将式 (3) 代入式 (5) 可知 $v_{x}$,$v_{y}$ 是关于 $\beta $ 和 $\alpha $ 的函数,又由式 (6) 可知 $i$ 是关于 $\gamma $ 和 $\varphi $ 的函数. 因此,${\pmb r}_{f}$ 矢径可以表示为
(20) ${\pmb r}_f = {\pmb r}\left( {f,\alpha ,\gamma ,\varphi } \right){\pmb p}\left( {\gamma ,\varphi } \right)$
其中 ${\pmb r}_{f}$ 表示 ${\pmb r} _{f}$ 矢径大小,${\pmb p}$ 表示 ${\pmb r}_{f}$ 方向单位矢量
(21) ${\pmb p}=\left[ {\sin \gamma \cos \varphi } \ \ {\cos \gamma \cos \varphi } \ \ {\sin \varphi } \right]^{T}$
当机动位置 $f$,终端位置方向 $\gamma $, $\varphi $ 确定后,${\pmb r}_{f}$ 矢径式 (20) 是关于变量 $\alpha $ 的一元函数,因此只需选择合适的 $\alpha$ 取值,使得式 (16) 取极值即可. 式 (16) 对 $\alpha$ 求导得
(22) $ \dfrac{\partial { r}_f }{\partial \alpha } = \dfrac{{ r}_0 { r}_f^2 }{h^2} \left\{ {\left[ {2\dfrac{\mu }{h}\left( {1 - \cos \theta } \right) - v_{1x} \sin \theta } \right] \dfrac{\partial v_{1y} }{\partial \alpha }+ } \right. \\ \left. { v_{1y} \sin \theta \dfrac{\partial v_{1x} }{\partial \alpha }} \right\}$
将式 (3) 代入式 (5),并对 $\alpha $ 求偏导得
(23) $\left. \dfrac{\partial v_{1x} }{\partial \alpha } = - \Delta v_M \sin \alpha \\ \dfrac{\partial v_{1y} }{\partial \alpha } = \Delta v_M \cos \alpha \right\}$
(24) $ \dfrac{\partial r_f }{\partial \alpha } = \dfrac{r_0 r_f^2 v_{1y} \Delta v_M }{h^2}\Bigg\{ \left[ {2\dfrac{\mu }{hv_{1y} }\left( {1 - \cos \theta } \right) - \dfrac{v_{1x} }{v_{1y} }\sin \theta } \right]\cdot \\ \cos \alpha - \sin \theta \sin \alpha \Bigg\}$
其中 $\dfrac{r_0 r_f^2 v_{1y} \Delta v_M }{h^2}$ 为非零项,定义表达式
(25) $ P\left( \alpha \right) = \left[ {2\dfrac{\mu }{hv_{1y} }\left( {1 - \cos \theta } \right) - \dfrac {v_{1x}}{v_{1y}} \sin \theta } \right]\cdot \\ \dfrac{\partial v_{1y} }{\partial \alpha } + \sin \theta \dfrac{\partial v_{1x} }{\partial \alpha }$
则可将极值求解问题转化为求表达式 $P ( \alpha )=0$ 的零点的问题. 求解完成后,将所得 $\alpha$ 解代入式 (16) 即得到 ${\pmb r}_{f}$ 矢径极值.
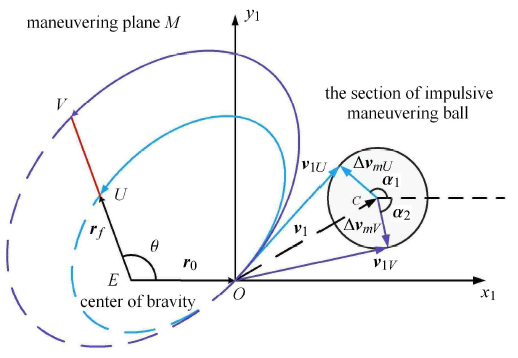
在满足可达性判据的前提下,终端位置 ${\pmb r}_{f}$ 方向上可达位置点构成 可达线段 ${UV}$,如图12 所示.${EU}$ 和 ${EV}$ 是 ${\pmb r}_{f}$ 矢径两个不同的极值,因此,在 $[- \infty , + \infty]$ 范围内,至少存在两个 $\alpha $ 值满足式 (25).
图12
图12
$\vert \vert {\pmb r}_{f }\vert \vert $ 极值与 $\alpha $ 取值关系
Fig. 12
Relationship between $\vert \vert {\pmb r}_{f }\vert\vert $ and $\alpha $
在采用数值迭代法求解式 (25) 的零点时,不同的迭代初值会得到不同的 $\alpha $ 可行解. 对于式 (16),只需从这些可行的 $\alpha $ 取值中选取两个,能够分别对应 ${\pmb r}_{f}$ 矢径的极大值和极小值即可,本文迭代计算的初值按照下式给定
(26) $\alpha _{10} = \dfrac{\pi }{2} , \ \ \ \alpha _{20} = - \dfrac{\pi }{2}$
按照式 (26) 中两个初值分别迭代求解,可以得到两个备选的可行解 $\alpha_{1}$, $\alpha _{2}$,分别代入式 (16),得到 $r_{f 1}$ 和 $r_{f 2}$,将两个 $\vert \vert {\pmb r}_{f }\vert \vert $ 的值中较大的记为 $r_{f \max}$,较小的记为 $r_{f \min}$. 通过式 (27) 进一步计算 $S_{g}$ 坐标系下的极值点位置坐标
(27) $\left.\begin{array}{l} {\pmb r}_{f\max } = {\pmb r}_{f\max } {\pmb p} \\ {\pmb r}_{f\min } = {\pmb r}_{f\min } {\pmb p} \end{array}\!\!\right\}$
2.2 可达域求解流程
本文可达域算法求解流程如算法 1 所示. $\gamma $ 在 $[0, 2 \pi ]$ 范围内取值, $\varphi$ 在 $[- \pi /2, \pi /2] $ 范围内取值, 由 1.3 节包络对称性,可以缩小 $\varphi$ 计算范围至 $[0, \pi /2]$.
最近,温昶煊等[25 -28 ] 、陈奇等[29 ] 对单脉冲轨道机动可达域问题进行了研究,温昶煊等的方法通过证明转移相位角和速度机动方向的对应关系,分别针对可达域内外包络建立了可达域直接求解模型. 陈奇等的方法以初始轨道为基础,将可达域定义为围绕在初始轨道周围的管道模型,并给出了通过求解非线性方程组计算可达域 的方法.为便于对比分析,本文将这两种方法的求解流程简要总结如算法 2 和算法 3 所示,其中温昶煊方法记为已有算法一,陈奇方法记为已有算法二.
步骤 1:给定初始轨道参数,由式 (1) 计算 ${\pmb r}_{0}$.
步骤 2:$\gamma $ 在 $[0, 2 \pi ]$ 范围内任意取值, $\varphi $ 在 $[0$, $\pi/2]$ 范围内任意取值,由式 (21) 确定单位矢量 ${\pmb p}$.
步骤 3:根据式 (10) 判断当前方向是否可达,若不可达则返回步骤 2 重新取值.
步骤 4:由表达式 (25) 迭代计算使当前 ${\pmb r}_{f}$ 方向矢径取极值的 $\alpha$ 取值,迭代初值按照式 (26) 确定.
步骤 5:将式 (16) 计算 ${\pmb r}_{f}$ 方向矢径极值.
步骤 6:将矢径极值和当前方向矢量 ${\pmb p}$ 代入式 (27) 计算极值点在 $S_{g}$ 坐标系中的位置坐标.
步骤 7:重复步骤 2 至步骤 6 直至角度序列 $[ \gamma , \varphi]$ 覆盖整个空间范围,将所有极值点坐标汇总得到可达域.
步骤 1:确定转移轨道面倾角$i$的允许上下界,$i_{\min}$和$i_{\max}$, $\theta $ 允许取值范围$[0, 2 \pi ]$.
步骤 2:计算中间参量 $F( i)$ 和 $Q$.
步骤 3:求解中间变量 $\alpha_{c}$,$\alpha_{\pi 1}$,$\alpha_{\pi 2}$.
步骤 4:确定 $\alpha $ 和 $\theta $ 之间的转化关系 $\theta ( \alpha)$,按照内包络与外包络分为 $\theta_{in} (\alpha)$ 和 $\theta_{out} (\alpha)$.
步骤 5:由 $\alpha_{c}$ 确定 $\alpha_{1}$, $\alpha_{2}$,定义 $[\alpha_{1}$,$\alpha_{2}]$ 对应远地包络,定义 $[\alpha_{2}$, $\alpha_{1} +2 \pi ]$ 对应近地包络.
(a) 在 $[ \alpha_{1}, \alpha_{2}]$ 区间内任取角度 $\alpha $,由 $\theta _{out}(\alpha )$ 计算 $\theta_{out}$;
(b) 由 $\alpha $, $\theta $ 计算包络半径 $r$,并确定远地包络坐标;
(c) 重复步骤(a),(b) 直至 $\alpha $ 覆盖区间 $[\alpha_{1}$, $\alpha_{2}]$.
(a) 在 $[\alpha_{2}, \alpha_{1}+2\pi]$ 区间内任取角度 $\alpha $,由 $\theta_{in}(\alpha)$ 计算 $\theta_{in}$;
(b)由 $\alpha $, $\theta $ 计算包络半径 $r$,并确定近地包络点坐标;
(c)重复步骤 (a),(b) 直至 $\alpha $ 覆盖区间 $[\alpha_{2}, \alpha_{1}+2\pi ]$.
步骤 8:重复执行步骤 2 到步骤 7 直至角度 $i$ 覆盖整个区间 $[i_{\min}$,$i_{\max}$].
步骤 1:给定初始轨道参数,确定 ${\pmb r}_{0}$ 和 ${\pmb h}_{0}$.
步骤 2:$\alpha $ 在 $[0, 2 \pi ]$ 范围内任意取值, $\varphi $ 在 $[0$, $2 \pi]$ 范围内任意取值.
步骤 3:由正弦定理确定控制变量 $\lambda $ 和 $\kappa $ 满足的约束关系 $G(\lambda $, $\kappa) = 0$.
步骤 4:将极值表达式 $R( \lambda , \kappa ) $ 分别对 $\lambda$ 和 $\kappa$ 求偏导,得到两个非线性方程 $H _{1} =0$, $H_{2}=0$.
步骤 5: 确定初值 $\lambda _{0}$ 和 $\kappa_{0}$,求解方程 $F=[G \ \ H_{1} \ \ H_{2}]=$ $0$.
步骤 6:将所求 $\lambda $ 和 $\kappa $ 的值代入矢径极值表达式,并转化为在坐标系下的坐标形式.
步骤 7:重复执行步骤 2 到 6 直至角度 $i$ 覆盖整个空间.
由算法 1~算法 3 可知,针对单脉冲轨道机动可达域求解问题,两种已有算法与本文算法相比,相同之处是 3 种算法均设置了两个角度变量,用于描述未来可达位置矢量 ${\pmb r}_{f}$ 的指向,角度变量定义各有不同:{算法 2} 定义了转移轨道面倾角 $i$ 和转移轨道面的转移相位角 $\theta $ 用以描述 ${\pmb r}_{f}$ 指向; {算法 3} 定义了角度 $\alpha $ 描述初始轨道上某点的位置,定义角度 $\varphi$ 表示以该点为起点的空间指向;本文提出的 {算法 1} 定义两个角度 $\gamma $ 和 $\varphi$ 分别表示 ${\pmb r}_{f}$ 相对于 $x_{g}$ 轴的方位角和相对初始轨道面的俯仰角.综上,无论采用哪种角度定义方式,均可使 ${\pmb r}_{f}$ 指向空间任意方向.
3种算法的不同之处在于:算法 2首先确定一个变量 $i$ 的取值范围,然后按转移轨道的未来走势不同把另一个变量 $\alpha $ 在 $[0, 2\pi ]$ 范围内分类,分别求得可达域内包络和外包络; {算法 3} 是对每一个目标方向 $[\alpha,\varphi]$,用数值方法求解关于 $\lambda $, $\kappa $ 的非线性方程组,求得控制变量 $\lambda $, $\kappa$ 的解后回代入可达矢径表达式求得可达域包络;而本文 {算法 1} 设计了不同的方向序列选取方案,提出了更加简洁的可达性判定方法,将可达域内外包络的求解统一为通过对单一变量求解非线性方程得到,相对于 {算法 2} 和 {算法 3} 均有所改进.与这两种已有算法对比,本文方法的优势在于:(1) 相比于 {算法 2},不涉及复杂的变量关系推导,模型更加简单;可达性证明及可达性判据的推导过程更加简洁,并且将内外包络的计算方法进行了统一.(2) 相比于 {算法 3},虽然两者都需要采用数值方法进行求解,但是本文只有一个待求参数,不需要求解微分方程组,初值敏感性低,求解效果较好.
3 仿真分析
本节以二体模型下椭圆轨道为例,计算航天器单脉冲机动可达域,采用 MonteCarlo 打靶仿真验证本文方法的正确性,并将两种现有算法与本文算法求解结果进行对比分析. 仿真算例采用的初始轨道参数: 半长轴 $a=10^{7}$ m, 轨道倾角 $i=0$ rad, 偏心 率 $e=0.2$,机动位置 $f=\pi/3$ rad. 最大速度脉冲 $\vert \vert \Delta {\pmb v} \vert \vert=500$ m/s,方向任意,即机动冲量限制在一个半径为 500 m/s 的空间球体内,如图13 所示.
图13
图13
速度机动球 $\vert \vert \Delta v\vert \vert =500$ m/s
Fig. 13
Impulsive maneuvering ball $\vert \vert \Delta v\vert \vert =500$ m/s
(1) 如图14 所示,在 $f_{0}=\pi /3$ 处,对脉冲机动大小 $\Delta v$、机动方向角度 $\delta $, $\xi $,采用均匀分布随机选取 10 000 个样本点;
图14
图14
机动方向角度 $\delta $ 和 $\xi $
Fig. 14
Maneuvering angle $\delta $ and $\xi $
(2) 将每一次样本机动量添加到航天器初始速度部分,采用二体轨道模型将初始位置速度外推一个轨道周期,得到一条机动后的样本轨道;
(3) 采用本文算法求解轨道机动可达域包络,通过观察所有机动后样本轨道是否完全落在求解的可达域包络内来判定求解结果的正确性.
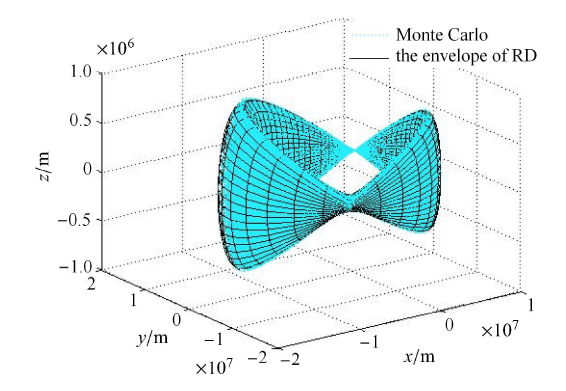
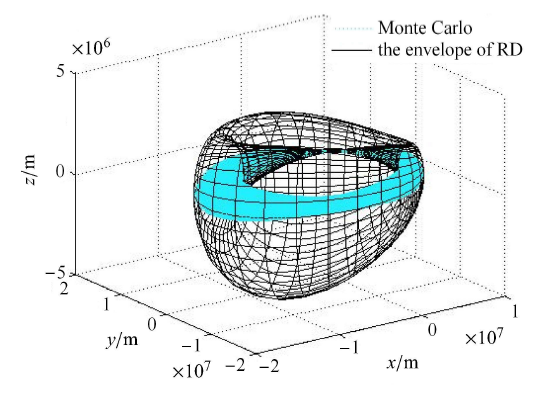
3种算法的计算结果如图15 ~图17 所示.需要说明的是,已有算法一求解过程不涉及数值迭代;已有算法二涉及非线性方程组数值求解,本算例中将初值取为 $\lambda_{0}=\pi /2$,$\kappa_{0}=0$;本文所提算法所涉及非线性方程数值求解,算例中将初值取为 $( \alpha_{0})_{1}=\pi/2$ 及 $(\alpha_{0})_{2}=-\pi /2$,分别对应该方向两个矢径极值的求解. 图15 ~图17 中,黑色实线网格为不同算法对可达域包络的求解结果,青色虚线为 Monte Carlo 仿真结果.
图15
图15
已有算法一仿真结果
Fig. 15
Results for existing algorithm 1
图16
图16
已有算法二仿真结果
Fig. 16
Results for existing algorithm 2
图17
图17
本文算法仿真结果
Fig. 17
Results for the algorithm of this paper
对比图15 ~图17 可知,算法一与本文算法求得的结果拟合性较好,基本与随机轨道分布区域贴合,而已有算法二在本章算例给定的初值条件下,所得结果拟合效果较保守,且离机动点位置越远,拟合效果越差.
为了更清晰直观地分析可达域求解结果,将三维可达域投影到初始轨道面内,得到可达域的二维投影如图18 所示.
图18
图18
三种算法仿真结果 $XY$ 视图
Fig. 18
Results for three algorithms in $XY$ plane
对比图18 可知,在 $XY$ 视图内,已有算法二在俯视图内,依然是在机动位置处拟合效果较好,但离机动位置越远,拟合效果越差,计算结果偏保守.已有算法一与本文算法的拟合效果相近且较好.
4 结论
本文提出了一种精度较高的航天器单脉冲轨道机动可达域求解算法. 首先定义了两个角度 $\gamma$ 和 $\varphi $ 描述未来终端位置矢量 ${\pmb r}_{f}$ 的指向,其次提出一种更为简洁的可达性判据判断 ${\pmb r}_{f}$ 方向可达性,然后通过极值求解算法计算可达位置矢量 ${\pmb r}_{f}$ 的矢径极值,最后将所有极值点的位置坐标排序汇总即可得到可达域.此外,根据球形机动冲量可达域包络的对称特性,减少了求解流程的计算量.本文算法通过合理选择可达矢径描述参数,简化了终端位置矢量的可达性证明方法并提出可达性判据,将可达域内外包络的求解算法进行了统一,同时将可达域求解问题转化为单一待求参数的非线性方程求解问题,提高了可达域求解的收敛性.最后采用 Monte Carlo 仿真验证了所提算法的正确有效性.仿真结果表明:本文所提航天器单脉冲机动可达域求解算法相比已有算法模型更简洁,计算精度更高.
参考文献
View Option
[1]
曹登庆 , 白坤朝 , 丁虎 等 . 大型柔性航天器动力学与振动控制研究进展
力学学报 , 2019 ,51 (1 ):1 -13
[本文引用: 1]
( Cao Dengqing Bai kunchao Ding Hu , et al . Advances in dynamics and vibration control of large-scale flexible spacecraft
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):1 -13 (in Chinese))
[本文引用: 1]
[2]
柳森 , 党雷宁 , 赵君尧 等 . 小行星撞击地球的超高速问题
力学学报 , 2018 ,50 (6 ):1311 -1327
[本文引用: 1]
( Liu Sen Dang Leining Zhao Junyao , et al . Hypervelocity issues of earth impact by asteroids
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (6 ):1311 -1327 (in Chinese))
[本文引用: 1]
[3]
王恩美 , 邬树楠 , 吴志刚 . 在轨组装空间结构面向主动控制的动力学建模
力学学报 , 2020 ,52 (3 ):805 -816
[本文引用: 1]
( Wang Enmei Wu Shunan Wu Zhigang . Active-control-oriented dynamic modelling for on-orbit assembly space structure
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (3 ):805 -816 (in Chinese))
[本文引用: 1]
[4]
Hughes SP Mailhe LM Guzman JJ . A comparison of trajectory optimization methods for the impulsive minimum propellant rendezvous problem
Advances in the Astronautical Sciences 2003 ,13 :85 -104
[本文引用: 1]
[5]
郗小宁 , 王威 , 高玉东 等 . 近地航天器轨道基础 . 长沙 : 国防科技大学出版社 , 2003 ,105
[本文引用: 1]
( Xi Xiaoning Wang Wei Gao Yudong , et al . Fundamentals of Near-Earth Spacecraft Orbit . Changsha : National University of Defense Technology Press , 2003 ,105 (in Chinese ))
[本文引用: 1]
[6]
李皓皓 , 张进 , 罗亚中 . 基于机动目标滤波估计的航天器主动规避策略
力学学报 , 2020 ,52 (6 )
[本文引用: 1]
( Li Haohao Zhang Jin Luo Yazhong . Spacecraft evasion strategy using active maneuvers based on maneuvering target acceleration estimation
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (6 ) (in Chinese))
[本文引用: 1]
[7]
范红旗 , 王胜 , 付强 . 目标机动检测算法综述
系统工程与电子技术 , 2009 ,31 (5 ):1064 -1070
URL
[本文引用: 1]
对机动目标跟踪中的机动检测技术进行了较为全面的综述.首先将机动检测表述为变化检测问题;然后给出了现有机动检测技术的三种分类方法;随后以检测器输入为主线对现有机动检测算法做了详细的介绍,指出了各种算法的基本原理、优缺点及相互关系;最后展望了机动检测技术的发展方向.
( Fan Honqi Wang Sheng Fu Qiang . Survey of algorithms of target maneuver detection
Systems Engineering and Electronics 2009 ,31 (5 ):1064 -1070 (in Chinese))
URL
[本文引用: 1]
A comprehensive and up-to-date survey of the techniques of maneuver detection in the filed of maneuvering target tracking is presented.The problem of maneuver detection is firstly described as change point detection.Then three classification methodologies of the techniques are proposed,and then various techniques of maneuver detection are surveyed according to the input information of the detector.This survey emphasizes the underlying ideas of the techniques,and their performances are also analyzed.Interrelationships among techniques and insight to the pros and cons are provided.Finally,the perspectives of maneuver detection are presented.
[8]
汪雄良 , 周海银 , 朱炬波 . 三状态样条滤波与平滑
数学理论与应用 , 2002 (1 ):109 -112
( Wang Xiongliang Zhou Haiyin Zhu Jubo . Three-state spline filter and smooth method
Mathematical Theory and Applications 2002 (1 ):109 -112 (in Chinese))
[9]
徐国亮 , 邓雅娟 . 机动目标建模及机动检测算法
情报指挥控制系统与仿真技术 , 2005 ,27 (4 ):81 -83
( Xu Guoliang Deng Yajuan . Mathematical models for maneuvering target tracking and maneuver detection algorithms
Information Command Control System & Simulation Technology 2005 ,27 (4 ):81 -83 (in Chinese))
[10]
李元凯 , 敬忠良 , 胡士强 . 基于瞬态相对模型的轨道机动目标运动参数估计
控制与决策 , 2009 ,24 (7 ):1059 -1064
[本文引用: 1]
( Li Yuankai Jing Zhongliang Hu Shiqiang . Transient relativemodel based kinematical parameter estimation for orbital maneuvering target
Control and Decision 2009 ,24 (7 ):1059 -1064 (in Chinese))
[本文引用: 1]
[11]
梁彦刚 , 王伟林 . 在轨服务航天器任务指派问题
国防科技大学学报 , 2013 ,35 (5 ):26 -30
[本文引用: 2]
( Liang Yangang Wang Weilin . Research on mission assignment of on-orbit servicing spacecraft
Journal of National University of Defense Technology 2013 ,35 (5 ):26 -30 (in Chinese))
[本文引用: 2]
[12]
Curtis HD . Orbital Mechanics for Engineering Students
Burlington: Elsevier Ltd , 2010
[本文引用: 1]
[13]
武凌斯 . 有翼导弹引论 . 北京 : 国防工业出版社 , 1979
[本文引用: 1]
( Wu Lingsi . Introduction to Winged Missiles . Beijing : National Defense Industry Press , 1979 (in Chinese))
[本文引用: 1]
[14]
Beckner FL . Regions Accessible to A Ballistic Weapon
Austin, TX: University of Texas at Austin
[本文引用: 1]
[15]
Battin RH . An introduction to the mathematics and methods of astrodynamics. rev
Reston, VA: AIAA , 1999
[本文引用: 3]
[16]
Vinh NX Lu P Howe RM , et al . Optimal interception with time constraint
Journal of Optimization Theory and Applications 1990 ,66 (3 ):361 -390
DOI
URL
[本文引用: 1]
[17]
Vinh NX Gilbert EG Howe RM , et al . Reachable domain for interception at hyperbolic speeds
Acta Astronautica 1995 ,35 (1 ):1 -8
[本文引用: 1]
[18]
陈茂良 , 周军 , 常燕 . 空间拦截攻击区和威胁区仿真研究
航天控制 , 2009 ,27 (1 ):41 -44
[本文引用: 1]
( Chen Maoliang Zhou Jun Chang Yan . Simulation study of attacking area and threatening area for space interception
Aerospace Control 2009 ,27 (1 ):41 -44 (in Chinese))
[本文引用: 1]
[19]
常燕 , 周军 . 空间飞行器追踪区设计
宇航学报 , 2006 ,27 (6 ):1228 -1231
[本文引用: 1]
( Chang Yan Zhou Jun . Tracing area design for spacecraft
Journal of Astronautics 2006 ,27 (6 ):1228 -1231 (in Chinese))
[本文引用: 1]
[20]
徐加瑞 , 陈勇 . 轨道机动的追踪区与机遇区仿真分析. 系统仿真技术及其应用学术会议论文集
北京: 中国系统仿真学会 , 2009
[本文引用: 1]
( Xu Jiarui Chen yong . Simulation analysis of tracking area and opportune area of the orbital maneuvering. System Simulation Technology & Application
Beijing: Chinese Society for System Simulation , 2009 (in Chinese))
[本文引用: 1]
[21]
雪丹 , 李俊峰 . 平面脉冲作用下卫星轨道的可达范围研究
宇航学报 , 2009 ,30 (1 ):88 -92
[本文引用: 1]
( Xue Dan Li Junfeng . Study on reachable domain for satellite trajectory with coplanar impulse applied
Journal of Astronautics 2009 ,30 (1 ):88 -92 (in Chinese))
DOI
URL
[本文引用: 1]
[22]
雪丹 , 李俊峰 . 确定卫星可达范围的优化方法
清华大学学报: 自然科学版 , 2009 (11 ):1852 -1855
[本文引用: 1]
( Xue Dan Li Junfeng . Optimization of the reachable domain of a satellite
Journal of Tsinghua University: Science & Technology 2009 (11 ):1852 -1855 (in Chinese))
[本文引用: 1]
[23]
雪丹 , 李俊峰 , 蒋方华 . 卫星在轨道平面内的可达范围研究
力学学报 , 2010 ,42 (2 ):337 -342
[本文引用: 1]
( Xue Dan Li Junfeng Jiang Fanghua . Reachable domain of a satellite with a coplanar impulse applied
Chinese Journal of Theoretical and Applied Mechanics 2010 ,42 (2 ):337 -342 (in Chinese))
[本文引用: 1]
[24]
Xue D Li J Baoyin H , et al . Reachable domain for spacecraft with a single impulse
Journal of Guidance, Control, and Dynamics 2010 ,33 (3 ):934 -942
DOI
URL
[本文引用: 1]
[25]
温昶煊 . 面向空间态势感知的可达范围理论和应用研究. [博士论文]
北京: 北京航空航天大学 , 2015
[本文引用: 5]
( Wen Changxuan . Space situational awareness oriented research on theory and application of reachable domain. [PhD Thesis]
Beijing: Beijing University of Aeronautics and Astronautics , 2015 (in Chinese))
[本文引用: 5]
[26]
Wen C Zhao Y Shi P . Precise determination of reachable domain for spacecraft with single impulse
Journal of Guidance,Control, and Dynamics 2014 ,37 (6 ):1767 -1779
DOI
URL
[27]
Wen C Zhao Y Shi P Hao Z , Orbital accessibility problem for spacecraft with a single impulse
Journal of Guidance,Control, and Dynamics 2014 ,37 (4 ):1260 -1271
DOI
URL
[28]
Wen C Peng C Gao Y , Reachable domain for spacecraft with ellipsoidal Delta-V distribution
Astrodynamics 2018 ,2 (3 ):265 -288
DOI
URL
[本文引用: 3]
[29]
Chen Q Qiao D Shang HB , et al . A new method for solving reachable domain of spacecraft with a single impulse
Acta Astronautica 2018 ,145 :153 -164
DOI
URL
[本文引用: 4]
[30]
张洪波 . 航天器轨道力学理论与方法 . 北京 : 国防工业出版社 , 2015
[本文引用: 2]
( Zhang Hongbo . Theories and Methods of Spacecraft Orbital Mechanics . Beijing : National Defense Industry Press , 2015 (in Chinese))
[本文引用: 2]
大型柔性航天器动力学与振动控制研究进展
1
2019
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
大型柔性航天器动力学与振动控制研究进展
1
2019
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
小行星撞击地球的超高速问题
1
2018
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
小行星撞击地球的超高速问题
1
2018
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
在轨组装空间结构面向主动控制的动力学建模
1
2020
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
在轨组装空间结构面向主动控制的动力学建模
1
2020
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
A comparison of trajectory optimization methods for the impulsive minimum propellant rendezvous problem
1
2003
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
1
2003
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
1
2003
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
基于机动目标滤波估计的航天器主动规避策略
1
2020
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
基于机动目标滤波估计的航天器主动规避策略
1
2020
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
目标机动检测算法综述
1
2009
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
目标机动检测算法综述
1
2009
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
基于瞬态相对模型的轨道机动目标运动参数估计
1
2009
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
基于瞬态相对模型的轨道机动目标运动参数估计
1
2009
... 随着人类太空活动日益频繁,空间目标 (航天器、空间碎片等) 数量不断增大,在轨航天器、乃至整个空间环境的安全面临新的挑战[1 -2 ] .一方面,在轨航天器存在与其他空间目标碰撞的危险[3 -4 ] ;另一方面,在轨航天器之间的对抗博弈活动越来越多[5 -6 ] ,这使得博弈双方需要尽可能多地掌握对方航天器的异动信息[7 -10 ] ,比如轨道机动后的可达范围及可能威胁区域. ...
在轨服务航天器任务指派问题
2
2013
... 航天器单脉冲轨道机动可达域是指航天器在某一位置施加机动冲量后,未来时间所有可能到达位置的集合[11 ] . 其中机动冲量满足一定约束条件[12 ] ,一般用速度机动球或速度机动椭球来描述,用以限制脉冲机动的大小和方向. ...
... 定义坐标系 $S_{0}$:原点 $O$ 位于航天器质心,$x_{0}$ 轴与 ${\pmb r}_{0}$ 重合,$z_{0}$ 轴指向初始轨道角动量方向,$y_{0}$ 轴与 $x_{0}$ 轴、$z_{0}$ 轴构成右手直角坐标系. 航天器初始轨道速度 ${\pmb v}_{0}$ 在 $S_{0}$ 坐标系下可表示为[11 ] ...
在轨服务航天器任务指派问题
2
2013
... 航天器单脉冲轨道机动可达域是指航天器在某一位置施加机动冲量后,未来时间所有可能到达位置的集合[11 ] . 其中机动冲量满足一定约束条件[12 ] ,一般用速度机动球或速度机动椭球来描述,用以限制脉冲机动的大小和方向. ...
... 定义坐标系 $S_{0}$:原点 $O$ 位于航天器质心,$x_{0}$ 轴与 ${\pmb r}_{0}$ 重合,$z_{0}$ 轴指向初始轨道角动量方向,$y_{0}$ 轴与 $x_{0}$ 轴、$z_{0}$ 轴构成右手直角坐标系. 航天器初始轨道速度 ${\pmb v}_{0}$ 在 $S_{0}$ 坐标系下可表示为[11 ] ...
Orbital Mechanics for Engineering Students
1
2010
... 航天器单脉冲轨道机动可达域是指航天器在某一位置施加机动冲量后,未来时间所有可能到达位置的集合[11 ] . 其中机动冲量满足一定约束条件[12 ] ,一般用速度机动球或速度机动椭球来描述,用以限制脉冲机动的大小和方向. ...
1
1979
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
1
1979
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
Regions Accessible to A Ballistic Weapon
1
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
An introduction to the mathematics and methods of astrodynamics. rev
3
1999
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... 以轨道机动位置 ${\pmb r}_{0}$ 为起点,终端位置 ${\pmb r}_{f}$ 为终点,二点之间的转移过程可以看做是两点边值问题,Battin[15 ] 证明轨道两点边值问题满足如下等式 ...
... 由等式 (6) 可得轨道两点边值问题的重要结论[15 ] :能到达给定目标位置矢量的所有可能转移轨道,其初始速度矢量的轨迹是一条边界速度双曲线 (terminal velocity hyperbola,TVH),该双曲线两条渐近线分别为弦和初始位置矢量 ${\pmb r}_{0}$ 所在的直线. 因此,为使得 ${\pmb r}_{f}$ 目标方向可达,需保证机动后的速度始端能够落在边界速度双曲线上,如图5 所示. ...
Optimal interception with time constraint
1
1990
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
Reachable domain for interception at hyperbolic speeds
1
1995
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
空间拦截攻击区和威胁区仿真研究
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
空间拦截攻击区和威胁区仿真研究
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
空间飞行器追踪区设计
1
2006
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
空间飞行器追踪区设计
1
2006
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
轨道机动的追踪区与机遇区仿真分析. 系统仿真技术及其应用学术会议论文集
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
轨道机动的追踪区与机遇区仿真分析. 系统仿真技术及其应用学术会议论文集
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
平面脉冲作用下卫星轨道的可达范围研究
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
平面脉冲作用下卫星轨道的可达范围研究
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
确定卫星可达范围的优化方法
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
确定卫星可达范围的优化方法
1
2009
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
卫星在轨道平面内的可达范围研究
1
2010
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
卫星在轨道平面内的可达范围研究
1
2010
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
Reachable domain for spacecraft with a single impulse
1
2010
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
面向空间态势感知的可达范围理论和应用研究. [博士论文]
5
2015
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... [25 -28 ]的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... 基于二体轨道动力学模型可得目标位置矢量 ${\pmb r}_{f}$ 可表示为[25 ] ...
... 最近,温昶煊等[25 -28 ] 、陈奇等[29 ] 对单脉冲轨道机动可达域问题进行了研究,温昶煊等的方法通过证明转移相位角和速度机动方向的对应关系,分别针对可达域内外包络建立了可达域直接求解模型. 陈奇等的方法以初始轨道为基础,将可达域定义为围绕在初始轨道周围的管道模型,并给出了通过求解非线性方程组计算可达域 的方法.为便于对比分析,本文将这两种方法的求解流程简要总结如算法 2 和算法 3 所示,其中温昶煊方法记为已有算法一,陈奇方法记为已有算法二. ...
... 算法 2 已有算法一求解流程[25 ] ...
面向空间态势感知的可达范围理论和应用研究. [博士论文]
5
2015
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... [25 -28 ]的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... 基于二体轨道动力学模型可得目标位置矢量 ${\pmb r}_{f}$ 可表示为[25 ] ...
... 最近,温昶煊等[25 -28 ] 、陈奇等[29 ] 对单脉冲轨道机动可达域问题进行了研究,温昶煊等的方法通过证明转移相位角和速度机动方向的对应关系,分别针对可达域内外包络建立了可达域直接求解模型. 陈奇等的方法以初始轨道为基础,将可达域定义为围绕在初始轨道周围的管道模型,并给出了通过求解非线性方程组计算可达域 的方法.为便于对比分析,本文将这两种方法的求解流程简要总结如算法 2 和算法 3 所示,其中温昶煊方法记为已有算法一,陈奇方法记为已有算法二. ...
... 算法 2 已有算法一求解流程[25 ] ...
Precise determination of reachable domain for spacecraft with single impulse
0
2014
Orbital accessibility problem for spacecraft with a single impulse
0
2014
Reachable domain for spacecraft with ellipsoidal Delta-V distribution
3
2018
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... -28 ]的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... 最近,温昶煊等[25 -28 ] 、陈奇等[29 ] 对单脉冲轨道机动可达域问题进行了研究,温昶煊等的方法通过证明转移相位角和速度机动方向的对应关系,分别针对可达域内外包络建立了可达域直接求解模型. 陈奇等的方法以初始轨道为基础,将可达域定义为围绕在初始轨道周围的管道模型,并给出了通过求解非线性方程组计算可达域 的方法.为便于对比分析,本文将这两种方法的求解流程简要总结如算法 2 和算法 3 所示,其中温昶煊方法记为已有算法一,陈奇方法记为已有算法二. ...
A new method for solving reachable domain of spacecraft with a single impulse
4
2018
... 航天器可达域的研究由常规导弹攻击区和弹道导弹可达区的研究拓展演变而来. 导弹攻击区[13 ] 是指导弹攻击目标的可能范围. Beckner[14 ] 给出了基于椭圆轨道上某点发射弹道武器,发射速度固定情况下的可达区计 算公式.Battin[15 ] 进一步研究并给出弹道导弹在初始静止、发射速度方向任意,大小受限情况下轨道可达 包络的确定方法.随着航天技术发展,基于天基平台的导弹拦截受到一定关注,1994年,Vinh 等[16 -17 ] 采用可达域概念研究了天基导弹对地面发射弹道导弹的拦截区域问题. 常燕等[18 -19 ] 提出了追踪区的概念,用于描述满足约束的可行变轨点集. 徐加瑞等[20 ] 对追踪区和机遇区进行了进一步研究. 随后,可达域研究进一步向具有空间机动能力的航天器拓展. 2009 年,雪丹等[21 -22 ] 提出了航天器可达范围的概念,在不考虑拦截目标和时间约束情况下,研究航天器所有可能到达的最大区域,文献[23 ] 给出了共面可达范围的精确求解,主要针对二维平面情况,此后作者在文献[24 ] 中进一步研究了三维空间的可达范围求解方法,但是该方法仅能给出可达范围的保守上界,不能精确地确定可达范围. 针对此不足,温昶煊等[25 -28 ] 通过参量转化进一步研究了三维空间可达域问题,该方法通过分别计算内外包络获得可达域,但求解模型较为复杂,涉及较多的变量代换关系;陈奇等[29 ] 基于初始轨道建立模型,通过增加几何约束条件,求解非线性方程组获得了航天器单脉冲机动的可达域包络,进一步研究了航天器机动位置不确定但限制在某一区段情况下的可达域计算方法.针对航天器单脉冲轨道可达域的计算,温昶煊等[25 -28 ] 的方法计算操作简单,但求解模型的可达性证明较复杂,涉及复杂的角度转化关系证明,且针对可达域内外包络有不同的计算公式;陈奇等[29 ] 的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... [29 ]的方法模型普适性更好,但是非线性方程组求解对初值选取的要求较高,初值选取不合适会使得部分计算结果偏保守从而导致精度降低. 因此需要模型更加精简,拟合效果更好的求解算法. ...
... 最近,温昶煊等[25 -28 ] 、陈奇等[29 ] 对单脉冲轨道机动可达域问题进行了研究,温昶煊等的方法通过证明转移相位角和速度机动方向的对应关系,分别针对可达域内外包络建立了可达域直接求解模型. 陈奇等的方法以初始轨道为基础,将可达域定义为围绕在初始轨道周围的管道模型,并给出了通过求解非线性方程组计算可达域 的方法.为便于对比分析,本文将这两种方法的求解流程简要总结如算法 2 和算法 3 所示,其中温昶煊方法记为已有算法一,陈奇方法记为已有算法二. ...
... 算法 3 已有算法二求解流程[29 ] ...
2
2015
... 在二体轨道初值问题中,设经过一段时间后,两条轨道的位置相对于初始位置的真近角差均为 $\Delta f$,则该时刻轨道位置可以表示为[30 ] ...
... 其中,$F$ 与 $G$ 为拉格朗日系数,仅与 $\Delta f$ 取值相关[30 ] ,当 $\Delta f$ 相同时,可作为常系数处理. ...
2
2015
... 在二体轨道初值问题中,设经过一段时间后,两条轨道的位置相对于初始位置的真近角差均为 $\Delta f$,则该时刻轨道位置可以表示为[30 ] ...
... 其中,$F$ 与 $G$ 为拉格朗日系数,仅与 $\Delta f$ 取值相关[30 ] ,当 $\Delta f$ 相同时,可作为常系数处理. ...