引言
再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行,期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束,使其轨迹规划问题成为了一个极富挑战性的问题,引起了国内外许多学者的研究兴趣[1 ] . 传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2 ] 等优化算法,两者或因巨大的计算量,或因不易收敛,都只适合离线的轨迹优化[3 -6 ] . 虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7 ] ,曾取得过辉煌的成绩,但该方法的简化过程限制了飞行器的机动能力. 总的来说,基于极大值原理的直接法推导最优解的过程较为繁琐,对于复杂问题几乎无法得到解析解;以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦;而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题,需反复交叉、变异、迭代,计算效率较低.
强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] .
近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败.
针对上述序列凸优化的不足之处,本文提出了几种改善其收敛性的方法. 首先通过增加虚拟控制量,可避免迭代初期由于控制能力的不足带来的"伪不可行"问题,降低该算法对初始参考轨迹的依赖.其次通过 B 样条曲线离散控制量,抑制由于离散带来的锯齿化现象.最后,引入一种"回溯搜索"的方法,改善迭代过程中状态量的振动,从而加快算法的收敛.
在高超声速飞行器实际的再入飞行过程中,大气参数扰动以及外界随机干扰都会对再入轨迹产生一定的影响. 现有的基于序列凸优化的轨迹优化方法,均属于确定性轨迹优化方法,即在优化的过程中未考虑参数扰动和初值不确定性对优化轨迹的影响. 在上述方法设计的最优输入的控制下,高超声速飞行器一旦受到不确定扰动或干扰的影响,可能会偏离预定优化轨迹,难以满足预期设定的过程约束、终端约束以及禁飞区等地理约束,甚至可能出现飞行器烧蚀坠落的事故. 因此,在轨迹优化设计的过程中,除了确定性的动力学建模分析之外,还需要综合考虑参数扰动的影响,完成复杂不确定条件下的高超声速再入轨迹的优化设计,提高再入飞行轨迹的鲁棒性.
目前鲁棒轨迹优化方法在高超声速领域应用较少. Rangaraj 等[21 ] 利用多项式混沌方法设计了一种改进粒子滤波器,与传统的粒子滤波器相比,计算效率大大提高. Xiong 等[22 ] 针对一类具有不确定性的轨迹优化问题,将不确定的路径约束使用多项式混沌方法表示为均值和方差的约束,提高了设计效率. Li 等[23 ] 设计了一种将不确定约束转化为确定性优化的非侵入的多项式混沌飞行轨迹优化方法. Michael 等[24 ] 对直接法进行改进,提出了一种快速鲁棒轨迹优化方法. 此外结合高斯伪谱法和多项式混沌理论的鲁棒轨迹优化方法也成为研究的热点[24 -26 ] .
本文为研究飞行器再入过程中的气动参数扰动问题,提出了采样点少、易于实现,计算效率高的广义混沌多项式理论研究方法,建立了基于广义混沌多项式和凸优化相结合的再入轨迹鲁棒优化模型,该模型可有效降低优化轨迹对气动参数扰动的敏感程度,在不确定条件的干扰下,展现出了较强的鲁棒稳定性.
1 确定性轨迹优化模型
1.1 再入动力学方程
考虑地球自转的影响,建立如下再入飞行器无量纲运动方程
(1a) $\left.\!\!\begin{array}{l} \dot {r} = V\sin \gamma \\ \dot {\theta } = \dfrac{V\cos \gamma \sin \psi }{r\cos \phi }\\ \dot {\phi } = \dfrac{V\cos \gamma \cos \psi }{r} \\ \dot {V} = - D - \dfrac{\sin \gamma }{r^2} + \varOmega _{g}^2r\cos \phi \sin \gamma \cos \phi - \\ \cos \gamma \sin \phi \cos \psi \\ \dot {\gamma } = \dfrac{L\cos \sigma }{V} + \left( {\dfrac{V}{r} - \dfrac{1}{r^2}} \right)\cos \gamma + 2\varOmega _{g} \cos \phi \sin \psi +\\ \dfrac{\varOmega _{g}^2r}{V}\cos \phi \left( {\cos \gamma \cos \phi + \sin \gamma \sin \phi \cos \psi } \right) \end{array} \right \} $
(1b) $ \dot {\psi } = \dfrac{L\sin \sigma }{V\cos \gamma } + \dfrac{V}{r}\cos \gamma \sin \psi \tan \phi - \\ 2\varOmega _{g} \left( {\cos \phi \cos \psi \tan \gamma - \sin \phi } \right) + \\ \dfrac{\varOmega _{g}^2r}{V\cos \gamma }\sin \varphi \cos \phi \sin \psi $
其中,$r,\theta ,\phi ,V,\gamma ,\psi $ 分别为无量纲化的地心距、经度、纬度、对地速度、航迹角、航向角,地心距按地球平均半径归一化,对地速度按第一宇宙速度归一化. 速度 $\sigma $ 为倾侧角,$\varOmega _{g} $ 为地球自转角速度,其对 $\sqrt {{g_0 } /{R_0 }}$ 归一化,无量纲化升力 $L$、阻力 $D$ 的表达式为
(2) $\left.\begin{array}{l} L = \dfrac{1}{2}R_0 \rho V^2S C_{L} \\ D = \dfrac{1}{2}R_0 \rho V^2S C_{D} \end{array} \!\! \right \}$
其中,$\rho $ 是大气密度,为简化问题,采用指数形式的大气模型 $\rho = \rho _{0} \exp \left( { - \beta h}\right)$,$S$ 为飞行器的气动参考面积,升力系数 $C_{L} $、阻力系数 $C_{D}$ 均认为是攻角和马赫数的函数.
1.2 基本约束
飞行器再入过程中,为保证飞行任务的成功,需满足热流、动压、过载等路径约束,可表示为
(3) $ \dot {Q} = k_Q \sqrt \rho V^{3.15} \leqslant \dot {Q}_{\max }$
(4) $ q = 0.5\rho V^2 \leqslant q_{\max }$
(5) $ n = \sqrt {L^2 + D^2} \leqslant n_{\max }$
其中,$\dot {Q}$, $ q$ 和 $n$ 分别为热流密度、动压及过载,$ k_Q $ 为热流密度系数,$\dot{Q}_{\max }$, $ q_{\max } $ 和 $n_{\max } $ 分别为峰值热流密度、峰值动压及过载峰值.
考虑伺服结构的约束,保证优化结果光滑可行,选择倾侧角的变化率为控制量,式 (1) 中需增加一个额外的状态方程 $\dot {\sigma } = u$,则状态变量为 ${\pmb x} = \left[ {r;\theta ;\phi ;V;\gamma ;\psi ;\sigma } \right]$,该策略可避免对控制量进行凸化处理.
(6) $\min \ \ J = \varphi \left[ {x\left( {t_{f} } \right)} \right] + \int_{t_0 }^{t_{f}} {\psi \left( {x,\sigma } \right)} \text{d} t$
(7) ${subject \ to} \ \ \dot {x} = f\left( {x,\sigma } \right)$
(8) $ \left.\begin{array}{ll} x\left( {t_0 } \right) = x_0 , & x\left( {t_{f} } \right) = x_{f} \\ \sigma _{\min } \leqslant \sigma \leqslant \sigma _{\max } , & \dot {\sigma }_{\min } \leqslant \dot {\sigma } \leqslant \dot {\sigma }_{\max } \end{array} \!\! \right \}$
(9) $\left.\begin{array}{l} \dot {Q} = k_Q \sqrt \rho V^{3.15} \leqslant \dot {Q}_{\max } \\ q = 0.5\rho V^2 \leqslant q_{\max } \\ n = \sqrt {L^2 + D^2} \leqslant n_{\max } \end{array} \!\! \right \}$
(10) $\dot {x} = f\left( x \right)+Bu +f_\varOmega \left( x \right)$
其中,第一项是与状态变量相关的项,第二项是与控制量相关的项,第三项是与地球自旋相关项. 可以看出,选择倾侧角变化率为控制量,使得控制量与状态量自然解耦,更加有利于优化收敛.
1.2 凸化处理
由 1.2 节可知,P1是一个高度的非线性最优控制问题,无法直接采用凸优化方法求解. 目前针对这种复杂的多约束最优控制问题基本上均是通过线性化处理来求解. 因此本文采用基于信赖域约束的序列凸优化方法. 通过求解一系列的凸优化子问题,来逐渐逼近原有问题的解.
将式 (10) 一阶泰勒展开,由于地球自旋速度较慢,可认为 $f_\varOmega \left( x\right) \approx f_\varOmega \left( {x_k } \right)$ ,则线性化的动力学方程为
(11) $\dot {\pmb x} \approx f\left( {{\pmb x}_k } \right) + {\pmb A}\left( {{\pmb x}_k } \right)\left( {{\pmb x} - {\pmb x}_k } \right) + {\pmb B}{\pmb u } + f_\varOmega \left( {{\pmb x}_k } \right)$
(12) $ {\pmb A}\left( {{\pmb x}_k } \right) = \left[ \!\!\begin{array}{ccccccc} 0 & 0 & 0 & {\dfrac{\partial r}{\partial V}} & {\dfrac{\partial r}{\partial \gamma }} & 0 & 0 \\ {\dfrac{\partial \theta }{\partial r}} & 0 & {\dfrac{\partial \theta } {\partial \phi }} & {\dfrac{\partial \theta }{\partial V}} & {\dfrac{\partial \theta }{\partial \gamma }} & {\dfrac{\partial \theta }{\partial \psi }} & 0 \\ {\dfrac{\partial \phi }{\partial V}} & 0 & 0 & {\dfrac{\partial \phi }{\partial V}} & {\dfrac{\partial \phi }{\partial \gamma }} & {\dfrac{\partial \phi }{\partial \psi }} & 0 \\ {\dfrac{\partial V}{\partial r}} & 0 & 0 & {\dfrac{\partial V}{\partial V}} & {\dfrac{\partial V}{\partial \gamma }} & 0 & 0 \\ {\dfrac{\partial \gamma }{\partial r}} & 0 & 0 & {\dfrac{\partial \gamma }{\partial V}} & {\dfrac{\partial \gamma }{\partial \gamma }} & 0 & {\dfrac{\partial \gamma }{\partial \sigma }} \\ {\dfrac{\partial \psi }{\partial r}} & 0 & {\dfrac{\partial \psi }{\partial \phi }} & {\dfrac{\partial \psi }{\partial V}} & {\dfrac{\partial \psi }{\partial \gamma }} & {\dfrac{\partial \psi }{\partial \psi }} & {\dfrac{\partial \psi }{\partial \sigma }} \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array} \!\! \right]$
(13) ${\pmb B} = \left[ \!\! \begin{array}{ccccccc} 0 & 0 & 0 & 0 & 0 & 0 & {1} \end{array}\!\! \right]^{T}$
式 (3) $\sim$ 式 (5) 中的基本约束也可通过上述凸化方法处理,序列凸优化的迭代寻优过程是在给定的参考轨迹附近线性化,为保证子问题向原问题逼近,需增加信赖域约束 $\left\| {x - x_k } \right\| \leqslant \varDelta $.
为避免迭代初期"伪不可行"的问题,降低对初值的依赖程度,同时弥补线性化带来的误差,在式 (11) 中增加一个虚拟控制量 $w$,可得
(14) $\dot {\pmb x} \approx f\left( {{\pmb x}_k } \right) + {\pmb A}\left( {{\pmb x}_k } \right)\left( {{\pmb x} - {\pmb x}_k } \right) + {\pmb B}{\pmb u}+ f_\varOmega \left( {{\pmb x}_k } \right) + {\pmb C}{\pmb w}$
可在迭代过程中,在目标函数中控制虚拟控制量的范围,使其在迭代后期为小量,从而保证问题的准确性, 即
(15) ${J}'= J + \lambda \left\| {{\pmb C}{\pmb w}} \right\|_{2}$
2 算法表述
2.1 问题离散
为求解无限维最优控制问题的数值解,必须对其进行离散.为了简单起见,状态变量像通常一样离散成等距的数值点,各个数值点处的控制量则通过 B 样条曲线控制点的表达式表示,控制点个数的选取可在实际仿真中调整,优化过程中的积分项均采用梯形积分表示.仿真结果显示这种方法可以十分有效地抑制数值求解中控制量的锯齿化现象,更加有利于迭代收敛,并且减少了需要求解的变量个数.将时间$N$等份,可得离散后的动力学方程为
(16) $\begin{array}{l} {\pmb x}_i = {\pmb x}_{i - 1} +\dfrac{\Delta t}{2}\left[ {\left( {{\pmb A}_{i - 1}^{k - 1} {\pmb x}_{i - 1} + {\pmb B}{\pmb u}_{i - 1} + {\pmb f}_{i - 1}^{k - 1} - } \right.} \right. \\ \left. { {\pmb A}_{i - 1}^{k -1} {\pmb x}_{i - 1}^{k - 1} + {\pmb f}_{\Omega ,i - 1}^{k - 1} } \right) + \\ \left. { \left( {{\pmb A}_i^{k - 1} {\pmb x}_i + {\pmb B}{\pmb u}_i + {\pmb f}_i^{k - 1} - {\pmb A}_i^{k - 1} {\pmb x}_i^{k - 1} + {\pmb f}_{\Omega ,i}^{k - 1} } \right)} \right] \end{array}$
其中,上角标 $k$ 表示第 $k$ 次迭代,下角标 $i$ 表示 $t_i $ 时刻,${\pmb x}_i^k = {\pmb x}^k\left( {t_i } \right)$,${\pmb A}_i^k = {\pmb A}\left( {{\pmb x}_i^k } \right)$,${\pmb f}_i^k = {\pmb f}\left( {{\pmb x}_i^k } \right)$,${\pmb f}_{\Omega ,i}^k = {\pmb f}_\Omega \left( {{\pmb x}_i^k } \right)$. 将式 (13) 重新排列组合得
(17) $\begin{array}{l} \left( {I-\dfrac{\Delta t}{2}{\pmb A}_i^{k - 1} } \right) {\pmb x}_i- \left( {I +\dfrac{\Delta t}{2}{\pmb A}_{i- 1 }^{k - 1} } \right) {\pmb x}_{i - 1}- \\ \dfrac{\Delta t}{2}{\pmb B}{\pmb u} _i- \dfrac{\Delta t}{2}{\pmb B}{\pmb u }_{i - 1} = \\ \dfrac{\Delta t}{2}\left( {{\pmb f}_{i - 1}^{k - 1}-{\pmb A}_{i - 1}^{k - 1} {\pmb x}_{i - 1}^{k - 1} + {\pmb f}_{\Omega ,i - 1}^{k - 1}+ } \right. \\ \left. { {\pmb f}_i^{k - 1} - {\pmb A}_i^{k - 1} {\pmb x}_i^{k - 1} + {\pmb f}_{\Omega ,i}^{k - 1} +{\pmb C}{\pmb w}} \right)\end{array}$
2.2 回溯搜索
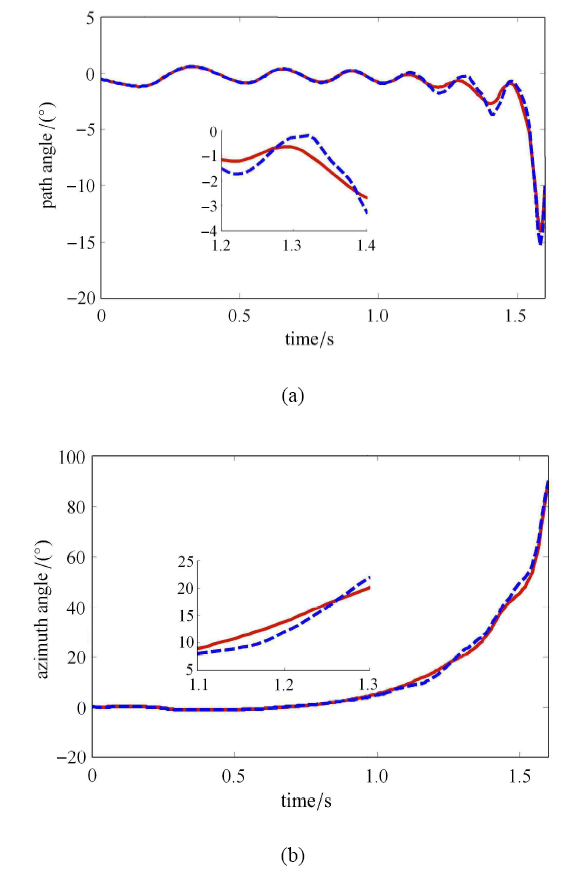
大气层内各个状态变量与控制量相互耦合,具有极强的非线性,且各个约束集也均为非凸,导致无法直接运用内点法进行求解. 受序列二次规划算法的的启发,国内外学者提出了基于信赖域约束的序列凸优化技术. 其信赖域约束也就是为了保障了线性化的可靠程度,当然每次外层迭代所使用的参考轨迹的不同使得每次迭代过程并不是同一个问题,也就是说并不是严格的最优解. 若取固定信赖域,且每次迭代间均采用全步长更新寻优结果,在迭代后期可能会出现如图1 和图2 的情况,各个状态变量在迭代后期产生剧烈振荡,难以符合停机准则,导致寻优失败.
图1
图1
振荡现象
Fig. 1
Vibration phenomena
图2
图2
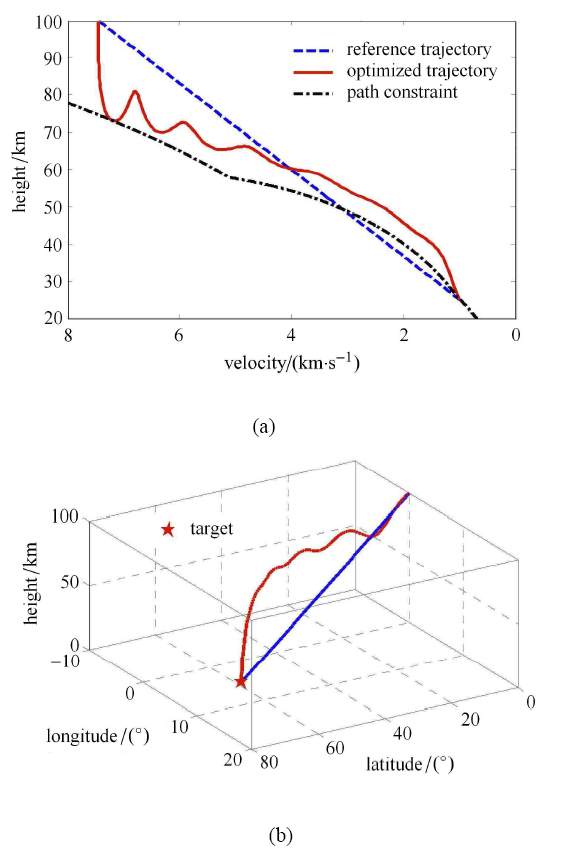
序列凸优化优化结果
Fig. 2
Results of sequential convex optimization
针对这种具有两个局部极小值,得益于牛顿法的启发,本文提出一种"回溯搜索"的收敛办法.通过设置阻尼步长 和回归搜索来快速处理这种局部极小值问题. 具体过程如下:
(1) 初值选取,并线性化,取两个回溯参数 $\alpha \in \left( {\left. {0,1} \right]} \right.,\beta \in \left({\left. {0,1} \right]} \right.$ 以及信赖域 $\varDelta _0 $
(2) 解决子 SOCP 问题,得到 $\varDelta _x $.
(4) 判断回溯条件:$If \ \ J\left( {k + 1} \right) > J\left( k \right)$,$x\left( {k + 1} \right) =x\left( k\right) + \alpha \varDelta _x $,$\varDelta _0 = \beta \varDelta _0 $,进入步骤一.
该回溯搜索的关键点在于信赖域的收缩权值以及阻尼步长权值的选取,调试初期可先设为黄金分割数,后期在具体的仿真过程中适当调整. 一方面信赖域的收缩速度不宜过快,否则可能及早地陷入局部最优点;另外一方面阻尼步长是在两次轨迹迭代轨迹之间的权衡,该值的选择决定了迭代收敛速度的快慢,回溯系数实质上代表了迭代搜索的方向,可决定收敛速度的快慢及计算结果的最优性.
3 考虑气动参数扰动的随机轨迹优化方法
3.1 广义混沌多项式理论
混沌多项式理论的基本思想是利用一系列特定分布的随机变量的正交多项式对随机过程与扰动进行逼近[27 -29 ] . 多项式混沌方法能够用于多种随机模型的求解过程,如集成电路的响应分析[30 ] 、不同类型流体问题研究[31 -32 ] 以及其他问题的研究中.
这里采用符号 $\omega $ 表示随机事件,$\varOmega $ 为随机事件的集合. 定义随机变量矢量为
(18) $\varDelta (\omega ) = [\delta _1 \left( \omega \right), \delta _2 \left( \omega \right),\cdots \delta _k \left( \omega \right), \cdots ]$
其中每个元素 $\delta _i \left( \omega\right)$ 均为随机变量. 同时在空间定义其内积为
(19) $\left\langle {\delta _1 \left( \omega \right) \vert \delta _k \left( \omega \right)} \right\rangle _{L_{2} (\varOmega )} = E\left( {\delta _1 \left( \omega \right),\delta _k \left( \omega \right)} \right)$
根据 Cameron-Martin 理论,这些随机变量 $\delta _i \left( \omega \right)$ 的多项式运算在 $L_{2}\left( \varOmega \right)$ 空间中是稠密的,也就是说任何随机过程都可以由 $L_{2} \left( \varOmega\right)$ 空间中随机变量的正交多项式逼近. 基于上述结论,任意随机过程 $X\left( \omega\right)$ 都可以由混沌多项式近似为
(20) $ X\left( \omega \right) = x_0 P_0 + \sum_{j = 1}^\infty {x_j P_1 \left( {\varDelta \left( \omega \right)} \right)} +\\ \sum_{j = 1}^\infty {\sum_{i = 1}^j {x_{ij} P_2 \left( {\varDelta \left( \omega \right)} \right)} } +\\ \sum_{j = 1}^\infty \sum_{i = 1}^j \sum_{k = 1}^i x_{ijk} P_3 \left( {\varDelta \left( \omega \right)} \right) + \cdots $
采用不高于 $p$ 阶的多项式进行有限项截断,并写成紧凑形式为
(21) $X\left( \omega \right) = \sum_{j = 0 }^{N_{PC} } {x_j \varPsi _j \left( {\varDelta \left( \omega \right)} \right)}$
其中,$P_j \left( {\varDelta \left( \omega \right)} \right)$ 为随机变量的第 $j$ 阶基底多项式,$x_j$ 为混沌多项式系数. 在随后的分析中将随机变量 $\varDelta \left( \omega \right)$ 简写为 $\varDelta$,混沌多项式 $\varPsi \left( {\varDelta \left( \omega \right)} \right)$ 简写为 $\varPsi $. $N_{PC}$ 是多项式展开式的项数,可由下式确定
(22) $N_{PC} = \dfrac{\left( {p + n} \right)!}{p!n!}-1$
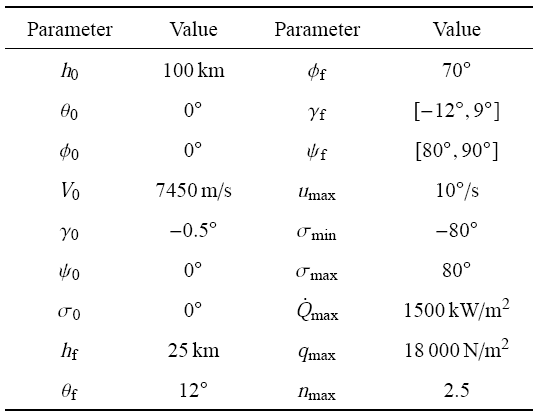
对于分布函数或者概率密度已知的随机变量,式中的系数为确定值. 多项式的选择依赖于随机变量的概率密度函数,根据 Askey 法则,对于不同概率密度函数,存在不同的最优多项式,具体对应形式如表1 所示[28 ] .
根据正交多项式法则,式 (20) 中的多项式展开系数可以表示为
(23) $\hat {x}_j = E\left( {X\left( \delta \right),\varPsi _j \left( \delta \right)} \right) = \int {X\left( \delta \right)\varPsi _j \left( \delta \right)\rho \left( \delta \right)} \text{d}\delta$
等式右侧的计算,可以使用配点法求解,将连续积分问题转化为离散点位置函数值的加权和. 配点和权重需要依据相关变量的分布类型进行选择. 对于均匀分布的随机变量,需要选择 Legendre-Gauss 点和 Gauss 权重. 则相应的积分计算为
(24) $\hat {x}_j = \sum_{m = 1}^Q {X\left( \delta \right)\varPsi _j \left( \delta \right)\tau _m }$
其中,$Q$ 为配点的总个数,相应的正交权重由 $\tau _m $ 表示.
应用混沌多项式可方便得到最优轨迹对应的随机变量的统计信息,这些信息可通过混沌多项式的系数得到,其均值可表示为
(25) $ E\left( {X\left( \delta \right)} \right) = \Big [\sum_{j = 1}^{N_{PC} } {x_j \varPsi _j \left( {\varDelta \left( \omega \right)} \right)} \Big ] =\\ \sum_{j = 1}^{N_{PC} } {\hat {x}_j \Big [\int {\varPsi _j \left( \delta \right)\rho \left( \delta \right)} \text{d}\delta } \Big] = \hat {x}_0 $
(26) $ D\left( {X\left( \delta \right)} \right) = E\left[ { X\left( \delta \right) - E\left( {X\left( \delta \right)} \right)^2 } \right] = \sum_{j = 1}^{N_{PC} } {\hat {x}_j^2 }$
3.2 基于广义混沌多项式的鲁棒轨迹优化
在飞行器再入飞行阶段,存在气动参数扰动等不确定性的作用,若仍然利用基于确定性系统的优化所得到的倾侧角控制律,热流、动压等路径约束将存在违背的情况,从而可能导致发射任务的失败. 因此考虑再入段的气动参数扰动不确定性扰动,本节提出再入段鲁棒轨迹优化方法,通过该方法可降低最优轨迹对扰动的敏感程度,确保优化结果满足所有规定约束.
考虑到非线性最优控制问题的复杂性,这里主要考虑采用状态的均值和标准差近似描述其分布特性. 将传统轨迹优化问题转化为鲁棒轨迹优化问题, 如下
(27) $ \left.\begin{array}{l} \min \ \ J = \bar {\varphi }\left[ {x\left( {t_f } \right)} \right] + \int_{t_0 }^{t_f } {\bar {\psi }\left( {x,\sigma } \right)} \text{d} t \\ {s.t.} \ \ \begin{cases} \dot {x} = f\left( {x,u,t,a} \right) \\ \bar {g}\left( {x,u,t,a} \right) + kg^\delta \left( {x,u,t,a} \right) \leqslant 0 \end{cases} \end{array} \right\}$
式中,$ \mathop{ (\cdot) }\limits^{\_} $ 与 $\left( \cdot \right)^\sigma$ 分别代表变量的均值与标准差,$a$ 为不确定的模型参数,系数 $k$ 描述约束满足情况对动力学模型不确定因素的鲁棒性,$k$ 值越大代表轨迹优化的鲁棒性越强,但最优性损失越大,可以发现求解鲁棒轨迹优化问题的关键是如何描述状态与标准差的变化.
为提高计算效率,本文采用回归法[30 ] 求解式 (20) 中的广义混沌多项式展开系数,首先通过配点法对随机变量 $\delta$ 进行采样,即 $\delta = \{ \delta ^{( 1)},\delta ^{( 2)}, \cdots$, $ \delta ^{\left( {N_S } \right)} \}$. 将优化过程中的 7 个状态变量 $x = [ r;\theta ;\varphi ;V;\gamma ;$ $\psi ;\sigma ]$ 通过混沌多项式展开,并将离散点代入式 (20) 可得
(28) $x_i^j \left( {\delta ^{\left( s \right)}} \right) = \sum_{j = 1}^p {\hat {x}_{ij} } \varPsi _j \left({\delta ^{\left( s \right)}} \right) , \ \ i = 1,2,\cdots , \ \ s = 1,2,\cdots ,N_s$
将式 (28) 代入动力学方程可表示为以下矩阵形式为
(29) $ \left[ \!\!\begin{array}{cccc} {\varPsi _{1} \left( {\delta ^{\left( {1} \right)}} \right)} amp; {\varPsi _{1} \left( {\delta ^{\left( {1} \right)}} \right)} amp; \cdots amp; {\varPsi _p \left( {\delta ^{\left( {1} \right)}} \right)} \\ {\varPsi _{1} \left( {\delta ^{\left( 2 \right)}} \right)} amp; {\varPsi _2 \left( {\delta ^{\left( 2 \right)}} \right)} amp; \cdots amp; {\varPsi _p \left( {\delta ^{\left( 2 \right)}} \right)} \\ \vdots amp; \vdots amp; amp; \vdots \\ {\varPsi _{1} \left( {\delta ^{\left( {N_S } \right)}} \right)} amp; {\varPsi _2 \left( {\delta ^{\left( {N_S } \right)}} \right)} amp; \cdots amp; {\varPsi _p \left( {\delta ^{\left( {N_S } \right)}} \right)} \end{array} \right]\left[ \begin{array}{l} \dot {\hat {x}}_{i1} \\ \dot {\hat {x}}_{i2} \\ \vdots \\ \dot {\hat {x}}_{in} \end{array} \right] =\\ \left[ f_i^{ ( 1 )} \ \ f_i^{ ( 2 )} \ \ \cdots \ \ f_i^{ ( N_S )} \right]^{T} $
可将式 (29) 简写为 ${\pmb A}\dot {\hat {\pmb x}}_i = {\pmb F}_i$,由于采样点的数目大于多项式混沌展开系数的个数,可通过最小二乘法求解
(30) $\dot {\hat {\pmb x}}_i = \left( {{\pmb A}^{T} \ \ {\pmb A}} \right)^{ - 1}{\pmb A}^{T}{\pmb F}_i$
非线性约束函数 ${\pmb g}\left( {{\pmb x}, {\pmb u},t, {\pmb a} }\right)$ 和目标函数 ${\pmb O}\left( {{\pmb x}, {\pmb u},t, {\pmb a}} \right)$ 也可采用类似的方法表示为混沌多项式的展开形式,从而得到相应的展开式系数
(31) $\hat {\pmb g}_i = \left( {{\pmb A}^{T} \ \ {\pmb A}} \right)^{ - 1}{\pmb A}^{T}{\pmb G}_i , \ \ \hat {\pmb o} = \left( {{\pmb A}^{T} \ \ {\pmb A}} \right)^{ - 1}{\pmb A}^{T}{\pmb O}$
各个系数向量计算完成后,可得到各个状态变量、非线性约束函数以及目标函数的均值、方差等统计特性.
4 仿真分析
本节以美国一可重复使用飞行器的再入轨迹优化为例,对第 3 节和第 4 节提出的确定性轨迹优化方法和考虑气动参数扰动条件的随机性轨迹优化方法进行仿真分析验证. 其质量 $m = 104 305$ kg,气动参考面积 $S=391.22$ m$^2$,气动模型如下
(32) $ C_{L} = - 0.041 065 + 0.016 292\alpha + 0.000 260 2\alpha ^2$
(33) $ C_{D} = 0.080 505 - 0.030 26C_{L} + 0.864 95C_{L} ^2$
借鉴航天飞机的程序攻角设计方法,采用典型的二次分段标称攻角剖面,其具体表达形式为
(34) $\alpha = \left\{ \!\!\begin{array}{ll} 40 , & V > 4570 {m/s} \\ 40 - 0.207 05\left( {V - 4570} \right)^2 / 340^2 , & { otherwise} \end{array} \right.$
仿真中暂不考虑飞行时间对轨迹的影响,规定总再入时间 $t_{f} = 1600$ s,离散点总数为 200,为保证计算的效率,设定最高迭代次数为 100 次. 仿真所需参数见表2 . 仿真中,序列凸优化算法中信赖域约束和收敛条件如下
(35) ${\pmb \varDelta} = \left[ {\dfrac{1000}{R_0 },\dfrac{20\pi }{180},\dfrac{20\pi }{180},\dfrac{500}{V_0 },\dfrac{20\pi }{180},\dfrac{20 \pi }{180},\dfrac{20\pi }{180}} \right]^{T}$
(36) ${\pmb\varepsilon } = \left[ {\dfrac{100}{R_0 },\dfrac{0.05\pi }{180},\dfrac{0.05\pi }{180},\dfrac{1}{V_0 },\dfrac{0.05\pi }{180},\dfrac{0.05\pi }{180},\dfrac{ \pi }{180}} \right]^{T}$
本文的仿真均是基于 matlab 环境,调用 Mosek8.0[34 ] 的求解子凸问题的求解器,以初始状态和末端状态的直线为初始参考轨迹,大约迭代 5$\sim$7 次就基 本收敛,说明该方法具有很强的鲁棒性.
4.1 确定性再入轨迹优化结果分析
假设气动参数没有扰动,利用序列凸技术进行再入轨迹优化,由于凸优化具有多项式时间复杂度,且局部最优解即全局最优解等特点,因此该寻优时间比较短,大约为 7 s.若在嵌入式 C 语言环境下,计算时间大概减少数倍,具有在线轨迹计算的 潜力.
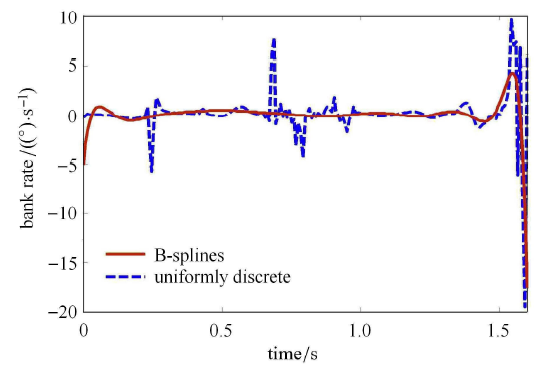
图2 (a) 是优化结果中的速度-高度曲线和热流、动压、过载等路径约束的示意图,在提供再入点与终点连线的轨迹作为初始参考值的情况下,序列凸优化技术也很好地求解出满足各非线性约束的最优轨迹,表明该方法对初值的依赖度较低,鲁棒性较强. 图3 是对控制量分别进行均匀离散和 B 样条曲线离散的寻优结果,可以发现,本文采取的方法有效避免了数值计算中锯 齿化现象,使得寻优结果更为光滑可行.
图3
图3
时间-控制量曲线
Fig. 3
Time-control curve
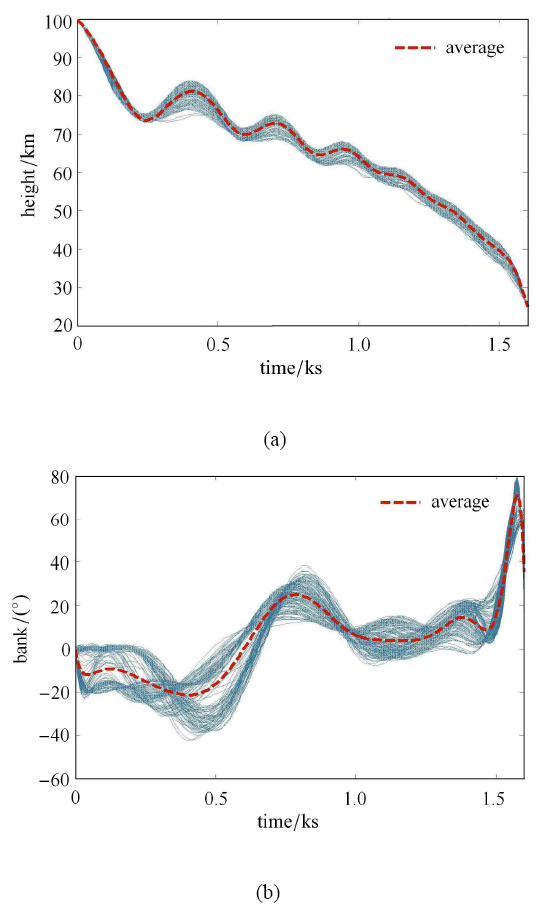
为验证序列凸优化的有效性和快速性,同时为计算状态量的的统计特性,比较广义混沌多项式与蒙特卡洛方法的特点,现对气动参数拉偏,进行 400 次打靶测试,拉偏范围 $K_{a}= \left[ {0.7,1.3} \right]$,$C_{L} =K_{a} C_{L}^0 $,$C_{D} = K_{a} C_{D}^0 $,测试结果如图4 所示.
图4
图4
打靶测试结果
Fig. 4
Results of target test
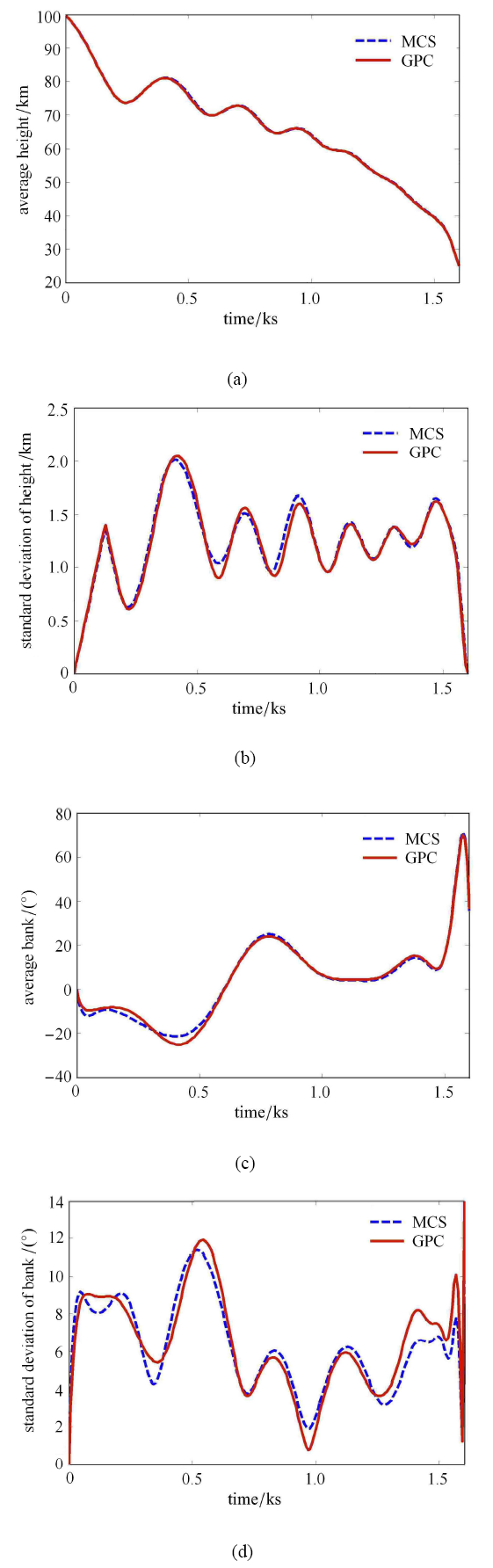
可以看出,序列凸优化可以适应各种拉偏情况,平均耗时 7.14 s 左右,算法本身的鲁棒性较强. 取 8 个 Gauss 配点的数据,通过最小二次回归求解广义混沌多项式的系数. 利用广义多项式混沌 GPC 和蒙特卡洛仿真 MCS 分别计算满足均匀分布的气动力符合系数扰动条件下的优化轨迹各状态变量 的统计特性.下图对比分析了不确定条件下状态变量的均值变化曲线与标准差变化曲线.可以看出,两种方法计算的各状态变量的均值变化曲线基本一致.
由图5 (b) 和图5 (d) 可知,在气动力扰动过程中,各状态变量的标准差均发生剧烈的变化. 其中高度扰动峰值超过 2000 m,倾侧角在飞行过程中也产生了超过 10$^\circ$ 的扰动,说明气动参数的扰动对飞行状态产生了较大的影响.
图5
图5
混沌多项式计算结果
Fig. 5
Results of chaotic polynomial calculation
综合分析两种方法计算所得的统计特性,不难发现广义多项式混沌方法与传统蒙特卡洛仿真方法的计算结果基本一致. 本节利用广义多项式混沌方法运用配点法计算统计特性的过程中,对于一维随机变量设置的配点个数为 8,而蒙特卡洛仿真方法达到收敛精度的采样次数较大,说明广义多项式混沌方法对于计算气动参数扰动条件下状态变量的统计特性具有很大的计算优势.
4.2 考虑气动参数扰动的再入轨迹优化仿真分析
上一小节的仿真结果验证了序列凸优化的快速性和有效性,但是再入过程中如果存在气动参数扰动,若依然利用基于确定性模型的轨迹优化问题所得到的倾侧角控制量,路径约束如热流、动压等将存在违背的情况. 因此本节主要研究在飞行器再入过程中考虑气动参数扰动的轨迹优化问题,力争降低最优轨迹对不确定扰动的敏感程度,提高寻优结果的鲁棒性,从而保证飞行任务的圆满成功.
由式 (20) 知,混沌多项式的复杂度随着展开项的增多而急剧增大,为保证计算效率,本节的优化过程中只考虑 10% 的气动参数扰动,并且基底取一阶 Legendre 多项式,仅取 3 个 Gauss 点的样本值进行展开式的系数计算. 考虑到鲁棒性的要求与控制能力有限的条件,现将最大热流密度调整至 $\dot {Q}_{\max } = 16$ kW/m$^2$,式 (27) 中参数 $k = 1$.
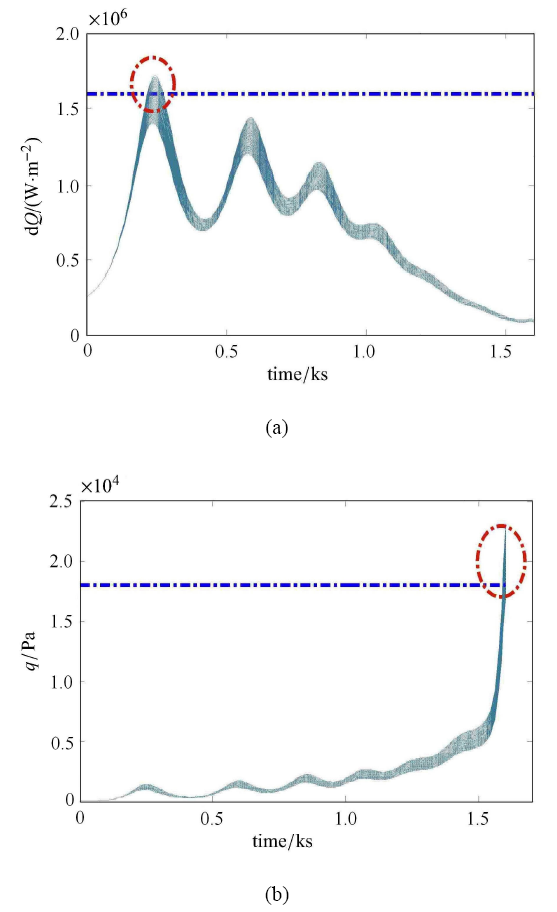
图6 是利用确定性模型下所得到的控制量进行打靶测试所得到热流与动压的结果. 可以发现,确定性模型的优化结果并不能满足所有扰动工况的路径约束,在实际飞行时,可能会使飞行器遭到损坏,导致任务失败.
图6
图6
确定性优化的热流和动压约束
Fig. 6
$\dot {Q}$ and $q$ of the deterministic optimization
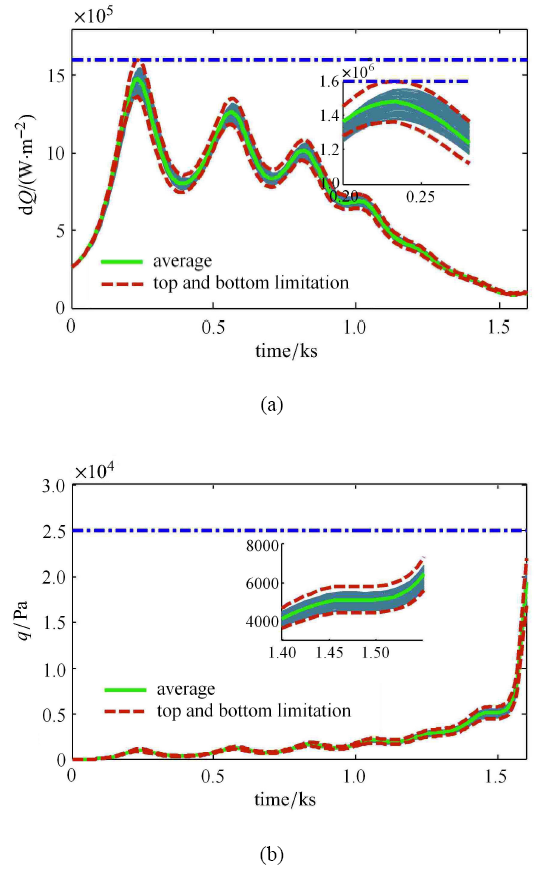
为提高寻优结果的稳定性和鲁棒性,本节利用 3.2 节提出的鲁棒轨迹优化方法进行仿真验证. 在序列凸优化的技术上,充分考虑气动参数的干扰,利用混沌多项式计算得到非线性约束函数的统计特性,在寻优过程中将其包含在内,并将优化所得的控制量进行气动参数拉偏打靶测试,继而得到如图7 的打靶结果.
图7
图7
确定性优化的热流和动压约束
Fig. 7
$\dot {Q}$ and $q$ of the robust optimization
由图7 可知,经打靶测试优化所得的控制量可以满足所有既定工况的路径约束,通过广义混沌多项式所估计的非线性约束函数的统计特性基本符合事实,测试中所有的约束都在估计范围内,这也说明了混沌多项式在描述不确定度传播方面的优势. 图7 中所估计的上下偏差虽然包含所有工况的约束,在一定程度上保证了满足非线性约束的裕度,但估计量仍与真实值存在偏差. 这是由于计算能力的限制,仿真过程中只采用了一阶多项式且采样点仅有 3 个 Gauss 点,计算精度较为有限. 同时需要说明的是,这里只考虑了 10% 的气动参数扰动,且认为该扰动服从均匀分布,虽然已验证了所提出的鲁棒轨迹优化方法的可行性,但若进一步增加其干扰程度,可能会导致无可行解的情况. 另外本次仿真中,取 $k$ 值为 1,$k$值越大,考虑的干扰裕度越大即轨迹优化的鲁棒性越强,但最优性损失越多,在实际应用过程中,需要在最优性和鲁棒性之间作出权衡.
3 结论
本文以考虑气动参数扰动的再入鲁棒轨迹优化设计为主要研究内容,通过广义混沌多项式方法对随机变量的统计特性进行有效估计,同时结合一种改进的序列凸优化技术进行鲁棒轨迹优化设计策略. 轨迹优化过程中以倾侧角的变化率作为控制量,为抑制数值优化过程中的锯齿化现象,采用 B 样条曲线离散控制量,同时增加额外虚拟控制量,通过一种"回溯直线"搜索的方法,提高算法的稳定性、快速性和寻优结果的光滑性. 在考虑气动参数扰动条件的寻优过程中,满足热流、动压等多重约束的同时,降低气动参数扰动对优化结果的影响,提出了基于广义混沌多项式与序列凸优化技术相结合的鲁棒轨迹优化方法. 仿真结果表明,该策略可以有效降低优化结果对气动参数扰动的敏感程度,可以适应既定的所有工况,表现出较强的鲁棒稳定性,具有一定的工程应用价值.
参考文献
View Option
[1]
Richie G . The common aero vehicle: Space delivery system of the future
// AIAA Space Technology Conference and Exposition, Albuquerque, NM , 1999
[本文引用: 1]
[2]
Hermant A . Homotopy algorithm for optimal control problems with a second-order state constraint
Applied Mathematics & Optimization 2010 ,61 (1 ):85 -127
[本文引用: 1]
[3]
Istratie V . Optimal profound entry into atmosphere with minimum heat and Constraints
// AIAA Atmospheric Flight Mechanics Conference and Exhibit , 2001 : 4069
[本文引用: 1]
[4]
Bollino K Oppenheimer M Doman D . Optimal guidance command generation and tracking for reusable launch vehicle reentry
// AIAA Guidance, Navigation, and Control Conference and Exhibit , 2006 : 6691
[5]
黄长强 , 国海峰 , 丁达理 . 高超声速滑翔飞行器轨迹优化与制导综述
宇航学报 , 2014 ,35 (4 ):369 -379
( Huang Changqiang Guo Haifang Ding Dali . A survey of trajectory optimization and guidance for hypersonic gliding vehicle
Journal of Astronautics 2014 ,35 (4 ):369 -379 (in Chinese))
[6]
Rea J . Launch vehicle trajectory optimization using a Legendre pseudo-spectral method
// AIAA Guidance, Navigation, and Control Conference and Exhibit , 2003 : 5640
[本文引用: 1]
[7]
Harpold JC Gavert DE . Space shuttle entry guidance performance results
Journal of Guidance, Control & Dynamics 1983 ,6 (6 ):442 -447
[本文引用: 1]
[8]
Boyd S Vandenberghe L . Convex Optimization . Cambridge : Cambridge University Press , 2004 : 157 -160
[本文引用: 1]
[9]
Nesterov Y Nemirovskii A . Interior-point Polynomial Algorithms in Convex Programming
Society for Industrial and Applied Mathematics Press , 1994 : 102 -137
[本文引用: 1]
[10]
Ploen SR . Convex programming approach to powered descent guidance for mars landing
Journal of Guidance Control & Dynamics 2007 ,30 (5 ):1353 -1366
DOI
URL
[本文引用: 2]
[11]
Aç$\imath$kmese B Carson JM Blackmore L . Lossless convexification of nonconvex control bound and pointing constraints of the soft landing optimal control problem
IEEE Transactions on Control Systems Technology 2013 ,21 (6 ):2104 -2113
DOI
URL
[本文引用: 1]
Planetary soft landing is one of the benchmark problems of optimal control theory and is gaining renewed interest due to the increased focus on the exploration of planets in the solar system, such as Mars. The soft landing problem with all relevant constraints can be posed as a finite-horizon optimal control problem with state and control constraints. The real-time generation of fuel-optimal paths to a prescribed location on a planet's surface is a challenging problem due to the constraints on the fuel, the control inputs, and the states. The main difficulty in solving this constrained problem is the existence of nonconvex constraints on the control input, which are due to a nonzero lower bound on the control input magnitude and a nonconvex constraint on its direction. This paper introduces a convexification of the control constraints that is proven to be lossless; i.e., an optimal solution of the soft landing problem can be obtained via solution of the proposed convex relaxation of the problem. The lossless convexification enables the use of interior point methods of convex optimization to obtain optimal solutions of the original nonconvex optimal control problem.
[12]
Harris MW Aç$\imath$kmese B . Lossless convexification of non-convex optimal control problems for state constrained linear systems
Automatica 2014 ,50 (9 ):2304 -2311
DOI
URL
[本文引用: 1]
This paper analyzes a class of finite horizon optimal control problems with mixed non-convex and convex control constraints and linear state constraints. A convex relaxation of the problem is proposed, and it is proved that a solution of the relaxed problem is also a solution of the original problem. This process is called lossless convexification, and its generalization for problems with state constraints is the primary contribution of the paper. Doing so enables the use of interior point methods of convex optimization to obtain global optimal solutions of the original non-convex problem. The approach is also demonstrated on example problems. (C) 2014 Elsevier Ltd.
[13]
Harris MW Aç$\imath$kmese B . Lossless convexification for a class of optimal control problems with linear state constraints
// Decision and Control IEEE , 2013 : 7113 -7118
[本文引用: 1]
[14]
Scharf DP Regehr MW Vaughan GM , et al . ADAPT demonstrations of onboard large-divert Guidance with a VTVL rocket
// Aerospace Conference IEEE , 2014
[本文引用: 1]
[15]
Liu X Shen Z Lu P . Entry trajectory optimization by second-order cone programming
Journal of Guidance Control & Dynamics 2015 ,39 (2 ):227 -241
DOI
URL
[本文引用: 3]
[16]
Wang Z Grant MJ . Constrained trajectory optimization for planetary entry via sequential convex programming
// AIAA Atmospheric Flight Mechanics Conference , 2016 : 3241
[本文引用: 1]
[17]
林晓辉 , 于文进 . 基于凸优化理论的含约束月球定点着陆轨道优化
宇航学报 , 2013 ,34 (7 ):901 -908
DOI
URL
[本文引用: 1]
针对月球精确定点软着陆问题,考虑导航及障碍检测敏感器视场约束及制动发动机推力大小约束,对月球动力下降段轨道优化方法进行了研究。首先建立了含约束条件的三维定点软着陆轨道优化问题模型,根据庞德亚金极小值原理推导了最优推力开关方程,并给出了推力奇异区间不存在的证明。针对优化模型中的复杂非线性约束,引入凸优化理论将问题转化为二阶锥优化问题,并采用内点法求解了最优标称轨迹。最后给出了月球软着陆制动段、接近段的仿真结果,验证了该着陆轨道优化方法的有效性。
( Lin Xiaohui Yu Wenjin . Constrained trajectory optimization for lunar pin point landing based on convex optimization theory
Journal of Astronautics 2013 ,34 (7 ):901 -908 (in Chinese))
DOI
URL
[本文引用: 1]
Taking account of the navigation and hazard detecting sensor FOV (Filed of View) constraint and the thrust constraint, the trajectory optimization algorithm for lunar pin point landing is studied in this paper. Firstly, a three dimensional trajectory optimization model is established, the optimal thrust switch function is given out according to the Pontryagin maximum principle. Also, the singular interval of thrust is proved to be nonexistent. Then the nonlinear constrained optimal control problem is transformed into a second order cone parameter optimization problem through convex transformation and discretization. In the meanwhile, the parameter optimization problem is solved by using interior point method. The feasibility and validity of the algorithm are verified by simulation results of different scenarios.
[18]
樊朋飞 , 郭云鹤 , 凡永华 等 . HGV 平衡滑翔式轨迹可达区域计算方法研究
计算机测量与控制 , 2019 ,27 (5 ):136 -140
( Fan Pengfei Guo Yunhe Fan Yonghua , et al . Footprint calculation of HGV with equilibrium gliding trajectory
Computer Measurement and Control 2019 ,27 (5 ):136 -140 (in Chinese))
[19]
邵楠 , 闫晓东 . 火箭垂直回收多阶段最优轨迹规划方法
宇航学报 , 2019 ,40 (10 ):1187 -1196
( Shao Nan Yan Xiaodong . Multi-stage trajectory optimization for vertical pin-point landing of a reusable launch vehicle
Journal of Astronautics 2014 ,35 (4 ):369 -379 (in Chinese))
DOI
URL
Aiming at the trajectory optimization and guidance (TOG) of a hypersonic gliding vehicle considering under the condition of multi constrains, the methods of TOG are divided into off line TOG and on line TOG, and the prospect is brought forward. The mathematical models with stochastic disturbances of the TOG for the hypersonic gliding vehicle are first built. The off line TOG is summarized from two sides of determinacy and robustness, according to whether considering stochastic disturbances or not. The on line TOG is classified as reference guidance and predictive guidance, and the principle of the reference guidance is reference trajectory on line generation and reference trajectory tracking. Finally, it is pointed out that the future research of the TOG should be enhanced at the model, calculational efficiency, multitask, and high accuracy guidance and so on.
[20]
李俊 , 江振宇 . 一种高超声速滑翔再入在线轨迹规划算法
北京航空航天大学学报 , 2020 ,46 (3 ):579 -587
[本文引用: 1]
( Li Jun Jiang Zhenyu . Online trajectory planning algorithm for hypersonic glide re-entry problem
Journal of Beijing University of Aeronautics and Astronautics 2020 ,46 (3 ):579 -587 (in Chinese))
[本文引用: 1]
[21]
Rangaraj R Chaudhuri A Gupta S . The use of polynomial chaos for parameter identification from measurements in nonlinear dynamical systems
Zamm Journal of Applied Mathematics & Mechanics 2015 ,12 (1 ):1372 -1392
[本文引用: 1]
[22]
Xiong F Xiong Y Xue B . Trajectory optimization under uncertainty based on polynomial chaos expansion
// AIAA Guidance, Navigation, and Control Conference, Kissimmee, Florida , 2015
[本文引用: 1]
[23]
Li X Nair PB Zhang ZG , et al . Aircraft robust trajectory optimization using nonintrusive polynomial chaos
Journal of Aircraft 2014 ,51 (51 ):1592 -1603
DOI
URL
[本文引用: 1]
[24]
Grant MJ Bolender MA . Rapid, robust trajectory design using indirect optimization methods
// AIAA Atmospheric Flight Mechanics Conference, Dallas, USA , 2015
[本文引用: 2]
[25]
Yu Z Zhao Z Cui P . An observability-based trajectory optimization considering disturbance for atmospheric entry
// AIAA Guidance, Navigation, and Control Conference, California, USA , 2016
[26]
Jones BA Doostan A Born GH . Nonlinear propagation of orbit uncertainty using non-intrusive polynomial chaos
Journal of Guidance Control & Dynamics 2013 ,36 (2 ):430 -444
DOI
URL
[本文引用: 1]
[27]
Xiu D Karniadakis GE . The Wiener-Askey polynomial chaos for stochastic differential equations
SIAM Journal on Scientific Computing 2002 ,24 (2 ):619 -644
DOI
URL
[本文引用: 1]
[28]
Eldred MS Webster CG Constantine P . Evaluation of non-intrusive approaches for Wiener-Askey generalized polynomial chaos
// Structural Dynamical and Materials Conference , 2008
[本文引用: 1]
[29]
Cottrill GC . Hybrid solution of stochastic optimal control problems using Gauss pseudospectral method and generalized polynomial chaos algorithms
Air Force Institute of Technology . 2012
[本文引用: 1]
[30]
Tao J Zeng X Cai W , et al . Stochastic sparse-grid collocation algorithm for periodic steady-state analysis of nonlinear system with process variations
// Proceedings of the 2007 Asia and South Pacific Design Automation Conference , 2007
[本文引用: 2]
[31]
Gottlieb D Xiu D . Galerkin method for wave equations with uncertain coefficients
Communications in Computational Physics 2008 ,3 (2 ):505 -518
[本文引用: 1]
[32]
Knio OM Najm HN Ghanem RG . A stochastic projection method for fluid flow: I. Basic formulation
Journal of computational Physics 2001 ,173 (2 ):481 -511
DOI
URL
[本文引用: 1]
[33]
熊芬芬 , 杨树兴 , 刘宇 等 . 工程概率不确定性分析方法 . 北京 : 科学出版社 , 2015
( Xiong Fenfen Yang Shuxing Liu Yu , et al . Engineering Probability Uncertainty Analysis Method . Beijing : Science Press , 2015 (in Chinese))
[34]
Andersen ED Andersen KD . The MOSEK interior point optimizer for linear programming: An implementation of the homogeneous algorithm
// High Performance Optimization, Springer, Boston, MA , 2000 : 197 -232
[本文引用: 1]
The common aero vehicle: Space delivery system of the future
1
1999
... 再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行,期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束,使其轨迹规划问题成为了一个极富挑战性的问题,引起了国内外许多学者的研究兴趣[1 ] . 传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2 ] 等优化算法,两者或因巨大的计算量,或因不易收敛,都只适合离线的轨迹优化[3 -6 ] . 虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7 ] ,曾取得过辉煌的成绩,但该方法的简化过程限制了飞行器的机动能力. 总的来说,基于极大值原理的直接法推导最优解的过程较为繁琐,对于复杂问题几乎无法得到解析解;以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦;而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题,需反复交叉、变异、迭代,计算效率较低. ...
Homotopy algorithm for optimal control problems with a second-order state constraint
1
2010
... 再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行,期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束,使其轨迹规划问题成为了一个极富挑战性的问题,引起了国内外许多学者的研究兴趣[1 ] . 传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2 ] 等优化算法,两者或因巨大的计算量,或因不易收敛,都只适合离线的轨迹优化[3 -6 ] . 虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7 ] ,曾取得过辉煌的成绩,但该方法的简化过程限制了飞行器的机动能力. 总的来说,基于极大值原理的直接法推导最优解的过程较为繁琐,对于复杂问题几乎无法得到解析解;以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦;而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题,需反复交叉、变异、迭代,计算效率较低. ...
Optimal profound entry into atmosphere with minimum heat and Constraints
1
2001
... 再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行,期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束,使其轨迹规划问题成为了一个极富挑战性的问题,引起了国内外许多学者的研究兴趣[1 ] . 传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2 ] 等优化算法,两者或因巨大的计算量,或因不易收敛,都只适合离线的轨迹优化[3 -6 ] . 虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7 ] ,曾取得过辉煌的成绩,但该方法的简化过程限制了飞行器的机动能力. 总的来说,基于极大值原理的直接法推导最优解的过程较为繁琐,对于复杂问题几乎无法得到解析解;以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦;而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题,需反复交叉、变异、迭代,计算效率较低. ...
Optimal guidance command generation and tracking for reusable launch vehicle reentry
0
2006
高超声速滑翔飞行器轨迹优化与制导综述
0
2014
高超声速滑翔飞行器轨迹优化与制导综述
0
2014
Launch vehicle trajectory optimization using a Legendre pseudo-spectral method
1
2003
... 再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行,期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束,使其轨迹规划问题成为了一个极富挑战性的问题,引起了国内外许多学者的研究兴趣[1 ] . 传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2 ] 等优化算法,两者或因巨大的计算量,或因不易收敛,都只适合离线的轨迹优化[3 -6 ] . 虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7 ] ,曾取得过辉煌的成绩,但该方法的简化过程限制了飞行器的机动能力. 总的来说,基于极大值原理的直接法推导最优解的过程较为繁琐,对于复杂问题几乎无法得到解析解;以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦;而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题,需反复交叉、变异、迭代,计算效率较低. ...
Space shuttle entry guidance performance results
1
1983
... 再入飞行器利用气动力在大气层内进行长时间、远距离、高马赫数的飞行,期间会受到极其复杂的非线性热流、动压、过载约束以及终端的高精度约束,使其轨迹规划问题成为了一个极富挑战性的问题,引起了国内外许多学者的研究兴趣[1 ] . 传统的再入弹道优化设计方法主要有基于极大值原理的间接法和基于非线性规划理论的直接法[2 ] 等优化算法,两者或因巨大的计算量,或因不易收敛,都只适合离线的轨迹优化[3 -6 ] . 虽然航天飞机所采用的基于阻力加速度剖面的轨迹规划[7 ] ,曾取得过辉煌的成绩,但该方法的简化过程限制了飞行器的机动能力. 总的来说,基于极大值原理的直接法推导最优解的过程较为繁琐,对于复杂问题几乎无法得到解析解;以伪谱法为代表的直接法对多阶段等复杂问题的建模过程比较麻烦;而以粒子群法等现代启发式算法对于计算量大、优化参数多的复杂模型优化问题,需反复交叉、变异、迭代,计算效率较低. ...
1
2004
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
Interior-point Polynomial Algorithms in Convex Programming
1
1994
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
Convex programming approach to powered descent guidance for mars landing
2
2007
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
... [10 -11 ]针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
Lossless convexification of nonconvex control bound and pointing constraints of the soft landing optimal control problem
1
2013
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
Lossless convexification of non-convex optimal control problems for state constrained linear systems
1
2014
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
Lossless convexification for a class of optimal control problems with linear state constraints
1
2013
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
ADAPT demonstrations of onboard large-divert Guidance with a VTVL rocket
1
2014
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
Entry trajectory optimization by second-order cone programming
3
2015
... 强耦合性、强非线性决定了再入轨迹规划问题难以直接求解,通常需要采用一系列易于求解的子问题逼近原问题. 凸优化具有多项式复杂度,局部最优解即全局最优解等特点,加上独特的内点法,使得数学上所有易解的规划问题几乎都指向了凸优化[8 -9 ] . 美国加州理工大学的Acikmese 等[10 -15 ] 最早开展了基于凸优化的轨迹优化研究.Acikmese 等[10 -11 ] 针对火星软着陆问题最先提出了无损凸化 (losslessconvexification) 的概念,使用松弛的凸形式约束代替原非凸约束,将原问题转化为凸问题,并利用极大值原理对二者的等价性进行了证明,保证转化过程的"无损性".针对具有非凸约束的一般形式线性系统最优控制问题,Acikmese 等[12 -13 ] 讨论了无损凸化的方法,对原问题与凸优化问题的等价性进行了证明. 相关理论研究成果已经在 NASA 的 G-FOLD 飞行试验中得到了成功应用[14 ] . ...
... 近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
... [15 ]在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
Constrained trajectory optimization for planetary entry via sequential convex programming
1
2016
... 近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
基于凸优化理论的含约束月球定点着陆轨道优化
1
2013
... 近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
基于凸优化理论的含约束月球定点着陆轨道优化
1
2013
... 近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
HGV 平衡滑翔式轨迹可达区域计算方法研究
0
2019
HGV 平衡滑翔式轨迹可达区域计算方法研究
0
2019
一种高超声速滑翔再入在线轨迹规划算法
1
2020
... 近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
一种高超声速滑翔再入在线轨迹规划算法
1
2020
... 近年来,许多学者都在尝试将凸优化引入到再入轨迹规划问题中来[15 -20 ] .Liu 等[15 ] 在给定攻角剖面的条件下,通过变量替换得到以能量为自变量的动力学方程,采用序列凸优化解决了再入轨迹优化问题.Wang 等[16 ] 则以时间为自变量并以倾侧角的导数为控制量,求解了终端时间固定的轨迹规划.现有的基于凸优化的滑翔再入轨迹规划方法基本上都直接使用了小扰动线性化来处理微分方程的非线性同时相应的添加了信赖域约束来保证子问题向原问题逼近.虽然目前的序列凸优化技术简单可行,寻优时间较传统直接法有一定优势,但是在实际仿真计算中还会遇到以下问题: (1)反复迭代的序列凸优化技术本质上还是牛顿法,其收敛范围小,并且在迭代后期可能会出现类似与牛顿法的 Maratos 效应,导致迭代寻优失败; (2)当初值给的比较粗糙时,子问题的可行性将是一个严峻的问题,可能出现"伪不可行"[17 ] (artificialinfeasibility),的情况使得迭代失败. ...
The use of polynomial chaos for parameter identification from measurements in nonlinear dynamical systems
1
2015
... 目前鲁棒轨迹优化方法在高超声速领域应用较少. Rangaraj 等[21 ] 利用多项式混沌方法设计了一种改进粒子滤波器,与传统的粒子滤波器相比,计算效率大大提高. Xiong 等[22 ] 针对一类具有不确定性的轨迹优化问题,将不确定的路径约束使用多项式混沌方法表示为均值和方差的约束,提高了设计效率. Li 等[23 ] 设计了一种将不确定约束转化为确定性优化的非侵入的多项式混沌飞行轨迹优化方法. Michael 等[24 ] 对直接法进行改进,提出了一种快速鲁棒轨迹优化方法. 此外结合高斯伪谱法和多项式混沌理论的鲁棒轨迹优化方法也成为研究的热点[24 -26 ] . ...
Trajectory optimization under uncertainty based on polynomial chaos expansion
1
2015
... 目前鲁棒轨迹优化方法在高超声速领域应用较少. Rangaraj 等[21 ] 利用多项式混沌方法设计了一种改进粒子滤波器,与传统的粒子滤波器相比,计算效率大大提高. Xiong 等[22 ] 针对一类具有不确定性的轨迹优化问题,将不确定的路径约束使用多项式混沌方法表示为均值和方差的约束,提高了设计效率. Li 等[23 ] 设计了一种将不确定约束转化为确定性优化的非侵入的多项式混沌飞行轨迹优化方法. Michael 等[24 ] 对直接法进行改进,提出了一种快速鲁棒轨迹优化方法. 此外结合高斯伪谱法和多项式混沌理论的鲁棒轨迹优化方法也成为研究的热点[24 -26 ] . ...
Aircraft robust trajectory optimization using nonintrusive polynomial chaos
1
2014
... 目前鲁棒轨迹优化方法在高超声速领域应用较少. Rangaraj 等[21 ] 利用多项式混沌方法设计了一种改进粒子滤波器,与传统的粒子滤波器相比,计算效率大大提高. Xiong 等[22 ] 针对一类具有不确定性的轨迹优化问题,将不确定的路径约束使用多项式混沌方法表示为均值和方差的约束,提高了设计效率. Li 等[23 ] 设计了一种将不确定约束转化为确定性优化的非侵入的多项式混沌飞行轨迹优化方法. Michael 等[24 ] 对直接法进行改进,提出了一种快速鲁棒轨迹优化方法. 此外结合高斯伪谱法和多项式混沌理论的鲁棒轨迹优化方法也成为研究的热点[24 -26 ] . ...
Rapid, robust trajectory design using indirect optimization methods
2
2015
... 目前鲁棒轨迹优化方法在高超声速领域应用较少. Rangaraj 等[21 ] 利用多项式混沌方法设计了一种改进粒子滤波器,与传统的粒子滤波器相比,计算效率大大提高. Xiong 等[22 ] 针对一类具有不确定性的轨迹优化问题,将不确定的路径约束使用多项式混沌方法表示为均值和方差的约束,提高了设计效率. Li 等[23 ] 设计了一种将不确定约束转化为确定性优化的非侵入的多项式混沌飞行轨迹优化方法. Michael 等[24 ] 对直接法进行改进,提出了一种快速鲁棒轨迹优化方法. 此外结合高斯伪谱法和多项式混沌理论的鲁棒轨迹优化方法也成为研究的热点[24 -26 ] . ...
... [24 -26 ]. ...
An observability-based trajectory optimization considering disturbance for atmospheric entry
0
2016
Nonlinear propagation of orbit uncertainty using non-intrusive polynomial chaos
1
2013
... 目前鲁棒轨迹优化方法在高超声速领域应用较少. Rangaraj 等[21 ] 利用多项式混沌方法设计了一种改进粒子滤波器,与传统的粒子滤波器相比,计算效率大大提高. Xiong 等[22 ] 针对一类具有不确定性的轨迹优化问题,将不确定的路径约束使用多项式混沌方法表示为均值和方差的约束,提高了设计效率. Li 等[23 ] 设计了一种将不确定约束转化为确定性优化的非侵入的多项式混沌飞行轨迹优化方法. Michael 等[24 ] 对直接法进行改进,提出了一种快速鲁棒轨迹优化方法. 此外结合高斯伪谱法和多项式混沌理论的鲁棒轨迹优化方法也成为研究的热点[24 -26 ] . ...
The Wiener-Askey polynomial chaos for stochastic differential equations
1
2002
... 混沌多项式理论的基本思想是利用一系列特定分布的随机变量的正交多项式对随机过程与扰动进行逼近[27 -29 ] . 多项式混沌方法能够用于多种随机模型的求解过程,如集成电路的响应分析[30 ] 、不同类型流体问题研究[31 -32 ] 以及其他问题的研究中. ...
Evaluation of non-intrusive approaches for Wiener-Askey generalized polynomial chaos
1
2008
... 对于分布函数或者概率密度已知的随机变量,式中的系数为确定值. 多项式的选择依赖于随机变量的概率密度函数,根据 Askey 法则,对于不同概率密度函数,存在不同的最优多项式,具体对应形式如表1 所示[28 ] . ...
Hybrid solution of stochastic optimal control problems using Gauss pseudospectral method and generalized polynomial chaos algorithms
1
2012
... 混沌多项式理论的基本思想是利用一系列特定分布的随机变量的正交多项式对随机过程与扰动进行逼近[27 -29 ] . 多项式混沌方法能够用于多种随机模型的求解过程,如集成电路的响应分析[30 ] 、不同类型流体问题研究[31 -32 ] 以及其他问题的研究中. ...
Stochastic sparse-grid collocation algorithm for periodic steady-state analysis of nonlinear system with process variations
2
2007
... 混沌多项式理论的基本思想是利用一系列特定分布的随机变量的正交多项式对随机过程与扰动进行逼近[27 -29 ] . 多项式混沌方法能够用于多种随机模型的求解过程,如集成电路的响应分析[30 ] 、不同类型流体问题研究[31 -32 ] 以及其他问题的研究中. ...
... 为提高计算效率,本文采用回归法[30 ] 求解式 (20) 中的广义混沌多项式展开系数,首先通过配点法对随机变量 $\delta$ 进行采样,即 $\delta = \{ \delta ^{( 1)},\delta ^{( 2)}, \cdots$, $ \delta ^{\left( {N_S } \right)} \}$. 将优化过程中的 7 个状态变量 $x = [ r;\theta ;\varphi ;V;\gamma ;$ $\psi ;\sigma ]$ 通过混沌多项式展开,并将离散点代入式 (20) 可得 ...
Galerkin method for wave equations with uncertain coefficients
1
2008
... 混沌多项式理论的基本思想是利用一系列特定分布的随机变量的正交多项式对随机过程与扰动进行逼近[27 -29 ] . 多项式混沌方法能够用于多种随机模型的求解过程,如集成电路的响应分析[30 ] 、不同类型流体问题研究[31 -32 ] 以及其他问题的研究中. ...
A stochastic projection method for fluid flow: I. Basic formulation
1
2001
... 混沌多项式理论的基本思想是利用一系列特定分布的随机变量的正交多项式对随机过程与扰动进行逼近[27 -29 ] . 多项式混沌方法能够用于多种随机模型的求解过程,如集成电路的响应分析[30 ] 、不同类型流体问题研究[31 -32 ] 以及其他问题的研究中. ...
The MOSEK interior point optimizer for linear programming: An implementation of the homogeneous algorithm
1
2000
... 本文的仿真均是基于 matlab 环境,调用 Mosek8.0[34 ] 的求解子凸问题的求解器,以初始状态和末端状态的直线为初始参考轨迹,大约迭代 5$\sim$7 次就基 本收敛,说明该方法具有很强的鲁棒性. ...