引言
近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题.
航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取.
逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差.
追踪器的追踪策略(主要体现为追踪制导率)同样是追逃问题的关键因素,然而本文主要研究逃逸器的规避策略, 因此采用经典的比例导引律(proportional navigation)作为追踪器的制导率.比例导引律具有简单、高效而且易于工程实现的特点,广泛应用于导弹拦截、空间交会问题[26 -28 ] .本文主要研究在追踪器采用比例导引律接近逃逸器, 追逃双方信息不透明的情况下,逃逸器基于当前统计模型自适应滤波算法对追踪器状态进行滤波估计,同时最大化视线转率以降低追踪器制导率作用的航天器主动机动规避策略.
1 机动目标滤波算法
1.1 相对导航观测模型
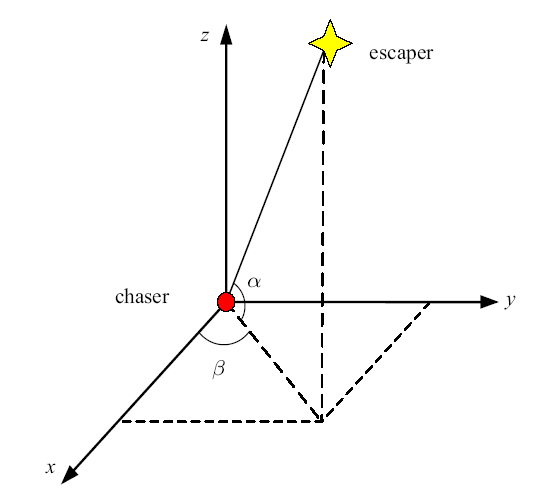
由于追逃双方采用相同的机动目标滤波算法获取相对状态, 因此本文以逃逸器为例进行说明. 以逃逸器质心为原点建立VVLH相对导航坐标系$O_c$-$xyz$, 其中$O_c$-$x$轴指向逃逸器V-bar方向, $O_c$-$y$轴指向逃逸器$-$H-bar方向, $O_c$-$z$轴指向逃逸器$-$R-bar方向.相对导航测量量为相对距离和相对角位置. 在VVLH坐标系中对相对角位置进行定义,如图1 所示, 定义追踪器相对于逃逸器的视线方向与导航坐标系中$xy$平面的夹角为俯仰角$\alpha \in(-{\pi}/{2} ,{\pi}/{2})$, 视线方向在$xy$平面的投影与$x$轴方向的夹角(从$x$轴开始沿逆时针方向度量)为方位角$\beta\in (-\pi ,\pi)$.
图1
图1
相对导航坐标系
Fig. 1
Relative navigation coordinate system
在上述定义下, 逃逸器对追踪器进行观测可得观测方程为
(1) $Z=\left[ {\begin{array}{l} r \\ \alpha \\ \beta \\ \end{array}} \right]=h(X)=\left[ {\begin{array}{l} \sqrt {x^2+y^2+z^2} \\ \tan ^{-1}\dfrac{z}{\sqrt {x^2+y^2} } \\ \tan ^{-1}\dfrac{y}{x} \\ \end{array}} \right]$
其中, $X$为位置、速度和加速度等状态变量, $X=[x,y,z,v_x ,v_y ,v_z ,a_x ,a_y,a_z ]^{T}$, 对应的观测敏感性矩阵为
(2) $H=\frac{\partial h(X)}{\partial X^{T}}= \begin{bmatrix} h_{11} & h_{12} & h_{13} & \cr h_{21} & h_{22} & h_{23} & {\bf0}_{3\times 6} \cr h_{31} & h_{32} & h_{33} & \cr \end{bmatrix}$
$ h_{11} =\dfrac{x}{\sqrt {x^2+y^2+z^2} } $
$ h_{12} =\dfrac{y}{\sqrt {x^2+y^2+z^2} }$
$ h_{13} =\dfrac{z}{\sqrt {x^2+y^2+z^2} } $
$ h_{21} =-\dfrac{xz}{\sqrt {x^2+y^2} \left( {x^2+y^2+z^2} \right)} $
$ h_{22} =-\dfrac{yz}{\sqrt {x^2+y^2} \left( {x^2+y^2+z^2} \right)} $
$ h_{23} =\dfrac{\sqrt {x^2+y^2} }{x^2+y^2+z^2}$
$ h_{31} =-\dfrac{y}{x^2+y^2}$
$ h_{32} =\dfrac{x}{x^2+y^2}$
1.2 基于当前统计模型的自适应滤波算法
逃逸器对追踪器的跟踪滤波是空间三维过程, 为便于表达与论述, 以$x$方向为例进行公式推导. 考虑加速度均值非零的时间相关模型,$x$方向的动力学方程为
(3) $\dot{{a}}_x (t)=-\alpha _x a_x (t)+\alpha _x \bar{{a}}_x +\omega _x (t)$
其中$\alpha _x $ 为根据经验设定的机动频率. 令$X_x (t)=\left[{x(t)} \ \ {v_x (t)} \ \ {a_x (t)} \right]^{T}$, 根据式(3)建立滤波状态方程如下
(4) $\dot{{X}}_x (t)=A_x X_x (t)+B_x F_x +B_x G_x (t)$
其中, $A_x =\left( {{\begin{array}{c@{\ \ }c@{\ \ }c} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & {-\alpha _x } \\ \end{array} }} \right)$, $B_x =\left( {{\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} }} \right)$, $F_x =\alpha _x \bar{{a}}_x $, $G_x (t)=\omega _x (t)$. 设采样周期为$\Delta t$, 求解上述方程
$\varPhi _x (\Delta t)={e}^{A_x \Delta t}$
$U_x (\Delta t)=(\int_{k \Delta t}^{(k+1)\Delta t} {{e}^{[(k+1)\Delta t-\tau ]A_x }} {d}\tau )B_x F_x$
$W_x (k+1,k)=\int_{k \Delta t}^{(k+1)\Delta t} {{e}^{[(k+1)\Delta t-\tau ]A_x }B_x G_x (\tau )} {d}\tau$
令$X_x (k)=[x(k),v_x (k),a_x (k)]^{T}$,可得离散状态方程为
(5) $X_x (k+1)=\varPhi _x (k+1,k)X_x (k)+U_x (k)F_x +W_x (k+1,k)$
$\varPhi _x (k+1,k)=\left( {{\begin{array}{c@{\quad }c@{\quad }c} 1 & {\Delta t} & {\dfrac{-1+\alpha _x \Delta t+{e}^{-\alpha _x \Delta t}}{\alpha _x ^2}} \\ 0 & 1 & {\dfrac{1-{e}^{-\alpha _x \Delta t}}{\alpha _x }} \\ 0 & 0 & {{e}^{-\alpha _x \Delta t}} \\ \end{array} }} \right)$
$U_x (k)=\left( {{\begin{array}{*{20}c} {\dfrac{\bar{{a}}_x \left[ {2-2{e}^{-\alpha _x \Delta t}+\alpha _x \Delta t\left( {-2+\alpha _x \Delta t} \right)} \right]}{2\alpha _x ^2}}\\ {\dfrac{\bar{{a}}_x \left( {-1+{e}^{-\alpha _x \Delta t}+\alpha _x \Delta t} \right)}{\alpha _x }} \\ {\bar{{a}}_x -\bar{{a}}_x {e}^{-\alpha _x \Delta t}} \\ \end{array} }} \right)$
令$N_x (\Delta t)={e}^{[(k+1)\Delta t-\tau ]A_x }B_x$, 则$W_x (k)=\int_{k \Delta t}^{(k+1)\Delta t}N_x(\tau )$ $G_x (\tau ) {d}\tau $, $W_x (k)$为离散时间白噪声序列, 即$E[W_x (k)$ $W_x^{T}(k+j)]=0\ (\forall j\ne 0)$. 由噪声$W_x (k)$可求得系统误差协方差矩阵为
(6) $Q_x (k)=E[W_x (k)W_x^{T} (k)]=\\ E\Bigg[\int_{k \Delta t}^{(k+1)\Delta t} \int_{k \Delta t}^{(k+1)\Delta t} N_x (\tau )G_x (\tau )G_x^{T} (s)\cdot\\ N_x^{T} (s) {d}\tau {d}s\Bigg] =[q_{ij} ]_{3\times 3}$
$Q_x (k)=[q_{ij} ]_{3\times 3}$的具体表达式限于篇幅不再详细给出.
根据当前统计模型的意义, 将$a(k)$在滤波流程中的一步预测值$a(k$+1$\vert k)$看作在$k\Delta t$ 时刻瞬时的当前加速度, 即随机机动加速度的均值,便可得到加速度的均值自适应算法, 即设$\bar{{a}}_x =a_x (k+1\vert k)$. 此时,将加速度的瞬时均值$\bar{{a}}_x $代入卡尔曼滤波公式$X_x (k+1\vert k)=\varPhi _x(k+1,k)X_x (k\vert k)+U_x (k)$, 便可对状态转移矩阵$\varPhi _x (k+1,k)$进行化简,得到均值自适应的状态转移矩阵
(7) $\varPhi _{x1} (k+1,k)=\left( {{\begin{array}{c@{\quad }c@{\quad }c} 1 & {\Delta t} & {\dfrac{\Delta t^2}{2}} \\ 0 & 1 & {\Delta t} \\ 0 & 0 & 1 \\ \end{array} }} \right)$
此时, 状态转移方程简化为$X_x (k+1\vert k)=\varPhi _{x1} (k+1,$ $k)X_x (k\vert k)$.
考虑$y$与$z$方向时, 公式推导是类似的, 注意此时$X(t)=[x,y,z,v_x ,v_y ,v_z ,a_x ,a_y,a_z ]^{T}$, $F=[\alpha _x \bar{{a}}_x ,\alpha _y \bar{{a}}_y ,$ $\alpha_z \bar{{a}}_z ]^{T}$, $G(t)=[\omega _x (t),\omega _y (t),\omega _z(t)]^{T}$,加速度均值$\bar{{a}}$仍然为滤波流程中的一步预测值$a$ ($k+1\vert k$).按照同样的步骤进行积分即可. 值得注意的是, 此时系统误差协方差矩阵$Q$ $(k)$的推导为
(8) $\left.\begin{array}{l} Q(k)=E[W(k)W^{T}(k)]=E\Bigg[\int_{k \Delta t}^{(k+1)\Delta t} \int_{k \Delta t}^{(k+1)\Delta t} \\ N(\tau )G(\tau )G^{T}(s) N^{T}(s) {d}\tau {d}s\Bigg] =\\ \int_{k \Delta t}^{(k+1)\Delta t} {\int_{k \Delta t}^{(k+1)\Delta t} {N(\tau )} }\ \ \cdot \\ E\left[ \left( \begin{array}{*{20}c} {\omega _x (\tau )} \\ {\omega _y (\tau )} \\ {\omega _z (\tau )} \\ \end{array} \right)\left( {{\begin{array}{*{20}c} {\omega _x (s)} & {\omega _y (s)} & {\omega _z (s)} \\ \end{array} }} \right) \right]N^{T}(s){d}\tau {d}s =\\ \int_{k \Delta t}^{(k+1)\Delta t} \int_{k \Delta t}^{(k+1)\Delta t} {N(\tau )\left( {{\begin{array}{*{20}c} {\sigma _{\omega x}^2 } & 0 & 0 \\ 0 & {\sigma _{\omega y}^2 } & 0 \\ 0 & 0 & {\sigma _{\omega z}^2 } \\ \end{array} }} \right)} \\ \delta (\tau -s)N^{T}(s){d}\tau {d}s =\\ \int_{k \Delta t}^{(k+1)\Delta t} N(\tau)\left(\begin{array}{*{20}c} {\sigma _{\omega x}^2 } & 0 & 0 \\ 0 & {\sigma _{\omega y}^2 } & 0 \\ 0 & 0 & {\sigma _{\omega z}^2 } \\ \end{array}\right)N^{T}(\tau ) {d}\tau \\ \end{array}\right\}$
$Q(k)$为$9\times9$的矩阵, 具体表达式限于篇幅不再详细给出.
2 主动机动规避策略设计
假设追踪器采用比例导引律对逃逸器进行追踪接近,比例导引律的原理在于抑制追踪器相对于逃逸器的视线偏转,使追踪器一直对准逃逸器. 逃逸器想要通过机动规避追踪器的接近时,可以通过施加适当方向的加速度使视线偏转率最大, 限制追踪器机动的作用,使脱靶量最大从而达到规避的效果.
2.1 追踪器比例导引制导指令加速度
为便于描述视线偏转和构造制导指令加速度, 建立视线坐标系. 以追踪器质心为原点,$X$轴指向视线方向, $Y$轴在轨道面内垂直于$X$轴, $Z$轴与$X$, $Y$轴构成右手系. 按照此定义,易知惯性系首先绕$Y$轴旋转$q_\beta $角, 再绕$Z$轴旋转$q_\varepsilon $角,便可得到视线系. 因此, 视线系的$x_A ,y_A ,z_A $三个坐标轴方向可表示为
(9) $\left. {\begin{array}{l} x_s =\cos q_\varepsilon \cos q_\theta \cdot x_A +\sin q_\varepsilon \cdot y_A -\\ \cos q_\varepsilon \sin q_\theta \cdot z_A \\ y_s =-\sin q_\varepsilon \cos q_\theta \cdot x_A +\cos q_\varepsilon \cdot y_A +\\ \sin q_\varepsilon \sin q_\theta \cdot z_A \\ z_s =\sin q_\theta \cdot x_A +\cos q_\theta \cdot z_A \\ \end{array}} \right\}$
三维比例导引律在视线坐标系内的指令加速度为[29 ]
(10) $\left.\begin{array}{l} a_{mx} =0 \\ a_{my} =Nv_s \dot{{q}}_\varepsilon \\ a_{mz} =-Nv_s \dot{{q}}_\theta \cos (q_\varepsilon ) \\ a_{c} =a_{my} y_s +a_{mz} z_s \\ \end{array}\right\}$
2.2 逃逸器追踪器视线角及视线角速率
在视线坐标系中, 视线角$q_\varepsilon $和$q_\theta$以及视线角速率$\dot{{q}}_\varepsilon $和$\dot{{q}}_\theta$可用以下公式计算[29 ]
(11) $\left.\begin{array}{l} q_\varepsilon =\tan^{-1}\left[ \dfrac{y}{\sqrt {x^2 +z^2 } } \right] \\ q_\theta =\tan ^{-1}\left[ {\dfrac{-z}{x}} \right] \\ \dot{{q}}_\varepsilon =\dfrac{(x^2 +z^2 )v_y -y(xv_x +zv_z )}{(x^2 +y^2 +z^2 )\sqrt {x^2 +z^2 } } \\ \dot{{q}}_\theta =\dfrac{zv_x -xv_z }{x^2 +z^2 } \\ \end{array}\right\}$
其中, $(x, y, z)$表示追踪器相对于逃逸器的位置, $(v_x ,$ $ v_y , v_z)$表示追踪器相对于逃逸器的速度.
2.3 主动规避控制加速度
追踪器采用比例导引率对逃逸器进行追踪接近, 逃逸器采用测角加测距的测量方式,考虑空间中测角和测距的测量误差, 采用当前统计模型对追踪器进行滤波分析,得到追踪器在VVLH坐标系中的位置$(x_{r}^V , y_{r}^V , z_{r}^V)$、速度$(v_{{r}x}^V , v_{{r}y}^V , v_{{r}z}^V )$等滤波信息,将其转换到惯性系$(x_{c}^A , y_{c}^A , z_{c}^A )$、$(v_{{c}x}^A , v_{{c}y}^A, v_{{c}z}^A )$. 假设逃逸器自身的位置$(x_{t}^A , y_{t}^A , z_{t}^A)$、速度$(v_{{t}x}^A , v_{{t}y}^A , v_{{t}z}^A )$已知.通过惯性系中的导航数据, 根据式(10)和式(11)计算追踪器当前的指令加速度方向,以此为逃逸器当前的逃逸方向. 则逃逸器的制导加速度为
(12) $a_{t} = a_{Nt} \frac{a_{c} }{\left| {a_{c} } \right|}$
其中, $a_{Nt}$为逃逸器的最大推力加速度, 即逃逸器始终以最大加速度进行机动.
3 算例分析
3.1 问题配置
逃逸器的初始轨道根数如表1 所示, 逃逸器采用光学相机和激光测距仪对追踪器进行测量, 可以获得相对距离、俯仰角和方位角. 当前统计模型中, $x$, $y$, $z$三个方向的机动频率设为$\alpha _x =\alpha _y =\alpha _z =0.001$ Hz, 滤波最大加速度设为1.8 m/s$^{2}$. 定义逃逸器的安全距离$d = 100$ m,当追踪器与逃逸器之间的距离$\vert r\vert < d$时, 认为追踪器成功接近逃逸器. 追踪器采用比例导引率追踪逃逸器,当追踪器与逃逸器视线方向的相对速度大于0时, 认为发生脱靶, 仿真结束.
3.2 仿真分析
本文首先验证提出的规避策略的有效性, 然后从观测设备(光学相机、激光测距仪)的测量精度、工作频率、逃逸器与追踪器的初始状态、逃逸器的机动能力等方面进行敏感性分析,以保证仿真的全面性和可靠性.
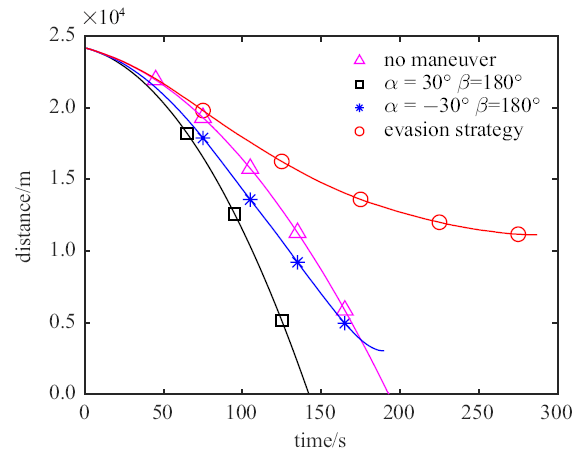
设光学相机的角度测量误差标准差为$\varepsilon _{r} = 0.001$ rad,激光测距仪的距离测量误差标准差为$\varepsilon _{d} = 10$ m.光学相机和激光测距仪的工作频率设为$f =$ 1 Hz.在以逃逸器质心为原点的VVLH坐标系中, 追踪器相对于逃逸器的位置为$r_{rel}=$ $[-21 000 \mbox{m}, 0 \mbox{m}, 12 000.0 \mbox{m}]^{T}$,速度为$v_{rel}=[23.0 \mbox{m/s},$ $0 \mbox{m/s}, -14.0 \mbox{m/s}]^{T}$.逃逸器的最大推力加速度为$a_{Nt} = 1.0$ m/s$^{2}$,追踪器的最大推力加速度为$a_{Nc} = 1.05$ m/s$^{2}$.为有效分析提出的规避策略的有效性, 设计以下4组对比工况:(1) 逃逸器不机动;(2) 逃逸器按照固定方向机动($\alpha =30^{\circ}, \beta =180^{\circ})$;(3) 逃逸器按照固定方向机动($\alpha =-30^{\circ}, \beta =180^{\circ})$;(4) 逃逸器按照最大化视线偏转率的主动规避策略进行机动.
仿真结果如图2 所示, 其中, 横轴表示仿真时间, 纵轴表示追踪器相对于逃逸器的距离(下同).
图2
图2
规避策略有效性验证
Fig. 2
Validation of evasion strategies
由图2 可知, 逃逸器不机动时, 追踪器在193 s成功接近逃逸器; 逃逸器按照$\alpha=30^{\circ}$, $\beta =180^{\circ}$的固定方向机动时, 追踪器在142 s成功接近逃逸器; 逃逸器按照$\alpha =-30^{\circ}$, $\beta=180^{\circ}$的固定方向机动时, 追踪器无法接近到逃逸器的安全距离以内, 在190 s时, 追踪器与逃逸器视线方向的相对速度变为大于0时, 发生脱靶,此时追踪器与逃逸器的相对距离为3 038 m; 逃逸器按照机动规避策略进行机动时,追踪器无法接近到逃逸器的安全距离以内, 在287 s,追踪器与逃逸器视线方向的相对速度变为大于0时, 发生脱靶,此时追踪器与逃逸器的相对距离为11 142 m. 综上分析,最大化视线偏转率的主动规避策略可以有效提高逃逸器的生存能力.
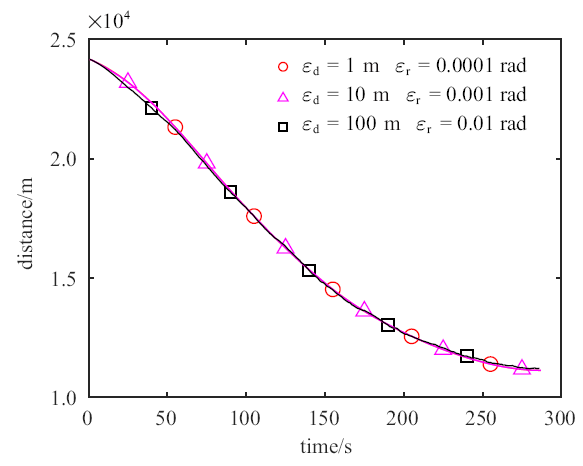
分析光学相机和激光测距仪的测量精度对规避策略的影响. 设计三组对比工况,角度测量误差标准差$\varepsilon _r $和距离测量误差标准差$\varepsilon _{d}$分别为(1) $\varepsilon _{d} =1$ m, $\varepsilon _{r} =0.000 1$ rad; (2) $\varepsilon _{d}=10$ m, $\varepsilon _{r} =0.001$ rad; (3) $\varepsilon _{d} =100$ m, $\varepsilon_{r} =0.01$ rad. 其余参数设置与3.2.1相同. 仿真结果如图3 所示.
图3
图3
测量精度敏感性分析
Fig. 3
Measurement accuracy sensitivity analysis
由图3 可知, 测量精度下降导致滤波精度下降, $\varepsilon _d=100$ m, $\varepsilon _r =0.01$ rad对应的曲线不如其余两种情况平滑,但是逃逸器规避机动的效果并无明显区别, 即说明规避策略对观测设备的测量精度不敏感.
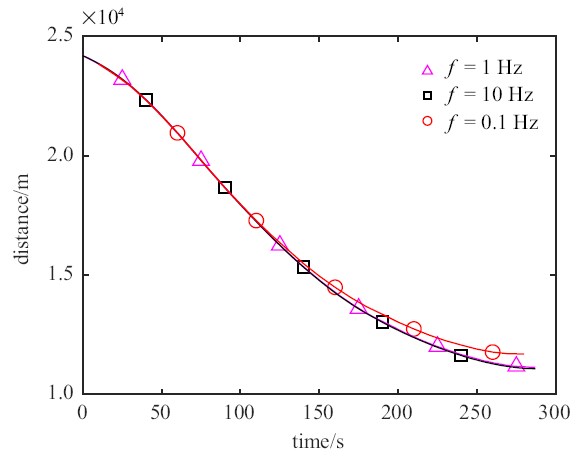
分析光学相机和激光测距仪的工作频率对规避策略的影响. 设计3组对比工况,工作频率$f$分别取(1) $f=1$ Hz; (2) $f=10$ Hz; (3) $f=0.1$ Hz. 其余参数设置与3.2.1节相同.仿真结果如图4 所示.
图4
图4
工作频率敏感性分析
Fig. 4
Frequency sensitivity analysis
由图4 可知, 工作频率降低同样导致滤波精度下降, 仿真后期$f=0.1$ Hz对应的曲线与其余两种工况有一定误差,但是逃逸器规避机动的效果并无明显区别, 即说明规避策略对观测设备的工作频率不敏感.
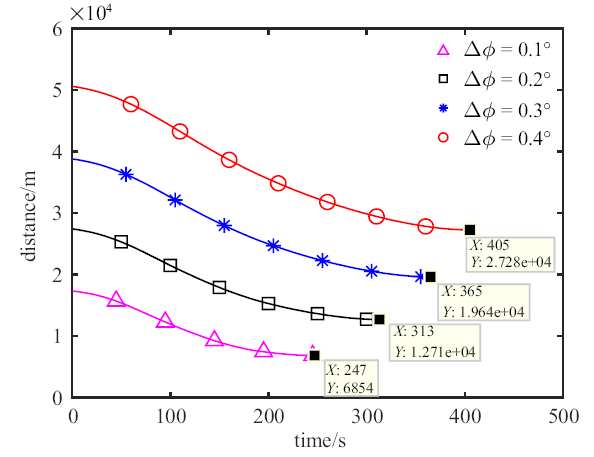
分析追踪器相对于逃逸器的初始状态对规避策略的影响.设追踪器的轨道低于逃逸器120 km, 追踪器位于逃逸器后方, 相位相差$\Delta \phi $, 其余轨道根数相同. 设计四组对比工况, 相位差$\Delta \phi$分别取(1) $\Delta \phi =0.1^{\circ}$, (2) $\Delta \phi =0.2^{\circ}$, (3) $\Delta\phi =0.3^{\circ}$, (4) $\Delta \phi =0.4^{\circ}$, 其余参数设置与3.2.1节相同. 仿真结果如图5 所示.
图5
图5
初始状态敏感性分析
Fig. 5
Sensitivity analysis of initial state
相位差$\Delta \phi $越大, 意味着逃逸器越早收到预警信息开始机动. 由图5 可知, 逃逸器收到预警信息越早, 发生脱靶时, 追踪器相对于逃逸器的距离越远, 即逃逸器的安全性越高, 规避效果越好.
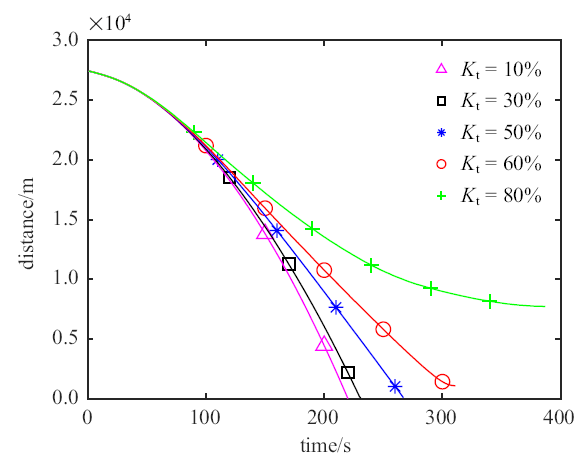
分析逃逸器机动能力对规避策略的影响. 设追踪器的最大推力加速度为$a_{Nc} = 1.0$ m/s$^{2}$, 逃逸器的最大推力加速度为$a_{Nt} =k_{t} \times a_{Nc}$, 其余参数设置与3.2.1节相同. 针对不同的系数$k_{t}$设计5组对比工况, 分别为(1) $k_{t} = 10\%$, (2) $k_{t} = 30\%$, (3) $k_{t} = 50\%$, (4) $k_{t} = 60\%$, (5) $k_{t} = 80\%$. 仿真结果如图6 所示.
图6
图6
逃逸器机动能力敏感性分析
Fig. 6
Sensitivity analysis of escaper maneuverability
由图6 可知, 随着$k_{t}$变大, 逃逸器机动能力逐渐增强, 当$k_{t} = 50\%$, 逃逸器不能逃脱追踪器的跟踪, 当$k_{t} = 60\%$, 逃逸器可有效规避追踪器的异常接近. 因此可取门限值$k_{t} = 60\%$, 即逃逸器的机动能力达到追踪器的60%以上时, 逃逸器的最大化视线偏转率的规避策略有效.
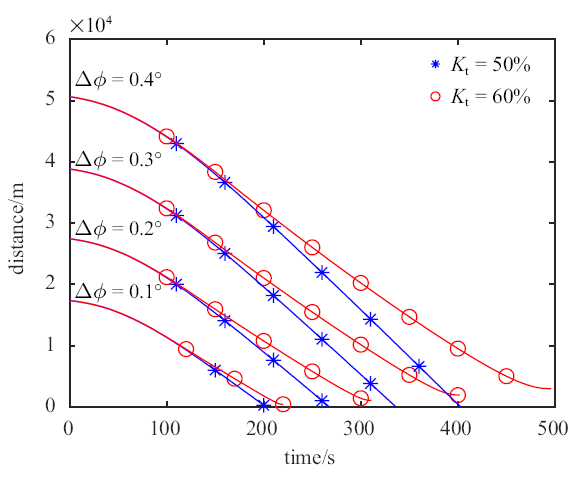
设置不同的工况验证60%的门限值是否有效. 针对$\Delta \phi =0.1^{\circ}$, $\Delta \phi =0.2^{\circ}$, $\Delta \phi =0.3^{\circ}$, $\Delta \phi =0.4^{\circ}$四种情况分别设计(1) $k_{t} = 50\%$, (2) $k_{t} =60\%$两组对比工况, 仿真结果如图7 所示.
图7
图7
不同初始状态对$k_{t}$的影响
Fig. 7
The influence of different initial states on $k_{t}$
由图7 可知, 针对不同的相位差$\Delta \phi $, 逃逸器的机动能力达到追踪器的60%时, 逃逸器可有效规避追踪器的异常接近,即60%的门限值有效.
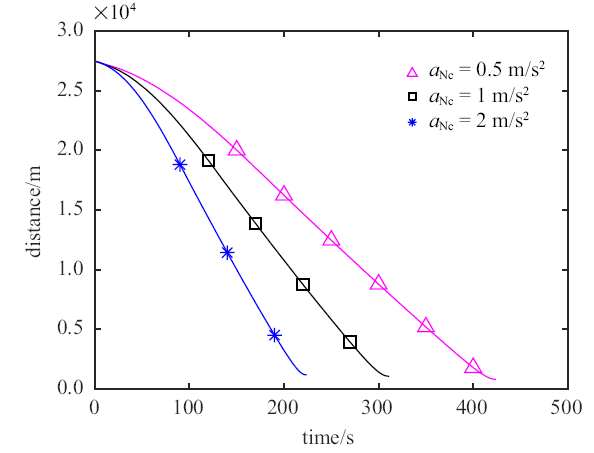
针对追踪器不同的机动能力$a_{Nc}$设计3组对比工况, 逃逸器机动能力为$a_{Nt}=60\% \times a_{Nc} $, 追踪器机动能力取(1) $a_{Nc} = 0.5$ m/s$^{2}$, (2) $a_{Nc} = 1$ m/s$^{2}$, (3) $a_{Nc} = 2$ m/s$^{2}$.
仿真结果如图8 所示. 分析可知, 针对追踪器不同的机动能力$a_{Nc}$, 逃逸器的机动能力达到追踪器的60%以上时, 逃逸器可有效规避追踪器的异常接近, 即60%的门限值有效.
图8
图8
追踪器机动能力对$k_{t}$的影响
Fig. 8
The influence of chaser's maneuverability on $k_{t}$
综上分析, 对于提出的最大化视线偏转率的主动规避策略, 可以设置门限值为60%, 即逃逸器的机动能力达到追踪器的60%以上时, 规避策略有效.
4 结论
本文在航天器近距离追逃博弈的背景下, 对逃逸器的主动规避策略进行了研究. 建立了基于当前统计模型的机动目标滤波算法,基于比例导引律抑制视线偏转率的基本原理, 从最大化视线偏转率的角度入手得到了逃逸器的规避加速度, 降低了追踪器比例导引制导率的有效性. 通过仿真分析可得出以下结论: 设追踪器通过比例导引率异常接近逃逸器, 安全距离为100 m, 则逃逸器的机动能力达到追踪器的60%以上时, 逃逸器采用基于最大化视线偏转率的规避策略进行机动可有效规避追踪器的异常接近;规避策略对观测设备的测量精度和工作频率不敏感; 逃逸器收到预警信息越早,规避效果越好. 提出的规避策略意义明确、形式解析、易于工程实现.
参考文献
View Option
[1]
曹登庆 , 白坤朝 , 丁虎 等 . 大型柔性航天器动力学与振动控制研究进展
力学学报 , 2019 ,51 (1 ):1 -13
[本文引用: 1]
( Cao Dengqing Bai Kunchao Ding Hu , et al . Advances in dynamics and vibration control of large-scale flexible spacecraft
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (1 ):1 -13 (in Chinese))
[本文引用: 1]
[2]
尹婷婷 , 邓子辰 , 胡伟鹏 等 . 空间刚性杆--弹簧组合结构轨道、姿态耦合动力学分析
力学学报 , 2018 ,50 (1 ):87 -98
[本文引用: 1]
( Yin Tingting Deng Zichen Hu Weipeng , et al . Dynamic modelling and simulation of orbit and attitude coupling problems for structure combined of spatial rigid rods and spring
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (1 ):87 -98 (in Chinese))
[本文引用: 1]
[3]
王恩美 , 邬树楠 , 吴志刚 . 在轨组装空间结构面向主动控制的动力学建模
力学学报 , 2020 ,52 (3 ):805 -816
[本文引用: 1]
( Wang Enmei Wu Shunan Wu Zhigang . Active-control-oriented dynamic modelling for on-orbit assembly space structure
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (3 ):805 -816 (in Chinese))
[本文引用: 1]
[4]
敬忠良 . 航天器自主操作的测量与控制 . 北京 : 中国宇航出版社 , 2011
[本文引用: 1]
( Jing Zhongliang . Measurement and Control of Autonomous Operation of Spacecraft . Beijing : China Aerospace Press , 2011 (in Chinese))
[本文引用: 1]
[5]
Li XR Jilkov VP . Survey of maneuvering target tracking. Part I. Dynamic models
IEEE Transactions on Aerospace and Electronic Systems 2003 ,39 (4 ):1333 -1364
DOI
URL
[本文引用: 1]
[6]
Singer RA . Estimating optimal tracking filter performance for manned maneuvering targets
IEEE Transactions on Aerospace and Electronic Systems 1970 (4 ):473 -483
[本文引用: 1]
[7]
周宏仁 , 敬忠良 , 王培德 等 . 机动目标跟踪 . 北京 : 国防工业出版社 , 1991
[本文引用: 1]
( Zhou Hongren Jin Zhongliang Wang Peide , et al . Tracking of Maneuvering Target . Beijing : National Defense Industry Press , 1991 (in Chinese))
[本文引用: 1]
[8]
李菲 , 潘平俊 . 机动目标模型的研究进展
火力与指挥控制 , 2007 ,32 (10 ):17 -21
[本文引用: 1]
( Li Fei Pan Pingjun . The research and progress of dynamic models for maneuvering target tracking
Fire Control and Command Control 2007 ,32 (10 ):17 -21 (in Chinese))
[本文引用: 1]
[9]
Zhou WM Wang H Tang GJ , et al . Inverse simulation system for manual-controlled rendezvous and docking based on artificial neural network
Advances in Space Research 2016 ,58 (6 ):938 -949
[本文引用: 1]
[10]
姚党鼐 , 王振国 . 航天器在轨防碰撞自主规避策略
国防科技大学学报 , 2012 ,34 (6 ):100 -110
[本文引用: 1]
( Yao Dingnai Wang Zhenguo . Active collision avoidance maneuver strategy for on-orbit spacecraft
Journal of National University of Defense Technology 2012 ,34 (6 ):100 -110 (in Chinese))
[本文引用: 1]
[11]
Bombardelli C . Analytical formulation of impulsive collision avoidance dynamics
Celestial Mechanics and Dynamical Astronomy 2013 ,118 (2 ):99 -114
[本文引用: 1]
[12]
Wang S Schaub H . Spacecraft collision avoidance using coulomb forces with separation distance and rate feedback
Journal of Guidance, Control, and Dynamics 2012 ,31 (3 ):740 -750
DOI
URL
[本文引用: 1]
[13]
郑重 , 宋申民 . 考虑避免碰撞的编队卫星自适应协同控制
航空学报 , 2013 ,34 (8 ):1934 -1943
DOI
URL
[本文引用: 1]
基于势函数法研究具有模型不确定性的编队飞行卫星避免碰撞的自适应协同控制。势函数法的思想为设计碰撞区域势函数值较大,所设计的控制律使得系统势函数具有减小的趋势,从而实现避免碰撞的编队飞行任务。首先,在无外部参考轨迹的情况下,通过引入避免碰撞势函数,提出一种自适应协同控制器,编队卫星最终实现速度一致和避免碰撞。进一步,考虑已知外部参考轨迹的情形,基于新的势函数方法,设计新的自适应协同控制器,能够同时实现避免碰撞、速度一致、卫星跟踪参考轨迹的目的。对于所提出的两种控制方法,均通过合理地应用Lyapunov稳定性理论分析了闭环系统的稳定性。仿真结果表明了所设计控制方法的有效性。
( Zheng Zhong Song Shenming . Adaptive coordination control of satellites within formation considering collision avoidance
Acta Aeronautica Et Astronautica Sinica 2013 ,34 (8 ):1934 -1943 (in Chinese))
DOI
URL
[本文引用: 1]
The adaptive coordination control based on potential function method associated with collision avoidance is investigated for formation flying satellites with model uncertainty. The idea of potential function method is designing the bigger value of potential function in the collision area. The potential function of the system declines with the designed control law, thus the mission of formation flying with collision avoidance can be satisfied. Firstly, an adaptive coordinated controller is proposed by introducing a collision avoidance potential function in the absence of external reference trajectories, so that formation flying satellites can achieve velocity consensus and collision avoidance eventually. Then, taking into consideration an external reference trajectory, a new adaptive coordinated controller is designed based on a new potential function, and the objective of collision avoidance, velocity consensus and satellites tracking the reference trajectory is realized simultaneously. For the two presented control approaches, the stability of the closed loop system is both analyzed by using Lyapunov stability theory. Simulation results demonstrate the effectiveness of the designed control methods.
[14]
PMID
[本文引用: 1]
( Luo Yazhong Li Zhenyu Zhu Hai . Survey on spacecraft orbital pursuit-evasion differential games
Science China Technological Sciences , doi:10.1360/SST-2019-0174 (in Chinese))
URL
PMID
[本文引用: 1]
The anti-virus and anti-bacteria active components were extracted from some Chinese medicine, such as the honeysuckle, forsythia and the licorice. Using a w/o/w emulsion method, the active components were fabricated to uniform particulate microcapsule with sustained-release properties. The polypropylene punched felt was finished with the finishing agent of microcapsule, nano ZnO and TiO2 and polymer adhesive, and the composite air filter with anti-virus and anti-bacteria properties were formed, staphylococcus aureus, colibacillus and candida albicans were applied to antibacterial experiments. The results indicate that the anti-bacteria rate are all 100%, and the virus inactivation rate also reaches 100% to pandemic influenza A virus.
[15]
张秋华 , 孙松涛 , 谌颖 等 . 时间固定的两航天器追逃策略及数值求解
宇航学报 , 2014 ,35 (5 ):537 -544
DOI
URL
[本文引用: 1]
针对时间固定的两航天器追逃问题,基于微分对策理论研究了追逃双方的最优控制策略及求解方法。研究在两航天器均为连续小推力假设条件下,以终端距离为支付函数,追踪器希望支付最小,逃逸器希望支付最大,并考虑时变的轨道高度及时变的角速度建立对策模型,模型具有高维时变特征;由对策必要条件,对策研究最终转化为高维时变非线性两点边值问题的求解。 提出采用多重打靶法和多目标遗传算法的混合算法,可以解决航天器追逃这类两点边值问题,并给出数值求解的具体方法。方法中,涉及边值问题中的协态变量初值估计时,采用多目标遗传算法给出初值估计,再由多重打靶法求两点边值问题的解。仿真实例表明:混合算法针对这类追逃问题,既能保证计算精度,又具有较好的鲁棒性,算例最终给出了追逃双方的最优控制策略和相应的追逃轨迹。
( Zhang Qiuhua Sun Songtao Chen Yin , et al . Strategy and numerical solution of pursuit-evasion with fixed duration for two spacecraft
Journal of Astronautics 2014 ,35 (5 ):537 -544 (in Chinese))
DOI
URL
[本文引用: 1]
For the problem of pursuit\|evasion with fixed duration for two spacecraft, an optimal control strategy and its numerical solution method are investigated based on the differential game theory. The two spacecraft are conflicted with each other under the assumed condition of low continuous thrust in a dynamics system with time dependent angular velocity and trajectory altitude. The terminal distance is taken as a payoff. The pursuer tries to minimize the payoff, and the evader tries to maximize it. Consequently, a high order time dependent nonlinear two point boundary value problem is introduced by using the necessary condition of the differential game. In this paper, a hybrid algorithm is presented by combining the multiple shooting method with the genetic algorithm for solving this type of pursuit evasion problem. In this hybrid algorithm, an improved multi objective genetic algorithm is adopted to obtain the initial estimation of the costate variables, and the result of the genetic algorithm is used as a feeder for the multiple shooting method to solve the solution of the complex two point boundary value problem. It is shown by the simulations that this hybrid algorithm has guarantee accuracy and robustness for the problem. Simultaneously, the optimal strategies and the corresponding pursuit evasion trajectory are obtained.
[16]
郝志伟 , 孙松涛 , 张秋华 等 . 半直接配点法在航天器追逃问题求解中的应用
宇航学报 , 2019 ,40 (6 ):628 -635
[本文引用: 1]
( Hao Zhiwei Sun Songtao Zhang Qiuhua , et al . Application of semi-direct collocation method for solving pursuit-evasion problems of spacecraft
Journal of Astronautics 2019 40 (6 ):628 -635 (in Chinese))
[本文引用: 1]
[17]
刘源 , 李玉玲 , 郝勇 等 . 航天器三维空间追逃问题研究
系统工程与电子技术 , 2018 ,40 (4 ):868 -877
[本文引用: 1]
( Liu Yuan Li Yuling Hao Yong , et al . Research on three dimensional space pursuit-evasion of spacecraft
Systems Engineering & Electronics 2018 ,40 (4 ):868 -877 (in Chinese))
[本文引用: 1]
[18]
Yu DT Luo YZ Jiang ZC , et al . Multi-objective evolutionary optimization of evasive maneuvers including observability performance
// 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan , May 25-28, 2015
[本文引用: 1]
[19]
于大腾 , 王华 , 周晚萌 . 考虑空间几何关系的反交会规避机动方法
国防科技大学学报 , 2016 ,38 (6 ):89 -94
[本文引用: 1]
( Yu Dateng Wang Hua Zhou Wanmeng . Anti-rendezvous evasive maneuver method considering space geometrical relationship
Journal of National University of Defense Technology 2016 ,38 (6 ):89 -94 (in Chinese))
[本文引用: 1]
[20]
Shen HX Casalino L . Revisit of the three-dimensional orbital pursuit-evasion game
Journal of Guidance, Control, and Dynamics 2018 ,41 (8 ):1823 -1831
[本文引用: 1]
[21]
Li Z Zhu H Yang Z , et al . A dimension-reduction solution of free-time differential games for spacecraft pursuit-evasion
Acta Astronautica 2019 : 201 -210
DOI
URL
PMID
[本文引用: 1]
The seed embryo of Arabidopsis thaliana, the favorite plant of up-to-date molecular developmental biology, represents a valuable model system for space radiation research with heavy ions. For several years, densely ionizing particles have been available for basic studies in nuclear physics and radiation biology through special accelerators as well as through space flight missions. Because of the great variability of the available radiation spectra, the induced relative biological effect (RBE-value) has to be differentiated with respect to the effective charge (z) and the linear energy transfer (LET) deposited in a certain volume of matter, and to the biological targets which differ in size, structure and function. The results of comparative studies of 8 space flight experiments, here by example show increasing damage produced by single heavy ions and/or cosmic background radiation (protons, neutrons, X-rays). These results offer new prospects for molecular investigation of the RBE of heavy ions in space.
[22]
Ye D Shi MM Sun ZW . Satellite proximate interception vector guidance based on differential games
Chinese Journal Aeronautic 2018 ,31 :1352 -1361
[本文引用: 1]
[23]
Weiss M Shima T . Minimum effort pursuit/evasion guidance with specified miss distance
Journal of Guidance, Control, and Dynamics 2016 ,39 (5 ):1069 -1079
DOI
URL
[本文引用: 1]
[24]
Weiss M Shima T . Minimum effort intercept and evasion guidance algorithms for active aircraft defense
Journal of Guidance, Control, and Dynamics 2016 ,39 (10 ):2297 -2311
[本文引用: 1]
[25]
祝海 . 基于微分对策理论的航天器追逃博弈研究. [硕士论文]
长沙: 国防科学技术大学 , 2017
[本文引用: 1]
( Zhu Hai . Spacecraft orbital pursuit-evasion based on differential game theory. [Master Thesis]
Changsha: National University of Defense Technology , 2017 (in Chinese))
[本文引用: 1]
[26]
陈文胜 , 陈新海 . 比例导引法在航天器交会中的应用
西北工业大学学报 , 1994 ,12 (1 ):31 -36
[本文引用: 1]
( Chen Wensheng Chen Xinhai . Application of proportional navigation to rendezvous problems
Journal of Northwestern Polytechnical University 1994 ,12 (1 ):31 -36 (in Chinese))
[本文引用: 1]
[27]
李九人 , 李海阳 , 陈磊 等 . 基于比例导引的空间交会寻的段飞行任务设计
飞行力学 , 2009 ,27 (4 ):58 -61
( Li Jiuren Li Haiyang Chen Lei , et al . Homing mission design of space rendezvous based on proportional guidance
Flight Dynamics 2009 ,27 (4 ):58 -61 (in Chinese))
[28]
Li KB Liang YG Su WS , et al . Performance of 3D TPN against true-arbitrarily maneuvering target for exoatmospheric interception
Science China Technological Sciences 2018 ,61 :1161 -1174
[本文引用: 1]
[29]
黎克波 . 拦截机动目标的制导律研究. [博士论文]
长沙: 国防科学技术大学 , 2016
[本文引用: 2]
( Li Kebo . Research on guidance laws for intercepting maneuvering targets. [PhD thesis]
Changsha: National University of Defense Technology , 2016 (in Chinese))
[本文引用: 2]
大型柔性航天器动力学与振动控制研究进展
1
2019
... 近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题. ...
大型柔性航天器动力学与振动控制研究进展
1
2019
... 近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题. ...
空间刚性杆--弹簧组合结构轨道、姿态耦合动力学分析
1
2018
... 近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题. ...
空间刚性杆--弹簧组合结构轨道、姿态耦合动力学分析
1
2018
... 近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题. ...
在轨组装空间结构面向主动控制的动力学建模
1
2020
... 近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题. ...
在轨组装空间结构面向主动控制的动力学建模
1
2020
... 近年来, 航天器操控技术日新月异.面向空间大型柔性结构[1 ] 、多体系统[2 ] 以及大型空间结构在轨组装[3 ] 等技术层出不穷,导致各个航天大国对太空资产安全问题越来越重视.具有主动机动能力的空间非合作航天器对己方航天器的自主异常接近是对己方航天器安全的重大威胁.当追踪航天器(简称为追踪器)异常接近时,逃逸航天器(简称为逃逸器)需要通过机动进行规避,规避策略包括施加机动的时机、大小和方向, 其优劣直接影响逃逸器的生存能力.因此, 规避策略的研究是逃逸器主动规避的核心问题. ...
1
2011
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
1
2011
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
Survey of maneuvering target tracking. Part I. Dynamic models
1
2003
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
Estimating optimal tracking filter performance for manned maneuvering targets
1
1970
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
1
1991
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
1
1991
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
机动目标模型的研究进展
1
2007
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
机动目标模型的研究进展
1
2007
... 航天器相对导航是空间近距离操作任务的基础[4 ] .逃逸器的规避策略同样离不开对追踪器状态的估计. 当追踪器持续机动时,传统的导航滤波算法收敛较慢甚至会发散,因此在追踪器持续机动时需要研究新的导航滤波算法.机动目标跟踪问题的核心是对目标的不确定性运动进行建模,主要思路是将目标的真实非随机机动加速度近似为一种随机过程[5 ] .最简单的目标机动模型是白噪声加速度模型, 也叫匀加速模型,它假设目标做匀加速运动, 将目标加速度变化量建模为白噪声.Singer[6 ] 于1970年提出了著名的Singer模型,其本质是将机动加速度建模为零均值一阶马尔可夫过程,采用更符合实际的有色噪声代替白噪声描述机动加速度.我国周宏仁教授在Singer模型的基础上提出了当前统计模型[7 ] ,其本质是非零均值的一阶马尔可夫模型,用修正的瑞利分布描述机动加速度的当前概率密度. 目前,当前统计模型在机动目标跟踪领域显示出了强大的生命力[8 ] .本文基于当前统计模型发展机动目标滤波算法,应用于逃逸器对于追踪器导航信息的获取. ...
Inverse simulation system for manual-controlled rendezvous and docking based on artificial neural network
1
2016
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
航天器在轨防碰撞自主规避策略
1
2012
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
航天器在轨防碰撞自主规避策略
1
2012
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Analytical formulation of impulsive collision avoidance dynamics
1
2013
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Spacecraft collision avoidance using coulomb forces with separation distance and rate feedback
1
2012
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
考虑避免碰撞的编队卫星自适应协同控制
1
2013
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
考虑避免碰撞的编队卫星自适应协同控制
1
2013
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
航天器轨道追逃微分对策研究综述
1
2020
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
航天器轨道追逃微分对策研究综述
1
2020
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
时间固定的两航天器追逃策略及数值求解
1
2014
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
时间固定的两航天器追逃策略及数值求解
1
2014
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
半直接配点法在航天器追逃问题求解中的应用
1
2019
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
半直接配点法在航天器追逃问题求解中的应用
1
2019
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
航天器三维空间追逃问题研究
1
2018
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
航天器三维空间追逃问题研究
1
2018
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Multi-objective evolutionary optimization of evasive maneuvers including observability performance
1
2015
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
考虑空间几何关系的反交会规避机动方法
1
2016
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
考虑空间几何关系的反交会规避机动方法
1
2016
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Revisit of the three-dimensional orbital pursuit-evasion game
1
2018
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
A dimension-reduction solution of free-time differential games for spacecraft pursuit-evasion
1
2019
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Satellite proximate interception vector guidance based on differential games
1
2018
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Minimum effort pursuit/evasion guidance with specified miss distance
1
2016
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
Minimum effort intercept and evasion guidance algorithms for active aircraft defense
1
2016
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
基于微分对策理论的航天器追逃博弈研究. [硕士论文]
1
2017
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
基于微分对策理论的航天器追逃博弈研究. [硕士论文]
1
2017
... 逃逸器的规避策略目前已有较多研究[9 -10 ] ,主要的研究思路是假设初始时刻追踪器的位置、速度等导航信息已知,通过设定终端脱靶量和碰撞概率等优化指标,将机动规避问题转化为优化问题进行处理.Bombardelli等[11 ] 构建了机动点与预测碰撞点之间关于距离的函数,求解脱靶量的最大值, 以此为施加机动方向. 此外,Wang等[12 ] 、郑重等[13 ] 通过相对距离、势函数等方法研究了卫星编队飞行中的规避机动策略.上述文献的研究对于逃逸器主动规避策略具有一定的参考价值,但其研究对象多是空间碎片或失效航天器等无机动能力的空间目标,规避策略也是考虑碰撞概率和相对距离等传统规避指标.若逃逸器在逃逸过程中考虑追踪器的机动策略,那规避逃逸问题将从单边规划问题变为追逃博弈双边规划问题[14 ] .张秋华等[15 ] 在时间固定的情况下,基于定量和定性方法研究了追逃双方航天器的追逃策略以及追逃界栅.郝志伟等[16 ] 采用半直接配点的数值方法求解追逃双方最优控制策略,避免了求解非线性两点边值问题.刘源等[17 ] 采用协同进化算法研究了固定时间下的两航天器三维空间追逃问题,思路是将最优双边规划问题简化为对追逃过程中纳什均衡点的搜索.于大腾等[18 -19 ] 研究了相对运动对系统可观测性的影响,设计系统可观测度, 以此为优化目标对最优规避进行了求解.沈红新等[20 ] 考虑了航天器质量变化,将三维追逃问题拓展为28维, 采用间接打靶法求解了鞍点.李振瑜等[21 ] 在近圆轨道、自由时间的情况下,提出了一种求解两航天器追逃博弈鞍点解的降维方法.Dong等[22 ] 通过零效脱靶量估算剩余捕获时间,解决了捕获时间最优化问题. 此外,Shima等[23 -24 ] 研究了考虑加速度估计延迟的导弹拦截微分对策制导律.上述文献的研究简化了相对动力学模型,并以信息透明为前提[25 ] ,即逃逸器已知追踪器的相对位置、速度等控制输入量, 然而对于非合作航天器,这些信息是无法实时已知的, 因此本文考虑实际工程情况,逃逸器通过测量和滤波获得追踪器的状态信息, 且状态信息具有一定误差. ...
比例导引法在航天器交会中的应用
1
1994
... 追踪器的追踪策略(主要体现为追踪制导率)同样是追逃问题的关键因素,然而本文主要研究逃逸器的规避策略, 因此采用经典的比例导引律(proportional navigation)作为追踪器的制导率.比例导引律具有简单、高效而且易于工程实现的特点,广泛应用于导弹拦截、空间交会问题[26 -28 ] .本文主要研究在追踪器采用比例导引律接近逃逸器, 追逃双方信息不透明的情况下,逃逸器基于当前统计模型自适应滤波算法对追踪器状态进行滤波估计,同时最大化视线转率以降低追踪器制导率作用的航天器主动机动规避策略. ...
比例导引法在航天器交会中的应用
1
1994
... 追踪器的追踪策略(主要体现为追踪制导率)同样是追逃问题的关键因素,然而本文主要研究逃逸器的规避策略, 因此采用经典的比例导引律(proportional navigation)作为追踪器的制导率.比例导引律具有简单、高效而且易于工程实现的特点,广泛应用于导弹拦截、空间交会问题[26 -28 ] .本文主要研究在追踪器采用比例导引律接近逃逸器, 追逃双方信息不透明的情况下,逃逸器基于当前统计模型自适应滤波算法对追踪器状态进行滤波估计,同时最大化视线转率以降低追踪器制导率作用的航天器主动机动规避策略. ...
基于比例导引的空间交会寻的段飞行任务设计
0
2009
基于比例导引的空间交会寻的段飞行任务设计
0
2009
Performance of 3D TPN against true-arbitrarily maneuvering target for exoatmospheric interception
1
2018
... 追踪器的追踪策略(主要体现为追踪制导率)同样是追逃问题的关键因素,然而本文主要研究逃逸器的规避策略, 因此采用经典的比例导引律(proportional navigation)作为追踪器的制导率.比例导引律具有简单、高效而且易于工程实现的特点,广泛应用于导弹拦截、空间交会问题[26 -28 ] .本文主要研究在追踪器采用比例导引律接近逃逸器, 追逃双方信息不透明的情况下,逃逸器基于当前统计模型自适应滤波算法对追踪器状态进行滤波估计,同时最大化视线转率以降低追踪器制导率作用的航天器主动机动规避策略. ...
拦截机动目标的制导律研究. [博士论文]
2
2016
... 三维比例导引律在视线坐标系内的指令加速度为[29 ] ...
... 在视线坐标系中, 视线角$q_\varepsilon $和$q_\theta$以及视线角速率$\dot{{q}}_\varepsilon $和$\dot{{q}}_\theta$可用以下公式计算[29 ] ...
拦截机动目标的制导律研究. [博士论文]
2
2016
... 三维比例导引律在视线坐标系内的指令加速度为[29 ] ...
... 在视线坐标系中, 视线角$q_\varepsilon $和$q_\theta$以及视线角速率$\dot{{q}}_\varepsilon $和$\dot{{q}}_\theta$可用以下公式计算[29 ] ...