引言
层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解.
准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解.
层合圆柱壳具有重量轻、强度高等特点, 是工程中常用的结构元件之一. 目前, 关于准晶层状结构的动态和静态问题研究多数是基于矩形层合板开展的[21 -23 ] . 此外, 同时考虑热电弹耦合效应和材料不均匀性的准晶层合圆柱壳的研究开展的很少. 因此, 本文采用类Stroh理论和传递矩阵方法, 获得了一维准晶功能梯度层合圆柱壳的热电弹性精确解, 讨论了功能梯度指数因子对层合圆柱壳物理量的影响, 以期为准晶功能梯度层合圆柱壳的多场耦合效应及非均匀性分析提供可靠的参考依据.
1 基本方程
图1 是柱坐标系($r$, $\theta$, $z)$中一维准晶功能梯度层合圆柱壳的示意图, 准周期方向和极化方向均沿着$r $轴, 其外表面半径为$r_{b}$, 内表面半径为$r_{a}$, 沿$z$向长度远远大于层合圆柱壳半径, 层合圆柱壳的角度跨度为$\theta_{0}$, 第$j$层的内外半径分别为$r_{j}$和$r_{j+1}$.
图1
图1
一维准晶功能梯度层合圆柱壳的示意图
Fig.1
Schematic of functionally graded layered 1Dquasicrystal cylindrical shells
对于考虑热-电-弹耦合的一维正交准晶材料, 本构方程为[24 ]
(1) $ \begin{eqnarray} \label{eq1} \left. \begin{array}{ll} \sigma _{rr} =C_{33} \varepsilon _{rr} +C_{13} \varepsilon _{\theta \theta } +C_{23} \varepsilon _{zz} +R_3 w_{rr} -\\ \qquad e_{33} E_r -\beta _3 T \\ \sigma _{\theta \theta } =C_{13} \varepsilon _{rr} +C_{11} \varepsilon _{\theta \theta } +C_{12} \varepsilon _{zz} +R_1 w_{rr} -\\ \qquad e_{31} E_r -\beta _1 T \\ \sigma _{zz} =C_{23} \varepsilon _{rr} +C_{12} \varepsilon _{\theta \theta } +C_{22} \varepsilon _{zz} +R_2 w_{rr} -\\ \qquad e_{32} E_r -\beta _1 T \\ \sigma _{\theta z} =\sigma _{z\theta } =2C_{66} \varepsilon _{\theta z} \\ \sigma _{rz} =\sigma _{zr} =2C_{44} \varepsilon _{zr} +R_5 w_{rz} -e_{24} E_z \\ \sigma _{r\theta } =\sigma _{\theta r} =2C_{55} \varepsilon _{r\theta } +R_6 w_{r\theta } -e_{15} E_\theta \\ H_{rr} =R_3 \varepsilon _{rr} +R_1 \varepsilon _{\theta \theta } +R_2 \varepsilon _{zz} +K_3 w_{rr} -d_{33} E_r \\ H_{rz} =2R_5 \varepsilon _{zr} +K_2 w_{rz} -d_{24} E_z \\ H_{r\theta } =2R_6 \varepsilon _{r\theta } +K_1 w_{r\theta } -d_{15} E_\theta \\ D_r =e_{33} \varepsilon _{rr} +e_{31} \varepsilon _{\theta \theta } +e_{32} \varepsilon _{zz} +d_{33} w_{rr} +\\ \qquad \xi _{33} E_r +p_3 T \\ D_\theta =2e_{15} \varepsilon _{r\theta } +d_{15} w_{r\theta } +\xi _{11} E_\theta \\ D_z =2e_{24} \varepsilon _{zr} +d_{24} w_{rz} +\xi _{11} E_z \\ \end{array} \right\} \end{eqnarray}$
式中, $\sigma _{kl} $为声子场应力; $\varepsilon _{kl} $为声子场应变; $H_{il} $为相位子场应力; $w_{il} $为相位子场应变; $D_k $为电位移; $E_k $为电场强度; $T$为温度变化; $C_{kl} $, $R_{kl} $, $K_{kl} $分别为声子场弹性常数, 声子场-相位子场耦合弹性常数和相位子场弹性常数; $e_{kl} $, $d_{kl} $, $\xi _{ll} $分别为声子场压电系数, 相位子场压电系数和介电系数; $p_3 $和$\beta _k $分别为热电系数和导热系数.
忽略体力、自由电荷以及内部热源, 静态平衡方程可写为
(2) $ \begin{eqnarray} \label{eq2} \left. \begin{array}{ll} \sigma _{rr,r} +{\sigma _{r\theta ,\theta } } / r+\sigma _{rz,z} +{\left( {\sigma _{rr} -\sigma _{\theta \theta } } \right)} / r=0 \\ \sigma _{r\theta ,r} +{\sigma _{\theta \theta ,\theta } } / r+\sigma _{\theta z,z} +{2\sigma _{r\theta } } / r=0 \\ \sigma _{rz,r} +{\sigma _{\theta z,\theta } } / r+\sigma _{zz,z} +{\sigma _{rz} } / r=0 \\ H_{rr,r} +{H_{r\theta ,\theta } } / r+H_{rz,z} +{H_{rr} } / r=0 \\ D_{r,r} +{D_{\theta ,\theta } } / r+D_{z,z} +{D_r } / r=0 \\ q_{r,r} +{q_{\theta ,\theta } } / r+q_{z,z} +{q_r } / r=0 \\ \end{array} \right\} \end{eqnarray}$
式中, $q_r $, $q_\theta $, $q_z $为热流. 热流与温度的关系, 可以表示为[25 ]
(3) $ \begin{eqnarray} \label{eq3} q_r =-k_{11} T_{,r},\ \ q_\theta =-k_{22} T_{,\theta} / r,\ \ q_z =-k_{33} T_{,z} \end{eqnarray}$
式中, $k_{ll} $为热传导系数. 几何方程为
(4) $ \begin{eqnarray} \label{eq4} \left. \begin{array}{ll} \varepsilon _{rr} =u_{r,r} , \ \ \varepsilon _{\theta \theta } ={\left( {u_{\theta,\theta } +u_r } \right)} / r, \ \ \varepsilon _{zz} =u_{z,z}\\ \varepsilon _{\theta z} =\varepsilon _{z\theta } =0.5\left( {u_{\theta ,z} +{u_{z,\theta } } / r} \right) \\ \varepsilon _{rz} =\varepsilon _{zr} =0.5\left( {u_{z,r} +u_{r,z} } \right)\\ \varepsilon _{\theta r} =\varepsilon _{r\theta } =0.5\left( {{u_{r,\theta }} / r+u_{\theta ,r} -{u_\theta } / r} \right) \\ w_{rr} =w_{r,r} , \ \ w_{r\theta } =w_{r,\theta}/r, \ \ w_{rz} =w_{r,z} \\ E_r =-\phi _{,r}, \ \ E_\theta =-\phi _{,\theta } / r, \ \ E_z =-\phi _{,z} \\ \end{array} \right\} \end{eqnarray}$
式中, $u_r $, $u_\theta $, $u_z $为声子场位移; $w_r $为相位子场位移; $\phi$为电势. 考虑层合圆柱壳两侧边简支的边界条件[24 ] , 即
(5) $ \begin{eqnarray} \label{eq5} \theta =0,\ \ \theta _0;\ \ \ u_r =w_r =\phi =T=0 \end{eqnarray}$
对于一维准晶功能梯度材料, 假设其材料参数沿着径向呈现幂函数分布, 即
(6) $ \begin{eqnarray} \label{eq6} \left. \begin{array}{ll} C_{kl} (r)=C_{kl}^0 (r/r_j )^\alpha , \ \ R_{kl} (r)=R_{kl}^0 (r/r_j )^\alpha \\ K_{kl} (r)=K_{kl}^0 (r/r_j )^\alpha , \ \ e_{kl} (r)=e_{kl}^0 (r/r_j )^\alpha \\ d_{kl} (r)=d_{kl}^0 (r/r_j )^\alpha , \ \ \xi _{ll} (r)=\xi _{ll}^0 (r/r_j )^\alpha \ \\ \beta _k (r)=\beta _k^0 (r/r_j )^\alpha , \ \ k_{ll} (r)=k_{ll}^0 (r/r_j )^\alpha \\ p_3 (r)=p_3^0 (r/r_j )^\alpha \\ \end{array} \right\} \end{eqnarray}$
式中, $\alpha $为功能梯度指数因子, 表示材料参数在半径$r$方向的梯度分布程度, 后文中$\alpha $均表示功能梯度指数因子; 上标带"0"的物理量表示均质材料对应的材料参数.
2 单层圆柱壳的热电弹性精确解
2.1 温度场的精确解
(7) $ \begin{eqnarray} \label{eq7} T=\bar{{T}}\left( r \right)\sin \left( {p\theta } \right)=f\rho ^\eta \sin \left( {p\theta } \right) \end{eqnarray}$
式中, $\rho = r/r_j $, $p = m\pi/\theta _0 $, $\bar{{T}}\left( r \right)$为与圆柱壳角度$\theta $无关的温度, 文中其他顶部带横线的物理量均表示独立于圆柱壳角度的物理量.
(8) $ \begin{eqnarray} \label{eq8} \left( {k_{11}^0 \eta ^2+k_{11}^0 \alpha \eta -k_{22}^0 p^2} \right)f=0 \end{eqnarray}$
(9) $ \begin{eqnarray} \label{eq9} \eta _1 =\frac{-\alpha +\sqrt {\alpha ^2+4k_{22}^0 p^2/k_{11}^0 }}{2}, \ \ \eta _2 =-\eta _1 -\alpha \end{eqnarray}$
(10) $ \begin{eqnarray} \label{eq10} \left[ {{\begin{array}{cc} 0 & {{-1} / {k_{11}^0 }} \\ {-p^2k_{22}^0 } & {-\alpha } \\ \end{array} }} \right]\left[ {{\begin{array}{c} f \\ g \\ \end{array} }} \right]=\eta \left[ {{\begin{array}{c} f \\ g \\ \end{array} }} \right] \end{eqnarray}$
式中, $\left[ {f,g} \right]^{\rm T}$为特征向量. 为了令特征向量和特征值对应, 对特征向量加下标, 即$\eta _1 $对应$\left[ {f_1 ,g_1 } \right]^{\rm T}$, $\eta _2 $对应$\left[ {f_2 ,g_2 } \right]^{\rm T}$, 式中上标"T"表示矩阵的转置.
利用特征值和特征向量, 可得到一维准晶功能梯度单层圆柱壳温度场的精确解
(11) $ \begin{eqnarray} \label{eq11} \left[ {{\begin{array}{*{20}c} {\bar{{T}}} \\ {r\bar{{q}}_r } \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} 1 & 0 \\ 0 & {\rho ^\alpha } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\rho ^{\eta _1 }} & 0 \\ 0 & {\rho ^{\eta _2 }} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\chi _1 } \\ {\chi _2 } \\ \end{array} }} \right] \end{eqnarray}$
式中, $\chi _1 $和$\chi _2 $为待定未知量.
2.2 电弹耦合场的精确解
(12) $ \begin{eqnarray} \label{eq12} && { u}=\left[ {{\begin{array}{*{20}c} {u_r } \\ {u_\theta } \\ {u_z } \\ {w_r } \\ \phi \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} {\bar{{u}}_r \sin \left( {p\theta } \right)} \\ {\bar{{u}}_\theta \cos \left( {p\theta } \right)} \\ {\bar{{u}}_z \cos \left( {p\theta } \right)} \\ {\bar{{w}}_r \sin \left( {p\theta } \right)} \\ {\bar{{\phi }}\sin \left( {p\theta } \right)} \\ \end{array} }} \right]= \rho ^s\left[ {{\begin{array}{*{20}c} {a_1 \sin \left( {p\theta } \right)} \\ {a_2 \cos \left( {p\theta } \right)} \\ {a_3 \cos \left( {p\theta } \right)} \\ {a_4 \sin \left( {p\theta } \right)} \\ {a_5 \sin \left( {p\theta } \right)} \\ \end{array} }} \right]+ \\ &&\qquad f\rho ^{1+\eta }\left[ {{\begin{array}{*{20}c} {c_1 \sin \left( {p\theta } \right)} \\ {c_2 \cos \left( {p\theta } \right)} \\ {c_3 \cos \left( {p\theta } \right)} \\ {c_4 \sin \left( {p\theta } \right)} \\ {c_5 \sin \left( {p\theta } \right)} \\ \end{array} }} \right] \end{eqnarray}$
将式(12)代入式(4), 然后代入式(1), 得到径向的广义应力矢量
(13) $ \begin{eqnarray} \label{eq13} && r{ t}=r\left[ {{\begin{array}{*{20}c} {\sigma _{rr} } \\ {\sigma _{\theta r} } \\ {\sigma _{zr} } \\ {H_{rr} } \\ {D_r } \\ \end{array} }} \right]=r\left[ {{\begin{array}{*{20}c} {\bar{{\sigma }}_{rr} \sin \left( {p\theta } \right)} \\ {\bar{{\sigma }}_{\theta r} \cos \left( {p\theta } \right)} \\ {\bar{{\sigma }}_{zr} \cos \left( {p\theta } \right)} \\ {\bar{{H}}_{rr} \sin \left( {p\theta } \right)} \\ {\bar{{D}}_r \sin \left( {p\theta } \right)} \\ \end{array} }} \right] =\rho ^{s+\alpha }\left[ {{\begin{array}{*{20}c} {b_1 \sin \left( {p\theta } \right)} \\ {b_2 \cos \left( {p\theta } \right)} \\ {b_3 \cos \left( {p\theta } \right)} \\ {b_4 \sin \left( {p\theta } \right)} \\ {b_5 \sin \left( {p\theta } \right)} \\ \end{array} }} \right]+ \\ &&\qquad f\rho ^{1+\eta +\alpha }\left[ {{\begin{array}{*{20}c} {d_1 \sin \left( {p\theta } \right)} \\ {d_2 \cos \left( {p\theta } \right)} \\ {d_3 \cos \left( {p\theta } \right)} \\ {d_4 \sin \left( {p\theta } \right)} \\ {d_5 \sin \left( {p\theta } \right)} \\ \end{array} }} \right] \end{eqnarray}$
(14) $ \begin{eqnarray} \label{eq14} \left. \begin{array}{ll} { a}=\left[ {a_1 ,a_2 ,a_3 ,a_4 ,a_5 } \right]^{\rm T}, { b}=\left[ {b_1 ,b_2 ,b_3 ,b_4 ,b_5 } \right]^{\rm T} \\ { c}=\left[ {c_1 ,c_2 ,c_3 ,c_4 ,c_5 } \right]^{\rm T}, { d}=\left[ {d_1 ,d_2 ,d_3 ,d_4 ,d_5 } \right]^{\rm T} \\ \end{array} \right\} \end{eqnarray}$
(15) $ \begin{eqnarray} \label{eq15} \left. \begin{array}{ll} { b}=\left( {-{ P}^{\rm T}+s{ T}} \right){ a} \\ { d} \ \ =\left[ {-{ P}^{\rm T}+\left( {1+\eta } \right){ T}} \right]{ c}-{ \beta }_2 \\ \end{array} \right\} \end{eqnarray}$
利用基本方程和式(12), 推导出满足一维热-电-弹性准晶功能梯度层合圆柱壳的类Stroh公式[26 ]
(16) $ \begin{eqnarray} \label{eq16} \left. \begin{array}{ll} \left[ {{ Q}-\alpha { P}^T+s\left( {{ P}-{ P}^T+\alpha { T}} \right)+s^2{ T}} \right]{ a}={\bf 0} \\ \left[{ Q}-\alpha { P}^T+\left( {1+\eta } \right)\left( {{ P}-{ P}^T+\alpha { T}} \right)+ \\ \qquad \left( {1+\eta } \right)^2{ T} \right]{ c}={ \beta }_1 +\left( {1+\eta +\alpha } \right){ \beta }_2 \\ \end{array} \right\} \end{eqnarray}$
(17) $ \begin{eqnarray} \label{eq17} \left. \begin{array}{ll} { Q}=\left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c} {-\left( {C_{55}^0 p^2+C_{11}^0 } \right)} & {\left( {C_{55}^0 +C_{11}^0 } \right)p} & 0 & {-R_6^0 p^2} & {-e_{15}^0 p^2} \\ {\left( {C_{55}^0 +C_{11}^0 } \right)p} & {-\left( {C_{11}^0 p^2+C_{55}^0 } \right)} & 0 & {R_6^0 p} & {e_{15}^0 p} \\ 0 & 0 & {-C_{66}^0 p^2} & 0 & 0 \\ {-R_6^0 p^2} & {R_6^0 p} & 0 & {-K_1^0 p^2} & {-d_{15}^0 p^2} \\ {-e_{15}^0 p^2} & {e_{15}^0 p} & 0 & {-d_{15}^0 p^2} & {\xi _{11}^0 p^2} \\ \end{array} }} \right], \ \ { P}=\left[ {{\begin{array}{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c} {-C_{13}^0 } & {-C_{55}^0 p} & 0 & {-R_1^0 } & {-e_{31}^0 } \\ {C_{13}^0 p} & {C_{55}^0 } & 0 & {R_1^0 p} & {e_{31}^0 p} \\ 0 & 0 & 0 & 0 & 0 \\ 0 & {-R_6^0 p} & 0 & 0 & 0 \\ 0 & {-e_{15}^0 p} & 0 & 0 & 0 \\ \end{array} }} \right]\\[10mm] { T}=\left[ {{\begin{array}{{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c}} {C_{33}^0 } & 0 & 0 & {R_3^0 } & {e_{33}^0 } \\ 0 & {C_{55}^0 } & 0 & 0 & 0 \\ 0 & 0 & {C_{44}^0 } & 0 & 0 \\ {R_3^0 } & 0 & 0 & {K_3^0 } & {d_{33}^0 } \\ {e_{33}^0 } & 0 & 0 & {d_{33}^0 } & {-\xi _{33}^0 } \\ \end{array} }} \right], \ \ { \beta }_1 =r_j \left[ {{\begin{array}{*{20}c} {-\beta _1^0 } \\ {\beta _1^0 p} \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right], \ \ { \beta }_2 =r_j \left[ {{\begin{array}{*{20}c} {\beta _3^0 } \\ 0 \\ 0 \\ 0 \\ {-p_3^0 } \\ \end{array} }} \right] \\ \end{array} \right\} \end{eqnarray}$
为了便于求解, 将式(16)转换为对应的标准特征关系
(18) $ \begin{eqnarray} \label{eq18} { N}\left[ {\begin{array}{l} { a} \\ { b} \\ \end{array}} \right]=s\left[ {\begin{array}{l} { a} \\ { b} \\ \end{array}} \right], \ \ { N}\left[ {\begin{array}{l} { c} \\ { d} \\ \end{array}} \right]=\left( {1+\eta } \right)\left[ {\begin{array}{l} { c} \\ { d} \\ \end{array}} \right]+{ \beta } \end{eqnarray}$
式中, 矩阵${ N}$和${ \beta }$分别为
(19) $ \begin{eqnarray} \label{eq19} \begin{array}{l} { N}=\left[ {{\begin{array}{*{20}c} {{ T}^{-1}{ P}^{\rm T}} & {{ T}^{-1}} \\ {-{ Q}-{ PT}^{-1}{ P}^{\rm T}} & {-{ PT}^{-1}-\alpha { I}} \\ \end{array} }} \right] \\ { \beta }=-\left[ {{\begin{array}{*{20}c} {\bf 0} & {{ T}^{-1}} \\ { I} & {-{ PT}^{-1}} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{ \beta }_1 } \\ {{ \beta }_2 } \\ \end{array} }} \right] \\ \end{array} \end{eqnarray}$
求解式(18), 可得到电-弹耦合场对应的特征值$s$和特征向量$[{ a}\ \ { b}]^{\rm T}$, $[{ c} \ \ { d}]^{\rm T}$. 因此, 一维准晶功能梯度单层圆柱壳电-弹耦合场的精确解为
(20) $ \begin{eqnarray} \label{eq20} && \left[ {{\begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r{\bar{{ t}}}} \\ \end{array} }} \right]=\left[ {{\begin{array}{*{20}c} { I} & {\bf 0} \\ {\bf 0} & {\rho ^\alpha { I}} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{ A}_1 } & {{ A}_2 } \\ {{ B}_1 } & {{ B}_2 } \\ \end{array} }} \right]\left\langle {\rho ^{s\ast }} \right\rangle \left[ {\begin{array}{l} { K}_1 \\ { K}_2 \\ \end{array}} \right]+ \left[ {{\begin{array}{*{20}c} {\rho { I}} & {\bf 0} \\ {\bf 0} & {\rho ^{1+\alpha }{ I}} \\ \end{array} }} \right]\cdot \\&&\qquad \left[ {{\begin{array}{*{20}c} {{ c}_1 } & {{ c}_2 } \\ {{ d}_1 } & {{ d}_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\rho ^{\eta _1 }} & 0 \\ 0 & {\rho ^{\eta _2 }} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & 0 \\ 0 & {f_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\chi _1 } \\ {\chi _2 } \\ \end{array} }} \right] \end{eqnarray}$
(21) $ \begin{eqnarray} \label{eq21} \left. \begin{array}{ll} \left[ \begin{array}{*{20}c} {{\bar{{ u}}}} & {r{\bar{{ t}}}} \\ \end{array} \right]^{\rm T}=\left[ \bar{{u}}_r ,\ \ \bar{{u}}_\theta ,\ \ \bar{{u}}_z ,\ \ \bar{{w}}_r , \ \ \bar{{\phi }}, \ \ r\bar{{\sigma }}_{rr} , \ \ r\bar{{\sigma }}_{\theta r} , \\\qquad r\bar{{\sigma }}_{zr} ,\ \ r\bar{{H}}_{rr} , \ \ r\bar{{D}}_r \right]^{\rm T} \\ { A}_1 =\left[ {{ a}_1 , \ \ { a}_2 , \ \ { a}_3 , \ \ { a}_4 , \ \ { a}_5 } \right]\\ { A}_2 =\left[ { \ \ \ { a}_6 , \ \ { a}_7 , \ \ { a}_8 , \ \ { a}_9 , \ \ { a}_{10} } \right] \\ { B}_1 =\left[ {{ b}_1 , \ \ { b}_2 , \ \ { b}_3 , \ \ { b}_4 , \ \ { b}_5 } \right]\\{ B}_2 =\left[ {{ b}_6 , \ \ { b}_7 , \ \ { b}_8 , \ \ { b}_9 , \ \ { b}_{10} } \right] \\ \left\langle {\rho ^{s^\ast }} \right\rangle = \mbox{diag}\left[ \rho ^{s_1 }, \ \ \rho ^{s_2 }, \ \ \rho ^{s_3 }, \ \ \rho ^{s_4 },\ \ \rho ^{s_5 }, \ \ \rho ^{-s_1 -\alpha }, \\\qquad \rho ^{-s_2 -\alpha }, \ \ \rho ^{-s_3 -\alpha }, \ \ \rho ^{-s_4 -\alpha },\ \ \rho ^{-s_5 -\alpha } \right] \\ \end{array} \right\} \end{eqnarray}$
3 层合圆柱壳的热电弹性精确解
本节引入传递矩阵方法[26 ] , 用于处理层状结构问题. 假设层间界面为完美连接, 首先处理温度场的传递问题, 然后求解电-弹耦合场多层结构问题, 最后将温度场、电场和弹性场的结果合并, 得到一维准晶功能梯度层合圆柱壳的热-电-弹性精确解.
考虑温度场, 对于层合圆柱壳第$j$层, 利用式(11), 有
(22) $ \begin{eqnarray} \label{eq22} && \left[ {{\begin{array}{*{20}c} {\chi _1 } \\ {\chi _2 } \\ \end{array} }} \right]_j =\left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]^{-1}\left[ {{\begin{array}{*{20}c} {\bar{{T}}} \\ {r_j \bar{{q}}_r } \\ \end{array} }} \right]_{r_j } =\left[ {{\begin{array}{*{20}c} {(r_{j+1} /r_j )^{-\eta _1 }} & 0 \\ 0 & {(r_{j+1} /r_j )^{-\eta _2 }} \\ \end{array} }} \right]\cdot \\&&\qquad \left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]^{-1}\left[ {{\begin{array}{*{20}c} 1 & 0 \\ 0 & {(r_{j+1} /r_j )^{-\alpha }} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\bar{{T}}} \\ {r_{j+1} \bar{{q}}_r } \\ \end{array} }} \right]_{r_{j+1} } \end{eqnarray}$
利用式(22), 圆柱壳$j$层任意半径处的物理量为
(23) $ \begin{eqnarray} \label{eq23} \left[ {{\begin{array}{*{20}c} {\bar{{T}}} \\ {r\bar{{q}}_r } \\ \end{array} }} \right]={ T}_j (r/r_j )\left[ {{\begin{array}{*{20}c} {\bar{{T}}} \\ {r_j \bar{{q}}_r } \\ \end{array} }} \right]_{r_j } \end{eqnarray}$
(24) $ \begin{eqnarray} \label{eq24} && { T}_j (r/r_j )=\left[ {{\begin{array}{*{20}c} 1 & 0 \\ 0 & {(r/r_j )^\alpha } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]\cdot \\&&\qquad \left[ {{\begin{array}{*{20}c} {(r/r_j )^{\eta _1 }} & 0 \\ 0 & {(r/r_j )^{\eta _2 }} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]^{-1} \end{eqnarray}$
考虑电-弹耦合场, 对于圆柱壳$j$层, 借助式(20), 可以得到
(25) $ \begin{eqnarray} \label{eq25} && \left[ {\begin{array}{l} { k}_1 \\ { k}_2 \\ \end{array}} \right]_j =\left[ {{\begin{array}{*{20}c} {{ a}_1 } & {{ a}_2 } \\ {{ b}_1 } & {{ b}_2 } \\ \end{array} }} \right]^{-1}\left[ {{\begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r_j {\bar{{ t}}}} \\ \end{array} }} \right]_{r_j } -\left[ {{\begin{array}{*{20}c} {{ a}_1 } & {{ a}_2 } \\ {{ b}_1 } & {{ b}_2 } \\ \end{array} }} \right]^{-1}\left[ {{\begin{array}{*{20}c} {{ c}_1 } & {{ c}_2 } \\ {{ d}_1 } & {{ d}_2 } \\ \end{array} }} \right]\cdot \\&&\qquad \left[ {{\begin{array}{*{20}c} {f_1 } & 0 \\ 0 & {f_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\chi _1 } \\ {\chi _2 } \\ \end{array} }} \right]_j =\left\langle {(r_{j+1} /r_j )^{-s\ast }} \right\rangle \left[ {{\begin{array}{*{20}c} {{ a}_1 } & {{ a}_2 } \\ {{ b}_1 } & {{ b}_2 } \\ \end{array} }} \right]^{-1}\cdot \\&&\qquad \left[ {{\begin{array}{*{20}c} { i} & {\bf 0} \\ {\bf 0} & {(r_{j+1} /r_j )^{-\alpha }{ i}} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r_{j+1} {\bar{{ t}}}} \\ \end{array} }} \right]_{r_{j+1} } -\left\langle {(r_{j+1} /r_j )^{-s\ast }} \right\rangle\cdot \\&&\qquad\left[ {{\begin{array}{*{20}c} {{ a}_1 } & {{ a}_2 } \\ {{ b}_1 } & {{ b}_2 } \\ \end{array} }} \right]^{-1} \left[ {{\begin{array}{*{20}c} { i} & {\bf 0} \\ {\bf 0} & {(r_{j+1} /r_j )^{-\alpha }{ i}} \\ \end{array} }} \right]\cdot \\&&\qquad\left[ {{\begin{array}{*{20}c} {(r_{j+1} /r_j ){ i}} & {\bf 0} \\ {\bf 0} & {(r_{j+1} /r_j )^{1+\alpha }{ i}} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{ c}_1 } & {{ c}_2 } \\ {{ d}_1 } & {{ d}_2 } \\ \end{array} }} \right]\cdot \\&&\qquad \left[ {{\begin{array}{*{20}c} {(r_{j+1} /r_j )^{\eta _1 }} & 0 \\ 0 & {(r_{j+1} /r_j )^{\eta _2 }} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & 0 \\ 0 & {f_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {\chi _1 } \\ {\chi _2 } \\ \end{array} }} \right]_j \end{eqnarray}$
利用式(25), 层合圆柱壳$j$层任意半径处的物理量可以表示为
(26) $ \begin{eqnarray} \label{eq26} \left[ {{\begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r{\bar{{ t}}}} \\ \end{array} }} \right]={ E}_j (r/r_j )\left[ {{\begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r_j {\bar{{ t}}}} \\ \end{array} }} \right]_{r_j } +{ S}_j (r/r_j )\left[ {{\begin{array}{*{20}c} {\bar{{T}}} \\ {r_j \bar{{q}}_r } \\ \end{array} }} \right]_{r_j } \end{eqnarray}$
式中, 矩阵${ E}_j $和${ S}_j $分别为
(27) $ \begin{eqnarray} \label{eq27} \left. \begin{array}{ll} { E}_j (r/r_j )=\left[ {{\begin{array}{*{20}c} { I} & {\bf 0} \\ {\bf 0} & {(r/r_j )^\alpha { I}} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{ A}_1 } & {{ A}_2 } \\ {{ B}_1 } & {{ B}_2 } \\ \end{array} }} \right]\left\langle {(r/r_j )^{s\ast }} \right\rangle\cdot\\\qquad \left[ {{\begin{array}{*{20}c} {{ A}_1 } & {{ A}_2 } \\ {{ B}_1 } & {{ B}_2 } \\ \end{array} }} \right]^{-1} \\ { S}_j (r/r_j )=\left[ {{\begin{array}{*{20}c} {(r/r_j ){ I}} & {\bf 0} \\ {\bf 0} & {(r/r_j )^{1+\alpha }{ I}} \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {{ c}_1 } & {{ c}_2 } \\ {{ d}_1 } & {{ d}_2 } \\ \end{array} }} \right]\\ \qquad\left[ {{\begin{array}{*{20}c} {(r/r_j )^{\eta _1 }} & 0 \\ 0 & {(r/r_j )^{\eta _2 }} \\ \end{array} }} \right] \left[ {{\begin{array}{*{20}c} {f_1 } & 0 \\ 0 & {f_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]^{-1}-\\ \qquad{ E}_j (r/r_j )\left[ {{\begin{array}{*{20}c} {{ c}_1 } & {{ c}_2 } \\ {{ d}_1 } & {{ d}_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & 0 \\ 0 & {f_2 } \\ \end{array} }} \right]\left[ {{\begin{array}{*{20}c} {f_1 } & {f_2 } \\ {g_1 } & {g_2 } \\ \end{array} }} \right]^{-1} \\ \end{array} \right\} \end{eqnarray}$
将式(23)和式(26)中精确解合并, 同时重复利用传递矩阵, 得到一维准晶功能梯度层合圆柱壳的热电弹性精确解
(28) $ \begin{eqnarray} \label{eq28} &&\left[ \begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r_b {\bar{{ t}}}} \\ {\bar{{T}}} \\ {r_b \bar{{q}}_r } \\ \end{array} \right]_{r_b } ={ G}_N (\delta _N ){ G}_{N-1} (\delta _{N-1} )\cdot \cdot \cdot { G}_2 (\delta _2 ){ G}_1 (\delta _1 )\cdot \\&&\qquad\left[ {{\begin{array}{*{20}c} {{\bar{{ u}}}} \\ {r_a {\bar{{ t}}}} \\ {\bar{{T}}} \\ {r_a \bar{{q}}_r } \\ \end{array} }} \right]_{r_a } \end{eqnarray}$
式中, $\delta _j =r_{j+1} /r_j $, 传递矩阵${ G}_j (\delta _j )$为
(29) $ { G}_j (\delta _j )=\left[ {{\begin{array}{c@{\quad }c} {{ E}_j (\delta _j )} & {{ S}_j (\delta _j )} \\ {\bf 0} & {{ T}_j (\delta _j )} \\ \end{array} }} \right]$
4 数值算例
本节主要讨论功能梯度指数因子对温度场、电场、声子场和相位子场的影响. 考虑3层功能梯度圆柱壳, 第一层和第三层为功能梯度准晶材料Al-Ni-Co, 第二层为均质压电材料BaTiO$_{3}$, 且每层厚度相等, 材料常数见表1 [27 -29 ] . 计算中为避免产生奇异矩阵, 晶体的相位子场弹性常数按照10$^{-8}$倍的准晶相位子场弹性常数选取[30 ] , 同时晶体中声子场-相位子场耦合弹性常数为0.
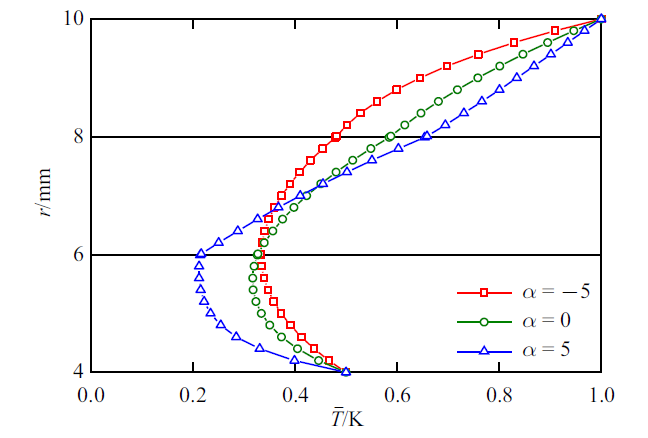
层合圆柱壳的几何参数为: 内表面半径$r_{a}= 4$ mm, 外表面半径$r_{b }= 10$ mm, 角度跨度$\theta_{0 }= 1$ rad. 假设在功能梯度层合圆柱壳的内外表面同时施加温度载荷, 外表面载荷为$T(r_b ) = 1K$, 内表面载荷为$T(r_a )=0.5K$. 令$m = 1$, 指数因子分别为$\alpha = -5$, 0, 5. 当$\alpha = 0$时, 功能梯度材料退化为均质材料. 数值算例中给出的物理量均独立于圆柱壳角度$\theta $.
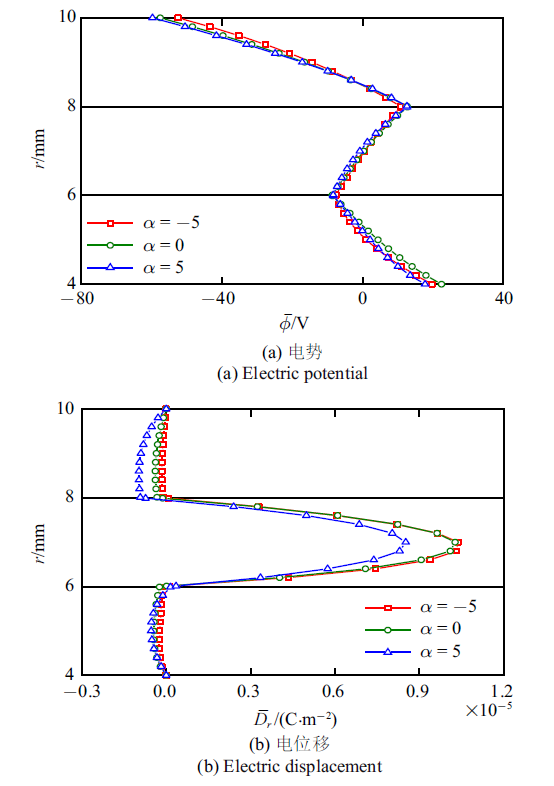
图2 给出指数因子$\alpha $对温度$\bar{{T}}$的影响, 图3 为电势$\bar{{\phi }}$和电位移$\bar{{D}}_r $随着指数因子$\alpha $的变化曲线. 从图2 可以看到, $\bar{{T}}$在功能梯度层合圆柱壳的内表面为0.5, 外表面为1.0. 同时, 图3 (b)显示电位移$\bar{{D}}_r $在功能梯度层合圆柱壳的内外表面均为0. 上述物理量在圆柱壳内外表面的数值满足加载的边界条件. 文中考虑了温度场对弹性场、电场的单向耦合问题, 根据温度场传递矩阵关系, 图2 所示$\bar{{T}}$与$\alpha $和特征值$\eta $有关. 同时考虑层合圆柱壳内外表面加载的温度边界条件. 因此, 不同$\alpha $对应的$\bar{{T}}$曲线出现交叉现象. 此外, $\alpha = -5$对应的温度$\bar{{T}}$在界面处更光滑, 是因为不同层间的热传导系数差异性减小导致的. 在图3 (a)中, 最外层的$\bar{{\phi }}$随着$\alpha $的增大略有增大. 图3 (b)所示中间层的$\bar{{D}}_r $数值随着$\alpha $的减小而增大, 并且数值远大于外层和内层, 这主要是因为晶体的热电系数大于准晶材料的热电系数导致.
图2
图2
指数因子对温度的影响
Fig.2
Influence of exponential factor on temperature
图3
图3
指数因子对电场的影响
Fig.3
Influence of exponential factor on electric field
图4 为不同指数因子$\alpha $对应的声子场和相位子场应力沿半径方向的变化曲线. 图4 (a)为在圆柱壳界面处连续的声子场应力$\bar{{\sigma }}_{rr} $. 和$\alpha =-5$对应的$\bar{{\sigma }}_{rr} $相比, $\alpha = 5$对应的$\bar{{\sigma }}_{rr} $最大值更大. 此外, $\alpha = 5$对应的$\bar{{\sigma }}_{rr} $在靠近内表面处数值最小, 在靠近外表面处数值最大. 从图4 (b)可以看到, 相位子场应力$\bar{{H}}_{rr} $在中间层为0, 因为晶体中不存在相位子场. 准晶层中的$\bar{{H}}_{rr} $随着$\alpha $的增大而增大.
图4
图4
指数因子对声子场和相位子场应力的影响
Fig.4
Influence of exponential factor on phonon and phason stresses
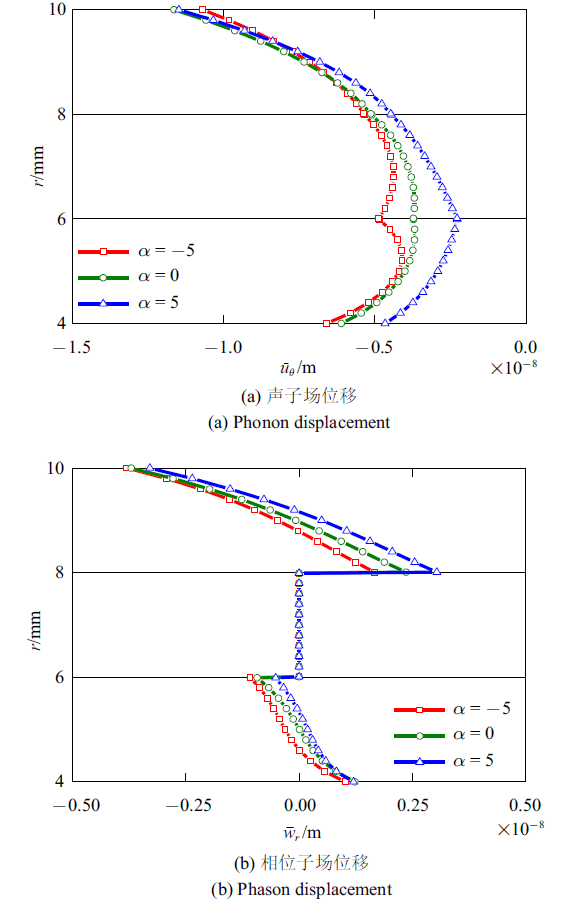
图5 给出指数因子$\alpha $对声子场和相位子场位移的影响. 图5 (a)显示声子场位移$\bar{{u}}_\theta $在界面处是连续的. 文中功能梯度材料参数遵循幂函数变化规律, 当指数因子$\alpha >0$时, 功能梯度材料性质呈现渐变硬化趋势, $\alpha <0$ 则呈现渐变软化特性. 所以层合圆柱壳内表面$\bar{{u}}_\theta $随着$\alpha $增大而变小. 同时, $\bar{{u}}_\theta$的大小还与层合圆柱壳半径有关. 因此, 不同的指数因子对应的$\bar{{u}}_\theta $在最外层出现交点. 此外, 和$\alpha =-5$对应的$\bar{{u}}_\theta $相比, $\alpha = 5$对应的$\bar{{u}}_\theta $在界面处曲线更光滑. 在图5 (b)中, 和$\alpha$对$\bar{{u}}_\theta $的影响相比, $\alpha $对内外表面处的相位子场位移$\bar{{w}}_r $的影响较小.
图5
图5
指数因子对声子场和相位子场位移的影响
Fig.5
Influence of exponential factor on phonon and phason displacements
5 结论
本文利用类Stroh理论和传递矩阵方法, 研究了一维准晶功能梯度层合圆柱壳的热电弹性耦合问题, 基于材料参数沿径向呈现幂函数分布特点, 得到了简支边界条件下的一维准晶功能梯度层合圆柱壳的热电弹性精确解. 数值算例中讨论了功能梯度指数因子对温度场、电场、声子场和相位子场的影响. 所得结论如下:
(1) 指数因子的变化影响层合圆柱壳的材料性质分布情况, 进而对温度、电势、电位移、声子场和相位子场应力和位移产生较大的影响.
(2) 随着指数因子的增大, 径向声子场应力增大, 且最大值出现在层合圆柱壳外层. 外层中较大的应力易于被外层凸面分散, 从而提升层合圆柱壳的承载能力.
(3) 随着指数因子的增大, 层合圆柱壳外表面周向声子场位移略有增大, 内表面周向声子场位移减小. 此外, 周向位移在界面处更为光滑, 可有效减缓层合圆柱壳在界面处出现开裂和分层等现象.
参考文献
View Option
[1]
叶天贵 , 靳国永 , 刘志刚 . 多层复合壳体三维振动分析的谱--微分求积混合法
力学学报 , 2018 ,50 (4 ):847 -852
[本文引用: 1]
( Ye Tiangui Jin Guoyong Liu Zhigang . A spectral-differential quadrature method for 3-d vibration analysis of multilayered shells
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (4 ):847 -852 (in Chinese))
[本文引用: 1]
[2]
仲政 , 吴林志 , 陈伟球 . 功能梯度材料与结构的若干力学问题研究进展
力学进展 , 2010 ,40 (5 ):528 -541
[本文引用: 2]
( Zhong Zheng Wu Linzhi Chen Weiqiu . Progress in the study of mechanics problems of functionally graded materials and structures
Advances in Mechanics 2010 ,40 (5 ):528 -541 (in Chinese))
[本文引用: 2]
[3]
柯燎亮 , 汪越胜 . 功能梯度材料接触力学若干基本问题的研究进展
科学通报 , 2015 ,60 (17 ):1565 -1573
[本文引用: 2]
( Ke Liaoliang Wang Yuesheng . Progress in some basic problems on contact mechanics of functionally graded materials
Chin Sci Bull 2015 ,60 :1565 -1573 (in Chinese))
[本文引用: 2]
[4]
郑保敬 , 梁钰 , 高效伟 等 . 功能梯度材料动力学问题的POD模型降阶分析
力学学报 , 2018 ,50 (4 ):787 -797
[本文引用: 1]
( Zheng Baojing Liang Yu Gao Xiaowei , et al . Analysis for dynamic response of functionally graded materials using pod based reduced order model
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (4 ):787 -797 (in Chinese))
[本文引用: 1]
[5]
杨健鹏 , 王惠明 . 功能梯度球形水凝胶的化学力学耦合分析
力学学报 , 2019 ,51 (4 ):1054 -1063
[本文引用: 1]
( Yang Jianpeng Wang Huiming . Chemomechanical analysis of a functionally graded spherical hydrogel
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):1054 -1063 (in Chinese))
[本文引用: 1]
[6]
Yang QQ Gao CF . Reduction of the stress concentration around an elliptic hole by using a functionally graded layer
Acta Mechanica 2016 ,227 (9 ):2427 -2437
DOI
URL
[本文引用: 1]
[7]
Yang B Chen WQ Ding HJ . Approximate elasticity solutions for functionally graded circular plates subject to a concentrated force at the center
Mathematics and Mechanics of Solids 2014 ,19 (3 ):277 -288
[本文引用: 1]
[8]
Pan E Han F . Exact solution for functionally graded and layered magneto-electro-elastic plates
International Journal of Engineering Science 2005 ,43 (3-4 ):321 -339
[本文引用: 1]
[9]
Shechtman D Blech I Gratias D , et al . Metallic phase with long-range orientational order and no translational symmetry
Physical Review Letters 1984 ,53 (20 ):1951 -1953
[本文引用: 1]
[10]
范天佑 . 准晶数学弹性力学和缺陷力学
力学进展 , 2000 ,30 (2 ):161 -174
[本文引用: 1]
( Fan Tianyou . Mathematical theory of elasticity and defects of quasicrystals
Advances in Mechanics 2000 ,30 (2 ):161 -174 (in Chinese))
[本文引用: 1]
[11]
Bak P . Symmetry, stability, and elastic properties of icosahedral incommensurate crystals
Physical Review B 1985 ,32 (9 ):5764 -5772
[本文引用: 1]
[12]
Gao Y Ricoeur A . Three-dimensional Green's functions for two-dimensional quasi-crystal bimaterials
Proceedings of the Royal Society A 2011 ,467 (2133 ):2622 -2642
[本文引用: 1]
[13]
Jaric M . Introduction to Quasicrystals
Elsevier , 2012
[本文引用: 1]
[14]
Fan TY . A study on the specific heat of a one-dimensional hexagonal quasicrystal
Journal of Physics-Condensed Matter 1999 ,11 (45 ):513 -517
[本文引用: 1]
[15]
Dubois JM . Properties- and applications of quasicrystals and complex metallic alloys
Chemical Society Reviews 2012 ,41 (20 ):6760 -6777
DOI
URL
PMID
[本文引用: 1]
This article aims at an account of what is known about the potential for applications of quasicrystals and related compounds, the so-called family of Complex Metallic Alloys (CMAsdouble dagger). Attention is focused at aluminium-based CMAs, which comprise a large number of crystalline compounds and quasicrystals made of aluminium alloyed with transition metals (like Fe or Cu) or normal metals like Mg. Depending on composition, the structural complexity varies from a few atoms per unit cell up to thousands of atoms. Quasicrystals appear then as CMAs of ultimate complexity and exhibit a lattice that shows no periodicity anymore in the usual 3-dimensional space. Properties change dramatically with lattice complexity and turn the metal-type behaviour of simple Al-based crystals into a far more complex behaviour, with a fingerprint of semi-conductors that may be exploited in various applications, potential or realised. An account of the ones known to the author is given in the light of the relevant properties, namely light absorption, reduced adhesion and friction, heat insulation, reinforcement of composites for mechanical devices, and few more exotic ones. The role played by the search for applications of quasicrystals in the development of the field is briefly addressed in the concluding section.
[16]
Maugin GA . A note on the thermo-mechanics of elastic quasi-crystals
Archive of Applied Mechanics 2016 ,86 (1 ):245 -251
[本文引用: 1]
[17]
Li XY Wang YW Li PD , et al . Three-dimensional fundamental thermo-elastic field in an infinite space of two-dimensional hexagonal quasi-crystal with a penny-shaped/half-infinite plane crack
Theoretical and Applied Fracture Mechanics 2017 ,88 :18 -30
[本文引用: 1]
[18]
Guo JH Yu J Xing YM , et al . Thermoelastic analysis of a two-dimensional decagonal quasicrystal with a conductive elliptic hole
Acta Mechanica 2016 ,227 (9 ):2595 -2607
[本文引用: 1]
[19]
Li Y Qin QH Zhao MH . Analysis of 3D planar crack problems in one-dimensional hexagonal piezoelectric quasicrystals with thermal effect. part I: Theoretical formulations
International Journal of Solids and Structures 2020 , 188-189 :269 -281
[本文引用: 1]
[20]
Li Y Qin QH Zhao MH . Analysis of 3D planar crack problems of one-dimensional hexagonal piezoelectric quasicrystals with thermal effect. part II: Numerical approach
International Journal of Solids and Structures 2020 , 188-189 :223 -232
[本文引用: 1]
[21]
Zhang L Guo JH Xing YM . Bending deformation of multilayered one-dimensional hexagonal piezoelectric quasicrystal nanoplates with nonlocal effect
International Journal of Solids and Structures 2018 ,132 :278 -302
[本文引用: 1]
[22]
Yang LZ Li Y Gao Y , et al . Three-dimensional exact thermo-elastic analysis of multilayered two-dimensional quasicrystal nanoplates
Applied Mathematical Modelling 2018 ,63 :203 -218
[23]
Waksmanski N Pan E Yang LZ , et al . Free vibration of a multilayered one-dimensional quasi-crystal plate
Journal of Vibration and Acoustics 2014 ,136 (4 ):041019
[本文引用: 1]
[24]
Li Y Yang LZ Zhang LL , et al . Exact thermoelectroelastic solution of layered one-dimensional quasicrystal cylindrical shells
Journal of Thermal Stresses 2018 ,41 (10-12 ):1450 -1467
[本文引用: 2]
[25]
杨世铭 , 陶文铨 . 传热学 . 北京 :高等教育出版社 , 2006
[本文引用: 1]
[26]
Pan E . Exact solution for simply supported and multilayered magneto-electro-elastic plates
Journal of Applied Mechanics 2001 ,68 (4 ):608 -618
[本文引用: 2]
[27]
Li XY Wang T Zheng RF , et al . Fundamental thermo-electro-elastic solutions for 1D hexagonal QC
Zeitschrift für Angewandte Mathematik und Mechanik 2015 ,95 (5 ):457 -468
[本文引用: 1]
[28]
Ootao Y Ishihara M . Exact solution of transient thermal stress problem of a multilayered magneto-electro-thermoelastic hollow cylinder
Journal of Solid Mechanics and Materials Engineering 2011 ,5 (2 ):90 -103
[29]
Li Y Yang LZ Gao Y . Thermo-elastic analysis of functionally graded multilayered two-dimensional decagonal quasicrystal plates
Zeitschrift für Angewandte Mathematik und Mechanik 2018 ,98 (9 ):1585 -1602
[本文引用: 1]
[30]
Waksmanski N Pan E Yang LZ , et al . Harmonic response of multilayered one-dimensional quasicrystal plates subjected to patch loading
Journal of Sound and Vibration 2016 ,375 :237 -253
DOI
URL
[本文引用: 1]
多层复合壳体三维振动分析的谱--微分求积混合法
1
2018
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
多层复合壳体三维振动分析的谱--微分求积混合法
1
2018
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度材料与结构的若干力学问题研究进展
2
2010
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
... [2 ]对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度材料与结构的若干力学问题研究进展
2
2010
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
... [2 ]对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度材料接触力学若干基本问题的研究进展
2
2015
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
... [3 ]结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度材料接触力学若干基本问题的研究进展
2
2015
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
... [3 ]结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度材料动力学问题的POD模型降阶分析
1
2018
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度材料动力学问题的POD模型降阶分析
1
2018
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度球形水凝胶的化学力学耦合分析
1
2019
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
功能梯度球形水凝胶的化学力学耦合分析
1
2019
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
Reduction of the stress concentration around an elliptic hole by using a functionally graded layer
1
2016
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
Approximate elasticity solutions for functionally graded circular plates subject to a concentrated force at the center
1
2014
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
Exact solution for functionally graded and layered magneto-electro-elastic plates
1
2005
... 层状结构因其优异的性能被广泛应用于航空、航天、土木和机械等领域[1 ] . 常规的层状结构是由均质材料层组合而成, 以期获得更好的机械和热力学性能. 但是, 这种层状结构界面处材料参数的突然变化会产生较大的层间应力, 从而导致应力集中、裂纹和分层等问题. 为了克服这些不利影响, 科学家们提出功能梯度材料的概念, 即利用连续变化的组分梯度来代替突变界面, 进而消除界面处的物理性能突变, 达到提高结构强度和优化结构性能的目的[2 -3 ] . 鉴于功能梯度材料具有组成结构连续变化和可设计性的特点, 越来越多的科研人员对功能梯度材料表现出极大的兴趣. 仲政等[2 ] 对功能梯度材料与结构若干力学问题的最新研究进展进行了综述, 并对非均匀介质力学研究进行了展望. 柯燎亮和汪越胜[3 ] 结合功能梯度材料接触力学的若干基本问题, 综述了相关理论的研究进展. 郑保敬等[4 ] 提出一种模型降阶方法用于分析非均质材料结构在复杂载荷作用下的动态响应. 杨健鹏和王惠明[5 ] 研究了功能梯度球形水凝胶在一定条件下的非均匀大变形溶胀行为. Yang等[6 ] 利用复变函数方法研究了含有功能梯度层加固椭圆孔的无限大板的应力集中问题, 并获得了其通解. 基于广义England方法, Yang等[7 ] 研究了功能梯度圆板在中心承受集中力作用下的轴对称弯曲问题. Pan和Han[8 ] 提出类Stroh理论用于研究功能梯度磁电弹层合板的弯曲问题, 获得了材料常数沿厚度方向呈现指数函数分布的精确解. ...
Metallic phase with long-range orientational order and no translational symmetry
1
1984
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
准晶数学弹性力学和缺陷力学
1
2000
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
准晶数学弹性力学和缺陷力学
1
2000
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Symmetry, stability, and elastic properties of icosahedral incommensurate crystals
1
1985
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Three-dimensional Green's functions for two-dimensional quasi-crystal bimaterials
1
2011
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Introduction to Quasicrystals
1
2012
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
A study on the specific heat of a one-dimensional hexagonal quasicrystal
1
1999
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Properties- and applications of quasicrystals and complex metallic alloys
1
2012
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
A note on the thermo-mechanics of elastic quasi-crystals
1
2016
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Three-dimensional fundamental thermo-elastic field in an infinite space of two-dimensional hexagonal quasi-crystal with a penny-shaped/half-infinite plane crack
1
2017
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Thermoelastic analysis of a two-dimensional decagonal quasicrystal with a conductive elliptic hole
1
2016
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Analysis of 3D planar crack problems in one-dimensional hexagonal piezoelectric quasicrystals with thermal effect. part I: Theoretical formulations
1
2020
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Analysis of 3D planar crack problems of one-dimensional hexagonal piezoelectric quasicrystals with thermal effect. part II: Numerical approach
1
2020
... 准晶由以色列科学家Shechtman教授首次在急冷的Al-Mn 合金电子衍射图形中发现[9 ] . 准晶是一种不同于晶体和非晶体的新型固体材料, 具有长程有序的原子排列, 但不具备平移对称性[10 ] . 基于Landau的元激发唯象理论, 准晶中存在两个低能元激发: 声子和相位子[11 -12 ] . 相位子场的引入, 使准晶表现出不同于晶体和非晶体的多种性能, 如: 高强度、高硬度、耐磨性、耐腐蚀、低摩擦系数和低导热率等[13 -14 ] . 由于准晶表现出来的优异性能, 其主要用作表面涂层、薄膜以及复合材料增强相[15 ] . 随着准晶应用的推广, 准晶材料的性能研究受到许多学者的关注. Maugin[16 ] 将提出的准晶弹性方程扩展到准晶热弹性问题中. Li等[17 ] 利用广义势能理论, 研究了二维六方准晶中的三维热弹性平面裂纹问题, 并获得了解析解. Guo等[18 ] 基于Stroh理论, 研究了二维十次热弹性准晶的缺陷问题. Li等[19 -20 ] 分别给出了考虑热效应的一维六方压电准晶中平面裂纹问题的理论解和数值解. ...
Bending deformation of multilayered one-dimensional hexagonal piezoelectric quasicrystal nanoplates with nonlocal effect
1
2018
... 层合圆柱壳具有重量轻、强度高等特点, 是工程中常用的结构元件之一. 目前, 关于准晶层状结构的动态和静态问题研究多数是基于矩形层合板开展的[21 -23 ] . 此外, 同时考虑热电弹耦合效应和材料不均匀性的准晶层合圆柱壳的研究开展的很少. 因此, 本文采用类Stroh理论和传递矩阵方法, 获得了一维准晶功能梯度层合圆柱壳的热电弹性精确解, 讨论了功能梯度指数因子对层合圆柱壳物理量的影响, 以期为准晶功能梯度层合圆柱壳的多场耦合效应及非均匀性分析提供可靠的参考依据. ...
Three-dimensional exact thermo-elastic analysis of multilayered two-dimensional quasicrystal nanoplates
2018
Free vibration of a multilayered one-dimensional quasi-crystal plate
1
2014
... 层合圆柱壳具有重量轻、强度高等特点, 是工程中常用的结构元件之一. 目前, 关于准晶层状结构的动态和静态问题研究多数是基于矩形层合板开展的[21 -23 ] . 此外, 同时考虑热电弹耦合效应和材料不均匀性的准晶层合圆柱壳的研究开展的很少. 因此, 本文采用类Stroh理论和传递矩阵方法, 获得了一维准晶功能梯度层合圆柱壳的热电弹性精确解, 讨论了功能梯度指数因子对层合圆柱壳物理量的影响, 以期为准晶功能梯度层合圆柱壳的多场耦合效应及非均匀性分析提供可靠的参考依据. ...
Exact thermoelectroelastic solution of layered one-dimensional quasicrystal cylindrical shells
2
2018
... 对于考虑热-电-弹耦合的一维正交准晶材料, 本构方程为[24 ] ...
... 式中, $u_r $, $u_\theta $, $u_z $为声子场位移; $w_r $为相位子场位移; $\phi$为电势. 考虑层合圆柱壳两侧边简支的边界条件[24 ] , 即 ...
1
2006
... 式中, $q_r $, $q_\theta $, $q_z $为热流. 热流与温度的关系, 可以表示为[25 ] ...
Exact solution for simply supported and multilayered magneto-electro-elastic plates
2
2001
... 利用基本方程和式(12), 推导出满足一维热-电-弹性准晶功能梯度层合圆柱壳的类Stroh公式[26 ] ...
... 本节引入传递矩阵方法[26 ] , 用于处理层状结构问题. 假设层间界面为完美连接, 首先处理温度场的传递问题, 然后求解电-弹耦合场多层结构问题, 最后将温度场、电场和弹性场的结果合并, 得到一维准晶功能梯度层合圆柱壳的热-电-弹性精确解. ...
Fundamental thermo-electro-elastic solutions for 1D hexagonal QC
1
2015
... 本节主要讨论功能梯度指数因子对温度场、电场、声子场和相位子场的影响. 考虑3层功能梯度圆柱壳, 第一层和第三层为功能梯度准晶材料Al-Ni-Co, 第二层为均质压电材料BaTiO$_{3}$, 且每层厚度相等, 材料常数见表1 [27 -29 ] . 计算中为避免产生奇异矩阵, 晶体的相位子场弹性常数按照10$^{-8}$倍的准晶相位子场弹性常数选取[30 ] , 同时晶体中声子场-相位子场耦合弹性常数为0. ...
Exact solution of transient thermal stress problem of a multilayered magneto-electro-thermoelastic hollow cylinder
2011
Thermo-elastic analysis of functionally graded multilayered two-dimensional decagonal quasicrystal plates
1
2018
... 本节主要讨论功能梯度指数因子对温度场、电场、声子场和相位子场的影响. 考虑3层功能梯度圆柱壳, 第一层和第三层为功能梯度准晶材料Al-Ni-Co, 第二层为均质压电材料BaTiO$_{3}$, 且每层厚度相等, 材料常数见表1 [27 -29 ] . 计算中为避免产生奇异矩阵, 晶体的相位子场弹性常数按照10$^{-8}$倍的准晶相位子场弹性常数选取[30 ] , 同时晶体中声子场-相位子场耦合弹性常数为0. ...
Harmonic response of multilayered one-dimensional quasicrystal plates subjected to patch loading
1
2016
... 本节主要讨论功能梯度指数因子对温度场、电场、声子场和相位子场的影响. 考虑3层功能梯度圆柱壳, 第一层和第三层为功能梯度准晶材料Al-Ni-Co, 第二层为均质压电材料BaTiO$_{3}$, 且每层厚度相等, 材料常数见表1 [27 -29 ] . 计算中为避免产生奇异矩阵, 晶体的相位子场弹性常数按照10$^{-8}$倍的准晶相位子场弹性常数选取[30 ] , 同时晶体中声子场-相位子场耦合弹性常数为0. ...