考虑应变率的广义压电热弹理论及其应用 1)

doi:10.6052/0459-1879-20-120

考虑应变率的广义压电热弹理论及其应用 ¹⁾

李吉伟, 何天虎^,²⁾

兰州理工大学理学院, 兰州 730050

A GENERALIZED PIEZOELECTRIC-THERMOELASTIC THEORY WITH STRAIN RATE AND ITS APPLICATION ¹⁾

Li Jiwei, He Tianhu^,²⁾

School of Science, Lanzhou University of Technology, Lanzhou 730050, China

通讯作者: 2)何天虎, 教授, 主要研究方向: 广义热弹性理论. E-mail:heth@lut.edu.cn

收稿日期: 2020-04-15 接受日期: 2020-04-15 网络出版日期: 2020-09-18

基金资助:

1)国家自然科学基金资助项目. 11972176

Received: 2020-04-15 Accepted: 2020-04-15 Online: 2020-09-18

作者简介 About authors

摘要

工程中大量材料的形变介于弹性与黏性之间, 既具有弹性固体特性, 又具有黏性流体特点, 即为黏弹性. 黏弹性使得材料出现很多力学松弛现象, 如应变松弛、滞后损耗等行为. 在研究受热载荷作用的多场耦合问题的瞬态响应时, 考虑此类问题中的热松弛和应变松弛现象, 对准确描述其瞬态响应尤为重要. 针对广义压电热弹问题的瞬态响应, 尽管已有学者建立了考虑热松弛的广义压电热弹模型, 但迄今, 尚未计入应变松弛. 本文中, 考虑到材料变形时的应变松弛, 通过引入应变率, 在Chandrasekharaiah广义压电热弹理论的基础之上, 经拓展, 建立了考虑应变率的广义压电热弹理论. 借助热力学定律, 给出了理论的建立过程并得到了相应的状态方程及控制方程. 在本构方程中, 引入了应变松弛时间与应变率的乘积项, 同时, 分别在本构方程和能量方程中引入了热松弛时间因子. 其后, 该理论被用于研究受移动热源作用的压电热弹一维问题的动态响应问题. 采用拉普拉斯变换及其数值反变换, 对问题进行了求解, 得到了不同应变松弛时间和热源移动速度下的瞬态响应, 即无量纲温度、位移、应力和电势的分布规律, 并重点考察了应变率对各物理量的影响效应, 将结果以图形形式进行了表示. 结果表明: 应变率对温度、位移、应力和电势的分布规律有显著影响.

关键词： 应变率 ; 松弛时间 ; 非傅里叶效应 ; 瞬态响应 ; 压电热弹性

Abstract

The deformation of a large number of materials in engineering is between elasticity and viscosity, which exhibits both features of elastic solid and viscous fluid, that is, viscoelasticity. Viscoelasticity causes many mechanical relaxation phenomena, such as strain relaxation and hysteresis loss. In the investigation of transient response of multi-field problems subjected to thermal loading, it is especially important to take the phenomena such as thermal relaxation and the strain relaxation into consideration to accurately describe their transient response. For the transient response of the generalized piezoelectric-thermoelastic problems, although the generalized piezoelectric-thermoelastic model was established by taking into account the thermal relaxation, no strain relaxation is included so far. In present paper, by considering the strain relaxation in the process of deformation, a generalized piezoelectric-thermoelastic theory is theoretically established by extending Chandrasekharaiah's theory through taking strain rate into consideration. By means of the thermodynamic laws, the theory is formulated and the corresponding state equations and governing equations are obtained. In constitutive equation, a term of the product of a strain relaxation time and the strain rate is introduced, meanwhile, thermal relaxation time factors are included in constitutive equation and energy equation respectively. Subsequently, this theory is applied to investigating the dynamic response of a one-dimensional piezoelectric-thermoelastic problem subjected to a moving heat source. The Laplace transform and its numerical inverse transform are used to solve the problem, and the transient response under different strain relaxation time and heat source moving speed is obtained, that is, the distribution law of dimensionless temperature, displacement, stress and electric potential. The effect of strain rate on each physical quantity was investigated, and the results were presented in graphical form. The results show that the strain rate has a significant effect on the distributions of temperature, displacement, stress and electric potential.

Keywords： strain rate ; relaxation times ; non-Fourier's effect ; transient response ; piezoelectric-thermoelasticity

PDF (1163KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

李吉伟, 何天虎. 考虑应变率的广义压电热弹理论及其应用 ¹⁾. 力学学报[J], 2020, 52(5): 1267-1276 DOI:10.6052/0459-1879-20-120

Li Jiwei, He Tianhu. A GENERALIZED PIEZOELECTRIC-THERMOELASTIC THEORY WITH STRAIN RATE AND ITS APPLICATION ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(5): 1267-1276 DOI:10.6052/0459-1879-20-120

引言

随着器件小型化及现代加热技术的发展, 如超短激光脉冲, 微波等, 用于模拟材料在极短时间内^[1-9]的热力学行为的经典热弹性理论令人质疑. 针对极端条件下的传热问题, 学者们对傅里叶定律进行了修正, 基于不同机理, 得到了形式各异的非傅里叶热传导模型. 第一个修正的模型是由Cattaneo^[10]和Vernotte^[11] (C-V)提出的, 他们通过引入热松弛时间因子和热流率的乘积项对经典傅里叶定律进行了修正, 得到了波型的热传导方程. 此后, Lord 和Shulman(L-S)^[12]及Green 和Lindsay(G-L)^[13]发展得到了广义的热弹性理论. 其他的广义热弹理论模型包括: 考虑或不考虑耗散的G--N^[14-16]模型、惯性熵模型^[17]、热质模型^[18]等. 在过去的数十年间, 分数阶微积分在描述反常扩散等问题方面得到了长足发展, 并被学者们引入了热弹性理论, 建立了分数阶型的广义热弹性理论, 如Povstenko^[19]提出的分数阶热弹性理论, Youssef ^[20]提出的L-S型分数阶理论, Sherief等^[21]、Ezzat^[22]和于亚军等^[23]的分数阶理论, 以及G-L型分数阶理论^[24]等. 许光映等^[25]基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和应力场的解析解. 针对电磁介质, 学者也建立了广义电磁热弹理论来研究相关问题, 如Sherief和Anwar^[26]将第三类热边界条件应用于圆环的内外表面, 研究了无限传导和有限传导圆环的动态响应问题. 何天虎等^[27]求解了无限长圆柱体的广义电磁热弹问题. 除此之外, 在广义热弹问题中, 考虑记忆依赖效应, 也引起了学者们的关注. 张培等^[28]基于记忆依赖非局部广义热弹理论, 研究了两段固定、受移动热源作用的有限长热弹杆的瞬态响应. 李妍等^[29]基于L-S广义热弹扩散理论, 建立了考虑材料记忆依赖效应和空间非局部效应的记忆依赖型非局部广义热弹扩散耦合理论.

压电陶瓷^[30-31]广泛用于各种智能结构, 由于压电效应, 常被用作传感器和致动器等. 为描述压电材料的热弹行为, Mindlin^[32]建立了经典热压电理论, 研究了热压电板的热弹行为; 在1988年, Chandrasekharaiah^[33]对基于热力学定律和G-L热弹性理论, 对Mindlin^[32]理论进行了拓展, 建立了广义压电热弹耦合的线性理论, 其中的热传导方程包含温度变化率, 同时在本构方程和能量方程中各引入了一个热松弛时间因子, 描述热以波的形式以有限速度进行传播. 基于Chandrasekharaiah理论, He等^[34]等运用拉普拉斯变换, 结合有限元方法, 研究了二维广义热压电问题; 此外, Majhi^[35]提出了一种势函数, 基于L-S型广义热弹压电理论, 研究了半无限长压电杆受局部热源作用的动态响应; 何天虎等^[36]基于L-S型广义热弹压电理论, 研究了热源移动时热压电杆的动态响应; Babaei和Chen^[37]在何天虎等^[36]的研究工作基础上, 经细化, 进一步研究了受移动热源作用的有限长热压电杆的动态响应问题.

工程中大量材料的形变介于弹性与黏性之间, 既具有弹性固体特性, 又具有黏性流体特点, 即为黏弹性. 黏弹性使得材料出现很多力学松弛现象, 如应变松弛、滞后损耗等行为. 在材料变形时由于分子间有内摩擦, 分子链运动时损耗能量, 除弹性形变外, 还有黏性形变和损耗, 应力和形变也不能建立平衡对应关系, 而有一个松弛过程, 因此出现应变滞后于应力的现象. 在广义热弹耦合问题的诸多研究中, 结果表明, 位移在弹性波和热波前不连续^[18-24], 这与连续体力学的位移连续性假设相矛盾. Yu等^[38]的研究工作进一步表明, 考虑应变率, 可消除位移的不连续性现象. 因此, 建立广义热弹性理论模型时, 考虑应变松弛, 是非常必要的. 考虑应变率的主旨, 便是考虑材料本身的应变松弛现象, 从而更加真实地反映材料变形机理.

本文在Chandrasekharaiah广义压电热弹理论的基础之上, 考虑材料变形时的应变迟滞现象, 通过引入应变率, 经拓展, 建立了考虑应变率的广义压电热弹理论. 理论中除考虑了应变率之外, 还考虑了温度变化率, Mindlin热压电理论^[32]以及Green和Lindsay^[13]热弹性理论都可经该理论退化后得到. 基于新建立的理论, 再次对受移动热源作用的一维压电杆的广义压电热弹瞬态响应问题进行了研究, 得到了压电杆中无量纲温度、位移、应力、电势等的分布规律, 并重点考察了应变率对各物理量的影响效应.

1 基本方程

1.1 理论推导

基于热弹理论基本方程, 借助热力学定律, 下面来建立考虑应变率的广义压电热弹耦合理论.

运动方程

(1) $ \begin{eqnarray} \sigma _{ij,j} +f_i =\rho \ddot{{u}}_i \end{eqnarray} $

其中, $\sigma _{ij} $是应力分量, $f_i $是体力, $\rho $是质量密度, $u_i$是位移矢量.

应变位移关系

(2) $ \begin{eqnarray} \varepsilon _{ij} =\frac{1}{2}\left( {u_{i,j} +u_{j,i} } \right) \end{eqnarray}$

压电材料能量守恒方程

(3) $ \begin{eqnarray} \rho \dot{{e}}=\sigma _{ij} \dot{{\chi }}_{ij} -q_{i,i} +E_i \dot{{D}}_i +r \end{eqnarray}$

其中, $e$是体积比内能, $q_i $是热流矢量, $r$是内热源, $\chi _{{ij}}$是一个包含应变及应变率的二阶张量, 其形式为

(4) $ \begin{eqnarray} \chi _{{ij}} =\chi _{{ij}} \left( {\varepsilon _{ij},\dot{{\varepsilon }}_{ij} } \right) \end{eqnarray}$

熵不等式

(5) $ \begin{eqnarray} \rho \dot{{\eta }}\geqslant -\left( {\frac{q_i }{\phi }} \right)_{,i}+\frac{r}{\phi } \end{eqnarray}$

其中, $\phi $是取决于温度及其速率的场变量的正标量函数, 其形式为

(6) $ \begin{eqnarray} \phi =\phi \left( {\theta,\dot{{\theta }}} \right) \end{eqnarray}$

高斯方程及电场电势关系

(7) $ \begin{eqnarray} D_i =0,\ \ E_i =-\varphi _{,i} \end{eqnarray}$

其中, $D_i $是电位移, $E_i $是电场强度.

从式(4)和式(6)可以得到

(8) $ \begin{eqnarray} \left. \begin{array}{ll} \dot{{\chi }}_{ij} =\dfrac{\partial \chi _{kl} }{\partial \varepsilon _{ij} }\dot{{\varepsilon }}_{kl} +\dfrac{\partial \chi _{kl} }{\partial \dot{{\varepsilon }}_{ij} }\ddot{{\varepsilon }}_{kl} \\ \dot{{\phi }}=\dfrac{\partial \phi }{\partial \theta }\dot{{\theta }}+\dfrac{\partial \phi }{\partial \dot{{\theta }}}\ddot{{\theta }} \\ \phi _{,i} =\dfrac{\partial \phi }{\partial \theta }\theta _{,i} +\dfrac{\partial \phi }{\partial \dot{{\theta }}}\dot{{\theta }}_{,i} \\ \end{array} \right\} \end{eqnarray}$

引入广义自由能表达式

(9) $ \begin{eqnarray} \rho \psi =\rho e-\rho \eta \phi -D_i E_i \end{eqnarray}$

将式(9)代入式(3)中, 可以得到能量守恒方程, 即热力学第一定律

(10) $ \begin{eqnarray} \rho \dot{{\psi }}+\rho \dot{{\eta }}\phi +\rho \eta \dot{{\phi }}+\dot{{E}}_i D_i =\sigma _{ij} \dot{{\chi }}_{ij} -q_{i,i} +r \end{eqnarray}$

克劳修斯不等式也可以改写为

(11) $ \begin{eqnarray} \sigma _{ij} \dot{{\chi }}_{ij} -\left( {\rho \dot{{\psi }}+\rho \eta \dot{{\phi }}} \right)-\dot{{E}}_i D_i -\frac{q_i }{\phi}\phi_{,i} \geqslant 0 \end{eqnarray}$

将式(8)代入式(10)和式(11)中, 可以得到

(12) $ \begin{eqnarray} &&\sigma _{ij} \left( {\frac{\partial \chi _{kl} }{\partial \varepsilon _{ij} }\dot{{\varepsilon }}_{kl} +\frac{\partial \chi _{kl} }{\partial \dot{{\varepsilon }}_{ij} }\ddot{{\varepsilon }}_{kl} } \right)-\rho \dot{{\psi }}-\rho \dot{{\eta }}\phi - \\&&\qquad \rho \eta \left( {\frac{\partial \phi }{\partial \theta }\dot{{\theta }}+\frac{\partial \phi }{\partial \dot{{\theta }}}\ddot{{\theta }}} \right)-q_{i,i} -D_i \dot{{E}}_i +r=0 \end{eqnarray}$

(13) $ \begin{eqnarray} \sigma _{ij} \left( {\frac{\partial \chi _{kl} }{\partial \varepsilon _{ij} }\dot{{\varepsilon }}_{kl} +\frac{\partial \chi _{kl} }{\partial \dot{{\varepsilon }}_{ij} }\ddot{{\varepsilon }}_{kl} } \right)-\rho \dot{{\psi }}-\rho \eta \left( {\frac{\partial \phi }{\partial \theta }\dot{{\theta }}+\frac{\partial \phi }{\partial \dot{{\theta }}}\ddot{{\theta }}} \right)- && \\ \qquad -\frac{q_i }{\phi }\left( {\frac{\partial \phi }{\partial \theta }\theta _{,i} +\frac{\partial \phi }{\partial \dot{{\theta }}}\dot{{\theta }}_{,i} } \right)-D_i \dot{{E}}_i \geqslant 0 \end{eqnarray}$

广义自由能可以假定为如下形式

(14) $ \begin{eqnarray} \rho \psi =\rho \psi \left( {\varepsilon _{ij},\dot{{\varepsilon }}_{ij},\theta,\dot{{\theta }},\theta _{,i},E_i } \right) \end{eqnarray}$

显然, 可以得到

(15) $ \begin{eqnarray} &&\rho \dot{{\psi }}=\rho \frac{\partial \psi }{\partial \varepsilon _{ij} }\dot{{\varepsilon }}_{ij} +\rho \frac{\partial \psi }{\partial \dot{{\varepsilon }}_{ij} }\ddot{{\varepsilon }}_{ij} +\rho \frac{\partial \psi }{\partial \theta }\dot{{\theta }}+ \\&&\qquad\rho \frac{\partial \psi }{\partial \dot{{\theta }}}\ddot{{\theta }}+\rho \frac{\partial \psi }{\partial \theta _{,i} }\dot{{\theta }}_{,i} +\rho \frac{\partial \psi }{\partial E_i }\dot{{E}}_i \end{eqnarray}$

将式(15)代入式(12)以及式(13), 可以得到如下的本构关系

(16) $ \begin{eqnarray} \left. \begin{array}{ll} \sigma _{{ij}} =\rho \dfrac{\partial \psi }{\partial\dot{{\varepsilon }}_{kl} }\left( {\dfrac{\partial \chi _{ij} }{\partial \dot{{\varepsilon }}_{kl} }} \right)^{-1} \\ \rho \eta =-\rho \dfrac{\partial \psi }{\partial \dot{{\theta }}}\left( {\dfrac{\partial \phi }{\partial \dot{{\theta }}}} \right)^{-1} \\ D_i =-\rho \dfrac{\partial \psi }{\partial E_i },\ \ \dfrac{q_i }{\phi }=-\rho \dfrac{\partial \psi }{\partial \theta _{,i} }\left( {\dfrac{\partial \phi }{\partial \dot{{\theta }}}} \right)^{-1} \\ \end{array} \right\} \end{eqnarray}$

于是, 式(12)和式(13)可以被写作

(17) $ \begin{eqnarray} && \left( {\sigma _{ij} \frac{\partial \chi _{ij} }{\partial \varepsilon _{kl} }-\rho \frac{\partial \psi }{\partial \varepsilon _{kl} }} \right)\dot{{\varepsilon }}_{kl} -\left( {\rho \frac{\partial \psi }{\partial \theta }+\rho \eta \frac{\partial \phi }{\partial \theta }} \right)\dot{{\theta }} - \\&&\qquad\rho \frac{\partial \psi }{\partial \theta _{,i} }\dot{{\theta }}_{,i} -\rho \dot{{\eta }}\phi -q_{i,i} +r=0 \end{eqnarray}$

(18) $ \begin{eqnarray} \left( {\sigma _{ij} \frac{\partial \chi _{ij} }{\partial \varepsilon _{kl} }-\rho \frac{\partial \psi }{\partial \varepsilon _{kl} }} \right)\dot{{\varepsilon }}_{kl} -\left( {\rho \frac{\partial \psi }{\partial \theta }+\rho \eta \frac{\partial \phi }{\partial \theta }} \right)\dot{{\theta }} - &&\\ \qquad\frac{q_i }{\varphi }\frac{\partial \varphi }{\partial \theta }\theta _{,i} \geqslant 0 \end{eqnarray}$

到目前为止, 已获得了考虑应变率的压电热弹理论的基本方程, 即平衡方程(1), 几何方程(2), 本构方程(16)和能量守恒方程(17). 不等式(18)会自动成立, 稍后将予以证明.

对于线性热弹性问题, 式(4)和式(6)可以被写作

(19) $ \chi _{ij} =\varepsilon _{ij} +\tau _0 \dot{{\varepsilon }}_{ij} $

(20) $ \phi =\theta _0 +\theta +\tau _1 \dot{{\theta }} $

在上两式中, $\tau _0 $和$\tau _1 $是两个时间迟滞因子, 他们之间满足如下关系

(21) $ \begin{eqnarray} \tau _1 \geqslant \tau _0 >0 \end{eqnarray}$

从式(19)和式(20)中, 可以得到

(22) $ \begin{eqnarray} &&\frac{\partial \chi _{ij} }{\partial \varepsilon _{kl} }=\delta _{ik} \delta _{jl},\ \ \frac{\partial \chi _{ij} }{\partial \dot{{\varepsilon }}_{kl} }=\tau _0 \delta _{ik} \delta _{jl}\end{eqnarray}$

(23) $ \begin{eqnarray} \frac{\partial \phi }{\partial \theta }=1,\ \ \frac{\partial \phi }{\partial \dot{{\theta }}}=\tau _1 \end{eqnarray}$

此处, 进一步写出广义自由能的显式表达式

(24) $ \begin{eqnarray} && \rho \psi =\frac{1}{2}C_{ijkl} \varepsilon _{ij} \varepsilon _{kl} -\gamma _{ij} \varepsilon _{ij} \theta -\frac{1}{2}\frac{\rho c_E }{\theta _0 }\theta ^2+ \\&&\qquad\tau _0 C_{ijkl} \dot{{\varepsilon }}_{ij} \varepsilon _{kl} +\frac{1}{2}\tau _0 \tau _0 C_{ijkl} \dot{{\varepsilon }}_{ij} \dot{{\varepsilon }}_{kl} -\tau _0 \gamma _{ij} \theta \dot{{\varepsilon }}_{ij} - \\&&\qquad\tau _1 \gamma _{ij} \varepsilon _{ij} \dot{{\theta }}-\tau _0 \tau _1 \gamma _{ij} \dot{{\varepsilon }}_{ij} \dot{{\theta }}-\tau _1 \theta \gamma _{kl} \varepsilon _{kl} - \\&&\qquad \tau _0 h_{ijk} E_k \dot{{\varepsilon }}_{kl} -\tau _1 p_i E_i \dot{{\theta }}-p_i E_i \theta -h_{ijk} E_i \varepsilon _{jk} - \\&&\qquad\frac{1}{2}\omega _{ij} E_i E_j -\frac{\rho c_E }{\theta _0 }\tau _1 \theta \dot{{\theta }}-\frac{1}{2}\frac{\rho c_E }{\theta _0 }\tau _1 \tau _1 \dot{{\theta }}\dot{{\theta }} + \\&&\qquad\frac{1}{2}\frac{\tau _1 }{\theta _0 }\theta _{,i} \kappa _{ij} \theta _{,j} \end{eqnarray}$

将方程(22)$\sim$(24)代入式(26)中, 可以得到本构方程的显式表达式, 如下所示:

应力本构方程为

(25) $ \begin{eqnarray} \sigma _{ij} =C_{ijkl} \left( {\varepsilon _{kl} +\tau _0 \dot{{\varepsilon }}_{kl} } \right)-\gamma _{ij} \left( {\theta +\tau _1 \dot{{\theta }}} \right)-h_{ijk} E_k \end{eqnarray}$

熵本构方程

(26) $ \begin{eqnarray} && \rho \theta _0 \eta =\rho c_E \left( {\theta +\tau _1 \dot{{\theta }}} \right)+\gamma _{ij} \theta _0 \left( {\varepsilon _{ij} +\tau _0 \dot{{\varepsilon }}_{ij} } \right)+\theta _0 p_i E_i \end{eqnarray}$

广义傅里叶定律

(27) $ \begin{eqnarray} q_i =-\frac{1}{\theta _0 }\kappa _{ij} \theta _{,j} \left( {\theta _0 +\theta +\tau _1 \dot{{\theta }}} \right) \end{eqnarray}$

电位移表达式

(28) $ \begin{eqnarray} D_i =h_{ijk} \left( {\varepsilon _{jk} +\tau _0 \dot{{\varepsilon }}_{jk} } \right)+\omega _{ij} E_j +p_i \left( {\theta +\tau _1 \dot{{\theta }}} \right) \end{eqnarray}$

理论推导的最后一步是关于不等式(18)的证明, 由方程(24)和(25)可得

(29) $ \begin{eqnarray} \sigma _{ij} \frac{\partial \chi _{ij} }{\partial \varepsilon _{kl} }-\rho \frac{\partial \psi }{\partial \varepsilon _{kl} }=C_{ijkl} \left( {\tau _1 -\tau _0 } \right)\dot{{\varepsilon }}_{kl} \end{eqnarray}$

因为$\tau _1 \geqslant \tau _0 >0$, 因此式(18)的第一项$\left( {\sigma _{ij} \partial \chi _{ij} /\partial \varepsilon _{kl} -\rho \partial \psi /\partial \varepsilon _{kl} } \right)\dot{{\varepsilon }}_{kl} $为正.

同理, 由表达式$\left( {\rho \partial \psi /\partial \theta +\rho \eta \partial \phi /\partial \theta } \right)$也可以得到

(30) $ \begin{eqnarray} \rho \frac{\partial \psi }{\partial \theta }+\rho \eta \frac{\partial \phi }{\partial \theta }=-\frac{\rho c_E }{\theta _0 }\left( {\tau _1 -\tau _0 } \right)\dot{{\theta }} \end{eqnarray}$

因此, 式(18)的第二项也为正, 式(18)的最后一项可以被写作

(31) $ \begin{eqnarray} -\frac{q_i }{\phi }\frac{\partial \phi }{\partial \theta }\theta _{,i} \approx \frac{1}{\theta _0 }\theta _{,i} \kappa _{ij} \theta _{,j} \end{eqnarray}$

这一项显然恒正, 因此, 式(18)自然成立. 至此, 理论推导结束. 现将如上理论的基本方和归纳如下:

运动方程

(32) $ \begin{eqnarray} \sigma _{ij,j} +\rho F_i =\rho \ddot{{u}}_i \end{eqnarray}$

应变位移关系

(33) $ \begin{eqnarray} \varepsilon _{ij} =\frac{1}{2}\left( {u_{i,j} +u_{j,i} } \right) \end{eqnarray}$

因为$\theta \theta _{,j} $和 $\dot{{\theta }}\theta _{,j} $相当小, 如果将它们忽略不计, 那么式(28)将退化为傅里叶定律

(34) $ \begin{eqnarray} q_i =-\kappa _{ij} \theta _{,j} \end{eqnarray}$

能量守恒方程

(35) $ \begin{eqnarray} \rho \dot{{\eta }}\theta _0 =-q_{i,i} +r \end{eqnarray}$

应力本构方程为

(36) $ \begin{eqnarray} \sigma _{ij} =C_{ijkl} \left( {\varepsilon _{kl} +\tau _0 \dot{{\varepsilon }}_{kl} } \right)-\gamma _{ij} \left( {\theta +\tau _1 \dot{{\theta }}} \right)-h_{ijk} E_k \end{eqnarray}$

熵本构方程

(37) $ \begin{eqnarray} && \rho \theta _0 \eta =\rho c_E \left( {\theta +\tau _1 \dot{{\theta }}} \right)+\gamma _{ij} \theta _0 \left( {\varepsilon _{ij} +\tau _0 \dot{{\varepsilon }}_{ij} } \right)+\theta _0 p_i E_i \end{eqnarray}$

电位移表达式

(38) $ \begin{eqnarray} D_i =h_{ijk} \left( {\varepsilon _{jk} +\tau _0 \dot{{\varepsilon }}_{jk} } \right)+\omega _{ij} E_j +p_i \left( {\theta +\tau _1 \dot{{\theta }}} \right) \end{eqnarray}$

如果不考虑应变率, 那么当前的理论可退化为已有的热压电理论. 如果是各向同性材料, 那么$C_{ijkl} \varepsilon _{kl} =2\mu \varepsilon _{ij} +\lambda \varepsilon _{kk} \delta _{ij}, \gamma _{ij} =\left( {3\lambda +2\mu } \right)\alpha _\theta \delta _{ij}, \kappa _{ij} =\kappa \delta_{ij}$, 其中$\lambda $和$\mu $是拉梅系数, $\alpha _\theta $是热膨胀系数.

1.2 问题描述

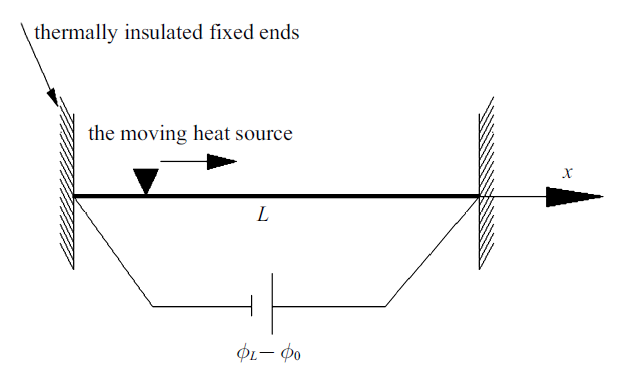
基于新建立的考虑应变率的广义压电热弹理论, 来研究一维压电杆的压电热弹性瞬态响应问题. 压电杆长为$L$, 两端固定, 受沿着轴向的移动热源作用, 如模型图1所示. 沿杆轴线方向建立一维坐标系($x$轴向右为正).

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 移动热源作用下的压电杆

Fig.1 A thermopiezoelectric rod subjected to a moving heat source

在不计自由电荷及体力的情况下, 对于一维热压电杆, 基本方程可写作

(39) $ \sigma _{xx,x} =\rho \ddot{{u}} $

(40) $ \varepsilon _{xx} =u_{,x} $

(41) $ D_{x,x} =0,E_x =-\varphi _{,x} $

(42) $ \rho \left( {\eta _{,t} \theta _0 -R} \right)+q_{x,x} =0 $

(43) $ q_x =-\kappa _{11} \theta _{,x} $

(44) $ \sigma _{xx} =c_{11} \left( {\varepsilon _{xx} +\tau _0 \dot{{\varepsilon }}_{xx} } \right)-h_{11} E_x -\gamma _{11} \left( {\theta +\tau _1 \dot{{\theta }}} \right) $

(45) $ D_x =h_{11} \left( {\varepsilon _{xx} +\tau _0 \dot{{\varepsilon }}_{xx} } \right)+\omega _{11} E_x +p_1 \left( {\theta +\tau _1 \dot{{\theta }}} \right) $

(46) $ \rho \eta =\frac{\rho c_E }{\theta _0 }\left( {\theta +\tau _1 \dot{{\theta }}} \right)+\gamma _{11} \left( {\varepsilon _{xx} +\tau _0 \dot{{\varepsilon }}_{xx} } \right)+p_1 E_x $

通过以上方程, 可得到

(47) $ \begin{eqnarray} && c_{11} \left( {\frac{\partial ^2u}{\partial x^2}+\tau _0 \frac{\partial ^3u}{\partial x^2\partial t}} \right)+h_{11} \frac{\partial ^2\varphi }{\partial x^2}- \\ &&\qquad \gamma _{11} \left( {\frac{\partial \theta }{\partial x}+\tau _1 \frac{\partial ^2\theta }{\partial x\partial t}} \right)=\rho \frac{\partial ^2u}{\partial t^2} \end{eqnarray} $

(48) $ \begin{eqnarray} h_{11} \left( {\frac{\partial ^2u}{\partial x^2}+\tau _0 \frac{\partial ^3u}{\partial x^2\partial t}} \right)-\omega _{11} \frac{\partial ^2\varphi }{\partial x^2}+p_1 && \\ \qquad\left( {\frac{\partial \theta }{\partial x}+\tau _1 \frac{\partial ^2\theta }{\partial x\partial t}} \right)=0 \end{eqnarray} $

(49) $ \begin{eqnarray} \kappa _{11} \frac{\partial ^2\theta }{\partial x^2}+\rho R+p_1 \theta _0 \frac{\partial ^2\varphi }{\partial x\partial t}-\rho c_E \left( {\frac{\partial \theta }{\partial t}+\tau _1 \frac{\partial ^2\theta }{\partial t^2}} \right)- && \\ \qquad\gamma _{11} \theta _0 \left( {\frac{\partial ^2u}{\partial x\partial t}+\tau _0 \frac{\partial ^3u}{\partial x\partial t^2}} \right)=0 \end{eqnarray}$

为简洁起见, 引入如下的无量纲量

(50) $ \begin{eqnarray} \left. \begin{array}{ll} x^\ast =c_0 s_0 x,\ u^\ast =c_0 s_0 u,\ L^\ast =c_0 s_0 L,\ t^\ast =c_0^2 s_0 t \\ \tau _i^\ast =c_0^2 s_0 \tau _i,\ \theta ^\ast =\dfrac{\theta }{\theta _0 },\ \sigma _{xx}^\ast =\dfrac{\sigma _{xx} }{c_{11} },\ D_x^\ast =\dfrac{D_x }{h_{11} } \\ R^\ast =\dfrac{R}{\kappa _{11} \theta _0 c_0^2 s_0^2 },\ c_0^2 =\dfrac{c_{11} }{\rho },\ s_0 =\dfrac{\rho c_E }{\kappa _{11} },\ \phi ^\ast =\dfrac{\omega _{11} }{h_{11} L}\varphi \\ \end{array} \right\}\quad \end{eqnarray}$

利用以上的无量纲量, 式(47)~式(49)变为

(51) $ \begin{eqnarray} &&\frac{\partial ^2u}{\partial x^2}+\tau _0 \frac{\partial ^3u}{\partial x^2\partial t}+g_1 \frac{\partial ^2\varphi }{\partial x^2}- \\ && \qquad g_2 \left( {\frac{\partial \theta }{\partial x}+\tau _1 \frac{\partial ^2\theta }{\partial x\partial t}} \right)=\frac{\partial ^2u}{\partial t^2} \end{eqnarray}$

(52) $ \begin{eqnarray} \frac{\partial ^2u}{\partial x^2}+\tau _0 \frac{\partial ^3u}{\partial x^2\partial t}-g_3 \frac{\partial ^2\varphi }{\partial x^2}+ &&\\ \qquad f_1 \left( {\frac{\partial \theta }{\partial x}+\tau _1 \frac{\partial ^2\theta }{\partial x\partial t}} \right)=0 \end{eqnarray} $

(53) $ \begin{eqnarray} \frac{\partial ^2\theta }{\partial x^2}+\rho R-\left( {\frac{\partial \theta }{\partial t}+\tau _1 \frac{\partial ^2\theta }{\partial t^2}} \right)- &&\\ \qquad f_2 \left( {\frac{\partial ^2u}{\partial x\partial t}+\tau _0 \frac{\partial ^3u}{\partial x\partial t^2}} \right) +f_3 \frac{\partial ^2\varphi }{\partial x\partial t}=0 \end{eqnarray}$

其中

(54) $ \begin{eqnarray} \left. \begin{array}{ll} g_1 =\dfrac{c_0 s_0 Lh_{11}^2 }{\omega _{11} c_{11} },\ \ g_2 =\dfrac{\gamma _{11} \theta _0 }{c_{11} },\ \ g_3 =c_0 s_0 L \\ f_1 =\dfrac{p_1 \theta _0 }{h_{11} },\ \ f_2 =\dfrac{\gamma _{11} }{\rho c_E },\ \ f_3 =\dfrac{p_1 c_0 Lh_{11} }{\kappa _{11} \omega _{11} } \\ \end{array} \right\} \end{eqnarray}$

问题的初始条件为

(55) $ \begin{eqnarray} \left. \begin{array}{ll} u\left( {x,0} \right)=\dot{{u}}\left( {x,0} \right)=0,\ \ \theta \left( {x,0} \right)=\dot{{\theta }}\left( {x,0} \right)=0 \\ \varphi \left( {x,0} \right)=\dot{{\varphi }}\left( {x,0} \right)=0 \\ \end{array} \right\} \end{eqnarray}$

边界条件为

(56) $ \begin{eqnarray} \left. \begin{array}{ll} u\left( {0,t} \right)=u\left( {L,t} \right)=0,\ \ \varphi \left( {0,t} \right)=\varphi \left( {L,t} \right)=0 \\ \dfrac{\partial \theta \left( {0,t} \right)}{\partial x}=\dfrac{\partial \theta \left( {L,t} \right)}{\partial x}=0 \\ \end{array} \right\} \end{eqnarray}$

另外, 假定无量纲热源具有以下形式

(57) $ \begin{eqnarray} R=R_0 \delta \left( {x-\nu t} \right) \end{eqnarray}$

其中, $R_0 $是移动热源的无量纲幅值的大小, $\delta $是狄克拉函数, $\nu $是热源的移动速度.

1.3 在拉氏域内的求解

引入拉普拉斯变换公式

(58) $ \begin{eqnarray} L\left[ {f(t)} \right]=\bar{{f}}(s)=\int_0^\infty{\rm e}^{-st}f(t){\rm d}t,\ \ {\rm Re}(s)>0 \end{eqnarray}$

其中, $s$是拉式变换中的参数, Re是实部.

对方程(51)$\sim$(53)进行拉普拉斯变换

(59) $ \begin{eqnarray} &&\left[ {\left( {1+\tau _0 s} \right)\frac{{\rm d}^2}{{\rm d}x^2}-g_4 s^2} \right]\bar{{u}}+g_1 \frac{{\rm d}^2}{{\rm d}x^2}\bar{{\varphi }}- \\&&\qquad g_2 \left( {1+\tau _1 s} \right)\frac{{\rm d}}{{\rm d}x}\bar{{\theta }}=0 \end{eqnarray} $

(60) $ \begin{eqnarray} \left( {1+\tau _0 s} \right)\frac{{\rm d}^2}{{\rm d}x^2}\bar{{u}}-g_3 \frac{{\rm d}^2}{{\rm d}x^2}\bar{{\varphi }} + &&\\ \qquad f_1 \left( {1+\tau _1 s} \right)\frac{{\rm d}}{{\rm d}x}\bar{{\theta }}=0 \end{eqnarray} $

(61) $ \begin{eqnarray} \left( {\frac{{\rm d}^2}{{\rm d}x^2}-s-\tau _1 s^2} \right)\bar{{\theta }}-f_2 s\left( {1+\tau _0 s} \right)\frac{{\rm d}}{{\rm d}x}\bar{{u}}+ &&\\ \qquad f_3 s\frac{{\rm d}}{{\rm d}x}\bar{{\varphi }}=-f_4 {\rm e}^{-\frac{s}{\nu }x} \end{eqnarray}$

其中, $g_4 ={\rho c_0^2 }/{c_{11}}$, $f_4 ={\rho R_0 }/{\nu }$.

从方程(58)$\sim$(60)中消去$\bar{{\theta }}$和$\bar{{\varphi }}$, 可得到

(62) $ \begin{eqnarray} \frac{{\rm d}^4}{{\rm d}x^4}\bar{{u}}+\frac{n_2 }{n_1 }\frac{{\rm d}^2}{{\rm d}x^2}\bar{{u}}+\frac{n_3 }{n_1 }\bar{{u}}=\frac{n}{n_1 }{\rm e}^{-\frac{s}{\nu }x} \end{eqnarray}$

其中

(63a) $ \begin{eqnarray} &&n_1 =\dfrac{f_1(1+\tau_1s)}{g_2s(1+\tau_0s)}- \\ && \qquad\dfrac{f_1g_1[g_2(1+\tau_0s)+f_1(1+\tau_1s)]}{g_2s(1+\tau_0s)(f_1g_1-g_2g_3)} \end{eqnarray} $

(63b) $ \begin{eqnarray} &&n_2 =1+\tau _0 s-f_1 \left( {1+\tau _1 s} \right)\cdot \\ &&\qquad\left[ {f_2 +\dfrac{g_4 s}{g_2 \left( {1+\tau _1 s} \right)\left( {1+\tau _0 s} \right)}} \right]+ \\ &&\qquad \dfrac{g_1 g_4 f_1^2 s}{g_2 \left( {1+\tau _1 s} \right)\left( {1+\tau _0 s} \right)}- \\ &&\qquad \left[ {\dfrac{f_1 f_3 \left( {1+\tau _1 s} \right)}{\left( {1+\tau _0 s} \right)}-g_3 } \right]\cdot \\ &&\qquad\dfrac{g_2 \left( {1+\tau _0 s} \right)+f_1 \left( {1+\tau _1 s} \right)}{\left( {f_1 g_1 -g_2 g_3 } \right)} \end{eqnarray} $

(63c) $ \begin{eqnarray} n_3=\left[\dfrac{f_1f_3(1+\tau_1s)}{(1+\tau_0s)}-g_3 \right]\dfrac{f_1g_4s^2}{(f_1g_1-g_2g_3)} \end{eqnarray} $

(63d) $ \begin{eqnarray} n=\dfrac{f_1f_4(1+\tau_1s)}{v(1+\tau_0s)} \end{eqnarray} $

方程(62)的通解为

(64) $ \begin{eqnarray} \bar{{u}}=C_1 {\rm e}^{\lambda _1 x}+C_2 {\rm e}^{\lambda _2 x}+C_3 {\rm e}^{\lambda _3 x}+C_4 {\rm e}^{\lambda _4 x}+K{\rm e}^{-\frac{s}{\nu }x} \end{eqnarray}$

其中$C_1$, $C_2$, $C_3$, $C_4$是待定的常数, $K$的表达式如下

(65) $ \begin{eqnarray} K=\frac{n}{n_1 \left( {\dfrac{s}{\nu }} \right)^4+n_2 \left( {\dfrac{s}{\nu }}\right)^2+n_3 } \end{eqnarray}$

而$\lambda _1$, $\lambda _2$, $\lambda _3$, $\lambda _4 $是如下特征方程的根

(66) $ \begin{eqnarray} \lambda ^4+\frac{n_2 }{n_1 }\lambda ^2+\frac{n_3 }{n_1 }=0 \end{eqnarray}$

特征根可表示为

(67) $ \begin{eqnarray} \left. \begin{array}{ll} \lambda _1 =-\lambda _2 =\sqrt {\dfrac{-n_2 +\sqrt {n_2^2 -4n_1 n_3 } }{2n_1 }} \\ \lambda _3 =-\lambda _4 =\sqrt {\dfrac{-n_2 -\sqrt {n_2^2 -4n_1 n_3 } }{2n_1 }} \\ \end{array} \right\} \end{eqnarray}$

消去方程(59)和(60)中的$\bar{{\theta }}$, 可得到

(68) $ \begin{eqnarray} &&\left[ {f_1 \left( {1+\tau _1 s} \right)+g_2 \left( {1+\tau _0 s} \right)} \right]\frac{{\rm d}^2}{{\rm d}x^2}\bar{{u}}-f_1 g_4 s^2\bar{{u}}+ \\&&\qquad \left( {f_1 g_1 -g_2 g_3 } \right)\frac{{\rm d}^2}{{\rm d}x^2}\bar{{\varphi}}=0 \end{eqnarray}$

将式(63)代入式(67)中, 可得到

(69) $ \begin{eqnarray} &&\bar{{\varphi }}=a_1 C_1 {\rm e}^{\lambda _1 x}+a_2 C_2 {\rm e}^{\lambda _2 x}+a_3 C_3 {\rm e}^{\lambda _3 x}+a_4 C_4 {\rm e}^{\lambda _4 x}+ \\&&\qquad aK{\rm e}^{-\frac{s}{\nu }x}+N_1 x+N_2 \end{eqnarray}$

进一步, 可得到$\bar{{\theta }}$的表达式

(70) $ \begin{eqnarray} && \bar{{\theta }}=b_1 C_1 {\rm e}^{\lambda _1 x}+b_2 C_2 {\rm e}^{\lambda _2 x}+b_3 C_3 {\rm e}^{\lambda _3 x}+b_4 C_4 {\rm e}^{\lambda _4 x}+ \\&&\qquad bK{\rm e}^{-\frac{s}{\nu }x}+\frac{g_3 N_1 }{f_1 \left( {1+\tau _1 s} \right)}+N_3 \end{eqnarray}$

在以上方程中

(71) $ \begin{eqnarray} \left. \begin{array}{ll} a=\dfrac{f_1g_4v^2-[f_1(1+\tau _1 s)+g_2(1+\tau _0 s)]}{f_1g_1-g_2g_3}\\ a_1=a_2=\dfrac{1}{f_1g_1-g_2g_3}\Bigg\{\dfrac{f_1g_4s^2}{\lambda_1^2}-\\ \qquad[f_1(1+\tau _1 s)+g_2(1+\tau _0 s)]\Bigg\}\\ a_3=a_4=\dfrac{1}{f_1g_1-g_2g_3}\Bigg\{\dfrac{f_1g_4s^2}{\lambda_3^2}-\\ \qquad[f_1(1+\tau _1 s)+g_2(1+\tau _0 s)]\Bigg\}\\ b=\dfrac{s[(1+\tau _0 s)-ag_3]}{v_1f_1(1+\tau _1 s)}\\ b_1=-b_2=\dfrac{\lambda_1[ag_3-(1+\tau _0 s)]}{f_1(1+\tau _1 s)}\\ b_3=-b_4=\dfrac{\lambda_3[ag_3-(1+\tau _0 s)]}{f_1(1+\tau _1 s)} \end{array} \right\} \end{eqnarray}$

结合电位移表达式以及应力本构方程, 可得到

(72) $ \begin{eqnarray} &&\bar{{\sigma }}_{xx} =C_i \left[ {\lambda _i \left( {1+\tau _1 s+a_i \frac{h_{11}^2 c_0 s_0 L}{\omega _{11} c_{11} }} \right)-\frac{\gamma _{11} \theta _0 }{c_{11} }b_i } \right]{\rm e}^{\lambda _i x}+ \\ &&\qquad K\left[ {-\frac{s}{\nu }\left( {1+\tau _1 s+a\frac{h_{11}^2 c_0 s_0 L}{\omega _{11} c_{11} }} \right)-\frac{\gamma _{11} \theta _0 }{c_{11} }b} \right]{\rm e}^{-\frac{s}{\nu }x} + \\ &&\qquad N_1 \left[ {\frac{h_{11}^2 c_0 s_0 L}{\omega _{11} c_{11} }-\frac{g_3 \gamma _{11} \theta _0 }{f_1 \left( {1+\tau _1 s} \right)c_{11} }} \right]- \\ &&\qquad\frac{\gamma _{11} \theta _0 }{c_{11} }N_3 -\frac{\gamma _{11} \theta _0 }{c_{11} }\tau _1 s \end{eqnarray} $

(73) $ \begin{eqnarray} && \bar{{D}}_x =C_i \left[ {\lambda _i \left( {1+\tau _0 s-a_i c_0 s_0 L} \right)+\frac{p_1 \theta _0 }{h_{11} }b_i } \right]{\rm e}^{\lambda _i x}+ \\ &&\qquad K\left[ {-\frac{s}{\nu }\left( {1+\tau _0 s-ac_0 s_0 L} \right)+\frac{p_1 \theta _0 }{h_{11} }b} \right]{\rm e}^{-\frac{s}{\nu }x}+ \\ &&\qquad N_1 \left[ {\frac{p_1 \theta _0 g_3 }{h_{11} f_1 \left( {1+\tau _1 s} \right)}-c_0 s_0 L} \right]+ \\ &&\qquad\frac{p_1 \theta _0 }{h_{11} }N_3 +\frac{p_1 \theta _0 }{h_{11} }\tau _1 s \end{eqnarray}$

其中, $i=1,2,3,4.$

将式(64)、式(69)、式(70)代入式(61)中, 得到

(74) $ \begin{eqnarray} \frac{f_1 f_3 \left( {1+\tau _1 s} \right)-g_3 }{f_1 \left( {1+\tau _1 s} \right)}N_1 -N_3 =0 \end{eqnarray}$

结合边界条件(56), 可得到

(75) $ \begin{eqnarray} &&C_1+C_2+C_3+C_4+K=0 \end{eqnarray} $

(76) $ \begin{eqnarray} &&C_1{\rm e}^{\lambda_1c_0s_0L}+C_2{\rm e}^{\lambda_2c_0s_0L}+C_3{\rm e}^{\lambda_3c_0s_0L}+ C_4{\rm e}^{\lambda_4c_0s_0L}+ \\&&\qquad K{\rm e}^{-(s/v)c_0s_0L}=0 \end{eqnarray} $

(77) $ \begin{eqnarray} &&a_1C_1+a_2C_2+a_3C_3+a_4C_4+aK+N_2=0 \end{eqnarray} $

(78) $ \begin{eqnarray} &&a_1C_1{\rm e}^{\lambda_1c_0s_0L}\!+\!a_2C_2{\rm e}^{\lambda_2c_0s_0L}\!+\!a_3C_3{\rm e}^{\lambda_3c_0s_0L}\!+\! a_4C_4{\rm e}^{\lambda_4c_0s_0L}\!+\! \\&&\qquad aK{\rm e}^{-(s/v)c_0s_0L}+N_1c_0s_0L+N_2=0 \end{eqnarray} $

(79) $ \begin{eqnarray} &&b_1\lambda_1C_1+b_2\lambda_2C_2+b_3\lambda_3C_3+b_4\lambda_4C_4-\frac{s}{v}bK=0 \end{eqnarray} $

(80) $ \begin{eqnarray} &&b_1\lambda_1C_1{\rm e}^{\lambda_1c_0s_0L}+b_2\lambda_2C_2{\rm e}^{\lambda_2c_0s_0L}+b_3\lambda_3C_3{\rm e}^{\lambda_3c_0s_0L}+ \\&&\qquad b_4\lambda_4C_4{\rm e}^{\lambda_4c_0s_0L}-\frac{s}{v}bK{\rm e}^{-(s/v)c_0s_0L}=0 \end{eqnarray} $

通过求解以上方程, 可以得到$C_i$ $(i=1,2,3,4)$, $N_i$ $(i=1,2,3)$和$K$, 由于所得表达式过于繁琐, 此处省略未列出.

1.4 拉普拉斯反变换

为得到各物理量在时域中的解, 引入拉普拉斯数值反变换对各物理量表达式进行反变换, 可得

(81) $ \begin{eqnarray} &&f\left( {x,t} \right)=\frac{{\rm e}^{\beta _0 t}}{t}\Bigg[\frac{1}{2}\tilde{{f}}\left( {x,\beta _0 } \right)+ \\&&\qquad Re\sum\limits_{n=1}^N {\tilde{{f}}\left( {x,\beta _0 +\frac{{\rm i}n\pi }{t}} \right)\left( {-1} \right)^n} \Bigg] \end{eqnarray}$

为了能快速收敛, 大量的数据试验表明, $\beta _0 $应满足$\beta _0 t\approx 4.7$^[39].

1.5 结果及讨论

为进行数值计算, 需引入如下的压电杆材料特性参数: $c_{11} =8.674\times 10^{10}~{\rm N/m}^{2}$, $\gamma _{11} =1.16\times10^6~{\rm N}/({\rm m}^{2}\cdot {\rm K})$, $\rho =2.65\times 10^3~{\rm kg/m}^{3}$, $c_E =782~{\rm J}/({\rm kg}\cdot{\rm K})$, $h_{11} =0.2~{\rm C/m}^{2}$, $\omega _{11} =0.392\times 10^{-10}~{\rm F/m}$, $p_1 =4\times 10^{-4}~{\rm C}/({\rm m}^{2}\cdot {\rm K})$, $\kappa _{11} =1.4~{\rm W}/({\rm m}\cdot {\rm K})$. 计算中, 其他参数取值如下

$$\begin{eqnarray*} R_0 =\frac{10}{\rho },\theta _0 =293,L=10 \end{eqnarray*}$$

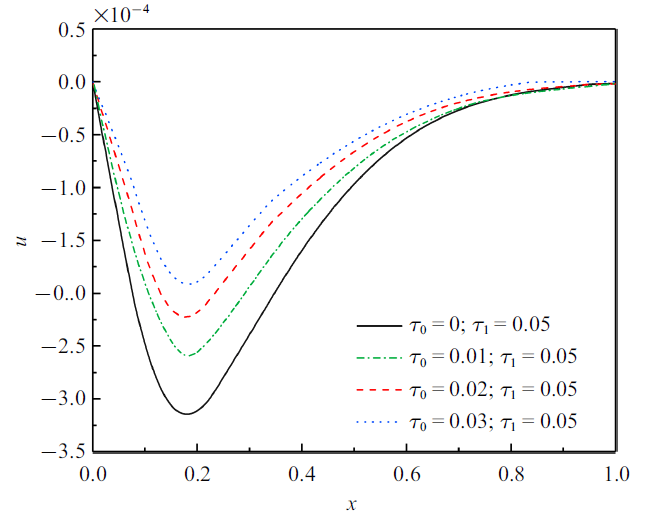
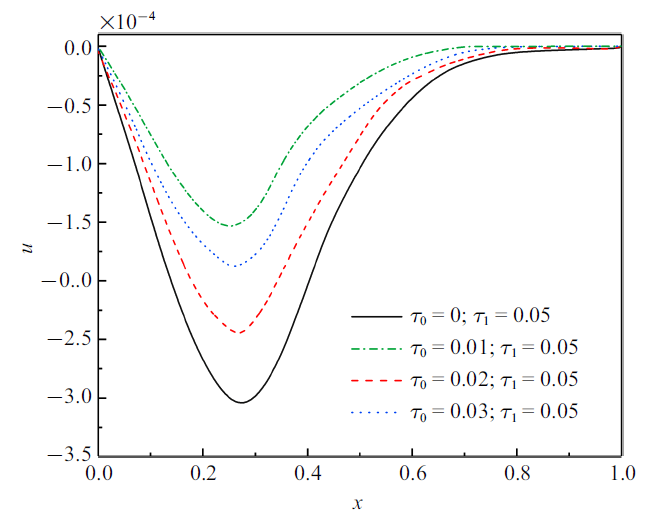
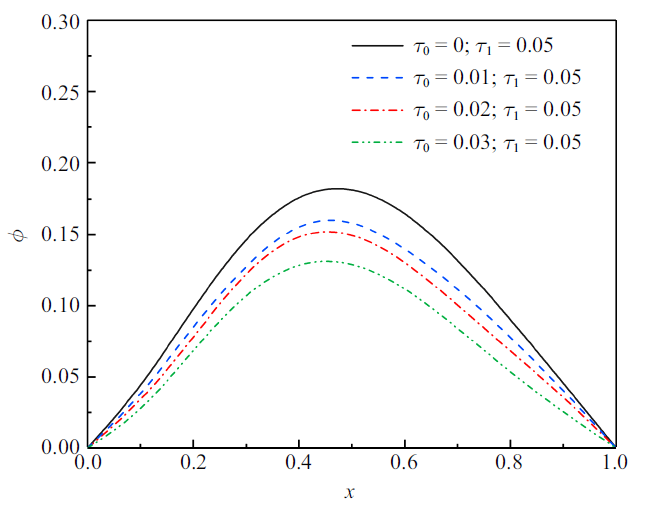
经计算, 得到了压电杆中无量纲温度、应力、位移、电势的分布规律. 计算中, 着重考察了应变率和热源移动速度对各物理量分布规律的影响效应, 应变率的影响效应是通过应变松弛时间因子来体现的. 计算中, 无量纲时间$t=0.1$, 热松弛时间因子$\tau _1 =0.05$, 应变松弛时间因子分别是$\tau _0 =0$, 0.01, 0.02, 0.03, 移动热源速度取了两不同值, 分别是$v=2, 3$. 各物理量的分布图如图2~图9所示.

图2

新窗口打开| 下载原图ZIP| 生成PPT

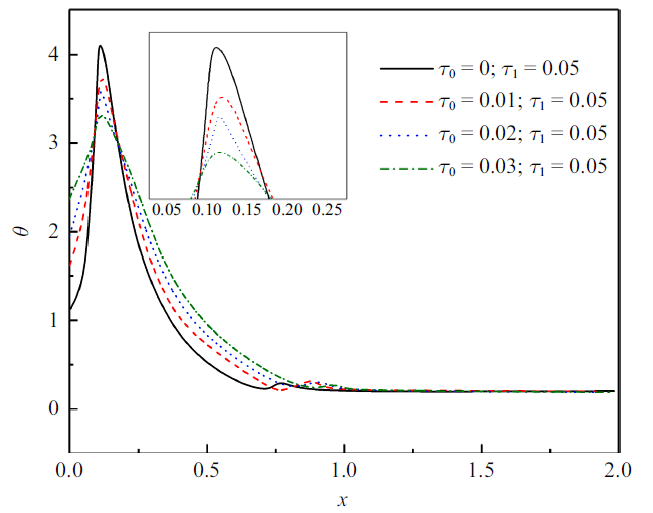
图2 无量纲温度($\nu =2$)

Fig.2 The non-dimensional temperature

图3

新窗口打开| 下载原图ZIP| 生成PPT

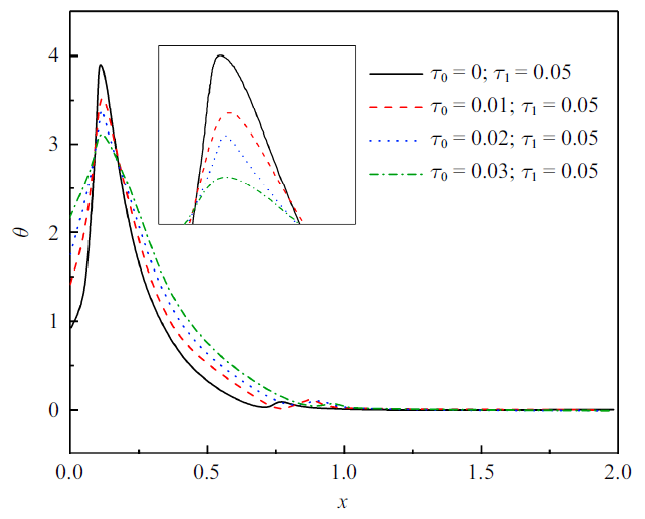
图3 无量纲温度($\nu =3$)

Fig.3 The non-dimensional temperature

图4

新窗口打开| 下载原图ZIP| 生成PPT

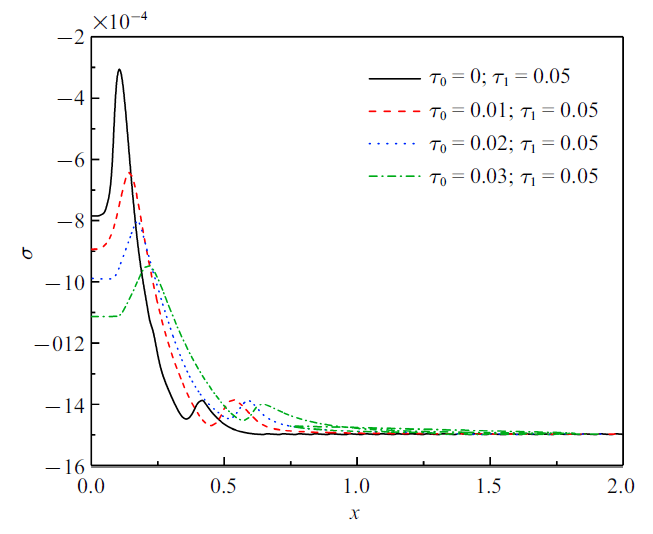
图4 无量纲应力($\nu =2$)

Fig.4 The non-dimensional stress

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 无量纲应力($\nu =3$)

Fig.5 The non-dimensional stress

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 无量纲位移($\nu =2$)

Fig.6 The non-dimensional displacement

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 无量纲位移($\nu =3$)

Fig.7 The non-dimensional displacement

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 无量纲电势($\nu =2$)

Fig.8 The non-dimensional electric potential

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 无量纲电势($\nu =3$)

Fig.9 The non-dimensional electric potential

图2和图3显示无量纲温度分布规律. 可以看到, 同样的热源移动速度下, 温度的峰值随着$\tau _0 $的增大向左侧移动并且减小. 因为左侧有移动热源的作用, 温度从非零值到达峰值而后逐渐趋于零. 同样的迟滞因子下, 温度会随着热源速度的增大而降低, 因为一段时间内热源释放的能量是不变的, 导致分配到单位杆长上的能量会随着热源速度的增大而减小. 每一温度分布曲线遵循如下规律: 从零开始迅速增加到峰值, 然后持续降低趋近于零.

图4和图5显示无量纲应力的分布规律. 可以看出杆中出现的是压应力, 这是由于热膨胀和固定端的缘故. 在同一热源速度下, 应力峰值绝对值会随着$\tau _0 $的增加而增加, 在同样的迟滞因子下, 应力峰值会随着热源速度的增大而下降. 每一应力分布曲线遵循以下规律: 应力缓慢增大到达峰值而后持续降低趋近于零.

图6和图7显示无量纲位移的分布规律. 从图中可以看出, 同一热源速度下, 位移峰值绝对值随着$\tau _0 $的增大而减小, 而同一迟滞因子下, 位移峰值绝对值会随着热源速度的增大而降低. 还可以看到, 杆的两端位移仍然为零, 这是由于杆的两端固定. 每一位移分布曲线满足如下规律: 从零开始缓慢增大达到峰值然后逐渐降低趋近于零.

图8和图9显示热压电杆中无量纲电势分别在$v=2$和$v=3$的分布规律. 压电材料有其特有的性质, 即压电效应. 由于热膨胀及杆端固定, 杆内产生压电效应, 导致在杆中产生电势. 可以看出, 同样的热源速度下, 电势的峰值随着$\tau _0$的增大而减小. 相同的迟滞因子, 不同移动热源速度下, 电势峰值所在的位置会不同, 峰值会随着移动速度的增大而减小. 每一电势分布曲线遵循以下规律: 从零开始缓慢增大到峰值而后持续降低趋近于零.

2 结论

本文借助热力学定律, 建立了考虑应变率的广义压电热弹理论, 并应用该理论研究了两端固定的一维压电杆在移动热源作用下的瞬态响应问题. 得到了无量纲电势、温度、应力、位移在不同热源速度下的分布规律并作图说明. 研究了不同应变迟滞因子$\tau _0 $对瞬态响应的影响. 结果表明:

(1) 在同一热源速度下, 无量纲电势的峰值会随着$\tau _0 $的增大而减小; 同时, 保持$\tau _0 $不变时, 电势的峰值随着热源速度的增加而降低;

(2) 在同一热源速度下, 无量纲温度的峰值会随着迟滞因子$\tau _0 $的增大而减小; 同样的迟滞因子和温度会随着热源速度的增大而减小;

(3) 同一热源速度下, 杆内产生压应力, 无量纲应力的峰值随着$\tau _0 $的增大而增大; 在同样的迟滞因子下, 应力峰值会随着热源速度的增大而下降;

(4) 在同一热源速度下, 位移峰值绝对值随着$\tau _0 $的增大而减小; 而同一迟滞因子下, 位移峰值绝对值会随着热源速度的增大而降低.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

Afrin

, Zhang

, Chen

Dual-phase lag behavior of a gas-saturated porous-medium heated by a short-pulsed laser

International Journal of Thermal Sciences, 2014,75:21-27