引言
超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构.
扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应.
Sherief等[12 ] 发展的整数阶广义热弹扩散理论只能描述力学过程某时刻的变化和力学过程在空间某一确定位置的局部性质, 对于某些反常扩散现象, 即本构关系不服从标准梯度率的现象, 其物理和力学过程通常涉及记忆和遗传、路径依赖以及全局相关性, 此时, 由分数阶广义热弹扩散理论描述结构的热弹扩散响应则更为恰当. Caputo型分数阶微分的形式如下[17 ]
(1) $ \begin{eqnarray} \label{eq1} \hspace{-4mm}D_{a_0}^\alpha f\left( t \right)\!=\!\int_{a_0 }^t {K_\alpha \left( {t-s} \right)f^{\left( m \right)}\left( s \right)\mbox{d}s},\ t\in \left[ {a_0 ,b_0 } \right],\alpha >0 \end{eqnarray}$
$$\begin{eqnarray*} K_\alpha \left( {t-s} \right)=\frac{\left( {t-s} \right)^{^{m-\alpha -1}}}{\Gamma \left( {m-\alpha } \right)} \end{eqnarray*}$$
$f\left( t \right)$在区间$\left[ {a_0 ,b_0 } \right]$内可积, $m$为整数, $\alpha $的取值范围为$m-1<\alpha \leqslant m$, $K_\alpha \left( {t-s} \right)$是核函数, $\Gamma $是Gamma函数, $f^{\left( m \right)}$表示对函数$f$求$m$阶微分. 上式可准确描述物理过程的"记忆依赖效应", 即: 系统的瞬时变化率依赖于过去状态.
Wang和Li[18 ] 认为, 式(1)有以下两个方面的局限性: 第一, 对于一个给定的实数$\alpha $, 核函数$K_\alpha \left( {t-s} \right)$是一个固定的函数, 但从应用的观点来看, 不同的物理过程需要不同的核函数来反映记忆依赖效应, 因此用可变的核函数来描述此过程就显得尤为重要; 第二, 分数阶微分定义在区间$\left[ {a_0 ,t} \right]$上, 且$a_0 $是一个固定的实数, 因此, 上式对于描述发生在长时间$t$范围内的记忆效应无效. 事实上, 一个真实物理过程的记忆依赖效应通常发生在一个时间区间里, 即迟滞区间$\left[ {t-\omega ,t} \right](\omega $表示迟滞时间)内. 受此启发, Wang和Li[18 ] 引入记忆依赖微分(MDD)的概念来反映记忆效应, 函数$f$的一阶记忆依赖微分定义为: 在一个可变迟滞区间上, 核函数与函数导数积的积分. 形式如下
(2) $ \begin{eqnarray} \label{eq2} D_\omega f\left( t \right)=\frac{1}{\omega }\int_{t-\omega }^t K\left( {t-\xi } \right)f'\left( \xi \right)\mbox{d}\xi \end{eqnarray}$
其中, $\omega $是时间迟滞因子, $K\left( {t-\xi } \right)$是可变的核函数. 式(2)的右侧可以理解为: 在迟滞区间$\left[ {t-\omega ,t} \right]$内, $f'\left( \xi \right)$取不同权重时的平均值. 从应用的观点来看, 对于某时刻$\xi \in \left[ {t-\omega ,t} \right)$, 记忆依赖效应权重的取值范围为$0\leqslant K\left( {t-\xi } \right)\leqslant 1$, 因此, 记忆依赖微分$D_\omega f\left( t \right)$通常小于微分$f'\left( t \right)$. 核函数可以根据实际情况选择, 例如可取: $1,\xi -t+1,\left[ {\left( {\left( {\xi -t} \right)/\omega } \right)+1} \right]^p$, 其中$p=0.25,1,2$等. 核函数$K\left( {t-\xi } \right)$是单调函数, 对于过去时刻$t-\xi $, 核函数$K=0$; 对于现在时刻$t$, 核函数$K=1$. 当$K\left( {t-\xi } \right)\equiv 1$时, 可以得到
(3) $ \begin{eqnarray} \label{eq3} \hspace{-4mm}D_\omega f\left( t \right)\!=\!\frac{1}{\omega }\int_{t-\omega }^t {f'\left( \xi \right)\mbox{d}\xi } =\frac{f\left( t \right)-f\left( {t-\omega } \right)}{\omega }\to f'\left( t \right) \end{eqnarray}$
这表明: 微分$\mbox{d}/\mbox{d}t$可以看作$\omega \to 0$时$D_\omega $的极限,因此
(4) $ \begin{eqnarray} \label{eq4} \left| {D_\omega f\left( t \right)} \right|\leqslant \left| {\frac{\mbox{d}f\left( t \right)}{\mbox{d}t}} \right|=\left| {\mathop {\lim }\limits_{\omega \to 0} \frac{f\left( t \right)-f\left( {t-\omega } \right)}{\omega }} \right| \end{eqnarray}$
Yu等[19 ] 将记忆依赖微分(MDD)引入L-S型广义热弹理论, 相比于分数阶广义热弹, 其优势在于: 第一, 新模型在形式上是唯一的; 第二, 新模型更能反映出记忆依赖效应的本质; 第三, 新模型是由整数阶微积分定义的, 因此在数值计算时更加方便; 最后, 核函数和时间迟滞因子可以根据实际情况选择, 这对于描述材料的实际响应来说更加灵活. Ezzat等[20 ] 将含有时间迟滞因子的MDD引入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态), 基于此, Ezzat[21 -24 ] 进行了一系列相关研究. Shaw和Mukhopadhyay[25 ] 提出了MDD热传导模型的不连续性, 并将记忆依赖模型应用于瞬态热力响应的研究.
当外部特征尺寸大于内部特征尺寸时, 经典力学适用; 外部特征尺寸接近于内部特征尺寸时, 结构的力学响应会呈现出很强的尺寸相关性, 此时, 经典力学不再适用. 例如: 石墨烯、碳纳米管等微纳尺度结构, 在受热冲击时, 空间尺度效应十分显著, 经典的热力学定律和广义热弹理论已无法准确预测结构的热弹响应. 为了描述微纳尺度结构的空间非局部特性, Eringen等[26 ] 提出了非局部弹性理论, Eringen认为: 变形体内某点处的应力不仅与该点处的应变相关, 还与变形体内其他点的应变(包括应变的历史)相关, 只是这种作用效应随距离的增大而逐渐衰减. 他提出了一种积分型的本构关系
(5) $ \begin{eqnarray} \label{eq5} \sigma _{ij} \left( r \right)=\int_V {K\left( { r, r',\chi } \right)} \sigma _{ij}' \left( { r'} \right)\mbox{d}V\left( { r'} \right) \end{eqnarray}$
其中, $\sigma _{ij} $是非局部应力; $\sigma _{ij}' $是经典应力; $K\left( { r, r',\chi } \right)$是核函数, 它是由质点$ r$和$ r'$间的距离$\left| { r'- r} \right|$及$\chi $决定的; $\chi $的定义为: $\chi =ea/l$, $l$为外部特征尺寸, 代表整个研究对象的大小, $a$为内部特征尺寸, 代表非局部空间的大小. 根据研究对象的不同, $l$可以取为裂纹长度、位错宽度、应力波波长等; $a$可以取为化学键长、晶格尺寸等. $e$为材料特性参数, 由不同的材料性质所决定; $ea$代表非局部参数.
非局部算子作用会导致微分-积分型控制方程, 不便于求解. 为了将其简化, Eringen[27 ] 引入新的核函数和非局部算子, 将积分型本构方程改写为微分形式
(6) $ \begin{eqnarray} \label{eq6} \lt[ 1-\lt(e_0 a )^2\nabla ^2 ]\sigma _{ij} \left( r\right)=\sigma _{ij}' \left( { r'} \right) \end{eqnarray}$
Yu等[28 -29 ] 将Eringen非局部理论与非局部热传导方程相结合, 建立了新的非局部广义热弹性理论, 并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30 ] 基于非局部热弹性理论, 研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应, 考虑了非局部参数对各个物理量的影响; 张培等[31 ] 基于记忆依赖非局部广义热弹理论, 研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应.
文献[32 ] 虽然建立了考虑记忆依赖效应的广义热弹扩散理论, 但未考虑材料的空间非局部效应, 无法准确预测内外部特征尺寸相近结构的热弹扩散响应. 本文将空间非局部算子引入本构方程, 建立记忆依赖非局部广义热弹扩散理论, 它可以准确描述热传导和扩散效应的记忆依赖效应和空间非局部效应. 利用所建理论研究了受到非Gaussian激光脉冲加热和化学势冲击联合作用半无限大薄板的热弹扩散响应. 获得了结构的温度、化学势、位移、应力、浓度等随非局部参数和时间迟滞因子变化的分布规律.
1 记忆依赖非局部广义热弹扩散理论
(7) $ \begin{eqnarray} \label{eq7} \sigma _{ij,j} =\rho \ddot{{u}}_i \end{eqnarray}$
式中物理量上方的点表示对时间求导, 右下角的撇表示对物质坐标求导.
(8) $ \begin{eqnarray} \label{eq8} e_{ij} =\frac{1}{2}\left( {u_{i,j} +u_{j,i} } \right) \end{eqnarray}$
(9) $ \left[ {1-\left( {e_0 a} \right)^2\nabla ^2} \right]\sigma _{ij} \!=\!2\mu e_{ij} +\delta _{ij} \left( {\lambda _0 e_{kk} -\gamma _1 \theta -\gamma _2 P} \right) $
(10) $ \rho S=\gamma _1 e_{kk} +l_1 \theta +dP $
(11) $ C=\gamma _2 e_{kk} +d\theta +nP $
(12) $ \begin{eqnarray} \label{eq12} q_{i,i} =-\rho T_0 \dot{{S}}+Q \end{eqnarray}$
(13) $ \begin{eqnarray} \label{eq13} \eta _{i,i} =-\dot{{C}} \end{eqnarray}$
(14) $ \begin{eqnarray} \label{eq14} q_i +\omega _1 D_{\omega _1 } q_i =-\kappa _{ij} \theta _{,j} \end{eqnarray}$
(15) $ \begin{eqnarray} \label{eq15} \eta _i +\omega _2 D_{\omega _2 } \eta _i =-D_{ij} P_{,j} \end{eqnarray}$
其中, $\rho $是密度, $u_i $是位移分量, $e_{ij} $是应变分量, $\lambda ,\mu $是拉梅系数, $\delta _{ij} $是克罗内克记号, $e_{kk} $是体应变, $\theta $是温度增量, $P$是化学势, $S$是熵密度, $C$是浓度, $q_i $是热流矢量的分量, $T_0 $是参考温度, $Q$是热源强度, $\eta _i $是扩散流矢量的分量, $\omega _1 $是热时间迟滞因子, $\kappa _{ij} $是热传导系数, $\omega _2 $是扩散时间迟滞因子, $D_{ij} $是扩散系数.
将式(7)和式(8)代入式(9), 式(10)和式(12)代入式(14), 式(11)和式(13)代入式(15), 可得到记忆依赖非局部广义热弹扩散理论的控制方程
(16) $ \rho \left[ {1-\left( {e_0 a} \right)^2\nabla ^2} \right]\ddot{{u}}_i = \\ \qquad\left( {\lambda _0 +\mu } \right)u_{j,ij} +\mu u_{i,jj} -\gamma _1 \theta _{,i} -\gamma _2 P_{,i} $
(17) $ \kappa\theta_{,ii}=\left( {1+\omega _1 D_{\omega _1 } } \right)\lt(T_0\gamma_1\dot{e}_{kk}+T_0l_1\dot{\theta}+T_0d\dot{P}-Q ) $
(18) $ DP_{,ii} =\left( {1+\omega _2 D_{\omega _2 } } \right)\left( {\gamma _2 \dot{{e}}_{kk} +d\dot{{\theta }}+n\dot{{P}}} \right) $
$$\begin{eqnarray*} &&\theta =T-T_0 ,\ \ \lambda _0 =\lambda -\frac{\beta _2^2 }{b},\ \ \gamma _1 =\beta _1 +\frac{a}{b}\beta _2\\&&\gamma _2 =\frac{\beta _2 }{b},\ \ d=\frac{a}{b} \ \ n=\frac{1}{b},\ \ l_1 =\frac{\rho C_E }{T_0 }+\frac{a^2}{b}\\&&\beta _1 =\left( {3\lambda +2\mu } \right)\alpha _t ,\ \ \beta _2 =\left( {3\lambda +2\mu } \right)\alpha _c \end{eqnarray*}$$
式中, $T$是绝对温度, $a$是热扩散效应度量, $b$是扩散效应度量, $C_E $是比热容, $\alpha_t $是线性热膨胀系数, $\alpha _c $是线性扩散膨胀系数.
至此, 能同时描述记忆依赖效应和空间尺度效应的记忆依赖非局部广义热弹扩散理论被建立.
(19) $ \begin{eqnarray} \label{eq17} Q\left( {x,t} \right)=\frac{R_a L_0 }{\delta t_p^2 }t\exp \left( {-\frac{x}{\delta }-\frac{t}{t_p }} \right) \end{eqnarray}$
其中, $R_a $是表面反射率, $L_0 $是镭射强度, $\delta $是热源吸收深度, $t_p$是特征时间.
2 问题的求解
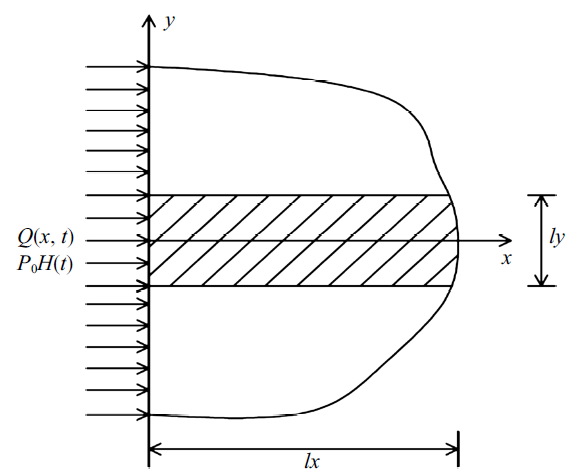
作为算例, 利用所建理论研究了边界受非高斯热源$Q\left( {x,t} \right)$和化学势冲击$P=P_0 H\left( t\right)$的联合作用半无限大薄板的热弹扩散瞬态响应问题, 其中, $H\left( t \right)$代表单位阶跃函数, $P_0 $代表化学势冲击的幅值. 该结构初始静止, 边界面应力自由. 根据结构和载荷特点, 问题可被简化为一维问题(仅与坐标$x$有关). 如图1 取薄板上的一窄条作为研究对象, 除左边界面外, 其他3个边界均为理想的热绝缘和化学势绝缘条件.
图1
图1
半无限大薄板边界受到热和化学冲击
Fig.1
Schematic of the semi-infinite thin plate subjected to a non-Gaussian heat source and a chemical shock
(20) $ \begin{eqnarray} \label{eq20} u_x =u\left( {x,t} \right),u_y =u_z =0 \end{eqnarray}$
(21) $ \begin{eqnarray} \label{eq21} e=e_{xx} =\frac{\partial u\left( {x,t} \right)}{\partial x} \end{eqnarray}$
(22) $ \begin{eqnarray} &&\rho \left[ {1-\left( {e_0 a} \right)^2\frac{\partial ^2}{\partial x^2}} \right]\frac{\partial ^2u}{\partial t^2}=\left( {\lambda _0 +2\mu } \right)\frac{\partial ^2u}{\partial x^2}- \\&&\qquad\gamma _1 \frac{\partial \theta }{\partial x}-\gamma _2 \frac{\partial P}{\partial x} \end{eqnarray}$
(23) $ \begin{eqnarray} \kappa \frac{\partial ^2\theta }{\partial x^2}=\left( {1+\omega _1 D_{\omega _1 } } \right)\left( T_0 \gamma _1 \frac{\partial ^2u}{\partial x\partial t}+T_0 l_1 \frac{\partial \theta }{\partial t}+ \\ \qquad T_0 d\frac{\partial P}{\partial t}-Q \right) \end{eqnarray}$
(24) $ \begin{eqnarray} D\frac{\partial ^2P}{\partial x^2}=\left( {1+\omega _2 D_{\omega _2 } } \right)\left( \gamma _2 \frac{\partial ^2u}{\partial x\partial t}+ \\ \qquad d\frac{\partial \theta }{\partial t}+n\frac{\partial P}{\partial t} \right) \end{eqnarray}$
(25) $ \begin{eqnarray} &&\left[ {1-\left( {e_0 a} \right)^2\frac{\partial ^2}{\partial x^2}} \right]\sigma =\left( {\lambda _0 +2\mu } \right)\frac{\partial u}{\partial x}-\gamma _1 \theta -\gamma _2 P\quad \end{eqnarray}$
(26) $ \begin{eqnarray} C=\gamma _2 \frac{\partial u}{\partial x}+d\theta +nP \end{eqnarray}$
(27) $ \left. \begin{array}{ll} x^\ast \left( {u^\ast ,\delta ^\ast ,\left( {e_0 a} \right)^\ast } \right)=c_0 \eta _0 x,\left( {u,\delta ,\left( {e_0 a} \right)} \right) \\ t^\ast \left( {t_p^\ast } \right)=c_0^2 \eta _0 t\left( {t_p } \right),\ \ \theta ^\ast =\dfrac{\beta _1 \theta }{\rho c_0^2 },\ \ P^\ast =\dfrac{P}{\beta _2 } \\ C^\ast =\dfrac{\beta _2 C}{\rho c_0^2 },\ \ \sigma ^\ast =\dfrac{\sigma }{\rho c_0^2 },\ \ q^\ast =\dfrac{q}{\kappa T_0 c_0 \eta _0 } \\[5mm] L_0^\ast =\dfrac{c_0 \eta _0 L_0 }{C_E \rho T_0 },\ \ c_0^2 =\dfrac{\lambda +2\mu }{\rho },\ \ \eta _0 =\dfrac{\rho C_E }{\kappa } \\ \end{array} \right\} $
为简化表述, 下文中在不引起混淆的情况下将去掉无量纲量右上角的星号. 式(22)$\sim$式(26)和式(14)经无量纲化处理后为
(28) $ \begin{eqnarray} \label{eq28} &&\left[ {1-\left( {e_0 a} \right)^2\frac{\partial ^2}{\partial x^2}} \right]\varepsilon \frac{\partial ^2u}{\partial t^2}=\frac{\partial ^2u}{\partial x^2}-\varepsilon \alpha _1 \frac{\partial \theta }{\partial x}-\varepsilon _1 \frac{\partial P}{\partial x} \end{eqnarray}$
(29) $ \begin{eqnarray} \frac{\partial ^2\theta }{\partial x^2}=\left( {1+\omega _1 D_{\omega _1 } } \right)\left[ W_1 \frac{\partial ^2u}{\partial x\partial t}+W_2 \frac{\partial \theta }{\partial t}+W_3 \frac{\partial P}{\partial t}- \\ \qquad W_4 t\exp \left( {-\frac{x}{\delta }-\frac{t}{t_p }} \right) \right] \end{eqnarray}$
(30) $ \begin{eqnarray} \label{eq30} \frac{\partial ^2P}{\partial x^2}=\left( {1+\omega _2 D_{\omega _2 } } \right)\left( {V_1 \frac{\partial ^2u}{\partial x\partial t}+V_2 \frac{\partial \theta }{\partial t}+V_3 \frac{\partial P}{\partial t}} \right) \end{eqnarray}$
(31) $ \begin{eqnarray} \left[ {1-\left( {e_0 a} \right)^2\frac{\partial ^2}{\partial x^2}} \right]\sigma =\frac{\beta ^{'2}}{\beta ^2}\frac{\partial u}{\partial x}-\alpha _1 \theta -\frac{\alpha _2 }{\beta ^2}P \end{eqnarray}$
(32) $ \begin{eqnarray} C=\frac{\alpha _2 }{\beta ^2}\left( {\frac{\partial u}{\partial x}+P} \right)+\frac{d\beta _2 }{\beta _1 }\theta \end{eqnarray}$
(33) $ \begin{eqnarray} \left( {1+\omega _1 D_{\omega _1 } } \right)q_i =-q_0 \frac{\partial \theta }{\partial x} \end{eqnarray} $
$$\begin{eqnarray*} &&\varepsilon =\frac{\beta ^2}{\beta ^{'2}},\ \ \varepsilon _1 =\frac{\alpha _2 }{\beta ^{'2}},\ \ \beta ^2=\frac{\lambda +2\mu }{\mu },\ \ \beta ^{'2}=\frac{\lambda _0 +2\mu }{\mu } \\&& \alpha _1 =\frac{\gamma _1 }{\beta _1 },\ \ \alpha _2 =\frac{\gamma _2 \beta _2 }{\mu },\ \ W_1 =\frac{T_0 \beta _1 \gamma _1 }{\kappa \eta _0 \left( {\lambda +2\mu } \right)},\ \ W_2 =\frac{T_0 l_1 }{\kappa \eta _0 } \\&& W_3 =\frac{T_0 d\beta _1 \beta _2 }{\kappa \eta _0 \left( {\lambda +2\mu } \right)},\ \ W_4 =\frac{\beta _1 T_0 R_a L_0 }{\left( {\lambda +2\mu } \right)\delta t_p^2 },\ \ V_1 =\frac{\gamma _2 }{D\eta _0 \beta _2 } \\&& V_2 =\frac{d\left( {\lambda +2\mu } \right)}{D\eta _0 \beta _1 \beta _2 },\ \ V_3 =\frac{n}{D\eta _0 },q_0 =\frac{\lambda +2\mu }{\beta _1 T_0 } \end{eqnarray*}$$
(34) $ \left. \begin{array}{ll} u\left( {x,0} \right)=\dot{{u}}\left( {x,0} \right)=0 \\ \theta \left( {x,0} \right)=\dot{{\theta }}\left( {x,0} \right)=0 \\ P\left( {x,0} \right)=\dot{{P}}\left( {x,0} \right)=0 \\ \end{array} \right\} $
(35) $ \begin{eqnarray} \label{eq35} \left. \begin{array}{ll} \sigma \left( {0,t} \right)=0,q\left( {0,t} \right)=0,P\left( {0,t} \right)=P_0 H\left( t \right) \\ u\left( {\infty ,t} \right)=0,q\left( {\infty ,t} \right)=0,P\left( {\infty ,t} \right)=0 \\ \end{array} \right\} \end{eqnarray}$
(36) $ \begin{eqnarray} \label{eq36} L\left[ {f\left( t \right)} \right]=\bar{{f}}\left( s \right)=\int_0^\infty {\mbox{e}^{-st}f\left( t \right)\mbox{d}t},\ \ Re\left( s \right)>0 \end{eqnarray}$
对式(28)$\sim$式(33)进行拉普拉斯变换
(37) $ \begin{eqnarray} \hspace{-3mm}&&\left\{ {\left[ {1+\varepsilon s^2\left( {e_0 a} \right)^2} \right]\frac{\mbox{d}^2}{\mbox{d}x^2}-\varepsilon s^2} \right\}\bar{{u}}=\varepsilon \alpha _1 \frac{\mbox{d}\bar{{\theta }}}{\mbox{d}x}+\varepsilon _1 \frac{\mbox{d}\bar{{P}}}{\mbox{d}x} \end{eqnarray}$
(38) $ \begin{eqnarray} \frac{\mbox{d}^2\bar{{\theta }}}{\mbox{d}x^2}=\left( {1+G_1 } \right)\left( {W_1 s\frac{\mbox{d}\bar{{u}}}{\mbox{d}x}+W_2 s\bar{{\theta }}+W_3 s\bar{{P}}-F\left( {x,s} \right)} \right)\qquad \end{eqnarray}$
(39) $ \begin{eqnarray} \frac{\mbox{d}^2\bar{{P}}}{\mbox{d}x^2}=s\left( {1+G_2 } \right)\left( {V_1 \frac{\mbox{d}\bar{{u}}}{\mbox{d}x}+V_2 \bar{{\theta }}+V_3 \bar{{P}}} \right) \end{eqnarray}$
(40) $ \begin{eqnarray} \left[ {1-\left( {e_0 a} \right)^2\frac{\mbox{d}^2}{\mbox{d}x^2}} \right]\bar{{\sigma }}=\frac{1}{\beta ^2}\left( {\beta ^{'2}\frac{\mbox{d}\bar{{u}}}{\mbox{d}x}-\alpha _1 \beta ^2\bar{{\theta }}-\alpha _2 \bar{{P}}} \right)\end{eqnarray}$
(41) $ \begin{eqnarray} \bar{{C}}=\frac{\alpha _2 }{\beta ^2}\left( {\frac{\mbox{d}\bar{{u}}}{\mbox{d}x}+\bar{{P}}} \right)+\frac{d\beta _2 }{\beta _1 }\bar{{\theta }} \end{eqnarray}$
(42) $ \begin{eqnarray} \left( {1+G_1 } \right)\bar{{q}}=-q_0 \frac{\mbox{d}\bar{{\theta }}}{\mbox{d}x} \end{eqnarray}$
$$\begin{eqnarray*} \begin{array}{l} F\left( {x,s} \right)=\dfrac{W_4 \exp \left( {-\dfrac{x}{\delta }} \right)}{\left( {s+1/t_p } \right)^2} \\ G_1 \left( s \right)=\left( {1-\mbox{e}^{-s\omega _1 }} \right)\left( {1-\dfrac{2q}{\omega _1 s}+\dfrac{2p^2}{\omega _1^2 s^2}} \right)-\\ \qquad\mbox{e}^{-s\omega _1 }\left( {p^2-2q+\dfrac{2p^2}{\omega _1 s}} \right) \\ G_2 \left( s \right)=\left( {1-\mbox{e}^{-s\omega _2 }} \right)\left( {1-\dfrac{2q}{\omega _2 s}+\dfrac{2p^2}{\omega _2^2 s^2}} \right)-\\ \qquad\mbox{e}^{-s\omega _2 }\left( {p^2-2q+\dfrac{2p^2}{\omega _2 s}} \right) \\ \end{array} \end{eqnarray*}$$
(43) $ \begin{eqnarray} &&L\left\{ {\omega _1 D_{\omega _1 } f_1 \left( t \right)} \right\}= \\&&\qquad F_1 \left( s \right)\left\{ {\begin{array}{l} 1-\mbox{e}^{-s\omega _1 },\ \ p=q=0 \\ 1-\dfrac{1}{\omega _1 s}\left( {1-\mbox{e}^{-s\omega _1 }} \right),\ \ p=0,\ \ q=\dfrac{1}{2} \\ \left( {1-\mbox{e}^{-s\omega _1 }} \right)-\dfrac{1}{s}\left( {1-\mbox{e}^{-s\omega _1 }} \right)+\omega _1 \mbox{e}^{-s\omega _1 },\\\qquad p=0,\ \ q=\dfrac{\omega _1 }{2} \\ \left( {1-\dfrac{2}{\omega _1 s}} \right)+\dfrac{2}{\omega _1^2 s^2}\left( {1-\mbox{e}^{-s\omega _1 }} \right),\\\qquad p=q=1 \\ \end{array}} \right. \end{eqnarray}$
(44) $ \begin{eqnarray} L\left\{ {f_1 \left( t \right)} \right\}=F_1 \left( s \right) = L\left\{ W_1 \dfrac{\partial ^2u}{\partial x\partial t}+W_2 \dfrac{\partial \theta }{\partial t}+W_3 \dfrac{\partial P}{\partial t}- . \\ \qquad W_4 t\exp \left( {-\dfrac{x}{\delta }-\dfrac{t}{t_p }} \right) \right\} = W_1 s\dfrac{\mbox{d}\bar{{u}}}{\mbox{d}x}+W_2 s\bar{{\theta }}+ \\ \qquad W_3 s\bar{{P}}-F\left( {x,s} \right) \end{eqnarray}$
(45) $ \begin{eqnarray} && L\left\{ {\omega _2 D_{\omega _2 } f_2 \left( t \right)} \right\}= \\&&\qquad F_2 \left( s \right)\left\{ \begin{array}{l} 1-\mbox{e}^{-s\omega _2 },\ \ p=q=0 \\ 1-\dfrac{1}{\omega _2 s}\left( {1-\mbox{e}^{-s\omega _2 }} \right),\ \ p=0,\ \ q=\dfrac{1}{2} \\ \left( {1-\mbox{e}^{-s\omega _2 }} \right)-\dfrac{1}{s}\left( {1-\mbox{e}^{-s\omega _2 }} \right)+\omega _2 \mbox{e}^{-s\omega _2 }\\\qquad p=0,\ \ q=\dfrac{\omega _2 }{2} \\ \left( {1-\dfrac{2}{\omega _2 s}} \right)+\dfrac{2}{\omega _2^2 s^2}\left( {1-\mbox{e}^{-s\omega _2 }} \right)\\\qquad p=q=1 \\ \end{array} \right. \end{eqnarray}$
(46) $ \begin{eqnarray} &&L\left\{ {f_2 \left( t \right)} \right\}=F_2 \left( s \right)=L\left\{ {V_1 \dfrac{\partial ^2u}{\partial x\partial t}+V_2 \dfrac{\partial \theta }{\partial t}+V_3 \dfrac{\partial P}{\partial t}} \right\} = \\&&\qquad s\left( {V_1 \dfrac{\mbox{d}\bar{{u}}}{\mbox{d}x}+V_2 \bar{{\theta }}+V_3 \bar{{P}}} \right) \end{eqnarray}$
(47) $ \left. \begin{array}{ll} \bar{{\sigma }}\left( {0,s} \right)=0,\bar{{q}}\left( {0,s} \right)=0,\bar{{P}}\left( {0,s} \right)=P_0 H\left( s \right) \\ \bar{{u}}\left( {\infty ,s} \right)=0,\bar{{q}}\left( {\infty ,s} \right)=0,\bar{{P}}\left( {\infty ,s} \right)=0 \\ \end{array} \right\} $
从式(37)$\sim$式(39)中消去$\bar{{\theta }}$和$\bar{{P}}$, 可得到关于$\bar{{u}}$的六阶常微分方程
(48) $ \begin{eqnarray} \label{eq48} &&\hspace{-5mm}\left( {\frac{\mbox{d}^6}{\mbox{d}x^6}-m_1 \frac{\mbox{d}^4}{\mbox{d}x^4}+m_2 \frac{\mbox{d}^2}{\mbox{d}x^2}-m_3 } \right)\bar{{u}}=m_4 \exp \left( {-\frac{x}{\delta }} \right) \end{eqnarray}$
$$m_1 =\Big[\varepsilon s^2+s\left( {1+G_1 } \right)\left( {W_2 g+\varepsilon \alpha _1 W_1 } \right)+ \\ s\left( {1+G_2 } \right)\left( {V_3 g+\varepsilon _1 V_1 } \right)\Big]\Big/g$$
$$m_2 =\left\{s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)\left[g\left( {W_2 V_3 -W_3 V_2 } \right)+ \\ \varepsilon _1 \left( {W_2 V_1 -W_1 V_2 } \right)+\varepsilon \alpha _1 \left( {W_1 V_3 -W_3 V_1 } \right)\right]+ \\ \varepsilon s^2\left[ s\left( {1+G_1 } \right)W_2 +s\left( {1+G_2 } \right)V_3 \right]\right\}\Big/g$$
$$m_3 =\left[ {\varepsilon s^4\left( {1+G_1 } \right)\left( {1+G_2 } \right)\left( {W_2 V_3 -W_3 V_2 } \right)} \right]\Big/g$$
$$m_4 =\left[ {s\left( {1+G_1 } \right)^2W_3 W_4 \varepsilon \alpha _1 } \right]\Big/\Big[ {\left( {s+1/t_p } \right)^2\delta ^3} \Big] - \\ \Big\{ \left[ s^2\left( {1+G_1 } \right)^2\left( {1+G_2 } \right)W_3 V_3 \varepsilon \alpha _1 -\varepsilon _1 s^2\left( {1+G_1 } \right)^2\cdot \\ \left( {1+G_2 } \right)W_3 V_2\right]W_4 \Big\}\Big/\Big[ \left( {s+1/t_p }\right)^2\delta \Big] \\ g=1+\varepsilon s^2\left( {e_0 a} \right)^2$$
考虑边界条件$\bar{{u}}\left( {\infty ,s} \right)=0$, 满足式(48)的$\bar{{u}}$的表达式如下
(49) $ \begin{eqnarray} \label{eq49} \bar{{u}}=u_1 \mbox{e}^{-k_1 x}+u_2 \mbox{e}^{-k_2 x}+u_3 \mbox{e}^{-k_3 x}+u_4 \mbox{e}^{-x/\delta } \end{eqnarray}$
$$\begin{eqnarray*} u_4 =\frac{m_4 \delta ^6}{1-m_1 \delta ^2+m_2 \delta ^4-m_3 \delta ^6} \end{eqnarray*}$$
$k_1 ,k_2 ,k_3 $为满足下列特征方程的根
(50) $ \begin{eqnarray} \label{eq50} k^6-m_1 k^4+m_2 k^2-m_3 =0 \end{eqnarray}$
(51) $ \begin{eqnarray} k_1 =\sqrt {\frac{1}{3}\left( {2\vartheta \sin \varsigma +m_1 } \right)} \end{eqnarray}$
(52) $ \begin{eqnarray} k_2 =\sqrt {-\frac{\vartheta }{3}\left( {\sqrt 3 \cos \varsigma +\sin \varsigma } \right)+\frac{m_1 }{3}} \end{eqnarray}$
(53) $ \begin{eqnarray} k_3 =\sqrt {\frac{\vartheta }{3}\left( {\sqrt 3 \cos \varsigma -\sin \varsigma } \right)+\frac{m_1 }{3}} \end{eqnarray}$
$$\begin{eqnarray*} \begin{array}{l} \vartheta =\sqrt {m_1^2 -3m_2 } ,\varsigma =\dfrac{1}{3}\sin ^{-1}R\\ R=\dfrac{-2m_1^3 +9m_1 m_2 -27m_3 }{3\vartheta ^3} \end{array} \end{eqnarray*}$$
同样地, $\bar{{\theta }}$和$\bar{{P}}$的表达式如下
(54) $ \begin{eqnarray} \bar{{\theta }}=\theta _1 \mbox{e}^{-k_1 x}+\theta _2 \mbox{e}^{-k_2 x}+\theta _3 \mbox{e}^{-k_3 x}+\theta _4 \mbox{e}^{-x/\delta } \end{eqnarray} $
(55) $ \begin{eqnarray} \bar{{P}}=P_1 \mbox{e}^{-k_1 x}+P_2 \mbox{e}^{-k_2 x}+P_3 \mbox{e}^{-k_3 x}+P_4 \mbox{e}^{-x/\delta }\end{eqnarray} $
将式(49)、式(54)和式(55)代入式(38)和式(39), 可以得到
(56) $ \begin{eqnarray} \label{eq56} \theta _i =A_i u_i ,\ \ P_i =B_i u_i \end{eqnarray}$
$$\begin{eqnarray} && A_i =-k_i \Big[ W_3 V_1 s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)+W_1 s\left( {1+G_1 } \right)\cdot \\&&\qquad\left( {k_i^2 -V_3 s\left( {1+G_2 } \right)} \right)\Big]\Big/\Big\{\left[ {k_i^2 -W_2 s\left( {1+G_1 } \right)} \right]\cdot \\&&\qquad\left[ {k_i^2 -V_3 s\left( {1+G_2 } \right)} \right]-s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)W_3 V_2\Big\} \\ &&B_i =-k_i \Big[ V_1 s\left( {1+G_2 } \right)\left( {k_i^2 -W_2 s\left( {1+G_1 } \right)} \right)+ W_1 V_2 s^2\cdot \\&&\qquad\left( {1+G_1 } \right)\left( {1+G_2 } \right) \Big]\Big/\Big\{\left[ {k_i^2 -W_2 s\left( {1+G_1 } \right)} \right]\cdot \\&&\qquad\left[ {k_i^2 -V_3 s\left( {1+G_2 } \right)} \right]-s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)W_3 V_2\Big\} \\ &&\qquad \left( {i=1,2,3} \right) \end{eqnarray}$$
(57) $ \begin{eqnarray} \theta _4 =\Big\{\left[1/\delta ^2-s\left( {1+G_2 } \right)V_3\right]s\left( {1+G_1 } \right)W_1 u_4 /\delta + && \\ \qquad s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)W_3 V_1 u_4 /\delta +\Big[ 1/\delta ^2- && \\ \qquad s\left( {1+G_2 } \right)V_3 \Big]\left( {1+G_1 } \right)W_4 \Big/\left( {s+1/t_p } \right)^2 \Big\}\Big/ && \\ \qquad\Big\{s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)W_3 V_2 -\Big[ 1/\delta ^2- && \\ \qquad s\left( {1+G_2 } \right)V_3\Big]\left[ 1/\delta ^2-s\left( {1+G_1 } \right)W_2 \right]\Big\} \end{eqnarray}$
(58) $ \begin{eqnarray} P_4 =\Big\{ \left[ {1/\delta ^2-s\left( {1+G_1 } \right)W_2 } \right]s\left( {1+G_2 } \right)V_1 u_4 /\delta+ && \\ \qquad s^2\left( {1+G_1 } \right)\left( {1+G_2 } \right)W_1 V_2 u_4 \Big/\delta +s\left( {1+G_1 } \right)\cdot && \\ \qquad\left( {1+G_2 } \right)V_2 W_4 /\left( {s+1/t_p } \right)^2\Big\}\Big/\Big\{s^2\left( {1+G_1 } \right)\cdot && \\ \qquad\left( {1+G_2 } \right)W_3 V_2 -\left[ {1/\delta ^2-s\left( {1+G_2 } \right)V_3 } \right]\cdot && \\ \qquad\left[ {1/\delta ^2-s\left( {1+G_1 } \right)W_2 } \right]\Big\} \end{eqnarray}$
$\bar{{\sigma }},\bar{{C}},\bar{{q}}$的表达式如下
(59) $ \begin{eqnarray} \bar{{\sigma }}=\sigma _1 \mbox{e}^{-k_1 x}+\sigma _2 \mbox{e}^{-k_2 x}+\sigma _3 \mbox{e}^{-k_3 x}+\sigma _4 \mbox{e}^{-x/\delta } \end{eqnarray}$
(60) $ \begin{eqnarray} \bar{{C}}=C_1 \mbox{e}^{-k_1 x}+C_2 \mbox{e}^{-k_2 x}+C_3 \mbox{e}^{-k_3 x}+C_4 \mbox{e}^{-x/\delta } \end{eqnarray}$
(61) $ \begin{eqnarray} \bar{{q}}=q_1 \mbox{e}^{-k_1 x}+q_2 \mbox{e}^{-k_2 x}+q_3 \mbox{e}^{-k_3 x}+q_4 \mbox{e}^{-x/\delta } \end{eqnarray}$
将温度、化学势和位移的解代入式(40)$\sim$式(42), 可以得到
(62) $ \begin{eqnarray} \label{eq62} \sigma _i =H_i u_i ,\ \ C_i =O_i u_i ,\ \ q_i =Q_i u_i \end{eqnarray}$
(63) $ \begin{eqnarray} \left. \begin{array}{ll} H_i =\dfrac{-\beta ^{'2}k_i /\beta ^2-\alpha _1 A_i -\alpha _2 B_i /\beta ^2}{1-\left( {e_0 a} \right)^2k_i^2 } \\ O_i =\dfrac{\alpha _2 }{\beta ^2}\left( {B_i -k_i } \right)+\dfrac{d\beta _2 }{\beta _1 }A_i \\ Q_i =\dfrac{q_0 }{\left( {1+G_1 } \right)}k_i A_i \\ \qquad\left( {i=1,2,3} \right) \\ \sigma _4 =-\left( {\dfrac{\beta ^{'2}}{\beta ^2\delta }u_4 +\alpha _1 \theta _4 +\dfrac{\alpha _2 }{\beta ^2}P_4 } \right)\Bigg/\\ \qquad \left[ {1-\left( {e_0 a} \right)^2\left( {1/\delta ^2} \right)} \right] \end{array} \right\} \end{eqnarray}$
(64) $ \begin{eqnarray} C_4 =-\frac{\alpha _2 }{\beta ^2\delta }u_4 +\frac{d\beta _2 }{\beta _1 }\theta _4 +\frac{\alpha _2 }{\beta ^2}P_4 \end{eqnarray}$
(65) $ \begin{eqnarray} q_4 =\frac{q_0 }{\left( {1+G_1 } \right)\delta }\theta _4 \end{eqnarray}$
由$\bar{{\sigma }}\left( {0,s} \right)=0$, $\bar{{q}}\left( {0,s} \right)=0$, $\bar{{P}}\left( {0,s} \right)=P_0 H\left( s \right)$确定$u_1$, $u_2$, $u_3$
(66) $ H_1 u_1 +H_2 u_2 +H_3 u_3 +\sigma _4 =0 $
(67) $ Q_1 u_1 +Q_2 u_2 +Q_3 u_3 +q_4 =0 $
(68) $ B_1 u_1 +B_2 u_2 +B_3 u_3 +P_4 =1/s $
3 拉普拉斯数值反变换
为了将所求得的物理量从拉氏域转换到时间域中, 还需进行拉普拉斯反变换. 由于拉氏域中所得结果的复杂性, 不便求其解析解, 而应用数值计算的方法可以将求解过程简化. 本文中, 采用Brancik[33 ] 提出的Matlab程序进行拉普拉斯数值反变换.
4 模型验证及算例分析
考虑材料的记忆依赖效应和空间非局部效应, 且边界面受非高斯激光脉冲加热和化学势冲击联合作用的半无限大薄板, 其瞬态响应与时间$t$、非局部参数$e_0 a$、热时间迟滞因子$\omega _1 $、扩散时间迟滞因子$\omega _2 $、热核函数$K_1 \left( {t-\xi } \right)$以及扩散核函数$K_2 \left( {t-\xi } \right)$有关. 本文重点研究非局部参数、热时间迟滞因子和扩散时间迟滞因子的变化对结构温度、化学势、位移、应力和浓度的影响. 分析中用到的常量如下$ \lambda =7.76\times 10^{10}$ kg/m$\cdot$s$^{2}$, $\mu =3.86\times 10^{10}$ kg/m$\cdot$s$^{2}$, $\kappa =386$ W/(m$\cdot$K), $D=8.5\times 10^{-9}$ kg$\cdot$s/m$^{3}$, $\alpha _c =1.98\times 10^{-4}$ m$^3$/kg, $\rho =8954$ kg/m$^{3}$, $\alpha _t =1.78\times 10^{-5}$ K$^{-1}$, $C_E =383.1$ J/(kg$\cdot$K), $a=1.2\times 10^4$ m$^{2}$/(s$^{2}$$\cdot$K), $b=9.0\times 10^5$ m$^5$/(kg$\cdot$s$^2$), $T_0 =293$ K, $L_0 =1.0\times 10^5$ J/m$^{2}$, $R_a =0.5$, $\delta =0.01$ m, $t_p =2.0$ ps.
以下分析中所述量均为无量纲量, 无量纲化学势幅值$P_0 =1$.
4.1 模型验证
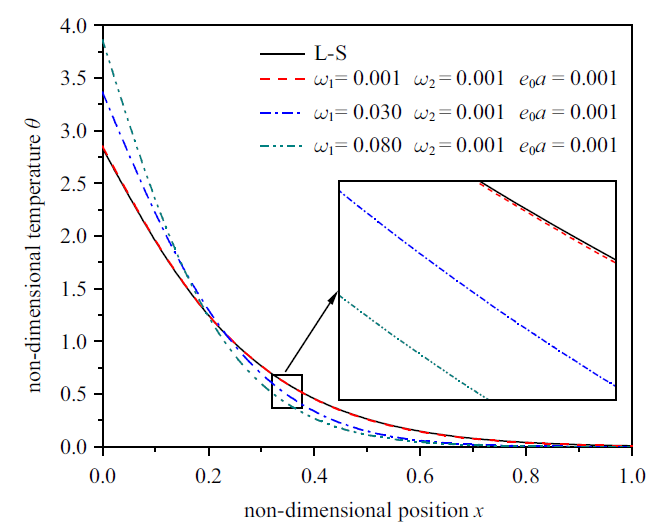
为验证所建模型的准确性, 基于本文所建模型分析了边界受热和化学冲击时板的响应, 并与L-S广义热弹扩散理论所得结果进行比较, 分析中, 热核函数和扩散核函数均取为1. $t=0.1$时刻模型取不同参数时板的温度分布如图2 所示. 由理论可知, 当所建模型的热时间迟滞因子$\omega _1 $、扩散时间迟滞因子$\omega _2 $及非局部参数$e_0 a$均趋近于0时, 所建模型将退化为L-S模型. 由图2 可知, 当$\omega _1$, $\omega _2 $和$e_0 a$的取值趋近于0时, 本文模型所得结果向L-S模型结果靠近. 如图中所示, 当它们取0.001时, 本文结果几乎于L-S结果重合. 由此验证了本文模型的准确性.
图2
图2
记忆依赖非局部模型与L-S模型的对比
Fig.2
Comparison between memory-dependent nonlocal model and L-S model
4.2 非局部参数$e_0 a$的影响
研究非局部参数$e_0 a$的变化对温度、化学势、位移、应力和浓度分布规律的影响. 在计算中, 非局部参数分别取: $e_0 a=0$, $e_0 a=0.045$和$e_0 a=0.09$, 时间、热时间迟滞因子、扩散时间迟滞因子、热核函数和扩散核函数的取值分别为: $t=0.05$, $\omega _1 =0.02$, $\omega _2 =0.02$, $K_1 \left( {t-\xi } \right)=1$和$K_2 \left( {t-\xi } \right)=1$. 得到的结果如图3 所示.
图3
图3
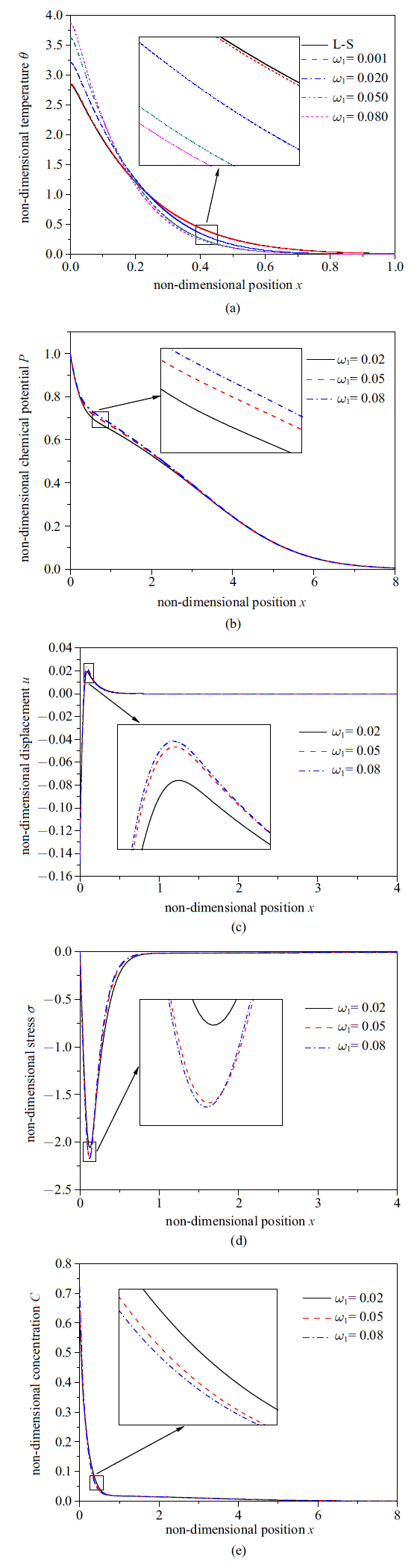
随非局部参数的变化. (a)无量纲温度, (b)无量纲化学势, (c)无量纲位移, (d)无量纲应力, (e)无量纲浓度的分布规律
Fig.3
The distributions of the non-dimensional temperature (a), chemical potential (b), displacement (c), stress (d) and concentration (e) with different nonlocal parameters
从图3 可以看出: 非局部参数取不同值时, 位移和应力图像变化显著, 而温度、化学势和浓度图像几乎不受非局部参数的影响. 这是由于: 非局部参数表征的是空间非局部效应, 即它对本构方程影响显著, 对传热和传质方程影响较小, 而结构中的温度和化学势是由热传导方程和扩散方程控制的, 故非局部参数的变化对位移和应力的影响显著, 对温度、化学势和浓度的影响不显著.
由图3 (c)可知, 位移的峰值随非局部参数的增大而减小, 在靠近边界处, 位移的最大值随非局部参数的增大而减小. 当$e_0a$的取值为小量($1.0\times 10^{-5})$时, 记忆依赖非局部模型与L-S模型的位移曲线接近, 此结论与理论预测一致, 可验证本文模型的准确性. 由图3 (d)可知, 应力峰值的绝对值随非局部参数的增大而减小. 图3 (e)表明: 温度达到零值前浓度的减小速率远远大于温度达到零值后浓度的减小速率.
4.3 热时间迟滞因子$\omega _1 $的影响
研究热时间迟滞因子$\omega _1$的变化对温度、化学势、位移、应力和浓度分布规律的影响. 在计算中, 热时间迟滞因子分别取: $\omega _1 =0.02$, $\omega _1 =0.05$和$\omega _1=0.08$, 时间、非局部参数、扩散时间迟滞因子、热核函数和扩散核函数的取值分别为: $t=0.1$, $e_0 a=0$, $\omega _2 =0.02$, $K_1 \left( {t-\xi } \right)=1$和$K_2 \left( {t-\xi } \right)=1$. 得到的结果如图4 所示.
图4
图4
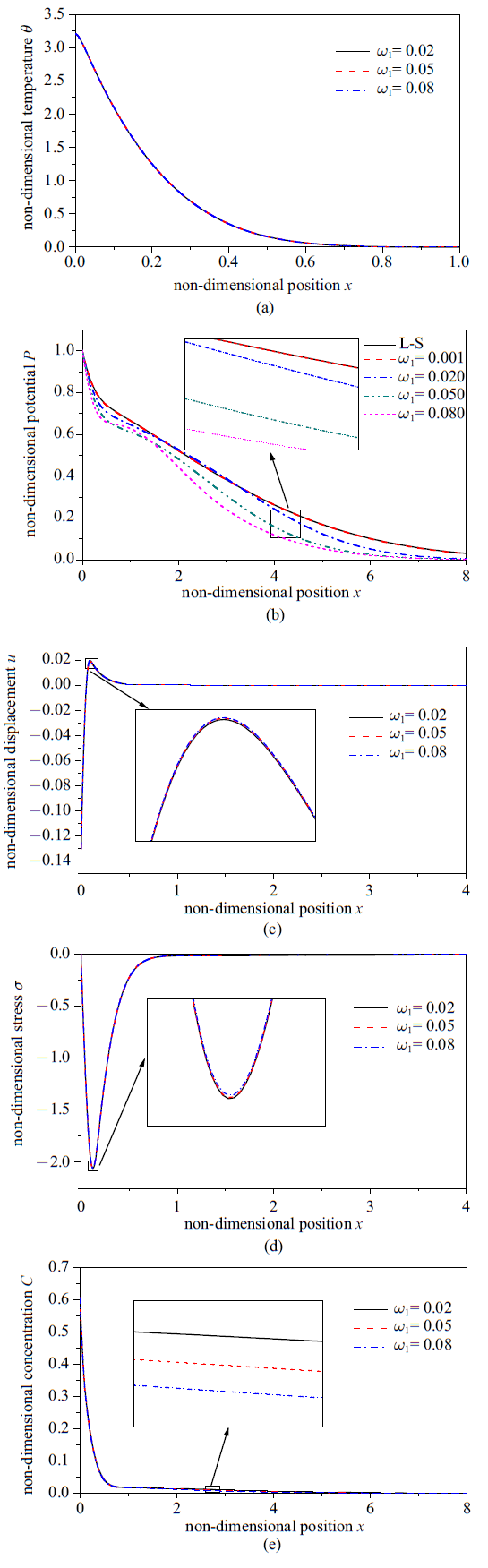
随热时间迟滞因子的变化. (a)无量纲温度, (b)无量纲化学势, (c)无量纲位移, (d)无量纲应力, (e)无量纲浓度的分布规律
Fig.4
The distributions of the non-dimensional temperature (a), chemical potential (b), displacement (c), stress (d) and concentration (e) under different thermal time delay factors
由图4 (a)可知, 温度在靠近边界处随热时间迟滞因子的增大而增大, 在$x=0.15$直至热弹波传播至零的过程中, 温度随热时间迟滞因子的增大而减小. 当$\omega _1 $的取值为小量(0.001)时, 记忆依赖非局部模型与L-S模型的温度曲线接近, 此结论与理论预测一致, 可验证本文模型的准确性. 图4 (b)表明: 化学势随热时间迟滞因子的增大而增大. 由图4 (c)和图4 (d)可知, 位移峰值和应力峰值的绝对值均随热时间迟滞因子的增大而增大, 在靠近边界处, 位移的最大值随热时间迟滞因子的增大而增大. 图4 (e)表明: 浓度随热时间迟滞因子的增大而减小.
4.4 扩散时间迟滞因子$\omega _2 $的影响
研究扩散时间迟滞因子$\omega _2$的变化对温度、化学势、位移、应力和浓度分布规律的影响. 在计算中, 扩散时间迟滞因子分别取: $\omega _2 =0.02$, $\omega _2 =0.05$和$\omega _2 =0.08$, 时间、非局部参数、热时间迟滞因子、热核函数和扩散核函数的取值分别为: $t=0.1$, $e_0 a=0$, $\omega _1 =0.02$, $K_1 \left( {t-\xi } \right)=1$和$K_2 \left( {t-\xi } \right)=1$. 得到的结果如图5 所示.
图5
图5
随扩散时间迟滞因子的变化. (a)无量纲温度, (b)无量纲化学势, (c)无量纲位移, (d)无量纲应力, (e)无量纲浓度的分布规律
Fig.5
The distributions of the non-dimensional temperature (a), chemical potential (b), displacement (c), stress (d) and concentration (e) under different diffusion time delay factors
比较图5 (a)和图4 (b)可知, 随热时间迟滞因子$\omega _1 $的变化, 化学势图像变化显著, 随扩散时间迟滞因子$\omega _2 $的变化, 温度图像几乎重合, 此现象表明: 传热对传质过程影响显著, 而传质对传热过程影响甚微. 由图5 (b)可知, 扩散时间迟滞因子越小, 扩散波传播的距离越远, 其原因是: 迟滞时间越短, 意味着过去态越接近于现在状态, 即时间越长, 波传播的距离就越远. 当$\omega _2 $的取值为小量(0.001)时, 记忆依赖非局部模型与L-S模型的化学势曲线接近, 此结论与理论预测一致, 可验证本文模型的准确性. 图5 (c)、图5 (d)和图5 (e)表明: 位移峰值随扩散时间迟滞因子的增大而增大, 在靠近边界处, 位移最大值随扩散时间迟滞因子的增大而增大; 应力峰值的绝对值和浓度随扩散时间迟滞因子的增大而减小.
5 结论
本文将空间非局部算子引入本构方程, 建立记忆依赖非局部广义热弹扩散理论, 采取拉普拉斯变换及其数值反变换的方法求解广义热弹扩散耦合的一维问题, 分析了不同参数对响应的影响, 可以得到如下结论:
(1) 在给定时刻, 热和扩散的扰动区域有限, 这表明热和扩散的传输呈现波动性, 即热弹波和扩散波均以有限大速度传播;
(2) 由于非局部参数仅仅修正本构方程, 故非局部参数的变化对位移和应力的影响显著, 对温度、化学势和浓度影响;
(3) 传热对传质过程影响显著, 传质对传热过程影响甚微.
参考文献
View Option
[1]
Maiman TH . Stimulated optical radiation in ruby
Nature 1960 ,187 (4736 ):493 -494
DOI
URL
[本文引用: 1]
[2]
Sun Y Fang D Saka M , et al . Laser-induced vibrations of micro-beams under different boundary conditions
International Journal of Solids & Structures2008 ,45 (7-8 ):1993 -2013
[本文引用: 1]
[3]
Wang X Xu X . Thermoelastic wave induced by pulsed laser heating
Applied Physics A 2001 ,73 (1 ):107 -114
[本文引用: 1]
[4]
Youssef HM El-Bary AA . Thermoelastic material response due to laser pulse heating in context of four theorems of thermoelasticity
Journal of Thermal Stresses 2014 ,37 (12 ):1379 -1389
DOI
URL
[本文引用: 1]
This article describes the study of induced temperature and stress fields in an elastic half-space in the context of classical coupled thermoelasticity (Biot) and generalized thermoelasticity (Lord-Shulman, Green-Lindsay and Green-Naghdi) in a unified system of equations. The medium is considered to be made of an isotropic homogeneous thermoelastic half-space. The bounding plane of the surface is heated by a non-Gaussian laser beam with pulse duration of 2 ps. An exact solution of the problem is first obtained in Laplace transform space. Because the response is of more interest in the transient state, the inversion of Laplace transforms were carried out numerically. The derived expressions were computed numerically for copper, and the results are presented in graphical form.
[5]
Elhagary MA . A two-dimensional generalized thermoelastic diffusion problem for a thick plate subjected to thermal loading due to laser pulse
Journal of Thermal Stresses 2014 ,37 (12 ):1416 -1432
DOI
URL
[本文引用: 1]
A two-dimensional problem for a thermoelastic thick plate is considered within the context of the theory of generalized thermoelastic diffusion with one relaxation time. The upper surface of the thick plate is taken to be traction free and heated by a laser beam. The chemical potential is also assumed to be a known function of time on the bounding plane. The lower surface is taken to be in contact with a rigid surface and is thermally insulated and impermeable. Laplace and Fourier transform techniques are used. The solution in the transformed domain is obtained by a direct approach. Numerical inversion techniques are used to obtain the inverse double transforms; numerical results are discussed and represented graphically.
[6]
Othman MIA Eraki EEM . Effect of gravity on generalized thermoelastic diffusion due to laser pulse using dual-phase-lag model
Multidiscipline Modeling in Materials and Structures 2018 , MMMS-08-2017-0087
[本文引用: 1]
[7]
许光映 , 王晋宝 , 薛大文 . 短脉冲激光加热分数阶导热及其热应力研究
力学学报 , 2020 ,52 (2 ):491 -502
[本文引用: 1]
( Xu Guangyin Wang Jinbao Xue Dawen . Investigations on the thermal behavior and associated thermal stresses of the fractional heat conduction for short pulse laser heating
Chinese Journal of Theoretical ad Applied Mechanics 2020 ,52 (2 ):491 -502 (in Chinese))
[本文引用: 1]
[8]
王殿恺 , 文明 , 王伟东 等 . 脉冲激光与正激波相互作用过程和减阻机理的实验研究
力学学报 , 2018 ,50 (6 ):1337 -1345
[本文引用: 1]
( Wang Diankai Wen Ming Wang Weidong , et al . Experimental study on process and mechanisms of wave drag reduction during pulsed laser interacting with normal shock
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (6 ):1337 -1345 (in Chinese))
[本文引用: 1]
[9]
Nowacki W . Dynamic problems of thermodiffusion in elastic solids
Proc Vibration Problems 1974 ,15 (2 ):105 -128
[本文引用: 1]
[10]
Maxwell JC . On the dynamic theory of gases
Philosophical Transactions of the Royal Society of London 1867 ,157 :49 -88
DOI
URL
[本文引用: 1]
[11]
Peshkov V . Second sound in helium II
Journal of Physics 1944 ,8 :381 -386
[本文引用: 1]
[12]
Sherief HH Hamza FA Saleh HA . The theory of generalized thermoelastic diffusion
International Journal of Engineering Science 2004 ,42 (5 ):591 -608
DOI
URL
[本文引用: 2]
[13]
Xia RH Tian XG Shen YP . The influence of diffusion on generalized thermoelastic problems of infinite body with a cylindrical cavity
International Journal of Engineering Science 2009 ,47 (5-6 ):669 -679
DOI
URL
[本文引用: 1]
[14]
Li CL Guo HL Tian X , et al . Transient response for a half-space with variable thermal conductivity and diffusivity under thermal and chemical shock
Journal of Thermal Stresses 2017 ,40 (3 ):389 -401
DOI
URL
[本文引用: 1]
[15]
Li CL Yu YJ Tian XG . Effect of rotation on plane waves of generalized electromagnetothermoelastics with diffusion for a half-space
Journal of Thermal Stresses 2016 ,39 (1 ):27 -43
DOI
URL
[本文引用: 1]
[16]
Li CL Guo HL Tian XG . Transient responses of generalized magnetothermoelasto-diffusive problems with rotation using Laplace transform-finite element method
Journal of Thermal Stresses 2017 ,40 (9 ):1152 -1165
DOI
URL
[本文引用: 1]
[17]
Diethelm K . Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type
Berlin, Heidelberg: Springer-Verlag , 2010
[本文引用: 1]
[18]
Wang JL Li HF . Surpassing the fractional derivative: Concept of the memory-dependent derivative
Comput Math Appl 2011 ,62 (3 ):1562 -1567
DOI
URL
[本文引用: 2]
[19]
Yu YJ Hu W Tian XG . A novel generalized thermoelasticity model based on memory-dependent derivative
International Journal of Engineering Science 2014 ,81 (811 ):123 -134
DOI
URL
[本文引用: 1]
[20]
Ezzat MA El-Karamany AS El-Bary AA . Generalized thermo-viscoelasticity with memory-dependent derivatives
International Journal of Mechanical Sciences 2014 ,89 :470 -475
DOI
URL
[本文引用: 1]
A new generalized thermo-viscoelasticity theory with memory-dependent derivatives is constructed. The governing coupled equations with time-delay and kernel function, which can be chosen freely according to the necessity of applications, are applied to one-dimensional problem of a half-space. The bounding surface is taken traction free and subjected to a time dependent thermal shock. The Laplace transforms technique is used to obtain the general solution in a closed form. A numerical method is employed for the inversion of the Laplace transforms. According to the numerical results and its graphs, conclusions about the new theory are given. The predictions of the theory are discussed and compared with dynamic classical coupled theory. (C) 2014 Elsevier Ltd.
[21]
Ezzat MA El-Karamany AS El-Bary AA . A novel magneto-thermoelasticity theory with memory-dependent derivative
Journal of Electromagnetic Waves & Applications2015 ,29 (8 ):1018 -1031
[本文引用: 1]
[22]
Ezzat MA El-Karamany AS El-Bary AA . Electro-thermoelasticity theory with memory-dependent derivative heat transfer
International Journal of Engineering Science 2016 ,99 :22 -38
DOI
URL
[23]
Ezzat MA El-Bary AA . Magneto-thermoelectric viscoelastic materials with memory-dependent derivative involving two-temperature
International Journal of Applied Electromagnetics & Mechanics2016 ,50 (4 ):549 -567
[24]
Ezzat MA El-Karamany AS El-Bary AA . On dual-phase-lag thermoelasticity theory with memory-dependent derivative
Mechanics of Composite Materials & Structures2017 ,24 (11 ):908 -916
[本文引用: 1]
[25]
Shaw S Mukhopadhyay B . A discontinuity analysis of generalized thermoelasticity theory with memory-dependent derivatives
Acta Mechanica 2017 ,228 (7 ):1 -15
DOI
URL
[本文引用: 1]
[26]
Eringen AC Wegner J . Nonlocal Continuum Field Theories
Applied Mechanics Reviews 2003 ,56 (2 ):391 -398
[本文引用: 1]
[27]
Eringen AC . On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves
Journal of Applied Physics 1983 ,54 (9 ):4703 -4710
DOI
URL
[本文引用: 1]
[28]
Yu YJ Tian XG Xiong QL . Nonlocal thermoelasticity based on nonlocal heat conduction and nonlocal elasticity
European Journal of Mechanics-A/Solids 2016 ,60 :238 -253
DOI
URL
[本文引用: 1]
[29]
Yu YJ Xue ZN Li CL , et al . Buckling of nanobeams under nonuniform temperature based on nonlocal thermoelasticity
Composite Structures 2016 ,146 :108 -113
DOI
URL
[本文引用: 1]
[30]
Zenkour AM . Effect of temperature-dependent physical properties on nanobeam structures induced by ramp-type heating
KSCE Journal of Civil Engineering 2017 ,21 (5 ):1820 -1828
DOI
URL
[本文引用: 1]
[31]
张培 , 何天虎 . 考虑非局部效应和记忆依赖微分的广义热弹问题
力学学报 , 2018 ,50 (3 ):508 -516
[本文引用: 1]
( Zhang Pei He Tianhu . A generalized thermoelastic problem with nonlocal effect and memory- dependent derivative
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (3 ):508 -516 (in Chinese))
[本文引用: 1]
[32]
Li Y He TH . A generalized thermoelastic diffusion problem with memory-dependent derivative
Mathematics and Mechanics of Solids 2019 ,24 (5 ):1438 -1462
DOI
URL
[本文引用: 1]
[33]
Brancik L . Programs for fast numerical inversion of Laplace transforms in Matlab language environment
// Proceedings of the 7th conference MATLAB'99, Czech Republic, Prague , 1999 : 27 -39
[本文引用: 1]
Stimulated optical radiation in ruby
1
1960
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
Laser-induced vibrations of micro-beams under different boundary conditions
1
2008
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
Thermoelastic wave induced by pulsed laser heating
1
2001
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
Thermoelastic material response due to laser pulse heating in context of four theorems of thermoelasticity
1
2014
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
A two-dimensional generalized thermoelastic diffusion problem for a thick plate subjected to thermal loading due to laser pulse
1
2014
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
Effect of gravity on generalized thermoelastic diffusion due to laser pulse using dual-phase-lag model
1
2018
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
短脉冲激光加热分数阶导热及其热应力研究
1
2020
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
短脉冲激光加热分数阶导热及其热应力研究
1
2020
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
脉冲激光与正激波相互作用过程和减阻机理的实验研究
1
2018
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
脉冲激光与正激波相互作用过程和减阻机理的实验研究
1
2018
... 超短激光脉冲是指脉冲持续时间在飞秒到皮秒的激光脉冲, 其具有功率密度高、持续时间短、加工精度高等优势. 自1960年Maiman[1 ] 发现激光以来, 超短激光脉冲技术已广泛应用于钻孔、切割、微纳尺度加工、微电子器件制造等领域, 并在生物医疗、核聚变和光通信等领域有着广阔的应用前景. 在超短激光脉冲加热时, 高强度的能量通量会在边界上引起极大的温度梯度和超高的加热速度[2 ] , 并会引起材料中产生传质现象. 因此, 超短激光脉冲热源加热所产生的热应力问题在其实际应用中不容小觑. Wang和Xu[3 ] 研究了受激光脉冲加热的半无限大体中平面波的广义热弹问题, 并说明了温度与应变率之间的耦合效应; Youssef和El-Bary[4 ] 在广义热弹性理论(L-S, G-L和G-N)的背景下, 研究了受非Gaussian激光脉冲加热(脉冲持续时间为2 ps)的均匀各向同性半无限大体的温度场和应力场; Elhagary[5 ] 基于考虑一个松弛时间的广义热弹扩散理论, 研究了边界面受激光脉冲束加热和时间相关的化学势冲击的厚板, 结果表明: 扩散对温度和位移影响较小, 而对应力影响显著; Othman和Eraki[6 ] 基于双相位滞后(DPL)模型, 研究了受非Gaussian激光脉冲加热的各向异性半无限大体的热弹响应; 许光映等[7 ] 基于分数阶理论, 研究了非高斯分布激光热源辐射下半无限大体内部的复杂传热过程及热变形, 给出了温度场和热应力场的解析解; 王殿恺等[8 ] 以深刻揭示减阻机理为目的, 针对激光与正激波相互作用这一基本物理现象开展了实验研究, 发展高精度纹影技术以测量复杂激波结构. ...
Dynamic problems of thermodiffusion in elastic solids
1
1974
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
On the dynamic theory of gases
1
1867
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
Second sound in helium II
1
1944
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
The theory of generalized thermoelastic diffusion
2
2004
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
... Sherief等[12 ] 发展的整数阶广义热弹扩散理论只能描述力学过程某时刻的变化和力学过程在空间某一确定位置的局部性质, 对于某些反常扩散现象, 即本构关系不服从标准梯度率的现象, 其物理和力学过程通常涉及记忆和遗传、路径依赖以及全局相关性, 此时, 由分数阶广义热弹扩散理论描述结构的热弹扩散响应则更为恰当. Caputo型分数阶微分的形式如下[17 ] ...
The influence of diffusion on generalized thermoelastic problems of infinite body with a cylindrical cavity
1
2009
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
Transient response for a half-space with variable thermal conductivity and diffusivity under thermal and chemical shock
1
2017
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
Effect of rotation on plane waves of generalized electromagnetothermoelastics with diffusion for a half-space
1
2016
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
Transient responses of generalized magnetothermoelasto-diffusive problems with rotation using Laplace transform-finite element method
1
2017
... 扩散现象是指物质分子从高浓度区域向低浓度区域转移直至均匀分布的现象, 钢件的表面渗碳法(提高钢件的硬度)、渗铝法(提高钢件的耐热性), 都利用了扩散现象. 扩散现象由菲克定律描述, 但菲克定律只考虑了扩散过程中传质通量与浓度梯度间的关系, 并未考虑物质与基体间的相互作用以及电、磁、热、弹等多物理场间的耦合效应. 为了克服上述缺陷, Nowacki[9 ] 提出耦合热弹扩散理论, 该理论认为: 不论物体中传热传质过程的机理如何, 都应服从经典的傅里叶定律和菲克定律. 然而, 由傅里叶热传导定律的控制方程$q(r,t)=-\kappa \nabla T(r,t)$可知: 热流矢量与温度梯度同步, 这预测着热在介质中以无限大速度传播, 即: 当介质中某一点受到热扰动时, 这种扰动效应瞬间会在无限远处被感知, 这一点与实验观测相悖. Maxwell[10 ] 提出热以波的形式进行传播, Peshkov[11 ] 在超流液态He中发现了热波, 有力证明了热量传播过程中波动效应的存在, 即热以有限大速度传播. 与此同时, 对于某些极端传热传质过程, 例如: 极短时间、极高温度梯度、时间空间皆属微尺度的问题, 傅里叶定律和菲克定律不再适用. 鉴于此, Sherief等[12 ] 建立了广义热弹扩散理论, 该理论预测热传导和扩散均以有限速度传播, 可准确描述极端条件下的传热传质过程. 基于广义热弹扩散理论, Xia和Tian[13 ] 采用有限单元法, 研究了表面受热冲击的无限长中空柱的瞬态响应, 结果表明: 对于广义热弹扩散问题, 有限元法是一种有效且精确的数值方法. Li等[14 ] 研究了具有可变热传导系数和扩散系数的半无限大体的瞬态热弹扩散响应, 该结构表面应力自由且受时间相关的热和化学势冲击. Li 和Yu[15 ] 建立了广义电磁热弹扩散耦合控制方程, 研究了各向同性导电半无限大体中旋转效应对热弹扩散响应的影响. Li 和Guo[16 ] 利用混合拉普拉斯变换-有限元方法, 研究了考虑旋转效应的磁热弹扩散问题的瞬态响应. ...
Analysis of Fractional Differential Equations: An Application-Oriented Exposition Using Differential Operators of Caputo Type
1
2010
... Sherief等[12 ] 发展的整数阶广义热弹扩散理论只能描述力学过程某时刻的变化和力学过程在空间某一确定位置的局部性质, 对于某些反常扩散现象, 即本构关系不服从标准梯度率的现象, 其物理和力学过程通常涉及记忆和遗传、路径依赖以及全局相关性, 此时, 由分数阶广义热弹扩散理论描述结构的热弹扩散响应则更为恰当. Caputo型分数阶微分的形式如下[17 ] ...
Surpassing the fractional derivative: Concept of the memory-dependent derivative
2
2011
... Wang和Li[18 ] 认为, 式(1)有以下两个方面的局限性: 第一, 对于一个给定的实数$\alpha $, 核函数$K_\alpha \left( {t-s} \right)$是一个固定的函数, 但从应用的观点来看, 不同的物理过程需要不同的核函数来反映记忆依赖效应, 因此用可变的核函数来描述此过程就显得尤为重要; 第二, 分数阶微分定义在区间$\left[ {a_0 ,t} \right]$上, 且$a_0 $是一个固定的实数, 因此, 上式对于描述发生在长时间$t$范围内的记忆效应无效. 事实上, 一个真实物理过程的记忆依赖效应通常发生在一个时间区间里, 即迟滞区间$\left[ {t-\omega ,t} \right](\omega $表示迟滞时间)内. 受此启发, Wang和Li[18 ] 引入记忆依赖微分(MDD)的概念来反映记忆效应, 函数$f$的一阶记忆依赖微分定义为: 在一个可变迟滞区间上, 核函数与函数导数积的积分. 形式如下 ...
... [18 ]引入记忆依赖微分(MDD)的概念来反映记忆效应, 函数$f$的一阶记忆依赖微分定义为: 在一个可变迟滞区间上, 核函数与函数导数积的积分. 形式如下 ...
A novel generalized thermoelasticity model based on memory-dependent derivative
1
2014
... Yu等[19 ] 将记忆依赖微分(MDD)引入L-S型广义热弹理论, 相比于分数阶广义热弹, 其优势在于: 第一, 新模型在形式上是唯一的; 第二, 新模型更能反映出记忆依赖效应的本质; 第三, 新模型是由整数阶微积分定义的, 因此在数值计算时更加方便; 最后, 核函数和时间迟滞因子可以根据实际情况选择, 这对于描述材料的实际响应来说更加灵活. Ezzat等[20 ] 将含有时间迟滞因子的MDD引入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态), 基于此, Ezzat[21 -24 ] 进行了一系列相关研究. Shaw和Mukhopadhyay[25 ] 提出了MDD热传导模型的不连续性, 并将记忆依赖模型应用于瞬态热力响应的研究. ...
Generalized thermo-viscoelasticity with memory-dependent derivatives
1
2014
... Yu等[19 ] 将记忆依赖微分(MDD)引入L-S型广义热弹理论, 相比于分数阶广义热弹, 其优势在于: 第一, 新模型在形式上是唯一的; 第二, 新模型更能反映出记忆依赖效应的本质; 第三, 新模型是由整数阶微积分定义的, 因此在数值计算时更加方便; 最后, 核函数和时间迟滞因子可以根据实际情况选择, 这对于描述材料的实际响应来说更加灵活. Ezzat等[20 ] 将含有时间迟滞因子的MDD引入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态), 基于此, Ezzat[21 -24 ] 进行了一系列相关研究. Shaw和Mukhopadhyay[25 ] 提出了MDD热传导模型的不连续性, 并将记忆依赖模型应用于瞬态热力响应的研究. ...
A novel magneto-thermoelasticity theory with memory-dependent derivative
1
2015
... Yu等[19 ] 将记忆依赖微分(MDD)引入L-S型广义热弹理论, 相比于分数阶广义热弹, 其优势在于: 第一, 新模型在形式上是唯一的; 第二, 新模型更能反映出记忆依赖效应的本质; 第三, 新模型是由整数阶微积分定义的, 因此在数值计算时更加方便; 最后, 核函数和时间迟滞因子可以根据实际情况选择, 这对于描述材料的实际响应来说更加灵活. Ezzat等[20 ] 将含有时间迟滞因子的MDD引入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态), 基于此, Ezzat[21 -24 ] 进行了一系列相关研究. Shaw和Mukhopadhyay[25 ] 提出了MDD热传导模型的不连续性, 并将记忆依赖模型应用于瞬态热力响应的研究. ...
Electro-thermoelasticity theory with memory-dependent derivative heat transfer
2016
Magneto-thermoelectric viscoelastic materials with memory-dependent derivative involving two-temperature
2016
On dual-phase-lag thermoelasticity theory with memory-dependent derivative
1
2017
... Yu等[19 ] 将记忆依赖微分(MDD)引入L-S型广义热弹理论, 相比于分数阶广义热弹, 其优势在于: 第一, 新模型在形式上是唯一的; 第二, 新模型更能反映出记忆依赖效应的本质; 第三, 新模型是由整数阶微积分定义的, 因此在数值计算时更加方便; 最后, 核函数和时间迟滞因子可以根据实际情况选择, 这对于描述材料的实际响应来说更加灵活. Ezzat等[20 ] 将含有时间迟滞因子的MDD引入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态), 基于此, Ezzat[21 -24 ] 进行了一系列相关研究. Shaw和Mukhopadhyay[25 ] 提出了MDD热传导模型的不连续性, 并将记忆依赖模型应用于瞬态热力响应的研究. ...
A discontinuity analysis of generalized thermoelasticity theory with memory-dependent derivatives
1
2017
... Yu等[19 ] 将记忆依赖微分(MDD)引入L-S型广义热弹理论, 相比于分数阶广义热弹, 其优势在于: 第一, 新模型在形式上是唯一的; 第二, 新模型更能反映出记忆依赖效应的本质; 第三, 新模型是由整数阶微积分定义的, 因此在数值计算时更加方便; 最后, 核函数和时间迟滞因子可以根据实际情况选择, 这对于描述材料的实际响应来说更加灵活. Ezzat等[20 ] 将含有时间迟滞因子的MDD引入广义热传导方程来描述记忆依赖效应(系统的瞬时变化率依赖于过去状态), 基于此, Ezzat[21 -24 ] 进行了一系列相关研究. Shaw和Mukhopadhyay[25 ] 提出了MDD热传导模型的不连续性, 并将记忆依赖模型应用于瞬态热力响应的研究. ...
Nonlocal Continuum Field Theories
1
2003
... 当外部特征尺寸大于内部特征尺寸时, 经典力学适用; 外部特征尺寸接近于内部特征尺寸时, 结构的力学响应会呈现出很强的尺寸相关性, 此时, 经典力学不再适用. 例如: 石墨烯、碳纳米管等微纳尺度结构, 在受热冲击时, 空间尺度效应十分显著, 经典的热力学定律和广义热弹理论已无法准确预测结构的热弹响应. 为了描述微纳尺度结构的空间非局部特性, Eringen等[26 ] 提出了非局部弹性理论, Eringen认为: 变形体内某点处的应力不仅与该点处的应变相关, 还与变形体内其他点的应变(包括应变的历史)相关, 只是这种作用效应随距离的增大而逐渐衰减. 他提出了一种积分型的本构关系 ...
On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves
1
1983
... 非局部算子作用会导致微分-积分型控制方程, 不便于求解. 为了将其简化, Eringen[27 ] 引入新的核函数和非局部算子, 将积分型本构方程改写为微分形式 ...
Nonlocal thermoelasticity based on nonlocal heat conduction and nonlocal elasticity
1
2016
... Yu等[28 -29 ] 将Eringen非局部理论与非局部热传导方程相结合, 建立了新的非局部广义热弹性理论, 并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30 ] 基于非局部热弹性理论, 研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应, 考虑了非局部参数对各个物理量的影响; 张培等[31 ] 基于记忆依赖非局部广义热弹理论, 研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应. ...
Buckling of nanobeams under nonuniform temperature based on nonlocal thermoelasticity
1
2016
... Yu等[28 -29 ] 将Eringen非局部理论与非局部热传导方程相结合, 建立了新的非局部广义热弹性理论, 并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30 ] 基于非局部热弹性理论, 研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应, 考虑了非局部参数对各个物理量的影响; 张培等[31 ] 基于记忆依赖非局部广义热弹理论, 研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应. ...
Effect of temperature-dependent physical properties on nanobeam structures induced by ramp-type heating
1
2017
... Yu等[28 -29 ] 将Eringen非局部理论与非局部热传导方程相结合, 建立了新的非局部广义热弹性理论, 并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30 ] 基于非局部热弹性理论, 研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应, 考虑了非局部参数对各个物理量的影响; 张培等[31 ] 基于记忆依赖非局部广义热弹理论, 研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应. ...
考虑非局部效应和记忆依赖微分的广义热弹问题
1
2018
... Yu等[28 -29 ] 将Eringen非局部理论与非局部热传导方程相结合, 建立了新的非局部广义热弹性理论, 并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30 ] 基于非局部热弹性理论, 研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应, 考虑了非局部参数对各个物理量的影响; 张培等[31 ] 基于记忆依赖非局部广义热弹理论, 研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应. ...
考虑非局部效应和记忆依赖微分的广义热弹问题
1
2018
... Yu等[28 -29 ] 将Eringen非局部理论与非局部热传导方程相结合, 建立了新的非局部广义热弹性理论, 并考虑了非局部热传导对纳米梁屈曲性能的影响; Zenkour[30 ] 基于非局部热弹性理论, 研究了受到斜坡式加热的经典欧拉伯努利纳米梁的瞬态响应, 考虑了非局部参数对各个物理量的影响; 张培等[31 ] 基于记忆依赖非局部广义热弹理论, 研究了两端固定、受移动热源作用的有限长热弹杆的瞬态响应. ...
A generalized thermoelastic diffusion problem with memory-dependent derivative
1
2019
... 文献[32 ] 虽然建立了考虑记忆依赖效应的广义热弹扩散理论, 但未考虑材料的空间非局部效应, 无法准确预测内外部特征尺寸相近结构的热弹扩散响应. 本文将空间非局部算子引入本构方程, 建立记忆依赖非局部广义热弹扩散理论, 它可以准确描述热传导和扩散效应的记忆依赖效应和空间非局部效应. 利用所建理论研究了受到非Gaussian激光脉冲加热和化学势冲击联合作用半无限大薄板的热弹扩散响应. 获得了结构的温度、化学势、位移、应力、浓度等随非局部参数和时间迟滞因子变化的分布规律. ...
Programs for fast numerical inversion of Laplace transforms in Matlab language environment
1
1999
... 为了将所求得的物理量从拉氏域转换到时间域中, 还需进行拉普拉斯反变换. 由于拉氏域中所得结果的复杂性, 不便求其解析解, 而应用数值计算的方法可以将求解过程简化. 本文中, 采用Brancik[33 ] 提出的Matlab程序进行拉普拉斯数值反变换. ...