引言
近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义.
随着ABAQUS、ANASYS等商业有限元软件的普及, 轮轨滑动接触温升的有限元模拟研究受到了学者们的广泛关注. 然而, 由于轮轨接触斑非常狭小, 为了准确地模拟接触斑内的温度场, 在有限元模拟过程中必须对这一区域进行大规模网格加密处理, 从而所花费的时间成本较为高昂. 因此, 针对轮轨滑动接触温升问题的解析或半解析研究也得到了大量开展. 例如, Tanvir[7 ] 忽略了传热参数的温度相关性, 将Hertz接触压力的椭圆型分布函数近似成四阶多项式级数形式, 通过拉普拉斯变换给出了二维轮轨滑动摩擦温升分布的解析解. 基于相同的材料属性温度无关性假设, Knothe和Liebelt[8 ] 通过拉普拉斯变换和格林函数法, 给出了任意接触压力下的轮轨滑动温升问题的解析解, 讨论了法向接触压力分布形式和表面粗糙度对钢轨表面温度的影响. 基于Hertz弹性接触理论, Ertz和Knothe[9 ] 讨论了轮轨间换热系数等因素对轮轨摩擦温升的影响. Fischer等[10 ] 同时考虑了摩擦功和局部塑性变形对接触界面热源的贡献, 给出了轮轨滑动接触闪温的解析表达式. 此外, 考虑到轮轨间存在磨屑等杂物, Wu等[11 ] 基于三体微接触模型和接触温升理论, 讨论了杂物尺寸、杂物密度、表面粗糙度、相对速度以及法向载荷等参数对接触界面温度场的影响.
由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解.
由上述分析可见, 已有研究存在不足: (1)接触压力通常被假定为满足Hertz弹性接触理论中的半椭圆型分布形式, 而在实际轮轨接触载荷作用下, 接触斑内将发生塑性变形, 其接触压力不再满足半椭圆型分布形式, 必须进行塑性修正[23 -25 ] . (2)材料参数往往被简化为温度无关的常量, 或仅考虑某一个材料参数的温度相关性. 实际上, 包含摩擦系数在内的多种材料属性均会随温度的改变而发生变化[26 ] , 在温升计算模型中同时考虑多种材料属性的温度相关性, 有望提升温升计算结果的准确性.
因此, 本文通过拟合实验数据, 获得了热导率、比热容以及摩擦系数的温度相关性函数, 并基于弹塑性接触理论, 构建了二维轮轨滑动温升有限差分计算模型, 分别讨论了对流换热系数、法向载荷、蠕滑率以及行车速度对钢轨表面温升的影响, 可为轮轨滑动温升的准确预测提供参考.
1 计算模型
在列车运行过程中, 经过一段时间的磨损和变形, 轮轨接触斑会变得比较狭长, 可近似为矩形形状, 从而可在二维框架下讨论轮轨滑动温升问题[1 ] . 忽略车轮和钢轨的内部热源, 考虑热导率和比热容的温度相关性, 基于傅里叶导热定律, 二维情况下的轮轨摩擦导热方程可以写成
(1) $ \begin{eqnarray} \label{eq1} \frac{\partial }{\partial X}\left({\lambda \left( T \right)\frac{\partial T}{\partial X}} \right)+\frac{\partial }{\partial Z}\left( {\lambda \left( T \right)\frac{\partial T}{\partial Z}} \right)=\rho c\left( T \right)\frac{\mbox{d}T}{\mbox{d}t} \end{eqnarray}$
其中, $\lambda \left( T \right)$, $c\left( T \right)$和$\rho $分别表示热导率、比热容和密度, 温度场$T$是位置坐标$(x, z)$和时间$t$的函数, 即$T=T\left({x,z;t} \right)$. 令$a$表示接触斑纵向宽度的一半, $\left( {X, Z} \right)$为固定在钢轨表面的绝对坐标系, $\left( {x, z} \right)$是原点处于接触斑前沿的随动坐标系, 如图1 所示.
图1
图1
二维轮轨接触示意图
Fig.1
Schematic of a two-dimensional wheel-rail contact system
当行车速度$v$保持恒定时, 坐标$\left( {X, Z} \right)$和$\left( {x, z} \right)$满足关系式$\left( {X,Z} \right)=\left( {x-vt,z} \right)$, 即
(2) $ \begin{eqnarray} \label{eq2} \left. \begin{array}{ll} {\dfrac{\partial T}{\partial X}=\dfrac{\partial T}{\partial x}, \dfrac{\partial T}{\partial Z}=\dfrac{\partial T}{\partial z} } \\[2mm] {\dfrac{\mbox{d}T}{\mbox{d}t}=\dfrac{\partial T}{\partial x}\dfrac{\mbox{d}x}{\mbox{d}t}+\dfrac{\partial T}{\partial t}=v\dfrac{\partial T}{\partial x}+\dfrac{\partial T}{\partial t}} \\ \end{array} \right\} \end{eqnarray}$
(3) $ \begin{eqnarray} \label{eq3} &&\frac{\partial }{\partial x}\left( {\lambda \left( T \right)\frac{\partial T}{\partial x}} \right)+\frac{\partial }{\partial z}\left( {\lambda \left( T \right)\frac{\partial T}{\partial z}} \right)= \\&&\qquad \rho c\left( T \right)\left( {v\frac{\partial T}{\partial x}+\frac{\partial T}{\partial t}} \right) \end{eqnarray}$
在稳态情况下, ${\partial T} / {\partial t}=0$, 方程(3)退化为
(4) $ \begin{eqnarray} \label{eq4} \frac{\partial }{\partial x}\left( {\lambda \left( T \right)\frac{\partial T}{\partial x}} \right)+\frac{\partial }{\partial z}\left( {\lambda \left( T \right)\frac{\partial T}{\partial z}} \right)=\rho c\left( T \right)v\frac{\partial T}{\partial x} \end{eqnarray}$
(5) $ \begin{eqnarray} \left. \begin{array}{ll} \tilde{{\lambda }}=\dfrac{\lambda \left( T \right)}{\lambda \left( {T_{\max } } \right)},\ \tilde{{c}}=\dfrac{c\left( T \right)}{c\left( {T_{\max } } \right)}\\[2mm] \tilde{{T}}=\dfrac{T}{T_{\max } },\ \tilde{{x}}=\dfrac{x}{2a},\ \tilde{{z}}=\dfrac{z}{\delta } \end{array} \right\} \end{eqnarray}$
其中, $T_{\max } $为最高温度, $\delta =\sqrt {{2a\lambda \left( {T_{\max } } \right)} / {\left[ {\rho c\left( {T_{\max } } \right)v} \right]}}$为对应的热穿透深度[8 ] , 则方程(4)可简化为
(6) $ \begin{eqnarray} \label{eq6} \frac{\lambda \left( {T_{\max } } \right)}{2a\rho c\left( {T_{\max } } \right)v}\frac{\partial }{\partial \tilde{{x}}}\left( {\tilde{{\lambda }}\frac{\partial \tilde{{T}}}{\partial \tilde{{x}}}} \right)+\frac{\partial }{\partial \tilde{{z}}}\left( {\tilde{{\lambda }}\frac{\partial \tilde{{T}}}{\partial \tilde{{z}}}} \right)=\tilde{{c}}\frac{\partial \tilde{{T}}}{\partial \tilde{{x}}} \end{eqnarray}$
对于本文所采用的轮轨材料(见3.1节), 系数${\lambda \left( {T_{\max } } \right)} / {\left[ {2a\rho c\left( {T_{\max } } \right)v} \right]}<3.6\times 10^{-5}$, 因此方程(4)中的第一项可忽略[8 ] , 对应的方程(4)退化为
(7) $ \begin{eqnarray} \label{eq7} \frac{\partial }{\partial z}\left( {\lambda \left( T \right)\frac{\partial T}{\partial z}} \right)=\rho c\left( T \right)v\frac{\partial T}{\partial x} \end{eqnarray}$
在接触区域内, 轮轨之间因相对滑动而发生摩擦做功, 假设因轮轨滑动摩擦而损失的机械能全部转化为热能, 并以热传导的方式平均传递给车轮和钢轨, 忽略轮轨间的相互导热作用, 而接触区之外的表面则与空气发生对流换热. 因此, 边界条件可表示为
(8) $ \begin{eqnarray} \label{eq8} \left. \begin{array}{ll} T\left( {x=0,z} \right)=T\left( {x,z=\infty } \right)=T_0 \\ -\left[ {\lambda \left( T \right)\dfrac{\partial T}{\partial z}} \right]_{z=0} =q=\left\{ {{\begin{array}{ll} 0.5\mu \left( T \right)p\left( x \right)v_{\rm s}, & 0\leqslant x<2a \\ h\left( {T_{z=0} -T_0 } \right), & x\geqslant 2a \\ \end{array} }} \right. \\ \end{array} \right\}\ \ \ \end{eqnarray}$
式中, $q$为热通量; $\mu \left( T \right)$为摩擦系数; $h$为对流换热系数; $T_0 $为环境温度; $v_{\rm s}$为轮轨间的相对滑动速度, 且$v_{\rm s} =sv$, $s$为纵向蠕滑率; $p\left( x \right)$表示接触压力.
当轮轨材料满足双线性各向同性强化本构关系时, 接触压力$p\left( x \right)$可以写成[27 ]
(9) $ \begin{eqnarray} \label{eq9} p\left( x \right)=\left\{\begin{array}{l} p_0^\ast \sqrt{1-\left( {\dfrac{x-a}{a}} \right)^2} ,\\\qquad a_{\rm p} \leqslant \left| {x-a} \right|<a \\ \left( 1-\dfrac{H^\ast }{E^\ast }\right)p_{\rm y} +\dfrac{H^\ast }{E^\ast }p_0^\ast \sqrt {1-\left( {\dfrac{x-a}{a}} \right)^2} ,\\\qquad 0\leqslant \left| {x-a} \right|<a_{\rm p} \\ \end{array} \right. \end{eqnarray}$
式中, $p_0^\ast$表示Hertz弹性接触下使得接触斑宽度达到$2a$时所对应的接触压力峰值; $p_{\rm y} $为临界接触压力, 且$p_{\rm y} \approx 1.6\sigma _{\rm y} $, $\sigma _{\rm y} $为屈服强度[28 ] . 该模型假设当接触压力峰值超过$p_{\rm y} $时, 接触斑内开始出现局部塑性区域[27 ] . $a_{\rm p} $为接触斑内塑性区域纵向宽度的一半
(10) $ \begin{eqnarray} \label{eq10} a_{\rm p} =a\sqrt {1-\left( {\frac{p_{\rm y} }{p_0^\ast }} \right)^2} \end{eqnarray}$
位于区域$0\leqslant \left| {x-a} \right|<a_{\rm p} $中的表面材料已发生塑性变形, 而位于区域$a_{\rm p} \leqslant \left| {x-a} \right|\leqslant a$中的表面材料仍处于弹性接触状态. $H^\ast $和$E^\ast $分别满足
(11) $ \begin{eqnarray} \label{eq11} \frac{1}{H^\ast }=\frac{1-\nu _1^2 }{H_1 }+\frac{1-\nu _2^2 }{H_2 }, \frac{1}{E^\ast }=\frac{1-\nu _1^2 }{E_1 }+\frac{1-\nu _2^2 }{E_2 } \end{eqnarray}$
式中, $\nu _1$和$\nu _2$分别表示车轮和钢轨的泊松比, $E_1 $和$E_2$分别为车轮和钢轨的弹性模量, $H_1 $和$H_2$分别为车轮和钢轨的塑性硬化模量.
(12) $ \begin{eqnarray} \label{eq12} &&P_z -\frac{\pi E^\ast a^2}{4R}-\left( {1-\frac{H^\ast }{E^\ast }} \right)p_{\rm y} a\sqrt {1-\left( {\frac{2p_{\rm y} R}{E^\ast a}} \right)^2} + \\&&\qquad \frac{\left( {E^\ast -H^\ast } \right)a^2}{2R}\arcsin \sqrt {1-\left( {\frac{2p_{\rm y} R}{E^\ast a}} \right)^2} =0 \end{eqnarray}$
式中, $R$为车轮滚动半径; $P_z $为横向单位长度上的法向载荷, $P_z =P / {b_0 }$, $P$表示总法向载荷, $b_0$为矩形接触斑的横向等效宽度. 当$H^\ast =E^\ast $时, 方程(12)退化为
(13) $ \begin{eqnarray} \label{eq13} a=\sqrt {\frac{4RP_z}{\pi E^\ast}} \end{eqnarray}$
这与Hertz弹性接触理论在二维接触状态下的计算结果完全一致[1 ,29 ] .
由于速度$v$的影响, 车轮高速行进时的总法向载荷(动载)会高于车轮静止时的总法向载荷(静载), 二者之间满足[30 ]
(14) $ \begin{eqnarray} \label{eq14} P=KP_{\rm s} ,\ \ K=1+\frac{0.4v}{100} \end{eqnarray}$
式中, $P_{\rm s}$为静载, 等于轴重之半.
2 计算模型的求解
观察式(7)和式(8)可以发现, 同时考虑热导率、比热容和摩擦系数的温度相关性, 使得方程(7)成为具有复杂边界条件(8)的含多个变系数的非线性抛物型偏微分方程, 直接进行求解十分困难. 因此, 基于基尔霍夫变换法, 对热导率的温度相关性函数进行积分
(15) $ \begin{eqnarray} \label{eq15} \vartheta =\vartheta \left( T \right)=\int_{T_0 }^T {\lambda \left( T \right)\mbox{d}T} \end{eqnarray}$
(16) $ \begin{eqnarray} \label{eq16} \frac{\kappa \left( \vartheta \right)}{v} {\frac{\partial ^2\vartheta }{\partial z^2}}=\frac{\partial \vartheta }{\partial x},\ \ \kappa \left( \vartheta \right)=\frac{\lambda \left( {\vartheta ^{-1}\left( T \right)} \right)}{\rho c\left( {\vartheta ^{-1}\left( T \right)} \right)} \end{eqnarray}$
其中$\vartheta ^{-1}\left( T \right)$表示$\vartheta \left( T \right)$的反函数.
(17) $ \begin{eqnarray} \label{eq17} \left. \begin{array}{ll} \vartheta \left( {x=0,z} \right)=\vartheta \left( {x,z=\infty } \right)=0\\ -\left[ {\dfrac{\partial \vartheta }{\partial z}} \right]_{z=0} =q=\\ \qquad \left\{ \begin{array}{ll} 0.5sv\mu \left( {\vartheta ^{-1}\left( T \right)} \right)p\left( x \right), & 0\leqslant x<2a \\ h\left( {\left[ {\vartheta ^{-1}\left( T \right)} \right]_{z=0} -T_0 } \right), &x\geqslant 2a \\ \end{array}\right. \\ \end{array} \right\} \end{eqnarray}$
真实材料的$\kappa \left( \vartheta \right)$和$\mu \left( \vartheta \right)$需要通过拟合实验结果获得, 可能并不总是满足线性函数等简单形式, 这意味着摄动法以及拉普拉斯变换等常见方法可能不再适用于方程(16)的求解. 因此, 具有更强适用性的隐式差分法被用于该问题的求解.
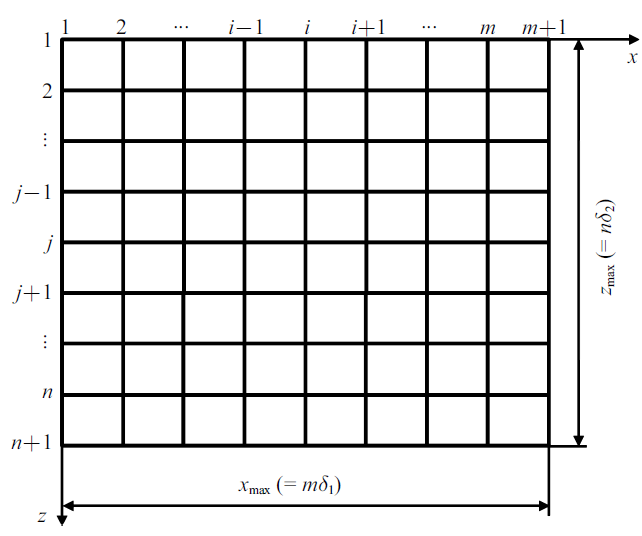
根据边界条件(17), 可令计算区域为$\bar{\varOmega}=\lt[0,x_{\max} ]\times\lt[0, \bar{z}_{\max} ]$, 其中$x_{\max } $和$\bar{z}_{\max}$分别表示$x$和$z$的取值上限, $\bar{z}_{\max}=\infty$. 然而, 数学意义上的$\infty $并不能直接用于实际计算, 可用有限大值$z_{\max } $来近似替代. 因此, 实际计算区域为$\varOmega =\left[ {0,x_{\max } } \right]\times \left[ {0,z_{\max } } \right]$, 如图2 所示. 用矩形网格对区域$\varOmega $进行离散, 沿$x$方向设置$m$+1个节点, 步长$\delta _1 ={x_{\max } } / m$; 沿$z$方向设置$n$+1个节点, 步长$\delta _2 ={z_{\max } } / n$. $\vartheta_j^i $表示在节点$\left( {i,j} \right)$, 即$x=\left( {i-1} \right)\delta _1 $且$z=\left( {j-1} \right)\delta _2 $处$\vartheta $的取值, $i=1$, 2, $\cdots$, $m+1$, $j=1$, 2, $\cdots$, $n+1$.
图2
图2
计算区域的离散
Fig.2
Schematic of calculation domain discretization
基于以差商近似代替微商的有限差分思想, 可将方程(16)和(17)转化成对应的差分方程形式
(18) $ \begin{eqnarray} \label{eq18} &&\left. \begin{array}{ll} \dfrac{\kappa _{j+0.5}^{i-1} }{v}\left[ {\dfrac{\vartheta _{j+1}^i -2\vartheta _j^i +\vartheta _{j-1}^i }{\left( {\delta _2 } \right)^2}} \right]=\dfrac{\vartheta _j^i -\vartheta _j^{i-1} }{\delta _1 } \\ \kappa _{j+0.5}^{i-1} =\kappa \left( {\dfrac{\vartheta _j^{i-1} +\vartheta _{j+1}^{i-1} }{2}} \right) \\ \end{array} \right\} \end{eqnarray}$
(19) $ \begin{eqnarray} \label{eq19} &&\left. \begin{array}{ll} \vartheta _j^1 =\vartheta _{n+1}^i =0 \\[2mm] -\dfrac{\vartheta _2^i -\vartheta _1^i }{\delta _2 }=q^{i-1}=\left\{ \begin{array}{l} {0.5sv\mu _1^{i-1} p^i, 0\leqslant x<2a} \\[1mm] {h\left( {T_1^{i-1} -T_0 } \right), x\geqslant 2a} \\ \end{array} \right. \\ \end{array} \right\} \end{eqnarray}$
其中, $\mu _1^{i-1} =\mu \left( {\vartheta _1^{i-1} } \right)$, $p^i=p\left({\left( {i-1} \right)\delta _1 } \right)$, $T_1^{i-1} =T\left( {\vartheta _1^{i-1} } \right)$, $i=2,3$, $\cdots$, $m+1$, $j=2,3$, $\cdots$, $n+1$.
将方程(19)代入方程(18)中, 便可以推导出非线性热传导方程(16)的二层隐式差分格式
(20) $ \begin{eqnarray} \label{eq20} A^{i-1}\bar{ \vartheta}^i+ F^{i-1}=\bar{ \vartheta}^{i-1} \end{eqnarray}$
其中, $ F^{i-1}=\left[ -\varepsilon \kappa _{2+0.5}^{i-1}\ \ q^{i-1}\delta _2 \ \ 0\ \ \cdots \ \ 0\ \ 0 \right]^{\rm T}$, $\bar{\vartheta}^{i-1}=\left[\vartheta^{i-1}_2\ \ \vartheta^{i-1}_3\ \ \cdots\ \ \vartheta^{i-1}_{n-1}\ \ \vartheta^{i-1}_n\right]^{\rm T}$, 上标T为转置符号, $ A^{i-1}$满足
(21) $ A^{i-1}=\begin{equation*} \begin{bmatrix} 1+\varepsilon \kappa _{2+0.5}^{i-1} & -\kappa _{2+0.5}^{i-1} & 0 & 0 & {\cdots } &0 & 0 & 0 \\ -\varepsilon \kappa _{3+0.5}^{i-1} & 1+2\varepsilon \kappa _{3+0.5}^{i-1} &-\varepsilon \kappa _{3+0.5}^{i-1} & 0 & {\cdots }&0 & 0 & 0 \\ 0 & -\varepsilon \kappa _{4+0.5}^{i-1} & 1+2\varepsilon \kappa _{4+0.5}^{i-1} & -\varepsilon \kappa _{4+0.5}^{i-1}& {\cdots }&0 & 0 & 0 \\ {\cdots } & {\cdots } & {\cdots } & {\cdots } & {\cdots } &{\cdots } & {\cdots } & {\cdots } \\ 0 & 0 & 0 & 0 & {\cdots } & -\varepsilon \kappa _{n-1+0.5}^{i-1} & 1+2\varepsilon \kappa _{n-1+0.5}^{i-1} & -\varepsilon \kappa _{n-1+0.5}^{i-1} \\ 0 & 0 & 0 & 0 & {\cdots } &0 & -\varepsilon \kappa _{n+0.5}^{i-1} & 1+2\varepsilon \kappa _{n+0.5}^{i-1} \end{bmatrix} \end{equation*} \\ \varepsilon ={\delta _1 } \Big/\left[ {\left( {\delta _2 } \right)^2v} \right], \ \ i=2,3, \cdots, m+1. $
在上述推导过程中, 并没有提前给定温度相关性函数$\lambda \left( T \right)$, $c\left( T \right)$和$\mu \left( T \right)$的形式, 这表明所给出的隐式差分格式(20)可以适用于具有任意温度相关性函数形式的热导率、比热容和摩擦系数. 联立求解方程(15)和(20), 便可获得任意节点位置处的温度$T_j^i $, $i=1$, 2, $\cdots$, $m+1$, $j=1$, 2, $\cdots$, $n+1$.
需要说明的是, 隐式差分法没有计算区域维度的限制, 当三维弹塑性接触压力分布函数已知时, 上述计算方法可较容易地推广至三维轮轨滑动接触温升的求解.
3 结果与讨论
3.1 材料属性的确定
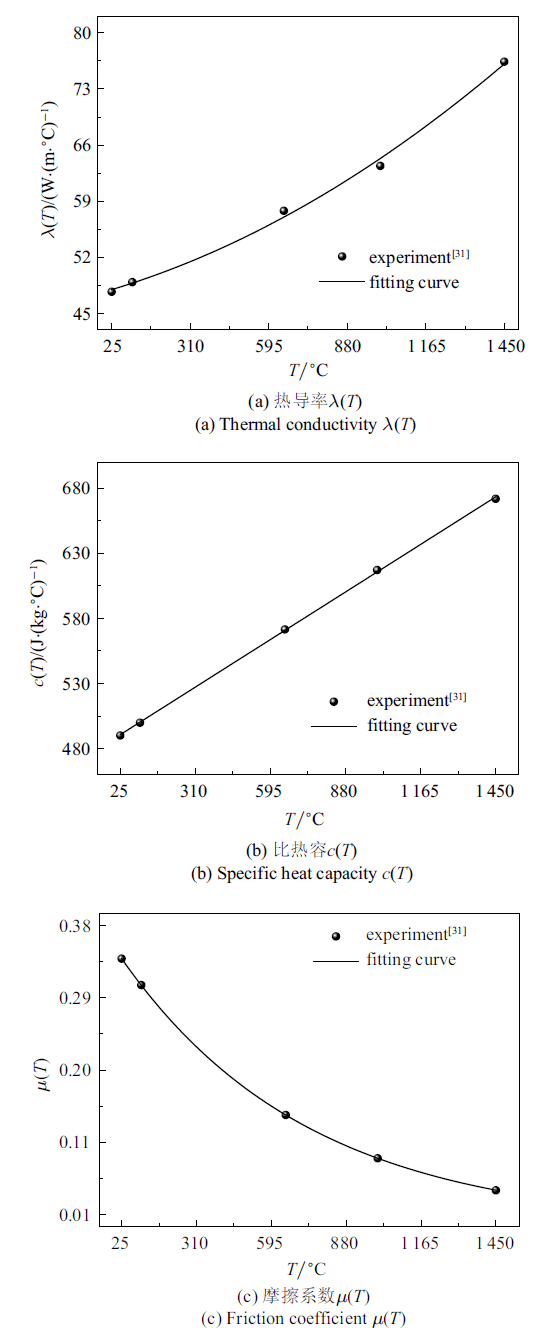
考虑CHN60N型钢轨和轮径(2$R)$为890 mm的LM$_{\rm A}$型车轮. 环境温度$T_{0}=25{^\circ}$C, 材料密度$\rho =7790$ kg/m$^{3}$, 弹性模量$E_1 =E_2 = 209$ GPa, 硬化模量$H_1 =H_2 =20.9$ GPa, 泊松比$\nu _1 =\nu _2 =0.3$, 屈服强度$\sigma _{\rm y} =608$ MPa. 根据文献[31 ] 中的实验数据, 热导率$\lambda \left( T \right)$、比热容$c\left( T \right)$和摩擦系数$\mu \left( T\right)$的拟合曲线如图3 (a)$\sim$图3 (c)所示, 对应的拟合函数为
(22) $ \begin{eqnarray} \label{eq22} \left.\begin{array}{l} {\lambda \left( T \right)=a_{11} T^2+a_{12} T+a_{13} } \\ {c\left( T \right)=a_{21} T+a_{22} } \\ {\mu \left( T \right)=a_{31} \exp \left( {a_{32} T} \right)} \\ \end{array}\right\} \end{eqnarray}$
图3
图3
热导率、比热容和摩擦系数的拟合曲线
Fig.3
The fitting curves of thermal conductivity, specific heat capacity and friction coefficient
其中, 拟合系数$a_{11} =6.61\times 10^{-6}$, $a_{12} =0.01$, $a_{13} =47.71$, $a_{21} =0.13$, $a_{22} =487.50$, $a_{31}=0.35$, $a_{32}= -1.40\times 10^{-3}$.
尽管实际材料的屈服强度和弹性模量也会表现出温度相关性, 但其温度相关性函数的引入会大大增加弹塑性接触问题的复杂性, 导致接触压力分布函数的显式形式不再存在, 进而使轮轨滑动温升的计算变得更加困难. 因此, 出于简化问题的考虑, 这里忽略了屈服强度和弹性模量的温度相关性.
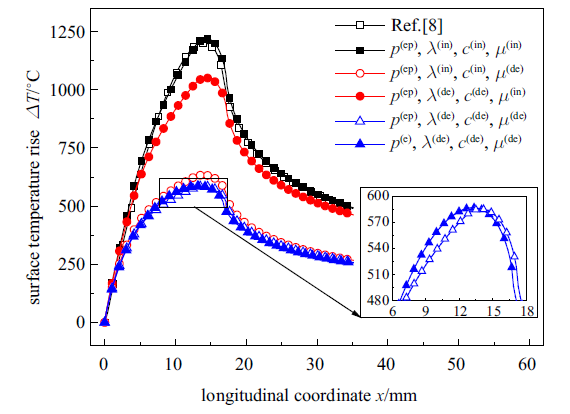
3.2 不同模型间的比较
不同轮轨滑动温升计算模型下的钢轨表面温升曲线如图4 所示. 图中上标(ep), (e), (de)和(in)分别表示弹塑性接触、弹性接触、温度相关性和温度无关性, 后文亦同. 由于钢轨的摩擦热影响区深度很浅, 仅为2 mm左右[32 -33 ] , 为了兼顾计算精度与工作效率, 此处可先试取计算区域深度$z_{\max }=4$ mm. 可以发现, 当忽略材料属性的温度相关性时, 所提出方法计算的温升曲线与文献[8 ] 得到的曲线符合较好, 表明本文所采用的隐式差分法和选取的计算区域深度是可行的. 同时, 考虑材料属性温度相关性时的温升曲线明显偏离忽略材料属性温度相关性时的曲线, 二者峰值温升之间的差值甚至可达640${^\circ}$C. 由此可见, 在轮轨温升计算模型中考虑材料属性的温度相关性是非常有必要的. 另外, 在较高温升下, 摩擦系数会出现剧烈的衰减现象(见图3 (c)), 对应的热通量随之降低, 进而对钢轨表面温度的继续升高产生抑制作用, 最终造成考虑摩擦系数温度相关性时的温升计算结果远远低于忽略该特性时的计算结果. 因此, 在轮轨滑动温升模拟中十分有必要考虑摩擦系数的温度相关性.
图4
图4
不同轮轨滑动温升计算模型下的钢轨表面温升曲线($P_{\rm s} =90$ kN, $h=100$ W$\cdot$(m$^{2}\cdot {^\circ}{\rm C})^{-1}$, $v=350$ km/h, $s=8$%)
Fig.4
The temperature rise curves of rail surface for different calculation models of wheel-rail sliding temperature rise ($P_{\rm s} =90$ kN, $h=100$ W$\cdot$(m$^{2}\cdot {^\circ}{\rm C})^{-1}$, $v=350$ km/h, $s=8$%)
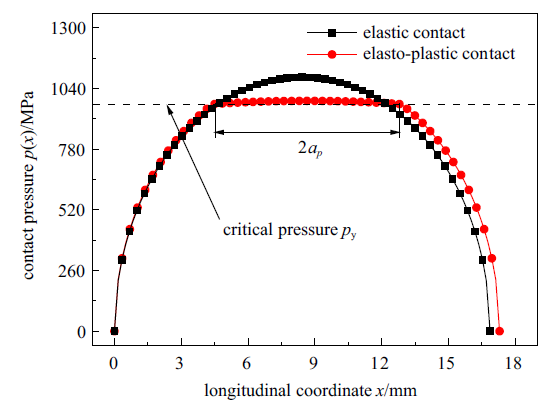
另外, 与Hertz弹性接触理论相比, 当法向载荷过大、接触斑内表面材料出现局部塑性变形时, 弹塑性接触理论所给出的峰值接触压力更小、接触斑宽度更大(见图5 ), 进而造成钢轨表面峰值温度所在位置朝接触斑后沿方向移动. 由于所采用的高强度钢轨CHN60N具有很高的临界接触压力, 相应的塑性变形区域很小, 因而两种接触压力形式下的最大滑动温升比较接近. 但对于屈服强度或临界接触压力较小的接触体材料, 这两种温升计算结果间的差异将更加显著.
图5
图5
弹性接触压力与弹塑性接触压力的比较
Fig.5
The comparison of elastic contact pressure and elasto-plastic contact pressure
3.3 对流换热系数对滑动温升的影响
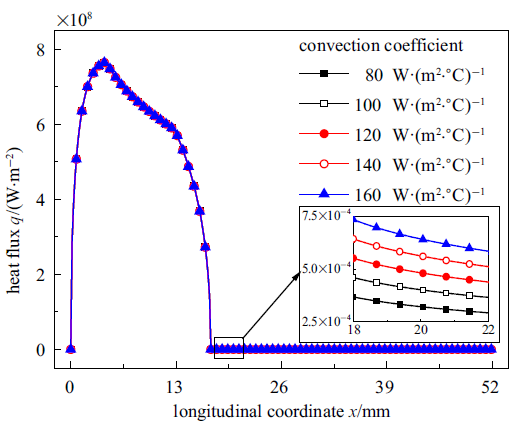
在轮轨滑动温升计算模型中, 钢轨非接触区域表面的边界条件直接取决于对流换热系数, 然而该物理参数往往受到车速、风速以及环境温度等诸多因素的影响, 其具体取值尚无定论[34 ] . Wang等[35 ] 通过比例模型实验测得了钢轨表面对流换热系数在列车高速行驶下的取值范围为80$\sim $160 W/(m$^{2}\cdot {^\circ}{\rm C})$. 因此, 图6 和图7 给出了不同对流换热系数下的钢轨表面温升和热通量分布曲线.
图6
图6
不同对流换热系数下的钢轨表面温升曲线($P_{\rm s}=90$ kN, $v=350$ km/h, $s=8$%)
Fig.6
The temperature rise curves of rail surface with different convection coefficients ($P_{\rm s}=90$ kN, $v=350$ km/h, $s=8$%)
图7
图7
不同对流换热系数下的钢轨表面热通量分布曲线($P_{\rm s}=90$ kN, $v=350$ km/h, $s=8$%)
Fig.7
The heat flux distribution of rail surface with different convection coefficients ($P_{\rm s}=90$ kN, $v=350$ km/h, $s=8$%)
不难看出, 钢轨表面峰值温度一直出现在接触斑内, 并靠近接触斑后沿, 这与文献[36 ,37 ] 的结论相一致. 同时, 不同对流换热系数下的温升曲线几乎完全重合, 表明当列车高速行驶时, 所讨论的对流换热系数变化对轮轨滑动温升的影响甚微, 这与文献[38 ] 的结论一致. 进一步观察图7 可知: 在车轮高速行进情况下, 摩擦功率对热通量的影响会显著高于对流换热系数变化的影响, 进而体现为轮轨滑动温升对对流换热系数变化的不敏感性, 因此在后续的讨论中对流换热系数将被设为定值100 W/(m$^{2}\cdot{^\circ}{\rm C})$.
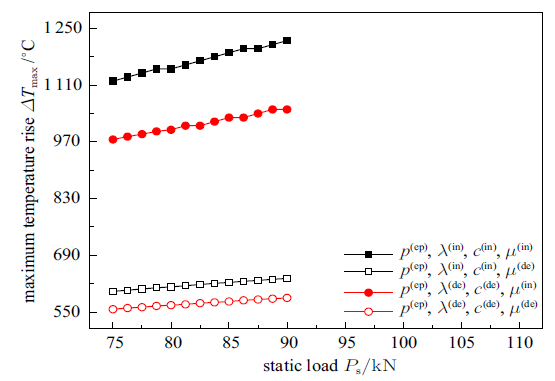
3.4 法向载荷对滑动温升峰值的影响
不同法向载荷下的钢轨表面温升峰值如图8 所示. 从图8 中可以发现, 在不同计算模型下, 对应的温升峰值均会随法向载荷的增大近似呈线性上升, 但温升取值则存在明显的差异. 与其他计算模型相比, 忽略材料属性温度相关性时的温升峰值计算结果最大, 表明忽略材料属性的温度相关性会大大高估轮轨间的滑动温升, 考虑材料属性的温度相关性可以减小这种高估程度, 进而提高温升计算结果的准确性. 同时, 仅考虑摩擦系数温度相关性时的温升峰值计算结果明显低于仅考虑热导率和比热容的温度相关性时的结果, 与同时考虑热导率、比热容和摩擦系数的温度相关性时的温升计算结果更为接近, 表明就式(22)所表征的材料而言, 摩擦系数的温度相关性对最终温升计算结果的影响显著强于热导率和比热容. 然而, 即便已经在温升计算模型中引入了温度相关的摩擦系数, 继续考虑热导率和比热容的温度相关性仍会影响最终的温升峰值计算结果, 二者之间的差值可接近70${^\circ}$C, 这再一次凸显了同时考虑多种材料属性的温度相关性对于提高轮轨滑动温升模拟结果准确性的意义.
图8
图8
钢轨表面最大温升随法向载荷的变化($v=350$ km/h, $s=8$%)
Fig.8
The maximum temperature rises of rail surface versus vertical loads ($v=350$ km/h, $s=8$%)
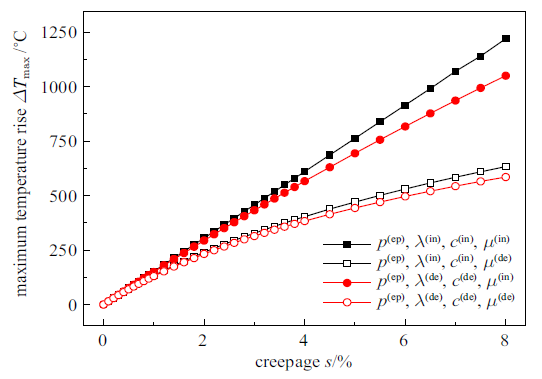
3.5 蠕滑率对滑动温升峰值的影响
钢轨表面温升峰值随蠕滑率的变化曲线如图9 所示. 可以看出, 温升峰值随蠕滑率的增大而上升, 这是因为在相同接触压力和行车速度的情况下, 蠕滑率的增大会引起轮轨接触点对间相对速度的增大, 提高摩擦热通量, 进而导致钢轨表面温度的上升. 当蠕滑率较低($s\leqslant 1$%)时, 轮轨滑动温升并不显著, 热导率、比热容和摩擦系数的变化量很小, 不同计算模型的温升峰值曲线接近重合; 但随着蠕滑率的进一步增大, 钢轨表面温度达到较高水平, 材料属性的温度相关性开始凸显, 因而该4组曲线互相偏离, 且偏离差异随蠕滑率的增加而增大. 忽略材料属性温度相关性时的钢轨滑动温升峰值与蠕滑率呈线性关系, 这与文献[8 ] 中的结论相一致; 考虑材料属性温度相关性时的温升峰值-蠕滑率曲线则体现出非线性特征, 且位于考虑材料属性温度无关性时的曲线的下方.
图9
图9
钢轨表面最大温升随蠕滑率的变化($P_{\rm s}=90$ kN, $v=350$ km/h)
Fig.9
The maximum temperature rises of rail surface versus creepages ($P_{\rm s}=90$ kN, $v=350$ km/h)
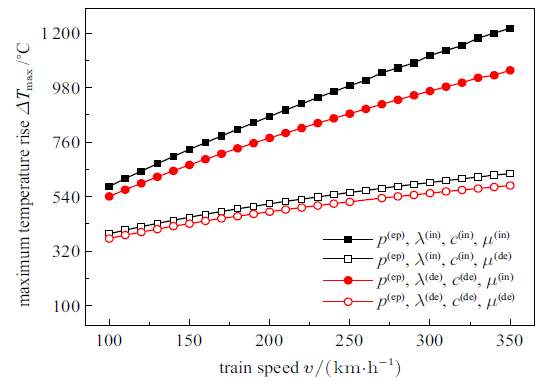
3.6 行车速度对滑动温升峰值的影响
图10 给出了钢轨表面温升峰值随行车速度的变化曲线. 与蠕滑率对钢轨温升峰值的影响相类似, 当法向载荷和蠕滑率恒定时, 行车速度的增大会引起轮轨接触点对间相对速度的增大, 提高摩擦热通量, 进而导致钢轨表面温升峰值的增加. 因此, 热导率、比热容和摩擦系数在高速下的变化量比低速情况更为显著, 从而导致不同温升模型计算结果之间的差异随行车速度的增大而加大. 在轮轨滑动温升计算模型中引入材料属性的温度相关性函数, 可以避免做出过分高估的温升评价, 这一特征在图10 中表现为考虑材料属性温度相关性时的温升峰值计算结果明显低于忽略温度相关性时的计算结果. 同时, 仅考虑摩擦系数温度相关性时的温升峰值曲线远远低于仅考虑热导率和比热容温度相关性时的结果, 并接近于同时考虑这三者的温度相关性时的曲线, 表明图3 (c)所呈现出的摩擦系数热衰减特性对温升计算结果的影响显著高于热导率和比热容. 因此, 在计算模型中增加摩擦系数的温度相关性函数可大幅提高温升预测的准确性.
图10
图10
钢轨表面最大温升随行车速度的变化($P_{\rm s}=90$ kN, $s=8$%)
Fig.10
The maximum temperature rises of rail surface versus train speeds ($P_{\rm s}=90$ kN, $s=8$%)
尽管所构建的二维轮轨滑动接触温升计算模型同时考虑了接触压力的塑性修正和热导率、比热容以及摩擦系数的温度相关性, 但忽略了屈服强度和弹性模量的温度相关性等因素对温升结果的影响, 与真实的轮轨传热状态尚有一定的偏差; 同时, 为了便于获得接触压力的解析解, 材料模型采用了简化的双线性各向同性强化模型来考虑车轮和钢轨的弹塑性响应, 而实际的车轮和钢轨的弹塑性响应是非线性的, 这将对计算结果产生一定的影响. 上述不足之处在目前提出的计算模型中尚无法被考虑, 需要在进一步的工作中予以完善.
4 结论
在二维弹塑性接触模型框架下, 同时考虑热导率、比热容和摩擦系数的温度相关性, 基于基尔霍夫变换方法, 将复杂的非线性Fourier导热方程转化成一种以热导率关于温度的积分函数为待求量的简单方程形式, 进而构建了相应的轮轨滑动接触温升计算模型. 基于隐式差分法, 推导出了一种不限材料温度相关性函数形式的统一差分求解格式, 并分别讨论了对流换热系数、法向载荷、蠕滑率以及行车速度对钢轨表面滑动温升的影响, 主要结论如下:
(1) 由于钢轨温升峰值总是位于接触斑内的后沿附近, 并且当接触斑内出现塑性变形区域时, 弹塑性接触理论所给出的接触斑宽度较弹性接触理论更大, 相应的温升峰值所在位置距接触斑前沿更远.
(2) 当行车速度处于较高水平时, 对流换热系数对轮轨滑动温升的影响甚微, 在温升计算模型中将对流换热系数设为定值是可行的. 蠕滑率和行车速度的增加, 均会引起轮轨接触点对间相对速度的增大, 摩擦热通量随之上升, 进而导致钢轨表面温升峰值的增加. 另外, 钢轨的温升峰值也会随法向载荷的增加而近似线性上升.
(3) 当实际的轮轨滑动温升处于较低水平时, 材料属性的温度相关性对温升计算结果的影响并不明显; 当实际温升较显著时, 在计算模型中同时考虑多种材料属性的温度相关性可以避免过分高估的温升评价, 且摩擦系数的温度相关性对温升计算结果的影响会明显高于热导率和比热容.
参考文献
View Option
[1]
金学松 , 刘启跃 . 轮轨摩擦学 . 北京 : 中国铁道出版社 , 2004
[本文引用: 3]
( Jin Xuesong Liu Qiyue Tribology of Wheel and Rail . Beijing : China Railway Publishing House , 2004 (in Chinese))
[本文引用: 3]
[2]
Wu L Wen ZF Li W , et al . Thermo-elastic-plastic finite element analysis of wheel/rail sliding contact
Wear 2011 ,271 :437 -443
DOI
URL
[本文引用: 1]
[3]
Srivastava JP Sarkar PK Ranjan V . Effects of thermal load on wheel-rail contacts: A review
Journal of Thermal Stresses 2016 ,39 :1389 -1418
DOI
URL
[本文引用: 1]
[4]
Ahlström J Karlsson B . Modelling of heat conduction and phase transformations during sliding of railway wheels
Wear 2002 ,253 :291 -300
DOI
URL
[本文引用: 1]
[5]
Chen YZ He CG Zhao XJ , et al . The influence of wheel flats formed from different braking conditions on rolling contact fatigue of railway wheel
Engineering Failure Analysis 2018 ,93 :183 -199
[本文引用: 1]
[6]
Chen S Zhao GT Wang HY , et al . Study of wheel wear influenced by tread temperature rising during tread braking
Wear 2019 , 438-439 :203046
[本文引用: 1]
[7]
Tanvir MA . Temperature rise due to slip between wheel and rail—An analytical solution for Hertzian contact
Wear 1980 ,61 :295 -308
[本文引用: 1]
[8]
Knothe K Liebelt S . Determination of temperatures for sliding contact with applications for wheel-rail systems
Wear 1995 ,189 :91 -99
[本文引用: 5]
[9]
Ertz M Knothe K . A comparison of analytical and numerical methods for the calculation of temperatures in wheel/rail contact
Wear 2002 ,253 :498 -508
[本文引用: 1]
[10]
Fischer FD Daves W Werner EA . On the temperature in the wheel-rail rolling contact
Fatigue & Fracture of Engineering Materials & Structures2003 ,26 (10 ):999 -1006
[本文引用: 1]
[11]
Wu HW Chen YY Horong JH . Contact temperature under three-body dry friction conditions
Wear 2015 , 330-331 :85 -92
[本文引用: 1]
[12]
Ling FF Rice JS . Surface temperature with temperature-dependent thermal properties
ASLE Transactions 1966 ,9 (2 ):195 -201
[本文引用: 1]
[13]
梁钰 , 郑保敬 , 高效伟 等 . 基于POD模型降阶法的非线性瞬态热传导分析
中国科学: 物理学力学天文学 , 2018 ,48 (12 ):124603
[本文引用: 1]
( Liang Yu Zheng Baojing Gao Xiaowei , et al . Reduced order model analysis method via proper orthogonal decomposition for nonlinear transient heat conduction problems
Scientia Sinica Physica, Mechanica & Astronomica2018 ,48 (12 ):124603 (in Chinese))
[本文引用: 1]
[14]
朱强华 , 杨恺 , 梁钰 等 . 基于特征正交分解的一类瞬态非线性热传导问题的新型快速分析方法
力学学报 , 2020 ,52 (1 ):124 -138
[本文引用: 1]
( Zhu Qianghua Yang Kai Liang Yu , et al . A novel fast algorithm based on model order reduction for one class of transient nonlinear heat conduction problem
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):124 -138 (in Chinese))
[本文引用: 1]
[15]
戴婷 , 戴宏亮 , 李军剑 等 . 含孔隙变厚度FG圆板的湿热力学响应
力学学报 , 2019 ,51 (2 ):512 -523
[本文引用: 1]
( Dai Ting Dai Hongliang Li Junjian , et al . Hygrothermal mechanical behavior of a FG circular plate with variable thickness
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):512 -523 (in Chinese))
[本文引用: 1]
[16]
Fabre A Hristov J . On the integral-balance approach to the transient heat conduction with linearly temperature-dependent thermal diffusivity
Heat and Mass Transfer 2017 ,53 (1 ):177 -204
[本文引用: 1]
[17]
林府标 , 张千宏 , 张俊 等 . 一维广义热传导方程的精确解
重庆师范大学学报(自然科学版) , 2018 ,35 (4 ):88 -92
[本文引用: 1]
( Lin Fubiao Zhang Qianhong Zhang Jun , et al . Exact solutions of one-dimensional general heat conduction equation
Journal of Chongqing Normal University $($Natural Science$)$ 2018 ,35 (4 ):88 -92 (in Chinese))
[本文引用: 1]
[18]
Ghasemi SE Zolfagharian A Hatami M , et al . Analytical thermal study on nonlinear fundamental heat transfer cases using a novel computational technique
Applied Thermal Engineering 2016 ,98 :88 -97
[本文引用: 1]
[19]
Pasha AV Jalili P Ganji DD . Analysis of unsteady heat transfer of specific longitudinal fins with temperature-dependent thermal coefficients by DTM
Alexandria Engineering Journal 2018 ,57 (4 ):3509 -3521
[本文引用: 1]
[20]
张英琦 , 乐贵高 , 马大为 等 . 同心筒热发射非线性热传导研究
工程热物理学报 , 2018 ,39 (10 ):2251 -2259
[本文引用: 1]
( Zhang Yingqi Le Guigao Ma Dawei , et al . Research on nonlinear thermal conduction of concentric canister launcher
Journal of Engineering Thermophysics 2018 ,39 (10 ):2251 -2259 (in Chinese))
[本文引用: 1]
[21]
李艾伦 , 傅卓佳 , 李柏纬 等 . 含肿瘤皮肤组织传热分析的广义有限差分法
力学学报 , 2018 ,50 (5 ):1198 -1205
[本文引用: 1]
( Li Ailun Fu Zhuojia Li Powei , et al . Generalized finite difference method for bioheat transfer analysis on skin tissue with tumors
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (5 ):1198 -1205 (in Chinese))
[本文引用: 1]
[22]
刘硕 , 方国东 , 王兵 等 . 近场动力学与有限元方法耦合求解热传导问题
力学学报 , 2018 ,50 (2 ):339 -348
[本文引用: 1]
( Liu Shuo Fang Guodong Wang Bing , et al . Study of thermal conduction problem using coupled peridynamics and finite element method
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):339 -348 (in Chinese))
[本文引用: 1]
[23]
Wiest M Kassa E Daves W , et al . Assessment of methods for calculating contact pressure in wheel-rail/switch contact
Wear 2008 ,265 (9-10 ):1439 -1445
[本文引用: 1]
[24]
Skrypnyk R Ekh M Nielsen JCO , et al . Prediction of plastic deformation and wear in railway crossings—Comparing the performance of two rail steel grades
Wear 2019 , 428-429 :302 -314
DOI
URL
[25]
王雯 , 吴洁蓓 , 高志强 等 . 机械结合面切向接触阻尼计算模型
力学学报 , 2018 ,50 (3 ):633 -642
[本文引用: 1]
( Wang Wen Wu Jiebei Gao Zhiqiang , et al . A calculation model for tangential contact damping of machine joint interfaces
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (3 ):633 -642 (in Chinese))
[本文引用: 1]
[26]
Wei YP Wu YP Chen K , et al . Experiment research on friction coefficient between a steel plate and rail in transient sliding thermal contact through a pendulum
Results in Physics 2018 ,11 :763 -768
DOI
URL
[本文引用: 1]
[27]
Zhu HB Zhao YT He ZF , et al . An elastic-plastic contact model for line contact structures
Science China Physics, Mechanics & Astronomy2018 ,61 :054611
DOI
URL
[本文引用: 2]
[28]
Brizmer V Kligerman Y Etsion I . The effect of contact conditions and material properties on the elasticity terminus of a spherical contact
International Journal of Solids and Structures 2006 ,43 (18-19 ):5736 -5749
DOI
URL
[本文引用: 1]
[29]
Carter FW . On the action of a locomotive driving wheel
Proceedings of the Royal Society A-Mathematical, Physical and Engineering Sciences 1926 ,112 (760 ):151 -157
[本文引用: 1]
[30]
Xiao JH Zhang FC Qian LH . Numerical simulation of stress and deformation in a railway crossing
Engineering Failure Analysis 2011 ,18 (8 ):2296 -2304
[本文引用: 1]
[31]
Chen YC Lee SY . Elastic-plastic wheel-rail thermal contact on corrugated rails during wheel braking
Journal of Tribology 2009 ,131 :011401
[本文引用: 1]
[32]
李伟 , 温泽峰 , 吴磊 等 . 车轮滑动时钢轨热弹塑性有限元分析
机械工程学报 , 2010 ,46 (10 ):95 -101
[本文引用: 1]
( Li Wei Wen Zefeng Wu Lei , et al . Thermo-elasto-plastic finite element analysis of rail during wheel sliding
Journal of Mechanical Engineering 2010 ,46 (10 ):95 -101 (in Chinese))
[本文引用: 1]
[33]
刘洋 , 刘振 , 吴亚平 等 . 考虑变摩擦系数的轮轨系统滑动接触热弹塑性应力分析
中国铁道科学 , 2015 ,36 (5 ):87 -93
[本文引用: 1]
( Liu Yang Liu Zhen Wu Yaping , et al . Thermo-elastic-plastic analysis of wheel-rail sliding contact stress with variable friction coefficient
China Railway Science 2015 ,36 (5 ):87 -93 (in Chinese))
[本文引用: 1]
[34]
Wu Y Wu MG Zhang YH , et al . Experimental study of heat and mass transfer of a rolling wheel
Heat and Mass Transfer 2014 ,50 (2 ):151 -159
[本文引用: 1]
[35]
Wang M Zhang YH Bai J , et al . Experimental study of convective heat transfer at the surface of a rail due to train passage
Proceedings of the Institution of Mechanical Engineers, Part F$:$ Journal of Rail and Rapid Transit 2015 ,229 (2 ):201 -209
[本文引用: 1]
[36]
Wu YP Wei YP Liu Y , et al . 3-D analysis of thermal-mechanical behavior of wheel/rail sliding contact considering temperature characteristics of materials
Applied Thermal Engineering 2017 ,115 :455 -462
[本文引用: 1]
[37]
Naeimi M Li SG Li ZL , et al . Thermomechanical analysis of the wheel-rail contact using a coupled modelling procedure
Tribology International 2018 ,117 :250 -260
[本文引用: 1]
[38]
王海新 , 吴亚平 , 刘振 等 . 对流换热系数对轮轨滑动接触特性的影响分析
铁道科学与工程学报 , 2018 ,15 (2 ):336 -342
[本文引用: 1]
( Wang Haixin Wu Yaping Liu Zhen , et al . Influence analysis of coefficients of convective heat transfer on the characteristic of wheel/rail sliding contact
Journal of Railway Science and Engineering 2018 ,15 (2 ):336 -342 (in Chinese))
[本文引用: 1]
3
2004
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
... 在列车运行过程中, 经过一段时间的磨损和变形, 轮轨接触斑会变得比较狭长, 可近似为矩形形状, 从而可在二维框架下讨论轮轨滑动温升问题[1 ] . 忽略车轮和钢轨的内部热源, 考虑热导率和比热容的温度相关性, 基于傅里叶导热定律, 二维情况下的轮轨摩擦导热方程可以写成 ...
... 这与Hertz弹性接触理论在二维接触状态下的计算结果完全一致[1 ,29 ] . ...
3
2004
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
... 在列车运行过程中, 经过一段时间的磨损和变形, 轮轨接触斑会变得比较狭长, 可近似为矩形形状, 从而可在二维框架下讨论轮轨滑动温升问题[1 ] . 忽略车轮和钢轨的内部热源, 考虑热导率和比热容的温度相关性, 基于傅里叶导热定律, 二维情况下的轮轨摩擦导热方程可以写成 ...
... 这与Hertz弹性接触理论在二维接触状态下的计算结果完全一致[1 ,29 ] . ...
Thermo-elastic-plastic finite element analysis of wheel/rail sliding contact
1
2011
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
Effects of thermal load on wheel-rail contacts: A review
1
2016
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
Modelling of heat conduction and phase transformations during sliding of railway wheels
1
2002
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
The influence of wheel flats formed from different braking conditions on rolling contact fatigue of railway wheel
1
2018
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
Study of wheel wear influenced by tread temperature rising during tread braking
1
2019
... 近年来, 随着我国轨道交通行业的迅速发展, 列车的行驶速度和运量均不断提升, 这对列车的牵引和制动性能提出了越来越高的要求. 列车的牵引和制动性能通过轮轨之间的接触关系来实现, 一旦列车的牵引力或制动力超过轮轨接触关系所能提供的粘着力时, 轮轨间便会发生相对滑动[1 ] . 在滑动过程中, 轮轨接触斑内的温度会因摩擦生热而迅速上升, 并随着车轮的进一步滑动脱离接触而快速衰减, 导致热应力出现交变变化. 这种交变的温升诱发热应力, 叠加在轴重引起的机械应力上, 将大幅度降低钢轨和车轮的服役寿命[2 -3 ] . 同时, 当滑动温升足够高时, 轮轨表层材料发生马氏体相变, 并伴随着后续的快速冷却过程而形成脆硬的马氏体组织. 在轮轨接触载荷的作用下, 这些脆硬组织容易发生脱落, 造成轮轨表面的扁疤和材料剥离, 进而影响列车行驶的安全性[4 -5 ] . 另外, 过高的轮轨表面温度也会导致材料硬度等力学性能的显著下降, 从而对轮轨表面的耐磨损性能带来不利影响[6 ] . 由于对轮轨滑动接触温升进行实验测量往往比较困难, 因此通过数值模拟和解析分析等非测试方式开展相应的温升研究具有重要的工程意义. ...
Temperature rise due to slip between wheel and rail—An analytical solution for Hertzian contact
1
1980
... 随着ABAQUS、ANASYS等商业有限元软件的普及, 轮轨滑动接触温升的有限元模拟研究受到了学者们的广泛关注. 然而, 由于轮轨接触斑非常狭小, 为了准确地模拟接触斑内的温度场, 在有限元模拟过程中必须对这一区域进行大规模网格加密处理, 从而所花费的时间成本较为高昂. 因此, 针对轮轨滑动接触温升问题的解析或半解析研究也得到了大量开展. 例如, Tanvir[7 ] 忽略了传热参数的温度相关性, 将Hertz接触压力的椭圆型分布函数近似成四阶多项式级数形式, 通过拉普拉斯变换给出了二维轮轨滑动摩擦温升分布的解析解. 基于相同的材料属性温度无关性假设, Knothe和Liebelt[8 ] 通过拉普拉斯变换和格林函数法, 给出了任意接触压力下的轮轨滑动温升问题的解析解, 讨论了法向接触压力分布形式和表面粗糙度对钢轨表面温度的影响. 基于Hertz弹性接触理论, Ertz和Knothe[9 ] 讨论了轮轨间换热系数等因素对轮轨摩擦温升的影响. Fischer等[10 ] 同时考虑了摩擦功和局部塑性变形对接触界面热源的贡献, 给出了轮轨滑动接触闪温的解析表达式. 此外, 考虑到轮轨间存在磨屑等杂物, Wu等[11 ] 基于三体微接触模型和接触温升理论, 讨论了杂物尺寸、杂物密度、表面粗糙度、相对速度以及法向载荷等参数对接触界面温度场的影响. ...
Determination of temperatures for sliding contact with applications for wheel-rail systems
5
1995
... 随着ABAQUS、ANASYS等商业有限元软件的普及, 轮轨滑动接触温升的有限元模拟研究受到了学者们的广泛关注. 然而, 由于轮轨接触斑非常狭小, 为了准确地模拟接触斑内的温度场, 在有限元模拟过程中必须对这一区域进行大规模网格加密处理, 从而所花费的时间成本较为高昂. 因此, 针对轮轨滑动接触温升问题的解析或半解析研究也得到了大量开展. 例如, Tanvir[7 ] 忽略了传热参数的温度相关性, 将Hertz接触压力的椭圆型分布函数近似成四阶多项式级数形式, 通过拉普拉斯变换给出了二维轮轨滑动摩擦温升分布的解析解. 基于相同的材料属性温度无关性假设, Knothe和Liebelt[8 ] 通过拉普拉斯变换和格林函数法, 给出了任意接触压力下的轮轨滑动温升问题的解析解, 讨论了法向接触压力分布形式和表面粗糙度对钢轨表面温度的影响. 基于Hertz弹性接触理论, Ertz和Knothe[9 ] 讨论了轮轨间换热系数等因素对轮轨摩擦温升的影响. Fischer等[10 ] 同时考虑了摩擦功和局部塑性变形对接触界面热源的贡献, 给出了轮轨滑动接触闪温的解析表达式. 此外, 考虑到轮轨间存在磨屑等杂物, Wu等[11 ] 基于三体微接触模型和接触温升理论, 讨论了杂物尺寸、杂物密度、表面粗糙度、相对速度以及法向载荷等参数对接触界面温度场的影响. ...
... 其中, $T_{\max } $为最高温度, $\delta =\sqrt {{2a\lambda \left( {T_{\max } } \right)} / {\left[ {\rho c\left( {T_{\max } } \right)v} \right]}}$为对应的热穿透深度[8 ] , 则方程(4)可简化为 ...
... 对于本文所采用的轮轨材料(见3.1节), 系数${\lambda \left( {T_{\max } } \right)} / {\left[ {2a\rho c\left( {T_{\max } } \right)v} \right]}<3.6\times 10^{-5}$, 因此方程(4)中的第一项可忽略[8 ] , 对应的方程(4)退化为 ...
... 不同轮轨滑动温升计算模型下的钢轨表面温升曲线如图4 所示. 图中上标(ep), (e), (de)和(in)分别表示弹塑性接触、弹性接触、温度相关性和温度无关性, 后文亦同. 由于钢轨的摩擦热影响区深度很浅, 仅为2 mm左右[32 -33 ] , 为了兼顾计算精度与工作效率, 此处可先试取计算区域深度$z_{\max }=4$ mm. 可以发现, 当忽略材料属性的温度相关性时, 所提出方法计算的温升曲线与文献[8 ] 得到的曲线符合较好, 表明本文所采用的隐式差分法和选取的计算区域深度是可行的. 同时, 考虑材料属性温度相关性时的温升曲线明显偏离忽略材料属性温度相关性时的曲线, 二者峰值温升之间的差值甚至可达640${^\circ}$C. 由此可见, 在轮轨温升计算模型中考虑材料属性的温度相关性是非常有必要的. 另外, 在较高温升下, 摩擦系数会出现剧烈的衰减现象(见图3 (c)), 对应的热通量随之降低, 进而对钢轨表面温度的继续升高产生抑制作用, 最终造成考虑摩擦系数温度相关性时的温升计算结果远远低于忽略该特性时的计算结果. 因此, 在轮轨滑动温升模拟中十分有必要考虑摩擦系数的温度相关性. ...
... 钢轨表面温升峰值随蠕滑率的变化曲线如图9 所示. 可以看出, 温升峰值随蠕滑率的增大而上升, 这是因为在相同接触压力和行车速度的情况下, 蠕滑率的增大会引起轮轨接触点对间相对速度的增大, 提高摩擦热通量, 进而导致钢轨表面温度的上升. 当蠕滑率较低($s\leqslant 1$%)时, 轮轨滑动温升并不显著, 热导率、比热容和摩擦系数的变化量很小, 不同计算模型的温升峰值曲线接近重合; 但随着蠕滑率的进一步增大, 钢轨表面温度达到较高水平, 材料属性的温度相关性开始凸显, 因而该4组曲线互相偏离, 且偏离差异随蠕滑率的增加而增大. 忽略材料属性温度相关性时的钢轨滑动温升峰值与蠕滑率呈线性关系, 这与文献[8 ] 中的结论相一致; 考虑材料属性温度相关性时的温升峰值-蠕滑率曲线则体现出非线性特征, 且位于考虑材料属性温度无关性时的曲线的下方. ...
A comparison of analytical and numerical methods for the calculation of temperatures in wheel/rail contact
1
2002
... 随着ABAQUS、ANASYS等商业有限元软件的普及, 轮轨滑动接触温升的有限元模拟研究受到了学者们的广泛关注. 然而, 由于轮轨接触斑非常狭小, 为了准确地模拟接触斑内的温度场, 在有限元模拟过程中必须对这一区域进行大规模网格加密处理, 从而所花费的时间成本较为高昂. 因此, 针对轮轨滑动接触温升问题的解析或半解析研究也得到了大量开展. 例如, Tanvir[7 ] 忽略了传热参数的温度相关性, 将Hertz接触压力的椭圆型分布函数近似成四阶多项式级数形式, 通过拉普拉斯变换给出了二维轮轨滑动摩擦温升分布的解析解. 基于相同的材料属性温度无关性假设, Knothe和Liebelt[8 ] 通过拉普拉斯变换和格林函数法, 给出了任意接触压力下的轮轨滑动温升问题的解析解, 讨论了法向接触压力分布形式和表面粗糙度对钢轨表面温度的影响. 基于Hertz弹性接触理论, Ertz和Knothe[9 ] 讨论了轮轨间换热系数等因素对轮轨摩擦温升的影响. Fischer等[10 ] 同时考虑了摩擦功和局部塑性变形对接触界面热源的贡献, 给出了轮轨滑动接触闪温的解析表达式. 此外, 考虑到轮轨间存在磨屑等杂物, Wu等[11 ] 基于三体微接触模型和接触温升理论, 讨论了杂物尺寸、杂物密度、表面粗糙度、相对速度以及法向载荷等参数对接触界面温度场的影响. ...
On the temperature in the wheel-rail rolling contact
1
2003
... 随着ABAQUS、ANASYS等商业有限元软件的普及, 轮轨滑动接触温升的有限元模拟研究受到了学者们的广泛关注. 然而, 由于轮轨接触斑非常狭小, 为了准确地模拟接触斑内的温度场, 在有限元模拟过程中必须对这一区域进行大规模网格加密处理, 从而所花费的时间成本较为高昂. 因此, 针对轮轨滑动接触温升问题的解析或半解析研究也得到了大量开展. 例如, Tanvir[7 ] 忽略了传热参数的温度相关性, 将Hertz接触压力的椭圆型分布函数近似成四阶多项式级数形式, 通过拉普拉斯变换给出了二维轮轨滑动摩擦温升分布的解析解. 基于相同的材料属性温度无关性假设, Knothe和Liebelt[8 ] 通过拉普拉斯变换和格林函数法, 给出了任意接触压力下的轮轨滑动温升问题的解析解, 讨论了法向接触压力分布形式和表面粗糙度对钢轨表面温度的影响. 基于Hertz弹性接触理论, Ertz和Knothe[9 ] 讨论了轮轨间换热系数等因素对轮轨摩擦温升的影响. Fischer等[10 ] 同时考虑了摩擦功和局部塑性变形对接触界面热源的贡献, 给出了轮轨滑动接触闪温的解析表达式. 此外, 考虑到轮轨间存在磨屑等杂物, Wu等[11 ] 基于三体微接触模型和接触温升理论, 讨论了杂物尺寸、杂物密度、表面粗糙度、相对速度以及法向载荷等参数对接触界面温度场的影响. ...
Contact temperature under three-body dry friction conditions
1
2015
... 随着ABAQUS、ANASYS等商业有限元软件的普及, 轮轨滑动接触温升的有限元模拟研究受到了学者们的广泛关注. 然而, 由于轮轨接触斑非常狭小, 为了准确地模拟接触斑内的温度场, 在有限元模拟过程中必须对这一区域进行大规模网格加密处理, 从而所花费的时间成本较为高昂. 因此, 针对轮轨滑动接触温升问题的解析或半解析研究也得到了大量开展. 例如, Tanvir[7 ] 忽略了传热参数的温度相关性, 将Hertz接触压力的椭圆型分布函数近似成四阶多项式级数形式, 通过拉普拉斯变换给出了二维轮轨滑动摩擦温升分布的解析解. 基于相同的材料属性温度无关性假设, Knothe和Liebelt[8 ] 通过拉普拉斯变换和格林函数法, 给出了任意接触压力下的轮轨滑动温升问题的解析解, 讨论了法向接触压力分布形式和表面粗糙度对钢轨表面温度的影响. 基于Hertz弹性接触理论, Ertz和Knothe[9 ] 讨论了轮轨间换热系数等因素对轮轨摩擦温升的影响. Fischer等[10 ] 同时考虑了摩擦功和局部塑性变形对接触界面热源的贡献, 给出了轮轨滑动接触闪温的解析表达式. 此外, 考虑到轮轨间存在磨屑等杂物, Wu等[11 ] 基于三体微接触模型和接触温升理论, 讨论了杂物尺寸、杂物密度、表面粗糙度、相对速度以及法向载荷等参数对接触界面温度场的影响. ...
Surface temperature with temperature-dependent thermal properties
1
1966
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
基于POD模型降阶法的非线性瞬态热传导分析
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
基于POD模型降阶法的非线性瞬态热传导分析
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
基于特征正交分解的一类瞬态非线性热传导问题的新型快速分析方法
1
2020
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
基于特征正交分解的一类瞬态非线性热传导问题的新型快速分析方法
1
2020
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
含孔隙变厚度FG圆板的湿热力学响应
1
2019
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
含孔隙变厚度FG圆板的湿热力学响应
1
2019
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
On the integral-balance approach to the transient heat conduction with linearly temperature-dependent thermal diffusivity
1
2017
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
一维广义热传导方程的精确解
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
一维广义热传导方程的精确解
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
Analytical thermal study on nonlinear fundamental heat transfer cases using a novel computational technique
1
2016
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
Analysis of unsteady heat transfer of specific longitudinal fins with temperature-dependent thermal coefficients by DTM
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
同心筒热发射非线性热传导研究
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
同心筒热发射非线性热传导研究
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
含肿瘤皮肤组织传热分析的广义有限差分法
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
含肿瘤皮肤组织传热分析的广义有限差分法
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
近场动力学与有限元方法耦合求解热传导问题
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
近场动力学与有限元方法耦合求解热传导问题
1
2018
... 由于材料属性的温度相关性, 摩擦副材料的热力学性质在摩擦温升过程中也会发生变化, 考虑材料属性的温度相关性将进一步提升温升计算结果的准确性. 然而, 材料属性温度相关性的引入会导致热传导方程的非线性化, 大大增加了温升求解的困难性. 因此, 考虑材料属性的温度相关性, 必须首先求解非线性热传导方程. Ling和Rice[12 ] 考虑了热导率和比热容的温度相关性, 通过傅里叶余弦变换, 给出了表面具有移动热源半无限大体的准稳态温度场的迭代数值解法. 这种求解方法允许任意形式的温度相关性函数, 但相应的计算成本高, 在实际应用中受到一定的限制. 梁钰等[13 -14 ] 基于特征正交分解方法, 对非线性瞬态热传导问题的有限元离散格式进行降阶处理, 从而提出了一种求解考虑传热参数温度相关性的二维非线性瞬态热传导问题的高效算法. 通过假设组份材料和孔隙填充物的热导率均随温度呈三次函数变化, 戴婷等[15 ] 采用微分求积法求解了一类含孔隙变厚度功能梯度圆盘的稳态温度场. 当热扩散系数随温度线性变化时, Fabre和Hristov[16 ] 基于热平衡积分法给出了一类一维热传导方程的解析解. 林府标等[17 ] 通过李群分析法, 考虑扩散率关于温度的幂函数形式, 得到了该类一维广义热传导方程的显示解析解和行波解. Ghasemi等[18 ] 则假定热导率是温度的线性函数, 将其斜率作为扰动小量, 也给出了一类一维非线性热传导问题的摄动解法. 此外, 微分变换法[19 ] 、有限差分法[20 -21 ] 和近场动力学法[22 ] 也被应用于非线性热传导温度场的求解. ...
Assessment of methods for calculating contact pressure in wheel-rail/switch contact
1
2008
... 由上述分析可见, 已有研究存在不足: (1)接触压力通常被假定为满足Hertz弹性接触理论中的半椭圆型分布形式, 而在实际轮轨接触载荷作用下, 接触斑内将发生塑性变形, 其接触压力不再满足半椭圆型分布形式, 必须进行塑性修正[23 -25 ] . (2)材料参数往往被简化为温度无关的常量, 或仅考虑某一个材料参数的温度相关性. 实际上, 包含摩擦系数在内的多种材料属性均会随温度的改变而发生变化[26 ] , 在温升计算模型中同时考虑多种材料属性的温度相关性, 有望提升温升计算结果的准确性. ...
Prediction of plastic deformation and wear in railway crossings—Comparing the performance of two rail steel grades
2019
机械结合面切向接触阻尼计算模型
1
2018
... 由上述分析可见, 已有研究存在不足: (1)接触压力通常被假定为满足Hertz弹性接触理论中的半椭圆型分布形式, 而在实际轮轨接触载荷作用下, 接触斑内将发生塑性变形, 其接触压力不再满足半椭圆型分布形式, 必须进行塑性修正[23 -25 ] . (2)材料参数往往被简化为温度无关的常量, 或仅考虑某一个材料参数的温度相关性. 实际上, 包含摩擦系数在内的多种材料属性均会随温度的改变而发生变化[26 ] , 在温升计算模型中同时考虑多种材料属性的温度相关性, 有望提升温升计算结果的准确性. ...
机械结合面切向接触阻尼计算模型
1
2018
... 由上述分析可见, 已有研究存在不足: (1)接触压力通常被假定为满足Hertz弹性接触理论中的半椭圆型分布形式, 而在实际轮轨接触载荷作用下, 接触斑内将发生塑性变形, 其接触压力不再满足半椭圆型分布形式, 必须进行塑性修正[23 -25 ] . (2)材料参数往往被简化为温度无关的常量, 或仅考虑某一个材料参数的温度相关性. 实际上, 包含摩擦系数在内的多种材料属性均会随温度的改变而发生变化[26 ] , 在温升计算模型中同时考虑多种材料属性的温度相关性, 有望提升温升计算结果的准确性. ...
Experiment research on friction coefficient between a steel plate and rail in transient sliding thermal contact through a pendulum
1
2018
... 由上述分析可见, 已有研究存在不足: (1)接触压力通常被假定为满足Hertz弹性接触理论中的半椭圆型分布形式, 而在实际轮轨接触载荷作用下, 接触斑内将发生塑性变形, 其接触压力不再满足半椭圆型分布形式, 必须进行塑性修正[23 -25 ] . (2)材料参数往往被简化为温度无关的常量, 或仅考虑某一个材料参数的温度相关性. 实际上, 包含摩擦系数在内的多种材料属性均会随温度的改变而发生变化[26 ] , 在温升计算模型中同时考虑多种材料属性的温度相关性, 有望提升温升计算结果的准确性. ...
An elastic-plastic contact model for line contact structures
2
2018
... 当轮轨材料满足双线性各向同性强化本构关系时, 接触压力$p\left( x \right)$可以写成[27 ] ...
... 式中, $p_0^\ast$表示Hertz弹性接触下使得接触斑宽度达到$2a$时所对应的接触压力峰值; $p_{\rm y} $为临界接触压力, 且$p_{\rm y} \approx 1.6\sigma _{\rm y} $, $\sigma _{\rm y} $为屈服强度[28 ] . 该模型假设当接触压力峰值超过$p_{\rm y} $时, 接触斑内开始出现局部塑性区域[27 ] . $a_{\rm p} $为接触斑内塑性区域纵向宽度的一半 ...
The effect of contact conditions and material properties on the elasticity terminus of a spherical contact
1
2006
... 式中, $p_0^\ast$表示Hertz弹性接触下使得接触斑宽度达到$2a$时所对应的接触压力峰值; $p_{\rm y} $为临界接触压力, 且$p_{\rm y} \approx 1.6\sigma _{\rm y} $, $\sigma _{\rm y} $为屈服强度[28 ] . 该模型假设当接触压力峰值超过$p_{\rm y} $时, 接触斑内开始出现局部塑性区域[27 ] . $a_{\rm p} $为接触斑内塑性区域纵向宽度的一半 ...
On the action of a locomotive driving wheel
1
1926
... 这与Hertz弹性接触理论在二维接触状态下的计算结果完全一致[1 ,29 ] . ...
Numerical simulation of stress and deformation in a railway crossing
1
2011
... 由于速度$v$的影响, 车轮高速行进时的总法向载荷(动载)会高于车轮静止时的总法向载荷(静载), 二者之间满足[30 ] ...
Elastic-plastic wheel-rail thermal contact on corrugated rails during wheel braking
1
2009
... 考虑CHN60N型钢轨和轮径(2$R)$为890 mm的LM$_{\rm A}$型车轮. 环境温度$T_{0}=25{^\circ}$C, 材料密度$\rho =7790$ kg/m$^{3}$, 弹性模量$E_1 =E_2 = 209$ GPa, 硬化模量$H_1 =H_2 =20.9$ GPa, 泊松比$\nu _1 =\nu _2 =0.3$, 屈服强度$\sigma _{\rm y} =608$ MPa. 根据文献[31 ] 中的实验数据, 热导率$\lambda \left( T \right)$、比热容$c\left( T \right)$和摩擦系数$\mu \left( T\right)$的拟合曲线如图3 (a)$\sim$图3 (c)所示, 对应的拟合函数为 ...
车轮滑动时钢轨热弹塑性有限元分析
1
2010
... 不同轮轨滑动温升计算模型下的钢轨表面温升曲线如图4 所示. 图中上标(ep), (e), (de)和(in)分别表示弹塑性接触、弹性接触、温度相关性和温度无关性, 后文亦同. 由于钢轨的摩擦热影响区深度很浅, 仅为2 mm左右[32 -33 ] , 为了兼顾计算精度与工作效率, 此处可先试取计算区域深度$z_{\max }=4$ mm. 可以发现, 当忽略材料属性的温度相关性时, 所提出方法计算的温升曲线与文献[8 ] 得到的曲线符合较好, 表明本文所采用的隐式差分法和选取的计算区域深度是可行的. 同时, 考虑材料属性温度相关性时的温升曲线明显偏离忽略材料属性温度相关性时的曲线, 二者峰值温升之间的差值甚至可达640${^\circ}$C. 由此可见, 在轮轨温升计算模型中考虑材料属性的温度相关性是非常有必要的. 另外, 在较高温升下, 摩擦系数会出现剧烈的衰减现象(见图3 (c)), 对应的热通量随之降低, 进而对钢轨表面温度的继续升高产生抑制作用, 最终造成考虑摩擦系数温度相关性时的温升计算结果远远低于忽略该特性时的计算结果. 因此, 在轮轨滑动温升模拟中十分有必要考虑摩擦系数的温度相关性. ...
车轮滑动时钢轨热弹塑性有限元分析
1
2010
... 不同轮轨滑动温升计算模型下的钢轨表面温升曲线如图4 所示. 图中上标(ep), (e), (de)和(in)分别表示弹塑性接触、弹性接触、温度相关性和温度无关性, 后文亦同. 由于钢轨的摩擦热影响区深度很浅, 仅为2 mm左右[32 -33 ] , 为了兼顾计算精度与工作效率, 此处可先试取计算区域深度$z_{\max }=4$ mm. 可以发现, 当忽略材料属性的温度相关性时, 所提出方法计算的温升曲线与文献[8 ] 得到的曲线符合较好, 表明本文所采用的隐式差分法和选取的计算区域深度是可行的. 同时, 考虑材料属性温度相关性时的温升曲线明显偏离忽略材料属性温度相关性时的曲线, 二者峰值温升之间的差值甚至可达640${^\circ}$C. 由此可见, 在轮轨温升计算模型中考虑材料属性的温度相关性是非常有必要的. 另外, 在较高温升下, 摩擦系数会出现剧烈的衰减现象(见图3 (c)), 对应的热通量随之降低, 进而对钢轨表面温度的继续升高产生抑制作用, 最终造成考虑摩擦系数温度相关性时的温升计算结果远远低于忽略该特性时的计算结果. 因此, 在轮轨滑动温升模拟中十分有必要考虑摩擦系数的温度相关性. ...
考虑变摩擦系数的轮轨系统滑动接触热弹塑性应力分析
1
2015
... 不同轮轨滑动温升计算模型下的钢轨表面温升曲线如图4 所示. 图中上标(ep), (e), (de)和(in)分别表示弹塑性接触、弹性接触、温度相关性和温度无关性, 后文亦同. 由于钢轨的摩擦热影响区深度很浅, 仅为2 mm左右[32 -33 ] , 为了兼顾计算精度与工作效率, 此处可先试取计算区域深度$z_{\max }=4$ mm. 可以发现, 当忽略材料属性的温度相关性时, 所提出方法计算的温升曲线与文献[8 ] 得到的曲线符合较好, 表明本文所采用的隐式差分法和选取的计算区域深度是可行的. 同时, 考虑材料属性温度相关性时的温升曲线明显偏离忽略材料属性温度相关性时的曲线, 二者峰值温升之间的差值甚至可达640${^\circ}$C. 由此可见, 在轮轨温升计算模型中考虑材料属性的温度相关性是非常有必要的. 另外, 在较高温升下, 摩擦系数会出现剧烈的衰减现象(见图3 (c)), 对应的热通量随之降低, 进而对钢轨表面温度的继续升高产生抑制作用, 最终造成考虑摩擦系数温度相关性时的温升计算结果远远低于忽略该特性时的计算结果. 因此, 在轮轨滑动温升模拟中十分有必要考虑摩擦系数的温度相关性. ...
考虑变摩擦系数的轮轨系统滑动接触热弹塑性应力分析
1
2015
... 不同轮轨滑动温升计算模型下的钢轨表面温升曲线如图4 所示. 图中上标(ep), (e), (de)和(in)分别表示弹塑性接触、弹性接触、温度相关性和温度无关性, 后文亦同. 由于钢轨的摩擦热影响区深度很浅, 仅为2 mm左右[32 -33 ] , 为了兼顾计算精度与工作效率, 此处可先试取计算区域深度$z_{\max }=4$ mm. 可以发现, 当忽略材料属性的温度相关性时, 所提出方法计算的温升曲线与文献[8 ] 得到的曲线符合较好, 表明本文所采用的隐式差分法和选取的计算区域深度是可行的. 同时, 考虑材料属性温度相关性时的温升曲线明显偏离忽略材料属性温度相关性时的曲线, 二者峰值温升之间的差值甚至可达640${^\circ}$C. 由此可见, 在轮轨温升计算模型中考虑材料属性的温度相关性是非常有必要的. 另外, 在较高温升下, 摩擦系数会出现剧烈的衰减现象(见图3 (c)), 对应的热通量随之降低, 进而对钢轨表面温度的继续升高产生抑制作用, 最终造成考虑摩擦系数温度相关性时的温升计算结果远远低于忽略该特性时的计算结果. 因此, 在轮轨滑动温升模拟中十分有必要考虑摩擦系数的温度相关性. ...
Experimental study of heat and mass transfer of a rolling wheel
1
2014
... 在轮轨滑动温升计算模型中, 钢轨非接触区域表面的边界条件直接取决于对流换热系数, 然而该物理参数往往受到车速、风速以及环境温度等诸多因素的影响, 其具体取值尚无定论[34 ] . Wang等[35 ] 通过比例模型实验测得了钢轨表面对流换热系数在列车高速行驶下的取值范围为80$\sim $160 W/(m$^{2}\cdot {^\circ}{\rm C})$. 因此, 图6 和图7 给出了不同对流换热系数下的钢轨表面温升和热通量分布曲线. ...
Experimental study of convective heat transfer at the surface of a rail due to train passage
1
2015
... 在轮轨滑动温升计算模型中, 钢轨非接触区域表面的边界条件直接取决于对流换热系数, 然而该物理参数往往受到车速、风速以及环境温度等诸多因素的影响, 其具体取值尚无定论[34 ] . Wang等[35 ] 通过比例模型实验测得了钢轨表面对流换热系数在列车高速行驶下的取值范围为80$\sim $160 W/(m$^{2}\cdot {^\circ}{\rm C})$. 因此, 图6 和图7 给出了不同对流换热系数下的钢轨表面温升和热通量分布曲线. ...
3-D analysis of thermal-mechanical behavior of wheel/rail sliding contact considering temperature characteristics of materials
1
2017
... 不难看出, 钢轨表面峰值温度一直出现在接触斑内, 并靠近接触斑后沿, 这与文献[36 ,37 ] 的结论相一致. 同时, 不同对流换热系数下的温升曲线几乎完全重合, 表明当列车高速行驶时, 所讨论的对流换热系数变化对轮轨滑动温升的影响甚微, 这与文献[38 ] 的结论一致. 进一步观察图7 可知: 在车轮高速行进情况下, 摩擦功率对热通量的影响会显著高于对流换热系数变化的影响, 进而体现为轮轨滑动温升对对流换热系数变化的不敏感性, 因此在后续的讨论中对流换热系数将被设为定值100 W/(m$^{2}\cdot{^\circ}{\rm C})$. ...
Thermomechanical analysis of the wheel-rail contact using a coupled modelling procedure
1
2018
... 不难看出, 钢轨表面峰值温度一直出现在接触斑内, 并靠近接触斑后沿, 这与文献[36 ,37 ] 的结论相一致. 同时, 不同对流换热系数下的温升曲线几乎完全重合, 表明当列车高速行驶时, 所讨论的对流换热系数变化对轮轨滑动温升的影响甚微, 这与文献[38 ] 的结论一致. 进一步观察图7 可知: 在车轮高速行进情况下, 摩擦功率对热通量的影响会显著高于对流换热系数变化的影响, 进而体现为轮轨滑动温升对对流换热系数变化的不敏感性, 因此在后续的讨论中对流换热系数将被设为定值100 W/(m$^{2}\cdot{^\circ}{\rm C})$. ...
对流换热系数对轮轨滑动接触特性的影响分析
1
2018
... 不难看出, 钢轨表面峰值温度一直出现在接触斑内, 并靠近接触斑后沿, 这与文献[36 ,37 ] 的结论相一致. 同时, 不同对流换热系数下的温升曲线几乎完全重合, 表明当列车高速行驶时, 所讨论的对流换热系数变化对轮轨滑动温升的影响甚微, 这与文献[38 ] 的结论一致. 进一步观察图7 可知: 在车轮高速行进情况下, 摩擦功率对热通量的影响会显著高于对流换热系数变化的影响, 进而体现为轮轨滑动温升对对流换热系数变化的不敏感性, 因此在后续的讨论中对流换热系数将被设为定值100 W/(m$^{2}\cdot{^\circ}{\rm C})$. ...
对流换热系数对轮轨滑动接触特性的影响分析
1
2018
... 不难看出, 钢轨表面峰值温度一直出现在接触斑内, 并靠近接触斑后沿, 这与文献[36 ,37 ] 的结论相一致. 同时, 不同对流换热系数下的温升曲线几乎完全重合, 表明当列车高速行驶时, 所讨论的对流换热系数变化对轮轨滑动温升的影响甚微, 这与文献[38 ] 的结论一致. 进一步观察图7 可知: 在车轮高速行进情况下, 摩擦功率对热通量的影响会显著高于对流换热系数变化的影响, 进而体现为轮轨滑动温升对对流换热系数变化的不敏感性, 因此在后续的讨论中对流换热系数将被设为定值100 W/(m$^{2}\cdot{^\circ}{\rm C})$. ...