引言
磁-电-弹性材料是一种同时具有压电压磁磁电耦合效应的复合材料, 这种材料在工程结构中, 尤其是在智能材料和结构系统中, 有越来越广泛的应用. 磁-电-弹性材料所固有的力电磁耦合特性使它们成为智能结构中传感与执行元件的首选材料, 广泛应用于传感器、执行器、滤波器、换能器和其他智能器件, 在能量转换系统中有着非常可观的潜在的应用前景[1 -8 ] . 由于这些智能器件通常在复杂的力、电、磁和热耦合载荷环境下工作, 因此对磁-电-弹性材料在多场耦合环境下的响应问题研究具有重要的意义.
近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解.
鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响.
从检索到的相关文献资料来看, 现有的工作主要集中在求解无限大磁-电-弹性体中的力学问题或者相应的热载荷是作用在全部边界上的情形, 而考虑边界的影响以及局部范围内分布载荷的作用则更具有实际意义. 本文利用积分变换方法推导并求解了磁-电-弹性半空间在边界上作用轴对称温度载荷时的热传导和控制方程, 得到了磁-电-弹性半空间中的温度场、应力、电位移和磁通量的解析解. 本文结果对磁-电-弹性材料在热环境中的应用具有重要的指导意义.
1 基本公式
考虑一个横观各向同性的磁-电-弹性材料, 其极化方向沿$z$轴方向, 各向同性平面为$xy$平面, 如图1 所示. 对于轴对称问题, 线性磁-电-弹性介质的本构方程为
(1) $ \begin{eqnarray} \label{eq1} && \left\{ {{\begin{array}{*{20}c} {\sigma _{rr} } \\ {\sigma _{\theta \theta } } \\ {\sigma _{zz} } \\ {D_z } \\ {B_z } \\ \end{array} }} \right\}=\left[ {{\begin{array}{*{20}c} {c_{11} } & {c_{12} } & {c_{13} } & {e_{31} } & {h_{31} } \\ {c_{12} } & {c_{11} } & {c_{13} } & {e_{31} } & {h_{31} } \\ {c_{13} } & {c_{13} } & {c_{33} } & {e_{33} } & {h_{33} } \\ {e_{31} } & {e_{31} } & {e_{33} } & {-\varepsilon _{33} } & {-d_{33} } \\ {h_{31} } & {h_{31} } & {h_{33} } & {-d_{33} } & {-\mu _{33} } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {u_{r,r} } \\ {{u_r } / r} \\ {u_{z,z} } \\ {\phi _{,z} } \\ {\varphi _{,z} } \\ \end{array} }} \right\}- \\&&\qquad \left[ {{\begin{array}{*{20}c} {\beta _1 } & {\beta _2 } & {\beta _3 } & {\beta _4 } & {\beta _5 } \\ \end{array} }} \right]'\Delta T \end{eqnarray}$
(2) $ \begin{eqnarray}\label{eq2} \left\{ {{\begin{array}{*{20}c} {\sigma _{rz} } \\ {D_r } \\ {B_r } \\ \end{array} }} \right\}=\left[ {{\begin{array}{*{20}c} {c_{44} } & {e_{15} } & {h_{15} } \\ {e_{15} } & {-\varepsilon _{11} } & {-d_{11} } \\ {h_{15} } & {-d_{11} } & {-\mu _{11} } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {u_{z,r} +u_{r,z} } \\ {\phi _{,r} } \\ {\varphi _{,r} } \\ \end{array} }} \right\} \end{eqnarray}$
图1
图1
轴对称热载荷作用下的磁-电-弹性半空间
Fig.1
A magnetoelectroelastic half-space under axisymmetric thermal loading
其中, 场变量为$r$和的$z$函数, 与角度$\theta $无关; $u_r $和$u_z $分别是径向和轴向弹性位移的分量; $\phi $和$\varphi $分别是电势和磁势; $\sigma _{rr}$, $\sigma _{\theta \theta}$, $\sigma _{zz}$, $\sigma _{rz}$为应力张量的分量; $D_r $和$D_z $为电位移的分量; $B_r $和$B_z$为磁通量的分量; $c_{11}$, $c_{12}$, $c_{13}$, $c_{33}$, $c_{44}$为弹性模量; $e_{15}$, $e_{31}$, $e_{33} $ 为压电常数; $\varepsilon _{11}$, $\varepsilon _{33} $ 为介电常数; $d_{11}$, $d_{33} $ 为电磁常数; $\mu _{11}$, $\mu _{33} $ 为磁渗透系数; $\beta _j$ $(j=1,2,...,5)$是热应力系数; $\Delta T$是温度变化量; $[\ ]'$表示矩阵的转置; $(\ )$表示对相应坐标的求偏导.
电场$E_j (j=r,z)$和磁场$H_j (j=r,z)$可以分别由电势和磁势的偏导数表示为
(3) $ \left. \begin{array}{ll} E_r =-\phi _{,r} ,\ \ E_z =-\phi _{,z} \\ H_r =-\varphi _{,r} ,\ \ H_z =-\varphi _{,z} \end{array} \right\} $
(4) $ \left. \begin{array}{ll} \sigma _{rr,r} +\sigma _{rz,z} +{(\sigma _{rr} -\sigma _{\theta \theta } )}/ r=0 \\ \sigma _{rz,r} +\sigma _{zz,z} +{\sigma _{rz} } / r=0 \\ D_{r,r} +D_{z,z} +{D_r } / r=0 \\ B_{r,r} +B_{z,z} +{B_r } / r=0 \\ \end{array} \right\} $
将方程(1)和(2)代入以上方程可以得到关于位移$u_r $, $u_z $, 电势$\phi$和磁势$\varphi $的控制方程如下
(5) $ \left. \begin{array}{ll} c_{11} \left( {u_{r,rr} +\dfrac{u_{r,r} }{r}-\dfrac{u_r }{r^2}} \right)+c_{44} u_{r,zz} +(c_{13} +c_{44} )u_{z,rz} + \\[2mm]\qquad (e_{15} +e_{31} )\phi _{,rz} +(h_{15} +h_{31} )\varphi _{,rz} =\beta _1 \Delta T_{,r} \\[2mm] c_{44} \left( {u_{z,rr} +\dfrac{u_{z,r} }{r}} \right)+(c_{13} +c_{44} )\left( {u_{r,rz} +\dfrac{u_{r,z} }{r}} \right)+\\[2mm]\qquad c_{33} u_{z,zz} + e_{15} \left( {\phi _{,rr} +\dfrac{\phi _{,r} }{r}} \right)+ e_{33} \phi _{,zz} +\\[2mm]\qquad h_{15} \left( {\varphi _{,rr} +\dfrac{\varphi _{,r} }{r}} \right)+ h_{33} \varphi _{,zz} =\beta _3 \Delta T_{,z} \\[2mm] (e_{15} +e_{31} )\left( {u_{r,rz} +\dfrac{u_{r,z} }{r}} \right)+e_{15} \left( {u_{z,rr} +\dfrac{u_{z,r} }{r}} \right)+\\[2mm]\qquad e_{33} u_{z,zz} -\varepsilon _{11} \left( {\phi _{,rr} +\dfrac{\phi _{,r} }{r}} \right)-\varepsilon _{33} \phi _{,zz} -\\[2mm]\qquad d_{11} \left( {\varphi _{,rr} +\dfrac{\varphi _{,r} }{r}} \right)- d_{33} \varphi _{,zz} =\beta _4 \Delta T_{,z} \\[2mm] (h_{15} +h_{31} )\left( {u_{r,rz} +\dfrac{u_{r,z} }{r}} \right)+h_{15} \left( {u_{z,rr} +\dfrac{u_{z,r} }{r}} \right)+\\[2mm]\qquad h_{33} u_{z,zz} - d_{11} \left( {\phi _{,rr} +\dfrac{\phi _{,r} }{r}} \right)-d_{33} \phi _{,zz} -\\[2mm]\qquad \mu _{11} \left( {\varphi _{,rr} +\dfrac{\varphi _{,r} }{r}} \right)- \mu _{33} \varphi _{,zz}=\beta _5 \Delta T_{,z} \\ \end{array} \right\} $
2 问题求解
考虑一个在其边界表面上作用有轴对称热载荷的磁-电-弹性半空间, 如图1 所示. 采用柱坐标($r$, $\theta$, $z)$, 并假定极化方向沿$z$轴方向; $T_B(r)$是一个定义在圆域($r\leqslant a, z=0)$内的轴对称函数.
(6) $ \begin{eqnarray} \label{eq6} T_{,rr} +{T_{,r} } / r+{k_z T_{,zz} } / {k_r }=0 \end{eqnarray}$
其中, $T=T(r,z)$是介质中的温度分布函数, $k_r $和$k_z $ 分别为$r$ 和 $z$方向的热传导系数. 应用Hankel 变换可以得到温度的表达式为
(7) $ \begin{eqnarray} \label{eq7} T(r,z)=A_0 +\int_0^\infty {A(\xi )\exp \left( {-\lambda \xi z} \right)} {\rm J}_0 (\xi r){\rm d}\xi \end{eqnarray}$
其中, $A(\xi )$为待求函数, $A_0 $是一个可以由远场边界条件确定的常数, J$_0 (\ )$ 是第一类零阶Bessel 函数, 系数$\lambda $定义为
(8) $ \begin{eqnarray} \label{eq8} \lambda =\sqrt {{k_r } / {k_z }} \end{eqnarray}$
假设无穷远处的温度为一有限值$T_I $并且作用于磁-电-弹性介质边界上有界区域内的温度为$T_B $, 即
(9) $ \begin{eqnarray} \label{eq9} T(r,\infty )=T_I,\ \ T(r,0)=T_B (r) \end{eqnarray}$
(10) $ \begin{eqnarray} \begin{array}{ll} A_0 =T_I \\ A(\xi )=\xi \int_0^\infty {r\left[ {T_B (r)-T_I } \right]{\rm J}_0 (\xi r){\rm d}r} =\\\qquad \xi \int_0^\infty {rT_0 (r){\rm J}_0 (\xi r){\rm d}r} \\ \end{array} \end{eqnarray}$
将方程(10)代入方程(7) 可以得到温度场的表达式为
(11) $ \begin{eqnarray} \label{eq10} &&T(r,z)=T_I+\int_0^\infty \xi \exp ( -\lambda \xi z){\rm J}_0 (\xi r)\cdot \\&&\qquad \int_0^\infty \eta T_0 (\eta ){\rm J}_0 (\xi \eta ){\rm d}\eta {\rm d}\xi \end{eqnarray}$
(12) $ \begin{eqnarray} \label{eq11} &&\Delta T=T(r,z)-T_I=\int_0^\infty \xi \exp \left( {-\lambda \xi z} \right){\rm J}_0 (\xi r)\cdot \\&&\qquad\int_0^\infty \eta T_0 (\eta ){\rm J}_0 (\xi \eta ){\rm d}\eta {\rm d}\xi \end{eqnarray}$
对方程(5)做Hankel变换, 可以得到弹性位移, 电势和磁势的通解如下
(13) $ u_r (r,z)=\int_0^\infty {\rm J}_1 (\xi r)\Bigg[B(\xi )\exp (-\lambda \xi z)+ \\ \qquad\sum\limits_{j=1}^4 {a_j A_j (\xi )\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi $
(14) $ u_z (r,z)=\int_0^\infty {\rm J}_0 (\xi r)\Bigg[ C(\xi )\exp (-\lambda \xi z) + \\ \qquad\sum\limits_{j=1}^4 {\frac{A_j (\xi )}{\gamma _j }\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi $
(15) $ \phi (r,z)=\int_0^\infty {\rm J}_0 (\xi r)\Bigg[ D(\xi )\exp (-\lambda \xi z) - \\ \qquad\sum\limits_{j=1}^4 {\frac{b_j A_j (\xi )}{\gamma _j }\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi $
(16) $ \varphi (r,z)=\int_0^\infty {\rm J}_0 (\xi r)\Bigg[ E(\xi )\exp (-\lambda \xi z)- \\ \qquad\sum\limits_{j=1}^4 {\frac{d_j A_j (\xi )}{\gamma _j }\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi $
其中, $A_j (\xi )$ $(j=1,2,3,4)$, $B(\xi )$, $C(\xi )$, $D(\xi )$, $E(\xi)$为待求的未知函数, $a_j $, $b_j $, $d_j $, ($j=1,2,3,4)$ 是与材料系数相关的已知的系数, 见附录; ${\rm J}_1 (\ )$ 是第一类的一阶Bessel函数, $\gamma _j $ ($j=1,2,3,4)$ 为以下特征方程的特征根
(17) $ \begin{eqnarray} \label{eq17} \left| {{\begin{array}{*{20}c} {c_{11} -c_{44} \gamma ^2} & {(c_{13} +c_{44} )\gamma } & {(e_{31} +e_{15} )\gamma } & {(h_{31} +h_{15} )\gamma } \\ {(c_{13} +c_{44} )\gamma } & {c_{33} \gamma ^2-c_{44} } & {e_{33} \gamma ^2-e_{15} } & {h_{33} \gamma ^2-h_{15} } \\ {(e_{31} +e_{15} )\gamma } & {e_{33} \gamma ^2-e_{15} } & {\varepsilon _{11} -\varepsilon _{33} \gamma ^2} & {d_{11} -d_{33} \gamma ^2} \\ {(h_{31} +h_{15} )\gamma } & {h_{33} \gamma ^2-h_{15} } & {d_{11} -d_{33} \gamma ^2} & {\mu _{11} -\mu _{33} \gamma ^2} \\ \end{array} }} \right| =0 \\ \end{eqnarray}$
其中, $\left| {M} \right|$ 表示矩阵${M}$的行列式值. 这里需要指出的是, 八阶特征方程(17)有8个特征根成对出现, 每一对大小相同符号相反, 复根以共轭形式成对出现. 在式(13)$\sim$式(16)中, 取特征根$\gamma _j $ ($j=1,2,3,4)$ 的实部为正, 以确保稳定系统的内能正定[31 -32 ] .
利用本构方程, 可以得到应力, 电位移及磁通量的各个分量为
(18) $ \begin{eqnarray} &&\sigma _{zz} (r,z) =\int_0^\infty {\rm J}_0 (\xi r)\Bigg[ K_{10} (\xi )\exp (-\lambda \xi z)+ \\&&\qquad\sum\limits_{j=1}^4 {K_{1j} (\xi )\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi -\beta _3 \Delta T \\ \end{eqnarray}$
(19) $ \begin{eqnarray} &&\sigma _{rz} (r,z) =\int_0^\infty {\rm J}_1 (\xi r)\Bigg[ K_{20} (\xi )\exp (-\lambda \xi z)+ \\&&\qquad\sum\limits_{j=1}^4 {K_{2j} (\xi )\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi \\ \end{eqnarray}$
(20) $ \begin{eqnarray} && D_z (r,z)=\int_0^\infty {\rm J}_0 (\xi r)\Bigg[ K_{30} (\xi )\exp (-\lambda \xi z)+ \\&&\qquad\sum\limits_{j=1}^4 {K_{3j} (\xi )\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi -\beta _4 \Delta T\\ \end{eqnarray}$
(21) $ \begin{eqnarray} && B_z (r,z)=\int_0^\infty {\rm J}_0 (\xi r)\Bigg[ K_{40} (\xi )\exp (-\lambda \xi z)+ \\&&\qquad\sum\limits_{j=1}^4 {K_{4j} (\xi )\exp (-\gamma _j \xi z)}\Bigg]{\rm d}\xi -\beta _5 \Delta T \end{eqnarray}$
(22a) $ \left. \begin{array}{ll} K_{10} (\xi )=\xi \lt\{c_{13} B(\xi )-\lambda \lt[c_{33} C(\xi )+e_{33} D(\xi )+ \\ h_{33} E(\xi ) ] \} \\ K_{1j} (\xi )=\xi \left[ {c_{13} a_j -c_{33} +e_{33} b_j +h_{33} d_j }\right]A_j (\xi ) \\ \end{array} \right\} $
(22b) $ \left. \begin{array}{ll} K_{20} (\xi )=-\xi \lt[c_{44} \lambda B(\xi )+c_{44} C(\xi )+e_{15} D(\xi )+ \\ h_{15} E(\xi ) ] \\ K_{2j} (\xi )=\xi \bigg[ -c_{44} \left( {a_j \gamma _j +\dfrac{1}{\gamma _j }} \right) +e_{15} \dfrac{b_j }{\gamma _j }+\\\qquad h_{15} \dfrac{d_j }{\gamma _j } \bigg]A_j (\xi ) \\ \end{array} \right\} $
(22c) $ \left. \begin{array}{ll} K_{30} (\xi )=\xi \bigg\{ e_{31} B(\xi )+\lambda \bigg[ \varepsilon _{33} D(\xi ) +h_{33} E(\xi )-\\ \qquad e_{33} C(\xi ) \bigg] \bigg\}\\ K_{3j} (\xi )=\xi \left[e_{31} a_j -e_{33} -\varepsilon _{33} b_j -h_{33} d_j \right]A_j (\xi ) \\ \end{array} \right\} $
(22d) $ \left. \begin{array}{ll} K_{40} (\xi )=\xi \lt\{ h_{31} B(\xi )+\lambda \lt[d_{33} D(\xi ) +\mu _{33} E(\xi )- \\ h_{33} C(\xi ) ] \} \\ K_{4j} (\xi )=\xi \left[ h_{31} a_j -h_{33} -d_{33} b_j -\mu _{33} d_j \right]A_j (\xi ) \\ \end{array} \right\} $
当在半无限大体的表面只作用有热载荷作用时, 磁-电-弹性半空间表面上电、磁和机械边界条件为
(23) $ \left. \begin{array}{ll} D_z (r,0)=0 \\ B_z (r,0)=0 \\ \sigma _{rz} (r,0)=0 \\ \sigma _{zz} (r,0)=0 \\ \end{array} \right\}$
将方程(18)$\sim$(21)代入方程(23), 可以得到以下关系式
(24a) $ \left. \begin{array}{ll} \sum\limits_{j=1}^4 {X_{1j} A_j (\xi )} =Y_1 \\ Y_1 =-c_{13} B(\xi )+\lambda \left[ c_{33} C(\xi )+e_{33} D(\xi )+ \\ \qquad h_{33} E(\xi )\right]+\beta _3 \dfrac{A(\xi )}{\xi } \\ \end{array} \right\} $
(24b) $ \left. \begin{array}{ll} \sum\limits_{j=1}^4 {X_{2j} A_j (\xi )} =Y_2 \\ Y_2 =c_{44} \lambda B(\xi )+c_{44} C(\xi )+e_{15} D(\xi )+h_{15} E(\xi ) \\ \end{array} \right\} $
(24c) $ \left. \begin{array}{ll} \sum\limits_{j=1}^4 {X_{3j} A_j (\xi )} =Y_3 \\ Y_3 =-e_{31} B(\xi )+\lambda \left[ e_{33} C(\xi )-\varepsilon _{33} D(\xi )- \\ \qquad h_{33} E(\xi )\right]+\beta _4 \dfrac{A(\xi )}{\xi } \\ \end{array} \right\} $
(24d) $ \left. \begin{array}{ll} \sum\limits_{j=1}^4 {X_{4j} A_j (\xi )} =Y_4 \\ Y_4 =-h_{31} B(\xi )+\lambda \left[ h_{33} C(\xi ) -d_{33} D(\xi )- \\ \qquad \mu _{33} E(\xi )\right]+\beta _5 \dfrac{A(\xi )}{\xi } \\ \end{array} \right\} $
(25a) $ X_{1j} =c_{13} a_j -c_{33} +e_{33} b_j +h_{33} d_j $
(25b) $ X_{2j} (\xi )=-c_{44} \left( {a_j \gamma _j +\frac{1}{\gamma _j }} \right) +e_{15} \frac{b_j }{\gamma _j }+h_{15} \frac{d_j }{\gamma _j } $
(25c) $ X_{3j} =e_{31} a_j -e_{33} -\varepsilon _{33} b_j -h_{33} d_j $
(25d) $ X_{4j} =h_{31} a_j -h_{33} -d_{33} b_j -\mu _{33} d_j $
未知函数$B(\xi )$, $C(\xi )$, $D(\xi )$, $E(\xi )$可以由函数$A(\xi )$表示为
(26) $ \begin{eqnarray} \label{eq26} \left\{ {{\begin{array}{*{20}c} {B(\xi )} \\ {C(\xi )} \\ {D(\xi )} \\ {E(\xi )} \\ \end{array} }} \right\}=\left\{ {{\begin{array}{*{20}c} {\varDelta _1 } \\ {\varDelta _2 } \\ {\varDelta _3 } \\ {\varDelta _4 } \\ \end{array} }} \right\}\frac{A(\xi )}{\xi } \end{eqnarray}$
其中, $\Delta _j $ ($j=1,2,3,4)$ 的表达式在附录中给出.
$Y_j $ ($j=1,2,3,4)$ 可以表示为$A(\xi )$的函数
(27) $ \begin{eqnarray} \label{eq27} \left\{ {{\begin{array}{*{20}c} {Y_1 } \\ {Y_2 } \\ {Y_3 } \\ {Y_4 } \\ \end{array} }} \right\}=\left\{ {{\begin{array}{*{20}c} {\delta _1 } \\ {\delta _2 } \\ {\delta _3 } \\ {\delta _4 } \\ \end{array} }} \right\}\frac{A(\xi )}{\xi } \end{eqnarray}$
(28a) $ \delta _1 =-c_{13} \varDelta _1 +c_{33} \lambda \varDelta _2 +e_{33} \lambda \varDelta _3 +h_{33} \lambda \varDelta _4 +\beta _3 $
(28b) $ \delta _2 =c_{44} \lambda \varDelta _1 +c_{44} \varDelta _2 +e_{15} \varDelta _3 +h_{15} \varDelta _4 $
(28c) $ \delta _3 =-e_{31} \varDelta _1 +e_{33} \lambda \varDelta _2 -\varepsilon _{33} \lambda \varDelta _3 -h_{33} \lambda \varDelta _4 +\beta _4 $
(28d) $ \delta _4 =-h_{31} \varDelta _1 +h_{33} \lambda \varDelta _2 -d_{33} \lambda \varDelta _3 -\mu _{33} \lambda \varDelta _4 +\beta _5 $
$A_j (\xi )\ (j=1,2,3,4)$与$A(\xi )$的关系为
(29) $ \begin{eqnarray} \label{eq28} \left[ {{\begin{array}{*{20}c} {X_{11} } & {X_{12} } & {X_{13} } & {X_{14} }\\ {X_{21} } & {X_{22} } & {X_{23} } & {X_{24} }\\ {X_{31} } & {X_{32} } & {X_{33} } & {X_{34} }\\ {X_{41} } & {X_{42} } & {X_{43} } & {X_{44} }\\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {A_1 (\xi )} \\ {A_2 (\xi )} \\ {A_3 (\xi )} \\ {A_4 (\xi )} \\ \end{array} }} \right\}=\left\{ {{\begin{array}{*{20}c} {\delta _1 } \\ {\delta _2 } \\ {\delta _3 } \\ {\delta _4 } \\ \end{array} }} \right\}\frac{A(\xi )}{\xi } \end{eqnarray}$
(30) $ \begin{eqnarray} \label{eq29} \left\{ {{\begin{array}{*{20}c} {A_1 (\xi )} \\ {A_2 (\xi )} \\ {A_3 (\xi )} \\ {A_4 (\xi )} \\ \end{array} }} \right\}=\left\{ {{\begin{array}{*{20}c} {\varOmega _1 } \\ {\varOmega _2 } \\ {\varOmega _3 } \\ {\varOmega _4 } \\ \end{array} }} \right\}\frac{A(\xi )}{\xi } \end{eqnarray}$
其中, $\varOmega _j $ ($j=1,2,3,4)$ 在附录中给出.
本文考虑如下定常相对温度作用在磁-电-弹性半空间表面上一个圆域上的情形
(31) $ \begin{eqnarray} \label{eq30} T_0 (r)=\left\{ {{\begin{array}{ll} T_0,\ \ & 0\leqslant r\leqslant a \\ 0,\ \ & r>a \\ \end{array} }} \right. \end{eqnarray}$
需要指出的是, $T_0 $是作用在圆域上的温度与圆域外的温度的相对值, 而所考查的半空间中的磁-电-弹性场的变化与$T_0 $有关.
(32) $ \begin{eqnarray} \label{eq32} A(\xi )=T_0 a{\rm J}_1 (\xi a) \end{eqnarray}$
温度场的积分表达式如方程(7)所示, 利用关系式(26)和式(30), 可以得到位移、电势、磁势、应力、电位移和磁通量的解析形式的表达式. 在此略去具体的细节, 应力、电位移和磁通量的分量可以表示为
(33) $ \sigma _{zz} (r,z)=T_0 a\left[ {(V_1 -\beta _3 )I_1 (\lambda )+\sum\limits_{j=1}^4 {E_j I_1 (\gamma _j )} } \right] $
(34) $ D_z (r,z)=T_0 a\left[ {(V_2 -\beta _4 )I_1 (\lambda )+\sum\limits_{j=1}^4 {F_j I_1 (\gamma _j )} } \right] $
(35) $ B_z (r,z)=T_0 a\left[ {(V_3 -\beta _5 )I_1 (\lambda )+\sum\limits_{j=1}^4 {G_j I_1 (\gamma _j )} } \right] $
(36) $ \sigma _{rz} (r,z)=T_0 a\left[ {V_4 I_2 (\lambda )+\sum\limits_{j=1}^4 {H_j I_2 (\gamma _j )} } \right] $
(37) $ D_r (r,z)=T_0 a\left[ {V_5 I_2 (\lambda )+\sum\limits_{j=1}^4 {K_j I_2 (\gamma _j )} } \right] $
(38) $ B_r (r,z)=T_0 a\left[ {V_6 I_2 (\lambda )+\sum\limits_{j=1}^4 {L_j I_2 (\gamma _j )} } \right] $
其中, 系数$V_k$ $(k=1,2,\dots, 6)$, $E_j$, $F_j$, $G_j $, $H_j$, $K_j $, $L_j$ ($j=1,2, 3,4)$在附录中给出, 积分算子$I_j \left( \lambda \right)$ $(j=1,2)$定义为
(39) $ \left. \begin{array}{ll} I_1 (\lambda )=\int_0^\infty {{\rm J}_1 (\xi a){\rm J}_0 (\xi r)\exp (-\lambda \xi z){\rm d}\xi } =\\[2mm]\qquad \dfrac{a}{2}\dfrac{\lambda z}{\left[ {r^2+\left( {\lambda z} \right)^2} \right]^{3 / 2}} \\[4mm] I_2 (\lambda )=\int_0^\infty {{\rm J}_1 (\xi a){\rm J}_1 (\xi r)\exp (-\lambda \xi z){\rm d}\xi } =\\[2mm]\qquad \dfrac{ar}{2}\dfrac{1}{\left[{r^2+\left( {\lambda z} \right)^2} \right]^{3 / 2}} \\ \end{array} \right\}$
常数$\beta _j$ $(j=1,2,3,4,5)$可表示为
(40) $ \left. \begin{array}{ll} \beta _1 =c_{11} \alpha _r +c_{12} \alpha _\theta +c_{13} \alpha _z \\ \beta _2 =c_{12} \alpha _r +c_{11} \alpha _\theta +c_{13} \alpha _z \\ \beta _3 =c_{13} \alpha _r +c_{13} \alpha _\theta +c_{33} \alpha _z \\ \beta _4 =e_{31} \alpha _r +e_{31} \alpha _\theta +e_{33} \alpha _z \\ \beta _5 =h_{31} \alpha _r +h_{31} \alpha _\theta +h_{33} \alpha _z \\ \end{array} \right\} $
其中, $\alpha _i$ $(i=r,\theta ,z)$为热膨胀系数.
由以上所得到的磁、电、热弹性场的解析表达式可知, 对于在任意区域作用任意温度载荷的情形, 本文的结果可以作为一个基本解, 在线弹性和小变形范围内利用叠加原理可以得到一般温度载荷情形的解. 需要指出的是, 由于解的表达式中含有无限积分项, 在不能获得精确积分结果的情况下, 数值积分可能会产生一定的误差.
3 数值计算及分析
在数值计算中, 不失一般性, 我们取一具有完全的机械、电和磁场耦合作用的横观各向同性性质的磁-电-弹性材料-复合材料BaTiO$_{3}$-CoFe$_{2}$O$_{4}$, 其材料常数为[31 ]
(41) $ \left. \begin{array}{ll} c_{11} =22.6\times 10^{10}~{\rm N} / {{\rm m}^{2}},\\ c_{13} =12.4\times 10^{10}~{\rm N} / {{\rm m}^{2}} \\ c_{33} =21.6\times 10^{10}~{\rm N} / {{\rm m}^{2}},\\ c_{44} =4.4\times 10^{10}~{\rm N} / {{\rm m}^{2}} \\ e_{15} =5.8~{\rm C} / {{\rm m}^{2}},\ \ e_{31} =-2.2~{\rm C} / {{\rm m}^{2}} \\ e_{33} =9.3~{\rm C} / {{\rm m}^{2}},\ \ h_{15} =275~{\rm N} /{{\rm Am}} \\ h_{31} =290.2~{\rm N} / {{\rm Am}},\ \ h_{33} =350~{\rm N} / {{\rm Am}} \\ \lambda _{11} =5.6\times 10^{-9}~{{\rm C}^{2}} / {{\rm Nm}^{2}},\\ \lambda _{33} =6.3\times 10^{-9}~{{\rm C}^{2}} / {{\rm Nm}^{2}} \\ \mu _{11} =29.7\times 10^{-5}~{{\rm Ns}^{2}} / {{\rm C}^{2}},\\ \mu _{33} =8.3\times 10^{-5}~{{\rm Ns}^{2}} / {{\rm C}^{2}} \\ d_{11} =4.0\times 10^{-9}~{{\rm Ns}} / {{\rm VC}},\\ d_{33} =4.7\times 10^{-9}~{{\rm Ns}} / {{\rm VC}} \\ \end{array} \right\}$
对于以$z$轴为极化方向的横观各向同性材料, 径向和切向的热膨胀系数相同, 即$\alpha _r =\alpha _\theta $. 因此, 由方程(40)可知$\beta _1 =\beta _2 $. 在以下的数值计算中, 热膨胀系数假定为$\alpha _r =\alpha _z =7.0\times 10^{-6}$ K$^{-1}$, 圆域内的相对温度值假设为$T_0 =100$ K.
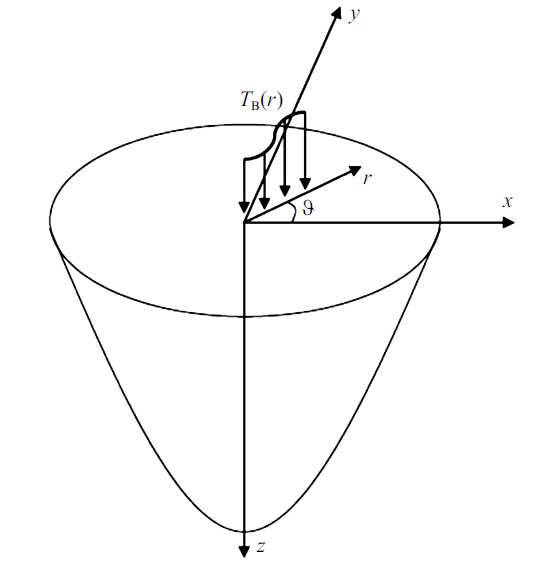
图2 给出了磁-电-弹性半空间中的无量纲化的正应力的分布. 图中显示最大应力发生在沿-轴方向距离半空间边界约$z\approx 1.3a$的位置. 可以推断当温度载荷作用的圆域半径增大时($a$增大), 最大应力发生的位置会远离半无限大体的边界, 即最大应力会发生在更深处; 反之当温度载荷作用的圆域半径减小时($a$减小), 最大应力发生的位置会靠近半无限大体的边界, 即最大应力会发生在靠近边界的位置. 需要指出的是, 在圆域外($r>a)$的正应力很小.
图2
图2
正应力${\sigma _{zz} } / {\beta _3 }T_0 $的分布
Fig.2
Distributions of the normalized stress ${\sigma _{zz} } / {\beta _3}T_0 $
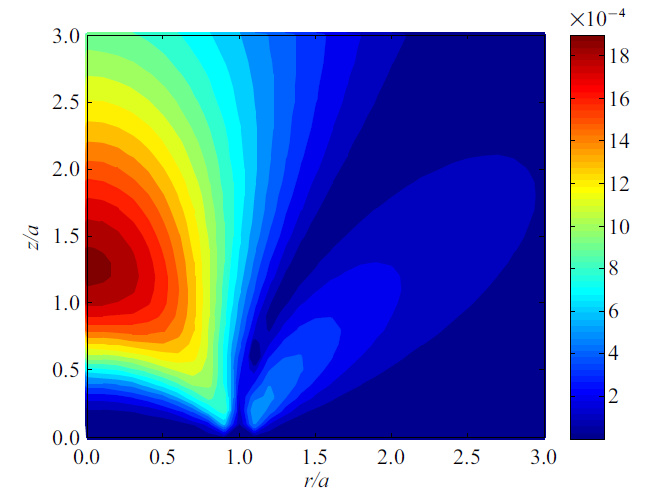
图3 显示了在圆域温度载荷作用下磁-电-弹性半空间中最大剪应力${\sigma _{rz} } /{\beta _3 }T_0 $的分布. 最大剪应力发生在靠近边界表面大约在圆形区域的边上($r\approx a)$. 在远离温度载荷作用区域($r>2a$, $z>a)$时, 剪应力变得相当小.
图3
图3
剪应力${\sigma _{rz} } / {\beta _3 }\Delta T$的分布
Fig.3
Distributions of the shear stress ${\sigma _{rz} } / {\beta _3 }\Delta T$
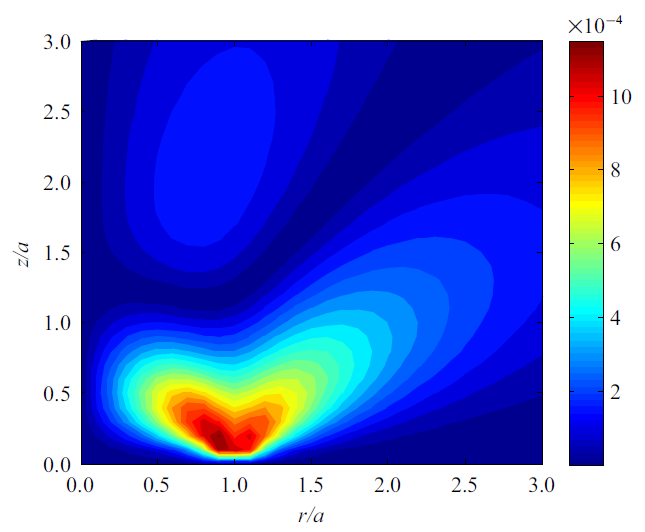
图4 给出了无量纲化的电场的分布, 可以看出, 电场在温度载荷作用的圆域内在边界表面附近有明显的强化. 这一结果预示在高温载荷情形时, 高温度区域可能会出现电击穿的情形. 图5 显示了半无限大空间中磁场的分布, 正的和负的磁场在不同的区域都得到了强化: 负的磁场在$z$轴附近约的区域强化显著, 而正的磁场在$z\approx 0.1a$, $r=1.2a$的区域得到了强化.
图4
图4
电场${e_{33} E_z } / {\beta _3 }\Delta T$的分布
Fig.4
Distributions of the normalized electric field ${e_{33} E_z } /{\beta _3 }\Delta T$
图5
图5
磁场${h_{33} H_z } / {\beta _3 }\Delta T$的分布
Fig.5
Distributions of the normalized magnetic field ${h_{33} H_z } / {\beta _3 }\Delta T$
4 结论
本文给出了磁-电-弹性半空间在轴对称温度载荷作用下的磁-电-热-弹性多场耦合的解析解. 利用变换法成功求解了磁-电-弹性介质中的热传导方程和控制方程, 得到了温度场分布的解析表达式, 并进一步获得了应力, 电位移和磁通量在半空间中的场分布. 数值结果表明在温度载荷作用下应力, 电位移和磁通量在各自特定的区域内会得到强化, 磁-电-弹性场强化区域的强化程度跟温度载荷的大小和作用区域大小相关. 本文结果对磁-电-弹性材料和结构的设计和应用具有重要的理论指导意义.
附录
方程(13), 方程(15)和(16)中的常数 $a_j$, $b_j$, $d_j $ ($j=1,2,3,4)$ 定义为
(A1) $\begin{eqnarray}\%A1 &&\left\{ {{\begin{array}{*{20}c} {a_j } \\ {b_j } \\ {d_j } \\ \end{array} }} \right\}=\left[ {{\begin{array}{*{20}c} {C_{11} -C_{44} \gamma _j^2 } & {e_{31} +e_{15} } & {h_{31} +h_{15} } \\ {(C_{13} +C_{44} )\gamma _j^2 } & {e_{33} \gamma _j^2 -e_{15} } & {h_{33} \gamma _j^2 -h_{15} } \\ {(e_{31} +e_{15} )\gamma _j^2 } & {\lambda _{11} -\lambda _{33} \gamma _j^2 } & {d_{11} -d_{33} \gamma _j^2 } \\ \end{array} }} \right]^{-1}\cdot \\&&\qquad \left\{ {{\begin{array}{*{20}c} {C_{13} +C_{44} } \\ {C_{33} \gamma _j^2 -C_{44} } \\ {e_{33} \gamma _j^2 -e_{15} } \\ \end{array} }} \right\}\ \ (j=1,2,3,4) \end{eqnarray}$
其中, $\gamma _j $ ($j=1,2,3)$ 为特征方程(17)的特征根. 在方程(26)中$\Delta _j$ ($j=1,2,3,4)$ 定义为
(A2a) $\begin{eqnarray} && \varDelta _1 = \frac{1}{\varDelta }\cdot\left| {{\begin{array}{*{20}c} {-\beta _1 } & {(C_{13} +C_{44} )\lambda } & {(e_{31} +e_{15} )\lambda } & {(h_{31} +h_{15} )\lambda } \\[1.5mm] {\beta _3 \lambda } & {C_{44} -C_{33} \lambda ^2} & {e_{15} -e_{33} \lambda ^2} & {h_{15} -h_{33} \lambda ^2} \\[1.5mm] {\beta _4 \lambda } & {e_{15} -e_{33} \lambda ^2} & {\varepsilon _{33} \lambda ^2-\varepsilon _{11} } & {d_{33} \lambda ^2-d_{11} } \\[1.5mm] {\beta _5 \lambda } & {h_{15} -h_{33} \lambda ^2} & {d_{33} \lambda ^2-d_{11} } & {\mu _{33} \lambda ^2-\mu _{11} } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A2b) $\begin{eqnarray} && \varDelta _2 = \frac{1}{\varDelta }\cdot\left| {{\begin{array}{*{20}c} {C_{44} \lambda ^2-C_{11} } & {-\beta _1 } & {(e_{31} +e_{15} )\lambda } & {(h_{31} +h_{15} )\lambda } \\[1.5mm] {(C_{13} +C_{44} )\lambda } & {\beta _3 \lambda } & {e_{15} -e_{33} \lambda ^2} & {h_{15} -h_{33} \lambda ^2} \\[1.5mm] {(e_{31} +e_{15} )\lambda } & {\beta _4 \lambda } & {\varepsilon _{33} \lambda ^2-\varepsilon _{11} } & {d_{33} \lambda ^2-d_{11} } \\[1.5mm] {(h_{31} +h_{15} )\lambda } & {\beta _5 \lambda } & {d_{33} \lambda ^2-d_{11} } & {\mu _{33} \lambda ^2-\mu _{11} } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A2c) $\begin{eqnarray} && \varDelta _3 = \frac{1}{\varDelta }\cdot\left| {{\begin{array}{*{20}c} {C_{44} \lambda ^2-C_{11} } & {(C_{13} +C_{44} )\lambda } & {-\beta _1 } & {(h_{31} +h_{15} )\lambda } \\[1.5mm] {(C_{13} +C_{44} )\lambda } & {C_{44} -C_{33} \lambda ^2} & {\beta _3 \lambda } & {h_{15} -h_{33} \lambda ^2} \\[1.5mm] {(e_{31} +e_{15} )\lambda } & {e_{15} -e_{33} \lambda ^2} & {\beta _4 \lambda } & {d_{33} \lambda ^2-d_{11} } \\[1.5mm] {(h_{31} +h_{15} )\lambda } & {h_{15} -h_{33} \lambda ^2} & {\beta _5 \lambda } & {\mu _{33} \lambda ^2-\mu _{11} } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A2d) $\begin{eqnarray} && \varDelta _4 = \frac{1}{\varDelta }\cdot\left| {{\begin{array}{*{20}c} {C_{44} \lambda ^2-C_{11} } & {(C_{13} +C_{44} )\lambda } & {(e_{31} +e_{15} )\lambda } & {-\beta _1 } \\[1.5mm] {(C_{13} +C_{44} )\lambda } & {C_{44} -C_{33} \lambda ^2} & {e_{15} -e_{33} \lambda ^2} & {\beta _3 \lambda } \\[1.5mm] {(e_{31} +e_{15} )\lambda } & {e_{15} -e_{33} \lambda ^2} & {\varepsilon _{33} \lambda ^2-\varepsilon _{11} } & {\beta _4 \lambda } \\[1.5mm] {(h_{31} +h_{15} )\lambda } & {h_{15} -h_{33} \lambda ^2} & {d_{33} \lambda ^2-d_{11} } & {\beta _5 \lambda } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A2e) $\left. \begin{array}{ll} \varDelta =\left| { \varDelta } \right| \\ { \varDelta }(1,1)=C_{44} \lambda ^2-C_{11}, { \varDelta }(1,2)={ \varDelta }(2,1)=(C_{13} +C_{44} )\lambda \\ { \varDelta }(1,3)={ \varDelta }(3,1)=(e_{31} +e_{15} )\lambda \\ { \varDelta }(1,4)={ \varDelta }(4,1)=(h_{31} +h_{15} )\lambda \\ { \varDelta }(2,2)=C_{44} -C_{33} \lambda ^2, \ \ { \varDelta }(2,3)={ \varDelta }(3,2)=e_{15} -e_{33} \lambda ^2 \\ { \varDelta }(2,4)={ \varDelta }(4,2)=h_{15} -h_{33} \lambda ^2 \\ { \varDelta }(3,3)=\varepsilon _{33} \lambda ^2-\varepsilon _{11}, { \varDelta }(3,4)={ \varDelta }(4,3)=d_{33} \lambda ^2-d_{11} \\ { \varDelta }(4,4)=\mu _{33} \lambda ^2-\mu _{11} \\ \end{array} \right\} $
在方程(30)中$\varOmega _j (j=1,2,3,4)$定义为
(A3a) $\begin{eqnarray} && \varOmega _1 =\frac{1}{\varDelta _X }\left| {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {\delta _1 } & {X_{12} } & {X_{13} } & {X_{14} } \\[1.5mm] {\delta _2 } & {X_{22} } & {X_{23} } & {X_{24} } \\[1.5mm] {\delta _3 } & {X_{32} } & {X_{33} } & {X_{34} } \\[1.5mm] {\delta _4 } & {X_{42} } & {X_{43} } & {X_{44} } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A3b) $\begin{eqnarray} && \varOmega _2 =\frac{1}{\varDelta _X }\left| {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {X_{11} } & {\delta _1 } & {X_{13} } & {X_{14} } \\[1.5mm] {X_{21} } & {\delta _2 } & {X_{23} } & {X_{24} } \\[1.5mm] {X_{31} } & {\delta _3 } & {X_{33} } & {X_{34} } \\[1.5mm] {X_{41} } & {\delta _4 } & {X_{43} } & {X_{44} } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A3c) $\begin{eqnarray} && \varOmega _3 =\frac{1}{\varDelta _X }\left| {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {X_{11} } & {X_{12} } & {\delta _1 } & {X_{14} } \\[1.5mm] {X_{21} } & {X_{22} } & {\delta _2 } & {X_{24} } \\[1.5mm] {X_{31} } & {X_{32} } & {\delta _3 } & {X_{34} } \\[1.5mm] {X_{41} } & {X_{42} } & {\delta _4 } & {X_{44} } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A3d) $\begin{eqnarray} && \varOmega _4 =\frac{1}{\varDelta _X }\left| {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {X_{11} } & {X_{12} } & {X_{13} } & {\delta _1 } \\[1.5mm] {X_{21} } & {X_{22} } & {X_{23} } & {\delta _2 } \\[1.5mm] {X_{31} } & {X_{32} } & {X_{33} } & {\delta _3 } \\[1.5mm] {X_{41} } & {X_{42} } & {X_{43} } & {\delta _4 } \\[1.5mm] \end{array} }} \right|\\[1.5mm] \end{eqnarray}$
(A3e) $\begin{eqnarray} && \varDelta _X =\left| {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {X_{11} } & {X_{12} } & {X_{13} } & {X_{14} } \\[1.5mm] {X_{21} } & {X_{22} } & {X_{23} } & {X_{24} } \\[1.5mm] {X_{31} } & {X_{32} } & {X_{33} } & {X_{34} } \\[1.5mm] {X_{41} } & {X_{42} } & {X_{43} } & {X_{44} } \\[1.5mm] \end{array} }} \right| \end{eqnarray} $
其中分量$X_{ij}$ $(i,j=1,2,3,4)$在方程(25)中定义.
方程(33)$\sim$(38)中的系数$V_k$ $(k=1,2,\dots, 6)$定义为
(A4) $\begin{eqnarray}\%A4 \left\{ {{\begin{array}{*{20}c} {V_1 } \\[.5mm] {V_2 } \\[.5mm] {V_3 } \\[.5mm] {V_4 } \\[.5mm] {V_5 } \\[.5mm] {V_6 } \\[.5mm] \end{array} }} \right\}=\left[ {{\begin{array}{*{20}c} {c_{13} } & {-\lambda c_{33} } & {-\lambda e_{33} } & {-\lambda h_{33} } \\[.5mm] {e_{31} } & {-\lambda e_{33} } & {\lambda \varepsilon _{33} } & {\lambda h_{33} } \\[.5mm] {h_{31} } & {-\lambda h_{33} } & {\lambda d_{33} } & {\lambda \mu _{33} } \\[.5mm] {-\lambda c_{44} } & {-c_{44} } & {-e_{15} } & {-h_{15} } \\[.5mm] {-\lambda e_{15} } & {-e_{15} } & {\varepsilon _{11} } & {d_{11} } \\[.5mm] {-\lambda h_{15} } & {-h_{15} } & {d_{11} } & {\mu _{11} } \\[.5mm] \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} { \varDelta _1 } \\[.5mm] { \varDelta _2 } \\[.5mm] { \varDelta _3 } \\[.5mm] { \varDelta _4 } \\[.5mm] \end{array} }} \right\} \end{eqnarray}$
$E_j$, $F_j$, $G_j$, $H_j$, $K_j$, $L_j$ ($j=1,2,3,4)$定义为
(A5) $\left. \begin{array}{ll} E_j =X_{1j} \varOmega _j,\ \ F_j =X_{3j} \varOmega _j \\[.5mm] G_j =X_{4j} \varOmega _j,\ \ H_j =X_{2j} \varOmega _j \\[.5mm] K_j =X_{5j} \varOmega _j,\ \ L_j =X_{6j} \varOmega _j \\[.5mm] \end{array} \right\}$
(A6a) $\begin{eqnarray} && X_{5j} (\xi )=-e_{15} \left( {a_j \gamma _j +\frac{1}{\gamma _j }} \right) -\varepsilon _{11} \frac{b_j }{\gamma _j }-d_{11} \frac{d_j }{\gamma _j }\end{eqnarray}$
(A6b) $\begin{eqnarray} X_{6j} (\xi )=-h_{15} \left( {a_j \gamma _j +\frac{1}{\gamma _j }} \right) -d_{11} \frac{b_j }{\gamma _j }-\mu _{11} \frac{d_j }{\gamma _j} \end{eqnarray} $
参考文献
View Option
[1]
Huang JH Kuo WS . The analysis of piezoelectric/piezomagnetic composite materials containing an ellipsoidal inclusion
Journal of Applied Physics 1997 ,81 :1378 -1386
DOI
URL
[本文引用: 1]
[2]
Benveniste Y . Magnetoelectric effect in fibrous composites with piezoelectric and piezomagnetic phases
Physics Review B 1995 ,B51 :16424 -16427
[3]
Liu SL Li YD . Fracture of a multiferroic semicylinder with a magnetoelectroelastic interlayer: Piezoelectric stiffening/softening effects and peak removal of stress intensity factor
International Journal of Solids and Structures 2016 , 88-89 :110 -118
DOI
URL
[4]
詹世革 , 方岱宁 , 李法新 等 . 层状电磁复合材料的界面结构与力学行为 -- 国家自然科学基金重大项目成果综述
中国科学基金 , 2015 ,5 :332 -336
( Zhan Shige Fang Daining Li Faxin , et al . Final report of key project of NSFC "The interfacial structure and mechanics of laminated magnetoelectric composites"
National Science Foundation of China 2015 ,5 :332 -336 (in Chinese))
[5]
Arefi M Amir HAS . Higher order shear deformation bending results of a magnetoelectrothermoelastic functionally graded nanobeam in thermal, mechanical, electrical, and magnetic environments
Mechanics Based Design of Structures and Machines 2018 ,46 (6 ):669 -692
[6]
胡骏 , 亢战 . 考虑可控性的压电作动器拓扑优化设计
力学学报 , 2019 ,51 (4 ):1073 -1081
( Hu Jun Kang Zhan . Topology optimization of piezoelectric actuator considering controllability
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (4 ):324 -332 (in Chinese))
[7]
牛牧青 , 杨斌堂 , 杨诣坤 等 . 磁致伸缩主被动隔振装置中的磁机耦合效应研究
力学学报 , 2019 ,51 (2 ):324 -332
( Niu Muqing Yang Bintang Yang Yikun , et al . Research on the magneto-mechanical effect in active and passive magnetostrictive vibration isolator
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):324 -332 (in Chinese))
[8]
张乐乐 , 刘响林 , 刘金喜 . 压电纳米板中SH型导波的传播特性
力学学报 , 2019 ,51 (2 ):503 -511
[本文引用: 1]
( Zhang Lele Liu Xianglin Liu Jinxi . Propagation characteristics of SH guided waves in a piezoelectric nanoplate
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):324 -332 (in Chinese))
[本文引用: 1]
[9]
Wang HM Pan E Sangghaleh A , et al . Circular loadings on the surface of an anisotropic and magentoelectroelastic half-space
Smart Materials and Structures 2012 ,21 :075003
[本文引用: 1]
[10]
Qin QH . Green's functions of magnetoelastic solids with a half-plane boundary or biomaterial interface
Philosophical Magazine Letters 2004 ,84 :771 -779
[本文引用: 1]
[11]
Hu KQ Chen ZT Zhong Z . Interface crack between magnetoelectroelastic and orthotropic half-spaces under in-plane loading
Theoretical and Applied Fracture Mechanics 2018 ,96 :285 -295
[本文引用: 1]
[12]
段淑敏 , 周敏娟 , 薛雁 等 . 加层电磁弹性材料界面裂纹瞬态响应
工程力学 , 2007 ,24 (8 ):101 -107
[本文引用: 1]
( Duan Shumin Zhou Minjuan Xue Yan , et al . Transient response of an interface crack between magneto-electro-elastic layer and dissimilar half-infinite medium
Engineering Mechanics 2007 ,24 (8 ):101 -107 (in Chinese))
[本文引用: 1]
[13]
Ma P Su RKL Feng WJ . Crack tip enrichment functions for extended finite element analysis of two-dimensional interface cracks in anisotropic magnetoelectroelastic bimaterials
Engineering Fracture Mechanics 2016 ,161 :21 -39
DOI
URL
[本文引用: 1]
[14]
Yang Y Li XF . Bending and free vibration of a circular magnetoelectroelastic plate with surface effects
International Journal of Mechanical Sciences 2019 , 157-158 :858 -871
[本文引用: 1]
[15]
Chen WQ Zhu J Li XY . General solutions for elasticity of transversely isotropic materials with thermal and other effects: A review
Journal of Thermal Stresses 2019 ,42 (1 ):90 -106
[本文引用: 1]
[16]
Hou PF Yi T Wang L . 2D general solution and fundamental solution for orthotropic electro-magneto-thermo-elastic materials
Journal of Thermal Stresses 2008 ,31 :807 -822
[本文引用: 1]
[17]
Chen WQ Lee KY Ding HJ . General solution for transversely isotropic magneto-electro-thermo-elasticity and the potential theory method
International Journal of Engineering Science 2004 ,42 :1361 -1379
[本文引用: 1]
[18]
Carman GP Cheung KS Wang D . Micro-mechanical model of a composite containing a conservative nonlinear electro-magneto-thermo- mechanical material
Journal of Intelligent Material Systems and Structures 1995 ,6 :691 -698
[本文引用: 1]
[19]
Li JY Dunn ML . Micromechanics of magnetoelectroelastic composite materials: Average field and effective behavior
Journal of Intelligent Material Systems and Structures 1998 ,9 :404 -416
[本文引用: 1]
[20]
Aboudi J . Micromechanical analysis of fully coupled electro-magneto-thermo-elastic multiphase composites
Smart Materials and Structures 2001 ,10 :867 -877
DOI
URL
[本文引用: 1]
[21]
Ke LL Wang YS . Free vibration of size-dependent magneto-electro- elastic nanobeams based on the nonlocal theory
Acta Mechanica Sinica 2014 ,30 (4 ):516 -525
DOI
URL
[本文引用: 1]
In this paper, the free vibration of magnetoelectro-elastic (MEE) nanoplates is investigated based on the nonlocal theory and Kirchhoff plate theory. The MEE nanoplate is assumed as all edges simply supported rectangular plate subjected to the biaxial force, external electric potential, external magnetic potential, and temperature rise. By using the Hamilton's principle, the governing equations and boundary conditions are derived and then solved analytically to obtain the natural frequencies of MEE nanoplates. A parametric study is presented to examine the effect of the nonlocal parameter, thermo-magneto-electro-mechanical loadings and aspect ratio on the vibration characteristics of MEE nanoplates. It is found that the natural frequency is quite sensitive to the mechanical loading, electric loading and magnetic loading, while it is insensitive to the thermal loading.
[22]
田晓耕 , 沈亚鹏 . 广义热弹性问题研究进展
力学进展 , 2012 ,42 (1 ):18 -28
[本文引用: 1]
( Tian Xiaogeng Shen Yapeng . Research progress in generalized thermoelastic problems
Advances in Mechanics 2012 ,42 (1 ):18 -28 (in Chinese))
[本文引用: 1]
[23]
He TH Ma JT Li Y . The generalized electromagnetic-thermoelastic coupling problem of hollow cylindrical conductor based on the memory-dependent derivative
International Journal of Applied Electromagnetics and Mechanics 2019 ,61 :357 -375
[本文引用: 1]
[24]
Ootao Y Tanigawa Y . Transient analysis of multilayered magneto electrothermoelastic strip due to nonuniform heat supply
Composite Structures 2005 ,68 :471 -480
[本文引用: 1]
[25]
Karimi M Shahidi AR . Nonlocal, refined plate, and surface effects used to analyze vibration of magnetoelectroelastic nanoplates under thermo-mechanical and shear loading
Applied Physics A 2017 ,123 (5 ):304
[本文引用: 1]
[26]
Gao CF Kessler H Balke H . Fracture analysis of electromagnetic thermoelastic solids
European Journal of Mechanics A/Solids 2003 ,22 :433 -442
DOI
URL
[本文引用: 1]
[27]
Niraula OP Wang BL . Thermal stress analysis in magneto-electro-thermoelasticity with a penny-shaped crack under uniform heat flow
Journal of Thermal Stresses 2006 ,29 :423 -437
DOI
URL
[本文引用: 1]
[28]
Li PD Li XY Kang GZ , et al . Three-dimensional fundamental solution of a penny-shaped crack in an infinite thermo-magneto-electro- elastic medium with transverse isotropy
International Journal of Mechanical Sciences 2017 ,130 :203 -220
DOI
URL
[本文引用: 1]
[29]
Zhao MH Dang HY Fan CY , et al . Analysis of an interface crack of arbitrary shape in a three-dimensional transversely isotropic magnetoelectrothermoelastic biomaterial -- part 1: Theoretical solution
Journal of Thermal Stresses 2017 ,40 (8 ):929 -952
[本文引用: 1]
[30]
Zhao MH Dang HY Fan CY , et al . Analysis of an interface crack of arbitrary shape in a three-dimensional transversely isotropic magnetoelectrothermoelastic biomaterial -- part 2: Numerical method
Journal of Thermal Stresses 2017 ,40 (8 ):953 -972
DOI
URL
[本文引用: 1]
[31]
Hu KQ Chen ZT . Pre-kinking of a moving crack in a magnetoelectroelastic material under in-plane loading
International Journal of Solids and Structures 2013 ,50 :2667 -2677
DOI
URL
[本文引用: 2]
A constant moving crack in a magnetoelectroelastic material under in-plane mechanical, electric and magnetic loading is studied for impermeable crack surface boundary conditions. Fourier transform is employed to reduce the mixed boundary value problem of the crack to dual integral equations, which are solved exactly. Steady-state asymptotic fields near the crack tip are obtained in closed form and the corresponding field intensity factors are expressed explicitly. The crack speed influences the singular field distribution around the crack tip and the effects of electric and magnetic loading on the crack tip fields are discussed. The crack kinking phenomena is investigated using the maximum hoop stress intensity factor criterion. The magnitude of the maximum hoop stress intensity factor tends to increase as the crack speed increases. (C) 2013 Elsevier Ltd. All rights reserved,
[32]
Hu KQ Chen ZT Zhong Z . Pre-kinking analysis of a constant moving crack in a magnetoelectroelastic strip under in-plane loading
European Journal of Mechanics-A/Solids 2014 ,43 :25 -43
DOI
URL
[本文引用: 1]
The analysis of piezoelectric/piezomagnetic composite materials containing an ellipsoidal inclusion
1
1997
... 磁-电-弹性材料是一种同时具有压电压磁磁电耦合效应的复合材料, 这种材料在工程结构中, 尤其是在智能材料和结构系统中, 有越来越广泛的应用. 磁-电-弹性材料所固有的力电磁耦合特性使它们成为智能结构中传感与执行元件的首选材料, 广泛应用于传感器、执行器、滤波器、换能器和其他智能器件, 在能量转换系统中有着非常可观的潜在的应用前景[1 -8 ] . 由于这些智能器件通常在复杂的力、电、磁和热耦合载荷环境下工作, 因此对磁-电-弹性材料在多场耦合环境下的响应问题研究具有重要的意义. ...
Magnetoelectric effect in fibrous composites with piezoelectric and piezomagnetic phases
1995
Fracture of a multiferroic semicylinder with a magnetoelectroelastic interlayer: Piezoelectric stiffening/softening effects and peak removal of stress intensity factor
2016
层状电磁复合材料的界面结构与力学行为 -- 国家自然科学基金重大项目成果综述
2015
层状电磁复合材料的界面结构与力学行为 -- 国家自然科学基金重大项目成果综述
2015
Higher order shear deformation bending results of a magnetoelectrothermoelastic functionally graded nanobeam in thermal, mechanical, electrical, and magnetic environments
2018
磁致伸缩主被动隔振装置中的磁机耦合效应研究
2019
磁致伸缩主被动隔振装置中的磁机耦合效应研究
2019
压电纳米板中SH型导波的传播特性
1
2019
... 磁-电-弹性材料是一种同时具有压电压磁磁电耦合效应的复合材料, 这种材料在工程结构中, 尤其是在智能材料和结构系统中, 有越来越广泛的应用. 磁-电-弹性材料所固有的力电磁耦合特性使它们成为智能结构中传感与执行元件的首选材料, 广泛应用于传感器、执行器、滤波器、换能器和其他智能器件, 在能量转换系统中有着非常可观的潜在的应用前景[1 -8 ] . 由于这些智能器件通常在复杂的力、电、磁和热耦合载荷环境下工作, 因此对磁-电-弹性材料在多场耦合环境下的响应问题研究具有重要的意义. ...
压电纳米板中SH型导波的传播特性
1
2019
... 磁-电-弹性材料是一种同时具有压电压磁磁电耦合效应的复合材料, 这种材料在工程结构中, 尤其是在智能材料和结构系统中, 有越来越广泛的应用. 磁-电-弹性材料所固有的力电磁耦合特性使它们成为智能结构中传感与执行元件的首选材料, 广泛应用于传感器、执行器、滤波器、换能器和其他智能器件, 在能量转换系统中有着非常可观的潜在的应用前景[1 -8 ] . 由于这些智能器件通常在复杂的力、电、磁和热耦合载荷环境下工作, 因此对磁-电-弹性材料在多场耦合环境下的响应问题研究具有重要的意义. ...
Circular loadings on the surface of an anisotropic and magentoelectroelastic half-space
1
2012
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
Green's functions of magnetoelastic solids with a half-plane boundary or biomaterial interface
1
2004
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
Interface crack between magnetoelectroelastic and orthotropic half-spaces under in-plane loading
1
2018
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
加层电磁弹性材料界面裂纹瞬态响应
1
2007
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
加层电磁弹性材料界面裂纹瞬态响应
1
2007
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
Crack tip enrichment functions for extended finite element analysis of two-dimensional interface cracks in anisotropic magnetoelectroelastic bimaterials
1
2016
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
Bending and free vibration of a circular magnetoelectroelastic plate with surface effects
1
2019
... 近年来, 关于磁-电-弹性材料力学问题的研究备受关注. Wang等[9 ] 推出了各向异性磁-电-弹性半空间在圆周方向载荷作用下的解析解. 利用推广的Stroh公式和坐标变换技术, Qin[10 ] 求得了磁-电-弹性介质中含有任意方向半平面或双材料界面时的Green函数解. 利用积分变换和奇异积分方程方法, Hu等[11 ] 研究了磁-电-弹性和正交各向异性半空间中的界面裂纹问题, 发现裂纹尖端的振荡奇异性或非振荡奇异性取决于双材料的特定材料属性组合. 段淑敏等[12 ] 用奇异积分方程法求解了磁-电-弹性材料与加层间的界面裂纹在反平面剪切冲击载荷和面内电磁冲击载荷作用下的动态响应问题, 讨论了载荷、材料及几何参数对能量释放率的影响. Ma等[13 ] 用扩展有限元法分析了磁-电-弹性双材料界面裂纹的静态断裂和多场耦合效应. Yang和Li[14 ] 通过考虑表面效应并利用Kirchhoff薄板理论, 获得了纳米尺度圆盘状磁-电-弹性薄板弯曲和自由振动的解析解. ...
General solutions for elasticity of transversely isotropic materials with thermal and other effects: A review
1
2019
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
2D general solution and fundamental solution for orthotropic electro-magneto-thermo-elastic materials
1
2008
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
General solution for transversely isotropic magneto-electro-thermo-elasticity and the potential theory method
1
2004
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Micro-mechanical model of a composite containing a conservative nonlinear electro-magneto-thermo- mechanical material
1
1995
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Micromechanics of magnetoelectroelastic composite materials: Average field and effective behavior
1
1998
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Micromechanical analysis of fully coupled electro-magneto-thermo-elastic multiphase composites
1
2001
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Free vibration of size-dependent magneto-electro- elastic nanobeams based on the nonlocal theory
1
2014
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
广义热弹性问题研究进展
1
2012
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
广义热弹性问题研究进展
1
2012
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
The generalized electromagnetic-thermoelastic coupling problem of hollow cylindrical conductor based on the memory-dependent derivative
1
2019
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Transient analysis of multilayered magneto electrothermoelastic strip due to nonuniform heat supply
1
2005
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Nonlocal, refined plate, and surface effects used to analyze vibration of magnetoelectroelastic nanoplates under thermo-mechanical and shear loading
1
2017
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Fracture analysis of electromagnetic thermoelastic solids
1
2003
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Thermal stress analysis in magneto-electro-thermoelasticity with a penny-shaped crack under uniform heat flow
1
2006
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Three-dimensional fundamental solution of a penny-shaped crack in an infinite thermo-magneto-electro- elastic medium with transverse isotropy
1
2017
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Analysis of an interface crack of arbitrary shape in a three-dimensional transversely isotropic magnetoelectrothermoelastic biomaterial -- part 1: Theoretical solution
1
2017
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Analysis of an interface crack of arbitrary shape in a three-dimensional transversely isotropic magnetoelectrothermoelastic biomaterial -- part 2: Numerical method
1
2017
... 鉴于磁-电-弹性材料和结构通常会用在磁场、电场和温度场等多场耦合的载荷环境中, 而其性能通常会受到温度载荷显著的影响, 因此有必要对其热效应进行深入的研究[15 ] . Hou等[16 ] 求得了各向同性磁-电-弹性材料中的二维形式的通解和基本解. 通过引入5个调和函数, Chen等[17 ] 推导出了横观各向同性磁-电-热弹性体的一般解并得到了各耦合场的表达式. Carman等[18 ] 提出了一个含有保守非线性的磁-电-弹性材料中的微观机械模型. 利用微观机械方法可以对完全耦合的磁-电-热弹性多相复合材料的性能进行系统的分析[19 -20 ] . Ke和Wang[21 ] 基于非局部理论和Kirchhoff板理论研究了磁-电-弹性纳米板的自由振动, 发现其固有频率对于力、电和磁载荷很敏感但对热载荷不敏感. 田晓耕和沈亚鹏[22 ] 讨论并综述了磁-电多场耦合的广义电磁热弹性耦合问题方面的研究以及计及扩散效应和黏弹性效应的广义热弹性理论的发展. He等[23 ] 研究了无限长空心圆柱体中的广义电磁热弹性问题. Ootao和Tanigama[24 ] 研究了多层磁-电-热弹性板条在非稳定及非均匀热载荷作用下的动态响应. Karimi和Shahidi[25 ] 利用非局部理论研究了磁-电-弹性纳米板在外加磁势、面内剪切和热载荷作用时的自由振动及表面效应. Gao等[26 ] 根据广义Stroh公式研究了完全耦合的磁-电-弹性介质中的共线电渗透型裂纹问题并给出了在远场均匀热流作用时磁-电-弹性场强度因子的简洁表达式. 利用积分方程法, Niraula和Wang[27 ] 求得了磁-电-弹性介质中的圆币型裂纹在均匀热流作用下的精确解. Li等[28 ] 求得了具有横观各向同性性质的无限大热-磁-电-弹性介质中的圆币型裂纹的三维基本解. Zhao等[29 -30 ] 用扩展的位移间断边界积分方程法分析了三维横观各向同性热-磁-电-弹性双材料中任意形状的界面裂纹问题并讨论了电-磁场边界条件对各个场强度因子的影响. ...
Pre-kinking of a moving crack in a magnetoelectroelastic material under in-plane loading
2
2013
... 其中, $\left| {M} \right|$ 表示矩阵${M}$的行列式值. 这里需要指出的是, 八阶特征方程(17)有8个特征根成对出现, 每一对大小相同符号相反, 复根以共轭形式成对出现. 在式(13)$\sim$式(16)中, 取特征根$\gamma _j $ ($j=1,2,3,4)$ 的实部为正, 以确保稳定系统的内能正定[31 -32 ] . ...
... 在数值计算中, 不失一般性, 我们取一具有完全的机械、电和磁场耦合作用的横观各向同性性质的磁-电-弹性材料-复合材料BaTiO$_{3}$-CoFe$_{2}$O$_{4}$, 其材料常数为[31 ] ...
Pre-kinking analysis of a constant moving crack in a magnetoelectroelastic strip under in-plane loading
1
2014
... 其中, $\left| {M} \right|$ 表示矩阵${M}$的行列式值. 这里需要指出的是, 八阶特征方程(17)有8个特征根成对出现, 每一对大小相同符号相反, 复根以共轭形式成对出现. 在式(13)$\sim$式(16)中, 取特征根$\gamma _j $ ($j=1,2,3,4)$ 的实部为正, 以确保稳定系统的内能正定[31 -32 ] . ...