引言
地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析.
采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献.
基于以上分析, 本文考虑地基土的固流耦合效应和孔隙水的渗透作用, 基于Kirchhoff理论和Biot多孔介质理论建立矩形板与饱和多孔地基动力相互作用的计算模型. 并且考虑了一种混合透水边界, 即板土接触面为不透水界面, 其余表面为透水界面. 针对接触面和非接触面的混合边值问题, 通过双重Fourier变换构造出两对二维对偶积分方程, 并利用Hilbert正交化定理和Schmidt法对二维对偶积分方程进行求解, 最终推导出板土系统在动力作用下的位移和应力解析式. 通过数值计算, 对饱和多孔地基上矩形板的振动响应和参数影响做了分析和讨论. 将计算结果与弹性地基上矩形板的振动响应进行对比分析, 总结出相关结论.
1 计算模型及基本方程求解
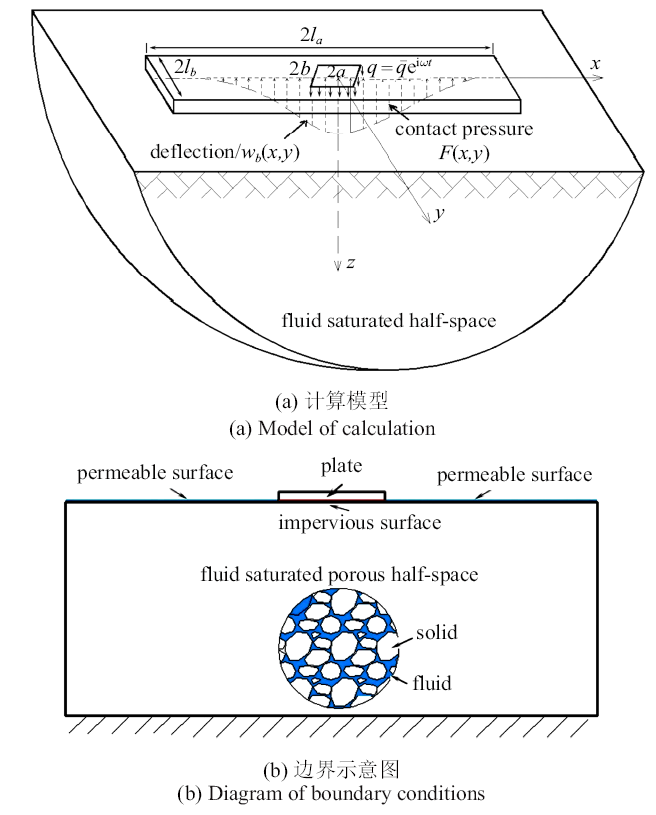
如图1 所示, 长、宽分别为$2l_a$和$2l_b $的矩形弹性板支撑在饱和多孔半空间表面. 板长方向为$x$轴, 板宽方向为$y$轴, $z$轴指向地基. 板中心作用有长为$2a$宽为$2b$的简谐分布载荷$q=\bar{{q}}{\rm e}^{{\rm i}\omega t}$. 图1 (b)表示板-土接触面为不透水界面, 其余地表为透水界面. 当板-地基系统受到简谐载荷$\bar{{q}}{\rm e}^{{\rm i}\omega t}$激励时, 系统中各场量存在如下关系
(1) \begin{eqnarray} \left[ {w_b ,F,u,w,\sigma ,\tau ,p} \right]^{\rm T}=\left[ {\bar{{w}}_b ,\bar{{F}},\bar{{u}},\bar{{w}},\bar{{\sigma }},\bar{{\tau }},\bar{{p}}} \right]^{\rm T}{\rm e}^{{\rm i}\omega t} \end{eqnarray}
图1
图1
模型示意图
Fig. 1
Diagram of calculation model
式中, $w_b $为矩形板挠度, $F$为接触反力, $u$为地基土骨架位移, $w$为孔隙水位移, $\sigma $和$\tau $分别为土骨架正应力和切应力, $p$为孔隙水压力. $\bar{{w}}_b$, $\bar{{F}}$, $\bar{{u}}$, $\bar{{w}}$, $\bar{{\sigma }}$, $\bar{{\tau}}$, $\bar{{p}}$为对应物理量的幅值. ${\rm e}^{{\rm i}\omega t}$为谐和因子, $\omega$为角频率, $t$为时间, i为虚数单位.
1.1 矩形板基本方程求解
根据Kirchhoff理论, 矩形板挠曲方程表示为
(2) \begin{eqnarray} && D\nabla ^4\bar{{w}}_b (x,y)-\bar{{m}}\omega ^2\bar{{w}}_b +\bar{{F}}(x,y) = H(a-\left| x \right|)H(b-\left| y \right|)\bar{{q}} \end{eqnarray}
式中, 已根据式(1)将谐和因子${\rm e}^{{\rm i}\omega t}$约去; $D$为矩形板的挠曲刚度, $\nabla ^4={\partial ^4}/({\partial x^4})+2{\partial ^4}/({\partial x^2\partial y^2})+{\partial ^4}/({\partial y^4})$; $H(\ )$为 Heaviside阶跃函数. 对$x$, $y$坐标引入以下双重Fourier变换
(3) \begin{eqnarray} \left. \begin{array}{l} \tilde{{\tilde{{f}}}}\left( {\xi ,\eta ,z} \right)=\displaystyle\int_{-\infty }^{+\infty } {\displaystyle\int_{-\infty }^{+\infty } {f\left( {x,y,z} \right)} } {\rm e}^{-{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}x{\rm d}y \\ f\left( {x,y,z} \right)=\dfrac{1}{4\pi ^2}\displaystyle\int_{-\infty }^{+\infty } {\displaystyle\int_{-\infty }^{+\infty } {\tilde{{\tilde{{f}}}}\left( {\xi ,\eta ,z} \right)} } {\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta \\ \end{array}\ \ \right\}\ \ \end{eqnarray}
(4) \begin{eqnarray} \tilde{{\tilde{{\bar{{w}}}}}}_b (\xi ,\eta )=\frac{4\bar{{q}}\sin \left( {\xi a} \right)\sin \left( {\eta b} \right)-\xi \eta \tilde{{\tilde{{\bar{{F}}}}}}(\xi ,\eta )}{\xi \eta [D(\xi ^2+\eta ^2)^2-\bar{{m}}\omega ^2]} \end{eqnarray}
式中, $\xi$和$\eta $为Fourier变换参数, $\tilde{{\tilde{{\bar{{w}}}}}}_b (\xi ,\eta )$和$\tilde{{\tilde{{\bar{{F}}}}}}(\xi ,\eta )$ 为对应物理量的双重Fourier变换.
1.2 饱和多孔地基控制方程及求解
考虑孔隙流体压缩性和流体与骨架的相对运动, 并忽略体力作用, Biot饱和多孔介质波动方程写为[19 -23 ]
(5a) $\left( {\lambda +G} \right)\frac{\partial \theta }{\partial x}+G\nabla ^2u_x -\frac{\partial p}{\partial x}=\rho \ddot{{u}}_x +\rho _{\rm f} \ddot{{w}}_x $
(5b) $ \left( {\lambda +G} \right)\frac{\partial \theta }{\partial y}+G\nabla ^2u_y -\frac{\partial p}{\partial y}=\rho \ddot{{u}}_y +\rho _{\rm f} \ddot{{w}}_y $
(5c) $ \left( {\lambda +G} \right)\frac{\partial \theta }{\partial z}+G\nabla ^2u_z -\frac{\partial p}{\partial z}=\rho \ddot{{u}}_z +\rho _{\rm f} \ddot{{w}}_z $
(5d) $ -\frac{\partial p}{\partial x}=\frac{\rho _{\rm f} g}{k_{\rm d} }\dot{{w}}_x +\rho _{\rm f} \ddot{{u}}_x +\frac{\rho _{\rm f} }{n}\ddot{{w}}_x $
(5e) $ -\frac{\partial p}{\partial y}=\frac{\rho _{\rm f} g}{k_{\rm d} }\dot{{w}}_y +\rho _{\rm f} \ddot{{u}}_y +\frac{\rho _{\rm f} }{n}\ddot{{w}}_y $
(5f) $ -\frac{\partial p}{\partial z}=\frac{\rho _{\rm f} g}{k_{\rm d} }\dot{{w}}_z +\rho _{\rm f} \ddot{{u}}_z +\frac{\rho _{\rm f} }{n}\ddot{{w}}_z $
(6a) $\sigma _x =\lambda \left( {\frac{\partial u_y }{\partial y}+\frac{\partial u_z }{\partial z}} \right)+\left( {\lambda +2G} \right)\frac{\partial u_x }{\partial x}-\alpha p $
(6b) $ \sigma _y =\lambda \left( {\frac{\partial u_x }{\partial x}+\frac{\partial u_z }{\partial z}} \right)+\left( {\lambda +2G} \right)\frac{\partial u_y }{\partial y}-\alpha p $
(6c) $ \sigma _z =\lambda \left( {\frac{\partial u_x }{\partial x}+\frac{\partial u_y }{\partial y}} \right)+\left( {\lambda +2G} \right)\frac{\partial u_z }{\partial z}-\alpha p $
(6d) $ \tau _{xy} =G\left( {\frac{\partial u_x }{\partial y}+\frac{\partial u_y }{\partial x}} \right) $
(6e) $ \tau _{xz} =G\left( {\frac{\partial u_x }{\partial z}+\frac{\partial u_z }{\partial x}} \right) $
(6f) $ \tau _{yz} =G\left( {\frac{\partial u_y }{\partial z}+\frac{\partial u_z }{\partial y}} \right)$
(7) \begin{eqnarray} \frac{\partial ^2u_x }{\partial x\partial t}+\frac{\partial ^2u_y }{\partial y\partial t}+\frac{\partial ^2u_z }{\partial z\partial t}=-\left( {\frac{\partial ^2w_x }{\partial x\partial t}+\frac{\partial ^2w_y }{\partial y\partial t}+\frac{\partial ^2w_z }{\partial z\partial t}} \right) \end{eqnarray}
式中, $\theta ={\partial u_x }/({\partial x})+{\partial u_y }/({\partial y})+{\partial u_z }/({\partial z})$为固体骨架的体应变; $\lambda $和$G$为Lamb常数; $\rho =n\rho _{\rm f} +\left({1-n} \right)\rho _{\rm s} $为土体总质量密度, 其中$\rho _{\rm s} $和$\rho _{\rm f} $分别为固体颗粒和孔隙水的质量密度; $n$为孔隙率; $k_{\rm d} $为渗透系数; $\alpha$为表征固体颗粒压缩性的常数, 当考虑颗粒不可压缩时$\alpha =1$.
对式(5a)$\sim\!$式(5c)施以${\partial }({\rm 5a})/({\partial x})+{\partial}({\rm 5b})/({\partial y})+{\partial}({\rm 5c})/{\partial z}$运算, 并考虑式(7), 得到
(8) \begin{eqnarray}\nabla ^2p=\left( {\lambda +2G} \right)\nabla ^2\theta -\left( {\rho -\rho _{\rm f} } \right)\ddot{{\theta }}\end{eqnarray}
对式(5d)$\sim\!$式(5f)施以${\partial}(5d)/({\partial x})+{\partial }(5e)/({\partial y})+{\partial }(5f)/({\partial z})$运算, 得到
(9) \begin{eqnarray}\nabla ^2p=\frac{\rho _{\rm f} g}{k_{\rm d} }\dot{{\theta }}+\left( {\rho _{\rm f} -\frac{\rho _{\rm f} }{n}} \right)\ddot{{\theta }}\end{eqnarray}
(10) \begin{eqnarray}\left( {\lambda +2G} \right)\nabla ^2\bar{{\theta }}+\left[ {\omega ^2\left( {\rho -\frac{\rho _{\rm f} }{n}} \right)-{\rm i}\omega \frac{\rho _{\rm f} g}{k_{\rm d} }}\right]\bar{{\theta }}=0\end{eqnarray}
(11) \begin{eqnarray} \left( {\frac{\partial ^2}{\partial z^2}-r_1^2 } \right)\tilde{{\tilde{{\bar{{\theta }}}}}}=0 \end{eqnarray}
(12) \begin{eqnarray}\tilde{{\tilde{{\bar{{\theta }}}}}}\left( {\xi ,\eta ,z} \right)=A_1 {\rm e}^{-r_1 z}\end{eqnarray}
式中, $r_1 =\sqrt{\xi ^2+\eta ^2-M_0}$, 取$Re\left( {r_1 }\right)>0$,以满足波的辐射条件, $Re$表示取实部; $\varphi ={\rho _{\rm f}\omega ^2}/{n}+{\rm i}\omega{\rho _{\rm f} g}/{k_{\rm d} }$; $M_0 ={\left( {\rho \omega ^2-\varphi } \right)} / {\left( {\lambda +2G} \right)}.$
对式(9)做Fourier变换, 再将式(12)代入, 即可求出孔隙压力的变换域解
(13) \begin{eqnarray}\tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,z} \right)=A_2 {\rm e}^{-r_2 \cdot z}+M_1 A_1 {\rm e}^{-r_1 \cdot z}\end{eqnarray}
式中, $r_2 =\sqrt {\xi ^2+\eta ^2} $, $M_1 =({\rho _{\rm f} \omega ^2-\varphi})/{M_0 }$.
(14a) $\bar{{w}}_x ={\left( {\frac{\partial \bar{{p}}}{\partial x}-\rho _{\rm f} \omega ^2\bar{{u}}_x } \right)} \Bigg/ {\left( {\omega ^2\frac{\rho _{\rm f} }{n}-{\rm i}\omega \frac{\rho _{\rm f} g}{k_{\rm d} }} \right)} $
(14b) $ \bar{{w}}_y ={\left( {\frac{\partial \bar{{p}}}{\partial y}-\rho _{\rm f} \omega ^2\bar{{u}}_y } \right)} \Bigg/ {\left( {\omega ^2\frac{\rho _{\rm f} }{n}-{\rm i}\omega \frac{\rho _{\rm f} g}{k_{\rm d} }} \right)} $
(14c) $ \bar{{w}}_z ={\left( {\frac{\partial \bar{{p}}}{\partial z}-\rho _{\rm f} \omega ^2\bar{{u}}_z } \right)} \Bigg/ {\left( {\omega ^2\frac{\rho _{\rm f} }{n}-{\rm i}\omega \frac{\rho _{\rm f} g}{k_{\rm d} }} \right)}$
将式(14)分别代入式(5a)$\sim\!$式(5c), 消去$w_x$, $w_y $和$w_z $后进行双重Fourier变换, 得到
(15) \begin{eqnarray} \left. {\begin{array}{l} \dfrac{\partial ^2}{\partial z^2}\tilde{{\tilde{{\bar{{u}}}}}}_x -\left( {r_2 ^2-M_4 } \right)\tilde{{\tilde{{\bar{{u}}}}}}_x =-{\rm i}\xi M_2 A_1 {\rm e}^{-r_1 z}-{\rm i}\xi M_3 A_2 {\rm e}^{-r_2 z}\\ \dfrac{\partial ^2}{\partial z^2}\tilde{{\tilde{{\bar{{u}}}}}}_y -\left( {r_2 ^2-M_4 } \right)\tilde{{\tilde{{\bar{{u}}}}}}_y = -{\rm i}\eta M_2 A_1 {\rm e}^{-r_1 z}-{\rm i}\eta M_3 A_2 {\rm e}^{-r_2 z} \\ \dfrac{\partial ^2}{\partial z^2}\tilde{{\tilde{{\bar{{u}}}}}}_z -\left( {r_2 ^2-M_4 } \right)\tilde{{\tilde{{\bar{{u}}}}}}_z = r_1 M_2 A_1 {\rm e}^{-r_1 z}+r_2 M_3 A_2 {\rm e}^{-r_2 z} \\ \end{array}} \right\} \end{eqnarray}
式中, $M_2 =\lambda +G+M_1 M_3 $, $M_3 ={\rho _{\rm f} \omega ^2} / \phi -1$, $M_4 =\rho \omega ^2-{\rho _{\rm f} ^2\omega ^4} / \phi$, $\phi ={\rho _{\rm f} \omega ^2} / n-{\rm i}\omega {\rho _{\rm f} g} / {k_{\rm d}}$.
(16a) $\tilde{{\tilde{{\bar{{u}}}}}}_x =A_3 {\rm e}^{-r_3 z}-\frac{{\rm i}\xi M_3 A_2 }{M_4 }{\rm e}^{-r_2 z}-\frac{{\rm i}\xi M_2 A_1 }{r_1^2 -r_2^2 +M_4 }{\rm e}^{-r_1 z}\qquad $
(16b) $ \tilde{{\tilde{{\bar{{u}}}}}}_y =A_4 {\rm e}^{-r_3 z}-\frac{{\rm i}\eta M_3 A_2 }{M_4 }{\rm e}^{-r_2 z}-\frac{{\rm i}\eta M_2 A_1 }{r_1^2 -r_2^2 +M_4 }{\rm e}^{-r_1 z} $
(16c) $ \begin{array}{l} \tilde{{\tilde{{\bar{{u}}}}}}_z =\dfrac{r_1 M_2 A_1 }{r_1^2 -r_2^2 +M_4 }\cdot {\rm e}^{-r_1 z}+\dfrac{r_2 M_3 A_2 }{M_4 }\cdot {\rm e}^{-r_2 \cdot z}- \qquad \dfrac{1}{r_1 }\left[ {{\rm i}\left( {\xi A_3 +\eta A_4 } \right)+\dfrac{2-M_2 }{2}A_1 } \right]\cdot {\rm e}^{-r_3 \cdot z}- \qquad \dfrac{1}{r_2 }\left[ {{\rm i}\left( {\xi A_3 +\eta A_4 } \right)+\dfrac{2-M_3 }{2}A_2 } \right]\cdot {\rm e}^{-r_3 \cdot z} \\ \end{array} $
式中, $r_3 =\sqrt {r_2^2 -M_4 } $, $A_1 \sim A_4 $为积分常量, 由边界条件确定; 对本构方程(6)做双重Fourier变换, 并将位移解式(16a)$\sim\!$式(16c)代入, 得到变换域的应力解
(17a) $\tilde{{\tilde{{\bar{{\sigma }}}}}}_z =-{\rm i}\lambda \left( {\xi \tilde{{\tilde{{\bar{{u}}}}}}_x +\eta \tilde{{\tilde{{\bar{{u}}}}}}_y } \right)+\left( {\lambda +2G} \right)\frac{\partial \tilde{{\tilde{{\bar{{u}}}}}}_z }{\partial z}-\tilde{{\tilde{{\bar{{p}}}}}} $
(17b) $ \tilde{{\tilde{{\bar{{\tau }}}}}}_{xz} =G\left( {\frac{\partial \tilde{{\tilde{{\bar{{u}}}}}}_x }{\partial z}-{\rm i}\xi \tilde{{\tilde{{\bar{{u}}}}}}_z } \right) $
(17c) $ \tilde{{\tilde{{\bar{{\tau }}}}}}_{yz} =G\left( {\frac{\partial \tilde{{\tilde{{\bar{{u}}}}}}_y }{\partial z}-{\rm i}\eta \tilde{{\tilde{{\bar{{u}}}}}}_z } \right) $
1.3 混合边值问题求解
考虑矩形板与半空间表面光滑接触, 且不会发生脱离; 并考虑板土接触面为不透水边界, 其余表面为透水边界. 将接触面区域$\left( {\left| x \right|\leqslant l_a ,\left| y \right|\leqslant l_b ,z=0} \right)$记为$\varOmega _1 $, 接触面以外区域$\left( {\left| x \right|>l_a ,\left| y \right|>l_b ,z=0} \right)$记为$\varOmega _2 $, 则半空间表面$z$=0处的边界条件写为
(18a) $\left. \begin{array}{l} \tau _{xz}(x,y,0)=\tau _{yz} (x,y,0)=0 \\ \sigma _z (x,y,0)=-F(x,y) \\ u_z (x,y,0)=w_b (x,y) \\ w_z (x,y,0)=0 \\ \end{array}\quad \begin{array}{l} (x,y\in \varOmega _1)\\ \end{array} \right\} $
(18b) $ \left. \begin{array}{l} \sigma _z(x,y,0)=0 \\ p(x,y,0)=0 \\ \end{array}\quad\begin{array}{l} (x,y\in \varOmega _2) \end{array} \right\} $
(19a) $A_1 =\frac{N_{11} }{N_0 }\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)-\frac{N_{12} +N_{13} }{N_0 }\tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) $
(19b) $ A_2 =\frac{N_{21} }{N_0 }\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+\left( {\frac{N_{22} +N_{23} }{N_0 }} \right)\tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) $
(19c) $ A_3 =\xi \Bigg[ \frac{N_{31} }{N_0 }\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+\left( {\frac{N_{31} +N_{32} +N_{33} }{N_0 }} \right)\cdot \tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) \Bigg] $
(19d) $ A_4 =\eta \Bigg[ \frac{N_{31} }{N_0 }\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+\left( {\frac{N_{31} +N_{32} +N_{33} }{N_0 }} \right)\cdot \tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) \Bigg] $
其中, $N_0$及$N_{11}$$\sim$$N_{33}$见附录. 将式(19)代入式(4)、式(14)、式(16)中并进行Fourier变换, 得到
(20a) $\tilde{{\tilde{{\bar{{w}}}}}}_b \left( {\xi ,\eta } \right)=h\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+\varDelta $
(20b) $ \tilde{{\tilde{{\bar{{u}}}}}}_z \left( {\xi ,\eta ,0} \right)=E_1 \tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+H_1 \tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) $
(20c) $ \tilde{{\tilde{{\bar{{w}}}}}}_z \left( {\xi ,\eta ,0} \right)=E_2 \tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+H_2 \tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) $
式中, $h$, $\varDelta$, $E_1$, $E_2$, $H_1$, $H_2$均为$\xi$和$\eta$的已函数, 形式见附录.
对式(20)做Fourier逆变换, 而后代入式(18a)和式(18b), 整理出两对二维对偶积分方程
(21a) $\left.\begin{array}{l} \int_{-\infty }^{+\infty } \int_{-\infty }^{+\infty } \left[ \left( E_1 +h \right)\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)+H_1 \tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) \right]{\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta =\int_{-\infty }^{+\infty } \int_{-\infty }^{+\infty }\varDelta {\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta \\ \int_{-\infty }^{+\infty} \int_{-\infty }^{+\infty } \left[ E_2 \left(\xi ,\eta \right)\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( \xi ,\eta,0 \right)+ H_2 \left( {\xi ,\eta } \right)\tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right) \right]{\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta =0\\ \end{array}\quad \begin{array}{l}(x,y\in \varOmega _1) \end{array} \right\}\\ $
(21b) $ \left. \begin{array}{l} \int_{-\infty }^{+\infty } {\int_{-\infty }^{+\infty } {\tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right){\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta =0} } \\ \int_{-\infty }^{+\infty } {\int_{-\infty }^{+\infty } {\tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right){\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta =0} } \\ \end{array}\quad \begin{array}{l}(x,y\in \varOmega _2) \end{array}\right\} $
为求解对偶积分方程(21), 根据Hilbert正交化定理[38 ] , 利用Jacobi正交多项式将积分核$\bar{{\sigma }}_z \left( {x,y,0}\right)$和$\bar{{p}}\left( {x,y,0} \right)$展为如下级数形式[39 ]
(22a) $\left. \begin{array}{l} \bar{{\sigma }}_z \left( {x,y,0} \right)=\sum\limits_{m=0}^\infty {\sum\limits_{n=0}^\infty {c_{mn} \left( {1-\frac{x^2}{l_a^2 }} \right)^{{1}/{2}}P_{2m+1}^{\left( {{1}/{2},{1}/{2}} \right)} \left( {\frac{x}{l_a }} \right)} } \cdot \left( {1-\frac{y^2}{l_b^2 }} \right)^{{1}/{2}}P_{2n}^{\left( {{1}/{2},{1}/{2}} \right)} \left( {\frac{y}{l_b }} \right)\\ \bar{{p}}\left( {x,y,0} \right)=\sum\limits_{m=0}^\infty {\sum\limits_{n=0}^\infty {d_{mn} \left( {1-\frac{x^2}{l_a^2 }} \right)^{{1}/{2}}P_{2m}^{\left( {{1}/{2},{1}/{2}} \right)} \left( {\frac{x}{l_a }} \right)} } \cdot \left( {1-\frac{y^2}{l_b^2 }} \right)^{{1}/{2}}P_{2n+1}^{\left( {{1}/{2},{1}/{2}} \right)} \left( {\frac{y}{l_b }} \right) \\ \end{array}\quad \begin{array}{l}(x,y\in \varOmega _1) \end{array} \right\} $
(22b) $ \left.\begin{array}{l} \bar{{\sigma }}_z \left( {x,y,0} \right)=0 \\ \bar{{p}}\left( {x,y,0} \right)=0 \\ \end{array}\quad \begin{array}{l}( x,y\in \varOmega _2) \end{array}\right\} $
式中, $c_{mn}$和$d_{mn}$为未知系数, $P_{2m+1}^{\left({{1}/{2},{1}/{2}} \right)} $为Jacobi多项式.
对式(22)进行双重Fourier变换得到[40 ]
(23a) $\left.\begin{array}{l} \tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {\xi ,\eta ,0} \right)=\sum\limits_{n=0}^\infty {\sum\limits_{m=0}^\infty {c_{mn} G_{mn}^{\left( 1 \right)} \frac{1}{\xi \eta }{\rm J}_{2m+2} \left( {\xi l_a } \right){\rm J}_{2n+1} \left( {\eta l_b } \right)} } \\ \tilde{{\tilde{{\bar{{p}}}}}}\left( {\xi ,\eta ,0} \right)=\sum\limits_{n=0}^\infty {\sum\limits_{m=0}^\infty {d_{mn} G_{mn}^{\left( 2 \right)} \frac{1}{\xi \eta }{\rm J}_{2m+1} \left( {\xi l_a } \right){\rm J}_{2n+2} \left( {\eta l_b } \right)} } \\ \end{array} \begin{array}{l} \left( {x,y\in \varOmega _1 } \right) \end{array}\right\} $
(23b) $ \left. \begin{array}{l} \tilde{{\tilde{{\bar{{\sigma }}}}}}_z \left( {x,y,0} \right)=0 \\ \tilde{{\tilde{{\bar{{p}}}}}}\left( {x,y,0} \right)=0 \\ \end{array}\quad \begin{array}{l} \left( {x,y\in \varOmega _2 } \right) \end{array} \right\} $
$\begin{eqnarray*} &&G_{mn}^{\left( 1 \right)} =\pi \left( {-1} \right)^{\left( {m+n} \right)}\frac{\Gamma \left( {2m+2+{1}/{2}} \right)}{\left( {2m+1} \right)!}\frac{\Gamma \left( {2n+1+{1}/{2}} \right)}{\left( {2n} \right)!} \\&&G_{mn}^{\left( 2 \right)} =\pi \left( {-1} \right)^{\left( {m+n} \right)}\frac{\Gamma \left( {2m+2+{1}/{2}} \right)}{\left( {2m} \right)!}\frac{\Gamma \left( {2n+1+{1}/{2}} \right)}{\left( {2n+1} \right)!} \end{eqnarray*}$
其中, $\Gamma \left( \cdot \right)$, ${\rm J}_n \left( \cdot\right)$分别为Gamma函数和Bessel函数. 将式(23b)代入式(21), 发现自动满足, 将式(23b)代入式(21)后, 则得到
(24) $\begin{eqnarray} \left. \begin{array}{l} \sum\limits_{n=0}^\infty {\sum\limits_{m=0}^\infty {c_{mn} } } K_1 \left( {x,y} \right)+\sum\limits_{n=0}^\infty {\sum\limits_{m=0}^\infty {d_{mn} } } Q_1 \left( {x,y} \right)=\hat{{\varDelta }}\left( {x,y} \right) \\ \sum\limits_{n=0}^\infty {\sum\limits_{m=0}^\infty {c_{mn} } } K_2 \left( {x,y} \right)+\sum\limits_{n=0}^\infty {\sum\limits_{m=0}^\infty {d_{mn} } } Q_2 \left( {x,y} \right)=0 \\ \end{array} \right\}\quad\ \end{eqnarray}$
式中, $\hat{{\varDelta }}\left( {x,y} \right)$, $K_1 \left( {x,y}\right)$, $K_2 \left( {x,y} \right)$, $Q_1 \left( {x,y} \right)$, $Q_2 \left( {x,y} \right)$都是以Fourier逆变换的形式给出(见附录), 其无穷积分可通过快速Fourier逆变换得到. 利用Schmidt法[41 -42 ] 可求解出式(24)中的系数$c_{mn}$和$d_{mn}$, 再将$c_{mn}$和$d_{mn}$依次回代到式(22)和式(18a)可得出接触反力
$\begin{eqnarray*} &&\bar{{F}}=\sum\limits_{m=0}^\infty {\sum\limits_{n=0}^\infty {c_{mn} \left( {1-\frac{x^2}{l_a^2 }} \right)^{{1}/{2}}P_{2m+1}^{\left( {{1}/{2},{1}/{2}} \right)} \left( {\frac{x}{l_a }} \right)} } \left( {1-\frac{y^2}{l_b^2 }} \right)^{{1}/{2}}\cdot P_{2n}^{\left( {{1}/{2},{1}/{2}} \right)} \left( {\frac{y}{l_b }} \right) \end{eqnarray*}$
然后利用式(4)、式(16)、式(17)可分别得到矩形板和地基的位移和应力解.
2 收敛性和正确性验证
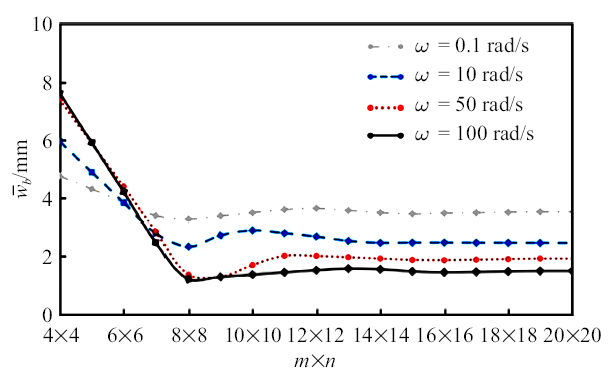
首先进行收敛性分析, 以确定式(24)的级数项数$m$和$n$. 为了便于比较, 矩形板和地基的计算参数按文献[20 ] 取值. 取矩形板边长$2l_{a}=2l_{b}=4$ m, 板厚为0.2 m; 板的泊松比为 0.167, 弹性模量$E_{b} = 34300$ MPa; 地基泊松比为 0.4, 弹性模量$Es=343$ MPa; 板中心作用均布载荷$q=0.98$ MPa. 本文考虑的地基为两相饱和多孔地基, 所以还需补充土体孔隙率$n=0.6$, 固体骨架密度$\rho_{\rm s}=2700$ kg/m$^{3}$、孔隙水密度$\rho_{\rm f}=1000$ kg/m$^{3}$, 渗透系数$k_{\rm d}=10^{-5}$ m/s. 通过MATLAB编程, 对本文推导结果进行数值计算. 图2 给出了矩形板中心点挠度幅值与网格数目$m\times n$的关系曲线, 图中反映出本方法收敛速度很快, 只需取$m\times n =16\times 16$个网格点足以得到收敛结果.
图2
图2
结果收敛性试算
Fig. 2
Verification of convergence
若取孔隙水密度$\rho _{\rm f}=0$, 代表地基中无水, 则本文的地基模型退化为单一弹性地基, 可与文献[20 ] 的结果进行对应比较. 表1 列出了本文退化解与文献解的对比, 从表1 的对比结果可知, 本文退化解与文献[20 ] 很好吻合, 由此验证了本文推导方法和数值计算程序的正确性.
3 数值结果和讨论
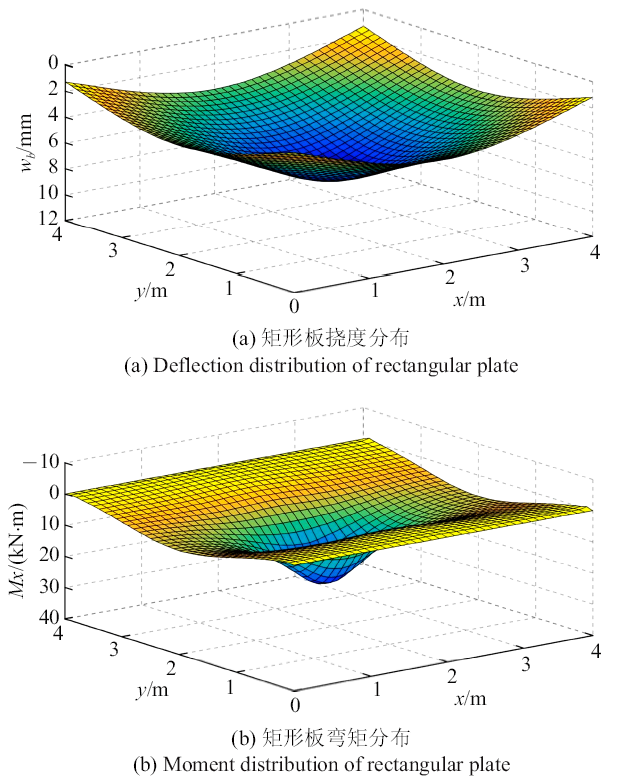
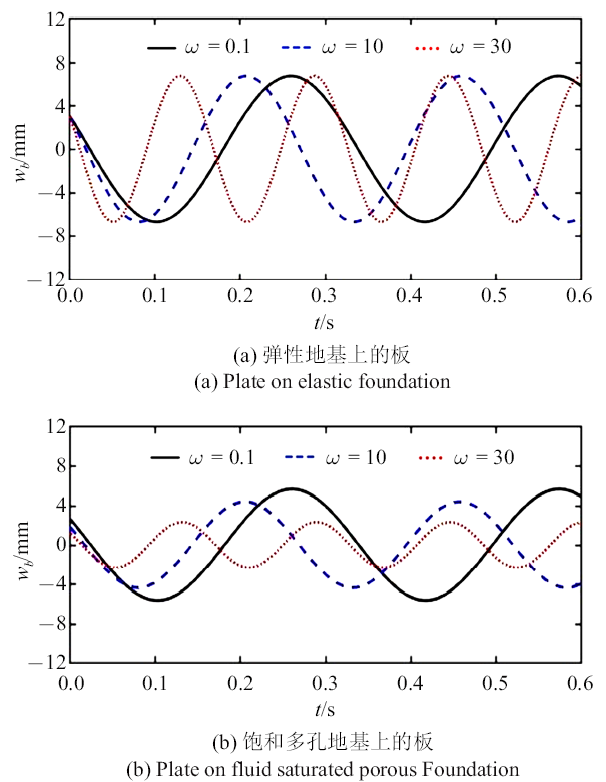
利用前文确定的计算参数和程序, 对本文模型进行数值计算图3 给出了部分计算结果. 图4 为不同载荷激励频率下板中心位置的挠度时程曲线, 为了进行对比分析, 在图4 (a)中绘出了对应于弹性地基的计算结果. 对比图4 (a)和图4 (b)可知, 对于弹性地基, 载荷激励频率的变化会造成板振动频率的变化, 但不会改变其振动幅值. 而对于两相饱和多孔地基, 激励频率的变化不仅引起板振动频率的变化, 其振动幅值也发生大的变化. 出现这一现象的机理可理解为, 在载荷作用下, 饱和多孔地基中固体骨架发生压缩变形, 孔隙受到挤压, 孔隙压力进而升高, 而孔隙压力会阻碍固体骨架进一步变形. 若孔隙中的水能及时渗透, 则孔隙压力将得以消散, 这种阻碍效应将不存在. 试想一下, 当振动频率较高时, 孔隙水来不及渗透, 则孔隙压力持续升高, 这种阻碍效应将增大, 地基将难以发生变形, 地基刚性从而增大, 板的挠曲幅值将随之减小.
图3
图3
数值计算结果($\omega =10$ rad/s, $t=0$ s)
Fig. 3
Results of numerical computation with ($\omega =10$ rad/s, $t=0$ s)
图4
图4
矩形板中心点挠度时程曲线
Fig. 4
Variation of deflection with time at the center of rectangular plate
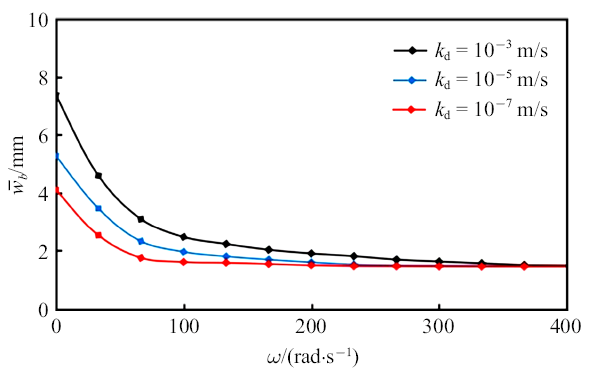
为进一步考察饱和多孔地基上矩形板的振动挠曲与激励频率的关系, 图5 给出激励频率与挠度幅值的关系曲线. 分析图5 可知, 随着激励频率增大, 板的挠度幅值随之减小. 当载荷激励频率达到极限时, 板的挠度幅值收敛于一固定值. 图中还反映出, 挠度幅值的收敛速度与地基渗透系数有密切关系. 为考察挠度幅值的最终收敛值, 尝试取地基渗透系数$k_{\rm d} \to 0$. 计算发现, 激励频率达到极限时, 板的挠度幅值与地基渗透系数趋于0时的结果近似相等(即$w_{\rm b}|_{\omega \to \infty }\approx w_{\rm b}|_{kd\to 0}$). 这说明, 当载荷激励频率达到极限时, 地基土体相当于一个固流耦合的封闭系统(孔隙水不发生渗透).
图5
图5
挠度幅值与激励频率关系图
Fig. 5
Deflection amplitude relative to frequency
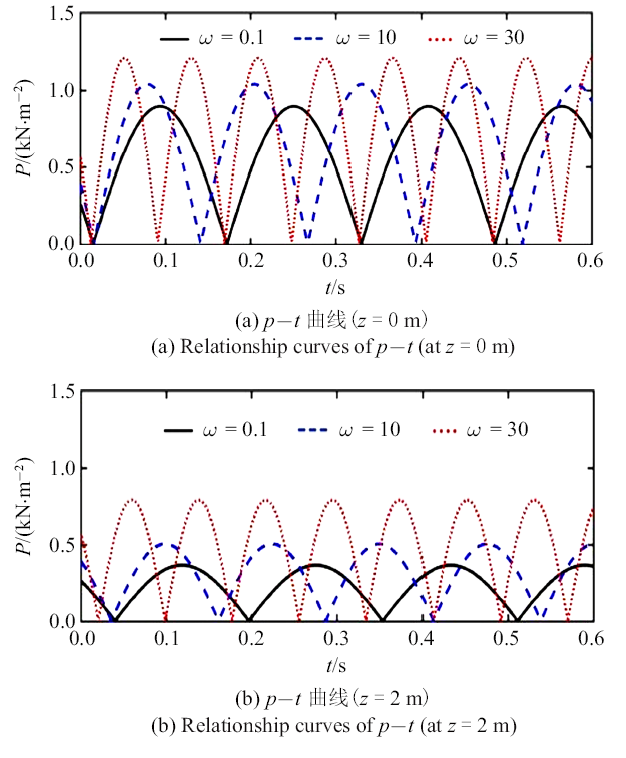
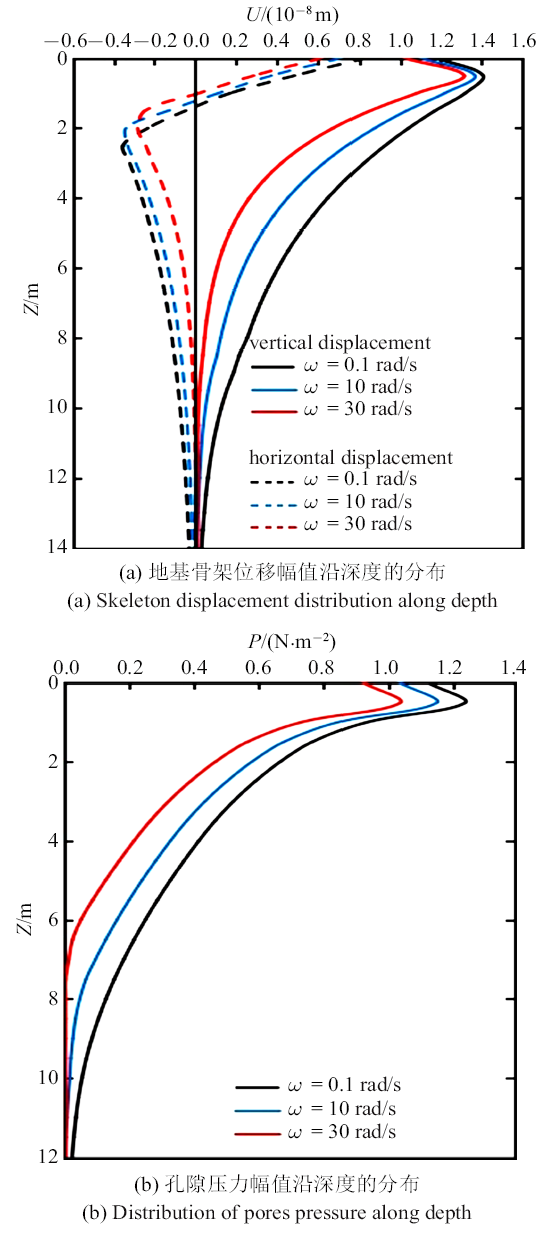
图6 (a)和图6 (b)分别为矩形板中心点下0 m和2 m处地基土中孔压随时间的变化曲线. 图7 (a)和图7 (b)为矩形板中心点下土体中固体骨架位移幅值$U$和孔隙压力幅值$P$沿深度的分布曲线. 图中可以看出, 随着载荷激励频率增大, 地基中固体骨架的水平方向和竖直方向位移幅值都随之减小, 位移响应深度也随即减小. 但孔隙压力幅值却随激励频率的增大而增大, 这一结果也印证了前文的机理解释.
图6
图6
板中心点下地基中空隙压力时程曲线
Fig. 6
Variation of pores pressure with time below the center point of rectangular plate
图7
图7
地基中变形和孔隙压力
Fig. 7
Displacement and pore pressure of foundation
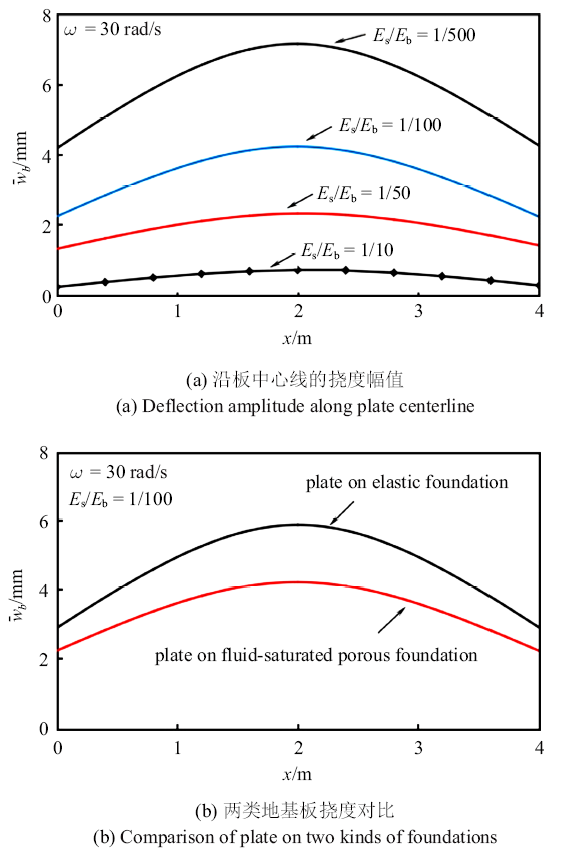
图8 为激励频率$\omega =30$ rad/s时, 土-板模量比($E_{\rm s}/E_{\rm b})$与板的挠度幅值的关系. 图中可看出, $E_{\rm s}/E_{\rm b}$取值越小, 地基土相对于板越松软, 板的变形越大. 图7 (b)比较了相同模量比取值下弹性地基与饱和多孔地基上的板挠曲变形, 进一步说明了饱和多孔地基中孔隙压力对地基刚性的贡献.
图8
图8
模量比($E_{\rm s}/E_{\rm b})$对地基板挠度的影响
Fig. 8
Influence of modulus ratio on plate deflection
4 结论
本文建立了具有混合透水边界的板土接触模型, 利用Hilbert定理和Schmidt法解决了非轴对称混合边值问题的求解, 从而得出饱和多孔地基上矩形板振动弯曲的解析解. 通过数值计算, 发现饱和多孔地基中由于孔隙压力的作用, 地基刚性将随激励频率的增大而提高. 而地基板的振动变形将随载荷激励频率的增大而减小. 本文提出的非轴对称混合边值问题的解析法, 具有一般性, 可广泛应用于复杂接触问题和多场耦合问题的求解.
附录
$ N_0 =\frac{r_3 G^2}{2}\left( {\lambda M_4 -2r_3^2 G} \right)\left[ {\frac{2-M_2 }{r_1 }-\frac{\left( {2-M_3 } \right)M_1 }{r_2 }} \right]+ N_{11} \left[ {\frac{2r_2^2 GM_1 M_3 }{M_4 }+\frac{\left( {\lambda M_0 -2r_1^2 G} \right)M_2 }{M_4 -M_0 }} \right] $
$N_{11} =-r_3 G^2\left[ {r_3 +r_2^2 \left( {\frac{1}{r_1 }+\frac{1}{r_2 }} \right)} \right] $
$N_{12} =N_{11} \left[ {1-\frac{r_3 \left( {\lambda +2G} \right)\left( {2-M_3 } \right)}{2r_2 }+\frac{2r_2^2 GM_3 }{M_4 }} \right] $
$N_{13} =-\frac{r_2 r_3 G^2\left( {2-M_3 } \right)}{2}\left[ {\lambda +r_3 \left( {\lambda +2G} \right)\left( {\frac{1}{r_1 }+\frac{1}{r_2 }} \right)} \right] $
$N_{21} =-M_1 \cdot N_{11} $
$N_{22} =N_{11} \left[ {\frac{\left( {\lambda M_0 -2r_1^2 G} \right)M_2 }{M_4 -M_0 }+\frac{r_3 \left( {\lambda +2G} \right)\left( {2-M_2 } \right)}{2r_1 }-M_1 } \right] $
$ N_{23} =\frac{r_2^2 r_3 G^2\left( {2-M_2 } \right)}{2r_1 }\left[ {\lambda +r_3 \left( {\lambda +2G} \right)\left( {\frac{1}{r_1 }+\frac{1}{r_2 }} \right)} \right] $
$N_{31} =\frac{{\rm i}r_3 G^2}{2}\left[ {\frac{\left( {2-M_3 } \right)M_1 }{r_2 }-\frac{2-M_2 }{r_1 }} \right] $
$N_{32} =\frac{ir_3 G^2\left( {2-M_2 } \right)}{2r_1 }\left[ {\frac{{\rm i}r_3 \left( {\lambda +2G} \right)\left( {2-M_3 } \right)}{2r_2 }-\frac{2r_2^2 GM_3 }{M_4 }} \right] $
$ N_{33} =-\frac{{\rm i}r_3 G^2\left( {2-M_3 } \right)}{2r_2 }\left[ {\frac{\left( {\lambda M_0 -2r_1^2 G} \right)M_2 }{M_4 -M_0 }+\frac{r_3 \left( {\lambda +2G} \right)\left( {2-M_2 } \right)}{2r_1 }} \right] $
$h\left( {\xi ,\eta } \right)=1 / {(Dr_2 ^4-\bar{{m}}\omega ^2)} $
$\varDelta \left( {\xi ,\eta } \right)=\frac{4q\sin \left( {\xi a} \right)\sin \left( {\eta b} \right)}{\xi \eta [Dr_2 ^4-\bar{{m}}\omega ^2]} $
$E_1 \left( {\xi ,\eta } \right)=\frac{N_{11} }{N_0 }\left( {\frac{r_1 M_2 }{M_4 -M_0 }-\frac{2-M_2 }{2r_1 }} \right)+\frac{N_{21} }{N_0 }\left( {\frac{r_2 M_3 }{M_4 }-\frac{2-M_3 }{2r_2 }} \right)- \frac{{\rm i}r_2 N_{31} }{N_0 }\left( {\frac{r_2 }{r_1 }+1} \right) $
$ H_1 \left( {\xi ,\eta } \right)=\frac{N_{22} +N_{23} }{N_0 }\left( {\frac{r_2 M_3 }{M_4 }-\frac{2-M_3 }{2r_2 }} \right)- \frac{{\rm i}r_2 \left( {N_{31} +N_{32} +N_{33} } \right)}{N_0 }\left( {\frac{r_2 }{r_1 }+1} \right) + \frac{N_{12} +N_{13} }{N_0 }\left( {\frac{r_1 M_2 }{M_4 -M_0 }-\frac{2-M_2 }{2r_1 }} \right) $
$ E_2 \left( {\xi ,\eta } \right)=-\frac{1}{\phi }\left[ {\frac{1}{N_0 }\left( {r_1 M_1 N_{11} +r_2 N_{21} } \right)+\rho _{\rm f} \omega ^2E_1 } \right] $
$ H_2 \left( {\xi ,\eta } \right)=-\frac{1}{\phi }\left[ {\frac{r_1 M_1 }{N_0 }\left( {N_{12} +N_{13} } \right)+\frac{r_2 }{N_0 }\left( {N_{22} +N_{23} } \right)} \right]-\frac{\rho _{\rm f} \omega ^2H_1 }{\phi } $
$\hat{{\varDelta }}\left( {x,y} \right)=\int_0^{+\infty } \int_0^{+\infty } \varDelta{\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta $
$K_1 \left( {x,y} \right)=\int_0^{+\infty } {\int_0^{+\infty } {\frac{1}{\xi \eta }\left( {E_1 +h} \right)} } G_{mn}^{\left( 1 \right)} {\rm J}_{2m+2} \left( {\xi l_a } \right)\cdot {\rm J}_{2n+1} \left( {\eta l_b } \right){\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta $
$K_2 \left( {x,y} \right)=\int_0^{+\infty } {\int_0^{+\infty } {\frac{1}{\xi \eta }E_2 } } G_{mn}^{\left( 1 \right)} {\rm J}_{2m+2} \left( {\xi l_a } \right){\rm J}_{2n+1} \left( {\eta l_b } \right){\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta $
$Q_1 \left( {x,y} \right)=\int_0^{+\infty } {\int_0^{+\infty } {\frac{1}{\xi \eta }H_1 } } G_{mn}^{\left( 2 \right)} {\rm J}_{2m+1} \left( {\xi l_a } \right){\rm J}_{2n+2} \left( {\eta l_b } \right){\rm e}^{{\rm i}\left( {\xi x+\eta y} \right)}{\rm d}\xi {\rm d}\eta $
$Q_2 \left( {x,y} \right)=\int_0^{+\infty } {\int_0^{+\infty } {\frac{1}{\xi \eta }H_2 } } G_{mn}^{\left( 2 \right)} {\rm J}_{2m+1} \left( {\xi l_a } \right){\rm J}_{2n+2} \left( {\eta l_b } \right)H_1 {\rm d}\xi {\rm d}\eta$
参考文献
View Option
[1]
陈叔陶 . 弹性地基上的自由边矩形板
力学学报 , 1960 ,4 (1 ):23 -35
URL
[本文引用: 1]
本文利用黎茲的变分原理,提供了弹性地基上自由边矩形板的計算方法。文中将变分方程写成簡单的形式,将11×11个点的位移函数及其二阶导数列成表格,读者只须将板的尺寸a,b、刚度D、荷载P(x/a,y/b)、地基的弹性模量k代入,經过簡单的計算即可求得板各处的位移及挠矩。
( Chen Shutao . Rectangular plate with free edge on elastic foundation
Chinese Journal of Theoretical and Applied Mechanics 1960 ,4 (1 ):23 -35 (in Chinese))
URL
[本文引用: 1]
本文利用黎茲的变分原理,提供了弹性地基上自由边矩形板的計算方法。文中将变分方程写成簡单的形式,将11×11个点的位移函数及其二阶导数列成表格,读者只须将板的尺寸a,b、刚度D、荷载P(x/a,y/b)、地基的弹性模量k代入,經过簡单的計算即可求得板各处的位移及挠矩。
[2]
滕兆春 , 衡亚洲 , 崔盼 等 . 变刚度Winkler地基上受压非均质矩形板的自由振动与屈曲特性
振动与冲击 , 2019 ,38 (3 ):258 -266
( Teng Zhaochun Heng Yazhou Cui Pan , et al . Free vibration and buckling characteristics of compressed non-homogeneous rectangular plates on Winkler foundation with variable stiffness
Journal of Vibration and Shock 2019 ,38 (3 ):258 -266 (in Chinese))
[3]
卢正 , 姚海林 , 吴莎 等 . 黏弹性地基板在矩形变速载荷作用下的振动分析
岩土力学 , 2010 ,31 (11 ):3613 -3619
( Lu Zheng Yao Hailin Wu Sha , et al . Vibration analysis of a plate on viscoelastic foundation under moving rectangular loads with variable speeds
Rock and Soil Mechanics 2010 ,31 (11 ):3613 -3619 (in Chinese))
[4]
Huang XL Dong L Wei GZ . Nonlinear free and forced vibrations of porous sigmoid functionally graded plates on nonlinear elastic foundations
Composite Structures 2019 : 1 -11
[5]
Yue F Wu ZY Yang HF . Iterative technique for circular thin plates on Gibson elastic foundation using modified Vlasov model
Theoretical and Applied Mechanics Letters 2019 : 312 -319
[6]
Fan JH Rong DL Xu CH . Exact solutions for forced vibration of completely free orthotropic rectangular nanoplates resting on viscoelastic foundation
European Journal of Mechanics 2019 : 22 -33
[本文引用: 1]
[7]
艾智勇 , 慕金晶 . 竖向简谐载荷下二维层状饱和地基的解析层元解
岩土力学 , 2018 ,39 (7 ):2632 -2639
[本文引用: 1]
( Ai Zhiyong Mu Jinjing . Analytical layer element solution for two-dimensional multilayered saturated subsoils under a vertical time-harmonic load
Rock and Soil Mechanics 2018 ,39 (7 ):2632 -2639 (in Chinese))
[本文引用: 1]
[8]
王立安 , 赵建昌 , 余云燕 . 瑞利波在非均匀饱和地基中的传播特性
岩土力学 , 2020 ,41 (6 ):32 -41
( Wang Li'an Zhao Jianchang Yu Yunyan . Propagation characteristics of Rayleigh wave in non-homogeneous saturated foundation
Rock and Soil Mechanics 2020 ,41 (6 ):32 -41 (in Chinese))
[9]
Ba ZN Wu MT Liang JW . 3D dynamic responses of a multi-layered transversely isotropic saturated half-space under concentrated forces and pore pressure
Applied Mathematical Modelling 2019 : 1 -42
[10]
Liang JW Wu MT Ba ZN . Three-dimensional dynamic Green's functions for transversely isotropic saturated half-space subjected to buried loads
Engineering Analysis with Boundary Elements 2019 : 301 -320
[本文引用: 1]
[11]
王元汉 , 邱先敏 . 弹性地基板的等参有限元法计算
岩土工程学报 , 1998 ,20 (4 ):7 -11
[本文引用: 1]
( Wang Yuanhan Qiu Xianmin . Isoparametric finite element calculation of elastic foundation plate
Chinese Journal of Geotechnical Engineering 1998 ,20 (4 ):7 -11 (in Chinese))
[本文引用: 1]
[12]
刘晶波 , 谭辉 , 宝鑫 等 . 土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
力学学报 , 2018 ,50 (1 ):32 -44
URL
( Liu Jinbo Tan Hui Bo Xin , et al . The seismic wave input method for soil-structure dynamic interaction analysis based on artificial boundary substructure
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (1 ):32 -44 (in Chinese))
URL
[13]
Lombaert G Degrande G Louteau D . Numerical modelling of free field traffic-induced vibrations
Soil Dynamic and Earthquake Engineering 2000 ,19 (7 ):473 -488
[14]
Yang YB Huang HH Chang DW . Train-induced wave propagation in layered soils using finite/infinite element simulation
Soil Dynamics and Earthquake Engineering 2003 ,23 (4 ) : 263 -278
DOI
URL
[本文引用: 1]
[15]
何涛 . 基于 ALE 有限元法的流固耦合强耦合数值模拟
力学学报 , 2018 ,50 (2 ):395 -404
[本文引用: 1]
( He Tao . A partitioned strong coupling algorithm for fluid-structure interaction using arbitrary lagrangian-eulerian finite element formulation
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):395 -404 (in Chinese))
[本文引用: 1]
[16]
陈少林 , 柯小飞 , 张洪翔 . 海洋地震工程流固耦合问题统一计算框架
力学学报 , 2019 ,51 (2 ):594 -606
URL
[本文引用: 1]
( Chen Shaolin Ke Xiaofei Zhang Hongxiang . A unified calculation framework for fluid structure coupling problems in marine seismic engineering
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (2 ):594 -606 (in Chinese))
URL
[本文引用: 1]
[17]
陈少林 , 程书林 , 柯小飞 . 海洋地震工程流固耦合问题统一计算框架-不规则界面情形
力学学报 , 2019 ,51 (5 ):1517 -1529
[本文引用: 1]
( Chen Shaolin Cheng Shulin Ke Xiaofei . A unified calculation framework for fluid structure coupling problems in marine seismic engineering: Irregular interface case
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (5 ):1517 -1529 (in Chinese))
[本文引用: 1]
[18]
康建宏 , 谭文长 . 多孔介质内黏弹性流体的热对流稳定性研究
力学学报 , 2018 ,50 (6 ):1436 -1457
[本文引用: 1]
( Kang Jianhong Tan Wenchang . Thermal instability of viscoelastic fluids in porous media
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (6 ):1436 -1457 (in Chinese))
[本文引用: 1]
[19]
Biot MA . Theory of propagation of elastic waves in a fluid-saturated porous solid II. Higher frequency range
Journal of the Acoustical Society of America 1956 ,28 (2 ):179 -191
DOI
URL
[本文引用: 2]
[20]
Biot MA . Mechanics of deformation and acoustic propagation in porous media
Journal of Applied Physics 1962 ,33 (4 ):1482 -1498
DOI
URL
[本文引用: 5]
[21]
Zhang ZG Huang M Zhang CP , et al . Analytical prediction of tunneling-induced ground movements and liner deformation in saturated soils considering influences of shield air pressure
Applied Mathematical Modelling 2020 : 749 -772
[本文引用: 1]
[22]
陈少林 , 赵宇昕 . 一种三维饱和土-基础-结构动力相互作用分析方法
力学学报 , 2016 ,48 (6 ):1362 -1372
DOI
URL
[本文引用: 1]
Analysis of soil-structure dynamic interaction subjected to seismic wave is a key problem in earthquake engineering. In general, the soil stratum consists of two-phase saturated porous zones and single-phase viscoelastic zones due to ground water. In most cases of soil-structure dynamic interaction analysis, the soil has been assumed to be a singlephase viscoelastic medium for simplicity and little attention has been paid to the saturated porous soil case, even less to case of the viscoelastic soil layered on saturated soil. In this study, an effcient method for three-dimensional saturated soil-foundation-structure dynamic interaction analysis is proposed. The unbounded saturated soil is modelled by lumpedmass explicit finite element method and transmitting boundary condition the structure is analysed through implicit finite element method, and response of the rigid foundation is calculated through explicit time integration scheme. The different time steps can be chosen for the explicit and implicit integration scheme, which can greatly improve the effciency. In addition, based on the fact that single-phase soil is a special case of two-phase saturated soil, the dynamic analysis of single-phase soil can be unified into the analysis of saturated soil by setting the bulk modulus of pore fluid and porosity to be zero. Thus, the soil-structure interaction analysis for the viscoelastic soil layered on saturated soil case is realized, which can approximate the ground water table in practice. The effects of ground water on the response of foundation and structure are examined through numerical examples of soil-structure interaction analysis for saturated soil, single-phase viscoelastic soil and the viscoelastic soil layered on saturated soil, and the results show that the ground water influences the structure and foundation responses greatly.
( Chen Shaolin Zhao Yuxin . A method for three-dimensional saturated soil-foundation-structure dynamic interaction analysis
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (6 ):1362 -1372 (in Chinese))
DOI
URL
[本文引用: 1]
Analysis of soil-structure dynamic interaction subjected to seismic wave is a key problem in earthquake engineering. In general, the soil stratum consists of two-phase saturated porous zones and single-phase viscoelastic zones due to ground water. In most cases of soil-structure dynamic interaction analysis, the soil has been assumed to be a singlephase viscoelastic medium for simplicity and little attention has been paid to the saturated porous soil case, even less to case of the viscoelastic soil layered on saturated soil. In this study, an effcient method for three-dimensional saturated soil-foundation-structure dynamic interaction analysis is proposed. The unbounded saturated soil is modelled by lumpedmass explicit finite element method and transmitting boundary condition the structure is analysed through implicit finite element method, and response of the rigid foundation is calculated through explicit time integration scheme. The different time steps can be chosen for the explicit and implicit integration scheme, which can greatly improve the effciency. In addition, based on the fact that single-phase soil is a special case of two-phase saturated soil, the dynamic analysis of single-phase soil can be unified into the analysis of saturated soil by setting the bulk modulus of pore fluid and porosity to be zero. Thus, the soil-structure interaction analysis for the viscoelastic soil layered on saturated soil case is realized, which can approximate the ground water table in practice. The effects of ground water on the response of foundation and structure are examined through numerical examples of soil-structure interaction analysis for saturated soil, single-phase viscoelastic soil and the viscoelastic soil layered on saturated soil, and the results show that the ground water influences the structure and foundation responses greatly.
[23]
陈少林 , 郭琪超 , 周国良 . 核电结构土-结相互作用分析分区混合计算方法
力学学报 , 2020 ,52 (1 ):258 -282
[本文引用: 2]
( Chen Shaolin Guo Qichao Zhou Guoliang . Partitioned hybrid method for soil-structure interaction analysis of nuclear power structure
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):258 -282 (in Chinese))
[本文引用: 2]
[24]
Slvadurai APS . Elastic Analysis of a Soil Structure Interaction
New Jersey: Preenice-Hall , 1978
[本文引用: 1]
[25]
王春玲 , 黄义 . 弹性半空间地基上四边自由矩形板的弯曲解析解
岩土工程学报 , 2005 ,27 (12 ):1402 -1408
URL
[本文引用: 1]
The method of double Fourier transform was introduced for the analysis of an elastic half space loaded with vertical force,and an integral representation for displacements of an elastic half space was presented.The analytic solution of an elastic rectangular plate on an elastic half space was also given by combining the analytic solution of an elastic rectangular plate with four free edges.Some examples were analyzed and the results were compared with those from the literature which used other methods such as finite element method.The agreement was found to be satisfactory which proved the validity of the new method in solving the problem of a rectangular plate on an elastic half space with four free edges.This new method would be feasible in practical applications.
( Wang Chunling Huang Yi . Analytic solution of rectangular plates loaded with vertical force on an elastic half space
Chinese Journal of Geotechnical Engineering 2005 ,27 (12 ):1402 -1408 (in Chinese))
URL
[本文引用: 1]
The method of double Fourier transform was introduced for the analysis of an elastic half space loaded with vertical force,and an integral representation for displacements of an elastic half space was presented.The analytic solution of an elastic rectangular plate on an elastic half space was also given by combining the analytic solution of an elastic rectangular plate with four free edges.Some examples were analyzed and the results were compared with those from the literature which used other methods such as finite element method.The agreement was found to be satisfactory which proved the validity of the new method in solving the problem of a rectangular plate on an elastic half space with four free edges.This new method would be feasible in practical applications.
[26]
王春玲 , 赵鲁珂 , 李东波 . 非饱和地基上多层矩形板稳态响应解析研究
岩土工程学报 , 2019 ,4 (2 ):1 -9
[本文引用: 1]
( Wang Chunling Zhao Luke Li Dongpo . Analytical study for dynamic response of multi-layered plate on unsaturated half-space
Chinese Journal of Geotechnical Engineering 2019 ,4 (2 ):1 -9 (in Chinese))
[本文引用: 1]
[27]
李刚 , 王贻荪 , 尚守平 . 弹性半空间上矩形基础稳态振动积分变换解
湖南大学学报 , 2000 ,27 (4 ):88 -93
[本文引用: 1]
( Li Gang Wang Yisun Shang Shouping . Integral transformation solution of steady state vibration of rectangular foundation in elastic half space
Journal of Hunan University 2000 ,27 (4 ):88 -93 (in Chinese))
[本文引用: 1]
[28]
Ba ZN Liang JW Vincent W Lee , et al . Dynamic impedance functions for a rigid strip footing resting on a multi-layered transversely isotropic saturated half-space
Engineering Analysis with Boundary Elements 2018 : 31 -44
[29]
Niki DB George AP Athanasios PC . Seismic analysis of rigid walls retaining a cross-anisotropic poroelastic soil layer over bedrock
Soil Dynamic and Earthquake Engineering 2018 : 615 -624
[本文引用: 1]
[30]
孙璐 , 邓学钧 . 弹性基础无限大板对移动载荷的响应
力学学报 , 1996 ,28 (6 ):756 -760
URL
[本文引用: 1]
Integral transform method is used to obtain general solution for steady dynamic response of infinite plate on an elastic foundation causing by a moving arbitrary load. Dynamic response of plate suffering with a moving stationary random load is also discussed. It's found that the plate is not a linear time-variant system in this case. Even if the excitation of plate is a stationary process, the output of it is still a non-stationary process.
( Sun Lu Deng Xuejun . General theory forsteady dynamic problem of infinite plate on an elastic foundation
Chinese Journal of Theoretical and Applied Mechanics 1996 ,28 (6 ):756 -760 (in Chinese))
URL
[本文引用: 1]
Integral transform method is used to obtain general solution for steady dynamic response of infinite plate on an elastic foundation causing by a moving arbitrary load. Dynamic response of plate suffering with a moving stationary random load is also discussed. It's found that the plate is not a linear time-variant system in this case. Even if the excitation of plate is a stationary process, the output of it is still a non-stationary process.
[31]
蔡袁强 , 孙宏磊 , 徐长节 . 移动载荷下上覆弹性板饱和地基的动力响应
计算力学学报 , 2008 ,25 (2 ):156 -162
[本文引用: 1]
( Cai Yuanqiang Song Honglei Xu Changjie . Dynamic response of saturated foundation with elastic plate under moving load
Chinese Journal of Computational Mechanics 2008 ,25 (2 ):156 -162 (in Chinese))
[本文引用: 1]
[32]
Cai YQ Chen Y Cao ZG . Dynamic responses of a saturated poroelastic half-space generated by a moving truck on the uneven pavement
Soil Dynamic and Earthquake Engineering 2015 : 172 -181
[本文引用: 1]
[33]
张春丽 , 王博 , 祝彦知 . 移动载荷下正交各向异性地基无限大板的动力响应
岩土工程学报 , 2017 ,39 (2 ):352 -359
[本文引用: 1]
( Zhang Chunli Wang Bo Zhu Yanzhi . Dynamic response of infinite plate on orthotropic half-plane medium under moving loads
Chinese Journal of Geotechnical Engineering 2017 ,39 (2 ):352 -359 (in Chinese))
[本文引用: 1]
[34]
金波 , 徐植信 . 多孔饱和半空间上刚体垂直振动的轴对称混合边值问题
力学学报 , 1997 ,29 (6 ):711 -719
URL
[本文引用: 1]
研究圆柱形刚体在多孔饱和半空间上的垂直振动.首先应用Hankel变换求解多孔饱和固体的动力基本方程———Biot波动方程.然后按混合边值条件建立多孔饱和半空间上刚体垂直振动的对偶积分方程,用Abel变换化对偶积分方程为第二类Fredholm积分方程.文末给出了多孔饱和半空间表面动力柔度系数的计算曲线.
( Jin Bo Xu Zhixin . Axisymmetric mixed boundary value problem for vertical vibration of rigid body in porous saturated half space
Journal of Theoretical and Applied Mechanics 1997 ,29 (6 ):711 -719 (in Chinese))
URL
[本文引用: 1]
研究圆柱形刚体在多孔饱和半空间上的垂直振动.首先应用Hankel变换求解多孔饱和固体的动力基本方程———Biot波动方程.然后按混合边值条件建立多孔饱和半空间上刚体垂直振动的对偶积分方程,用Abel变换化对偶积分方程为第二类Fredholm积分方程.文末给出了多孔饱和半空间表面动力柔度系数的计算曲线.
[35]
金波 . 多孔饱和半空间上弹性圆板垂直振动的积分方程
力学学报 , 2000 ,32 (1 ):78 -86
URL
[本文引用: 1]
( Jin Bo . Integral equation of vertical vibration of elastic circular plate on porous saturated half-space
Journal of Theoretical and Applied Mechanics 2000 ,32 (1 ):78 -86 (in Chinese))
URL
[本文引用: 1]
[36]
陈龙珠 , 陈胜利 . 饱和地基上弹性圆板的动力响应
力学学报 , 2001 ,33 (6 ):821 -827
[本文引用: 1]
( Chen Longzhu Chen Shenli . Dynamic response of elastic circular plate on saturated ground
Journal of Theoretical and Applied Mechanics 2001 ,33 (6 ):821 -827 (in Chinese))
[本文引用: 1]
[37]
郭树起 . 应用边界积分法求圆形夹杂问题的解析解
力学学报 , 2020 ,52 (1 ):73 -81
[本文引用: 1]
( Guo Shuqi . Exact solution of circular inclusion problems by a boundary integral method
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):73 -81 (in Chinese))
[本文引用: 1]
[38]
沈以淡 . 积分方程 . 北京 : 清华大学出版社 , 2011
[本文引用: 1]
( Shen Yidan . Integral Equation . Beijing : Tsinghua University Press , 2011 (in Chinese)
[本文引用: 1]
[39]
Gradshteyn IS Ryzhik IM . Table of Integrals, Series and Products . New York : Academic Press , 1980
[本文引用: 1]
[40]
Erdelyi A . Tables of Integral Transforms
New York: McGraw-Hill , 1954
[本文引用: 1]
[41]
Morse PM Feshbach H . Methods of Theoretical Physics
New York: McGraw-Hill , 1958
[本文引用: 1]
[42]
Yau WF . Axisymmetric slipless indentation of an infinite elastic cylinder
SIAM Journal on Applied Mathematics 1967 ,15 :219 -227
DOI
URL
[本文引用: 1]
弹性地基上的自由边矩形板
1
1960
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
弹性地基上的自由边矩形板
1
1960
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
变刚度Winkler地基上受压非均质矩形板的自由振动与屈曲特性
2019
变刚度Winkler地基上受压非均质矩形板的自由振动与屈曲特性
2019
黏弹性地基板在矩形变速载荷作用下的振动分析
2010
黏弹性地基板在矩形变速载荷作用下的振动分析
2010
Nonlinear free and forced vibrations of porous sigmoid functionally graded plates on nonlinear elastic foundations
2019
Iterative technique for circular thin plates on Gibson elastic foundation using modified Vlasov model
2019
Exact solutions for forced vibration of completely free orthotropic rectangular nanoplates resting on viscoelastic foundation
1
2019
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
竖向简谐载荷下二维层状饱和地基的解析层元解
1
2018
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
竖向简谐载荷下二维层状饱和地基的解析层元解
1
2018
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
3D dynamic responses of a multi-layered transversely isotropic saturated half-space under concentrated forces and pore pressure
2019
Three-dimensional dynamic Green's functions for transversely isotropic saturated half-space subjected to buried loads
1
2019
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
弹性地基板的等参有限元法计算
1
1998
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
弹性地基板的等参有限元法计算
1
1998
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
2018
土-结构动力相互作用分析中基于人工边界子结构的地震波动输入方法
2018
Numerical modelling of free field traffic-induced vibrations
2000
Train-induced wave propagation in layered soils using finite/infinite element simulation
1
2003
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
1
2018
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
1
2018
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
海洋地震工程流固耦合问题统一计算框架
1
2019
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
海洋地震工程流固耦合问题统一计算框架
1
2019
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
海洋地震工程流固耦合问题统一计算框架-不规则界面情形
1
2019
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
海洋地震工程流固耦合问题统一计算框架-不规则界面情形
1
2019
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
多孔介质内黏弹性流体的热对流稳定性研究
1
2018
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
多孔介质内黏弹性流体的热对流稳定性研究
1
2018
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
Theory of propagation of elastic waves in a fluid-saturated porous solid II. Higher frequency range
2
1956
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
... 考虑孔隙流体压缩性和流体与骨架的相对运动, 并忽略体力作用, Biot饱和多孔介质波动方程写为[19 -23 ] ...
Mechanics of deformation and acoustic propagation in porous media
5
1962
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
... 首先进行收敛性分析, 以确定式(24)的级数项数$m$和$n$. 为了便于比较, 矩形板和地基的计算参数按文献[20 ] 取值. 取矩形板边长$2l_{a}=2l_{b}=4$ m, 板厚为0.2 m; 板的泊松比为 0.167, 弹性模量$E_{b} = 34300$ MPa; 地基泊松比为 0.4, 弹性模量$Es=343$ MPa; 板中心作用均布载荷$q=0.98$ MPa. 本文考虑的地基为两相饱和多孔地基, 所以还需补充土体孔隙率$n=0.6$, 固体骨架密度$\rho_{\rm s}=2700$ kg/m$^{3}$、孔隙水密度$\rho_{\rm f}=1000$ kg/m$^{3}$, 渗透系数$k_{\rm d}=10^{-5}$ m/s. 通过MATLAB编程, 对本文推导结果进行数值计算. 图2 给出了矩形板中心点挠度幅值与网格数目$m\times n$的关系曲线, 图中反映出本方法收敛速度很快, 只需取$m\times n =16\times 16$个网格点足以得到收敛结果. ...
... 若取孔隙水密度$\rho _{\rm f}=0$, 代表地基中无水, 则本文的地基模型退化为单一弹性地基, 可与文献[20 ] 的结果进行对应比较. 表1 列出了本文退化解与文献解的对比, 从表1 的对比结果可知, 本文退化解与文献[20 ] 很好吻合, 由此验证了本文推导方法和数值计算程序的正确性. ...
... [20 ]很好吻合, 由此验证了本文推导方法和数值计算程序的正确性. ...
... 板中心挠度幅值及弯矩与文献[20 ] 对比 ...
Analytical prediction of tunneling-induced ground movements and liner deformation in saturated soils considering influences of shield air pressure
1
2020
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
一种三维饱和土-基础-结构动力相互作用分析方法
1
2016
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
一种三维饱和土-基础-结构动力相互作用分析方法
1
2016
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
核电结构土-结相互作用分析分区混合计算方法
2
2020
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
... 考虑孔隙流体压缩性和流体与骨架的相对运动, 并忽略体力作用, Biot饱和多孔介质波动方程写为[19 -23 ] ...
核电结构土-结相互作用分析分区混合计算方法
2
2020
... 地基板(梁)在动力作用下的振动弯曲问题在诸多工程领域有着重要的实践应用, 如建筑物的筏板基础、公路或市政道路的路面板、铁路的轨道板以及飞机跑道等都可视为这类问题. 以往研究中, 通常采用线弹性、弹塑性或黏弹性本构来模拟地基(如Winkler地基), 通过在板-土接触面上添加弹簧支撑和阻尼黏壶来模拟接触关系[1 -6 ] . 众所周知, 土体是一种具有多相组成和骨架孔隙结构的介质, 采用弹(塑)性或黏弹性本构来模拟土地基, 是将土体视为单相介质, 无法真实反映土体的力学性质. 尤其在动力作用下, 土体中孔隙水的渗透作用以及固流耦合效应对其动力行为起到重要影响[7 -10 ] . 而且采用添加弹簧支撑和黏壶的方式, 使得计算结果完全依赖于地基弹性系数和阻尼比的选取, 无法考虑板土接触的真实情况. 采用有限元分析地基板问题时, 同样需要输入地基弹性系数和阻尼比, 而且传统有限元软件也没有提供可模拟渗透和孔隙压力的本构单元, 因此无法实现板土接触分析的有限元模拟[11 -14 ] . 何涛[15 ] 基于任意拉格朗日-欧拉(ALE)有限元技术, 给出一种数值模拟固流耦合效应的方法, 但无法适用于土体. 陈少林等[16 -17 ] 采用集中质量显式有限元方法, 并结合透射边界条件给出一种针对海洋地震工程流固耦合问题的统一计算框架. 康建宏等[18 ] 基于修正Darcy模型, 分析了多孔介质内黏弹性流体的热对流问题. Biot[19 -20 ] 提出的多孔介质理论为研究土体动力响应提供了理论基础. Zhang等[21 ] 给出一种分析饱和土与隧道结构动力相互作用的理论模型. 陈少林等[22 -23 ] 基于Biot理论对土-基础-结构系统在地震作用下的动力响应做了整体分析. ...
... 考虑孔隙流体压缩性和流体与骨架的相对运动, 并忽略体力作用, Biot饱和多孔介质波动方程写为[19 -23 ] ...
Elastic Analysis of a Soil Structure Interaction
1
1978
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
弹性半空间地基上四边自由矩形板的弯曲解析解
1
2005
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
弹性半空间地基上四边自由矩形板的弯曲解析解
1
2005
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
非饱和地基上多层矩形板稳态响应解析研究
1
2019
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
非饱和地基上多层矩形板稳态响应解析研究
1
2019
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
弹性半空间上矩形基础稳态振动积分变换解
1
2000
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
弹性半空间上矩形基础稳态振动积分变换解
1
2000
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
Dynamic impedance functions for a rigid strip footing resting on a multi-layered transversely isotropic saturated half-space
2018
Seismic analysis of rigid walls retaining a cross-anisotropic poroelastic soil layer over bedrock
1
2018
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
弹性基础无限大板对移动载荷的响应
1
1996
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
弹性基础无限大板对移动载荷的响应
1
1996
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
移动载荷下上覆弹性板饱和地基的动力响应
1
2008
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
移动载荷下上覆弹性板饱和地基的动力响应
1
2008
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
Dynamic responses of a saturated poroelastic half-space generated by a moving truck on the uneven pavement
1
2015
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
移动载荷下正交各向异性地基无限大板的动力响应
1
2017
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
移动载荷下正交各向异性地基无限大板的动力响应
1
2017
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
多孔饱和半空间上刚体垂直振动的轴对称混合边值问题
1
1997
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
多孔饱和半空间上刚体垂直振动的轴对称混合边值问题
1
1997
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
多孔饱和半空间上弹性圆板垂直振动的积分方程
1
2000
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
多孔饱和半空间上弹性圆板垂直振动的积分方程
1
2000
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
饱和地基上弹性圆板的动力响应
1
2001
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
饱和地基上弹性圆板的动力响应
1
2001
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
应用边界积分法求圆形夹杂问题的解析解
1
2020
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
应用边界积分法求圆形夹杂问题的解析解
1
2020
... 采用接触分析法求解地基板问题时, 关键是接触反力的确定. 早期研究中, 前苏联学者哥尔布诺夫波沙道夫[24 ] 采用双重幂级数展开给出弹性地基上矩形板的完全解析解, 但这种解法形式太过复杂, 并没有在实践中得到应用. 王春玲等[25 -26 ] 采用双重三角级数展开的方法, 分别给出了弹性地基和饱和多孔地基上矩形板动力弯曲的解析解. 这种方法与波沙道夫的方法相似, 形式复杂存在收敛问题, 而且无法求解复杂边界条件的情形. 一些学者将矩形板刚性化, 假定接触反力均匀分布, 从而使问题简化为平面应变问题进行求解, 对地基上刚性基础的振动问题做了解析研究[27 -29 ] . 还有一些学者将矩形板视为无限大 使问题简化为单一边界问题从而进行解析求解. 孙璐等[30 ] 给出弹性半空间上无限板的解析解; 蔡袁强等[31 -32 ] 给出饱和多孔地基上无限大板的动力弯曲解; 张春丽等[33 ] 给出各向异性弹性地基上无限大板的解析解. 金波等[34 -35 ] 、陈龙珠等[36 ] 利用Abel变换给出了轴对称混合边值问题的求解方法, 并由此得出饱和多孔地基上圆形板振动弯曲的解析解. 应注意, 对于圆形地基板的轴对称问题, 放在圆柱坐标系下事实上是二维问题, 其一般性将受到限制. 此外, 郭树起[37 ] 也给出了适用于轴对称问题的边界积分法. 而对应于矩形地基板的三维非轴对称混合边值问题的完全解析解, 目前仍未见相关文献. ...
1
2011
... 为求解对偶积分方程(21), 根据Hilbert正交化定理[38 ] , 利用Jacobi正交多项式将积分核$\bar{{\sigma }}_z \left( {x,y,0}\right)$和$\bar{{p}}\left( {x,y,0} \right)$展为如下级数形式[39 ] ...
1
2011
... 为求解对偶积分方程(21), 根据Hilbert正交化定理[38 ] , 利用Jacobi正交多项式将积分核$\bar{{\sigma }}_z \left( {x,y,0}\right)$和$\bar{{p}}\left( {x,y,0} \right)$展为如下级数形式[39 ] ...
1
1980
... 为求解对偶积分方程(21), 根据Hilbert正交化定理[38 ] , 利用Jacobi正交多项式将积分核$\bar{{\sigma }}_z \left( {x,y,0}\right)$和$\bar{{p}}\left( {x,y,0} \right)$展为如下级数形式[39 ] ...
Tables of Integral Transforms
1
1954
... 对式(22)进行双重Fourier变换得到[40 ] ...
Methods of Theoretical Physics
1
1958
... 式中, $\hat{{\varDelta }}\left( {x,y} \right)$, $K_1 \left( {x,y}\right)$, $K_2 \left( {x,y} \right)$, $Q_1 \left( {x,y} \right)$, $Q_2 \left( {x,y} \right)$都是以Fourier逆变换的形式给出(见附录), 其无穷积分可通过快速Fourier逆变换得到. 利用Schmidt法[41 -42 ] 可求解出式(24)中的系数$c_{mn}$和$d_{mn}$, 再将$c_{mn}$和$d_{mn}$依次回代到式(22)和式(18a)可得出接触反力 ...
Axisymmetric slipless indentation of an infinite elastic cylinder
1
1967
... 式中, $\hat{{\varDelta }}\left( {x,y} \right)$, $K_1 \left( {x,y}\right)$, $K_2 \left( {x,y} \right)$, $Q_1 \left( {x,y} \right)$, $Q_2 \left( {x,y} \right)$都是以Fourier逆变换的形式给出(见附录), 其无穷积分可通过快速Fourier逆变换得到. 利用Schmidt法[41 -42 ] 可求解出式(24)中的系数$c_{mn}$和$d_{mn}$, 再将$c_{mn}$和$d_{mn}$依次回代到式(22)和式(18a)可得出接触反力 ...