引言
轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器.
具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题.
要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪.
为了设计控制器使轮式移动结构能精确地沿着给定目标轨迹曲线运动,首先应分析清楚轮式移动结构的非完整约束本质,以及机械结构在轮式非完整约束下的运动规律. 然后将得到的运动规律与动力学方程有机结合起来,再利用现代控制理论设计合适的轨迹跟踪控制器. 本文工作从质点连续光滑运动出发,认清轮式非完整约束的本质及理清各类轮式移动结构的运动学方程,并在此基础上给出求解动力学方程的一般方法. 另一方面,利用平面曲线基本理论分析轮式移动结构在非完整约束下的运动规律,然后通过引入相对曲率为任务目标曲线设计动态轨迹跟踪目标. 基于该动态轨迹跟踪目标,可以将实际问题中的目标轨迹曲线、运动学方程和动力学方程有机结合起来,为轮式移动结构设计精确高效的轨迹跟踪控制器以实现给定的运动任务.
1 质点沿光滑曲线运动的特征
1.1 质点连续光滑运动满足的条件
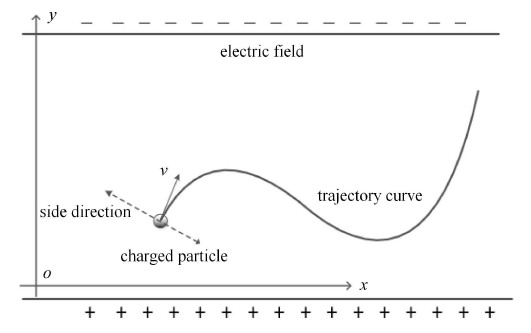
如图 1 所示,一个质量为 $m$ 的带电质点,在电场的作用下在平面上做光滑曲线运动. 若要使该质点沿给定的光滑曲线运动,该如何控制电场力才能精确地实现运动任务?这是一个简单的轨迹跟踪控制问题,该质点好像没有受到任何约束作用,我们直接利用牛顿第二定律就可以得到其动力学方程
(1) $\left.\begin{array}{l} m\ddot {x} = T_x \\ m\ddot {y} = T_y \end{array} \right \}$
其中,$T_x$, $T_y $ 分别是沿坐标方向的电场控制力.
图1
图1
带电质点在平面电场中运动简图
Fig.1
Motion schematic diagram of a charged particle in a plane with electric field
假设给定的光滑曲线是平面上的一个轨道槽,质点在该曲线槽里运动,那么该质点是否受到了约束作用呢? 答案是 肯定的. 此时该约束是完整约束还是非完整约束呢? 注意到质点沿该曲线运动时,其沿与切向垂直的横向方向的速度为 0,即
(2) $-\dot {x}\sin \theta + \dot {y}\cos \theta = 0$
其中,$\theta $ 为运动曲线的切向量与$x$轴的夹角,$\dot {\theta }$ 可以理解为质点运动的偏航 转速. 事实上,质点在光滑曲线槽中运动时,受到槽对它的约束作用,使其速度满足约束方程 (2),因此质点受到槽对它的非完整约束力. 但如果没有轨道槽,质点在平面上做光滑曲线运动时,其运动速度也必须满足方程 (2). 若某时刻质点突然有一个不为零的横向速度,就会导致质点的运动轨迹出现一个尖点,不是光滑曲线.
假设质点在平面运动时坐标表示为光滑曲线 $r = \left( {x\left( t \right), y(t)} \right)$,令该运动轨迹曲线切向量长度为
(3) $v: = \sqrt {\dot {x}^2 + \dot {y}^2}$
(4) $\left.\begin{array}{l} - \dot {x}\sin \theta + \dot {y}\cos \theta = 0 \\ v = \dot {x}\cos \theta + \dot {y}\sin \theta \end{array} \!\! \right \}$
方程 (4) 表明了质点沿光滑轨迹曲线运动的主要特征:沿与切向垂直的横向速度为零,轨迹曲线的切向量就是质点沿该曲线运动的前向速度.
(5) $\left.\begin{array}{l} \dot {x} = v\cos \theta = \sqrt {\dot {x}^2 + \dot {y}^2} \cos \theta \\ \dot {y} = v\sin \theta = \sqrt {\dot {x}^2 + \dot {y}^2} \sin \theta \end{array} \!\! \right \}$
方程 (2) 是质点运动轨迹是光滑曲线的必要条件. 当质点运动满足方程 (4) 时,可以推出其前向速度和偏航转速与实际运动轨迹曲线之间的关系.
1.2 质点的运动速度与实际运动轨迹曲线的关系
给定光滑曲线 $\hat {r} = \left( {\hat {x}(t), \hat {y}\left( t \right)} \right)$, 将曲线看成是某质点的运动轨迹,则质点沿坐标方向速度分量为
(6) $\left.\begin{array}{l} \dot {\hat {x}} = \hat {v}\cos \hat {\theta } = \sqrt {\dot {\hat {x}}^2 + \dot {\hat {y}}^2} \cos \hat {\theta } \\ \dot {\hat {y}} = \hat {v}\sin \hat {\theta } = \sqrt {\dot {\hat {x}}^2 + \dot {\hat {y}}^2} \sin \hat {\theta } \end{array}\!\! \right \}$
其中,$\hat {v}$ 是曲线的切向量长度,其物理意义就是质点运动的前向速度,$\hat {\theta }$ 是曲线切向量与 $x$ 轴的夹角.
(7) $\left.\begin{array}{l} \ddot {\hat {x}} = \dfrac{1}{v}\left( {\dot {\hat {x}}\ddot {\hat {x}} + \dot {\hat {y}}\ddot {\hat {y}}} \right)\cos \hat {\theta } - \hat {v}\sin \hat {\theta }\dot {\hat {\theta }} \\ \ddot {\hat {y}} = \dfrac{1}{v}\left( {\dot {\hat {x}}\ddot {\hat {x}} + \dot {\hat {y}}\ddot {\hat {y}}} \right)\sin \hat {\theta } + \hat {v}\cos \hat {\theta }\dot {\hat {\theta }} \end{array}\!\! \right \}$
(8) $\dot {\hat {x}}\ddot {\hat {y}} - \ddot {\hat {x}}\dot {\hat {y}} = \left( {\dot {\hat {x}}^2 + \dot {\hat {y}}^2} \right)\dot {\hat {\theta }}$
(9) $\left.\begin{array}{l} \hat {v} = \sqrt {\dot {\hat {x}}^2 + \dot {\hat {y}}^2} \\ \dot {\hat {\theta }} = \dfrac{\dot {\hat {x}}\ddot {\hat {y}} - \ddot {\hat {x}}\dot {\hat {y}}}{\dot {\hat {x}}^2 + \dot {\hat {y}}^2} \end{array}\!\! \right \}$
从 式 (9) 可以看出,给定一个运动轨迹曲线可以确定质点运动的前向速度和偏航转速;反之,根据式 (6),给定质点运动的前向速度和偏航转速,可以确定质点运动轨迹的参数方程. 因此,利用式 (9),可以将参数曲线 $\hat {r} = \left( {\hat {x}(t), \hat {y}(t)} \right)$ 表示成速度形式.
事实上,对于一般的机械力学系统,利用 Euler-Lagrange 方程建模得到的动力学方程基本上都是关于速度的,所以将目标轨迹曲线转化为速度目标后,能非常方便地设计力或力矩控制器.
2 独轮的约束方程与动力学方程
如图 2 所示,假设独轮足够宽且无侧翻和侧滑,则独轮的中心$O$在平面上做连续光滑运动. 假设该中心坐标为 $\left( {x(t), y(t)} \right)$,故其运动需满足方程 (2). 在这个实际问题中,要使得中心 $O$ 的运动满足方程 (2),整个力学系统要受到非完整约束力的作用才能实现. 因此,约束方程 (2)是独轮运动受到的非完整约束. 考虑到独轮的运动是通过驱动轮子转动来实现的,所以必须引入轮子转速这个变量. 假设轮子不打滑和不空转,则独轮还受到如下完整约束
(10) $r\dot {\theta }_{\rm f} = v$
其中,$r$ 是独轮半径,$\dot {\theta }_{\rm f}$ 是独轮转速.
图2
图2
独轮运动结构简图
Fig.2
Motion schematic diagram of the single-wheel
因此,独轮总共受到两个约束作用, 式 (10) 是一个完整约束,而 式 (2) 是独轮受到的非完整约束.
(11) $\left.\begin{array}{l} I_\omega \ddot {\theta }_{\rm f} = T_\omega \\ I_z \ddot {\theta } = T_z \end{array} \right \}$
其中,$I_\omega , I_z $ 分别是轮子绕中心轴和绕过中心且平行 $z$ 轴的轴线的转动惯量,$T_\omega $ 是驱动轮子转动的力矩,$T_z $ 是使得独轮偏转的力矩.
要使中心点 $O$ 沿给定轨迹曲线 $\hat {r} = ( \hat {x} ( t ), \hat {y}(t) )$ 运动,该如何设计控制力矩 $\left( {T_\omega , T_z } \right)$ 呢? 由于中心 $O$ 的运动满足方程 (2),由式 (9) 可将目标曲线转化为速度目标,将式 (10) 代入式 (11),动力学方程转化为
(12) $\left.\begin{array}{l} \dot {v} = r\dfrac{T_\omega }{I_\omega } \\ \ddot {\theta } = \dfrac{T_z }{I_z } \end{array} \right \}$
这样就将原问题转化为线性系统 (12) 关于速度目标 (9) 的一般轨迹跟踪控制问题.
3 两轮式倒立摆的约束方程与动力学方程
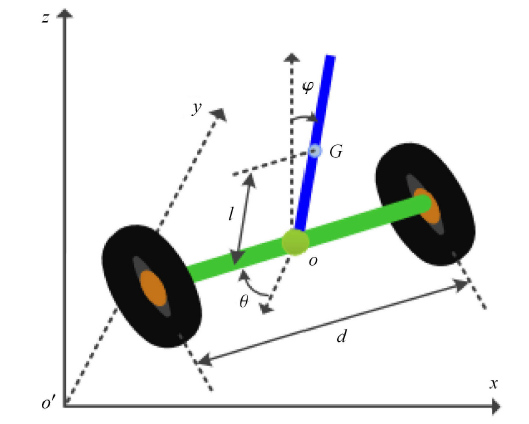
两轮式倒立摆是一类经典欠驱动的非完整系统,在实际中应用广泛,相应的运动规划和控制研究非常多[1 ,22 ] . 如图 3 所示,假设两轮无侧滑无空转,左右两轮各安装一个驱动马达,通过驱动左右两轮转动来实现两轮式倒立摆的运动和摆杆平衡.
图3
图3
两轮式倒立摆结构简图
Fig.3
Schematic diagram of the two-wheeled inverted pendulum
3.1 两轮运动的约束方程
设中心 $O$ 坐标为 $\left( {x(t), y(t)} \right)$,当两轮式倒立摆在平面上无侧滑时,$O$ 在平面上沿光滑曲线运动,故其运动必须满足约束方程 (2). 另外,当两轮不打滑不空转时,有如下速度关系式
(13) $\left.\begin{array}{l} v = \dfrac{r}{2}(\dot {\theta }_{\rm l} + \dot {\theta }_{\rm r} ) \\ \dot {\theta } = \dfrac{r}{d}(\dot {\theta }_{\rm l} - \dot {\theta }_{\rm r} ) \end{array} \!\! \right \}$
其中,$\dot {\theta }_{\rm l}, \dot {\theta }_{\rm r}$ 分别是左右两轮转速.
因此,两轮移动结构在运动时总共受到一个非完整约束 (2) 和两个完整约束 (13). 从方程 (13) 中将 $\dot\theta_l$ 和 $\dot\theta_r$ 反解出来,并结合方程 (5),则可将两轮式移动结构运动时所受约束方程总结为
(14) $\left.\begin{array}{l} \dot {x} = v\cos \theta \\ \dot {y} = v\sin \theta \\ \dot {\theta }_{\rm l}= \dfrac{1}{r}v + \dfrac{d}{2r}\dot {\theta }\\ \dot {\theta }_{\rm r} = \dfrac{1}{r}v - \dfrac{d}{2r}\dot {\theta } \end{array} \!\! \right \}$
实际上两轮式移动结构只受到 3 个约束作用, 式 (14) 中其实包含了一个赋值关系式 (3).
3.2 两轮式倒立摆的动力学方程
两轮式倒立摆的摆杆稳定是通过整个结构前后运动的耦合作用来实现的,这里面受力分析比较复杂. 目前求解其动力学方程的方法主要有 Newton 法[23 ] 、Kane 法[24 ] 和 Euler-Lagrange 方法. 相对来说,Newton 法和 Kane 法都比较繁琐. 这里我们采用 Euler-Lagrange 方程来建立其动力学方程[22 ] .
将式 (4) 的第二式代入式 (14) 的第三、四式,并结合 式 (2),得到两轮结构运动约束的另一种形式
(15) $\left.\begin{array}{l} - \dot {x}\sin \theta + \dot {y}\cos \theta = 0 \\ \dot {x}\cos \theta + \dot {y}\sin \theta + \dfrac{d}{2}\dot {\theta } - r\dot {\theta }_{\rm l} = 0 \\ \dot {x}\cos \theta + \dot {y}\sin \theta - \dfrac{d}{2}\dot {\theta } - r\dot {\theta }_{\rm r} = 0 \end{array} \right \}$
令 ${\pmb q}=\left( {x, y, \theta , \varphi , \theta _{\rm l} , \theta _{\rm r} } \right)^{\rm T}$ 是两轮式倒立摆的广义坐标,则运动约束方程 (15) 可以写成矩阵形式 ${\pmb F}({\pmb q} )_{3\times 6} \dot{\pmb q} = {\bf 0 }_{3\times 1} $,其中
${\pmb F} ({\pmb q} ) = \left[\!\!\begin{array}{cccccc} { - \sin \theta } & {\cos \theta } & 0 & 0 & 0 & 0 \\ {\cos \theta } & {\sin \theta } & {\dfrac{d}{2}} & 0 & { - r} & 0 \\ {\cos \theta } & {\sin \theta } & { - \dfrac{d}{2}} & 0 & 0 & { - r} \end{array} \!\! \right] $
另一方面,令 ${\pmb V} = \left( {\dot {\varphi },v,\dot {\theta }} \right)^{\rm T}$,约束 (14) 写成矩阵形式
(16) $\dot{\pmb q} ={\pmb S} ({\pmb q} ) {\pmb V}$
${\pmb S}({\pmb q}) = \left[\!\!\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0 \\ {\cos \theta } & {\sin \theta } & 0 & 0 & {\dfrac{1}{r}} & {\dfrac{1}{r}} \\ 0 & 0 & 1 & 0 & {\dfrac{d}{2r}} & { - \dfrac{d}{2r}} \end{array} \!\!\right]^{\rm T} $
事实上,$ \dot{\pmb q}$ 在 ${\pmb F}({\pmb q})$ 的零空间中,且
(17) ${\pmb F}({\pmb q}) \cdot {\pmb S}({\pmb q}) = {\bf 0}_{3\times 3}$
采用 Euler-Lagrange 方程来求解两轮式倒立摆的动力学方程[22 ] . 假设 $M_\omega $ 和 $M$ 分别是轮子和中间体质量,$I_\omega $ 和 $I_{\omega d} $ 分别是轮子绕轮轴方向和 $z$ 轴方向的转动惯量,$I_B $ 和 $I_{z} $ 分别是中间体绕轮轴方向和 $z$ 轴方向的转动惯量.
$ T_\omega = \dfrac{1}{2}M_\omega r^2\dot {\theta }_{\rm l}^2 + \dfrac{1}{2}M_\omega r^2\dot {\theta }_{\rm r}^2 + \dfrac{1}{2}I_\omega \dot {\theta }_{\rm r}^2 + \dfrac{1}{2}I_\omega \dot {\theta }_{\rm l}^2 + I_{\omega d} \dot {\theta }^2 $
$ T_{\rm B}^{\rm T} = \dfrac{ 1 }{ 2 }M\left[ {\dot {\varphi }l\cos \varphi + \dfrac{ 1 }{ 2 }r(\dot {\theta }_{\rm l} + \dot {\theta }_{\rm r} )} \right]^2 + \dfrac{ 1 }{ 2 }M(\dot {\theta }l\sin \varphi )^2 + \dfrac{ 1 }{ 2 } M (-\dot {\varphi }l\sin \varphi)^2 \\ T_{\rm B}^{\rm R} = \dfrac{ 1 }{ 2 }I_{\rm B} \dot {\varphi }^2 + \dfrac{ 1 }{ 2 }I_z \dot {\theta }^2 $
转动惯量 $I_z $ 是和摆角 $\varphi $ 相关的,在摆角较小的情况下,$I_z $ 近似一个常量. 两轮式倒立摆重力势能为
$L = T_\omega + T_{\rm B}^{\rm T} + T_{\rm B}^{\rm R}-P $
利用非完整力学系统的 Euler-Lagrange 方程
(18) $\dfrac{\text{d}}{\text{d}t}\left( {\dfrac{\partial L}{\partial \dot{\pmb q}} } \right) - \dfrac{\partial L}{\partial {\pmb q}} = {\pmb E}( {\pmb q}){\pmb T} + {\pmb F}^{\rm T}({\pmb q})\lambda$
其中,$\lambda $ 是 Lagrange 乘子,${\pmb T}$ 是输入力矩向量,${\pmb E}({\pmb q})$ 是输入匹配矩阵
${\pmb T} = \left[\!\! \begin{array}{l} {T_l } \\ {T_r } \end{array} \!\! \right] ,\quad {\pmb E} ({\pmb q} ) = \left[ \!\!\begin{array}{cccccc} 0 & 0 & 0 & { - 1} & 1 & 0 \\ 0 & 0 & 0 & { - 1} & 0 & 1 \end{array} \!\! \right]^{\rm T} $
计算 式 (18) 并按照状态变量的各阶导数整理成
(19) ${\pmb A}({\pmb q}) \ddot{\pmb q} + {\pmb U}\left( {{\pmb q}, \dot{\pmb q}} \right) \dot{\pmb q} = {\pmb E}({\pmb q}){\pmb T} + {\pmb F}^{\rm T}({\pmb q})\lambda$
为了消去式 (19) 中的 Lagrange 乘子,将 式 (16) 的左右两端分别对 $t$ 求导并代入 式 (19) 得
(20) ${\pmb A \pmb S}\dot{\pmb V} + {\pmb A}\dot{\pmb S}{\pmb V} + {\pmb U} \left( { {\pmb q }, \dot{\pmb q} } \right){\pmb S}{\pmb V} = {\pmb E} ({\pmb q} ){\pmb T} + {\pmb F }^{\rm T}({\pmb q })\lambda$
对 式 (20) 左右两边同时左乘 ${\pmb S}^{\rm T}({\pmb q})$,并利用式 (17) 将 Lagrange 乘子消去得
(21) ${\pmb S}^{\rm T}{\pmb A}{\pmb S}\dot{\pmb V} + {\pmb S }^{\rm T}( {\pmb A}\dot{\pmb S}{\pmb V} + {\pmb U} \left( {{\pmb q }, \dot{\pmb q}} \right){\pmb S}{\pmb V} ) = {\pmb S }^{\rm T}{\pmb E }({\pmb q}){\pmb T}$
注意到 ${\pmb S}^{\rm T}{\pmb A}\dot{\pmb S} = {\bf 0}_{3\times 3} $,化简 式 (21) 得到动力学方程
(22) $\dot{\pmb V} = - \bar{\pmb A}^{ - 1}{\pmb S}^{\rm T}{\pmb U}({\pmb q}, \dot{\pmb q}){\pmb S}{\pmb V} + \bar{\pmb A}^{ - 1}{\pmb S}^{\rm T}{\pmb E}({\pmb q}) {\pmb T}$
其中,$\bar{\pmb A} = {\pmb S}^{\rm T}{\pmb A}({\pmb q}){\pmb S}$.
(23) $ \left.\begin{array}{l} \ddot {\varphi } = \dfrac{ - Ml(\dot {\theta }^2l\cos \varphi + g)\left( {Mr^2\sin \varphi + 2I_\omega \sin \varphi + 2M_\omega r^2\sin \varphi } \right)}{\varDelta + M^2l^2r^2\cos ^2\varphi } +\dfrac{M^2l^2r^2\dot {\varphi }^2\sin \varphi \cos \varphi }{\varDelta + M^2l^2r^2\cos ^2\varphi } + \\ \qquad \dfrac{Mr^2 + 2I_\omega + 2M_\omega r^2 + Mlr\cos \varphi }{\varDelta + M^2l^2r^2\cos ^2\varphi }u_2 \\ \dot {v} = \dfrac{Mlr^2\left[ {Ml\sin \varphi \cos \varphi (\dot {\theta }^2l\cos \varphi + g) - \dot {\varphi }^2\sin \varphi Ml^2 - \dot {\varphi }^2\sin \varphi I_{\rm B} } \right]}{\varDelta + M^2l^2r^2\cos ^2\varphi } - \dfrac{Mlr^2\cos \varphi + Mrl^2 + I_{\rm B} r}{\varDelta + M^2l^2r^2\cos ^2\varphi }u_2 \\ \ddot {\theta } = \dfrac{2Ml^2r^2\dot {\theta }\dot {\varphi }\sin 2\varphi }{\varOmega + 2M^2l^2r^2\cos ^2\varphi } + \dfrac{rd}{\varOmega + 2M^2l^2r^2\cos ^2\varphi }u_1 \end{array} \!\! \right \} $
$\begin{array}{l} \varDelta = - M^2l^2r^2 - 2Ml^2I_\omega - 2Ml^2M_\omega r^2 -\\ \qquad I_{\rm B} Mr^2 - 2I_{\rm B} I_\omega - 2M_\omega r^2I_{\rm B} \\ \varOmega = - M_\omega d^2r^2 - 4I_{\omega d} r^2 - 2I_z r^2 - d^2I_\omega - 2Ml^2r^2 \\ u_1 = T_{\rm l} - T_{\rm r} ,\quad u_2 = T_{\rm l} + T_{\rm r} \end{array} $
3.3 两轮式倒立摆的运动控制
要使两轮式倒立摆的中心点 $O$ 沿给定的轨迹曲线运动,并且整个运动过程中摆角 $\varphi $ 始终保持足够小,该如何设计控制器 $(u_1 ,u_2)$ 呢? 利用 式 (9) 将目标轨迹曲线 $\hat {r} = (\hat {x}(t), \hat {y}(t))$ 转化为速度目标的形式,结合式 (23) 的后两式可将原问题转化为一般的轨迹跟踪控制问题. 另外,动力学方程 (23) 可以解耦成两个控制子系统,可以分别设计控制器 $u_2 $ 和 $u_1 $. 在文献[25 ] 中, 通过引入关于摆角 $\varphi$ 的大权重性能指标,对摆角 $\varphi $ 进行线性化后将得到的线性系统看成标称系统,然后设计关于性能指标的最优积分滑模控制器以实现两轮式倒立摆的往返运动.
4 三四轮移动结构的约束方程与动力学方程
4.1 三四轮移动结构的运动约束
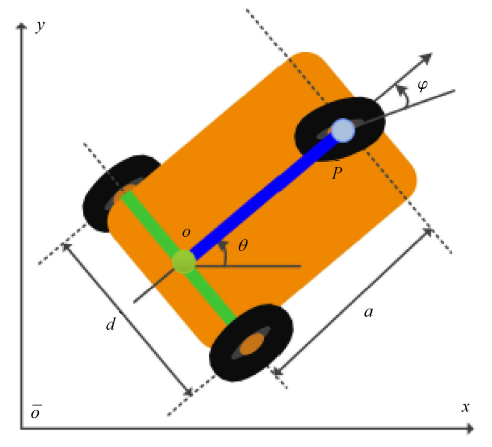
如图 4 和图 5 所示三轮和四轮移动结构,假设驱动马达都安装在后两轮上,前轮可以通过控制方向盘进行转向.后两轮所受到的约束和两轮式倒立摆是一样的,都可以用 式 (14) 表示.
图4
图4
三轮移动结构简图
Fig.4
Schematic diagram of the three-wheeled mobile structure
图5
图5
四轮移动结构简图
Fig.5
Schematic diagram of the four-wheeled mobile structure
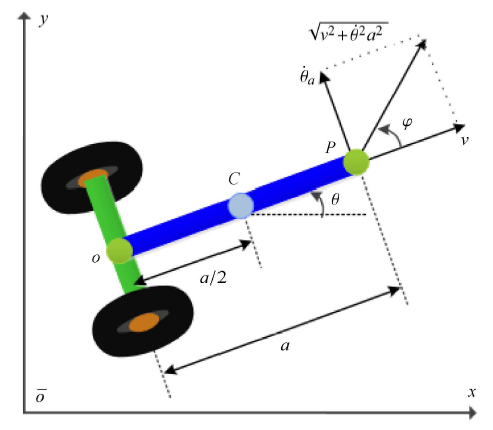
对于前轮所受约束,考虑中间杆的前端点 $P(x_P, y_P )$ 的运动. 注意到 $P$ 点有两重身份,首先作为前轮的中心点,它的运动满足横向速度为零
(24) $-\dot {x}_P \sin \varphi + \dot {y}_P \cos \varphi = 0$
另一方面,$P$ 作为中间杆前端点,它的运动速度如图 6 所示,结合 式 (24) 有如下关系
(25) $\dfrac{\dot {y}_P }{\dot {x}_P } = \tan \varphi = \dfrac{\dot {\theta }a}{v}$
(26) $\dot{\theta} = \dfrac{v\tan \varphi }{a}$
方程 (26) 是一个非完整约束,它刻画了前轮转向角与中心点 $O$ 的速度之间的关系. 若将 $\dot{x} = v\cos \theta $ 代入式 (26),还可以将该非完整约束改写为
$-\tan \varphi \dot {x} + a\dot {\theta }\cos \theta = 0 $
图6
图6
$P$ 点速度示意图
Fig.6
Schematic diagram of the velocity of $P$
4.2 三轮移动结构的动力学方程
由于图 4 和图 5 中三、四轮结构所受的约束方程完全相同,因此利用方程 (18) 求解动力学方程的过程完全一样. 仅以三轮为例,$\varphi$ 是通过方向盘人为进行控制的,所以将 $\varphi $ 看成控制变量. 结合式 (14) 和式 (26),三轮移动结构所受到的所有运动约束为
(27) $\left.\begin{array}{l} \dot {x} = v\cos \theta \\ \dot {y} = v\sin \theta \\ \dot {\theta }_{\rm l} = \dfrac{1}{r}v + \dfrac{d}{2r}\dot {\theta }\\ \dot {\theta }_{\rm r} = \dfrac{1}{r}v - \dfrac{d}{2r}\dot {\theta }\\ \dot {\theta } = \dfrac{v\tan \varphi }{a} \end{array} \!\! \right \}$
令 ${\pmb q} = \left( {x,y,\theta ,\theta _l ,\theta _r } \right)^{\rm T}$, ${\pmb V} = (v,\dot {\theta })^{\rm T}$,将约束方程 (27) 写成矩阵形式
(28) $\dot{\pmb q} = {\pmb S} ({\pmb q }){\pmb V}$
其中, ${\pmb S}({\pmb q}) = \left[\!\! \begin{array}{cc} {\cos \theta } & 0 \\ {\sin \theta } & 0 \\ {\dfrac{\tan \varphi }{a}} & 0 \\ {\dfrac{1}{r}} & {\dfrac{d}{2r}} \\ {\dfrac{1}{r}} & { - \dfrac{d}{2r}} \end{array} \!\! \right] $ .
从式 (27) 来看,三轮移动结构似乎一共受到四个约束作用,但其实不然,约束方程 (26) 和 (13) 的第二式并不是相互独立的,而是互相影响的. 在两轮式移动结构的情形中,两轮式的三个约束分别是横向速度为零,两轮转速之和决定前向速度,两轮转速之差决定偏航转速. 而在本文的三轮移动结构中,3 个约束作用实际上分别是横向速度为零,两轮转速之和决定前向速度,前向速度 $v$ 和 $\varphi $ 决定偏航转速,此时对应的 $\dot {\theta }_{\rm l} , \dot {\theta }_{\rm r} $ 就是确定的了. 因此,我们将这两个约束整合在一起,将三轮移动结构受到的约束作用总结成如下形式
$\left\{\begin{array}{l} - \dot {x}\sin \theta + \dot {y}\cos \theta = 0 \\ \dot {x}\cos \theta + \dot {y}\sin \theta - \dfrac{r}{2}(\dot {\theta }_{\rm l} + \dot {\theta }_{\rm r} ) = 0 \\ - \tan \varphi \dot {x} + a\dot {\theta }\cos \theta = 0 \end{array} \right. $
${\pmb F}({\pmb q})_{3\times 5} \dot{\pmb q} = {\bf 0 }_{3\times 1} $
${\pmb F}({\pmb q}) = \left[\begin{array}{ccccc} { - \sin \theta } & {\cos \theta } & 0 & 0 & 0 \\ {\cos \theta } & {\sin \theta } & 0 & { - \dfrac{r}{2}} & { - \dfrac{r}{2}} \\ { - \tan \theta } & 0 & {a\cos \theta } & 0 & 0 \end{array} \right] $
注意到,${\pmb F}({\pmb q}), {\pmb S}({\pmb q})$ 满足如下关系
(29) ${\pmb F}_{3\times 5} ({\pmb q}) \cdot {\pmb S}_{5\times 2 } \left( {\pmb q} \right) = {\bf 0}_{3\times 2}$
为了利用 Euler-Lagrange 方程来计算三轮移动结构的动力学方程, 首先需要分别计算各个部分 的动能. 如图 6 所示,可以得到如下位置关系
$ \begin{array}{l} \begin{array}{l} x_{\omega \rm l} = x + \dfrac{d}{2}\sin \theta ,\\ y_{\omega \rm l} = y - \dfrac{d}{2}\cos \theta , \end{array} \quad \begin{array}{l} x_{\omega \rm r} = x - \dfrac{d}{2}\sin \theta \\ y_{\omega \rm r} = y + \dfrac{d}{2}\cos \theta \end{array} \\ \begin{array}{l} x_C = x + \dfrac{a}{2}\cos \theta ,\\ y_C = y + \dfrac{a}{2}\sin \theta, \end{array} \quad \begin{array}{l} x_P = x + a\cos \theta \\ y_P = y + a\sin \theta \end{array} \end{array} $
其中,$(x_{\omega \rm l} , y_{\omega \rm l} ), (x_{\omega \rm r} , y_{\omega \rm r} )$ 分别是左右后轮的中心坐标,$v_{\omega \rm l} , v_{\omega \rm r} , v_C $ 和 $v_P $ 分别为后两轮中心点的速度,中间杆的中心点 $C$ 和前轮中心 $P$ 的速度. 这样,可以得到各中心点速度的平方分别为
$\begin{array}{l} v_{\omega \rm l}^2 = \dot {x}^2 + \dot {y}^2 + \dfrac{d^2}{ 4 }\dot {\theta }^2 + d\dot {\theta }(\dot {x}\cos \theta + \dot {y}\sin \theta ) \\ v_{\omega \rm r}^2 = \dot {x}^2 + \dot {y}^2 + \dfrac{d^2} {4} \dot {\theta }^2 - d\dot {\theta }(\dot {x}\cos \theta + \dot {y}\sin \theta ) \\ v_C^2 = \dot {x}^2 + \dot {y}^2 + \dfrac{a^2}{ {4}}\dot {\theta }^2 - a\dot {\theta }(\dot {x}\sin \theta - \dot {y}\cos \theta ) \\ v_P^2 = \dot {x}^2 + \dot {y}^2 + a^2\dot {\theta }^2 - 2a\dot {\theta }(\dot {x}\sin \theta - \dot {y}\cos \theta ) \end{array} $
$T_\omega = M_\omega (\dot {x}^2 + \dot {y}^2 + \dfrac{d^2}{4}\dot {\theta }^2) + \dfrac{ 1 }{ 2 }I_\omega (\dot {\theta }_{\rm r}^2 + \dot {\theta }_{\rm l}^2 ) + I_{\omega d} \dot {\theta }^2 $
$\begin{array}{l} T_{\rm B} = \dfrac{1}{2}M_{\rm B} \Big[ \dot {x}^2 + \dot {y}^2 + \dfrac{a^2}{4}\dot {\theta }^2 - a\dot {\theta }(\dot {x}\sin \theta - \dot {y}\cos \theta ) \Big ] + \dfrac{1}{2}I_{\rm B} \dot {\theta }^2 \\ T_{\rm f} = \dfrac{1}{2}\Big(M_\omega + \dfrac{I_\omega }{r^2}\Big )\left[ {\dot {x}^2 + \dot {y}^2 + a^2\dot {\theta }^2 - }\right. \left.{ 2a\dot {\theta }(\dot {x}\sin \theta - \dot {y}\cos \theta )} \right] \end{array}$
其中,$M_{\rm B}$ 是中间杆的质量,$I_{\rm B}$ 是中间杆绕 $O$ 点在 $x - y$ 平面上的转动惯量.
将 Lagrange 函数 $L=T_\omega + T_{\rm B} + T_{\rm f} $ 代入式 (18), 此时输入力矩向量 ${\pmb T}$ 和匹配矩阵 ${\pmb E}( {\pmb q})$ 分别为
${\pmb T} = \left[\!\!\begin{array}{c} {T_{\rm l} } \\ {T_{\rm r} } \end{array}\!\! \right],\quad {\pmb E}({\pmb q}) = \left[\!\! \begin{array}{ccccc} 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array} \!\!\right]^{\rm T} $
计算 式 (18),并按状态变量的各阶导数进行整理得
(30) ${\pmb A}({\pmb q}) \ddot{\pmb q} + {\pmb U }({\pmb q }, \dot{\pmb q} ) \dot{\pmb q} = {\pmb E} ({\pmb q }){\pmb T} + {\pmb F }^{\rm T}({\pmb q} )\lambda$
$ \begin{array}{l} {\pmb A}({\pmb q}) = \left[ \!\!\begin{array}{ccccc} {M_1 } & 0 & { - M_2 a\sin \theta } & 0 & 0 \\ 0 & {M_1 } & {M_2 a\cos \theta } & 0 & 0 \\ { - M_2 a\sin \theta } & {M_2 a\cos \theta } & I & 0 & 0 \\ 0 & 0 & 0 & {I_\omega } & 0\\ 0 & 0 & 0 & 0 & {I_\omega } \end{array} \!\! \right] \\ {\pmb U}({\pmb q}, \dot{\pmb q}) = \left[ \!\!\begin{array}{ccccc} 0 & 0 & { - M_2 a\dot {\theta }\cos \theta } & 0 & 0 \\ 0 & 0 & { - M_2 a\dot {\theta }\sin \theta } & 0 & 0\\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 \end{array}\!\! \right] \\ M_1 = M_{\rm B} + 3M_\omega + \dfrac{I_\omega }{r^2} \\ M_2 = \dfrac{M_{\rm B} }{ 2 } + M_\omega + \dfrac{I_\omega }{r^2} \\ I = I_{\rm B} + 2I_{\omega d} + \dfrac{a^2}{4}M_{\rm B} + \dfrac{d^2}{ 2 }M_\omega + a^2M_\omega + \dfrac{I_\omega a^2}{r^2} \end{array} $
对式 (28) 关于 $t$ 求导,然后代入 式 (30) 得
(31) ${\pmb A}{\pmb S}\dot{\pmb V} + {\pmb A}\dot{\pmb S}{\pmb V} + {\pmb U}({\pmb q}, \dot{\pmb q}){\pmb S}{\pmb V} = {\pmb E}({\pmb q}){\pmb T} + {\pmb F}^{\rm T}({\pmb q})\lambda$
对 式 (31) 左右两边同时左乘 ${\pmb S}^{\rm T}({\pmb q})$,并利用 式 (29) 将 Lagrange 乘子消去得三轮移动结构动力学方程为
(32) ${\pmb S}^{\rm T}{\pmb A}{\pmb S}\dot{\pmb V} + ({\pmb S}^{\rm T} {\pmb A}\dot{\pmb S} + {\pmb S}^{\rm T}{\pmb U}({\pmb q}, \dot{\pmb q}){\pmb S}){\pmb V} = {\pmb S}^{\rm T}{\pmb E}({\pmb q}){\pmb T}$
$ {\pmb S}^{\rm T}{\pmb A}{\pmb S} = \left[\!\! \begin{array}{cc}{\dfrac{M_1 a^2r^2\cos ^2\varphi + 2I_\omega a^2\cos ^2\varphi + Ir^2\sin ^2\varphi }{a^2r^2\cos ^2\varphi }} & 0 \\ 0 & {\dfrac{d^2I_\omega }{2r^2}} \end{array} \!\! \right] \\ {\pmb S}^{\rm T}{\pmb A}\dot{\pmb S} + {\pmb S}^{\rm T}{\pmb U}({\pmb q}, \dot{\pmb q}){\pmb S} = \left[\!\! \begin{array}{cc} {\dfrac{I\dot {\varphi }\sin \varphi }{a\cos ^3\varphi }} & 0 \\ 0 & 0 \end{array} \!\! \right] \\ {\pmb S}^{\rm T}{\pmb E}({\pmb q}){\pmb T} = \left[\!\! \begin{array}{c} {\dfrac{T_{\rm l} + T_{\rm r} }{r}} \\ {\dfrac{d(T_{\rm l} - T_{\rm r} )}{2r}} \end{array} \!\! \right] $
4.3 三轮移动结构的运动控制
(33) $\left.\begin{array}{l} \dot {v} = - \dfrac{Iar^2\dot {\varphi }\sin \varphi }{\varDelta \cos \varphi }v + \dfrac{ra^2\cos ^2\varphi }{\varDelta }u_2 \\ \ddot {\theta } = cu_1 \end{array} \right \}$
$\begin{array}{l} \varDelta = M_1 a^2r^2\cos ^2\varphi + 2I_\omega a^2\cos ^2\varphi + Ir^2\sin ^2\varphi \\ c = \dfrac{r}{dI_\omega },\quad u_1 = T_{\rm l} - T_{\rm r} ,\quad u_2 = T_{\rm l} + T_{\rm r} \end{array} $
利用 式 (9) 将目标轨迹曲线转化成速度形式,结合控制系统 (33) 得到一般的轨迹跟踪控制问题. 注意这里 $u_1 $ 是中间控制变量,而最终需要设计的控制变量是 $\varphi $ 和 $u_2 $. 由于方程 (33) 是解耦的,因此可先根据第二个方程设计 $u_1 $,然后结合方程 (26) 得
(34) $\dot {\theta } = \dfrac{v\tan \varphi }{a} = \int_0^t {cu_1 } \text{d}s$
方程 (34) 给出了控制变量 $u_1 $ 和 $\varphi $ 的关系. 将得到的控制变量 $\varphi $ 代入式 (33) 的第一式,再设计控制变量 $u_2 $ 完成最终的轨迹跟踪控制设计任务.
5 动态跟踪目标与运动控制设计
前面几节内容已经系统地分析了各类轮式移动结构的约束方程及其动力学方程. 实际上约束方程 (2) 是所有轮式移动结构在无横向滑动时必须满足的非完整约束. 通过分析该约束条件,我们可以利用式 (9) 将轮式移动结构的任务轨迹曲线转化为成速度目标的形式,然后结合其动力学方程将原运动任务转化为一般的轨迹跟踪控制问题. 如文献[26 ] 在考虑轮式倒立摆的避障运动控制时,就将设计好的分段多项式轨迹曲线转化成近似的速度目标形式,然后结合动力学方程设计轨迹跟踪控制器. 文献[27 ,28 ,29 ] 在考虑拖-挂车的轨迹曲线跟踪和避障运动时,就是先将目标轨迹曲线转化为 式 (9) 这样的速度目标,然后采用模型预测等控制方法实现给定的运动任务. 但从这些论文的仿真结果来看,不管采用多么先进的控制设计方法,实际运动轨迹总是会有一些偏离目标轨迹曲线,尤其是在最初始的一段时间内. 出现这样的结果主要原因之一在于所采用的速度目标 (9) 在初始时刻和实际速度相比具有比较大的差值,这个速度误差会累计成很大的位置误差. 另外,如果采用静态速度目标 (9),当前向速度误差控制系统受到未知扰动影响时,会导致实际前向速度偏离给定的前向速度目标,而此时偏航转速目标不能时时地进行调整,这就会导致轮式移动结构偏离目标轨迹曲线. 为了同时解决这两个问题,使轮式移动结构能精确地沿着给定目标轨迹曲线运动,我们将静态速度目标 (9) 改进为动态跟踪目标.
5.1 动态跟踪目标设计
对于给定的目标轨迹曲线 $\hat {r} = (\hat {x}(t), \hat {y}(t))$,利用式(9)将其转化为速度目标. 进一步地改写成
(35) $\left.\begin{array}{l} \hat {v} = \sqrt {\dot{\hat {x}}^2 + \dot{\hat {y}}^2} \\ \dot{\hat{\theta }} = k(s(t))\hat{v},\quad s(t) = \int_0^t \hat{v}(\tau ) \text{d}\tau \end{array} \!\! \right \}$
其中 $k(s(t)) = \dfrac{\dot {\hat {x}}\ddot {\hat {y}} - \ddot {\hat {x}}\dot {\hat {y}}}{(\dot {\hat {x}}^2 + \dot {\hat {y}}^2)^{\tfrac{3}{2}}}$ 是目标曲线的相对曲率.
事实上,曲率函数 $k(s(t))$ 是曲线 $\hat {r} = (\hat {x}(t), \hat {y}(t))$ 的核心特征. 当参数 $t = s$ 是弧长参数时,前向速度目标 $\hat {v}(s)$ 是单位速度,此时曲率函数 $k(s)$ 在平面上唯一确定一条光滑曲线. 当 $t$ 不是弧长参数时,由前向速度 $\hat {v}(t)$ 和曲率函数 $k(t) = k(s(t))$ 可以在平面上唯一确定一条光滑曲线. 对曲线 $\hat {r} = (\hat {x}(t), \hat {y}(t))$ 引入新的时间变量 $\eta$, 它由 $t = \phi (\eta )$ 确定,其中 $\phi $ 是一一对应的光滑函数,则可将原参数曲线转化为 $\hat {r} = (\hat {x}(\eta ), \hat {y}(\eta ))$. 由复合函数求导关系
$\dfrac{\text{d}\hat {x}}{\text{d}\eta } = \dfrac{\text{d}\hat {x}}{\text{d}t}\dfrac{\text{d}t}{\text{d}\eta },\quad \dfrac{\text{d}\hat {y}}{\text{d}\eta } = \dfrac{\text{d}\hat {y}}{\text{d}t}\dfrac{\text{d}t}{\text{d}\eta } $
结合方程 (35) 得到 $\hat {r} = (\hat {x}(\eta ), \hat {y}(\eta ))$ 的前向速度为
$\hat {v}_\eta = \dot {\phi }(\eta )\hat {v} $
从上式可看出,方程 (35) 中的前向速度目标是可以通过参数变换进行调整的. 因此方程 (35) 中涉及到曲线曲率的第二式才是轨迹曲线的本质刻画.
在实际跟踪过程中,如果我们只需要轮式移动结构精确沿给定轨迹曲线 $\hat{r}$ 运动,而并不在乎整个过程中运动速度的快慢,那么可以放弃对前向速度目标 $\hat{v}$ 的精确跟踪,集中精力跟踪方程 (35) 的第二式. 此时可以将跟踪目标 (35) 改进为动态跟踪目标
(36) $\left. \!\! \begin{array}{l} \hat {v} = \dot {\phi }(t) \\ \dot {\hat {\theta }} = k(s)v(t),\quad s = \int_0^t {v(\tau )d\tau } \\ \end{array} \!\! \right \}$
这里,$\hat v=\dot \phi(t)$ 可以根据实际需要进行设计,$v(t)$ 是实际前向速度, 式 (36) 可称之为动态跟踪目标.
$\phi (t) = - (\beta t + 1)l{\rm e}^{ - \beta t} + l $
(37) $\dot {\phi }(t) = l\beta ^2t {\rm e}^{ - \beta t}$
在实际应用中,由于初始时刻轮式移动结构都是静止的,利用前向速度目标 (37) 可以使得跟踪控制问题的初始速度误差为零,并可以根据实际需要调节参数 $\beta$ 使得整个过程跟踪控制的效果最好.
5.2 动态跟踪目标的优点
与静态速度目标 (9) 相比,采用动态跟踪目标 (36) 具有两个明显的优点:
(1) 速度误差 (尤其初始速度误差) 不会累积成越来越大的位置误差. 由于动态跟踪目标直接指向目标曲线的本质-曲率,当实际前向速度偏大时,方程 (36) 第二式所给的偏航转速目标也变得更大,只要控制过程中的偏航转速误差足够小,也即曲率跟踪误差足够小,就能保证轮式移动结构不偏离给定轨道向外偏转. 反之,若实际前向速度偏小,那么方程 (36) 第二式所给出的偏航转速目标也会相应变小,只要曲率跟踪误差小就能保证轮式移动结构不偏离给定轨道向内偏转. 因此,尽管在整个运动过程中存在很大的前向速度误差,但采用动态跟踪目标能够保证轮式移动结构始终在给定轨道上运动.
(2) 前向速度目标可以根据实际需要进行设计,这在实际应用中非常重要. 由于对前向速度目标无限制要求,而采用不同的前向速度目标,所导致的结果仅仅是整个运动过程中轮式移动结构运动快慢不同而已. 另外,考虑到轮胎最大静摩擦力是有限的,因此实际控制力矩最好不要超过该最大静摩擦力. 这里我们可以通过设计小一些的前向速度目标,使得实际需要的控制力矩尽量小于轮胎的最大静摩擦力,以免轮胎打滑严重影响跟踪控制效果.
5.3 基于动态跟踪目标的控制仿真
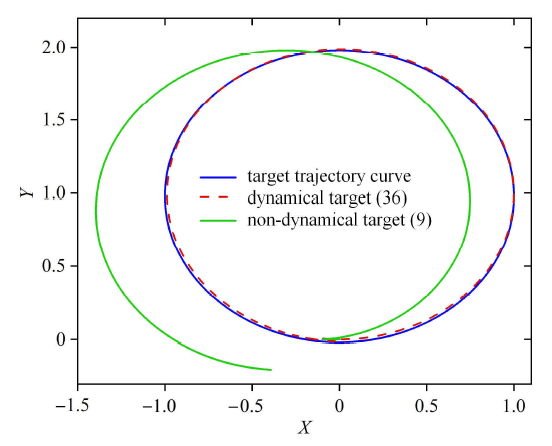
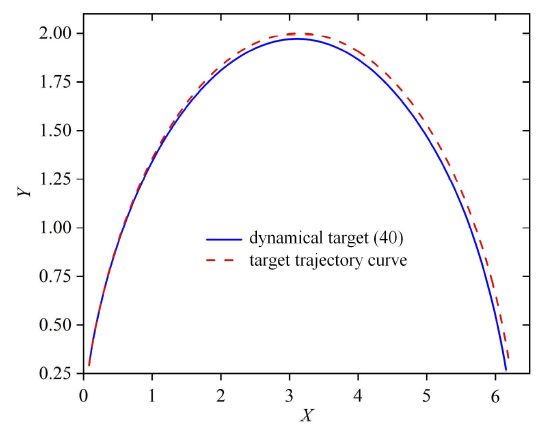
以单位圆为目标轨迹曲线为例,由于目标 曲线的相对曲率是常数 1,文献[30 ] 中将偏航转速目标设计为实际的前向速度,这样设计的动态跟踪目标恰好是 式 (36) 的特殊情形. 由于两轮式倒立摆的动力学方程是非线性的,原问题转化为非线性系统的轨迹跟踪控制问题. 为此,我们先利用反馈线性化方法将系统 转化为线性系统,然后基于线性系统利用预测反馈处理输入时滞的影响. 而线性化误差和外部有界扰动整体打包后利用积分滑模控制来处理. 由于所设计的积分滑模面就是两轮式倒立摆需要完成的运动任务对应的状态,因此最终设计的积分滑模控制不但能使两轮式倒立摆在保持摆杆稳定下很好地完成给定的运动任务,整个运动过程还具有很强的鲁 棒性. 如图 7 所示,实际运动轨迹几乎和单位圆是重合的,而采用静态速度目标 (9) 时,实际运动轨迹和目标曲线会有很大的偏差.
图7
图7
两轮式倒立摆在平面上实际运动轨迹
Fig.7
Actual motion trajectory of the two-wheeled inverted pendulum in a plane
文献[30 ] 中给定的目标轨迹曲线是单位圆,是具有常数曲率的特殊曲线. 为了更好地说明采用动态跟踪目标的控制效果,我们考虑独轮沿一个非常数曲率的光滑曲线运动. 假设初始时刻独轮是静止的,需要完成的运动任务轨迹曲线是摆线
$\hat {r} = (\hat {x}(t),\hat {y}(t)) = (t - \sin t,1 - \cos t),\quad t \in \left[ {0,2\pi } \right] $
$k(t) = - \dfrac{1}{4\sin(t / 2)} $
注意到该曲线在端点处的曲率趋于无穷,在应用动态跟踪目标 (36) 进行控制时,会出现极大的数值计算误差. 因此我们选取摆线中不包含上述端点的一段曲线作为目标轨迹曲线
$\hat {r} = \Bigg (t + \dfrac{\pi }{4} - \sin \Big (t + \dfrac{\pi }{4}\Big ), 1 - \cos \Big (t + \dfrac{\pi }{4}\Big )\Bigg ), \ t \in \left[ {0, \dfrac{3}{ 2 }\pi } \right] $
(38) $k(t) = - \dfrac{1}{4\sin \dfrac{t + {\pi }/{4}}{2}}$
$s(t) = \int_0^t \!\!{\sqrt {2 \Big [1-\cos \Big (u + \dfrac{\pi }{4}\Big )\Big ]} } \text{d}u = 4\cos \dfrac{\pi }{ 8}- 4\cos \dfrac{t + {\pi }/{4}}{2} $
整个曲线的弧长为 $l = s\Big (\dfrac{3}{ 2 }\pi \Big ) = 8\cos \dfrac{\pi }{8}$. 将上式反解出 $\cos \dfrac{t + {\pi }/{4}}{2}$,然后解出 $\sin \dfrac{t + {\pi }/{4}}{2}$ 代入 式 (38) 得
(39) $k(s) = - \dfrac{1}{\sqrt {16 - 16\cos ^2\dfrac{\pi }{8} - s^2 + 8s\cos \dfrac{\pi }{8}} }$
(40) $\left.\begin{array}{l} \hat {v} = 2t{\rm e}^{ - \tfrac{1}{2}t} \\ \hat {\omega } = k(s)v(t) \end{array} , \quad s \in \left[ {0, 8\cos \dfrac{\pi }{ 8 }} \right] \right\}$
其中,$s = \int_0^t {v(\tau )} \text{d}\tau $, $\hat {\omega } = \dot {\hat {\theta }}$. 独轮的动力学方程为
(41) $\left.\begin{array}{l} \dot {v} = u_1 \\ \dot {\omega } = u_2 \end{array} \right \}$
其中,$\omega = \dot {\theta }$, $u_1 = \dfrac{r}{I_\omega }T_\omega$, $u_2 = \dfrac{ 1 }{I_z }T_z $. 注意到控制方程 (41) 是解耦的,因此可以先设计 $u_1 $,然后基于实际的前向速度,设计 $u_2 $ 跟踪偏航转速目标.
令 ${\pmb X} = \left[ {x_1 ,x_2 } \right]^{\rm T} = \left[ {s,v} \right]^{\rm T}$,前向速度控制方程改写为二阶状态方程
(42) $\dot{\pmb X} (t) = {\pmb A}{\pmb X} (t) + {\pmb B}{ u}_1 (t)$
其中,${\pmb A} = \left[ \!\!\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array} \!\! \right]$, ${\pmb B} = \left[\begin{array}{c} 0 \\ 1 \end{array}\!\! \right] $.
$\begin{array}{l} \hat {s} = \int_0^t {\hat {v}(\tau )} \text{d}\tau ,\quad \hat{\pmb X} = \left[ {\hat {x}_1 ,\hat {x}_2 } \right]^{\rm T} = \left[ {\hat {s},\hat {v}} \right]^{\rm T} \\ {\pmb Y} (t) = \left[ {y_1 ,y_2 } \right] = {\pmb X} (t) - \hat{\pmb X}(t),\quad {\pmb \eta }(t): = {\pmb A}\hat{\pmb X} - \dot {\hat {\pmb X}} \end{array} $
(43) $\dot{\pmb Y}(t) = {\pmb A}{\pmb Y}(t) + {\pmb B}{ u}_1 (t) + {\pmb \eta }(t)$
要使得整个运动过程中前向速度误差一直保持足够小,可以采用文献[22 ] 中的思想,利用线性二次型最优控制的权重来调节. 由于 式 (40) 中前向速度目标 $\hat {v}$ 是逐渐趋近于零的,且其无穷积分是收敛. 因此可以引入一个无限时域线性二次型性能指标
$J = \dfrac{ 1 }{ 2 }\int_0^{ + \infty } {\left[ {{\pmb Y}^{\rm T}(t){\pmb Q}{\pmb Y}(t) + { u}_1^{\rm T} (t){\pmb R}{ u}_1 (t)} \right]} \text{d}t $
该性能指标中关于前向速度误差的权重取足够大,这样所设计的最优控制能使前向速度误差尽量小. 利用线性二次型最优控制理论,$u_1 $ 设计为
(44) $u_1 (t) = - {\pmb R}^{ - 1}{\pmb B}^T\left[ {{\pmb P} {\pmb Y}(t) + {\pmb b}(t)} \right]$
其中,${\pmb P} \in \mathbb{R}^{2\times 2}, {\pmb b}(t) \in \mathbb{R}^2$ 满足如下方程
$\begin{array}{l} - {\pmb P}{\pmb A} - {\pmb A}^{\rm T}{\pmb P} + {\pmb P}{\pmb B}{\pmb R}^{ - 1}{\pmb B}^{\rm T}{\pmb P} - {\pmb Q} = 0 [2mm] \dot{\pmb b} = - \left[ {{\pmb A} - {\pmb B}{\pmb R}^{ - 1} {\pmb B}^{\rm T}{\pmb P}} \right]^{\rm T}{\pmb b} - {\pmb P}{\pmb \eta }(t),\quad {\pmb b}( + \infty ) = {\bf 0} \end{array} $
针对偏航转速控制系统,可以采用文献[25 ] 中的积分滑模思想设计积分滑模控制器. 令 $z = \omega - \hat {\omega }$,则系统 (41) 的第二式可转化为误差控制系统
其中,$\hat {u}_2 = u_2 - \dot {\hat {\omega }}$,而
$\dot {\hat {\omega }} = \dfrac{4\cos \dfrac{\pi }{8} - s}{\Big (8 - 4\sqrt 2 - s^2 + 8s\cos \dfrac{\pi }{8}\Big )^{\tfrac{3}{2}}}v^2 + k(s)u_1 $
将 $\hat {u}_2 $ 设计为 $\hat {u}_2 = - kz$,则原偏航转速系统的控制器的基础部分可以设计为
$u_{20} = - kz + \dot {\hat {\omega }} $
其中 $k$ 是控制增益参数 (后面所有仿真中 $k = 40)$. 然后将动态跟踪目标设计为积分滑模面 $\varGamma (\omega (t)) = 0$,其中 $G > 0$ 是合适的常数
$\varGamma (\omega (t)): = G\left[ {\omega (t) - \omega (0)} \right] - G\int_0^t {\dot {\hat {\omega }}(\rho )} \text{d}\rho $
$u_{21} (t) = - G^{ - 1}(\mu + GD\left| {\hat {\omega } - \omega } \right|) \cdot {\rm sgn} [\varGamma (\omega (t))] $
其中 $\mu $ 是滑模控制参数,$D$ 是外部扰动的最大振幅. 最终 $u_2 $ 设计为
(45) $u_2 (t) = u_{20} (t) + u_{21} (t)$
(46) $\left.\begin{array}{l} \hat {v} = 2\sin \dfrac{t + {\pi }/{4}}{ 2 } ,\\ \hat {\omega } = k(t)\hat {v}(t) = - \dfrac{ 1 }{ 2 }, \\ \end{array} \quad t \in \left[ {0, \dfrac{3}{ 2 }\pi } \right] \right\}$
若同样采用式 (44) 和式 (45) 作为控制器,由于 $\hat v$ 不是逐渐趋于零的,从文献[22 ] 的分析可知,此时不能采用无限时域的性能指标,而必须采用有限时域性能指标,导致对应的黎卡提微分方程很难求解,控制器设计变得困难. 而采用动态目标 (40) 时,只需求解代数黎卡提方程,控制器设计变得简单.
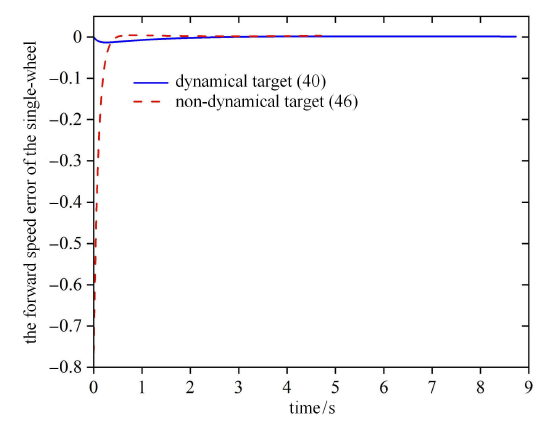
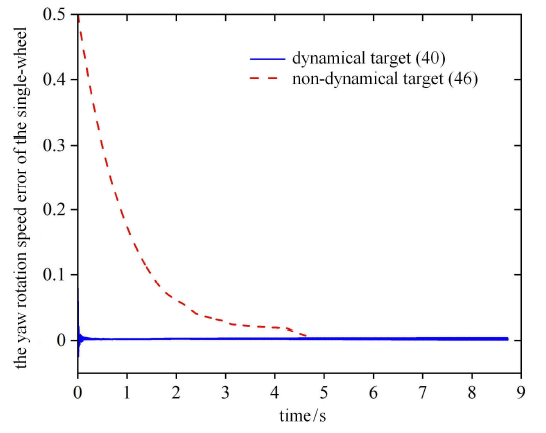
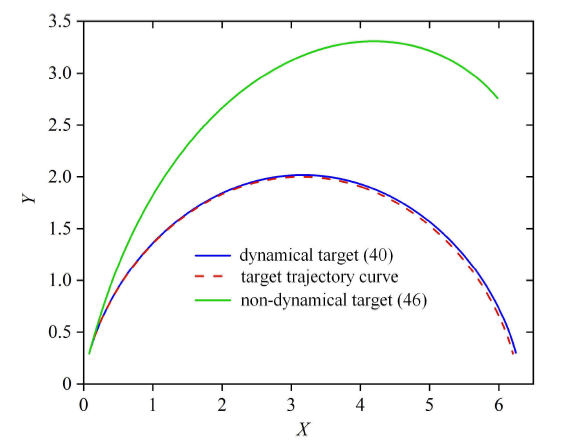
一般来说,采用静态目标 (46) 时,会使得误差系统的初始值不为零. 而采用动态目标 (40) 时,可以根据实际需要设计合适的前向速度目标,使得初始速度误差为零. 如图 8 和图 9 所示,明显采用静态跟踪目标时的速度累积误差会远远大于采用动态跟踪目标时. 而累积速度误差大自然会导致累积位置误差也很大,使最终得到的实际轨迹曲线严重偏离目标曲线. 如图 10 所示,采用动态跟踪目标 (40) 时,实际轨迹偏差非常小,而采用静态跟踪目标 (46) 时,实际轨迹严重偏离目标曲线. 另外,图8 和图 9 中红色的线在大概一半的时间时就结束了,这是因为采用静态目标 (46) 时的实际平均速度要比采用动态目标 (40) 时更快,提前完成了运动任务.
图8
图8
独轮的前向速度误差
Fig.8
Forward speed error of the single-wheel
图9
图9
独轮的偏航转速误差
Fig.9
Yaw rotation speed error of the single-wheel
图10
图10
独轮在平面上实际运动轨迹
Fig.10
Actual motion trajectory of the single-wheel
实事上,在采用动态跟踪目标 (40) 时,由于偏航转速目标是根据实际前向速度时时调整的,能够极大地减少累积位置误差. 即使前向速度误差非常大甚至误差系统不稳定,只要偏航转速目标能被精确跟踪,就能保证独轮沿着给定的目标轨迹曲线运动. 考虑误差系统 (43) 受到未知扰动 $ {\pmb d}(t)$ 影响的情形
(47) $\dot{\pmb Y}(t) = {\pmb A}{\pmb Y}(t) + {\pmb B}{\pmb u}_1 (t) + {\pmb \eta }(t) + {\pmb d}(t)$
当 ${\pmb d}(t) = \left[ {5y_ 1 ,10.5y_2 } \right]^{\rm T}$时,若在${\pmb d}(t)$ 的影响下继续采用控制器 (44) 和 (45),则此时误差系统 (47) 会变得不稳定,其前向速度误差如图 11 所示. 但从图 12 可以看出,虽然前向速度误差很大,但由于采用了动态跟踪目标 (40),其实际运动轨迹依然和目标曲线非常接近,实现了任务目标精确跟踪的目的.
图11
图11
${\pmb d}(t)$ 影响下独轮的前向速度误差
Fig.11
Forward speed error of the single-wheel under the effect of ${\pmb d}(t)$
图12
图12
${\pmb d}(t)$ 影响下独轮在平面上实际运动轨迹
Fig.12
Actual motion trajectory of the single-wheel under the effect of ${\pmb d}(t)$
6 结论
不同类型轮式移动结构在平面上不发生横向滑动时都会受到一个共同的非完整约束,该非完整约束本质上就是质点沿平面光滑曲线运动时沿与切向垂直的横向方向的速度为零. 本文理清了各轮式移动结构的所有约束方程,在此基础上,给出了基于 Euler-Lagrange 方程建立不同轮式移动结构动力学方程的一般方法. 另外,基于该非完整约束,我们可以将目标轨迹曲线转化为速度目标的形式,然后引入相对曲率设计动态跟踪目标. 仿真结果显示,即使前向速度跟踪误差非常大,甚至前向速度误差系统不稳定,采用动态跟踪目标都能保证轮式移动结构不偏离给定目标轨迹曲线. 还可以通过设计合适的前向速度目标使得跟踪的效果达到最好.
本文所提出的动态跟踪目标方法从根本上解决了轨迹曲线精确跟踪的问题,其他任何先进控制设计方法仅仅从控制设计的角度是达不到这样的精确效果的. 实事上,受到该非完整约束的各类型机械结构的精确运动控制问题都可以采用动态跟踪目标方法. 甚至只要是需要精确跟踪给定光滑轨迹曲线的控制问题,都可以采用该方法,达到精确跟踪的目的. 进一步地,后续工作还可以引入挠率,将动态跟踪目标方法推广到空间轨迹曲线的情形,这将大大扩展动态跟踪目标思想的应用范围.
致谢
衷心地感谢审稿人认真审阅我们的论文,给出的宝贵意见使论文得到极大的改进.
参考文献
View Option
[1]
Chan RPM Stol KA Halkyard CR . Review of modelling and control of two-wheeled robots
Annual Reviews in Control 2013 ,37 (1 ):89 -103
DOI
URL
[本文引用: 2]
In the past decade, there has been much more research in two-wheeled robots which actively stabilize themselves. Various models and controllers have been applied both to explain and control the dynamics of two-wheeled robots. We explore the methods which have been investigated and the controllers which have been used, first for balancing and movement of two-wheeled robots on flat terrain, then for two-wheeled robots in other situations, where terrain may not be flat, where there may be secondary objectives and where the robots may have additional actuators. (C) 2013 Elsevier Ltd. All rights reserved,
[2]
Li ZJ Yang CG Fan LP . Advanced Control of Wheeled Inverted Pendulum Systems
London, Springer , 2013
[3]
Cui RX Guo J Mao ZY . Adaptive backstepping control of wheeled inverted pendulums models
Nonlinear Dynamics 2015 ,79 (1 ):501 -511
DOI
URL
[本文引用: 1]
[4]
阮晓钢 , 蔡建羡 , 李欣源 等 . 两轮自平衡机器人的研究与设计 . 北京 : 科学出版社 , 2012 : 1 -12
[本文引用: 1]
( Ruan Xiaogang Cai Jianxin Li Xinyuan , et al . The Study and Design of Two-Wheeled Self-Balancing Robot . Beijing : Science Press , 2012 : 1 -12 (in Chinese))
[本文引用: 1]
[5]
Grasser F D'Arrigo A Colombi S , et al . JOE: A mobile inverted pendulum
IEEE Transaction on Industrial Electronics 2012 ,49 (1 ):107 -114
DOI
URL
[本文引用: 1]
[6]
侯忠生 , 许建新 . 数据驱动控制理论及方法的回顾和展望
自动化学报 , 2009 ,35 (6 ):650 -667
DOI
URL
[本文引用: 1]
The definitions and concepts of data-driven controltheories and designs are described in this paper. The motivation andnecessity for data-driven control are discussed from the aspects oftheory, applications and the history of system control. Thestate-of-art of the existing data-driven control methods arepresented with appropriate classifications and insights, and thedifferences among these methods and the application scopes are alsohighlighted. Finally, the perspective of data-driven control andassociated research topics are also briefly explored and discussed.
( Hou Zhongsheng Xu Jianxin . On data-driven control theory: the state of the art and perspective
Acta Automatica Sinica 2009 ,35 (6 ):650 -667 (in Chinese))
DOI
URL
[本文引用: 1]
The definitions and concepts of data-driven controltheories and designs are described in this paper. The motivation andnecessity for data-driven control are discussed from the aspects oftheory, applications and the history of system control. Thestate-of-art of the existing data-driven control methods arepresented with appropriate classifications and insights, and thedifferences among these methods and the application scopes are alsohighlighted. Finally, the perspective of data-driven control andassociated research topics are also briefly explored and discussed.
[7]
谭跃刚 . 非完整机器人的原理与控制 . 北京 : 科学出版社 , 2011 : 12 -32
[本文引用: 1]
( Tan Yuegang . The Principle and Control of Nonholonomic Robots . Beijing : Science Press , 2011 : 12 -32 (in Chinese))
[本文引用: 1]
[8]
胡海岩 . 论力学系统的自由度
力学学报 , 2018 ,50 (5 ):1135 -1144
[本文引用: 1]
( Hu Haiyan . On the degrees of freedom of a mechanical system
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (5 ):1135 -1144 (in Chinese))
[本文引用: 1]
[9]
葛一敏 , 袁海辉 , 甘春标 . 基于步态切换的欠驱动双足机器人控制方法
力学学报 , 2018 ,50 (4 ):871 -879
URL
[本文引用: 1]
( Ge Yimin Yuan Haihui Gan Chunbiao . Control method of an underactuated biped robot based on gait transition
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (4 ):871 -879 (in Chinese))
URL
[本文引用: 1]
[10]
付晓东 , 陈力 . 全柔性空间机器人运动振动一体化输入受限重复学习控制
力学学报 , 2020 ,52 (1 ):171 -183
[本文引用: 1]
( Fu Xiaodong Chen Li . An input limited repetitive learning control of flexible-base two-flexible-link and two-flexible-joint space robot with integration of motion and vibration
Chinese Journal of Theoretical and Applied Mechanics 2020 ,52 (1 ):171 -183 (in Chinese))
[本文引用: 1]
[11]
Bloch AM Bailliewl J Crouch P , et al . Nonholonomic Mechanics and Control
Second Edition, New York: Springer-verlag , 2004
[本文引用: 1]
[12]
Liu HG Shi DH . Optimal control of a mobile robot on sphere
Theoretical & Applied Mechanics Letters 2019 ,9 (1 ):34 -38
[本文引用: 1]
[13]
Murry RM Sastry SS . Nonholonomic motion planning: Steering using sinusoids
IEEE Transaction on Automatic Control 1993 ,38 (5 ):700 -716
DOI
URL
[本文引用: 1]
[14]
Godhavn J Egeland O . A Lyapunov approach to exponential stabilization of nonholonomic systems in power form
IEEE Transactions on Automatic Control 1997 ,42 (7 ):1028 -1032
DOI
URL
[本文引用: 1]
[15]
Tilbury R Murray RM Sastry SS . Trajectory generation for the n-trailer problem using goursat normat form
IEEE Transactions on Automatic Control 1995 ,40 (5 ):802 -819
DOI
URL
[本文引用: 1]
[16]
Yang CG Li ZJ Cui RX , et al . Neural network-based motion control of underactuated wheeled inverted pendulum models
IEEE Transactions on Neural Networks and Learning Systems 2014 ,25 (11 ):2004 -2016
DOI
URL
[本文引用: 1]
In this paper, automatic motion control is investigated for wheeled inverted pendulum (WIP) models, which have been widely applied for modeling of a large range of two wheeled modern vehicles. First, the underactuated WIP model is decomposed into a fully actuated second-order subsystem Sigma(a) consisting of planar movement of vehicle forward motion and yaw angular motions, and a passive (nonactuated) first-order subsystem Sigma(b) of pendulum tilt motion. Due to the unknown dynamics of subsystem Sigma(a) and universal approximation ability of neural network (NN), an adaptive NN scheme has been employed for motion control of subsystem Sigma(a). Model reference approach has been used, whereas the reference model is optimized by finite time linear quadratic regulation technique. Inspired by human control strategy of inverted pendulum, the tilt angular motion in the passive subsystem Sigma(b) has been indirectly controlled using the dynamic coupling with planar forward motion of subsystem Sigma(a), such that the satisfactory tracking of set tilt angle can be guaranteed. Rigorous theoretic analysis has been established, and simulation studies have been performed to demonstrate the developed method.
[17]
Huang J Ri MH Wu DR . Interval type-2 fuzzy logic modeling and control of a mobile two-wheeled inverted pendulum
IEEE Transactions on Fuzzy Systems 2018 ,26 (4 ):2030 -2038
DOI
URL
[本文引用: 1]
[18]
Yue M An C Da Y , et al . Indirect adaptive fuzzy control for a nonholonomic/underactuated wheeled inverted pendulum vehicle based on a data-driven trajectory planner
Fuzzy Sets & Systems 2016 ,290 :158 -177
[本文引用: 1]
[19]
Yue M Wang S Sun JZ . Simultaneous balancing and trajectory tracking control for two-wheeled inverted pendulum vehicles: A composite control approach
Neurocomputing 2016 ,191 :44 -54
DOI
URL
[本文引用: 1]
[20]
Wen CY Huang JS Wang W , et al . Adaptive output feedback tracking control of a nonholonomic mobile robot
Automatica 2014 ,50 (3 ):821 -831
DOI
URL
[本文引用: 1]
An adaptive output feedback tracking controller for nonholonomic mobile robots is proposed to guarantee that the tracking errors are confined to an arbitrarily small ball. The major difficulties are caused by simultaneous existence of nonholonomic constraints, unknown system parameters and a quadratic term of unmeasurable states in the mobile robot dynamic system as well as their couplings. To overcome these difficulties, we propose a new adaptive control scheme including designing a new adaptive state feedback controller and two high-gain observers to estimate the unknown linear and angular velocities respectively. It is shown that the closed loop adaptive system is stable and the tracking errors are guaranteed to be within the pre-specified bounds which can be arbitrarily small. Simulation results also verify the effectiveness of the proposed scheme. (C) 2014 Elsevier Ltd.
[21]
彭海军 , 李飞 , 高强 等 . 多体系统轨迹跟踪的瞬时最优控制保辛方法
力学学报 , 2016 ,48 (4 ):784 -791
DOI
URL
[本文引用: 1]
With the wide application of robot in various fields, the new requirement on dynamics and control performance for robot has been continually proposed. Especially for the intelligent robot with much more complex system and flexibility of operation, the high accuracy of trajectory tracking should be satisfied for practical mission requirement. Therefore, the aim of this paper is to satisfy the requirement of trajectory tracking mission of robot multibody system, and then the symplectic method based on differential-algebraic equations for instantaneous optimal control is proposed. First, the general dynamic equation of robot should be established by absolute coordinates of multibody system, i.e., differential-algebraic equations; then, the differential-algebraic equations are discretized in the domain of continuoustime by symplectic method, and then the present position/velocity/Lagrange multiplier are taken as unknown variables of nonlinear equations; afterward, the combination of objective tracking trajectory and weighted control input are introduced as the performance of instantaneous optimal control. The optimal control input is obtained by the theory of instantaneous optimal control; finally, the tracking mission for the objective trajectory can be continuously implemented with the updated time step. In order to test the effectiveness of the proposed method, the trajectory tacking problem of double pendulum is taken as an example, and numerical simulations show that the proposed symplectic method for instantaneous optimal control can obtain high accuracy tracking results, meanwhile, the proposed symplectic method based on differential-algebraic equations can be applied for other trajectory tracking mission of complex multibody system.
( Peng Haijun Li Hui Gao Qiang , et al . Symplectic method for instantaneous optimal control of multibody system trajectory tracking
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (4 ):784 -791 (in Chinese))
DOI
URL
[本文引用: 1]
With the wide application of robot in various fields, the new requirement on dynamics and control performance for robot has been continually proposed. Especially for the intelligent robot with much more complex system and flexibility of operation, the high accuracy of trajectory tracking should be satisfied for practical mission requirement. Therefore, the aim of this paper is to satisfy the requirement of trajectory tracking mission of robot multibody system, and then the symplectic method based on differential-algebraic equations for instantaneous optimal control is proposed. First, the general dynamic equation of robot should be established by absolute coordinates of multibody system, i.e., differential-algebraic equations; then, the differential-algebraic equations are discretized in the domain of continuoustime by symplectic method, and then the present position/velocity/Lagrange multiplier are taken as unknown variables of nonlinear equations; afterward, the combination of objective tracking trajectory and weighted control input are introduced as the performance of instantaneous optimal control. The optimal control input is obtained by the theory of instantaneous optimal control; finally, the tracking mission for the objective trajectory can be continuously implemented with the updated time step. In order to test the effectiveness of the proposed method, the trajectory tacking problem of double pendulum is taken as an example, and numerical simulations show that the proposed symplectic method for instantaneous optimal control can obtain high accuracy tracking results, meanwhile, the proposed symplectic method based on differential-algebraic equations can be applied for other trajectory tracking mission of complex multibody system.
[22]
Zhou YS Wang ZH . Motion controller design of wheeled inverted pendulum with an input delay via optimal control theory
Journal of Optimization Theory and Applications 2016 ,168 (2 ):625 -645
DOI
URL
[本文引用: 5]
[23]
Kim Y Kim SH Kwak YK . Dynamic analysis of a nonholonomic two-wheeled inverted pendulum robot
Journal of Intelligent and Robotic Systems 2005 ,44 (1 ):25 -46
DOI
URL
[本文引用: 1]
[24]
Kim S Kwon SJ . Dynamic modeling of a two-wheeled inverted pendulum balancing mobile robot
International Journal of Control, Automation and Systems 2015 ,13 (4 ):926 -933
[本文引用: 1]
[25]
Zhou YS Wang ZH . Robust motion control of a two-wheeled inverted pendulum with an input delay based on optimal integral sliding mode manifold
Nonlinear Dynamics 2016 ,85 (3 ):2065 -2074
DOI
URL
[本文引用: 2]
[26]
Ning YG Yue M Yang L , et al . A trajectory planning and tracking control approach for obstacle avoidance of wheeled inverted pendulum vehicles
International Journal of Control 2018 : 1 -11
[本文引用: 1]
[27]
Yue M Hou XQ Hou WB . Composite path tracking control for tractor-trailer vehicles via constrained model predictive control and direct adaptive fuzzy techniques
Journal of Dynamic Systems 2017 ,139 :111008 -1
[本文引用: 1]
[28]
Hou XQ Yue M Zhao J , et al . An ESO-based integrated trajectory tracking control for tractor-trailer vehicles with various constraints and physical limitations
International Journal of Systems Science 2018 ,49 (15 ):3202 -3215
DOI
URL
[本文引用: 1]
[29]
Yue M Hou XQ Gao RJ . Trajectory tracking control for tractor-trailer vehicles: A coordinated control approach
Nonlinear Dynamics 2018 ,91 :1061 -1074
DOI
URL
[本文引用: 1]
[30]
Zhou YS Wang ZH Chung KW . Turning motion control design of a two-wheeled inverted pendulum using curvature tracking and optimal control
Journal of Optimization Theory and Applications 2019 ,181 (2 ):634 -652
[本文引用: 2]
Review of modelling and control of two-wheeled robots
2
2013
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
... 两轮式倒立摆是一类经典欠驱动的非完整系统,在实际中应用广泛,相应的运动规划和控制研究非常多[1 ,22 ] . 如图 3 所示,假设两轮无侧滑无空转,左右两轮各安装一个驱动马达,通过驱动左右两轮转动来实现两轮式倒立摆的运动和摆杆平衡. ...
Advanced Control of Wheeled Inverted Pendulum Systems
2013
Adaptive backstepping control of wheeled inverted pendulums models
1
2015
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
1
2012
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
1
2012
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
JOE: A mobile inverted pendulum
1
2012
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
数据驱动控制理论及方法的回顾和展望
1
2009
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
数据驱动控制理论及方法的回顾和展望
1
2009
... 轮式移动结构是一种通过驱动轮子转动来实现运动功能的经典机械模型,具有能耗小和操作方便等优点. 尤其是独轮和两轮移动结构占地小且运动灵活,能够实现很多复杂的运动功能. 因此在很多机械结构中需要加入轮式滚动接触机构,尤其在机器人、航空航天和机械制造等领域应用十分广泛. 目前在商业领域中有独轮结构 Unicycle,两轮结构 Segway PT,三轮结构摩托车,四轮结构汽车和更多轮的拖-挂车. 轮式机器人在近二十年是一个非常热门的研究领域,相关的建模、路径规划和控制设计研究很多[1 -3 ] . 而在工业领域,很多公司研制了自己特色的轮式移动机器人[4 ] . 2002 年,Grasser 等[5 ] 研制了两轮式移动机器人 Joe,通过解耦分别驱动控制两轮转速,使得机器人的灵活性达到前所未有的水平. 2007 年,德国 Fraunhofer 等研制出一款货物搬运机器人,该机器人配备了红外线传感器,能到达指定地点搬运货物. 2017 年,谷歌母公司 Alphabet 发布了一款集轮子和腿为一体的机器人 Handle,能够俯身跳跃和货物搬运,具有非常优秀的平衡能力. 虽然工业界研发的轮式机器人功能越来越强大,但这一切在很大程度上应归功于发达的测量技术和强大的数据处理能力. 从理论上来说,只要能够测量足够多的精确数据,并能很好地处理这些数据,就可以不需要实际模型,而直接基于数据驱动设计轨迹跟踪控制器[6 ] . 但毫无疑问,这样做的成本是高昂的,因为实际模型本身就是一种已知信息,放弃这么重要的信息无疑是一种巨大的浪费. 正确的做法应该是尽量利用实际模型和观测信息,结合现代控制理论设计精确高效的低成本控制器. ...
1
2011
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
1
2011
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
论力学系统的自由度
1
2018
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
论力学系统的自由度
1
2018
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
基于步态切换的欠驱动双足机器人控制方法
1
2018
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
基于步态切换的欠驱动双足机器人控制方法
1
2018
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
全柔性空间机器人运动振动一体化输入受限重复学习控制
1
2020
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
全柔性空间机器人运动振动一体化输入受限重复学习控制
1
2020
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
Nonholonomic Mechanics and Control
1
2004
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
Optimal control of a mobile robot on sphere
1
2019
... 具有滚动接触的结构在运动时会受到非完整约束[7 ] ,它是对系统运动速度的限制,并且不可积. 与完整约束限制系统的位形不同,非完整约束是系统状态空间上的约束,主要是对系统运动速度的限制. 在无任何约束的控制作用下,非完整移动结构可以在整个位形空间内运动. 因此,一般来说非完整约束的强度要比完整约束要弱,文献[8 ] 指出,在计算非完整约束力学系统的自由度时,每一个非完整约束可以使得系统减少 0.5 个自由度. 由于非完整约束结构本质上还是欠驱动的,导致其路径规划和跟踪控制设计都比较困难[9 -10 ] . 文献[11 ] 基于几何观点在拉格朗日和哈密顿框架下建立非完整约束力学系统的动力学方程,并讨论了在非完整约束下力学系统的可控性和控制器设计问题. 文献[12 ] 提出采用 Pontryagin 极大值原理的 Hamel 形式来解决移动机器人在球面上受非完整约束下的最优控制问题. ...
Nonholonomic motion planning: Steering using sinusoids
1
1993
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
A Lyapunov approach to exponential stabilization of nonholonomic systems in power form
1
1997
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Trajectory generation for the n-trailer problem using goursat normat form
1
1995
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Neural network-based motion control of underactuated wheeled inverted pendulum models
1
2014
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Interval type-2 fuzzy logic modeling and control of a mobile two-wheeled inverted pendulum
1
2018
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Indirect adaptive fuzzy control for a nonholonomic/underactuated wheeled inverted pendulum vehicle based on a data-driven trajectory planner
1
2016
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Simultaneous balancing and trajectory tracking control for two-wheeled inverted pendulum vehicles: A composite control approach
1
2016
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Adaptive output feedback tracking control of a nonholonomic mobile robot
1
2014
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
多体系统轨迹跟踪的瞬时最优控制保辛方法
1
2016
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
多体系统轨迹跟踪的瞬时最优控制保辛方法
1
2016
... 要想精确控制轮式移动结构的运动,必须同时 清楚其运动学方程和动力学方程,而其动力学方程又需要利用运动学方程结合 Euler-Lagrange 方程推导出来. 目前很多研究仅仅针对其运动学方程,将约束方程转化为标准链式系统的形式[13 ] ,然后利用相关链式或幂式系统的控制理论设计速度控制器[14 -15 ] . 但在实际问题中,实现运动任务所需要的速度是通过力或力矩来实现的,应该设计力或力矩控制器. 另外一些研究仅仅针对其动力学方程,考虑跟踪给定的前向速度和偏航转速目标,设计自适应模糊或神经网络控制实现给定跟踪任务[16 -17 ] . 但所给定的前向速度和偏航转速目标所对应的几何轨迹是什么并不清楚. 而实际问题需要设计跟踪控制使得轮式移动结构能够精确地沿着给定的目标轨迹曲线运动. 因此,必须同时考虑其运动学方程和动力学方程,设计力或力矩控制器使机器人实现给定的运动任务. 但是,目前已有的文献对轮式非完整约束的运动规律理解还不深入,很多研究成果侧重于从控制理论的角度进行控制设计与分析,很少有研究能将轮式非完整约束下的运动规律与机器人运动控制设计有机结合起来. 如文献[18 ,19 ] 中,将前向速度和偏航转速同时看成是运动方程的控制输入变量和动力学方程的状态输出变量,基于中间变量来设计自适应模糊跟踪控制器. 文献[20 ] 中利用两个高增益观测器来估计两轮式移动结构的前向速度和偏航转速,然后在此基础上设计自适应反馈控制器来实现圆周运动. 文献[21 ] 采用保辛算法将多体系统连续时间域内的动力学方程进行离散化,再用瞬时最优控制保辛方法实现对目标轨迹的高精度跟踪. ...
Motion controller design of wheeled inverted pendulum with an input delay via optimal control theory
5
2016
... 两轮式倒立摆是一类经典欠驱动的非完整系统,在实际中应用广泛,相应的运动规划和控制研究非常多[1 ,22 ] . 如图 3 所示,假设两轮无侧滑无空转,左右两轮各安装一个驱动马达,通过驱动左右两轮转动来实现两轮式倒立摆的运动和摆杆平衡. ...
... 两轮式倒立摆的摆杆稳定是通过整个结构前后运动的耦合作用来实现的,这里面受力分析比较复杂. 目前求解其动力学方程的方法主要有 Newton 法[23 ] 、Kane 法[24 ] 和 Euler-Lagrange 方法. 相对来说,Newton 法和 Kane 法都比较繁琐. 这里我们采用 Euler-Lagrange 方程来建立其动力学方程[22 ] . ...
... 采用 Euler-Lagrange 方程来求解两轮式倒立摆的动力学方程[22 ] . 假设 $M_\omega $ 和 $M$ 分别是轮子和中间体质量,$I_\omega $ 和 $I_{\omega d} $ 分别是轮子绕轮轴方向和 $z$ 轴方向的转动惯量,$I_B $ 和 $I_{z} $ 分别是中间体绕轮轴方向和 $z$ 轴方向的转动惯量. ...
... 要使得整个运动过程中前向速度误差一直保持足够小,可以采用文献[22 ] 中的思想,利用线性二次型最优控制的权重来调节. 由于 式 (40) 中前向速度目标 $\hat {v}$ 是逐渐趋近于零的,且其无穷积分是收敛. 因此可以引入一个无限时域线性二次型性能指标 ...
... 若同样采用式 (44) 和式 (45) 作为控制器,由于 $\hat v$ 不是逐渐趋于零的,从文献[22 ] 的分析可知,此时不能采用无限时域的性能指标,而必须采用有限时域性能指标,导致对应的黎卡提微分方程很难求解,控制器设计变得困难. 而采用动态目标 (40) 时,只需求解代数黎卡提方程,控制器设计变得简单. ...
Dynamic analysis of a nonholonomic two-wheeled inverted pendulum robot
1
2005
... 两轮式倒立摆的摆杆稳定是通过整个结构前后运动的耦合作用来实现的,这里面受力分析比较复杂. 目前求解其动力学方程的方法主要有 Newton 法[23 ] 、Kane 法[24 ] 和 Euler-Lagrange 方法. 相对来说,Newton 法和 Kane 法都比较繁琐. 这里我们采用 Euler-Lagrange 方程来建立其动力学方程[22 ] . ...
Dynamic modeling of a two-wheeled inverted pendulum balancing mobile robot
1
2015
... 两轮式倒立摆的摆杆稳定是通过整个结构前后运动的耦合作用来实现的,这里面受力分析比较复杂. 目前求解其动力学方程的方法主要有 Newton 法[23 ] 、Kane 法[24 ] 和 Euler-Lagrange 方法. 相对来说,Newton 法和 Kane 法都比较繁琐. 这里我们采用 Euler-Lagrange 方程来建立其动力学方程[22 ] . ...
Robust motion control of a two-wheeled inverted pendulum with an input delay based on optimal integral sliding mode manifold
2
2016
... 要使两轮式倒立摆的中心点 $O$ 沿给定的轨迹曲线运动,并且整个运动过程中摆角 $\varphi $ 始终保持足够小,该如何设计控制器 $(u_1 ,u_2)$ 呢? 利用 式 (9) 将目标轨迹曲线 $\hat {r} = (\hat {x}(t), \hat {y}(t))$ 转化为速度目标的形式,结合式 (23) 的后两式可将原问题转化为一般的轨迹跟踪控制问题. 另外,动力学方程 (23) 可以解耦成两个控制子系统,可以分别设计控制器 $u_2 $ 和 $u_1 $. 在文献[25 ] 中, 通过引入关于摆角 $\varphi$ 的大权重性能指标,对摆角 $\varphi $ 进行线性化后将得到的线性系统看成标称系统,然后设计关于性能指标的最优积分滑模控制器以实现两轮式倒立摆的往返运动. ...
... 针对偏航转速控制系统,可以采用文献[25 ] 中的积分滑模思想设计积分滑模控制器. 令 $z = \omega - \hat {\omega }$,则系统 (41) 的第二式可转化为误差控制系统 ...
A trajectory planning and tracking control approach for obstacle avoidance of wheeled inverted pendulum vehicles
1
2018
... 前面几节内容已经系统地分析了各类轮式移动结构的约束方程及其动力学方程. 实际上约束方程 (2) 是所有轮式移动结构在无横向滑动时必须满足的非完整约束. 通过分析该约束条件,我们可以利用式 (9) 将轮式移动结构的任务轨迹曲线转化为成速度目标的形式,然后结合其动力学方程将原运动任务转化为一般的轨迹跟踪控制问题. 如文献[26 ] 在考虑轮式倒立摆的避障运动控制时,就将设计好的分段多项式轨迹曲线转化成近似的速度目标形式,然后结合动力学方程设计轨迹跟踪控制器. 文献[27 ,28 ,29 ] 在考虑拖-挂车的轨迹曲线跟踪和避障运动时,就是先将目标轨迹曲线转化为 式 (9) 这样的速度目标,然后采用模型预测等控制方法实现给定的运动任务. 但从这些论文的仿真结果来看,不管采用多么先进的控制设计方法,实际运动轨迹总是会有一些偏离目标轨迹曲线,尤其是在最初始的一段时间内. 出现这样的结果主要原因之一在于所采用的速度目标 (9) 在初始时刻和实际速度相比具有比较大的差值,这个速度误差会累计成很大的位置误差. 另外,如果采用静态速度目标 (9),当前向速度误差控制系统受到未知扰动影响时,会导致实际前向速度偏离给定的前向速度目标,而此时偏航转速目标不能时时地进行调整,这就会导致轮式移动结构偏离目标轨迹曲线. 为了同时解决这两个问题,使轮式移动结构能精确地沿着给定目标轨迹曲线运动,我们将静态速度目标 (9) 改进为动态跟踪目标. ...
Composite path tracking control for tractor-trailer vehicles via constrained model predictive control and direct adaptive fuzzy techniques
1
2017
... 前面几节内容已经系统地分析了各类轮式移动结构的约束方程及其动力学方程. 实际上约束方程 (2) 是所有轮式移动结构在无横向滑动时必须满足的非完整约束. 通过分析该约束条件,我们可以利用式 (9) 将轮式移动结构的任务轨迹曲线转化为成速度目标的形式,然后结合其动力学方程将原运动任务转化为一般的轨迹跟踪控制问题. 如文献[26 ] 在考虑轮式倒立摆的避障运动控制时,就将设计好的分段多项式轨迹曲线转化成近似的速度目标形式,然后结合动力学方程设计轨迹跟踪控制器. 文献[27 ,28 ,29 ] 在考虑拖-挂车的轨迹曲线跟踪和避障运动时,就是先将目标轨迹曲线转化为 式 (9) 这样的速度目标,然后采用模型预测等控制方法实现给定的运动任务. 但从这些论文的仿真结果来看,不管采用多么先进的控制设计方法,实际运动轨迹总是会有一些偏离目标轨迹曲线,尤其是在最初始的一段时间内. 出现这样的结果主要原因之一在于所采用的速度目标 (9) 在初始时刻和实际速度相比具有比较大的差值,这个速度误差会累计成很大的位置误差. 另外,如果采用静态速度目标 (9),当前向速度误差控制系统受到未知扰动影响时,会导致实际前向速度偏离给定的前向速度目标,而此时偏航转速目标不能时时地进行调整,这就会导致轮式移动结构偏离目标轨迹曲线. 为了同时解决这两个问题,使轮式移动结构能精确地沿着给定目标轨迹曲线运动,我们将静态速度目标 (9) 改进为动态跟踪目标. ...
An ESO-based integrated trajectory tracking control for tractor-trailer vehicles with various constraints and physical limitations
1
2018
... 前面几节内容已经系统地分析了各类轮式移动结构的约束方程及其动力学方程. 实际上约束方程 (2) 是所有轮式移动结构在无横向滑动时必须满足的非完整约束. 通过分析该约束条件,我们可以利用式 (9) 将轮式移动结构的任务轨迹曲线转化为成速度目标的形式,然后结合其动力学方程将原运动任务转化为一般的轨迹跟踪控制问题. 如文献[26 ] 在考虑轮式倒立摆的避障运动控制时,就将设计好的分段多项式轨迹曲线转化成近似的速度目标形式,然后结合动力学方程设计轨迹跟踪控制器. 文献[27 ,28 ,29 ] 在考虑拖-挂车的轨迹曲线跟踪和避障运动时,就是先将目标轨迹曲线转化为 式 (9) 这样的速度目标,然后采用模型预测等控制方法实现给定的运动任务. 但从这些论文的仿真结果来看,不管采用多么先进的控制设计方法,实际运动轨迹总是会有一些偏离目标轨迹曲线,尤其是在最初始的一段时间内. 出现这样的结果主要原因之一在于所采用的速度目标 (9) 在初始时刻和实际速度相比具有比较大的差值,这个速度误差会累计成很大的位置误差. 另外,如果采用静态速度目标 (9),当前向速度误差控制系统受到未知扰动影响时,会导致实际前向速度偏离给定的前向速度目标,而此时偏航转速目标不能时时地进行调整,这就会导致轮式移动结构偏离目标轨迹曲线. 为了同时解决这两个问题,使轮式移动结构能精确地沿着给定目标轨迹曲线运动,我们将静态速度目标 (9) 改进为动态跟踪目标. ...
Trajectory tracking control for tractor-trailer vehicles: A coordinated control approach
1
2018
... 前面几节内容已经系统地分析了各类轮式移动结构的约束方程及其动力学方程. 实际上约束方程 (2) 是所有轮式移动结构在无横向滑动时必须满足的非完整约束. 通过分析该约束条件,我们可以利用式 (9) 将轮式移动结构的任务轨迹曲线转化为成速度目标的形式,然后结合其动力学方程将原运动任务转化为一般的轨迹跟踪控制问题. 如文献[26 ] 在考虑轮式倒立摆的避障运动控制时,就将设计好的分段多项式轨迹曲线转化成近似的速度目标形式,然后结合动力学方程设计轨迹跟踪控制器. 文献[27 ,28 ,29 ] 在考虑拖-挂车的轨迹曲线跟踪和避障运动时,就是先将目标轨迹曲线转化为 式 (9) 这样的速度目标,然后采用模型预测等控制方法实现给定的运动任务. 但从这些论文的仿真结果来看,不管采用多么先进的控制设计方法,实际运动轨迹总是会有一些偏离目标轨迹曲线,尤其是在最初始的一段时间内. 出现这样的结果主要原因之一在于所采用的速度目标 (9) 在初始时刻和实际速度相比具有比较大的差值,这个速度误差会累计成很大的位置误差. 另外,如果采用静态速度目标 (9),当前向速度误差控制系统受到未知扰动影响时,会导致实际前向速度偏离给定的前向速度目标,而此时偏航转速目标不能时时地进行调整,这就会导致轮式移动结构偏离目标轨迹曲线. 为了同时解决这两个问题,使轮式移动结构能精确地沿着给定目标轨迹曲线运动,我们将静态速度目标 (9) 改进为动态跟踪目标. ...
Turning motion control design of a two-wheeled inverted pendulum using curvature tracking and optimal control
2
2019
... 以单位圆为目标轨迹曲线为例,由于目标 曲线的相对曲率是常数 1,文献[30 ] 中将偏航转速目标设计为实际的前向速度,这样设计的动态跟踪目标恰好是 式 (36) 的特殊情形. 由于两轮式倒立摆的动力学方程是非线性的,原问题转化为非线性系统的轨迹跟踪控制问题. 为此,我们先利用反馈线性化方法将系统 转化为线性系统,然后基于线性系统利用预测反馈处理输入时滞的影响. 而线性化误差和外部有界扰动整体打包后利用积分滑模控制来处理. 由于所设计的积分滑模面就是两轮式倒立摆需要完成的运动任务对应的状态,因此最终设计的积分滑模控制不但能使两轮式倒立摆在保持摆杆稳定下很好地完成给定的运动任务,整个运动过程还具有很强的鲁 棒性. 如图 7 所示,实际运动轨迹几乎和单位圆是重合的,而采用静态速度目标 (9) 时,实际运动轨迹和目标曲线会有很大的偏差. ...
... 文献[30 ] 中给定的目标轨迹曲线是单位圆,是具有常数曲率的特殊曲线. 为了更好地说明采用动态跟踪目标的控制效果,我们考虑独轮沿一个非常数曲率的光滑曲线运动. 假设初始时刻独轮是静止的,需要完成的运动任务轨迹曲线是摆线 ...