引言
多介质大变形问题广泛存在于军事和民用领域,例如爆炸力学效应、高速冲击问题、武器设计以及自然灾害的防护等. 上述问题通常存在多种介质间强烈的相互作用,具有强耦合、大变形、高度非线性等特点,物理现象极其复杂. 由于各介质之间的物理特性、初始状态差异极大,很多对单介质问题比较有效的数值方法在处理多介质问题时,通常会引起较大的数值震荡和误差[1 -2 ] ,甚至导致计算无法继续,因此需要研究合适的多介质数值计算方法,准确描述不同介质间的相互作用.
多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理.
本文提出了一种基于 Euler 坐标系的非结构网格、具有锐利界面的二维和三维守恒型多介质流动数值方法,可用于模拟可压缩流体和弹塑性固体在极端物理条件下的大变形动力学行为. 利用分片线性的 Level Set 函数清晰重构出分段线性的相界面,建立了单纯形网格内具有多种介质的相界面拓扑结构,理论上可以处理全局任意种介质、局部 3 种介质的多介质流动问题. 提出了一种守恒型的相界面两侧介质相互作用的处理方法,能够保证不同介质间的通量守恒. 提出了一种非结构网格上的单元聚合算法,通过对每个碎片单元建立至少包含一个完整单元的同介质单元片,并对该单元片内的守恒量进行基于单元体积的加权平均,扩大了碎片单元的特征尺度,消除了由于网格被相界面分割成较小碎片、违反 CFL 条件,进而可能带来数值不稳定的问题. 最后对激波-气泡相互作用、浅埋爆炸、空中强爆炸冲击波和典型坑道内冲击波传播问题开展了数值模拟,验证了数值方法的可靠性和计算效率.
1 物理模型
1.1 控制方程
考虑二、三维计算区域上的多介质流动问题,基于 Euler 坐标系描述可压缩流体和弹塑性固体的大变形动力学行为,其控制方程组如式 (1) 所示
(1) $\dfrac{\partial {\pmb U}}{\partial t}+\nabla \cdot {\pmb F}({\pmb U})={\pmb H}({\pmb U})$
$ {\pmb U} = \left( \!\! \begin{array}{l} \rho \\ \rho {\pmb u} \\ E \end{array} \!\! \right), \ {\pmb F}({\pmb U}) = \left(\!\! \begin{array}{l} \rho {\pmb u}^{\rm T} \\ \rho {\pmb u} \otimes {\pmb u} + p{\pmb I} - {\pmb S} \\ (E + p) {\pmb u} - {\pmb S} \cdot {\pmb u} \end{array} \!\! \right), \ {\pmb H}({\pmb U}) = \left(\!\! \begin{array}{c} 0 \\ {\bf 0} \\ 0 \end{array} \!\! \right) $
其中, $\rho $ 表示密度,${\pmb u}$ 表示速度矢量,$E$ 表示单位体积总能量,$p$ 表示压力,${\pmb S}$ 表示固体的偏应力张量,对于流体 ${\pmb S}$ 设为 ${\bf 0}$,以下同.
1.2 状态方程
除了描述物质 (流体或固体) 的质量、动量和能量守恒的控制方程外,物质动力学行为的完整描述还需要提供描述物质自身热力学状态的本构方程 (状态方程). 本文涉及到的状态方程包括 JWL 状态方程、理想气体状态方程以及刚性气体状态方程等. 其中,JWL 状态方程用于描述 TNT 爆轰产物,如式(2)所示
(2) $p = A_1 \left( {1 - \dfrac{\omega \rho }{R_1 \rho _0 }} \right)\exp \left( { - R_1 \dfrac{\rho _0 }{\rho }} \right) +\\ \qquad B_1 \left( {1 - \dfrac{\omega \rho }{R_2 \rho _0 }} \right)\exp \left( { - R_2 \dfrac{\rho _0 }{\rho }} \right) + \omega \rho e $
其中,$\rho_{0}$表示初始密度,$e$表示质量比内能,且满足 $e = E / \rho - (u^2 + v^2) / 2 $$A_{1}$, $B_{1}$, $R_{1}$, $R_{2}$, $\omega $ 为 JWL 状态方程的参数, 其值分别为 3.712, 0.0323, 4.15, 0.95 和 0.3.
(3) $p = (\gamma - 1)\rho e$
刚性气体状态方程 (4) 可用于描述典型的固体等在受到爆炸或冲击时的动态响应问题
(4) $p = (\gamma - 1)\rho e - \gamma p_\infty$
和流体不同的是,固体材料除了能够承受压缩或膨胀带来的体积变化外,还能够承受一定程度的剪切变形 (形状改变). 流体弹塑性模型将固体的力学响应过程分解为两个独立部分:体积变形和剪切变形,其中体积变形仍然由状态方程来确定,而剪切变形在受到强冲击或者爆炸载荷作用时可能经历 3 个过程:弹性变形阶段、塑性变形阶段以及流体动力学阶段,如式 (5) 所示
(5) $s_{ij}^{n + 1} = \left\{ \begin{array}{ll} s_{ij}^n + 2\mu ^{\rm e}\dot {\varepsilon }'_{ij} , & | s_{\rm eff} | < Y^{\rm e} \\ s_{ij}^n + 2\mu ^{\rm p}\dot {\varepsilon }'_{ij} , & Y^{\rm e} \leqslant | s_{\rm eff} | < Y^{\rm p} \\ s_{ij}^n , & | s_{\rm eff} | = Y^{\rm p} \end{array} \right.$
其中,${ s}_{ij}$ 表示偏应力分量,$| s_{\rm eff} |$ 表示 Von Mises 等效应力,$\dot {\varepsilon }'_{ij} $ 表示偏 应变率,$\mu ^{\rm e}$ 和 $\mu ^{\rm p}$ 分别表示弹性和塑形剪切模量,$Y^{\rm e}$ 和 $Y^{\rm p}$ 分别表 示弹性和塑形屈服应力.
2 多介质流动数值方法
采用基于欧拉坐标系、具有互不相溶特征的二、三维多介质流动计算模型来进行数值离散. 在任意时刻,整个计算区域 $\varOmega $ 可以分成两个子区域 $\varOmega ^ + (t)$ 和 $\varOmega ^ - (t)$,且满足
$\varOmega ^ + (t) \cup \varOmega ^ - (t) = \varOmega , \quad \varOmega ^ + (t) \cap \varOmega ^ - (t) = \varGamma (t) $
其中,$\varGamma (t)$ 是两种互不相溶介质之间的相界面.
利用有限体积方法求解每种介质的控制方程组,采用 Level Set 方法捕捉不同介质之间的相界面,并通过在界面法向上求解局部一维多介质 Riemann 问题的精确解来计算相界面上的数值通量. 整个计算流程如下.
2.1 相界面追踪
Level Set 方法把随时间运动的相界面 $\varGamma (t)$ 定义为距离函数 $\varphi ({\pmb x},t)$ 的零等值面[30 ] . 本文利用特征线方法求解 Level Set 函数的演化方程
(6) $\dfrac{\partial \varphi }{\partial t} + \tilde {\pmb u} \cdot \nabla \varphi = 0$
式中,$\tilde {\pmb u}$ 为由物质界面的运动速度延拓得到的速度场[31 ] .
根据特征线方法的思想,只要知道 $t_{n + 1} $ 时刻网格顶点 $X_i $ 上的流体在 $t_n $ 时刻的位置 ${\pmb x}(t_{n + 1} )$,就可以得到新的 Level Set 函数在 $X_i $ 上的值 $\varphi ({\pmb x},t_{n + 1} )$. 对每个顶点 $X_i $,利用特征线方法可得
${\pmb x}\left( {t_{n + 1} } \right) = {\pmb x}\left( {t_n } \right) - \left( {t_{n + 1} - t_n } \right)\tilde {\pmb u}_n $
再利用代数平均,可得新的 Level Set 函数
$\varphi ({\pmb x},t_{n + 1} ) = \sum_{X_i \in \tau _i^n } \varphi ({\pmb x},t_n ) \Bigg / \sum_{X_i \in \tau _i^n } 1 $
其中,$\tau _i^n $ 表示顶点 ${ X}_{i}$ 所处于的单元.
利用显式正系数格式[31 ] 求解如下所示的重新初始化方程
$\left\{\!\! \begin{array}{c}\varphi _t + {\rm sgn} (\varphi _0 )(| \nabla \varphi | - 1) = 0 \\ \varphi (x,0) = \varphi _0 \\ {\rm sgn} (\varphi _0 ) = \dfrac{\varphi _0 }{\sqrt {\varphi _0^2 + \varepsilon ^2} } \end{array}\right. $
以保持 Level Set 函数的符号距离性质. 其中, $\varphi_{0}$ 为重新初始化前 $\varphi ({\pmb x},t)$ 的值,$\varepsilon $ 为一很小的正数 (例如 10$^{-6}$).
2.2 相界面几何重构
当得到 $t_{n}$ 时刻的 Level Set 函数 $\varphi_{n}$ 后,根据其分片线性的特征重构出界面单元内分片线性的相界面,包括:二维两相、二维三相、三维两相和三维三相情形,具体如下.
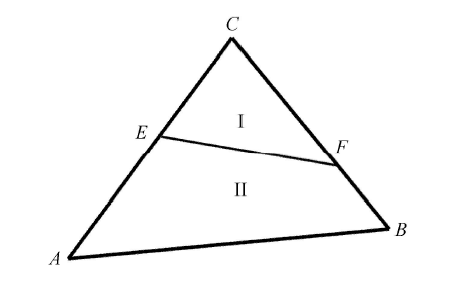
图 1 给出了二维情形下单元内包含两种介质时的相界面几何结构. 假设在三角形 $\varDelta ABC$ 中,顶 点 $A,B, C$ 处的 Level Set 函数值分别为 $\varphi_{A}$, $\varphi _{B}$, $\varphi _{C}$. 如果某个顶点的函数值与其他两个顶点具有相反的符号,该单元一定为相界面单元,且该单元中存在两种介质.
图1
图1
二维相界面拓扑结构 (两相情形)
Fig.1
Two-dimensional topology of phase interface (two-phase case)
不失一般性,假设在三角形 $\varDelta {ABC}$ 中,$C$ 点的相编号为 I,$A$,$B$ 两点的相编号为 II,且存在相界面 ${EF}$. 根据水平集函数分片线性的特征,可计算 $E, F$ 的坐标
$\begin{array}{l} x_E = x_A + \dfrac{\varphi _A - 0}{\varphi _A - \varphi _C }\left( {x_C - x_A } \right) \\ x_F = x_B + \dfrac{\varphi _B - 0}{\varphi _B - \varphi _C }\left( {x_C - x_B } \right) \end{array} $
$\begin{array}{l} A_{\rm I} = A_{\varDelta CEF} = \dfrac{1}{2} \overline{CE}\times \overline{CF} \\ A_{\rm II} = A_{\varDelta ABC} - A_{\varDelta CEF} \end{array} $
采用向量型水平集函数来描述超过两相情形时的相界面. 对任一点 $x$,向量型水平集函数在该点的取值为 $\varphi (x,t) = ( \varphi 1(x,t), \varphi 2(x,t), \cdots , \varphi n(x,t))$,如果其最大分量为 $\varphi i(x,t)$,则该点的相编号为 $i$. 其中,$n$ 表示相数.
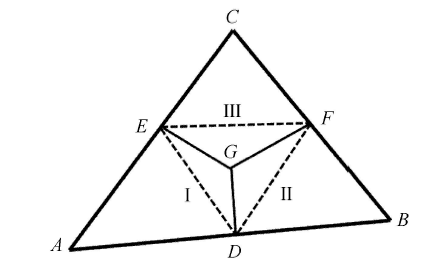
如果三角形 $ABC$ 中 3 个顶点的相编号各不相同,该单元中存在 3 种介质,如图 2 所示. 不失一般性,假设 $A, B, C$ 三点的相编号分别为 I, II, III. 根据水平集函数的分片线性特征,可得单元 3 条边上的相界面分界点 $D, E, F$ 的位置
$\begin{array}{l} x_D = x_A + \dfrac{\varphi _{\rm I} (x_A ) - \varphi _{{\rm II}} (x_A )}{\left( {\varphi _{\rm I} (x_A ) - \varphi _{{\rm II}} (x_A )} \right) - \left( {\varphi _{\rm I} (x_B ) - \varphi _{{\rm II}} (x_B )} \right)} \overline{AB} \\ x_E = x_A + \dfrac{\varphi _{\rm I} (x_A ) - \varphi _{{\rm III}} (x_A )}{\left( {\varphi _{\rm I} (x_A ) - \varphi _{{\rm III}} (x_A )} \right) - \left( {\varphi _{\rm I} (x_C ) - \varphi _{{\rm III}} (x_C )} \right)} \overline{AC} \\ x_F = x_B + \dfrac{\varphi _{{\rm II}} (x_B ) - \varphi _{{\rm III}} (x_B ) - 0}{\left( {\varphi _{{\rm II}} (x_B ) - \varphi _{{\rm III}} (x_B )} \right) - \left( {\varphi _{{\rm II}} (x_C ) - \varphi _{{\rm III}} (x_C )} \right)} \overline{BC} \\ \end{array} $
图2
图2
二维相界面拓扑结构 (两相情形)
Fig.2
Two-dimensional topology of phase interface (three-phase case)
$A_1 = A_{\varDelta ADE}, \ A_2 = A_{\varDelta BDF}, \ A_3 = A_{\varDelta CEF}, \ A = A_{\varDelta ABC} $
$\lambda _1 = A_1 / A,\quad \lambda _2 = A_2 / A,\quad \lambda _3 = A_3 / A $
来确定三相分界点的位置,然后计算各相所占的面积和两两之间的相界面. 其中 $G$ 的位置为
$x_G = \lambda _1 x_F + \lambda _2 x_E + \lambda _3 x_D $
此时,第 I 相所占的面积为 $A\varDelta ADE + A\varDelta DEG$,第 II 相所占的面积为 $A\varDelta BDF + A\varDelta DFG$,第 III 相所占的面积为 $A\varDelta CEF + A\varDelta EFG$. I, II 两相的相界面为线段 $DG$,I, III 两相的相界面为线段 $EG$,II, III 两相的相界面为线段 $FG$.
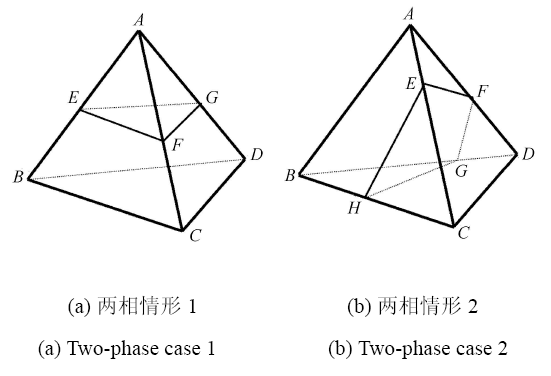
根据水平集函数与三维四面体网格的相交情况,可以将三维两相的相界面几何结构分为两种情形,分别如图 3 (a) 和图 3 (b) 所示.
图3
图3
三维相界面拓扑结构 (两相情形)
Fig.3
Three-dimensional topology of phase interface (two-phase case)
四面体 ${ABCD}$ 中有一个顶点与其他 3 个顶点的相编号不一样,不妨设 $A$ 点的相编号为 I,$B$, $C$, $D$ 三点的相编号为 II (如图 3 (a) 所示),此时
$\varphi (x_A ) > 0,\quad \varphi (x_\xi ) < 0\quad \left( {\xi = B,C,D} \right) $
根据水平集函数的分片线性特征,使用和二维两相情形类似的算法可得四面体棱上的相分界点 $E$, $F$, $G$,此时相界面为 $\varDelta EFG$,且第 I 相所占的体积为
$V_{\rm I} = \dfrac{1}{6}\overline{AE}\cdot \overline{AG}\cdot \overline{AF} $
$V_{\rm II} = \dfrac{1}{6}\overline{AB}\cdot \overline{AD}\cdot\overline{AC} - V_I $
四面体中 4 个顶点按相编号平均分为两组. 不妨设 $A$, $B$ 的相编号为 I,$C$, $D$ 的相编号为 II,如图 3 (b) 所示. 使用和情形 1 类似的算法,可以计算出四面体 棱上的相分界点 $E$, $F$, $G$, $H$,此时相界面为四边形 ${EFGH}$. 记
$ \lambda _{00} = \dfrac{ | AE | }{ | AC | }, \ \ \lambda _{01} = \dfrac{ | AF | }{ | AD | } \\ \lambda _{10} = \dfrac{ | BH | }{ | BC | }, \ \ \lambda _{11} = \dfrac{ | BG | }{ | BD | } \\ V = V_{ABCD} = \dfrac{1}{6}\overline{AB}\cdot \overline{AD}\cdot\overline{AC} $
$\begin{array}{l} V_{\rm II} = V_{E - CDGH} + V_{E - FDG} =\\ \qquad \left( {1 - \dfrac{ | BH | }{ | BC | }\dfrac{ | BG | }{ | BD | }} \right)\dfrac{ | EC | }{ | AC | }V + \dfrac{ | DG | }{ | DB | }\dfrac{ | DF | }{ | DA | }\dfrac{ | EF | }{ | CA | }V =\\ \qquad \left( {1 - \lambda _{10} \lambda _{11} } \right)\left( {1 - \lambda _{00} } \right)V + \left( {1 - \lambda _{11} } \right)\left( {1 - \lambda _{01} } \right)\lambda _{00} V =\\ \qquad \left( {1 - \lambda _{00} \lambda _{01} - \lambda _{01} \lambda _{10} - \lambda _{10} \lambda _{11} + \lambda _{00} \lambda _{01} \lambda _{10} + }\right. \left.{ \lambda _{01} \lambda _{10} \lambda _{11} } \right)V \end{array} $
$\begin{array}{l} V_I = V - V_{II} = \left( {\lambda _{00} \lambda _{01} + \lambda _{01} \lambda _{10} + \lambda _{10} \lambda _{11} - }\right. \left.{\lambda _{00} \lambda _{01} \lambda _{10} - \lambda _{01} \lambda _{10} \lambda _{11} } \right)V \end{array} $
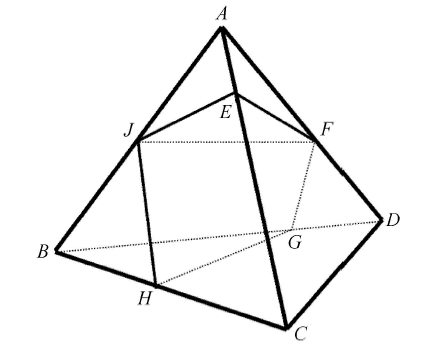
图 4 给出了三维情形下单元内包含 3 种介质时的相界面拓扑结构. 根据水平集函数的分片线性性质,四面体网格的四个顶点 中必然有两个为一相,另外两个顶点各占据一相. 不失一般性,不妨设 $A$ 的相编号为 I,$B$ 的相编号为 II,$C$, $D$ 的相编号为 III.
图4
图4
三维相界面拓扑结构 (三相情形)
Fig.4
Three-dimensional topology of phase interface (three-phase case)
使用和前面类似的算法,可以计算出四面体棱上的相分界点,包括:相 I 与相 III 的分界 点 $E$, $F$,相 II 与相 III 的分界点 $G$, $H$,以及相 I 与相 II 的分界点 $K$,此时四面体单元 ${ABCD}$ 内包含两个相界面:三角形 ${EFK}$ 和四边形 ${FGHK}$. 整个四面体单元的体积为
$V = V_{ABCD} = \dfrac{1}{6}\overline{AB}\cdot \overline{AD}\cdot\overline{AC} $
$V_{\rm I} = V_{A - EFJ} = \dfrac{1}{6}\overline{AJ}\cdot \overline{AF}\cdot\overline{AE} $
$\begin{array}{l} V_{\rm II} = V_{B - FGH} + V_{B - FHJ} = \dfrac{1}{6}\overline{BH}\cdot \overline{BG}\cdot\overline{BF} + \dfrac{1}{6}\overline{BJ}\cdot \overline{BH}\cdot\overline{BF} \end{array} $
$V_{\rm III} = V - V_{\rm I} - V_{\rm II} $
2.3 数值通量
在 Euler 坐标系下的多介质数值计算中,每个单元内守恒量的变化来自两个部分:(1) 单元内介质与单元外同相的介质在单元边界上通过流入流出或相互作用力而带来的守恒量变化,称为单元边界通量;(2) 不同相的介质在相界面处由于相互作用力带来的守恒量变化,称为相界面通量.
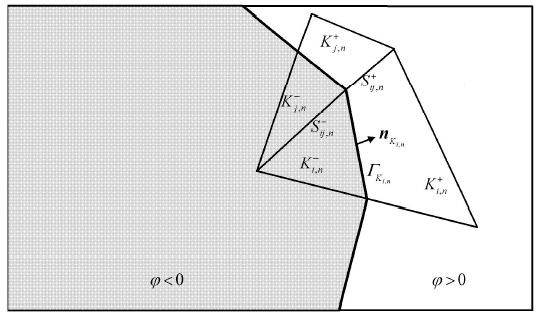
以二维两相情形为例 (如图 5 所示),假设单元 $K_{i,n}$ 与单元 $K_{j,n}$ 具有共边 $S_{ij,n}$,且包含物质界面 $\varGamma _{K_{i,n} } $. $\varGamma _{K_{i,n} } $ 将 $K_{i,n}$ 和 $S_{ij,n}$ 依次分为 2 个部分 $K_{i,n}^\pm $ 和 $S_{ij,n}^\pm $,此时单元包含 2 种介质,每种介质的守恒量分别定义为
${\pmb U}_{K_{i,n} }^\pm = \left[ {\rho _{K_{i,n} }^\pm } \ \ {\rho _{K_{i,n} }^\pm {\pmb u}_{K_{i,n} }^\pm } \ \ E_{K_{i,n} }^\pm \right]^{\rm T} $
其中,$\rho _{K_{i,n} }^\pm $, ${\pmb u}_{K_{i,n} }^\pm $ 和 $E_{K_{i,n} }^\pm $ 分别为每种介质的密度、速度和体积比总能,$n_{K_{i,n} } $ 为物质界面的单位法向.
图5
图5
多介质流动计算模型示意图
Fig.5
Schematic diagram for the multi-media flow calculation model
单元边界的数值通量是指单元边界上同种介质之间的数值通量,且满足
$\hat {\pmb F}_{ij,n}^\pm = \Delta t_n \left| {S_{ij,n}^\pm } \right|\hat {\pmb F}\left( {{\pmb U}_{K_{i,n} }^\pm , \ {\pmb U}_{K_{j,n} }^\pm ; \ {\pmb n}_{ij,n}^\pm } \right) $
式中,${\pmb n}_{ij,n}^\pm $为单元边界上的单位法向,$\Delta t_n $为时间步长,$\hat {\pmb F} ({\pmb U}_{K_{i,n} }^\pm , {\pmb U}_{K_{j,n} }^\pm ; {\pmb n}_{ij,n}^\pm )$ 为相容、单调的数值通量函数. 本文采用 local Lax-Friedrich 数值通量函数
$\begin{array}{l} \hat {\pmb F}({\pmb U}_{K_{i,n} }^\pm , {\pmb U}_{K_{j,n} }^\pm ; {\pmb n}_{ij,n}^\pm ) = \dfrac{1}{2}\left( {{\pmb F}({\pmb U}_{K_{i,n} }^\pm ) + {\pmb F}({\pmb U}_{K_{j,n} }^\pm )} \right) \cdot {\pmb n}_{ij,n}^\pm - \dfrac{1}{2}\lambda ({\pmb U}_{K_{j,n} }^\pm - {\pmb U}_{K_{i,n} }^\pm ) \end{array} $
且 $\lambda = \max \{\lambda _{K_{i,n} } ,\lambda _{K_{j,n} } \}$,$\lambda _{K_{i,n} } $ 和 $\lambda _{K_{j,n} } $ 分别为 ${\pmb U}_{K_{i,n} }^\pm $ 和 ${\pmb U}_{K_{j,n} }^\pm $ 的最大信号速度.
相界面数值通量是相界面两侧不同介质之间的数值通量,且满足
$\hat {\pmb F}_{K_{i,n} }^\pm = \Delta t_n \left| {\varGamma _{K_{i,n} } } \right|\left[ \!\!\begin{array}{c} 0 \\ {\sigma _{K_{i,n} }^* {\pmb n}_{K_{i,n} } }\\ {\sigma _{K_{i,n} }^* u_{K_{i,n} }^* } \end{array} \!\! \right] $
式中,${\pmb n}_{K_{i,n} } $ 为相界面的单位法向,$ | \varGamma _{K_{i,n} } | $ 为相界面的长度,$\sigma _{K_{i,n} }^* $ 和 $u_{K_{i,n} }^* $ 分别为相界面上的法向应力和法向速度,且通过在相界面法向上求解局部一维多介质 Riemann 问题的精确解 来获得,具体见文献[32 ,33 ] .
2.4 守恒量更新
当计算得到 $K_{i,n} $ 的单元边界数值通量和相界面数值通量后,可对该单元中每种介质的守恒量进行如下更新
(7) $U_{K_{i,n + 1} }^{\pm ,* } = \left\{ \!\! \begin{array}{ll} 0, & K_{i,n + 1}^\pm = 0 \\ \dfrac{1}{ | K_{i,n + 1}^\pm | }\left( { | K_{i,n}^\pm | U_{K_{i,n} }^\pm + \sum_{S_{ij,n}^\pm \subseteq K_{i,n}^\pm } {\hat {F}_{ij,n}^\pm } + \hat {F}_{K_{i,n} }^\pm } \right) , & \\ & K_{i,n + 1}^\pm \ne 0 \end{array} \!\! \right.$
式中,$U_{{K_{i,n} }^\pm {K_{i,n + 1} }^\pm }$ 和 $K_{i,n}^\pm K_{i,n + 1}^\pm $ 分别表示 $t_n$ 和 $t_{n + 1}$ 时刻单元内每种介质的守恒量和体积.
2.5 单元碎片聚合
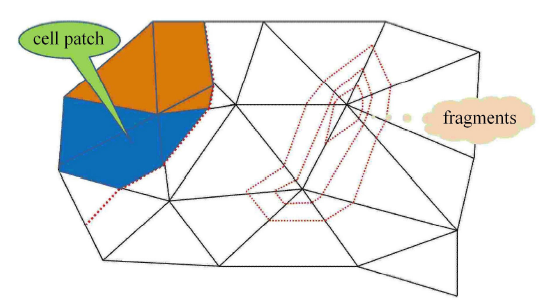
利用式 (7) 来更新守恒量,等价于在原始背景网格 $\varLambda $ 和相界面耦合的网格上求解控制方程组. 由于有些网格单元被相界面分割成一些碎片,这些碎片单元的尺寸比原始单元的尺寸小,导致 CFL 条件被破坏,可能造成数值不稳定.为了消除不稳定性,需要对 $U_{K_{i,n + 1} }^{\pm ,* } $ 进行特殊处理.首先建立单元片,使得每个碎片单元都处于同介质的单元片中,并且该单元片中至少包含一个完整单元;然后修正守恒量,对单元片中每个单元上的介质守恒量进行单元体积的加权平均,以保证整体物理量的守恒.图 6 为网格聚合算法及碎片处理的示意图.
图6
图6
网格聚合算法及碎片处理
Fig.6
Cell aggregation and fragment process
提出如下的聚合算法来建立单元片. 首先把包含碎片的单元 (即界面单元) 收集起来
$E_{n + 1}^\pm = \left\{ {K_i \in \varLambda : K_{i,n + 1}^\pm \ne K_i \ \hbox{or} \ K_{i,n + 1}^\pm \ne \varPhi } \right\} $
再把与界面单元相邻并且只含有当前所考虑介质的单元收集起来,作为种子单元
$ B_{n + 1}^\pm = \left\{ {K_i \in \varLambda : K_{i,n + 1}^\pm = K_i \ \ \hbox{and} }\right. \left.{ \bar {K}_i \cap \bar {K}_j \ne \varPhi , \bar {K}_j \in E_{n + 1}^\pm } \right\} $
其中,$\varPhi $ 表示空集合,$\bar {K}_i \cap \bar {K}_j \ne \varPhi $ 表示单元 $K_i $ 与单元 $K_j $ 具有一条共边.
单元片是由 $E_{n + 1}^\pm $ 和 $B_{n + 1}^\pm $ 中的某些单元构成的一簇单元. 聚合算法刚开始时,每个单元片中只包含一个界面单元,即
$P_{n + 1}^\pm = \left\{ {P_{n + 1,i}^\pm : P_{n + 1}^\pm = \left\{ {K_i } \right\} , K_i \in E_{n + 1}^\pm } \right\} $
(1) 对 $\forall K_i \in B_{n + 1}^\pm $,为其指定唯一编号 $I_{K_i } $;
(2) 对 $\forall K_i \in B_{n + 1}^\pm $,$\forall \kappa \in \partial K_i $,如果 $\kappa $ 上没有设定编号,就为 $\kappa $ 设定编号为 $I_{K_i } $;
(3) 对 $\forall K_i \in E_{n + 1}^\pm $,如果 $\exists \kappa \in \partial K_i $,则给 $K_i $ 设置编号为 $I_\kappa $,令 $E_{n + 1}^\pm = E_{n + 1}^\pm \backslash \left\{ {K_i } \right\}$,$B_{n + 1}^\pm = B_{n + 1}^\pm \cup \left\{ {K_i } \right\}$;
(4) 如果 $E_n^\pm = \varPhi $,则单元片建立完成,流程终止;如果上一步给 $E_n^\pm $ 中的单元设置了编号,转步骤 (2);
(5) 对 $\forall K_i \in E_n^\pm $,为 $K_i $ 设置一个唯一的编号$I_{K_i } $,且 $I_{K_i } > \max _{K_i \in B_{n + 1}^\pm } I_{K_i } $;
(6) 对 $\forall K_i \in E_n^\pm $,$\forall \kappa \in \partial K_i $,如果 $\kappa $ 上没有设置编号,为其设置编号 $I_G $,令 $I_G = I_{K_i } $;否则如果 $I_G > I_{K_i } $,令 $I_G = I_{K_i } $;
(7) 对 $\forall K_i \!\in\! E_{n + 1}^\pm $,令其单元编号 $I_{K_i } \!>\! \min _{G \in \partial K_i } I_G $;
(8) 如果过程 (7) 中 $\forall K_i \in E_{n + 1}^\pm $,$K_i $ 的编号 没有变化,令 $B_{n + 1}^\pm = B_{n + 1}^\pm \cup E_{n + 1}^\pm $,单元片建立完成; 否则,转过程 (6). 上述过程结束后,$B_{n + 1}^\pm $ 中编号相同的单元就构成了一个单元片 $P_{n + 1,i}^\pm $.
将单元片 $P_{n + 1,i}^\pm $ 中每个单元 $K_i $ 上的守恒量设为
(8) $U_{K_i ,n + 1}^\pm = \dfrac{ \sum_{\hat {K}_i \in P_{n + 1,i}^\pm } \left| {\hat {K}_{i,n + 1}^\pm } \right|U_{K_i ,n + 1}^{\pm ,* } }{\sum _{\hat {K}_i \in P_{n + 1,i}^\pm } \left| {\hat {K}_{i,n + 1}^\pm } \right|},\quad \forall K_i \in P_{n + 1,i}^\pm$
$\sum _{K_i \in \varLambda } \left| {K_{i,n + 1}^\pm } \right|U_{K_i ,n + 1}^{\pm ,* } = \sum _{K_i \in \varLambda } \left| {K_{i,n + 1}^\pm } \right|U_{K_i ,n + 1}^\pm $
后处理过程 (8) 实际上消去了同一单元片内部单元间的数值通量,将过程 (7) 的更新改为只考虑单元片边界上的通量. 由于每个单元片中至少有一个完整单元,因而满足 CFL 条件,整个算法的数值稳定性得到了保证.
如果一个小的单元碎片孤立存在于其他介质单元中,有可能整个单元片中没有一个完整的单元与它含有相同的介质. 因此,有些 $P_{n + 1,i}^\pm $ 在算法完成之后只有一个单元,将这些单元合起来作为一个单元片,称之为 "孤岛". 如果孤岛的体积小于预设的忍量 (原始单元体积的10$^{ - 8})$,直接将孤岛上该介质的守恒量设为缺省的极低压状态,计算过程中孤岛会逐渐缩小直至消失,这种做法可以有效地消除过于复杂的相界面,因此总的计算量得到控制.
3 数值算例
本节给出一些数值算例来对数值方法进行测试,包括多介质 Riemann 问题、激波与气泡相互作用、触地浅埋爆炸以及典型坑道内的冲击波传播等问题,验证数值方法的可靠性和计算效率.
3.1 多介质 Riemann 问题
首先计算一个 JWL 状态方程的单介质 Riemann问题,来自文献[34 ] . 计算 区域为 [0 , 1 ] $\times $ [0, 5.0 $\times $ 10$^{ - 3}$], 网格尺寸为 2.5$\times $10$^{ - 3}$. 其中,JWL 状态方程参数取 $A_{1} =854.5$GPa,$A_{2} =20.5$GPa, $\omega =0.25$,$R_{1} =4.6$, $R_{2} =1.35$, $\rho_{0} =1840$kg/m$^{3}$. 初值条件如下
$ \left[ {\rho ,u,v,p} \right] = \left\{ \!\!\begin{array}{ll} {[1700, 0, 0,10^{12}]} , & {x < 0.5 } \\ {[1000, 0, 0,5\times 10^{10}]} , & {x > 0.5 } \end{array} \right. $
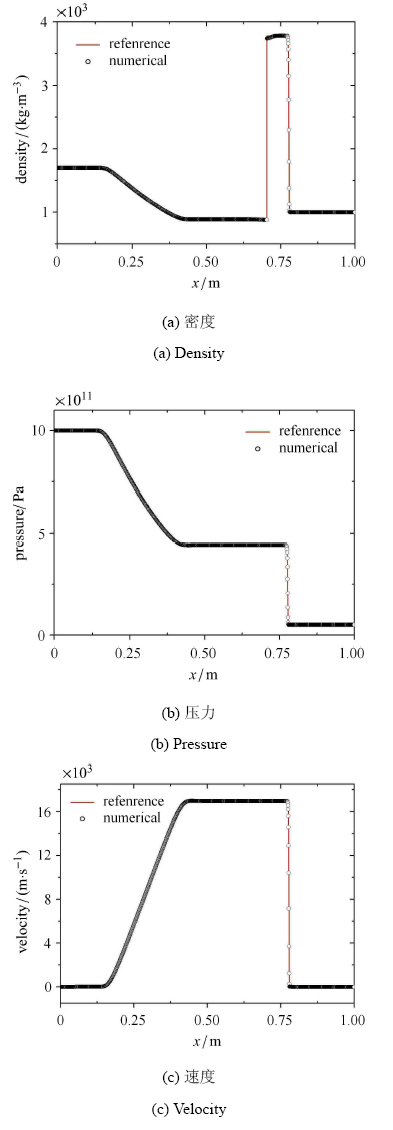
计算时间为 $t =1.2 \times 10^{ - 5}$. 计算结果与文献[34 ] 参考解的对比如图 7 所示,对比表明本文结果 与文献中的高精度参考解符合较好,且在相界面处密度具有高分辨率.
图7
图7
Shyue 激波管问题
Fig.7
Shyue shock tube problem
再计算一个 JWL - 弹性固体的 Riemann 问题,其中气体相用JWL状态方程来描述,参数为 $A_{1}=854.5$GPa,$A_{2} =20.50$GPa, $\omega =0.25$,$R_{1} =4.6$, $R_{2} =1.35$, $\rho _{0}=1840$kg/m$^{3}$. 固体相的静水压力用刚性气体状态方程描述,且 $\gamma =4.4$,$p_{\infty } = 600$MPa,固体的偏应力遵守 Hooke 定律,且 $\beta ^{e} =10^{14}$Pa$\cdot $kg/m$^{3}$[35 ] . 初 值条件如下
$ \left[ {\rho ,u,v,p} \right] = \left\{ \!\!\begin{array}{ll} {[1630, 0, 0,10^9]} , & {x < 0.5 } \\ {[7800, 0, 0,10^5]} , & {x > 0.5 } \end{array} \right. $
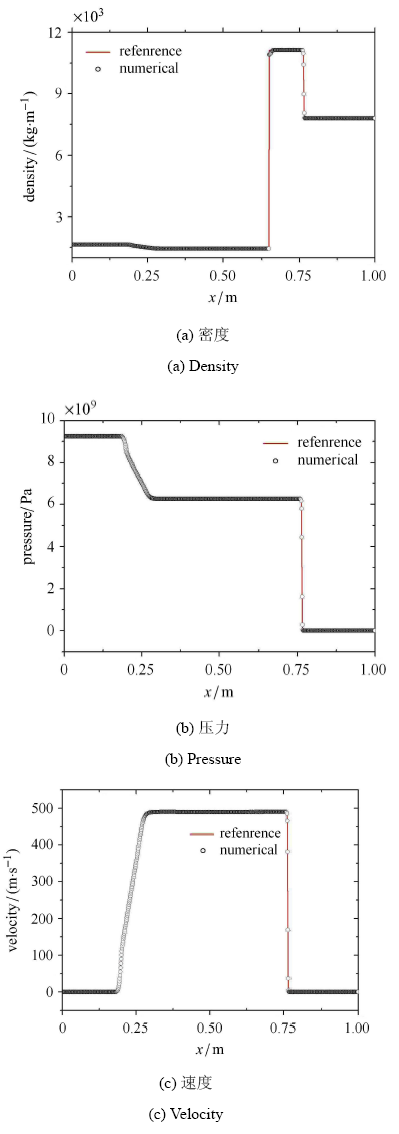
计算时间为 $t =10^{ - 4}$. 图 8 给出了计算结果与参考解[35 ] 的对比,从对比分析可知数值结果与参考解符合较好,且在接触间断和激波附近具有较高的分辨率.
图8
图8
JWL-弹性固体 Riemann 问题
Fig.8
JWL-elastic solid Riemann problem
3.2 激波与气泡相互作用
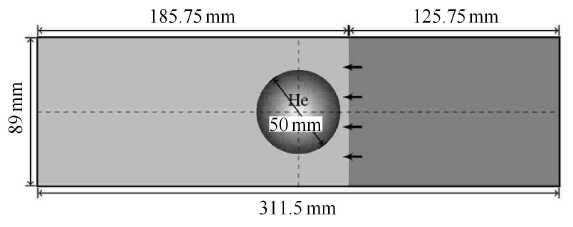
激波与气泡作用问题是可压缩多介质流体问题的一个经典算例[36 -38 ] . 初值条件如下:一个直径为 50mm 的圆形气泡放置在长 311.5mm、宽 89mm 的激波管的正中间,其余地方充满空气 (如图 9 所示). 初始时刻,气泡右侧 5mm 处有一个马赫数为 $Ma=1.22$、向左运动的平面激波. 初始物理参数如表 2 所示. 计算模型的上、下边界设为反射边界条件,左、右边界设为出流边界条件,网格尺寸为 1mm.
图9
图9
激波与气泡相互作用问题示意图
Fig.9
Computational model of gas-bubble interaction problem
图 10 给出了不同时刻的数值结果,并与 Haas 和 Sturtevant 的实验结果[38 ] 进行了比较.图中第一列为实验纹影图,第二列为数值计算得到的密度等值线图.
图10
图10
激波与气泡相互作用问题. 第一列从上到下依次为32$\mu $s, 53$\mu $s, 62$\mu $s, 72$\mu $s, 82$\mu $s, 102$\mu $s, 245$\mu $s, 427$\mu $s, 674$\mu $s和983$\mu $s; 第二 列从上到下依次为23$\mu $s, 43$\mu $s, 53$\mu $s, 66$\mu $s, 75$\mu $s, 102$\mu $s, 260$\mu $s, 445$\mu $s, 674$\mu $s和983$\mu $s
Fig.10
Gas-bubble interaction problem. First column: 32$\mu $s, 53$\mu $s, 62$\mu $s, 72$\mu $s, 82$\mu $s, 102$\mu $s, 245$\mu $s, 427$\mu $s, 674$\mu $s and 983$\mu $s; Second column: 23$\mu $s, 43$\mu $s, 53$\mu $s, 66$\mu $s, 75$\mu $s, 102$\mu $s, 260$\mu $s, 445$\mu $s, 674$\mu $s and 983$\mu $s
从图 10 可以看出,数值计算结果与实验结果定性吻合.当激波从密度大的空气进入密度小的氦气时,气泡的上游边缘呈现出 Richtmyer-Meshkov 不稳定性,其蘑菇形状在 445$\mu$s 时刻发生. 从 427$\mu$s 开始气泡发生严重变形,到 674$\mu$s 时空气的上尖峰和下尖峰形成. 随后气泡变得越来越薄,直至发生破裂.算例中的气泡大变形问题对数值计算提出了很大的挑战,但计算结果表明,本文的数值方法可以很好的追踪相界面,同时能够保持 $y$ 方向上解的对称性,证明了数值方法的正确性.
3.3 浅埋爆炸问题
计算一个二维三相问题-浅埋爆炸,用于测试本文方法在处理三相问题时的能力. 计算区域内包含 3 种介质:爆炸产物、空气和地介质. 爆炸产物初始半径为 0.1m,初始时刻位于地下 0.1m 处. 爆炸产物和空气采用理想气体状态方程,绝热指数均为 1.4. 地介质的静水压力部分采用刚性气体状态方程,偏应力部分采用理想弹塑性材料模型,且 $\gamma = 4.4$,$p_{\infty } = 6$kPa, $\mu ^{e } = 853$kPa, $\mu ^{p}= 0$,$Y^{e }= 6.5$kPa. 初值条件如下
$ \left[ {\rho ,u,v,p,\gamma } \right] =\left\{ \!\! \begin{array}{ll} {[1.0,0,0,10^5,1.4]} , & {\sqrt {x^2 + (y + 0.1)^2} \leqslant 0.1 } \\ {[26.7,0,0,1.0,4.4]} , & {\sqrt {x^2 + (y + 0.1)^2} > 0.1 \cap y < 0 } \\ {[1.0,0,0,1.0,1.4]} , & {\sqrt {x^2 + (y + 0.1)^2} > 0.1 \cap y \geqslant 0 } \end{array} \right. $
图 11 和图 12 分别给出了浅埋爆炸条件下,典型时刻整个计算区域内的密度和压力分布情况. 在浅埋爆炸问题中,炸药爆炸产生的冲击波会剧烈压缩地介质,并在地介质中形成应力波. 当冲击波突破地表面后,形成弹坑,并喷射到空气中形成强冲击波. 从计算结果来看,本文的数值方法能够正确反映浅埋爆炸时的实际物理过程,表明本文的三相数值方法是正确的.
图11
图11
浅埋爆炸典型时刻的密度云图
Fig.11
Density contours of sub-surface blast problem
图12
图12
浅埋爆炸典型时刻的压力云图
Fig.12
Pressure contours of sub-surface blast problem
3.4 空中强爆炸冲击波传播
计算一个当量为 1kt TNT、爆高为 200m 的空中强爆炸冲击波传播问题. 强爆炸产物采用等温等压球模型,取爆炸总当量的 85% 作为强爆炸的力学初始能量[39 ] . 空气采用理想气体状态方程,初始压力为 101.3kPa,初始密度为 1.29kg/m$^{3}$. 计算区域在 $x =0$ 和 $y =0$ 设为固壁反射边界条件,其余边界设为无反射边界条件.
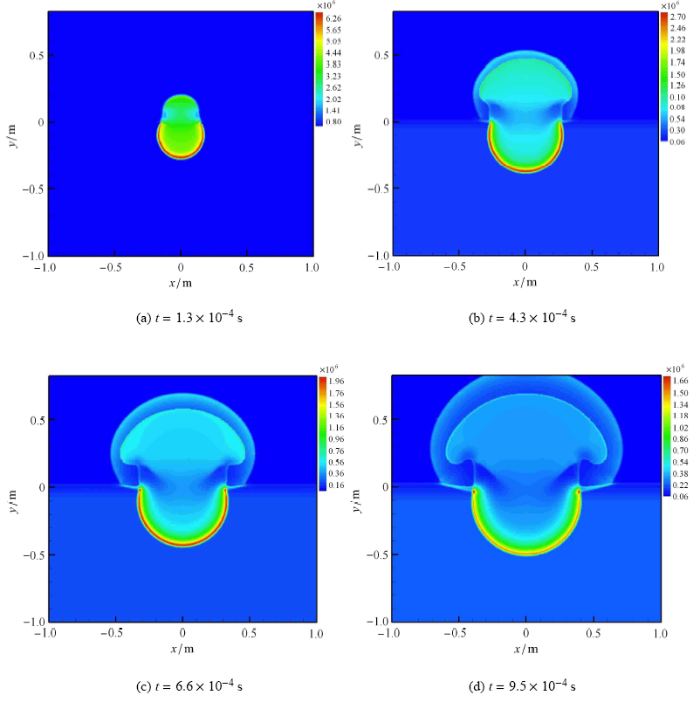
计算得到典型时刻的冲击波压力等值线如图 13 所示,当空中强爆炸产生的冲击波传播到地面时,最早在爆心投影点发生正反射,然后以逐渐增大的入射角发生斜反射,产生双激波结构的规则反射 (图 13 (a)). 随着冲击波向外继续传播,入射角不断增大. 当入射角增大到临界角附近时将发生马赫反射,此时反射波阵面和入射波阵面的交点离开地面,形成垂直于地面的马赫杆 (图 13 (b)). 随着冲击波的进一步传播,马赫杆不断增长. 图 14 给出了数值计算得到的地面冲击波载荷分布 (峰值超压和冲量) 与实测结果拟合的经验公式[40 ] 的对比情况. 由对比可知,计算得到的地面冲击波参数与实测结果符合得较好,最大误差不超过 40%.
图13
图13
空中强爆炸典型时刻的压力云图
Fig.13
Pressure contours of air blast at typical time
图14
图14
地面不同距离处的冲击波参数
Fig.14
Blast wave parameters on the ground at different radii
3.5 三维坑道中冲击波传播
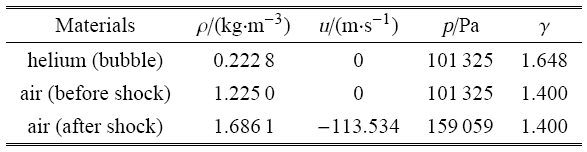
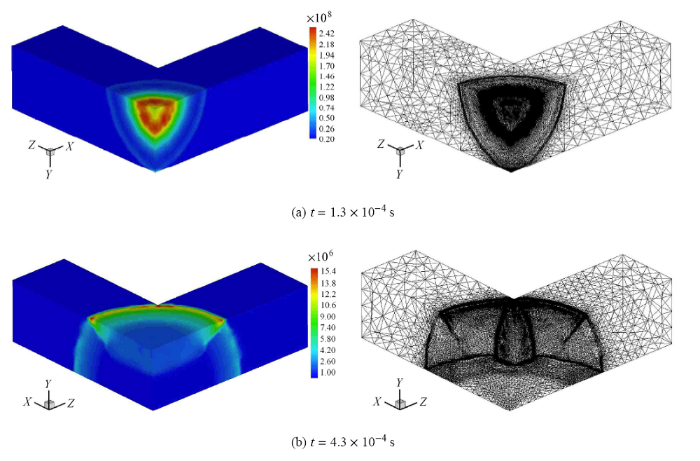
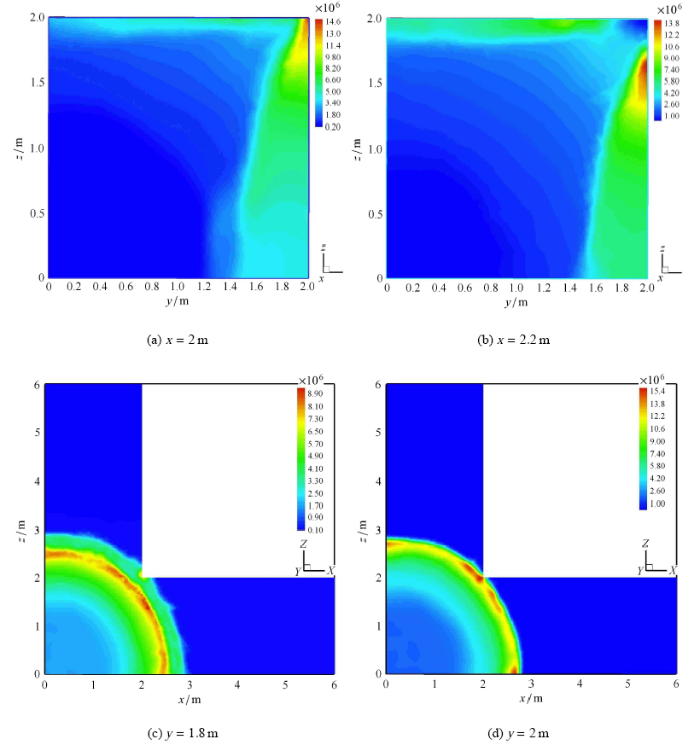
计算了 1kg TNT 爆炸产生的冲击波在一个"十" 字形三维密闭空间中的传播过程. 考虑空间结构的对称性,将其简化为一个 "$L$" 型的结构 $E_{1} \cup E_{2}$. 其中,$E_{1} =[0, 2] \times [0, 2] \times [0, 6]$m, $E_{2} =[0, 6] \times [0, 2] \times [0, 2]$m. TNT 和空气分别采用JWL状态方程和理想气体状态方程来描述. 由于三维的计算量很大,本文采用了网格自适应技术并结合基于区域分解的并行计算策略,有效提高了计算效率. 图 15 给出了典型时刻的冲击波流场压力云图,图 16 给出了 $t =9.2 \times 10^{ - 4}$s时刻典型位置处的冲击波压力切面图. 计算结果表明,TNT 爆炸后将在空气中产生强冲击波,起初波阵 面以球面波的形式向外传播. 当冲击波遇到固壁时,将发生反射并沿壁面继续向前传播,最终在整个密闭空间中形成非常复杂的载荷分布.
图15
图15
典型时刻的三维冲击波压力云图和网格自适应图
Fig.15
Pressure contours and adaptive meshes of three-dimensional blast wave propagation
图16
图16
$t=9.2\times 10^{ - 4}$s 时的冲击波压力切面图
Fig.16
Typical pressure sections of blast wave at $t=9.2\times 10^{ - 4}$s
4 结论
本文提出了一种基于 Euler 坐标系的非结构网格上互不相溶的、具有锐利相界面的守恒型多介质流动数值方法,建立了二维和三维单纯形网格上的多介质流动数值模拟程序,可用于模拟可压缩流体和弹塑性固体在爆炸与冲击等极端物理条件下的大变形动力学行为. 本文提出的多介质流动数值方法采用了向量型的水平集函数,理论上可以处理全局任意种介质、局部三种介质的多介质流动问题,且能够保持锐利的相界面. 此外,提出的基于非结构网格上的聚合算法能够从本质上消除由于网格被相界面分割成较小碎片而带来的数值不稳定性,有效提高了数值计算的效率和健壮性. 最后结合具有代表性的数值算例和实际应用问题,验证了数值方法在处理多介质大变形和相界面大变形问题中的能力.
参考文献
View Option
[1]
王昭 , 严红 . 基于气液相界面捕捉的统一气体动理学格式
力学学报 , 2018 ,50 (4 ):711 -721
URL
[本文引用: 2]
( Wang Zhao Yan Hong . Unified gaskinetic scheme for two phase interface capturing
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (4 ):711 -721 (in Chinese))
URL
[本文引用: 2]
[2]
刘文超 , 刘曰武 . 低渗透煤层气藏中气-水两相不稳定渗流动态分析
力学学报 , 2017 ,49 (4 ):828 -835
URL
[本文引用: 1]
( Liu Wenchao Liu Yuewu . Dynamic analysis on gas--water two-phase unsteady seepage flow in low-permeable coalbed gas reservoirs
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (4 ):828 -835 (in Chinese))
URL
[本文引用: 1]
[3]
Benson D . Computational methods in Lagrangian and Eulerian hydrocodes
Computer Methods in Applied Mechanics and Engineering 1992 ,99 (2-3 ):235 -394
DOI
URL
[本文引用: 1]
[4]
贾祖鹏 , 张树道 , 蔚喜军 . 多介质流体动力学计算方法 . 北京 : 科学出版社 , 2014
[本文引用: 1]
( Jia Zupeng Zhang Shudao Yu Xijun . Numerical methods of multi-material flow dynamics . Beijing : Science Press , 2014 (in Chinese))
[本文引用: 1]
[5]
Hirt C Amsden A Cook J . An arbitrary Lagrangian-Eulerian computing method for all flow speeds
Journal of Computational Physics 1974 ,14 (3 ):227 -253 .
DOI
URL
[本文引用: 1]
[6]
何涛 . 基于 ALE 有限元法的流固耦合强耦合数值模拟
力学学报 , 2018 ,50 (2 ):395 -404
[本文引用: 1]
( He Tao . A partitioned strong coupling algorithm for fluid-structure interaction using arbitrary Lagrangian-Eulerian finite element formulation
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (2 ):395 -404 (in Chinese))
[本文引用: 1]
[7]
Arienti M . A level set approach to Eulerian--Lagrangian coupling
Journal of Computational Physics 2003 ,185 (1 ):213 -251
DOI
URL
[本文引用: 1]
[8]
Hirts C Nichols B . Volume of fluid (VOF) method for the dynamics of free boundaries
Journal of Computational Physics 1981 ,39 (1 ):201 -225
[本文引用: 1]
[9]
张嫚嫚 , 孙姣 , 陈文义 . 一种基于几何重构的 Youngs-VOF 耦合水平集追踪方法
力学学报 , 2019 ,51 (3 ):775 -786
[本文引用: 1]
( Zhang Manman Sun Jiao Chen Wenyi . An interface tracking method of coupled Youngs-VOF and level set based on geometric reconstruction
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ):775 -786 (in Chinese))
[本文引用: 1]
[10]
Dyadechko V Shashkov M . Moment-of-fluid interface reconstruction
Los Alamos report A-UR-05-7571 , 2005
[本文引用: 1]
[11]
Glimm J Grove J Li X . Three-dimensional front tracking
SIAM Journal on Scientific Computing 1998 ,19 (3 ):1703 -727
[本文引用: 1]
[12]
Tryggvason G Bunner B Esmaeeli A . A front-tracking method for the computations of multiphase flow
Journal of Computational Physics 2001 ,169 (2 ):708 -759
DOI
URL
[本文引用: 1]
[13]
Osher S Sethian J . Fronts propagating with curvature-dependent speed: algorithms based on Hamilton- Jacobi formulations
Journal of Computational Physics 1988 ,79 (1 ):12 -49
DOI
URL
[本文引用: 1]
[14]
Sethian J . Level set methods and fast marching methods: evolving interfaces in computational geometry, fluid mechanics, computer vision, and materials science . Cambridge : Cambridge University Press , 1999
[本文引用: 1]
[15]
Fedkiw R . A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method)
Journal of Computational Physics 1999 ,152 (2 ):457 -492
DOI
URL
[本文引用: 1]
[16]
Liu TG Khoo BC Wang CW . The ghost fluid method for compressible gas--water simulation
Journal of Computational Physics 2005 ,204 (1 ):193 -221
[本文引用: 1]
[17]
Liu TG Khoo BC Xie WF . Isentropic one-fluid modelling of unsteady cavitating flow
Journal of Computational Physics 2004 ,201 (1 ):80 -108
DOI
URL
[18]
Liu TG Khoo BC Yeo K . Ghost fluid method for strong shock impacting on material interface
Journal of Computational Physics 2003 ,190 (2 ):651 -681
DOI
URL
[19]
Liu TG Khoo BC Yeo K . Ghost fluid method for strong shock impacting on material interface
Journal of Computational Physics 2003 ,190 (2 ):651 -681
DOI
URL
[20]
Liu TG Khoo BC Yeo K . The simulation of compressible multi-medium flow. I. A new methodology with test applications to 1D gas-gas and gas-water cases
Computers & Fluids 2001 ,30 (3 ):291 -314
[本文引用: 1]
[21]
Wang CW Liu TG Khoo BC . A real ghost fluid method for the simulation of multimedium compressible flow
SIAM Journal on Scientific Computing 2006 ,28 (1 ):278 -302
DOI
URL
[本文引用: 1]
[22]
Gao S Liu TG Yao CB . A complete list of exact solutions for one-dimensional elasticperfectly plastic solid Riemann problem without vacuum
Communications in Nonlinear Science and Numerical Simulation 2018 ,63 :205 -227
DOI
URL
[本文引用: 1]
[23]
Nourgaliev R Liou M Theofanous T . Numerical prediction of interfacial instabilities: Sharp interface method (SIM)
Journal of Computational Physics 2008 ,227 (8 ):3940 -3970
DOI
URL
[本文引用: 1]
[24]
Liu C Hu C . Adaptive THINC-GFM for compressible multi-medium flows
Journal of Computational Physics 2017 ,342 :43 -65
[本文引用: 1]
[25]
白晓 . 可压缩多相流问题的数值研究及应用
合肥:中国科学技术大学 , 2016
[本文引用: 1]
( Bai Xiao . Numerical Investigation of compressible multi-phase flows and application
Hefei: University of Science and Technology of China , 2016 (in Chinese))
[本文引用: 1]
[26]
Hu XY Khoo BC Adams NA , et al . A conservative interface method for compressible flows
Journal of Computational Physics 2006 ,219 (2 ):553 -578
[本文引用: 1]
[27]
Hu XY Adams NA Laccarino G . On the HLLC Riemann solver for interface interaction in compressible multi-fluid flow
Journal of Computational Physics 2009 ,228 (17 ):6572 -6589
[本文引用: 1]
[28]
Meyer M Devesa A Hickel S , et al . A conservative immersed interface method for large-eddy simulation of incompressible flows
Journal of Computational Physics 2010 ,229 (18 ):6300 -6317
DOI
URL
[本文引用: 1]
[29]
Lauer E Hu XY Hickel S , et al . Numerical modelling and investigation of symmetric and asymmetric cavitation bubble dynamics
Computers & Fluids 2012 ,69 (2 ):1 -19
[本文引用: 1]
[30]
Tryggvason G Bunner B Esmaeeli A . A front-tracking method for the computations of multiphase flow
Journal of Computational Physics 2001 ,169 (2 ):708 -759
DOI
URL
[本文引用: 1]
[31]
Di YN Li R Tang T . Level set calculations for incompressible two-phase flows on a dynamically adaptive grid
Journal of Scientific Computing 2007 ,31 (1 ):75 -98
[本文引用: 2]
[32]
Eleuteuo FT . Riemann Solvers and Numerical Methods for Fluid Dynamics
USA: Springer , 2009 : 102 -200
[本文引用: 1]
[33]
Guo YH Li R Yao CB . A numerical method on Eulerian grids for two-phase compressible flow
Advances in Applied Mathematics and Mechanics 2016 ,8 (2 ):187 -212
DOI
URL
[本文引用: 1]
[34]
Shyue K . A fluid-mixture type algorithm for compressible multicomponent flow with Mie-Grüneisen equation of state
Journal of Computational Physics 2001 ,171 (2 ):678 -707
DOI
URL
[本文引用: 2]
[35]
Gavrilyuk SL Favrie N Saurel R . Modelling wave dynamics of compressible elastic materials
Journal of Computational Physics 2008 ,227 (5 ):2941 -2969
[本文引用: 2]
[36]
Quirk J Karni S . On the dynamics of a shock-bubble interaction
Journal of Fluid Mechanics 1996 ,318 :129 -163
DOI
URL
[本文引用: 1]
[37]
Ullah M Gao W Mao D . Towards front-tracking based on conservation in two space dimensions III, tracking interfaces
Journal of Computational Physics 2013 ,242 :268 -303
DOI
URL
This is the third paper in the series of our conservative front-tracking method. In this paper, we describe how our method tracks fluid interfaces in multi-fluid flows. Two important ingredients in our conservative front-tracking method in tracking fluid interfaces are: (1) the velocities and pressures of the left and right cell-averages in a discontinuity cell are respectively maintained to be equal to each other, and in doing so the physics that the normal velocity and pressure are continuous cross the interface is simulated but that the tangential velocity may be discontinuous is ignored, and (2) a so-called numerical surface dissipation is designed on the tracked interface to eliminate possible numerical instability there, and we believe that this numerical surface dissipation is a good substitute for the missing physical dissipation acting on the interface. We then present numerical simulation of Haas-Sturtevant's two shock-bubble interaction experiments [J.F. Haas, B. Sturtevant, Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities, J. Fluid Mech. 181 (1987) 41-76] using this method. Our numerical results are in good agreement with the experimental and other numerical results in the early times of the flow. Moreover, our numerical results are also in good agreement with the experimental results in the later times of the flow and give clear pictures of the bubble deformation then, which show that the right boundaries of the bubble behave just as Rychtmyer-Meshkov instabilities with the shock coming from either heavy or light gases. (C) 2013 Elsevier Inc.
[38]
Haas J Sturtevant B . Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities
Journal of Fluid Mechanics 1987 ,181 :41 -76
DOI
URL
[本文引用: 2]
[39]
乔登江 . 核爆炸物理概论 . 北京 : 国防工业出版社 , 2003 : 51 -55
[本文引用: 1]
( Qiao Dengjiang . An Introduction to Nuclear Explosion Physics . Beijing : National Defence Industry Press , 2003 : 51 -55 (in Chinese))
[本文引用: 1]
[40]
Glasstone S Dolan PJ . Effects of nuclear weapons
USA United States Department of Defense and the Energy Research and Development Administration , 1977 : 453 -501
[本文引用: 1]
基于气液相界面捕捉的统一气体动理学格式
2
2018
... 多介质大变形问题广泛存在于军事和民用领域,例如爆炸力学效应、高速冲击问题、武器设计以及自然灾害的防护等. 上述问题通常存在多种介质间强烈的相互作用,具有强耦合、大变形、高度非线性等特点,物理现象极其复杂. 由于各介质之间的物理特性、初始状态差异极大,很多对单介质问题比较有效的数值方法在处理多介质问题时,通常会引起较大的数值震荡和误差[1 -2 ] ,甚至导致计算无法继续,因此需要研究合适的多介质数值计算方法,准确描述不同介质间的相互作用. ...
... 首先计算一个 JWL 状态方程的单介质 Riemann问题,来自文献[34 ] . 计算 区域为 [0 , 1 ] $\times $ [0, 5.0 $\times $ 10$^{ - 3}$], 网格尺寸为 2.5$\times $10$^{ - 3}$. 其中,JWL 状态方程参数取 $A_{1} =854.5$GPa,$A_{2} =20.5$GPa, $\omega =0.25$,$R_{1} =4.6$, $R_{2} =1.35$, $\rho_{0} =1840$kg/m$^{3}$. 初值条件如下 ...
基于气液相界面捕捉的统一气体动理学格式
2
2018
... 多介质大变形问题广泛存在于军事和民用领域,例如爆炸力学效应、高速冲击问题、武器设计以及自然灾害的防护等. 上述问题通常存在多种介质间强烈的相互作用,具有强耦合、大变形、高度非线性等特点,物理现象极其复杂. 由于各介质之间的物理特性、初始状态差异极大,很多对单介质问题比较有效的数值方法在处理多介质问题时,通常会引起较大的数值震荡和误差[1 -2 ] ,甚至导致计算无法继续,因此需要研究合适的多介质数值计算方法,准确描述不同介质间的相互作用. ...
... 首先计算一个 JWL 状态方程的单介质 Riemann问题,来自文献[34 ] . 计算 区域为 [0 , 1 ] $\times $ [0, 5.0 $\times $ 10$^{ - 3}$], 网格尺寸为 2.5$\times $10$^{ - 3}$. 其中,JWL 状态方程参数取 $A_{1} =854.5$GPa,$A_{2} =20.5$GPa, $\omega =0.25$,$R_{1} =4.6$, $R_{2} =1.35$, $\rho_{0} =1840$kg/m$^{3}$. 初值条件如下 ...
低渗透煤层气藏中气-水两相不稳定渗流动态分析
1
2017
... 多介质大变形问题广泛存在于军事和民用领域,例如爆炸力学效应、高速冲击问题、武器设计以及自然灾害的防护等. 上述问题通常存在多种介质间强烈的相互作用,具有强耦合、大变形、高度非线性等特点,物理现象极其复杂. 由于各介质之间的物理特性、初始状态差异极大,很多对单介质问题比较有效的数值方法在处理多介质问题时,通常会引起较大的数值震荡和误差[1 -2 ] ,甚至导致计算无法继续,因此需要研究合适的多介质数值计算方法,准确描述不同介质间的相互作用. ...
低渗透煤层气藏中气-水两相不稳定渗流动态分析
1
2017
... 多介质大变形问题广泛存在于军事和民用领域,例如爆炸力学效应、高速冲击问题、武器设计以及自然灾害的防护等. 上述问题通常存在多种介质间强烈的相互作用,具有强耦合、大变形、高度非线性等特点,物理现象极其复杂. 由于各介质之间的物理特性、初始状态差异极大,很多对单介质问题比较有效的数值方法在处理多介质问题时,通常会引起较大的数值震荡和误差[1 -2 ] ,甚至导致计算无法继续,因此需要研究合适的多介质数值计算方法,准确描述不同介质间的相互作用. ...
Computational methods in Lagrangian and Eulerian hydrocodes
1
1992
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
1
2014
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
1
2014
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
An arbitrary Lagrangian-Eulerian computing method for all flow speeds
1
1974
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
1
2018
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
基于 ALE 有限元法的流固耦合强耦合数值模拟
1
2018
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A level set approach to Eulerian--Lagrangian coupling
1
2003
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Volume of fluid (VOF) method for the dynamics of free boundaries
1
1981
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
一种基于几何重构的 Youngs-VOF 耦合水平集追踪方法
1
2019
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
一种基于几何重构的 Youngs-VOF 耦合水平集追踪方法
1
2019
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Moment-of-fluid interface reconstruction
1
2005
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Three-dimensional front tracking
1
1998
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A front-tracking method for the computations of multiphase flow
1
2001
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Fronts propagating with curvature-dependent speed: algorithms based on Hamilton- Jacobi formulations
1
1988
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
1
1999
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method)
1
1999
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
The ghost fluid method for compressible gas--water simulation
1
2005
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Isentropic one-fluid modelling of unsteady cavitating flow
2004
Ghost fluid method for strong shock impacting on material interface
2003
Ghost fluid method for strong shock impacting on material interface
2003
The simulation of compressible multi-medium flow. I. A new methodology with test applications to 1D gas-gas and gas-water cases
1
2001
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A real ghost fluid method for the simulation of multimedium compressible flow
1
2006
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A complete list of exact solutions for one-dimensional elasticperfectly plastic solid Riemann problem without vacuum
1
2018
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Numerical prediction of interfacial instabilities: Sharp interface method (SIM)
1
2008
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Adaptive THINC-GFM for compressible multi-medium flows
1
2017
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
可压缩多相流问题的数值研究及应用
1
2016
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
可压缩多相流问题的数值研究及应用
1
2016
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A conservative interface method for compressible flows
1
2006
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
On the HLLC Riemann solver for interface interaction in compressible multi-fluid flow
1
2009
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A conservative immersed interface method for large-eddy simulation of incompressible flows
1
2010
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
Numerical modelling and investigation of symmetric and asymmetric cavitation bubble dynamics
1
2012
... 多介质流动数值方法按其采用的坐标系可以分为 Lagrange 方法[3 ] 、Euler 方法[4 ] 、ALE 方法[5 -6 ] 以及 Euler-Lagrange 耦合方法[7 ] 等. 由于 Euler 方法的坐标系固定在空间中,计算网格不随介质的运动而运动,不发生网格畸变,因此适合处理大变形问题. 但由于介质在网格间流动,如果计算区域内存在多种介质,则有可能出现同一网格中包含多种介质的情况. 如何描述相界面的位置以及混合网格中各介质之间的相互作用,是 Euler 方法求解多介质问题的难点. 目前比较流行的、用于描述和追踪自由面和相界面运动轨迹的方法包括:VOF (volume of fluid) 方法[8 -9 ] 、MOF (moment of fluid) 方法[10 ] 、Front Tracking 方法[11 -12 ] 以及 Level Set 方法[13 -14 ] 等.此外,当网格中包含多种介质时,如果不同介质的密度和状态方程差异很大,在相界面附近容易产生速度和压力的非物理震荡,因此在Euler坐标系下求解多介质问题时,应尽可能避免直接利用相界面两侧介质的状态参数来求解控制方程,而是需要对混合网格进行特殊处理,尽可能抑制和消除非物理震荡. 目前主要的处理方法包括两类.第一类方法是虚拟流体类方法 (包括 GFM[15 ] 、MGFM[16 -20 ] 和 RGFM[21 -22 ] 等),其假设在相界面的另一侧存在相同介质的虚拟流体,介质穿过相界面时满足等熵关系,且压力和法向速度连续.第二类方法是切割单元法 (cut cell method),该方法根据求解精度显式地重构出相界面,并将含有多种介质的单元切割成几个部分.切割单元法的优点是能够清晰的描述相界面的位置和拓扑结构,而且能处理比较复杂的相界面以及拓扑结构发生变化时的情形,但缺点是单元会被相界面切割成几个部分,人为地形成碎片单元.当碎片单元的尺寸过小时,会严重影响数值计算的稳定性和效率,此时需要采用额外的技术来克服上述困难.例如,Nourgaliev 等[23 ] 采用了两套网格来存储数据,其中一套网格为非结构网格,另一套为结构网格.数值计算时,相界面对结构网格进行切割,并通过对切割过程中产生的碎片单元进行网格融合,得到另一套非结构网格,在一定程度上克服了 CFL 条件对时间步长的限制.Liu 等[24 ] 引入了一个混合方法,通过对碎片单元相邻网格的守恒量进行再分配,来达到数值稳定的目的.白晓等[25 ] 在切割单元过程中引入了虚拟流体方法,每种介质切割单元的状态可以覆盖到一个完整的单元,实现了碎片单元的状态量更新,并克服了数值不稳定性.Hu 等[26 -27 ] 在二维交错型结构网格中提出了一种守恒型的混合技术,对体积分数小于 0.5 的碎片单元,根据界面的法向确定碎片单元在 $x$,$y$ 方向以及对角线方向的同介质相邻单元,并以界面的法向分量和各相邻单元的体积分数作为权重来计算这 3 个单元与目标碎片单元之间的守恒量交换,从而对碎片单元的守恒量进行了修正,提高了数值计算的稳定性. Meyer 等[28 ] 在 Hu 的研究基础上进行了改进,并将算法拓展了三维情形.在对碎片单元的守恒量进行修正时,碎片单元的所有相邻单元都被用于进行混合操作,并将体积分数的幂函数形式加入到权重因子中,使得体积分数越大的的单元所占的权重越大,进一步提高了混合技术的稳定性.Lauer 等[29 ] 将 Meyer 的混合技术扩展到了非均匀的结构网格中,利用混合技术对体积分数小于 0.6 的碎片单元进行了满足守恒性质的修正处理. ...
A front-tracking method for the computations of multiphase flow
1
2001
... Level Set 方法把随时间运动的相界面 $\varGamma (t)$ 定义为距离函数 $\varphi ({\pmb x},t)$ 的零等值面[30 ] . 本文利用特征线方法求解 Level Set 函数的演化方程 ...
Level set calculations for incompressible two-phase flows on a dynamically adaptive grid
2
2007
... 式中,$\tilde {\pmb u}$ 为由物质界面的运动速度延拓得到的速度场[31 ] . ...
... 利用显式正系数格式[31 ] 求解如下所示的重新初始化方程 ...
Riemann Solvers and Numerical Methods for Fluid Dynamics
1
2009
... 式中,${\pmb n}_{K_{i,n} } $ 为相界面的单位法向,$ | \varGamma _{K_{i,n} } | $ 为相界面的长度,$\sigma _{K_{i,n} }^* $ 和 $u_{K_{i,n} }^* $ 分别为相界面上的法向应力和法向速度,且通过在相界面法向上求解局部一维多介质 Riemann 问题的精确解 来获得,具体见文献[32 ,33 ] . ...
A numerical method on Eulerian grids for two-phase compressible flow
1
2016
... 式中,${\pmb n}_{K_{i,n} } $ 为相界面的单位法向,$ | \varGamma _{K_{i,n} } | $ 为相界面的长度,$\sigma _{K_{i,n} }^* $ 和 $u_{K_{i,n} }^* $ 分别为相界面上的法向应力和法向速度,且通过在相界面法向上求解局部一维多介质 Riemann 问题的精确解 来获得,具体见文献[32 ,33 ] . ...
A fluid-mixture type algorithm for compressible multicomponent flow with Mie-Grüneisen equation of state
2
2001
... 首先计算一个 JWL 状态方程的单介质 Riemann问题,来自文献[34 ] . 计算 区域为 [0 , 1 ] $\times $ [0, 5.0 $\times $ 10$^{ - 3}$], 网格尺寸为 2.5$\times $10$^{ - 3}$. 其中,JWL 状态方程参数取 $A_{1} =854.5$GPa,$A_{2} =20.5$GPa, $\omega =0.25$,$R_{1} =4.6$, $R_{2} =1.35$, $\rho_{0} =1840$kg/m$^{3}$. 初值条件如下 ...
... 计算时间为 $t =1.2 \times 10^{ - 5}$. 计算结果与文献[34 ] 参考解的对比如图 7 所示,对比表明本文结果 与文献中的高精度参考解符合较好,且在相界面处密度具有高分辨率. ...
Modelling wave dynamics of compressible elastic materials
2
2008
... 再计算一个 JWL - 弹性固体的 Riemann 问题,其中气体相用JWL状态方程来描述,参数为 $A_{1}=854.5$GPa,$A_{2} =20.50$GPa, $\omega =0.25$,$R_{1} =4.6$, $R_{2} =1.35$, $\rho _{0}=1840$kg/m$^{3}$. 固体相的静水压力用刚性气体状态方程描述,且 $\gamma =4.4$,$p_{\infty } = 600$MPa,固体的偏应力遵守 Hooke 定律,且 $\beta ^{e} =10^{14}$Pa$\cdot $kg/m$^{3}$[35 ] . 初 值条件如下 ...
... 计算时间为 $t =10^{ - 4}$. 图 8 给出了计算结果与参考解[35 ] 的对比,从对比分析可知数值结果与参考解符合较好,且在接触间断和激波附近具有较高的分辨率. ...
On the dynamics of a shock-bubble interaction
1
1996
... 激波与气泡作用问题是可压缩多介质流体问题的一个经典算例[36 -38 ] . 初值条件如下:一个直径为 50mm 的圆形气泡放置在长 311.5mm、宽 89mm 的激波管的正中间,其余地方充满空气 (如图 9 所示). 初始时刻,气泡右侧 5mm 处有一个马赫数为 $Ma=1.22$、向左运动的平面激波. 初始物理参数如表 2 所示. 计算模型的上、下边界设为反射边界条件,左、右边界设为出流边界条件,网格尺寸为 1mm. ...
Towards front-tracking based on conservation in two space dimensions III, tracking interfaces
2013
Interaction of weak shock waves with cylindrical and spherical gas inhomogeneities
2
1987
... 激波与气泡作用问题是可压缩多介质流体问题的一个经典算例[36 -38 ] . 初值条件如下:一个直径为 50mm 的圆形气泡放置在长 311.5mm、宽 89mm 的激波管的正中间,其余地方充满空气 (如图 9 所示). 初始时刻,气泡右侧 5mm 处有一个马赫数为 $Ma=1.22$、向左运动的平面激波. 初始物理参数如表 2 所示. 计算模型的上、下边界设为反射边界条件,左、右边界设为出流边界条件,网格尺寸为 1mm. ...
... 图 10 给出了不同时刻的数值结果,并与 Haas 和 Sturtevant 的实验结果[38 ] 进行了比较.图中第一列为实验纹影图,第二列为数值计算得到的密度等值线图. ...
1
2003
... 计算一个当量为 1kt TNT、爆高为 200m 的空中强爆炸冲击波传播问题. 强爆炸产物采用等温等压球模型,取爆炸总当量的 85% 作为强爆炸的力学初始能量[39 ] . 空气采用理想气体状态方程,初始压力为 101.3kPa,初始密度为 1.29kg/m$^{3}$. 计算区域在 $x =0$ 和 $y =0$ 设为固壁反射边界条件,其余边界设为无反射边界条件. ...
1
2003
... 计算一个当量为 1kt TNT、爆高为 200m 的空中强爆炸冲击波传播问题. 强爆炸产物采用等温等压球模型,取爆炸总当量的 85% 作为强爆炸的力学初始能量[39 ] . 空气采用理想气体状态方程,初始压力为 101.3kPa,初始密度为 1.29kg/m$^{3}$. 计算区域在 $x =0$ 和 $y =0$ 设为固壁反射边界条件,其余边界设为无反射边界条件. ...
Effects of nuclear weapons
1
1977
... 计算得到典型时刻的冲击波压力等值线如图 13 所示,当空中强爆炸产生的冲击波传播到地面时,最早在爆心投影点发生正反射,然后以逐渐增大的入射角发生斜反射,产生双激波结构的规则反射 (图 13 (a)). 随着冲击波向外继续传播,入射角不断增大. 当入射角增大到临界角附近时将发生马赫反射,此时反射波阵面和入射波阵面的交点离开地面,形成垂直于地面的马赫杆 (图 13 (b)). 随着冲击波的进一步传播,马赫杆不断增长. 图 14 给出了数值计算得到的地面冲击波载荷分布 (峰值超压和冲量) 与实测结果拟合的经验公式[40 ] 的对比情况. 由对比可知,计算得到的地面冲击波参数与实测结果符合得较好,最大误差不超过 40%. ...