引言
在人们生活的三维世界中,从咖啡的溶解到威力巨大的台风,湍流现象是随处可见的. 而在一些自然界与工程应用的三维流动中,由于边界尺寸限制或者外力的作用,其中一个维度上的运动被抑制,流动呈现出近似二维流动的特征. 例如大气与海洋中的大尺度流动——由于地球半径约为 6400km, 而大气层和海洋的厚度仅为 10km 左右, 因此台风等的大尺度运动往往可以被看作二维流动. 无论是三维湍流还是二维湍流,湍流场都是一个耗散系统. 流场中的湍动能 $u^2/2$ 会不断被耗散,并需要不断的能量补充来维持稳定的流场. 在局部均匀湍流场中,欧拉场的二阶混合速度加速度结构函数 (velocity-acceleration structure function, VASF),表示两个粒子间相对湍动能的变化速率,与尺度间的能量传递率相关[1 -4 ]
(1) $\langle \delta u \cdot \delta a \rangle_{R_0} =\dfrac{\rm d}{{\rm d} t}\left\langle \dfrac{1}{2}\delta u^2 \right \rangle_{R_0} =-2\varepsilon$
其中,$\delta u$ 和 $\delta a$ 为两个粒子间的相对速度和相对加速度,$\langle \cdot \rangle$ 代表系综平均,下标 $R_0$ 表示是对相对距离 $R_0$ 在惯性区的粒子对进行条件统计; $\varepsilon$ 为湍流场的能量传递速率,其符号表示能量传递的方向[4 ] . 当能量从大尺度传到小尺度,$\varepsilon>0$;当能量从小尺度传到大尺度,$\varepsilon<0$.
在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证.
二维湍流除了能量的反向传递,另一个重要物理过程是拟涡能 (enstrophy,又称为涡量拟能) $\omega^2/2$ 的正向传递,其 中 $\omega$ 为涡量. 外力在作用尺度 $L_{\rm F}$ 以速率 $\beta$ 注入拟涡能,其不断往小尺度传递,最终在黏性作用尺度 $\eta$ 下被黏性耗散掉. 当初始距离在反向能量级串区 ($L_{\rm F}\ll R_0 \ll L_{\alpha}$),式 (1) 是成立的. 当初始距离在正向拟涡能级串区 ($\eta\ll R_0 \ll L_{\rm F}$),拟涡能传递率 $\beta$ 起主导. 量纲分析可得
(2) $\langle \delta u \cdot \delta a \rangle_{R_0} \sim \beta R_0^2$
其中,$R_0$ 为两个粒子的相对距离,正的 $\beta$ 代表拟涡能从大尺度往小尺度进行传递,上式左右两边存在待定的常系数. 式 (2) 只在均匀流场中成立,但实际中的许多湍流场是衰减的. 也即拟涡能只在初始时刻或者初始位置上注入,随后注入源消失. 例如海洋上形成的强台风,在登陆后由于耗散作用其气旋强度会逐渐降低.
本文将对二维湍流的 VASF 进行研究,并重点考察衰减对 VASF 的影响. 在第 1 节推导二维湍流场中正向级串区和反向级串区的 VASF 理论公式,发现除了式 (1) 或式 (2) 代表的能量或拟涡能在尺度间的传递项外,还存在衰减带来的非均匀项. 两者一正一负,呈现竞争关系. 第 2 节介绍基于皂膜的二维衰减湍流的实验装置. 为了获取速度,特别是加速度,以及粒子位置随时间的演化信息,本文采用拉格朗日粒子追踪法对流场进行测量. 并实现了在每一步时间匹配推进上,复杂度从 $N^2$ 到 $N\log_2 N$ 的算法优化. 第 3 节对 VASF 在正向拟涡能级串区的测量结果进行讨论. 实验发现尺度间拟涡能传递项是正的,但非均匀项为负的,并且占主导作用. 因此在二维衰减湍流中 VASF 甚至可能会小于 0,其符号也失去了表征涡量拟能传递方向的意义. 第 4 节对与 VASF 密切相关的弥散过程进行讨论,通过负的 VASF 解释了弥散过程后期变慢现象. 最后一节对本文工作进行总结.
1 理论
对于二维流场中的任意时刻上的任意两点 $(x, t)$ 和 $({x}', t')$,这里以及下文中的上标 ${ }'$ 表示另一个点的信息. 这两点距离为 $r=x-{x}'$,中间位置为 $X=(x+{x}')/2$. 时间间隔为 $\tau=t-t'$,平均时间为 $T=(t+t')/2$. 两点的速度为 $u_i(x,t)$ 和 $u'_i (x',t')$,加速度分别为 $a_i(x,t)=\dfrac{{\rm \partial} u_i}{{\rm \partial} t}+u_k\dfrac{{\rm \partial} u_i}{{\rm \partial} x_k}$ 和 $a'_i (x',t')=\dfrac{{\rm \partial} u'_i }{{\rm \partial} t'}+u_k'\dfrac{{\rm \partial} u'_i }{{\rm \partial} x'_k }$. 那么速度和加速度的混合结构函数为
(3) $\delta u_j \delta a_i =(u_j-u'_j )\left(\dfrac{{\rm \partial} u_i}{{\rm \partial} t}+u_k\dfrac{{\rm \partial} u_i}{{\rm \partial} x_k}- \dfrac{{\rm \partial} u'_i }{{\rm \partial} t'}-u'_k \dfrac{{\rm \partial} u'_i }{{\rm \partial} x'_k }\right)$
(4) $u_k\dfrac{{\rm \partial} u_i}{{\rm \partial} x_k}-u'_k \dfrac{{\rm \partial} u'_i }{{\rm \partial} x'_k }=\\ \qquad \dfrac{u_k+u'_k }{2}\dfrac{{\rm \partial} (u_i-u'_i )}{{\rm \partial} X_k} +(u_k-u'_k )\dfrac{{\rm \partial} (u_i-u'_i )}{{\rm \partial} r_k}$
上式中用到了空间坐标自变量 $(x,x' )$ 与 $(X,r)$ 的相互转化[13 ]
(5) $\left.\begin{array}{c} \dfrac{{\rm \partial} }{{\rm \partial} x} =\dfrac{1}{2}\dfrac{{\rm \partial} }{{\rm \partial} X}+\dfrac{{\rm \partial} }{{\rm \partial} r}, \ \ \ \dfrac{{\rm \partial} }{{\rm \partial} x^{\prime}} =\dfrac{1}{2}\dfrac{{\rm \partial} }{{\rm \partial} X}-\dfrac{{\rm \partial} }{{\rm \partial} r}\\ \dfrac{{\rm \partial} }{{\rm \partial} X} =\dfrac{{\rm \partial} }{{\rm \partial} x}+\dfrac{{\rm \partial} }{{\rm \partial} x'} , \ \ \ \dfrac{{\rm \partial} }{{\rm \partial} r} =\dfrac{1}{2}\Big(\dfrac{{\rm \partial} }{{\rm \partial} x}-\dfrac{{\rm \partial} }{{\rm \partial} x' }\Big) \end{array}\right\}$
(6) $\dfrac{{\rm \partial} u_i}{{\rm \partial} t}-\dfrac{{\rm \partial} u'_i }{{\rm \partial} t'} =\dfrac{{\rm \partial} (u_i+u_i^{\prime})}{{\rm \partial} \tau} +\dfrac{1}{2}\dfrac{{\rm \partial} (u_i-u'_i )}{{\rm \partial} T} = \dfrac{{\rm \partial} (u_i-u'_i )}{{\rm \partial} T}$
将式 (4) 和式 (6) 代入到式 (3),取其缩并,系综平均得到
(7) $\langle \delta u_i\delta a_i \rangle = \underbrace{\dfrac{1}{2}\dfrac{{\rm \partial} D_{ii}}{{\rm \partial} T}}_{\rm unsteady} + \underbrace{\dfrac{U_k}{2}\dfrac{{\rm \partial} D_{ii} }{{\rm \partial} X_k}}_{\rm inhomogeneous} +\underbrace{\dfrac{1}{2}\dfrac{{\rm \partial} D_{iik}}{{\rm \partial} r_k}}_{\rm scale transfer}$
其中,$U=(u+u' )/2$ 是流场的平均速度,$D_{ii}=\langle \delta u_i \delta u_i \rangle$ 和 $D_{iik}=\langle \delta u_i \delta u_i \delta u_k \rangle$ 分别为二阶和三阶的欧拉速度结构函数. 上式的推导是一个通用的表达式,并未用到任何假设. VASF 虽然是绝对坐标 $X$ 和相对距离 $r$ 的多元函数,但是这两个自变量之间没有显著耦合 (即使 $D_{ii}, D_{iik}$ 是这两个自变量的二元函数),这为实验数据的分析带来了极大的便利. 可以看到 $\langle \delta u_i\delta a_i \rangle$ 由 3 部分组成. 第 1 项为时间的非稳态项,在稳态流场中为 0. 第 2 项是非均匀项,在局部均匀流场中结构函数 $D_{ii}$ 只是相对距离 $r$ 的函数,对当地绝对位置 $X$ 微分为 0. 因此在稳态局部均匀流场中,只剩下第 3 项. 同三阶速度结构函数物理含义一样,该项代表能量或拟涡能在尺度间的传递. 第 3 项在任意流场中是没有普适表达式的. 为进一步对该项进行分析,本文讨论该项在不可压均匀各向同性湍流的条件下的表达式. 参考三维湍流中相关推导[14 -16 ] ,本文得到二维和三维湍流中该项的通用表达式
(8) $\dfrac{{\rm \partial} D_{iik}}{{\rm \partial} r_k} =\dfrac{{\rm \partial} D_{iiL}}{{\rm \partial} r} +\dfrac{(d-1) D_{iiL}}{r} =\\ \qquad \dfrac{1}{3}\left[r\dfrac{{\rm \partial}^2 D_{LLL}}{{\rm \partial} r^2}+(2d+1)\dfrac{{\rm \partial} D_{LLL}}{{\rm \partial} r}+(d^2-1)\dfrac{D_{LLL}}{r}\right]$
其中,$d$ 代表维数,在二维湍流中 $d=2$,在三维湍流中 $d=3$. $D_{iiL}=\langle \delta u_i \delta u_i \delta u_L \rangle =\langle \delta u_i \delta u_i \delta u_k r_k/|{r}| \rangle$,下标 $L$ 表示相对速度在相对距离径向方向 $r_k/|{r}|$ 的投影. 进一步的,$D_{LLL}=\langle \delta u_L \delta u_L \delta u_L \rangle$ 为三阶径向速度结构函数,在能量和拟涡能惯性区分别为[16 -17 ]
(9) $D_{LLL}=\left\{\!\!\begin{array}{cl} -\dfrac{12}{d(d+2)}\varepsilon r & \text{(energy range in 2D/3D)} \\ \dfrac{1}{8}\beta r^3 & \text{(enstrophy range in 2D)} \end{array}\right.$
将式 (9) 代入式 (8),得到 VASF 中的能量/拟涡能在尺度间传递项的表达式
(10) $\dfrac{1}{2}\dfrac{{\rm \partial} D_{iik}}{{\rm \partial} r_k}= \left\{\!\!\begin{array}{cl} -2\varepsilon<0 & \text{(3D energy range)} \\ -2\varepsilon>0 & \text{(2D energy range)} \\ \beta r^2/2>0 & \text{(2D enstrophy range)} \end{array}\right.$
式中,$\varepsilon>0$, $\beta>0$ 代表着能量和拟涡能分别从大尺度传向小尺度. 在三维均匀各向同性湍流中,能量往小尺度传递,$\langle \delta u_i \delta a_i \rangle=-2\varepsilon<0$. 而在二维均匀各向同性湍流中,能量往大尺度传递,拟涡能往小尺度传递,所以两个惯性区间 $\langle \delta u_i \delta a_i \rangle>0$ 皆成立[18 -19 ] .
本文从相对速度和相对加速度的定义出发,重现了在均匀各向同性湍流中式 (1) 和式 (2) 的VASF 表达式,并确定了 在拟涡能级串惯性区表达式前的系数 “1/2”. 而在一般湍流场中,VASF更普适的表达式中包含时间维度 (非稳态项),空间维度 (非均匀项),尺度维度 (尺度间传递项) 三者共同的影响. 为比较这三项的相对大小,本文开展了基于皂膜的二维衰减湍流实验研究. 为此接下来一小节先对实验装置及流场测量方法进行介绍.
2 实验方法和粒子跟踪技术
二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s.
为了形成强湍流场,类似于三维风洞中插入平面栅格的方式,本文在皂膜上游处水平插入一排栅格,如图 1 (a) 中虚线方框中所示. 栅格间距 $M=5$mm,组成栅格的圆棒直径为 1.14mm. 栅格的布置实物图如图 1 (b) 所示,栅格是以一块铝板为基底,在表面通过线切割开半圆形槽,放入不锈钢针作为圆柱小棒制成,并以磁铁加以固定. 图中两根竖直的亮线为构成皂膜的两根尼龙绳,皂膜在两根尼龙绳中间往下流动.
当皂膜流过栅格后,会形成强烈湍流脉动. 本文在距离栅格为 $S\!=\!(12.5 \sim 67.5)M$ 的下游位置对流场进行测量,如图 1 (a) 中的绿色区域. 在对流场进行速度测量时,粒子图像测速法 (particle image velocimetry, PIV) 是一个成熟和普遍使用的方法,该方法可以获得速度的欧拉场. 但利用欧拉速度场求取加速度时,涉及到对流项的空间求导,要求流场空间分辨率应达到拟涡能耗散尺度的量级. 此外湍流中的非稳态项 ${\rm \partial} u_i/{\rm \partial} t$和对流项$u_k {\rm \partial} u_i/{\rm \partial} x_k$ 两者十分接近且正负相反,利用这两者的和得到的加速度不确定度往往极大[30 ] . 为此本文采用拉格朗日粒子追踪法 (lagrangian particle tracking, LPT) 对速度和加速度进行测量[31 ] . 首先在皂液中加入直径 $1\mu$m 的示踪粒子,粒子直径小于皂膜厚度,因此可以忽略对皂膜的影响. 一台波长 532nm,功率为 100W 的脉冲激光器照亮待测流场区域中的示踪粒子. 如图 1 (a) 所示,两台高速相机沿流向依次排列,在保证分辨率的情况下获得足够长的流场视野. 两台相机的合成分辨率为 $(2\times)2560\times 472$,可以拍得 100mm$\times $12mm 的狭长流场区域. 通过移动相机和栅格的相对位置实现更长范围内的测量. 采用同步器将两台相机和激光器进行同步,采样频率为 5000Hz. 整个实验系统通过基于 $Qt$ 环境下编写的数据采集平台进行控制,实现 数据的自动采集、传输和存储.
图1
图1
(a) 二维水洞装置图,$x$ 方向为重力方向,$y$ 方向为水平方向,$z$ 方向为皂膜厚度方向. 皂膜平面由两根直径为 0.32mm 的尼龙绳组成. 为了形成湍流场,在皂膜上游水平插入一排栅格. 激光器照亮距离栅格为 $S$ 的下游绿色区域,该区域内的流场轨迹信息被两台高速相机捕捉. (b) 栅格布置的实物图. 上方水平排列的圆柱小棒为栅格,竖直的亮线为尼龙绳,两根尼龙绳中间为竖直往下流动的皂膜. 由于 532nm 激光的散射,整个流场呈现绿色背景
Fig.1
(a) Two-dimensional water tunnel setup, $x$ axis is the gravity direction, $y$ axis is the horizontal direction, $z$ axis is the film thickness direction. The plane of soap film is consisted by two nylon ropes whose diameter are 0.32mm. To create turbulent flow, we insert a comb in the upstream. The laser illuminates the downstream regions below the comb, whose flow trajectories are recorded by two high speed cameras. (b) The real image of comb equipment. The upper cylinders make up a comb, the vertical bright lines are nylon ropes, and the soap film flows down between the ropes. The whole flow are in green background, owing the scatter from 532nm laser
在获得原始的粒子图像后,首先通过亚像素定位获得示踪粒子在像素坐标系上的位置. 第二步经过标定还原到真实的物理空间 坐标系. 对于单台相机的二维标定,一般是假设皂膜平面和标定板平面重合. 但在两台相机的二维标定中,可以求得皂膜平面和标定板平面的距离并调节使之真正重合. 接下来一个重要的步骤是实现粒子在不同时刻的匹配,这是LPT算法的核心以及计算资源消耗最大的一步. 每一个瞬时场都有数百个粒子,从上一个时刻到下一个时刻需要实现这上百个粒子的一一匹配. 由于粒子的形态大小是无法区分的,因此一般是通过历史的位置、速度和加速度场信息进行匹配[31 ] . 假设每个时刻粒子平均个数为 $N$. 若采用暴力匹配算法,对 $t$ 时刻的 $N_t$ 个粒子,需匹配 $t+1$ 时刻的 $N_{t+1}$ 个粒子,每推进一个时间步的复杂度为 $N^2$. 但本文注意到皂膜流场是长 100mm 的狭长形区域. 流场的竖向脉动速度方差约为 0.2m/s,考虑到大约 5 倍脉动速度的事件概率很低以致可忽略不计. 那么在高达 5000Hz 的拍摄频率下,粒子的位置波动为 $0.2\times 5/5000=0.2$mm. 因此本文事先就可以预估出粒子下一个时刻的位置限定在 $\pm 0.2$mm 范围内,而不必在整个 100mm 的流场范围内进行匹配.
基于上面的分析,本文提出实现粒子时间匹配的两步走快速匹配算法. 首先对每一个时刻内的流场粒子以 $x$ 坐标为基准进行排序,例如快速排序等,复杂度为 $N\log_2 N$. 其次在已经排序好的 $t+1$ 时刻流场中,通过二分查找等算法迅速完成 $\pm 0.2$mm 位置范围的定位,复杂度为 $\log_2 N$. 对这 $\pm 0.2$mm 预判区的粒子进行一一匹配,一般预判区内粒子个数为 $O(1)$. 这一个步骤需要对 $t$ 时刻的每一个粒子进行依次操作. 因此每推进一个时间步的复杂度为
(11) $N\log_2 N+N_{t}\log_2 N_{t+1}=O(N\log_2 N)$
为此基于对特定流场的分析实现了快速的 LPT 算法. 其实也可以在亚像素定位步骤中,按照 $x$ 坐标依次遍历识别粒子,从而节省上述算法中的空间排序步骤. 此外实际计算中,为了保证匹配准确率,本文会同时验证 $t+1$ 时刻和 $t+2$ 时刻的粒子信息. 为了表述方便,上文中只阐述根据 $t+1$ 时刻信息进行匹配的算法. 但两种算法都可以通过上面的思路进行改善,将推进复杂度从 $O(N^2)$ 降低至 $O(N\log_2 N)$. 匹配问题体现在生产生活中的方方面面,本文提出的 $O(N\log_2 N)$ 匹配算法是基于粒子位置信息的强预测性. 对于有着同样性质的问题,可以将本文思路进行推广并应用.
在获得流场轨迹信息后,最后一步是通过位置场进行速度和加速度场的计算. 根据粒子轨迹信息,可以通过对空间位置的一次时间微分得到速度. 进一步地,直接对空间位置的二次时间微分得到加速度,而不需要通过速度场再来计算加速度,从而LPT方法实现了加速度的准确测量. 实际计算中,由于轨迹信息在时间上是离散的,一般是通过对位置信息卷积速度核函数和加速度核函数以分别得到速度和加速度[31 ] .
3 VASF实验结果与讨论
通过LPT测量,本文获得了皂膜流场中粒子轨迹上的速度和加速度. 进一步对轨迹进行时间排序,得到速度和加速度 的欧拉场. 假如本文对欧拉场中任取两点来计算式 (7) 中的 VASF 或者两阶及三阶速度结构函数,那么得到的将是待测区域的统计特性的平均值. 但皂膜流场的脉动速度在主流 $x$ 方向是不断衰减的,$\beta$ 和 $\varepsilon$ 都是空间位置 $x$ 的递减函数. 理想情况下,按照定义式 (7),要想计算各部分在当地位置 $x$ 的值,需要选取 $x-r/2$ 和 $x+r/2$ 两个点的速度进行计算. 但实际上这样的数据点极少,难以形成收敛的统计量. 为了获取收敛的结构函数,本文采用泰勒冻结假设. 流场的脉动速度 $u$ 虽然在不断衰减,但平均速度 $U=2.7$m/s 几乎保持不变. 流场的湍流强度 $u/U=5%\sim 10% \ll 1$,因此满足泰勒冻结假设[32 ] . 泰勒冻结假设并非适用于所有的流场,但在三维风洞中的运用已经得到广泛的认可[33 ] . Belmonte 等[34 ] 在二维皂膜流动中,也已经验证了泰勒冻结假设的正确性. 该假设认为湍流场的信息被冻结着以对流速度进行传递,那么
(12) $u(x+r,t+\tau)=u(x+r-U\tau,t)$
(13) $D_{ii}(r,\tau;x) =\langle [u_i(x+r,t+\tau)-u_i(x,t)]^2 \rangle =\\ \qquad \langle [u_i(x+r-U\tau,t)-u_i(x,t)]^2\rangle = \\ \qquad D_{ii}(r-U\tau,0;x)$
在风洞中使用热线法测速时,也是利用泰勒冻结假设获得在热线当地位置处的结构函数[35 ] ,自变量相对距离只包含时间距离. 相同的, 式 (13) 参与运算的是两个在当地位置 $x$ 的点的脉动速度信息,得到的是当地 $x$ 的二阶结构函数. 唯一不同的是,这里自变量相对距离 $r-U\tau$ 既包含两点之间的空间距离$r$,也包含时间距离 $\tau$. 为了获得当地位置 $x$ 上的真实条件统计,空间波动范围 $r$ 的选取不宜太大. 一般的,本文设置其最大值为 $r=0.2$mm,也即计算在位置 $x\pm 0.2$mm 处的当地统计特性. $r$ 的范围是根据拟涡能耗散率尺度选定的,其值为 $ 0.3\sim 0.5$mm[28 ] ,并随着往下游的发展而逐渐增长.
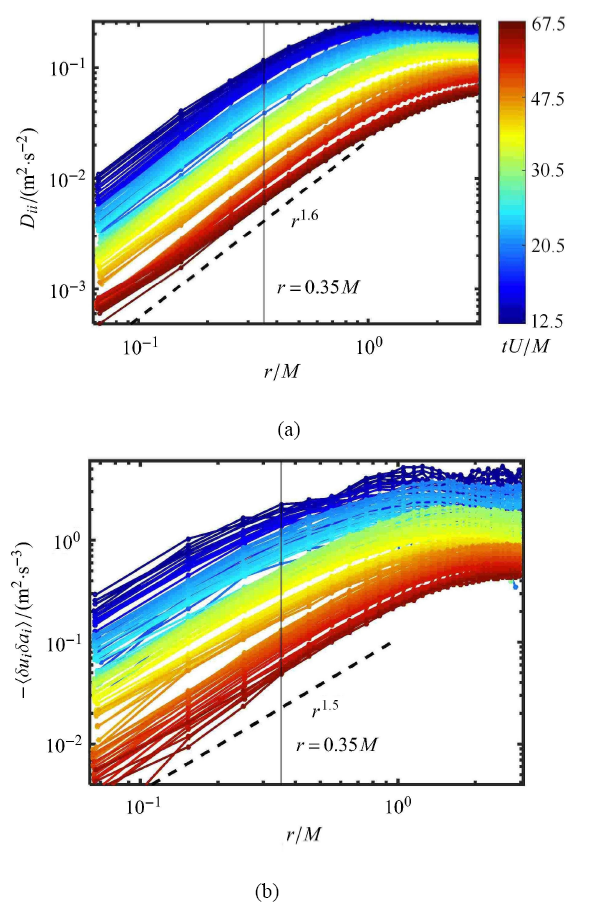
图 2 (a) 展示的是利用泰勒冻结假设计算得到的,当地位置 $x$ 的二阶结构函数 $D_{ii}(r;x)$. 如右边的颜色坐标所示,不同的颜色代表不同的当地位置 $x$. 在距离栅格下游的 $12.5M$ 一直增长到 $67.5M$,颜色也从深蓝变为深红. 根据 Kraichnan 的理论[7 ] ,在正向拟涡能级串区 $(\eta \ll r \ll L_{\rm F})$,结构函数由 $\beta$ 控制. 量纲分析得到 $D_{ii}\sim \beta^{2/3}r^2 $. 图 2 (a) 显示在 $r<M$ 区间存在 $D_{ii}\sim r^{1.6}$ 幂次律,对应着流场中的正向级串区. 偏小的幂次律在其他皂膜实验中也被普遍观察到,并被认为是由于有限雷诺数等原因导致[11 ,36 ] . 在衰减过程中,理论上,正向级串区的雷诺数 ${ Re}_{\omega}=u_{\rm F}L_{\rm F}/\nu=(L_{\rm F}/\eta)^2\sim t^0$. $L_{\rm F}$ 和 $\eta$ 均以 $t^{1/2}$ 的幂次律进行增长,整个正向级串惯性区的宽度不会发生显著变化. 实验中发现 $r^{1.6}$ 的幂次律得到自相似的往下游发展,并未得到显著升高或降低. 不变的惯性区间宽度和不变的幂次律和理论预测是一致的,但为了明确有限雷诺数的影响还需进一步实验. 此外,拟涡能是由栅格带来的扰动注入,一般认为拟涡能注入尺度 $L_{\rm F}\sim M$,这也与本文观察的一致. 栅格不仅在尺度$L_{\rm F}$上注入拟涡能,同时也注入能量,并往大尺度传递. Kraichnan 指出在反向级串区 $(L_{\rm F} \ll r \ll L_{\alpha})$,结构函数由能量耗散率决定,量纲分析得到 $D_{ii}\sim (\varepsilon r)^{2/3}$. $r^{2/3}$ 的幂次律十分平缓,并受到有限惯性区间的影响,本文的实验结果并没有看到一段清晰的 $r^{2/3}$ 幂次律. 但本文仍可以看到在 $r=M$ 附近,正向级串区和反向级串区的转变. 并且随着往下游的衰减,转折点在不断增大. 表征有效注入尺度的增长,这是二维湍流和三维湍流的一个重要差别,这一现象在衰减能谱上也可以看到[28 ] .
图2
图2
(a) 运用泰勒冻结假设,计算当地下游位置 $x\pm 0.2$mm 处的 $D_{ii}$ 与尺度 $r$ 的关系. 不同的颜色 代表对应的距离栅格的距离 $x/M$. 两台相机一次的拍摄视野只有 $ 100{\rm mm}=20 M$. 为获得距离栅格更宽范围 的统计特性,本文通过移动栅格使相机距离栅格 $S/M=12$, 20, 30 和 50,分 4 次实验完成. (b) $-\langle \delta u_i \delta a_i \rangle$ 与尺度 $r$ 的关系,在正向级串区表现出 $r^{1.5}$ 的幂次律. 图中的各 颜色代表不同的空间位置,同 (a) 中一致. 本图和上图的竖直实线为尺度 $r=0.35 M$,其与各种颜色线的交点即为各 下游位置在 $r=0.35 M$ 上的 $-\langle \delta u_i \delta a_i \rangle$ 和 $D_{ii}$
Fig.2
(a) Using Taylor frozen flow hypothesis, we calculate the relationship between $D_{ii}$ and $r$ in local downstream location $x\pm 0.2$mm. Different colors correspond to different separation below the comb $x/M$. The capture window of two cameras is 100mm =20M in each time. To obtain a wider regions statistics, we set the relative separation between camera and comb as $S/M=12$, 20, 30 and 50. (b) The relationship between $-\langle \delta u_i \delta a_i \rangle$ and $r$, which shows $r^{1.5}$ power law in direct enstrophy range. The colors mean different downstream locations which are the same with (a). The vertical solid line lies in $r=0.35 M$, whose cross points with different colorful lines are $-\langle \delta u_i \delta a_i \rangle$ and $D_{ii}$ in $r=0.35 M$
同计算式 (13) 一样,运用泰勒冻结假设,本文也计算了各下游位置的 VASF,如图 2 (b) 所示. 在二维均匀各向同性湍流中,式 (10) 表明无论在正向级串区还是反向级串区,VASF 的尺度间传递项,$\dfrac{1}{2}\dfrac{{\rm \partial} D_{iik}}{{\rm \partial} r_k}>0$. 但实验结果显示所有下游位置的所有尺度上 VASF $<$ 0. 而皂膜实验是稳态的,构成 VASF 的第一项为零. 因此这告诉人们构成 VASF 的第二项,非均匀项不可忽略. 并且非均匀项为负,即使尺度间传递项为正,但由于非均匀项绝对值更大,导致整体的 VASF 为负. 在正向级串区中,非均匀项
(14) $\dfrac{U_k}{2}\dfrac{{\rm \partial} D_{ii} }{{\rm \partial} X_k}\approx \dfrac{2}{3}\dfrac{{\rm \partial} D_{NN} }{{\rm \partial} t} \sim \dfrac{{\rm \partial} \langle \omega^2 r^2 \rangle }{{\rm \partial} t} \sim -\beta r^2$
其中,$D_{NN}=\langle \delta u_N \delta u_N \rangle$ 为二阶横向结构函数,$\delta u_N$ 为相对速度在垂直于相对距离方向上的横向分量. 由于皂膜平均速度 $U=2.7$m/s 几乎保持不变,因此本文将空间变量换为时间变量 $x=Ut$. 在均匀各向同性二维湍流的正向级串区,$D_{ii}=4D_{NN}/3$. 上式第二个关系是考虑到正向区的速度场是线性的,将相对速度进行泰勒展开并只保留第一阶项,$\delta_r u \sim \omega r$. 最后一个关系是由于 $\beta=-{\rm d} (\omega^2/2)/{\rm d}t$. 可见非均匀项对 VASF 是负的贡献,与预期一致. 此外在均匀各向同性湍流场中,其随尺度的幂次律为 $r^2$. 非均匀项与尺度间传递项虽然有着相反的符号,但有着相近的幂次律,也与图 2 (b) 实验测得的综合 VASF 的 $r^{1.5}$ 幂次律十分接近. 出现的幂次律偏差可能和 $D_{ii}$ 一样,是由于有限惯性区间等因素导致.
通过上述的分析,本文发现实验结果中负的 VASF 很有可能是流场非均匀性导致. 接下来,本文对此进行定量的计算和比较. 对于 VASF,实验中可以直接测得在不同位置和不同尺度下的值,如图 2 (b) 所示. 选定正向级串区的某一个尺度 $r=0.35M$,图 2 (b) 中的竖向与各颜色曲线的交点,即为不同位置 $x$ 处 $-\langle \delta u_i \delta a_i \rangle$ 在 $r=0.35 M$ 的值. 这些值如图 2 (a) 中的红色圆圈所示,其随着往下游的发展而逐渐衰减. 对于组成 VASF 三部分分量,如式 (7) 所示. 其第一项为 0. 对于第二项,在均匀各向同性湍流中,本文可以得到其理论的表达式 (14). 而皂膜流场并不满足均匀各向同性的条件,本文转而采用实验直接测量的方式. 同 VASF 一样,图 2 (a)中的竖向与各颜色曲线的交点,即为不同位置处 $D_{ii}(x)=D_{ii}(tU)$ 在 $r=0.35 M$ 的值. 对其进行对空间求导,可获得非均匀项 $\langle (U_n/2){\rm \partial} D_{ii} /{\rm \partial} X_n\rangle$. 其值小于 0,本文对其取负号,如图 3 (a) 的绿色方块. 因为采样点比较离散 (分辨率为 0.5mm),进行微分操作后数据点有一定的离散. 但不难看出,非均匀项的值与VASF的值十分接近,且变化趋势高度一致. 进一步的,将两者画成散点图,如图 3 (b) 所示,中间的实线表示两者完全相等. 而实验数据几乎落在直线附近,表明两者几乎相等,两者的相关系数为 0.905,平均值相差 $6%$. 在正向级串惯性区的其他尺寸,如 $r=0.15M$ 和 $r=0.85M$ 也观察到同样的现象.
图3
图3
(a) 在尺度 $r/M=0.35$ 下,红色圆圈为 VASF,对其取负号使之为正. 绿色方块为构成 VASF 的第二项,非均 匀项,并也对其取负号. 蓝色星形为构成 VASF 的第三项,尺度间传递项的实验值. 这三者在不同空间位置 $tU/M$ 的值. (b) 纵坐标为 $-\langle \delta u_i \delta a_i \rangle$ 的对数值,横坐标为 $-\langle (U_n/2){\rm \partial} D_{ii} /{\rm \partial} X_n\rangle$ 的对数值,数据基本都落在图中等值线附近
Fig.3
(a) In scale $r/M=0.35$, the red circles are VASF which have been multiplied by $-1$. Green squares are inhomogeneous term which is the second term of VASF. Blue stars are the scale-to-scale transfer term which is the third term of VASF. We plot their values in different downstream location $tU/M$. (b) The ordinate is the logarithmic value of $-\langle \delta u_i \delta a_i \rangle$, the abscissa is the logarithmic value of $-\langle (U_n/2){\rm \partial} D_{ii} /{\rm \partial} X_n\rangle$, most of the data lies around the contour line
现对构成 VASF 的第三部分,代表能量和拟涡能传递的 $(1/2){\rm \partial} D_{iik}/{\rm \partial} r_k$ 进行讨论. 流动的衰减主要是在主流$x$方向,因此本文可以通过对 $x$ 方向求导,进而获得非均匀项. 但能量和拟涡能的传递在各个方向是同量级的,在均匀各向同性湍流场中是相等的,本文无法选择球坐标系中某一个方向 $r_k$ 进行求 $D_{iik}$ 的微分. 为评估该式大小,本文采用均匀各向同性湍流场中的结果. 根据式 (10),在正向级串区, $(1/2){\rm \partial} D_{iik}/{\rm \partial} r_k =\beta r^2/2=4D_{LLL}/r$. 通过泰勒冻结假设, 获得 $D_{LLL}(t;r \!=\! 0.35M)$. 从而得到 $(1/2){\rm \partial} D_{iik}/$ ${\rm \partial} r_k$ 在尺度 $r=0.35 M$ 上的值,如图 3 (a) 中的蓝色星形所示. 可以看到代表拟涡能在尺度间传递的该项在各空间位置上都为正数. 由于数据是在长度为 $\pm 0.2$mm 的狭窄区域进行统计,并且三阶矩收敛性较二阶矩更差,因此数据的波动比较大. 但依然可以看到蓝色数据约为红色和绿色数据的 $1/2 \sim 1/4$. 并且随着往下游的衰减,相差会越来越大. 可见在衰减的皂膜流场中,是非均匀项对 VASF 占主导.
在二维衰减湍流中,尺度间的传递项始终为正. 说明了即使是在衰减流场中,拟涡能也是往小尺度传递. 衰减效应对二维湍流拟涡能的传递方向不会造成本质的影响. 但衰减会对 VASF 造成显著的影响. 由于非均匀项为负值,即使尺度间的拟涡能传递项为正值,VASF 仍为负值. 在非均匀二维湍流中,本文从理论上发现不可以忽略非均匀项的效果,进一步从实验上发现该项甚至会主导 VASF. 关于三维湍流中非均匀项对 VASF 的影响还有待进一步研究.
4 弥散
VASF除了表征尺度间的能量/拟涡能传递,也和湍流场的弥散作用密切相关. 弥散过程描述了粒子位置随时间的演化. 这是人们 日常生活中的一种常见的物理现象. 例如 PM 2.5 颗粒在大气中的运动,污染物在海洋中的扩散,病毒在人群中的传播. 研究弥散过程可以帮助人们理解、预测、还原追踪这些过程. 其可通过考察两点的相对距离平方 $\langle R^2(t) \rangle =\langle(x' (t)-x(t))^2\rangle_{R_0}$ 随时间的演化来进行研究,其中 $x' (t)$ 和 $x(t)$ 分别为两个粒子在时刻$t$的空间位置. 下标 $R_0$ 表示对初始距离为 $R(0)=R_0$ 且在惯性区的两个粒子做系综平均. 当弥散时间不太长时,本文对 $R(t)$ 进行在 $t=0$ 时刻进行泰勒展开[6 ,37 ]
(15) $\langle (R(t)-R_0)^2 \rangle =\langle (\delta u_0 t+\delta a_0 t^2/2+O(t^3))^2 \rangle =\\ \qquad \langle \delta ^2 u_0 \rangle t^2 +\langle \delta u_0 \delta a_0 \rangle t^3+O(t^4)$
其中,$\delta u_0$ 和 $\delta a_0$ 分别为 $t\!=\!0$ 时刻的相对速度和相对加速度. 那么 $\langle \delta ^2 u_0 \rangle=D_{ii}(R_0)$, $\langle \delta u_0 \delta a_0 \rangle=\langle \delta u_i \delta a_i \rangle(R_0)$.本文接下来只选取在正向级串区的 $R_0$ 粒子对进行讨论. 主要是考虑到,在皂膜流场中,空气阻力带来的能量衰减主要集中在大尺度. 此外若初始尺度 $R_0$ 在反向级串区,$R(t)$ 很快将会超过流场的相关尺度. 此时两个粒子不再相关,会进入 Taylor 线性弥散区间,也即 $\langle R^2(t) \rangle\sim t$[38 ] .
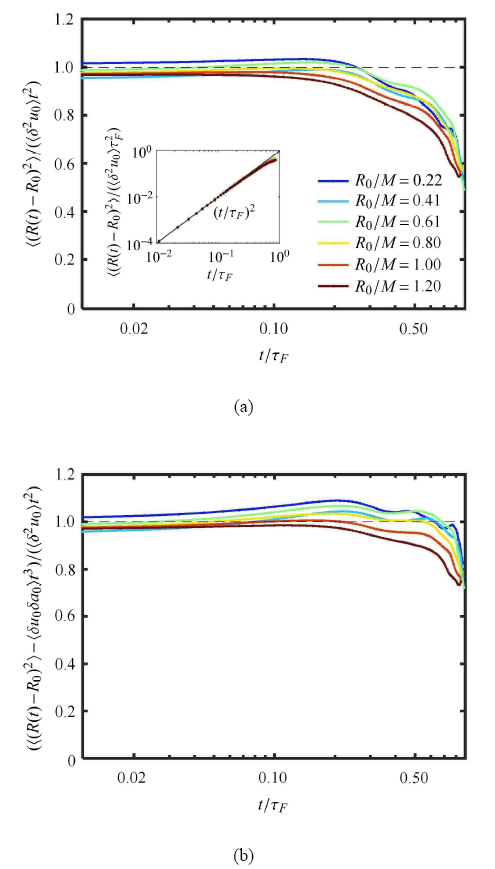
图 4 (a) 展示了两个粒子对的相对距离平方 $\langle (R(t)-R_0)^2 \rangle $ 随着时间的关系. 并用正向区的特征时间 $\tau_{\rm F}=\beta^{-1/3}=18$ms 来无量纲化 $t$,其中 $\beta=8D_{LLL}/r^3$ 为测量区域 $20M\sim 40M$ 的平均拟涡能耗散率. 所有粒子对的初始距离都在正向级串区内,并用不同的颜色表示.
图4
图4
(a) 在距离栅格 $20M\sim40 M$ 范围内,两个粒子对的相对距离平方 $\langle (R(t)-R_0)^2 \rangle $ 随着时 间的关系. 不同的颜色代表不同的初始距离 $R_0$. 子图的黑色直线为 $(t/\tau_{\rm F})^2$,并不是数据拟合曲线. (b) 考虑 VASF 对相对距离的影响后,补偿的弥散关系
Fig.4
(a) In the region which lies in $20M\sim40 M$ below the comb, the dispersion relationship of two particles $\langle (R(t)-R_0)^2 \rangle $ with time. Different colors correspond to different initial separations $R_0$. The black line in sub-figure is $(t/\tau_{\rm F})^2$, which is not the fitting curve. (b) Considering the effect of VASF, the compensated dispersion relationships
从子图中可以看到在各个尺度上, 相对距离平方都呈现出 $t^2$ 的增长规律,表明式 (15) 中的第一阶 $t^2$ 项在初始 时刻是明显的主导作用. 当用 $\langle \delta ^2 u_0 \rangle \tau_{\rm F}^2$ 来归一化纵坐标,各个尺度的数据都落在同一条黑色直线 $(t/\tau_{\rm F})^2$ 上,进一步验证了式 (15),并与 Batchelor[39 ] 提出的弥散过程中 $t^2$ 理论一致. 但发展一段时间之后,例如 $t>0.8\tau_{\rm F}$,可以看到相对距离平方的发展比 $t^2$ 要慢. 这种变慢的弥散过程可以从主图中更明显地看出来,主图是用 $\langle \delta ^2 u_0 \rangle t^2$ 来无量纲化纵坐标. 假如式 (15) 中只有 $t^2$ 项,那么数据应该落在值为“1”的水平虚线上. 但在 $t>0.2\tau_{\rm F}$ 之后,出现了更加缓慢的增长. 此时 $(R(t)-R_0)^2=1\sim 2$mm,相对距离 $R(t)$ 仍在惯性区范围内,甚至还是在正向级串区. 两个粒子还表现出相关性,大尺度的影响也应该很微弱. 说明主要是式 (15) 中的 $t^3$ 项起到显著影响. $t^3$ 项和 $t^2$ 项的相对关系为
(16) $\dfrac{\langle \delta u_0 \delta a_0 \rangle t^3}{\langle \delta ^2 u_0 \rangle t^2} \sim\dfrac{C_1 \beta R_0^2 t^3}{C_2 \beta^{2/3} R_0^2 t^2} =\dfrac{C_1 }{C_2 }\dfrac{t}{\tau_{\rm F}}$
其中 $C_1=O(1),C_2=O(1)$ 分别为 VASF 和二阶速度结构函数的常系数. 可见在 $t=C_2\tau_{\rm F}/C_1$ 时 $t^3$ 项将不可被忽略,这与本文的观察一致. 在二维均匀各向同性湍流场中,$\langle \delta u_0 \delta a_0 \rangle>0$,从而 $t^3$ 项是正的,会使得后期的弥散过程比 $t^2$ 更快,与本文的实验观察相反. 对于这一矛盾,本文可以 通过上一节关于 VASF 的讨论来解释. 在衰减流场中,VASF 是负的非均匀项和正的尺度间传递项相互竞争的结果. 若衰减效应足够强烈,非均匀项足够大,VASF 是可能小于零. 因此本文在弥散过程中看到的负的 VASF 和二维湍流中正的尺度间拟涡能传递两者并不矛盾.
为了进一步验证VASF对弥散过程的影响,本文绘制补偿VASF的粒子相对距离平方随时间的演化,如图 4 (b) 所示. 可以看到各个尺度都很好的落在理论值“1”附近. 出现的些许波动可能是由于粒子对的初始距离选取有一定的容差 $R_0\pm 0.5$mm. 在 $t>0.5t_{\rm F}$ 之后,粒子的相对距离 $R(t)\approx 10$mm,相关性逐渐减弱,转到泰勒线性扩散区间. 由于初始尺度$R_0$ 越大,越快进入该区间,因此可以看到红色曲线代表的大初始尺度也越早出现偏离. 由此本文定量上解释了弥散过程在后期变慢是由于负的 VASF 项导致.
5 结论
一直以来,湍流场中的二阶速度加速度结构函数 (VASF) 被认为与能量或者拟涡能在尺度间的传递相关. 本文从加速度定义 出发,发现 VASF 除了尺度间传递项,还有非稳态项和非均匀项. 在稳态的局部均匀各向同性湍流中,只有尺度间传递项. 但实际湍流流动中,很多都是衰减的非均匀湍流. 为研究非均匀项对 VASF 的影响,本文搭建了基于皂膜的二维衰减湍流. 通过 LPT 测量方法及改进的 $N \log_2 N$ 的粒子匹配算法,获得了速度场和加速度场. 实验数据显示二维湍流尺度间传递项在正向级串区的尺度间传递项均为正,证实了拟涡能往小尺度传递,说明衰减并不影响其传递方向. 采用泰勒冻结假设,得到当地空间位置的非均匀项. 在衰减湍流中,非均匀项为负,并且大于正的尺度间传递项. 因此是非均匀项主导二维衰减湍流的 VASF,使之为负数. 最后本文对与 VASF 密切相关的弥散过程进行了讨论,实验观察到两个粒子相对距离平方先以 $t^2$ 幂次律增长,之后变为更缓慢的增长. 这种缓慢增长可以用负的 VASF 来解释,也即是由于衰减放缓了弥散过程. 总的来说,本文通过理论分析和LPT的实验结果发现衰减不改变拟涡能的传递方向. 但是衰减在 VASF 和弥散过程等问题上会产生显著的影响,在这些问题的讨论上衰减作用将不可忽略.
致谢
感谢徐海涛教授对本工作的指导和建议,感谢清华大学对本工作的资助. 由衷感谢审稿人给出的宝贵意见使得本文得到进一步的改善.
参考文献
View Option
[1]
Mann J Ott S Andersen JS . Experimental study of relative, turbulent diffusion
Risø National Laboratory , 1999
[本文引用: 1]
[2]
Falkovich G Dzki KG Vergassola M . Particles and fields in fluid turbulence
Reviews of Modern Physics 2001 ,73 (4 ):913 -975
DOI
URL
[3]
Pumir A Shraiman BI Chertkov M . The Lagrangian view of energy transfer in turbulent flow
Europhysics Letters 2001 ,56 (3 ):379 -385
DOI
URL
[4]
Xu H Pumir A Bodenschatz E . Lagrangian view of time irreversibility of fluid turbulence
Science China-Physics Mechanics & Astronomy 2016 ,59 (1 ):614702
[本文引用: 2]
[5]
Kolmogorov AN . The local structure of turbulence in Incompressible viscous fluid for very large Reynolds numbers
Doklady Akademii Nauk Sssr 1941 ,30 :301 -305
[本文引用: 1]
[6]
Ouellette NT Xu H Bourgoin M , et al . An experimental study of turbulent relative dispersion models
New Journal of Physics 2006 ,8 (6 ):109
DOI
URL
[本文引用: 2]
[7]
Kraichnan RH . Inertial ranges in two-dimensional turbulence
Physics of Fluids 1967 ,10 (7 ):1417 -1423
[本文引用: 2]
[8]
Batchelor GK . Computation of the energy spectrum in homogeneous two-dimensional turbulence
Physics of Fluids 1969 ,12 (12 ):233 -239
DOI
URL
[9]
Chen S Ecke RE Eyink GL , et al . Physical mechanism of the two-dimensional inverse energy cascade
Physical Review Letters 2006 ,96 (8 ):84502
[本文引用: 1]
[10]
Boffetta G Musacchio S . Evidence for the double cascade scenario in two-dimensional turbulence
Physical Review E 2010 ,82 (1 ):16307
DOI
URL
[本文引用: 1]
[11]
Belmonte A Goldburg WI Kellay H , et al . Velocity fluctuations in a turbulent soap film: The third moment in two dimensions
Physics of Fluids 1999 ,11 (5 ):1196 -1200
[本文引用: 2]
[12]
Fang L Ouellette NT . Advection and the efficiency of spectral energy transfer in two-dimensional turbulence
Physical Review Letters 2016 ,117 (10 ):104501
URL
PMID
[本文引用: 1]
[13]
Hill RJ . Opportunities for use of exact statistical equations
Journal of Turbulence 2006 ,7 (43 ):1 -13
[本文引用: 1]
[14]
Landau L Lifshitz E . A Course of Theoretical Physics . Pergamon Press , Vol. 6 , 1959
[本文引用: 1]
[15]
Monin AS Yaglom AM . Statistical Fluid Mechanics, Volume II: Mechanics of Turbulence
Courier Corporation , 1975
[16]
Frisch U . Turbulence: The legacy of A. N. Kolmogorov . Cambridge, England : Cambridge University Press , 1995
[本文引用: 2]
[17]
Davidson P . Turbulence: An Introduction for Scientists and Engineers . Oxford : Oxford University Press , 2015
[本文引用: 1]
[18]
Lindborg E . Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence?
Journal of Fluid Mechanics 1999 ,388 :259 -288
DOI
URL
[本文引用: 1]
[19]
Bragg AD De Lillo F Boffetta G . Irreversibility inversions in two-dimensional turbulence
Physical Review Fluids 2018 ,3 (2 ):24302
[本文引用: 1]
[20]
Gao P Lu X . Instability of an oscillatory fluid layer with insoluble surfactants
Journal of Fluid Mechanics 2008 ,595 :461 -490
[本文引用: 1]
[21]
Zhou Q Huang Y Lu Z , et al . Scale-to-scale energy and enstrophy transport in two-dimensional Rayleigh-Taylor turbulence
Journal of Fluid Mechanics 2016 ,786 :294 -308
[本文引用: 1]
[22]
Couder Y Chomaz J Rabaud M . On the hydrodynamics of soap films
Physica D 1989 ,37 (3 ):384 -405
[本文引用: 1]
[23]
Zhang J Childress S Libchaber A , et al . Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind
Nature 2000 ,408 (6814 ):835 -839
URL
PMID
[本文引用: 1]
[24]
杨义红 , 尹协振 , 陆夕云 . 肥皂膜水洞实验技术
实验流体力学 , 2005 ,19 (4 ):36 -41
( Yang Yihong Yin Xiezhen Lu Xiyun . Experimental methods in a soap film tunnel
Journal of Experimental in Fluid Mechanics 2005 ,19 (4 ):36 -41 (in Chinese))
[25]
Jia L Yin X . Passive oscillations of two tandem flexible filaments in a flowing soap film
Physical Review Letters 2008 ,100 (22 ):228104
DOI
URL
PMID
The passive oscillations of flexible filaments in a flowing soap film were investigated to learn the serial interaction between them. When arranged in tandem, the downstream filament flaps at the same frequency as that of the upstream one, but with a larger amplitude, whereas the upstream one is almost unaffected compared to the single filament case. The data analysis shows the downstream filament indeed extracts energy from the vortex street and receives greater force than the upstream one or a single filament in a uniform flow.
[26]
王显圣 , 司廷 , 罗喜胜 等 . 柱形汇聚激波冲击球形重气体界面的实验研究
力学学报 , 2012 ,44 (3 ):473 -480
( Wang Xiansheng Si Ting Luo Xisheng , et al . Experimental inverstigation on a spherical heavy-gas interface accelerated by a cylindeical converging shock wave
Chinese Journal of Theoretical and Applied Mechanics 2012 ,44 (3 ):473 -480 (in Chinese))
[27]
Wang M Si T Luo X . Generation of polygonal gas interfaces by soap film for Richtmyer-Meshkov instability study
Experiments in Fluids 2013 ,54 (1 ):1427
DOI
URL
[本文引用: 1]
[28]
Zhou Z Fang L Ouellette NT , et al . Vorticity gradient stretching in the direct enstrophy transfer process of two-dimensional turbulence
Physical Review Fluids 2020 ,5 (5 ):054602
DOI
URL
[本文引用: 3]
[29]
周泽友 , 万冬梅 , 徐海涛 . 平面流动皂膜的表面张力系数及厚度测量
实验流体力学 , 2020 ,34 (3 ):90 -96
[本文引用: 2]
( Zhou Zeyou Wan Dongmei Xu Haitao . Surface tension coefficient and thickness measurements in planar soap-film flows
Journal of Experimental in Fluid Mechanics 2020 ,34 (3 ):90 -96 (in Chinese))
[本文引用: 2]
[30]
Pumir A Xu H Bodenschatz E , et al . Single-particle motion and vortex stretching in three-dimensional turbulent flows
Physical Review Letters 2016 ,116 (12 ):124502
URL
PMID
[本文引用: 1]
[31]
Ouellette NT Xu HT Bodenschatz E . A quantitative study of three-dimensional Lagrangian particle tracking algorithms
Experiments in Fluids 2006 ,40 (2 ):301 -313
[本文引用: 3]
[32]
Pope SB . Turbulent Fow . Cambridge, England : Cambridge University Press , 2000
[本文引用: 1]
[33]
He G Jin G Yang Y . Space-time correlations and dynamic coupling in turbulent flows
Annual Review of Fluid Mechanics 2017 ,49 (1 ):51 -70
DOI
URL
[本文引用: 1]
[34]
Belmonte A Martin B Goldburg WI . Experimental study of Taylor's hypothesis in a turbulent soap film
Physics of Fluids 2000 ,12 (4 ):835 -845
DOI
URL
[本文引用: 1]
[35]
Sinhuber M Bewley GP Bodenschatz E . Dissipative effects on inertial-range statistics at high Reynolds numbers
Physical Review Letters 2017 ,119 (13 ):134502
URL
PMID
[本文引用: 1]
[36]
Rivera M Vorobieff P Ecke RE . Turbulence in flowing soap films: velocity, vorticity, and thickness fields
Physical Review Letters 1998 ,81 (7 ):1417 -1420
DOI
URL
[本文引用: 1]
[37]
Jucha J Xu H Pumir A , et al . Time-reversal-symmetry breaking in turbulence
Physical Review Letters 2014 ,113 (5 ):54501
DOI
URL
[本文引用: 1]
[38]
Taylor GI . Diffusion by continuous movements
Proceedings of the London Mathematical Society 1922 ,2 (1 ):196 -212
[本文引用: 1]
[39]
Batchelor GK . The Application of the similarity theory of turbulence to atmosperic diffusion
Quarterly Journal of the Royal Meteorological Society 1950 ,76 (328 ):133 -146
DOI
URL
[本文引用: 1]
Experimental study of relative, turbulent diffusion
1
1999
... 在人们生活的三维世界中,从咖啡的溶解到威力巨大的台风,湍流现象是随处可见的. 而在一些自然界与工程应用的三维流动中,由于边界尺寸限制或者外力的作用,其中一个维度上的运动被抑制,流动呈现出近似二维流动的特征. 例如大气与海洋中的大尺度流动——由于地球半径约为 6400km, 而大气层和海洋的厚度仅为 10km 左右, 因此台风等的大尺度运动往往可以被看作二维流动. 无论是三维湍流还是二维湍流,湍流场都是一个耗散系统. 流场中的湍动能 $u^2/2$ 会不断被耗散,并需要不断的能量补充来维持稳定的流场. 在局部均匀湍流场中,欧拉场的二阶混合速度加速度结构函数 (velocity-acceleration structure function, VASF),表示两个粒子间相对湍动能的变化速率,与尺度间的能量传递率相关[1 -4 ] ...
Particles and fields in fluid turbulence
2001
The Lagrangian view of energy transfer in turbulent flow
2001
Lagrangian view of time irreversibility of fluid turbulence
2
2016
... 在人们生活的三维世界中,从咖啡的溶解到威力巨大的台风,湍流现象是随处可见的. 而在一些自然界与工程应用的三维流动中,由于边界尺寸限制或者外力的作用,其中一个维度上的运动被抑制,流动呈现出近似二维流动的特征. 例如大气与海洋中的大尺度流动——由于地球半径约为 6400km, 而大气层和海洋的厚度仅为 10km 左右, 因此台风等的大尺度运动往往可以被看作二维流动. 无论是三维湍流还是二维湍流,湍流场都是一个耗散系统. 流场中的湍动能 $u^2/2$ 会不断被耗散,并需要不断的能量补充来维持稳定的流场. 在局部均匀湍流场中,欧拉场的二阶混合速度加速度结构函数 (velocity-acceleration structure function, VASF),表示两个粒子间相对湍动能的变化速率,与尺度间的能量传递率相关[1 -4 ] ...
... 其中,$\delta u$ 和 $\delta a$ 为两个粒子间的相对速度和相对加速度,$\langle \cdot \rangle$ 代表系综平均,下标 $R_0$ 表示是对相对距离 $R_0$ 在惯性区的粒子对进行条件统计; $\varepsilon$ 为湍流场的能量传递速率,其符号表示能量传递的方向[4 ] . 当能量从大尺度传到小尺度,$\varepsilon>0$;当能量从小尺度传到大尺度,$\varepsilon<0$. ...
The local structure of turbulence in Incompressible viscous fluid for very large Reynolds numbers
1
1941
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
An experimental study of turbulent relative dispersion models
2
2006
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
... VASF除了表征尺度间的能量/拟涡能传递,也和湍流场的弥散作用密切相关. 弥散过程描述了粒子位置随时间的演化. 这是人们 日常生活中的一种常见的物理现象. 例如 PM 2.5 颗粒在大气中的运动,污染物在海洋中的扩散,病毒在人群中的传播. 研究弥散过程可以帮助人们理解、预测、还原追踪这些过程. 其可通过考察两点的相对距离平方 $\langle R^2(t) \rangle =\langle(x' (t)-x(t))^2\rangle_{R_0}$ 随时间的演化来进行研究,其中 $x' (t)$ 和 $x(t)$ 分别为两个粒子在时刻$t$的空间位置. 下标 $R_0$ 表示对初始距离为 $R(0)=R_0$ 且在惯性区的两个粒子做系综平均. 当弥散时间不太长时,本文对 $R(t)$ 进行在 $t=0$ 时刻进行泰勒展开[6 ,37 ] ...
Inertial ranges in two-dimensional turbulence
2
1967
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
... 图 2 (a) 展示的是利用泰勒冻结假设计算得到的,当地位置 $x$ 的二阶结构函数 $D_{ii}(r;x)$. 如右边的颜色坐标所示,不同的颜色代表不同的当地位置 $x$. 在距离栅格下游的 $12.5M$ 一直增长到 $67.5M$,颜色也从深蓝变为深红. 根据 Kraichnan 的理论[7 ] ,在正向拟涡能级串区 $(\eta \ll r \ll L_{\rm F})$,结构函数由 $\beta$ 控制. 量纲分析得到 $D_{ii}\sim \beta^{2/3}r^2 $. 图 2 (a) 显示在 $r<M$ 区间存在 $D_{ii}\sim r^{1.6}$ 幂次律,对应着流场中的正向级串区. 偏小的幂次律在其他皂膜实验中也被普遍观察到,并被认为是由于有限雷诺数等原因导致[11 ,36 ] . 在衰减过程中,理论上,正向级串区的雷诺数 ${ Re}_{\omega}=u_{\rm F}L_{\rm F}/\nu=(L_{\rm F}/\eta)^2\sim t^0$. $L_{\rm F}$ 和 $\eta$ 均以 $t^{1/2}$ 的幂次律进行增长,整个正向级串惯性区的宽度不会发生显著变化. 实验中发现 $r^{1.6}$ 的幂次律得到自相似的往下游发展,并未得到显著升高或降低. 不变的惯性区间宽度和不变的幂次律和理论预测是一致的,但为了明确有限雷诺数的影响还需进一步实验. 此外,拟涡能是由栅格带来的扰动注入,一般认为拟涡能注入尺度 $L_{\rm F}\sim M$,这也与本文观察的一致. 栅格不仅在尺度$L_{\rm F}$上注入拟涡能,同时也注入能量,并往大尺度传递. Kraichnan 指出在反向级串区 $(L_{\rm F} \ll r \ll L_{\alpha})$,结构函数由能量耗散率决定,量纲分析得到 $D_{ii}\sim (\varepsilon r)^{2/3}$. $r^{2/3}$ 的幂次律十分平缓,并受到有限惯性区间的影响,本文的实验结果并没有看到一段清晰的 $r^{2/3}$ 幂次律. 但本文仍可以看到在 $r=M$ 附近,正向级串区和反向级串区的转变. 并且随着往下游的衰减,转折点在不断增大. 表征有效注入尺度的增长,这是二维湍流和三维湍流的一个重要差别,这一现象在衰减能谱上也可以看到[28 ] . ...
Computation of the energy spectrum in homogeneous two-dimensional turbulence
1969
Physical mechanism of the two-dimensional inverse energy cascade
1
2006
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
Evidence for the double cascade scenario in two-dimensional turbulence
1
2010
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
Velocity fluctuations in a turbulent soap film: The third moment in two dimensions
2
1999
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
... 图 2 (a) 展示的是利用泰勒冻结假设计算得到的,当地位置 $x$ 的二阶结构函数 $D_{ii}(r;x)$. 如右边的颜色坐标所示,不同的颜色代表不同的当地位置 $x$. 在距离栅格下游的 $12.5M$ 一直增长到 $67.5M$,颜色也从深蓝变为深红. 根据 Kraichnan 的理论[7 ] ,在正向拟涡能级串区 $(\eta \ll r \ll L_{\rm F})$,结构函数由 $\beta$ 控制. 量纲分析得到 $D_{ii}\sim \beta^{2/3}r^2 $. 图 2 (a) 显示在 $r<M$ 区间存在 $D_{ii}\sim r^{1.6}$ 幂次律,对应着流场中的正向级串区. 偏小的幂次律在其他皂膜实验中也被普遍观察到,并被认为是由于有限雷诺数等原因导致[11 ,36 ] . 在衰减过程中,理论上,正向级串区的雷诺数 ${ Re}_{\omega}=u_{\rm F}L_{\rm F}/\nu=(L_{\rm F}/\eta)^2\sim t^0$. $L_{\rm F}$ 和 $\eta$ 均以 $t^{1/2}$ 的幂次律进行增长,整个正向级串惯性区的宽度不会发生显著变化. 实验中发现 $r^{1.6}$ 的幂次律得到自相似的往下游发展,并未得到显著升高或降低. 不变的惯性区间宽度和不变的幂次律和理论预测是一致的,但为了明确有限雷诺数的影响还需进一步实验. 此外,拟涡能是由栅格带来的扰动注入,一般认为拟涡能注入尺度 $L_{\rm F}\sim M$,这也与本文观察的一致. 栅格不仅在尺度$L_{\rm F}$上注入拟涡能,同时也注入能量,并往大尺度传递. Kraichnan 指出在反向级串区 $(L_{\rm F} \ll r \ll L_{\alpha})$,结构函数由能量耗散率决定,量纲分析得到 $D_{ii}\sim (\varepsilon r)^{2/3}$. $r^{2/3}$ 的幂次律十分平缓,并受到有限惯性区间的影响,本文的实验结果并没有看到一段清晰的 $r^{2/3}$ 幂次律. 但本文仍可以看到在 $r=M$ 附近,正向级串区和反向级串区的转变. 并且随着往下游的衰减,转折点在不断增大. 表征有效注入尺度的增长,这是二维湍流和三维湍流的一个重要差别,这一现象在衰减能谱上也可以看到[28 ] . ...
Advection and the efficiency of spectral energy transfer in two-dimensional turbulence
1
2016
... 在三维湍流中,能量从大尺度向小尺度传递形成正向的能量级串[5 ] ,能量耗散率 $\varepsilon>0, \langle \delta u \cdot \delta a \rangle<0$,并且两者之间的常系数 “$-2$” 也在实验中得到验证[6 ] . 自然地,人们将式 (1) 推广到二维湍流的能量惯性区. 在二维湍流中,涡量拉伸 (vortex stretching) 不复存在,湍动能的小尺度黏性耗散几乎为零,此时大尺度的摩擦耗散起到主导作用. 湍动能将从能量注入尺度 $L_{\rm F}$ 向更大的摩擦耗散尺度 $L_{\alpha}$ 传递,形成反向的能量级串[7 -9 ] . 此时 $\varepsilon<0$,这一点已经在能谱[10 ] ,三阶结构函数[11 ] ,尺度间的能量传递[12 ] 等方面都得到了证实. 但 $\langle \delta u \cdot \delta a \rangle>0$ 则有待进一步的验证. ...
Opportunities for use of exact statistical equations
1
2006
... 上式中用到了空间坐标自变量 $(x,x' )$ 与 $(X,r)$ 的相互转化[13 ] ...
1
1959
... 其中,$U=(u+u' )/2$ 是流场的平均速度,$D_{ii}=\langle \delta u_i \delta u_i \rangle$ 和 $D_{iik}=\langle \delta u_i \delta u_i \delta u_k \rangle$ 分别为二阶和三阶的欧拉速度结构函数. 上式的推导是一个通用的表达式,并未用到任何假设. VASF 虽然是绝对坐标 $X$ 和相对距离 $r$ 的多元函数,但是这两个自变量之间没有显著耦合 (即使 $D_{ii}, D_{iik}$ 是这两个自变量的二元函数),这为实验数据的分析带来了极大的便利. 可以看到 $\langle \delta u_i\delta a_i \rangle$ 由 3 部分组成. 第 1 项为时间的非稳态项,在稳态流场中为 0. 第 2 项是非均匀项,在局部均匀流场中结构函数 $D_{ii}$ 只是相对距离 $r$ 的函数,对当地绝对位置 $X$ 微分为 0. 因此在稳态局部均匀流场中,只剩下第 3 项. 同三阶速度结构函数物理含义一样,该项代表能量或拟涡能在尺度间的传递. 第 3 项在任意流场中是没有普适表达式的. 为进一步对该项进行分析,本文讨论该项在不可压均匀各向同性湍流的条件下的表达式. 参考三维湍流中相关推导[14 -16 ] ,本文得到二维和三维湍流中该项的通用表达式 ...
Statistical Fluid Mechanics, Volume II: Mechanics of Turbulence
1975
2
1995
... 其中,$U=(u+u' )/2$ 是流场的平均速度,$D_{ii}=\langle \delta u_i \delta u_i \rangle$ 和 $D_{iik}=\langle \delta u_i \delta u_i \delta u_k \rangle$ 分别为二阶和三阶的欧拉速度结构函数. 上式的推导是一个通用的表达式,并未用到任何假设. VASF 虽然是绝对坐标 $X$ 和相对距离 $r$ 的多元函数,但是这两个自变量之间没有显著耦合 (即使 $D_{ii}, D_{iik}$ 是这两个自变量的二元函数),这为实验数据的分析带来了极大的便利. 可以看到 $\langle \delta u_i\delta a_i \rangle$ 由 3 部分组成. 第 1 项为时间的非稳态项,在稳态流场中为 0. 第 2 项是非均匀项,在局部均匀流场中结构函数 $D_{ii}$ 只是相对距离 $r$ 的函数,对当地绝对位置 $X$ 微分为 0. 因此在稳态局部均匀流场中,只剩下第 3 项. 同三阶速度结构函数物理含义一样,该项代表能量或拟涡能在尺度间的传递. 第 3 项在任意流场中是没有普适表达式的. 为进一步对该项进行分析,本文讨论该项在不可压均匀各向同性湍流的条件下的表达式. 参考三维湍流中相关推导[14 -16 ] ,本文得到二维和三维湍流中该项的通用表达式 ...
... 其中,$d$ 代表维数,在二维湍流中 $d=2$,在三维湍流中 $d=3$. $D_{iiL}=\langle \delta u_i \delta u_i \delta u_L \rangle =\langle \delta u_i \delta u_i \delta u_k r_k/|{r}| \rangle$,下标 $L$ 表示相对速度在相对距离径向方向 $r_k/|{r}|$ 的投影. 进一步的,$D_{LLL}=\langle \delta u_L \delta u_L \delta u_L \rangle$ 为三阶径向速度结构函数,在能量和拟涡能惯性区分别为[16 -17 ] ...
1
2015
... 其中,$d$ 代表维数,在二维湍流中 $d=2$,在三维湍流中 $d=3$. $D_{iiL}=\langle \delta u_i \delta u_i \delta u_L \rangle =\langle \delta u_i \delta u_i \delta u_k r_k/|{r}| \rangle$,下标 $L$ 表示相对速度在相对距离径向方向 $r_k/|{r}|$ 的投影. 进一步的,$D_{LLL}=\langle \delta u_L \delta u_L \delta u_L \rangle$ 为三阶径向速度结构函数,在能量和拟涡能惯性区分别为[16 -17 ] ...
Can the atmospheric kinetic energy spectrum be explained by two-dimensional turbulence?
1
1999
... 式中,$\varepsilon>0$, $\beta>0$ 代表着能量和拟涡能分别从大尺度传向小尺度. 在三维均匀各向同性湍流中,能量往小尺度传递,$\langle \delta u_i \delta a_i \rangle=-2\varepsilon<0$. 而在二维均匀各向同性湍流中,能量往大尺度传递,拟涡能往小尺度传递,所以两个惯性区间 $\langle \delta u_i \delta a_i \rangle>0$ 皆成立[18 -19 ] . ...
Irreversibility inversions in two-dimensional turbulence
1
2018
... 式中,$\varepsilon>0$, $\beta>0$ 代表着能量和拟涡能分别从大尺度传向小尺度. 在三维均匀各向同性湍流中,能量往小尺度传递,$\langle \delta u_i \delta a_i \rangle=-2\varepsilon<0$. 而在二维均匀各向同性湍流中,能量往大尺度传递,拟涡能往小尺度传递,所以两个惯性区间 $\langle \delta u_i \delta a_i \rangle>0$ 皆成立[18 -19 ] . ...
Instability of an oscillatory fluid layer with insoluble surfactants
1
2008
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
Scale-to-scale energy and enstrophy transport in two-dimensional Rayleigh-Taylor turbulence
1
2016
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
On the hydrodynamics of soap films
1
1989
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
Flexible filaments in a flowing soap film as a model for one-dimensional flags in a two-dimensional wind
1
2000
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
Passive oscillations of two tandem flexible filaments in a flowing soap film
2008
柱形汇聚激波冲击球形重气体界面的实验研究
2012
柱形汇聚激波冲击球形重气体界面的实验研究
2012
Generation of polygonal gas interfaces by soap film for Richtmyer-Meshkov instability study
1
2013
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
Vorticity gradient stretching in the direct enstrophy transfer process of two-dimensional turbulence
3
2020
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
... 在风洞中使用热线法测速时,也是利用泰勒冻结假设获得在热线当地位置处的结构函数[35 ] ,自变量相对距离只包含时间距离. 相同的, 式 (13) 参与运算的是两个在当地位置 $x$ 的点的脉动速度信息,得到的是当地 $x$ 的二阶结构函数. 唯一不同的是,这里自变量相对距离 $r-U\tau$ 既包含两点之间的空间距离$r$,也包含时间距离 $\tau$. 为了获得当地位置 $x$ 上的真实条件统计,空间波动范围 $r$ 的选取不宜太大. 一般的,本文设置其最大值为 $r=0.2$mm,也即计算在位置 $x\pm 0.2$mm 处的当地统计特性. $r$ 的范围是根据拟涡能耗散率尺度选定的,其值为 $ 0.3\sim 0.5$mm[28 ] ,并随着往下游的发展而逐渐增长. ...
... 图 2 (a) 展示的是利用泰勒冻结假设计算得到的,当地位置 $x$ 的二阶结构函数 $D_{ii}(r;x)$. 如右边的颜色坐标所示,不同的颜色代表不同的当地位置 $x$. 在距离栅格下游的 $12.5M$ 一直增长到 $67.5M$,颜色也从深蓝变为深红. 根据 Kraichnan 的理论[7 ] ,在正向拟涡能级串区 $(\eta \ll r \ll L_{\rm F})$,结构函数由 $\beta$ 控制. 量纲分析得到 $D_{ii}\sim \beta^{2/3}r^2 $. 图 2 (a) 显示在 $r<M$ 区间存在 $D_{ii}\sim r^{1.6}$ 幂次律,对应着流场中的正向级串区. 偏小的幂次律在其他皂膜实验中也被普遍观察到,并被认为是由于有限雷诺数等原因导致[11 ,36 ] . 在衰减过程中,理论上,正向级串区的雷诺数 ${ Re}_{\omega}=u_{\rm F}L_{\rm F}/\nu=(L_{\rm F}/\eta)^2\sim t^0$. $L_{\rm F}$ 和 $\eta$ 均以 $t^{1/2}$ 的幂次律进行增长,整个正向级串惯性区的宽度不会发生显著变化. 实验中发现 $r^{1.6}$ 的幂次律得到自相似的往下游发展,并未得到显著升高或降低. 不变的惯性区间宽度和不变的幂次律和理论预测是一致的,但为了明确有限雷诺数的影响还需进一步实验. 此外,拟涡能是由栅格带来的扰动注入,一般认为拟涡能注入尺度 $L_{\rm F}\sim M$,这也与本文观察的一致. 栅格不仅在尺度$L_{\rm F}$上注入拟涡能,同时也注入能量,并往大尺度传递. Kraichnan 指出在反向级串区 $(L_{\rm F} \ll r \ll L_{\alpha})$,结构函数由能量耗散率决定,量纲分析得到 $D_{ii}\sim (\varepsilon r)^{2/3}$. $r^{2/3}$ 的幂次律十分平缓,并受到有限惯性区间的影响,本文的实验结果并没有看到一段清晰的 $r^{2/3}$ 幂次律. 但本文仍可以看到在 $r=M$ 附近,正向级串区和反向级串区的转变. 并且随着往下游的衰减,转折点在不断增大. 表征有效注入尺度的增长,这是二维湍流和三维湍流的一个重要差别,这一现象在衰减能谱上也可以看到[28 ] . ...
平面流动皂膜的表面张力系数及厚度测量
2
2020
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
... [29 ],小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
平面流动皂膜的表面张力系数及厚度测量
2
2020
... 二维湍流的研究,已经在理论和数值计算上开展了大量的工作[20 -21 ] . 实验上,Couder 提出了基于皂膜的实验装置[22 ] ,并得到了广泛应用[23 -27 ] . 在前人工作的基础上,本文搭建了皂膜流动实验台. 其详细描述可参考之前的报道[28 -29 ] ,本文在此进行补充说明. 皂膜实验装置如图 1 (a) 所示. 含 2% Dawn 洗碗液的皂液沿着直径为 6mm 的狭长喷嘴流出. 在喷嘴出口处,两根直径为 0.32mm 的红色尼龙绳组成了长 $X_1=106$cm 的逐渐扩张平面. 皂液在此逐渐展开形成皂膜,并被重力不断加速. 在长 $X_2=194$cm,宽 $W=5$cm 的实验段达到充分发展. 最后流入下水箱,被蠕动泵送入上水箱,形成往复循环. 通过调整泵的流量,皂膜的平均速度可在 $1 \sim 3$m/s 的范围内进行调整,根据干涉条纹和速度剖面测得皂膜的平均厚度在 $4 \sim 9\mu$m 之间[29 ] ,小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
... [29 ],小于另外两个维度四到六个量级,因此可以被视为二维湍流. 本文的皂膜流量工况为 40ml/min,平均流速为 2.7m/s. ...
Single-particle motion and vortex stretching in three-dimensional turbulent flows
1
2016
... 当皂膜流过栅格后,会形成强烈湍流脉动. 本文在距离栅格为 $S\!=\!(12.5 \sim 67.5)M$ 的下游位置对流场进行测量,如图 1 (a) 中的绿色区域. 在对流场进行速度测量时,粒子图像测速法 (particle image velocimetry, PIV) 是一个成熟和普遍使用的方法,该方法可以获得速度的欧拉场. 但利用欧拉速度场求取加速度时,涉及到对流项的空间求导,要求流场空间分辨率应达到拟涡能耗散尺度的量级. 此外湍流中的非稳态项 ${\rm \partial} u_i/{\rm \partial} t$和对流项$u_k {\rm \partial} u_i/{\rm \partial} x_k$ 两者十分接近且正负相反,利用这两者的和得到的加速度不确定度往往极大[30 ] . 为此本文采用拉格朗日粒子追踪法 (lagrangian particle tracking, LPT) 对速度和加速度进行测量[31 ] . 首先在皂液中加入直径 $1\mu$m 的示踪粒子,粒子直径小于皂膜厚度,因此可以忽略对皂膜的影响. 一台波长 532nm,功率为 100W 的脉冲激光器照亮待测流场区域中的示踪粒子. 如图 1 (a) 所示,两台高速相机沿流向依次排列,在保证分辨率的情况下获得足够长的流场视野. 两台相机的合成分辨率为 $(2\times)2560\times 472$,可以拍得 100mm$\times $12mm 的狭长流场区域. 通过移动相机和栅格的相对位置实现更长范围内的测量. 采用同步器将两台相机和激光器进行同步,采样频率为 5000Hz. 整个实验系统通过基于 $Qt$ 环境下编写的数据采集平台进行控制,实现 数据的自动采集、传输和存储. ...
A quantitative study of three-dimensional Lagrangian particle tracking algorithms
3
2006
... 当皂膜流过栅格后,会形成强烈湍流脉动. 本文在距离栅格为 $S\!=\!(12.5 \sim 67.5)M$ 的下游位置对流场进行测量,如图 1 (a) 中的绿色区域. 在对流场进行速度测量时,粒子图像测速法 (particle image velocimetry, PIV) 是一个成熟和普遍使用的方法,该方法可以获得速度的欧拉场. 但利用欧拉速度场求取加速度时,涉及到对流项的空间求导,要求流场空间分辨率应达到拟涡能耗散尺度的量级. 此外湍流中的非稳态项 ${\rm \partial} u_i/{\rm \partial} t$和对流项$u_k {\rm \partial} u_i/{\rm \partial} x_k$ 两者十分接近且正负相反,利用这两者的和得到的加速度不确定度往往极大[30 ] . 为此本文采用拉格朗日粒子追踪法 (lagrangian particle tracking, LPT) 对速度和加速度进行测量[31 ] . 首先在皂液中加入直径 $1\mu$m 的示踪粒子,粒子直径小于皂膜厚度,因此可以忽略对皂膜的影响. 一台波长 532nm,功率为 100W 的脉冲激光器照亮待测流场区域中的示踪粒子. 如图 1 (a) 所示,两台高速相机沿流向依次排列,在保证分辨率的情况下获得足够长的流场视野. 两台相机的合成分辨率为 $(2\times)2560\times 472$,可以拍得 100mm$\times $12mm 的狭长流场区域. 通过移动相机和栅格的相对位置实现更长范围内的测量. 采用同步器将两台相机和激光器进行同步,采样频率为 5000Hz. 整个实验系统通过基于 $Qt$ 环境下编写的数据采集平台进行控制,实现 数据的自动采集、传输和存储. ...
... 在获得原始的粒子图像后,首先通过亚像素定位获得示踪粒子在像素坐标系上的位置. 第二步经过标定还原到真实的物理空间 坐标系. 对于单台相机的二维标定,一般是假设皂膜平面和标定板平面重合. 但在两台相机的二维标定中,可以求得皂膜平面和标定板平面的距离并调节使之真正重合. 接下来一个重要的步骤是实现粒子在不同时刻的匹配,这是LPT算法的核心以及计算资源消耗最大的一步. 每一个瞬时场都有数百个粒子,从上一个时刻到下一个时刻需要实现这上百个粒子的一一匹配. 由于粒子的形态大小是无法区分的,因此一般是通过历史的位置、速度和加速度场信息进行匹配[31 ] . 假设每个时刻粒子平均个数为 $N$. 若采用暴力匹配算法,对 $t$ 时刻的 $N_t$ 个粒子,需匹配 $t+1$ 时刻的 $N_{t+1}$ 个粒子,每推进一个时间步的复杂度为 $N^2$. 但本文注意到皂膜流场是长 100mm 的狭长形区域. 流场的竖向脉动速度方差约为 0.2m/s,考虑到大约 5 倍脉动速度的事件概率很低以致可忽略不计. 那么在高达 5000Hz 的拍摄频率下,粒子的位置波动为 $0.2\times 5/5000=0.2$mm. 因此本文事先就可以预估出粒子下一个时刻的位置限定在 $\pm 0.2$mm 范围内,而不必在整个 100mm 的流场范围内进行匹配. ...
... 在获得流场轨迹信息后,最后一步是通过位置场进行速度和加速度场的计算. 根据粒子轨迹信息,可以通过对空间位置的一次时间微分得到速度. 进一步地,直接对空间位置的二次时间微分得到加速度,而不需要通过速度场再来计算加速度,从而LPT方法实现了加速度的准确测量. 实际计算中,由于轨迹信息在时间上是离散的,一般是通过对位置信息卷积速度核函数和加速度核函数以分别得到速度和加速度[31 ] . ...
1
2000
... 通过LPT测量,本文获得了皂膜流场中粒子轨迹上的速度和加速度. 进一步对轨迹进行时间排序,得到速度和加速度 的欧拉场. 假如本文对欧拉场中任取两点来计算式 (7) 中的 VASF 或者两阶及三阶速度结构函数,那么得到的将是待测区域的统计特性的平均值. 但皂膜流场的脉动速度在主流 $x$ 方向是不断衰减的,$\beta$ 和 $\varepsilon$ 都是空间位置 $x$ 的递减函数. 理想情况下,按照定义式 (7),要想计算各部分在当地位置 $x$ 的值,需要选取 $x-r/2$ 和 $x+r/2$ 两个点的速度进行计算. 但实际上这样的数据点极少,难以形成收敛的统计量. 为了获取收敛的结构函数,本文采用泰勒冻结假设. 流场的脉动速度 $u$ 虽然在不断衰减,但平均速度 $U=2.7$m/s 几乎保持不变. 流场的湍流强度 $u/U=5%\sim 10% \ll 1$,因此满足泰勒冻结假设[32 ] . 泰勒冻结假设并非适用于所有的流场,但在三维风洞中的运用已经得到广泛的认可[33 ] . Belmonte 等[34 ] 在二维皂膜流动中,也已经验证了泰勒冻结假设的正确性. 该假设认为湍流场的信息被冻结着以对流速度进行传递,那么 ...
Space-time correlations and dynamic coupling in turbulent flows
1
2017
... 通过LPT测量,本文获得了皂膜流场中粒子轨迹上的速度和加速度. 进一步对轨迹进行时间排序,得到速度和加速度 的欧拉场. 假如本文对欧拉场中任取两点来计算式 (7) 中的 VASF 或者两阶及三阶速度结构函数,那么得到的将是待测区域的统计特性的平均值. 但皂膜流场的脉动速度在主流 $x$ 方向是不断衰减的,$\beta$ 和 $\varepsilon$ 都是空间位置 $x$ 的递减函数. 理想情况下,按照定义式 (7),要想计算各部分在当地位置 $x$ 的值,需要选取 $x-r/2$ 和 $x+r/2$ 两个点的速度进行计算. 但实际上这样的数据点极少,难以形成收敛的统计量. 为了获取收敛的结构函数,本文采用泰勒冻结假设. 流场的脉动速度 $u$ 虽然在不断衰减,但平均速度 $U=2.7$m/s 几乎保持不变. 流场的湍流强度 $u/U=5%\sim 10% \ll 1$,因此满足泰勒冻结假设[32 ] . 泰勒冻结假设并非适用于所有的流场,但在三维风洞中的运用已经得到广泛的认可[33 ] . Belmonte 等[34 ] 在二维皂膜流动中,也已经验证了泰勒冻结假设的正确性. 该假设认为湍流场的信息被冻结着以对流速度进行传递,那么 ...
Experimental study of Taylor's hypothesis in a turbulent soap film
1
2000
... 通过LPT测量,本文获得了皂膜流场中粒子轨迹上的速度和加速度. 进一步对轨迹进行时间排序,得到速度和加速度 的欧拉场. 假如本文对欧拉场中任取两点来计算式 (7) 中的 VASF 或者两阶及三阶速度结构函数,那么得到的将是待测区域的统计特性的平均值. 但皂膜流场的脉动速度在主流 $x$ 方向是不断衰减的,$\beta$ 和 $\varepsilon$ 都是空间位置 $x$ 的递减函数. 理想情况下,按照定义式 (7),要想计算各部分在当地位置 $x$ 的值,需要选取 $x-r/2$ 和 $x+r/2$ 两个点的速度进行计算. 但实际上这样的数据点极少,难以形成收敛的统计量. 为了获取收敛的结构函数,本文采用泰勒冻结假设. 流场的脉动速度 $u$ 虽然在不断衰减,但平均速度 $U=2.7$m/s 几乎保持不变. 流场的湍流强度 $u/U=5%\sim 10% \ll 1$,因此满足泰勒冻结假设[32 ] . 泰勒冻结假设并非适用于所有的流场,但在三维风洞中的运用已经得到广泛的认可[33 ] . Belmonte 等[34 ] 在二维皂膜流动中,也已经验证了泰勒冻结假设的正确性. 该假设认为湍流场的信息被冻结着以对流速度进行传递,那么 ...
Dissipative effects on inertial-range statistics at high Reynolds numbers
1
2017
... 在风洞中使用热线法测速时,也是利用泰勒冻结假设获得在热线当地位置处的结构函数[35 ] ,自变量相对距离只包含时间距离. 相同的, 式 (13) 参与运算的是两个在当地位置 $x$ 的点的脉动速度信息,得到的是当地 $x$ 的二阶结构函数. 唯一不同的是,这里自变量相对距离 $r-U\tau$ 既包含两点之间的空间距离$r$,也包含时间距离 $\tau$. 为了获得当地位置 $x$ 上的真实条件统计,空间波动范围 $r$ 的选取不宜太大. 一般的,本文设置其最大值为 $r=0.2$mm,也即计算在位置 $x\pm 0.2$mm 处的当地统计特性. $r$ 的范围是根据拟涡能耗散率尺度选定的,其值为 $ 0.3\sim 0.5$mm[28 ] ,并随着往下游的发展而逐渐增长. ...
Turbulence in flowing soap films: velocity, vorticity, and thickness fields
1
1998
... 图 2 (a) 展示的是利用泰勒冻结假设计算得到的,当地位置 $x$ 的二阶结构函数 $D_{ii}(r;x)$. 如右边的颜色坐标所示,不同的颜色代表不同的当地位置 $x$. 在距离栅格下游的 $12.5M$ 一直增长到 $67.5M$,颜色也从深蓝变为深红. 根据 Kraichnan 的理论[7 ] ,在正向拟涡能级串区 $(\eta \ll r \ll L_{\rm F})$,结构函数由 $\beta$ 控制. 量纲分析得到 $D_{ii}\sim \beta^{2/3}r^2 $. 图 2 (a) 显示在 $r<M$ 区间存在 $D_{ii}\sim r^{1.6}$ 幂次律,对应着流场中的正向级串区. 偏小的幂次律在其他皂膜实验中也被普遍观察到,并被认为是由于有限雷诺数等原因导致[11 ,36 ] . 在衰减过程中,理论上,正向级串区的雷诺数 ${ Re}_{\omega}=u_{\rm F}L_{\rm F}/\nu=(L_{\rm F}/\eta)^2\sim t^0$. $L_{\rm F}$ 和 $\eta$ 均以 $t^{1/2}$ 的幂次律进行增长,整个正向级串惯性区的宽度不会发生显著变化. 实验中发现 $r^{1.6}$ 的幂次律得到自相似的往下游发展,并未得到显著升高或降低. 不变的惯性区间宽度和不变的幂次律和理论预测是一致的,但为了明确有限雷诺数的影响还需进一步实验. 此外,拟涡能是由栅格带来的扰动注入,一般认为拟涡能注入尺度 $L_{\rm F}\sim M$,这也与本文观察的一致. 栅格不仅在尺度$L_{\rm F}$上注入拟涡能,同时也注入能量,并往大尺度传递. Kraichnan 指出在反向级串区 $(L_{\rm F} \ll r \ll L_{\alpha})$,结构函数由能量耗散率决定,量纲分析得到 $D_{ii}\sim (\varepsilon r)^{2/3}$. $r^{2/3}$ 的幂次律十分平缓,并受到有限惯性区间的影响,本文的实验结果并没有看到一段清晰的 $r^{2/3}$ 幂次律. 但本文仍可以看到在 $r=M$ 附近,正向级串区和反向级串区的转变. 并且随着往下游的衰减,转折点在不断增大. 表征有效注入尺度的增长,这是二维湍流和三维湍流的一个重要差别,这一现象在衰减能谱上也可以看到[28 ] . ...
Time-reversal-symmetry breaking in turbulence
1
2014
... VASF除了表征尺度间的能量/拟涡能传递,也和湍流场的弥散作用密切相关. 弥散过程描述了粒子位置随时间的演化. 这是人们 日常生活中的一种常见的物理现象. 例如 PM 2.5 颗粒在大气中的运动,污染物在海洋中的扩散,病毒在人群中的传播. 研究弥散过程可以帮助人们理解、预测、还原追踪这些过程. 其可通过考察两点的相对距离平方 $\langle R^2(t) \rangle =\langle(x' (t)-x(t))^2\rangle_{R_0}$ 随时间的演化来进行研究,其中 $x' (t)$ 和 $x(t)$ 分别为两个粒子在时刻$t$的空间位置. 下标 $R_0$ 表示对初始距离为 $R(0)=R_0$ 且在惯性区的两个粒子做系综平均. 当弥散时间不太长时,本文对 $R(t)$ 进行在 $t=0$ 时刻进行泰勒展开[6 ,37 ] ...
Diffusion by continuous movements
1
1922
... 其中,$\delta u_0$ 和 $\delta a_0$ 分别为 $t\!=\!0$ 时刻的相对速度和相对加速度. 那么 $\langle \delta ^2 u_0 \rangle=D_{ii}(R_0)$, $\langle \delta u_0 \delta a_0 \rangle=\langle \delta u_i \delta a_i \rangle(R_0)$.本文接下来只选取在正向级串区的 $R_0$ 粒子对进行讨论. 主要是考虑到,在皂膜流场中,空气阻力带来的能量衰减主要集中在大尺度. 此外若初始尺度 $R_0$ 在反向级串区,$R(t)$ 很快将会超过流场的相关尺度. 此时两个粒子不再相关,会进入 Taylor 线性弥散区间,也即 $\langle R^2(t) \rangle\sim t$[38 ] . ...
The Application of the similarity theory of turbulence to atmosperic diffusion
1
1950
... 从子图中可以看到在各个尺度上, 相对距离平方都呈现出 $t^2$ 的增长规律,表明式 (15) 中的第一阶 $t^2$ 项在初始 时刻是明显的主导作用. 当用 $\langle \delta ^2 u_0 \rangle \tau_{\rm F}^2$ 来归一化纵坐标,各个尺度的数据都落在同一条黑色直线 $(t/\tau_{\rm F})^2$ 上,进一步验证了式 (15),并与 Batchelor[39 ] 提出的弥散过程中 $t^2$ 理论一致. 但发展一段时间之后,例如 $t>0.8\tau_{\rm F}$,可以看到相对距离平方的发展比 $t^2$ 要慢. 这种变慢的弥散过程可以从主图中更明显地看出来,主图是用 $\langle \delta ^2 u_0 \rangle t^2$ 来无量纲化纵坐标. 假如式 (15) 中只有 $t^2$ 项,那么数据应该落在值为“1”的水平虚线上. 但在 $t>0.2\tau_{\rm F}$ 之后,出现了更加缓慢的增长. 此时 $(R(t)-R_0)^2=1\sim 2$mm,相对距离 $R(t)$ 仍在惯性区范围内,甚至还是在正向级串区. 两个粒子还表现出相关性,大尺度的影响也应该很微弱. 说明主要是式 (15) 中的 $t^3$ 项起到显著影响. $t^3$ 项和 $t^2$ 项的相对关系为 ...