引言
针对描述围岩的时效变形, 采用物理模型是一种十分有效的方法. 这些模型通常是由几个代表性元件组合而成, 如: 胡克弹性体、牛顿黏体和圣维南塑性体, 具有明确的物理意义[3]. 但是由于传统元件的简单性, 尽管通过不同方式的组合或叠加, 往往岩体的复杂变形行为仍不能得到较好的描述. 因此, 国内外学者采用了不同的方法对传统的流变物理模型不断改进. 徐卫亚等[4]基于岩体非线性加速蠕变的特征, 提出了NVPB元件, 并与五元件模型串联, 建立了河海模型. 夏才初等[5]建立了包含15个流变力学模型的同一流变模型, 并给出了参数的确定方法. 近年来众多学者尝试将分数阶微积分理论研究应用于描述岩石的流变本构模型研究[6-8]. Zhou等[9]通过利用分数阶Abel黏壶替代西原模型中Newton黏壶, 建立了盐岩的分数阶流变模型. 刘泉声等[10]亦采用Abel黏壶替代了Burgers流变模型中的Kelvin体, 并在修正的Burgers模型上串联了非线性黏塑性体, 建立了改进的分数阶流变模型.
目前, 在应对高地应力软岩隧道大变形问题时, 主流的支护理念是"强支硬顶", 即采用大刚度、高强度的支护结构, 以期能够尽早地约束围岩变形[11]. 但是, 众多工程实践表明该种支护方法达到的效果往往并不尽如人意, 围岩变形总是在经历多次支护、破坏、拆除后才能得到一定控制, 造成了大量的资源浪费. 例如: 日本的Enasan隧道在前期建设过程中采用重型H型钢架及厚度达1.2 m的钢筋混凝土二衬, 但是由于过大的围岩挤压变形, 支护仍出现大面积破坏[12]; 国内的家竹箐隧道在施工中也发生了极大的变形, 但一味地增大支护刚度并未有效地解决支护失效问题[13]. 近年来, 基于围岩"能量吸收、变形释放"的支护理念, 让压支护(亦称柔性支护)方案开始在科研与实践工程中得以探索和实施[12-16]. 所谓让压支护, 即要求支护结构具有适应围岩变形的能力, 在提供较高支护阻力的同时, 又能够允许围岩产生一定的变形, 释放部分围岩压力, 以达到充分发挥围岩的自承载能力, 优化支护结构受力, 保障隧道安全的目的[17-19]. 刚性支护与让压支护作用下围岩-支护曲线如图1所示. Cantieni和Anagnostou[20]认为穿越高地应力软弱岩层的隧道其支护结构必须具备让压能力并辅以扩挖才能解决变形难题. 目前, 让压支护型式可分为: 主动让压支护和被动让压支护. 主动让压支护主要为让压锚杆. 2014年, Li等[21]对几种经典的让压锚杆性能做了对比分析. 何满潮等[22]研发了一种具有负泊松比效应的新型恒阻大变形锚杆. Cantieni和Anagnostou[18]根据被动让压结构的让压方式, 总结了其基本类型: (a)设置可压缩层; (b)具有滑动接头的钢架; (c)内置高压缩性元件的混凝土衬砌. 其中, 设置可压缩层又称为径向让压, 可压缩层在承担围岩形变压力时, 能够产生较大的压缩变形, 允许围岩的变形向刚性衬砌的外缘发展[19]. Wang等[23-25]利用泡沫混凝土作为可压缩层填充材料, 采用数值模拟分析了泡沫混凝土层的设置对隧道衬砌的影响. 内置高压缩性元件或者使用具有滑动接头的钢架属于环向让压. 内置高压缩性元件的混凝土衬砌在承受压力的同时, 能够通过高压缩性元件的压缩来适应大变形[26]. 雷升祥等[27]从能量转化的角度, 阐明了该种支护环向让压的基本原理. Tian等[28]利用数值模拟技术探究了内置高压缩性元件(泡沫混凝土)的对衬砌的影响. 仇文革等[29]自主研发了限阻耗能型支护结构, 并应用到深埋老黄土隧道和高地应力水平岩层隧道, 成功解决了初支开裂问题. 对于具有滑动接头的钢架, 以U型钢为代表, 可利用钢架间的接头滑动产生收缩来释放围岩的变形[30-31]. 李雪峰等[32]通过室内试验研究了对不同位置设置可缩接头的U型钢架的承载特性. 尤春安[33]通过理论分析探究了U型钢可缩型支架稳定性的承载能力问题. 对于支护结构与围岩的相互作用, 目前也有许多学者给出了力学分析的理论解答[34-39]. 但是, 尽管让压支护已经在科研与工程中得到越来越多的探索与实践, 而围岩-让压支护相互作用力学机制并不明确, 也少有文献涉及在让压支护作用下隧道力学行为的研究.
图1
图1
刚性与让压支护作用下围岩-支护曲线
Fig.1
Curves for surrounding rock and stiff or yielding supports
本文以改进的分数阶Burgers蠕变模型表征围岩的变形特征, 以环向让压支护为例, 通过在支护结构不同变形阶段引入了刚度修正系数, 推导了考虑支护安装延迟作用下, 不同变形阶段的支护压力和隧道位移的理论解. 此外, 基于理论解答, 本文还探讨了围岩本构模型的分数阶阶数、让压变形和刚度修正系数等参数对支护效果的影响.
1 理论前提
1.1 基本假设
(1)围岩与支护为均质、连续且各向同性材料, 围岩的力学行为可采用黏弹性本构模型描述; 在围岩荷载作用下, 支护的变形始终处于线弹性状态;
(2)隧道深埋, 忽略重力梯度影响, 则可认为隧道在无穷远处受静水压力作用;
(3)隧道的开挖与支护的安装都是瞬时的.
1.2 分数阶岩石本构模型
分数阶微积分最常用的定义为Riemann-Liouville (R-L)分数阶微积分定义方法, 其定义为: 设$f$在$(0, +\infty)$上逐段连续, 且在$(0, +\infty)$的任何子区间上可积, 对$t>0$, Re$(\gamma )>0$, 则函数$f(t)$的$\gamma$阶R-L分数阶积分可表示为[10]
式中, $\varGamma \left( \gamma \right) = \int_0^\infty {t^{\gamma -1}{e}^{-t}{d}t} $.
R-L分数阶导数为其积分的逆运算, 定义为: 设$f\in C$, $\nu >0$, $m$为大于$\gamma $的最小整数, 记$\nu = m-\gamma >0$, 则函数$f\left( t \right)$的$\gamma $阶R-L分数阶导数为
Abel黏壶是一种可用于描述介于理想弹性体和牛顿流体之间的物体力学性质的黏性元件, 如图2所示, 其本构方程可表示为
式中, $\zeta $为黏滞系数, $\beta $为求导阶数. 若$\beta =0$时, Abel黏壶退化成理想胡克弹性体; 当$\beta =1$时, Abel黏壶等同于牛顿黏壶.
图2
由R-L型微积分理论可反算得到
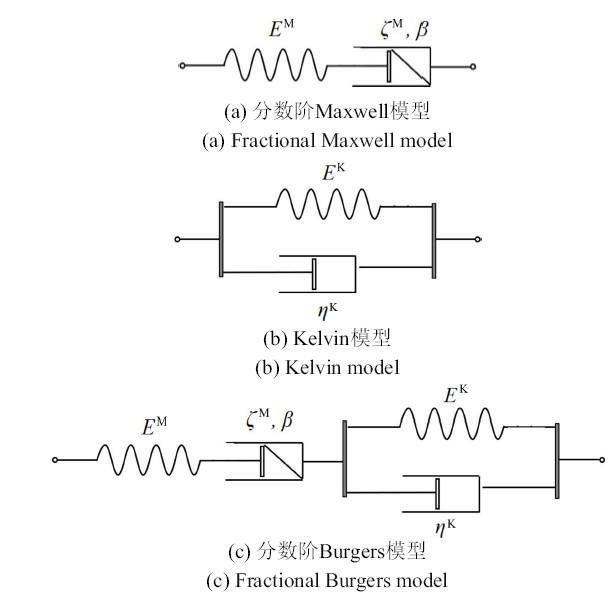
Burgers模型由一Maxwell体和Kelvin体串联而成, 根据Goodman[40]等的研究, 因为Burgers蠕变模型简单, 涉及参数少, 且能较为全面地描述岩石材料不同阶段的蠕变行为, 包括加速和稳定蠕变, 特别适用于工程分析. 该模型主要应用于软岩, 包括泥质页岩、板岩等. 但是, 由于Burgers模型中包含的均为整数阶微积分黏、弹性元件, 而岩石材料的 应变状态是与其所经历的整个应力历史相关的; 分数阶时间导数表现为微分-积分卷积算子, 可充分地展现系统函数发展的历史依赖性[10]. 据此, 本文将Maxwell体中的牛顿黏壶采用Abel黏壶代替, 构成了改进的分数阶Burgers流变模型(见图3), 以能够更好地描述岩石材料的流变力学性能. 此外, 可以发现改进后的Burgers模型并未造成参数复杂化的困难.
图3
根据流变元件串联法则, 有
式中, $\varepsilon$和$\sigma$分别表示应力和应变分量. 上标M和K分别表征修正的Maxwell模型和Kelvin模型相应的分量.
基于改进的Maxwell模型和Kelvin模型, 通过拉式变换, 其蠕变本构方程可分别表示为
式中, $E$和$\eta $分别代表胡克弹性体的常数和牛顿黏壶的黏滞系数.
将方程(6)代入方程(5)中可以得到分数阶Burgers模型的蠕变本构方程为
式中, $J(t)$为蠕变柔量, 其表达式可写为
2 理论解
2.1 未安装支护
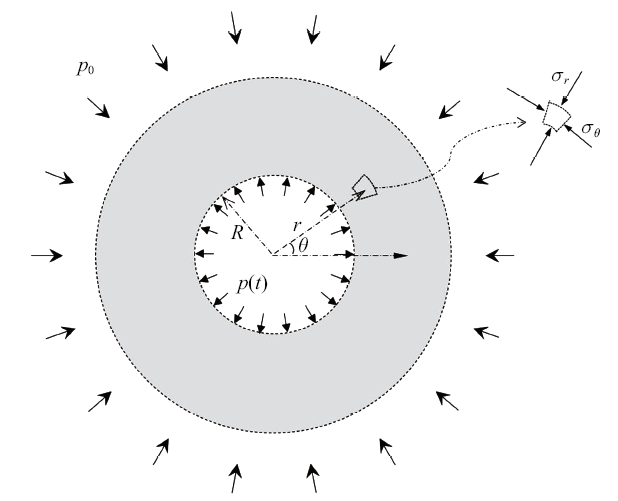
如图4所示, 为一圆形衬砌隧道力学模型示意图. 对于未安装支护结构的隧道而言, 其支护作用力$p(t)$大小等于0. 基于弹性理论, 利用黏弹性对应原理, 未安装支护结构的圆形隧道应力场的表达式可写为
式中, $\sigma$$_{r}$和$\sigma$$_{\theta }$分别为径向和切向应力. $p_{0}$表示初始地应力. $R$和$r$分别表示隧道半径和距隧道中心的距离.
图4
隧道$z$轴纵向应力表达式为
则平均应力为
利用方程(9)和(11)可得到围岩的偏应力场表达式
式中, $\sigma _r^{dev} $和$\sigma _\theta ^{dev} $分别表示径向和切向偏应力.
将方程(12)中的径向偏应力代入分数阶Burgers模型蠕变本构方程中, 得到围岩的径向应变表达式为
其中
式中, $G$表示剪切模量.
将方程(14)代入方程(13)可得到
对围岩径向应变积分, 可得到隧道径向位移表达式$u_{r}(t)$, 如下
将$r=R$代入上式, 则隧道洞周的位移方程为
利用方程(17), 隧道开挖后, 隧道的瞬时弹性变形等于
2.2 弹性变形阶段I
若在隧道开挖后$t=t_{0}$时刻安装支护, 支护结构的力学表达式可写为
式中, $p(t)$为支护结构与围岩之间相互作用力. $K_{S}$表示支护结构的支护刚度, 其表达式为
式中, $E'$和$\nu '$分别表示为支护材料的弹性模量和泊松比. $R$和$R_{1}$表示支护结构的内外半径, 在数值上支护结构外半径与隧道开挖半径相等.
于是, 在施加支护结构完毕后, 从$t=t_{0}$时刻开始, 围岩的径向偏应力改变为
则围岩的径向应变表达式改写为
对式(22)进行积分, 且另$r=R$, 得到在安装支护结构后隧道洞周处的位移表达式为
从方程(23)可以看出, 该式为一隐式解. 利用方程(19)和(23)可以解得
方程({24})和({25})分别为从安装支护结构$t=t_{0}$时刻开始, 支护结构的作用力与隧道位移的表达式.
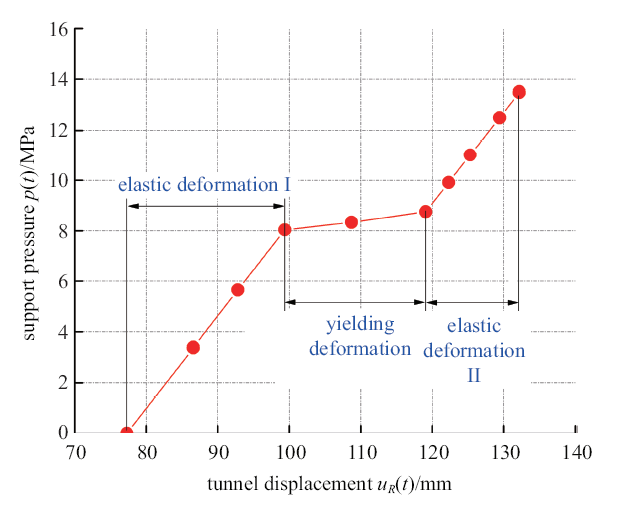
2.3 让压阶段
由于支护具备让压功能, 当作用在支护结构上的作用力$p\left( t \right)\geqslant p_1 $的时候(此刻$t=t_{1}$, $u_{R}(t_{1})=u_{1})$, 支护能够允许围岩产生变形, 但作用在支护上的压力将不会增加或仅引起较小的上升. 相较于弹性变形阶段I, 在该让压阶段, 支护结构的刚度发生突变, 为此, 本文引入支护刚度修正系数$\lambda_{1}$, 则在该阶段支护结构的受力表达式变换为
利用方程(23)隧道洞周处的位移表达式, 方程(26)可改写为
显然, 式(27)是关于$p(t)$ 的一元函数方程. 由式(27)可解得在让压阶段支护结构的作用力表达式为
将式(28)代入方程(23)中, 得到让压阶段隧道洞周处的位移函数为
2.4 弹性变形阶段II
若在$t=t_{2}$时刻, 支护的让压变形结束, 此时$p(t)=p_{2}$, $u_{R}(t_{2})=u_{2}$, 支护再次进入弹性变形阶段. 在这一阶段, 支护将继续提供较大的支护阻力来约束围岩的变形, 即较小隧道位移的增加将引起较大支护阻力的提高, 支护的刚度再次产生突变. 在这一阶段, 引入支护刚度修正系数$\lambda_{2}$, 则支护的力-位移表达式为
同理, 利用方程(23)隧道洞周处的位移表达式, 方程(30)可改写为
则解方程(31)可以得到弹性变形阶段II的支护结构压力表达式如下
将方程(32)代入方程(23)中, 该阶段隧道洞周处位移的表达式为
综上, 让压支护的计算主要分为弹性变形阶段I、让压阶段以及弹性变形阶段II. 图5给出了隧道支护计算的流程图, 若在刚性(工程许可范围内)条件下, 支护满足承载力要求, 则可选刚性支护, 否则可采用让压支护, 并通过不断地调整让压阶段的支护参数, 使结构最终能满足各项要求.
图5
3 结果与讨论
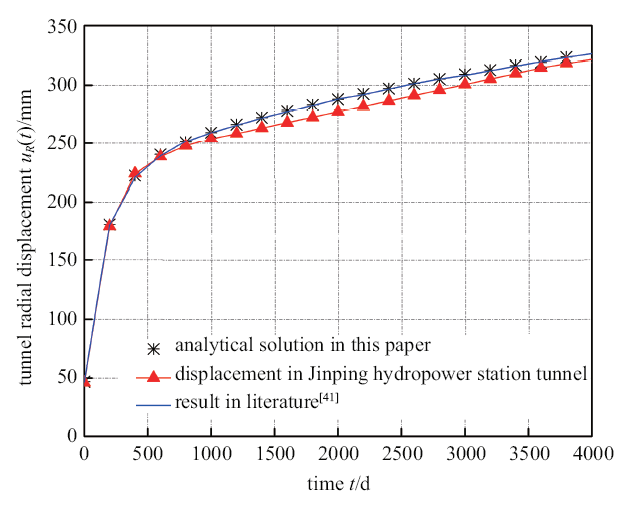
3.1 理论验证
为了验证理论推导的正确性, 本文选取文献[41]中的结果和锦屏二级水电站引水隧洞绿泥石片岩围岩洞壁处位移进行对比分析. 由于本文上述理论考虑了支护作用, 为了有效对比, 假设支护结构在$t_{0}=0$时刻安装, 支护结构的刚度$K_{S}$取0.001、支护刚度修正参数$\lambda_{1}$和$\lambda_{2}$均为1(即支护刚度极小的传统支护), 以模拟未安装支护时的工况. 隧道半径、初始地应力和围岩参数为[41]: 初始地应力$p_{0}=40$ MPa, 隧道半径$R=7$ m, 剪切模量$GM=3$ GPa, 剪切模量$GK=1070.6$ MPa, 黏滞系数$\eta K=172$ GPa$\cdot$d, 黏滞系数$\zeta =37.5$ GPa$\cdot$d, 分数阶阶数$\beta =0.43$.
图6
3.2 参数分析
3.2.1 非定常参数
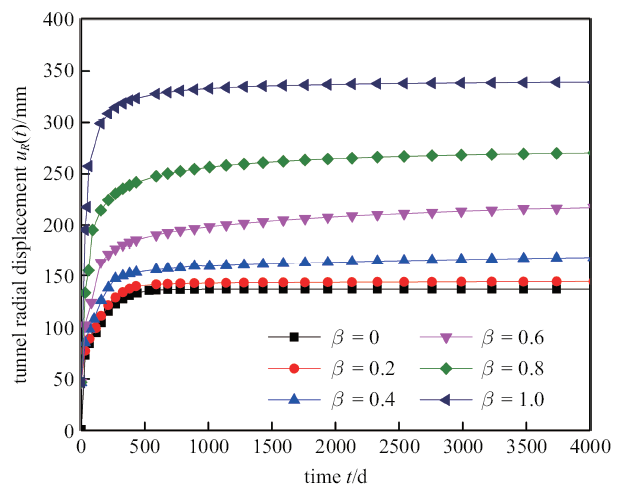
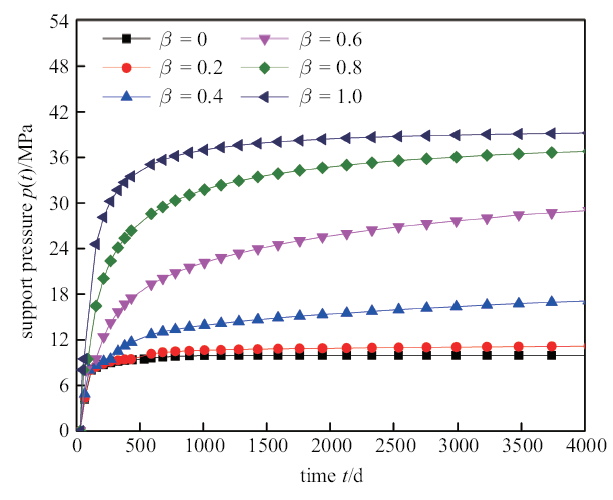
图7
图7
不同分数阶阶数工况下隧道位移曲线图
Fig.7
Curves for tunnel displacement under the cases of different derivative orders
图8
图8
不同分数阶阶数工况下支护压力曲线图
Fig.8
Curves for support under the cases of different derivative orders
3.2.2 刚性支护与让压支护效果对比
图9
图9
传统刚性支护下隧道位移和支护压力曲线
Fig.9
Curves for tunnel displacement and support pressure with traditional stiff support
图10
图10
让压支护作用下隧道压力-位移曲线
Fig.10
Curve for load-displacement of tunnel supported by yielding supports
由此表明, 通过支护结构的让压来减小支护压力, 保持隧道稳定, 是一种可行且有效的方法.
3.2.3 让压位移
图11
图11
让压支护与刚性支护作用下隧道位移比率
Fig.11
Ratio of tunnel displacement under conditions of yielding supports to traditional stiff supports
图12
图12
让压支护与刚性支护作用下支护压力比率
Fig.12
Ratio of support pressure under conditions of yielding supports to traditional stiff supports
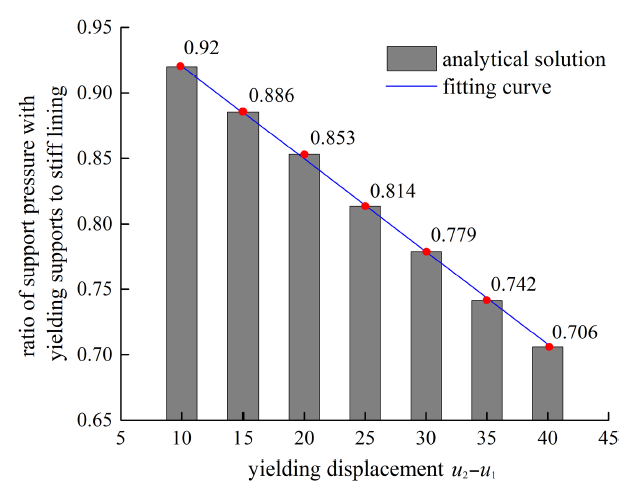
图12给出了支护压力随让压位移变化的曲线图. 显然地, 支护压力与让压位移存在线性减小的关系, 即随着让压位移的增加, 支护压力线性减小. 由图10, 当让压位移达到40 mm的时候, 支护压力与刚性状态相比, 仅为后者的70.6${\%}$, 减幅接近30${\%}$. 由此可以得出, 在大变形隧道中, 若刚性支护, 甚至重型支护不能承受由于围岩大变形所造成的支护荷载, 相较而言, 让压支护则是最优选择. 让压支护能够通过允许围岩变形, 释放围岩变形能量, 以减小作用在支护结构上的内力, 且随着让压位移的不断增大, 支护载荷可不断减小, 最终能够使得作用在支护结构上的压力小于支护承载力. 但是, 必须强调的是, 由于围岩在变形释放的过程中存在由"松弛"到"离散"突变的风险, 因此, 在让压过程中可能存在离散岩体形成的不确定性. 在实际工程在, 让压位移的选择是一较为复杂的判断过程, 应该结合围岩自身的性质, 支护特性及隧道设计的要求等, 而一味地增大让压位移以达到减小支护结构受力的目的并不可取.
3.2.4 修正刚度
让压阶段是让压支护区别于传统刚性支护结构的重要特征. 在让压阶段, 随着位移逐渐地增大, 但作用在支护结构上的力并不增加, 或者呈较小幅度的增大. 因此, 该阶段支护刚度修正系数$\lambda_{1}$应保持在较小水平内. 为了研究支护效果对支护刚度修正系数$\lambda_{1}$的参数敏感性, 本文取$\lambda_{1}=0$, 0.05, 0.1, 0.15, 0.2, 作为计算工况. 在该计算中, 认为支护是在隧道开挖30 d后完成的, $\beta$取0.2, 支护在压力$p(t)$达到8 MPa后开始产生让压变形, 让压位移为40 mm. 支护刚度修正系数$\lambda_{2}$取1. 不同支护刚度修正系数$\lambda_{1}$情况下支护结构的压力与隧道位移如图13和图14所示.
图13
图13
不同支护刚度修正系数($\lambda_{1})$条件下隧道位移曲线
Fig.13
Curve for tunnel displacement with different correction coefficients of support stiffness $\lambda_{1}$
图14
图14
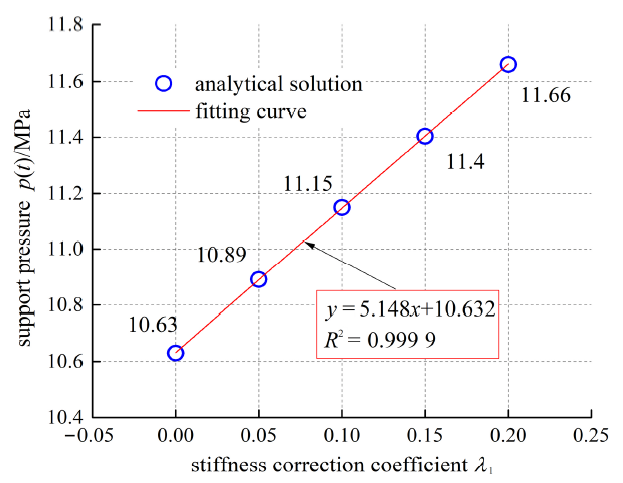
不同支护刚度修正系数($\lambda_{1})$条件下支护压力曲线
Fig.14
Curve for support pressure with different correction coefficients of support stiffness $\lambda_{1}$
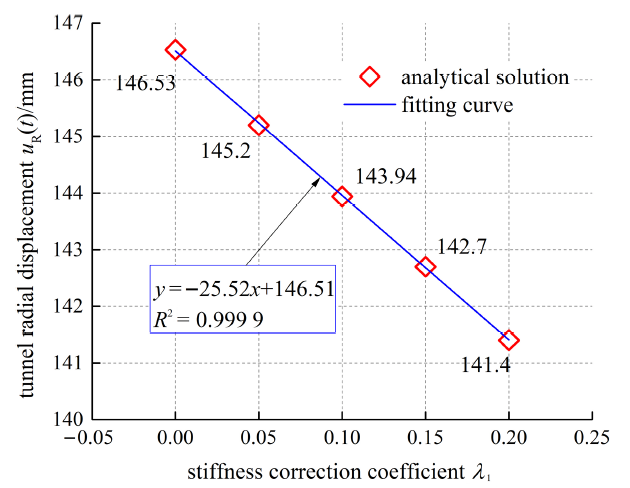
图13和图14给出了在相同让压位移下, 隧道位移和支护压力随支护刚度修正参数$\lambda_{1}$的演化规律. 从图13和图14中可以看出, 隧道位移和支护压力与支护刚度修正系数$\lambda_{1}$也存在线性关系, 隧道位移随着修正系数的增加而减小, 支护压力则呈相反趋势. 这种情况可以解释为: 由于在让压阶段, 支护刚度修正系数$\lambda_{1}$可表征在该阶段支护结构约束变形的能力, 若该系数越大, 则让压支护的力学性能就越接近越刚性支护. 因此, 刚度修正系数$\lambda_{1}$越大, 意味着支护对围岩变形的约束就越强, 从而导致隧道变形越小, 但作用在支护结构上的荷载越大. 但是, 由于刚度修正系数$\lambda_{1}$仅保持在较小的变化范围内, 隧道位移和支护压力的降低或增加并不剧烈.
4 结论
让压支护是解决深埋高地应力软岩隧道大变形问题的有效方法. 针对让压支护对隧道力学行为的影响, 本文展开了相应的理论分析. 基于理论解答, 进一步讨论了岩石变形参数、让压支护参数对支护效果的影响. 得到的主要结论如下:
(1) 采用改进的分数阶Burgers蠕变模型, 通过在支护结构不同变形阶段引入了刚度修正系数$\lambda_{1}$和$\lambda_{2}$, 推导了考虑支护安装延迟作用下, 不同变形阶段的支护压力和隧道位移的解析解.
(2) 随着围岩本构模型分数阶阶数$\beta $的增大, 围岩的时效变形能力也不断增大, 隧洞的位移和支护压力也呈不断增大的趋势.
(3) 随着让压位移的增大, 隧道位移、支护压力与让压位移存在线性关系. 隧道位移随着让压位移的增大而减小, 而支护压力呈相反趋势. 实际工程中将采取扩挖的方式来满足隧道的变形, 以达到不会造成侵限的目标. 由于围岩在释放变形的过程中存在由"松弛"到"离散"突变的风险, 一味的地增大让压位移以达到减小支护结构受力的目的并不可取, 应视具体情况来确定最优让压位移.
(4) 隧道位移和支护压力与支护刚度修正系数$\lambda _{1}$也存在线性关系, 隧道位移随着修正系数的增大而减小, 支护压力则呈相反趋势. 但是, 由于刚度修正系数$\lambda_{1}$仅保持在较小的变化范围内, 隧道位移和支护压力的降低或增加并不显著.