引言
混凝土、岩石及陶瓷等脆性材料存在严重的拉压不对称性, 其拉伸强度一般远小于压缩强度. 大多情况下这类材料和结构的破坏是由拉伸断裂引起的, 如弯曲破坏、压缩碎裂、应力波在界面反射引起的层裂等, 因此, 脆性材料的拉伸强度是人们关注的重要参数[1-3]. 目前, 关于脆性或准脆性材料的拉伸强度测定主要有直接拉伸法[4]和间接拉伸法[5-12]. 其中, 巴西圆盘劈裂实验具有加载简单方便、可利用Hopkinson压杆加载用于动态拉伸强度测试等优点, 是目前使用最广泛的间接拉伸实验方法, 已被国际岩石力学学会(ISRM)、美国材料和试验协会(ASTM)、英国的BS标准和国际ISO标准作为岩石抗拉强度测试的推荐方法[7-8], 日本则更将其定为混凝土拉伸强度的测试方法[9]. 因应用广泛, 巴西圆盘劈裂实验自提出以来, 对该方法的验证、改进以及扩展研究就没有停止, 一直是研究的热点[10-21].
巴西劈裂实验分析中, 抗拉强度的计算是基于弹性力学平面问题解析解. 由于巴西劈裂不是通常意义上的一维拉伸实验, 巴西圆盘实验中试件各点处于复杂应力状态, 拉伸强度值的确定还与破坏准则的选择有关, 因此规定巴西劈裂实验数据有效性必须满足: 断裂是在载荷最大点处从圆盘试件的中心处起始, 沿着加载方向瞬态扩展到上、下加载两端[4,7-9], 这样按Griffith脆性破坏准则[22], 试样中心点应力状态满足的起裂条件才与一维应力拉伸实验得到的强度一致. 因此, 试样几何特征、尺寸(如径厚比等)对实验结果可靠性、敏感性影响等一直是研究热点之一[14,23]. 另一方面, 在巴西圆盘劈裂实验中, 集中力载荷易导致试样加载处附近应力集中而发生压溃破坏, 不再满足中心起裂假设[24-25]. 为减小巴西劈裂实验中线载荷所引起的应力集中, 许多研究者采用弧形加载[26-27]、垫条加载[7,28-30]及采用平台巴西试样[11-12,19]等以改变加载接触面. 这些方法可改善应力集中引起的破坏, 但应力状态也发生了变化. 为此, 国内外研究者开展大量工作, 包括不同载荷作用下试样应力场弹性解的表征, 分析不同加载边界下试样中心起裂条件及其对拉伸强度测试的影响等, 但结果仍存在较大差异[14,25-26,31]. 这些研究中, 较多的是采用理论及数值分析方法探讨, 比较实验数据资料尚显不足[14].
为此, 本文对平板加载及垫条加载下混凝土巴西劈裂实验开展比较分析, 采用高速相机与试验机同步器同步采集加载力、试样表面变形及裂纹起始、断裂过程, 结合DIC技术分析试样表面应变场演化, 探讨了不同加载边界下混凝土特性、应力状态、破坏的起始演化等对拉伸强度的影响, 研究对于巴西劈裂实验应用及混凝土劈裂强度理解具有重要意义.
1 实验方案及试样
1.1 实验设计与测试
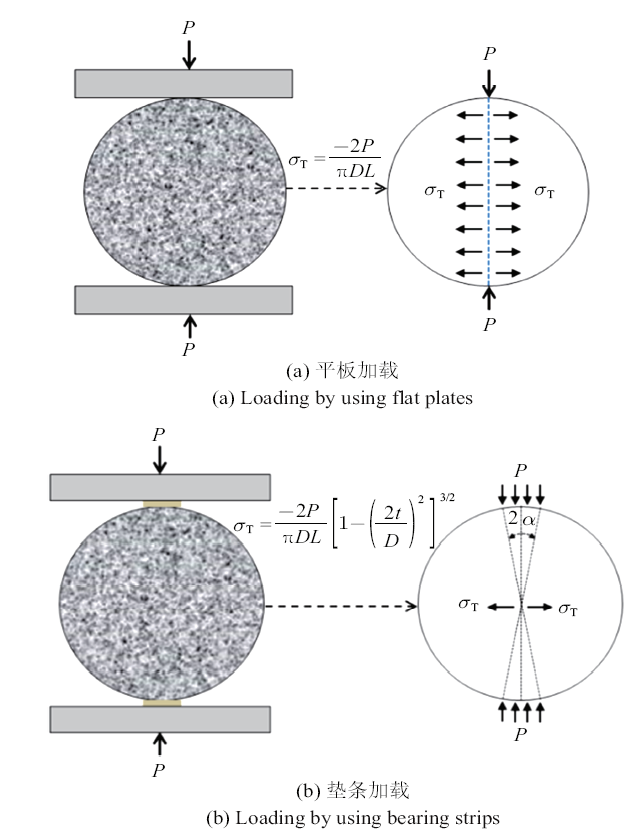
在混凝土、岩石及陶瓷等巴西劈裂实验中国内外学术和工程界常采用方法有平板直接加载、弧形压模加载、垫条加载及平台圆盘试样等, 但载荷接触条件对实验结果有很大影响[32]. 尽管不同的技术规范和文献对实施巴西实验的条件还没有达成完全一致的共识, 但文献中对实验取得理想结果提出了许多有益的建议. 对于不同的加载方式, ASTM[8]阐述垫条加载与弧形压模加载具有相近的理论解和实验结果, 认为其劈裂强度与平板直接加载接近. 对近期发展的平台试样也认为与垫条加载结果相近[31]. 一般认为: 在保证中心起裂的情况下, 接触角越小越好. 为此, 本文设计巴西圆盘直接加载及垫条加载劈裂实验开展比较分析, 如图1所示. 其中, 垫条采用宽度为6 mm的软木条. 对于巴西圆盘劈裂实验, 通常测试其载荷峰值并采用圆盘在不同加载边界下的弹性理论解直接给出材料的拉伸强度.
图1
图1
平板加载与垫条加载示意图
Fig.1
Schematic diagram of loading by flat plates and bearing strips
实验在MTS-180-5T液压伺服材料试验机上完成, 加载采用位移控制为使两种加载方式获得相近的加载率, 调整平板加载速度为0.1 mm/s, 垫条加载速度为0.15 mm/s. 巴西实验要求起裂前必须近似满足线弹性状态, 否则按弹性理论解计算的拉伸强度会存在较大误差, 为分析加载边界、应力状态演化等对劈裂过程及劈裂强度的影响, 建立试验机与相机的同步采集系统, 采用FASTCAM SA1.1高速相机同步记录载荷历时及相对应的变形及起裂过程, 并利用DIC分析劈裂实验加载过程中巴西圆盘试样的应变演化特征, 考察实验条件满足情况. 高速相机采样频率为8000 f/s, 像素为$512\times528$, 能较精确获取、比对加载过程试样表面的变形演化. 需要说明: 即使在准静态加载下混凝土试样劈裂破坏过程也是瞬态发生, 8000 f/s的采样频率还无法记录高分辨的裂纹的起始、发展过程, 为此实验还设置高速相机36 000 f/s的采样频率, 用于记录劈裂过程的裂纹演化特征.
混凝土试件表面喷涂散斑, 利用二维数字图像相关法(digital image correlation, DIC-2D)分析试样破坏全程表面应变场演化[33]. 实验采用MatchID-Zero-Normalized Sum of Squared Differences (ZNSSD)算法(subset size为31像素, step size为5像素), 单位像素对应试样上的长度为0.167 mm.
1.2 试样
巴西圆盘试样采用相同的C40混凝土, 水灰比0.5, 普通硅酸盐(P.I 42.5)水泥, 粗骨料为5$\sim$15 mm连续级配石灰岩, 细骨料为河沙(中沙). 浇筑成直径74 mm、厚35 mm圆盘试样, 标准条件养护28 d.
同步制备150 mm $\times$ 150 mm $\times $ 150 mm混凝土标准立方体试样, 利用MTS材料试验机测量混凝土压缩性能等基本参数. 实验中采用DIC测试压缩过程试样的轴向压缩应变及横向应变, 根据压缩应力应变曲线及试样轴向应变-横向应变曲线, 计算混凝土材料的弹性模量、泊松比, 4组重复实验测得准静态下材料的平均压缩性能如表1.
2 实验结果及分析
2.1 加载率
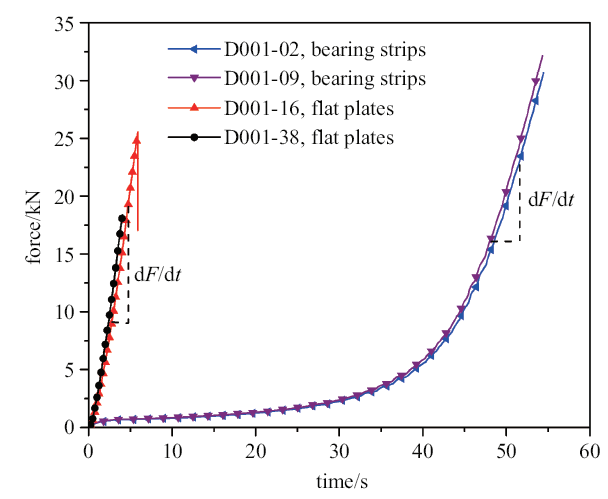
对混凝土试样在相同加载速率下开展系列平板及软木垫条加载劈裂实验, 图2为一组典型的载\lb 荷-时间曲线. 可见实验重复性很好, 可近似采用$\dot{F}={d}F/{d}t$作为加载率. 平板加载、软木垫条加载实验的加载率分别为5.52 kN/s, 2.24 kN/s, 按$\dot{\varepsilon}=\dot{\sigma}/E$计算两者应变率基本一致.
图2
2.2 劈裂破坏过程及强度
图3
图3
压缩直径上拉伸应力分布示意图
Fig.3
Schematics of tensile stress distribution on the compressed diameter
对于平板直接加载情况, 相当于垫条宽度$2t$趋于0的集中载荷(如图3). 按平面弹性解, 沿压缩直径上的拉伸应力是均匀分布的, 其最大拉伸应力为
式中, $P$是加载力, $D$和$L$分别是试样直径及厚度, $\sigma_1$为第一主应力(以拉伸为正). 如试样满足"中心起裂", 可将材料抗拉强度$\sigma_{T}$表征为试样中心应力状态的最大拉伸张量, 即
式中, $P_{c}$ 为峰值载荷.
对于软木垫条加载, 可近似假设为均布载荷加载情况, 试样沿压缩直径上的拉伸应力分布不是均匀的, 与垫条宽度$2t$相关. Tang[34]较早采用理论与有限元比较的方法分析了不同宽度均布载荷作用对加载直径$AB$上拉伸应力分量的影响, 给出修正的分析解
式(2)和式(3)给出了两种不同加载边界下混凝土巴西劈裂强度计算公式. 形式上集中载荷试样中心拉伸应力弹性解式(2)为均布载荷式(3)的一个特例, 对于 $2t/D\leqslant0.16$, 式(2)与式(3)的差别不会超过4${\%}$. 因此, 在实际应用中也有实验直接采用式(2)近似进行计算.
2.2.1 平板加载
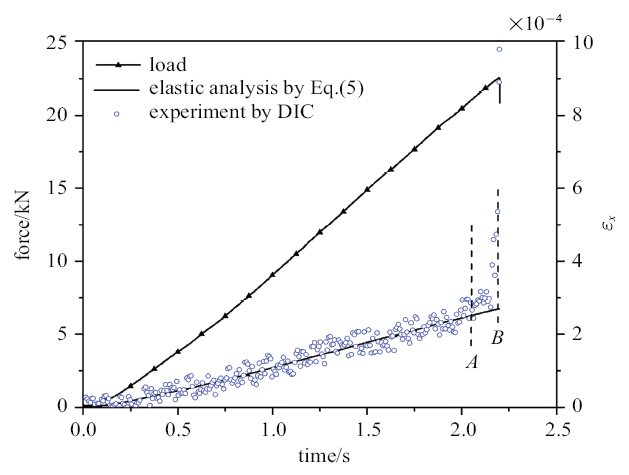
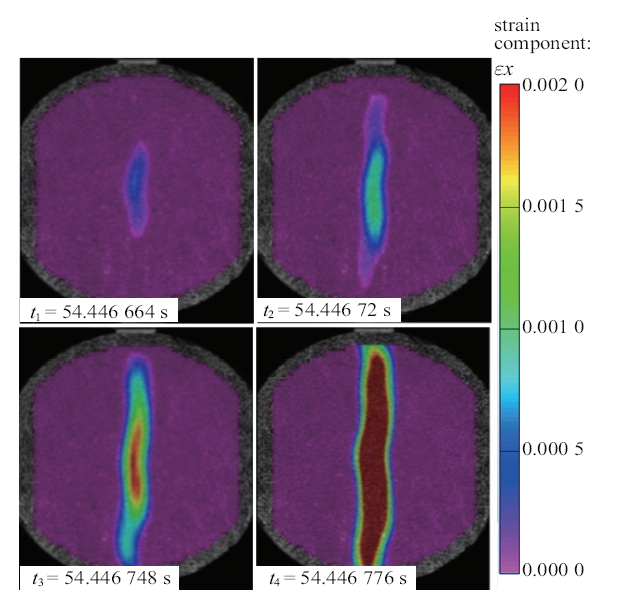
图4(a)和图4(b)为平板加载时, 试样中心点典型的拉伸应力-时间曲线及高速相机记录的试样表面裂纹演化特征. 高速相机记录该试样(编号D001-04)满足中心起裂. 其中, 图4(b)裂纹扩展过程的时刻与图4(a)中的时刻$t_{1}-t_{4}$对应. 可见: (1)在载荷峰值点前($t_{1}< 2.192 375$ s), 试样表面未见裂纹; (2)劈裂发生在最大应力峰值之后的$t_{2}=2.199 125$ s时刻, 裂纹从中心起始并向加载点扩展, 至$t_{3}$ $(t_{3}=2.199 250$ s)时刻贯穿整个试样. 随后, 试样左右两个部分分离, 拉伸应力陡然下降. 值得注意的是: 在裂纹起裂、扩展过程中($t_{1}-t_{3}$时刻)试样发生瞬态的断裂. 从$t_{2}=2.199 125$ s裂纹起始至$t_{3}=2.199 250$ s时扩展至整个试样, 拉伸应力几乎没有明显变化, 几乎在恒定拉伸应力$\sigma=5.55$ MPa下, 裂纹平均扩展速度约为290 m/s.
图4
图4
载荷-时程曲线与表面裂纹发展过程
Fig.4
The history of load and the develop process of surface crack
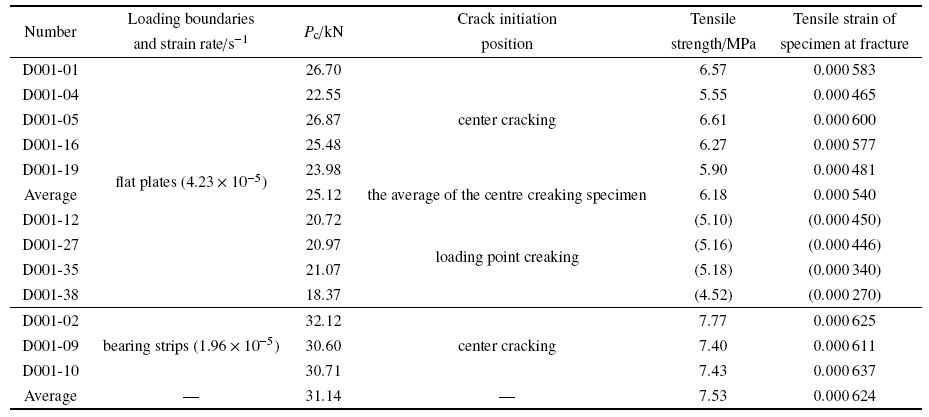
实验中, 混凝土平板加载试样并不总是中心起裂, 部分从靠近试样加载点附近位置起裂并向另一端扩展的情况, 如图5. 扩展过程中还会继续产生多重裂纹, 不满足巴西劈裂实验要求的"中心起裂"假定, 这与文献[35]观察到的结果一致. 其中, 9次重复实验中有5个试样为中心起裂、4个为近加载点的位置起裂, 存在较大的随机性. 按式(2)所计算拉伸强度汇总在表2中. 结果显示: (1)平板加载情况下, 混凝土巴西劈裂实验裂纹起始位置有较大的随机性, 存在中心起裂及近加载点起裂两种情况; (2)从统计看, 中心起裂试样的最大压缩载荷$P_{c}$大于近加载点起裂的情况; (3)满足中心起裂的有效实验得到的强度分散性较大, 约为10.2%.
图5
图5
底端起裂试样表面裂纹发展过程
Fig.5
Surface cracks develop process of the sample cracking from the bottom
2.2.2 软木垫条加载
图6
两种不同加载边界混凝土劈裂实验结果比较显示: (1)软木垫条加载情况, 起裂稳定, 均能保证从中心起裂; (2)加载边界、应力状态等差别对混凝土试样裂纹演化、拉伸强度表征有显著影响, 软木垫条加载得到的平均抗拉强度为7.53 MPa, 明显大于平板加载的6.18 MPa, 相差17.9%. 有必要对不同加载条件下应力场、材料破坏演化及其影响开展进一步分析讨论.
3 基于DIC的劈裂过程及应变场演化分析
3.1 理论分析
尽管圆盘试样的几何形状及其边界条件相对简单, 但不同加载边界条件下应力场的弹性理论一直是一个经典问题. 赫兹解[36]表明圆盘内部的应力分布与固体的弹性常数无关. 随后, 人们发展了各种数学方法来确定二维空间中的应力、应变场[37-38]. 随载荷配置更为复杂和多样, 经典弹性理论解决这些问题变得困难许多学者发展新的方法(如airy函数、应变函数、位移函数或势函数)等方法来求解给出不同加载几何下试样的应力场[27-28,31,38-39]. 对同一问题使用不同的数学方法求解, 形式虽有差异, 但得出的结论趋于相同. 表3中选择给出了分析中常被采用的应力场解的形式. 巴西劈裂实验中, 只有沿压缩直径$AB$上发生破坏时, 结果才是有效的, 因此, 沿直径$AB$线上的应力分布最为重要, 表中给出该直径上的应力场分布表达式及其中心满足Griffith失效准则的拉伸强度确定公式.
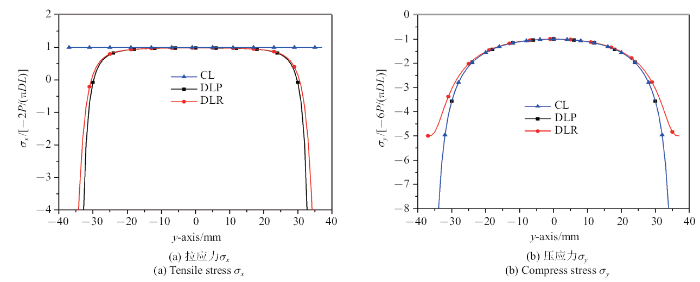
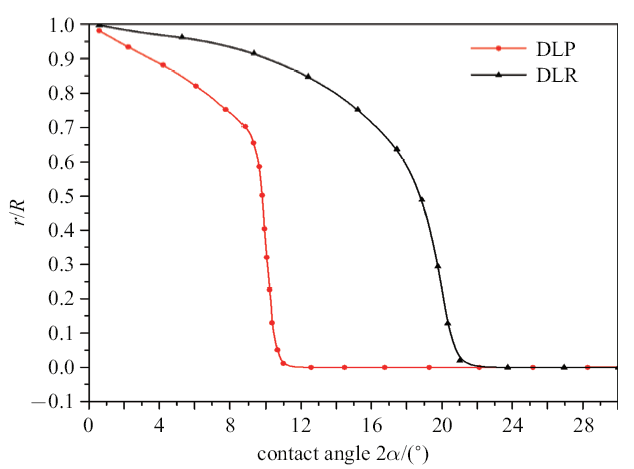
刚性平板与试样之间加入软木垫条后, 载荷形式可假设为沿软木宽度的径向均匀分布的载荷(DLR), 也可近似按轴向平行均布载荷(DLP)简化. 对于本文实验设计软木条原始宽度为6 mm的加载条件, 加载过程软木条会产生变形变宽, 平均宽度为8.07 mm, 对应的接触角近似为$2\alpha=12.42^\circ$. 相应地, 按DLR或DLP两种分布载荷简化假设下得到的沿加载直径方向拉应力$\sigma_{ x}$与压应力$\sigma_{y}$应力场分布特征与平板加载(CL)的比较如图7(a)和图7(b)所示. 可见: (1)在加载直径上, 试样中间大部分区域3者的拉伸应力分量$\sigma_{x}$分布趋势相近, 分布较为均匀, 所不同的是在加载端附近, 在CL载荷下$\sigma_{ x}$恒定不变, 但DLP和DLR的理论解在加载端附近$\sigma_{x}$从拉伸变为压缩, 并且越近加载端压应力分量越大; (2) 3种加载边界下, $\sigma_{y}$应力场的分布趋势也基本相同, 中心最小且在数值上基本均为最大拉伸应力张量的3倍. 图8给出了DLR、DLP两种均布载荷加载假设下归一化拉伸强度随接触角$2\alpha$的变化. 可见: 在$\alpha<25^\circ$范围内, 两者无明显差别. 因此, 从理论解分析, 在实验所采用的软木条加载下, 采用DLR或DLP简化计算应力分量$\sigma_{x}$和$\sigma_{y}$影响不大.
图7
图7
不同加载边界下应力分布($2\alpha=12.42^\circ)$
Fig.7
Stress distribution under different loading boundaries ($2\alpha=12.42^\circ)$
图8
另一方面, 巴西劈裂实验基本前提是材料假定是均匀、各向同性的, 在破坏发生前为线弹性应力场已确定. 忽略应力集中, 脆性或准脆性材料破坏满足Griffith裂纹准则
式中, $\sigma_1$和$\sigma_3$分别为第一和第三主应力(以拉伸为正), $\sigma_{T}$为材料拉伸强度.
理论上, 对于平板直接加载实验, 加载直径$AB$上拉伸应力为恒定均匀场, 试样中心$3\sigma_1=-\sigma_3$, 圆盘的几何中心是满足拉伸破坏条件的唯一点, 其值等于单轴拉伸强度. 但平板加载下, 加载端压缩应力远大于拉伸应力, 可能会导致试样从加载端发生压溃或剪切破坏. 另外, 混凝土材料起裂还易出现在混凝土圆盘试样中的孔隙、裂缝或多相界面应力集中处, 因此使得起裂位置出现较为随机.
而对于软木垫条加载情况, 根据DLR及DLP假设给出的应力场分析, 按Griffith准则得到理论失效起始位置与接触角$2\alpha$相关, 如图9所示. 对于DLP加载情况, 只要接触角$2\alpha$大于11$^{\circ}$时, 理论上即能满足中心起裂条件. 而对于DLR加载情况, 需保证接触角$2\alpha$大于21$^{\circ}$才能保证中心起裂. 本文实验设计软木垫条接触角为12.42$^\circ$, 加载实验观察的均满足中心起裂, 形式上更符合DLP分布载荷假设.
图9
只要满足中心起裂, 理论上分析, CL, DLR及DLP三种加载情况试样中心有相近的应力场, 计算的拉伸强度也应是相同的. 但事实上, 实验中混凝土劈裂实验测试得到的平均拉伸强度差别达到17.9%.
3.2 基于DIC的应变演化实验分析
假设该混凝土断裂前为线弹性, 试样表面满足平面应力条件, 则在试样加载直径$AB$上沿$x$方向上的应变$\varepsilon_{ x}$与$y$方向上应变$\varepsilon_{y}$分别为
实验中采用DIC技术对高速相机记录的试样表面变形进行分析, 可得到表面应变场, 与弹性解(5)和(6)进行比较.
3.2.1 平板加载
图10
图10
平板加载试样表面拉伸应变场演化
Fig.10
Tensile strain field evolution under plate loading of the sample surface
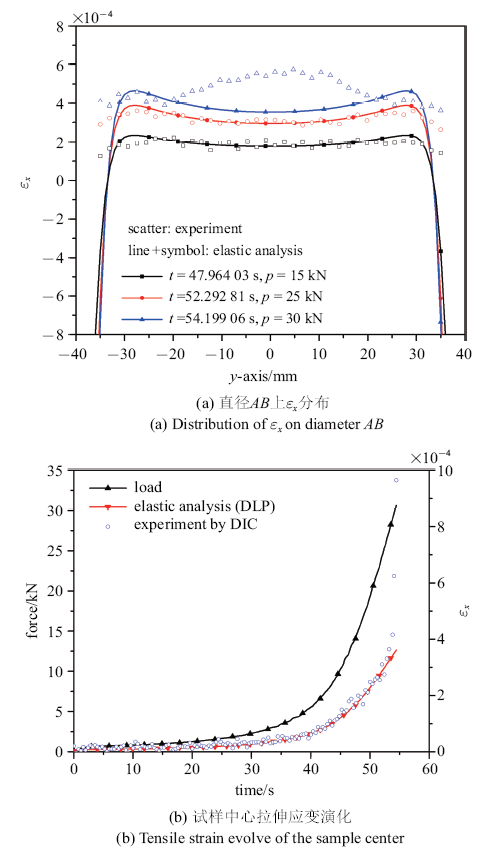
图11(a)和图11(b)给出了按式(5)和式(6)计算得到的理论解应变场与实验DIC分析得到应变场的比较. 虽然混凝土为多相非均质材料, 在加载初期, DIC实测的应变场$\varepsilon_{x}$和$\varepsilon_{y}$与理论解的分布特征趋势基本符合, 试样中部区域($-30$ mm $<y<$ 30 mm)拉伸应变较为均匀, 与弹性理论应变分布趋势基本一致. 但随着加载逐渐增大至最大载荷前, $\varepsilon_{x}$场与理论解开始出现明显分离. 由于出现应变集中, 实测的应变值显著大于理论解, 距中心位置越远偏离越大, 应变场已不满足材料线弹性假设. 这时, 近加载端的压缩应变$\varepsilon_{y}$减小, 小于弹性解.
图11
图11
$\varepsilon_{x}$和$\varepsilon_{y}$场理论解与实验DIC结果比较
Fig.11
Comparison of $\varepsilon_{x}$ and $\varepsilon_{y}$ field theoretical solutions with experimental DIC results
图12
图12
载荷与试样中心点拉伸应变$\varepsilon_{x}$时程曲线
Fig.12
The history of load and tensile strain $\varepsilon_{x}$ of sample centre point
图13
3.2.2 软木垫条加载
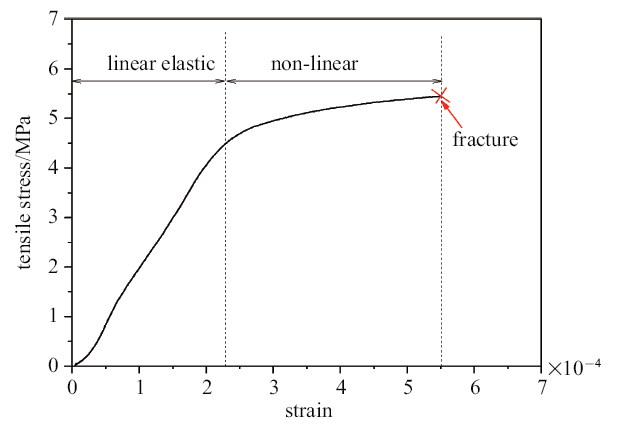
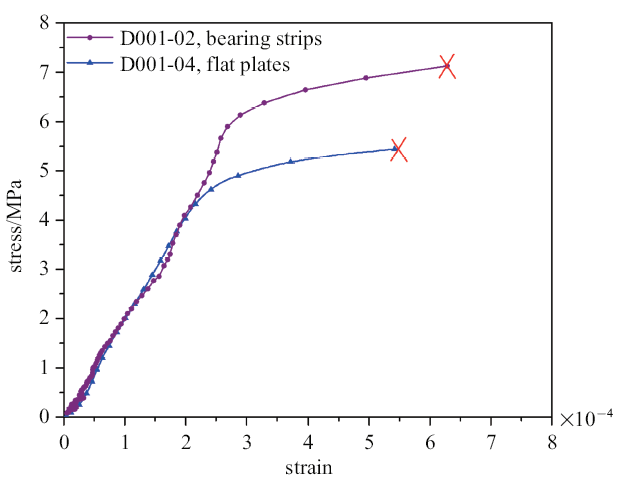
图14为软木垫条加载下试样D001-02应变演化云图. 与平板加载不同, 断裂前拉伸应变最先在试样中心开始集中, 向加载端延伸、贯穿试样. 图15(a)和图15(b)为实验DIC分析得到直径$AB$及中心处应变$\varepsilon_{x}$与按式(5)计算得到理论解的对比, 可见: (1)软木垫条加载下, 在加载直径中部区域拉伸应变分布、大小与线弹性解相近, 但与平板加载不同, 加载端附近$\varepsilon_{x}$是压缩的; (2)当载荷接近最大值, 材料发生塑性损伤, 试样中心应变$\varepsilon_{x}$首先开始集中, 明显大于弹性解. 图16为试样中心点的拉伸应力-应变曲线, 同样存在损伤演化的非线性段, 发生应变集中时的载荷$P$大于平板直接加载情况.
图14
图14
软木垫条加载试样表面拉伸应变场演化
Fig.14
Tensile strain field evolve under bearing strips loading of the sample surface
图15
图15
拉伸应变DIC结果与DLP理论比较
Fig.15
Comparison of tensile strain DIC result and DLP theoretical solution
图16
图16
不同加载条件下的应力-应变曲线
Fig.16
Stress-strain curve under different loading boundaries
4 分析讨论
实验分析显示: (1)混凝土材料拉伸断裂前, 存在明显非线性演化, 已不满足巴西劈裂分析的线弹性假设; (2)无论均布载荷还是集中载荷, 试样断裂前存在应变非线性集中发展, 当达到载荷最大点后, 裂纹在应变集中区中起始、扩展直至发生断裂. (3)在较小载荷的弹性段, 平板加载(CL)与软木垫条加载(DLP)两者的弹性应力理论场相近, 实验DIC分析得到的试样中心应变场也几乎相同. 需要关注是, 应变开始集中演化到发生断裂的最大载荷点, 虽然载荷幅值变化都不大, 大约只有10${\%}$左右, 如图16. 但对于平板加载, 即使裂纹从中心起裂, 损伤集中发展也不是从中心起始, 而总是从靠近集中载荷端附近首先起始. 可见由于集中加载端附近应力集中, 加载端将在较低的载荷幅值下提早发生应变塑性损伤集中, 导致试样应力场分布及对称性破坏, 使得载荷峰值降低. 而混凝土为多相不均匀材料, 骨料界面或孔隙位置处易产生应力集中起裂, 使得起裂位置出现随机性, 并产生多重裂纹. 因此, 按式(2)计算得到的劈裂强度偏低, 实验误差及分散性较大. 而软木垫条加载减小了加载端应力集中, 应变场发展更稳定, 应变非线性演化与裂纹起始位置相同, 均从中心开始形成、发展. 试样能够在较高的载荷下保持理想弹性场, 应变集中起始的载荷及试样断裂时的载荷峰值提高, 使得表观强度高于平板加载情况, 因此, 均布载荷巴西劈裂实验测得的拉伸强度较高. 另外, DLP加载下应变集中从中心起始, 易保证中心起裂条件, 应力场也更对称稳定, 结果分散性小.
综上可见: 巴西劈裂演化过程的非线性对加载条件敏感, 试样破坏过程的非线性导致表征的混凝土拉伸强度有明显差别, 实验中仅观察是否满足"中心起裂"是不够的, 设计时必须谨慎考虑.
5 结论
巴西劈裂实验采用垫条、圆弧压模及平台加载, 将载荷均匀地分布在接触区域上, 可减少加载端附近失效的倾向, 保证测试中心起裂的条件, 理论分析显示它们的弹性应力场相近. 但即使采用文献或相关标准所建议的加载接触角$2\alpha$, 不同加载边界下得到强度仍存在差别, 实验结果到目前存在争议. 本文对平板及软垫条加载下的巴西劈裂实验开展研究, 分析表明在满足中心起裂条件下, 该两种实验加载方式, 形式上可代表典型的集中载荷和不同分布载荷加载条件. 实验采用高速相机结合数字图像相关法(DIC)分析比较了两种加载方式的应变、裂纹演化特征, 探讨其对拉伸强度的影响. 结果显示: (1)混凝土劈裂拉伸存在明显的非线性特性; (2)虽然从非线性起始载荷到最大断裂载荷只有不到10${\%}$, 对按弹性假设计算材料拉伸强度影响不大, 但非线性应变集中演化对加载边界敏感, 对劈裂强度测试有显著影响, 软木垫条加载比平板加载实验测得的强度高17.9%; (3)对于平板加载, 即使满足中心起裂, 由于其应变集中总是从加载端提前起始, 破坏了试样弹性场, 导致得到的拉伸强度低于垫条加载情况, 起裂位置随机性大, 结果分散; (4)软木垫条加载下, 只要接触角$2\alpha$设计合理, 弹性应力场发展稳定, 保证应变集中及裂纹演化均从中心起始, 能更好符合巴西劈裂实验要求; (5)对于巴西劈裂实验, 由于存在非线性演化, 仅校验"中心起裂"有效性条件是不够的. 实验阐明了不同加载条件下巴西劈裂实验结果差异的原因, 对脆性材料巴西劈裂实验应用设计、拉伸特性测试具有参考意义.