引言
近年来,人们对骨细胞的空间特性(包括密度和形态)以及这些特性与疾病和衰老的潜在关系越来越感兴趣. 体外实验研 究表明,骨细胞几何形状影响其应变响应[10]. Carter等发现股骨的前侧,后侧,内侧和外侧的骨细胞的密度,形状和方向都有较大差别,其可能原因是与负载的局 部变化有关[11]. 骨质疏松症已经成为世界范围内的一个严重问题,最近有研究表明患有骨质疏松的病人的骨 细胞形状更不规则[12-13],骨小管更弯曲[13],而其骨细胞膜上感受的流体剪应力和流体速度也 发生较大的变化[14]. 年龄也是影响骨细胞形状的一个重要因素,年龄增大会导致骨细胞面积减小且形 状偏扁平[15-16]. 以前的研究一般都认为骨陷窝-骨细胞的方向与骨中胶原纤维的方向一致[9, 17-19],即渗透率主方向与坐标轴方向一致. 事实上, 二者方向会有不一致的情况[11, 20- 21],这会使得骨内液体流动主方向(即渗透率主方向)与胶原纤维的方向成一定的夹角. 骨陷窝-骨细胞-骨小管的这种形态和方向变化会导致骨组织内渗透率的各向异性行为. 在进行有限元多孔弹性力学分析时,需要准确量化骨陷窝-小管孔隙的渗透性来捕捉骨的各向异性流体流动行为,才能 更真实地预测孔隙流体压力和流速响应.
因此,为了更精确地阐明骨内液体流动的具体形式,本研究开发一种基于骨组织微观结构的多孔弹性力学有限元模型. 首先根据骨陷窝的形状,方向和其他微观结构生理参数,计算得到骨的三维渗透率. 然后,基于多孔弹性力学理论建立骨单元的有限元模型,计算在轴向载荷作用下骨单元内液体的压力和流速,以期为骨的力传导与骨的功能适应性机制提供一个更深入的理解.
1 基于骨单元微观结构计算其渗透率
1.1 骨单元渗透率的计算
图1
$A_{1}$和$B_{1}$由以下方程得出
其中,${I}_{0}$,${K}_{0}$,${I}_{1}$和$ {K}_{1}$是第1类和第2类的修正贝塞尔函数.
$L$表示两个骨陷窝之间的距离,也是CPUC的边长,可由以下公式得出
其中,$a, b, c$分别为骨陷窝长半轴、中半轴和短半轴. 则骨陷窝-小管的孔隙率$\varphi $为
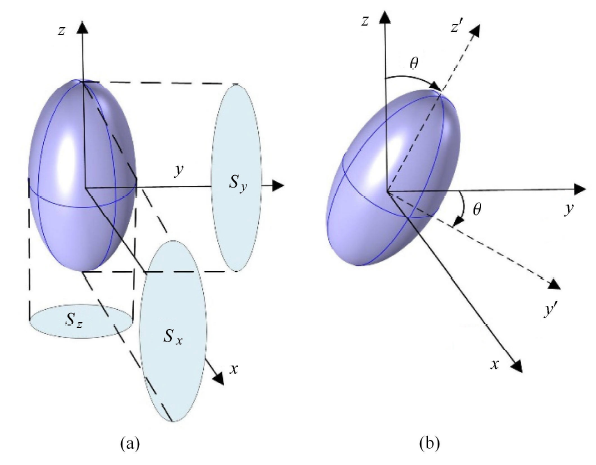
其中,$n_{x}$,$n_{y}$和$n_{z}$分别是平行于$x$,$y$和$z$轴穿过CUPC各面的小管数;$S_{x}$,$S_{y}$和$S_{z}$分别是$x$,$y$和$z$方向上骨陷窝的投影表面积,$N$是一个骨陷窝周围的骨小管总数. 如图2(b)所示,当骨陷窝绕$x$轴偏转$\theta $角时,骨陷窝在$x'$,$y'$和$z'$轴上的投影面积和骨小管的三维分布同样可由式(6)求出.
图2
图2
(a) 骨陷窝沿着$x$轴,$y$轴和$z$轴的投影面积 ($S_x$,$S_y$和$S_z$). (b) 骨陷窝绕$x$轴旋转$\theta $角
Fig.2
(a) Projected surface areas of the lacuna-osteocyte in the $x, y,$ and $z$ directions ($S_x$, $S_y$ and $S_z$) were used to determine the distribution of canaliculi; (b) The lacuna-osteocyte rotates around $x$-axis by $\theta $
1.2 骨陷窝形状
图3
图3
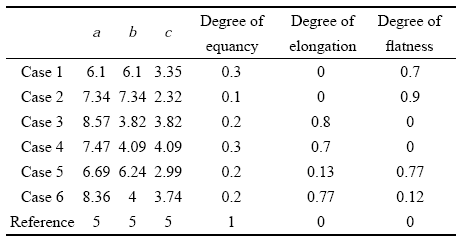
骨陷窝形状的代表性示例. 骨陷窝在不同平面的投影形状 (a) $x$-$y$面,(b) $y$-$z$面,(c) $x$-$z$面
Fig.3
Representative cases of lacunae shapes. The project of lacunae shapes are shown schematically in (a) the $x$-$y$ plane, (b) the $y$-$z$ plane, and (c) the $x$-$z$ plane
当3个特征值相等(EV1= EV2= EV3)时,骨陷窝的形状即为球形(reference). 当前两个特征值相等,第3个特征值较小(EV1= EV2$>$EV3)时,骨陷窝的形状呈扁平形(Case 1和Case 2);第1个特征值较大,后两个特征值相等(EV1$>$EV2= EV3)时,骨陷窝的形状呈伸长形(Case 3和Case 4);3个特征值都不相同(EV1$>$EV2$>$EV3),形状偏向取决于伸长度和扁平度的大小(Case 5和Case 6).
根据表1中骨陷窝形状参数计算得到Case1-Case 6的渗透率分别为${\pmb K}_{1}$,${\pmb K}_{2}$,${\pmb K}_{3}$,${\pmb K}_{4}$,${\pmb K}_{5}$和${\pmb K}_{6}$
${\pmb K}_1 = \left( \!\!\begin{array}{ccc} 8.25\times 10^{ - 21} & 0 & 0 \\ 0 & 8.25\times 10^{ - 21} & 0 \\ 0 & 0& 1.50\times 10^{ - 20} \end{array}\!\!\right){m}^2 \\ {\pmb K}_2 = \left(\!\! \begin{array}{ccc} 6.10\times 10^{ - 21} & 0 & 0 \\ 0 & 6.10\times 10^{ - 21} &0 \\ 0 & 0 & 1.93\times 10^{ - 20} \end{array} \!\! \right){m}^2 \\ {\pmb K}_3 = \left(\!\! \begin{array}{ccc} 5.74 \times 10^{ - 21} & 0 & 0 \\ 0 & 1.29 \times 10^{ - 20} & 0 \\ 0 &0 & 1.29 \times 10^{ - 20} \end{array} \!\! \right){m}^2 \\ {\pmb K}_4 = \left(\!\! \begin{array}{ccc} 6.77 \times 10^{ - 21} & 0 & 0 \\ 0 & 1.28 \times 10^{ - 20} & 0 \\ 0 & 0 & 1.28 \times 10^{ - 20} \end{array}\!\!\right){m}^2\\ {\pmb K}_5 = \left(\!\! \begin{array}{ccc} 7.31 \times 10^{ - 21} & 0 & 0 \\ 0 & 7.84 \times 10^{ - 21} &0 \\ 0 & 0 & 1.64 \times 10^{ - 20} \end{array} \!\!\right){m}^2 \\ {\pmb K}_6 = \left(\!\! \begin{array}{ccc} 5.91 \times 10^{ - 21} & 0 & 0 \\ 0 & 1.24 \times 10^{ - 20} & 0 \\ 0 & 0 & 1.32 \times 10^{ - 20} \end{array} \!\! \right) {m}^2 $
参考模型(reference)模型的渗透率是各向同性的 其值计算得:1.05$\times$10$^{ - 20}$ m$^{2}$.
1.3 骨陷窝方向
${\pmb K} = \left(\!\!\begin{array}{ccc} {k_{xx} } & {k_{xy} } & {k_{xz} } \\ {k_{yx} } & {k_{yy} } & {k_{yz} } \\ {k_{zx} } & {k_{zy} } & {k_{zz} } \end{array} \!\! \right)$
在空间直角坐标系$o$-$x'y'z'$中,渗透率主方向与坐标轴方向一致,其渗透率主值$k_{x}$, $k_{y}$和$k_{z}$可由式(6)求得. 在坐标系$o$-$xyz$中$x$与$x'$重合,则$k_{xx}=k_{x}$, $k_{xy}=k_{xz}=k_{yx}=k_{zx}= 0$, 而$k_{yy}, k_{yz}, k_{zy}$和$k_{zz}$可由以下公式求得[32]
当$\theta $角分别为0$^\circ$,30$^\circ$,45$^\circ$,60$^\circ$和90$^\circ$时, 对应于$o$-$xyz$坐标 下渗透率分别为
${\pmb K}_{0^{\circ}} = \left(\!\! \begin{array}{ccc} 4.84 \times 10^{ - 21} & 0 & 0\\ 0 & 8.06 \times 10^{ - 21} &0 \\ 0 & 0 & 1.86 \times 10^{ - 20} \end{array} \!\! \right) {m}^2 \\ {\pmb K}_{30^{\circ}} = \left(\!\! \begin{array}{ccc} 4.84 \times 10^{ - 21} \!&\! 0 \!&\! 0 \\ 0 \!&\! 1.07 \times 10^{ - 20} \!&\! -4.56 \times 10^{ - 21} \\ 0 \!&\! - 4.56 \times 10^{ - 21} \!&\! 1.60 \times 10^{- 20} \end{array}\!\! \right) {m}^2 \\ {\pmb K}_{45^{\circ}} = \left(\!\! \begin{array}{ccc} 4.84 \times 10^{ - 21} \!&\! 0 \!&\! 0 \\ 0 \!&\! 1.33 \times 10^{ - 20} \!&\! - 2.64 \times 10^{ - 21} \\ 0 \!&\! - 2.64 \times 10^{ - 21} \!&\! 1.33\times 10^{- 20} \end{array} \!\! \right) {m}^2 \\ {\pmb K}_{60^{\circ}} = \left(\!\! \begin{array}{ccc} 4.84 \times 10^{ - 21} \!&\! 0 \!&\! 0\\ 0 \!&\! 1.60 \times 10^{ - 20} \!&\! - 4.56 \times 10^{ - 21} \\ 0 \!&\! - 4.56 \times 10^{ - 21} \!&\! 1.07 \times 10^{ - 20} \end{array} \!\! \right) {m}^2 \\ {\pmb K}_{90^{\circ}} = \left(\!\!\begin{array}{ccc} 4.84 \times 10^{ - 21} \!&\! 0 \!&\! 0 \\ 0 \!&\! 1.86 \times 10^{ - 20} \!&\! 0 \\ 0 \!&\! 0 \!&\! 8.06 \times 10^{ - 21} \end{array} \!\! \right) {m}^2$
2 骨单元控制方程及有限元模型的建立
2.1 控制方程
其中, ${\pmb\sigma}$是整个多孔介质对应的应力张量, ${\pmb\varepsilon}$为应变张量. ${\pmb M}$是多孔介质脱水的4阶弹性矩阵, ${\pmb\alpha }$和$M$分别是Biot有效应力系数张 量和模量. $p$为多孔介质孔隙内液体压力, $\xi $为单位体积内液体含量的改变量. tr ( ) 表示矩阵的迹算子.
在不考虑体积力的情况下的平衡方程[8]
液体质量守恒方程
式中,$\ddot {\pmb u}^s$表示固体骨架对应的位移矢量对时间的二阶导数. $\rho $是整个多孔介质的密度,由液体密度$\rho _{f}$、固体密度$\rho_{s}$及孔隙率$\varphi $的关系来确定
$\rho = \varphi \rho _{f} + (1 - \varphi )\rho _{s}$
达西定律可写为[36]
式中,${\pmb V}$是流速矢量,${\pmb k}$和$\mu $分别是渗透张量和液体的黏度. 将式(8)代入式(10),式(9)和式(12)代入式(11)得到骨单元的控制方程
2.2 有限元模型的建立
图4
图4
骨单元模型的建立(a)和网格划分(b)
Fig.4
Establishment of osteon model (a) and mesh generation (b)
考虑到载荷频率较低,哈弗氏管像蓄水池一样起到储蓄的作用,能够维持流体正常的流进流出,其内的压力可设置为0,用作参考压力. 哈弗氏管的孔隙尺寸远大于骨陷窝-小管孔隙,骨单元壁的孔隙压力可以由此释放. 哈弗氏管表面的应力可以忽略不计,这也导致在哈弗氏管处应力为0的边界条件[37]. 骨单元外壁设置刚性约束(位移为0),表示骨单元受周围骨间质约束不能移动[33]. 如图4(a)和方程(14),轴向对称的循环载荷代表纵向压缩的生理运动,其谐波幅值$(w)$和频率$(f)$分别为0.5 $\mu $m和 1 Hz. 在一个周期内的最大轴向应变($\varepsilon )$发生在 0.5 s时,其幅度为0.001[33].
如图4(b)所示,借助扫掠的网格剖分方法来生成精确有效的有限元网格,网格包含20 880个单元. 最小单元质量为0.601 5;平均单元质量为0.847 4.
3 结果
3.1 骨陷窝形状的影响
根据本文的加载形式,当$t=0.25$ s时,应变率达到最大值0.001 s$^{ -1}$,骨单元内孔隙液体压力和流速的变化规律有最大响应[12, 33]. 如图5绘制了$t=0.25$ s时考虑不同形状骨陷窝CUPC的骨单元孔隙压力及流速的分布图. 在轴向的对称载荷下,参考模型呈现的是对称分布与之前的研究结果吻合[12, 33, 36]. 由于内部骨陷窝形状的不同,Case 1 $\sim $ Case 6的液体的压力和流速(靠近哈弗氏管部位较为明显)的大小与分布规律均与参考模型有较大差别,且最大的孔隙压力值均大于参考模型. 这说明在骨陷窝体积相同的情况下,形状的差异程度会影响压力和流速的大小和分布规律. Case 1,Case 2和Case 5的骨陷窝形状都是扁平形的,Case 3, Case 4和Case 6的骨陷窝形状都是伸长形的. Case 1,Case 2和Case 5的压力和流速在分布上与参考模型有些类似,沿着$y-z$面和$x-z$面的分布差异不大. Case 3,Case 4和Case 6的模型的压力和流速在$y-z$面和$x-z$面的分布差异较大.
图5
图5
骨陷窝形状影响下的骨单元孔隙压力($p)$及流速($v)$的分布图
Fig.5
The pore pressure ($p)$ and flow velocity ($v)$ distribution of osteon due to the influence of lacunae shape
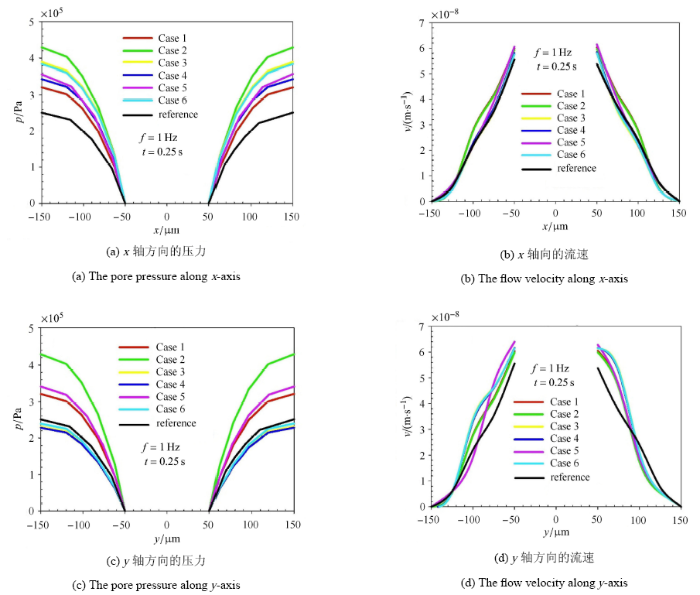
由图6可以看出,在$t=0.25$ s时,Case 1-参考 模型的压力和流速分别为 3.21 $\times $ 10$^{5}$ Pa,4.29 $\times $ 10$^{5}$ Pa,3.9 $\times $ 10$^{5}$ Pa,3.43 $\times $ 10$^{5}$ Pa,3.57 $\times $ 10$^{5}$ Pa,3.84 $\times $ 10$^{5}$ Pa,2.51 $\times $ 10$^{5}$ Pa和6.34 $\times $ 10$^{ - 8}$ m/s和6.57 $\times $ 10$^{ - 8}$ m/s, 6.5 $\times $ 10$^{ - 8}$ m/s,6.81 $\times $ 10$^{ - 8}$ m/s,6.74 $\times $ 10$^{ - 8}$ m/s, 6.4 $\times $ 10$^{ - 8}$ m/s,6.72 $\times $ 10$^{ - 8}$ m/s和5.85 $\times $ 10$^{ - 8}$ m/s. 在不同Case模型中,Case 2和Case 4模型沿$y$轴的压力差距最大,增大了86${\%}$,Case 5和参考模型沿$y$轴流速差距最大,增大了18${\%}$. 在单个Case模型上,Case 1, Case 2,Case 5和参考模型沿$x$轴和$y$轴的最大压力和流速差别不大,而Case 3,Case 4和Case 6沿$x$轴和$y$轴的压力有明显区别,分别增大了62${\%}$,47${\%}$和58${\%}$,而流速差别不大.
图6
图6
骨陷窝形状对骨单元孔隙压力和流速沿着不同方向的影响
Fig.6
Effect of the lacunae shape on the pore pressure and flow velocity along the different directions of osteon
3.2 骨陷窝方向的影响
图7绘制了$t=0.25$ s时考虑具有不同方向骨陷窝CUPC的骨单元孔隙压力及流速的分布图. 在我们所研究参数范围内, 0$^\circ$$\sim $90$^\circ$模型的液体的压力和流速的大小与分布规律均有较大差别. 随着骨陷窝旋转角度的增加其沿着$y-z$面和$x-z$面的压力分布差距越大. 30$^\circ$,45$^\circ$,60$^\circ$模型的流速在哈弗氏管处出现流速局部增大的情况.
图7
图7
骨陷窝方向影响下的骨单元孔隙压力$(p)$及流速$(v)$的分布图
Fig.7
The pore pressure ($p)$ and flow velocity ($v)$ distribution of osteon due to the influence of lacunae direction
由图8可以看出,骨陷窝在0$^\circ$$\sim $90$^\circ$的旋转过程中导致骨单元的模型的压力值逐渐减小. 在$y$轴方向上30$^\circ$,45$^\circ$和60$^\circ$的模型流速出现明显的不均匀分布. 渗透率的 主值方向与坐标轴方向出现偏转,即液体流动主方向($x', y'$和$z'$方向)与骨胶原纤维方 向($x,y$和$z)$ 成$\theta $角时会导致骨组织内压力和流速大小和分布规律的变化. 根据 所选择的骨陷窝($a=15 mu$m,$b=9 mu$m,$c=3.9 mu$m)及其偏转的角 度(绕$x$轴偏转0$^\circ$ $\sim$ 90$^\circ$),不同模型之间的最大的压力和流速有着较大差异,其中0$^\circ$沿$y$轴的压力比90$^\circ$增大了125${\%}$;30$^\circ$沿$y$轴的流速比90$^\circ$增大了56${\%}$. 同一模型中由于偏转角度的不同,沿不同坐标轴方向最大压力和流速也存在这较大差异,其中60$^\circ$模型$x$轴上的最大压力比$y$轴上增大了58${\%}$; 30$^\circ$模型沿$y$轴上的流速比$x$轴上增大了50${\%}$. 可见,骨陷窝角度的不同,可明显使得局部的压力和流速发生改变.
图8
图8
骨陷窝方向对骨单元孔隙压力和流速沿着不同方向的影响
Fig.8
Effects of the lacunae direction on the pore pressure and flow velocity along the different directions of osteon
4 讨论
骨组织的渗透率是骨陷窝-小管流体流动空间的渗透率,不能脱离流体流动通道独立存在,也不可简单矢量合成. 本研究首先通过估计不同形状和方向的骨陷窝中骨小管的数量,其次利用这些骨小管的三维分布以及骨组织其他微结构参数(骨陷窝密度,骨小管半径和骨细胞突触的半径等)来计算骨组织的渗透率和孔隙率等参数,最后根据计算所得的参数建立骨单元的多孔弹性有限元模型. 结果表明,由于骨陷窝形状和方向的不同对骨单元内液体压力和流速的大小和分布规律有着明显的影响.
孔隙流体压力是骨陷窝-小管系统中的一种重要负荷诱导现象,它在很大程度上干预骨细胞生长,分化和化学物质运输[7, 38]. 骨陷窝的形状和方向发生变化时,孔隙压力行为有着明显的改变. 具体来说,对于形状改变的模型,Case 3,Case 4和Case 6在$x$和$y$方向上的压力差距最大,而Case1 Case2,Case5和参考模型差距不大. 这种情况和骨陷窝形状的改变引起的渗透率的各向异性有关,可以发现,Case 3,Case 4和Case 6模型在$x$和$y$方向的渗透率差了一个数量级,而Case1 Case2,Case5和参考模型在$x$和$y$方向的渗透率在一个数量级且差距不大. 而在$z$方向上所有的模型的压力都没有明显的变化,这是因为负载诱导产生流体压力的机制使得液体通过骨陷窝-小管流入哈弗氏管,使孔隙压力得到释放,即骨单元内液体的主要流动是在骨单元外壁和哈弗氏管之间,而在$z$方向上几乎没有流动.
对于角度不同的模型,设定的是骨陷窝绕$x$轴旋转$\theta $角. 实际上,两个坐标系中$x$轴与$x'$轴是重合的,因此骨单元在$x$方向上的渗透率是相同的. 如图8(a)和图8 (c)可以看到,沿$x$轴上的压力变化远小于沿$y$轴的变化. 在$y$方向的渗透率变化大约在一个数量级左右. 如图8(c),在$y$轴方向上0$^\circ$$\sim $90$^\circ$的模型的渗透率是逐渐增大的,其压力是逐渐减小的. 在30$^\circ$,45$^\circ$和60$^\circ$时,骨中胶原纤维的方向与骨陷窝的方向不在一个方向,会导致$y$-$z$方向的渗流行为,引起流速局部增大的情况. 总体来看,压力大小的变化与渗透率有很大相关性,随着渗透率的减小,压力有增大的趋势.
虽然骨陷窝方向的改变,使得30$^\circ$,45$^\circ$和60$^\circ$模型局部的流速发生较大的变化,但就整体来看骨陷窝形状和方向的改变对流速的影响都不超过一个数量级. 这种现象可以解释为,渗 透性由1.0 $\times$ 10$^{ - 20}$ m$^{2}$降低到1.0 $\times $ 10$^{ - 21}$ m$^{2}$的过程中抑制了流体流动,但孔隙压力和压力梯度相应的增加维持了流体速度的大小,从而维持了骨陷窝-小管内正常的对流运输,因此骨内达西流速变化不大.
在典型的人类日常生理活动的载荷(1.0 $\times $ 10$^{3}\mu \varepsilon )$和频率(1 Hz)下[39],分别计算出了各向异性骨陷 窝-小管孔隙的最大孔隙压力和流速响应,压力范围从 2.6 $\times $ 10$^{5}$ Pa 到 4.8 $\times $ 10$^{5}$ Pa,流速范 围从4.7 $\times $ 10$^{ - 8}$ m/s到9.8 $\times $ 10$^{ -8}$ m/s. 压力的大小足以驱动流体跨皮质流动(大于6.0 $\times $ 10$^{3}$ Pa)[7]. 流速大小也足以直接刺激骨细胞(大于2.0 $\times$ 10$^{ - 8}$ m/s)[36]. 每一个骨单元(哈弗氏系统)都可以充当其自身的排水系统,并通过哈弗氏管释放因骨组织变形产生的流体压力. 尽管单个骨单元在整体骨组织中受到骨外膜到骨内膜产生的跨皮质压力梯度的影响,但一个哈弗氏系统产生的局部的压力梯度完全可以控制本身骨陷 窝-骨小管流体的流动. 因此,本文未考虑相邻骨单元之间的耦合程度,选用不透水的粘合线计算流体压力和速度大小是符合生理值要求的.
我们研究的一个局限性是骨小管被理想化为直管. 实际上,骨细胞突触是通过弯曲的小管从骨陷窝延伸到CUPC表面[40]. 这项研究没有考虑到骨小管弯曲的影响,因为精确计算弯曲的骨小管非常困难. 这个限制可以在模型的下一步改进中解决. 另一个局限性是本文把骨单元看成是由一个个相同的CUPC组成,但是实际上每个CUPC内的骨陷窝形状和方向会有区别,这将引起局部的液体流动的变化. 虽然理论上模型需要确定每个CUPC内骨陷窝的形状和方向,但据实验观察了解到,在骨组织的一定区域内骨陷窝的形状是类似的[11],且骨中胶原纤维的方向与骨陷窝的方向有一定的相关性[18-19]. 这样的区域大到包含一个或者几个骨单元大小[11],因此本研究的结果可用于建立骨单元的各向异性多孔弹性有限元模型. 因此,只要确定所分析的特定区域内骨陷窝形状和方向,就可以把本研究中计算的各向异性渗透率应用到有限元模型中,以求解载荷诱导的流体压力和速度场.
5 结论
本研究提出了一种根据骨陷窝形状和方向估计骨单元内骨陷窝-骨小管孔隙各向异性渗透性的方法,并通过确定的骨陷窝-小管渗透率来描述骨单元内液体各向异性的流动. 结果表明,骨陷窝的形状和方向以及骨小管的三维分布情况是决定骨陷窝-小管孔隙内液体流动的各向异性程度的重要参数. 形状不同的模型最大压力和流速的差异分别可达86${\%}$和18${\%}$;方向不同的模型最大压力和流速的差异分别可达125${\%}$和56${\%}$. 本文的研究对进一步理解骨力传导机制和一些像骨质疏松之类的骨质疾病具有重要参考价值.