引言
冲击现象广泛存在, 促使人们寻求更有效、经济、可靠的防护结构[1-3]. 当理论和数值研究受到限制, 结构冲击的实验测试则变得必不可少. 在实验设计中, 结构冲击相似理论是备受青睐的研究领域, 这主要在于通过小尺寸模型预测全尺寸结构响应的实验具有经济成本低、实验周期短、实验环境易实现等明显优势[4]. 经典的冲击相似理论已广为人知, 它通过单一的几何比例因子联系比例模型与原型的物理量, 并被广泛应用于汽车、高铁、船舶、飞机、核电站等工程结构受冲击的安全防护设计中[5-6]. 此外, Johnson[5, 7]提出著名的损伤数$Dn$, 用来测量冲击结构的损伤程度. 赵亚溥[8-9]在损伤数$Dn$的基础上, 提出了考虑结构几何的响应数$Rn$, 被广泛应用于弹塑性结构的冲击动力响应分析. 这些无量纲数的提出, 进一步扩充了经典冲击相似理论的基础. 然而, 当考虑比例模型材料的应变率敏感性效应、屈服应力、密度等不同于原型, 以及考虑重力、断裂效应时, 经典的相似理论则会发生畸变[5-6,10-14]. 因此, 有必要发展处理畸变问题的冲击相似理论.
针对材料的畸变问题, Drazetic等[15-19]使用一组基于VSG (initial impact velocity-dynamic flow stress-impact mass $G)$量纲分析的无量纲数, 在几何比例因子的基础上, 增加了速度比例因子, 并通过一种间接相似方法修正比例模型的冲击速度或冲击质量, 进而补偿材料应变率敏感性效应引起的畸变. 然而这种间接相似方法, 存在需要预先测试比例模型响应信息的困难, 因而并不实用. Oshiro和 Alves[20]进一步使用幂律形式的Norton-Hoff本构方程, 发展了一种直接相似方法, 无需测试结构响应信息即可获得修正冲击速度的比例因子, 克服了间接相似法的缺陷. Mazzariol等[21]在VSG体系中增加了结构质量的无量纲数以及密度比例因子, 并使用一种新的直接相似方法修正冲击速度, 进而补偿应变率敏感性效应以及屈服应力和密度不同时的不同材料引起的畸变. Oshiro等[22-24]对船舶碰撞与搁浅的大型结构工程冲击问题, 使用1/100的比例模型试验, 验证了VSG不同材料畸变理论的有效性以及其对复杂问题的适应能力. Mazzariol等[25-26]在VSG的基础上, 对不同材料的畸变问题, 研究了同时考虑几何畸变的相似途径. 张振华等[27-32]针对船舰结构加筋板受爆炸载荷, 研究了考虑流固耦合、应变率敏感性效应、不同材料引起的畸变问题, 通过VSG间接相似方法修正冲击速度, 验证了VSG理论对加筋板结构受爆炸冲击载荷的有效性. 姜正荣等[33-34]对单层网壳结构, 考虑了应变率敏感性效应引起的畸变以及重力引起的畸变, 并提出通过附加质量修正结构密度的缩放技术, 为大型结构的相似试验提供了新的技术手段. 魏德敏和胡晨曦[35]使用一种部分相似的技术, 发展了修正密度的方法, 结合间接相似方法改变结构质量和冲击质量, 处理应变率敏感性效应引起的畸变. 苏子星和何继业[36]基于Cowper-Symonds方程, 修正了VSG不同材料畸变问题中冲击速度的计算方法. Sadeghi等[37-41]使用一组连续介质力学的输运方程, 提出了有限相似(finite similitude)理论, 从方程分析的角度验证了VSG不同材料畸变体系的合理性, 并同时考虑了材料的应变硬化效应以及断裂的相似性问题. 王帅等[42]提出了DLV (density-length-velocity)量纲分析体系替代VSG体系, 从无量纲数、响应方程和相似分析的角度进一步扩展了应用范围, 并修正冲击速度和密度以补偿不同材料引起的畸变.
本工作采用VSG冲击畸变相似理论体系和最佳平方逼近方法, 推导了不同材料引起的畸变问题的一种直接相似方法, 研究了本构模型中材料参数对流动屈服应力动态相似关系的影响, 以期为结构冲击安全防护设计中使用比例模型试验提供一种处理畸变问题的直接相似技术.
1 直接相似方法
1.1 传统的相似方法
对于不同材料引起的畸变问题, 通常使用一组基于VSG[16,20-21,43]或DLV[42]的量纲分析体系来解决, 它们具有相同的比例因子. 在此, 本工作使用较为简洁的DLV体系简要回顾结构冲击问题的相似律. 该理论由一组基于密度($\rho $)、长度($L)$、速度($V)$为基本量的无量纲数构成, 其中几个主要的无量纲数为: 应力($\sigma$), $\varPi_{\sigma } = \rho V^{2}/\sigma $; 应变($\varepsilon$), $\varPi_{\varepsilon} = \varepsilon $; 角度($\theta $), $\varPi_{\theta } = \theta $; 应变率($\dot{{\varepsilon }})$, $\varPi_{\dot{\varepsilon}} =\dot{{\varepsilon }}L/V$; 时间($t)$, $\varPi_{t} = tV/L$; 位移($\delta $), $\varPi_{\delta } = \delta /L$; 质量($M)$, $\varPi_{M }= M/\rho L^{3}$. 与此对应, 该理论由一组基于几何比例因子$\beta = L_{m}/L_{p}$、速度比例因子$\beta_{V}= V_{m}/V_{p}$、密度比例因子$\beta_{\rho} = \rho_{m}/\rho_{p}$为基础的比例关系表达物理量的相似关系, 其中几个主要的比例因子为: 应力$\beta_\sigma =\beta_\rho \beta_V^2$; 应变$\beta_{\varepsilon}= 1$; 角度$\beta_{\theta }= 1$; 应变率$\beta_{\dot{{\varepsilon }}} =\beta_V /\beta $; 时间$\beta_{t} = \beta /\beta_{V}$; 位移$\beta_{\delta } = \beta $; 质量$\beta_{M} = \beta_{\rho}\beta^{3}$. 式中, 下标m和p分别代表比例模型和原型.
基于这组无量纲数和比例因子, 在进行比例模型试验时, 由于几何比例因子、密度比例因子是已知的, 因而应用该理论的关键技术在于通过本构方程合理地计算速度比例因子, 进而修正比例模型的冲击速度. 在VSG体系中, 通过对本构方程$\sigma_{d} =f(\dot{{\varepsilon }})$应用比例关系$\beta_\sigma =\beta_\rho \beta_V^2 $和$\beta_{\dot{{\varepsilon }}} =\beta_V /\beta$来计算速度比例因子$\beta_{V}$, 进而修正比例模型的冲击速度, 补偿不同材料引起的畸变. 需强调的是, 应变率敏感性效应畸变已包含在不同材料畸变中, 因而不再刻意区分.
式中, $\dot{{\varepsilon }}_{m}^{c}$代表速度修正后的比例模型所测得的平均应变率, $\dot{{\varepsilon }}_{m}^{nc} $代表速度未修正的比例模型所测得的平均应变率. 显然, 这种间接相似方法需要通过一个过渡模型预先测试结构响应的平均应变率信息, 作为求解$\beta_{V}$的已知条件, 因而并不实用.
为克服间接相似方法的缺陷, Oshiro和Alves[20]对应变率敏感性效应引起的畸变, 通过使用特殊形式的Norton-Hoff 幂律本构方程$\sigma_{d} =\sigma_0 (\dot{{\varepsilon }}/\dot{{\varepsilon }}_0 )^q$, 定义速度因子为
式中, $\sigma_{0}$为屈服应力, $\dot{{\varepsilon }}_0 $为$\sigma_{0}$对应的参考应变率, $q$为应变率敏感性特征参数. 显然, 该方法定义的速度因子$\beta_{V}$, 仅由几何比例因子$\beta $及材料参数$q$确定, 无需预先测试结构的任何响应信息, 是一种直接相似方法. 然而, 对于其他形式的本构方程, 不能直接获得速度比例因子, 通用性有限.
Mazzariol等[21]考虑材料应变率敏感性效应、屈服应力、密度不同引起的不同材料的畸变, 定义速度因子为
式中, $\beta_{\sigma_0} =(\sigma_0 )_{m} /(\sigma_0 )_{p}$是屈服应力比例因子, $\beta_{visco} =f_{m} (\dot{{\varepsilon }}_{m} )/f_{p}(\dot{{\varepsilon }}_{m} \beta /\beta_V)$是本构方程中应变率敏感性黏性项的比例因子. 对直接相似, 文献中针对Johnson-Cook本构模型简单设定$\dot{{\varepsilon }}=1$ s$^{-1}$ 从而简化获取结构平均应变率的间接过程. 然而, 这种对平均应变率的简单设定, 忽略了结构应变率在冲击过程中随时间和空间变化的动态特性, 因而不能反映结构冲击的动态相似性质.
1.2 直接相似方法的推导
本文对VSG体系中计算修正冲击速度或修正密度的比例因子的关键技术问题, 提出一种基于最佳平方逼近关系的直接相似法, 可适用于任何形式的应变率敏感性的本构方程$\sigma_{d} =f(\dot{{\varepsilon}})$.
在VSG相似理论下, 比例模型和原型的流动屈服应力和应变率关系为
和
当使用比例模型的流动屈服应力预测原型时, 将式(5)代入式(4)中, 预测值为
式中, $({\sigma }'_{d} )_{p} $代表通过比例模型的流动屈服应力($\sigma_{d})_{m}$所预测的原型流动屈服应力. 由于几何比例因子$\beta $和密度比例因子$\beta_{\rho }$已知, 因而$({\sigma }'_{d} )_{p}$仅取决于原型的应变率$\dot{{\varepsilon }}_{p} $和速度比例因子$\beta_{V}$.
考虑在冲击过程中, 动态屈服应力和应变率随位置和运动时间而变化. 因而, 对于冲击问题的相似性, 应包含这种动态过程的连续相似. 这就要求比例模型预测的流动屈服应力$({\sigma }'_{d} )_{p} $与原型的流动屈服应力$(\sigma_{d} )_{p} =f_{p} (\dot{{\varepsilon }}_{p})$在应变率区间上应始终重合. 显然, 对大多数由试验拟合的本构方程, 实现这种严格意义的精确重合并不现实. 对此, 可采用函数逼近的方法近似描述这个动态相似过程, 使得在一个连续的应变率区间上它们的平均误差最小. 因而可在应变率区间$[\dot{{\varepsilon }}_a ,\dot{{\varepsilon }}_b ]$上, 通过预测动态屈服应力$({\sigma }'_{d} )_{p} $与原型动态屈服应力($\sigma_{d})_{p}$的最佳平方逼近, 来描述这种动态相似过程.
假定对一个结构冲击的缩放问题, 原型响应的应变率$\dot{{\varepsilon }}_{p}$在区间$[\dot{{\varepsilon }}_a ,\dot{{\varepsilon }}_b]$上变化, 且$\beta$和$\beta_{\rho}$是已知的, 那么对于比例模型存在一个最佳逼近$({\sigma }'_{d} )_{p}^* =f_{m} (\dot{{\varepsilon }}_{p} \beta_V^* /\beta )/\beta_\rho \beta_V^{*2}$, 使得关系$\vert \vert ({\sigma }'_{d} )_{p}^* -(\sigma_{d} )_{p} \vert \vert_2 =\mathop {\min }\limits_{\beta_V \in {\mathbb{R}}} \vert \vert ({\sigma }'_{d} )_{p} -(\sigma_{d} )_{p} \vert \vert_2 $成立, 即
其中, $\beta_V^* $是使得$({\sigma }'_{d} )_{p}^* $对($\sigma_{d})_{p}$最佳逼近时的速度比例因子$\beta_{V}$, $\vert \vert \cdot \vert \vert_2 $代表2-范数, ${R}$是实数集.
对于式(7), 当$\dot{{\varepsilon }}_a $和$\dot{{\varepsilon }}_b $已知时, 可使用无约束最优化方法进行数值求解, 此时$\beta_{V}$是目标函数$\min \vert \vert \cdot \vert \vert_2 $唯一的设计变量. 为此, 合理地选择积分区间$[\dot{{\varepsilon }}_a ,\dot{{\varepsilon }}_b]$是计算$\beta_V^* $的基础. 典型的方法是将$[\dot{{\varepsilon }}_a ,\dot{{\varepsilon }}_b ]$取为原型结构真实的应变率区间, 以获得最佳逼近效果. 然而, 在比例模型试验前, 原型响应通常是未知的, 也很难通过试验来测试. 为解决预先获取原型信息的不合理性, 这里使用粗略的数量级应变率区间, 来代替原型精确的真实应变率区间. 为此, 我们分析应变率区间的选择对最佳逼近关系的影响. 假设几何比例因子为1/10, 结构原型的真实应变率区间为[0 s$^{-1}$, $2.0\times 10^{3}$ s$^{-1}$], 则结构原型应变率区间均值的量级为$1.0\times 10^{3}$ s$^{-1}$. 本构模型选用Cowper-Symonds本构, 即$\sigma_{d} =\sigma_0[1+(\dot{{\varepsilon }}/D)^{1/P}]$, 式中, $P$为应变率敏感性特征参数; $D$为材料的特征应变率参数, 通常表示为$\sigma_{d} = 2\sigma_{0}$时的应变率. 比例模型和原型选用典型的应变率敏感的软钢材料, $D = 40.4$ s$^{-1}$、$P = 5$[5]. 对式(7), 选用不同的数量级应变率区间求解$\beta_V^* $, 并使用式(6)的比例模型预测的流动屈服应力$({\sigma }'_{d} )_{p}$与原型流动屈服应力($\sigma_{d})_{p}$进行比较. 图1显示了使用不同的应变率区间得到的比例模型无量纲预测流动屈服应力$({\sigma }'_{d} )_{p} /(\sigma_0 )_{p} $对原型的动态逼近结果(图中, 原型流动屈服应力($\sigma_{d})_{p}$即是原型预测的流动屈服应力$({\sigma }'_{d} )_{p} $, 原型应变率$\dot{{\varepsilon }}_{p} $即是原型预测的应变率${\dot{{\varepsilon }}}'_{p} $, 以后对它们不做区分).
图1
图1
不同应变率区间对流动屈服应力-应变率曲线预测结果的比较
Fig.1
Comparison of the prediction results for the function curves between the flow yield stress and the strain rate curves by the different strain rate intervals
可见, 当$\dot{{\varepsilon }}_a $为0 s$^{-1}$, 且$\dot{{\varepsilon }}_b $分别为10 s$^{-1}$, 100 s$^{-1}$时, 应变率区间均值的量级分别为$5.0$ s$^{-1}$, $50$ s$^{-1}$, 此时预测结果与原型误差较为显著. 这说明, 式(7)中使用与原型数量级不一致的应变率积分区间, 不能获得最佳逼近效果. 当$\dot{{\varepsilon }}_a $为0 s$^{-1}$且$\dot{{\varepsilon }}_b $为$1.0\times10^{3}$ s$^{-1}$, $5.0\times 10^{3}$ s$^{-1}$, $1.0\times10^{4}$ s$^{-1}$时, 应变率均值的量级为$500$ s$^{-1}$, $2.5\times 10^{3}$ s$^{-1}$, $5.0\times 10^{3}$ s$^{-1}$, 此时预测结果与原型较为接近, 可近似认为得到了最佳逼近效果. 因而, $\dot{{\varepsilon }}_b $与原型应变率数量级一致时, 能够获得最佳逼近效果. 当$\dot{{\varepsilon }}_a $为$1.0\times10^{3}$ s$^{-1}$, $\dot{{\varepsilon }}_b $为$5.0\times 10^{3 }$ s$^{-1}$数量级时, 应变率区间均值的量级为$3.0\times 10^{3 }$ s$^{-1}$, 其获得的逼近效果与$\dot{{\varepsilon }}_a $为0 s$^{-1}$, $\dot{{\varepsilon }}_b $为$5.0\times 10^{3}$ s$^{-1}$时基本相同. 可见, $\dot{{\varepsilon }}_a$取值对最佳逼近效果影响不显著.
以上分析表明, 当应变率积分区间均值的数量级与结构原型相同或相近时, 可获得最佳逼近效果. 因而, 使用粗略的应变率数量级区间替代原型精确的真实应变率区间的方法是合理的. 为此, 我们对$\dot{{\varepsilon }}_a $取为0 s$^{-1}$, $\dot{{\varepsilon }}_b$取为结构原型应变率均值所在数量级, 如10 s$^{-1}$, 100 s$^{-1}$, $200$ s$^{-1}$, $500$ s$^{-1}$, 1000 s$^{-1}$, 5000 s$^{-1}$, $1.0\times10^{4}$ s$^{-1}$等. 此时, 在比例模型测试前, 一个简单粗糙的原型应变率数量级估计, 就可以使用式(7)直接求出速度比例因子. 相比文献[37]对应变率使用一个非常宽的固定窗口[0 s$^{-1}$, $1.0\times10^{4}$ s$^{-1}$]的做法, 本文提出的应变率数量级区间的方法, 明确了应变率区间数量级对最佳逼近效果的影响, 更为合理.
此外, 式(7)还可以进一步扩展. 针对文献提出的修正材料密度的方法, 可在式(7)中预先固定$\beta_{V}$, 将$\beta_{\rho }$作为未知量, 从而求出最佳逼近时的新的密度比例因子$\beta_\rho ^* $, 进而修正比例模型结构质量和冲击质量. 本文只讨论修正模型冲击速度的方法.
1.3 考虑材料参数后的直接相似方法
当使用式(7)定义的直接相似方法时, 为获得比例模型预测流动屈服应力$({\sigma}'_{d} )_{p} $与原型流动屈服应力($\sigma_{d})_{p}$的最佳逼近效果, 还需考虑具体材料参数的影响, 从而使得这种动态相似性始终存在.
下面取3种经典的材料本构模型, 来展示直接相似法在考虑材料参数后的应用过程.
(1)当使用Norton-Hoff本构, 根据式(7)得到
代入$(\sigma_0 )_{m} =\beta_{\sigma_0 } (\sigma_0 )_{p} $, $(\dot{{\varepsilon }}_0 )_{m} =\beta_{\dot{{\varepsilon }}_0 } (\dot{{\varepsilon }}_0 )_{p} $, $q_{m}= \beta_{q}q_{p}$, 上式变为
此时, 除了比例因子$\beta $, 最佳逼近关系受$\beta_{q}$, $\beta_{\dot{{\varepsilon }}_0}$和$\beta_{\sigma_0 } /\beta_\rho $的影响.
为进一步导出考虑材料参数后的最佳逼近条件, 假设$\beta_{q }= 1$, 由式(9)得到
显然, 上式最佳逼近关系成立的条件是$\beta_V^* =(\beta_{\sigma_0 } /\beta_\rho )^{1/(2-q)}(\beta \beta_{\dot{{\varepsilon }}_0 } )^{q/(q-2)}$, 此时比例模型预测流动屈服应力与原型流动屈服应力随应变率的变化总是相等的, 是一种理想的动态相似情况.
当比例模型与原型材料相同, 则比例模型材料应变率敏感性特征参数$q$、参考应变率$\dot{{\varepsilon }}_0$、屈服应力$\sigma_{0}$、密度$\rho $与原型相同. 对相同材料, $\beta_V^* $退化为$\beta_V^* =\beta ^{q/(q-2)}$, 即式(2)给出的速度修正因子. 此时, 无论$q$, $\dot{{\varepsilon }}_0 $, $\sigma_{0}$, $\rho $取何值, 比例模型与原型始终是理想动态相似的.
当比例模型与原型材料不同, 则比例模型材料的应变率敏感性特征参数$q$、参考应变率$\dot{{\varepsilon }}_0$、屈服应力$\sigma_{0}$、密度$\rho $与原型不同. 对不同材料, 式(10)分析表明, 比例模型材料的参考应变率$\dot{{\varepsilon }}_0 $、屈服应力$\sigma_{0}$、密度$\rho$取值对最佳逼近效果没有影响, 而应变率敏感性特征参数$q$具有主导作用. 当比例模型$q$取值越接近原型, 最佳逼近效果越接近理想相似情况, 对原型逼近程度越好.
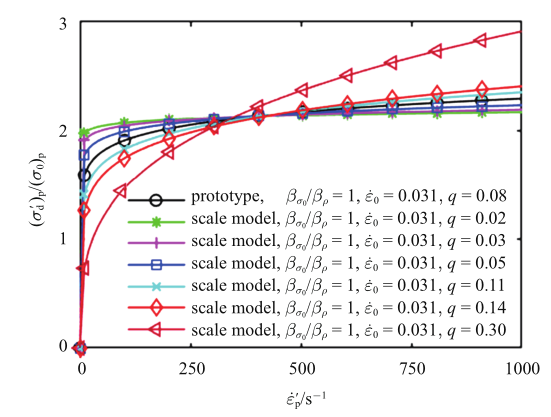
对于比例模型材料参数$q$与原型不同的情况, 我们通过具体例子进一步分析. 对原型, 根据参考文献[22]给定的1008软钢的Norton-Hoff本构, 取$\dot{{\varepsilon }}_0=0.031$ s$^{-1}$, $q = 0.08$. 对比例模型, $\dot{{\varepsilon }}_0 =0.031$ s$^{-1}$, $q$为0.02$\sim$0.30. 此外, 假定$\beta_{\sigma_0 } /\beta_\rho =1$, $\beta = 1/10$, 应变率区间为0$\sim$1000 s$^{-1}$, 从而使用式(9)求解$\beta_V^* $. 图2显示了比例模型材料参数$q$的变化对无量纲预测流动屈服应力$({\sigma }'_{d} )_{p}/(\sigma_0 )_{p} $与预测应变率${\dot{{\varepsilon }}}'_{p} $关系曲线的影响.
图2
图2
材料参数$q$对预测流动屈服应力-预测应变率曲线的影响(Norton-Hoff本构)
Fig.2
The influence of material parameter $q$ for the function curves between the flow yield stress and the strain rate curves (Norton-Hoff equation)
从图2可见, 当比例模型参数$q$与原型接近时, 逼近效果最佳, 这与式(10)的分析结果完全一致. 当比例模型与原型参数$q$相差较大时, 比例模型预测流动屈服应力与原型流动屈服应力的误差明显增大. 可见, 对使用不同材料的缩放试验, 选取参数$q$与原型接近的材料是缩放试验成功进行的必要条件, 这意味着比例模型需选用与原型具有相同应变率硬化能力的材料.
(2) 当使用Cowper-Symonds本构, 根据式(7)\lb 得到
代入$(\sigma_0 )_{m} =\beta_{\sigma_0 } (\sigma_0 )_{p} $, $D_{m}= \beta_{D}D_{p}$, $P_{m}= \beta_{P}P_{p}$, 上式变为
此时, 除比例因子$\beta $, 最佳逼近关系受$\beta_{P}$, $\beta_{D}$和$\beta_{\sigma_0 } /\beta_\rho $的影响.
为进一步从材料角度定义式(12)的动态相似关系, 我们分析材料应变率敏感性特征参数$P$、特征应变率$D$ (类似于Norton-Hoff中参考应变率$\dot{{\varepsilon }}_0 )$、屈服应力$\sigma $、密度$\rho $对$({\sigma }'_{d} )_{p} $和$(\sigma_{d} )_{p} $动态逼近程度的影响.
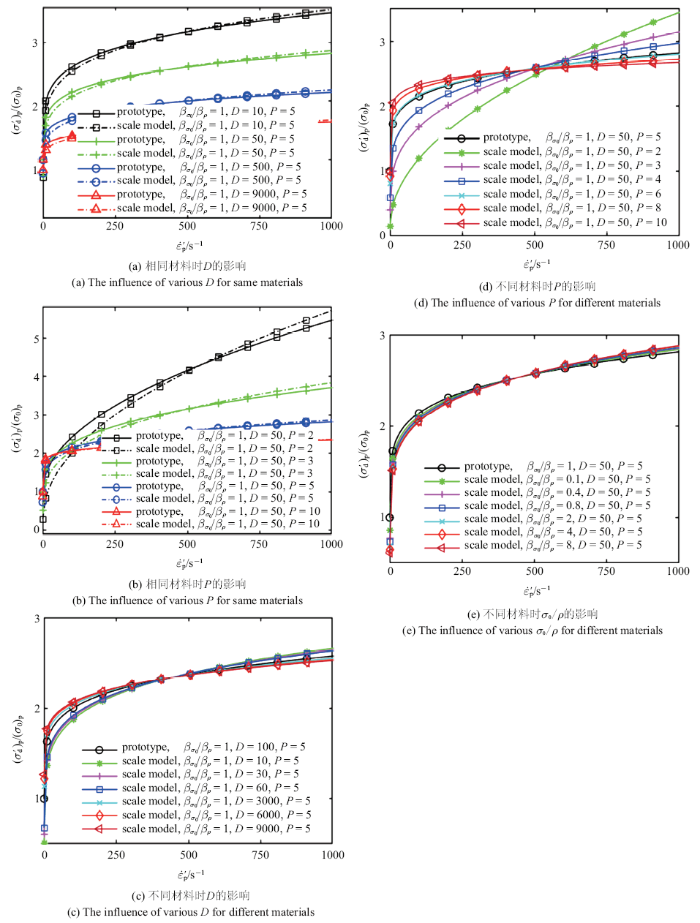
对比例模型和原型, 根据参考文献[5]给定的几种典型金属材料的Cowper-Symonds本构参数, 分别选取参数范围: $D$从10$\sim$9000, $P$从2$\sim$10, $\beta_{\sigma_0 } /\beta_\rho $从0.2$\sim$8. 几何比例因子$\beta $为1/10, 应变率区间为0$\sim$1000 s$^{-1}$, 从而使用式(12)求解$\beta_V^* $. 图3显示了材料参数$D$, $P$, $\sigma_0 $, $\rho $的变化对无量纲预测流动屈服应力$({\sigma}'_{d} )_{p} /(\sigma_0 )_{p} $与预测应变率${\dot{{\varepsilon }}}'_{p} $关系曲线的影响.
从图3(a)和图3(b)可见, 当比例模型与原型使用相同材料, 无论特征应变率$D$、应变率敏感性特征参数$P$的取值如何变化, 比例模型预测流动屈服应力与原型流动屈服应力都显现出良好的一致性. 此外, 从图3(a)还可看到, 当$D$取值由小变大, 流动屈服应力对应变率越不敏感, 而动态逼近效果基本不受影响; 从图3(b)还可看到, 当$P$取值越大, 流动屈服应力对应变率越不敏感, 动态逼近效果越好. 从图3(c)和图3(d)可见, 当比例模型与原型使用不同材料时, 不同的特征应变率$D$均能获得良好的动态逼近效果, 而不同的应变率敏感性特征参数$P$的动态逼近效果差异显著. 当比例模型与原型参数$P$相差较大时, 预测流动屈服应力与原型流动屈服应力两者误差明显增大. 此外, 当比例模型参数$P$大于原型, 更容易获得最佳逼近效果. 从图3(e)可见, 比例模型材料参数$\sigma_0$, $\rho$的变化几乎不影响比例模型与原型的动态相似性. 以上分析表明, 对于Cowper-Symonds本构, 当比例模型选用与原型应变率硬化能力相同的材料时, 逼近效果最佳. 此时, 应变率敏感性特征参数$P$起主导作用.
图3
图3
材料参数对预测流动屈服应力-预测应变率曲线的影响 (Cowper-Symonds本构)
Fig.3
The influence of material parameters for the function curves between the flow yield stress and the strain rate curves (Cowper-Symonds equation)
(3) 当使用简化后的Johnson-Cook本构模型(忽略应变硬化效应和温度效应), 即$\sigma _{d} =\sigma_0 [1+C\ln (\dot{{\varepsilon }}/\dot{{\varepsilon }}_0 )]$, 式中, $C$为应变率敏感性特征参数、$\dot{{\varepsilon }}_0 $为参考应变率参数, 通常设定为1 s$^{-1}$. 根据式(7)得到
代入$(\sigma_0 )_{m} =\beta_{\sigma_0 } (\sigma_0 )_{p} $, $C_{m} = \beta_{C }C_{p}$, $(\dot{{\varepsilon }}_0 )_{m} =\beta_{\dot{{\varepsilon }}_0 }(\dot{{\varepsilon }}_0 )_{p} $, 上式变为
此时, 除比例因子$\beta$, 最佳逼近关系受$\beta_{C}$, $\beta_{\dot{\varepsilon}_0}$, $\beta_{\sigma_0}/\beta_\rho$的影响. 由于Johnson-Cook本构中参考应变率一般取为1 s$^{-1}$, 因而得到$\beta_{\dot{{\varepsilon }}_0} =1$. 此时, 只需关注变量$\beta_{C}$和$\beta_{\sigma_0} /\beta_\rho $即可. 对此, 我们分析应变率敏感性特征参数$C$、 屈服应力$\sigma_{0}$、 密度$\rho$对$({\sigma }'_{d} )_{p}$和$(\sigma_{d} )_{p} $动态逼近程度的影响.
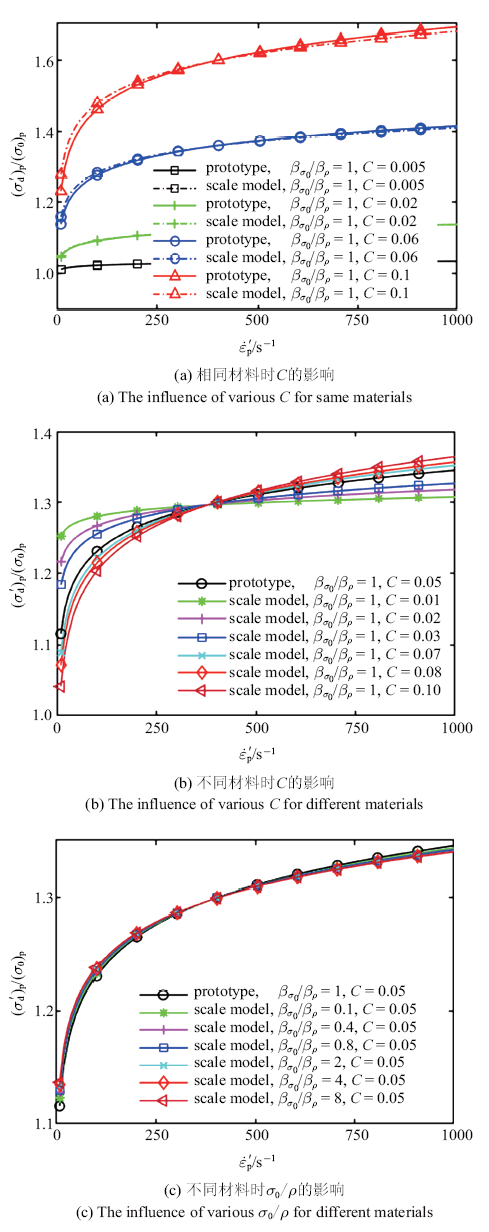
对比例模型和原型, 根据参考文献[21]给定的几种典型金属材料的Johnson-Cook本构参数, 分别选取参数范围为: $C$为0.001$\sim$0.1, $\beta_{\sigma_0 } /\beta_\rho$为0.2$\sim$8. 几何比例因子$\beta $为1/10, 应变率区间为0$\sim$1000 s$^{-1}$, 从而使用式(14)求解$\beta_V^* $. 图4显示了材料参数$C$, $\sigma/\rho$的变化对无量纲预测流动屈服应力$({\sigma }'_{d} )_{p} /(\sigma_0 )_{p} $与预测应变率${\dot{{\varepsilon }}}'_{p}$关系曲线的影响.
图4
图4
材料参数对预测流动屈服应力-预测应变率曲线的影响 (Johnson-Cook本构)
Fig.4
The influence of material parameters for the function curves between the flow yield stress and the strain rate curves (Johnson-Cook equation)
从图4(a)可见, 当比例模型与原型使用相同材料, 无论应变率敏感性特征参数$C$取值如何变化, 比例模型预测流动屈服应力与原型流动屈服应力都显现出良好的一致性. 从图4(b)可见, 当比例模型与原型使用不同材料, 比例模型不同的应变率敏感性特征参数$C$的取值对原型的动态逼近效果差异显著. 当二者相差较大时, 预测误差明显增大. 此外, 当比例模型参数$C$的值大于原型时, 更容易获得最佳逼近. 从图4(c)可见, 材料参数$\sigma_0$、$\rho $的变化几乎不影响比例模型与原型的动态相似性. 以上分析表明, 当比例模型选用与原型应变率硬化能力相同的材料时, 逼近效果最佳, 此时参数$C$起主导作用.
以上对3种经典材料本构模型的定性分析表明, 比例模型参考应变率、屈服应力、密度这些材料参数的变化对式(7)定义的动态最佳逼近相似关系影响很小, 而应变率敏感性特征参数(对Norton-Hoff为$q$, 对Cowper-Symonds为$P$, 对Johnson-Cook为$C$)影响较大. 比例模型的应变率敏感性特征参数越接近原型, 即两者具有相同的应变率硬化能力, 越容易获得动态最佳逼近效果.
更一般地, 对任何形式的本构方程$\sigma_{d} =f(\dot{{\varepsilon }})$, 假定$X$为其应变率敏感性特征参数, 那么式(7)在考虑这个主导性的材料因素后, 可重新定义为
式中, $\beta_X^* $是使得$({\sigma }'_{d} )_{p}^* $对($\sigma_{d})_{p}$最佳逼近时应变率敏感性特征参数的比例因子$\beta_{X}$. 式(15)表明, 通过调整比例模型的冲击速度$V_{m}$(亦可调整比例模型的密度$\rho_{m}$)和比例模型的应变率敏感性特征参数$X_{m}$, 可获得最佳的动态逼近效果. 在实际操作中, 对一个特定的材料, 调整其应变率敏感性特征参数并不现实. 根据前面的分析可知, 通过选择应变率敏感性与原型接近的其他类型的材料, 作为调整比例模型应变率敏感性特征参数的途径, 来获得最佳的动态逼近效果.
1.4 方法对比
为验证直接相似方法的有效性, 对比使用不同方法时比例模型对原型流动屈服应力的预测精度. 选用几何比例因子1/10, 应变率数量级区间0$\sim$2000 s$^{-1}$. 比例模型与原型材料相同, 均为Cowper-Symonds本构, 且$D = 40$ s$^{-1}$, $P= 5$. 对Oshiro和Alves的方法(式(2)), 根据文献[20], 给出$\beta_{V} = \beta^{q/(q-2)}= (1/10)^{0.077/(0.077-2)}= 1.097$. 对Mazzariol等[21]的方法, 采用Cowper-Symonds本构且代入$\dot{{\varepsilon }}_{m} =1$, 由式(3)计算得到$\beta_{V}= 1.067$. 对本文的最佳逼近直接相似法, 根据式(7)得到$\beta_{V}= 1.1904$. 此外, 由于$\beta_{P}= 1$, 根据1.3节分析可知, 此时动态逼近效果最佳, 因而不需要考虑调整比例模型的应变率敏感性特征参数. 不同方法下, 比例模型预测的无量纲动态流动屈服应力-应变率曲线与原型的比较, 如图5所示.
图5
图5
不同方法对流动屈服应力-应变率曲线预测结果的比较
Fig.5
Comparison of the prediction results for the function curves between the flow yield stress and the strain rate curves by different scaling methods
从图5可见, 当预测应变率${\dot{{\varepsilon }}}'_{p} =1010$ s$^{-1}$时, 对无量纲预测流动屈服应力$({\sigma }'_{d} )_{p} /(\sigma_0 )_{p} $, 原型为2.91. Oshiro和Alves的方法预测结果为3.39, 误差达到16.49 ${\%}$. Mazzariol等[21] 的方法预测结果为3.57, 误差达到24.68 ${\%}$. 本文的最佳逼近直接相似法预测结果为2.92, 误差仅为0.34 ${\%}$. 可见, 本文的直接相似法较Oshiro和Alves[30]的方法以及Mazzariol等[21]的方法, 预测精度有很大的提高, 准确预测了Cowper-Symonds本构下原型的流动屈服应力.
2 数值算例验证
2.1 数值模型
图6
图6
折板结构受轴向质量冲击 (a)运动第一阶段, (b)运动第二阶段
Fig.6
Crooked plates under axial impact. (a) First phase of motion, (b) second phase of motion
Tam和Calladine[44]对第一阶段的运动进行了分析, 给出结构的运动方程为
其中, $\gamma = (3N_{p}/Lm)^{1/2}$, $N_{p}= \sigma_{d}A$为半板的轴向力, $A = BH$是板的截面积, $w_{0 }=L\sin\theta_{0}$是初始水平位移, $\sigma_{d}$是使用Cowper--Symonds本构方程得到的流动屈服应力. 在这个阶段, 应变率被简化为$V_0/L$, 横向位移为$w_{1}=w_{0}\cos(\gamma t$), 当转角较小时, $\sin\theta = w/L\to \theta \approx w/L$, 因而该阶段的转角和角速度分别为
当轴向压缩$\dot{{c}}=0$时, 第一阶段的运动停止. 根据式(16)可求得第一阶段的运动时间$\tau_{1}$, 根据式(17)和式(18)可分别求出第一阶段的最终转角$\theta_1 (\tau_1)$和$\dot{{\theta }}_1 (\tau_1 )$, 它们可被作为第二阶段运动的初始条件.
Zhang 和 Yu[45]给出了第二阶段的运动方程
式中, $M_{1}$和$M_{2}$是塑性铰 1和塑性铰2处的弯矩, 当使用Cowper-Symonds本构方程时, 分别为
当$\dot{{\theta }}=0$, 此阶段运动结束. 结合式(19) $\sim\!$式(21), 可用数值方法求出第二阶段的转角$\theta_{2}$和运动时间$\tau_{2}$.
2.2 结果分析
对折板结构简单的量纲分析, 输入参数为: 半长$L$、厚度$H$、宽度$B$、初始夹角$\theta_{0}$; 冲击质量$G$、冲击速度$V_0$; 密度$\rho $、流动屈服应力$\sigma_{d}$. 输出参数选为: 时间$t$、转角$\theta$. 当使用$\rho$, $L$, $V_0$为基本量, 输入和输出参数的无量纲数为$H/L$, $B/L$, $\theta_{0}$, $G/\rho L^{3}$, $\rho V_0^2 /\sigma_{d}$, $tV/L$, $\theta $, 这与1.1节中给出的DLV无量纲数是一致的. 因而, 可使用1.1节中的比例关系对折板结构进行缩放模型试验.
假定原型结构, $L_{p} = 0.025$ m, $H_{p} = 0.001 6$ m, $B_{p }= 0.051$ m, ($\theta_{0})_{p} = 1.15^\circ$, $G_{p} = 4.55$ kg, ($V_0)_{p} = 7.33$ m/s. 对比例模型, $L_{m}$, $H_{m}$, $B_{m}$, ($\theta_{0})_{m}$, $G_{m}$, ($V_0)_{m}$分别按照1.1节的比例关系进行缩放; 其中, $\beta $分别取1/4, 1/10, 1/20, 1/100四种工况, $\beta_{\rho }$根据具体材料得到, $\beta_{V}$由式(7)计算得到. 结构原型的真实应变率区间为$(\dot{{\varepsilon }}_a)_{p} =0$ s$^{-1}$, $(\dot{{\varepsilon }}_b )_{p} =(V_0 )_{p} /2L_{p} =146.6$ s$^{-1}$, 可得真实应变率区间均值为73.3 s$^{-1}$. 为验证直接相似方法的有效性, 粗略的应变率区间取为[0 s$^{-1}$, 200 s$^{-1}$], 其区间均值为100 s$^{-1}$, 与真实区间均值量级一致, 据此可使用式(7)计算速度比例因子$\beta_{V}$. 为验证材料应变率敏感性效应引起的畸变, 比例模型和原型均选用典型的应变率敏感的软钢. 为验证比例模型材料不同于原型引起的畸变, 原型选用典型的应变率敏感的软钢, 比例模型选用典型的应变率不敏感的铝合金材料. 两种材料的参数如表1所示. 根据1.3节的分析, 最优比例模型材料应取参数$P$与原型较为接近的材料, 显然比例模型无论选用软钢还是铝合金材料, 都是合理的. 对不同比例的模型, 计算得到的$\beta_{V}$如表2所示. 数值计算得到的转角时间曲线, 如图7所示.
表2 不同比例折板结构模型的速度因子
Table 2
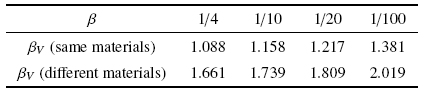 |
图7
图7
不同比例的折板结构转角-时间曲线
Fig.7
Evolution of the rotation with movement time for the various geometric crooked plates
从图7(a)和图7(b)可以看出, 当比例模型使用与原型相同的材料还是不同的材料, 折板结构的"时间转角"响应与原型明显不同; 当几何比例因子从1/4 缩放到 1/100时, 两者的"时间-转角"响应差别明显增大. 从图7(c)和图7(d)可以看出, 当使用时间、转角的无量纲数$tV_0/L$、$\theta$校正有量纲的结构动态响应后, 无论比例模型使用与原型相同的应变率敏感的软钢材料, 还是使用与原型不同的应变率不敏感的铝合金材料, 都显示与原型近乎精确的重合. 此外, 当几何比例从1/4缩放到1/100时, 这种动态响应的相似关系仍然是较为精确的. 以上分析表明, 使用本文提出的直接相似方法进行材料畸变问题的比例模型试验时, 能够准确预测结构原型在冲击载荷下的动态响应.
3 结论
基于VSG结构冲击相似理论, 提出了比例模型材料应变率敏感性效应、屈服应力、密度不同于原型引起的畸变问题的一种直接相似方法. 与传统的相似方法相比, 该方法不需要预先测试结构响应的信息, 适用于不同形式的本构方程, 重点强调应变率区间上材料流动屈服应力-应变率曲线的动态相似关系以及材料参数对这种动态相似关系的影响.
首先, 针对传统相似方法存在的缺陷, 提出了基于最佳平方逼近的直接相似方法, 建立了应变率区间上比例模型预测的流动屈服应力与原型流动屈服应力之间的动态相似关系, 并使用结构原型的应变率数量级的积分区间替代真实应变率积分区间, 直接获得了修正冲击速度的速度比例因子或修正密度的密度比例因子.
其次, 基于Norton-Hoff、Cowper-Symonds和Johnson-Cook三种经典的材料本构模型, 定性地研究了应变率敏感性特征参数以及参考应变率、屈服应力、密度的变化对动态相似性的影响. 分析表明, 动态相似关系最佳逼近效果主要受材料应变率敏感性特征参数的控制, 而参考应变率、屈服应力、密度的影响不大. 比例模型选择应变率敏感性特征参数与原型接近的材料, 可获得最佳动态逼近效果. 在此基础上, 进一步定义了同时调整材料应变率敏感性特征参数及调整冲击速度(或调整密度)的直接相似方法.
最后, 基于Cowper-Symonds本构模型, 比较了本文提出的最佳逼近直接相似方法和传统直接相似方法的预测精度, 并使用受集中质量冲击的折板结构, 进一步验证了本文提出的直接相似方法的优势. 结果表明, 传统的直接相似方法对流动屈服应力预测误差较大, 而本文提出的直接相似方法预测精度较高. 对于应变率敏感性效应、屈服应力、密度不同引起的畸变问题, 本文提出的直接相似方法, 即便对1/100的折板结构比例模型, 仍能够准确预测原型的动态响应.