引言
碳纤维增强聚合物基(carbon fiber reinforced polymer, CFRP)复合材料, 简称碳纤维复合材料, 具有密度低、比刚度高、比强度高、可设计性强等优点, 能够很好地实现结构的轻量化和高性能设计[1 ] . 作为一种新型轻质复合材料, 碳纤维复合材料因其优异的力学性能在航空航天、汽车、船舶等行业得到了广泛的应用[2 -3 ] . 平纹机织CFRP的制备过程包括编织、铺层、浸润和固化等, 得到的材料在结构上具有多尺度特征. 在CFRP的制备过程中, 由于存储条件和组成相成分、批次的不同导致组成相材料性能有所差异, 同时由于织物和预浸织布的生产、存储和搬运等过程导致纺织结构的变动. 这种材料和结构的不确定性反映到CFRP性质上表现为各尺度力学性能均有一定的随机性, 并最终影响材料的宏观性能[4 -7 ] . 因此, 有必要发展可靠的CFRP随机力学性能预测方法, 充分考虑各尺度材料和结构参数的不确定性, 研究其对材料宏观力学性能预测结果的影响作用.
为了实现对考虑随机性的复合材料力学性能的准确预测, 国内外学者开展了广泛的研究工作. 与有限元技术相结合的计算细观力学方法可以在各个尺度上建立考虑随机性的精细仿真模型来进行力学性能预测[8 -11 ] . 在纤维束尺度上, 目前研究主要是通过纤维角度和位移等参数的扰动来生成满足给定参数组合和约束条件下不规则排列结构. Zhu等[12 ] 提出了基于序列随机扰动算法生成纤维随机分布结构, 并基于有限元模型研究了纤维随机分布对纤维束力学性能的影响. 类似的研究还包括Yang等[13 ] 提出的随机序列展开方法, Zhang等[14 ] 提出的结合随机分布和完全弹性碰撞的生成算法. 在介观尺度上, 主要是基于图像分析与几何参数统计学描述方法相结合的方法生成具有结构随机性的代表性体积单元(representative volume element, RVE)进行仿真分析. Bale等[15 ] 基于微计算机断层扫描技术得到三维图像并对纤维束位置和形状进行了统计学描述. Blacklock等[16 ] 则在此基础上重构了具有随机性的RVE模型. Zhu等[17 ] 则进一步考虑了参数之间的相关性, 提出了基于相关性混合高斯随机序列的平纹机织CFRP的RVE重构算法.
基于计算细观力学的方法本质上是建立多个能够满足统计学表征的有限元模型并统计仿真分析的结果, 因此计算代价过高. 而解析细观力学方法由于具有较高的计算效率, 在进行考虑不确定性的预测研究时具有很大的优势. Chakraborty等[18 ] 采用多项式相关函数展开实现了复合材料层合板的随机自由振动分析. 考虑到微观结构的不确定性, 随机有限元[19 ] 被采用进行有效的预测. Cui等[20 ] 采用Copula函数表征复合材料中的纤维铺设角度和材料参数之间的相关性, 并基于摄动法进行不确定性分析. Mehrez等[21 ] 提出了基于混沌多项式展开(polynomial chaos expansion, PCE)的层级式传递方法得到宏观材料力学性能的不确定性. Xu等[22 ] 则在层级传递的过程中进一步考虑了分布的真实形式和分布之间的高维相关性, 并应用于三维正交机织复合材料的力学性能预测中.
现有的面向平纹机织CFRP的研究主要存在以下几个问题: 一是所考虑的随机参数不够全面, 大多研究仅考虑部分尺度的随机参数. 且采用的不确定性传递方法大多具有局限性: 随机有限元法, 作为一种嵌入式的不确定性算法, 对问题不具备很好的适应性; 摄动法则对概率分布形式具有要求; 二是在力学性能预测中对随机参数之间的相关性考虑不够充分. 针对以上这些问题, 本文提出一种基于PCE和Vine Copula的平纹机织CFRP随机力学性能预测方法, 该方法考虑了微观和介观尺度中不确定性材料、结构参数, 基于自下而上层级传递的策略逐层研究平纹机织CFRP的各尺度力学性能参数的不确定性. 所采用的非嵌入式PCE方法能够高效准确地实现不确定性地传递. 此外, Vine Copula函数能准确构造相关随机参数之间的高维联合概率分布, 从而有效掌握相关性对性能响应的影响, 提高平纹机织CFRP力学性能参数预测的精度和可靠性.
1 确定性模型构建
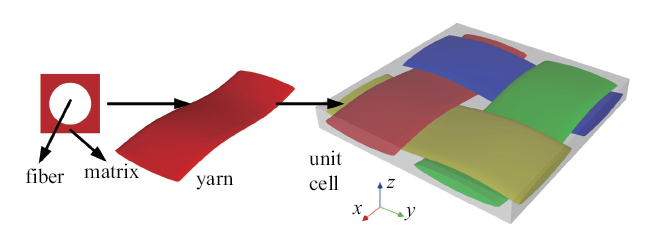
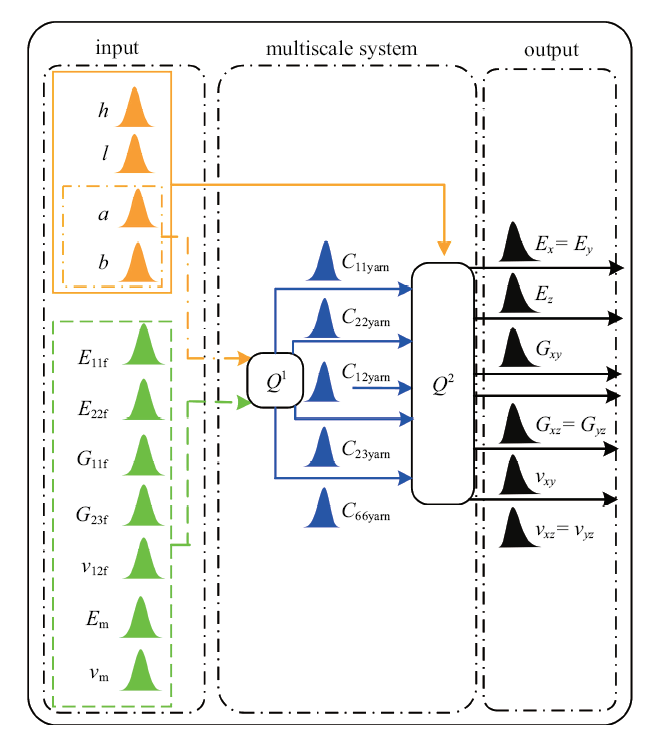
采用解析细观力学方法实现平纹机织 CFRP 的多尺度确定性随机弹性力学性能预测, 该方法能充分考虑影响平纹机织 CFRP 力学性能的因素, 包括组分材料的力学性能、 各尺度的几何参数、 体积分数等[23 ] . 尺度包括纤维丝尺度(微观尺度)、 纤维束尺度(介观尺度)和单胞尺度(宏观尺度), 如图1 所示. 该方法基于连续介质力学及均匀化理论, 采用自下而上多尺度式串行的策略逐级预测力学性能.
图1
图1
平纹机织CFRP多尺度特征
Fig.1
Multiscale characteristics of plain woven CFRP
1.1 纤维束模型
平纹机织CFRP中, 每一根浸润过的纤维束都包含了嵌入在基体中的许多单向纤维, 浸润纤维束被认为是单向复合材料. 若纤维束的纤维丝体积分数为$V_{f}$, 则力学性能可由下述Chamis方程得到[24 ]
(1) $\left. \begin{array}{ll} V_{m} =1-V_{f} \\ E_{11} =E_{11f} V_{f} +E_{m} V_{m} \\ E_{22} ={E_{m} } \Big/ {\left[ {1-\sqrt {V_{f} } \left( {1-E_{m} /E_{22f} } \right)} \right]} \\ G_{12} ={G_{m} } \Big/ {\left[ {1-\sqrt {V_{f} } \left( {1-G_{m} /G_{12f} } \right)} \right]} \\ G_{23} ={G_{m} } \Big/ {\left[ {1-\sqrt {V_{f} } \left( {1-G_{m} /G_{23f} } \right)} \right]} \\ v_{12} =v_{12f} V_{f} +v_{m} V_{m},\ v_{23} ={E_{22} } / {\left( {2G_{23} } \right)}-1\end{array} \right\}$
式中, 下标f和m分别表示纤维丝和基体, $V$表示体积分数, $E$表示弹性模量, $G$表示剪切模量, $u$表示泊松比.
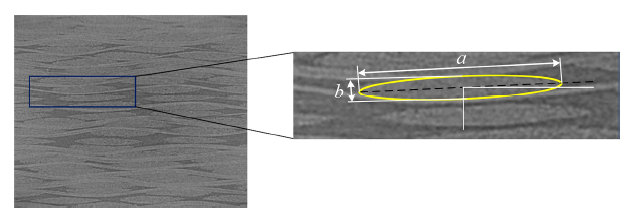
(2) $V_{f} ={S_{f} } / {\left( {\pi ab/4} \right)},\ \ S_{f} =N_{fiber} \pi d^2/4$
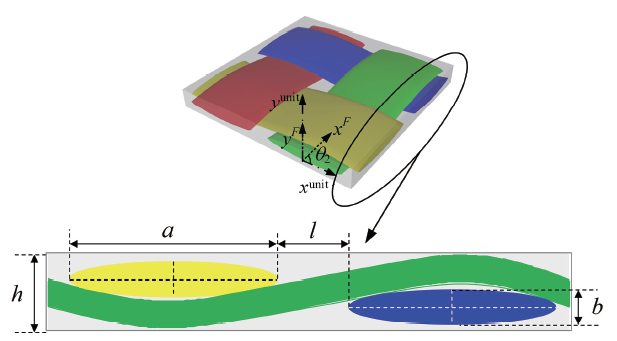
其中, $S_{f}$表示纤维束中纤维丝的总截面面积, $d$表示纤维丝直径, $N_{fiber}$表示纤维束中纤维丝数量, $a$和$b$分别表示纤维束的长轴和短轴长度, 如图2 所示.
图2
图2
单胞截面
Fig.2
Cross section of unit cell
由于纤维束通常被假设为横向各向同性的, 故其刚度矩阵可以定义为
(3) $\begin{eqnarray} \label{eq3} C=\left[ \begin{array}{c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c@{\ \ \ }c} {C_{11} } & {C_{12} } & {C_{12} } & 0 & 0 & 0\\ {C_{12} } & {C_{22} } & {C_{23} } & 0 & 0 & 0\\ {C_{12} } & {C_{23} } & {C_{22} } & 0 & 0 & 0\\ 0 & 0 & 0 & {\left( {C_{22} -C_{23} } \right)/2} & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{66} } & 0\\ 0 & 0 & 0 &0 & 0 & {C_{66} } \\ \end{array}\right] \end{eqnarray}$
(4a) $\left. {\begin{array}{l} C_{11} =\left( {1-v_{23}^2 } \right)E_{11} /\varDelta \\ C_{12} =C_{13} =v_{12} \left( {1+v_{23} } \right)E_{22} /\varDelta \\ C_{23} =\left( {v_{23} +v_{12}^2 E_{22} /E_{11} } \right)E_{22} /\varDelta \\ C_{22} =C_{33} =\left( {1-v_{12}^2 E_{22} /E_{11} } \right)E_{22} /\varDelta \\ \end{array}} \right\}$
(4b) $\left. {\begin{array}{l} C_{44} =G_{23} =E_{22} \big/\left[ {2\left( {1+v_{23} } \right)} \right] \\ C_{55} =C_{66} =G_{12} \\ \varDelta = {\left( {1+v_{23} } \right)\left( {1-v_{23} -2v_{12}^2 } \right)\dfrac{E_{22} }{E_{11} }} \\ \end{array}} \right\}$
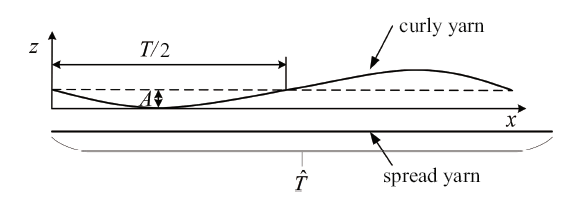
由于平纹机织CFRP的纤维束存在卷曲变形, 对于卷曲的纤维束, 如图3 所示.
图3
图3
纤维束的正弦函数表达
Fig.3
Sinusoidal expression for yarn
(5) $\hat{{x}}=A\sin \left( {{2\pi x} / T} \right)$
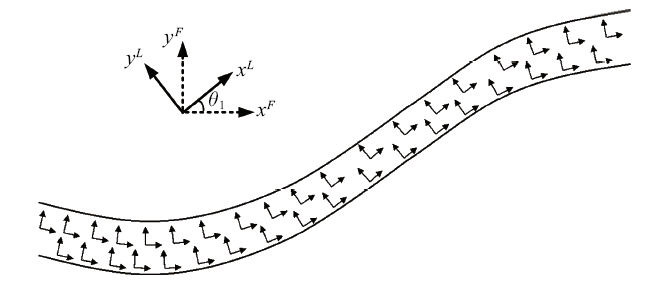
式中, $T$表示周期, $A$表示幅度. 综合图2 和图3 可以得到$T=2(a+l)$, $A=(h-b)/2$. 将卷曲纤维束划分为无数的微段, 各微段沿纤维主方向均可视作单向纤维复合材料, 如图4 所示, $x^{L}$方向即为主方向.
图4
图4
纤维束材料主方向
Fig.4
Material principal orientation in yarn
定义第$N$微段在其局部坐标系下的刚度矩阵\lb 为$C_N^L$
(6) $C_N^F =H_N C_N^L H_N^{T}$
式中, 上标$L$表示微段纤维局部坐标系($x^{L}$, $y^{L})$, 上标$F$表示纤维束坐标系($x^{F}$, $y^{F})$, 上标T表示转置, $H$为转换矩阵, 其求解公式为
(7) $\begin{eqnarray} \label{eq7} H_N^{T} =\left[ {{\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} {h_1^2 } & 0 & {h_2^2 } & 0 & {2h_1 h_2 } & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ {h_2^2 } & 0 & {h_1^2 } & 0 & {-2h_1 h_2 } & 0 \\ 0 & 0 & 0 & {h_1 } & 0 & {h_2 } \\ {-h_1 h_2 } & 0 & {h_1 h_2 } & 0 & {h_1^2 -h_2^2 } & 0 \\ 0 & 0 & 0 & {h_2 } & 0 & {h_1 } \\ \end{array} }} \right] \end{eqnarray}$
(8) $\begin{eqnarray} \label{eq8} \left. {\begin{array}{l} h_1 =1 \big/ {\sqrt {1+\tan ^2 {\theta _1 } } } \\ h_2 ={\tan {\theta _1 }} \big/ {\sqrt {1+\tan ^2 {\theta _1 }} } \\ \end{array}} \right\} \end{eqnarray}$
(9) $\tan {\theta _1 }={2\pi A} / {T \cos \left( {{2\pi x} / T} \right)}$
式中$\theta _1 $代表微段纤维局部坐标系与纤维束坐标系的夹角, 如图4 所示. 在纤维束坐标系下, 纤维束的等效刚度矩阵可通过对各微段沿$x$方向进行积分来\lb 获得
(10) $C^F=1 / T\left( {\int_0^{T} {C_N^F {d}x} } \right)$
1.2 单胞模型
对于CFRP, 在宏观尺度上选取单胞来表征其宏观性能. 由于平面机织CFRP是由经纱和纬纱机织而成, 单胞整体的刚度矩阵可根据各纤维束的平均性能计算得到, 由于经纱和纬纱的方向不同, 需通过坐标转换, 将纤维束刚度矩阵转化为单胞坐标系下的纤维束刚度矩阵
(11) $C^{unit}=H^{unit}C^FH^{unit}$
(12) $\begin{eqnarray} \label{eq12} H^{unit}=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} {h_3^2 } & {h_4^2 } & 0 & 0 & 0 & {2h_3 h_4 } \\ {h_4^2 } & {h_3^2 } & 0 & 0 & 0 & {-2h_3 h_4 } \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {h_3 } & {-h_4 } & 0 \\ 0 & 0 & 0 & {h_4 } & {h_3 } & 0 \\ {-h_3 h_4 } & {h_3 h_4 } & 0 & 0 & 0 & {h_3^2 -h_4^2 } \\ \end{array} }} \right] \end{eqnarray}$
(13) $\begin{eqnarray} \label{eq13} \left. {\begin{array}{l} h_3 =\cos {\theta _2 } \\ h_4 =\sin {\theta _2 } \\ \end{array}}\ \ \right\} \end{eqnarray}$
式中, $\theta _2$代表纤维束坐标系($x^{F}$, $y^{F})$与单胞坐标系($x^{unit}$, $y^{unit})$的夹角, 如图2 所示. 从而可得平纹机织CFRP的宏观刚度阵
(14) $C=1 / {V_{unit} }\left\{ {C_{warp}^{unit} V_{warp} +C_{weft}^{unit} V_{weft}+C_{m}^{unit} V_{m}^{unit} } \right\}$
式中, $V_{unit}$表示单胞的体积, 下标warp表示经纱, 下标weft表示纬纱, $V_{m}^{unit}$表示基体占单胞的体积分数. 由于纱线是卷曲的, 需要对其沿$x$方向的长度进行积分获得伸展的纤维束长度$\hat{{T}}$, 如图3 所示. 经纬纱和基体的体积分数可通过式(15)来获得
(15) $\begin{eqnarray} \label{eq15} \left. {\begin{array}{l} V_{warp} =V_{weft} ={\hat{{T}}\pi ab} / 4 \\ V_{m}^{unit} =1-2V_{warp} \\ \end{array}} \ \ \right\} \end{eqnarray}$
通过对宏观刚度矩阵进行求解, 可获得单胞的弹性模量、剪切模量和泊松比.
1.3 模型验证
本文所制备的平纹机织CFRP碳纤维丝和基体材料力学性能参数如表1 所示, 碳纤维丝选用台丽碳纤维TC33, 碳纤维以3K的形式集合成碳纤维束. 基体选择Huntsman公司的环氧树脂, 牌号为LY1564 SP, 对应的固化剂牌号为Aradur 3486, 两者的体积比为5:2. 采用真空导入工艺进行力学性能试验所用的平纹机织CFRP的成型. 通过上述工艺制备得到的CFRP的密度为1.47 g/cm$^{3}$.
为了从宏观上探究CFRP的力学性能, 分别根据试验标准ASTM D638[25 ] 和ASTM D7078[26 ] 进行平纹机织CFRP的轴向拉伸和面内剪切试验, 试验样件如图5 所示, 尺寸单位为mm. 准静态轴向拉伸力学性能试验使用岛津5 t EHF-UM电液伺服疲劳试验机进行, 准静态面内剪切试验采用SUNS电子万能试验机. 所有试验均采用位移控制方式, 并根据样件的尺寸设定加载速率, 保证对应的工程应变率在0.001 s$^{-1}$范围. 每种试验均保证测量得到5个有效试验数据并取平均值. 最终试验得到的宏观轴向拉伸弹性模量为60.89 GPa, 面内剪切模量为3.63 GPa.
图5
图5
准静态力学性能试验样件
Fig.5
Specimens for quasi-static mechanical tests
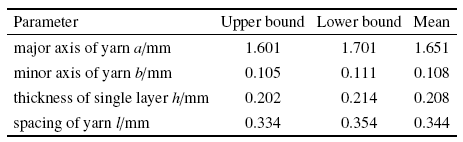
纤维丝和纤维束的几何参数通过对纤维束界面显微图像和Micro-CT图像(如图6 和图7 所示)进行数据统计可获得, 纤维丝的直径为$d=6.23$ $\mu$m, 纤维束的几何参数如表2 所示. 表中平均值为统计得到的均值, 上下限值为统计得到的$\pm 3\sigma $置信区域数值. 纤维丝占纤维束体积分数的均值为65.32${\%}$, 纤维束占单胞体积分数的均值为67.90${\%}$.
图6
图6
纤维束截面显微图像
Fig.6
Microscopic image of cross section for yarns
图7
图7
Micro-CT 图像
Fig.7
Micro-CT images
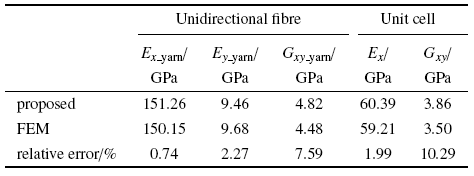
以各变量的均值为输入参数, 经过前述的解析模型预测得到的单向纤维和单胞的确定性力学性能如表3 所示, 通过与有限元仿真结果的对比可看出解析法的相对误差较小. 特别地, 解析法得到的结果与试验结果的相对误差分别为0.82${\%}$和6.33${\%}$, 预测结果与试验结果有较好的一致性.
2 纤维束随机力学性能预测
本文主要考虑组分材料力学性能和几何参数不确定性对单向纤维力学性能预测结果的影响, 组分材料的力学性能参数和几何参数的概率密度函数(probability density function, PDF)均设定为具有1${\%}$变异系数的高斯分布.
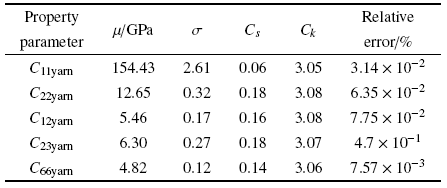
平纹机织CFRP的层级结构如图8 所示, 由于纤维束长轴和短轴既参与体积分数$V_{f}$的计算, 又参与了体积分数$V_{warp}$的计算, 属于跨尺度的共享变量. 单向纤维力学性能输入包括7个组分材料参数和几何参数$a$, $b$, 各参数之间相互独立, 故直接采用混沌多项式方法来进行预测. 考虑到单向纤维具有5个独立的材料参数, 分别选择$C_{11yarn}$, $C_{22yarn}$, $C_{12yarn}$, $C_{23yarn}$, $C_{66yarn}$作为纤维束尺度模型力学性能响应输出.
图8
图8
平纹机织CFRP层级结构
Fig.8
Hierarchical structure of plain woven CFRP
2.1 混沌多项式展开
PCE实质上是对随机变量构造一个具有随机性的代理模型[27 -29 ] . 为了描述的方便, 设定$X=(E_{11f}$, $E_{22f}$, $G_{11f}$, $G_{23f}$, $v_{12f}$, $E_{m}$, $v_{m}$, $a$, $b)$, 其任一元素设定为$X$. 采用PCE, 随机响应$Q$的截断的PCE可以简洁地表达如下
(16) $Q\left( X \right)\simeq Q_p \left( X \right)=\sum\limits_{i=0}^{P-1} {q_{\alpha _i } \psi _{\alpha _i } \left( X \right)}$
式中, $\left| \alpha \right|=\sum_{i=1}^{N_L } {\alpha _i } $且$0\leqslant \left| \alpha \right|\leqslant p$, $p$是多项式阶数, $N_{L}$是随机变量的数目, $P$是多项式项总数, 其计算表达式为$P={\left( {p+N_L } \right)!} / {\left( {p!N_L !} \right)}$, $q_\alpha $是待定的多项式系数, $\psi _\alpha $是服从概率分布$f_X \left( x \right)$的多元多项式项, 具有正交性质
(17) $E\left[ {\psi _\alpha \left( X \right)\psi _\beta \left( X \right)} \right]=\delta _{\alpha \beta }, \ \forall \ \alpha,\beta \in {N}^{N_L }$
式中, $\delta _{\alpha \beta } $是克罗内克符号, $E\left( \cdot\right)$表示期望算子. 式(16)所对应的截断集定义如下
(18) $A=\left\{ {\alpha \in {N}^{N_L},\left| \alpha \right|\leqslant p} \right\}$
利用PCE进行不确定性传递时, 最关键的步骤是求解式(16)中待定的多项式系数$q_\alpha $, 本文采用回归法求解待定系数, 其回归表达式为
(19) $q={arg}\min E\left[ {\left( {Q-q^{T}\psi } \right)^2} \right]$
求解上式得到多项式中的待定系数. 基于正交性质, 前四阶矩, 包括均值$\mu$、标准差$\sigma $、偏度系数$C_s $、峰度系数$C_k$可以通过下式结合多项式系数获得.
(20) $\left. \begin{array}{ll} \mu =q_{\alpha _0 } \\ \sigma =\sqrt {\sum\limits_{\alpha \in \tilde{{A}}} {E\left[ {\psi _\alpha } \right]^2} } \\ C_s =\frac{1}{\sigma ^3}\sum\limits_{\alpha \in \tilde{{A}}} {\sum\limits_{\beta \in \tilde{{A}}} {\sum\limits_{\gamma \in \tilde{{A}}} {E\left[ {\psi _\alpha \psi _\beta \psi _\gamma } \right]q_\alpha q_\beta q_\gamma } } } \\ C_k =\frac{1}{\sigma ^4}\sum\limits_{\alpha \in \tilde{{A}}} {\sum\limits_{\beta \in \tilde{{A}}} {\sum\limits_{\gamma \in \tilde{{A}}} {\sum\limits_{\eta \in \tilde{{A}}} {E\left[ {\psi _\alpha \psi _\beta \psi _\gamma \psi _\eta } \right]q_\alpha q_\beta q_\gamma q_\eta } } } }\end{array} \right\}$
式中, $\tilde{{A}}=A\backslash \left\{ 0 \right\}$.
基于前四阶并采用概率分布拟合方法可以获得响应的概率分布. 常用的概率分布方法包括最大熵原理, 鞍点逼近等[30 -32 ] . 若偏度系数约为0, 峰度系数约为3, 则可直接假设该分布服从正态分布从而得到概率分布.
本文采用留一交叉验证方法来验证所构造的PCE的预测精度. 假设原始数据有$N$个样本, 那么每个样本单独作为验证集, 其余的$N-1$个样本作为验证集. 留一交叉验证能充分利用所有样本, 并得到$N$个模型, 用这$N$个模型验证集的相对误差平均数作为验证误差以评估模型的精度.
2.2 预测结果分析
将PCE方法应用到平纹机织CFRP单向纤维的力学性能预测中, 设定多项式阶数为3, 基于拉丁超立方采样方法采取原始数据集, 包含50个样本. 预测得到的结果及模型验证误差如表4 所示.
所构造的PCE模型采用留一交叉验证方法来验证模型的精度, 由表4 可知, 力学性能参数预测模型的交叉验证误差最高为0.470, 模型精度很高. 偏度系数均在0左右, 峰度系数均在3左右, 说明单向纤维力学参数基本服从正态分布.
3 单胞随机力学性能预测
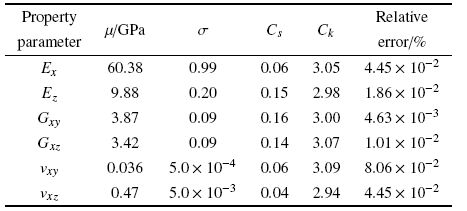
单胞尺度下, 纤维束预测得到的力学性能响应属于同一模型的不同响应, 故不可避免地存在变量相关性. 此外, 几何参数$a$, $b$由于既参与纤维丝占纤维束体积分数$V_{f}$的计算, 又参与纤维束占单胞体积分数$V_{warp}$和$V_{weft}$的计算; 而$V_{f}$又与$C_{11yarn}$等刚度矩阵元素存在因果关系, 故几何参数$a$, $b$与$C_{11yarn}$等刚度矩阵元素之间也存在相关性. 随机响应预测过程中若不考虑变量之间的相关性, 会使得预测结果出现较大的偏离[33 ] . 因此, 单胞尺度的力学性能预测需要充分考虑随机参数之间的相关性, 本文基于Vine Copula理论首先构造相关随机变量的联合概率分布, 然后基于Rosenblatt转换实现相关样本至独立样本的转换, 最后基于相互独立的样本并采用PCE来实现单胞尺度的拉伸弹性模量$E_{x}=E_{y}$, 拉伸弹性模量$E_{z}$和面内剪切模量$G_{xy}$, 面外剪切模量$G_{xz}=G_{yz}$, 泊松比$v_{xy}$, 及$v_{xz}=v_{yz}$的随机预测, 如图8 所示.
3.1 基于Vine Copula的相关性模型构建
Copula函数能够建立一元边缘累积概率分布与多元联合分布之间的关系[34 -35 ] , 为了描述的方便, 设定$Y=(C_{11yarn}$, $C_{22yarn}$, $C_{12yarn}$, $C_{23yarn}$, $C_{66yarn}$, $a$, $b$, $h$, $l)$, 其联合累积概率分布(cumulative distribution function, CDF)表达式为
(21) $F_Y \left( y \right)=\Pr \left( {Y_1 <y_1 ,Y_2 <y_2 ,\cdots ,Y_{N_U } <y_{N_U } } \right)$
式中, $N_{U}$为变量个数, $\Pr \left( \cdot \right)$为累积概率算子. 基于Sklar's理论, 联合CDF可以重构成一系列边缘CDF的函数.
(22) $F_Y \left( y \right)=C\left( {F_1 \left( {y_1 } \right),\cdots ,F_{N_U } \left( {y_{N_U } } \right)\left| \vartheta \right.} \right),\ \ y\in R^{N_U }$
式中, $C\left( \cdot \right)$表示Copula函数, 当所有的边缘CDF都是连续函数时, Copula函数是唯一的; $\vartheta $表示Copula参数向量. 式(22)可进一步写成
(23) $\left. \begin{array}{ll} C\left( u\left| \vartheta \right. \right)=F_Y \left( F_1^{-1} \left( u_1 \right), F_2^{-1} \left( u_2\right),\cdots, F_n^{-1} \left( u_n \right)\right)\quad\\ u\in \left[ {0,1} \right]^{N_U}\end{array} \right\}$
式中, $u$为累积概率值向量. Copula函数有其对应的Copula密度函数
(24) $c(u|\vartheta)=\partial ^{N_U }C(u|\vartheta)\big/(\partial u_1, \partial u_2,\cdots,\partial u_{N_U })$
(25) $f_Y \left( y \right)=c\left( {F_1 \left( {y_1 } \right),F_2 \left( {y_2 } \right),\cdots ,F_{N_U } \left( {y_{N_U } } \right)} \right)\prod\limits_{i=1}^{N_U } {f_i \left( {y_i } \right)}$
对于相关性测度, 本文采用一种非线性测度Kendall系数来进行描述. 相关模型的构建是基于累积概率样本集, 因此原始样本集需要转换到对应空间来进行相关模型的构造, 即$Y\to U$. Copula理论为多元相关建模提供了一种合理的方法, 但是目前主要针对二元Copula函数. 随着维度的增加, 构造一个合适的多元Copula会变得越来越困难. 为了克服上述局限性, 采用Vine Copula来将多元Copula函数分解为一系列二元Copula函数的组合来构造多元相关模型. 分解方法如下
(26) $\begin{eqnarray} \label{eq26} &&f_Y \left( y \right)=f_1 \left( {x_1 } \right)\cdots f_{N_U \left| {1,2,\cdots ,N_U -1} \right.}\cdot \\&&\qquad \left( {y_{N_U } \left| {y_1 ,y_2 ,\cdots ,y_{N_U -1} } \right.} \right) \end{eqnarray}$
式中, $f_{j\left| {1,2,\cdots ,j-1} \right.} \left( {y_j \left| {y_1 ,y_2,\cdots ,y_{j-1} } \right.} \right)$, $j=2,3,\cdots N_U $是边缘PDF, 其可以通过Copula密度函数的偏导求得
(27) $f_{i|j} \left( y_i | {y_j }\right)=\partial c_{ij} \left( {u_i ,u_j } \right)/\partial u_j$
观察式(26)不难发现通过改变分解变量的顺序, 多元Copula函数的分解方式多样. 本文采用基于图形模型的R-vine来进行结构构造[36 ] . 该方法通过分析变量之间的相关系数并基于最大生成树方法来确定R-Vine的结构[37 ] . 二元Copula函数存在多种形式, 如Gumbel Copula, Gaussian Copula, Frank Copula等, 且不同函数存在对应的Copula参数. 分别引入最大似然估计方法和赤池信息准则(Akaike information criterion, AIC)[38 ] 来确定最优Copula参数和函数.
(28) $\left. \begin{array}{l} \hat{{\vartheta }} = {arg} \mathop{\max}\limits_\vartheta L \\ L=\sum {\ln c\left( {F_1 \left( {y_{1i} } \right),\ F_2 \left( {y_{2i} } \right)| \vartheta } \right)} \\ \end{array}\ \ \right\}$
(29) $AIC=-2L+2k_\vartheta$
式中, $k_\vartheta $是需要确定的Copula 参数数目. 通过上述方法的组合可逐步构造二元Copula函数直到获得所需要的多元Copula函数.
3.2 独立性转换
基于Vine Copula理论构造相关性模型后, 可通过该模型生成相关累积概率样本集$u$, 该样本集无法直接用于后续的不确定性分析, 故须先通过独立性转换方法得到相互独立的样本集. 由于最大生成树方法已经确定了Vine Copula的结构, 即确定了随机变量的转换次序, 故此时采用Rosenblatt转换会得到唯一一组独立样本集. 转换方法如下
(30) $\left. \begin{array}{ll} \hat{{u}}_1 =u_1 \\ \hat{{u}}_2 =C\left( {u_2 \left| {u_1 } \right.} \right) \\ \cdots \\ \hat{{u}}_n =C\left( {u_n \left| {u_1 } \right.,u_2 ,\cdots ,u_{n-1} } \right) \end{array} \right\}$
式中, $\hat{{u}}=\left( {\hat{{u}}_1 ,\hat{{u}}_2 ,\cdots ,\hat{{u}}_n } \right)$转换后的独立样本集.
Rosenblatt转换实现了样本从相关到独立的转换, 即$U\to \hat{{U}}$. 进一步地采用$\hat{{y}}_i =\varPhi ^{-1}\left( {\hat{{u}}_i } \right)$可得到用于不确定性传递的样本集, 其转换表达式为$\hat{{U}}\to \hat{{Y}}$.
3.3 预测结果分析
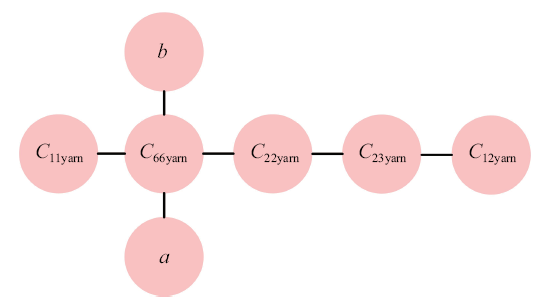
将Vine Copula理论应用到平纹机织CFRP单胞尺度力学性能预测的相关模型建模中. 具有相关性的参数为($C_{11yarn}$, $C_{22yarn}$, $C_{12yarn}$, $C_{23yarn}$, $C_{66yarn}$, $a$, $b)$, 几何参数$a$和$b$的PDF已设定为高斯分布, 力学性能参数($C_{11yarn}$, $C_{22yarn}$, $C_{12yarn}$, $C_{23yarn}$, $C_{66yarn})$的PDFs则已通过纤维束尺度的随机预测获得. 得到的R-Vine树结构1如图9 所示.
图9
图9
R-Vine树结构1
Fig.9
R-Vine tree structure 1
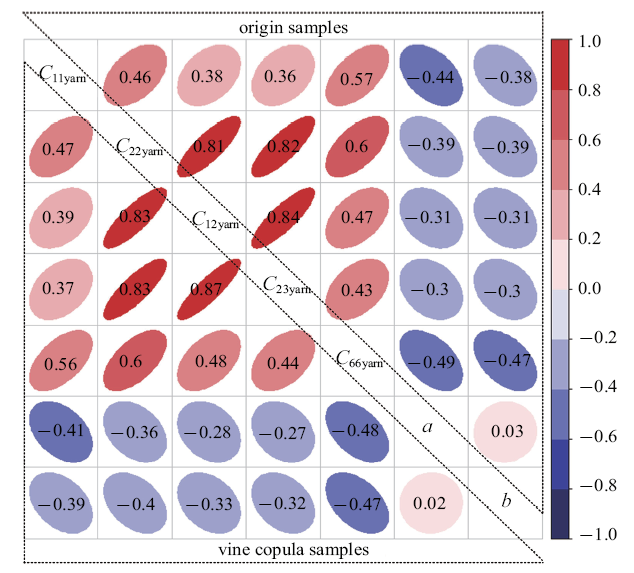
为了验证所构造的相关性模型的准确性, 基于该模型产生随机样本并求解得到相关性系数, 该相关性系数与原样本集相关性系数进行对比, 对比结果如图10 中相关性矩阵所示. 相关性矩阵上对角矩阵的相关性系数为原样本集计算得到的结果, 下三角矩阵的相关系数为Vine Copula模型计算得到的结果. 对比矩阵里面的元素可发现相关性系数几乎一致, 绝对误差最大仅为0.03, 说明构造的相关性模型精度很高.
图10
图10
相关性矩阵对比
Fig.10
Comparison of correlation matrix
基于独立性转换方法将原样本集$Y$转换为用于不确定性传递的样本集$\hat{{Y}}$, 图11 给出了($C_{11yarn}$, $C_{22yarn})$在空间$Y\to U\to \hat{{U}}\to \hat{{Y}}$转换过程. 可以看出, 最终获得了相互独立的样本集. 基于该样本集并采用前述的PCE方法来实现平纹机织CFRP单胞的力学性能预测. 设定多项式阶数为5, 预测得到的结果如表5 所示.
图11
图11
样本集转换过程
Fig.11
Transformation of samples
所构造的PCE模型的验证误差最大为0.080 6, 模型精度很高. 由于偏度系数值在0左右, 峰度系数值在3左右, 说明单胞弹性力学性能参数基本服从正态分布. 将单胞力学性能随机预测结果与表1 中的确定性结果进行对比可以发现, 随机预测结果的均值与确定性结果基本一致, 这说明了平纹机织CFRP轴向拉伸弹性模量和面内剪切模量的多尺度模型非线性程度较低, 使得随机预测结果的均值相对于确定性结果波动较小; 也从侧面证明了传统确定性方法实际上就是基于随机变量的均值来进行分析. 此外, 通过计算得到随机预测结果的变异系数分别为1.64${\%}$, 2.02${\%}$, 2.32${\%}$, 2.63${\%}$, 1.38${\%}$, 1.13${\%}$相比较于输入参数1${\%}$的变异系数来说均有所提高, 表明不确定性相互耦合且传递之后会对随机预测结果的方差产生放大的影响.
4 结论
本文针对现有平纹机织CFRP力学性能预测研究中的考虑随机参数不够全面, 不确定性传递方法大多具有局限性以及对随机参数之间的相关性考虑不够充分等问题, 提出一种基于PCE和Vine Copula的平纹机织CFRP随机力学性能多尺度预测方法. 具体工作与结论如下:
(1)该方法综合考虑了平纹机织CFRP微观及介观尺度的材料、结构随机参数, 基于层级传递的策略逐尺度地研究了力学性能参数的不确定性. 本方法从根源上量化了不确定性, 并逐尺度地揭示了参数的不确定性对各尺度力学性能的影响作用.
(2)随机力学性能预测结果表明, 所构造的各尺度PCE模型的交叉验证误差均很低, 说明非嵌入式PCE方法能够准确地实现各尺度力学性能的随机预测. 同时, 由于PCE模型能够解析地给出预测结果的均值、标准差、偏度系数和峰度系数, 能够进一步得到参数的PDF.
(3)该方法在预测过程中充分考虑了随机变量之间的高维相关性, 基于Vine Copula方法和Rosenblatt转换实现了对相关性的建模与转换. 相关性矩阵中系数之间的绝对误差最大为0.03, 表明所构造的相关性模型能够很好地反映原数据之间的相关性; 而Rosenblatt转换与所构造的相关性模型相结合则能够很好地实现样本集的独立性转换.