引言
工程结构的损伤、破坏和解体往往是微裂纹形核、萌生、发展和传播扩散的结果. 因此, 准确把握固体材料与结构中裂纹的产生和发展过程至关重要[1]. 自20世纪20年代初Griffith的开创工作[2]以来, 人们对此进行了大量的研究, 并先后发展了线弹性断裂力学[3-6]、弹塑性断裂力学[7-11]和损伤力学[12-18]. 然而, 固体中的裂纹萌生与传播的模拟, 迄今仍面临一系列挑战性问题. 例如, 经典断裂力学难以解决裂纹形核以及扩展方向等问题[19]. 20世纪末, 通过引入能量释放率最小化等准则和裂纹面密度连续化思想, 基于变分原理发展了脆性材料的相场理论, 为裂纹扩展模拟开辟了新的道路[20-21]. 最近, 结合损伤力学和相场理论, Wu等[22-25]提出了一类统一相场理论框架, 对准脆性材料的静力与动力裂纹扩展分析问题取得了重要突破. 这一途径, 从计算角度来看, 属于弥撒型裂纹模型的范畴. 在传统上, 人们认为断裂力学与损伤力学是分别处理和分析裂纹出现之后与产生之前的两种力学理论. 统一相场模型的成功, 从一个侧面表明, 这一认识存在局限性. 事实上, 二者之间是可以相容而相得益彰的. 与此同时, 人们意识到, 仅仅在宏观连续介质力学尺寸不足以把握材料损伤萌生与裂纹扩展的物理-力学本质, 要从根本上解决上述问题, 需要结合微细观机理的分析, 由此发展了宏微观断裂力学[1]. 另一方面, 人们逐步认识到非局部化性质对克服经典局部损伤力学中网格敏感性问题的根本性意义[26]. 鉴于裂纹本质上是不连续的, 20世纪末以来人们提出了一系列新的途径, 包括内聚裂纹模型[27]、扩展有限元方法[28]和无网格方法[29]. 自2000年以来, Silling提出peridynamics(近场动力学[30]或毗域动力学[31])理论[32], 将固体介质的相互作用采用积分和离散形式表达, 给出了一类新的、具有非局部化性质的离散裂纹萌生和扩展模拟方法, 并在一系列问题中取得了相当的成功[33-37].
虽然如此, 统一相场理论需要额外求解相场演化方程, 从而使得理论和求解的复杂程度较高. 另一方面, 近场动力学方法中本构模型的确定以及对准脆性裂纹的模拟尚存在困难. 为此, 结合统一相场理论和近场动力学的基本思想, 针对准脆性材料的裂纹模拟, 最近提出了一类新的非局部宏-微观损伤模型[38]. 在此基础上, 本文进一步修正微观损伤准则, 并对具有强非线性回弹特性的典型裂纹扩展问题进行分析, 验证了所改进模型的有效性.
1 宏-微观损伤模型的基本理论
从微细观层次来看, 裂纹的萌生和发展从几何上表现为出现了不连续性, 从宏观上虽依然可认为是连续体, 但与原初固体材料相比, 出现了宏观损伤. 这一损伤将引起材料自由能的变化, 使得本构关系中出现非线性, 因而导致材料表现出非线性行为. 本节将给出这一基本路径的理论刻画[38].
1.1 拓扑损伤
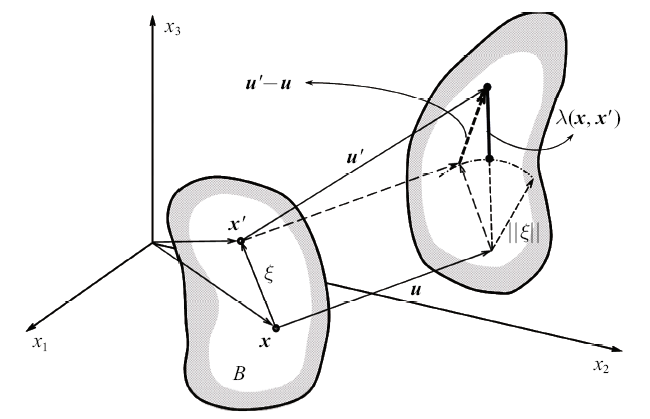
考虑连续固体$B$, 其边界为$\partial B$. 该连续体中的物质点记为${x}=(x_1 ,x_2 ,x_3 )\in B$. 考察物质点对$({x},{{x}'})$, 其中${{x}'}=({x}'_1 ,{x}'_2 ,{x}'_3 )\in B$, $\xi ={{x}'}-{x}$为两点之间的空间差, $\| \xi \|$则为相应的距离, 这里$\left\|\cdot \right\|$为向量的长度. 连续体发生变形后, 物质点${x}$和${{x}'}$的位移分别记为$u=u(x)$和${u}'=u({x}')$.
根据变形几何(如图1所示), 可以定义物质点对$({x},{{x}'})$之间的变形为
其中, $\nu =\xi /\left\| \xi \right\|$为物质点对的单位方向向量. 由此, 可定义物质点对的伸长量为
式中, $H(\cdot )$为Heaviside阶跃函数, 当$\lambda \leqslant 0$时, $H(\lambda)=0$, 否则$H(\lambda )=1$.
图1
可以合理地假设, 当伸长量超过给定阈值$\bar{{\lambda }}$时, 物质点对之间的联系(物质键)开始弱化, 直至完全分离, 即物质键断裂. 这一过程显然与单调非减的加载历史参数有关. 为此, 可定义加载历史参数为
即物质键变形历史的最大超越伸长量, 其中$t$为时间变量(对静力问题应理解为虚拟时间).
且满足$\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over {\omega }} (0)=0$, $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over {\omega }} (\infty )=1$以及$\partial _\kappa \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over {\omega }} \geqslant 0$.
注记2 从物理意义上看, $\omega $是微细观损伤的度量, 其具体形式可由分子动力学的相互作用势函数通过计算加以确定, 或者根据理性假设给出. 在本文中, 假设为如下形式
其中$\gamma >0$为模型参数, 它表征微细观损伤的发展速度. 不难注意到, $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\smile$}}\over {\omega }} (\kappa )$是以$\gamma $为参数的、Heaviside阶跃函数$H(\kappa )$的极限函数列, 而Heaviside阶跃函数表征了不连续性. 因此, 从这个意义上说, 微细观损伤刻画了固体在物质键层次的不连续程度, 这一点与李杰等[18]认为损伤变量应打破物质空间连续性的观点是一致的.
事实上, 连续体中某物质点处的损伤, 往往不仅取决于该点本身, 还必然与其周边一定邻域范围内的物质点相互作用有关. 换言之, 其损伤的变化, 本质上是非局部化的. 记存在影响的邻域(影响域)半径为$\ell $, 即$\ell =\mbox{diam}D_\ell ({x})/2$, 这里$D_\ell ({x})$表示物质点${x}$的影响域. 根据上述表述, 可以进一步提炼出损伤的数学语言:
定义1 设连续体$B\subset {R}^d$ $(d=1,2,3)$及其位移场${u}\subset R^d$, 若给定影响域半径$\ell >0$, 存在阈值$\bar{{\lambda}}>0$, 使得物质点${x}\in B$有
则称连续体在${x}$处发生损伤, 此时微细观损伤$\omega >0$. 它从数学上刻画了位移场${u}$在空间上关于方向$\nu $的不连续程度, 因此不妨称这一定义为$\bar{{\lambda }}-\ell $语言.
作为对照, 这里给出位移场${u}$作为$d$元$d$维向量值函数其连续性的$\epsilon-\delta $语言[41].
定义2 设${u}:B\subset {R}^d\to {R}^d$, 若对任意$\epsilon>0$, 存在$\delta >0$, 使得${x}\in B$有
其中$D_\delta ({x})=\{{{x}'}\in B:\left\| {{{x}'}-{x}}\right\|<\delta \}$, 则称向量值函数${u}$在${x}$处连续.
对$\forall {x}\in B$物质点给定的影响域$D_\ell ({x})$, 设任意两物质点之间的影响函数为$\phi ({x},{{x}'})$, 并满足如下条件
即非负性、定域性和归一性. 当考虑各向同性材料时, 可取$\phi =\phi (\left\| {{{x}'}-{x}} \right\|)$. 在本文中, 取
其中, vol[$\cdot$]表示体积测度.
从宏观上看, 对于固体$B$内任意物质点${x}$, 其损伤应是该物质点所连接的物质键之微细观损伤的加权平均. 因此, 对$\forall {x}\in B$定义宏观层次损伤为
即根据微细观层次的物质键$({x},{{x}'})$的断裂程度在局部空间上进行几何上的加权平均, 它连续地刻画了位移场在一点附近的整体不连续性. 不难注意到, 损伤区域$J_\varOmega =\{{x}\in B:\varOmega ({x})>0\}$构成了裂纹拓扑$J$ (其中$\dim J=d-1)$的非局部化邻域表达. 因此, 从这个意义上, 不妨称之为拓扑损伤.
的作用相同, 即采用非局部化思路将裂纹拓扑表示为含一定带宽的弥散型界面, 从而使得分析过程无需人为预设裂纹扩展路径. 其中, 式(11)的参数$\varphi $和$\alpha$分别为相场函数和裂纹几何函数.
进一步地, 可以证明以下命题:
命题1 设裂纹拓扑$J\subset {R}^d$, 以及$\varOmega $和$\varTheta$分别如式(10)和式(11)所定义, 则
式中, $\vartheta (d)=\varUpsilon (d)/2$, 其中$\varUpsilon(d)$表示$d$维单位球域$D_{\ell =1} ({\bf 0})$的表面积测度.
需要说明的是, 上式第一个等式(即椭圆泛函逼近)已经由Braides[44]给出了证明, 而第二个等式(拓扑损伤逼近)的具体证明因限于本文的篇幅而考虑另文给出.
1.2 能量退化因子
注意到, 连续体的自由能密度必然随着拓扑损伤的发展(即裂纹萌生和扩展)而退化. 设能量退化因子为$g$, 则有损连续体的自由能为
式中小应变张量$\varepsilon =\nabla ^{S}{u}$, 其中$\nabla^{S}(\cdot )$表示对称梯度算子, $\psi _0$为无损材料的自由能密度函数, 即
其中$E$为四阶弹性张量.
为简化计, 在本文中暂不考虑塑性的影响. 因此, 这里弹性应变和总应变相同, 后文对二者将不再加以区分.
其中, $g(0)=1$表示物质点处于线弹性无损状态; $g(1)=0$则是完全损伤的刻画, 即丧失了全部的储能能力; 此外, ${d}_\varOmega g<0$表示损伤总是耗能的; 而${d}_\varOmega g(1)=0$则保证当$\varOmega =1$时, 损伤驱动力$\partial _\varOmega \psi ={d}_\varOmega g(\varOmega )\psi _0 $趋于零, 即当一点的损伤发展完全后, 其驱动力应随之消失.
若从能量意义上说, 不妨称$\varPhi =1-g(\varOmega )$为基于能量的损伤. 事实上, 基于拓扑损伤的能量退化因子还可以进一步从物理上论证, $g$是$[\mbox{0,1}]$上的凸函数[38], 其定性的物理解释如下.
由于拓扑损伤$\varOmega $考虑的是影响域内所有方向上物质键损伤的几何"平均", 而各个方向上的物质键并非同时地发生损伤, 因为物质键的伸长量在各个方向上的分布一般是不均匀的. 在初始阶段, 只有位移场在空间变化剧烈方向上那些少数(相对于所有方向上的物质键总数而言)超过阈值的物质键率先进入损伤状态, 此时拓扑损伤$\varOmega $在数值上非常小, 但这些率先发生损伤的物质键因变形剧烈而储存了较大比重的变形能. 因此, 在$\varOmega=0$附近处基于能量的损伤$\varPhi $要大于拓扑损伤$\varOmega $, 即
随着其他方向物质键损伤的发展及其能量的释放, 逐渐地一点邻域内所能释放的变形能比重越来越小, 即能量退化因子$g$随着拓扑损伤$\varOmega $的增大而趋于平缓.
其中, $p$和$q$均为退化函数. 一些代表性取值的函数曲线如图2所示.
图2
2 控制方程
2.1 本构方程
根据Clausius-Duhem不等式[17], 有能量耗散率$d_t \varXi$不等式
其中, $\sigma $为Cauchy应力张量. 将式(13)代入上述不等式并稍作整理, 得
由前述拓扑损伤即能量退化因子的定义和性质可知, 上述积分项内第二项必然不大于零. 因此, 该不等式成立的充要条件是
式中, $\sigma _0 $为有效应力张量.
注记6 由此可见, 能量退化因子表征了材料的物性关系, 式(20)与传统损伤力学理论[18]的本构关系在形式上完全相同. 其中, 本文式(17)退化因子给出的是准脆性材料本构, $p$和$q$的取值刻画了材料的宏观脆性程度, 可认为是物性参数, 应根据标准试件进行标定.
2.2 平衡方程与边界条件
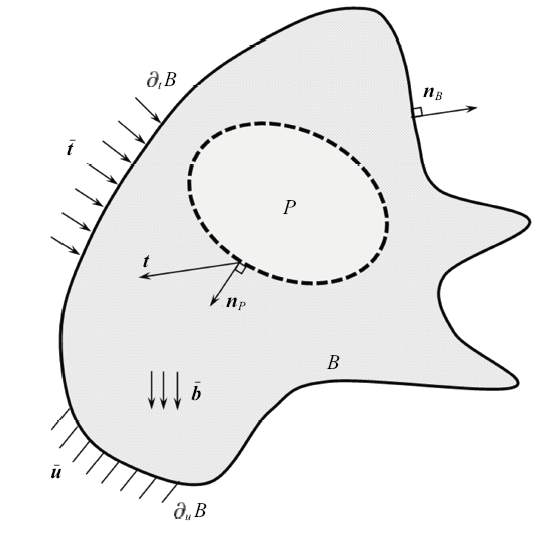
平衡方程和边界条件与常规连续介质力学的基本表达相同. 考虑图3所示固体$B$的参考构形, 容易列出平衡方程为
其中, ${t}$为内力向量, ${\bar{{b}}}$为体力密度向量(当不计体力时, ${\bar{{b}}}={0})$.
图3
根据Cauchy假定, 即${t}=\sigma \cdot n_P $, 其中${n}_P $为子集$P$的边界外法向向量. 由式(20)所表述的本构关系, 利用散度定理并注意到$P$的任意性, 可得
而在边界上则分别有
其中, ${n}_B $为固体的边界外法向向量, ${\bar{{t}}}$和${\bar{{u}}}$分别为给定的边界面力和边界位移.
3 数值求解方法
3.1 有限元离散方程
上述问题, 可以直接采用常规有限单元法进行离散和求解. 式(22)和式(23)这一边值问题经过弱形式逼近后, 可得单元的平衡方程为
式中, ${U}_{e} $为单元结点位移向量, ${K}_{e} $为单元刚度矩阵, $R_{e}$为单元结点力向量, 其中
这里$A_{e} $为单元区域, $\partial _{t} A_{e} $为边界单元的力边界, ${B}_{e} $和$\varPsi _{e} $分别为几何矩阵和形函数矩阵, 其表达式可在一般有限元专著中找到, 兹不赘述. 此外, ${D}_{e} $为弹性矩阵, 对于平面应力问题有
其中, $E$为弹性模量, $\mu $为泊松比.
根据单元组集规则, 可得结构整体平衡方程为
其中, 整体刚度矩阵${K}$、整体等效载荷向量${R}$和整体位移向量${U}$分别为
式中, $\varLambda _{e} $为单元转换矩阵, $N_{e} $为单元数目.
3.2 单元刚度矩阵的计算
在式(26)中, 为了计算单元刚度矩阵, 需要计算给定积分点的能量退化因子$g$. 这时, 应通过离散化方式计算式(10)中的拓扑损伤$\varOmega $, 然后将其代入能量退化因子式(17)中. 此时, 拓扑损伤可根据离散化后的各单元变形计算. 对于常应变单元, 有
其中, ${x}_{e} $和${x}_{{e}'} $分别为单元$A_{e} $和$A_{{e}'} $的形心坐标, 而$\bar{{V}}_{{e}'} =\mbox{vol}[D_\ell ({x}_{e} )\cap A_{{e}'} ]$. 若考虑采用等参单元进行离散, 则二者为相应的高斯点及其权重体积.
注意到, 能量退化因子是位移的函数. 由式(26)可知, 单元刚度矩阵也是位移的函数, 因而由式(30)给出的整体刚度矩阵亦为位移的函数. 因此, 平衡方程(29)是一个非线性方程. 在本文中, 采用改进局部弧长法进行求解. 限于篇幅, 兹不赘述.
注记8 在求解中, 拓扑损伤$\varOmega $是整体节点位移向量${U}$的"显式"函数, 即一旦求得整体节点位移向量${U}$已知, 直接将其代入式(31)就可以得到拓扑损伤$\varOmega $, 整个过程自始至终只需要求解(29)的平衡方程, 无需额外的待求解方程. 这一点比相场模型简单而高效, 因为相场模型中相场函数和位移场均是待求未知量, 需要采用联立或交替的策略求解平衡方程和额外的相场演化方程[49].
4 典型实例分析
以Ingraffea和Grigoriu所做的有机玻璃剪切梁试件[50]为例, 来验证和分析本模型的有效性. 注意到, 该试件以其强非线性回弹特性而著称, 是检验数值模型优良性的经典算例. 近些年来, 经过该算例检验的数值模型有基于混合(应变/位移)元的各向同性损伤模型[51]和统一相场模型[23]等. 分析中试件按平面应力问题处理, 其材料参数按文献[51]取: 弹性模量$E=3.102$ GPa, 泊松比$\mu =0.35$. 宏-微观损伤模型中的参数取: 影响域半径$\ell=4$ mm, 临界伸长量$\bar{{\lambda }}=1.38\times 10^{-2}$ mm, $\gamma =2.0\times 10^5$, 以及$p=4$和$q=4$.
4.1 不含圆孔情况
注意到, 经典的局部损伤力学存在网格敏感性[18]: 一旦所分析的固体存在或出现初始裂纹时, 当计算点的间距加密时, 基于经典局部损伤力学的分析结果, 将会出现即使是很微小的外力作用就可以引起严重的损伤(当网格非常密集时, 更甚者会出现不需要任何外力就可以使固体发生破坏的问题)这一违背物理真实的现象.
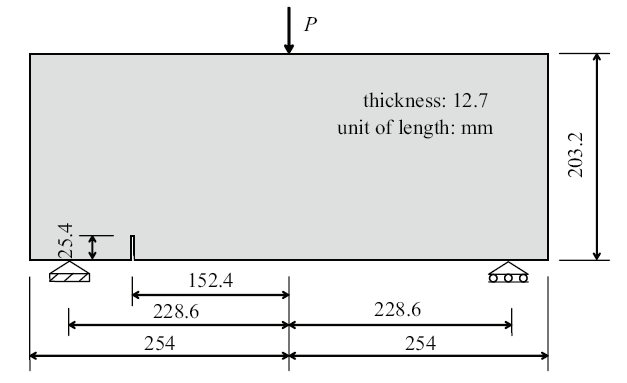
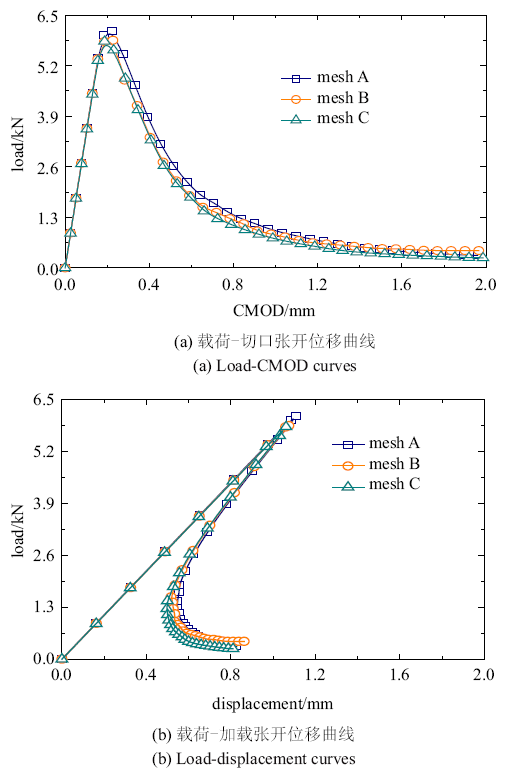
为了考察本文损伤模型的网格敏感性问题, 在有限元离散时采用3种不同疏密程度的三角形网格进行划分. 为此, 首先考虑不含圆孔的情况, 试件形状和尺寸如图4所示.
图4
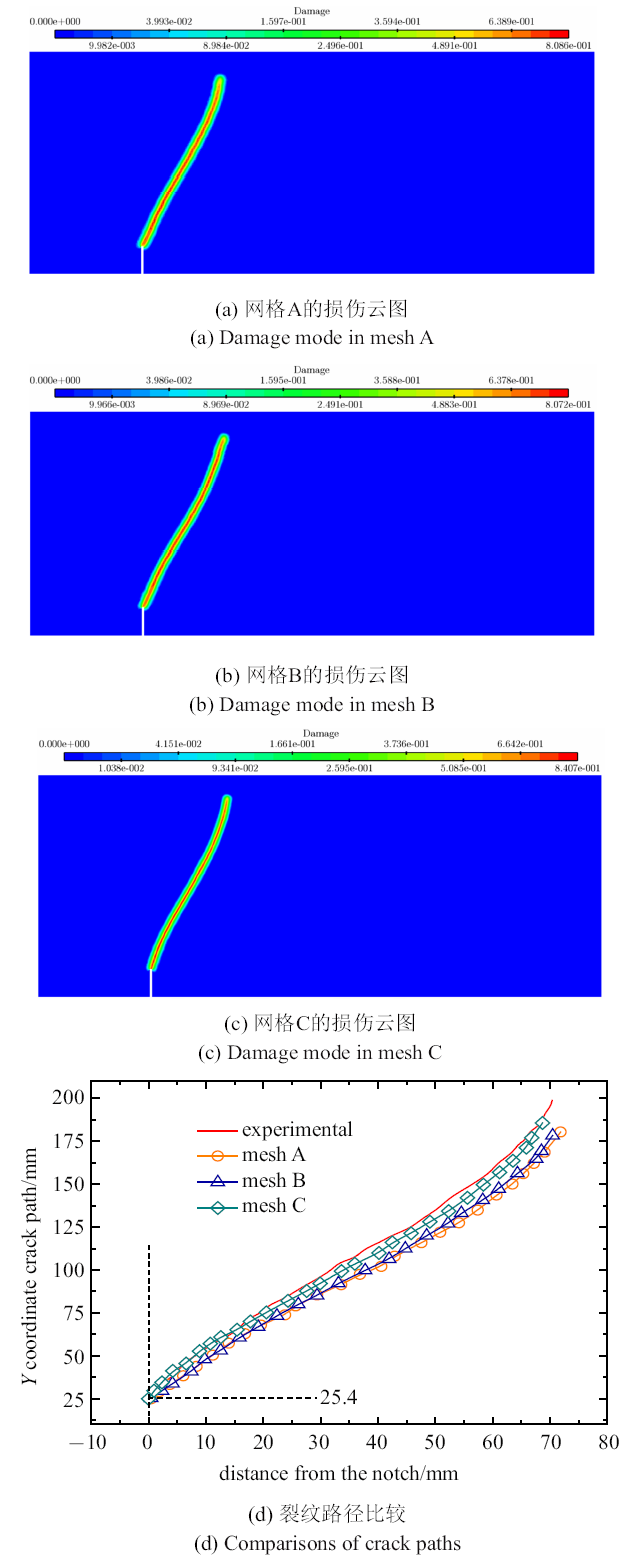
具体地, 考虑在切口一定范围的区域进行单元加密处理, 3种不同疏密程度的单元总数目分别为17 308, 23 564和55 262, 单元分布情况见图5.
图5
图6
图7
图8
图9
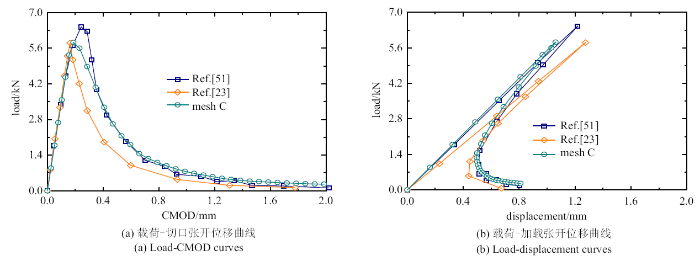
图9
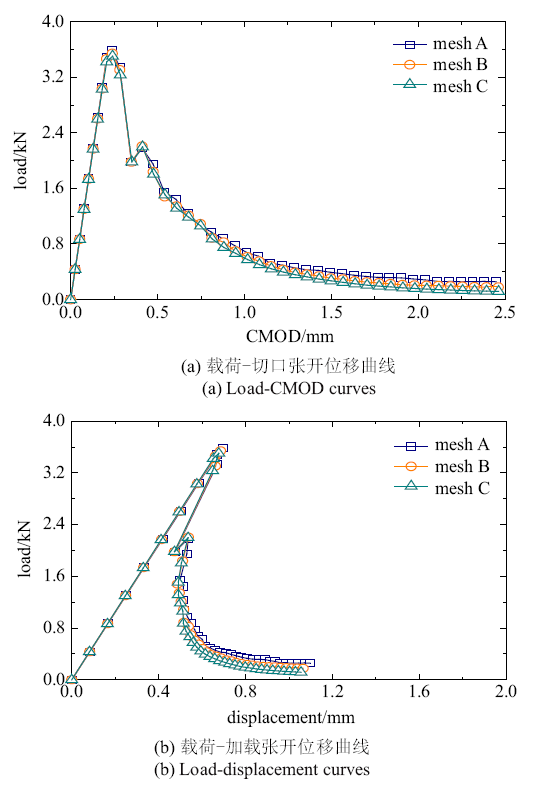
与其他数值模型的载荷-位移曲线比较
Fig.9
The load-deformation curves compared with other numerical models
图10
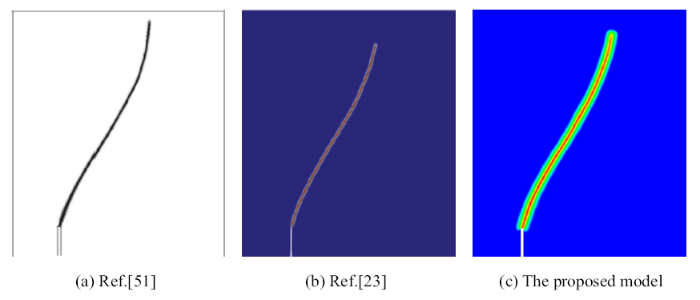
图10
与其他数值模型破坏模式的比较
Fig.10
The comparisons of failure modes with other numerical models
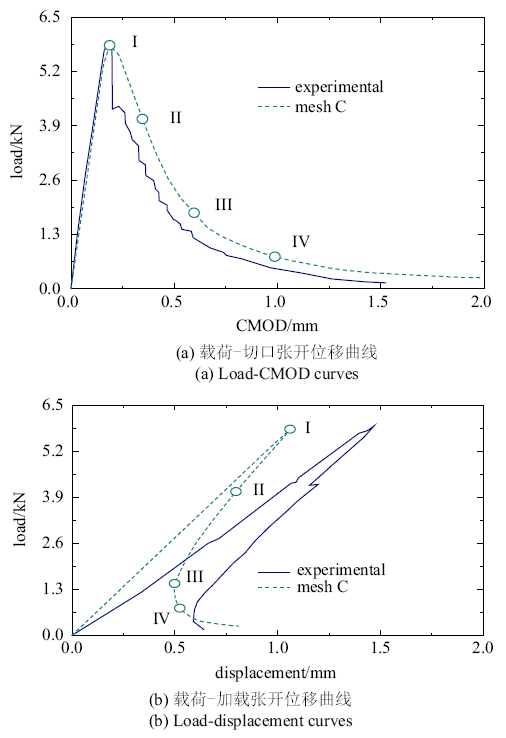
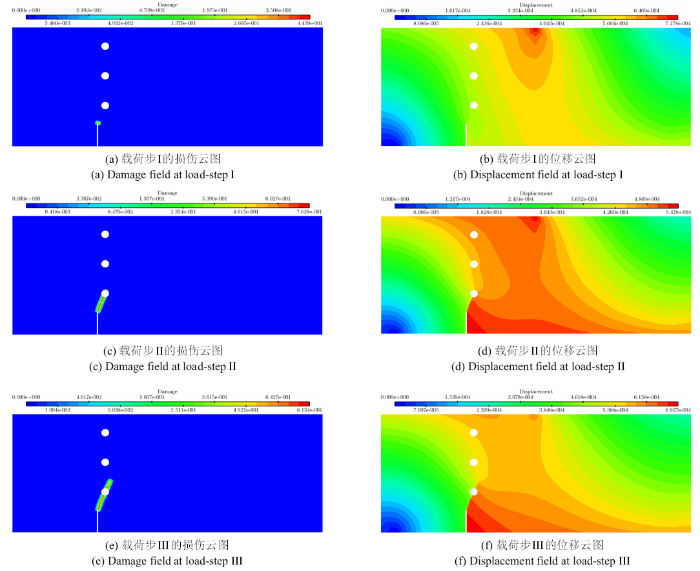
图11是图8的载荷-变形曲线中几个典型阶段的损伤云图和位移云图演化情况. 从图中可见, 裂纹随着加载过程而不断发展, 同时位移场在裂纹两侧出现显著的不连续性. 特别值得注意的是, 当外加载荷已经达到峰值的时候, 裂纹才刚刚具有肉眼可见的发展(图11(a)), 从图11(b)亦可见, 此时位移场尚未出现显著的不连续性. 当裂纹明显萌生和发展时(图11(c), 图11(e), 图11(g)), 试件的载荷-变形曲线已经进入显著的下降段(图8(a))或回弹段(图8(b)). 换言之, 对于此类问题, 当出现肉眼可见的裂纹时, 裂纹已经进入不稳定发展阶段. 这与人们从实际工程的损伤和断裂分析中获得的经验完全相符.
图11
图11
典型载荷步损伤与位移云图
Fig.11
Damage and displacement field at typical loading steps
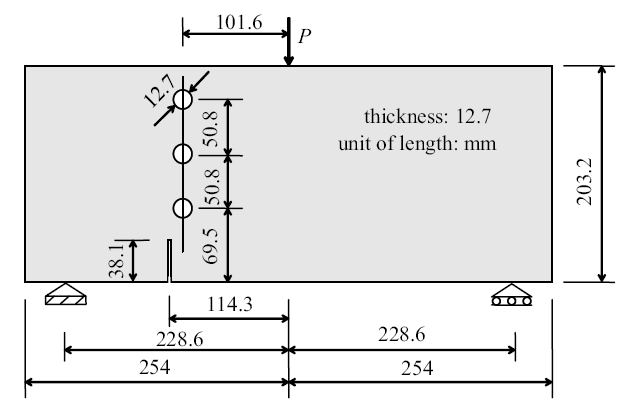
4.2 含圆孔情况
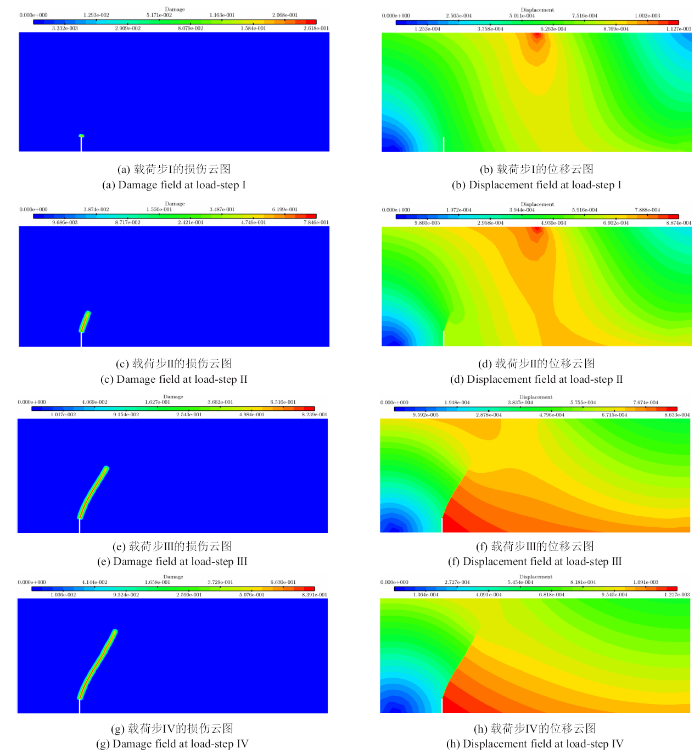
图12
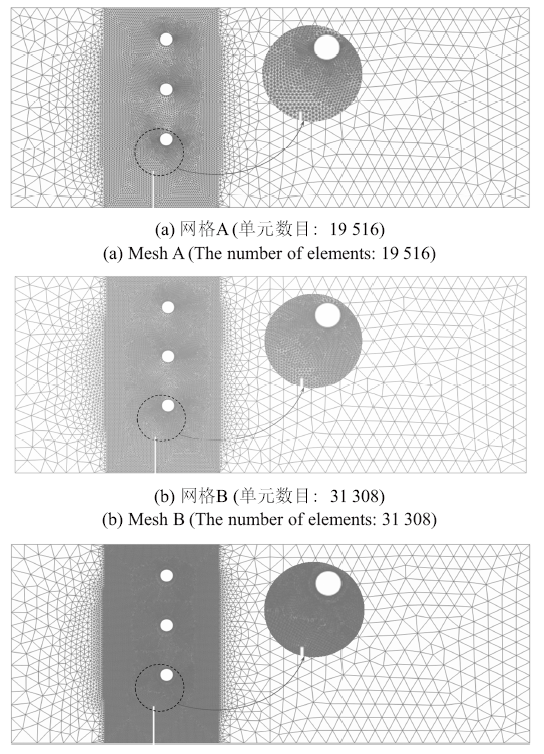
图13
图14
图15
图16
图17
图17
典型载荷步损伤与位移云图
Fig.17
Damage and displacement field at typical loading steps
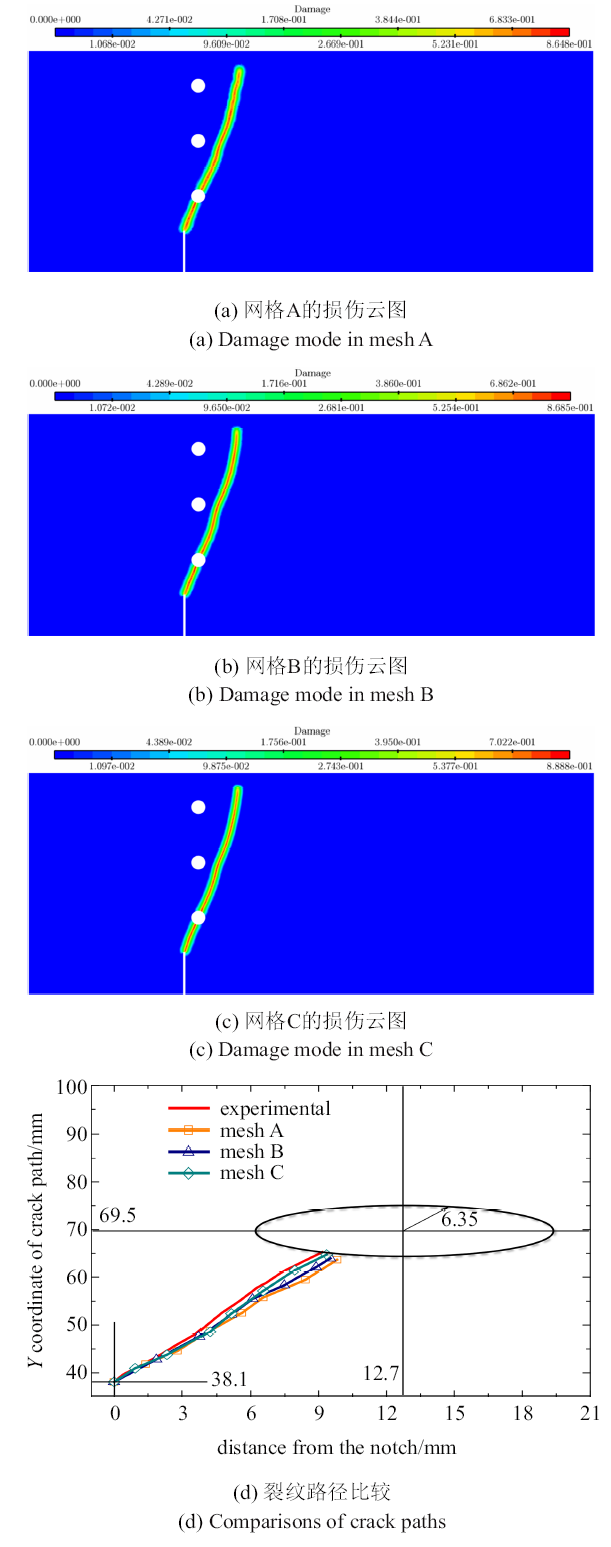
图18
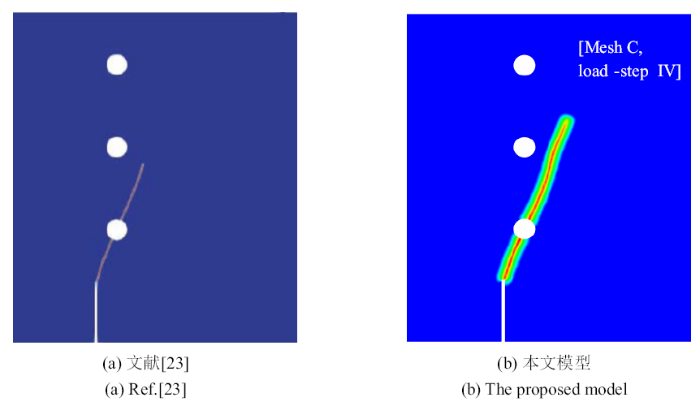
图18
与统一相场模型破坏模式的比较
Fig.18
The failure mode compared to that obtained by the unified phase field model
5 结论
在连续损伤力学的框架下, 结合相场理论与近场动力学的基本思想, 基于一类新的非局部宏-微观损伤模型, 实现了典型试件的裂纹发展过程模拟和分析. 主要结论如下.
(1)本文对非局部宏-微观损伤模型进行了改进. 该模型可以方便地在连续介质力学与有限元离散的框架下求解. 与统一相场模型相比, 不需要求解额外的相场演化方程. 与近场动力学相比, 不需要根据连续介质力学重新确定本构关系.
(2)应用该损伤模型分析固体破坏问题, 不需要人为预设裂纹扩展路径, 可自动描述和跟踪裂纹扩展. 不仅可以获得正确的裂纹模式, 而且可以定量地获得载荷-变形曲线.
(3)该损伤模型是一类非局部化模型, 不存在经典局部损伤力学所面临的网格敏感性问题.
本文的研究工作初步验证了非局部宏-微观损伤模型的有效性. 在未来工作中, 尚有大量研究工作需要深入推进, 例如基本参数与断裂能之间的内在关系、塑性变形的考虑、各向异性问题、动态裂纹扩展与分叉等挑战性问题.