引言
多颗粒流动广泛存在于自然现象和工业领域中, 比如植物种子的传播、大气污染物的扩散、流化床中颗粒的运动等. 多颗粒流动的行为取决于许多因素, 比如扰动、粒子之间的相互作用以及作用于不同尺度的自身动力 [1]. 这使得大量的多颗粒多尺度模型非常复杂并且依赖于对相关现象认知的进步. 在一些情况下单个颗粒的动力学行为对多颗粒流动行为有很重要的影响, 因此单个颗粒运动特性的研究对于进一步研究多颗粒运动行为有着重要的意义. 单个颗粒由于受到浮力和重力的作用, 往往呈现出不稳定的运动形态(比如摆动、翻滚、混沌、盘旋的运动状态), 这些现象背后潜在的物理机理引起了众多学者的关注, Ern等 [2]综述了球体、圆盘、圆柱等颗粒运动特性的实验和数值结果, 然而, 目前对于椭球体(包括长扁椭球体和椭球型圆盘)的研究甚少, 对其的研究将进一步促进对颗粒在液体中运动的特性的理解, 具有十分重要的研究价值.
在球体尾迹和路径方面, 文献[3,4,5,6]对均匀流中球体的各种尾迹结构进行了详细的数值研究, 但并未揭示流动不稳定发生的潜在机理. 随后Provansal等 [7-8]用实验验证了前人的数值结果: 当$Re_{d} < 212$, 球体的尾迹是轴对称结构, 当 $212 <Re_{d}<280$, 尾迹会演化成平面对称结构, 当$280 \leqslant Re_{d} <345$, 尾迹中会有一系列的发卡涡脱落现象, 当$Re_{d}> 345$时, 尾迹会变得不规则, 其中$Re_{d} =\overline u _z d/\nu$ $(\overline u _z $为颗粒平均下降速度, $d$为颗粒直径, $\nu $为流体运动黏度). 对于自由上升或下降的球体, Jenny [9]在$\overline \rho =\rho _{c} /\rho _{f} $ (其中$\rho_{c}$为物体密度, $\rho_{f}$为流体密度) 为$0\sim10$, $225 <Re_{d}<550$的范围对球体自由运动进行了数值模拟, 并且提出了5种路径, 分别是: 倾斜直线、 小震荡的倾斜、 Z字形振荡、 混沌运动、 Z字形和混沌运动之间的过渡运动. Schmiedel [10]和Veldhuis等 [11]分别用可视化技术和纹影法对自由上升和下降的球体尾迹进行可视化, 结果表明球体的尾迹中会形成涡环和流向涡, 但是没有定义其模式或和运动类型的联系. Horowitz等 [12]在大{\it Re}数范围内($Re_{d} = 100\sim15 000$)对球体尾迹进行了实验研究, 结果表明有3种涡脱落模式: $R$ (每个运动周期产生一个单侧涡环)、 $2R$ (每个运动周期产生一个双侧涡环)、 $4R$ (每个运动周期在不同的方向产生4个涡环), 3种涡脱落模式分别对应于倾斜直线、垂直直线、Z字形路径.
相比球体颗粒, 非球型颗粒由于其几何特征的各向异性, 其运动过程将产生不一样的运动特征, 相应的尾迹和路径不稳定性会变得更加复杂 [13-14]. Marshall等 [15]圆盘运动的实验表明当$Re_{d}$超过临界值时, 固定的圆盘尾迹中会有周期性发卡涡脱落; 这在文献[16,17,18]的数值结果里得到验证, 且球体不同的运动状态和尾迹结构也得到确认. Field等 [19]对自由下落圆盘进行实验研究后表明存在定常运动、周期运动、翻滚、混沌等4种运动类型, 随后Auguste [20]也在数值模拟中观察到了同样的结果. Willmarth等 [21]对于圆盘的实验表明, 当$Re_{d}<100$时圆盘的运动是稳定的, 随着雷诺数增大, 开始出现周期性运动. Zhong等 [22]对圆盘的研究发现在$40<Re_{d}< 105$时尾迹是轴对称的, 与Willmarth等 [21]在低雷诺数下观测的尾迹是吻合的, $Re_{d}>118$时, 尾迹结构的平面对称性会消失, $Re_{d}> 150$时, 会有周期性的发卡涡脱落. Feng等 [23]对下落的椭圆形圆盘进行了二维数值模拟表明椭圆形颗粒总是以长轴垂直于重力方向的形式下落, 并且随着粒子尺寸和密度的增加椭圆形颗粒会出现水平振荡, 三维情况在低雷诺数下也会出现这样的结果. Magnaudet等 [24]和Ern等 [2]解释椭球形粒子的路径不稳定性与尾迹不稳定性密切相关, 其涡的脱落会随着轴相对速度的方向的改变而改变.
圆柱颗粒的运动过程有别于圆盘的运动过程. Namkoong等 [25]对自由上升或下降的无限长圆柱进行了二维数值模拟, 在$0.5< \overline \rho < 4$, $65 < Re_{d}<185$下不稳定的尾迹会出现周期性涡脱落. Horowitz等 [26]在$3500 < Re_{d} <7000$范围内的实验表明, 对于密度比$\overline \rho >0.54$的圆柱实验发现路径为小振幅的震荡运动, 并且尾迹与卡门涡街符合很好; $\overline \rho <0.54$ 时, 路径为大振幅的震荡运动并且每个周期有两个涡对脱落. 随后Mathai等 [27]用数值模拟也验证了从小振幅到大振幅运动的过渡, 尾迹也会由两个单涡脱落模式到两个涡对脱落模式. Toupoint等 [28]对于$2 < L/d <20$, $200 <Ar<1100$范围内的圆柱进行了实验, 主要发现了3种运动: 直线下降、规则的振荡、不规则小振幅振荡.
然而当颗粒为细长椭球体时, 其形状介于球体与圆柱之间, 在流体中的运动形态将有明显的区别, 目前的研究还主要集中在数值模拟方面. Xia等 [29]研究了单个二维椭球体在牛顿流体中的下沉过程, 结果表明流体区域的宽度对椭球型颗粒的运动形态有着显著的影响. Mehdi等 [30]对单个细长椭球体进行了三维数值模拟, 结果表明细长椭球体运动过程中会绕其长轴旋转. Li等 [31]在研究椭球型颗粒在剪切流中的特性时也同样发现了这一旋转现象. Fornari等 [32]采用浸没边界法研究了多个椭球体的运动过程, 发现颗粒的平均下降速度随着颗粒的体积分数的增大而减小, 且均小于单个颗粒运动时的最终速度. 然而, 采用理论和数值模拟方法虽能非常深入地了解椭球体的运动特性, 但其中一些结果还有待实验的进一步验证. 本文主要通过实验对不同纵横比的细长椭球体的运动特性开展研究. 首先介绍了实验平台、实验材料和数据处理方法; 然后分别讨论了物体运动的路径、速度、振荡频率、尾涡结构; 最后总结了细长椭球体运动特点.
1 实验系统及数据处理方法
1.1 实验系统介绍
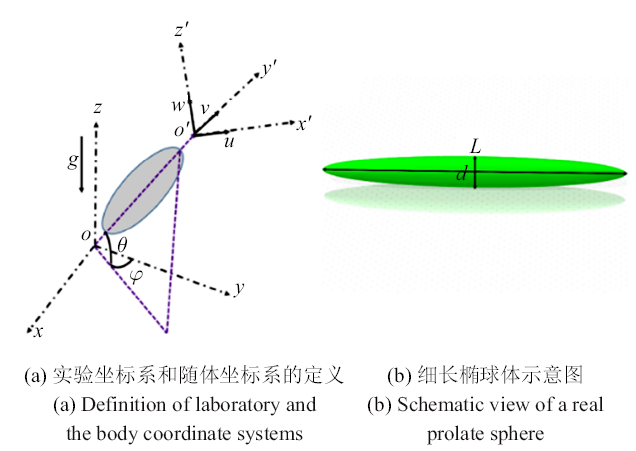
为了开展细长椭球体在水中自由下落的运动特性研究, 我们搭建了包含两台高速摄像机的颗粒追踪系统, 实验系统如图1所示, 由主体框架、水箱、高速摄像机、光源、释放装置等几大部分组成. 主体框架由铝合金制成, 作为整个实验系统的载体; 水箱为高1200 mm, 横截面为300 mm $\times$ 300 mm的有机玻璃制成, 作为颗粒在水箱中运动的实验段, 前人的大量实验已证明直径小于10 mm的小球在这种水箱中运动时, 壁面的影响可以忽略不计; 两台高速摄像机(Phantom MIRO LC 311, 实验所用分辨率1280 $\times $ 800, 拍摄帧频为25), 用于记录颗粒的整个运动过程; 两台LED灯与两台高速摄像机分别相互垂直放置在升降台上(升降平台运动速度可调, 并始终保持颗粒在运动过程中始终处于相机视野内)如图1(b)所示, 并且将有灯光一侧的水箱壁面贴上柔光纸(为了使灯光均匀的照射拍摄区域); 顶端的电动释放装置用于颗粒的释放, 并且与之相连的伸缩杆可以调整释放装置与液面的距离; 调平地脚用于调整系统水平, 底座用于放置水箱, 移动滚轮用于移动系统的位置.
图1
实验中所使用的细长椭球体是用树脂材料3D打印的, 树脂密度$\rho_{c} = 1.2\pm 0.05$ g/cm$^{3}$. 3D打印可以很好的控制椭球体的尺寸, 其真实物理形状如图2(b)所示, 其中$L$表示细长椭球体的长轴, $d$表示短轴, 在实验前会将打印的椭球体进行打磨以确保物体表面光滑, 然后测得的长短轴长度的打印误差在5%以下, 可以满足实验的要求, 每种工况打印两个椭球体. 椭球体的几何信息可以用两个参数来描述, 即纵横比$L/d$, 以及等效直径$D=\sqrt[3]{Ld^2}$在本实验中, 所选椭球体几何参数范围为: $L/d= 2\sim 10$, 等效直径为$D = 5\sim 10$ mm, ($L/d$, $D$)组合参数有30组. 本实验在有机玻璃制成的水箱中进行, 水箱中加入过滤后的自来水, 并保证液位高度在1150 mm, 实验在室温(20$\pm $5${^\circ}$C)环境下进行, 对应水的密度为$\rho_{f} = 0.996\pm 0.004$ g/cm$^{3}$,运动黏性$\nu = 1.02\times 10^{-6 }$ m$^{2}$/s.
图2
图2
实验颗粒形状以及相应的坐标系
Fig.2
Particle shape in experiments and the corresponding coordinate system
实验前将水箱中装满水并静置几个小时, 并将实验颗粒用电动夹爪夹紧, 且同时保证细长椭球体的长轴为水平状态并位于液面以下, 以保证颗粒无初速度入水. 每次实验过程中, 通过设定升降平台的运动速度以保证颗粒始终在相机的视野中, 后期在数据处理过程中, 将相机拍摄得到的颗粒运动速度与平台运动速度进行叠加, 进而得到颗粒的真实运动速度. 每组工况用两个不同的椭球体进行两次重复实验, 且保证两次实验的间隔时间为1 h左右, 以减小流体内部运动对固体颗粒运动特性的影响. 需要注意的是, 根据Toupoint等 [28]的研究表明, 对于圆柱体而言, 其初始的运动角度带来的影响对圆柱体下落的最终运动形态没有影响, 因此, 本文暂时不考虑细长椭球体在不同初始角度下落的情形.
实验中不考虑椭球颗粒和液体密度的影响, 因此颗粒的下沉状态完全由($Ar$, $L/d)$来决定, 其中$Ar$是阿基米德数, 表示颗粒所受重力和黏性力的比值, 其定义方式为
其中$\rho_{c}$和$\rho_{f}$分别表示椭球体和液体的密度, $\nu $表示液体的运动黏性系数. 值得注意的是, 颗粒下沉的终态雷诺数$Re_{d}$对研究其运动状态也很有意义, 因此我们对不同工况下的$Re_{d}$也进行了统计, 如表1所示. 为了研究方便, 在本文中若无特殊说明, 长度用$D$进行无量纲化, 时间用$D/u_{0}$进行无量纲化, 其中$u_0 =\left[ \left( \rho _{c} /\rho _{f} -1 \right)gd \right]^{1/2}$.
表1 不同工况下物体运动属性
Table 1
 |
1.2 图像处理方法
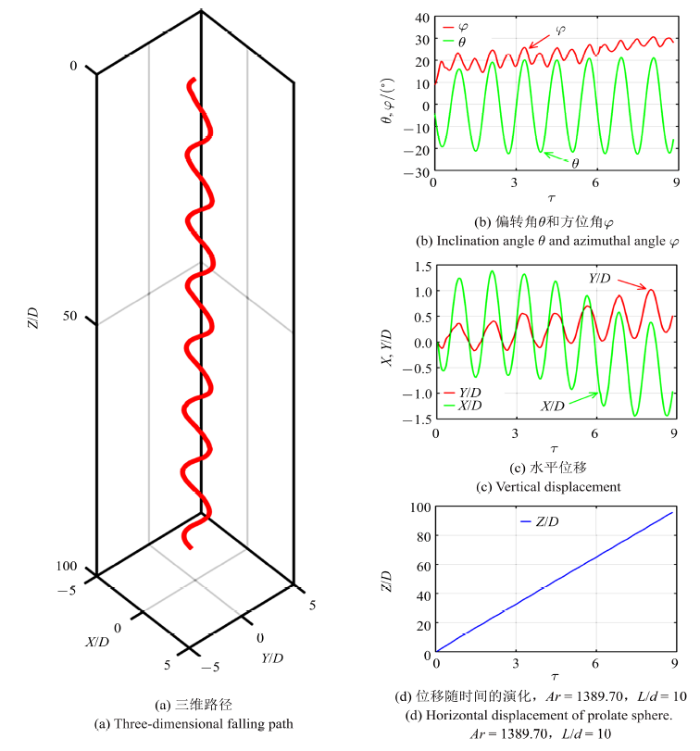
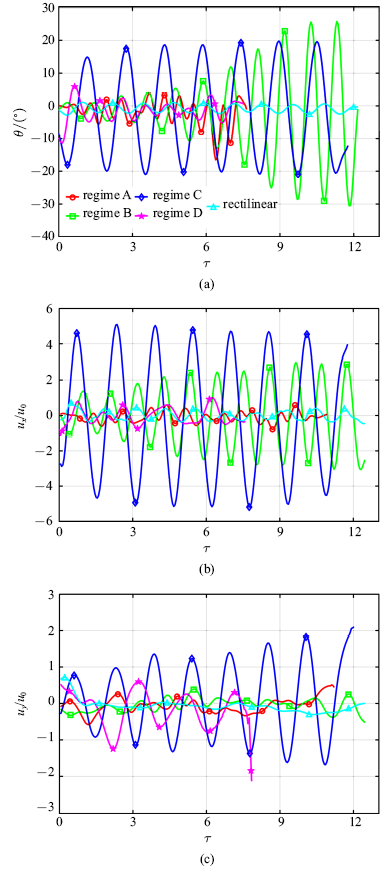
通过背光拍摄的方法, 采用两台相互垂直的高速摄像机获取物体两个方向上的投影图像, 相机输出的结果分别是($x$, $z)$和($y$, $z)$平面灰度图像, 其中$z$为垂直方向, ($x$, $y)$为水平面, 如图2(a)所示. 标定得到的图像空间分辨率为每个像素0.2 mm, 图像处理得到的物体尺寸与实际尺寸误差在10{\%}以下. 然后用两台高速摄像机跟踪拍摄得到物体在($x$, $z)$和($y$, $z)$两个平面的投影图像序列, 最后通过我们编写的MATLAB图像处理程序, 将灰度图像转化为二值化图像从而获取物体的边界, 得到物体5个自由度的信息. 图3为椭球体$L/d= 10$, $Ar= 1389.70$参数下($x$, $y$, $z$, $\theta $, $\varphi)$ 5个自由度随时间的演化情况, 图3(a)为实验室坐标系下该椭球体的三维路径图, 图3(b)为同一个椭球体偏转角$\theta $ (椭球体长轴与水平面的夹角, 如图2(a)所示)和方位角$\varphi $ (椭球体长轴在($x$, $y)$平面的投影与$y$轴的夹角)随时间的变化, 图3(c)和图3(d)为重心的三维坐标($x, y, z)$随时间的演化.
图3
图3
典型细长椭球体的运动特征
Fig.3
Time histories of the falling behaviors of a prolate sphere
图4
图4
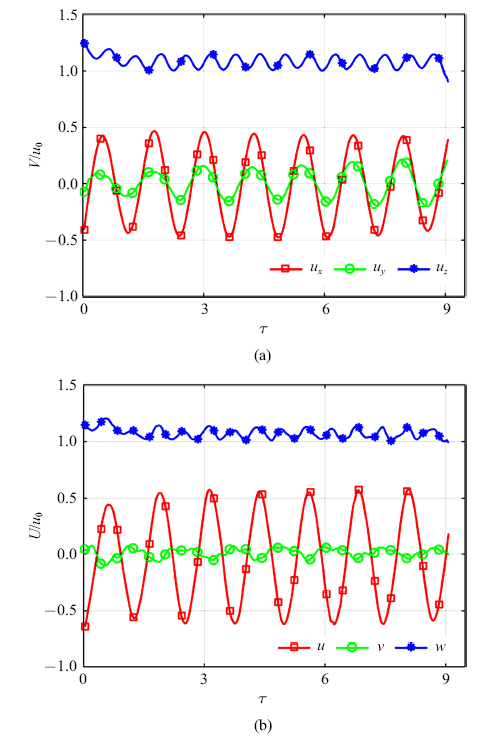
两个不同坐标系下各速度分量的对比(a) 实验室坐标系下 (b) 随体坐标系(
Fig.4
Comparison of the velocity components (a) in the laboratory frame; and (b) in the system of rotating with the body (defined in
2 实验结果与分析
2.1 细长椭球体的运动轨迹分析
在所研究的($Ar$, $L/d)$参数空间内, 我们进行了30种工况的实验(包括60次实验). 在$Ar = 400$$\sim$1400, $L/d = 2$$\sim$10参数范围内主要观察到了5种路径类型和Ern等 [2]定义的几种典型的运动特征保持一致, 分别是A状态: 小振幅不规则运动、B状态: 小振幅高频振荡运动、C状态: 大振幅低频振荡运动、D状态: 高度非线性运动和直线状态(包括垂直和倾斜直线).
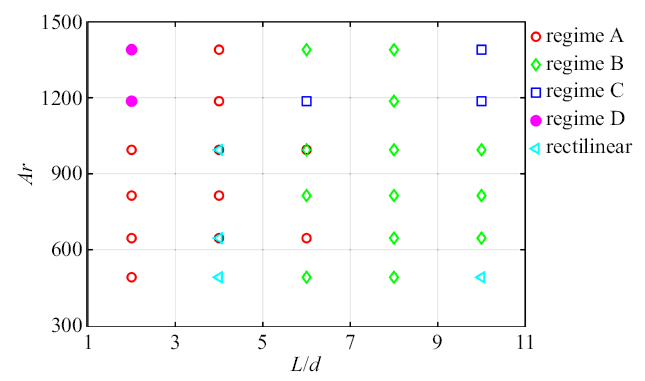
图5展示了不同路径在参数空间($Ar$, $L/d)$的分布情况. 直线运动主要发生在$L/d = 4$, 10; $Ar = 400$$\sim $1000, 其中$L/d =10$下路径为竖直的直线, $L/d = 4$下路径为倾斜的直线. Z字形振荡运动(包括B和C状态)主要发生在($Ar$, $L/d$) $\approx$ (400$\sim $1400, 6$\sim$10)范围内, 主要特点是作三维周期性震荡运动. 除此之外, 还有两种不规则运动状态, 包括小振幅不规则运动(A状态)和高度非线性运动(D状态). 其中A状态发生在($Ar$, $L/d$) $\approx$ (400$\sim $1400, 2$\sim $6), 而D状态发生在($Ar$, $L/d$) $\approx$ (400$\sim $1400, 2), 两个都是混沌运动. 需要指出的是, 图5中出现的数据点重叠现象是由于同样工况下小球运动产生的两种不同的状态.
图5
图5
不同路径在($Ar$, $L/d$)平面的相图
Fig.5
Map of the different paths observed in the plane ($Ar$, $L/d$)
图6给出了不同运动状态下偏转角和水平速度的演化过程. 从图中观察可以发现A状态的偏转角$\theta $在0$^{\circ}\sim 10^{\circ}$之间不规则振荡, 低于Z字形振荡运动(这与Toupoint [28]的不规则II很类似), 水平速度也都是小振幅不规则震荡; B状态的偏转角$\theta $在0$^{\circ}\sim 30^{\circ}$为振幅逐渐增加的谐波振荡, $u_{x}$对应的振幅先增加而后趋于稳定值, $u_{y}$对应的振幅较小, 且不规则; C状态的偏转角$\theta $是恒定振幅为20$^{\circ}$的谐波震荡, $u_{x}$是振幅为恒定值谐波振荡以及$u_{y}$为振幅增加的谐波振荡, 图3和图4分别描述了($Ar$, $L/d$) $\approx$ (1389.70, 10)的细长椭球颗粒在水中作Z字型振荡运动时其路径和速度随时间的变化规律, 从图3(a)和3(b)可以发现颗粒在水平方向的位移振幅在$1.5D\sim 3D$之间, 偏转角$\theta $的震荡频率为1.5 Hz 左右, 为状态B的1.5倍. 进一步从图4(a)也可发现竖直速度分量$u_{z}$是水平速度($u_{x}$, $u_{y})$振荡频率的两倍, 这些现象与Fernandes等 [34]和Toupoint等 [28]得到的结果一致, 这种现象是由颗粒在做Z字形运动时颗粒两侧周期性涡脱落引起的, 涡每脱落一次就会产生阻力的变化, 从而引起竖直速度的振荡, 而水平速度的振荡则与升力相关, 需要涡脱落两次才完成升力的一个周期性变化. 高度非线性运动的偏转角$\theta $在0$^{\circ}\sim 15^{\circ}$之间不规则振荡, $u_{x}$为小振幅不规则振荡以及$u_{y}$是大振幅不规则振荡; 直线运动的偏转角$\theta$为恒定振幅3$^{\circ}$的谐波振荡, 其水平速度都是小振幅不规则震荡. 这样通过不同路径的偏转角和水平速度随时间演化的特点可以对路径进行清晰地分类.
图6
图6
不同路径类型所对应的典型物体的偏转角$\theta $以及水平速度随时间的演化比较, A状态: 小振幅不规则运动($L/d$ = 2, $Re_{d}$ =449.02)、B状态: 小振幅振荡运动($L/d$ = 6, $Re_{d}$ =372.08)、C状态: 大振幅振荡运动($L/d$ = 10, $Re_{d}$ = 474.60)、D状态: 高度非线性运动($L/d$ = 2, $Re_{d}$ = 1304.29)、直线运动($L/d$ = 10, $Re_{d}$ = 149.76)
Fig.6
Comparison of the time of inclination angle$\theta $ and horizontal velocity of the typical prolate sphere corresponding to different path types, for the low-amplitude irregular motion ($L/d$ = 2, $Re_{d}$ = 449.02), for the low-amplitude fluttering ($L/d$ = 6, $Re_{d}$ = 372.08), for the high-amplitude fluttering ($L/d$ = 10, $Re_{d}$ =474.60), for the highly nonlinear motion ($L/d$ = 2, $Re_{d}$ = 1304.29), and for the rectilinear motion ($L/d$ = 10, $Re_{d}$ = 149.76)
2.2 速度和阻力分析
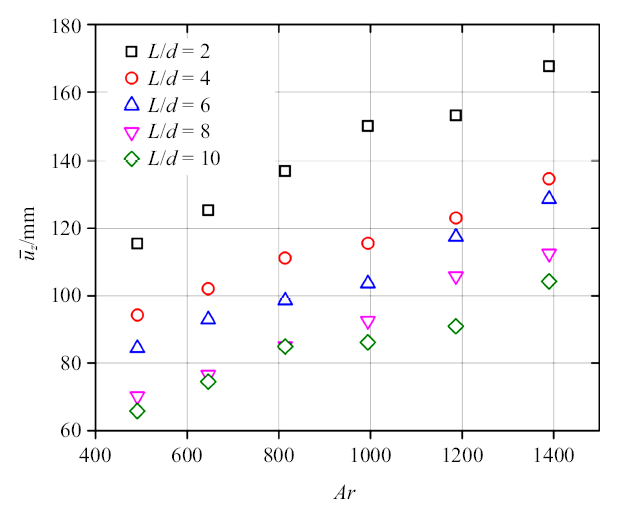
为了进一步研究其运动特性, 本节对物体的速度以及阻力进行定量的分析和讨论. 将物体从静止释放后, 我们将两次实验的垂直下降的最终速度进行平均得到$\overline u _z $, 速度的范围为65.8$\sim $167.62 mm/s. 对于给定的($Ar$, $L/d)$, 两次实验的平均速度相对误差在8{\%}以内, 通过两次数据平均的方法以降低实验误差.
图7给出了随着$Ar$和$L/d$的变化, 平均下落最终速度$\overline u _z $的变化情况, 可以从图中明显看出, 随着$Ar$的增加(颗粒体积增大), 颗粒的下落最终速度呈现线性的增加; 而当固定小球体积时($Ar$固定)随着细长椭球体的长短轴比$L/d$ 的增加, 其下落最终速度逐渐减小. 这一现象产生的主要原因是$L/d$的增加所带来的细长椭球体迎风面积增大, 进而导致其运动阻力增大、最终下落速度减小. 进一步地, 我们基于平均速度$\overline u _z $、椭球体的短轴长$d$定义了雷诺数$Re_{d} =\overline u _z d/\nu $, 并建立阻力与浮力的平衡关系如下面公式, 其中$C_{d}$表示阻力系数, 可以得
其中$\gamma = 4\pi(d/2)^{2}L/6$为细长椭球体的体积, $S =\pi dL/4$为椭球体在下落时的迎风面积.
图7
图7
不同$L/d$下终态速度与$Ar$之间的关系
Fig.7
Average terminal velocity versus Archimedes number for various $L/d$
图8
图8
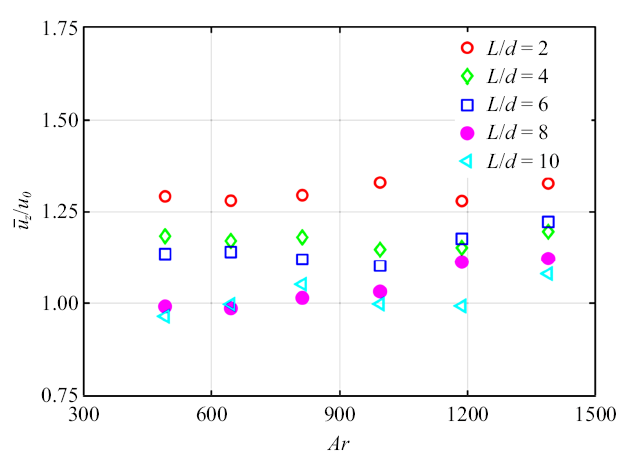
在不同$L/d$下无量纲化平均速度与$Ar$之间的关系
Fig.8
Average vertical velocity scaled by the gravitational velocity versus the Archimedes number for various elongation ratios
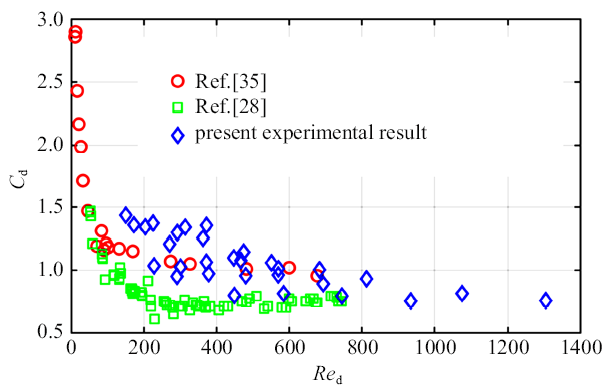
图9给出了各种实验工况下的阻力系数与$Re_{d}$的关系, 并将本实验结果与前人文献中圆柱自由下落的结果进行对比. 在实验参数范围内, 阻力系数$C_{d}=0.7$$\sim $1.5. 本文结果与Jayaweera等 [35] ($L/d >100$的金属圆柱在不同密度的液体中下落)和Toupoint等 [28] ($2\leqslant L/d \leqslant 20$的塑料圆柱在水中下落)的实验结果进行比较, 可以发现本文结果与Jayaweera等 [35]的结果符合较好, 而与Toupoint等 [28]的实验结果有一定的偏差. 产生这一现象的主要原因是实验过程中本文的细长椭球体的偏转角为$\theta = 0^{\circ}\sim 30^{\circ}$, 比Toupoint等 [28]的圆柱下落时的偏转角($\theta <25^{\circ})$要大一些, 较大的偏转角引起颗粒运动过程中产生更大的阻力. 从图9中还可以看出, 颗粒下落的阻力系数在$Re_{d}<200$时, 随着$Re_{d}$增大呈现急剧下降的趋势, 而当$Re_{d}\geqslant200$时, 颗粒下落的阻力系数变化趋于平缓.
图9
图9
自由下落的椭球体阻力系数$C_{d}$与$Re_{d}$之间的关系
Fig.9
Drag coefficient of the freely falling prolate spheres versus Reynolds number
2.3 振荡频率的分析
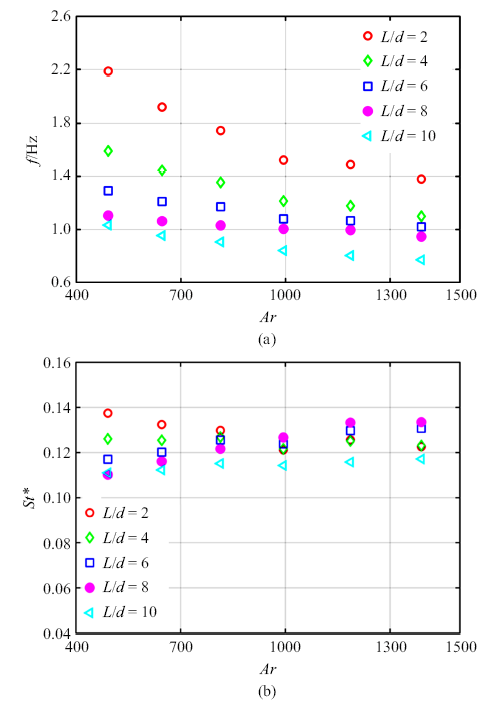
通过将细长椭球体的偏转角$\theta $进行频谱分析, 我们获得了其球体下落过程的摆动频率, 并绘制在图10(a)中. 从图中可以看出, 频率$f = \omega /2\pi $的范围为0.7$\sim $2.2 Hz, 且随着$Ar$数的增大而逐渐减小. 对比$L/d = 2$的短椭球体, 其摆动频率随$Ar$数的增大而迅速减小, 从2.2 Hz下降到1.4 Hz左右; 而对于较长的椭球体, $L/d$ = 10, 其摆动频率随$Ar$数增大减小较小, 从1.0 Hz左右下降到0.7 Hz左右. 若将无量纲长度变为$L_0 =\sqrt{dL} $, 特征速度不变, 将振荡频率$f$进行无量纲化得到$St^{\ast}= fL_{0}/u_{0}$. 从图10可以看出$St^{\ast }$几乎与$L/d$和$Ar$无关而趋于恒定的值0.12. 这与Fernandes等 [36]短圆柱的实验($L/d = 0.1\sim 0.5$)结果和Toupoint等 [28]细长圆柱的实验($L/d = 2\sim 20$)结果$St^{\ast}= 0.11$相比非常接近. 由于这些物体的振荡频率隐藏在固有的和附加的惯性项以及考虑黏性和尾迹效应的涡流贡献之间的复杂平衡中, 因此沿着这个思路进一步研究存在于物体表面的不稳定边界层特征.
图10
图10
不同$L/d$下偏转角, 振荡频率$f$及无量纲化后的$St^{\ast}$随$Ar$的演化对比
Fig.10
Comparison of the oscillations frequency $f$ and the $St^{\ast }$ of the body inclination angle versus the $Ar$ for various elongation ratio $L/d$
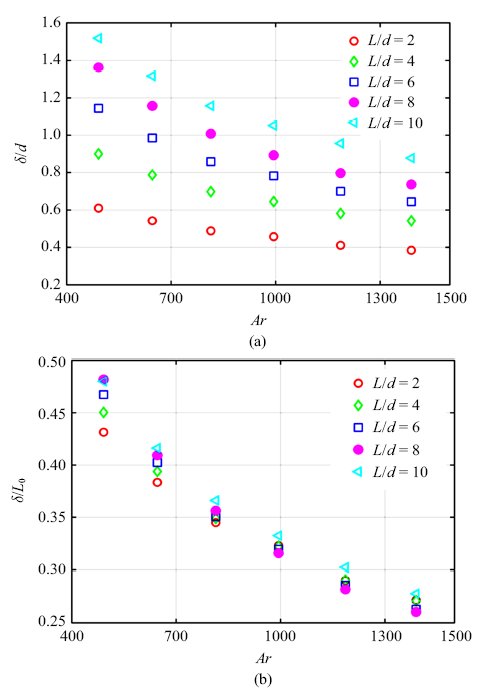
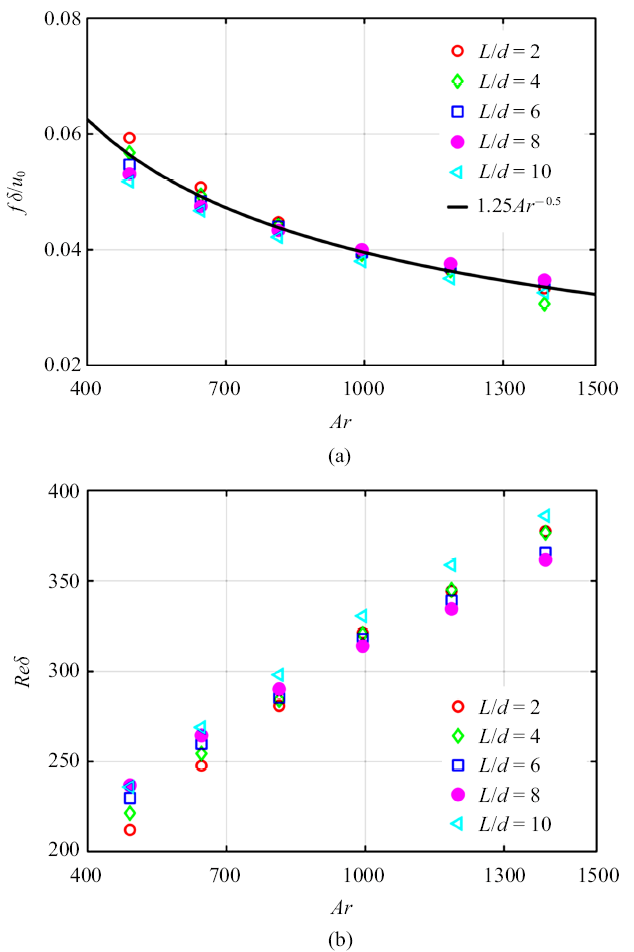
由于物体振荡的频率$f$大于黏性扩散频率$v/d^2$ (6倍$L/d =10$, $Ar=491.33$到175倍$L/d=10$, $Ar=1389.70$), 因此远离物体表面的涡黏性扩散就会受到限制以至于速度剧烈变化以适应无滑移边界条件. 下面引入非定常边界层厚度$\delta=2\pi\sqrt{2v/\omega}$作为相关的特征长度尺度 [25]. 图11(a)表明与椭球体的短轴$d$的尺度是相当的, 在相同$L/d$下, 随着$Ar$的增大而减小; 在相同体积下, 随着$L/d$的增大而增大. 鉴于这一变化关系我们将$\delta$用$L_0$无量纲化后发现$\delta$与$L/d$无关, 随着$Ar$的增大而线性减小, 如图11(b)所示. 因此$L/d$的作用可以通过特征长度$L_0$和$\delta$来获得, 图10和图11的结果可以用图12(a)和图12(b)两种形式来阐释. 图12(a)说明基于$\delta$无量纲化的$St^*_{\delta}=f\delta/u_0$是与$L/d$无关的, 并且和$Ar$的关系可以用$St^*_{\delta}=1.25Ar^{-0.5}$进行拟合, 随着$Ar$的增大而减小. 图12(b)是基于$\delta$的$Re_{\delta}=u_0\delta/v$也与$L/d$无关而随着$Ar$的增大而线性增大, 这与图7形成对比. 图12(a)和图12(b)中$St^*_{\delta}$和$Re_{\delta}$对于$Ar$的依赖性和对$L/d$的独立性说明物体的体积的重要性而不再是具体的形状, 以及椭球体的尖端在控制运动物体非定常边界层扩展具有重要的作用.
图11
图11
在不同的$L/d$下, 不稳定边界层厚度$\delta$分别在椭球体短轴长$d$和$L_0 =\sqrt {dL}$的无量纲化下随着$Ar$的演化
Fig.11
Thickness of the unsteady boundary layer $\delta$ versus $Ar$ for various elongation ratios, normalized with the prolate sphere minor axis $d$ and $L_0 =\sqrt{dL}$
图12
图12
基于不稳定边界层厚度$\delta$的$St^{\ast}= f\delta /u_{0}$, $Re_{d} =u_{0}\delta /\nu$与$Ar$的关系
Fig.12
Based on the thickness of the unsteady boundary. $St^{\ast}$ and Reynolds number versus $Ar$
2.4 物体尾涡可视化研究
最后对细长椭球体在水中自由下落过程中不同路径所对应的尾涡结构和特性进行定性的分析, 实验前先将椭球体放入高浓度的荧光素钠溶液中浸泡两个小时, 然后取出风干使其均匀的覆盖在椭球体表面, 主要为了使染色的球体运动足够远的距离以便能更好的观察涡演化的过程.
分别对小振幅不规则运动(A状态)、Z字形振荡运动(包括B和C状态, 由于Z字形运动的尾涡是类似的, 因此选取了一组大振幅振荡的尾涡)、高度非线性运动(D状态)、直线运动各选取一组典型椭球体进行尾涡可视化实验. 如图13所示, 左图为该椭球体重心的三维位置及其偏转角$\theta $演化的示意图, 右图为相应的尾涡随时间的演化图. 图13(a)对应于A状态, 其特征是会观察到不相连的发卡状涡交替从细长椭球体两侧交替脱落, 其脱落的频率为6$\sim $7 Hz, 这与 Veldhuis等 [37] (对于$Re_{d} = 608$, $\overline \rho =1.05$)的球体尾迹类似. 图13(b)对应于C状态, 由于尾迹与物体运动的耦合以及物体轴相对于速度方向的角度影响从而导致了明显不同的尾迹, 其特征是细长椭球体的两侧脱落涡时会产生一个周期性变化的升力从而导致物体周期性振荡运动; 涡脱落的频率和竖直速度振荡的频率是相同的, 偏转角$\theta $振荡频率是其一半, 这是因为物体两侧各脱落一次涡时分别对应于偏转角$\theta $一个周期的波峰和波谷; 涡刚开始从平衡位置脱落和脱落完成时对应的竖直速度达到最大值, 相应的加速度达到最小, 这与Toupoint等 [28]在$Re_{d} = 585$, $L/d = 5$的圆柱观察到的尾迹是类似的; 图13(c)对应于运动类型D, 其特征是在高雷诺数下尾迹呈现出混沌的状态, 这与Veldhuis等 [37] (对于$Re_{d} = 1261$, $\overline \rho =2.63$)的球体的尾迹类似, 同样类似的尾涡结构在Cano-Lozano等 [38]文中的气泡作混沌上升时也被观察到, 在他们的数值模拟中, 发现气泡在高雷诺数情况下做无规则的混沌运动, 但路径振幅显著小于气泡作Z字型或者螺旋型运动时, 大概只有气泡直径的1/10或者更小, 这些特征与图13(c)的结果相符. 图13(d)对应于直线运动类型, 其特征是在细长椭球体两侧会周期性地脱落出旋转方向相反、左右交替脱落的漩涡, 这种漩涡具有一定的脱落频率, 这也被称为卡门涡街; 这与Toupoint等 [28](对于$Re_{d} = 50$, $L/d = 10$的塑料圆柱)以及Jayaweera [35] (对于$Re_{d} = 70$, $L/d = 10$金属圆柱)实验中的尾迹几乎是一样的, 其脱落的频率也在6$\sim $7 Hz.
图13
图13
不同路径以及对应的尾迹随时间的演化, 每幅尾迹图的上下图分别为该时刻的正视图和侧视图 (a) 小振幅不规则振荡运动($L/d = 2$, $Re_{d} = 449.02$) (b)大振幅低频振荡运动($L/d = 10$, $Re_{d} = 474.60$) (c)高度非线性运动($L/d = 2$, $Re_{d} = 1304.29$) ($d)$直线运动($L/d = 10$, $Re_{d} =149.76$)
Fig.13
Examples of the time of evolution of three-dimensional path and corresponding wake , the upper and lower parts of each wake diagram are the front view and the side view of the time, respectively, (a) for the low-amplitude irregular motion ($L/d = 2$, $Re_{d}$ = 449.02); (b) for the high-amplitude fluttering ($L/d$ = 10, $Re_{d}$ = 474.60), (c) for the highly nonlinear motion ($L/d$ = 2, $Re_{d}$ = 1304.29); and (d) for the rectilinear motion ($L/d$ = 10, $Re_{d}$ = 149.76)
通过对不同细长椭球体尾迹的观察可以发现, 一方面随着雷诺数的增加, 尾迹会变得越来越不规则; 另一方面当$L/d \to 1$时, 细长椭球体的运动状态和球体的类似, $L/d \to 10$时, 细长椭球体的运动状态和细长圆柱($L/d = 10$)的类似. 由于实验参数范围有限, 因此没有观察到文献[28]中提到的条纹状涡($L/d$ = 3, $Re_{d}$ = 120)以及倾斜的涡脱落模式($L/d$ = 20, $Re_{d}$ = 130), 后面会扩大参数范围进一步理解和分析细长椭球体在液体中的运动特性.
3 结论
本文通过实验研究了细长椭球体在液体中自由下落的运动特性, 通过高速摄像机拍摄其运动过程和尾涡结构, 然后获取其运动路径、方向角度、振荡频率等的变化趋势, 并通过进一步分析得到以下结论:
(1) 对于所研究的参数范围($2\leqslant L/d \leqslant 10$, $400\leqslant Ar\leqslant1400$), 根据偏转角以及水平速度的演化特点将路径分为5类: 小振幅不规则运动(A状态)、包括小振幅高频振荡运动(B状态)、大振幅低频振荡(C状态)、高度非线性运动(D状态)、直线运动. 这五类运动路径与物体形状以及体积有关.
(2) 在相同参数范围下本文研究的细长椭球体受到的阻力系数$C_{d}$明显大于Toupoint等 [28]对于圆柱阻力系数的测量结果, 产生阻力增大的主要原因是本文研究的椭球体相比圆柱体在下落时的偏转角\lb 更大.
(3) 通过引入特征长度尺度$\delta =2\pi \sqrt {2\nu /\omega }$和特征速度尺度$u_0 =\left[ {\left( {\rho _{c} /\rho _{f} -1} \right)gd}\right]^{1/2}$, 发现$St^{\ast}= f\delta/u_{0}$和$Re_{d}=u_{0}\delta/\nu $取决于$Ar$变化而与$L/d$无关. 一方面说明物体的体积是很重要的参数而不再是具体的物体形状, 另一方面说明椭球体的尖端在控制运动物体附近的非定常边界层的扩展有很重要的作用, 这一点和细长圆柱体两端的作用类似.
(4) 通过对各种路径下尾涡的研究, 首先验证了Mehdi等 [30]中细长椭球体会绕垂直轴旋转这一结论. 其次通过对不同细长椭球体尾迹的观察可以发现, 一方面随着雷诺数的增大, 尾迹会变得越来越不规则; 另一方面当$L/d \to 1$时, 细长椭球体的运动状态和球体的类似, $L/d \to 10$时, 细长椭球体的运动状态和细长圆柱($L/d$ = 10)的类似.