引言
滚石灾害多发于斜坡,坡体既包括整体稳定的斜坡,也包括正在运动中的坡体和崩塌体等. 但是已有的碰撞理论模型中大多将滚石碰撞模型简化为质点的碰撞[20-22]或圆盘/球与静止平板的碰撞[7,23-27];而滚石与斜板碰撞理论模型比较少见[3]. 同时Pei等[28]在研究中发现坡体表层松散滑动易诱发小型基地岩块失稳,更容易发生滚石灾害. 张正雄等[29]也发现考虑滚石碰撞到运动滚石时可大大提高滚石落下的个数,且相较于单块岩体沿静止坡面滚下具有更大的冲击力. 也就是说运动中的坡体和崩塌体更易诱发和扩大滚石灾害,其坡体和崩塌体的运动情况对滚石碰撞过程的影响不容忽视. 但已有研究中关于滚石冲击到运动中坡体的碰撞理论模型鲜见报道. 因此导致了滚石碰撞理论模型预测结果与实际结果出入较大, 滚石碰撞模型精准预测仍面临着巨大挑战.
1 滚石颗粒随机撞击模型的建立
1.1 理论模型的选取
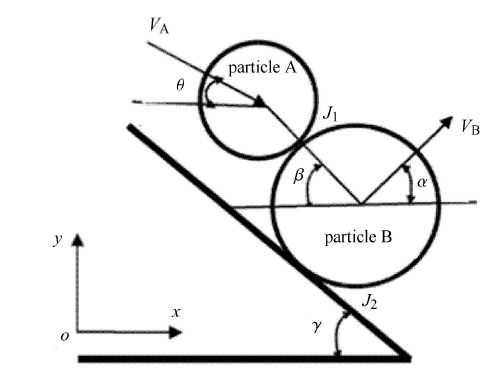
自然界中,崩塌的滚石颗粒带有一定的速度冲击到复杂地形的斜坡或者斜坡上的其他运动滚石颗粒上,入射速度和角度、碰撞位置等都是随机的,并且斜坡滚石颗粒碰撞过程时间短、受力复杂,滚石颗粒形状各异,使得直接建模困难较大. 为描述碰撞的 复杂性以及普遍性,将滚石与斜坡碰撞进行如下处理,建立等效模型. 虽然滚石运动为三维运动,但滚石运动的主方向仍可近 似认为是平行于入射速度平面内的二维运动[32]. 为简化模型,采用已有文献中常用的处理方法,将非规则形态的滚石颗粒碰撞简化为二维均质圆盘之间的碰撞,且碰撞为非弹性的[32],碰撞过程如图1所示,即:等效半径$R_{A}$的崩塌滚石颗粒A以某一速度直接与斜坡($R_{B} \to \infty $)或斜坡上某一运动的等效半径为$R_{B}$的滚石颗粒发生碰撞,碰撞的位置为$J_{1}$,其中崩塌滚石A的入射速度大小记为$V_{A}$,入射角度为$\theta $(将与水平方向$x$轴所成的角度记为$\theta $);为了反映运动坡体对滚石碰撞过程的作用,可由坡体上被碰颗粒B的运动情况来承载,将坡体上被碰颗粒B在碰撞前的速度作为运动坡体的速度记为$V_{B}$,坡体上被碰滚石颗粒B与斜坡的接触位置为$J_{2}$,且$V_{B}$与水平 方向的夹角记为启动角$\alpha $;将颗粒A,B质心连线与水平方向的夹角记为撞击角$\beta$,由于斜坡地 形复杂,撞击角$\beta $随着地形的变化而变化;斜坡坡角设为$\gamma $.
图1
在图1所示的滚石颗粒撞击模型中,斜坡角$\gamma $、滚石A的入射速度$V_{A}$、入射角$\theta$和斜 坡上滚石B的运动速度以及启动角$\alpha$均受滚石尺寸以及斜坡等因素决定且是随机变化的,滚石颗粒A和B的碰撞点$J_{1}$,颗粒B与斜坡的接触点$J_{2}$也是随机变化的,即碰撞角度$\beta$是随机变化的.
1.2 基本方程的建立
(1) 对于滚石A和B的碰撞压缩阶段,即:从碰撞开始到碰撞压缩量达到最大时,所遵循的力学方程如下:
颗粒A切向方向的碰撞冲量表示为
颗粒A法向方向的碰撞冲量表示为
颗粒A依据冲量矩定理得到
颗粒B的$x$方向的冲量为
颗粒B的$y$方向的冲量为
颗粒B依据冲量矩定理得
(2) 颗粒A和B碰撞完成后整个碰撞过程所遵循的力学方程如下:
颗粒A的碰撞后切向冲量表示为
颗粒A的碰撞后的法向冲量表示为
颗粒A依据冲量矩定理得
颗粒B的$x$方向的冲量为
颗粒B的$y$方向的冲量为
颗粒B依据冲量矩定理得
其中,$U'_{{A}x}$,$U'_{{A}y}$,$\omega'_{A}$分别是颗粒A在压缩结束时质心速度的水平与垂向分量以及角速度; $U'_{{B}x}, U'_{{B}y}, \omega'_{B}$分别是颗粒B在压缩结束时质心速度的水平与垂向分量以及角速度; $S'_\tau, S'_n$分别为颗粒A与B之间的切向和法向碰撞冲量; $U_{{A}x}, U_{{A}y}, \omega _{\rm A}$分别是颗粒A在碰撞结束时的质心速度的水平与垂向分量以及角速度; $U_{{B}x}, U_{{B}y}, \omega _{B}$分别是颗粒B在碰撞结束时的质心速度的水平与垂向分量以及角速度; $S_\tau , S_n $分别为颗粒A, B接触点处的切向和法向碰撞冲量; $S'_1, S'_2 $分别为在碰撞过程中压缩变形达到最大时,斜坡作用在颗粒B接触点处的切向和法向冲量; $S_1, S_2$分别为碰撞结束时B受到斜坡的切向和法向冲量.
1.3 连接条件
上述模型的基本方程共12个,但是有20个未知量,显然方程组不封闭,因此需要补充连接条件.
根据两颗粒碰撞时的接触点处的连接条件得到方程,对于两颗粒的接触点$J_{1}$得:
$x$方向的平衡方程
$y$方向的平衡方程
对于B颗粒与地面接触点$J_{2}$得:
$x$方向的平衡方程
$y$方向的平衡方程
各个冲量之间的关系为
由于碰撞为不完全非弹性碰撞,所以本文考虑的法向、切向碰撞恢复系数,即$k_{1}, k_{2}$采用的是Xie等[34]恢复系数公式,在此不再赘述.
2 结果分析
将方程(1)$\sim$(20)进行联立求解,得到含有坡角$\gamma $,入射速度$V_{A}$,入射角度$\theta $,碰撞角度$\beta $,颗粒B的速度$V_{B}$以及启动角度$\alpha $等参数的反弹颗粒速度($U_{{A}x}$,$U_{{A}y} $,$\omega _{A} $)的解析解.
我们利用等间距直方图理论[37]计算滚石颗粒反弹速度以及角度的频率. 假设样本空间包括所有的反弹速度和角度,将 其作为随机变量$X$,其中随机变量个数为$n$. 假设$a=\min\{X\}$,$b =\max \{ X \}$,将区间$[a-\varepsilon $, $b+\varepsilon ]$ 等分为$m$个小区间,其中$\varepsilon $是小的正数,统计出落在小区间$i$中$(i=1, 2, \cdots , m)$ 样本的频数$f_{i}$,得到频率$P(x_i ) = f_i / n$.
计算过程主要分为如下几个部分:(1) 划分入射角度$\theta $、碰撞角度$\beta $所在的区间,且假设上述随机变量在区间内为等概率分布. (2) 由于碰撞角度$\beta $范围与入射角度$\theta $有关,一个入射角$\theta$对应一个$\beta $的区间,选取$\beta $每个子区间中的均值代入反弹颗粒解析解中. (3) 重复过程(2)得到不同入射角$\theta $下每个子区间下的值作为样本. (4) 确定固定坡角下所有的样本空间并输出频率.
2.1 滚石-壁面碰撞模型验证与分析
表1 模型计算数据与试验数据对比
Table 1
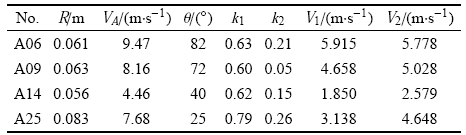 |
Notes: VA is the experimental incident velocity, V1 is the experimental rebound velocity, and V2 is the theoretical rebound velocity.
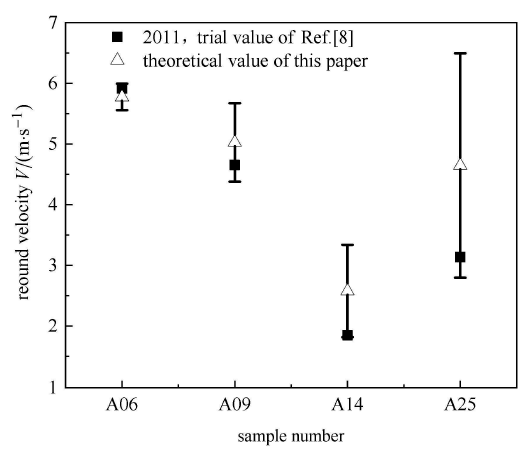
图2
图2
理论结果与试验结果对比
Fig.2
Comparison of theoretical results with experimental results
从图2可以看出,由于滚石碰撞的位置不同,即碰撞角不同,在相同的碰撞条件下,其反弹速度不是一个固定值,而是在一定范围内变化,再次说明了滚石碰撞位置影响颗粒反弹速度,颗粒反弹速度随撞击位置而变化,应有一个分布范围. 因此,上述对比分析说明了该理论模型具有适用性,同时表明影响滚石-壁面碰撞过程的因素都是随机的,且对滚石运动产生明显影响.
2.2 坡体上被碰颗粒B的速度${V}_{B}$对反弹滚石运动特性概率分布的影响
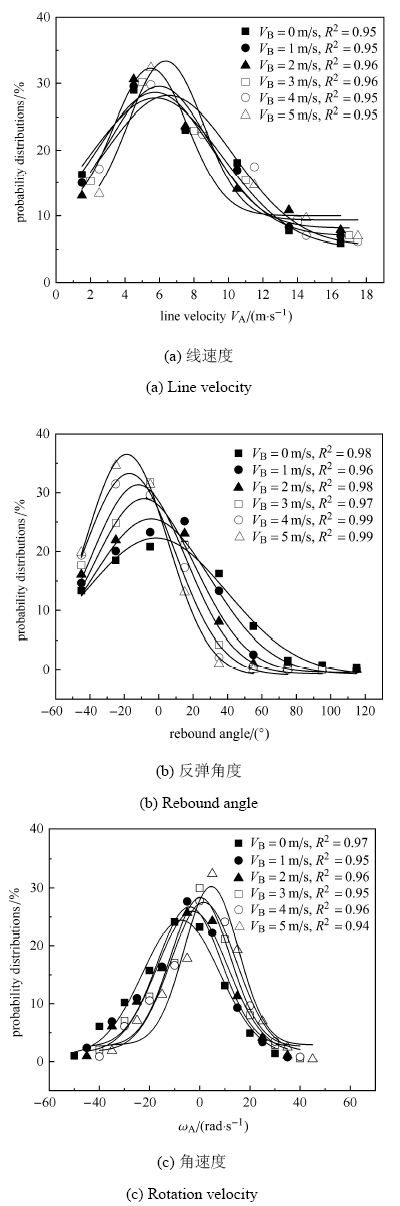
图3
图3
$V_{B}$不同时,碰后反弹颗粒速度以及角度概率分布 ($V_{B} =0$,1,2,3,4,5 m/s,$R_{A}=R_{B} =0.2$ m)
Fig.3
Rebound particle velocity and angular probability distribution after collision when the particle B' velocity is different ($V_{B} =0$,1,2,3,4,5 m/s, $R_{A}=R_{B}=0.2$ m)
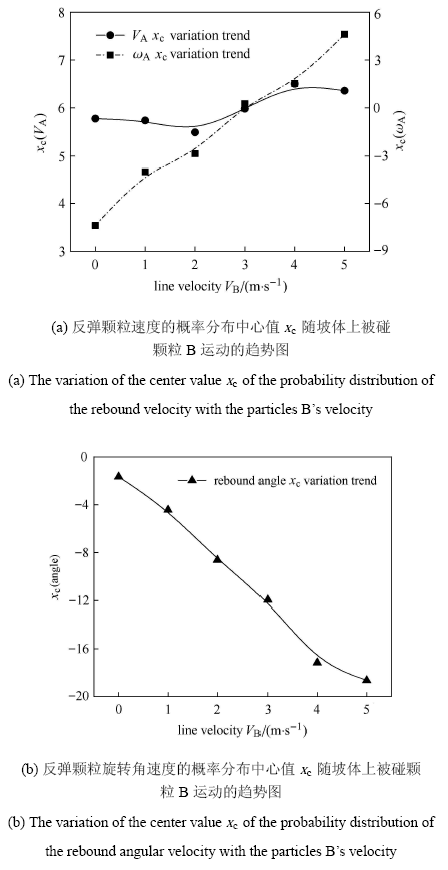
由图3可知,反弹滚石颗粒的速度和角度以及反弹旋转角速度均服从高斯分布$(y = y_0 + (A /$ $ (\sqrt{\pi / 2} w) {e}^{[ - 2(x - x_{c} ) / w]^2})$,坡体上被碰颗粒B的速度对反弹颗粒线速度和角度以及反弹角速度概率分布形式定性上影响不大,但对其概率分布定量上有显著影响,例如随着坡面运动速度逐渐增大,反弹速度和反弹旋转角速度的高斯分布的中心值$x_{c}$呈线性增大如图4(a)所示,其中反弹角速度的中心值影响显著;如图4(b)所示,反弹角度的高斯分布的中心值$x_{c}$呈线性减小. 即:当崩塌滚石碰撞到斜坡上其它运动滚石上时$(V_{B} \ne 0)$,反弹速度和旋转角速度均值均要高于碰撞到斜坡上其它静止滚石上$(V_{B}=0)$时的情况,坡体上被碰滚石颗粒的运 动更利于滚石颗粒的反弹,且反弹后速度和旋转角速度增大,这一结论与文献[29]中的结论一致. 也就是说在滚石灾害预测中,进入下一碰撞周期时的能量增大,灾害的破坏能力和范围也更大.
图4
图4
反弹颗粒速度和旋转角速度的概率分布的中心值$x_{c}$随坡体上颗粒B运动情况的趋势图 ($V_{B}=0$,1,2,3,4,5 m/s, $R_{A}=R_{B} =0.2$ m)
Fig.4
The variation of the center value $x_{c}$ of the probability distribution of the rebound velocity and angular velocity with the particles B velocity ($V_{B}=0$,1,2,3,4,5 m/s, $R_{A}=R_{B} =0.2$ m)
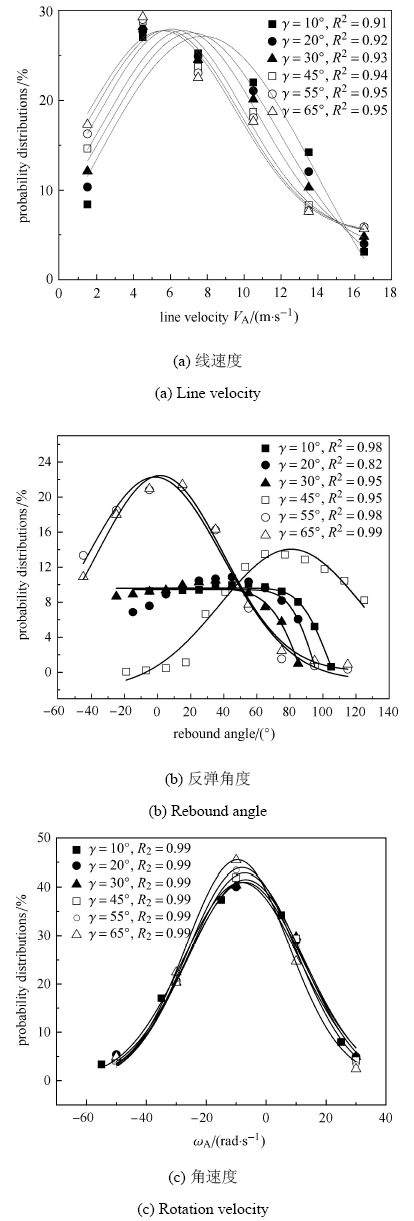
2.3 坡角对反弹滚石运动特性概率分布的影响
图5
图5
静止坡面,不同坡角下碰后反弹颗粒速度以及旋转角速度的概率分布 ($\gamma =10^\circ$,20$^\circ$,30$^\circ$,45$^\circ$,55$^\circ$,65$^\circ$,$R_{A}=R_{B} =0.2$ m)
Fig. 5
Probability distribution of rebound particle velocity and rotational angular velocity on a stationary slope with different slope angles ($\gamma =10^\circ$,20$^\circ$,30$^\circ$,45$^\circ$,55$^\circ$,65$^\circ$,$R_{A}=R_{B} =0.2$ m)
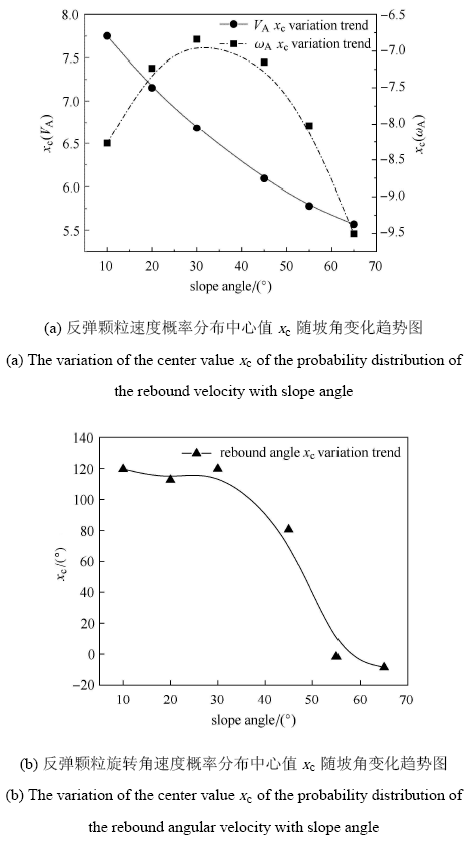
由图5可知,反弹滚石颗粒速度和角度以及反弹旋转角速度均服从高斯分布形式 $( y = y_0 + (A / (\sqrt{\pi / 2} w)){e}^{[ - 2(x - x_{c} ) / w]^2})$,从图5(b)中,可以看出坡角为45$^\circ$时,反弹角的概率密度曲线虽然仍服从高斯分布,但是与其他角度 的曲线图趋势有明显不同,由图5(b)可知, $\gamma =45^\circ$的反弹角度概率密度相比$\gamma =10^\circ$, $\gamma=20^\circ$和$\gamma=30^\circ$的反弹角度概率密度明显增大;而当坡角大于45$^\circ$时,反弹角度概率密度明显增高,且概率密度峰值发生左移. 即针对滚石反弹角度来说,坡角45$^\circ$是一个临界坡度值,这一结论与文献[39]定性上是一致的.
坡角对反弹线速度和角度以及反弹旋转角速度概率分布形式定性上影响不大,但对其概率分布定量上有明显影响,由图6所示,随着坡角的逐渐增大,反弹速度和角度的高斯分布的中心值$x_{c}$逐渐减小,反弹旋转角速度的高斯分布的中心值$x_{c}$先增大后逐渐减小.
图6
图6
反弹颗粒速度和旋转角速度的概率分布的中心值$x_{c}$随坡角变化趋势图 ($\gamma =10^\circ$,20$^\circ$,30$^\circ$,45$^\circ$,55$^\circ$,65$^\circ$,$R_{A}=R_{B} =0.2$ m)
Fig.6
The variation of the center value $x_{c}$ of the probability distribution of the rebound velocity and angular velocity with slope angle ($\gamma =10^\circ$,20$^\circ$,30$^\circ$,45$^\circ$,55$^\circ$,65$^\circ$,$R_{A}=R_{B} =0.2$ m)
3 结论与讨论
3.1 结论
基于上述理论分析,得出以下的初步结论:
(1) 本文建立了普适的斜坡滚石碰撞模型,该碰撞模型可描述滚石与斜坡、滚石与滚石、滚石与平板,滚石与运动床面的碰撞过程.
(2) 得到了滚石碰撞后反弹滚石颗粒速度解析解,这一解析解包含了影响滚石碰撞过程的6个随机因素,即:坡角、坡体上被碰颗粒B的速度和角 度、入射速度和角度、撞击角度等随机因素.
(3) 该理论模型结果显示,反弹滚石速度和角度以及反弹旋转角速度的概率分布均服从高斯分布形式,坡体上被碰滚石颗粒B的速度和坡角对反弹滚石速度和角度以及反弹旋转角速度的概率分布定性上没有影响,但对高斯分布的中心值参数有显著影响.
3.2 讨论
该理论碰撞模型反映的是滚石-斜坡单次碰撞过程,对滚石运动演化全过程的预测存在一定的局限性,不能直观表述滚石多次、连续的碰撞过程. 但是本模型中得到的碰后速度与滚石进入下次碰撞的入射速度和能量有密切关系,且碰后速度的变化是计算滚石冲击力、冲击能量以及运动距离的关键输入参数,可为滚石灾害范围预测以及被动防护装置结构设计提供一定的理论依据.
另外,实际落石运动演化过程是不规则形状滚石三维运动过程,简化后的二维圆盘碰撞理论模型在主要运动方向上可以体现碰撞过程的运动特性,反映碰后速度变化,但是仍然会忽视了垂直于圆盘方向上的速度变化和能量耗散,并且简化后的圆盘忽略了不规则滚石形心和质心不重合带来的接触点和力的作用点变化的影响,使得预测结果与实际落石速度以及运动轨迹存在一定的误差. 因此,在进一步的研究中,试图将二维圆盘碰撞拓展为三维球体,并将滚石的不规则形状考虑进去,使得滚石-斜坡碰撞模型更接近实际情况,进一步提高滚石-斜坡碰撞理论模型的预测精度.