引言
已于2019年12月通车运营的敦格铁路DK79-DK90段穿越库姆塔格沙漠东缘的沙山沟,沟谷两侧分布大量星形沙丘. 受到铁路设计标准和最小曲线半径的限制,部分线路位于沟谷西侧沙丘上,且铁路工程轨面高度与沙丘高度相近,受到风沙灾害的潜在威胁(图1).
图1
图1
敦格铁路沙山沟地貌及铁路桥梁图
Fig.1
Landform and railway bridge map of Shashangou railway
沙丘背风坡处的风场异常复杂且是风沙运动的主要影响因素之一. 当沙丘背风坡建造铁路路基工程或桥梁工程时,风场会受到工程的影响而改变,风沙运动也会相应变化,不同铁路结构形式对风场及风沙运动的影响成为重要的研究课题. 我国西北铁路施工地区大多地势平坦,铁路设计采用以路基为主、桥梁隧道为辅的结构形式. 为了防止风沙对路基本体的危害,路基两侧多设置PE网(草、石)方格等措施进行防沙固沙,费用较高且养护工作量大. 而敦格铁路沙山沟段采用以桥代路的方式来减小风沙危害尚属首次,为桥梁工程对风场及风沙运动的影响研究提供了工程样例.
1 数值模拟方法
1.1 连续性方程
空气连续性方程[28]
沙粒连续性方程
其中,$\phi _{a}$,$\phi _{s}$代表空气和沙粒的体积分数,即空气和沙粒在计算域中所占的比例,其和为1;$\rho_{a}$,$\rho _{s}$代表空气和沙粒的密度;$U_{a} $与$U_{s} $分别代表空气相与沙粒相的速度在某特定位置的速度.
1.2 动量方程
空气动量方程
沙粒动量方程
其中$f_{sa} = 1 / 8C_{D} \rho _{a} \pi d^2U_{r} $为空气与沙粒的相互作用力,$p$为空气压力,$p_{s} $为沙粒压力,$U_{r}$是风场与沙粒的相对速度,$d$是沙粒的粒径.
上式中, $\tau _{a} $与$\tau _{s}$分别是空气与沙粒相的应力张量,表征了各相中某点的应力与该点速度梯度之间的线性关系,其表达式如下
其中,${\pmb I}$为单位矩阵,$u_{a} $和$u'_{a}$是空气相的剪切和体积黏度,$u_{s} $和$u'_{s}$是沙粒相的剪切和体积黏度.
本文将沙粒视为球形,其拖曳力系数可表示为如下形式[29]
$Re$是相对运动雷诺数
沙粒动量方程(4)中需要求解沙粒压力项
上式中的$d_0 $是径向分布函数,表征沙粒间的碰撞概率[30]
$\theta _{s}$表示的沙粒的颗粒温度描述了沙粒随机运动的动能,其方程[31]如下
其中,$\left( {1 - p_{s} I + \tau _{s} } \right)\nabla U_{s}$为沙粒应力张量产生的能量,$k_{\theta _{s} } \nabla \theta _{s} $为能量扩散,$k_{\theta _{s}} $为扩散系数,$a_{\theta _{s} } $为随机能量交换系数, $\gamma _{\theta _{s} }$碰撞能量损失可表示为[32]
沙粒应力张量式(6)中,$u_{s}$和$u'_{s}$分别为沙粒的体积与剪切黏度
上式中$u_{scol} $与$u_{skin}$是沙粒碰撞与动力黏度[33]
其中,$e_{s}$代表沙粒间碰撞的恢复系数.
1.3 $k$-$\varepsilon$湍流模型
其中,$k_\alpha $为湍动能,$\varepsilon _\alpha $为湍动耗散率,$\mu _{t}$为湍动黏度,$G_{k _\alpha} = \mu _{t} \left( {\partial U_{ai} / \partial x_j + \partial U_{ai} / \partial x_i } \right)$为平均速度梯度引起的湍流动能产生, $G_{b _\alpha} = - \beta g_i \mu _{t} / \left( {\rho _a Pr _{t} } \right) \cdot \left( {\partial T / \partial x_i } \right)$为浮力影响引 起的湍动能产生,$\beta = - \rho _{a} \left( {\partial \rho _{a}/ \partial T} \right)$ 为热膨胀系数,$ Pr _t $为湍 动普朗数,$C_{1\varepsilon } $,$C_{2\varepsilon } $,$C_{3\varepsilon }$是常数,取值 分别为1.44,1.92和0.09,$\sigma _k $,$\sigma _\varepsilon $代表湍动能和耗散率对应的普朗特数,取值分别为1.0和1.3[28, 34].
1.4 边界条件
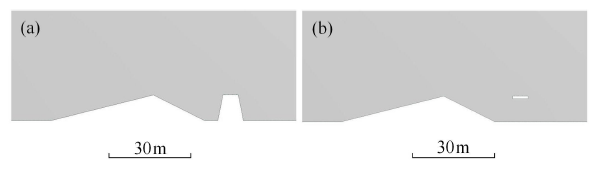
计算域尺寸为400m$\times $70m$\times $1m. 沙丘定义为高10m,底宽60m的三角形(图3). 路基工程的算例中路基模型为梯形,桥梁工程中桥梁模型为悬空的矩形(图2). 在入口到沙丘之间有100 m的距离以保证风沙流充分发展. 边界条件设置:(1) 地面、沙丘和桥梁表面均被定义为无滑移边界;(2) 计算区域的上边和两侧边界设置为对称边界条件,即速度和压强在边界法线方向的梯度都为0;(3) 入口风速沿高度符合对数分布规律,满足公式$u = u_* / k\ln \left( {z / z_0 } \right)$,入口处的湍流强度设置为5%,入口处沙粒相的体积分数给定为0.02[25];(4) 出口设置为自由出流.
图2
图2
位于沙丘背风侧铁路路基及桥梁工程模型
Fig.2
Two kinds of typical design for railway in a leeside region of sand dune
本文采用FLUENT对风沙流进行模拟,其采用有限体积法对控制方程进行离散. 模拟过程中离散格式采用二阶迎风格式,压力-速度耦合的修正采用SIMPLE方法. 采用非结构网格对计算域进行划分,网格总数为$2.2\times 10^6$,时间步长设置为0.1s,收敛标准为残差小于$1.0\times 10^{ - 4}$.
在模拟中,空气被定义为无热交换的不可压缩流体,温度25${^\circ}$C,密度1.225kg/m$^{3}$,黏度系数 1.7846kg/(m$\cdot$s);沙粒被定义为重流体,密度 2650kg/m$^{3}$,黏度系数0.047kg/(m$\cdot $s).
图3
图3
路基工程算例的计算域及网格划分
Fig.3
The simulation domain and grid system used in subgrade designs computational
1.5 模型验证
图4
图4
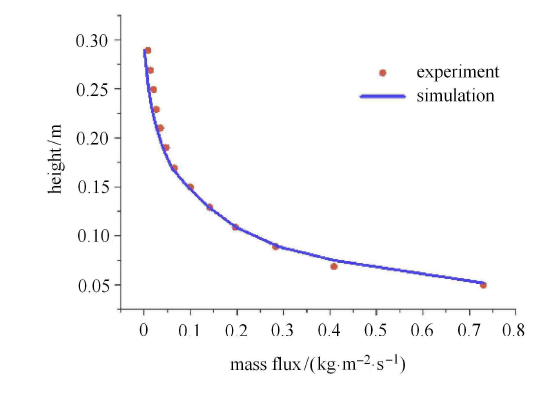
距离入口8m处数值模拟及风洞实验中随高度变化沙通量的对比图
Fig.4
The comparison of mass flux profile between simulation results and experiment results at the position of 8m downstream of the inlet
2 模拟结果及讨论
2.1 风场分析
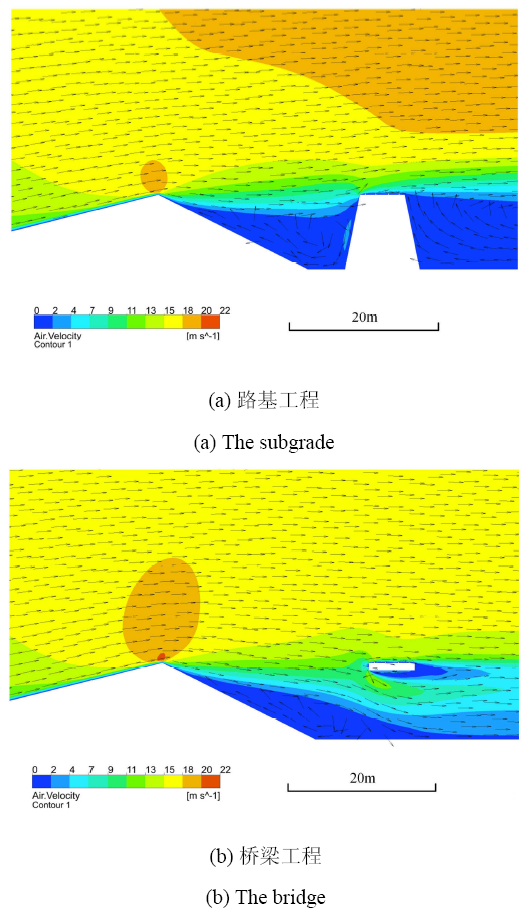
图5是摩阻风速为0.5 m/s时风场的速度大小云图和速度矢量图. 可以清楚地看到沙丘背风坡处有一个回流区,而这个回流区在不同结构形式下有明显的区别. 在路基工程中,沙丘背面的回流区被分为了两部分,在沙丘和路基之间有一个小的回流区,而路基下风侧则有一个较大的回流区. 铁路路基明显增大了回流区的范围,降低了地表区域的风速,同时也对路基顶面以上的风场有一个加速作用. 在桥梁模拟结果中,由于桥梁的导流效应,沙丘背风坡处的回流区被压缩,而且桥梁工程处的风速明显大于路基工程,可以得到相比路基工程,桥梁工程不会形成大范围回流低速区而造成宜积沙的条件.
图5
图5
摩阻风速为0.5m/s时风场的速度云图与矢量图
Fig.5
The velocity nephogram and vector diagram of wind field when the friction velocity is 0.5m/s
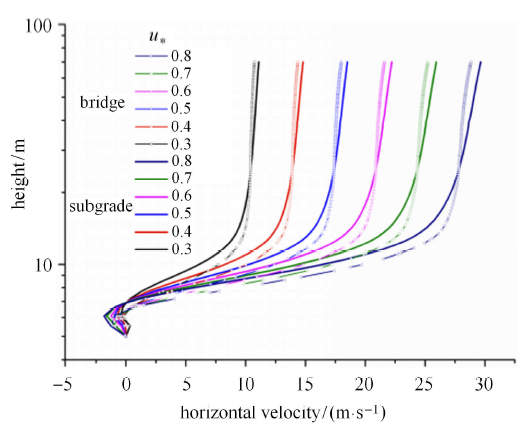
图6表示沙丘背风坡中点处(距离入口150m 处)水平风速随高度变化的模拟结果. 结果显示,无论是路基工程还是桥梁工程,在沙丘背风侧表面均有回流区,并且水平风速呈现出随高度变化的对数趋势. 在近地表范围内,路基工程回流区水平速度要小于桥梁工程. 在高度8$\sim$30m范围内,桥梁工程的水平风速大于路基工程;在高度30m以上的范围,路基工程的水平风速超过桥梁工程. 随着摩阻 风速的增加,桥梁工程与路基工程水平风速的差值同步增加.
图6
图6
沙丘背风坡中点处(距离入口150m处)水平风速随高度变化的模拟结果
Fig.6
The horizontal velocity profiles of wind field with height in the middle of sand dune leeside at the position $x =150$m. Straight lines are the profiles in the subgrade design, and the shape lines are in the bridge design
图7表示铁路桥梁或路基表面中点处(距离入口170m处)水平风速随高度变化的模拟结果. 不同于沙丘背风坡中点处的结果,铁路中点处的水平风速均是正值. 由于路基工程有很强的阻滞效应,在高度小于16m范围内水平风速小于桥梁工程;而在16m以上的区域,路基工程的水平风速超过了桥梁工程. 同样的,随着摩阻风速的增加,桥梁工程与路基工程水平风速的差值同步增加. 可以看出在铁路表面,桥梁工程受到更强的风场影响,而接下来我们将进一步讨论不同铁路结构形式时的积沙 情况.
图7
图7
铁路桥梁或路基表面中点处(距离入口170m处)水平风速随 高度变化的模拟结果
Fig.7
The horizontal velocity profiles of wind field with height in the middle of railway at the position $x =170$m. Straight lines are the profiles in the subgrade design, and the shape lines are in the bridge design
2.2 沙粒运动分析
图8表示当摩阻风速为0.3m/s时,铁路路基工程和桥梁工程的沙粒体积分数. 可以明显的看出不同的结构形式下风沙体积分数有着很大的差异. 结合风场分析,在路基两侧都有大量积沙情况出现,并且在路基迎风侧的积沙量要远大于路基背风侧的积沙量. 铁路轨道系统增加了铁路表面的粗糙度,有少量积沙出现在路基表面的轨道之间. 桥梁工程的导流效应使得更多的气流沿着梁上下通过,从而减小了回流区的范围. 因此在沙丘背风侧与桥梁之间只有少量积沙. 同样的,由于铁路轨道系统增加了铁路表面的粗糙度,有少量积沙出现在桥梁表面的轨道之间.
图8
图8
铁路路基工程和桥梁工程的沙粒体积分数(摩阻风速为0.3m/s)
Fig.8
The volume fraction of sand when the friction velocity is 0.3m/s with different design
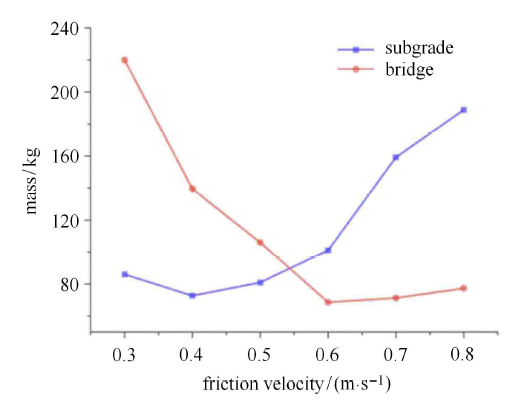
图9表示在10min内随着摩阻风速的增加路基工程表面以及桥梁工程表面的积沙量. 可以看出积沙量随着摩阻风速的增大呈现出非线性,表明风场和沙粒之间有着较为复杂的相互作用. 在路基工程中,随着摩阻风速的增大,积沙量首先轻微下降,随后明显增大. 这种现象的原因可以解释为路基工程有着很强的阻滞效应. 随着摩阻风速的增大进入该区域的沙粒也同步增加,但是由于路基工程阻滞作用,风蚀能力没有同幅度增大,因此有大量沙沉积下来. 而桥梁工程的模拟结果则相反,当摩阻风速从0.3m/s增大至0.6m/s时,桥梁工程的积沙量有着明显的下降,当摩阻风速增大至0.6m/s以上时,积沙量基本达到了一个平衡. 这种现象的原因可以解释为桥梁工程没有明显的阻滞效应,随着摩阻风速的增大,风蚀能力的增长幅度大于沙粒沉积的增长幅度,所以随着摩阻风速的增大桥梁工程处的积沙量有明显的下降.
图9
图9
铁路路基工程以及桥梁工程表面积沙量
Fig.9
The mass of sand accumulations on railway with friction velocity in two kinds of design forms
我国沙害严重的地区主要集中在甘肃、新疆、内蒙、青海等西部省区,而这些地区的铁路施工区域整体来说地形较为平坦,在铁路工程的设计过程当中往往形成了一种根深蒂固的思维定式,就是要以路基工程为主来降低铁路整体造价. 这种设计理念贯穿于整条线路,这样大风沙害地区就不可避免的同样采用路基工程通过,只不过是在沙害严重地段增设了风沙防护措施. 因此从我国第一条沙漠铁路包(头)兰(州)线开始,就从前苏联引进方格网固沙防护铁路,之后很多学者也进行了大量的研究,如根据不同地区的特点优化了方格网材料、研究了高立式沙障等立面防护设施、设置下导风措施加速风沙通过铁路路基、研究喷洒化学制剂固沙等,但这些研究均未跳出设置阻沙、固沙措施防止沙害威胁铁路路基的思维模式,至今还未有相关研究对比路基工程与桥梁工程对风沙环境的适应性.
而从我们上述对比铁路路基工程与桥梁工程的结果来看,路基工程阻滞效应加大的回流区以及低速区造成了路基坡脚的大量积沙,桥梁工程的导流效应则压缩了沙丘背风侧的回流区,且风速要明显大于路基工程,这种情况下沙粒会顺利从桥下通过不宜沉积下来.
在桥梁建设现场我们也重点实地观察了桥梁与路基过渡段的积沙情况,之所以选择观察路桥过渡段是因为可以直观地对比同一地段桥梁工程和路基工程的风沙环境适应性.
2015-2019年的4年间,如图10所示在敦煌台小里程方向路基工程范围(DK78+800-DK79+254.26)路基坡脚及路基面道碴间有大量积沙出现,因此2018年还对此段路基范围的积沙进行过清理;而在该桥敦煌台大里程方向(桥梁工程范围内DK79+254.26-DIK89+858.99)并未出现明显积沙,也未出现明显的风蚀现象. 从现场实际情况来看与本文的模拟结果吻合较好,也可以证实采用桥梁工程通过大风沙漠地区较之路基工程有着明显的优势.
图10
图10
铁路路基工程与桥梁工程的积沙情况对比
Fig.10
Comparison of sand deposition between subgrade and bridge
3 结论
本文采用多相流的方法模拟了当铁路位于沙丘背风侧时,风沙流越过沙丘对铁路工程的影响,讨论了路基工程和桥梁工程两种铁路结构形式对铁路表面积沙量的影响.
研究结果显示:(1) 在路基工程中,沙丘背风坡处的回流区被明显分成了两部分,且路基工程明显增大了回流区范围;在桥梁工程中,由于桥梁的导流效应使得沙丘背风侧回流区风速明显大于路基工程,且回流区范围相对路基工程也较小. (2) 在沙丘背风侧中点处,在高度8$\sim$30m范围内,桥梁工程的水平风速大于路基工程;而当高度超过30m时,路基工程的水平风速超过桥梁工程. (3) 在铁路桥梁或路基表面中点处,在高度小于16m范围内水平风速小于桥梁工程;而在16m以上的区域,路基工程的水平风速超过了桥梁工程. (4) 铁路轨道系统增加了铁路表面的粗糙度,有少量积沙出现在路基表面的轨道之间,而在路基工程两侧则有大量积沙. (5) 风场和沙粒之间的复杂相互作用使得积沙量呈现出非线性,在桥梁工程中,随着摩阻风速的增大,风蚀能力的增长幅度大于沙粒沉积的增长幅度,所以随着摩阻风速的增加桥梁工程处的积沙量有明显的下降,而路基工程的模拟结果则正好相反.
综上可认为在特定条件下,桥梁工程是通过大风沙漠地区铁路工程设计的较优方案. 本文的工作为风沙运动对铁路工程的影响提供了理论支持,为今后的铁路工程设计提供了新的思路与研究工具.