引言
对于自然环境大气边界层,数值模拟研究用于风沙流的高雷诺数湍流风场,需要足够大的计算规模,才能有效的反映出实际野外环境中沙尘颗粒在气流作用下的运动规律. 目前对高雷诺数湍流流动的数值模拟研究仍受到计算规模的限制. 因此,充分利用我国的超级计算机资源,发展高效率并行计算技术,对高雷诺数湍流风场以及进一步的风沙流数值模拟研究有重要的意义.
1 大涡模拟控制方程和亚网格模式
大气边界层中的空气流动,在Bussinesqe假定下可认为是分层的不可压缩流体. 风场大涡模拟控制方程是不可压NS方程. 无量纲化的不可压NS方程为
$\dfrac{\partial u_i}{\partial x_i}=0 \\ \dfrac{\partial u_i}{\partial t}+u_j \dfrac{\partial u_i}{\partial x_j} =-\dfrac{\partial P}{\partial x_i}+ \dfrac 1{Re} \dfrac{\partial^2 u_i}{\partial x_i\partial x_j} +\dfrac{\partial \tau_{ij}}{\partial x_j}$
其中,$u$为速度,$P$为压力,$Re$为雷诺数, $\tau_{ij }$是亚网格应力.
LES方程和NS方程的不同之处是LES方程包含了亚网格通量. 这些亚网格通量需要建立封闭模式,是大涡模拟的关键问题之一. 关于复杂湍流中的亚网格通量模式仍在继续研究和发展中,目前最常用的模式是涡黏和 涡扩散模型. Smagorinsky涡黏模式是最早提出的亚网格模式,并被工业界广泛应用. 涡黏模式的公式为
$\tau_{ij}=2 v_t \bar S_{ij} +\dfrac 13 \tau_{kk} \delta_{ij}$
其中Smagorinsky的涡黏模式
$v_t=C^2_s \varDelta^2 | \bar S |$
$C_{s}$是模式系数, $\varDelta $是网格尺度,$ | \bar S | =(2 \bar S_{ij} \bar S_{ij})^{1/2}$, 而 $\bar S_{ij}=(\partial \bar u_i/\partial x_j+ \partial \bar u_j / \partial x_i)/2$是可解尺度速度变形率张量. 各项同性湍流理论可确定模式系数$C_{s} =0.10$. 但在实际应用中发现,Smagorinsky涡黏模式在底边界壁面附近耗散过大,需要调整模式系数. 本文将采用Smagorinsky涡黏模式作为亚网格模式进行大涡模拟计算.
大涡模拟的控制方程特性与NS方程DNS模拟在求解过程中没有本质的区别,可以用相同的数值求解方法进行数值计算.
高雷诺数湍流风场的数值模拟研究受到计算规模的限制,一直是湍流数值模拟研究工作中的难题之一. 因此,在超级计算机上研究和应用高效的并行计算技术,对开展大规模高雷诺数湍流风场的模拟以及为后续沙尘颗粒等运动特性的联立求解,有着现实的意义.
2 不可压流动LES模拟的并行直接求解方法
在过去的八年里,我们开展了极高瑞利数湍流热对流的DNS模拟研究. 由于极高瑞利数湍流热对流问题的特殊性,要求DNS模拟的计算规模非常之大,使改进和发展新的并行模拟求解方法的工作成为必然. 2016年终于在规模并行计算技术上有了突破性进展,创建了不可压流动湍流热对流的并行直接求解方法(parallel direct method of DNS, PDM-DNS),并在"天河二号"超级计算机上实现了系列高瑞利数湍流热对流的DNS模拟计算,并得到了系列的高瑞利数湍流热对流特性的研究成果.
本文拟将湍流热对流DNS模拟的并行直接求解方法,扩展到湍流风场的LES模拟中,希望能显著有效的提高壁湍流风场LES模拟的计算效率,由此可进一步扩大壁湍流风场的计算规模,提高计算壁湍流风场的雷诺数.
2.1 不可压流动LES的并行直接求解方法
由于该计算方法只限用于水平采用等距网格的矩形计算区域,适用于风场的LES模拟计算,如图1所示的风场示意图.
图1
采用LES模拟不可压NS方程,本文采用投影法分步骤计算. 动量方程中预估速度的计算采用容易实现并行的显示格式. 联立压力驱动速度项和连续方程,得到压力泊松方程,需要全流场联立求解,是数值求解过程中计算工作量最大的部分,同时全场联立求解也给大规模并行造成困难. 大规模并行计算的压力泊松方程高效求解技术,是解决高雷诺数湍流风场大规模并行计算的关键.
在二维湍流热对流DNS模拟的并行直接求解方法PDM-DNS[26]中,压力泊松方程是二维的,因此仅需要在水平方向进行FFT变换解耦泊松方程,将方程变为三对角方程,再利用PPD并行算法,综合建立高效并行计算方法.
在"天河二号"超级计算机上,大规模的并行计算可以进行MPI和OpenMP混编,MPI并行计算需要交换分区边界的数据.
类似二维湍流热对流DNS的直接求解方法,在三维湍流风场的LES模拟中将矩形的风场计算区域沿水平面对$z$进行分割. 相邻的MPI分割区域在并行计算中需要数据通讯,区域内部可用OpenMP并行,无需数据通讯. 在此基础上进行压力泊松方程的水平面FFT变化时将不用并行计算,而是在纵向三对角方程求解时使用PDD技术进行并行计算. 因而大大的提高了泊松方程并行求解的计算效率.
由此可见,二维流动的并行直接求解方法扩展到三维计算,泊松方程的求解过程仅是在FFT解耦的过程上有所不同. 二维流动计算中用一维FFT,三维流动计算中用平面二维FFT变换,其它求解过程基本一致.
对三维湍流风场的LES模拟,同样并行计算的困难在于求解压力泊松方程. 三维泊松方程的直接求解方法的具体做法为,在三维空间的${xoy}$水平平面上使用二维平面FFT变换,将空间3个方向上都要求联立求解的压力泊松方程解耦,使泊松方程变换成为只在$z$方向上的三对角方程. 求解三对角方程后通过FFT反变换就可得到全场泊松方程解.
三维压力泊松方程为
$\dfrac{\partial^2 P}{\partial x^2}+\dfrac{\partial^2 P}{\partial y^2}+\dfrac{\partial^2P}{\partial z^2}=d$
其对应的上下压力无梯度边界条件为
$\dfrac{\partial P}{\partial n} \Big |_{\hbox{边界}}=0$
沿流向及展向方向的压力边界条件为周期边界条件.
在$x$和$y$方向使用等距网格,$z$方向可使用变距网格. 在点$(i,j,k)$对应的3个方向网格长度分别为$\Delta x$, $\Delta y$和$\Delta z_k$,压力泊松方程的二阶精度中心差分离散格式可写成如下形式
$\dfrac{P_{i-1,j,k}-2P_{i,j,k}+P_{i+1,j,k}}{\Delta x^2}+ \dfrac{P_{i,j-1,k}-2P_{i,j,k}+P_{i,j+1,k}}{\Delta y^2}+\\ \qquad \dfrac{2P_{i,j,k+1}}{(\Delta z_{k+1}+\Delta z_k)\Delta z_k}+ \dfrac{2P_{i,j,k-1}}{(\Delta z_{k-1}+\Delta z_k)\Delta z_k}-\\ \qquad \dfrac{2P_{i,j,k}}{\Delta z_k} \Big ( \dfrac 1{\Delta z_{k+1}+\Delta z_k}+\dfrac 1 {\Delta z_{k-1}+\Delta z_k } \Big ) =d_{i,j,k}$
根据以上离散泊松方程的特点,使用$xy$平面上的二维离散余弦傅里叶变换,可以对泊松方程的离散方程进行解耦. 为自动满足压力的边界条件,选用二维离散余弦傅里叶变换,表达式为
$\hat P_{p,q,k}=\dfrac 1{\sqrt{4MN}} \sum\limits^{M-1}_{i=0} \sum\limits^{N-1}_{j=0} 4P_{i,j,k}\cos \dfrac{\pi (i+1/2)p}M \cdot \\ \qquad \cos \dfrac{\pi(j+1/2)q}N$
$M$对应$x$方向的网格数$N_x$,$N$对应$y$方向的网格数$N_y$. 以上变换可以通过使用FFTW 软件包实现. 将上式变换应用到压力泊松方程中,可得到沿$z$方向联立的三对角方程
$a_{p,q,k}\cdot \hat P_{p,q,k-1}+b_{p,q,k}\cdot \hat P_{p,q,k}+c_{p,q,k}\cdot \hat p_{p,q,k+1}=\hat d_{p,q,k}$
对于给定的$p$和$q$,变换后的压力泊松方程在需要$xy$和$z$方向上解耦,变为系列的三对角方程组. 完成所有三对角方程组的求解后,通过对应的变换即可完成压力泊松方程的求解.
利用以上高效的压力泊松方程并行直接求解方法,联合其它易并行的动量方程等计算,本文将已创建的二维湍流热对流并行直接求解方法,扩展到三维不可压湍流风场的LES模拟中,建立LES模拟的并行直接求解方法,为大规模高效并行计算高雷诺数湍流流动,提供全新的数值计算技术和计算方法.
2.2 并行计算规模和计算效率
实际计算研究中,壁湍流风场的大涡模拟已有许多成熟的研究成果. 但在实际自然灾害问题的风场研究中,空间尺度都很大,从而导致风场具有很高的雷诺数,需要计算规模巨大. 如何实现大规模高雷诺数风场数值计算仍是一 个瓶颈问题. 本论文的研究特点主要在采用新的并行计算技术,建立了一个可进行大规模高效并行的计算方法,可以显著的提高风场大涡模拟的计算效率,为实现高$Re$风场以及由风带来的物质输运的计算研究提供有价值的计算工具.
采用半槽道壁湍流大涡模拟计算,对新方法PDM-LES的并行效率进行验证.
计算域为三维矩形. 作为验证计算,计算网格在($x,y,z$)方向均取256$\times$256$\times$256. 以$x$作为流动方向,$y$方向为与$x$方向垂直的另一水平方向,$z$方向为垂直地面方向. 边界条件为$x$方向上下游及$y$方向为周期边界,$z$方向下底面为无滑移边界,上边界为对称边界条件. 在计算过程中,采用定流量计算方法,以保证流动持续进行,即在每个时间迭代计算中对由于粘性摩擦损失的流量进行修正.
计算在"天河二号"超级计算机上进行. 每个计算机节点可以有32线程无需交换数据的并行计算,采用OpenMP方式进行并行计算. 节点间在并行计算是需要交换数据,采用MPI方式进行并行计算.
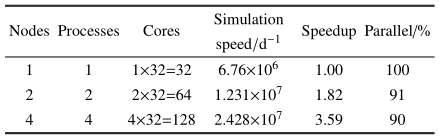
表1给出了采用不同节点数的计算结果,分别采用1,2和4个节点进行了计算效率的对比计算. 以1个节点的计算作为基础计算工作量,可以看到,采用1个节点每天可迭代71.6万个时间步长,当用4个节点共128核的并行计算,加速比为3.59,计算效率达到90${\%}$.
由此可见,本文建立的针对风场的壁湍流大涡模拟的并行直接求解方法(PDM-LES),具有较高的并行计算效率,可用于规模风场的数值计算研究.
3 三维风场的规模并行计算
采用建立的PDM-LES方法,对三维壁湍流风场进行大涡模拟计算. 取来流$Re=10000$进行试算,检验壁湍流计算结果的合理性. 在以高度为1的无量纲计算域中,计算域选取流动流向、展向和垂向长度分别为8$\times$2$\times$1,网格分别为$N_x\subseteq N_y \subseteq N_z = 1024 \subseteq 192 \subseteq 160$. 水平采用等距网格,垂向采用变距网格,计算网格规模约为3.800$\times$10$^7$.
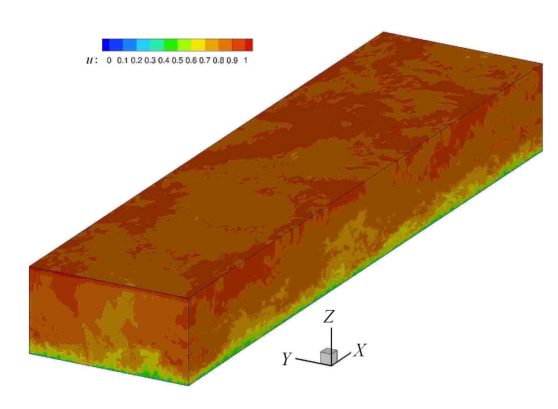
图2给出了来流${Re}=10000$时三维瞬时速度分布. 三维瞬时速度分布图中可以看到,湍流流动的速度分布存在明显的脉动特性. 计算结果得出,在现有计算条件下${Re}_{\tau } \approx 4000$.
图2
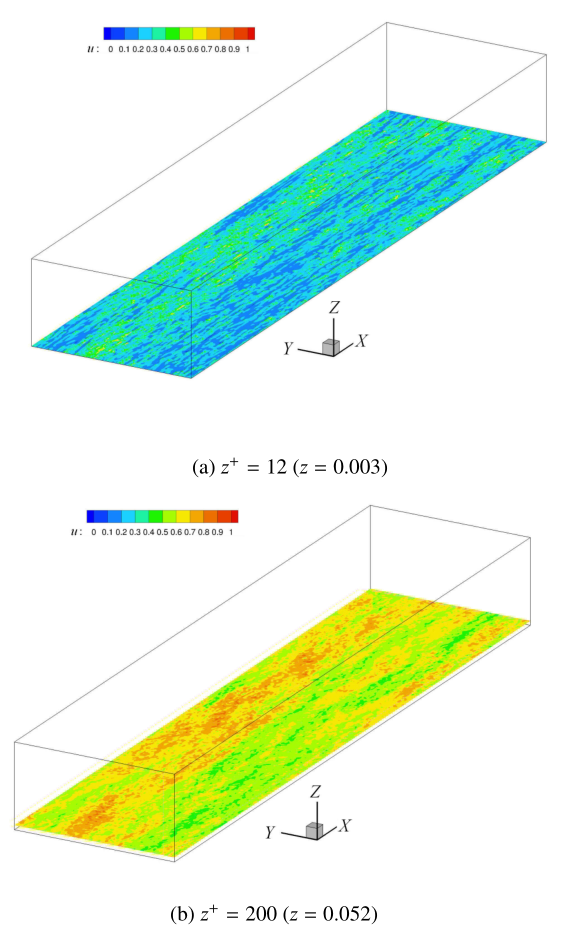
图3
图3
不同高度${xy}$平面的瞬时速度分布
Fig.3
Instant velocity distribution of ${xy}$ planes at different altitudes
计算湍流平均速度特性. 选用多个不同时刻的瞬时速度场取平均值,再对水平平面的速度进行平均计算,得到壁湍流流动在时间和空间上的平均速度场湍流特性纵向分布.
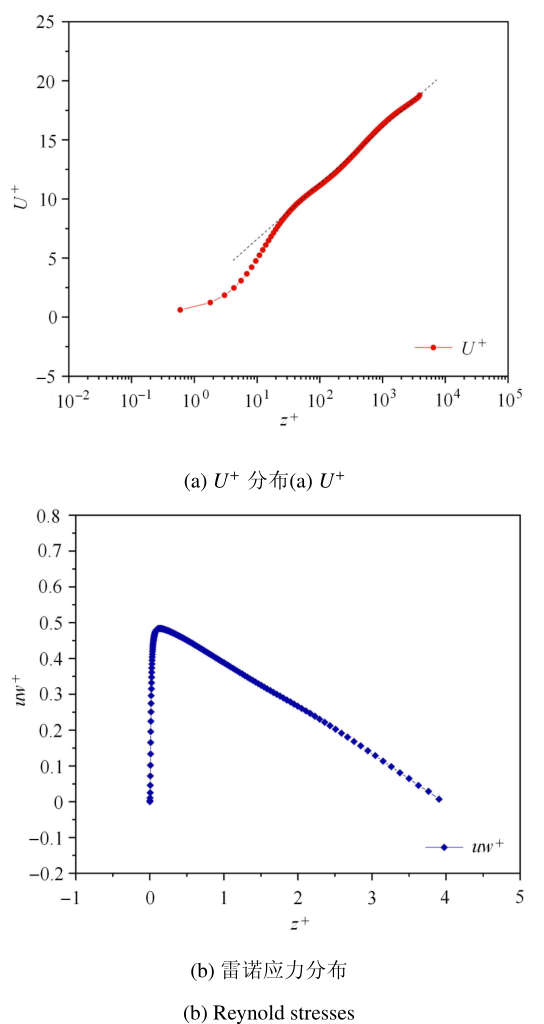
图4中给出了平均速度场$U^{ + }$和雷诺应力的纵向分布特性. 图4(a)为速度$U^{ + }$的纵向分布,纵向距离$z^{ + }$取对数. 可以看到,第一个数值点的距离小于1个$z^{ +}$,表明近壁面网格距离基本满足计算的要求,本算例的计算网格选取是合理的. $U^{+ }$的纵向分布在$z^{ + }\approx 20$处分为两段,近壁面区域$U^{ + }$的分布曲线是弯曲的,离开壁面区域$U^{ + }$随$z^{ +}$的分布在单对数坐标中呈现直线关系,表明速度分布存在对数律. 图4(b) 是雷诺应力的纵向分布情况. 雷诺应力的分布特性符合湍流边界层的特性规律,但雷诺应力的最大值偏小.
图4
总体上说,本文计算的壁湍流风场的湍流特性基本合理.
下一步工作是,在"天河二号"超级计算机上开展高雷诺数的壁湍流大涡模拟计算,增加计算网格规模,同时也增加有效的并行计算线程数,使得能在可接受的时间内完成高雷诺数的壁湍流大涡模拟计算,为风沙流的模拟计算等研究服务.
4 结论
利用大涡模拟数值研究三维高雷诺数风场特性,超大规模的数值模拟计算是十分必要的. 依靠超级计算机技术的发展,建立高效并行的计算方法,对更深入研究计算实际野外风沙流的物理和流动特性具有很重要的意义.
(1) 本文将高效的并行直接求解方法扩展到三维壁湍流风场的大涡模拟计算中,建立了三维壁湍流风场大涡模拟的高效并行直接求解方法PDM-LES.
(2) 对并行直接求解方法的并行计算效率进行的验证计算结果表明,在"天河二号"超级计算机上进行的1至4个节点,最大用到128核的并行计算效率达到90${\%}$.
(3) 计算${Re}=10 000$的结果显示,湍流风场瞬时速度分布在近壁区存在条带状的拟序结构,并远离壁面条带结构尺度增加. 平均场的速度分布符合湍流速度分布特性,即近壁面在$z^{ + } \approx 20$之内$U^{ + }$为线性分布,在外区$U^{ +}$满足对数律分布. 计算得到的风场湍流特性基本合理.