引言
近年来梯级溃决洪水过程受到了较大的关注, 研究集中在室内实验和数值模拟两方面. Xue等[4]开展了比较系统的室内梯级溃决室内实验, 主要探讨了坝间距、库容比对下游水库水流洪峰的影响. Niu等[5]在斜槽中堆积了梯形大坝, 研究了梯级大坝溃决形式和溃坝水流的传播过程. Chen等[6]通过实验研究了溃坝水流对下游坝体的冲击力作用, 指出针对下游不同库容存在3种冲击模式, 并给出了作用力拟合公式. 大量的工作集中在数值模拟方面, 主要可以分为水文方法、浅水动力学模拟, 以及三维Navier-Stokes方程模拟. 赵雪莹等[7]使用经验公式研究了贵阳柏山-花溪梯级水库发生梯级溃决的洪水演进, 分析了梯级水库群不同水位组合总计4种情况, 诱发溃坝洪水对下游的影响, 并指出降低库水位将有效减轻溃坝洪水对下游影响. 贺同坤等[8]使用Mike11软件模拟了澜沧江中游五个水库组成的梯级库的特大洪水演进过程, 指出当发生一万年一遇洪水时, 漫湾和景洪两个水库的最高水位接近坝顶. 刘庆红等[9]模拟了特定河流的梯级水库群的连锁响应以及向下游演进的过程. 黄卫等[10]建立了梯级大坝溃决洪水过程的浅水动力学模型, 研究了不同组合情况下梯级溃决洪水演进过程, 指出梯级溃决洪峰存在增强机制. 随后Cao等[11]进一步使用水沙耦合模型研究指出梯级溃决诱发洪水将更具威胁, 当前的单坝溃决预案需要改进. Wang等[12]比较了浅水动力学模型和Boussinesq模型模拟梯级溃决洪水的传播的爬升过程, 并指出Boussinesq在相对较大水深处能给出更加精确的解. Zhou等[13]使用VOF方法和湍流模型研究了梯级溃决洪水过程. Luo等[14]用近年来快速发展的无网格粒子方法(SPH)模拟了梯级溃决过程, 将溃坝洪水效应分为高速冲击区和传压区两个过程. 李仟[15]研究了梯级土石坝溃决洪水的演进和调洪过程, 对下游洪水过程进行了风险分析. 袁岳[16]用RANS模型和标准$k$-$\varepsilon$模型模拟了不同坡角, 坝间距及库容比对溃决过程的影响, 比较了单级溃决和梯级溃决不同溃决模式下水流流动特点. 赵丹[17]研究上寺水库大坝溃决的流量过程, 并对当前使用的常见模型模拟精度进行了比较.
综上所述, 当前对梯级溃决开展了一些机理性实验研究和各种不同类型的数值模拟, 主要研究溃坝洪水过程, 大部分都指出了梯级溃决相对单坝溃决存在增强现象, 但是对梯级溃决洪峰增强机制缺乏基本的物理和力学解释, 特别是缺少质量和能量转化如何增强梯级溃决洪水过程的认识. 本文使用浅水动力学方法研究梯级溃决洪水过程, 从梯级溃决上游来水对下游水库的质量和能量补充及分布方面入手, 对梯级溃决洪峰增强机制进行一些探索, 并给出了一个射流水塔单坝溃决模式等效梯级溃决洪水过程.
1 控制方程与数值方法
1.1 控制方程
由于溃坝洪水过程的水平尺度远大于垂向尺度, 并且本文对溃坝过程采取瞬间溃决的方式处理, 因此溃坝洪水演化过程可以用浅水动力学方程描述
其中, $h$和$u$分别表示水深和水平方向的垂向平均速度, $g$ 和$b$ 则分别表示重力加速度和地形高程. 本文考虑大尺度洪水演进过程和机理研究, 因此忽略摩擦作用.
1.2 数值方法
浅水动力学模型(1)和(2)是一组非线性双曲型偏微分方程, 其典型的特征是会出现水跃(激波), 同时由于源项的作用, 存在一个平衡解, 即所谓Well-Balance条件, 另一方面实际问题经常遇到一侧水深为零的情况, 即所谓的干湿条件, 因此这套控制方程的求解算法需要具备至少3个特征, 捕捉激波、满足Well-Balance条件, 以及捕捉干湿边界. 过去十年在非线性双曲守恒律的高分辨率数值格式方面取得了重要的进展[25-27], 本文综合考虑了这3方面的需求, 结合近期浅水动力学计算方法的进展, 融合了Kurganov的Riemann解[28-30]和Audusse[31-32]的单元插值模式, 构造了一套浅水动力学模型的离散格式.
首先将控制方程写成守恒形式, 如式(3)所示
其中, $U=(h,hu)^{T}$, $F=(hu,hu^2+gh^2/2)^{T}$, $s(U)=[0,-gh({\partial b}/{\partial x})]^{T}$.
采用一套满足Well-Balance行为的有限体积法[31]对守恒方程(3)进行离散, 得到以下的离散格式, 如式(4)所示
其中$U_j =(h_j ,q_j )^{T}$ 为第$j$个单元的单元平均值, 数值通量$F_{j+{1}/{2}}$的构造采用MUSCL方法[33], 如式(5)所示
这里$U_{j+({1}/{2})-} =(h_{j+({1}/{2})-}$, $h_{j+({1}/{2})-} u_{j,r} )^{T}$, $U_{j+({1}/{2})+} =(h_{j+({1}/{2})+}$, $h_{j+({1}/{2})+} u_{j+1,l})^{T}$.
采用满足Well-Balance特性的插值方式构造$h_{j+({1}/{2})-}$和$h_{j+({1}/{2})+} $, 其中$h_{j+({1}/{2})-} =max (0,h_{j,r} +b_{j,r} -b_{j+1/2})$, $h_{j+({1}/{2})+} =max (0,h_{j+1,l} +b_{j+1,l} -b_{j+1/2})$, 这里$b_{j+1/2} =max (b_{j,r} ,b_{j+1,l} )$. 所有的单元左右重构值均采用二阶MUSCL方法构造, 并采用Minmod限制器抑制虚假振荡[34].
这里的Riemann近似求解器可以采用任意形式的Riemann求解器, 本文考虑计算稳定性, 采用了近年来新发展的Kurganov近似解[30]. 源项部分包括两项, 其表达式分别如式(6)和式(7)所示
其中
$\begin{eqnarray*} &&S_{j+(1/2)-}=\lt(0,\frac{1}{2}gh_{j+(1/2)-}^2 -\frac{1}{2}gh_{i,r}^2 )^{T}\\ &&S_{j-(1/2)+}=\lt(0,\frac{1}{2}gh_{j,l}^2 -\frac{1}{2}gh_{j-(1/2)+}^2)^{T} \end{eqnarray*}$
时间离散采取二阶Runge-Kutta方法.
1.3 模型验证
本节采取两个典型的例子验证1.2中算法的有效性, 两个例子分别是溃坝问题和Well-Balance问题, 将给出两个问题的数值解和解析解的比较.
1.3.1 溃坝问题简单波解
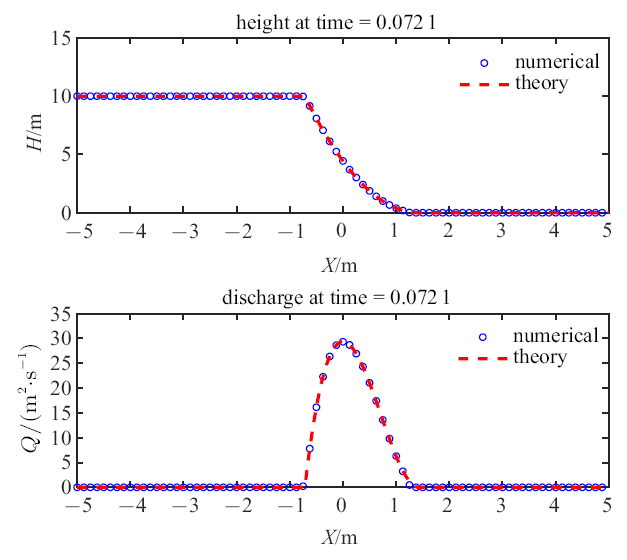
经典溃坝问题以一侧为水, 另一侧无水为初始情况, 瞬间抽除挡板后的水流运动演化过程. 该过程存在解析解, 称为简单波解[35]. 设计初始水深$h_0 =10$ m, $x=0$为初始挡板位置, 本例的解析解为$h=({h_0}/{9})(2-{x}/{ct})^2$ , $u={2}(c+{x}/{t})/{3}$, 其中波速$c=\sqrt{gh_0}$, 流量$Q=hu$.
图1给出了时刻0.072\,1 s的水深$h$和流量$Q$的计算结果, 可以发现计算结果和解析解基本吻合.
图1
图1
溃坝问题在时刻0.0721 s的水深和流量分布, 数值解和理论解的比较, $H$为水位, $Q$为流量
Fig.1
Height and discharge distribution of dam break flow at 0.0721 s, the red dashed line and blue symbols are analytical and numerical solutions respectively, where $H$ is water depth, and $Q$ is discharge
1.3.2 Well-Balance行为
地形变化情况的浅水动力学方程存在一个稳态解结构, 即$h+b={const}$, $q=0$, 即在流量为0的时候, 自由表面为常数. 这个结构在数值模型中需要保持, 称为Well-Balance问题. 本例给出了底部为一个高度为5 m的近似抛物线凸起, 自由水面高程为10 m例子的数值模拟. 图2给出了本例在时刻10.0932 s的数值解, 可以发现自由水面高程保持常数, 同时流量在凸起位置处为很小的值, 约10$^{-5}$ m$^{2}$/s量级, 这在后续的工程计算中是可以接受的.
图2
图2
Well-Balance问题的验证, $H+b$为水位, $Q$为流量, 绿色虚线为底床高程
Fig.2
Verification for Well-Balance behavior over a bump denoted by red dashed line, where $H+b$ is free surface elevation, and $Q$ is discharge
2 梯级坝溃决洪水演进
梯级水库是当前水资源开发利用中的常见模式, 上游坝体的溃决往往又会导致下游坝体的溃决, 其流动过程更为复杂. 针对这种梯级水库开发模式, 本文模拟了典型的两个梯级坝连续溃决的洪水演进过程, 重点分析梯级溃决引发的洪峰增强现象.
2.1 梯级坝溃决洪水演进过程
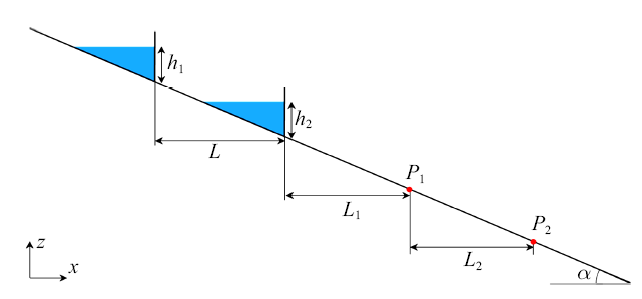
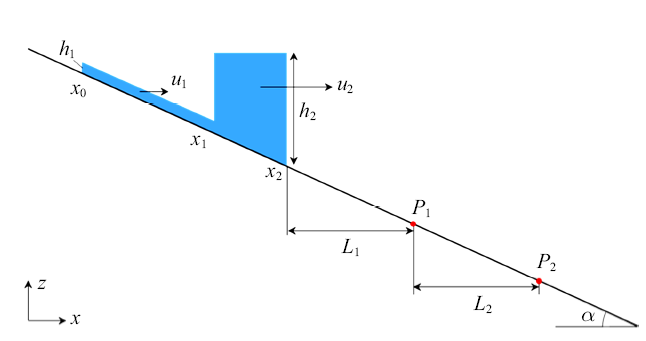
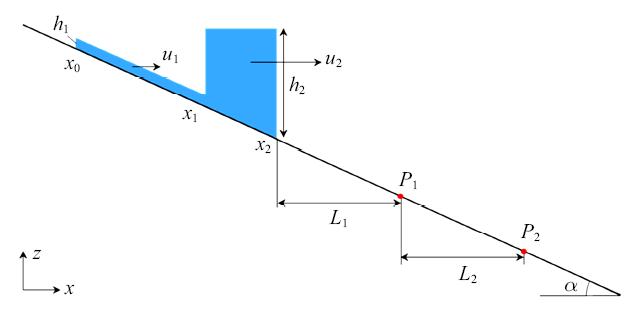
如图3所示, 在坡度为$\alpha $的河道上, 上下游存在两个坝体, 其间距为$L$, 两个坝体围成了两个水库, 其库容高度分别为$h_1 $和$h_2 $, 梯级溃决过程是, 首先上游坝体突然溃决, 水流往下游传播, 下游坝前水位超过坝体高度后下游坝体瞬间溃决, 形成溃坝洪水往下游传播. 主要关注溃坝洪水的演进过程及其对下游的影响, 因此在下游处设置两个测点$P_1$和$P_2 $, 测点$P_1 $距离下游水库的距离为$L_1 $, 测点$P_2 $距离测点$P_1 $的距离为$L_2 $.
图3
图3
梯级溃决问题描述以及测点
Fig.3
Cascade dam-break model and detection points $P_1 $ and $P_2 $
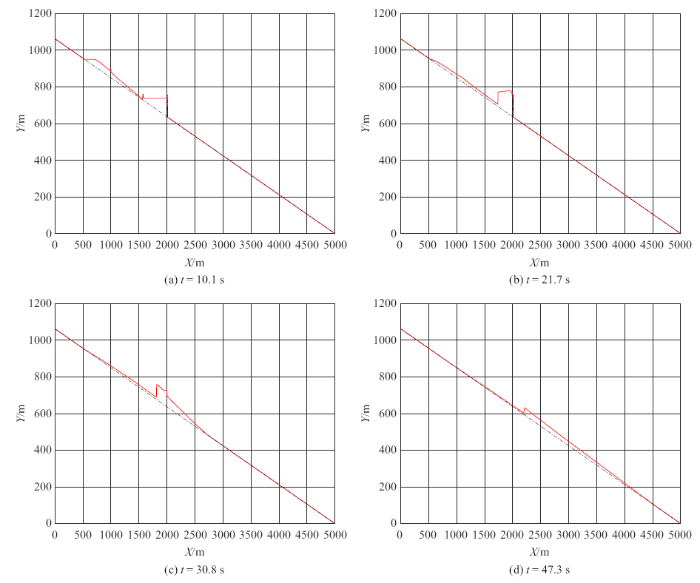
这里模拟一个梯级溃决的洪水演进过程, 其中$h_1 =h_2 =100$ m, $L=1000$ m, $L_1 =L_2 =1000$ m, $\alpha =12^\circ$, 图4给出了4个典型时刻的水位高程分布. 0 s时刻随着上游坝体的溃决, 上游水库水体向下倾泻而出, 向下游水库传播, 约10 s左右上游溃坝洪水传到下游水库, 如图4(a)所示; 形成一个稳定的向下游水库传播的水跃(激波), 如图4(b)所示; 水跃传播到下游坝体时候下游坝体溃决, 从而形成洪水往下游传播, 如图4(c)所示, 部分上游水体和下游水库合在一起宛如一个水塔为下游洪水提供充足的质量和动量来源; 最终如图4(d)所示, 洪水继续往下游传播, 直至消亡.
图4
图4
典型梯级溃决洪水演进过程水位分布
Fig.4
Water elevation distribution at four typical times of cascade dam break flow
2.2 梯级坝连续溃决洪峰增强现象
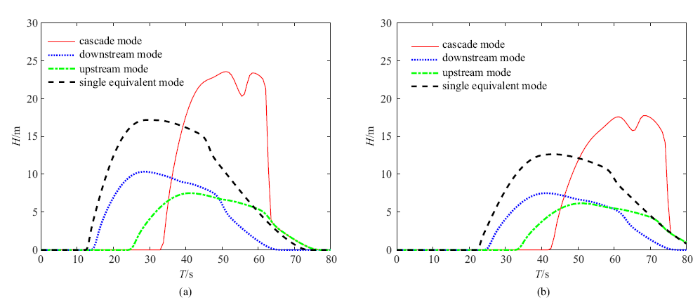
为研究梯级溃决下游河道的洪峰演化和增强现象, 选取两个参考测点$P_1 $和$P_2 $, 其距离下游坝体分别为1000 m和2000 m, 考察其洪水演进时间历程, 结果如图5所示. 为比较, 同时给出了另外3种溃决模式, 分别是上游和下游坝体单独溃决模式, 以及将上游水体体积加载在下游水库的单坝溃决模式(等体积溃决模式). 图5(a)表明梯级溃决模式在$P_1 $测点的最高水位能达到23.56 m, 下游单坝溃决模式在$P_1 $测点的最高洪峰为10.33 m, 上游单坝溃决模式在$P_1$测点的最高水位为7.50 m, 而等体积溃决模式在$P_1$测点的最高水位为17.19 m. 综合来看, 梯级溃决模式在$P_1 $诱发的洪峰大大超过单板溃决洪峰, 还超过上游下游单个溃决模式的最高洪峰之和, 也超过等体积溃决模式的最高洪峰, 在$P_2 $测点也有类似的规律. 这论证了梯级溃决模式存在洪峰增强现象, 上游水库不仅对下游水库进行了质量补充, 还进行了大量的能量补充, 但是这种质量和能量如何进行补充的, 又是如何分布的, 是梯级溃决洪水演进和洪峰增强的关键.
图5
图5
四种溃决模式下游测点$P_1 $(a)和$P_2 $(b)的洪水位时间演化, 其中Cascade Mode为梯级溃决模式, Downstream Mode和Upstream Mode分别为下游和上游单坝溃决模式, Single Equivalent Mode表示等体积溃决模式
Fig.5
Flood elevation evolution at detection points $P_1$ (a) and $P_2$ (b) for four dam break modes: cascade dam break mode, single downstream dam break mode, single upstream dam break mode, and single downstream dam break with full water mode
3 梯级坝溃决洪峰增强机制
第2节的计算分析表明梯级溃决诱发洪水洪峰超过单个坝体单独溃决洪峰的总和, 也超过将上游体积放到下游后等效的所谓等体积溃决模式的洪峰, 梯级溃决模式中, 下游水库实际上既从上游水库的溃坝洪水继承了部分质量, 而且继承了部分能量, 但是质量和能量是如何补充和分布的应当是梯级溃决洪峰增强的关键因素. 本节重点分析梯级溃决的质量和能量转化过程, 并给出几个关键机制的分析.
3.1 能量转化机制
图4的梯级溃决洪水演化过程表明上游坝体溃决对下游水库既增大了质量又增大了能量, 图6给出了下游坝体溃决瞬间的水深分布和速度分布, 下游水库形成了一个基本稳定的梯形水塔, 其自由面高程基本为常数(图4(b)), 由于底床为直线分布, 因此水深为线性分布如图6(a)所示, 其速度由后部至前部呈线性分布如图6(b)所示; 而后部实际拖了很长的一段水流, 其速度由尾部向前部逐渐增大, 前后两部分通过一个运动水跃(激波)连接. 因此初步的分析表明上游溃坝洪水对下游溃坝的效应体现在两个方面, 其一是增大了其质量, 其二是增大了其动量, 余下的水体质量和动量滞留在后部. 以上机制表明可以考虑将梯级溃决诱发洪水过程简化成一个带动量的初始水体的单坝溃决情况处理.
图6
图6
梯级溃决下游坝体溃决瞬间的高程(a)和速度分布(b)
Fig.6
Depth (a) and velocity (b) distribution of flood when downstream dam breaks
3.2 "水塔"机制
图7
图8
图8
梯级溃决洪水演进水塔模型的初始水深(a)和速度分布(b)
Fig.8
Initial water depth (a) and velocity (b) of water tower model for cascade dam break flow
图9
图9
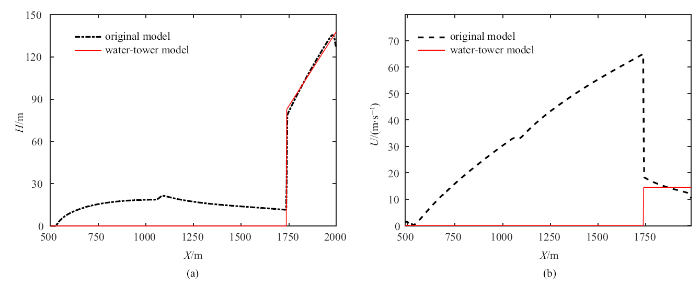
梯级溃决下游测点$P_1$ (a)和$P_2$ (b)洪水演进过程的水塔模型预测, 虚线为原始模型计算结果, 实线为水塔模型预测结果
Fig.9
Prediction of flood level at detection positions $P_1 $ (a) and $P_2 $ (b) of cascade dam break flow by water tower model, dashed line is shallow water flow model prediction, and solid line represents water tower model prediction
3.3 "射流-水塔"机制
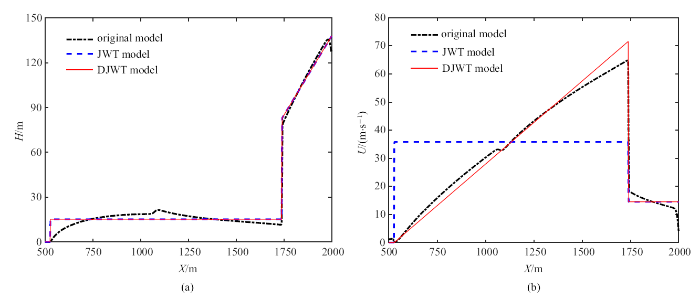
以上水塔模型低估了梯级溃决洪峰的能量, 进一步经过计算分析, 对于本例, 前部水塔的质量占总质量的61.2${\%}$, 动量则占总动量的37.7${\%}$, 后部水体的动量占据比例非常大, 类似一股射流作用, 对前部水塔有很强的质量、动量补充作用, 以维持洪峰的高度, 称之为梯级溃决的"射流-水塔"机制. 因此建立如图10所示的"射流-水塔"模型, 射流为一股带速度分布的等水深射流, 而水塔则和水塔模型一致. 射流的速度分布采取两种模型, 如图11所示, 第一种为常数分布, 第二种为线性分布, 分别称为射流水塔模型和分布式射流水塔模型. 两种模型模拟的洪水演进过程在测点$P_1 $和测点$P_2 $的洪峰演化如图12所示. 结果表明射流水塔模型的预测结果明显偏大, 而分布式射流水塔模型的洪峰过程更加接近实际洪峰过程, 但是依然存在一定的偏差. 由此可知, 分布式射流水塔模型相比于射流水塔模型、水塔模型以及单坝溃决洪峰叠加模式更能反映梯级溃决的洪水演进过程.
图10
图11
图11
梯级溃决射流水塔模型的水深(a)和速度分布(b), 其中蓝线虚线为射流水塔模型(JWT)的水深和速度分布, 而红线实线为分布式射流水塔模型(DJWT)的水深和速度分布, 黑色点划线是原始模型水深和速度分布
Fig.11
Initial water depth (a) and velocity (b) of jet-water tower model for cascade dam break flow, blue dashed line, red solid line and black dash dot line represent water depth and velocity of jet-water tower model (JWT), distributed jet-water tower model (DJWT), and original shallow water model, respectively
图12
图12
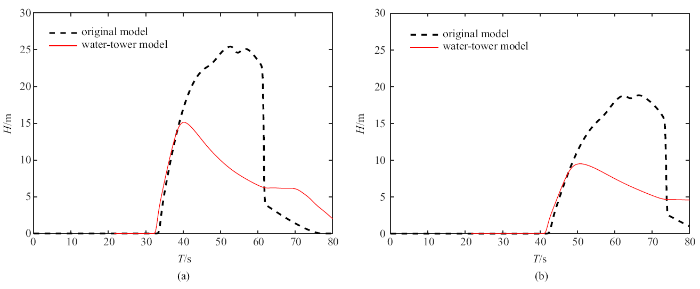
梯级溃决下游测点$P_1$ (a)和$P_2$ (b)洪水演进过程的两类射流水塔模型预测, 虚线为原始模型计算结果, 蓝线虚线为射流水塔模型(JWT)预测结果, 红线实线为分布式射流水塔模型(DJWT)预测结果, 黑色点划线为浅水动力学模拟结果
Fig.12
Prediction of flood level at detection positions $P_1$ (a) and $P_2$ (b) of cascade dam break flow by jet-water tower model (JWT) in blue dashed line and distributed jet-water tower model (DJWT) in red solid line, and black dash dot line is the shallow water model solution
4 分布式"射流-水塔"模型应用
梯级溃决洪水演进过程存在"射流-水塔"机制, 一方面上游溃坝洪水增大下游库容的质量和动量, 另一方面残余的水流构成一个高速的射流在下游溃坝洪水演进过程中不断补充质量和动量, 维持洪峰高度. 第3节总结了一个反映这种机制的分布式射流水塔模型, 本节应用该模型预测两组接近实际尺度的梯级坝溃决洪峰, 考察不同的库容比和坝间距的影响, 总共设计7组算例, 其中坡降$\tan \alpha =0.1\% $, 计算区域为800 km, 坝间距在100 km量级, 在距离下游坝处100 km和200 km处分别选取测点$P_1 $和测点$P_2 $, 分别考察洪峰水位和流量的演进过程, 同时选取原始浅水动力学模型的计算结果作为比较对象, 相关结果整理后如表1和表2所示.
表1 实际尺度梯级坝溃决洪峰水位预测
Table 1
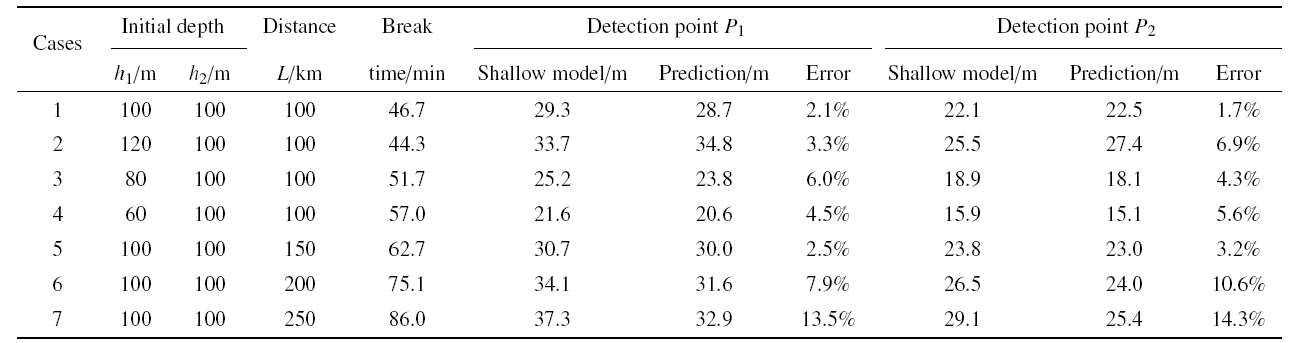 |
表2 实际尺度梯级坝溃决洪峰流量预测
Table 2
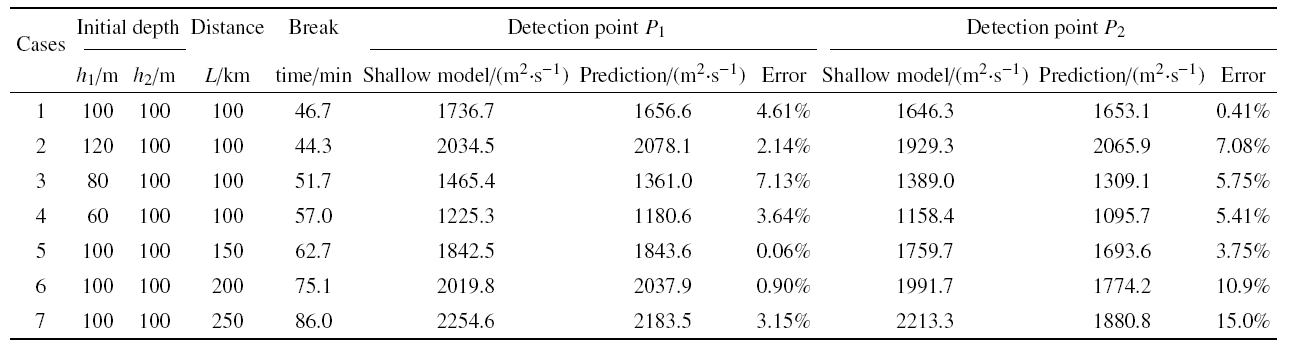 |
总体而言, 分布式射流水塔模型反映了梯级溃决的洪水峰值, 其预测的洪峰值和原始模型预测的洪峰值基本吻合. 对于间距为100 km的两个坝体, 库容比在0.6\,$\sim$\,1.2的范围内, 下游100 km处洪水峰值的预测值误差在6${\%}$以内, 200 km处洪峰的预测值误差小于7${\%}$; 对于库容比为1.0, 间距在100\,$\sim$\,250 km范围内的梯级溃决过程, 下游200 km以内, 分布式射流水塔模型预测的洪峰误差在15${\%}$以内. 对于下游100 km处测点, 由表2可知洪峰流量的预测值和浅水动力学模型计算结果吻合较好, 下游测点200 km的$P_2 $测点, 误差随着坝间距的增大而增大, 这主要是由于溃决模式和洪水增强机理存在差异所致.
5 结论
针对梯级溃坝洪水演进问题, 本文建立了一维浅水动力学方程和数值模型, 详细研究了梯级溃的洪峰增强机制, 并建立了一个梯级溃决洪水演进的单坝溃决等效模型. 主要结论如下:
(1) 梯级溃决的洪水过程存在增强机制, 下游洪峰不仅超过单坝溃决洪峰, 而且超过两个单坝溃决的峰值之和, 以及所谓等体积溃决模式的洪峰.
(2) 梯级溃决的洪峰增强由射流水塔机制控制, 上游溃决诱发的洪水不仅增大下游水库的质量和动量, 形成"水塔", 而且在尾部残留一个动量较大的射流, 稳定和维持下游溃决后"水塔"的质量和动量.
(3) 以梯级溃决洪水演进增强的射流-水塔机制为基础, 建立了一个等效的射流水塔单坝溃决等效模型, 预测结果基本能够反映梯级溃决下游洪峰演化过程, 对实际百公里量级间距的梯级溃决洪峰过程预测良好.
梯级溃坝洪水过程十分复杂, 溃决模式和增强机制方面依然还有待进一步研究, 如在可冲刷河床情况下梯级溃决的洪峰增强机制, 此外本文提出的射流水塔模型是否存在解析/半解析的参数化模型. 本文所建立的梯级溃决洪水过程的单坝溃决等效模型为实际梯级溃决洪峰过程提供了理论上的可能, 但是如何将本模型和实际河道如金沙江及其支流的梯级坝关键参数对应进行安全评估还有很多实际因素需要考虑, 如地形、河道截面和能量耗散.