引言
图1
图2
与传统的铝或铝合金等致密金属材料相比, 泡沫铝具有明显的不同特性, 前者在塑性阶段几乎不可压缩, 因此单轴压缩试样在大应变时表现出体积守恒的横向膨胀, 而泡沫铝具有明显的体积可压缩特性[13]. 存在这种差异的主要原因是泡沫铝自身特殊的孔隙结构, 因此泡沫铝的材料特性及力学性能表征也主要围绕其孔隙结构进行. 一般来说, 主要有以下几个参数或特征:
(1)相对密度或孔隙率;
(2)孔径大小及其不均匀性[14];
(3)胞孔形状及其不规则度[15].
作为材料参数, 相对密度、孔隙率的表达形式已为大家熟知. 其中, 孔隙率的计算公式
式中, $\theta $为材料孔隙率, $V_{o} $为材料总体积, $V_{p} $为材料中孔隙所占体积, $V_{s} $为材料中致密基材所占体积. 相对密度与孔隙率之间的关系为
式中, $\rho _{r} $为材料相对密度, $\rho ^* $为材料表观密度, $\rho _{s}$为材料致密基材密度.
1 泡沫铝试验研究进展
图3
总体来说, 已有的试验研究可按以下性质分类:
(1)加载方向: 单轴加荷、双轴加荷、三轴比例加荷以及静水加荷;
(2)加载方式: 压缩、拉伸、剪切、弯曲、扭转及简单的复合加载;
(3)加载速率: 静态、准静态、动态.
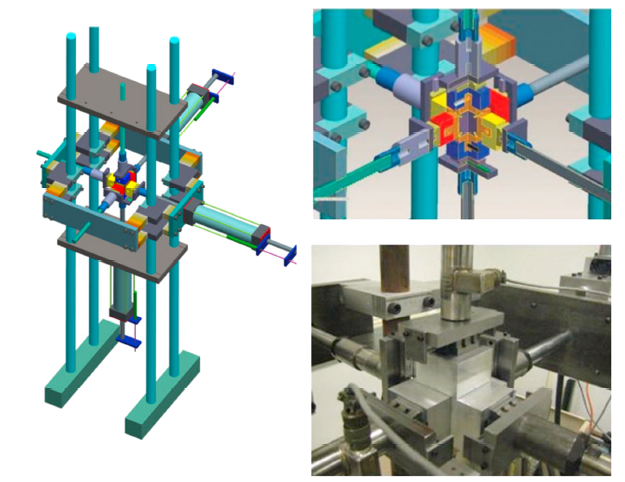
在单轴拉、压试验的同时, 三轴压缩试验也得到了进一步的发展. 泡沫铝三轴压缩边界条件主要通过两种方式实现: (1)围压装置, (2)三轴加载仪.
图4
主动围压装置所用试件需密封处理. Deshpand与Fleck[20]采用铝垫片(厚度25 $\mu$m)及橡胶薄膜包裹试件, 然后用楔形结构密封, 如图5所示, 首次成功进行了三轴压缩试验, 并提出了经典的自相似模型(self-similar model)及微分强化模型(differential hardening model). Ruan等[38]利用主动围压装置对泡沫铝多轴加载下的初始屈服面进行测试, 发现Deshpand和Fleck提出的自相似模型受塑性泊松比影响严重, 认为获得准确的塑性泊松比十分重要. 被动围压装置与SHPB结合, 可以实现泡沫铝的动态三轴加载, 如图6所示, 王二恒等[39-40]采用这种方式, 对Chen-Lu本构进行了应用验证.
图5
图6
图7
图8
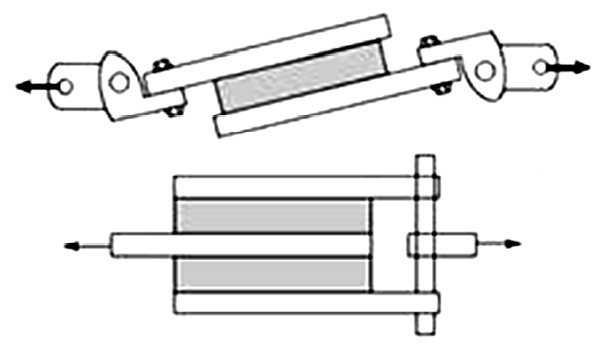
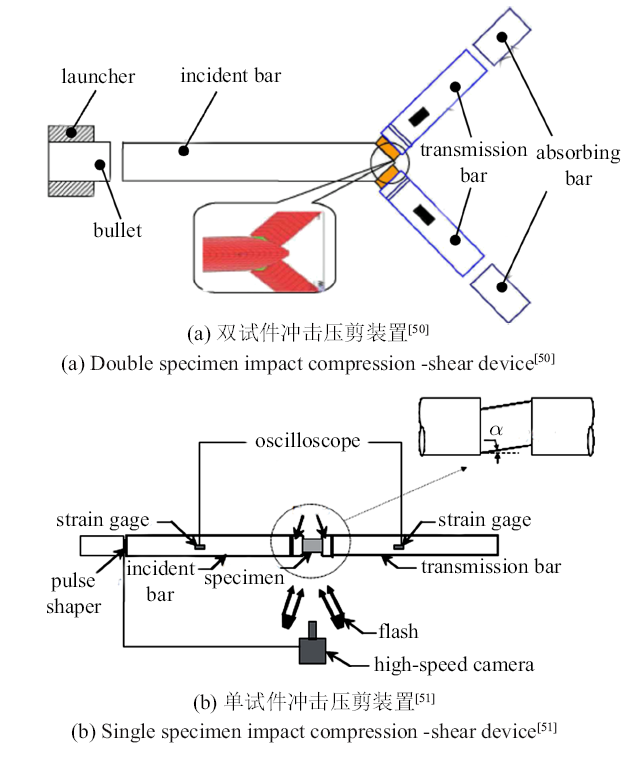
为了对泡沫铝的抗剪性能有深入的认识, 专家们还对泡沫铝进行了剪切、扭转、拉伸-扭转、压缩-剪切及拉伸-剪切等试验. Ashby等[44]通过图9所示原理的装置, 测试了泡沫金属的剪切强度. Blazy等[45]基于拉伸装置, 增加扭转机构, 研发了拉伸-扭转试验装置, 对泡沫铝进行了拉伸-扭转试验. Doyoyo等[46]及Zhou等[47]基于Arcan装置[48]的改进设备(图10), 对泡沫铝进行了压缩-剪切、拉伸-剪切试验. 通过对SHPB装置及落锤试验机的改造, 崔云霄等[49-50]实现了双试件的冲击压剪加载, 如图11(a)所示; Sun等[51]实现了单个试件的冲击压剪, 如图11(b)所示, 叶福庆等[52]以此试验装置为参考, 对泡沫铝的动态压剪性能进行了数值研究.
图9
图10
图11
图11
冲击压剪试验装置示意图
Fig.11
Schematic diagram of impact compression shear test device
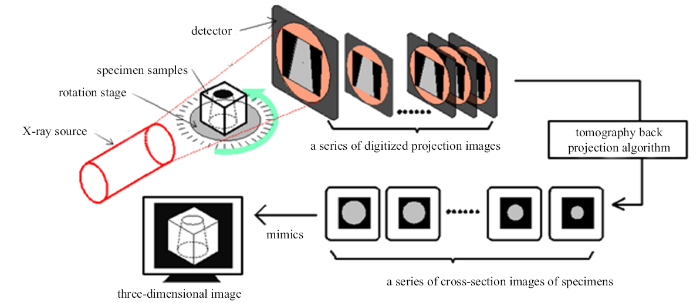
在对泡沫铝力学性能的试验研究中, 采用合理的试验方法, 准确观测其在各种边界条件下的变形是一个关键问题. 为了观察到泡沫铝在高速冲击载荷下的变形过程, 杨宝等[54]将高速摄影技术引入泡沫铝SHPB试验中. 由于泡沫铝试件的外表面并不平整, 接触式测量方式(应变片或机械引伸计)存在诸多困难. 为了准确获得泡沫铝试验过程的形貌特征及变形数据, 程洁[55]、Schüler等[56]将三维数字图像技术(3D digital image correlation, 3D DIC)引入试验研究中. 此外, 为了研究泡沫铝变形时内部微结构的演化规律, 汪敏等[57]将同步辐射X射线计算机断层扫描技术(synchrotron X-ray computed tomography, SXR-CT)引入到泡沫铝的压缩试验中.
通过大量且系统的试验研究, 人们获取了丰富的数据, 对泡沫金属变形机理及力学特性的认识逐渐加深. 这为泡沫铝本构模型的研究奠定了坚实基础.
2 有限元数值分析研究进展
2.1 细观模型研究现状
泡沫铝的另一个重要特点是其细观组织结构尺度在亚毫米或毫米级别, 容易辨识, 因此建立合适的细观模型, 采用有限元软件来研究泡沫铝的力学性能, 并服务于泡沫铝本构模型的构建及验证工作, 是一种常用的方法.
 |
*注: 3D-RVE的名义尺寸正方体, 2D-RVE的名义尺寸为正方形.
结构模型种类繁多, 实际使用中常与几何模型组合使用, 产生了众多混合模型. 混合模型可适用于高相对密度及低相对密度泡沫铝的数值分析[73]. 因此, 其应用愈来愈广泛.
离散模型(也称逆向重构模型)基于Micro CT断层扫描技术构建, 可更加真实地反应泡沫铝(或其他多孔材料)内部胞孔的形状及分布. 离散模型的数据与试验结果有良好的吻合度, 但是其建模过程复杂(图12), 模型计算量巨大. 随着建模技术的不断成熟, 越来越多的研究人员将其运用到泡沫铝(尤其是闭孔泡沫铝)力学性能及本构模型的研究中.
图12
2.2 数值分析研究现状
相较于试验研究, 有限元数值分析在参数控制、加载方式及边界条件的实现上, 有巨大的优势. 泡沫铝试件由于制备工艺的局限不可避免地存在分散性(或无序性)[1, 10], 包括胞孔形状、孔壁厚度、孔径及内部缺陷等在泡沫铝试件中分布的无序性, 使得试验结果有很大的离散性, 同时, 试验中无法清楚观测到试件高速变形的过程. 这些是泡沫铝本构模型的试验研究和验证工作的主要困难之一. 数值分析中, 可以根据研究对象和目的, 选取球体几何模型(geometric model)、结构模型(structural model)或离散模型(discrete model)[58]等, 合理设置和控制胞孔形状、孔壁厚度、孔径、孔隙率及内部缺陷等相关参数[9, 14-15], 实现参数的精准控制, 进而减轻或消除泡沫铝分散性的影响. 在此基础上, 通过一定的技术手段, 研究人员实现了对泡沫铝各种加载速度(或应变率)、加载方式及边界条件的数值分析, 包括单轴加载、侧面耦合单轴加载、双轴加载、三轴比例加载、三轴静水加载及其他特殊的边界条件. 对泡沫铝的宏观性能和细观结构、孔壁材料性能之间的关系, 包括杨氏模量、体积模量、屈服强度、塑性泊松比、屈服面及其强化规律等, 有了更深入的认识.
Grenestedt等[74]使用Kelvin模型研究了孔壁厚度对闭孔泡沫材料弹性刚度的影响. Youssef等[75]通过逆向重构模型研究了多孔材料压缩过程中的初始组织和局部变形机理. Bardenhagen等[76-77]采用物质点法模拟了开孔泡沫材料致密化的过程, 并分析了其物理特性. Demiray等[78]对开孔泡沫材料的初始及后继屈服面进行了数值计算. 刘耀东等[79]对多孔金属速率敏感性进行了数值研究. 宋延泽等[63]基于十四面体模型对闭孔泡沫材料的动态力学性能进行了有限元分析. Marcadon与Feyel [80]采用空心球堆叠模型, 讨论了模型结构体系及其对本构方程的影响. Giorgi等[81]对比分析了Kelvin十四面体及不规则分布椭球两种胞元结构对有限元计算结果的影响.
Machado等[82]将无网格伽辽金算法(element-free Galerkin method)引入到泡沫材料的力学性能研究中, 并将ABAQUS中体积强化可压缩本构模型的屈服面演化与ABAQUS中各向同性强化可压缩模型的非关联流动法则组合应用, 捕捉到了更高的变形和变形梯度. 宫伟伟[83]将自相似模型引进到物质点法程序中, 并加入了失效准则, 用于模拟泡沫铝的动态压缩试验. Zhang等[84]基于3D Voronoi技术, 分析了闭孔泡沫金属材料的倒塌与断裂行为的细观力学表现. 张健等[59,85]采用逆向重构泡沫铝模型, 确定了三种本构模型的材料参数, 并验证了其在多轴载荷下屈服面演化的适用性.
随着研究的深入和建模技术的发展, 采用离散模型进行泡沫铝本构行为的数值分析研究逐渐成为一大研究趋势. Jeon等[89]采用离散模型对闭孔泡沫铝的塑性破坏行为进行了研究, 发现塑性应变局部带的塑性铰是引起泡沫铝塑性破坏的主要原因. 张健等[85](2015)采用逆向重构模型, 确定了3个有代表性的泡沫铝本构模型的本构参数, 并对其在单轴压缩和静水压缩下的模型屈服面准确性进行了评估. 李侯贞强等[90]基于映射网格思想, 提出一种建立闭孔泡沫铝三维离散模型的简化方法, 实现了对泡沫铝试件在准静态和动态压缩下的受力、变形与破坏过程更加详细的模拟分析. 虽然基于Micro-CT断层扫描技术的离散模型建模复杂, 中间处理步骤繁多且往往需借助于多套大型商业软件来实施, 但是其可最大程度还原泡沫铝的胞孔形态和拓扑结构特征, 具有其他模型无法比拟的仿真程度, 因而备受青睐.
通过商业化有限元软件(包括ANSYS、ABAQ-US、 LS-DYNA等)及非商业开源软件提供的数据接口, 人们开发了多种描述多孔材料性能的本构子程序, 极大提高了分析效率并简化了操作流程, 同时也为泡沫铝在工程项目中的应用带来了方便, 推动了众多内置于有限元软件的数值分析模型的诞生. Reyes等[91]通过增加单元删除准则来模拟断裂和失效, 同时考虑材料质量的非均匀分布, 并通过用户子程序将其植入有限元软件LS-DYNA中. Shahbeyk等[92]针对自相似模型编制了ABAQUS的VUMAT接口子程序, 研究了泡沫金属填充铝管的压溃性能. 罗绍鸿[12]以自相似模型为基础, 增加材料破坏准则, 利用ABAQUS平台开发了一套包含弹塑性分析和破坏特征描述的泡沫铝VUMAT程序. 为描述高孔隙率泡沫铝的应变率效应, 寇玉亮等[94]建立了一种率相关的横观各向同性泡沫铝本构模型, 开发了基于ABAQUS平台的VUMAT子程序, 并采用一个单元和多个单元验证了计算结果的收敛和稳定性. 张健[59]基于各向同性可压缩泡沫本构模型框架, 采用特征应变、两参数对称屈服面、体积强化和非关联流动法则, 加入破坏准则, 建立了闭孔泡沫铝的唯象本构模型, 并编写了ABAQUS的VUMAT接口子程序.
采用有限元数值方法研究泡沫铝材料本构关系也有其局限性. 首先是数值分析计算精确性的问题. 不同软件、模型、边界条件等众多因素, 都会对计算结果的精确度造成影响. 其次, 是计算效率问题. 由于泡沫铝材料本身结构的复杂性, 为了得到可靠的分析结果, 人们往往倾向于选用简化程度较低的模型, 进而导致其计算效率降低. 为了提高计算效率, 在数值分析中常采用质量缩放(mass scaling)、对称性边界条件等[95-96]技术手段. 最后, 虽然在有限元软件中各种载荷边界条件相对于试验更容易实现, 但是, 泡沫铝的三轴比例加载(加载比例为1:1:$x$)及非比例加载(加载比例为1:$x$:$y$)依旧存在大变形下的应力比例难以维持恒定的问题[59].
3 现有本构模型概述
泡沫铝在宏观上具有非线性大变形、体积可压缩、拉压不对称和应变率相关等复杂特性. 以大量的试验研究、数值模拟及理论分析为基础, 人们建立了不同的本构模型来表征泡沫铝的应力-应变关系, 并确定了一些关键本构参数(杨氏模量、塑性泊松比、压缩及拉伸屈服强度等)与泡沫铝材料参数之间的关系. 其中, 有些模型最初并非是针对泡沫铝材料建立, 但是通过相关的试验研究和数值分析, 发现其对泡沫铝具有较好的适用性, 因此被一些学者用于泡沫铝力学性能及本构模型的研究中.
3.1 一维本构模型概述
一维本构模型主要用于分析泡沫铝的动态压缩行为及吸能性能. 应力增强和变形局部化是泡沫铝在动态压缩下最明显的两个特征, 基于此专家们提出了一系列的一维本构模型.
式中, $\sigma^{qs}$为准静态塑性压溃应力, $\rho _0 $为材料初始表观密度, $V_i$为初始冲击速度.
Tan等[30]认为泡沫铝在压缩吸能中经历的塑性变形远大于弹性变形, 因而可以忽略其弹性变形, 采用R-P-P (rigid-perfectly plastic)模型来表征其压缩行为更简便.
式中, $E_0 $为弹性模量, $\varepsilon _{\max} $为最大理论应变, 由泡沫金属的相对密度$\rho _{r} $确定, 即$\varepsilon _{\max} =1-\rho _{r} $, $U_{\max}^{Q-S} $为泡沫金属准静态压缩时的单位体积能. E-P-R模型关键参数最大理论应力$\sigma _{\max }$与塑性模量$E_{P}$的表达式分别为
式中, $\sigma _{cr}$为模型临界应力, $\varepsilon _{cr} $为临界应变.
式中, $\sigma _0$为初始压溃应力, $K$为强度指标, $n$为应变硬化指数.
Zheng等[101]提出用R-LHP-L (rigid-linearly hardening plastic-locking)模型研究泡沫金属在冲击模式和过渡模式下的动态力学行为, 成功预测并给出了泡沫金属3种变形模式(均匀模式、过渡模式和冲击模式)临界速度, 为R-P-P-L模型补充了解析解.
Wang等[29]考虑应变率效应的影响, 使用D-R-LHP-L (dynamic-rigid-linear hardening plastic-locking)模型和D-R-P-P-L (dynamic-rigid-perfectly plastic-locking)模型研究了泡沫金属杆内塑性波或冲击波产生的临界速度和能量守恒条件.
式中, $\sigma _0$为初始压溃应力, $C$为应变硬化参数.
3.2 一维本构模型总结
以是否忽略泡沫铝在压缩变形过程中的弹性变形为标准, 可以将一维本构模型分为两大类. R-P-P模型、R-P-P-L模型及R-PLH模型等忽略了泡沫铝压缩过程中的弹性变形阶段, 因而适用于高相对密度、高刚度的泡沫铝材料; 而低相对密度、低刚度的泡沫铝材料的弹性阶段相对较长, 因此更宜选取E-P-P-R模型、E-P-R模型或E-P-P-H模型.
事实上, 泡沫铝应力-应变曲线密实阶段是一个渐进的过程, 基于这个认识, 学者们提出了更加符合实际的一维模型, 以考虑非线性塑性硬化行为, 这是目前一维本构模型的一个主要发展方向.
3.3 三维本构模型概述
(1) GAZT模型
式中, $\sigma _{e} $为von Mises等效应力, $\sigma _{m} $为静水压力(平均应力), $\sigma _{y}$为泡沫铝单轴压缩平台应力, $\rho ^* $为泡沫铝表观密度, $\rho _{s} $为泡沫铝基材料密度. GAZT模型仅对初始屈服面进行了表征, 没有给出相应的强化及流动法则, 但其依旧是泡沫铝材料(及其他多孔材料)的经典本构模型之一.
图13
GAZT模型的屈服面在$\left( {\sigma _{m} ,\sigma _{e} } \right)$平面内为对称抛物线, 即认为泡沫材料单轴压缩屈服强度与单轴拉伸屈服强度相等. Triantafillou等[108]完成了模型的试验验证, 并发现其较好地描述了泡沫材料多轴行为的主要特征. 该模型基于规则模型得到, 特别适合形状规整且内部无缺陷的开孔泡沫材料, 但对闭孔泡沫铝的屈服面描述不够准确. Andrews等[110]比较了GAZT模型对开孔及闭孔泡沫铝的适用性, 发现模型会高估闭孔泡沫铝的杨氏模量和抗压强度, 但对于开孔泡沫铝有很好的适用性. Miller[13]认为GAZT模型屈服面几乎是不可压缩的, 单轴压缩情况下会产生严重的侧向变形, 无法模拟泡沫金属材料的贯入实验.
(2) Zhang模型
其中, $a$, $b$与$x_0$均为材料参数, $a$, $b$表示屈服面椭圆的长、短轴半轴的二次幂, $x_0 $表示椭圆中心位置, 三者均可以通过试验数据拟合得到. Peroni等[16]发现该屈服面能很好地吻合多轴试验的材料屈服数据.
Zhang模型采用非关联流动法则, 即塑性流动势函数$\varphi $与屈服面函数$f$不相等, 其塑性势函数为
式(11)中, $\beta $为控制体积塑性流动的材料参数. 参数$\beta $的表达式为
式(12)中, $\nu ^{pl}$为材料的塑性泊松比.
Zhang模型的强化通过体积强化实现, 并以塑性体积应变$\varepsilon _{vp}$为变量的材料参数$x_0 (\varepsilon _{vp} )$, $a(\varepsilon _{vp})$和$b(\varepsilon _{vp} )$来表征, 通过改变式(10)中的材料参数, 使屈服面随塑性体积应变的增大而增大.
张健[59]通过对闭孔泡沫铝逆向重构模型进行有限元数值分析发现, Zhang模型静水压缩下的屈服面演化与数值结果吻合较好, 单轴压缩和三轴等比加载(加载比例为1:1:$x$)的屈服点仅在应变较小时吻合较好.
(3) Miller模型
式中, $\gamma $, $\alpha $和$d$为待定参数, 通过试验的应力、应变数据确定.
由式(13)可知, Miller模型的屈服面是一个关于有效应力和平均应力的多项式, 其形状为$\left( {\sigma _{m} ,\sigma _{e} } \right)$平面内的不对称椭圆. 式(13)中存在一个平均应力的一次幂, 因而其屈服面可描述不同的拉伸和压缩屈服行为.
Miller模型采用关联流动法则, 即塑性流动势函数$\varphi $与屈服面函数$f$相等, 模型强化法则的核心思想表达式为
式中, $\bar{{\varepsilon }}_{pl} $为等效塑性应变, $\varepsilon _{vol}$为体积应变.
当满足式(15)时, Miller屈服面退化为GAZT屈服面
Ruan等[113]发现Miller模型在塑性泊松比$v_{pl}$较大时会形成一个马鞍形屈服面, 与屈服面应是外凸面的要求不符.
(4)自相似模型(self-similar model)
Deshpande和Fleck依据开孔泡沫铝Duocel (相对密度7${\%}$)和闭孔泡沫铝Alporas(相对密度8.4${\%}$, 16${\%}$)的多轴压缩试验数据, 提出了自相似模型(self-similat model)[20]. 自相似模型的屈服面表达式为
式中, $\hat{{\sigma }}$为等效应力, $Y$为单轴拉伸或压缩屈服应力, $\alpha$为屈服面形状参数, $v^{pl}$为塑性泊松比.
该模型为唯象模型. Deshpande和Fleck明确指出可将唯象理论引入到泡沫铝的本构模型研究中, 这对泡沫铝本构模型的后续研究具有深远的影响.
由式(16)及式(17)可知, 自相似模型的屈服面在$\left( {\sigma _{m} ,\sigma _{e} } \right)$平面为对称椭圆. 与Miller模型相同, 自相似模型同样采用了关联流动法则.
自相似模型的强化法则综合考虑了泡沫铝单轴压缩及静水压缩对其后继屈服面的影响, 其表达式为
式中, $Y_{0}$表示单轴压缩的初始屈服应力, $h_\sigma \left( {\varepsilon _u }\right)$和$h_{p} \left( {\varepsilon _{vol}}\right)$分别表示单轴和静水压缩下的切线模量, 用于表征泡沫铝压缩下的强化响应.
为了便于应用, 自相似模型有一个简化版. 简化版自相似模型(simplified version of the self-similar model)的强化响应直接由单轴压缩响应给出, 其原理如式(20)所示
式中, $H$表示强化函数, $\hat{{\varepsilon }}$为等效应变.
自相似模型及其简化版的屈服面均以几何自相似的方式演化, 这与试验观察并不完全一致[31]. 与GAZT模型一样, 自相似模型及其简化版本同样没有考虑泡沫铝单轴拉伸和压缩的不对称性.
(5)微分强化模型(differential hardening model)
为使屈服面的演化不受几何自相似方式的约束, 进而更准确地描述后继屈服面的演化, Deshpande和Fleck还提出了更复杂同时也更为精确的微分强化模型(differential hardening model)[33]. 微分强化模型的屈服面表达式为
式中, $S$, $P$分别为单轴压缩与静水压缩下的屈服\lb 强度.
微分强化模型的屈服面在$\left( {\sigma _{m} ,\sigma _{e} }\right)$平面同样为对称椭圆, 其流动法则也采用了关联的形式.
微分强化模型的特点在于其准确却极其复杂的强化法则. 该模型允许后继屈服面形状同时沿平均应力和有效应力两个方向演化, 因而能够细致地描述金属泡沫塑性屈服面演化的整个过程. 其强化法则如式(22)所示
式中, $h_{\alpha \beta } $为强化参数
由于其强化法则过于复杂, 微分强化模型的实用性受到限制.
(6) Chen-Lu模型
Chen和Lu[19]基于弹性余能表达式, 引入无量纲的特征应力和特征应变, 结合相应的应力势和屈服流动法则, 提出了可适用于泡沫金属塑性可压缩和塑性不可压缩材料的弹塑性本构模型理论框架.
Chen-Lu模型的应力势函数以特征应力及特征应变为参变量, 因而不用区分弹性部分与塑性部分, 也不需要任何初始屈服面的信息, 从而规避了唯象本构模型中将弹性阶段与塑性阶段分离的做法.
特征应力$\bar{{\sigma }}$、特征应变$\bar{{\varepsilon}}$的表达式及其关系如下
其中
Chen-Lu模型没有区分弹性和塑性, 不存在塑性本构框架内的屈服面, 因此定义类似"屈服面"的应力势函数如下
式中, $\varPhi _1 \left( {\bar{{\varepsilon }},\sigma _{ij} } \right)$和$Y\left( {\bar{{\varepsilon }}} \right)$是由实验确定的材料参数, 由两次特征实验确定. 对于各向同性材料来说, $\varPhi _1 \left( {\bar{{\varepsilon }},\sigma _{ij} } \right)$一般依赖于$\sigma _{m} $, $\sigma { }_{e}$和$J_3 $. 假设式(25)中的$\varPhi _1 =C\left( {\bar{{\varepsilon }}} \right)\sigma _{m}^2 $, 便得到其最常见的表征形式
此时, 特征参数由$\varPhi _1 \left( {\bar{{\varepsilon }},\sigma _{ij} } \right)$和$Y\left( {\bar{{\varepsilon }}} \right)$简化为$C\left( {\bar{{\varepsilon }}} \right)\sigma _{m}^2 $与$Y\left( {\bar{{\varepsilon }}} \right)$. 其在$\left( {\sigma _{m} ,\sigma _{e} } \right)$平面为对称椭圆.
Chen-Lu模型采用关联流动法则, 通过单轴压缩下的特征应力-特征应变曲线$\bar{{\sigma }}_{u} \left( {\bar{{\varepsilon }}} \right)$和静水压缩下的特征应力-特征应变曲线$\bar{{\sigma }}_{h} \left( {\bar{{\varepsilon }}} \right)$来表征后继屈服面的演化.
(7) Lode角模型
修正后的抛物线和椭圆屈服函数为
式(27)$\sim$式(29)中, $a_1 $, $a_2 $, $A$, $B$, $A_1 $, $B_1 $均为拟合参数, $\sigma _{c} $为单轴压缩屈服强度, $\theta $为Lode角.
这种修正的数据验证不足, 屈服函数是否合理有待商榷.
(8) Forest模型
Forest等[21]提出了一种基于可压缩塑性框架的连续介质模型, 主要基于以下3点的考虑: (1)基于椭圆势的可压缩塑性模型; (2)由层析图像导出的非均匀初始孔隙度图; (3)将固有长度尺度纳入连续体模型的正则化过程. 该模型适用于应变局部带化的模拟. 模型的屈服面函数如下
式中, $C$, $F$为取决于材料的孔隙度的参数, $R$为强化函数.
Forest模型的初始屈服面在$\left( {\sigma _{m} ,\sigma _{e} }\right)$平面内为对称椭圆, 模型采用关联流动法则, 其强化函数如下
式中, $R_{0}$、$H$为材料强化参数(文献[34]中给出的值为$R_{0} = 200$ MPa, $H=10$ MPa), $\mu $为剪切模量, $\varepsilon _u$为单轴压缩真实轴向应变.
3.4 三维本构模型总结
基于将泡沫铝作为一种各向同性材料的假设, 已经建立了多种体系成熟的本构模型. 但早在1999年, Deshpande和Fleck就发现, 当高相对密度泡沫铝Alporas单向压缩至对数轴向应变0.70时, 随后的横向强度约为轴向强度的两倍, 表明泡沫金属在较大塑性应变下呈现各向异性, 而各向同性硬化本构模型不能表征这种各向异性的发展趋势[20]. 对此, Gioux等[103]提出归一化方法, 其主要思路为将各向同性屈服函数的应力变量通过归一化替代为无量纲变量, 进而在保持屈服函数形式不变的前提下得到适合各向异性材料的屈服函数. Gioux等[103]考虑泡沫铝三个方向屈服强度的差异提出了如式(33)所示的归一化等效应力$\sigma _{e}^* $和平均应力$\sigma _{m}^* $
其中, $\sigma _{pl1} $, $\sigma _{pl2} $, $\sigma _{pl3}$是泡沫铝沿着3个方向的单轴屈服强度. 用归一化变量$\sigma _{e}^* $, $\sigma_{m}^* $代替变量$\sigma _{e}$, $\sigma _{m}$之后便得到适合各向异性材料的屈服准则. Doyoyo等[46]采用类似方法归一化应力第一不变量和偏应力第二不变量, 基于各向同性的屈服函数, 建立了适合各向异性的屈服准则. Alkhader和Vural[119-120]基于弹性应变能密度, 归一化推导出无量纲弹性能密度, 建立了针对2D多孔材料的屈服准则, 并进一步推导出三轴加载时横观各向同性泡沫材料屈服等效应力、等效应变以及屈服函数的表达式.
现有模型, 除Chen-Lu模型[19]外, 均采用了区分弹性阶段和塑性阶段的方法, 这就产生了屈服判断的问题[96]. 国内外学者基于各自的实验和数值分析数据特征, 提出的初始屈服判断依据可分为两大类. 第一类是根据材料应力-应变或载荷-位移曲线, 将某些特征应力状态定义为初始屈服状态. Deshpande和Fleck[121]双轴和立方体加载时, 将应力-应变曲线的弹性阶段和塑性阶段的交叉点定义为屈服强度; Doyoyo等[46]压缩/拉伸-剪切时, 定义垂直加载方向载荷-位移曲线的弹性极限位置为屈服状态. Chen等[122]基于2D细观结构双轴加载, 定义应力-应变曲线的峰值为屈服状态. 第二类是取特定数值的特征应变对应的状态定义为初始屈服状态. Deshpande和Fleck[20,123]三轴对称压缩时, 定义0.3${\%}$残余轴向应变对应的应力、应变状态为初始屈服状态. Combaz等[42,116]双轴和多轴加载时, 采用von Mises等效应力-等效应变曲线, 定义0.2${\%}$残余等效应变为初始屈服状态. Alkhader和Vural[119]研究2D多胞孔结构双轴加载时, 基于弹性应变能密度定义特征应力和特征应变, 进而定义0.02${\%}$塑性特征应变对应的状态为初始屈服状态. 但是, 这两类判断方式, 都存在一定的数据离散性问题. Wu等[124]为改善泡沫铝屈服面数据的离散性问题, 结合试验及3D Voronoi模型数值分析, 提出了在应变空间表征泡沫铝屈服面的思路. 张晓阳等[125]基于3D Voronoi模型研究了闭孔泡沫铝在三轴载荷作用下的屈服特性, 为泡沫铝本构模型研究中屈服面确定这一关键问题提供了思路.
与一维模型同样, 三维模型中考虑应变率效应的模型也占比较少, 因此, 将对泡沫铝率效应的研究成果引入三维本构模型中, 是一个十分重要的问题. 就目前被广泛应用的泡沫铝本构模型来说, 只有ABAQUS软件中的各向同性强化可压缩泡沫模型(crushable foam model with isotropic hardening)和体积强化可压缩泡沫模型(crushable foam model with volumetric hardening)明确提出可以通过应力指数法则(overstress power law)和列表输入屈服比(tabular input of yield ratio)两种方式将率效应引入模型中[72,106]. 率敏感性是泡沫铝本构行为研究中的核心科学问题之一, 也是近年来研究的重点和热点, 但是由于泡沫铝制备方法的多样性和动态实验技术的差异, 迄今为止国内外学者的研究没有得出一致的结论[91,126]. 甚至对于相同制备工艺(powder metallurgy technique)生产出的相同相对密度的泡沫铝(IFAM)会得出相悖的应变率敏感性结论[127-129]. 但是, 仍然有一些学者在这方面做出了努力, 提出了一些率相关本构模型[94,130].
现有本构模型在流动法则的选取及强化法则的侧重点上存在较大分歧, 且均不能准确表征泡沫铝后继屈服面的演化. 现有本构模型的塑性流动法则分为两类: 关联流动法则及非关联流动法则. 非关联流动法则使得材料刚度矩阵是非对称的[131], 因此当具有非关联流动法则的本构模型应用于有限元分析时, 应使用非对称矩阵存储器和求解策略[72, 132]. 强化法则主要考虑材料单轴压缩强化响应及静水压缩强化响应两方面, 不同本构模型对两者的权重考虑不同. Deshpand和Fleck [18]提出, 非比例加载下, 各向异性的发展可能成为重点且需要相应的硬化模型, 随动强化(kinematic hardening)是必要的, 并建议作为将来的一个研究主题.
本构模型的验证工作依旧是现阶段的工作重点. 验证工主要由3部分组成: 基材料及本构模型参数的确定、初始屈服面的验证及后继屈服面演化的验证. 张健等[59,86]根据泡沫铝单轴压缩试验及逆向重构模型的有限元分析, 确定了基体材料参数及3种模型(各向同性强化可压缩本构模型[72], Chen-Lu模型[19] 及Zhang模型[22,111])的本构参数. 验证结果发现, 各向同性强化可压缩本构模型[72]在单轴压缩时的结果吻合良好, 而静水压缩时只有初始屈服点吻合良好, 试件在特征塑性应变为0.1时, 预测的静水压缩屈服应力和数值计算结果相比就会产生超过20${\%}$的偏差, 而且随着特征塑性应变的增大而增大, 可见该模型屈服面在大变形时会严重低估闭孔泡沫铝静水压缩的屈服应力. Chen-Lu模型[19]在单轴压缩时的结果吻合良好, 静水压缩时初始屈服点吻合良好, 而在特征塑性应变为0.4时, 预测的静水压缩屈服应力和数值计算结果相比偏差超过20${\%}$, 该模型在大变形时略微低估闭孔泡沫铝静水压缩的屈服应力. Zhang模型[22,111]在静水压缩时的结果吻合很好, 单轴压缩和等比加载的屈服点在应变较小时吻合良好, 在大应变时虽然有一些偏差, 也都在屈服面附近, 该模型的屈服面有较好的精度. 此外, 对于将塑性泊松比引入其中并处理为常数的本构模型, 塑性泊松比在压缩过程中的倒S形走势[59,86]也会对其后继屈服面的演化造成显著影响[92].
现有泡沫铝本构模型众多, 适用性体系的建立至关重要. Hanssen和Hopperstad等[93]通过单轴压缩、单轴拉伸、压痕测试、对角加载及泡沫铝填充梁的弯曲试验等结果及有限元数值模拟结果的对比, 建立了一个关于泡沫铝和泡沫铝填充结构力学行为的实验数据库, 用于验证各种加载条件下泡沫铝本构模型的适用性, 并且对已有的9种泡沫铝材料模型进行了讨论和比较. 为了说明数据库的使用, 也通过数值模拟与实验数据的比较对LS-DYNA软件的4种模型进行了评估. 张健等[59,86]研究了各向同性强化可压缩本构模型[72], Chen-Lu模型[19] 及Zhang模型[22,111]单轴压缩及静水压缩下的适用性.
很多学者在已有本构模型的基础上进行了补充、修正. 王二恒等[39-40]以Chen-Lu模型为框架, 建立了泡沫铝的准静态本构模型, 并推导了三轴等比例加载和环向受约束轴向加载下的宏观应力-应变曲线. 寇玉亮等[94]基于Tagarielli等[133]提出的多孔材料横观各向同性率无关模型, 在屈服函数中考虑应变率的因素, 构建了一种泡沫铝率相关本构模型并编写了基于ABAQUS平台的VUMAT子程序. 罗绍鸿[12]以自相似模型为基础, 增加材料破坏准则, 提出了一个包含弹塑性分析和破坏特征描述的泡沫金属本构关系, 并编写了ABAQUS平台的VUMAT子程序. 习会峰等[134]简化六参数的Liu-Subhash模型[135]为五参数, 并将参数与温度关联, 提出了一种考虑温度效应的泡沫铝静态压缩本构模型. 王鹏飞等[130]基于Sherwood和Sherwood和Frost[136]提出的泡沫材料本构关系框架, 对常温下的应变率敏感系数进行了温度项修正, 得到一种泡沫铝在一定密度范围内包含温度项、应变率项的本构方程. 张健[59]基于各向同性可压缩泡沫本构模型框架, 加入破坏准则, 编写了基于ABAQUS平台的VUMAT子程序. 朱长峰[137]基于变化的椭圆率, 提出了修正的Deshpand-Fleck泡沫本构模型等等. 对于自相似本构模型、Zhang模型、Miller模型及各向同性强化可压缩泡沫模型等包含关键参数塑性泊松比$\nu ^{pl}$的确定也是一个重要的方向. 泡沫铝塑性泊松比的概念最早由Miller引入[13], 即轴对称试验中径向塑性应变率与轴向塑性应变率之比. 自相似本构模型、Zhang模型、Miller模型及各向同性强化可压缩泡沫模型等, 在泡沫铝的整个变形过程中均把$\nu ^{pl}$作为一个恒定值处理. 但是, 张乐等[87]、王长峰等[88]及张健等[59,86]分别在Kelvin模型、3D Voronoi模型及泡沫金属逆向重构模型的压缩过程中观察到泡沫铝的塑性泊松比呈现倒S形走势, 因此一些研究者尝试对此参数进行修正. 张健、张乐等[59,86-87]提出了平均塑性泊松比的概念, Fang等[138]将塑性泊松比作为应变的指数函数, 提出了一种修正模型, 并与LS-DYNA中的#63模型、#75模型与#154模型进行了对比, 发现这样修正后, 模型的数值稳定性和精度有了显著提高.
迄今为止, 描述泡沫铝本构关系的模型已经为数不少, 但仍然存在很多问题, 其中一个重要的原因是泡沫铝材料的可压缩性以及材料微结构的不规则性和随机性. 此外, 各因素之间的耦合作用, 如率效应与温度等[139], 也有一定影响. 因此, 确定各种影响因素的权重对于泡沫铝本构模型的后续研究具有重要的意义.