引言
作为潜力巨大的新材料, 其力学行为和机理的研究具有重要的理论价值和实际意义.得益于非晶合金合成与制备方法的不断进步,相继获得一系列体积大、热稳定性高的非晶合金,为非晶物质玻璃转变以及室温力学行为的研究提供了理想的模型合金.但由于非晶态合金不具有类似晶态结构中位错滑移机制,其在室温下形变高度局域化在剪切带内, 进而转变成裂纹,导致材料缺乏室温宏观塑性, 成为其实际应用的极大障碍.随着对非晶合金物理性能和力学行为的大量研究,研究者将这种形变高度局域化的物理起源归因于微观结构非均匀性[3,6].杨勇等[7]通过非晶合金在动态载荷下的滞弹性行为研究了非晶合金中的原子团簇和流动缺陷,发现排列松散的自由体积区域被排列紧密的弹性外壳所包裹,具有类似过冷液体的变形特征.Ichitsubo等[8]利用超声振动技术使Pd基非晶合金部分晶化,使得高分辨率电镜可以分辨非晶合金中晶化速度有差异的硬区与软区.陈明伟等[9]首次提供了非晶合金中纳米尺度黏弹性不均匀性的实验证据,利用动态原子力显微镜从实验中直接观察到了Zr基非晶合金的能量耗散不均匀和模量不均匀,测量到结构不均匀性的尺寸约为2.5 nm. 王云江等[10]对CuZr二元非晶合金进行了分子动力学模拟,认为无序固体的性能是由结构亚纳米级的空间关联特性所决定的.因此要研究非晶合金的变形行为,必须认识到微观非均匀的玻璃结构的重要性以及其在变形过程中的演化.普遍认为变形的基本单元要能够容纳剪切应变的原子局部重排,这种基本单元在晶体材料中是位错,在非晶合金中则是具有瞬时性定义的剪切转变区(shear transformation zone, STZ).金属宏观塑性变形的本质是由于STZ的作用和自由体积的再分配而产生的局部应变的积累[11-12].
非晶合金变形行为还会受到物理时效(退火)等行为的影响.在非晶合金物理时效过程中, 原子会跨越一系列的低能态,导致焓、熵和缺陷浓度等参量发生变化, 原子排列调整.非晶材料中这种微观结构变化的宏观反映, 就是非晶合金性能的变化. Nagel等[13]发现经过物理时效后,Zr$_{46.7}$Ti$_{8.3}$Cu$_{7.5}$Ni$_{10}$Be$_{27.5}$块体非晶合金的密度增大了0.1%.
1 实验方法
本实验所采用的模型体系是采用电弧熔炼-铜模吸铸方法制备的大块非晶合金,其名义组分为Zr$_{50}$Cu$_{40}$Al$_{10}$ (原子百分比).
研究采用Rigaku D/max 2500型X射线衍射仪(XRD)对样品进行X射线衍射实验,以确定样品的非晶特征. 模型合金热性能通过NetzschDSC404型差示扫描量热仪(DSC)来进行测定.
动态力学分析是指对材料施加交变载荷, 测量对应的的应变响应的技术.复模量可以表示为$E^\ast (G^\ast )=E'+{\rm i}E''=G'+{\rm i}G''$,其中储能模量$E'(G')$代表样品弹性变形而储存的能量,而$E''(G'')$是对应于黏弹性的损耗模量, 代表样品因黏性变形而损耗的能量.材料的内耗用$\tan \delta =E''/E'=G''/G'$表示.动态力学分析测试所用的样品尺寸约为30 mm (长) $\times$ 2 mm (宽) $\times$ 1\nbsmm (厚). 动态力学分析实验分两部分进行: (1)恒定加载频率和升温速率,观察损耗模量和储能模量随温度的演化. 该部分实验在商用动态力学分析仪(TADMA Q800上进行). (2)等温扫频实验, 将样品在某一温度恒定,观察储能模量和损耗模量随不同加载频率的演化过程.该部分实验在法国国立里昂应用科学学院(INSA Lyon) MATEIS实验室进行,设备为自行设计的高真空倒扭摆内耗仪, 等温扫频温度间隔为5 K.
条带拉伸试验在商用DMA Q800试验机的拉伸夹具模式下进行, DMA Q800试验机力控制范围为0.0001$\sim$18 N, 拉伸试样是母合金通过高真空单辊甩带设备制得厚度约50 $\mu $m的非晶薄带.
2 实验结果
2.1 结构和热力学信息表征
图1
图1
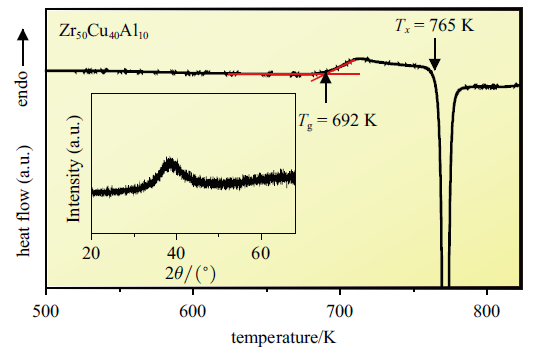
Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金的DSC曲线, 加热速率为10 K/min. 插图为X射线衍射图样
Fig. 1
DSC curve of Zr$_{50}$Cu$_{40}$Al$_{10}$ metallic glass with a heating rate of 10 K/min. Inset shows the XRD pattern of Zr$_{50}$Cu$_{40}$Al$_{10}$ metallic glass
2.2 动态力学分析
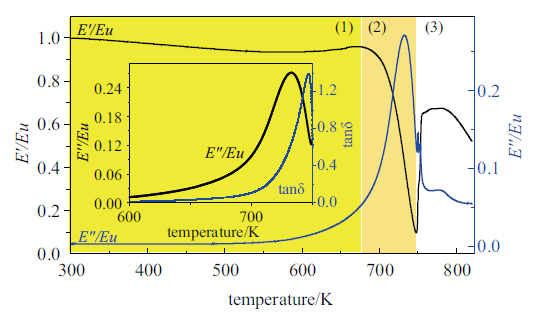
图2是储能模量、损耗模量和内耗在3 K/min 的升温速率下随温度的演化曲线, 给定的加载频率为1 Hz. $E_{u}$为室温下未弛豫时的储能模量.本研究模型合金的演化规律与其他非晶固体体系表现出的动力学特征类似[18]: (1)在低温区, 储能模量很高仅略微下降, 而损耗模量近乎为0,此时非晶合金的特性主要表现为弹性变形; (2)当温度升高至680 K时, 储能模量急剧降低, 损耗模量快速升高, 在732 K时模型体系的主弛豫($\alpha$弛豫)峰值出现. 主弛豫对应着非晶物质中的动态玻璃转变过程; (3)当温度升高至750 K以上时,储能模量与损耗模量均有先升后降的过程,该过程对应着非晶合金体系的晶化过程. 图2中的插图分别是升温过程中损耗模量与内耗随温度的变化,内耗与一个周期内材料耗散的能量直接相关, 这种能量耗散是由于外加的动态应力引发的原子运动, 因此对内耗的研究可以揭示黏弹性材料原子运动的微观机制与动力学过程[19]. 低温区原子被冻结, 原子移动性很低, 随温度升高, 原子移动性逐渐增大, 在过冷液相区, 伴随着大规模的原子协同运动, 非晶合金发生不可逆的结构演化.
图2
图2
Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金的归一化储能模量${E}'/Eu$和损耗模量${E}''/Eu$随温度的演化曲线(升温速率3 K/min, 加载频率1 Hz).插图是损耗模量和内耗在加热过程中的演化过程
Fig. 2
Evolution of the normalized storage modulus and loss modulus with temperature of Zr$_{50}$Cu$_{40}$Al$_{10}$ metallic glass (heating rate: 3 K/min, driving frequency: 1 Hz). $E_{u}$ is the unrelaxed modulus, assumed to be equal to the storage modulus at ambient temperature. Inset is the loss modulus and loss factor as a function of temperature
非晶合金的动态弛豫对其施加的频率非常敏感. 图3为600$\sim$730 K的温度区间内, 采用5 K的温度间隔, Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金损耗模量随测试频率的演化关系. 当温度低于680 K时, 损耗模量很低且变化量较小. 随着温度的升高,损耗模量峰(即$\alpha$弛豫峰)出现且随温度的升高而移向更高的频率, 其原因为随着温度的升高使得非晶合金中特征弛豫时间$\tau$降低. 众所周知,内耗的频率谱峰值对应着内耗的最大值, 此时观察时间$1/\omega_{\max}$与弛豫时间$\tau$相等, 即$\omega_{\max}\tau =1$.
图3
图3
Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金损耗模量$G''/Gu$的等温扫频曲线. 温度区间为600$\sim$730 K, 温度间隔为5 K
Fig. 3
Evolution of the normalized loss modulus $G''/Gu$ as a\\ function of frequency at different temperatures for Zr$_{50}$Cu$_{40}$Al$_{10}$ bulk metallic glass
图4
图4
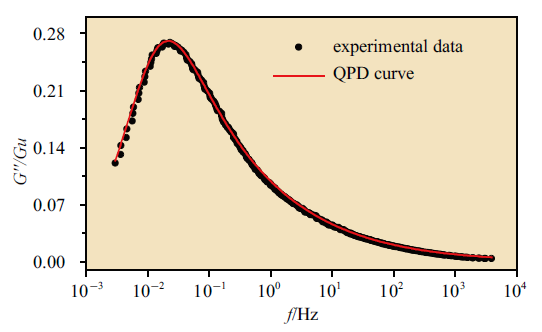
Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金损耗模量$G''/G_u $ 在710 K参考温度下的主曲线. 红色实线是公式 (1) 的拟合曲线
Fig. 4
The master curve of the loss modulus $G''/G_u$ of the Zr$_{50}$Cu$_{40}$Al$_{10}$ bulk metallic glass with the reference temperature of 710 K. The red solid line is the fit by the Eq.(1)
大量的模型被用来描述非晶物质的主弛豫行为, 早期用于研究固体材料中原子运动的Debye模型[21]已经被证明与实验结果相差较大, 可见非晶合金的主弛豫过程并非简单的Debye弛豫过程, 必须考虑弛豫时间的分布. 研究者又提出改进的Cole-Davidson(CD)模型[22]和Kohlrausch-Williams -Watts(KWW)模型[23], 均可以与实验结果较好的吻合,但这两个模型中引入的参数, 都没有明确的物理意义, 因而不能明晰非晶固体主弛豫过程中的微观物理机制. 为了更好对非晶固体主弛豫过程进行物理描述, Perez等[17, 24]基于"缺陷"概念推导了一套完整的理论, 提出了准点缺陷模型(quasi-points defects, QPDs), 最早用来描述非晶聚合物的弛豫行为及力学变形过程[18].根据准点缺陷理论, 在玻璃转变温度以下被冻结的玻璃结构中所存在纳米尺度上的焓、熵以及密度的起伏, 称之为准点缺陷. 非晶态物质的$\alpha$弛豫被描述为分级相关的原子或分子运动, 而对应局部分子或原子运动的弛豫过程则作为$\alpha$ 弛豫过程的前驱运动. 关联因子$\chi$对应着非晶固体中缺陷浓度, 缺陷浓度越高, 则$\chi$越大, 反之亦然. 根据准点缺陷理论,动态模量的复数形式可以表示为[25]
式中, $G^\ast $为复模量, $G_u$为未弛豫模量, $\lambda$为数字因子, 接近1, $\omega $为角频率($=2\pi f)$, $\tau _r $为整体特征时间.
式中, $U_\beta $为结构单元基本运动的激活能, $k$为玻尔兹曼常数, $T$为温度.
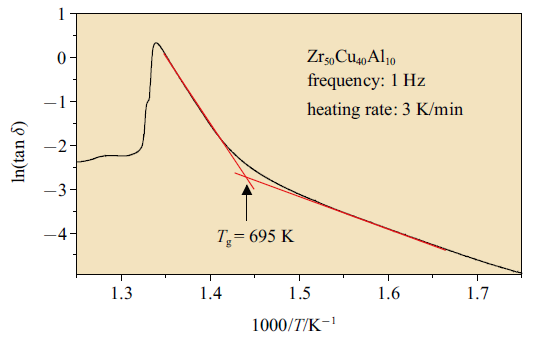
由式(2)还可以得知当温度低于玻璃转变温度时, 关联因子$\chi$基本为一常数, 因此在给定加载频率下, $\ln (\tan \delta)$对温度的倒数作图符合线性关系, 如图6所示. 根据斜率可以求得非晶合金模型体系在玻璃转变温度$T_{\rm g}$以下原子运动的激活能$U_\beta$为0.63 eV, 该值与其他非晶合金体系, 如Zr$_{41.2}$Ti$_{13.8}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$[26]和Pd$_{43}$Ni$_{10}$Cu$_{27}$P$_{20}$[25]激活能非常接近. 尤其需要注意的是, 采用DMA测定得到的动态玻璃转变温度(如图6所示)与采用DSC测得的玻璃转变温度吻合得很好(如图1).
图5
图5
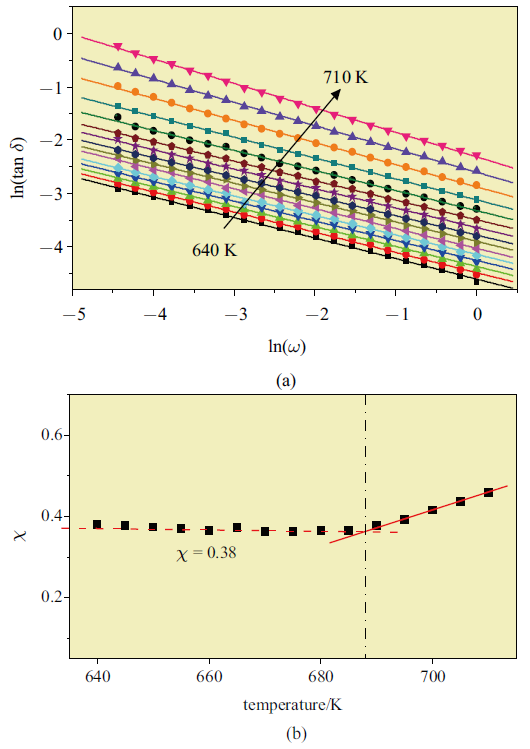
Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金内耗与频率的的相关性. (a) 不同温度下,内耗与频率的双对数坐标图. 实线是公式 (2) 的拟合直线.(b) 关联因子随温度的演化规律
Fig. 5
Correlation between the loss factor and the frequency. (a) Double\\ logarithmic plot of $\tan\delta$ and $\omega$ at the different temperature. The solid line is the fit by the Eq.(2). (b) The temperature dependence of correlation factor $\chi$
图6
图6
Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金在单频率升温过程中内耗随温度的演化按照$\ln\left( {\tan \delta } \right)$和$1000/T$作图
Fig. 6
The $\ln \left( {\tan \delta } \right)$ vs. $1000/T$ in the Zr$_{50}$Cu$_{40}$Al$_{10}$ bulk metallic glass. Driving frequency: 1 Hz; Heating rate: 3 K/min
2.3 高温流变行为
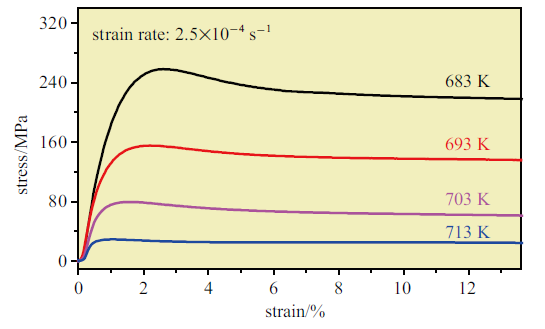
图7是Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金在拉伸实验中的真应力-应变曲线, 应变速率为$2.5\times 10^{-4 }$ s$^{-1}$. 与室温下脆性破坏不同, 在图7中所示的温度范围和应变率下, 样品表现出均匀流变行为. 应力-应变曲线的初始斜率随温度增大而降低, 表明初始杨氏模量随温度升高而降低. 而且稳态流变应力随温度的升高而降低, 表明高温流变是温度相关的热驱动过程. 在683 K, 样品的真拉伸应力-应变曲线上有一个屈服过程, 但随温度的升高, 应力过冲现象逐渐消失, 一般认为应力过冲现象与自由体积引起的结构松弛或流变缺陷形成有关[29,30]. 由于初始自由体积不足, 剪切变形的激活延迟,导致应力超过了稳态值[31].
图7
图7
不同测试温度下Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金的应力-应变曲线(测试应变: $2.5\times10^{-4}$ s$^{-1})$
Fig. 7
Compressive curves at different temperatures of Zr$_{50}$Cu$_{40}$Al$_{10}$ bulk metallic glass at strain rate $2.5\times 10^{-4}$ s$^{-1}$
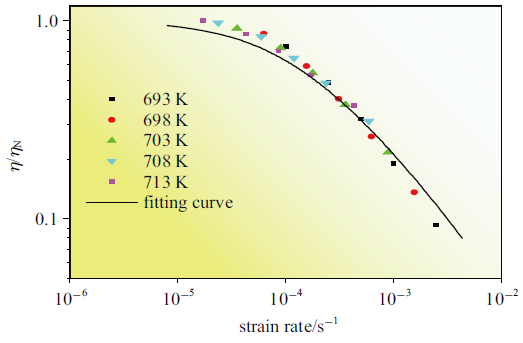
图8(a)是Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金在713 K应变率突变实验中获得的真应力-应变曲线, 应变率范围为$1.0\times 10^{-4}$\sim$2.5\times 10^{-3}$ s$^{-1}$. 可以看到在给定温度下, 稳态流变应力随应变率的增大而增大.基于准点缺陷模型, 拉伸应力-应变曲线表现出稳态流变现象对应着材料内部缺陷浓度的动态平衡,即缺陷产生和湮灭的量相等. 图8(b)是不同温度下Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金名义黏度随应变速率的变化规律. 名义黏度根据公式$\eta =\sigma _{\rm fiow}/(3\dot{\varepsilon})$计算, 其中$\sigma _{\rm fiow}$是流变应力, $\dot{\varepsilon}$是应变速率[32]. 从图8(b)中可以可看出黏度随应变速率的增大而降低. 事实上, 在高温低应变速率下, 黏度与应变速率基本无关. 当温度降低或应变速率增大时, 黏度随应变速率的增大而显著降低, 发生从牛顿流变向非牛顿流变的转变.每个温度下对应的牛顿黏度可由图8(b)外推得出.
图8
图8
Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金
Fig. 8
The Zr$_{50}$Cu$_{40}$Al$_{10}$ bulk metallic glass
图9
图9
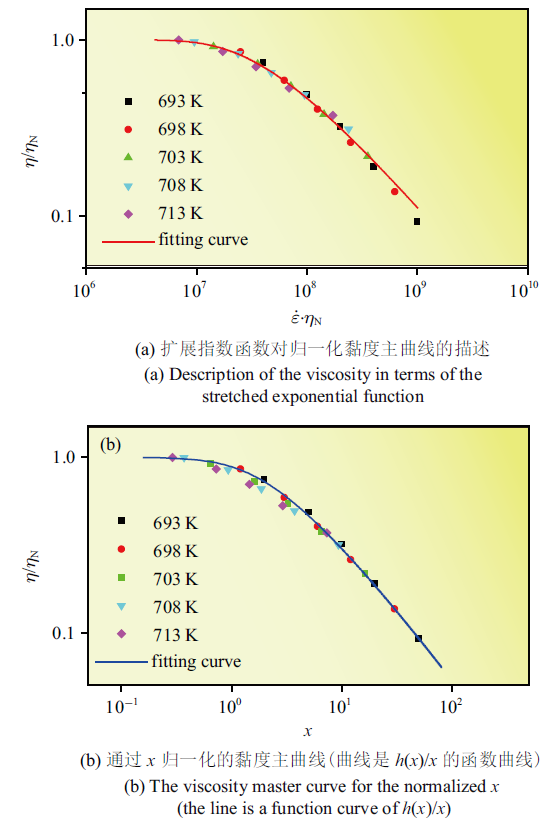
Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金在参考温度693 K时的黏度主曲线
Fig. 9
The viscosity master curve with the reference temperature of 693 K of Zr$_{50}$Cu$_{40}$Al$_{10}$ metallic glass
式中, $\dot{{\varepsilon }}$为应变速率, $\dot{{\varepsilon }}_0=2c_{\rm f} \nu _D (-{\Delta G^{\rm m}}/{kT})$为频率因子, $\sigma_{{\rm flow}} $为稳态流变应力, 为激活体积. 因此, 根据自由体积理论, 名义黏度可以表示为
在牛顿流变域内, $\sigma _{{\rm flow}} V$远小于$kT$, 因此, 牛顿黏度可以表示为
根据式(5)和式(6), 可以得到
图9(b)是$\eta / {\eta _N }$随$x={\dot{{\varepsilon }}} / {\dot{{\varepsilon}}_0 }$的变化趋势, 可以看出式(7)可以对黏度主曲线进行较好的描述.
其中, $\tau _\beta $是结构单元热激活跃迁所需的平均时间, 其与温度的关系满足Arrhenius关系. $\sigma _0 $是Frenkel极限, 即材料在0 K时的屈服极限. Pelletier等[25]由式(8)结合准点缺陷理论中的相关公式推导出黏度与应变速率的关系为
根据如前所述的动态弛豫实验, 可以得到式(9)中的参数$U_\beta =0.63$ eV和$\chi=0.38$. 图10为准点缺陷理论计算得到的预测曲线与实验得到的黏度主曲线的比较, 实验结果与理论模型吻合较好. 因此, 准点缺陷模型不仅可以用来描述非晶合金的主弛豫行为, 而且准点缺陷模型结合动态力学实验中得到的参数, 可以很好描述非晶合金中应变率对黏度的演化过程.
图10
图10
Zr$_{50}$Cu$_{40}$Al$_{10}$非晶合金在参考温度693 K时的黏度主曲线与准点缺陷理论的拟合曲线比较
Fig. 10
Comparison between experimental data the Zr$_{50}$Cu$_{40}$Al$_{10}$ metallic glass (master curve of the viscosity, the reference temperature is 693 K) and prediction of QPD model (Eq.(9))
3 结论
本文使用铜模吸铸和单辊甩带法制得的非晶合金进行了动态力学分析和高温拉伸实验, 系统研究了Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金的动态弛豫行为和高温流变行为. 主要结论如下:
(1)在固定频率下储能模量和剪切模量随温度的演化曲线表明在升温过程中有3个阶段: 在低温段的弹性主导区域, 过冷液相区附近的黏弹性主导区域,晶化温度以上的晶化过程.
(2)在等温扫频实验中, 准点缺陷模型可以在微观结构状态与动态力学弛豫行为之间进行定量描述. 在参考温度下损耗模量的等温扫频主曲线可以使用准点缺陷理论进行描述. 基于内耗数据, 可以得到结构单元基本运动的激活能$U_\beta=0.63$ eV,与准点缺陷浓度有关的关联因子$\chi$当温度$T\leqslant T_{\rm g}$时几乎恒定不变, 其值为0.38表明在玻璃转变温度以下, 非晶合金的缺陷浓几乎不变.而当温度$T>T_{\rm g}$时, 关联因子$\chi$随着温度增大而增大,表明准点缺陷浓度随温度升高而增大.
(3)在拉伸实验中, 非晶固体的高温变形受温度和应变速率的影响, 当温度降低或者应变速率增大时, 高温变形从牛顿流变到非牛顿流变的转变.Zr$_{50}$Cu$_{40}$Al$_{10}$大块非晶合金的高温流变行为不仅可以通过扩展指数函数和自由体积模型来描述, 还可以在动态力学分析实验获得的激活能$U_\beta $和关联因子$\chi$的基础上, 采用准点缺陷理论来描述其在参考温度下的黏度主曲线.结果表明在非晶聚合物中提出的准点缺陷理论也适用于非晶合金的高温变形. 准点缺陷模型不仅可以很好的描述非晶合金的动态力学行为和高温流变行为, 还为非晶合金微观结构非均匀性与宏观力学行为的进一步研究提供了新的思路.
参考文献
The elastic properties, elastic models and elastic perspectives of metallic glasses
Corrosion behavior of Fe-based ferromagnetic (Fe, Ni)-B-Si-Nb bulk glassy alloys in aqueous electrolytes
Structural heterogeneities and mechanical behavior of amorphous alloys
预压下锆基块体非晶合金的热冲击变形与破坏
Deformation and fracture of Zr$_{51}$Ti$_{5}$Ni$_{10}$Cu$_{25}$Al$_{9}$ bulk metallic glass under rapid heating and pre-load
非晶态物质的本质和特性
The nature and properties of amorphous mater
不均匀性:非晶合金的灵魂
Heterogeneity: The soul of metallic glasses
Atomistic free-volume zones and inelastic deformation of metallic glasses
Microstructure of fragile metallic glasses inferred from ultrasound-accelerated crystallization in Pd-based metallic glasses
Characterization of nanoscale mechanical heterogeneity in a metallic glass by dynamic force microscopy
非晶态固体的结构可以决定性能吗?
Does structure determine property in amorphous solids?
Mechanical behavior of amorphous alloys
基于原子体积场拉普拉斯算子对金属玻璃剪切转变区的预测
Prediction of Shear Transformation Zones in Metallic Glasses Based on Laplacian of Atomic Volume
Free-volume changes in the bulk metallic glass Zr$_{46.7}$Ti$_{8.3}$Cu$_{7.5}$Ni$_{10}$Be$_{27.5}$ and the undercooled liquid
Models of the glass transition
Liquid-glass transition: Dependence of the glass transition on heating and cooling rates
Correlation between the secondary $\beta $-relaxation time at $T_{\rm g}$ with the Kohlrausch exponent of the primary $\alpha $ relaxation or the fragility of glass-forming materials
Molecular theory for the rheology of glasses and polymers
Characterization and modeling of dynamic relaxation of a Zr-based bulk metallic glass
Dynamic mechanical properties in a Zr$_{46.8}$Ti$_{13.8}$Cu$_{12.5}$Ni$_{10}$Be$_{27.5}$ bulk metallic glass
Relaxation and diffusion in complex systems
Dielectric relaxation in glycerol, propylene glycol, and n-propanol
Compilation of the fragility parameters for several glass-forming metallic alloys
Nonlinear mechanical response of amorphous polymers below and through glass transition temperature
Viscoelasticity and viscosity of Pd-Ni-Cu-P bulk metallic glasses
Mechanical properties over the glass transition of Zr$_{41.2}$Ti$_{13.8}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$ bulk metallic glass.
Shear flow characteristics and crystallization kinetics during steady non-isothermal flow of Vitreloy-1
Deformation behavior of the Zr$_{41.2}$Ti$_{13.8}$Cu$_{12.5}$Ni$_{10}$Be$_{22.5}$ bulk metallic glass over a wide range of strain-rates and temperatures
大块非晶合金的力学行为及其微观机理研究. [博士论文]
Study of the mechanical behavior and its mecahnism of bulk amorphous alloys. [PhD Thesis]
A microscopic mechanism for steady state inhomogeneous flow in metallic glasses
Origin of stress overshoot in amorphous solids
Newtonian viscosity of supercooled liquid in a Pd40Ni40P20 metallic glass
Arrhenius activation of Zr$_{65}$Cu$_{18}$Ni$_{7}$Al$_{10}$ bulk metallic glass in the supercooled liquid region
Newtonian and non-Newtonian viscosity of supercooled liquid in metallic glasses
Free volume model: High-temperature deformation of a Zr-based bulk metallic glass
A mechanism for the flow and fracture of metallic glasses