Assessing the utility of structure in amorphous materials
2
2019
... 基于物质的微观结构解释其宏观物性是材料、物理、化学、固体力学等广义物理学的一个典型研究范式[1]. 该范式的基本思想是化学分子的构型决定其功能. 虽然, 单晶的宏观结构是基于晶体原胞, 按照一定的平移和旋转对称性, 在空间上周期排列而成. 但是, 基于原胞的化学成分与对称性信息就可以推断单晶性质, 比如基于电子能带特征就可以判断材料是导体、半导体还是绝缘体, 所以结构决定性能也适用于单晶体. 具体来说, 真实存在的晶体性质是由多种缺陷形式的萌生、运动决定的. 而缺陷本身即是一种结构, 表示实际原子位置对理想晶格位置的偏离, 所以同样遵循"结构决定性能"的范式. 进一步讲, 如果对于某种物质, 其所有原子位置和化学成分可知, 那么其性质就可以预测, 而无论材料本身是晶态还是非晶态. 所以, 斯坦福大学的蔡巍与Nix[2]在他们合著的《晶态固体缺陷》一书中指出, 材料科学的准确定义可以描述为"合成有用的工程材料, 并通过控制成分与微结构调控材料的宏观性能". ...
... 在之前的工作中, 基于以上3个方面对于材料结构物理意义的理解, 提出了3种新的定量评估非晶态材料结构有效性的普适方法[1]. 首先, 基于香农信息熵的概念, 即$S=\mathop \sum \nolimits_i P_i \ln P_i $, 其中$P_i $表示体系中某种特定的Voronoi多面体结构$n_3 ,n_4 ,n_5 ,n_6 $出现的概率, 定义了两个参量来定量描述非晶的结构, 即结构的多样性指数和效用指数; 这两个物理参数可以定量评价非晶结构, 以及结构在预测性质方面的效用. 发现随着受限程度增加或者能量降低, 非晶结构子集的多样性越来越低. 但是, 这种结构变化非常弱, 不足以说明某种特定结构是非晶合金物理性质的主要起因. ...
1
2016
... 基于物质的微观结构解释其宏观物性是材料、物理、化学、固体力学等广义物理学的一个典型研究范式[1]. 该范式的基本思想是化学分子的构型决定其功能. 虽然, 单晶的宏观结构是基于晶体原胞, 按照一定的平移和旋转对称性, 在空间上周期排列而成. 但是, 基于原胞的化学成分与对称性信息就可以推断单晶性质, 比如基于电子能带特征就可以判断材料是导体、半导体还是绝缘体, 所以结构决定性能也适用于单晶体. 具体来说, 真实存在的晶体性质是由多种缺陷形式的萌生、运动决定的. 而缺陷本身即是一种结构, 表示实际原子位置对理想晶格位置的偏离, 所以同样遵循"结构决定性能"的范式. 进一步讲, 如果对于某种物质, 其所有原子位置和化学成分可知, 那么其性质就可以预测, 而无论材料本身是晶态还是非晶态. 所以, 斯坦福大学的蔡巍与Nix[2]在他们合著的《晶态固体缺陷》一书中指出, 材料科学的准确定义可以描述为"合成有用的工程材料, 并通过控制成分与微结构调控材料的宏观性能". ...
Thermodynamics and kinetics of slip
1
1975
... 过去一个世纪以来, 人类对于传统晶态固体强度和弹塑性变形的认识取得了极大的进展[3-5]. 在位错被发现之前, 塑性的微观机理一直是困扰材料和力学界的重大难题之一. 科学上一个重大的困扰是材料的实际强度通常低于Frenkel理想强度数个数量级以下, 而模型是基于理想密排面整体滑移计算[6]. 19世纪30年代, Orowan等[4]3位科学家提出了塑性变形的位错理论, 极大地丰富了人类对于材料强度和塑性的认识, 从而解开了固体力学的一个谜团. 之后的塑性力学发展, 几乎均围绕位错的均匀与非均匀形核、位错相互作用与增殖、以及位错与不同尺度晶态缺陷的相互作用展开. 特别是固体力学与经典过渡态理论相结合, 考虑位错运动与形核的热激活属性, 该理论框架成为定量预测材料强度及其温度、应力依赖性和尺寸效应的经典物理模型. 基于热激活理论框架预测材料塑性变形的Orowan公式$\dot{\varepsilon}=\rho v b$ (其中$\dot{\varepsilon}$为塑性应变率, $\rho $为位错密度, $v$为应力和温度相关的位错运动速度, $b$为伯格斯矢量大小), 是固体塑性和强度物理模型的经典代表. ...
1
2008
... 过去一个世纪以来, 人类对于传统晶态固体强度和弹塑性变形的认识取得了极大的进展[3-5]. 在位错被发现之前, 塑性的微观机理一直是困扰材料和力学界的重大难题之一. 科学上一个重大的困扰是材料的实际强度通常低于Frenkel理想强度数个数量级以下, 而模型是基于理想密排面整体滑移计算[6]. 19世纪30年代, Orowan等[4]3位科学家提出了塑性变形的位错理论, 极大地丰富了人类对于材料强度和塑性的认识, 从而解开了固体力学的一个谜团. 之后的塑性力学发展, 几乎均围绕位错的均匀与非均匀形核、位错相互作用与增殖、以及位错与不同尺度晶态缺陷的相互作用展开. 特别是固体力学与经典过渡态理论相结合, 考虑位错运动与形核的热激活属性, 该理论框架成为定量预测材料强度及其温度、应力依赖性和尺寸效应的经典物理模型. 基于热激活理论框架预测材料塑性变形的Orowan公式$\dot{\varepsilon}=\rho v b$ (其中$\dot{\varepsilon}$为塑性应变率, $\rho $为位错密度, $v$为应力和温度相关的位错运动速度, $b$为伯格斯矢量大小), 是固体塑性和强度物理模型的经典代表. ...
Thermally Activated Mechanisms in Crystal Plasticity. vol. 8
2
2003
... 过去一个世纪以来, 人类对于传统晶态固体强度和弹塑性变形的认识取得了极大的进展[3-5]. 在位错被发现之前, 塑性的微观机理一直是困扰材料和力学界的重大难题之一. 科学上一个重大的困扰是材料的实际强度通常低于Frenkel理想强度数个数量级以下, 而模型是基于理想密排面整体滑移计算[6]. 19世纪30年代, Orowan等[4]3位科学家提出了塑性变形的位错理论, 极大地丰富了人类对于材料强度和塑性的认识, 从而解开了固体力学的一个谜团. 之后的塑性力学发展, 几乎均围绕位错的均匀与非均匀形核、位错相互作用与增殖、以及位错与不同尺度晶态缺陷的相互作用展开. 特别是固体力学与经典过渡态理论相结合, 考虑位错运动与形核的热激活属性, 该理论框架成为定量预测材料强度及其温度、应力依赖性和尺寸效应的经典物理模型. 基于热激活理论框架预测材料塑性变形的Orowan公式$\dot{\varepsilon}=\rho v b$ (其中$\dot{\varepsilon}$为塑性应变率, $\rho $为位错密度, $v$为应力和温度相关的位错运动速度, $b$为伯格斯矢量大小), 是固体塑性和强度物理模型的经典代表. ...
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Zur Theorie der Elastizit?tsgrenze und der Festigkeit kristallinischer K?rper
1
1926
... 过去一个世纪以来, 人类对于传统晶态固体强度和弹塑性变形的认识取得了极大的进展[3-5]. 在位错被发现之前, 塑性的微观机理一直是困扰材料和力学界的重大难题之一. 科学上一个重大的困扰是材料的实际强度通常低于Frenkel理想强度数个数量级以下, 而模型是基于理想密排面整体滑移计算[6]. 19世纪30年代, Orowan等[4]3位科学家提出了塑性变形的位错理论, 极大地丰富了人类对于材料强度和塑性的认识, 从而解开了固体力学的一个谜团. 之后的塑性力学发展, 几乎均围绕位错的均匀与非均匀形核、位错相互作用与增殖、以及位错与不同尺度晶态缺陷的相互作用展开. 特别是固体力学与经典过渡态理论相结合, 考虑位错运动与形核的热激活属性, 该理论框架成为定量预测材料强度及其温度、应力依赖性和尺寸效应的经典物理模型. 基于热激活理论框架预测材料塑性变形的Orowan公式$\dot{\varepsilon}=\rho v b$ (其中$\dot{\varepsilon}$为塑性应变率, $\rho $为位错密度, $v$为应力和温度相关的位错运动速度, $b$为伯格斯矢量大小), 是固体塑性和强度物理模型的经典代表. ...
Structural heterogeneities and mechanical behavior of amorphous alloys
1
2019
... 但是晶态固体只是自然界存在物质的一小部分, 更广泛的物质以非晶态呈现, 比如日常生活中常见的玻璃、橡胶、聚合物、沙粒等结构. 特别是近年来, 随着材料制备技术的进步, 新型金属结构材料形式不断涌现, 极大地提升了材料强度和塑性的调控自由度. 其中, 非晶合金(又称金属玻璃)作为典型的非晶态固体, 表现出与传统金属结构材料完全不同的新奇力学行为和优异的物理、化学性质, 并且该类材料隐藏着丰富的微观结构模型和未被充分认识的物理力学机制[7-10]. ...
Mechanical behavior of amorphous alloys
1
2007
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Deformation of metallic glasses: Recent developments in theory, simulations, and experiments
2
2016
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
... 其他的复杂非晶结构包括前文提到的基于短程结构空间排列方式的所谓中、长程结构信息[9,67].除此之外, 特别突出的一个成功的结构指标为两体过剩熵, 或称局部结构熵[68-69]. 以CuZr二元金属玻璃为例, 第$i$个原子的两体过剩熵定义为 ...
Deformation and flow of amorphous solids: a review of mesoscale elastoplastic models
1
2018
... 但是晶态固体只是自然界存在物质的一小部分, 更广泛的物质以非晶态呈现, 比如日常生活中常见的玻璃、橡胶、聚合物、沙粒等结构. 特别是近年来, 随着材料制备技术的进步, 新型金属结构材料形式不断涌现, 极大地提升了材料强度和塑性的调控自由度. 其中, 非晶合金(又称金属玻璃)作为典型的非晶态固体, 表现出与传统金属结构材料完全不同的新奇力学行为和优异的物理、化学性质, 并且该类材料隐藏着丰富的微观结构模型和未被充分认识的物理力学机制[7-10]. ...
Atomic-level structure and structure-property relationship in metallic glasses
2
2010
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
... 第一类结构指标完全基于原子的空间排列, 比如目前被广泛采用的原子Voronoi多面体结构分析算法[11-12,15]. Voronoi多面体结构从一个具体位置的原子出发, 用中心原子与其周围最近邻原子之间的中垂面围成一个多面体, 中心原子位于这个多面体中, 通过描述包围多面体的特征, 即Voronoi指数来描述中心原子所处短程结构环境. 另外, Voronoi多面体自然包含了配位数信息, 还可以定量描述原子所处的结构环境, 即最近邻原子空间分布情况. 通常, Voronoi指数标记为$n_3 ,n_4 ,n_5 ,n_6, \ldots $, 其中$n_i $表示这个多面体中$i$边形的数量. 一般来说, 取前4个指数, 即三、四、五、六边形的数量即可完备描述一个中心原子的结构信息. 此外, 这些多面体结构以某种隐含的规律, 在中、长程上堆积, 可以填满整个空间. 由Voronoi多面体分析衍生出的结构指标还包括配位数(coordination number, CN, 即$\mathop \sum \nolimits_i n_i )$、$N$重对称性参数($N$边形在多面体所有面中所占比例, 比如五重对称性为L5FS, 即$d_5 =n_5 /\mathop \sum \nolimits_i n_i )$、原子的Voronoi体积等, 以及由二十面体在空间上的堆积、连接方式形成的中程序结构[63-64]. 近来, 本文部分作者基于短程的Voronoi多面体分析, 提出了用于预测非晶态固体异常振动特征的方向序参量[65]. ...
Atomic level structure in multicomponent bulk metallic glass
2
2009
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
... 第一类结构指标完全基于原子的空间排列, 比如目前被广泛采用的原子Voronoi多面体结构分析算法[11-12,15]. Voronoi多面体结构从一个具体位置的原子出发, 用中心原子与其周围最近邻原子之间的中垂面围成一个多面体, 中心原子位于这个多面体中, 通过描述包围多面体的特征, 即Voronoi指数来描述中心原子所处短程结构环境. 另外, Voronoi多面体自然包含了配位数信息, 还可以定量描述原子所处的结构环境, 即最近邻原子空间分布情况. 通常, Voronoi指数标记为$n_3 ,n_4 ,n_5 ,n_6, \ldots $, 其中$n_i $表示这个多面体中$i$边形的数量. 一般来说, 取前4个指数, 即三、四、五、六边形的数量即可完备描述一个中心原子的结构信息. 此外, 这些多面体结构以某种隐含的规律, 在中、长程上堆积, 可以填满整个空间. 由Voronoi多面体分析衍生出的结构指标还包括配位数(coordination number, CN, 即$\mathop \sum \nolimits_i n_i )$、$N$重对称性参数($N$边形在多面体所有面中所占比例, 比如五重对称性为L5FS, 即$d_5 =n_5 /\mathop \sum \nolimits_i n_i )$、原子的Voronoi体积等, 以及由二十面体在空间上的堆积、连接方式形成的中程序结构[63-64]. 近来, 本文部分作者基于短程的Voronoi多面体分析, 提出了用于预测非晶态固体异常振动特征的方向序参量[65]. ...
Local order influences initiation of plastic flow in metallic glass: Effects of alloy composition and sample cooling history
2008
Relationship between structure, dynamics, and mechanical properties in metallic glass-forming alloys
2008
Atomic packing and short-to-medium-range order in metallic glasses
1
2006
... 第一类结构指标完全基于原子的空间排列, 比如目前被广泛采用的原子Voronoi多面体结构分析算法[11-12,15]. Voronoi多面体结构从一个具体位置的原子出发, 用中心原子与其周围最近邻原子之间的中垂面围成一个多面体, 中心原子位于这个多面体中, 通过描述包围多面体的特征, 即Voronoi指数来描述中心原子所处短程结构环境. 另外, Voronoi多面体自然包含了配位数信息, 还可以定量描述原子所处的结构环境, 即最近邻原子空间分布情况. 通常, Voronoi指数标记为$n_3 ,n_4 ,n_5 ,n_6, \ldots $, 其中$n_i $表示这个多面体中$i$边形的数量. 一般来说, 取前4个指数, 即三、四、五、六边形的数量即可完备描述一个中心原子的结构信息. 此外, 这些多面体结构以某种隐含的规律, 在中、长程上堆积, 可以填满整个空间. 由Voronoi多面体分析衍生出的结构指标还包括配位数(coordination number, CN, 即$\mathop \sum \nolimits_i n_i )$、$N$重对称性参数($N$边形在多面体所有面中所占比例, 比如五重对称性为L5FS, 即$d_5 =n_5 /\mathop \sum \nolimits_i n_i )$、原子的Voronoi体积等, 以及由二十面体在空间上的堆积、连接方式形成的中程序结构[63-64]. 近来, 本文部分作者基于短程的Voronoi多面体分析, 提出了用于预测非晶态固体异常振动特征的方向序参量[65]. ...
Correlation between local structure order and spatial heterogeneity in a metallic glass
2017
Direct observation of local atomic order in a metallic glass
2
2011
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
... 而从晶体中演化出的诸多概念, 并不完全适合于分析非晶态固体. 非晶态固体通常具有长程无序、短程有序的结构特点. 但是, 它并不存在直观的结构缺陷[17,37]. 所以从晶格上辨识结构缺陷, 基于缺陷运动规律分析材料性质的思路在非晶态材料中不易开展. 以典型的非晶态固体, 二元CuZr金属玻璃体系为例, 丰富的微观结构特征会引入独特的动力学拓扑信息, 如图1的局域黏度所示. 材料黏度可以通过过渡态理论与黏滞流动激活能计算, 即$\eta =\eta _0 \exp\left( \Delta Q/k_{\rm B} T \right)$, 其中$\eta _0 =1.0\times10^{-4}$ Pa$\cdot $s为特征黏度, 即黏度的高温上限; $\Delta Q$为局域原子重拍的热力学激活能, 其计算细节将在下文中详述; $k_{\rm B} $为玻尔兹曼常数, $T$为热力学温度, 故而$k_{\rm B} T$为热能. 图1显示该玻璃样品中存在不均匀动力学属性, 即黏度具有空间涨落特征. 在典型的实验室时间尺度(100 s), 人们通常以$\eta =1.0\times10^{12}$ Pa$\cdot$s作为液体与固体的临界黏度[25-26]. 黏度小于这个数量级的物质为液体, 而反之则为固体. 图1显示CuZr金属玻璃中同时存在类液体区域与类固体区域. 两类区域的特征尺寸均在纳米量级. 动力学不均匀性是非晶态固体区别于传统晶体的显著特征. 特别是非晶态固体的表面相对于块体的动力学快几个数量级以上[38]. 因为类液体区域的动力学较快, 对非晶态固体施加一定的外载时, 材料首先从类液体区域开始变形. 所以, 目前存在的比较成功的非晶态固体的塑性变形模型, 基本都是围绕类液体区域这个动力学缺陷开展的. ...
Metallic liquids and glasses: Atomic order and global packing
1
2010
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
Local structural mechanism for frozen-in dynamics in metallic glasses
2018
Atomistic structural mechanism for the glass transition: Entropic contribution
1
2020
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
Revealing key structural features hidden in liquids and glasses
2
2019
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
... 因为非晶态固体的原子结构非常复杂, 缺乏普适的平移和旋转对称性, 所以很难找到一个类似于晶体原胞的简洁结构信息作为整个材料的基本重复单元[21]. 在非晶态物理、材料等领域, 通常的做法是定位广义的"结构''用于描述非晶体系的动力学性质. 这些广义"结构"基本上分为3类, 具体包括原子结构指标、热力学指标和动力学指标. ...
The role of local structure in dynamical arrest
1
2015
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
Configuration correlation governs slow dynamics of supercooled metallic liquids
1
2018
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
Revealing hidden structural order controlling both fast and slow glassy dynamics in supercooled liquids
1
2018
... 按照传统研究范式, 与晶态固体类似, 自然期待使用非晶态物质的结构特征来解释其丰富的性能[11]. 实际上, 文献中已经有大量报道, 尝试鉴定出可以决定非晶态物质性能的短程结构信息. 比如, 模拟和实验结果显示可能存在二十面体或其他短程结构, 有利于稳定非晶态物质[12-17]; 玻璃转变或动力学冻结现象也与某些局域的结构序参量相关[18-20]. 但是, 对于典型的非晶态固体, 比如金属玻璃来说, 并不存在一种公认的主控结构可以决定玻璃的性质[21-22]. 相反, 近来的一些研究表明, 无序合金的动力学性质并不由某种短程结构决定[23-24]. ...
Signatures of distinct dynamical regimes in the energy landscape of a glass-forming liquid
2
1998
... 本文主要回答的科学问题为, 经典的"结构决定性能"研究范式适用于广泛的非晶态固体吗? 短程结构和复杂超结构可否关联非晶态固体的性能?背后隐藏的物理机制又是什么. 为此, 基于分子动力学模拟, 通过海量抽样无序固体势能图谱(potential energy landscape, PEL)上的局域原子重排的激活能[25-28], 定量探讨不同结构特征在决定玻璃性能方面的效用. 从介绍非晶态固体的基本变形模式出发, 然后简述文献中几类预测性能的非晶结构指标以及分子动力学计算细节, 通过比较简单结构和超结构揭示玻璃"结构-性能"关系蕴含的物理规律, 最终提出评估与筛选有效玻璃结构的普适方法. ...
... 而从晶体中演化出的诸多概念, 并不完全适合于分析非晶态固体. 非晶态固体通常具有长程无序、短程有序的结构特点. 但是, 它并不存在直观的结构缺陷[17,37]. 所以从晶格上辨识结构缺陷, 基于缺陷运动规律分析材料性质的思路在非晶态材料中不易开展. 以典型的非晶态固体, 二元CuZr金属玻璃体系为例, 丰富的微观结构特征会引入独特的动力学拓扑信息, 如图1的局域黏度所示. 材料黏度可以通过过渡态理论与黏滞流动激活能计算, 即$\eta =\eta _0 \exp\left( \Delta Q/k_{\rm B} T \right)$, 其中$\eta _0 =1.0\times10^{-4}$ Pa$\cdot $s为特征黏度, 即黏度的高温上限; $\Delta Q$为局域原子重拍的热力学激活能, 其计算细节将在下文中详述; $k_{\rm B} $为玻尔兹曼常数, $T$为热力学温度, 故而$k_{\rm B} T$为热能. 图1显示该玻璃样品中存在不均匀动力学属性, 即黏度具有空间涨落特征. 在典型的实验室时间尺度(100 s), 人们通常以$\eta =1.0\times10^{12}$ Pa$\cdot$s作为液体与固体的临界黏度[25-26]. 黏度小于这个数量级的物质为液体, 而反之则为固体. 图1显示CuZr金属玻璃中同时存在类液体区域与类固体区域. 两类区域的特征尺寸均在纳米量级. 动力学不均匀性是非晶态固体区别于传统晶体的显著特征. 特别是非晶态固体的表面相对于块体的动力学快几个数量级以上[38]. 因为类液体区域的动力学较快, 对非晶态固体施加一定的外载时, 材料首先从类液体区域开始变形. 所以, 目前存在的比较成功的非晶态固体的塑性变形模型, 基本都是围绕类液体区域这个动力学缺陷开展的. ...
Supercooled liquids and the glass transition
2
2001
... 而从晶体中演化出的诸多概念, 并不完全适合于分析非晶态固体. 非晶态固体通常具有长程无序、短程有序的结构特点. 但是, 它并不存在直观的结构缺陷[17,37]. 所以从晶格上辨识结构缺陷, 基于缺陷运动规律分析材料性质的思路在非晶态材料中不易开展. 以典型的非晶态固体, 二元CuZr金属玻璃体系为例, 丰富的微观结构特征会引入独特的动力学拓扑信息, 如图1的局域黏度所示. 材料黏度可以通过过渡态理论与黏滞流动激活能计算, 即$\eta =\eta _0 \exp\left( \Delta Q/k_{\rm B} T \right)$, 其中$\eta _0 =1.0\times10^{-4}$ Pa$\cdot $s为特征黏度, 即黏度的高温上限; $\Delta Q$为局域原子重拍的热力学激活能, 其计算细节将在下文中详述; $k_{\rm B} $为玻尔兹曼常数, $T$为热力学温度, 故而$k_{\rm B} T$为热能. 图1显示该玻璃样品中存在不均匀动力学属性, 即黏度具有空间涨落特征. 在典型的实验室时间尺度(100 s), 人们通常以$\eta =1.0\times10^{12}$ Pa$\cdot$s作为液体与固体的临界黏度[25-26]. 黏度小于这个数量级的物质为液体, 而反之则为固体. 图1显示CuZr金属玻璃中同时存在类液体区域与类固体区域. 两类区域的特征尺寸均在纳米量级. 动力学不均匀性是非晶态固体区别于传统晶体的显著特征. 特别是非晶态固体的表面相对于块体的动力学快几个数量级以上[38]. 因为类液体区域的动力学较快, 对非晶态固体施加一定的外载时, 材料首先从类液体区域开始变形. 所以, 目前存在的比较成功的非晶态固体的塑性变形模型, 基本都是围绕类液体区域这个动力学缺陷开展的. ...
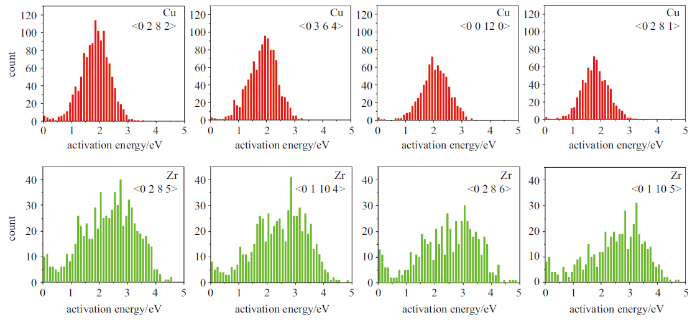
... 如前文所述, 非晶态固体的局部激活事件激活能是最直观和关键的动力学参数, 可以定量表征事件发生的难易程度, 这一点已经在之前的工作中得到充分验证[69]. 但是, 非晶态物质的PEL是个高自由度的、异常复杂的多维平面. 在3$N$维空间中, 高效、准确抽样PEL拓扑信息绝非易事[26-27,93]. 针对该问题, 加拿大蒙特利尔大学的Mousseau等[94-96]发展了ART(activation-relaxation technique)算法, 后又经过多人改进. 该算法可以通过随机抽样鞍点态来获得体系中不同事件的激活能, 从而克服了分子动力学模拟上的时间尺度限制, 属于加速分子动力学模拟的一类. 它的优势在于可以高效处理无序体系等复杂系统的PEL抽样, 而不依赖于原子晶格等信息, 也无需事先定义激活的初态与末态. 并且, 初始激活方向随机, 高效海量抽样后, 可以潜在穷尽所有可能的局部激活时间, 给出完备的激活能图谱. ...
2
2016
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
... 如前文所述, 非晶态固体的局部激活事件激活能是最直观和关键的动力学参数, 可以定量表征事件发生的难易程度, 这一点已经在之前的工作中得到充分验证[69]. 但是, 非晶态物质的PEL是个高自由度的、异常复杂的多维平面. 在3$N$维空间中, 高效、准确抽样PEL拓扑信息绝非易事[26-27,93]. 针对该问题, 加拿大蒙特利尔大学的Mousseau等[94-96]发展了ART(activation-relaxation technique)算法, 后又经过多人改进. 该算法可以通过随机抽样鞍点态来获得体系中不同事件的激活能, 从而克服了分子动力学模拟上的时间尺度限制, 属于加速分子动力学模拟的一类. 它的优势在于可以高效处理无序体系等复杂系统的PEL抽样, 而不依赖于原子晶格等信息, 也无需事先定义激活的初态与末态. 并且, 初始激活方向随机, 高效海量抽样后, 可以潜在穷尽所有可能的局部激活时间, 给出完备的激活能图谱. ...
2
2004
... 本文主要回答的科学问题为, 经典的"结构决定性能"研究范式适用于广泛的非晶态固体吗? 短程结构和复杂超结构可否关联非晶态固体的性能?背后隐藏的物理机制又是什么. 为此, 基于分子动力学模拟, 通过海量抽样无序固体势能图谱(potential energy landscape, PEL)上的局域原子重排的激活能[25-28], 定量探讨不同结构特征在决定玻璃性能方面的效用. 从介绍非晶态固体的基本变形模式出发, 然后简述文献中几类预测性能的非晶结构指标以及分子动力学计算细节, 通过比较简单结构和超结构揭示玻璃"结构-性能"关系蕴含的物理规律, 最终提出评估与筛选有效玻璃结构的普适方法. ...
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
A first report on deformation-mechanism maps
1
1972
... 传统晶体材料的塑性变形机制在20世纪中得到了充分的研究, 人类对于晶体变形的机理认识已经深入到了原子层次. 比如, 著名的M. F. Ashby变形图谱定义了不同的温度、应力、应变率条件下多晶材料的微观变形模式[29-30].随着外载应力水平的提高和温度的降低, 晶体的变形机制可能从晶界扩散、滑移等所谓扩散机制, 转换到位错、变形孪晶、相变等所谓位移机制[31-36]. 将不同形式晶体缺陷的几何特征, 与经典热力学和动力学理论相结合, 可以推断出晶体材料的力学性能与外部变量的定量关系, 比如引言中提到的关于位错塑性的Orowan方程, 就是其中一个典型代表. ...
Ultra-strength materials
1
2010
... 传统晶体材料的塑性变形机制在20世纪中得到了充分的研究, 人类对于晶体变形的机理认识已经深入到了原子层次. 比如, 著名的M. F. Ashby变形图谱定义了不同的温度、应力、应变率条件下多晶材料的微观变形模式[29-30].随着外载应力水平的提高和温度的降低, 晶体的变形机制可能从晶界扩散、滑移等所谓扩散机制, 转换到位错、变形孪晶、相变等所谓位移机制[31-36]. 将不同形式晶体缺陷的几何特征, 与经典热力学和动力学理论相结合, 可以推断出晶体材料的力学性能与外部变量的定量关系, 比如引言中提到的关于位错塑性的Orowan方程, 就是其中一个典型代表. ...
Time, stress, and temperature-dependent deformation in nanostructured copper: Stress relaxation tests and simulations
1
2016
... 传统晶体材料的塑性变形机制在20世纪中得到了充分的研究, 人类对于晶体变形的机理认识已经深入到了原子层次. 比如, 著名的M. F. Ashby变形图谱定义了不同的温度、应力、应变率条件下多晶材料的微观变形模式[29-30].随着外载应力水平的提高和温度的降低, 晶体的变形机制可能从晶界扩散、滑移等所谓扩散机制, 转换到位错、变形孪晶、相变等所谓位移机制[31-36]. 将不同形式晶体缺陷的几何特征, 与经典热力学和动力学理论相结合, 可以推断出晶体材料的力学性能与外部变量的定量关系, 比如引言中提到的关于位错塑性的Orowan方程, 就是其中一个典型代表. ...
Time-, stress-, and temperature-dependent deformation in nanostructured copper: Creep tests and simulations
2016
Atomistic understanding of diffusion kinetics in nanocrystals from molecular dynamics simulations
2013
Entropic effect on creep in nanocrystalline metals
2013
Transition of creep mechanism in nanocrystalline metals
2011
Grain size dependence of creep in nanocrystalline copper by molecular dynamics
1
2012
... 传统晶体材料的塑性变形机制在20世纪中得到了充分的研究, 人类对于晶体变形的机理认识已经深入到了原子层次. 比如, 著名的M. F. Ashby变形图谱定义了不同的温度、应力、应变率条件下多晶材料的微观变形模式[29-30].随着外载应力水平的提高和温度的降低, 晶体的变形机制可能从晶界扩散、滑移等所谓扩散机制, 转换到位错、变形孪晶、相变等所谓位移机制[31-36]. 将不同形式晶体缺陷的几何特征, 与经典热力学和动力学理论相结合, 可以推断出晶体材料的力学性能与外部变量的定量关系, 比如引言中提到的关于位错塑性的Orowan方程, 就是其中一个典型代表. ...
Geometric frustration of icosahedron in metallic glasses
1
2013
... 而从晶体中演化出的诸多概念, 并不完全适合于分析非晶态固体. 非晶态固体通常具有长程无序、短程有序的结构特点. 但是, 它并不存在直观的结构缺陷[17,37]. 所以从晶格上辨识结构缺陷, 基于缺陷运动规律分析材料性质的思路在非晶态材料中不易开展. 以典型的非晶态固体, 二元CuZr金属玻璃体系为例, 丰富的微观结构特征会引入独特的动力学拓扑信息, 如图1的局域黏度所示. 材料黏度可以通过过渡态理论与黏滞流动激活能计算, 即$\eta =\eta _0 \exp\left( \Delta Q/k_{\rm B} T \right)$, 其中$\eta _0 =1.0\times10^{-4}$ Pa$\cdot $s为特征黏度, 即黏度的高温上限; $\Delta Q$为局域原子重拍的热力学激活能, 其计算细节将在下文中详述; $k_{\rm B} $为玻尔兹曼常数, $T$为热力学温度, 故而$k_{\rm B} T$为热能. 图1显示该玻璃样品中存在不均匀动力学属性, 即黏度具有空间涨落特征. 在典型的实验室时间尺度(100 s), 人们通常以$\eta =1.0\times10^{12}$ Pa$\cdot$s作为液体与固体的临界黏度[25-26]. 黏度小于这个数量级的物质为液体, 而反之则为固体. 图1显示CuZr金属玻璃中同时存在类液体区域与类固体区域. 两类区域的特征尺寸均在纳米量级. 动力学不均匀性是非晶态固体区别于传统晶体的显著特征. 特别是非晶态固体的表面相对于块体的动力学快几个数量级以上[38]. 因为类液体区域的动力学较快, 对非晶态固体施加一定的外载时, 材料首先从类液体区域开始变形. 所以, 目前存在的比较成功的非晶态固体的塑性变形模型, 基本都是围绕类液体区域这个动力学缺陷开展的. ...
Fast surface dynamics enabled cold joining of metallic glasses
1
2019
... 而从晶体中演化出的诸多概念, 并不完全适合于分析非晶态固体. 非晶态固体通常具有长程无序、短程有序的结构特点. 但是, 它并不存在直观的结构缺陷[17,37]. 所以从晶格上辨识结构缺陷, 基于缺陷运动规律分析材料性质的思路在非晶态材料中不易开展. 以典型的非晶态固体, 二元CuZr金属玻璃体系为例, 丰富的微观结构特征会引入独特的动力学拓扑信息, 如图1的局域黏度所示. 材料黏度可以通过过渡态理论与黏滞流动激活能计算, 即$\eta =\eta _0 \exp\left( \Delta Q/k_{\rm B} T \right)$, 其中$\eta _0 =1.0\times10^{-4}$ Pa$\cdot $s为特征黏度, 即黏度的高温上限; $\Delta Q$为局域原子重拍的热力学激活能, 其计算细节将在下文中详述; $k_{\rm B} $为玻尔兹曼常数, $T$为热力学温度, 故而$k_{\rm B} T$为热能. 图1显示该玻璃样品中存在不均匀动力学属性, 即黏度具有空间涨落特征. 在典型的实验室时间尺度(100 s), 人们通常以$\eta =1.0\times10^{12}$ Pa$\cdot$s作为液体与固体的临界黏度[25-26]. 黏度小于这个数量级的物质为液体, 而反之则为固体. 图1显示CuZr金属玻璃中同时存在类液体区域与类固体区域. 两类区域的特征尺寸均在纳米量级. 动力学不均匀性是非晶态固体区别于传统晶体的显著特征. 特别是非晶态固体的表面相对于块体的动力学快几个数量级以上[38]. 因为类液体区域的动力学较快, 对非晶态固体施加一定的外载时, 材料首先从类液体区域开始变形. 所以, 目前存在的比较成功的非晶态固体的塑性变形模型, 基本都是围绕类液体区域这个动力学缺陷开展的. ...
A microscopic mechanism for steady state inhomogeneous flow in metallic glasses
1
1977
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Plastic deformation in metallic glasses
2
1979
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
... 因为剪切转变是热激活事件, 所以基于动力学参数预测非晶态固体的局部塑形激活是直观的, 虽然其物理意义和科学价值值得进一步的讨论. 实际上, 当Argon[40]提出剪切转变平均场模型时, 他就基于Eshelby夹杂的弹性应变能赋予了热激活事件的激活能显式表达式, 用以表征剪切事件发生的难易程度, 所以激活能是一个最关键的动力学参数. 之后Johnson的协同剪切模型, 启发于Frenkel关于晶体原子面间滑移的剪切强度理论, 将激活能与非晶态材料的STZ体积、模量等参数关联, 便可以很好地描述非晶态材料的屈服行为和随温度变化的趋势[41]. 所以激活能是最直接的描述非晶态塑性的动力学参量[79-83]. ...
A universal criterion for plastic yielding of metallic glasses with a ($T/T_{g})^{2/3}$ temperature dependence
2
2005
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
... 因为剪切转变是热激活事件, 所以基于动力学参数预测非晶态固体的局部塑形激活是直观的, 虽然其物理意义和科学价值值得进一步的讨论. 实际上, 当Argon[40]提出剪切转变平均场模型时, 他就基于Eshelby夹杂的弹性应变能赋予了热激活事件的激活能显式表达式, 用以表征剪切事件发生的难易程度, 所以激活能是一个最关键的动力学参数. 之后Johnson的协同剪切模型, 启发于Frenkel关于晶体原子面间滑移的剪切强度理论, 将激活能与非晶态材料的STZ体积、模量等参数关联, 便可以很好地描述非晶态材料的屈服行为和随温度变化的趋势[41]. 所以激活能是最直接的描述非晶态塑性的动力学参量[79-83]. ...
Dynamics of viscoplastic deformation in amorphous solids
1
1998
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Flow units as dynamic defects in metallic glassy materials
1
2018
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Soft spots and their structural signature in a metallic glass
3
2014
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
... 另外一个热力学指标为低频振动模式参与度(participation fraction of low-frequency vibrational modes)[44-45]. 与大多数晶体相比, 结构无序固体一般会有显著的过剩低频振动模式, 并且具有空间准局域特征[65]. 软模集中的区域通常在玻璃材料中被认为是"软点''(soft spots)[73,78]. 这种低频振动模式与非晶合金中的剪切转换事件密切相关. 塑形事件总是从某个低频振动模式的失稳开始. 那么, 软点理所当然也和过冷液体的不可逆结构重排相关[45]. 因此, 软模也常被作为一种能有效预测玻璃性质的结构指标. 原子$i$的低频振动模式参与度定义为 ...
Irreversible reorganization in a supercooled liquid originates from localized soft modes
3
2008
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
... 另外一个热力学指标为低频振动模式参与度(participation fraction of low-frequency vibrational modes)[44-45]. 与大多数晶体相比, 结构无序固体一般会有显著的过剩低频振动模式, 并且具有空间准局域特征[65]. 软模集中的区域通常在玻璃材料中被认为是"软点''(soft spots)[73,78]. 这种低频振动模式与非晶合金中的剪切转换事件密切相关. 塑形事件总是从某个低频振动模式的失稳开始. 那么, 软点理所当然也和过冷液体的不可逆结构重排相关[45]. 因此, 软模也常被作为一种能有效预测玻璃性质的结构指标. 原子$i$的低频振动模式参与度定义为 ...
... [45]. 因此, 软模也常被作为一种能有效预测玻璃性质的结构指标. 原子$i$的低频振动模式参与度定义为 ...
Universal link between the boson peak and transverse phonons in glass
1
2008
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
The "ension transformation zone'' model of amorphous alloys
1
2017
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Stress-temperature scaling for steady-State flow in metallic glasses
1
2010
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
Universal enthalpy-entropy compensation rule for the deformation of metallic glasses
2
2015
... 在典型的玻璃态中, 塑性通常被认为是包含几十到数百原子的一个区域中发生的集团原子重排[8-9]. 关于非晶态固体变形最典型的平均场描述包括F. Spaepen的过剩体积模型(free volume model)[39]和Argon的剪切转变模型(shear transformation model)[40], 以及之后发展的协同剪切模型[41]、剪切转变区模型(shear tranformation zone, STZ)[42]、流变单元模型[43]、振动软点模型[44-46]等, 以及本文部分作者提出的拉伸转变区模型[47]. 广义来说, 这些关于非晶态物质塑性变形的模型均会涉及到在应力、温度等外载条件下的热力学状态改变[48-49], 均可以理解为在势能图谱上的固有结构状态的改变, 对应于在外载条件下发生的从PEL上一个局部能量极小状态到临近局部能量极小状态的改变[27-28]. 塑性事件对应结构上的改变为应力、温度激励下的局域原子结构重排, 是一类典型的热激活事件[5]. ...
... 因为非晶态固体局域塑性具有热激活特征, 所以最关键的物理参数为激活自由能函数. 而激活自由能是温度、应力、化学势等热力学量的函数. 那么, 自然可以通过调控温度或应力激励塑性事件的发生[49,84]. 从这个角度看, 应力与温度具有一定的等价性, 前者通过对PEL的偏置实现自由能势垒的降低, 等效于温度升高. 从应力角度出发, Patinet等[85]提出了局域屈服应力的概念, 它可以作为一种有效预测塑性事件位置和大小的动力学参数, 其优势在于即使材料经历了大变形, 在数十个事件之后仍然具有一定的预测性. Xu等[86]从PEL抽样过程出发, 发现沿STZ事件发生的最小能量路径的应力梯度方向可以有效预测非晶态固体塑性事件发生的宏观应变、位置、结构变形形貌特征,也是一种用于预测非晶塑性的动力学指标. ...
Atomic theory of viscoelastic response and memory effects in metallic glasses
1
2017
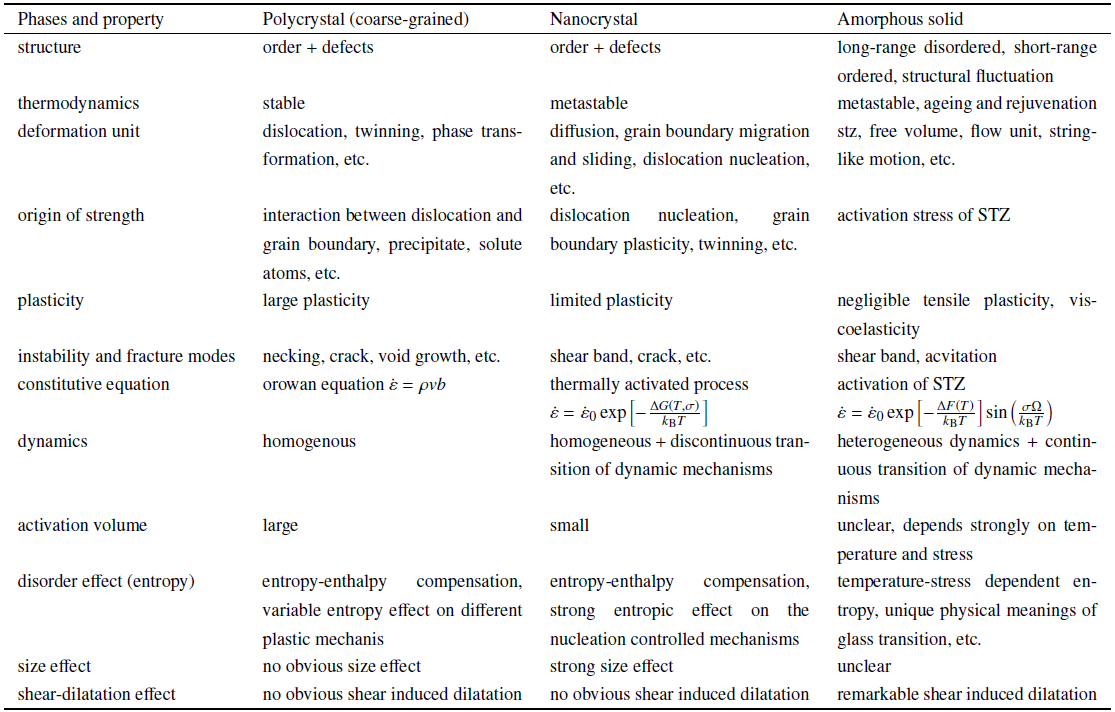
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Transition from stress-driven to thermally activated stress relaxation in metallic glasses
2
2016
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
... [51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
A comprehensive atomistic analysis of the experimental dynamic-mechanical response of a metallic glass
2014
Microscopic characterization of structural relaxation and cryogenic rejuvenation in metallic glasses
2019
Rangel DaCosta L, Liu M, et al. Shear transformation zone analysis of anelastic relaxation of a metallic glass reveals distinct properties of $\alpha $ and $\beta $ relaxations
1
2019
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Prediction of pressure-promoted thermal rejuvenation in metallic glasses
1
2016
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Extreme rejuvenation and softening in a bulk metallic glass
2018
Rejuvenation of metallic glasses by non-affine thermal strain
2015
Ultrafast extreme rejuvenation of metallic glasses by shock compression
1
2019
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Direct atomic-scale evidence for shear-dilatation correlation in metallic glasses
1
2016
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Shear band dilatation in amorphous alloys
1
2017
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Cavitation in amorphous solids
1
2013
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Shear bands in metallic glasses
1
2013
... 以上描述的独特结构和动力学特征, 使非晶态固体的塑性变形与传统多晶材料、纳米晶材料相比, 在结构、热力学和动力学上具有诸多新奇的特点, 几类显著的不同详细总结于表1中. 比如, 非晶态固体的变形具有显著的滞弹性特征[50], 变形与时间相关[51]. 晶体变形中, 扩散、位错等塑性具有迥异的时间尺度, 易于分辨, 而非晶态物质的变形则具有连续变化的时间弛豫谱[51-54]. 在合适的温度和应力区间, 结构无序材料可能会出现老化或年轻化趋势[55-58]. 并且, 非晶的局域塑性在几何上存在显著的剪胀效应[59-60], 即剪切变形通常会导致明显的局部物质密度涨落, 从而导致孔洞、剪切带形成等破坏和失稳模式[61-62]. ...
Hidden topological order and its correlation with glass-forming ability in metallic glasses
1
2015
... 第一类结构指标完全基于原子的空间排列, 比如目前被广泛采用的原子Voronoi多面体结构分析算法[11-12,15]. Voronoi多面体结构从一个具体位置的原子出发, 用中心原子与其周围最近邻原子之间的中垂面围成一个多面体, 中心原子位于这个多面体中, 通过描述包围多面体的特征, 即Voronoi指数来描述中心原子所处短程结构环境. 另外, Voronoi多面体自然包含了配位数信息, 还可以定量描述原子所处的结构环境, 即最近邻原子空间分布情况. 通常, Voronoi指数标记为$n_3 ,n_4 ,n_5 ,n_6, \ldots $, 其中$n_i $表示这个多面体中$i$边形的数量. 一般来说, 取前4个指数, 即三、四、五、六边形的数量即可完备描述一个中心原子的结构信息. 此外, 这些多面体结构以某种隐含的规律, 在中、长程上堆积, 可以填满整个空间. 由Voronoi多面体分析衍生出的结构指标还包括配位数(coordination number, CN, 即$\mathop \sum \nolimits_i n_i )$、$N$重对称性参数($N$边形在多面体所有面中所占比例, 比如五重对称性为L5FS, 即$d_5 =n_5 /\mathop \sum \nolimits_i n_i )$、原子的Voronoi体积等, 以及由二十面体在空间上的堆积、连接方式形成的中程序结构[63-64]. 近来, 本文部分作者基于短程的Voronoi多面体分析, 提出了用于预测非晶态固体异常振动特征的方向序参量[65]. ...
Stretched and compressed exponentials in the relaxation dynamics of a metallic glass-forming melt
1
2018
... 第一类结构指标完全基于原子的空间排列, 比如目前被广泛采用的原子Voronoi多面体结构分析算法[11-12,15]. Voronoi多面体结构从一个具体位置的原子出发, 用中心原子与其周围最近邻原子之间的中垂面围成一个多面体, 中心原子位于这个多面体中, 通过描述包围多面体的特征, 即Voronoi指数来描述中心原子所处短程结构环境. 另外, Voronoi多面体自然包含了配位数信息, 还可以定量描述原子所处的结构环境, 即最近邻原子空间分布情况. 通常, Voronoi指数标记为$n_3 ,n_4 ,n_5 ,n_6, \ldots $, 其中$n_i $表示这个多面体中$i$边形的数量. 一般来说, 取前4个指数, 即三、四、五、六边形的数量即可完备描述一个中心原子的结构信息. 此外, 这些多面体结构以某种隐含的规律, 在中、长程上堆积, 可以填满整个空间. 由Voronoi多面体分析衍生出的结构指标还包括配位数(coordination number, CN, 即$\mathop \sum \nolimits_i n_i )$、$N$重对称性参数($N$边形在多面体所有面中所占比例, 比如五重对称性为L5FS, 即$d_5 =n_5 /\mathop \sum \nolimits_i n_i )$、原子的Voronoi体积等, 以及由二十面体在空间上的堆积、连接方式形成的中程序结构[63-64]. 近来, 本文部分作者基于短程的Voronoi多面体分析, 提出了用于预测非晶态固体异常振动特征的方向序参量[65]. ...
Structural parameter of orientational order to predict the boson vibrational anomaly in glasses
3
2019
... 第一类结构指标完全基于原子的空间排列, 比如目前被广泛采用的原子Voronoi多面体结构分析算法[11-12,15]. Voronoi多面体结构从一个具体位置的原子出发, 用中心原子与其周围最近邻原子之间的中垂面围成一个多面体, 中心原子位于这个多面体中, 通过描述包围多面体的特征, 即Voronoi指数来描述中心原子所处短程结构环境. 另外, Voronoi多面体自然包含了配位数信息, 还可以定量描述原子所处的结构环境, 即最近邻原子空间分布情况. 通常, Voronoi指数标记为$n_3 ,n_4 ,n_5 ,n_6, \ldots $, 其中$n_i $表示这个多面体中$i$边形的数量. 一般来说, 取前4个指数, 即三、四、五、六边形的数量即可完备描述一个中心原子的结构信息. 此外, 这些多面体结构以某种隐含的规律, 在中、长程上堆积, 可以填满整个空间. 由Voronoi多面体分析衍生出的结构指标还包括配位数(coordination number, CN, 即$\mathop \sum \nolimits_i n_i )$、$N$重对称性参数($N$边形在多面体所有面中所占比例, 比如五重对称性为L5FS, 即$d_5 =n_5 /\mathop \sum \nolimits_i n_i )$、原子的Voronoi体积等, 以及由二十面体在空间上的堆积、连接方式形成的中程序结构[63-64]. 近来, 本文部分作者基于短程的Voronoi多面体分析, 提出了用于预测非晶态固体异常振动特征的方向序参量[65]. ...
... 另外一个热力学指标为低频振动模式参与度(participation fraction of low-frequency vibrational modes)[44-45]. 与大多数晶体相比, 结构无序固体一般会有显著的过剩低频振动模式, 并且具有空间准局域特征[65]. 软模集中的区域通常在玻璃材料中被认为是"软点''(soft spots)[73,78]. 这种低频振动模式与非晶合金中的剪切转换事件密切相关. 塑形事件总是从某个低频振动模式的失稳开始. 那么, 软点理所当然也和过冷液体的不可逆结构重排相关[45]. 因此, 软模也常被作为一种能有效预测玻璃性质的结构指标. 原子$i$的低频振动模式参与度定义为 ...
... 所以, 一个有效的非晶态固体结构参量, 必须具有一个公共的空间关联特征, 大概在亚纳米的量级. 从这个角度讲, 可以将广义结构参量的空间关联长度作为控制非晶态固体动力学性质的隐藏物理量[69,98-99]. 除非一个超级复杂玻璃结构, 具备了亚纳米量级的空间关联属性, 那么它在预测玻璃性能方面才是完备的. 然而这大概需要数百或数千量级的原子来定义这种复杂结构, 从而为建立有效的无序物质"结构-性能"关系带来了极大的挑战, 这也是为什么到目前为止探索非晶态物质的结构-性能关联仍是研究热点. 也许最近邻结构不能决定玻璃性质的结论听起来有点令人失望, 但从另外一个角度看, 这其实是一个好消息. 每个原子都有很多种可能的局部结构定义, 却只有一个振动MSD, 从而可以从广义"结构"的角度, 另辟蹊径建立起超越传统晶态物质的新型无序物质构效关系. 的数据和讨论显示, 在非晶态固体中受限比几何结构本身更关键. 最后, 空间关联的重要性是普遍的, 激活能、两体过剩熵、低频振动模式参与度、柔性体积、异常振动方向序等物理参量也被发现具有亚纳米的空间关联长度[65,69]. 基于机器学习的非晶结构参量-软度-也被发现在跨空间尺度多种材料中适用[99]. ...
Structural atomistic mechanism for the glass transition entropic scenario
1
2019
... 更精细的原子结构指标还包括诸多键序参量, 其中涵盖了原子间角度信息, 比如$Q_6$等键方向序(steinhard bond-orientational order, $Q_6 $为六重键方向序). 它们可以用以区分非晶和不同对称性的晶体结构, 适合描述晶化过程. 它通过球谐函数和键角参数定义, 即$Q_6 =\left( {\frac{4\pi }{13}\mathop \sum \nolimits_{-6}^6 \left| {\overline {Y_{6m} } } \right|^2} \right)$, 这里$Y_{6m} $是球谐函数, $\overline {Y_{6m} } $表示所有键的平均. 关于短程结构分析, 本文以Voronoi 多面体结构为例, 图2给出了典型的CuZr金属玻璃中主要的Voronoi多面体分布情况, 还有占比较少的结构没有列出. 对Cu原子为中心和Zr原子为中心的Voronoi多面体加以区分. 对于两类中心原子, 最常见的4种多面体原子结构已在图中展示. 虽然分子动力学模拟显示, 在某些化学成分中, 随着无序材料从液体到玻璃演化, 其中的二十面体结构$\left\langle {0,0,12,0} \right\rangle $显著增加, 但是没有任何结构相对于其他结构起到了主控作用[66]. 这个图像与晶体截然不同, 比如在类体心立方的B2晶体中, 主控团簇结构是$\left\langle {0,6,0,8} \right\rangle $. 此外, 非晶态固体的这些短程结构的分布还具有很强的化学成分依赖性. 显而易见, 在非晶态固体中任何一种多面体结构作为其他结构的所谓"缺陷"结构, 都比较牵强. 所以, 试图通过这些短程结构信息去理解非晶态固体的动力学行为具有极大的挑战性. ...
Cooling rates dependence of medium-range order development in Cu$_{64.5}$Zr$_{35.5}$ metallic glass
1
2015
... 其他的复杂非晶结构包括前文提到的基于短程结构空间排列方式的所谓中、长程结构信息[9,67].除此之外, 特别突出的一个成功的结构指标为两体过剩熵, 或称局部结构熵[68-69]. 以CuZr二元金属玻璃为例, 第$i$个原子的两体过剩熵定义为 ...
Structures of local rearrangements in soft colloidal glasses
2
2016
... 其他的复杂非晶结构包括前文提到的基于短程结构空间排列方式的所谓中、长程结构信息[9,67].除此之外, 特别突出的一个成功的结构指标为两体过剩熵, 或称局部结构熵[68-69]. 以CuZr二元金属玻璃为例, 第$i$个原子的两体过剩熵定义为 ...
... 两体过剩熵是过剩熵有限项展开后的两体部分, 为过剩熵最主要的部分, 它表示由于原子位置的相互关联导致的相对于理想气体状态的熵损失. 因为平衡态理想气体熵最大, 非晶态固体中的原子级别过剩熵总是负值, 绝对值越大, 则该原子越有序. 它曾被应用于预测玻璃形成液体的扩散行为和不均匀动力学, 以及软胶体玻璃的局部粒子重排[68]. 因此, 它可以作为一种纯结构参数来探索可能的结构-性能关联. 除此之外, 由于积分截断半径的选择具有灵活性, 该自由度为检测空间关联在调节结构-性能关系中的重要作用提供很大可能性. ...
Revisiting the structure-property relationship of metallic glasses: Common spatial correlation revealed as a hidden rule
7
2019
... 其他的复杂非晶结构包括前文提到的基于短程结构空间排列方式的所谓中、长程结构信息[9,67].除此之外, 特别突出的一个成功的结构指标为两体过剩熵, 或称局部结构熵[68-69]. 以CuZr二元金属玻璃为例, 第$i$个原子的两体过剩熵定义为 ...
... 其中, $e_\omega ^i $为原子$i$对应的极化矢量. 简正模分析可以通过对角化固有结构的动力学矩阵(Hessian matrix)完成, 而力常数矩阵从经验势函数中计算得到. 通常, 可以经验地选择将0.25%的最低频振动模式求和, 作为第$i$个原子的低频振动模式参与度[69]. ...
... 如前文所述, 非晶态固体的局部激活事件激活能是最直观和关键的动力学参数, 可以定量表征事件发生的难易程度, 这一点已经在之前的工作中得到充分验证[69]. 但是, 非晶态物质的PEL是个高自由度的、异常复杂的多维平面. 在3$N$维空间中, 高效、准确抽样PEL拓扑信息绝非易事[26-27,93]. 针对该问题, 加拿大蒙特利尔大学的Mousseau等[94-96]发展了ART(activation-relaxation technique)算法, 后又经过多人改进. 该算法可以通过随机抽样鞍点态来获得体系中不同事件的激活能, 从而克服了分子动力学模拟上的时间尺度限制, 属于加速分子动力学模拟的一类. 它的优势在于可以高效处理无序体系等复杂系统的PEL抽样, 而不依赖于原子晶格等信息, 也无需事先定义激活的初态与末态. 并且, 初始激活方向随机, 高效海量抽样后, 可以潜在穷尽所有可能的局部激活时间, 给出完备的激活能图谱. ...
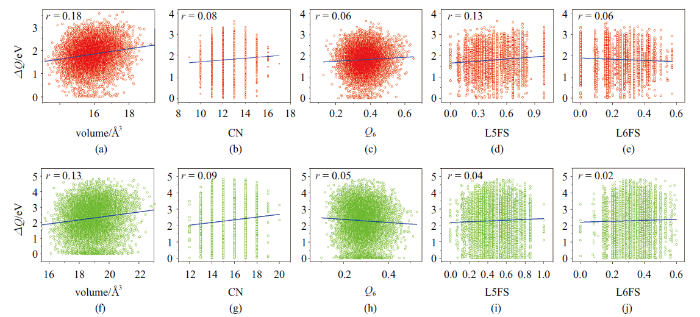
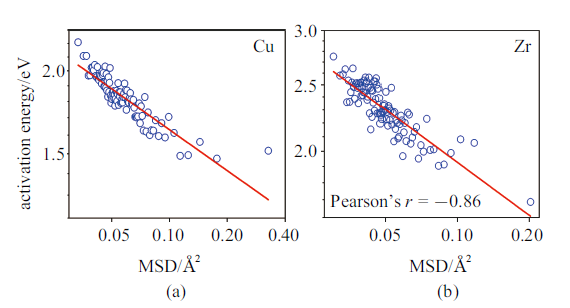
... 严格来说, 以上数据并没有从数学上严格推演出以下结构, 即非晶固体局部简单结构对于预测长时间性质无效. 但是, 至少它们已经表明了最标准的局部结构表征方法在预测非晶态物质热激活性能时大概是无效的. 所以, 应该从另外一个角度出发, 可能需要用更复杂的结构表征方法, 比如启用超越最近邻原子的复杂结构指标, 尝试与动力学性质建立更加有效的关联. 比如从一个原子出发, 基于数个近邻原子层, 定义式(1)中的原子级两体过剩熵$S_{2,i} $. 之前的研究发现, 如果用来定义这个结构参数的原子范围超过第四近邻(11.2 Å), 那么过剩熵与激活能之间就可以建立起非常强的关联, 其线性拟合的Pearson关联系数, 对于Cu原子为0.95, Zr原子为0.72, 说明完备的非晶结构信息是非局域的[69]. ...
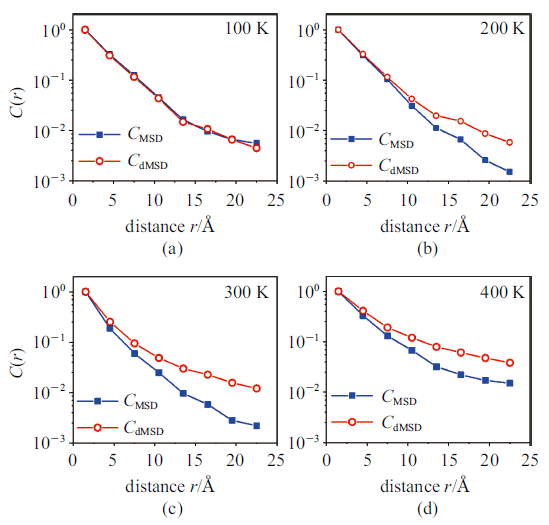
... 从图7中可以看出, 振动MSD的空间自关联函数衰减是连续的, 说明振动的相互作用是长程的, 所以没有理由将相互作用截断在某个空间位置. 但是很显然, 关联尺度远超过该CuZr体系的最近邻距离(即RDF第一高峰位置, 约2.8 Å). 作为初级近似, 采用经验函数描述, $C\left( r \right)\propto \exp\left( {-r/\xi } \right)$, 其中$\xi $为关联长度. 那么, 可以经验地认为, 当距离为$r_{\rm c} =3\xi $时, 关联函数衰减到$\exp\left( {-3} \right)\approx 0.05$, 这时自关联消失[98]. 如果采用此种定义, 那么vMSD的自关联长度$r_{\rm c} $大概在亚纳米的量级. 这与短程结构的空间关联函数具有极大的区别. 在之前的研究中发现, 短程结构, 例如五重对称性参数L5FS, 其空间关联函数随距离衰减很快, 远低于纳米的量级[69]. ...
... 所以, 一个有效的非晶态固体结构参量, 必须具有一个公共的空间关联特征, 大概在亚纳米的量级. 从这个角度讲, 可以将广义结构参量的空间关联长度作为控制非晶态固体动力学性质的隐藏物理量[69,98-99]. 除非一个超级复杂玻璃结构, 具备了亚纳米量级的空间关联属性, 那么它在预测玻璃性能方面才是完备的. 然而这大概需要数百或数千量级的原子来定义这种复杂结构, 从而为建立有效的无序物质"结构-性能"关系带来了极大的挑战, 这也是为什么到目前为止探索非晶态物质的结构-性能关联仍是研究热点. 也许最近邻结构不能决定玻璃性质的结论听起来有点令人失望, 但从另外一个角度看, 这其实是一个好消息. 每个原子都有很多种可能的局部结构定义, 却只有一个振动MSD, 从而可以从广义"结构"的角度, 另辟蹊径建立起超越传统晶态物质的新型无序物质构效关系. 的数据和讨论显示, 在非晶态固体中受限比几何结构本身更关键. 最后, 空间关联的重要性是普遍的, 激活能、两体过剩熵、低频振动模式参与度、柔性体积、异常振动方向序等物理参量也被发现具有亚纳米的空间关联长度[65,69]. 基于机器学习的非晶结构参量-软度-也被发现在跨空间尺度多种材料中适用[99]. ...
... ,69]. 基于机器学习的非晶结构参量-软度-也被发现在跨空间尺度多种材料中适用[99]. ...
Colloquium: The glass transition and elastic models of glass-forming liquids
1
2006
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
Quantitative relations between cooperative motion, emergent elasticity, and free volume in model glass-forming polymer materials
2015
Predicting the long-time dynamic heterogeneity in a supercooled liquid on the basis of short-time heterogeneities
1
2006
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
Universal structural parameter to quantitatively predict metallic glass properties
3
2016
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
... 其中, $\tau _0 $为有限的振动评估区间(100 ps量级, 对应几十个振动周期), 需要包含足够的振荡周期; $r_{i,\rm equil} $是第$i$个原子在某个非晶固有结构中(已用CG算法能量最小化)的平衡位置; $r_i \left( t \right)$是原子在300 K的温度下, $\tau _0 =100$ ps时间内的瞬时位置. 尖括号表示时间平均. 一个合适的时间段需要保证原子围绕着它们的热动力学平衡位置振动, 而又不会发生PEL上两个能量盆地之间的动力学跳跃, 所以评估时间也不能太长. 目前, 在玻璃形成液体中, vMSD已经被显示是一个好的动力学预测指标, 可以预测慢冷却现象和动力学不均匀性. 从 PEL角度分析, vMSD表示系统状态围绕着一个能量局部最小点的热平均偏差度, 它反应了这个能量盆地的曲率大小. 具体而言, 它的物理意义为局部构型的受限程度.因为$k_{\rm B} T/\Delta r^2$在简谐近似下为力常数, 所以, vMSD和非晶固体的局部刚度(弹性模量)相关. 特别是在协同剪切模型中, 固体的弹性模量直接用于计算剪切转变发生的能垒. 从这个意义上来说, vMSD可以作为玻璃的一个直接的结构指标,用于本文中有关非晶态固体"结构-性能''关联的探讨. 后来, 马恩等提出的柔性体积概念[73], 也是基于vMSD的一个体积量纲的扩展结构参数, 在其中振动部分起到了决定作用. ...
... 另外一个热力学指标为低频振动模式参与度(participation fraction of low-frequency vibrational modes)[44-45]. 与大多数晶体相比, 结构无序固体一般会有显著的过剩低频振动模式, 并且具有空间准局域特征[65]. 软模集中的区域通常在玻璃材料中被认为是"软点''(soft spots)[73,78]. 这种低频振动模式与非晶合金中的剪切转换事件密切相关. 塑形事件总是从某个低频振动模式的失稳开始. 那么, 软点理所当然也和过冷液体的不可逆结构重排相关[45]. 因此, 软模也常被作为一种能有效预测玻璃性质的结构指标. 原子$i$的低频振动模式参与度定义为 ...
Evolution of elastic heterogeneity during aging in metallic glasses
1
2014
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
Local elastic expansion model for viscous-flow activation energies of glass-forming molecular liquids
1996
Correlation between local elastic heterogeneities and overall elastic properties in metallic glasses
1
2016
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
Bar-sinai Y, et al. Local thermal energy as a structural indicator in glasses
1
2017
... 由于纯粹的原子结构信息描述非晶体系的动力学性质比较困难, 所以非晶物理领域常见的方法是定义广义的"结构", 文献中已经由大量的报道和成功范例. 比如, 基于热力学信息预测非晶态物质的动力学行为. 这类指标包括低频振动模式参与度[44-45]、振动均方位移[70-72]、柔性体积[73]、局域模量[74-76]、局域热能[77]等热力学参量. 下面简要介绍几种典型的热力学非晶"结构"参量. ...
Correlating the properties of amorphous silicon with its flexibility volume
1
2017
... 另外一个热力学指标为低频振动模式参与度(participation fraction of low-frequency vibrational modes)[44-45]. 与大多数晶体相比, 结构无序固体一般会有显著的过剩低频振动模式, 并且具有空间准局域特征[65]. 软模集中的区域通常在玻璃材料中被认为是"软点''(soft spots)[73,78]. 这种低频振动模式与非晶合金中的剪切转换事件密切相关. 塑形事件总是从某个低频振动模式的失稳开始. 那么, 软点理所当然也和过冷液体的不可逆结构重排相关[45]. 因此, 软模也常被作为一种能有效预测玻璃性质的结构指标. 原子$i$的低频振动模式参与度定义为 ...
Energy landscape-driven non-equilibrium evolution of inherent structure in disordered material
1
2017
... 因为剪切转变是热激活事件, 所以基于动力学参数预测非晶态固体的局部塑形激活是直观的, 虽然其物理意义和科学价值值得进一步的讨论. 实际上, 当Argon[40]提出剪切转变平均场模型时, 他就基于Eshelby夹杂的弹性应变能赋予了热激活事件的激活能显式表达式, 用以表征剪切事件发生的难易程度, 所以激活能是一个最关键的动力学参数. 之后Johnson的协同剪切模型, 启发于Frenkel关于晶体原子面间滑移的剪切强度理论, 将激活能与非晶态材料的STZ体积、模量等参数关联, 便可以很好地描述非晶态材料的屈服行为和随温度变化的趋势[41]. 所以激活能是最直接的描述非晶态塑性的动力学参量[79-83]. ...
How thermally activated deformation starts in metallic glass
2014
Crossover from localized to cascade relaxations in metallic glasses
2015
Distribution of thermally activated plastic events in a flowing glass
2009
Yield stress in metallic glasses: The jamming-unjamming transition studied through Monte Carlo simulations based on the activation-relaxation technique
1
2009
... 因为剪切转变是热激活事件, 所以基于动力学参数预测非晶态固体的局部塑形激活是直观的, 虽然其物理意义和科学价值值得进一步的讨论. 实际上, 当Argon[40]提出剪切转变平均场模型时, 他就基于Eshelby夹杂的弹性应变能赋予了热激活事件的激活能显式表达式, 用以表征剪切事件发生的难易程度, 所以激活能是一个最关键的动力学参数. 之后Johnson的协同剪切模型, 启发于Frenkel关于晶体原子面间滑移的剪切强度理论, 将激活能与非晶态材料的STZ体积、模量等参数关联, 便可以很好地描述非晶态材料的屈服行为和随温度变化的趋势[41]. 所以激活能是最直接的描述非晶态塑性的动力学参量[79-83]. ...
A free energy landscape perspective on the nature of collective diffusion in amorphous solids
2
2018
... 因为非晶态固体局域塑性具有热激活特征, 所以最关键的物理参数为激活自由能函数. 而激活自由能是温度、应力、化学势等热力学量的函数. 那么, 自然可以通过调控温度或应力激励塑性事件的发生[49,84]. 从这个角度看, 应力与温度具有一定的等价性, 前者通过对PEL的偏置实现自由能势垒的降低, 等效于温度升高. 从应力角度出发, Patinet等[85]提出了局域屈服应力的概念, 它可以作为一种有效预测塑性事件位置和大小的动力学参数, 其优势在于即使材料经历了大变形, 在数十个事件之后仍然具有一定的预测性. Xu等[86]从PEL抽样过程出发, 发现沿STZ事件发生的最小能量路径的应力梯度方向可以有效预测非晶态固体塑性事件发生的宏观应变、位置、结构变形形貌特征,也是一种用于预测非晶塑性的动力学指标. ...
... 除此之外, 还发现一个有趣的现象, 图7中所示的所有空间自关联函数总是正值. 这说明所谓的软点原子, 即具有比较大的vMSD的原子, 总是倾向于被另外一些软点原子所包围. 这反映了vMSD不仅仅是由最近邻结构控制的, 还具有协同性. 有趣的是, 如果观察方向解耦的vMSD, 它们的平均空间关联函数$C_{\Delta x^2,\Delta y^2,\Delta z^2} \left( r \right)$会延伸到更远的位置. 尤其是随着温度的升高, 方向vMSD空间关联尺度会变长, 这说明局部各向异性对于玻璃性质来说非常重要, 一维运动模式变得更可能发生, 这可能就是结构无序体系中经常发现类链式集体运动的物理起源[84,100]. ...
Connecting local yield stresses with plastic activity in amorphous solids
1
2016
... 因为非晶态固体局域塑性具有热激活特征, 所以最关键的物理参数为激活自由能函数. 而激活自由能是温度、应力、化学势等热力学量的函数. 那么, 自然可以通过调控温度或应力激励塑性事件的发生[49,84]. 从这个角度看, 应力与温度具有一定的等价性, 前者通过对PEL的偏置实现自由能势垒的降低, 等效于温度升高. 从应力角度出发, Patinet等[85]提出了局域屈服应力的概念, 它可以作为一种有效预测塑性事件位置和大小的动力学参数, 其优势在于即使材料经历了大变形, 在数十个事件之后仍然具有一定的预测性. Xu等[86]从PEL抽样过程出发, 发现沿STZ事件发生的最小能量路径的应力梯度方向可以有效预测非晶态固体塑性事件发生的宏观应变、位置、结构变形形貌特征,也是一种用于预测非晶塑性的动力学指标. ...
Predicting Shear Transformation Events in Metallic Glasses
1
2018
... 因为非晶态固体局域塑性具有热激活特征, 所以最关键的物理参数为激活自由能函数. 而激活自由能是温度、应力、化学势等热力学量的函数. 那么, 自然可以通过调控温度或应力激励塑性事件的发生[49,84]. 从这个角度看, 应力与温度具有一定的等价性, 前者通过对PEL的偏置实现自由能势垒的降低, 等效于温度升高. 从应力角度出发, Patinet等[85]提出了局域屈服应力的概念, 它可以作为一种有效预测塑性事件位置和大小的动力学参数, 其优势在于即使材料经历了大变形, 在数十个事件之后仍然具有一定的预测性. Xu等[86]从PEL抽样过程出发, 发现沿STZ事件发生的最小能量路径的应力梯度方向可以有效预测非晶态固体塑性事件发生的宏观应变、位置、结构变形形貌特征,也是一种用于预测非晶塑性的动力学指标. ...
Fast parallel algorithms for short-range molecular dynamics
1
1995
... 本文基于大规模分子动力学模拟和势能面抽样技术, 选用具有较好玻璃形成能力的二元金属玻璃体系, Cu$_{50}$Zr$_{50}$, 作为广义的非晶态固体模型, 探讨其"结构-性能''关系及其背后隐藏的物理机制. 非晶合金样品的制备采用分子动力学技术, 计算使用LAMMPS程序包开展[87]. 力场采用Finnis-Sinclair类型的嵌入原子经验势(embedded-atom method, EAM)描述[88]. 该经验势函数被广泛应用于研究玻璃结构、玻璃转变、热力学和动力学等性质. 本文研究的体系包含19 652个原子, 3个方向均为7 nm尺寸, 该尺寸远大于径向分布函数所显示的短、中程序. 分子动力学模拟中, 模型的3个方向都采用周期性边界条件描述. 分子动力学运动方程时间积分步长为2 fs. 首先, 将体系在液体态(2000 K)充分融化4 ns时间, 由于该时间远远大于体系的$\alpha $弛豫时间, 所以可以保证体系始终处于热力学平衡态. 然后将平衡液体以10$^{10}$ K/s的冷却速率快速冷却到0 K. 模拟采用等温等压系综, 过程中温度使用Nose-Hoover热浴控制[89-90], 每个方向的外部压力通过Parrinello-Rahman压浴保持为零应力状态[91]. 在冷却结束后, 通过共轭梯度算法, 将体系完全弛豫到局部势能极小点, 即玻璃形成液体的某个固有结构. 通过追踪体系热力学函数, 比如体积、势能的变化, 可以判断该二元体系的玻璃转变温度在650 K左右, 与实验结果吻合. 此外, 采用Voronoi多面体分析等方法分析该玻璃体系的短程原子结构, 并通过Ovito软件可视化[92], 结果如图2所示, 该体系中存在着广泛的短程结构. ...
Development of suitable interatomic potentials for simulation of liquid and amorphous Cu-Zr alloys
1
2009
... 本文基于大规模分子动力学模拟和势能面抽样技术, 选用具有较好玻璃形成能力的二元金属玻璃体系, Cu$_{50}$Zr$_{50}$, 作为广义的非晶态固体模型, 探讨其"结构-性能''关系及其背后隐藏的物理机制. 非晶合金样品的制备采用分子动力学技术, 计算使用LAMMPS程序包开展[87]. 力场采用Finnis-Sinclair类型的嵌入原子经验势(embedded-atom method, EAM)描述[88]. 该经验势函数被广泛应用于研究玻璃结构、玻璃转变、热力学和动力学等性质. 本文研究的体系包含19 652个原子, 3个方向均为7 nm尺寸, 该尺寸远大于径向分布函数所显示的短、中程序. 分子动力学模拟中, 模型的3个方向都采用周期性边界条件描述. 分子动力学运动方程时间积分步长为2 fs. 首先, 将体系在液体态(2000 K)充分融化4 ns时间, 由于该时间远远大于体系的$\alpha $弛豫时间, 所以可以保证体系始终处于热力学平衡态. 然后将平衡液体以10$^{10}$ K/s的冷却速率快速冷却到0 K. 模拟采用等温等压系综, 过程中温度使用Nose-Hoover热浴控制[89-90], 每个方向的外部压力通过Parrinello-Rahman压浴保持为零应力状态[91]. 在冷却结束后, 通过共轭梯度算法, 将体系完全弛豫到局部势能极小点, 即玻璃形成液体的某个固有结构. 通过追踪体系热力学函数, 比如体积、势能的变化, 可以判断该二元体系的玻璃转变温度在650 K左右, 与实验结果吻合. 此外, 采用Voronoi多面体分析等方法分析该玻璃体系的短程原子结构, 并通过Ovito软件可视化[92], 结果如图2所示, 该体系中存在着广泛的短程结构. ...
A molecular dynamics method for simulations in the canonical ensemble
1
1984
... 本文基于大规模分子动力学模拟和势能面抽样技术, 选用具有较好玻璃形成能力的二元金属玻璃体系, Cu$_{50}$Zr$_{50}$, 作为广义的非晶态固体模型, 探讨其"结构-性能''关系及其背后隐藏的物理机制. 非晶合金样品的制备采用分子动力学技术, 计算使用LAMMPS程序包开展[87]. 力场采用Finnis-Sinclair类型的嵌入原子经验势(embedded-atom method, EAM)描述[88]. 该经验势函数被广泛应用于研究玻璃结构、玻璃转变、热力学和动力学等性质. 本文研究的体系包含19 652个原子, 3个方向均为7 nm尺寸, 该尺寸远大于径向分布函数所显示的短、中程序. 分子动力学模拟中, 模型的3个方向都采用周期性边界条件描述. 分子动力学运动方程时间积分步长为2 fs. 首先, 将体系在液体态(2000 K)充分融化4 ns时间, 由于该时间远远大于体系的$\alpha $弛豫时间, 所以可以保证体系始终处于热力学平衡态. 然后将平衡液体以10$^{10}$ K/s的冷却速率快速冷却到0 K. 模拟采用等温等压系综, 过程中温度使用Nose-Hoover热浴控制[89-90], 每个方向的外部压力通过Parrinello-Rahman压浴保持为零应力状态[91]. 在冷却结束后, 通过共轭梯度算法, 将体系完全弛豫到局部势能极小点, 即玻璃形成液体的某个固有结构. 通过追踪体系热力学函数, 比如体积、势能的变化, 可以判断该二元体系的玻璃转变温度在650 K左右, 与实验结果吻合. 此外, 采用Voronoi多面体分析等方法分析该玻璃体系的短程原子结构, 并通过Ovito软件可视化[92], 结果如图2所示, 该体系中存在着广泛的短程结构. ...
Canonical dynamics: Equilibrium phase-space distributions
1
1985
... 本文基于大规模分子动力学模拟和势能面抽样技术, 选用具有较好玻璃形成能力的二元金属玻璃体系, Cu$_{50}$Zr$_{50}$, 作为广义的非晶态固体模型, 探讨其"结构-性能''关系及其背后隐藏的物理机制. 非晶合金样品的制备采用分子动力学技术, 计算使用LAMMPS程序包开展[87]. 力场采用Finnis-Sinclair类型的嵌入原子经验势(embedded-atom method, EAM)描述[88]. 该经验势函数被广泛应用于研究玻璃结构、玻璃转变、热力学和动力学等性质. 本文研究的体系包含19 652个原子, 3个方向均为7 nm尺寸, 该尺寸远大于径向分布函数所显示的短、中程序. 分子动力学模拟中, 模型的3个方向都采用周期性边界条件描述. 分子动力学运动方程时间积分步长为2 fs. 首先, 将体系在液体态(2000 K)充分融化4 ns时间, 由于该时间远远大于体系的$\alpha $弛豫时间, 所以可以保证体系始终处于热力学平衡态. 然后将平衡液体以10$^{10}$ K/s的冷却速率快速冷却到0 K. 模拟采用等温等压系综, 过程中温度使用Nose-Hoover热浴控制[89-90], 每个方向的外部压力通过Parrinello-Rahman压浴保持为零应力状态[91]. 在冷却结束后, 通过共轭梯度算法, 将体系完全弛豫到局部势能极小点, 即玻璃形成液体的某个固有结构. 通过追踪体系热力学函数, 比如体积、势能的变化, 可以判断该二元体系的玻璃转变温度在650 K左右, 与实验结果吻合. 此外, 采用Voronoi多面体分析等方法分析该玻璃体系的短程原子结构, 并通过Ovito软件可视化[92], 结果如图2所示, 该体系中存在着广泛的短程结构. ...
Polymorphic transitions in single crystals: A new molecular dynamics method
1
1981
... 本文基于大规模分子动力学模拟和势能面抽样技术, 选用具有较好玻璃形成能力的二元金属玻璃体系, Cu$_{50}$Zr$_{50}$, 作为广义的非晶态固体模型, 探讨其"结构-性能''关系及其背后隐藏的物理机制. 非晶合金样品的制备采用分子动力学技术, 计算使用LAMMPS程序包开展[87]. 力场采用Finnis-Sinclair类型的嵌入原子经验势(embedded-atom method, EAM)描述[88]. 该经验势函数被广泛应用于研究玻璃结构、玻璃转变、热力学和动力学等性质. 本文研究的体系包含19 652个原子, 3个方向均为7 nm尺寸, 该尺寸远大于径向分布函数所显示的短、中程序. 分子动力学模拟中, 模型的3个方向都采用周期性边界条件描述. 分子动力学运动方程时间积分步长为2 fs. 首先, 将体系在液体态(2000 K)充分融化4 ns时间, 由于该时间远远大于体系的$\alpha $弛豫时间, 所以可以保证体系始终处于热力学平衡态. 然后将平衡液体以10$^{10}$ K/s的冷却速率快速冷却到0 K. 模拟采用等温等压系综, 过程中温度使用Nose-Hoover热浴控制[89-90], 每个方向的外部压力通过Parrinello-Rahman压浴保持为零应力状态[91]. 在冷却结束后, 通过共轭梯度算法, 将体系完全弛豫到局部势能极小点, 即玻璃形成液体的某个固有结构. 通过追踪体系热力学函数, 比如体积、势能的变化, 可以判断该二元体系的玻璃转变温度在650 K左右, 与实验结果吻合. 此外, 采用Voronoi多面体分析等方法分析该玻璃体系的短程原子结构, 并通过Ovito软件可视化[92], 结果如图2所示, 该体系中存在着广泛的短程结构. ...
Visualization and analysis of atomistic simulation data with OVITO-the Open Visualization Tool
1
2010
... 本文基于大规模分子动力学模拟和势能面抽样技术, 选用具有较好玻璃形成能力的二元金属玻璃体系, Cu$_{50}$Zr$_{50}$, 作为广义的非晶态固体模型, 探讨其"结构-性能''关系及其背后隐藏的物理机制. 非晶合金样品的制备采用分子动力学技术, 计算使用LAMMPS程序包开展[87]. 力场采用Finnis-Sinclair类型的嵌入原子经验势(embedded-atom method, EAM)描述[88]. 该经验势函数被广泛应用于研究玻璃结构、玻璃转变、热力学和动力学等性质. 本文研究的体系包含19 652个原子, 3个方向均为7 nm尺寸, 该尺寸远大于径向分布函数所显示的短、中程序. 分子动力学模拟中, 模型的3个方向都采用周期性边界条件描述. 分子动力学运动方程时间积分步长为2 fs. 首先, 将体系在液体态(2000 K)充分融化4 ns时间, 由于该时间远远大于体系的$\alpha $弛豫时间, 所以可以保证体系始终处于热力学平衡态. 然后将平衡液体以10$^{10}$ K/s的冷却速率快速冷却到0 K. 模拟采用等温等压系综, 过程中温度使用Nose-Hoover热浴控制[89-90], 每个方向的外部压力通过Parrinello-Rahman压浴保持为零应力状态[91]. 在冷却结束后, 通过共轭梯度算法, 将体系完全弛豫到局部势能极小点, 即玻璃形成液体的某个固有结构. 通过追踪体系热力学函数, 比如体积、势能的变化, 可以判断该二元体系的玻璃转变温度在650 K左右, 与实验结果吻合. 此外, 采用Voronoi多面体分析等方法分析该玻璃体系的短程原子结构, 并通过Ovito软件可视化[92], 结果如图2所示, 该体系中存在着广泛的短程结构. ...
Exploring Energy Landscapes
1
2018
... 如前文所述, 非晶态固体的局部激活事件激活能是最直观和关键的动力学参数, 可以定量表征事件发生的难易程度, 这一点已经在之前的工作中得到充分验证[69]. 但是, 非晶态物质的PEL是个高自由度的、异常复杂的多维平面. 在3$N$维空间中, 高效、准确抽样PEL拓扑信息绝非易事[26-27,93]. 针对该问题, 加拿大蒙特利尔大学的Mousseau等[94-96]发展了ART(activation-relaxation technique)算法, 后又经过多人改进. 该算法可以通过随机抽样鞍点态来获得体系中不同事件的激活能, 从而克服了分子动力学模拟上的时间尺度限制, 属于加速分子动力学模拟的一类. 它的优势在于可以高效处理无序体系等复杂系统的PEL抽样, 而不依赖于原子晶格等信息, 也无需事先定义激活的初态与末态. 并且, 初始激活方向随机, 高效海量抽样后, 可以潜在穷尽所有可能的局部激活时间, 给出完备的激活能图谱. ...
Event-based relaxation of continuous disordered systems
1
1996
... 如前文所述, 非晶态固体的局部激活事件激活能是最直观和关键的动力学参数, 可以定量表征事件发生的难易程度, 这一点已经在之前的工作中得到充分验证[69]. 但是, 非晶态物质的PEL是个高自由度的、异常复杂的多维平面. 在3$N$维空间中, 高效、准确抽样PEL拓扑信息绝非易事[26-27,93]. 针对该问题, 加拿大蒙特利尔大学的Mousseau等[94-96]发展了ART(activation-relaxation technique)算法, 后又经过多人改进. 该算法可以通过随机抽样鞍点态来获得体系中不同事件的激活能, 从而克服了分子动力学模拟上的时间尺度限制, 属于加速分子动力学模拟的一类. 它的优势在于可以高效处理无序体系等复杂系统的PEL抽样, 而不依赖于原子晶格等信息, 也无需事先定义激活的初态与末态. 并且, 初始激活方向随机, 高效海量抽样后, 可以潜在穷尽所有可能的局部激活时间, 给出完备的激活能图谱. ...
Kinetic activation-relaxation technique: An off-lattice self-learning kinetic Monte Carlo algorithm
2008
Kinetic activation-relaxation technique
1
2011
... 如前文所述, 非晶态固体的局部激活事件激活能是最直观和关键的动力学参数, 可以定量表征事件发生的难易程度, 这一点已经在之前的工作中得到充分验证[69]. 但是, 非晶态物质的PEL是个高自由度的、异常复杂的多维平面. 在3$N$维空间中, 高效、准确抽样PEL拓扑信息绝非易事[26-27,93]. 针对该问题, 加拿大蒙特利尔大学的Mousseau等[94-96]发展了ART(activation-relaxation technique)算法, 后又经过多人改进. 该算法可以通过随机抽样鞍点态来获得体系中不同事件的激活能, 从而克服了分子动力学模拟上的时间尺度限制, 属于加速分子动力学模拟的一类. 它的优势在于可以高效处理无序体系等复杂系统的PEL抽样, 而不依赖于原子晶格等信息, 也无需事先定义激活的初态与末态. 并且, 初始激活方向随机, 高效海量抽样后, 可以潜在穷尽所有可能的局部激活时间, 给出完备的激活能图谱. ...
Following atomistic kinetics on experimental timescales with the kinetic Activation-Relaxation Technique
1
2015
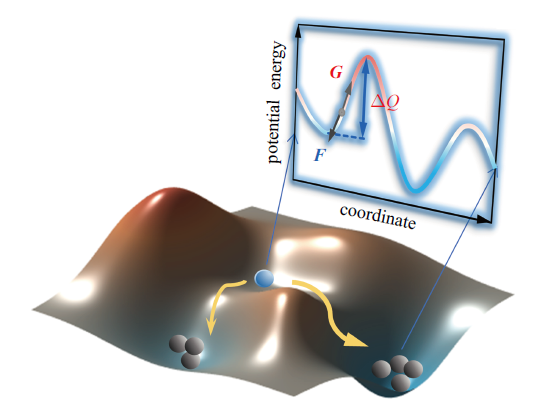
... ART算法的核心思想如图3所示. 产生事件以评估其激活能的过程包括3个基本步骤[97]. 首先, 从一个局部势能最小点开始, 以随机方向扰动某一集团原子使其离开势阱; 然后, 基于Lanczos算法, 通过Hessian矩阵求解, 评估可能能量路径的最弱方向, 即能量曲面的最小弧度方向, 并沿该方向收敛到鞍点, 鞍点能量与初态状态的势能相比, 获取该事件激活能; 最后, 将状态弛豫到一个新的相邻局部势能最小态. ...
Spatial correlation of elastic heterogeneity tunes the deformation behavior of metallic glasses
2
2018
... 从图7中可以看出, 振动MSD的空间自关联函数衰减是连续的, 说明振动的相互作用是长程的, 所以没有理由将相互作用截断在某个空间位置. 但是很显然, 关联尺度远超过该CuZr体系的最近邻距离(即RDF第一高峰位置, 约2.8 Å). 作为初级近似, 采用经验函数描述, $C\left( r \right)\propto \exp\left( {-r/\xi } \right)$, 其中$\xi $为关联长度. 那么, 可以经验地认为, 当距离为$r_{\rm c} =3\xi $时, 关联函数衰减到$\exp\left( {-3} \right)\approx 0.05$, 这时自关联消失[98]. 如果采用此种定义, 那么vMSD的自关联长度$r_{\rm c} $大概在亚纳米的量级. 这与短程结构的空间关联函数具有极大的区别. 在之前的研究中发现, 短程结构, 例如五重对称性参数L5FS, 其空间关联函数随距离衰减很快, 远低于纳米的量级[69]. ...
... 所以, 一个有效的非晶态固体结构参量, 必须具有一个公共的空间关联特征, 大概在亚纳米的量级. 从这个角度讲, 可以将广义结构参量的空间关联长度作为控制非晶态固体动力学性质的隐藏物理量[69,98-99]. 除非一个超级复杂玻璃结构, 具备了亚纳米量级的空间关联属性, 那么它在预测玻璃性能方面才是完备的. 然而这大概需要数百或数千量级的原子来定义这种复杂结构, 从而为建立有效的无序物质"结构-性能"关系带来了极大的挑战, 这也是为什么到目前为止探索非晶态物质的结构-性能关联仍是研究热点. 也许最近邻结构不能决定玻璃性质的结论听起来有点令人失望, 但从另外一个角度看, 这其实是一个好消息. 每个原子都有很多种可能的局部结构定义, 却只有一个振动MSD, 从而可以从广义"结构"的角度, 另辟蹊径建立起超越传统晶态物质的新型无序物质构效关系. 的数据和讨论显示, 在非晶态固体中受限比几何结构本身更关键. 最后, 空间关联的重要性是普遍的, 激活能、两体过剩熵、低频振动模式参与度、柔性体积、异常振动方向序等物理参量也被发现具有亚纳米的空间关联长度[65,69]. 基于机器学习的非晶结构参量-软度-也被发现在跨空间尺度多种材料中适用[99]. ...
Structure-property relationships from universal signatures of plasticity in disordered solids
3
2017
... 所以, 一个有效的非晶态固体结构参量, 必须具有一个公共的空间关联特征, 大概在亚纳米的量级. 从这个角度讲, 可以将广义结构参量的空间关联长度作为控制非晶态固体动力学性质的隐藏物理量[69,98-99]. 除非一个超级复杂玻璃结构, 具备了亚纳米量级的空间关联属性, 那么它在预测玻璃性能方面才是完备的. 然而这大概需要数百或数千量级的原子来定义这种复杂结构, 从而为建立有效的无序物质"结构-性能"关系带来了极大的挑战, 这也是为什么到目前为止探索非晶态物质的结构-性能关联仍是研究热点. 也许最近邻结构不能决定玻璃性质的结论听起来有点令人失望, 但从另外一个角度看, 这其实是一个好消息. 每个原子都有很多种可能的局部结构定义, 却只有一个振动MSD, 从而可以从广义"结构"的角度, 另辟蹊径建立起超越传统晶态物质的新型无序物质构效关系. 的数据和讨论显示, 在非晶态固体中受限比几何结构本身更关键. 最后, 空间关联的重要性是普遍的, 激活能、两体过剩熵、低频振动模式参与度、柔性体积、异常振动方向序等物理参量也被发现具有亚纳米的空间关联长度[65,69]. 基于机器学习的非晶结构参量-软度-也被发现在跨空间尺度多种材料中适用[99]. ...
... [99]. ...
... 鉴于此, 扩展更全面的结构度量方法也就成为一项重要的任务. 比如, 随着人工智能的发展, 机器学习已经被用于寻找更为合适的结构描述[99,102-106]. 机器学习的基本原理是通过调整不同类型结构在组合全局结构中的权重, 使组合结构与某些特定性质的一致性最大化, 从而达到用结构准确预测特定性质的目的, 而不关心结构是否复杂或是否可认知. 所以, 即使机器学习在超越人类认知的高维空间训练出可以准确描述玻璃某种性能的所谓"超结构", 如何将黑盒子信息翻译为人类可以理解的理性语言也是一大挑战. ...
Structural Rearrangements Governing Johari-Goldstein Relaxations in Metallic Glass
1
2017
... 除此之外, 还发现一个有趣的现象, 图7中所示的所有空间自关联函数总是正值. 这说明所谓的软点原子, 即具有比较大的vMSD的原子, 总是倾向于被另外一些软点原子所包围. 这反映了vMSD不仅仅是由最近邻结构控制的, 还具有协同性. 有趣的是, 如果观察方向解耦的vMSD, 它们的平均空间关联函数$C_{\Delta x^2,\Delta y^2,\Delta z^2} \left( r \right)$会延伸到更远的位置. 尤其是随着温度的升高, 方向vMSD空间关联尺度会变长, 这说明局部各向异性对于玻璃性质来说非常重要, 一维运动模式变得更可能发生, 这可能就是结构无序体系中经常发现类链式集体运动的物理起源[84,100]. ...
Supercooling of liquids
1
1952
... (3) 结构作为衡量体系有序程度的物理量. 比如Frank[101]于1952年提出局部二十面体可以有效稳定纯液体结构, 使其可以进入过冷态. 所以, 由于某些几何结构的存在, 同时导致了整体上无序结构的产生. 因此, 结构可以用来表示体系接近有序的程度, 即结构对于晶体对称性的相似度. ...
Identifying structural flow defects in disordered solids using machine-learning methods
1
2015
... 鉴于此, 扩展更全面的结构度量方法也就成为一项重要的任务. 比如, 随着人工智能的发展, 机器学习已经被用于寻找更为合适的结构描述[99,102-106]. 机器学习的基本原理是通过调整不同类型结构在组合全局结构中的权重, 使组合结构与某些特定性质的一致性最大化, 从而达到用结构准确预测特定性质的目的, 而不关心结构是否复杂或是否可认知. 所以, 即使机器学习在超越人类认知的高维空间训练出可以准确描述玻璃某种性能的所谓"超结构", 如何将黑盒子信息翻译为人类可以理解的理性语言也是一大挑战. ...
A structural approach to relaxation in glassy liquids
2016
The relationship between local structure and relaxation in out-of-equilibrium glassy systems
2016
Heterogeneous Activation, Local Structure, and Softness in Supercooled Colloidal Liquids
2019
A transferable machine-learning framework linking interstice distribution and plastic heterogeneity in metallic glasses
1
2019
... 鉴于此, 扩展更全面的结构度量方法也就成为一项重要的任务. 比如, 随着人工智能的发展, 机器学习已经被用于寻找更为合适的结构描述[99,102-106]. 机器学习的基本原理是通过调整不同类型结构在组合全局结构中的权重, 使组合结构与某些特定性质的一致性最大化, 从而达到用结构准确预测特定性质的目的, 而不关心结构是否复杂或是否可认知. 所以, 即使机器学习在超越人类认知的高维空间训练出可以准确描述玻璃某种性能的所谓"超结构", 如何将黑盒子信息翻译为人类可以理解的理性语言也是一大挑战. ...