引言
小冲杆试验(small punch test, SPT)[6-7]是一种近乎"无损"的微型试样试验方法, 其试样尺寸为$\varPhi$10 mm $\times$ 0.5 mm, 通过试验可以得到试样中心点的载荷-位移曲线、断口相关数据等,其中包含了材料的弹塑性变形行为与断裂特征. 在小冲杆试验发展历史上,Mao等[8]分别将小冲杆试验屈服载荷、最大载荷与材料屈服强度、抗拉强度相关联,给出了相对应的经验公式.Chica等[9]则对小冲杆试验载荷-位移曲线初始阶段进行分析,将初始阶段斜率与材料弹性模量相关联, 得到两者之间的经验公式.Peng等[10]基于等效能量原理, 对小冲杆试验载荷-位移曲线第三阶段进行分析,得到了材料的真应力-应变曲线与抗拉强度.Baik等[11]将载荷-位移曲线下的面积定义为小冲杆断裂能,并发现夏比V型缺口试验结果与小冲杆试验结果之间的相关性,确定了材料韧脆转变温度.Hurst等[10]提出了一种基于断裂能的环形缺口小冲杆试样$J$积分估算方法,并且采用标准小冲杆试验,对$J-R$抗弯曲线和断裂韧性$J_{\rm IC}$进行了局部分析模拟.众多学者基于自己的试验结果均采用经验关联的方式给出获取材料强度和断裂韧性的关联公式[12-19],然而由于试验所用材料、试验机结构、尺寸、加载方式,以及小冲杆试验载荷-位移曲线上屈服载荷定义方法[20]的差异,通过试验数据拟合得到的经验公式也不尽相同, 彼此之间并能不通用,造成重复研究与研究资源的浪费. 因此,亟待找到更合理和有效的方法关联小冲杆试验结果与常规试验结果.
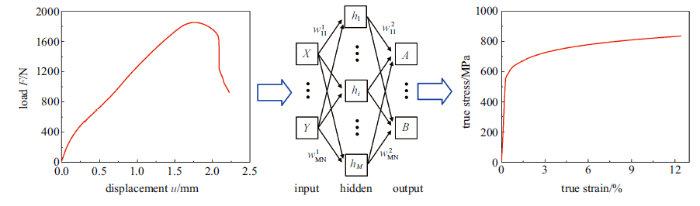
本文提出了一种利用小冲杆试验[21-23]、有限元模拟与人工智能BP (back-propagation)神经网络[24-26]相结合,准确获得材料真应力-应变曲线, 从而获得材料弹塑性力学性能的方法.通过经试验验证的含Gurson-Tvergaard-Needleman(GTN)损伤参数的小冲杆试验有限元模型得到457组假想材料小冲杆试验载荷-位移曲线,结合其对应的真应力-应变曲线对BP神经网络进行训练, 在两者之间建立关联关系.将小冲杆试验得到的X80管道钢载荷-位移曲线输入BP神经网络,得到X80管道钢的真应力-应变曲线, 从而得到其屈服强度与抗拉强度,并用单轴拉伸试验结果验证该方法的有效性与准确性.为了进一步推广得到的关联关系之广泛适用性, 利用训练好的BP神经网络,对已有文献[10, 27]中AISI 304L, P92, DP600等材料的小冲杆试验数据进行处理,将结果与文献中单轴拉伸试验结果相对比, 证明了相较于常规经验关联法,此方法获得材料力学性能具有准确性高、效率高、成本低等优点.
1 试验
1.1 单轴拉伸试验
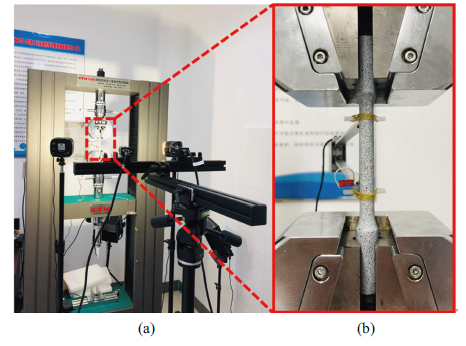
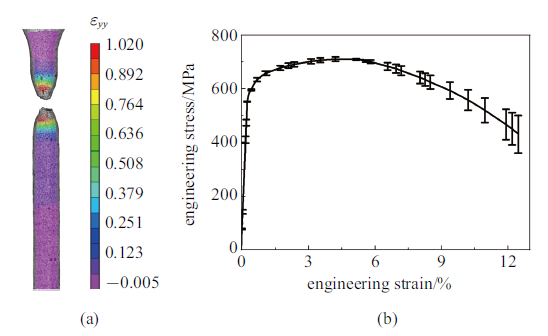
试验所用X80管道钢的化学元素C, Si, Mn, P, S, Cr, Mo, Ni, Nb, V, Ti, Cu含量分别为0.043%, 0.23%, 1.87%, 0.01%, 0.0028%, 0.025%, 0.27%, 0.23%, 0.06%, 0.006%, 0.017%, 0.13%. 采用数字图像相关(digital image correlation, DIC)方法获得X80管道钢的工程应力-应变曲线. DIC测试装置如图1所示,利用两台CCD (charge-coupled device)摄像机记录拉伸过程, 通过VIC-3D软件处理得到单轴拉伸试样在室温($T_{\rm r} = 23$℃)下的变形过程, 共进行了三组试验, 试样断裂时的应变分布和工程应力-应变曲线如图2(a)所示. 由此得到X80管道钢的弹性模量$E=206$ GPa, $R_{\rm eL}=594$ MPa, 抗拉强度$R_{\rm m}=713$ MPa.
图1
图1
(a) DIC装置 (b) X80管线钢拉伸试验散斑试样
Fig. 1
(a) The setup of digital image correlation (DIC) device, and (b) speckled specimen of X80 pipeline steel used in tensile test
图 2
图 2
(a)试样表面应变分布 (b) X80管道钢工程应力-应变曲线
Fig. 2
(a) Strain distribution on specimen surface and (b) engineering stress-strain curve of X80 pipeline steel
数值模拟所需X80管道钢材料塑性参数由真应力-应变得到. Hollomon公式可以用于描述大多数韧性材料的弹塑性本构关系[28]
式中, $R$为真应力, $K$为强度系数, $\varepsilon$为真应变, $n$为应变硬化指数. 材料真应力$R$与真应变$\varepsilon$可分别通过式(2)、式(3)计算得到
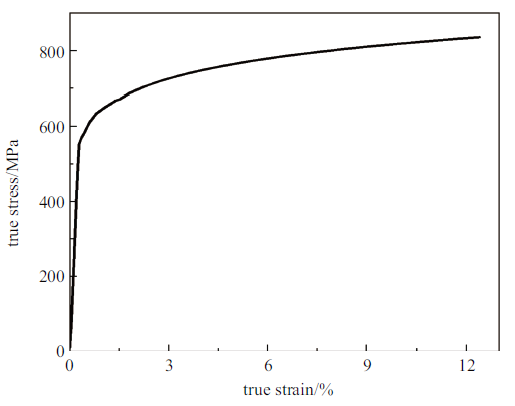
式中, $R_{\rm E}$为工程应力, $\varepsilon_{\rm E}$为工程应变. 得到如图3所示的材料真应力-应变曲线后, 将曲线处于屈服强度与抗拉强度之间的部分利用幂函数形式进行拟合, 得到Hollomon公式中的参数$K$与$n$.
图 3
此外对上述公式进行推导可得到工程应力与真应力应变之间的关系, 可表示为
由上述关系可知, 不同材料的抗拉强度可由其对应的Hollomon公式反推得到.
1.2 小冲杆试验
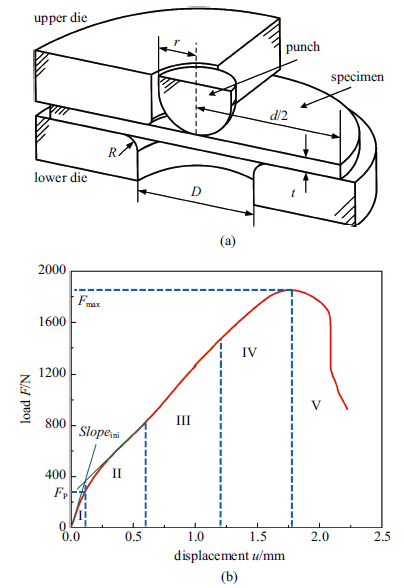
小冲杆装置如图4(a)所示, 冲杆头部为半球形, 半径$r=1.25$ mm, 下夹具孔径$D=4$ mm, 下夹具倒角半径$R=0.2$ mm, 试样厚度$t=0.500$ mm, 直径$d=10$ mm, 试样放于下夹具凹槽中, 并用上夹具压紧, 防止其在试验过程中出现滑动. 试验时冲杆向下施加载荷, 速率恒定为0.2 mm/min, 将试样中心下压直至试样发生断裂,记录整个试验过程试样所受载荷与冲头位移, 从而得到小冲杆试验载荷-位移曲线, 如图4(b)所示. 整条曲线可分为5部分: I. 弹性弯曲变形阶段; II. 弹塑性弯曲阶段;III. 塑性强化阶段; IV. 基于材料损伤的软化阶段; V. 裂纹生成直至试样断裂阶段[31-32]. 通过小冲杆试验载荷-位移曲线可得到表征材料弹塑性行为的相关参数,包括曲线第一阶段弹性段的初始斜率$slope_{\rm ini}$, 通过最小二乘法拟合第一、第二阶段得到的屈服载荷$F_{\rm P}$以及曲线最高点对应的最大载荷$F_{\max}$, 如图4(b)所示.
图 4
图 4
(a)小冲杆试验装置示意图和(b)小冲杆试验载荷-位移曲线
Fig. 4
(a) Schematic of the SPT device, and (b) load-displacement curve of SPT
式中, $t$为小冲杆试样初始厚度; $\alpha$, $\beta$, $\gamma_{1}$, $\gamma _{2}$为材料相关系数, 分别等于17.47, 0.36, 0.13, $-0.32$. 这些系数通过对不同材料试验结果进行回归分析而得到. 将从X80管道钢小冲杆试验结果获得的参数代入式(6) $\sim\!$式(8), 分别得到弹性模量$E=225$ GPa,屈服强度$R_{\rm eL}=473$ MPa, 抗拉强度$R_{\rm m}=983$ MPa, 与单轴拉伸试验结果相比, 误差分别为: 9.2%, 20.3%, 37.8%. 由此可发现,直接利用其他学者得到的经验公式获取X80管道钢材料力学性能参数, 与标准常规试验相比误差较大. 若要利用小冲杆试验较为准确地获取管道钢材料弹性模量、屈服强度、抗拉强度等力学性能参数,需对多种管道钢材料分别进行小冲杆试验与单轴拉伸试验, 拟合新的适用于管道钢的经验公式. 这样势必会进行重复研究, 不得不切取在役管道, 耗费大量的研究资源与成本, 并且总结的经验公式可能仅适用于管道钢材料. 基于以上原因, 亟待开发新的试验方法在保证管道完整性的情况下获取在役管道材料力学性能参数. 因此本研究采用人工智能BP神经网络结合小冲杆试验与数值模拟获取在役管道材料弹塑性力学性能参数.
2 BP神经网络
BP神经网络可对大量数据进行训练, 在两种不同因素之间建立合理、紧密的关联关系. 本文将小冲杆试验载荷-位移曲线作为输入集, 真应力-应变曲线作为输出集, 所采用的BP神经网络主要训练方案如图5所示.
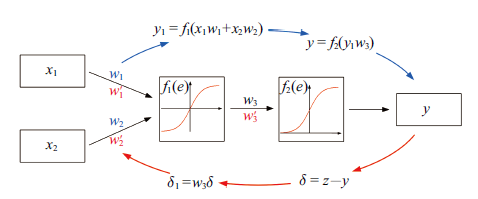
BP神经网络训练过程中, 需对输入数据进行计算, 不断减小误差, 如图6所示. 计算过程主要分为两部分: (1)首先设定目标误差值, 输入一组同种材料的小冲杆载荷-位移数据与真应力-应变数据, 第一层神经元接收小冲杆试验载荷-位移数据后, 通过本层对应的激活函数$f_{1}(e)$对其进行计算, 将计算结果$y_{1}$输出到第二层神经元. 输出集$y$由第二层神经元计算得到, 求出其与输入真应力-应变数据之间的误差$\delta $; (2)将计算得到的误差 $\delta $反馈回前两层神经元,通过式(9) $\sim\!$式(11)分别对每层神经元的权值进行修正, 并利用修正后的权值重复进行第(1)步运算, 直至误差小于预设的目标误差值
图 5
图 6
式中, $w_{1}$, $w_{2}$, $w_{3}$为第一次训练连接权值, ${w}'_1 $, ${w}'_2$, ${w}'_3 $为修正后的第二次训练权值, $\eta $为学习率, $f(e)$为激活函数, $\delta $为计算误差.
3 小冲杆试验有限元模拟与假想材料力学性能获取
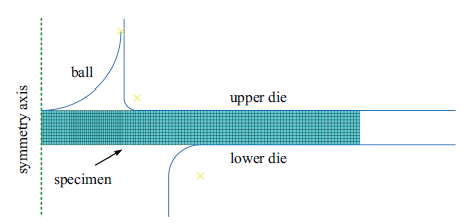
本研究采用有限元软件ABAQUS对小冲杆试验进行有限元模拟并获取大量假想材料的力学性能. 小冲杆试样为圆片状轴对称结构, 因此可直接简化为二维轴对称模型, 不考虑冲头、上夹具、下夹具的变形将其设为刚体, 上夹具与下夹具为固定约束, 控制冲头向下位移来对试件施加载荷. 建立试件与冲头、上夹具、下夹具之间的接触, 摩擦系数 $\mu =0.15$. 单元选择4节点二次缩减积分单元CAX4R, 厚度方向共划分10层网格, 如图7所示.
图 7
图 7
小冲杆试验轴对称有限元模型
Fig. 7
Axisymmetric finite element model of small punch test
3.1 材料参数
为了模拟小冲杆试验过程中试样的弹塑性变形、损伤与断裂行为, 有限元模型中导入了GTN连续损伤模型. 材料参数的定义分为两部分: (1)材料弹塑性参数定义; (2)材料损伤参数定义. 有限元模型中所需材料弹塑性参数包括弹性模量、泊松比与应力应变关系, 而这些参数可通过单轴拉伸试验得到.
GTN损伤模型的屈服函数可以表示为
式中, $f_{\rm c} $为孔洞开始发生聚合时的临界孔洞体积分数, $f_{\rm F} $为材料失效时的孔洞体积分数, 即应力承载能力为零时的极限孔洞体积分数, $f_{\rm F}^\ast =1/q_1 $. GTN模型中的孔洞体积分数包括两部分: (1)现有孔洞逐渐增长, 导致体积分数增大; (2)由于较大的塑性应变, 材料中产生新的孔洞. 因此, 如果考虑应变控制成核, 孔洞体积分数的增大可写为
现有孔隙率$\dot{{f}}_{\rm growth}$的增长由塑性应变控制, 而新孔洞的形核$\dot{{f}}_{\rm nucl} $取决于(1)孔洞形核时平均应变 $\varepsilon_{\rm n}$; (2)可形核孔洞的体积分数$f_{\rm N}$; (3)形核平均应变 $\varepsilon_{\rm n}$的标准差$S_{\rm N}$; (4)初始孔洞体积分数$f_{0}$. 式中$\varepsilon _{\rm m}^{\rm p} $与$\dot{{\varepsilon}}_{\rm m}^{\rm p} $分别为等效塑性应变及其变化率.
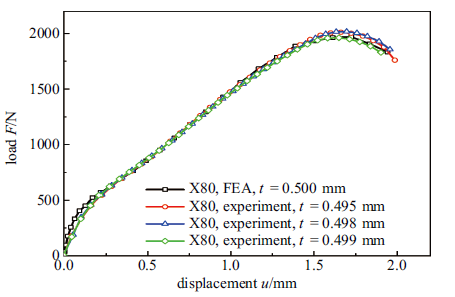
在小冲杆试验有限元模型中, X80管道钢材料的孔洞参数$f_{0}$, $f_{\rm N}$, $f_{\rm c} $, $f_{\rm F} $未知, 因此需确定这些参数的取值. 由于材料的微观损伤难以观测与测量[37],因此大多数学者通过多次调参试算, 将模拟得到的载荷-位移曲线与试验结果对比, 最佳匹配时所用参数作为此种材料的GTN损伤参数. 本文也使用此种方法确定材料损伤参数, 具体做法如下所述. 通过线切割从管道上切取直径10.0 mm、厚度0.600 mm的试片. 使用砂纸对切取的试片进行打磨, 去除试样表面过热和加工硬化影响区, 使试样中不含有任何裂纹和其他宏观缺陷. 为保证试验的准确性, 准备三组试验, 最终试样厚度$t$分别为0.495 mm, 0.498 mm和0.499 mm, 分别对其进行试验, 记录每个试样在整个试验过程中的载荷-位移数据, 得到三组小冲杆载荷-位移曲线. 对多组小冲杆试验有限元模型进行模拟, 保证其塑性参数不变, 只改变其GTN损伤参数, 将多个模拟结果与试验结果对比, 找到与试验结果匹配度最高的曲线, 如图8所示. 将此模型采用的GTN损伤参数作为X80管道钢材料的GTN损伤参数. 最终确定的GTN损伤参数为: $q_{1}$, $q_{2}$, $q_{3}$, $\varepsilon_{\rm N}$, $S_{\rm N}$, $f_{0}$, $f_{\rm N}$, $f_{\rm c}$, $f_{\rm F} $分别为1.5, 1, 2.25, 0.3, 0.1, 0.002 5, 0.000 8, 0.03, 0.15.
图 8
图 8
小冲杆试验结果与有限元模拟结果对比
Fig. 8
Comparisons between experimental and simulation results of small punch test
4 神经网络识别程序
4.1 数据库构建
采用上一节经过验证的有限元模型, 通过改变Hollomon公式中的$K$, $n$参数, 经过计算, 得到457种假想材料的真应力-应变曲线和小冲杆载荷-位移曲线. 将这些数据作为训练神经网络的数据库. BP神经网络训练集包括两部分: 小冲杆载荷-位移曲线作为输入集, 同种材料真应力-应变曲线作为输出集.其中真应力-应变曲线可以通过系统地改变Hollomon公式中的参数$K$与$n$得到. 若要得到较为准确的训练结果, 需保证训练集数据的准确性与全面性, 因此数据库应包含大部分常见金属材料真应力-应变曲线. 大多数金属材料的应变硬化指数$n$取值范围为[0.005, 0.6], 强度系数$K$的取值范围为[200, 2000][38]. 但由于$K$值较小时, 随着$n$值的减小, 真应变为0.002时对应的真应力即材料屈服强度变得极小, 此时材料屈强比变得极小, 而此类金属极为少见, 因此为提高神经网络训练的结果, 不考虑这类真应力-应变曲线. 最终确定的$K$与$n$参数取值范围如表1所示.
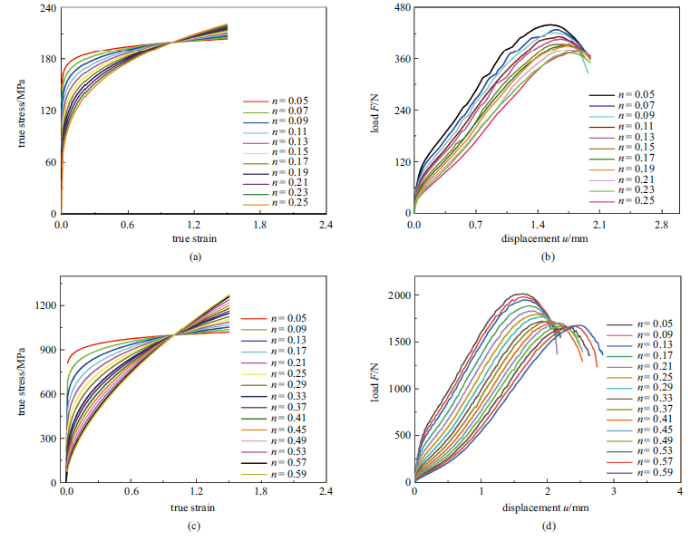
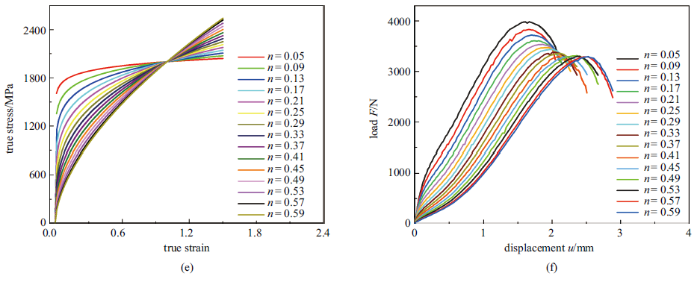
每改变一次参数$K$与$n$便可得到一条新的真应力-应变曲线, 将得到的每条真应力-应变曲线依次代入小冲杆试验有限元模型, 进行计算得到完整的载荷-位移曲线. 取小冲杆载荷-位移曲线下降段最终载荷大小为最大载荷的80%, 部分数据如图9所示. 建立数据库的过程中并未考虑材料GTN参数的变化, 因为根据已有文献, 不同管道钢微观组织与缺陷的分布基本一致, 故本研究中假设有限元模型中所有假想材料的GTN参数一致.
在训练BP神经网络时, 输入、输出数据只能分别为一个列矩阵. 小冲杆试验获得的材料载荷-位移曲线与真应力-应变曲线为独立的两组数据, 每组数据分别包含横坐标(试样中心点位移与真应变)与纵坐标(载荷与真应力). 因此需要将每组数据包含的横坐标与纵坐标转化为一个列矩阵. 具体转化方式如表2所示. 其中, 小冲杆试验载荷($X_{i, j}$, $Y_{i, j})$来表示, 真应力-应变曲线用($A_{m, n}$, $B_{m, n})$来表示, 每条载荷-位移曲线取120组坐标, 真应力-应变曲线取50组坐标, 下标$i$, $m$为输入数据点序号, $j$, $n$为输入训练集序号. 由此, 可以把($X_{1}$, $Y_{1})$, ($X_{2}$, $Y_{2})$, $\cdots$, ($X_{120}$,$Y_{120})$形式排列的小冲杆试验载荷-位移曲线坐标转化为[$X_{1}$, $X_{2}$, $\cdots$, $X_{120}$, $Y_{1}$, $Y_{2}$, $\cdots$, $Y_{120}$]形式的列矩阵,材料真应力-应变曲线转化方式与小冲杆试验载荷-位移曲线转化方式相同.全部457组假想材料的BP神经网络训练集数据库结构如表2所示.
图 9
图 9
BP神经网络训练集数据, 不同参数$n$对应的真应力-应变曲线: (a) $K$ = 200, (c) $K$ = 1000, (e) $K$ = 2000和不同参数$n$对应的小冲杆试验载荷-位移曲线(b) $K$ = 200, (d) $K$ = 1000, (f) $K$ = 2000
Fig. 9
BP neural network training set data: the true stress-strain curves corresponding to different parameters $n $(a) $K$ = 200, (c) $K$ = 1000, (e) $K$ = 2000, and the load-displacement curves of SPT corresponding to different parameters $n$ (b) $K$ = 200, (d) $K$ = 1000, (f) $K$ = 2000
图 9
图 9
BP神经网络训练集数据, 不同参数$n$对应的真应力-应变曲线: (a) $K$ = 200, (c) $K$ = 1000, (e) $K$ = 2000和不同参数$n$对应的小冲杆试验载荷-位移曲线(b) $K$ = 200, (d) $K$ = 1000, (f) $K$ = 2000 (续)
Fig. 9
BP neural network training set data: the true stress-strain curves corresponding to different parameters $n $(a) $K$ = 200, (c) $K$ = 1000, (e) $K$ = 2000, and the load-displacement curves of SPT corresponding to different parameters $n$ (b) $K$ = 200, (d) $K$ = 1000, (f) $K$ = 2000 (continued)
4.2 BP神经网络计算结果
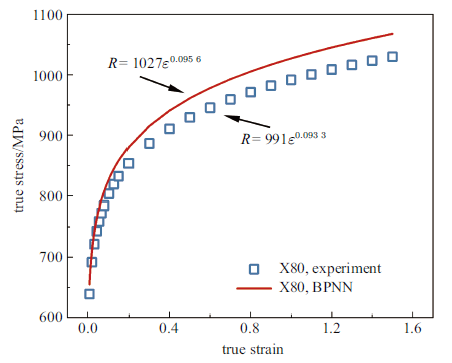
将转化完成的训练集数据输入BP神经网络进行训练, 当误差小于预设误差$1.0\times10^{-5}$时, 训练完成. 将小冲杆试验得到的X80管道钢载荷-位移曲线输入训练好的BP神经网络便得到相应的真应力-应变曲线. 该结果与单轴拉伸试验结果进行对比, 如图10所示. 通过对比发现, BP神经网络计算的结果与单轴拉伸试验所得材料真应力-应变曲线误差最大为3.7%, 最小为2.5%.
图 10
图 10
BP神经网络与单轴拉伸试验得到的X80管道钢真应力-应变曲线对比
Fig. 10
Comparison of true stress-strain curves of X80 pipeline steel obtained between BP neural network and uniaxial tensile tests
图 11
图 11
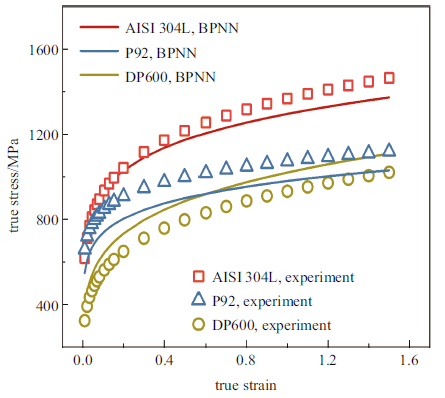
BP神经网络与单轴拉伸试验得到的文献中材料的真应力-应变曲线对比
Fig. 11
Comparison of true stress-strain curves of materials in reference obtained between BP neural network and uniaxial tensile tests
表 3 BP神经网络得到的材料力学性能参数
Table 3
 |
从上表数据可以看出, 由BP神经网络计算得到X80管道钢材料与其他常见金属材料的弹塑性力学性能参数与单轴拉伸试验结果相比, 最大误差为9.3%, 远小于利用常规经验关联法计算结果的误差37.8%. 并且, 也说明本文提出的BP神经网络关联方法不仅适用于管道钢材料, 也适用于其他常见金属材料. 只需将小冲杆试验得到材料的载荷-位移曲线输入训练好的BP神经网络, 经过计算, 便可获得材料真应力-应变曲线, 进而得到相应材料的弹塑性力学性能参数.
5 结论
本研究提出了一种利用小冲杆试验、有限元模拟与BP神经网络相结合, 准确获得材料真应力-应变曲线, 从而获得材料完整弹塑性力学性能的方法. 通过由试验验证的含GTN损伤参数的小冲杆试验有限元模型得到457组小冲杆试验载荷-位移曲线, 结合其相对应的真应力-应变曲线对BP神经网络进行训练, 在两者之间建立关联关系. 通过对比X80管道钢小冲杆试验与单轴拉伸试验结果以及现有文献中不同材料的试验数据, 验证该方法的准确性与广泛适用性, 得到以下结论:
(1)含有GTN损伤参数的小冲杆试验有限元模型得到的载荷-位移曲线与试验结果具有很高的吻合度, 可代替试验获取BP神经网络训练集数据.
(2)将X80管道钢小冲杆试验载荷-位移曲线代入BP神经网络计算得到其真应力-应变曲线, 进而得到屈服强度$R_{\rm eL_BPNN}= 567$ MPa, 抗拉强度$R_{\rm m_BPNN}= 746$ MPa,与单轴拉伸试验结果相比误差分别为-6.6%与4.6%, 证明BP神经网络结合小冲杆试验可以较准确地得到管道钢材料弹塑性力学性能.
(3)利用BP神经网络对文献中已有材料试验数据进行计算, 对比文献中单轴拉伸试验结果, 最大误差为9.3%, 低于常规经验关联法误差. 表明本文提出的方法广泛适用于在役管道钢以及多种金属材料真应力-应变曲线的获取.
参考文献
准静态条件下金属材料的临界断裂准则研究
The critical strength criterion of metal materials under quasi-static loading
The development of a miniaturized disk bend test for the determination of postirradiation mechanical properties
Small punch test evaluation methods for material characterisation
小冲杆试验摩擦力计算及抗拉强度公式改进
Calculation of frictional force and improvement of tensile strength formula for small punch test
金属材料的强度与应力-应变关系的球压入测试方法
Spherical indentation method to determine stress-strain relations and tensile strength of metallic materials
Determining tensile yield stresses from Small Punch tests: A numerical-based scheme
小冲杆试验技术研究现状与展望
Research status and prospects for small punch testing technique
Development of a further-miniaturized specimen of 3 mm diameter for tem disk ($\varPhi$3 mm) small punch tests
Improved correlation for elastic modulus prediction of metallic materials in the small punch test
A new method based on energy principle to predict uniaxial stress--strain relations of ductile materials by small punch testing
Small punch test evaluation of intergranular embrittlement of an alloy steel
Determination of fracture toughness from the small punch test using circular notched specimens
Small-punch and TEM-disc testing techniques and their application to characterization of radiation damage
Small punch tests on austenitic and martensitic steels irradiated in a spallation environment with 530 MeV protons
Small punch testing for assessing the fracture properties of the reactor vessel steel with different thicknesses
Mechanical properties characterization of heat-affected zone using the small punch test
Determination of fracture toughness and tensile properties of structural steels by small punch test and micro-tensile test
Mechanical behaviour and strain rate sensitivity analysis of TA2 by the small punch test
Developments in the estimation of tensile strength by small punch testing
Estimation of the mechanical properties of metallic materials by means of the small punch test
Evaluation of the ductile-brittle transition temperature of anisotropic materials by small punch test with un-notched and U-notched specimens
不同缺口形式小冲杆试样测试3Cr1MoV钢韧脆转变温度的对比
Comparison of ductile-brittle transition temperature testing of 3Cr1MoV steel with small punch specimens of different notch forms
基于Beremin模型的小冲杆试验技术估算Weibull参数的试样选取
Choice of specimen types and calculation of Weibull parameters of small punch test based on Beremin model
Determination of deformation and failure properties of ductile materials by means of the small punch test and neural networks
Prediction and sensitivity analysis of long-term skid resistance of epoxy asphalt mixture based on GA-BP neural network
A cellular automata traffic flow model combined with a BP neural network based microscopic lane changing decision model
The significance of specimen displacement definition on the mechanical properties derived from Small Punch Test
The effect of heat treatment and carbon content on the work hardening characteristics of several steels
Determination of tensile properties by instrumented indentation technique: Representative stress and strain approach
A strain-dependent ductile damage model and its application in the derivation of fracture toughness by micro-indentation
小冲杆试验方法标准化研究 (二)―材料室温拉伸性能的确定
Study on standardization of small punch test (2)-Tensile properties at room temperature
Development of an improved prediction method for the yield strength of steel alloys in the small punch test
Effect of confinement level on mechanical behaviour using the small punch test
Evaluation of damage in materials due to fatigue cycling through static and cyclic small punch testing//Small Specimen Test Techniques. 6th Volume
Influence of voids on shear band instabilities under plane strain conditions
基于M积分的脆性材料微缺陷等效损伤面积/体积表征
Lü junnan, Li qun. The calibration of microdefects induced equivalent damage area/volume of brittle materials by using the M-integral
GTN模型参数标定方法与应用
Parameters calibration and application of the GTN model
真应力-应变的定义及其力学特征
Definition and mechanical characteristics of true stress-strain
Plastic deformation and fracture behavior of X65 pipeline steel: Experiments and modeling
Effect of simulated welding thermal cycle on microstructure and mechanical properties of X90 pipeline steel
Investigation of local tensile strength and ductility properties of an X100 submerged arc seam weld