引言
海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用.
上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用.
在本文中,基于文献[2 ] 的研究成果及结合文献[23 ,24 ,25 ] 的分析方法,考虑均匀流对毛细重力波的调制作用.在第一节,将使用多重尺度法推导被均匀流调制的二维毛细重力波振幅在有限水深中所满足的NLSE.在第二节,通过使用NLSE,分析被均匀流调制的毛细重力波的不稳定性.第三节是本文的主要结论.由于毛细重力波与流的相互作用可以有效地改变海表粗糙度和海洋上层流场结构,所以这对海面风场、海表压强、海气通量交换等有重要意义.另外,了解海表面的这些短波动力机制,对卫星遥感的精确测量和海气耦合模式的改进等也有重要意义.
1 方程的推导
1.1 控制方程与边界条件
假设流体运动是无黏的、不可压的和无旋的.如图1 所示,考虑均匀流作用下二维毛细重力水波在有限水深中的传播,坐标原点$o$位于静止水面处,$x$方向是水波的传播方向,$y$方向垂直向上与重力方向相反,$z$垂直纸面向外.这里,把与波动方向一致的均匀流称为顺流,反之称为逆流.故二维水波基本方程组[39 -42 ] 可表述为
(1) $ \Delta \phi = 0 , \ \ - h < y < \zeta$
(2) $ \zeta _t + (U + \phi _x )\zeta _x = \phi _y , \ \ y = \zeta$
(3) $ \phi _t + g\zeta + \dfrac{1}{2}(\phi _x^2 + \phi _y^2 ) + U\phi _x = \dfrac{a}{\rho }\dfrac{\zeta _{xx} }{(1 + \zeta _x^2 )^{3/2}} , \ \ y = \zeta$
(4) $ \phi _y = 0 , \ \ y = - h$
图1
图1
二维毛细重力水波在均匀流作用下的传播.$\zeta (x,t)$是自由面波动,$c$是波速度
Fig. 1
Schematic of the Eulerian framework for two-dimensional propagating capillary-gravity waves with a uniform flow. $\zeta (x, t)$ is the free surface elevation and $c$ is the wave velocity
其中, $\phi $是速度势函数,$U $是均匀流为常数,$h $为流体的深度, $\zeta $为自由 面起伏,$g$是重力加速度,$a $为流体表面张力系数, $\rho $为流体的密度,$\Delta$为二维Laplace算子.其中下标表示对相应变量求导.式 (2)是自由面上的运动学边界条件,式 (3)是自由面上的动力学边界条件,式 (4)是底边界条件.
1.2 非线性Schrödinger方程
(5) $ \eta = \varepsilon (x - c_{\rm g} t) , \ \ \tau = \varepsilon ^2t$
其中,波陡$\varepsilon = kA $是度量非线性程度的小参数,$k $是载波波数,$A $是振幅,$c_{\rm g }$是群速 度.把式 (5)代入式 (1)~式 (4)中,得到新的方程组
(6) $ \phi _{xx} + 2\varepsilon \phi _{x\eta } + \varepsilon ^2\phi _{\eta \eta } + \phi _{yy} = 0 ,\quad - h < y < \zeta$
(7) $ (U + \phi _x + \varepsilon \phi _\eta )(\zeta _x + \varepsilon \zeta _\eta ) - \phi _y + \\ \zeta _t - \varepsilon c_g \zeta _\eta + \varepsilon ^2\zeta _\tau = 0 ,\quad y = \zeta$
(8) $ \phi _t - \varepsilon c_g \phi _\eta + \varepsilon ^2\phi _\tau + g\zeta + U(\phi _x + \varepsilon \phi _\eta ) - \\ \left( {a /\rho } \right)(\zeta _{xx} + 2\varepsilon \zeta _{x\eta } + \varepsilon ^2\zeta _{\eta \eta } - {3\zeta _{xx} \zeta _x^2 } /2) + \\ {(\phi _x^2 + 2\varepsilon \phi _x \phi _\eta + \varepsilon ^2\phi _\eta ^2 + \phi _y^2 )}/ 2 = 0 ,\quad y = \zeta$
其中式 (4)没有变化.对$\phi $在$y = 0$附近按$\zeta $幂次Taylor展开,进行线性化处理上 边界条件 (7)和 (8).假设方程组 (4),$ (6)\sim$(8)有如下的渐近解
(9) $ \left. \phi = \sum_{n = - \infty }^{ + \infty } {\phi _n } \exp \left[ {{\rm i} n\left( {kx - \omega t} \right)} \right] \\ \zeta = \sum_{n = - \infty }^{ + \infty } {\zeta _n } \exp \left[ {{\rm i}n\left( {kx - \omega t} \right)} \right] \right\}$
其中, $\omega $是角频率,$n $是谐波数, $\phi_{ - n }$和$\zeta_{ - n }$分别表示$\phi_{n}$和$\zeta_{n }$的共轭.然后把$\phi_{n }$和$\zeta_{n }$关于$\varepsilon $小级数展开
(10) $ \phi _n = \sum_{j = n}^{ + \infty } {\varepsilon ^j\phi _{nj} (\eta ,y,\tau )} , \ \ \zeta _n = \sum_{j = n}^{ + \infty } {\varepsilon ^j\zeta _{nj} (\eta ,\tau )}$
这里$j $是阶数,假设$\phi_{00 }= \zeta_{00} =0$.将式 (9)和式 (10)代入式 (4),式$ (6)\sim$式 (8)中,得到了前三阶摄动问题的方程组.
(1) $\varepsilon e^{1}$ (表示一阶一次谐波项):确定了频散关系
(11) $ \omega ^2\left( {1 - \bar {u}} \right)^2 = gk\sigma (1 + N)$
其中,$\bar {u}= U/c $是无量纲均匀流,$c = \omega /k $是波速 度, $\sigma = {\rm tanh} (kh)$,$N=ak^{2}/\rho g $代表了无量纲表面张力.同时得到了速度势和自由面起伏表达式
(12) $ \phi _{11} = A\dfrac{\cosh \left[ {k\left( {y + h} \right)} \right]}{\cosh \left( {kh} \right)} , \ \ \zeta _{11} = \dfrac{{\rm i}\omega \left( {1 - \bar {u}} \right)}{ g(1 + N )}A$
(2) $\varepsilon^{2}e^{1}$:确立了行波的群速度
(13) $ c_{\rm g} = \dfrac{\partial \omega }{\partial k} = \dfrac{c}{2\sigma }\left[ {\mu \left( {1 - \sigma ^2} \right) + \sigma \dfrac{1 + 3N}{1 + N}} \right]\left( {1 - \bar {u}} \right) + c\bar {u}$
其中, $\mu = kh $是划分浅水和深水的无量纲参量,一般认为$\mu >\pi $属于深水, $\mu <0.1\pi $是浅水,介于二者之间是有限水深.同时$\zeta _{01} =0$
(14) $ \phi _{12} = \dfrac{1}{\cosh \left( {kh} \right)}\Bigg \{ D\cosh \left[ {k\left( {y + h} \right)} \right] + \\ {\rm i} A_\eta h\sigma \cosh \left[ {k\left( {y + h} \right)} \right] - \\ {\rm i}A_\eta \left( {y + h} \right)\sinh \left[ {k\left( {y + h} \right)} \right] \Bigg \}$
(15) $ \zeta _{12} = \dfrac{1}{g\left( {1 + N} \right)}\left[ {c_g - c\bar {u} -\dfrac{2Nc}{1 + N}\left( {1 - \bar {u}} \right)} \right]A_\eta + \\ \dfrac{{\rm i}\omega \left( {1 - \bar {u}} \right)}{g\left( {1 + N} \right)}D$
(3) $\varepsilon^{2}e^{2}$:获得了$\phi_{22}$ 及 $\zeta_{22}$ 的表达式
(16) $ \phi _{22} = F\dfrac{\cosh \left[ {2k\left( {y + h} \right)} \right]}{\cosh \left( {2kh} \right)}$
(17) $ F = \dfrac{3{\rm i}k^2\left( {1 + \sigma ^2} \right)}{4\omega (1 - \bar {u})}\dfrac{1 - \sigma ^2 + \left( {3 - \sigma ^2} \right)N}{\sigma ^2 - (3 - \sigma ^2)N}A^2$
(18) $ \zeta _{22} = - \dfrac{k^2}{2g}\dfrac{3 - \sigma ^2}{\sigma ^2 - (3 - \sigma ^2)N}A^2$
(4) $\varepsilon ^{3}e^{0}$:得到一个由短波调制产生的平均流动势$\phi_{10 }$的长波方程
(19) $ \left[ {\left( {c_{\rm g} - U} \right)^2 - gh} \right] \phi _{01\eta } = \\ \qquad \left[ {\dfrac{2k\omega (1 - \bar {u})}{1 + N} + k^2\left( {1 - \sigma ^2} \right)\left( {c_{\rm g} - U} \right)} \right]\left| A \right|^2$
它描述以波速$U \pm (gh)^{1/2 }$向左右传播的长波所伴随的参数变化.同时
(20) $ g\zeta _{02} = \left( {c_{\rm g} - U} \right)\phi _{01\eta } - k^2\left( {1 - \sigma ^2} \right) \left| A \right|^2$
(5) \ $\varepsilon^{3}e^{1}$:经过繁琐的计算,由于频散关系,$B$和$D_{\eta }$被消除了,最终得到了描述波形包络演化的NLSE
(21) $ {\rm i}\dfrac{\partial A}{\partial \tau } + \alpha \dfrac{\partial ^2A}{\partial \eta ^2} = \beta \left| A \right|^2A$
$$ \alpha = \dfrac{\omega }{2k^2\sigma }\left\{ \dfrac{N}{1 + N}\left[ {3\sigma + 2\mu \left( {1 - \sigma ^2} \right)} \right]\left( {1 - \bar {u}} \right) + \\ {\mu \left( {1 - \sigma ^2} \right)\left( {1 - \mu \sigma } \right)\left( {1 - \bar {u}} \right) - \sigma \left( {\bar {c}_{\rm g} - \bar {u}} \right)^2\left( {1 - \bar {u}} \right)^{ - 1}} \right\} \\ \beta = \dfrac{k^4}{4\omega (1 - \bar {u})}\left\{ - 2\left( {1 + N} \right)\left( {1 - \sigma ^2} \right)^2 + \left( {8 - \dfrac{3N}{1 + N}} \right)\sigma ^2 + \\ \dfrac{(\sigma ^4 - 10\sigma ^2 + 9) + N(\sigma ^4 - 10\sigma ^2 + 21)}{\sigma ^2 - (3 - \sigma ^2)N} + \\ 2\left[ {\sigma \left( {1 + N} \right)\left( {1 - \sigma ^2} \right)\left( {\bar {c}_{\rm g} - \bar {u}} \right) + 2\sigma \left( {1 - \bar {u}} \right)} \right] \cdot \\ \dfrac{2\left( {1 - \bar {u}} \right) + \left( {\bar {c}_{\rm g} - \bar {u}} \right)\left( {1 - \sigma ^2} \right)\left( {1 + N} \right)}{\sigma \left( {\bar {c}_{\rm g} - \bar {u}} \right)^2\left( {1 + N} \right) - \mu \left( {1 - \bar {u}} \right)^2} \right\} $$
其中,$\bar c_{\rm g}=c_{\rm g}/c$是无量纲群速度, $\alpha $和$\beta $分别是频散系数和非线性系数,它们与 ($\bar u, N, \mu $)有关.若$\bar u= 0$,上述结果和文献[2 ] 给出的结果一致.通过观察$\beta $中各项,发现有两处奇异需要避免,一处是
(22) $ \sigma ^2 - (3 - \sigma ^2)N = 0$
它说明在$N = \sigma^{2}/(3-\sigma^{2})$处毛细重力波发生分叉,是一种Wilton涟漪现象,在深水情形下, $\sigma =1$, $N =1/2$.另一处是
(23) $ \sigma \left( {\bar {c}_{\rm g} - \bar {u}} \right)^2\left( {1 + N} \right) - \mu \left( {1 - \bar {u}} \right)^2 = 0$
(24) $ (c_{\rm g} - U)^2 = gh$
它反映了长重力波与短毛细重力波发生共振,此时短波的群速度与长波的相速度相一致.同样地可以得到 自由面$\zeta $的振幅$a$所满足的方程
(25) $ \zeta = \dfrac{1}{2}(\varepsilon a {\rm e}^{{\rm i}(kx - \omega t)} + c.c) + O(\varepsilon ^2)$
(26) $ {\rm i}\dfrac{\partial a}{\partial \tau } + \alpha \dfrac{\partial ^2a}{\partial \eta ^2} = \gamma \left| a \right|^2a , \quad \gamma = \dfrac{\omega ^2(1 - \overline u )^2}{4k^2\sigma ^2}\beta$
同时有必要考虑在深水情形下NLSE系数的变化,即$\mu \to \infty $时
(27) $ {\rm i}\dfrac{\partial a}{\partial \tau } + \dfrac{\omega }{8k^2}\left( {1 - \bar {u}} \right)\dfrac{3N^2 + 6N - 1}{\left( {1 + N} \right)^2}\dfrac{\partial ^2a}{\partial \eta ^2} =\\ \qquad \dfrac{k^2\omega }{16}\left( {1 - \bar {u}} \right)\dfrac{2N^2 + N + 8}{\left( {1 + N} \right)\left( {1 - 2N} \right)}\left| a \right|^2a$
2 稳定性分析
(28) $ a(\tau ) = a_0 \exp \left( { - {\rm i}\gamma a_0^2 \tau } \right)$
其中$a_{0 }$是初始振幅,考虑在振幅和相位上有小扰动的解
(29) $ a(\tau ) = a_0 \left( {1 + \delta _a } \right)\exp \left[ {{\rm i}\left( {\delta _p - \gamma a_0^2 \tau } \right)} \right]$
将上式代入式 (26)中,线性化Stokes波解,有
(30) $ {\rm i}\dfrac{\partial \delta _a }{\partial \tau } - \dfrac{\partial \delta _p }{\partial \tau } + \alpha \dfrac{\partial ^2\delta _a }{\partial \eta ^2} + {\rm i}\alpha \dfrac{\partial ^2\delta _p }{\partial \eta ^2} - 2\gamma a_0^2 \delta _a = 0$
分开上述方程实部和虚部,产生一个关于小扰动的常系数线性方程组
(31) $ \begin{eqnarray}\left. \begin{array}{l}\dfrac{\partial \delta _a }{\partial \tau } + \alpha \dfrac{\partial ^2\delta _p }{\partial \eta ^2} = 0 \\ - \dfrac{\partial \delta _p }{\partial \tau } + \alpha \dfrac{\partial ^2\delta _a }{\partial \eta ^2} - 2\gamma a_0^2 \delta _a = 0 \end{array}\!\!\right\}\end{eqnarray}$
(32) $ \begin{eqnarray}\left. \begin{array}{l}\delta _a (\eta ,\tau ) = \delta _{a_0 } \exp \left[ {{\rm i}\left( {L\eta - \varGamma \tau } \right)} \right]\\ \delta _p (\eta ,\tau ) = \delta _{p_0 } \exp \left[ { {\rm i}\left( {L\eta - \varGamma \tau } \right)} \right] \end{array}\!\!\right\}\end{eqnarray}$
其中,$L $和$\varGamma $分别是扰动波数和扰动角频率,将式 (32)代入方程组 (31)中,式 (31)有非零解的充要条件是
(33) $ \varGamma ^2 = \alpha L^2\left( {\alpha L^2 + 2\gamma a_0^2 } \right)$
显然,当$\alpha (\alpha L^{2}+2\gamma a_{0}^{2}) \geqslant 0 $时,$\varGamma $ 有实解,扰动是有界的且Stokes波解是稳定的,相反,当$\alpha (\alpha L^{2}+2\gamma a_{0}^{2}) <0 $时,解 是不稳定的.又因为$L$是个小量,所以上述分析暗含着当$\alpha \gamma \geqslant 0 $时,Stokes波解 是稳定的,当$\alpha \gamma <0 $时,Stokes波解是不稳定的[43 ] .故不稳定增长率是
(34) $ \varGamma _i = L\sqrt { - 2\alpha \gamma a_0^2 - \alpha ^2L^2}$
(35) $ \alpha = \bar {\alpha }\dfrac{\omega }{k^2} , \ \ \gamma = \bar {\gamma }\omega k^2 , \ \ L = \bar {L}a_0 k^2 , \ \ \varGamma _{\rm i} = \bar {\varGamma }_{\rm i} \omega a_0^2 k^2$
顶标横杠表示它们都是无量纲的,均与 ($\bar u, N, \mu $)有关.故无量纲不稳定增长率是
(36) $ \bar {\varGamma }_{\rm i} = \bar {L}\sqrt { - 2\bar {\alpha }\bar {\gamma } - \bar {\alpha }^2\bar {L}^2}$
(37) $ \bar {\varGamma }_{\rm i\max } = \sqrt { - \dfrac{\bar {\gamma }}{\bar {\alpha }}} \sqrt { - \bar {\alpha }\bar {\gamma }} = \left| \bar {\gamma } \right|$
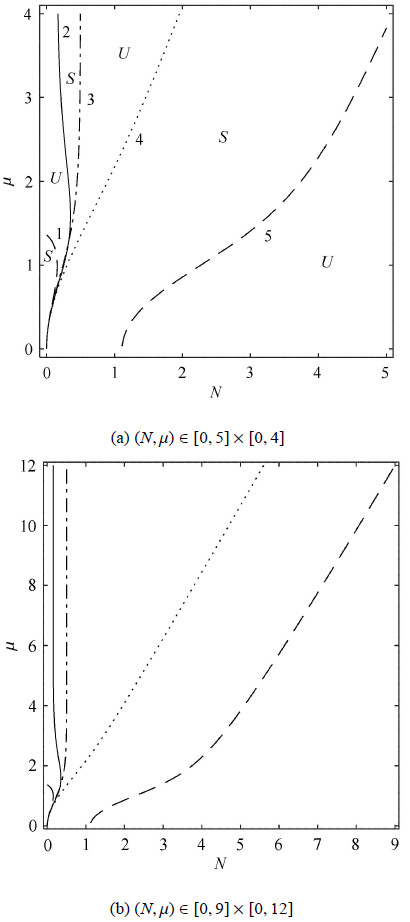
如图2 (a)所示,5条曲线将 ($N, \mu $)平面划分为6个区域,其中"S''表示Stokes波解是调制稳定的, 而"U''表示Stokes波解是调制不稳定的,但是均匀流不影响这个区域的划分.曲线1和曲线5表示非线性系数$\bar \gamma=0$,曲线1与$\mu $轴的交点为熟悉的$\mu =1.363$,表示在不考虑表面张力时,$\mu <1.363$,重力波是稳定的;$\mu >1.363$,它是不稳定的.曲线2表示耗散系数$\bar \alpha=0$,即相速度达到最小值且和群速度相一致.曲线3和4是$\bar\gamma$的奇异处,分别表示毛细重力波分 叉及长波和短波共振.由式 (27)知,曲线2和3的渐近线分别是$N=2/3^{1 / 2 }-1$,$N=1/2$,如图2 (b)所示,它们之间毛细重力波是稳定的;长短波共振曲线4有渐近线
(38) $ \mu = \dfrac{9}{4}N - \dfrac{3}{4}, \ \ \mu \gg 1$
图2
图2
Stokes毛细重力波稳定区域划分
Fig. 2
Stability diagram for Stokes capillary-gravity waves
(39) $ \mu = \dfrac{9}{4}N - \dfrac{35}{4}, \ \ \mu \gg 1$
值得注意的是,毛细重力波在曲线4和5渐近线之间是稳定的,但当$\mu \gg 1 $时,即深水时,它们在$\mu $轴上的截断3/4和35/4可以被忽略,这两条边界线重合在一起 (斜率相同),它们之间稳定区域消失,这也解释了长短 波共振在深水中消失的原因[2 ,25 ] .
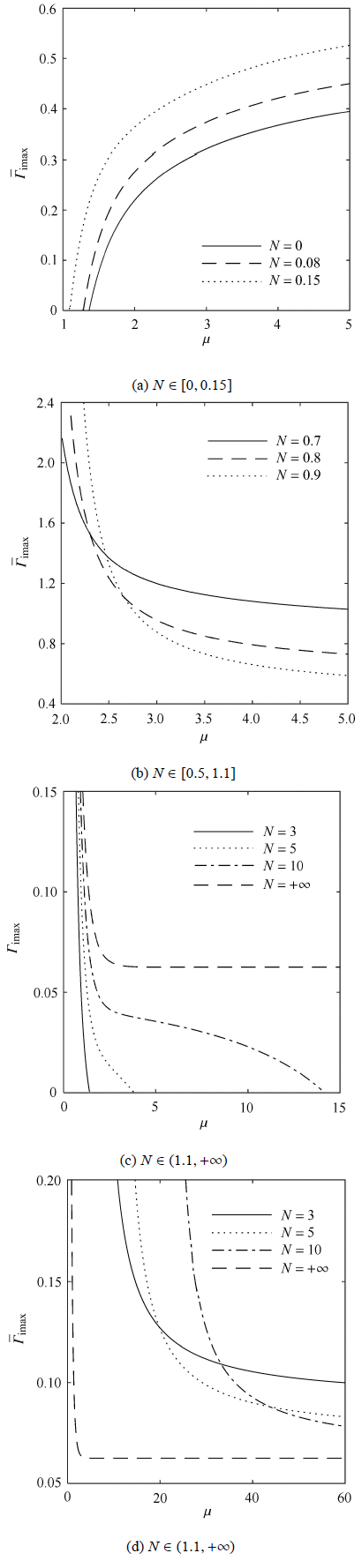
2.1 不稳定最大增长率
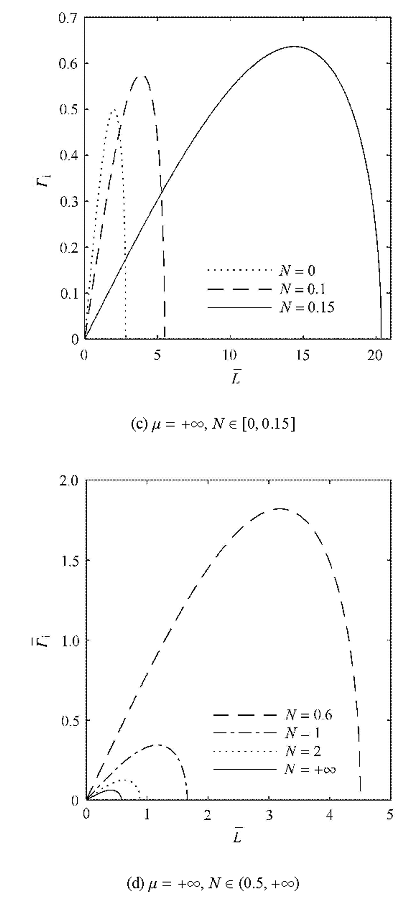
如图3 所示,知$N $大致上被划分为4个部分: [0,0.15], (0.15,0.5), [0.5,1.1], $(1.1,+\infty )$, 其中 (0.15,0.5) 是稳定区域.我们来分析不稳定最大增长率随水深的变化趋势.如图3 (a)所示,$N\!=\!0$ 时,实线与$\mu $轴的交点为$\mu\!=\!1.363$,随着$N $增大,交点$\mu $值变小,体现了调制不稳定的重新稳定;且$\bar\varGamma _{{\rm i}\max }$随着$\mu $变大而变大,逐渐趋于一个常值, $\bar\varGamma _{{\rm i}\max }$亦随着$N $增大 而增大.但 在$N \in [0.5,1.1] $中,如图3 (b)所示,$\bar\varGamma _{{\rm i}\max }$随着$\mu $变大而变小,且$N $越大下降的趋势越快,在深水时达到常值.曲线4及曲线5将$N \in (1.1,+ \infty )$不稳定区域隔开,所以$\bar\varGamma _{{\rm i}\max }$随$\mu $ 变化被分为两部分,如图3 (c)、图3 (d)所示,在$\mu $前半段,$\bar\varGamma _{{\rm i}\max }$随$\mu $增大而逐渐减小到0,随$N $增大,每条曲线向右边的$N=+\infty $靠近;在$\mu $后半段,$\bar\varGamma _{{\rm i}\max }$亦随 $\mu $增大而减小,但趋于一个常值,且随着$N $增大,曲线向右移动,远离 $N=+\infty $.
图3
图3
$\bar u= 0$时,无量纲最大增长率$\bar\varGamma _{\rm i \max }$随水深$\mu $的变化
Fig. 3
Dimensionless maximum growth rate $\bar\varGamma _{\rm i \max }$ as a function of dimensionless water depth $\mu $ for $\bar u= 0$}
如图4 (a)所示,在$N $前半段,$\bar\varGamma _{{\rm i}\max }$随$N $增大先减小后增大,且随着水深增大,$\bar\varGamma _{{\rm i}\max }$变化范围变大,逐渐向右偏移;但在$N $后半段,如 图4 (b)所示,$\bar\varGamma _{{\rm i}\max }$随$N $增大而增大,随水深增大而减小且向右偏移.
图4
图4
$\bar u= 0$时,无量纲最大增长率$\bar\varGamma _{\rm i \max }$随$N $的变化
Fig. 4
Dimensionless maximum growth rate $\bar\varGamma _{\rm i \max }$ as a function of $N $ for $\bar u= 0$ at different $\mu $
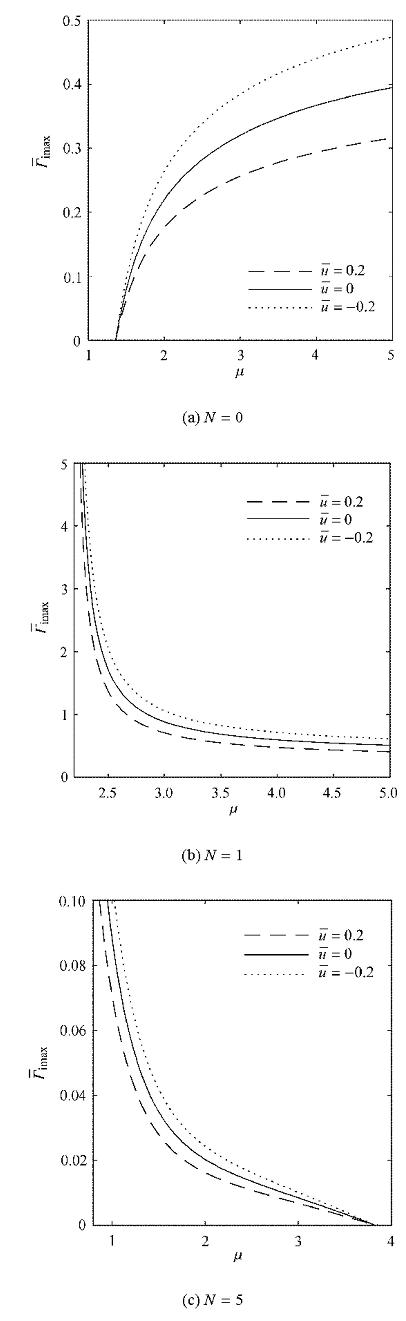
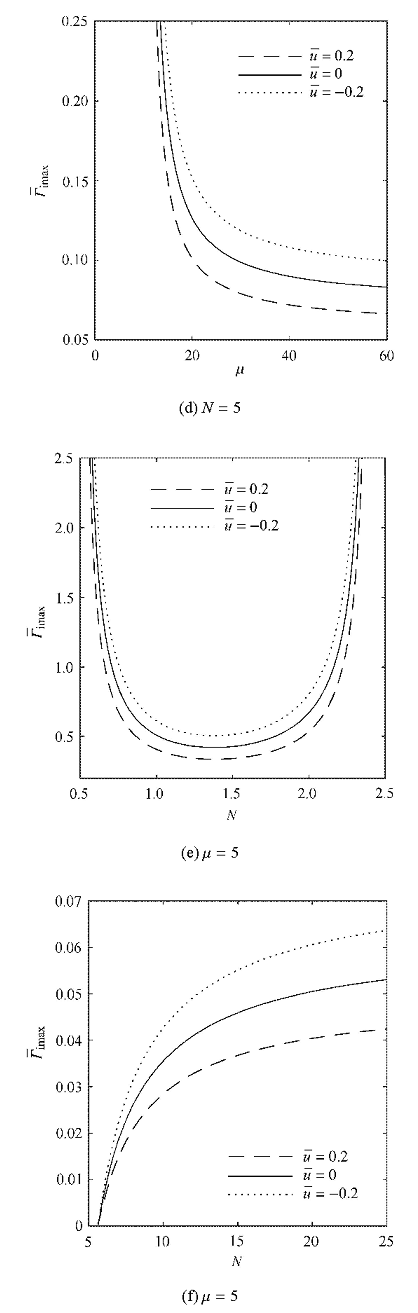
如图5 所示,顺流相对没有流动时,$\bar\varGamma _{{\rm i}\max }$变小,相反地,逆流使$\bar\varGamma _{{\rm i}\max }$变大,且相差的倍数都是$ 1-\bar u$.
图5
图5
无量纲最大增长率$\bar\varGamma _{\rm i\max }$的变化
Fig. 5
Dimensionless maximum growth rate $\bar\varGamma_{\rm i\max}$
图5
图5
无量纲最大增长率$\bar\varGamma _{\rm i\max }$的变化(续)
Fig. 5
Dimensionless maximum growth rate $\bar\varGamma_{\rm i\max}$ (continued)
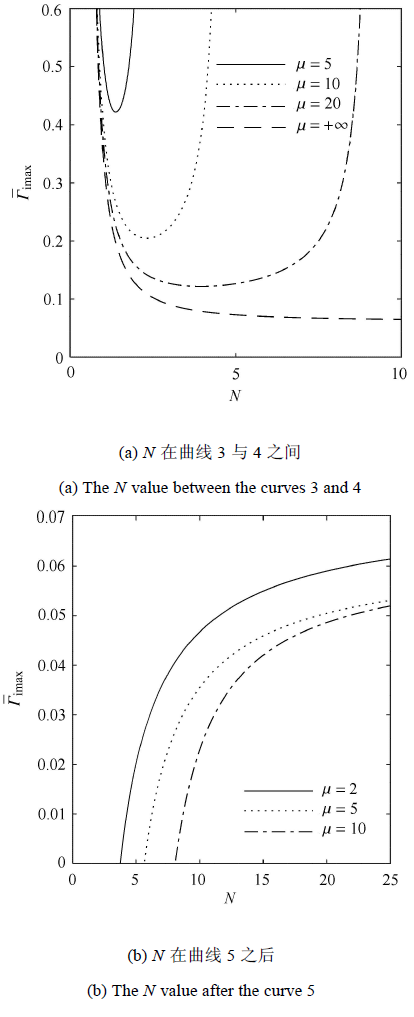
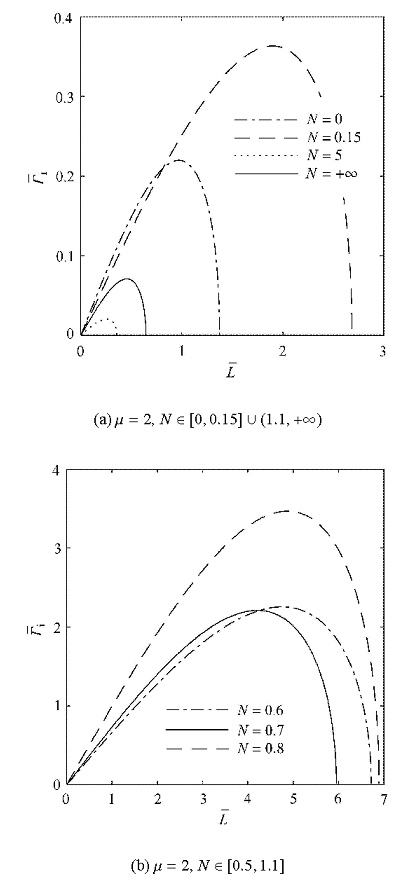
2.2 不稳定增长率
如图6 所示, $\bar\varGamma _{\rm i}$都是随着$\bar L$增大先增大后减小,都有一个最大$\bar\varGamma _{\rm i}$,且$\bar L$的取值范围是$[0, ( 2\bar\gamma/\bar\alpha) ^{1 /2}]$.在有限深水时,如图6 (a)和图6 (b)所示,当$N \!\in [0,0.15] $时,随着$N$增大,$\bar L$取值范围变大,但$\bar\varGamma _{\rm i}$增大的斜率变小一些;受到有限水深$\mu\!=\!2$的影响,在$N \in [0.5,1.1]$ 这部分,随着$N $增大, $\bar\varGamma _{i}$增大的斜率变大,但是$\bar L$ 取值范围却是在$N $的两端大中间小;当$N \in (1.1,+ \infty)$时,随着$N $增大,$\bar L$取值范围变大,且$\bar\varGamma _{i}$增大的斜率变大.在深水时,如图6 (c)和图6 (d)所示,当$N \in [0,0.15] $时, 随着$N$增大,$\bar L$取值范围变大,但$\bar\varGamma _{i }$增大的斜率变小且相差较大;当$N \in (0.5,+\infty )$时,随着$N $增大,$\bar L$取值范围变小,$\bar\varGamma _{i}$增大的斜率变小.
图6
图6
$\bar u= 0$时,无量纲增长率$\bar\varGamma _{\rm i}$随无量纲扰动波数$\bar L$的变化
Fig. 6
Dimensionless growth rate $\bar\varGamma _{\rm i}$ as a function of dimensionless perturbation wave number $\bar L$ for $\bar u= 0$ at different $N$
图6
图6
$\bar u= 0$时,无量纲增长率$\bar\varGamma _{\rm i}$随无量纲扰动波数$\bar L$的变化 (续)
Fig. 6
Dimensionless growth rate $\bar\varGamma _{\rm i}$ as a function of dimensionless perturbation wave number $\bar L$ for $\bar u= 0$ at different $N$ (continued)
如图7 所示,与图5 有类似的结果,顺流使无量纲不稳定增长率变小,逆流使之变大,且相差的倍数都是$1-\bar u$.
图7
图7
无量纲增长率$\bar\varGamma _{i}$随无量纲扰动波数$\bar L$的变化
Fig. 7
Dimensionless growth rate $\bar\varGamma _{i}$ as a function of dimensionless perturbation wave number $\bar L$ at different $\bar u$
3 结论
该文分析了均匀流对毛细重力波的调制作用.从水波基本方程出发,考虑了均匀流的作用,使用多重尺度分析方法导出了毛细重力波 振幅所满足的NLSE.通过毛细重力波调制稳定性分析,知NLSE中频散系数$\alpha$和非线性系数$\gamma $同号时,毛细重力波是调制稳定的; $\alpha $与$\gamma$异号时,它是调制不稳定的,此时会有钟型孤立波的产生.而$\alpha $和$\gamma$的大小是与均匀流、水深和表面张力有关的.通过对$\alpha $与$\gamma $符号的判断,知$\alpha=0$和$\gamma =0 $及它们的奇异处5条曲线将 ($N$, $\mu$)平面划分为6个区域,从左到右,稳定和不稳定依次交换;在深水时,$N$轴被划分为3个稳定和不稳定依次交替的片段,即$N \in [0,0.15] \cup (0.5,+ \infty )$ 时,毛细重力波是调制不稳定的;但$N \in (0.15,0.5]$时,它是调制稳定的.均匀流对这些区域的划分没有影响.同时也得到了微扰动的频散关系,给出了毛细重力波不稳定的增长率及最大增长率随水深、表面张力及扰动波数的变化趋势.指出了顺流会减小增长率及最大增长率,逆流会增加它们.
海洋上界面过程直接影响和调控着海气边界层结构与海气相互作用,特别是发生在海气界面的海洋表面波动在海气相互作用中发挥着重要作用.当风吹过海面时,会在海面产生切应力,这种摩擦应力会使海面形成毛细重力波和重力波,它们与海流的相互作用会有效地改变海表粗糙度和海洋上层流场结构,进而影响海气界面动量、热量及水汽的交换.尽管风浪频谱的主要能量集中于谱峰频率附近,但谱的高频率部分对研究海-气相互作用和海面的反射性能等有重要意义.本文建立了一个关于均匀流与毛细重力高频波相互作用的简单模型,来刻画实际海洋中复杂的海流与高频波的相互作用.了解海表这些短波动力机制,对卫星遥感的精确测量、海气相互作用的深入研究及海气耦合模式的改进等有重要意义.
参考文献
View Option
[1]
Larraza A Putterman S . Theory of non-propagating surface-wave solitons
Journal of Fluid Mechanics , 1984 ,148 :443 -449
[本文引用: 1]
[2]
Djordjevic AD Redekopp LG . On two-dimensional packets of capillary-gravity waves
Journal of Fluid Mechanics , 1977 ,79 :703 -714
[本文引用: 5]
[3]
刘应中 , 张乐 . 摄动理论在船舶流体力学中的应用 . 上海 : 上海交通大学出版社 , 1991
[本文引用: 1]
( Liu Yingzhong Zhang Le Application of Perturbation Theory in Ship Fluid Mechanics. Shanghai : Shanghai Jiaotong University Press , 1991 (in Chinese))
[本文引用: 1]
[4]
李家春 . 深水波理论的新进展
力学进展 , 1986 ,16 (2 ):175 -184
( Li Jiachun . Modern development on deep water waves
Advance in Mechanics , 1986 ,16 (2 ):175 -184 (in Chinese))
[5]
李家春 . 非线性力学与计算
力学进展 , 1993 ,23 (3 ):318 -326
[本文引用: 1]
( Li Jiachun . Nonlinear mechanics and computation
Advance in Mechanics , 1993 ,23 (3 ):318 -326 (in Chinese))
[本文引用: 1]
[6]
王本仁 , 魏荣爵 . 二模振荡激励下水槽中的孤立波
物理学报 , 1986 ,35 (12 ):1547 -1555
[本文引用: 1]
( Wang Benren Wei Rongjue . The solitary waves in trough excited by two frequency modes
Acta Physica Sinica , 1986 ,35 (12 ):1547 -1555 (in Chinese))
[本文引用: 1]
[7]
周显初 , 崔洪农 , 向隆万 . 考虑表面张力的非传播孤立波
力学学报 , 1991 ,23 (6 ):666 -673
[本文引用: 1]
( Zhou Xianchu Cui Hongnong Xiang Longwan . Non-propagating solitary waves with the consideration of surface tension
Chinese Journal of Theoretical and Applied Mechanics , 1991 ,23 (6 ):666 -673 (in Chinese))
[本文引用: 1]
[8]
周显初 . 非传播孤立波和表面张力
力学学报 , 1998 ,30 (6 ):672 -675
[本文引用: 1]
( Zhou Xianchu . Non-propagating soliton and surface tension
Chinese Journal of Theoretical and Applied Mechanics , 1998 ,30 (6 ):672 -675 (in Chinese))
[本文引用: 1]
[9]
颜家壬 , 黄国翔 . 计及表面张力的非传播孤波理论
应用数学和力学 , 1987 ,8 (10 ):925 -929
[本文引用: 1]
( Yan Jiaren Huang Guoxiang . Theory of non-propagation solitons including surface-tension effects
Applied Mathematics and Mechanics , 1987 ,8 (10 ):925 -929 (in Chinese))
[本文引用: 1]
[10]
Takuji K . Nonlinear interaction between short and long capillary-gravity waves
Journal of the Physical Society of Japan , 1975 ,39 (5 ):1379 -1386
[本文引用: 1]
[11]
Dias F Kharif C . Nonlinear gravity and capillary-gravity waves
Annual Review of Fluid Mechanics , 1999 ,31 :301 -346
[本文引用: 1]
[12]
Parau EI Vanden-Broeck MJ Cooker MJ . Nonlinear three-dimensional gravity-capillary solitary waves
Journal of Fluid Mechanics , 2005 ,536 :99 -105
[本文引用: 1]
[13]
Vanden-Broeck MJ Dias F . Gravity-capillary solitary waves in water of infinite depth and related free-surface flows
Journal of Fluid Mechanics , 1992 ,240 :549 -557
[本文引用: 1]
[14]
Kang Y Vanden-Broeck MJ . Gravity-capillary waves in the presence of constant vorticity.
European Journal of Mechanics B-Fluids , 2000 ,19 :253 -268
[本文引用: 1]
[15]
Wahlen E . Steady periodic capillary-gravity waves with vorticity
SIAM Journal on Mathematical Analysis , 2006 ,38 (3 ):921 -943
[本文引用: 1]
[16]
Wahlen E . Steady periodic capillary waves with vorticity
Arkiv for Mathematics , 2006 ,44 :367 -387
[17]
Wahlen E . On rotational water waves with surface tension
Philosophical Transactions of the Royal Society A , 2007 ,365 :2215 -2225 .
[本文引用: 1]
[18]
Martin CI . Resonant interactions of capillary-gravity water waves
Journal of Mathematical Fluid Mechanics , 2017 ,19 (4 ):807 -817
[本文引用: 1]
[19]
Martin CI Matioc BV . Existence of capillary-gravity water waves with piecewise constant vorticity
Journal of Differential Equations , 2014 ,256 :3086 -3114
[本文引用: 1]
[20]
Tiron R Choi W . Linear stability of finite-amplitude capillary waves on water of infinite depth
Journal of Fluid Mechanics , 2012 ,696 :402 -422
[本文引用: 1]
[21]
Li JC Hui WH Donelan MA . In Nonlinear Water Waves.
Berlin and Heidelberg: Spring-Verlag , 1987
[本文引用: 1]
[22]
Sedletsky YV . The modulational instability of Stokes waves on the surface of finite-depth fluid
Physics Letters A , 2005 ,343 :293 -299
[本文引用: 1]
[23]
Liao B Dong G Ma Y , et al . Linear-shear-current modified Schrödinger equation for gravity waves in finite water depth
Physical Review E , 2017 ,96 :043111
[本文引用: 2]
[24]
Li SF Chen J Cao AZ , et al . A nonlinear Schrödinger equation for gravity waves slowly modulated by linear shear flow
Chinese Physics B , 2019 ,28 :124701
[本文引用: 2]
[25]
Hsu HC Kharif C Abid M , et al . A nonlinear Schrödinger equation for gravity-capillary water waves on arbitrary depth with constant vorticity. Part 1
Journal of Fluid Mechanics , 2018 ,854 :146 -163
[本文引用: 3]
[26]
张卓 , 宋志尧 , 孔俊 . 波流共同作用下流速垂线分布及其影响因素分析
水科学进展 , 2010 ,21 (6 ):801 -807
[本文引用: 1]
( Zhang Zhuo Song Zhiyao Kong Jun . Wave-current interaction effects on velocity profiles and influencing factor analysis
Advances in Water Science , 2010 ,21 (6 ):801 -807 (in Chinese))
[本文引用: 1]
[27]
文锋 , 王建华 . 二维均匀流与重力短峰波相互作用解析
物理学报 , 2014 ,63 (9 ):094701 (in Chinese))
( Wen Feng Wang Jianhua . An analytical solution for the interaction of two-dimensional currents and gravity short-crest waves
Acta Physica Sinica , 2014 ,63 (9 ):094701 (in Chinese))
[28]
徐振山 , 陈永平 , 张长宽 等 . 波流环境中射流的大涡数值模拟
水科学进展 , 2014 ,25 (2 ):239 -245 (in Chinese))
( Xu Zhenshan Chen Yongping Zhang Changkuan , et al . Large eddy simulation of a jet in wave-current environment
Advances in Water Science , 2014 ,25 (2 ):239 -245 (in Chinese))
[29]
丁阳 , 马瑞 , 李宁 . 三维波流耦合水槽模拟模型
工程力学 , 2015 ,32 (10 ):68 -74
( Ding Yang Ma Rui Li Ning . A simulation model for three-dimensional coupled wave-current flumes
Engineering Mechanics , 2015 ,32 (10 ):68 -74 (in Chinese))
[30]
柏君励 , 马宁 , 顾解忡 . 波流对不同淹没深度水平圆柱的载荷分析
上海交通大学学报 , 2018 ,52 (8 ):938 -945
( Bai Junli Ma Ning Gu Xiechong . Wave-current loads on the horizontal cylinder with varying submergence depths
Journal of Shanghai Jiao Tong University , 2018 ,52 (8 ):938 -945 (in Chinese))
[31]
匡翠萍 , 韩雪健 , 李文斌 等 . 波流对人工岬头和海滩养护工程的响应
同济大学学报 (自然科学版) , 2019 ,47 (3 ):339 -346
( Kuang Cuiping Han Xuejian Li Wenbin , et al . Responses of wave and current to artificial headlands and a beach nourishment project
Journal of Tongji University (Natural Science) , 2019 ,47 (3 ):339 -346 (in Chinese))
[32]
任智源 , 侯京明 , 王培涛 等 . 精细化地震海啸波流实时预警系统研究与应用 , 2019 ,41 (9 ):145 -155
[本文引用: 1]
( Ren Zhiyuan Hou Jingming Wang Peitao , et al . Study and application of the refined tsunami real time warning system including tsunamigenic wave and current
Haiyang Xuebao , 2019 ,41 (9 ):145 -155 (in Chinese))
[本文引用: 1]
[33]
徐祥德 , 冉令坤 . 波流相互作用与波动传播模态
大气科学 , 2007 ,31 (6 ):1237 -1250
[本文引用: 1]
( Xu Xiangde Ran Lingkun . Wave-flow interaction and wave-propagation modes
Chinese Journal of Atmospheric Sciences , 2007 ,31 (6 ):1237 -1250 (in Chinese))
[本文引用: 1]
[34]
徐俊丽 , 宋金宝 . 高频表面波对定常Ekman流解的影响
海洋与湖沼 , 2014 ,45 (1 ):197 -205
[本文引用: 1]
( Xu Junli Song Jinbao . Effects of high frequency surface waves on the steady Ekman current solutions
Oceanologia Et Limnologia Sinica , 2014 ,45 (1 ):197 -205 (in Chinese))
[本文引用: 1]
[35]
杨衡 , 孙龙泉 , 刘莹 等 . 波流作用下圆柱体入水特性的三维数值模拟研究
船舶力学 , 2015 ,19 (10 ):1186 -1196
[本文引用: 1]
( Yang Heng Sun Longquan Liu Ying , et al . 3D numerical simulation on water entry of cylindrical under wave and stream action
Journal of Ship Mechanics , 2015 ,19 (10 ):1186 -1196 (in Chinese))
[本文引用: 1]
[36]
魏艳 , 王赤忠 . 二阶波-流和结构物相互作用的高阶有限元分析
华中科技大学学报(自然科学版) , 2018 ,46 (6 ):99 -104
[本文引用: 1]
( Wei Yan Wang Chizhong . Second order wave interactions with body in current through higher order finite element method
Journal of Huazhong University of Science and Technology (Natural Science Edition) , 2018 ,46 (6 ):99 -104 (in Chinese))
[本文引用: 1]
[37]
程永舟 , 吕行 , 王文森 等 . 波流作用下大直径淹没圆柱局部冲刷实验研究
水科学进展 , 2019 ,30 (6 ):872 -881
[本文引用: 1]
( Cheng Yongzhou Lü Xing Wang Wensen , et al . Experimental study on local scour around large- diameter submerged cylinders under combined waves and current action
Advances in Water Science , 2019 ,30 (6 ):872 -881 (in Chinese))
[本文引用: 1]
[38]
程永舟 , 吕行 , 王文森 等 . 波流作用下淹没圆柱局部冲深影响因素分析
水利水运工程学报 , 2019 , ( 6 ):69 -76
[本文引用: 1]
( Cheng Yongzhou Lü Xing Wang Wensen , et al . Research on the influencing factors of scour depth around submerged cylinder under combined action of wave and current.
Hydro-science and Engineering , 2019 , ( 6 ):69 -76 (in Chinese))
[本文引用: 1]
[39]
文圣常 , 余宙文 . 海浪理论与计算原理 . 北京 : 科学出版社 , 1985
[本文引用: 1]
( Weng Shenchang Yu Zhouwen Wave Theory and Calculation Principle. Beijing : Science Press , 1985 (in Chinese))
[本文引用: 1]
[40]
Yan JR You JQ . Wu's solition in a sloping trough
Chinese Physics Letters , 1990 ,7 (9 ):406 -409
[41]
梅强中 . 水波动力学 . 北京 : 科学出版社 , 1984
( Mei Qiangzhong Mei Qiangzhong. Water Wave Dynamics . Beijing : Science Press , 1984 (in Chinese))
[42]
颜家壬 , 周川汇 , 钟建新 等 . 表面张力、黏性和驱动对非传播表面孤立波的影响
力学学报 , 1994 ,26 (2 ):158 -164
[本文引用: 1]
( Yan Jiaren Zhou Chuanhui Zhong Jianxin , et al . Effect of surface tension, viscosity and driving on the non-propagating solitary surface waves
Chinese Journal of Theoretical and Applied Mechanics , 1994 ,26 (2 ):158 -164 (in Chinese))
[本文引用: 1]
[43]
Thomas R Kharif C Manna M . A nonlinear Schrödinger equation for water waves on finite depth with constant vorticity
Physics of Fluids , 2012 ,24 (12 ):127102
[本文引用: 1]
Theory of non-propagating surface-wave solitons
1
1984
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
On two-dimensional packets of capillary-gravity waves
5
1977
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
... 在本文中,基于文献[2 ] 的研究成果及结合文献[23 ,24 ,25 ] 的分析方法,考虑均匀流对毛细重力波的调制作用.在第一节,将使用多重尺度法推导被均匀流调制的二维毛细重力波振幅在有限水深中所满足的NLSE.在第二节,通过使用NLSE,分析被均匀流调制的毛细重力波的不稳定性.第三节是本文的主要结论.由于毛细重力波与流的相互作用可以有效地改变海表粗糙度和海洋上层流场结构,所以这对海面风场、海表压强、海气通量交换等有重要意义.另外,了解海表面的这些短波动力机制,对卫星遥感的精确测量和海气耦合模式的改进等也有重要意义. ...
... 引入下列多重尺度[2 ] ...
... 其中,$\bar c_{\rm g}=c_{\rm g}/c$是无量纲群速度, $\alpha $和$\beta $分别是频散系数和非线性系数,它们与 ($\bar u, N, \mu $)有关.若$\bar u= 0$,上述结果和文献[2 ] 给出的结果一致.通过观察$\beta $中各项,发现有两处奇异需要避免,一处是 ...
... 值得注意的是,毛细重力波在曲线4和5渐近线之间是稳定的,但当$\mu \gg 1 $时,即深水时,它们在$\mu $轴上的截断3/4和35/4可以被忽略,这两条边界线重合在一起 (斜率相同),它们之间稳定区域消失,这也解释了长短 波共振在深水中消失的原因[2 ,25 ] . ...
1
1991
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
1
1991
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
非线性力学与计算
1
1993
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
非线性力学与计算
1
1993
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
二模振荡激励下水槽中的孤立波
1
1986
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
二模振荡激励下水槽中的孤立波
1
1986
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
考虑表面张力的非传播孤立波
1
1991
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
考虑表面张力的非传播孤立波
1
1991
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
非传播孤立波和表面张力
1
1998
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
非传播孤立波和表面张力
1
1998
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
计及表面张力的非传播孤波理论
1
1987
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
计及表面张力的非传播孤波理论
1
1987
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Nonlinear interaction between short and long capillary-gravity waves
1
1975
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Nonlinear gravity and capillary-gravity waves
1
1999
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Nonlinear three-dimensional gravity-capillary solitary waves
1
2005
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Gravity-capillary solitary waves in water of infinite depth and related free-surface flows
1
1992
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Gravity-capillary waves in the presence of constant vorticity.
1
2000
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Steady periodic capillary-gravity waves with vorticity
1
2006
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Steady periodic capillary waves with vorticity
2006
On rotational water waves with surface tension
1
2007
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Resonant interactions of capillary-gravity water waves
1
2017
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Existence of capillary-gravity water waves with piecewise constant vorticity
1
2014
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
Linear stability of finite-amplitude capillary waves on water of infinite depth
1
2012
... 海洋中的波动现象十分丰富.如:海洋表面的波浪、海啸、潮汐和风暴潮等,这些不同尺度海洋波动的生成和演变通常与重力、地球的自转及月亮和太阳的引力等有关.LarrazA和Putterman[1 ] 对水槽中表面重力波进行了理论研究,用多重尺度法几乎是直接 给出了水波振幅所满足的立方非线性Schrödinger方程 (non-linear Schrödinger equation, NLSE)及其孤立波解,但是缺乏严密的推导和 论证,也没有考虑表面张力的影响.Djordjevic和Redekopp[2 ] 考虑到表面张力的作用,导出了有限水深中二维毛细重力波振幅所满足的NLSE,对其解进行了稳定性划分,揭示了短毛细重力波和长重力波的共振条件.多重尺度分析是一种处理水波问题的常用方法,可研究不同尺度下波浪的演化,大量学者[3 -5 ] 使用这种方法进行水波的研究.也有些学者,如王本仁和魏荣爵[6 ] 曾使用变分法研究水波.不管使用何种方法,诸多学者发展了毛细重力波的动力机制.周显初等[7 -8 ] 解释了毛细重力孤立波横向谐振中波峰尖、波谷平的原因.颜家壬等[9 ] 研究了两层流体中的毛细重力孤立波.Takuji等[10 ] 分析了短毛细重力波和长重力波的非线性相互作用,指出了在共振情况下短波和长波之间可以相互转化能量,此时短波的群速度和长波的相速度相匹配.Dias等[11 ] 详细地讨论了上述短波和长波之间的演变过程、分叉及稳定性.Parau等[12 ] 研究了三维毛细重力波,并与Vanden Broeck等[13 ] 给出的二维情况作了详细的对比,指出二维和三维有较好的相似性.Kang等[14 ] 给出了有限水深下,伴有恒定涡度 (代表流的剪切性)存在的周期性孤立毛细重力波.Wahlen等[15 -17 ] 使用分叉理论严密地证明了在伴有非恒定涡度条件下周期性毛细波和毛细重力波的存在性.Martin等[18 -19 ] 指出在伴有分段涡度分布的条件下,三波相互作用是可能的,然而调制不稳定性是和四波共振作用相一致的.Tiron等[20 ] 数值计算了毛细重力波之间的相互共振作用. ...
In Nonlinear Water Waves.
1
1987
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
The modulational instability of Stokes waves on the surface of finite-depth fluid
1
2005
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
Linear-shear-current modified Schr?dinger equation for gravity waves in finite water depth
2
2017
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
... 在本文中,基于文献[2 ] 的研究成果及结合文献[23 ,24 ,25 ] 的分析方法,考虑均匀流对毛细重力波的调制作用.在第一节,将使用多重尺度法推导被均匀流调制的二维毛细重力波振幅在有限水深中所满足的NLSE.在第二节,通过使用NLSE,分析被均匀流调制的毛细重力波的不稳定性.第三节是本文的主要结论.由于毛细重力波与流的相互作用可以有效地改变海表粗糙度和海洋上层流场结构,所以这对海面风场、海表压强、海气通量交换等有重要意义.另外,了解海表面的这些短波动力机制,对卫星遥感的精确测量和海气耦合模式的改进等也有重要意义. ...
A nonlinear Schr?dinger equation for gravity waves slowly modulated by linear shear flow
2
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
... 在本文中,基于文献[2 ] 的研究成果及结合文献[23 ,24 ,25 ] 的分析方法,考虑均匀流对毛细重力波的调制作用.在第一节,将使用多重尺度法推导被均匀流调制的二维毛细重力波振幅在有限水深中所满足的NLSE.在第二节,通过使用NLSE,分析被均匀流调制的毛细重力波的不稳定性.第三节是本文的主要结论.由于毛细重力波与流的相互作用可以有效地改变海表粗糙度和海洋上层流场结构,所以这对海面风场、海表压强、海气通量交换等有重要意义.另外,了解海表面的这些短波动力机制,对卫星遥感的精确测量和海气耦合模式的改进等也有重要意义. ...
A nonlinear Schr?dinger equation for gravity-capillary water waves on arbitrary depth with constant vorticity. Part 1
3
2018
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
... 在本文中,基于文献[2 ] 的研究成果及结合文献[23 ,24 ,25 ] 的分析方法,考虑均匀流对毛细重力波的调制作用.在第一节,将使用多重尺度法推导被均匀流调制的二维毛细重力波振幅在有限水深中所满足的NLSE.在第二节,通过使用NLSE,分析被均匀流调制的毛细重力波的不稳定性.第三节是本文的主要结论.由于毛细重力波与流的相互作用可以有效地改变海表粗糙度和海洋上层流场结构,所以这对海面风场、海表压强、海气通量交换等有重要意义.另外,了解海表面的这些短波动力机制,对卫星遥感的精确测量和海气耦合模式的改进等也有重要意义. ...
... 值得注意的是,毛细重力波在曲线4和5渐近线之间是稳定的,但当$\mu \gg 1 $时,即深水时,它们在$\mu $轴上的截断3/4和35/4可以被忽略,这两条边界线重合在一起 (斜率相同),它们之间稳定区域消失,这也解释了长短 波共振在深水中消失的原因[2 ,25 ] . ...
波流共同作用下流速垂线分布及其影响因素分析
1
2010
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流共同作用下流速垂线分布及其影响因素分析
1
2010
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
Study and application of the refined tsunami real time warning system including tsunamigenic wave and current
1
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
Study and application of the refined tsunami real time warning system including tsunamigenic wave and current
1
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流相互作用与波动传播模态
1
2007
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流相互作用与波动传播模态
1
2007
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
高频表面波对定常Ekman流解的影响
1
2014
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
高频表面波对定常Ekman流解的影响
1
2014
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流作用下圆柱体入水特性的三维数值模拟研究
1
2015
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流作用下圆柱体入水特性的三维数值模拟研究
1
2015
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
二阶波-流和结构物相互作用的高阶有限元分析
1
2018
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
二阶波-流和结构物相互作用的高阶有限元分析
1
2018
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流作用下大直径淹没圆柱局部冲刷实验研究
1
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流作用下大直径淹没圆柱局部冲刷实验研究
1
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流作用下淹没圆柱局部冲深影响因素分析
1
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
波流作用下淹没圆柱局部冲深影响因素分析
1
2019
... 上述文献虽然均没有考虑到均匀流对波的作用,但对本文关注的波流相互作用研究有重要的指导意义.早期,李家春等[21 ] 考虑深水中二维Stokes波边带不稳定性,通过实验观察发现边带不稳定增长率定性地和理论相一致,且微风会提高增长率,而强风却会抑制.Sedletsky[22 ] 分析了水深对高阶Stocks波调制不稳定性的影响,指出水深加深时非线性作用加强,小波数情形下调制不稳定会重新稳定.近来,廖波等[23 ] 、李少峰等[24 ] 研究了被线性剪切流缓慢调制的有限水深重力波,这里的剪切流是由均匀流和流的剪切组成的,其中流的剪切刻画了涡度.同时他们展示了剪切流对重力波稳定性区域划分的影响,发现了顺流增强调制不稳定,而逆流减弱它.Hsu等[25 ] 分析了被涡度缓慢调制的有限水深毛细重力波,他们指出毛细重力波稳定性区域划分被涡度有效地改变.另外,还有些学者[26 -32 ] 研究了不同物理背景下的波流相互作用,如徐祥德等[33 ] 详细介绍了大气中大尺度波流相互作用及波动传播模态;徐俊丽等[34 ] 分析了高频波对定常Ekman流解的影响;杨衡等[35 ] 、魏艳等[36 ] 、程永舟等[37 -38 ] 讨论了波流和结构物的相互作用. ...
1
1985
... 假设流体运动是无黏的、不可压的和无旋的.如图1 所示,考虑均匀流作用下二维毛细重力水波在有限水深中的传播,坐标原点$o$位于静止水面处,$x$方向是水波的传播方向,$y$方向垂直向上与重力方向相反,$z$垂直纸面向外.这里,把与波动方向一致的均匀流称为顺流,反之称为逆流.故二维水波基本方程组[39 -42 ] 可表述为 ...
1
1985
... 假设流体运动是无黏的、不可压的和无旋的.如图1 所示,考虑均匀流作用下二维毛细重力水波在有限水深中的传播,坐标原点$o$位于静止水面处,$x$方向是水波的传播方向,$y$方向垂直向上与重力方向相反,$z$垂直纸面向外.这里,把与波动方向一致的均匀流称为顺流,反之称为逆流.故二维水波基本方程组[39 -42 ] 可表述为 ...
Wu's solition in a sloping trough
1990
表面张力、黏性和驱动对非传播表面孤立波的影响
1
1994
... 假设流体运动是无黏的、不可压的和无旋的.如图1 所示,考虑均匀流作用下二维毛细重力水波在有限水深中的传播,坐标原点$o$位于静止水面处,$x$方向是水波的传播方向,$y$方向垂直向上与重力方向相反,$z$垂直纸面向外.这里,把与波动方向一致的均匀流称为顺流,反之称为逆流.故二维水波基本方程组[39 -42 ] 可表述为 ...
表面张力、黏性和驱动对非传播表面孤立波的影响
1
1994
... 假设流体运动是无黏的、不可压的和无旋的.如图1 所示,考虑均匀流作用下二维毛细重力水波在有限水深中的传播,坐标原点$o$位于静止水面处,$x$方向是水波的传播方向,$y$方向垂直向上与重力方向相反,$z$垂直纸面向外.这里,把与波动方向一致的均匀流称为顺流,反之称为逆流.故二维水波基本方程组[39 -42 ] 可表述为 ...
A nonlinear Schr?dinger equation for water waves on finite depth with constant vorticity
1
2012
... 显然,当$\alpha (\alpha L^{2}+2\gamma a_{0}^{2}) \geqslant 0 $时,$\varGamma $ 有实解,扰动是有界的且Stokes波解是稳定的,相反,当$\alpha (\alpha L^{2}+2\gamma a_{0}^{2}) <0 $时,解 是不稳定的.又因为$L$是个小量,所以上述分析暗含着当$\alpha \gamma \geqslant 0 $时,Stokes波解 是稳定的,当$\alpha \gamma <0 $时,Stokes波解是不稳定的[43 ] .故不稳定增长率是 ...