引言
规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性.
土-结动力相互作用分析可采用频域方法,如软件SASSI[18 ] .频域方法可直接采用具有试验观测基础的滞回阻尼模型,对于线性问题而言,可得到准确的结果,当考虑土体非线性时,需通过等效线性化进行处理.大多数研究表明,等效线性化适合于土体弱非线性,对于强非线性,宜采用时域逐步积分方法[19 ] .若采用时域分析之模态叠加法进行土-结动力相互作用分析,可以直接采用规范规定的模态阻尼比,当体系的反应主要由低阶模态控制时,具有运算速度快,阻尼输入准确等优点,但原则上不适合于非线性分析.
当采用时域逐步积分方法时,土体可采用非线性黏弹性本构,能较为合理地反应其非线性特性.对于结构而言,时步积分法常采用的阻尼模型为瑞利阻尼模型和Caughy阻尼模型.瑞利阻尼与质量和刚度成正比,通常称为比例阻尼,通过两阶模态的频率和阻尼比来确定两个比例常数.当对地震反应起主要贡献的结构模态数为两个时,采用这两个模态的频率和阻尼比确定的瑞利阻尼可以较准确地反应这两个模态的阻尼比,由瑞利阻尼模型计算的反应较为准确.但当对地震反应有贡献的模态数较多时,瑞利阻尼能较准确反应指定阻尼的两阶模态阻尼,其余模态阻尼与真实情况有误差,使得多数模态反应失真,造成地震反应与真实解有较大差异.邹德高等[16 ] 、李小军等[17 ] 分别改进了瑞利阻尼模型中两系数的确定方法,并分别对土石坝和核电厂房进行了地震反应分析,但本质上未改变瑞利阻尼模型的实质,仍是通过同样的函数来近似阻尼.Caughy阻尼模型通过级数形式描述阻尼,可以使得更多阶的模态阻尼比满足规定值,但在通过满足多个模态阻尼比确定级数的系数时,有时会出现系数矩阵为奇异的情形,造成系数求解的困难.另外,Caughy阻尼在高频时可能出现负阻尼情形,影响计算的失稳.Luco等[9 ] 提出了一种Caughy阻尼系数优化方法,可以避免上述相关问题.
综上所述,核电结构不允许进入非线性,采用模态叠加法可简便合理地记入模态阻尼.非基岩场地在地震作用下容易进入非线性,宜通过非线性黏弹性本构描述非基岩场地特性,采用时步积分法进行分析.目前土-结相互作用分析常用的软件SASSI[18 ] ,采用频域分析方法,通过等效线性化方法考虑土体非线性,在强震时不能很好地体现土体特性,且不能考虑土与基础间的接触非线性[20 -21 ] .采用ANSYS,ABAQUS,OpenSees等软件,结构和土体只能采用相同的分析方法 (要么都采用时步积分法,或都采用模态叠加法),且计算效率较低[22 ] (23 961个节点,18 200个单元,8000时步数,在Intel Core i72.93 GHz,8 GB内存的微机上用时4周).因此,有必要发展一种能合理考虑结构阻尼和土体非线性的高效时域土-结相互作用分析方法.
本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响.
1 基本理论
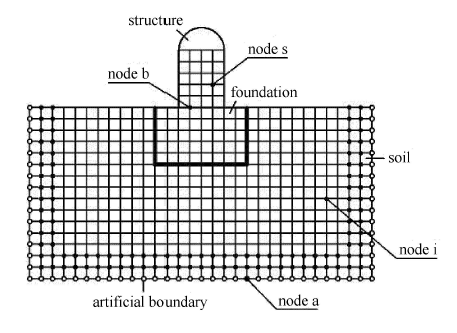
图1 为结构-基础-土体模型示意图,对该体系进行有限元离散,并将节点类型分为结构节点、结构与基础的界面点、土体和基础节点,以及人工边界点.则体系的运动方程可写为
(1) $ \left[\!\!\begin{array}{cccc} {\pmb M}_{\rm ss} & {\pmb M}_{\rm sb} & {\bf 0} & {\bf 0} \\ {\pmb M}_{\rm bs} & {\pmb M}^{\rm s}_{\rm bb}+{\pmb M}^{\rm g}_{\rm bb} & {\pmb M}_{\rm bi} & {\bf 0} \\ {\bf 0} & {\pmb M}_{\rm ib} & {\pmb M}_{\rm ii} & {\pmb M}_{\rm ia} \\ {\bf 0} & {\bf 0} & {\pmb M}_{\rm ai} & {\pmb M}_{\rm aa} \end{array}\!\!\right] \left\{\!\! \begin{array} \ddot{\pmb u}_{\rm s} \\ \ddot{\pmb u}_{\rm b} \\ \ddot{\pmb u}_{\rm i} \\ \ddot{\pmb u}_{\rm a} \end{array}\!\!\right\} + \\ \left[\!\!\begin{array}{cccc} {\pmb C}_{\rm ss} & {\pmb C}_{\rm sb} & {\bf 0} & {\bf 0} \\ {\pmb C}_{\rm bs} & {\pmb C}_{\rm bb}^{\rm s}+{\pmb C}_{\rm bb}^{\rm g} & {\pmb C}_{\rm bi} & {\bf 0} \\ {\bf 0} & {\pmb C}_{\rm ib} & {\pmb C}_{\rm ii} &{\pmb C}_{\rm ia} \\ {\bf 0} & {\bf 0} & {\pmb C}_{\rm ai} &{\pmb C}_{\rm aa} \end{array}\!\!\right] \left \{\!\!\begin{array} \dot{\pmb u}_{\rm s} \\ \dot{\pmb u}_{\rm b} \\ \dot{\pmb u}_{\rm i} \\ \dot{\pmb u}_{\rm a} \end{array}\!\!\right\} + \\ \left[\!\!\begin{array}{cccc} {\pmb K}_{\rm ss} & {\pmb K }_{\rm sb} & {\bf 0} & {\bf 0} \\ {\pmb K }_{\rm bs} & {\pmb K }_{\rm bb}^{\rm s}+{\pmb K }_{\rm bb}^{\rm g} & {\pmb K }_{\rm bi} & {\bf 0} \\ {\bf 0} & {\pmb K }_{\rm ib} & {\pmb K }_{\rm ii} &{\pmb K }_{\rm ia} \\ {\bf 0} & {\bf 0} & {\pmb K }_{\rm ai} &{\pmb K }_{\rm aa} \end{array}\!\!\right] \left \{\!\!\begin{array}{cccc} {\pmb u}_{\rm s} \\ {\pmb u}_{\rm b} \\ {\pmb u}_{\rm i} \\ {\pmb u}_{\rm a} \end{array}\!\!\right\} =\left\{ \!\!\begin{array} {\bf 0} \\ {\bf 0} \\ {\bf 0} \\ {\pmb f}_{\rm a} \end{array}\!\!\right\} $
式中,下标s, b, i和A分别表示结构节点、结构与基础的界面节点、土体节点和人工边界点.上标s和g分别表示结构和基础. 其中${\pmb K}_{\rm aa} $和${\pmb C}_{\rm aa}$分别为黏弹性边界的弹簧和阻尼系数矩阵,${\pmb f}_{\rm a}$为地震波输入时施加在人工边界节点上的等效载荷[3 -5 ] .若采用透射边界,可通过多次透射公式在人工边界上施加位移[2 ] .对方程 (1)通过时步积分方法直接进行求解,即为土-结相互作用的直接法或整体解法.若采用隐式解法,则需每时步求解大型方程组,计算量很大,十分耗时.若采用集中质量显式积分方法,每一时步不需求解大型方程组,但结构波速较大,稳定性要求时间步距较小,计算时步数较多,效率受影响.
图1
图1
土-基础-结构整体分析模型示意图
Fig. 1
Soil-foundation-structure model
(2) $ \left[\!\!\begin{array}{cccc} {\pmb S}_{\rm ss} & {\pmb S}_{\rm ss} & {\bf 0} & {\bf 0} \\ {\pmb S}_{\rm bs} & {\pmb S}_{\rm bb}^{\rm s}+{\pmb S}_{\rm bb}^{\rm g} & {\pmb S}_{\rm bi} & {\bf 0} \\ {\bf 0} & {\pmb S}_{\rm ib} & {\pmb S}_{\rm ii} & {\pmb S}_{\rm ia} \\ {\bf 0} & {\bf 0} & {\pmb S}_{\rm ai} & {\pmb S}_{\rm aa} \end{array}\!\!\right] \left \{\!\!\begin{array}{cccc} {\pmb U_s} \\ {\pmb U }_{\rm b} \\ {\pmb U }_{\rm i} \\ {\pmb U }_{\rm a} \end{array}\!\!\right\} =\left \{\!\!\begin{array}{cccc} {\bf 0} \\ {\bf 0} \\ {\bf 0} \\ {\pmb F_a} \end{array}\!\!\right\} $
(3) $ {\pmb S}={\pmb K}+{\rm i} \omega {\pmb C}-\omega^2 {\pmb M} $
式中,${\pmb U}$和${\pmb u}, {\pmb F}$和${\pmb f}$分别为傅里叶变换对.
(4) $ \left [\!\! \begin{array}{cc} {\pmb S}_{\rm ss} & {\pmb S}_{\rm sb} \\ {\pmb S}_{\rm bs} \ &{\pmb S}_{\rm bb}+{\pmb S}_{\rm bb}^{\infty} \end{array}\!\!\right] \left \{ \!\!\begin{array}{cc} {\pmb U}_{\rm s} \\ {\pmb U}_{\rm b} \end{array}\!\!\right\} =\left \{ \!\!\begin{array}{cc} {\bf 0} \\ {\pmb S}^{\infty}_{\rm bb}{\pmb U}^{\rm f}_{\rm b}+ {\pmb S}^{\rm e}_{\rm bb}{\pmb U}^{\rm f}_{\rm b}\end{array}\!\!\right\} $
注意,这里的下标s包含结构和基础的节点,下标b为基础与土体的界面点, ${\pmb S}^{\infty}_{\rm bb}$为基础的动力刚度, ${\pmb S}^{\rm e}_{\rm bb}$为开挖掉的土体动力刚度, ${\pmb U}^{\rm f}_{\rm b}$为土体与基础界面点的自由场位移.求得自由场和动力刚度后,即可由式 (4)求得结构和基础的频域响应,这种方法称为子结构方法.子结构法在频域内进行分析,原则上只适合于线性情形.
若将整个系统进行分区,分为上部结构、下部基础和土体,按此分区,将方程 (1)分开写成如下形式
(5) $ {\pmb M}_{\rm ss} \ddot {\pmb u}_{\rm s} + {\pmb C}_{\rm ss} \dot {\pmb u}_{\rm s} + {\pmb K}_{\rm ss} {\pmb u}_{\rm s} = - {\pmb M}_{\rm sb} \ddot {\pmb u}_{\rm b} - {\pmb C}_{\rm sb} \dot {\pmb u}_{\rm b} - {\pmb K}_{\rm sb} {\pmb u}_{\rm b} $
(6) $\left[ \!\!\begin{array}{cccc} {\pmb M}_{\rm bb}^{\rm s} + {\pmb M}_{\rm bb}^{\rm g} & {\pmb M}_{\rm bi} & {\bf 0} \\ {\pmb M}_{\rm ib} & {\pmb M}_{\rm ii} & {\pmb M}_{\rm ai} \\ {\bf 0} & {\pmb M}_{\rm ia} & {\pmb M}_{\rm aa} \end{array}\!\! \right]\left\{ \!\!\begin{array}{cccc} \ddot {\pmb u}_{\rm b } \\ \ddot{\pmb u}_{\rm i} \\ \ddot{\pmb u}_{\rm a} \end{array}\!\! \right\} + \\ \qquad \left[\!\!\begin{array}{ccc} {\pmb C}_{\rm bb}^{\rm s}+{\pmb C}_{\rm bb}^{\rm g} & {\pmb C}_{\rm bi} & {\bf 0} \\ {\pmb C}_{\rm ib} & {\pmb C}_{\rm ii} & {\pmb C}_{\rm ai} \\ {\bf 0} & {\pmb C}_{\rm ia} & {\pmb C}_{\rm aa} \end{array}\!\!\right] \left \{\!\! \begin{array}{ccc} \dot{\pmb u}_{\rm b} \\ \dot{\pmb u}_{\rm i} \\ \dot{\pmb u}_{\rm a} \end{array}\!\!\right\} + \\ \qquad \left[\!\!\begin{array}{ccc}{\pmb K }_{\rm bb}^{\rm s}+{\pmb K }_{\rm bb}^{\rm g} & {\pmb K }_{\rm bi} & {\bf 0} \\ {\pmb K }_{\rm ib} & {\pmb K }_{\rm ii} & {\pmb K }_{\rm ai} \\ {\bf 0} & {\pmb K }_{\rm ia} & {\pmb K }_{\rm aa} \end{array}\!\!\right] \left \{ \!\!\begin{array}{ccc} {\pmb u}_{\rm b} \\ {\pmb u}_{\rm i} \\ {\pmb u}_{\rm a} \end{array}\!\!\right\} = \\ \left\{ \!\!\begin{array}{c} -{\pmb M}_{\rm bs}\ddot{\pmb u}_{\rm s}-{\pmb C}_{\rm bs}\dot{\pmb u}_{\rm s}- {\pmb K}_{\rm bs}{\pmb u}_{\rm s} \\ {\bf 0} \\ {\pmb f}_{\rm a} \end{array} \right\} $
其中,式 (5)的右端项为基础对结构的作用力,式 (6)的右端项第一分量为结构给基础的作用力,两者为一对作用力和反作用力.
考虑到土体自由度数目较大,采用集中质量显式积分方法效率更高.因此,对式 (6)采用集中质量形式,并采用显式积分格式,如单边中心差分格式
(7) $ \ddot {\pmb u}^p = \dfrac{{\pmb u}^{p + 1} + {\pmb u}^{p - 1} - 2{\pmb u}^p}{\Delta t^2}$
(8) $ \dot{\pmb u}^p = \dfrac{{\pmb u}^p - {\pmb u}^{p - 1}}{\Delta t}$
则式 (6)中每一节点$k$的位移可通过如下方程求解
(9) $ {\pmb u}_k^{p + 1} = 2{\pmb u}_k^p - {\pmb u}_k^{p - 1} - \dfrac{\Delta t}{m_k }\sum_j^N {\pmb C}_{kj} \left( {{\pmb u}_j^p - {\pmb u}_j^{p - 1} } \right) - \\ \qquad \dfrac{\Delta t^2}{m_k }\sum_j^N {\pmb K}_{kj} {\pmb u}_j^p - {\pmb f}_k^p$
其中,$N$为与节点$k$相邻的节点总数. $\Delta t $为时间步距,$\ddot{\pmb u}_k^p $,$\dot{\pmb u}_k^p $和${\pmb u}_k^p$分别为节点$k$在$t = p\Delta t$时刻的加速度向量、速度向量和位移向量. $m_k$为集中于节点$k$的质量, ${\pmb C}_{kj} $和${\pmb K}_{kj}$分别为节点$k$与相邻节点$j$之间的阻尼阵和刚度阵, ${\pmb f}_k^p $为$p$时刻作用在节点$k$上的载荷向量.若$k$属于基础与结构相连的界面点,则${\pmb f}_k^p$为结构施加在基础上的载荷;若$k$属于人工边界点,当采用黏弹性边界时,${\pmb f}_k^p$为地震输入时的等效载荷,当采用透射边界时,该点的位移直接由多次透射公式求得;若$k$为基础和土体的其余节点,则${\pmb f}_k^p $为零.
由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法.
图2
图2
弱耦合示意图
Fig. 2
Illustration of loose coupling
求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下
(10) $ {\pmb M}_{\rm ss} \ddot {\pmb u}_{\rm s} + {\pmb C}_{\rm ss} \dot{\pmb u}_{\rm s} + {\pmb K}_{\rm ss} {\pmb u}_{\rm s} = \left\{ {\dfrac{0}{ {\pmb f}_{\rm b} }} \right\}$
(11) $ \bar{\pmb f}_{\rm b} = \bar{\pmb M}_{\rm bb} \ddot{\pmb u}_{\rm b}$
其中,$\bar{\pmb M}_{\rm bb} $为基底大质量矩阵. 对式 (10)采用模态叠加法进行分析,放开基底约束,考虑刚体模态,采用模态阻尼.
大质量法通过在大质量基础点上施加力载荷模拟地震作用;在数学处理上比较巧妙地通过在质量矩阵上"置大数"实现近似于真实 值的地震动输入,因此$\bar {\pmb M}_{\rm bb}$中的元素一般取结构总质量的10$^6$倍.
结构采用模态叠加方法,时间步距的选取满足精度要求即可,可较土体分析的时间步距大,即结构和土体可以采用不同的时间步距.已知$p$时步及以前各时步土、基础和结构的位移,求解$\left( {p + 1}\right)$时步各点的位移,土-结相互作用分析的基本步骤如下:
(1) 根据式 (7)~式 (9)可以计算土体和基础节点及人工边界节点$\left( {p +1} \right)$时步的响应,得到结构底部节点的加速度响应;
(2) 以结构底部节点$\left( {p + 1} \right)$ 时步的加速度为多点激励,通过大质量法得到施加在结构底部大质量点上的力 (式 (11)),对式 (10)采用模态叠加法,计算结构响应,并得到$\left( {p + 1} \right)$时步结构对基础的反力;
(3) 重复以上各步,即可得到土-基础-结构体系各时刻的反应.
2 算例分析
根据上述原理,我们编制了相应的计算程序,实现了模态叠加和时步积分结合的三维土-结相互作用分析的分区并行计算方法.对于无限域土体和基础的动力响应,采用自编的Fortran程序进行分析.对于结构响应,其每一时步的计算独立于土体的计算,因此可使用ANSYS等商业软件进行分析,结构和土体可分别采用不同的时间步距.通过耦合算法和Fortran程序与ANSYS之间的交互,实现土-结相互作用动力分析.由于采用分区计算方式,土体和结构可以独立进行建模,且在每一时步,两者独立进行计算.土体采用MPI协议,编程实现并行.结构可采用ANSYS中的并行计算方案.土体和结构之间的并行通过异步传输数据实现,具体见文献[17 ] .下面,通过一简单模型的算例对该方法进行验证,并对某非均匀场址上CAP1400核电结构的反应进行分析.
2.1 简单模型土-结相互作用分析
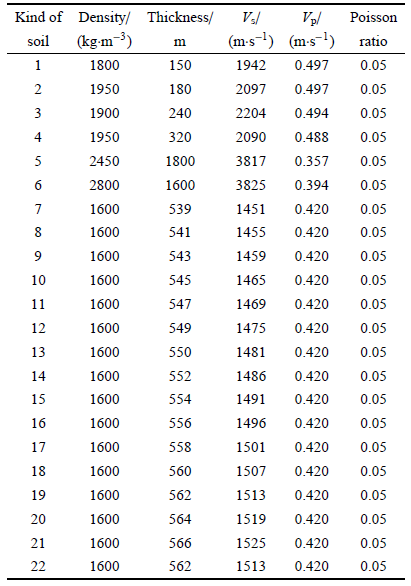
计算模型如图3 所示,上部结构尺寸为2 m$\times $2 m$\times $10 m,采用1 m$\times$1 m$\times $1 m的六面体八节点实体单元进行离散.选取三层水平成层场地,土层材料参数及相应厚度见表1 . 选取土体计算区 域的尺寸为40 m$\times$40 m$\times$18 m,将土体沿$X$方向划分为3个子区域:土体1,土体2和土体3,采用3个进程进行并行计算.土体离散为1 m$\times $1 m$\times$1 m的六面体八节点实体单元,单元总数为39 600,节点总数为31 939. 刚性埋置基础尺寸为6 m$\times$6 m$\times $4 m.
图3
图3
计算模型示意图
Fig. 3
Numerical model
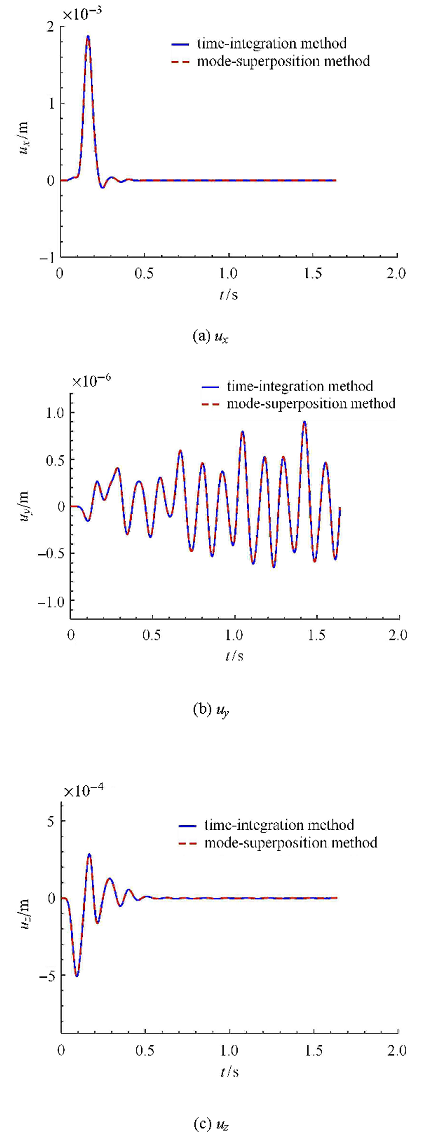
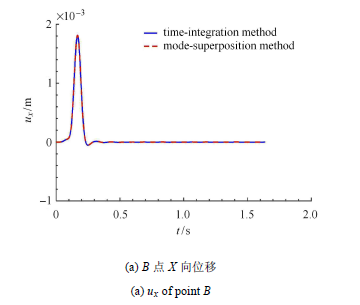
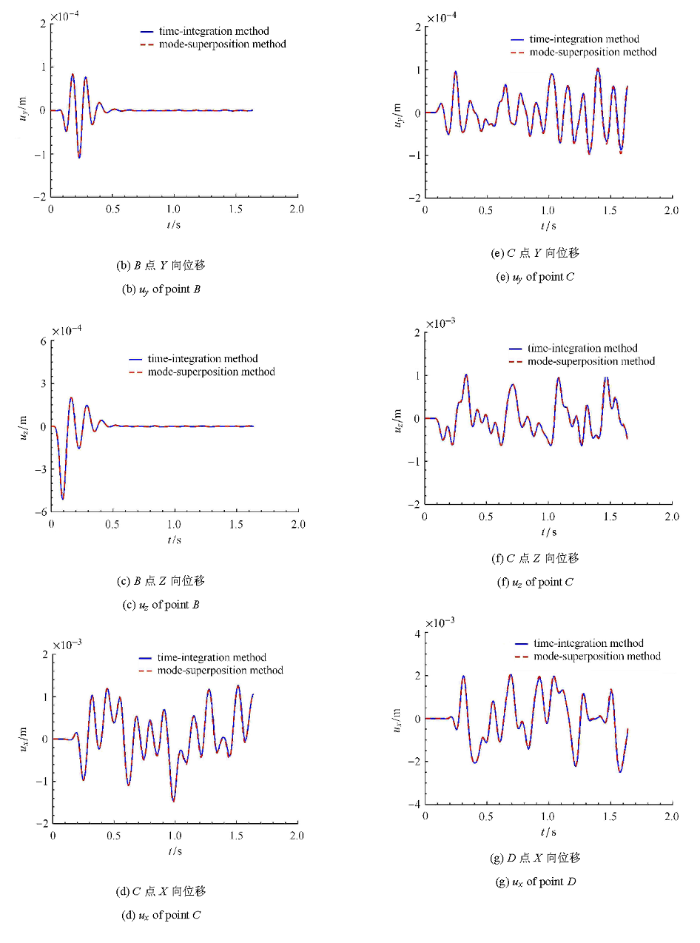
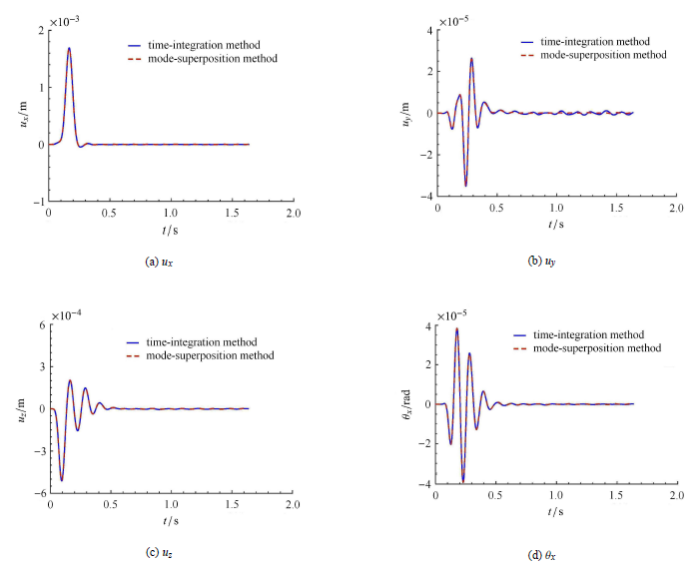
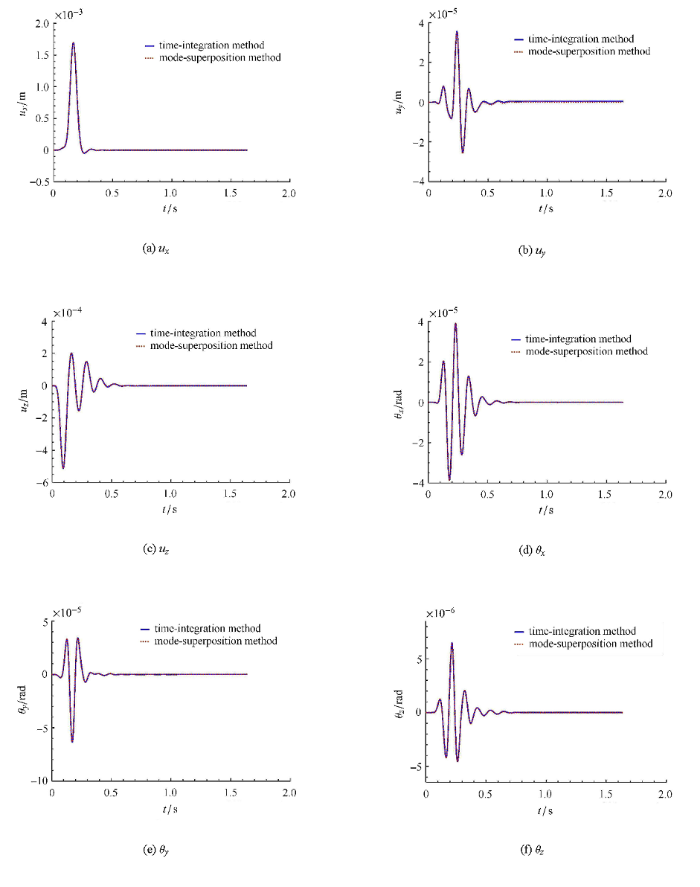
选取脉冲宽度0.15 s的单位脉冲波 (如图4 所示)作为SV波,垂直入射.土体采用显式中心差分格式,时间步距$\Delta t_1 = 2.0 \times 10^{ - 4}$,计算步数为8192步,结构分别采用Newmark隐式积分格式和模态叠加法进行分析,不考虑结构阻尼,用于验证模态叠加与时步积分结 合的土 - 结相互作用分区计算 方法的有效性.图5 ~图 7 分别为土体$A$点、结构$B, C, D$点 及基础的位移,点的位置如图3 所示.图5 ~图 7 中实线为 结构采用时步积分法的结果,虚线为结构采用模态叠加法的结果.从图5 ~图 7 可以看出,两种结果完全重合,这验证了模态叠加方 法结合时步积分法 进行土-结相互作用分析的有效性.
图4
图4
输入单位脉冲
Fig. 4
Pulse input
图5
图5
场地$A$点的位移反应
Fig. 5
Displacements of point $A$
图6
图6
结构点的位移反应
Fig. 6
Displacements of structure
图6
图6
结构点的位移反应(续)
Fig. 6
Displacements of structure (continued)
图6
图6
结构点的位移反应(续)
Fig. 6
Displacements of structure (continued)
图7
图7
基础位移反应
Fig. 7
Displacements of foundation
图7
图7
基础位移反应(续)
Fig. 7
Displacements of foundation (continued)
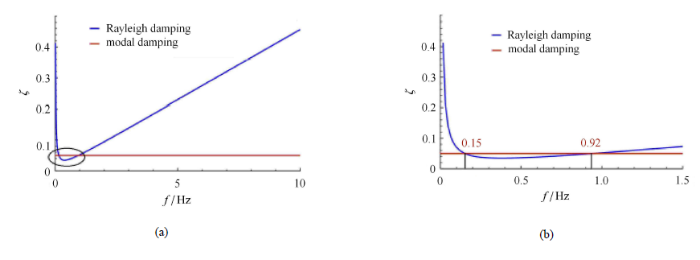
结构的阻尼分别采用Rayleigh阻尼和模态阻尼,计算模型及其余参数与3.1中相同.模态阻尼比取0.05,选取$X$方向质量影响系数最大的两阶自振频率 (分别为0.15 Hz和0.92 Hz),其对应的瑞利阻尼比同样取为0.05,对应的瑞利阻尼系数$\alpha=0.081$,$\beta =0.014$. 由此得到的阻尼如图8 所示.
图8
图8
阻尼曲线(右边为局部放大图)
Fig. 8
Damping curve(right: zoom in detail)
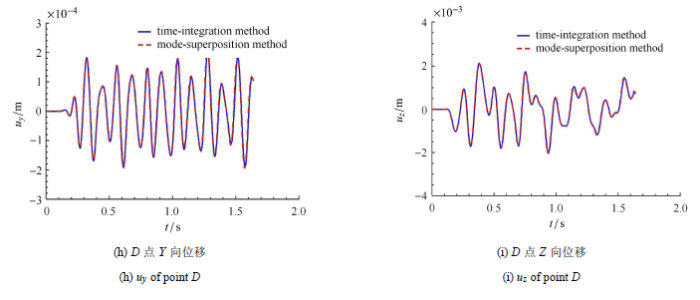
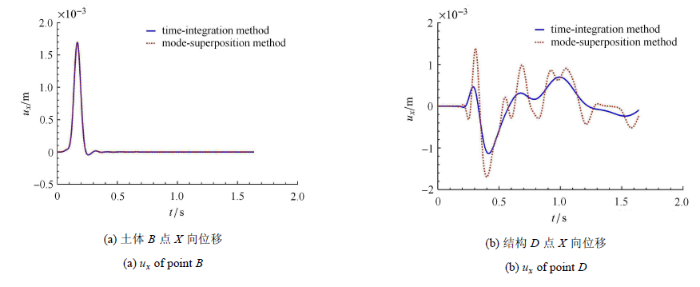
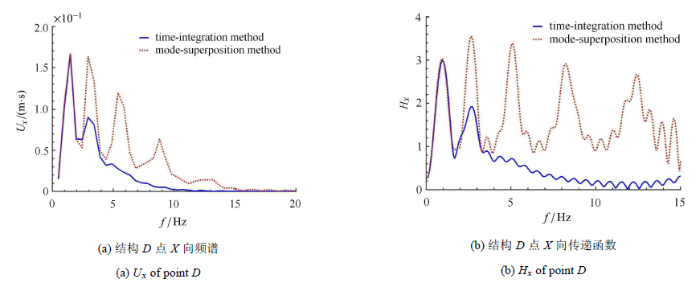
图9 为刚性基础的位移时程,其中实线为时步积分方法的结果,采用的是瑞利阻尼,虚线为模态叠加方法的结果,采用的是模态阻尼,后面的图例与此相同,不再说明.可以看出,结构阻尼模型对基础反应影响很小,可能是由于结构较小,土-结相互作用较小的原因.图10 为$B$点和$D$点 (位置如图3 所示)的$X$方向位移时程.由图中可以看出,结构阻尼模型对土体反应影响较小,但对结构反应影响较大.图11 为$D$点$X$方向的位移频谱,以及相对于基础的传递函数$H_X\left( f \right) = U_x \left( f \right) / U_{FX} \left( f\right)$,其中$U_{FX} \left( f \right)$为基础X方向的位移频谱.由图中结果可看出,频率大于2 Hz时,瑞利阻尼的结果要远小于模态阻尼的结果,这与图8 相一致,即大于2 Hz,瑞利阻尼远大于模态阻尼.
图9
图9
基础位移反应
Fig. 9
Displacements of foundation
图10
图10
土体$B$点与结构$D$点位移反应
Fig. 10
Displacements of point $B$ and $D$
图11
图11
结构$D$点的位移频谱和传递函数
Fig. 11
Spectrum and transfer function of point $D$
2.2 核电结构土-结相互作用分析
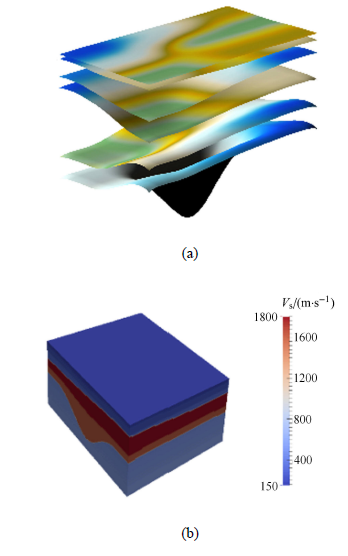
根据地脉动测试和钻孔资料,获得了某核电场地的剪切波速剖面,如图12 所示. 土体参数如表2 所示.选取土体计算区域的尺寸为640 m $\times $ 360 m $\times $194 m,边界采用黏弹性边界.土体离散为2 m $\times $ 2 m $\times $2 m的六面体八节点实体单元,单元总数为 5 587 200,节点总数为5 693 898.采用集中质量显式有限元方法进行分析,时间步距$ \Delta t_1 = 1.0\times 10^{ - 4}$ s.
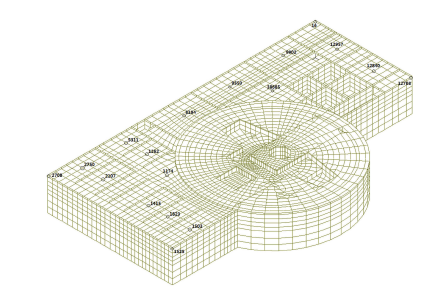
核电结构模型如图13 ,结构单元数为597 686,相应的节点数为700 194. 刚性基础尺寸为92 m$\times $60 m$\times$16 m.结构分别采用Newmark隐式时步积分方法和模态叠加方法进行分析,对应的阻尼分别采用瑞利阻尼和模态阻尼.模态阻尼比取为0.05,选取$X$方向质量影响系数最大的两阶自振频率 (分别为3.75 Hz和6.88 Hz),其对应的瑞利阻尼比同样取为0.05,对应的瑞利阻尼系数$\alpha=1.509$,$\beta =$0.001 5,由此得到的阻尼如图14 所示.采用模态叠加法,选取了六阶刚体模态以及300阶非刚体模态.结构分析的时间步距$\Delta t_2=25\Delta t_1 $,即$\Delta t_2 \!= 2.5\times 10^{ -3}$,本算例使用DELL-Optiplex小型工作站进行计算,CPU是Intel@Xeon(R)CPU@E5-2667v4@3.2 GHz$\times$32,主存大小为64 G,操作系统为Ubuntu16.04LTS. 土体采用5进程,结构采用2进程,并行计算.
图12
图12
场地剪切波速剖面图及模型
Fig. 12
Shear velocity profile and soil model
图13
图13
计算模型示意图
Fig. 13
Numerical model
图14
图14
阻尼曲线
Fig. 14
Damping curve
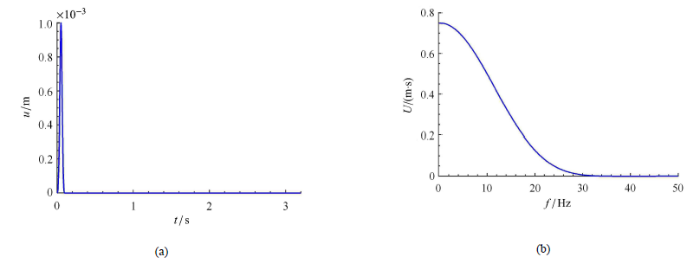
考虑SV波垂直入射,输入的脉冲位移时程图和频谱图如图15 所示.
图15
图15
脉冲波输入
Fig. 15
Pulse input
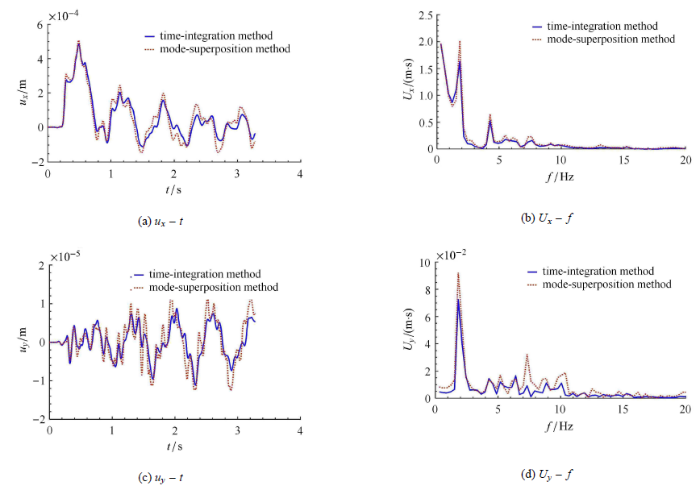
图16 为$C, D, E$三点(位置见图14 所示)的位移时程及频谱图.对比图中3点的位移时程及频谱图,可以看出,离基础越远,结构阻尼模型对土体反应的影响越小.从$C$点位移频谱图可知,小于3.75 Hz时,模态阻尼的结果要大于瑞利阻尼的结果,这与图 14 的阻尼曲线一致. 总体而言,结构阻尼模型对土体反应影响较小.图17 为基础的位移时程及频谱图,可以看出,结果阻尼模型对基础反应有较明显的影响.由基础$X$方向的位移频谱图可以看出,在结构自振频率处 (如3.75 Hz和6.88 Hz),基础的稳态反应接近零,符合土-结相互作用理论.结合图14 ,在3.75 Hz至10 Hz,瑞利阻尼与模态阻尼较为接近,所以两种阻尼模型对应的基础$X$方向稳态反应差别不大,但小于3.75 Hz时,瑞利阻尼远大于模态阻尼,因此在2 Hz左右,其反应明显小于模态阻尼.
图16
图16
场地$X$方向位移时程及频谱
Fig. 16
$X$-direction displacements on site
图16
图16
场地$X$方向位移时程及频谱(续)
Fig. 16
$X$-direction displacements on site (continued)
图17
图17
基础位移时程及频谱
Fig. 17
Displacements of foundation
图17
图17
基础位移时程及频谱(续)
Fig. 17
Displacements of foundation (continued)
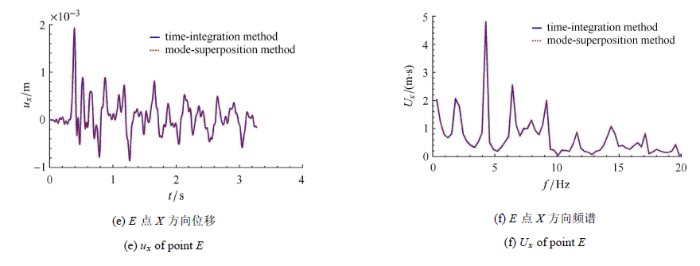
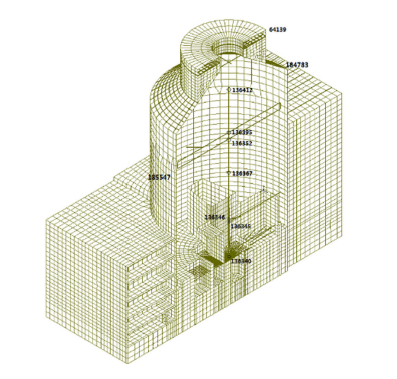
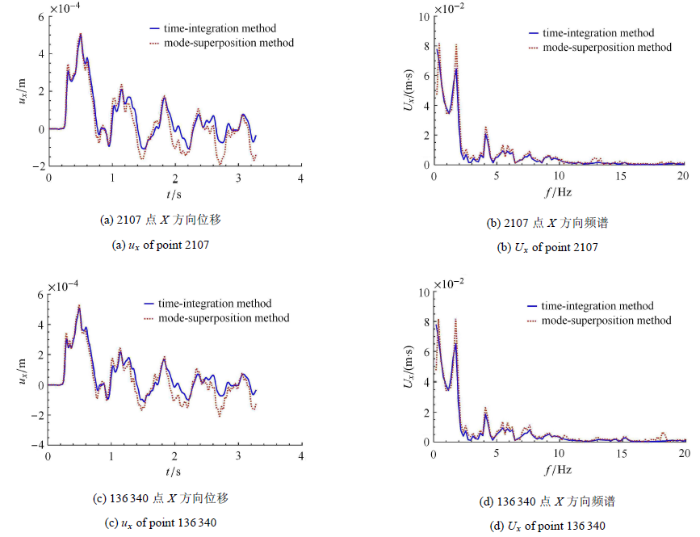
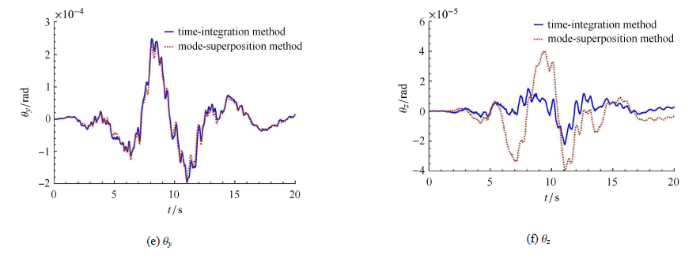
图18 为结构11 m高度处的截面图,给出其中2107号节点的反应.图19 为核岛结构屏蔽厂房剖面及参考点位置图,给出其中136 340,136 367,185 547,184 783,64 139号节点的反应.由于SV波垂直入射,主要产生$X$方向的位移,因此只给出上述节点$X$方向的位移及其频谱图,见图20 .
图18
图18
核岛11 m高度截面图及参考点位置
Fig. 18
11 m height section of nuclear island and reference point
图19
图19
核岛结构屏蔽厂房剖面及参考点位置
Fig.19
Section of nuclear island and reference points
图20
图20
结构点的位移时程及其频谱
Fig. 20
Displacements of structure
图20
图20
结构点的位移时程及其频谱(续)
Fig. 20
Displacements of structure (continued)
图20
图20
结构点的位移时程及其频谱(续)
Fig. 20
Displacements of structure (continued)
结合图15 与图20 进行分析,总体而言,在3.75 Hz至6.88 Hz,瑞利阻尼与模态阻尼较为接近,所以两种阻尼模型对应的稳态反应差别不大,但频率小于3.75 Hz或大于6.88 Hz时,瑞利阻尼远大于模态阻尼,因此其反应明显小于模态阻尼的反应,这种差异在结构中上部点越为明显.对于136 367点的反应,在5.5 Hz左右,模态叠加反应明显大于瑞利阻尼的结果,可能与局部模态有关.
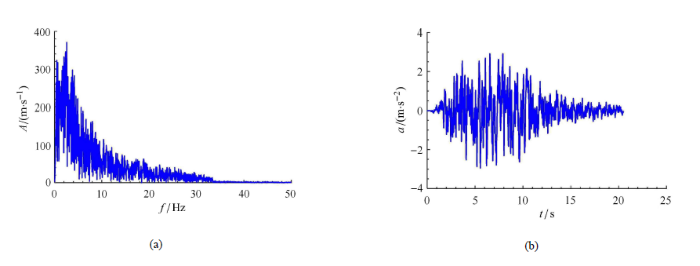
采用地震安全性评价得到的人工地震波.图21 是露头基岩处的$X$方向的加速度时程及其傅里叶幅值谱.这里假定为SV波垂直入射,在边界区近似为水平成层场地,将露头基岩处的地震波折减一半做为输入,采用传递矩阵方法,计算得到边界自由场,进而得到黏弹性边界的等效载荷,做为土-结相互作用分析的输入.
图21
图21
人工地震波加速度时程及其频谱
Fig. 21
Artificial seismic wave
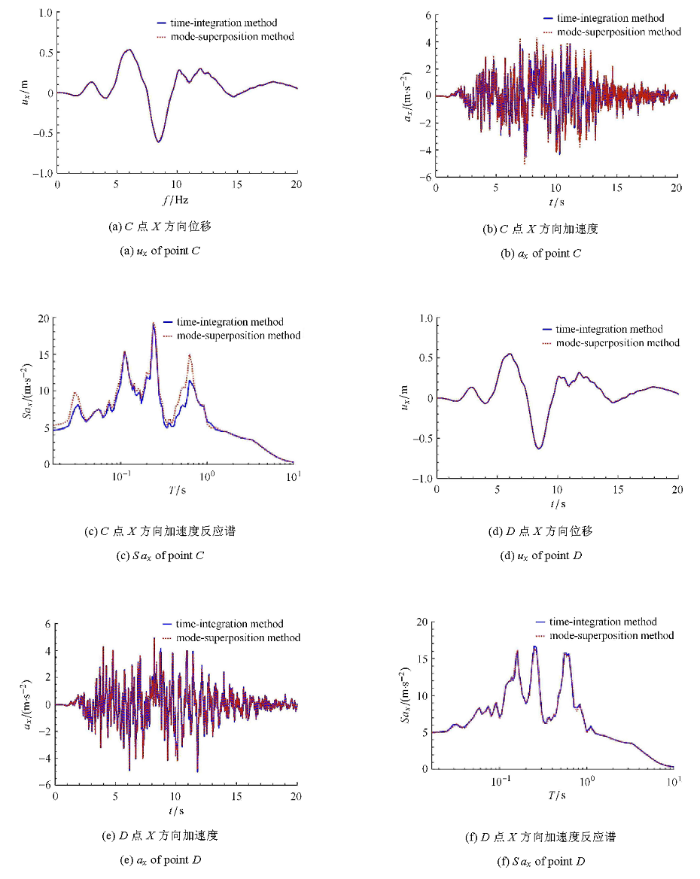
图 22 所示为$C, D,E$三点的位移、加速度和加速度反应谱 (阻尼比均为5%).从图22 可以看出,地震波输入时,结构阻尼模型对土体的位移响应基本没有影响.对离基础较近 ($C$点)的土体加速度存在影响,但对离基础较远的$D$和$E$点,则影响很小.
图22
图22
场地$X$方向反应时程及加速度反应谱
Fig. 22
$X$-direction displacements on site
图22
图22
场地$X$方向反应时程及加速度反应谱(续)
Fig. 22
$X$-direction displacements on site (continued)
图23 为基础的位移时程,由于SV波垂直入射,主要产生$X$方向的响应,其余方向的响应较小.从图中可以看出,阻尼模型对基础位移的影响较小.
图23
图23
基础位移时程
Fig. 23
Displacements of foundation
图23
图23
基础位移时程(续)
Fig. 23
Displacements of foundation (continued)
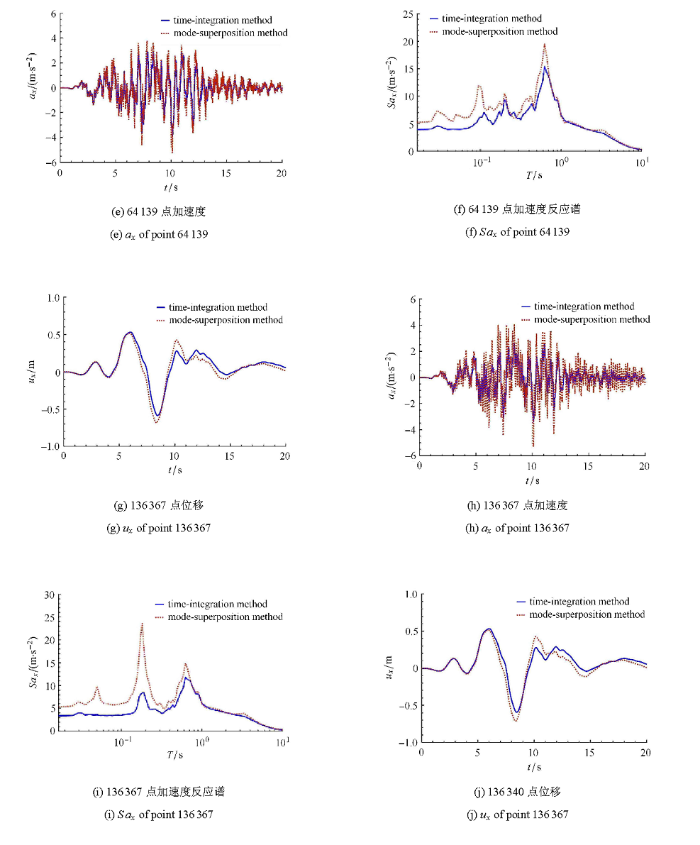
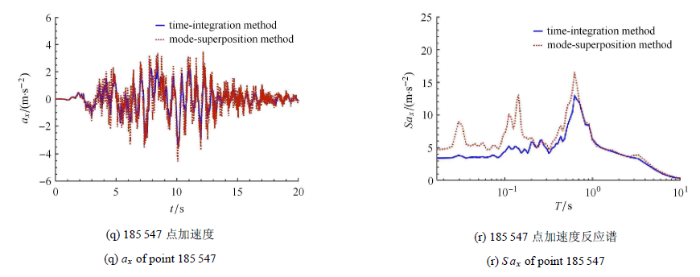
图24 为结构点的响应 (点号及位置见图18 和图19 ),从图中可以看出,结构阻尼模型对结构的响应影响较大,采用瑞利阻尼时结构的响应要比采用模态阻尼的小.从加速度反应谱可以看出,瑞利阻尼的结果要小于模态阻尼的结果,越靠近结构顶部越明显 (如图中185 547号点).这与图15 所示的核电结构各振型阻尼比一致,即尽在3.75 Hz至6.88 Hz的很小频段范围内,瑞利阻尼与模态阻尼较为接近,在其余频率,瑞利阻尼远大于模态阻尼,因此其反应明显小于模态阻尼的反应.
图24
图24
结构$X$方向位移、加速度及反应谱
Fig. 24
$X$-direction responses of structure
图24
图24
结构$X$方向位移、加速度及反应谱(续)
Fig. 24
$X$-direction responses of structure (continued)
图24
图24
结构$X$方向位移、加速度及反应谱(续)
Fig. 24
$X$-direction responses of structure (continued)
图24
图24
结构$X$方向位移、加速度及反应谱(续)
Fig. 24
$X$-direction responses of structure (continued)
3 结论
本文提出并实现了模态叠加和时步积分相结合的土-结动力相互作用分析的分区算法,可较为合理地考虑核电结构土-结相互作用分析中的阻尼. 该方法具有如下特点:(1)核电结构采用模态叠加法进行分析,可采用实测的模态阻尼;(2) 土体采用显式时步积分分析,可考虑土体的非线性和滞回阻尼;(3)半无限土体的辐射阻尼可通过黏弹性边界或透射边界计入;(4) 结构和土体可分别采用满足各自精度和稳定性要求的时间步距,且便于并行计算,效率较高.
通过算例验证了该分区算法的有效性.对某复杂场地上CAP1400核电模型的分析结果表明,结构分别采用瑞利阻尼和模态阻尼,对场地反应的影响不大,但对结构反应的影响较为明显. 因此,在核电结构的土-结相互作用分析中,需要合理选择阻尼模型.
参考文献
View Option
[1]
Seismic analysis of safety-related nuclear structure
ASCE standard, ASCE/SEI4-16
[本文引用: 1]
[2]
Liao ZP Wong HL . A transmitting boundary for the numerical simulation of elastic wave propagation
Soil Dynamics and Earthquake Engineering , 1984 ,3 :174 -183
[本文引用: 2]
[3]
刘晶波 , 李彬 . 三维黏弹性静-动力统一人工边界
中国科学: 工程科学材料科学 , 2005 ,35 (9 ):966 -980
[本文引用: 2]
( Liu Jingbo Li Bin . 3D viscoelastic static-dynamic unified artificial boundary
Chinese Science: Engineering Science Materials Science , 2005 ,35 (9 ):966 -980 (in Chinese))
[本文引用: 2]
[4]
谷音 , 刘晶波 , 杜义欣 . 三维一致黏弹性人工界及等效黏弹性边界单元
工程力学 , 2007 ,24 (12 ):31 -37
( Gu Yin Liu Jingbo Du Yixin . 3D consistent viscous-spring artificial boundary and viscous-spring boundary element
Engineering Mechanics , 2007 ,24 (12 ):31 -37 (in Chinese))
[5]
章小龙 , 李小军 , 陈国兴 等 . 黏弹性人工边界等效载荷算的改进方法
力学学报 , 2016 ,48 (5 ):1126 -1135
[本文引用: 2]
( Zhang Xiaolong Li Xiaojun Chen Guoxing , et al . An improved method for calculating equivalent load of viscoelastic artificial boundary
Chinese Journal of Theoretical and Applied Mechanics , 2016 ,48 (5 ):1126 -1135 (in Chinese))
[本文引用: 2]
[6]
Kausel E . Damping matrices revisited
Journal of Engineering Mechanics , 2014 ,140 (8 ):04014055
[本文引用: 1]
[7]
Luco JE . A note on classical damping matrices
Earthquake Engineering & Structural Dynamics , 2008 ,37 (4 ):615 -626
[8]
Chopra AK , McKenna F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation
Earthquake Engineering & Structural Dynamics , 2016 ,45 :193 -211
[9]
Luco JE Lanzi A . Optimal Caughey series representation of classical damping matrices
Soil Dynamics and Earthquake Engineering , 2017 ,92 :253 -265
[本文引用: 1]
[10]
Hall JF . Problems encountered from the use (or misues) of Rayleigh damping
Earthquake Engineering & Structural Dynamics , 2006 ,35 :525 -545
[11]
黄宗明 , 白绍良 , 赖明 . 结构地震反应时程分析中阻尼问题评述
地震工程与工程振动 , 1996 ,16 (2 ):95 -105
( Huang Zongming Bai Shaoling Lai Ming . Review of damping problems in time-history analysis of structural seismic response
Earthquake Engineering and Engineering Vibration , 1996 ,16 (2 ):95 -105 (in Chinese))
[12]
淡丹辉 , 孙利民 . 结构动力有限元分析的阻尼建模及评价
振动与冲击 , 2007 ,26 (2 ):121 -124
( Tan Danhui Sun Limin . Damping modeling and evaluation for dynamic finite element analysis of structures
Journal of Vibration and Shock , 2007 ,26 (2 ):121 -124 (in Chinese))
[13]
楼梦麟 , 张静 . 大跨度拱桥地震反应分析中阻尼模型的讨论
振动与冲击 , 2009 ,28 (5 ):22 -26
( Lou Menglin Zhang Jing . Discussion on damping models for seismic response analysis of long-span
Journal of Vibration and Shock , 2009 ,28 (5 ):22 -26 (in Chinese))
[14]
李田 . 结构时程动力分析中的阻尼取值研究
土木工程学报 , 1997 ,30 (3 ):68 -73
( Li Tian . Study on damping value in time-history dynamic analysis of structures
China Civil Engineering Journal , 1997 ,30 (3 ):68 -73 (in Chinese))
[15]
杨志勇 , 李桂清 , 瞿伟廉 . 结构阻尼的发展及其研究近况
武汉工业大学学报 , 2000 ,22 (3 ):38 -41
( Yang Zhiyong Li Guiqing Qu Weilian . Development of structural damping and recent research
Journal of Wuhan University of Technology , 2000 ,22 (3 ):38 -41 (in Chinese))
[16]
邹德高 , 徐斌 , 孔宪京 . 瑞利阻尼系数确定方法对高土石坝地震反应的影响研究
岩土力学 , 2011 ,32 (3 ):797 -803
[本文引用: 1]
( Zou Degao Xu Bin Kong Xianjing . Study of influence of different methods for calculating Rayleigh damping coefficient on high earth-rock dam seismic response
Rock and Soil Mechanics , 2011 ,32 (3 ):797 -803 (in Chinese))
[本文引用: 1]
[17]
李小军 , 侯春林 , 潘蓉 等 . 阻尼矩阵选取对核电厂结构地震响应的影响研究
振动与冲击 , 2015 ,34 (1 ):110 -116
[本文引用: 3]
( Li Xiaojun Hou Chunlin Pan Rong , et al . Effect analysis of damping matrix on seismic response of nuclear power plant structure
Journal of Vibration and Shock , 2015 ,34 (1 ):110 -116 (in Chinese))
[本文引用: 3]
[18]
Ostadan F Deng N . Computer Program: SASSI2010-A System for Analysis of Soil-Structure Interaction. Version1.1. Geotechnical and Hydraulic Engineering Services.
Bechtel National Inc., San Francisco, California , 2011
[本文引用: 2]
[19]
Bolisetti C Whittaker AS Mason HB , et al . Equivalent linear and nonlinear site response analysis for design and risk assessment of safety-related nuclear structures
Nuclear Engineering and Design , 2014 ,275 (8 ):107 -121
[本文引用: 1]
[20]
Coleman JL Bolisetti C Whittaker AS . Time-domain soil-structure interaction analysis of nuclear facilities
Nuclear Engineering and Design , 2016 ,298 :264 -270
[本文引用: 1]
[21]
Jeremic B Jie G Preisig M , et al . Time domain simulation of soil-foundation-structure interaction in non-uniform soils
Earthquake Engineering and Engineering Vibration , 2009 ,38 (5 ):699 -718
[本文引用: 1]
[22]
Kabanda J Kwon OS Kwon G . Time and frequency domain analyses of the Hualien large-scale seismic test
Nuclear Engineering and Design , 2015 ,295 :261 -275
[本文引用: 1]
[23]
陈少林 , 唐敢 , 刘启方 等 . 三维土-结构动力相作用的一种时域直接分析方法
地震工程与工程动 , 2010 ,30 (2 ):24 -31
[本文引用: 4]
( Chen Shaolin Tang Gang Liu Qifang , et al . A direct time-domain method for analysis of three-dimensional soil-structure dynamic interaction
Earthquake Engineering and Engineering Dynamics , 2010 ,30 (2 ):24 -31 (in Chinese))
[本文引用: 4]
[24]
陈少林 , 王俊泉 , 刘启方 等 . 基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法
中国科学:技术科学 , 2017 ,47 (12 ):1321 -1330
[本文引用: 4]
( Chen Shaolin Wang Junquan Liu Qifang , et al . Asynchronous parallel algorithm for three-dimensional soil-structure interaction analysis based on explicit-implicit integration scheme
Scientia Sinica Technologica , 2017 ,47 (12 ):1321 -1330 (in Chinese))
[本文引用: 4]
[25]
Leger P Ide IM Paultre P . Multiple support seismic analysis of large structures
Computers & Structures , 1990 ,36 (6 ):1153 -1158
[本文引用: 1]
[26]
胡聿贤 . 地震工程学. 第2版 . 北京 : 地震出版社 , 2006
( Hu Yixian . Seismic Engineering. Second Edition. Beijing : Seismological Press , 2006 (in Chinese))
[27]
周国良 , 李小军 , 刘必灯 等 . 大质量法在多点激励分析中的应用、误差分析及改进
工程力学 , 2011 ,28 (1 ):48 -54
[本文引用: 2]
( Zhou Guoliang Li Xiaojun Liu Bideng , et al . Error analysis and improvements of large mass method used in multi-support seismic excitation analysis
Engineering Mechanics , 2011 ,28 (1 ):48 -54 (in Chinese))
[本文引用: 2]
[28]
陈少林 , 朱学江 , 赵宇昕 等 . 考虑土骨架非线性的饱和土-结构相互作用分析
地震工程与工程振动 , 2019 ,39 (1 ):114 -127
[本文引用: 2]
( Chen Shaolin Zhu Xuejiang Zhao Yuxin , et al . Analysis of saturated soil-structure interaction considering nonlinearity of soil skeleton
Earthquake Engineering and Engineering Vibration , 2019 ,39 (1 ):114 -127 (in Chinese))
[本文引用: 2]
[29]
陈少林 , 赵宇昕 . 一种三维饱和土-基础-结构动力相互作用分析方法
力学学报 , 2016 ,48 (6 ):1362 -1371
[本文引用: 1]
( Chen Shaolin Zhao Yuxin . A method for three-dimensional saturated soil-foundation-structure dynamic interaction analysis
Chinese Journal of Theoretical and Applied Mechanics , 2016 ,48 (6 ):1362 -1371 (in Chinese))
[本文引用: 1]
[30]
Wolf JP . Dynamic Soil-Structure Interaction.
Prentice-Hall,Inc , 1985
[本文引用: 1]
Seismic analysis of safety-related nuclear structure
1
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
A transmitting boundary for the numerical simulation of elastic wave propagation
2
1984
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 式中,下标s, b, i和A分别表示结构节点、结构与基础的界面节点、土体节点和人工边界点.上标s和g分别表示结构和基础. 其中${\pmb K}_{\rm aa} $和${\pmb C}_{\rm aa}$分别为黏弹性边界的弹簧和阻尼系数矩阵,${\pmb f}_{\rm a}$为地震波输入时施加在人工边界节点上的等效载荷[3 -5 ] .若采用透射边界,可通过多次透射公式在人工边界上施加位移[2 ] .对方程 (1)通过时步积分方法直接进行求解,即为土-结相互作用的直接法或整体解法.若采用隐式解法,则需每时步求解大型方程组,计算量很大,十分耗时.若采用集中质量显式积分方法,每一时步不需求解大型方程组,但结构波速较大,稳定性要求时间步距较小,计算时步数较多,效率受影响. ...
三维黏弹性静-动力统一人工边界
2
2005
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 式中,下标s, b, i和A分别表示结构节点、结构与基础的界面节点、土体节点和人工边界点.上标s和g分别表示结构和基础. 其中${\pmb K}_{\rm aa} $和${\pmb C}_{\rm aa}$分别为黏弹性边界的弹簧和阻尼系数矩阵,${\pmb f}_{\rm a}$为地震波输入时施加在人工边界节点上的等效载荷[3 -5 ] .若采用透射边界,可通过多次透射公式在人工边界上施加位移[2 ] .对方程 (1)通过时步积分方法直接进行求解,即为土-结相互作用的直接法或整体解法.若采用隐式解法,则需每时步求解大型方程组,计算量很大,十分耗时.若采用集中质量显式积分方法,每一时步不需求解大型方程组,但结构波速较大,稳定性要求时间步距较小,计算时步数较多,效率受影响. ...
三维黏弹性静-动力统一人工边界
2
2005
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 式中,下标s, b, i和A分别表示结构节点、结构与基础的界面节点、土体节点和人工边界点.上标s和g分别表示结构和基础. 其中${\pmb K}_{\rm aa} $和${\pmb C}_{\rm aa}$分别为黏弹性边界的弹簧和阻尼系数矩阵,${\pmb f}_{\rm a}$为地震波输入时施加在人工边界节点上的等效载荷[3 -5 ] .若采用透射边界,可通过多次透射公式在人工边界上施加位移[2 ] .对方程 (1)通过时步积分方法直接进行求解,即为土-结相互作用的直接法或整体解法.若采用隐式解法,则需每时步求解大型方程组,计算量很大,十分耗时.若采用集中质量显式积分方法,每一时步不需求解大型方程组,但结构波速较大,稳定性要求时间步距较小,计算时步数较多,效率受影响. ...
三维一致黏弹性人工界及等效黏弹性边界单元
2007
三维一致黏弹性人工界及等效黏弹性边界单元
2007
黏弹性人工边界等效载荷算的改进方法
2
2016
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 式中,下标s, b, i和A分别表示结构节点、结构与基础的界面节点、土体节点和人工边界点.上标s和g分别表示结构和基础. 其中${\pmb K}_{\rm aa} $和${\pmb C}_{\rm aa}$分别为黏弹性边界的弹簧和阻尼系数矩阵,${\pmb f}_{\rm a}$为地震波输入时施加在人工边界节点上的等效载荷[3 -5 ] .若采用透射边界,可通过多次透射公式在人工边界上施加位移[2 ] .对方程 (1)通过时步积分方法直接进行求解,即为土-结相互作用的直接法或整体解法.若采用隐式解法,则需每时步求解大型方程组,计算量很大,十分耗时.若采用集中质量显式积分方法,每一时步不需求解大型方程组,但结构波速较大,稳定性要求时间步距较小,计算时步数较多,效率受影响. ...
黏弹性人工边界等效载荷算的改进方法
2
2016
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 式中,下标s, b, i和A分别表示结构节点、结构与基础的界面节点、土体节点和人工边界点.上标s和g分别表示结构和基础. 其中${\pmb K}_{\rm aa} $和${\pmb C}_{\rm aa}$分别为黏弹性边界的弹簧和阻尼系数矩阵,${\pmb f}_{\rm a}$为地震波输入时施加在人工边界节点上的等效载荷[3 -5 ] .若采用透射边界,可通过多次透射公式在人工边界上施加位移[2 ] .对方程 (1)通过时步积分方法直接进行求解,即为土-结相互作用的直接法或整体解法.若采用隐式解法,则需每时步求解大型方程组,计算量很大,十分耗时.若采用集中质量显式积分方法,每一时步不需求解大型方程组,但结构波速较大,稳定性要求时间步距较小,计算时步数较多,效率受影响. ...
Damping matrices revisited
1
2014
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
A note on classical damping matrices
2008
McKenna F. Modeling viscous damping in nonlinear response history analysis of buildings for earthquake excitation
2016
Optimal Caughey series representation of classical damping matrices
1
2017
... 当采用时域逐步积分方法时,土体可采用非线性黏弹性本构,能较为合理地反应其非线性特性.对于结构而言,时步积分法常采用的阻尼模型为瑞利阻尼模型和Caughy阻尼模型.瑞利阻尼与质量和刚度成正比,通常称为比例阻尼,通过两阶模态的频率和阻尼比来确定两个比例常数.当对地震反应起主要贡献的结构模态数为两个时,采用这两个模态的频率和阻尼比确定的瑞利阻尼可以较准确地反应这两个模态的阻尼比,由瑞利阻尼模型计算的反应较为准确.但当对地震反应有贡献的模态数较多时,瑞利阻尼能较准确反应指定阻尼的两阶模态阻尼,其余模态阻尼与真实情况有误差,使得多数模态反应失真,造成地震反应与真实解有较大差异.邹德高等[16 ] 、李小军等[17 ] 分别改进了瑞利阻尼模型中两系数的确定方法,并分别对土石坝和核电厂房进行了地震反应分析,但本质上未改变瑞利阻尼模型的实质,仍是通过同样的函数来近似阻尼.Caughy阻尼模型通过级数形式描述阻尼,可以使得更多阶的模态阻尼比满足规定值,但在通过满足多个模态阻尼比确定级数的系数时,有时会出现系数矩阵为奇异的情形,造成系数求解的困难.另外,Caughy阻尼在高频时可能出现负阻尼情形,影响计算的失稳.Luco等[9 ] 提出了一种Caughy阻尼系数优化方法,可以避免上述相关问题. ...
Problems encountered from the use (or misues) of Rayleigh damping
2006
瑞利阻尼系数确定方法对高土石坝地震反应的影响研究
1
2011
... 当采用时域逐步积分方法时,土体可采用非线性黏弹性本构,能较为合理地反应其非线性特性.对于结构而言,时步积分法常采用的阻尼模型为瑞利阻尼模型和Caughy阻尼模型.瑞利阻尼与质量和刚度成正比,通常称为比例阻尼,通过两阶模态的频率和阻尼比来确定两个比例常数.当对地震反应起主要贡献的结构模态数为两个时,采用这两个模态的频率和阻尼比确定的瑞利阻尼可以较准确地反应这两个模态的阻尼比,由瑞利阻尼模型计算的反应较为准确.但当对地震反应有贡献的模态数较多时,瑞利阻尼能较准确反应指定阻尼的两阶模态阻尼,其余模态阻尼与真实情况有误差,使得多数模态反应失真,造成地震反应与真实解有较大差异.邹德高等[16 ] 、李小军等[17 ] 分别改进了瑞利阻尼模型中两系数的确定方法,并分别对土石坝和核电厂房进行了地震反应分析,但本质上未改变瑞利阻尼模型的实质,仍是通过同样的函数来近似阻尼.Caughy阻尼模型通过级数形式描述阻尼,可以使得更多阶的模态阻尼比满足规定值,但在通过满足多个模态阻尼比确定级数的系数时,有时会出现系数矩阵为奇异的情形,造成系数求解的困难.另外,Caughy阻尼在高频时可能出现负阻尼情形,影响计算的失稳.Luco等[9 ] 提出了一种Caughy阻尼系数优化方法,可以避免上述相关问题. ...
瑞利阻尼系数确定方法对高土石坝地震反应的影响研究
1
2011
... 当采用时域逐步积分方法时,土体可采用非线性黏弹性本构,能较为合理地反应其非线性特性.对于结构而言,时步积分法常采用的阻尼模型为瑞利阻尼模型和Caughy阻尼模型.瑞利阻尼与质量和刚度成正比,通常称为比例阻尼,通过两阶模态的频率和阻尼比来确定两个比例常数.当对地震反应起主要贡献的结构模态数为两个时,采用这两个模态的频率和阻尼比确定的瑞利阻尼可以较准确地反应这两个模态的阻尼比,由瑞利阻尼模型计算的反应较为准确.但当对地震反应有贡献的模态数较多时,瑞利阻尼能较准确反应指定阻尼的两阶模态阻尼,其余模态阻尼与真实情况有误差,使得多数模态反应失真,造成地震反应与真实解有较大差异.邹德高等[16 ] 、李小军等[17 ] 分别改进了瑞利阻尼模型中两系数的确定方法,并分别对土石坝和核电厂房进行了地震反应分析,但本质上未改变瑞利阻尼模型的实质,仍是通过同样的函数来近似阻尼.Caughy阻尼模型通过级数形式描述阻尼,可以使得更多阶的模态阻尼比满足规定值,但在通过满足多个模态阻尼比确定级数的系数时,有时会出现系数矩阵为奇异的情形,造成系数求解的困难.另外,Caughy阻尼在高频时可能出现负阻尼情形,影响计算的失稳.Luco等[9 ] 提出了一种Caughy阻尼系数优化方法,可以避免上述相关问题. ...
阻尼矩阵选取对核电厂结构地震响应的影响研究
3
2015
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 当采用时域逐步积分方法时,土体可采用非线性黏弹性本构,能较为合理地反应其非线性特性.对于结构而言,时步积分法常采用的阻尼模型为瑞利阻尼模型和Caughy阻尼模型.瑞利阻尼与质量和刚度成正比,通常称为比例阻尼,通过两阶模态的频率和阻尼比来确定两个比例常数.当对地震反应起主要贡献的结构模态数为两个时,采用这两个模态的频率和阻尼比确定的瑞利阻尼可以较准确地反应这两个模态的阻尼比,由瑞利阻尼模型计算的反应较为准确.但当对地震反应有贡献的模态数较多时,瑞利阻尼能较准确反应指定阻尼的两阶模态阻尼,其余模态阻尼与真实情况有误差,使得多数模态反应失真,造成地震反应与真实解有较大差异.邹德高等[16 ] 、李小军等[17 ] 分别改进了瑞利阻尼模型中两系数的确定方法,并分别对土石坝和核电厂房进行了地震反应分析,但本质上未改变瑞利阻尼模型的实质,仍是通过同样的函数来近似阻尼.Caughy阻尼模型通过级数形式描述阻尼,可以使得更多阶的模态阻尼比满足规定值,但在通过满足多个模态阻尼比确定级数的系数时,有时会出现系数矩阵为奇异的情形,造成系数求解的困难.另外,Caughy阻尼在高频时可能出现负阻尼情形,影响计算的失稳.Luco等[9 ] 提出了一种Caughy阻尼系数优化方法,可以避免上述相关问题. ...
... 根据上述原理,我们编制了相应的计算程序,实现了模态叠加和时步积分结合的三维土-结相互作用分析的分区并行计算方法.对于无限域土体和基础的动力响应,采用自编的Fortran程序进行分析.对于结构响应,其每一时步的计算独立于土体的计算,因此可使用ANSYS等商业软件进行分析,结构和土体可分别采用不同的时间步距.通过耦合算法和Fortran程序与ANSYS之间的交互,实现土-结相互作用动力分析.由于采用分区计算方式,土体和结构可以独立进行建模,且在每一时步,两者独立进行计算.土体采用MPI协议,编程实现并行.结构可采用ANSYS中的并行计算方案.土体和结构之间的并行通过异步传输数据实现,具体见文献[17 ] .下面,通过一简单模型的算例对该方法进行验证,并对某非均匀场址上CAP1400核电结构的反应进行分析. ...
阻尼矩阵选取对核电厂结构地震响应的影响研究
3
2015
... 规范规定,核电屏蔽厂房的地震反应分析需要考虑土-结相互作用的影响[1 ] .在核电结构的土-结动力相互作用分析中,阻尼是影响结构反应的一个重要因素.另外,出于安全性考虑,核电结构一般不允许进入非线性;而土体在地震作用下,容易进入非线性,因此土体非线性是影响土-结系统反应的另一重要因素.如何合理考虑阻尼和土体非线性是土-结动力相互作用分析的关键问题.其中,辐射阻尼一般通过人工边界条件来考虑,如透射边界[2 ] ,黏弹性人工边界[3 -5 ] 等.这里主要讨论结构材料阻尼[6 -17 ] 和土体非线性. ...
... 当采用时域逐步积分方法时,土体可采用非线性黏弹性本构,能较为合理地反应其非线性特性.对于结构而言,时步积分法常采用的阻尼模型为瑞利阻尼模型和Caughy阻尼模型.瑞利阻尼与质量和刚度成正比,通常称为比例阻尼,通过两阶模态的频率和阻尼比来确定两个比例常数.当对地震反应起主要贡献的结构模态数为两个时,采用这两个模态的频率和阻尼比确定的瑞利阻尼可以较准确地反应这两个模态的阻尼比,由瑞利阻尼模型计算的反应较为准确.但当对地震反应有贡献的模态数较多时,瑞利阻尼能较准确反应指定阻尼的两阶模态阻尼,其余模态阻尼与真实情况有误差,使得多数模态反应失真,造成地震反应与真实解有较大差异.邹德高等[16 ] 、李小军等[17 ] 分别改进了瑞利阻尼模型中两系数的确定方法,并分别对土石坝和核电厂房进行了地震反应分析,但本质上未改变瑞利阻尼模型的实质,仍是通过同样的函数来近似阻尼.Caughy阻尼模型通过级数形式描述阻尼,可以使得更多阶的模态阻尼比满足规定值,但在通过满足多个模态阻尼比确定级数的系数时,有时会出现系数矩阵为奇异的情形,造成系数求解的困难.另外,Caughy阻尼在高频时可能出现负阻尼情形,影响计算的失稳.Luco等[9 ] 提出了一种Caughy阻尼系数优化方法,可以避免上述相关问题. ...
... 根据上述原理,我们编制了相应的计算程序,实现了模态叠加和时步积分结合的三维土-结相互作用分析的分区并行计算方法.对于无限域土体和基础的动力响应,采用自编的Fortran程序进行分析.对于结构响应,其每一时步的计算独立于土体的计算,因此可使用ANSYS等商业软件进行分析,结构和土体可分别采用不同的时间步距.通过耦合算法和Fortran程序与ANSYS之间的交互,实现土-结相互作用动力分析.由于采用分区计算方式,土体和结构可以独立进行建模,且在每一时步,两者独立进行计算.土体采用MPI协议,编程实现并行.结构可采用ANSYS中的并行计算方案.土体和结构之间的并行通过异步传输数据实现,具体见文献[17 ] .下面,通过一简单模型的算例对该方法进行验证,并对某非均匀场址上CAP1400核电结构的反应进行分析. ...
Computer Program: SASSI2010-A System for Analysis of Soil-Structure Interaction. Version1.1. Geotechnical and Hydraulic Engineering Services.
2
2011
... 土-结动力相互作用分析可采用频域方法,如软件SASSI[18 ] .频域方法可直接采用具有试验观测基础的滞回阻尼模型,对于线性问题而言,可得到准确的结果,当考虑土体非线性时,需通过等效线性化进行处理.大多数研究表明,等效线性化适合于土体弱非线性,对于强非线性,宜采用时域逐步积分方法[19 ] .若采用时域分析之模态叠加法进行土-结动力相互作用分析,可以直接采用规范规定的模态阻尼比,当体系的反应主要由低阶模态控制时,具有运算速度快,阻尼输入准确等优点,但原则上不适合于非线性分析. ...
... 综上所述,核电结构不允许进入非线性,采用模态叠加法可简便合理地记入模态阻尼.非基岩场地在地震作用下容易进入非线性,宜通过非线性黏弹性本构描述非基岩场地特性,采用时步积分法进行分析.目前土-结相互作用分析常用的软件SASSI[18 ] ,采用频域分析方法,通过等效线性化方法考虑土体非线性,在强震时不能很好地体现土体特性,且不能考虑土与基础间的接触非线性[20 -21 ] .采用ANSYS,ABAQUS,OpenSees等软件,结构和土体只能采用相同的分析方法 (要么都采用时步积分法,或都采用模态叠加法),且计算效率较低[22 ] (23 961个节点,18 200个单元,8000时步数,在Intel Core i72.93 GHz,8 GB内存的微机上用时4周).因此,有必要发展一种能合理考虑结构阻尼和土体非线性的高效时域土-结相互作用分析方法. ...
Equivalent linear and nonlinear site response analysis for design and risk assessment of safety-related nuclear structures
1
2014
... 土-结动力相互作用分析可采用频域方法,如软件SASSI[18 ] .频域方法可直接采用具有试验观测基础的滞回阻尼模型,对于线性问题而言,可得到准确的结果,当考虑土体非线性时,需通过等效线性化进行处理.大多数研究表明,等效线性化适合于土体弱非线性,对于强非线性,宜采用时域逐步积分方法[19 ] .若采用时域分析之模态叠加法进行土-结动力相互作用分析,可以直接采用规范规定的模态阻尼比,当体系的反应主要由低阶模态控制时,具有运算速度快,阻尼输入准确等优点,但原则上不适合于非线性分析. ...
Time-domain soil-structure interaction analysis of nuclear facilities
1
2016
... 综上所述,核电结构不允许进入非线性,采用模态叠加法可简便合理地记入模态阻尼.非基岩场地在地震作用下容易进入非线性,宜通过非线性黏弹性本构描述非基岩场地特性,采用时步积分法进行分析.目前土-结相互作用分析常用的软件SASSI[18 ] ,采用频域分析方法,通过等效线性化方法考虑土体非线性,在强震时不能很好地体现土体特性,且不能考虑土与基础间的接触非线性[20 -21 ] .采用ANSYS,ABAQUS,OpenSees等软件,结构和土体只能采用相同的分析方法 (要么都采用时步积分法,或都采用模态叠加法),且计算效率较低[22 ] (23 961个节点,18 200个单元,8000时步数,在Intel Core i72.93 GHz,8 GB内存的微机上用时4周).因此,有必要发展一种能合理考虑结构阻尼和土体非线性的高效时域土-结相互作用分析方法. ...
Time domain simulation of soil-foundation-structure interaction in non-uniform soils
1
2009
... 综上所述,核电结构不允许进入非线性,采用模态叠加法可简便合理地记入模态阻尼.非基岩场地在地震作用下容易进入非线性,宜通过非线性黏弹性本构描述非基岩场地特性,采用时步积分法进行分析.目前土-结相互作用分析常用的软件SASSI[18 ] ,采用频域分析方法,通过等效线性化方法考虑土体非线性,在强震时不能很好地体现土体特性,且不能考虑土与基础间的接触非线性[20 -21 ] .采用ANSYS,ABAQUS,OpenSees等软件,结构和土体只能采用相同的分析方法 (要么都采用时步积分法,或都采用模态叠加法),且计算效率较低[22 ] (23 961个节点,18 200个单元,8000时步数,在Intel Core i72.93 GHz,8 GB内存的微机上用时4周).因此,有必要发展一种能合理考虑结构阻尼和土体非线性的高效时域土-结相互作用分析方法. ...
Time and frequency domain analyses of the Hualien large-scale seismic test
1
2015
... 综上所述,核电结构不允许进入非线性,采用模态叠加法可简便合理地记入模态阻尼.非基岩场地在地震作用下容易进入非线性,宜通过非线性黏弹性本构描述非基岩场地特性,采用时步积分法进行分析.目前土-结相互作用分析常用的软件SASSI[18 ] ,采用频域分析方法,通过等效线性化方法考虑土体非线性,在强震时不能很好地体现土体特性,且不能考虑土与基础间的接触非线性[20 -21 ] .采用ANSYS,ABAQUS,OpenSees等软件,结构和土体只能采用相同的分析方法 (要么都采用时步积分法,或都采用模态叠加法),且计算效率较低[22 ] (23 961个节点,18 200个单元,8000时步数,在Intel Core i72.93 GHz,8 GB内存的微机上用时4周).因此,有必要发展一种能合理考虑结构阻尼和土体非线性的高效时域土-结相互作用分析方法. ...
三维土-结构动力相作用的一种时域直接分析方法
4
2010
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... [23 ,24 ]中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... 求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下 ...
三维土-结构动力相作用的一种时域直接分析方法
4
2010
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... [23 ,24 ]中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... 求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下 ...
基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法
4
2017
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... ,24 ]中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... 求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下 ...
基于显-隐式格式的三维时域土-结相互作用分析的异步并行算法
4
2017
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... ,24 ]中,结构采用Newmark积分方法,这里采用模态叠加法. ...
... 求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下 ...
Multiple support seismic analysis of large structures
1
1990
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
大质量法在多点激励分析中的应用、误差分析及改进
2
2011
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下 ...
大质量法在多点激励分析中的应用、误差分析及改进
2
2011
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 求得结构基底的反应后,即可得到式 (5)右端的载荷项,可由模态叠加法求得结构的响应以及结构给基础的反力.若结构模型较为复杂,则每一时步求得式 (5)右端项较为麻烦.由式 $ (7)\sim$式 (9)求得结构与基础界面点的加速度等响应后,由于连续条件,将界面点的响应施加于结构底部,相当于是多点激励下的结构分析,并将结构对基础的作用力反馈给基础,如图2 所示,关于刚性基础情形,见文献[23 ,24 ] .这里,我们考虑加速度连续,通过大质量法[27 ] 将加速度施加于结构底部,因此,上部结构的运动方程如下 ...
考虑土骨架非线性的饱和土-结构相互作用分析
2
2019
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
考虑土骨架非线性的饱和土-结构相互作用分析
2
2019
... 本文在显-隐式时域土-结相互作用分区算法的研究基础上[23 -24 ] ,改用模态叠加法进行结构分析,土体仍采用集中质量显式有限元方法结合人工边界条件进行模拟,在每一时步,通过大质量法[25 -27 ] 进行多点激励输入,实现了模态叠加和时步积分结合的土-结相互作用分区混合算法.该方法能合理地考虑辐射阻尼和结构的材料阻尼,也可考虑土体的非线性[28 ] .另外,结构和土体可采用不同的时间步距,且方便采用并行计算技术,具有较高的效率.通过简单算例对该方法进行了验证,并对某复杂场地上CAP1400核电模型进行了土-结相互作用分析,对比分析了结构阻尼模型对核电结构反应的影响. ...
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
一种三维饱和土-基础-结构动力相互作用分析方法
1
2016
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
一种三维饱和土-基础-结构动力相互作用分析方法
1
2016
... 由式 (7) ~式 (9)求得土体和基础$(p +1)$时刻的反应后,则式 (5)的右端项已知,可求得结构$(p +1)$时刻的反应,包括结 构作用在基础上$(p + 1)$时刻的载荷.我们称该方法为分区方法 (partitioned method),分区方法的优点是土体和结构可独立建模,采用适合各自特点的分析方法,在每一时步独立分析,且可采用不同的时间步距,便于独立开发各自的分析程序,或应用已有的分析程序,因此具有较大的灵活性和较高的效率.分区方法的缺点是有可能失稳,其失稳机理和稳定性条件还有待进一步研究.我们已编制相应的并行计算程序,实现了土-结相互作用的分区分析,称之为PASSI (partitioned analysisof soil-structure interaction) [23 -24 ,28 -29 ] .在文献[23 ,24 ] 中,结构采用Newmark积分方法,这里采用模态叠加法. ...
Dynamic Soil-Structure Interaction.
1
1985
... 消去方程 (2)中土体节点的自由度,可得[30 ] ...