引言
隧洞是广泛应用于水电、交通、矿山及军事工程领域的常用地下结构.近来,随着我国经济的持续发展及高新技术的不断应用,我国的隧洞工程得到了前所未有的迅速发展,支护-围岩相互作用,以及如何保证隧洞围岩的稳定性是我们要研究的基本问题[1 -2 ] .
利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解.
Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解.
隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触.
完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性.
本文同样将通过库仑摩擦模型模拟接触面上的切向力学行为,但不同于文献[28 ] ,本文在优化过程中减少了设计变量的个数,极大地简化了优化模型. 在弹性接触分析中,库仑摩擦模型可表述如下
(1) $ \left| {\tau _{r\theta } } \right| \leqslant f_r \left| {\sigma _r } \right|$
式中,$\tau _{r\theta } $ 接触面上的剪应力,$\sigma _r $为接触面法向压力,$f_r $ 为接触界面综合摩擦系数.该表达实质上是静摩擦力的屈服条件或接触面的滑移条件,将切向力与径向压力联系起来.这种接触条件最符合实际情况,即为摩擦滑动接触.本文基于平面应变假定,将围岩和衬砌视为各向同性线弹性体,考虑支护滞后效应,利用复变函数方法推导出深埋圆形隧洞在原始地应力和衬砌内部静水压力共同作用下围岩与衬砌在摩擦滑动接触情况下的解析解,为隧洞围岩和衬砌接触的支护设计计算提供理论基础.
1 基本原理及方法
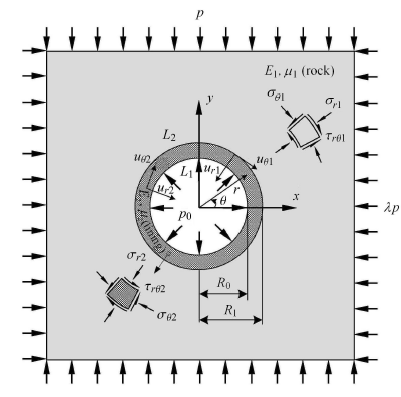
如图1 所示,为在原始地应力和静水压力共同作用下圆形衬砌支护隧洞.在开挖之前,围岩无穷远处水平和竖直方向的原始地应力分别为:$\sigma_h^\infty = \lambda p$,$\sigma _v^\infty = p$,$\lambda $为侧压力系数,定义拉应力为负,压应力为正.隧洞衬砌的内外半径分别为$R_0 $ 和$R_1$,定义径向和$x$方向的夹角为$\theta $,以逆时针为正.
图1
图1
原始地应力和静水压力共同作用下深埋圆形衬砌隧洞
Fig. 1
Lined circular tunnel under in situ stresses and uniform hydrostatic pressure
1.1 摩擦滑动接触的准则及数学模型
当围岩和衬砌间的接触为摩擦滑动接触时,由于围岩和衬砌之间的摩擦作用,接触面可以传递剪力,但允许围岩与衬砌之间的切向相对滑动,本文将通过最优化方法来处理这样的问题.当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,围岩和衬砌间接触面间将产生相对滑动,接触面两侧,即围岩一侧和衬砌一侧的切向位移将产生间断,即在$r = R_1 $的接触面上,会存在$u_{\theta 1} \ne u_{\theta 2} $ 的区域.本文作者提出在保证围岩与衬砌之间剪应力小于或者等于接触面所能提供的摩擦力前提下,将接触面间产生最小滑移量的状态作为衬砌的真实工作状态.这样的准则可以用最优化的数学模型表示为
(2) $ \left. \min F({\pmb X}),{\pmb X} \in D \\ D: \ \ b_j ({\pmb X}) \geqslant 0 \right\}$
其中,$F({\pmb X}) = \left| {u_{\theta 1} - u_{\theta 2} }\right|$,$b_j ({\pmb X}) \geqslant 0$为库仑摩擦模型表示的不等式组.
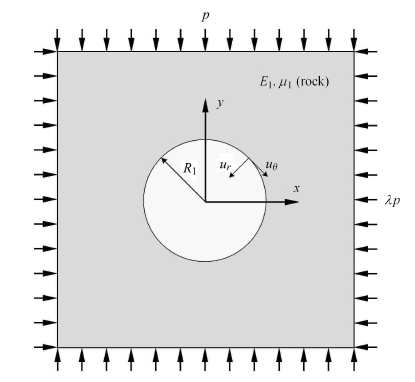
1.2 仅开挖作用时引起的围岩位移
如图2 所示在隧洞开挖之后,假设没有支护,围岩会完成相应的位移.此时围岩内任一点的径向位移$u_r $ 和切向位移$u_\theta $可以表示为[13 ]
(3) $ u_r + {\rm i}u_\theta = \dfrac{1}{2G_1 }{\rm e}^{ - {\rm i}\theta } \left[ {\kappa _1 \dfrac{ - p(1 - \lambda )}{2}\dfrac{R_1^2 }{z} - \dfrac{p(1 - \lambda)}{2}\dfrac{zR_1^2 }{\overline z ^2}} \right.+ \\ \left. { \dfrac{p(1 + \lambda )}{2}\dfrac{R_1^2 }{\overline z } + \dfrac{p(1 -\lambda )}{2}\dfrac{R_1^4 }{\overline z ^3}} \right]$
式中,$R_1 $ 为无支护隧洞的半径,$z$ 是一个复数且$z = R_1 {\rm e}^{{\rm i}\theta }$,$\kappa _1 = 3- 4\mu _1 $,$G_1 = E_1 / [2(1 + \mu _1 )]$,$\mu _1 $,$E_1 $和$G_1 $ 分别是岩石的泊松比、弹性模量和剪切模量. 式 (3)即隧洞开挖后无支护时围岩的全部位移.
图 2
图 2
开挖引起的围岩位移
Fig. 2
Surrounding rock displacement caused by excavation
1.3 求解围岩和衬砌解析函数的基本方程
(4) $ \sigma _r = 2 {\rm Re} \left[ {{\varphi }'_0 (z)} \right] - {\rm Re}\left\{ {{\rm e}^{2{\rm i}\theta } \left[ {\overline z {\varphi }''_0 (z) + {\psi }'_0 (z)} \right]} \right\}$
(5) $ \sigma _\theta = 2{\rm Re}\left[ {{\varphi }'_0 (z)} \right] + {\rm Re}\left\{ {{\rm e}^{2{\rm i}\theta } \left[ {\overline z {\varphi }''_0 (z) + {\psi }'_0 (z)} \right]} \right\}$
(6) $ \tau _{r\theta } = {\rm Im} \left\{ {{\rm e}^{2{\rm i}\theta } \left[ {\overline z {\varphi }''_0 (z) + {\psi }'_0 (z)} \right]} \right\}$
(7) $ u_r = \dfrac{1}{2G}{\rm Re}\left\{ {{\rm e}^{ - {\rm i}\theta } \left[ {\kappa \varphi _0 (z) - z\overline {{\varphi }'_0 (z)} - \overline {\psi _0 (z)} } \right]} \right\}$
(8) $ u_\theta = \dfrac{1}{2G}{\rm Im}\left\{ {{\rm e}^{-{\rm i}\theta } \left[ {\kappa \varphi _0 (z) - z\overline {{\varphi }'_0 (z)} - \overline {\psi _0 (z)} } \right]} \right\}$
其中,$\varphi _0 \left( z \right)$和$\psi _0\left( z \right)$ 是关于围岩或者衬砌的两个解析函数.若能求出满足边界条件的围岩和衬砌的两个解析函数,则应力分量和位移分量均可以利用上述结果得出.
隧洞开挖后进行支护,围岩和衬砌相互作用.围岩对应的两个解析函数为[13 ]
(9) $ \varphi _1 (z) = \sum_{k = 1}^\infty {c_k z^{ - k}} , \ \ \psi _1 (z) = \sum_{k = 1}^\infty {d_k z^{ - k}}$
(10) $ \left.\varphi _2 (z) = \sum_{k = 1}^\infty {e_k z^{ - k}} + \sum_{k =1}^\infty {f_k z^k} \\ psi _2 (z) = \sum_{k = 1}^\infty {g_k z^{ - k}} + \sum_{k =1}^\infty {h_k z^k} \right\}$
式 (9) 和式 (10) 中的系数$c_k $,$d_k $,$e_k $,$f_k $,$g_k $ 和$h_k $ 都是待求的实常数.
通过衬砌内边界$L_1 $ 的应力边界条件和围岩衬砌接触面$L_2 $ 的接触条件可以建立求解解析函数系数的基本方程.
用$\sigma _{r2} $,$\sigma _{\theta 2} $,$\tau _{r\theta 2} $分别表示衬砌的径向应力、环向应力和剪应力. 在衬砌内边界$L_1 $上,作用有大小为$p_0 $的静水压力,则其应力边界条件可以表示为 (式中$z = R_0 {\rm e}^{{\rm i}\theta }$)
(11) $ \sigma _{r2} = 2{\rm Re} \left[ {{\varphi }'_2 (z)} \right]-{\rm Re} \left\{ { {\rm e}^{2{\rm i}\theta }\left[ {\overline z {\varphi }''_2 (z) + {\psi }'_2 (z)} \right]} \right\} = p_0$
(12) $ \tau _{r\theta 2} = {\rm Im}\left\{ {{\rm e}^{2{\rm i}\theta } \left[ {\overline z {\varphi }''_2 (z) + {\psi }'_2 (z)} \right]} \right\} = 0$
用$\sigma _{r1} $,$\sigma _{\theta 1} $,$\tau _{r\theta 1} $分别表示围岩的径向应力,环向应力和剪应力. 在围岩衬砌接触面$L_2 $上,围岩和衬砌的径向应力和剪应力连续,其应力连续条件可以表示为
(13) $ \sigma _{r1} = \sigma _{r2}$
(14) $ \tau _{r\theta 1} = \tau _{r\theta 2}$
即 (式中$z = R_1 {\rm e}^{{\rm i}\theta }$)
(15) $ \!\! 2 {\rm Re} \left[ {{\varphi }'_1 (z)} \right]- {\rm Re} \left\{ {{\rm e}^{2{\rm i}\theta }\left[ {\overline z {\varphi }''_1 (z) + {\psi }'_1 (z)} \right]} \right\} = \\ \qquad 2{\rm Re}\left[ {{\varphi }'_2 (z)} \right] - {\rm Re}\left\{ {{\rm e}^{2{\rm i}\theta }\left[ {\overline z {\varphi }''_2 (z) + {\psi }'_2 (z)} \right]} \right\}$
(16) $ {\rm Im}\left\{ {{\rm e}^{2{\rm i}\theta } \left[ {\overline z {\varphi }''_1 (z) + {\psi }'_1 (z)} \right]} \right\} = {\rm Im}\left\{ {{\rm e}^{2{\rm i}\theta }\left[ {\overline z {\varphi }''_2 (z) + {\psi }'_2 (z)} \right]} \right\}$
本文考虑支护滞后的隧洞开挖过程,$\eta $为位移释放系数,如果$\eta =0$,即隧洞在开挖后立即进行支护,围岩在支护之前没有发生位移.明显这不符合工程实际,即使在开挖后立即安装支护,也不可避免地在围岩中发生了一部分变形.假设隧洞位移在完成了最大位移$u_r + {\rm i}u_\theta $ 的$\eta(0 \leqslant \eta \leqslant 1)$倍后,再进行支护,此时围岩完成的位移为$\eta (u_r + {i}u_\theta )$.设置衬砌以后,围岩和衬砌相互作用,支护限制了部分围岩位移的产生,此时围岩的位移表示为$u_{r1} + {\rm i}u_{\theta 1} $.而在围岩作用下,衬砌的位移可以表示为$u_{r2} + {\rm i}u_{\theta2} $.
在围岩衬砌接触面$L_2 $ 上,根据法向位移连续条件可得,其中$z =R_1 {\rm e}^{{\rm i}\theta }$
(17) $ (1 - \eta )u_r + \dfrac{1}{2G_1 }{\rm Re}\left\{ {{\rm e}^{-{\rm i}\theta } \left[ {\kappa _1 \varphi _1 (z) - z\overline {{\varphi }'_1 (z)}-\overline {\psi _1 (z)} } \right]} \right\} =\\ \dfrac{1}{2G_2 } {\rm Re}\left\{ {{\rm e}^{ - {\rm i}\theta }\left[ {\kappa _2 \varphi _2 (z) - z\overline {{\varphi }'_2 (z)} - \overline {\psi _2 (z)} } \right]} \right\}$
式中$\kappa _2 = 3 - 4\mu _2 $,$G_2 = E_2 / [2(1 + \mu _2 )]$. $\mu _2 $,$E_2 $ 和$G_2 $ 分别是衬砌的泊松比、弹性模量和剪切模量.
将相应的$z$值代入式 (9)~式 (12),式 (15)~式 (17),利用幂级数解法,比较$\theta$的同幂次项系数,可得到关于系数$c_k $,$d_{k + 2} $,$e_k$,$f_{k + 2} $,$g_{k + 2} $ 和$h_k $ 的方程,其中$k\geqslant 1$. 联立所有方程,整理后发现当$k \geqslant 2$ 时,$c_k$,$d_{k + 2} $,$e_k $,$f_{k + 2} $,$g_{k + 2} $ 和$h_k$都为0,只有$c_1 $,$d_1 $,$d_3 $,$e_1 $,$f_1 $,$f_3$,$g_1 $,$g_3 $ 和$h_1 $为非零实数,可得方程 (18)~式 (25)
(18) $ 2R_0^2 f_1 + g_1 = R_0^2 p_0$
(19) $ e_1 + 3R_0^4 f_3 + R_0^2 h_1 = {0}$
(20) $ R_0^2 e_1 - R_0^6 f_3 - g_3 = {0}$
(21) $ d_1 - 2R_1^2 f_1 - g_1 = 0$
(22) $ d_3 - 4R_1^6 f_3 - g_3 - R_1^4 h_1 = 0$
(23) $ 2R_1^2 c_1 - d_3 - 2R_1^2 e_1 - 2R_1^6 f_3 + g_3 - R_1^4 h_1 = 0$
(24) $ d_1 - \dfrac{G_1 }{G_2 }(1 - \kappa _2 )R_1^2 f_1 - \dfrac{G_1 }{G_2 }g_1 = \dfrac{1}{2}(1 - \eta )(1 + \lambda )pR_1^2$
(25) $ (\kappa _1 + 1)R_1^2 c_1 - \dfrac{G_1 }{G_2 }(\kappa _2 + 1)R_1^2 e_1 - \dfrac{G_1 }{G_2 }(\kappa _2 - 3)R_1^6 f_3 + \\ \dfrac{G_1 }{G_2 }g_3 + \dfrac{G_1 }{G_2 }R_1^4 h_1 - d_3 = \dfrac{1}{2}\kappa _1 (1 - \eta )(1 - \lambda )pR_1^4$
这样利用边界条件就得到了式 (18)~式 (25)共8个线性方程. 8个方程,9个未知量$c_1 $,$d_1 $,$d_3$,$e_1 $,$f_1 $,$f_3 $,$g_1 $,$g_3 $,$h_1$,只通过这8个方程,是不可能求解9个未知量的,如何求解这样的问题是本文的关键所在.
本文将用围岩一侧和衬砌一侧的切向位移间断值$u_{\theta 1} -u_{\theta 2} $ 的大小来衡量接触面间的滑移量,在式 (2)中用目标函数$F({\pmb X}) = \left| {u_{\theta 1} - u_{\theta 2} }\right|$ 表示. 由式 (8) 可得 (式中$z = R_1 {\rm e}^{{i}\theta }$)
(26) $ u_{\theta 1} = (1 - \eta )u_\theta + \dfrac{1}{2G_1 } {\rm Im}\left\{ {{\rm e}^{ - {\rm i}\theta }\left[ {\kappa _1 \varphi _1 (z) - z\overline {{\varphi }'_1 (z)} - \overline {\psi _1 (z)} } \right]} \right\}$
(27) $ u_{\theta 2} = \dfrac{1}{2G_2 }{\rm Im}\left\{ {{\rm e}^{-{\rm i}\theta }\left[ {\kappa _2\varphi _2 (z) - z\overline {{\varphi }'_2 (z)} - \overline {\psi _2 (z)} }\right]} \right\}$
(28) $ \begin{array} u_{\theta 1} = \dfrac{1}{4G_1 }\Big[ pR_1 \kappa _1 (1 - \eta )(1 - \lambda ) + \ \qquad 2(1 - \kappa _1 )c_1 R_1^{ - 1} - 2d_3 R_1^{ - 3} \Big ]\sin 2\theta \end{array}$
(29) $ \begin{array} u_{\theta 2} = \dfrac{1}{2G_2 }\left[ {(1 - \kappa _2 )e_1 R_1^{ - 1} + (3 + \kappa _2 )f_3 R_1^3 - } \right. \ \qquad \left. {g_3 R_1^{ - 3} + h_1 R_1 } \right]\sin 2\theta \end{array}$
(30) $\left| {u_{\theta 1} - u_{\theta 2} } \right| = \Bigg | \Bigg \{ \dfrac{1}{4G_1 }\Big [ pR_1 \kappa _1 (1 - \eta )(1 - \lambda ) + \\ \qquad 2(1 - \kappa _1 )c_1 R_1^{ - 1} - 2d_3 R_1^{ - 3} \Big ] - \\ \qquad \dfrac{1}{2G_2 }\left[ {(1 - \kappa _2 )e_1 R_1^{ - 1} - g_3 R_1^{ - 3} + }\right. \\ \qquad (3 + \kappa _2 )f_3 R_1^3 + h_1 R_1 \Big ] \Bigg \}\sin 2\theta \Bigg | $
由式 (30) 可以看出,对任意$\theta $,当$\left| {\left\{ \ \right\}} \right|$ 内的值达到最小值时,所产生的位移间断值都最小,只是对于不同$\theta $,位移间断值的最小值不同而已. 所以取目标函数$F$为
(31) $ F = \Bigg | \dfrac{1}{4G_1 }\Big[ pR_1 \kappa _1 (1 - \eta )(1 - \lambda ) + \\ \qquad 2(1 - \kappa _1 )c_1 R_1^{ - 1} - 2d_3 R_1^{ - 3} \Big ] - \\ \qquad \dfrac{1}{2G_2 }\Big [ (1 - \kappa _2 )e_1 R_1^{ - 1} - g_3 R_1^{ - 3} + \\ \qquad (3 + \kappa _2 )f_3 R_1^3 + h_1 R_1 \Big ] \Bigg | $
使式 (31) 达到最小的一组$c_1 $,$d_1 $,$d_3 $,$e_1 $,$f_1 $,$f_3 $,$g_1 $,$g_3 $ 和$h_1 $,可以保证接触面间产生最小的滑移量. 在接触面,必须满足库仑摩擦模型,式中$\tau _{r\theta } $ 和$\sigma _r $ 分别为接触面上的剪应力和径向正应力,由于在接触面上应力的连续性,因此$\tau _{r\theta } $,$\sigma _r $ 既可取$\tau _{r\theta 1} $,$\sigma _{r1} $,也可取$\tau _{r\theta 2} $,$\sigma _{r2} $. 本文取前者,则有
(32) $\begin{array} f_r \left| {d_1 R_1^{ - 2} + \left( {3d_3 R_1^{ - 4} - 4c_1 R_1^{ - 2} } \right)\cos 2\theta } \right| - \\ \qquad \left| {\left( {2c_1 R_1^{ - 2} - 3d_3 R_1^{ - 4} } \right)\sin 2\theta } \right| \geqslant 0 \end{array} $
对任意的$\theta $,式 (32) 都应该成立.由于问题的对称性,只考虑$\theta \in [0,\pi ]$ 的情形即可.将$[0,\pi ]$ 分为$m$ 等分 (本文取180),则式 (32)可化归为$m + 1$ 个约束条件
(33) $ \begin{array} f_r \left| {d_1 R_1^{ - 2} + \left( {3d_3 R_1^{ - 4} - 4c_1 R_1^{ - 2} } \right)\cos 2\theta _j } \right| - \\ \qquad \left| {\left( {2c_1 R_1^{ - 2} - 3d_3 R_1^{ - 4} } \right)\sin 2\theta _j } \right| \geqslant 0 \end{array}$
式中$\theta _j = \dfrac{\pi (j - 1)}{m}$, $j = 1,2, \cdots ,m + 1$. 式 (33)即为式 (2) 中$b_j ({\pmb X}) \geqslant 0$ 表示的不等式组.
2 摩擦滑动接触的解法
2.1 最优化问题的求解
文献[28 ] 使用混合罚函数方法来进行优化计算[29 -30 ] ,其数学模型为
(34) $ \left. \min F({\pmb X}),{\pmb X} \in D \\ D: \ \ a_j ({\pmb X}) = 0 , \ \ j = 1, 2, \cdots, 8 \\ \qquad b_j ({\pmb X}) \geqslant 0 , \ \ j = 1, 2, \cdots, m + 1 \right\}$
按照文献[28 ] 的求解过程,其将式 (18)~式 (25) 组成的8 个方程作为优化模型中的等式约束函数$a_j ({X})$, 而将式 (33)组成的不等式组作为不等式约束条件,然后将等式约束函数$a_j ({X})$ 和不等式约束函数$b_j ({\pmb X})$分别构成惩罚项加到目标函数$F({\pmb X})$构成一个新的无约束的称为罚函数的目标函数$p(x,r)$,其中$r$称为罚因子. 这样,就把原目标函数$F({\pmb X})$的约束极小值问题转为求罚函数$p(x,r)$ 的无约束极小值问题.其罚函数的具体形式为
(35) $ \begin{array} p({\pmb X},r) = F({\pmb X}) + r\sum_{j \in I_1 } {\ln \dfrac{1}{b_j ({\pmb X})}} + \\ \qquad \dfrac{1}{r}\left\{ {\sum_{j = 1}^8 {a_j^2 ({\pmb X})} + \sum_{j \in I_2 } {\left\{ {\min \left[ {0,b_j \left({\pmb X} \right)} \right]} \right\}^2} } \right\} \end{array}$
$$ I_1 = \left\{ {j\left| {b_j ({\pmb X}^{(0)}) > 0 , \ \ 1 \leqslant j \leqslant m + 1} \right.} \right\} \\ I_2 = \left\{ {j\left| {b_j ({\pmb X}^{(0)}) \leqslant 0 , \ \ 1 \leqslant j \leqslant m + 1} \right.} \right\} $$
其中${\pmb X}^{(0)}$ 是给出的原问题的计算初始点.在该模型中,${\pmb X} = [c_1 ,d_1 ,d_3 ,e_1 ,f_1,f_3 ,g_1 ,g_3 ,h_1]$,即所有的变量都需要参与到优化的过程中,计算初始点${X}^{(0)} = [c_1^0 ,d_1^0 ,d_3^0 ,e_1^0 ,f_1^0,f_3^0 ,g_1^0 ,g_3^0 ,h_1^0 ]$.我们知道,设计变量的增加会优化的数学模型更加复杂,从而增加优化的难度,有时甚至得不到满足约束的最优解.如果可以减少设计变量的个数,这将大大地简化优化的数学模型,从而使求解变得容易.
本文同样使用混合罚函数法来进行优化计算,不同的是本文将设计变量的个数从9个变为1个,极大地简化了优化模型.具体来说,本文可以将$c_1 $,$d_1 $,$d_3 $,$e_1 $,$f_1 $,$f_3 $,$g_1 $,$g_3 $和$h_1 $ 其中的任意一个作为设计变量,以$h_1 $ 为例,赋予$h_1$ 初值,根据式 (18)~式 (25)组成方程组即可以求解出$c_1 $,$d_1 $,$d_3 $,$e_1 $,$f_1$,$f_3 $,$g_1 $,$g_3 $ 这8 个变量,再将$c_1 $,$d_1 $,$d_3$,$e_1 $,$f_1 $,$f_3 $,$g_1 $,$g_3 $ 和$h_1 $代入如下的优化模型中,即可获得优化结果
(36) $ \left. \min F({\pmb X}),{\pmb X} \in D \\ D: \ \ b_j ({\pmb X}) \geqslant 0 , \ \ j = 1,2, \cdots ,m + 1 \right\}$
式中,$b_j ({\pmb X}) \geqslant 0$表示的是不等式约束条件,它由式 (33) 构成,而$F({\pmb X})$即为式 (31). 在该优化模型中,其罚函数的具体形式简化为
(37) $ \begin{array} p({\pmb X},r) = F({\pmb X}) + r\sum_{j \in I_1 } {\ln \dfrac{1}{b_j ({\pmb X})}} + \\ \qquad \dfrac{1}{r}\sum_{j \in I_2 } {\left\{ {\min \left[ {0,b_j \left( {\pmb X} \right)} \right]} \right\}^2} \end{array}$
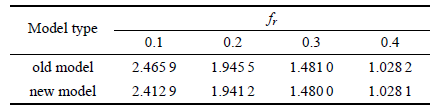
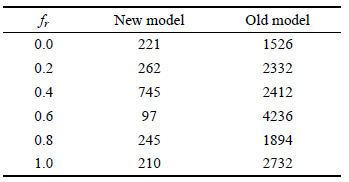
可以看出,较之文献[28 ] 中的罚函数的具体形式,本文的罚函数形式没有二次损失项中的$\sum_{j = 1}^8 {a_j^2 ({\pmb X})}$,并且计算初始点${\pmb X}^{(0)}$ 仅有$h_1^0$,这极大地简化了优化的数学模型. 模型中只有$h_1 $为设计变量,改变$h_1 $ 的值,使式 (36) 达到最小值的$\hat{h}_1 $即为该优化问题的解,此时其他8个变量可以由解方程组得出且分别表示为$\hat{c}_1 $,$\hat {d}_1 $,$\hat {d}_3 $,$\hat {e}_1 $,$\hat {f}_1$,$\hat {f}_3 $,$\hat {g}_1 $,$\hat {g}_3 $.为了比较两种模型的精确程度,我们以摩擦滑动接触为例,利用新旧两种模型分别计算出不同摩擦系数$f_r$对应的目标函数的值,其对比如表1 所示.
从表1 可以看出,比较不同摩擦系数$f_r $计算出的目标函数值,本文提出的新优化模型所得结果更小,这是因为本文通过解方程的方法可以使式 (34) 中的$a_j ({\pmb X}) = 0$精确满足,较之文献[28 ] 中的优化模型,该方法更加精确.
同时可以通过访问目标函数的次数来对比两种方法的迭代速度 (见表2 ),可以看出新优化模型较之旧模型有很大地提升.
利用新优化模型求解出的这样一组${\pmb X} = [c_1$, $d_1 ,d_3,e_1 ,f_1 ,f_3 ,g_1 ,g_3 ,h_1 ]$即为本文问题的解,从而完成了围岩支护后,围岩和衬砌中复势函数的求解.从以上的分析和求解过程可以看出,这种摩擦滑动接触的解法具有一般性,它包含了完全接触和光滑接触两种极限情形.
当$f_r = 0$ 时,由式 (32) 表示的不等式约束条件将变为
(38) $ 2c_1 R_1^{ - 2} - 3d_3 R_1^{ - 4} = 0$
若令$\tau _{r\theta 1} = 0$,则可以获得与式 (38)完全相同的方程,即式 (38) 表示的就是光滑接触的情形.
当$f_r $ 的值大于某个值时,式 (32)表示的不等式约束条件总会满足,式 (36) 达到最小值 (其值为零)时的解为
(39) $ \begin{array} \dfrac{1}{4G_1 }\left[ {pR_1 \kappa _1 (1 - \eta )(1 - \lambda ) - 2d_3 R_1^{ - 3} + 2(1 - \kappa _1 )c_1 R_1^{ - 1} } \right] = \\ \qquad \dfrac{1}{2G_2 }\left[ {(1 - \kappa _2 )e_1 R_1^{ - 1} - g_3 R_1^{ - 3} + (3 + \kappa _2 )f_3 R_1^3 + h_1 R_1 } \right] \end{array}$
则式 (39) 所表示的实际就是$u_{\theta 1} = u_{\theta 2}$,这由式 (26)、式 (27) 可以清晰地看出.由后面的算例可知,满足完全接触条件所需要的$f_r $值大小与侧压力系数$\lambda $ 密切相关,$\lambda $越接近于1,所需要的$f_r $ 值越小,理论上当$\lambda = 1 $ 时,$f_r = 0 $ 就可以满足完全接触条件.
2.2 衬砌和围岩中的应力
给定$R_0 $,$R_1 $,$p$,$\lambda $,$p_0 $,$G_1 $,$\mu _1$,$G_2 $,$\mu _2 $,$\eta $,可以求出待定的$c_1 $,$d_1$,$d_3 $,$e_1 $,$f_1 $,$f_3 $,$g_1 $,$g_3 $,$h_1 $.
(40) $ \sigma _{r2} = 2f_1 + g_1 r^{ - 2} + ( - 4e_1 r^{ - 2} + 3g_3 r^{ - 4} - h_1 )\cos 2\theta$
(41) $ \sigma _{\theta 2} = 2f_1 - g_1 r^{ - 2} + (12f_3 r^2 - 3g_3 r^{ - 4} + h_1 )\cos 2\theta$
(42) $ \tau _{r\theta 2} = (6f_3 r^2 - 2e_1 r^{ - 2} + 3g_3 r^{ - 4} + h_1 )\sin 2\theta$
围岩中的应力应由开挖前,开挖后,支护后三部分的应力进行迭加.迭加后的应力仍用$\sigma _{r1} $,$\sigma _{\theta 1} $,$\tau_{r\theta 1} $ 符号表示,可求得[13 ]
(43) $ \sigma _{r1} = \dfrac{ - (1 + \lambda )p}{2} + \left[ {\dfrac{(1 + \lambda )pR_1^2 }{2} + d_1 } \right]r^{ - 2} + \\ \qquad \left\{ {\dfrac{( {1}-\lambda )p}{2} - 2\left[ {(1 - \lambda )pR_1^2 + 2c_1 } \right]r^{ - 2} + } \right. \\ \qquad \left. {\left[ {\dfrac{3(1 - \lambda )pR_1^4 }{2} + 3d_3 } \right]r^{ - 4}} \right\} \cos 2\theta$
(44) $ \begin{array} \sigma _{\theta 1} = \dfrac{ - (1 + \lambda )p}{2} - \left[ {\dfrac{(1 + \lambda )pR_1^2 }{2} + d_1 } \right]r^{ - 2}- \\ \qquad \left\{ {\dfrac{( {1}-\lambda )p}{2} + \left[ {\dfrac{3(1 - \lambda )pR_1^4 }{2} + 3d_3 } \right]r^{ - 4}} \right\}\cos 2\theta \end{array}$
(45) $ \begin{array} \tau _{r\theta 1} = - \left\{ {\dfrac{( {1}-\lambda )p}{2} + \left[ {(1 - \lambda )pR_1^2 + 2c_1 } \right]r^{ - 2} - } \right. \\ \qquad \left. {\left[ {\dfrac{3(1 - \lambda )pR_1^4 }{2} + 3d_3 } \right]r^{ - 4}} \right\} \sin 2\theta \end{array}$
3 分析和讨论
3.1 围岩和衬砌接触面上的接触方式
取计算参数为:$p = 10.0$ MPa,$p_0 = 2.0$ MPa,$R_1 =3.0$ m,$R_0 = 2.7$ m,$\mu _1 = 0.25$,$\mu _2 = 0.20$,$E_2 /E_1 = 10.0$,$\eta = 0.20$. 对于不同的侧压力系数$\lambda $以及摩擦系数$f_r $,获得的解析函数的系数也不同. 由于问题的对称性,只需要分析$\theta \in [0^\circ, 90^\circ]$内的结果.
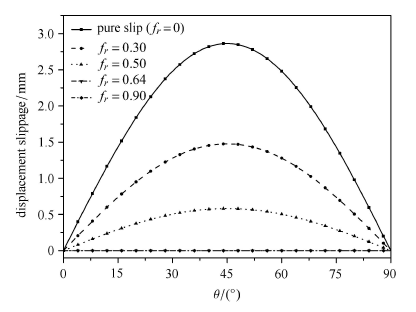
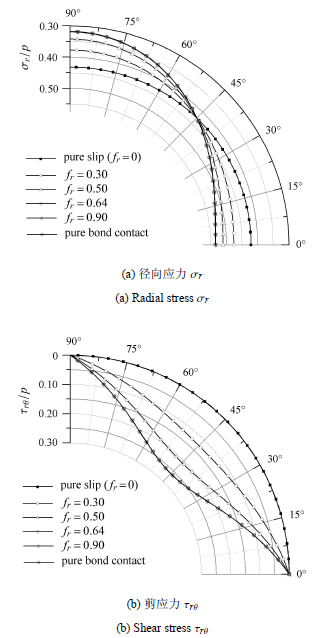
由前面的推导我们知道,本文作者提出的摩擦滑动接触可以计算光滑接触和完全接触两种极限的接触工况,并且这与摩擦系数$f_r$的取值相关. 取侧压力系数$\lambda = 0.5$,分析摩擦系数$f_r$取不同值时接触面上接触应力$\sigma _r $,$\tau _{r\theta }$和切向位移间断值$\left| {u_{\theta 1} - u_{\theta 2} } \right|$的变化规律,并将其与完全接触[13 ] 和光滑接触[14 ] 的结果进行对比.
从图3 可以看出,接触面上一旦发生滑动,除了对称点0$^\circ$和90$^\circ$,其余各点都会发生相对滑动,且在45$^\circ$处有最大值. 当摩擦系数$f_r $为零时,接触上发生最大的相对滑动,当$f_r \geqslant 0.64$时,接触面上的切向位移间断值$\left| {u_{\theta 1} - u_{\theta 2}} \right|$ 基本为零,即$u_{\theta 1} \approx u_{\theta 2}$,并且随着$f_r $ 的增大,$\left| {u_{\theta 1} - u_{\theta 2} }\right|$ 逐渐减小.
图3
图3
接触面上切向位移间断值$\left| {u_{\theta 1} - u_{\theta 2} } \right|$ 的分布
Fig. 3
Distributions of $\left| {u_{\theta 1} - u_{\theta 2} } \right|$ on the interface
如图4 (a) 所示,接触面上径向应力$\sigma _r $ 在45$^\circ$处为一定值,而当$f_r =0$ 即光滑接触时, $\sigma _r $的绝对值分别在0$^\circ$ 和90$^\circ$ 处取得极小值和极大值.当$f_r $ 较大时,$\sigma _r $ 的绝对值在$[0^\circ,90^\circ]$范围内单调递减.图 4 (b) 表明随着$f_r $的增大,接触面上的剪应力$\tau_{r\theta } $的绝对值也随之增大,且都在45$^\circ$ 处取得最大值. 当$f_r\geqslant 0.64$ 时,图4 中的$\sigma _r $,$\tau _{r\theta } $不再变化,且与完全接触的结果一致,结合图3 ,$f_r \geqslant 0.64$时,$u_{\theta 1} \approx u_{\theta 2}$,此时得到的解即为完全接触的解.
我们已经确定利用摩擦滑动接触解法可以求解完全接触和光滑接触两种极限接触问题, 而且通过推导已知当$f_r$ 的值大于某个值时,总能满足完全接触的条件,称这个值为阈值$f_r^t$,确定阈值$f_r^t $ 对判断接触面上的接触方式很有帮助. 文献[28 ] 通过反复试算的方式讨论了不同弹性模量和侧压力系数所确定的阈值$f_r^t$,但是这种方法不够精确,本文尝试利用一种精确的方法来确定阈值$f_r^t$.
图4
图4
接触面上接触应力随摩擦系数$f_r $ 变化的分布规律
Fig. 4
Distributions of the contact stresses on the interface for different $f_r $
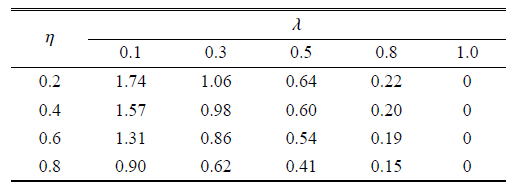
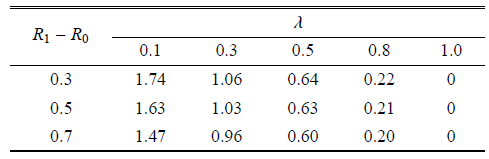
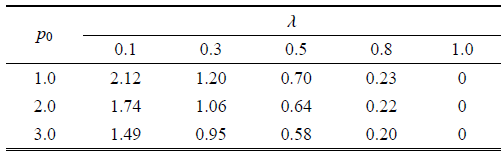
本文作者认为若接触面上所有的点都满足$\left| {\tau _{r\theta }^p} \right| < f_r \left| {\sigma _r^p } \right|$时,即接触面上的剪应力都小于接触面所能提供的最大摩擦力,此时,接触面不发上相对滑动,即为完全接触,其中$\sigma_r^p $,$\tau _{r\theta }^p $为完全接触时接触面上的径向应力和剪应力;当接触面上存在满足$\left|{\tau _{r\theta }^p } \right| \geqslant f_r \left| {\sigma _r^p }\right|$ 的点时,此时的摩擦系数即为阈值$f_r^t$,我们可以认为衬砌和围岩之间必定产生相对滑动,即为摩擦滑动接触.当摩擦系数$f_r $ 达到阈值$f_r^t $ 时,总是可以满足$\left|{\tau _{r\theta }^p } \right| < f_r^t \left| {\sigma _r^p }\right|$,即满足完全接触的条件. 利用该方法确定的阈值$f_r^t =0.64$,将其代入摩擦滑动解法程序中,得到接触面上的切向位移间断值$\left|{u_{\theta 1} - u_{\theta 2} } \right| \approx 0$ (图3 ),接触应力$\sigma _r $,$\tau _{r\theta } $ 如图4 所示,从图4 ,我们可以清晰地得到,当摩擦系数$f_r \geqslant0.64$,接触面上所有点都满足$\left| {\tau _{r\theta }^p } \right|< f_r \left| {\sigma _r^p } \right|$,即为完全接触.图 4 表示按照摩擦滑动接触解法获得的接触应力介于光滑接触和完全接触之间,且随着摩擦系数的增大,接触应力的结果趋于完全接触. 不同情况下获得阈值$f_r^t $ 也不同.表3 ~表6 分别是不同位移释放系数,不同衬砌厚度,不同水压力大小以及不同弹模比值情况下改变侧压力系数时所获得的阈值$f_r^t $.
同时,为了同文献[28 ] 中所得结果进行比较,取$R_0 =2.5$ m,侧压力系数分别为0.2,0.5,0.8,1.0,在不同弹模比值下所得阈值如表6 所示.
表3表明增大位移释放系数,阈值$f_r^t $逐渐减小,说明越晚支护,接触面上越不容易发生相对滑动;从表4 可以看出, 在洞径不变的前提下,增大衬砌厚度可以使阈值$f_r^t $减小. 表5 则很清晰地表示随着内水压力的增大,阈值$f_r^t $逐渐减小. 表6 说明当$E_2 / E_1 \leqslant10$,随着弹模比值的增大,阈值$f_r^t $ 也增大,而当$E_2 / E_1 >10$,阈值$f_r^t $ 随着弹模比值的增大而减小,而文献[28 ] 中利用试算方法所得阈值随着弹模比值的增大而增大,这与此处所得结论不同,说明了试算方法的局限性;从表3 ~表6 可以看出,侧压力系数$\lambda $ 对阈值的影响最大,随着$\lambda$ 的增大,满足完全接触的阈值$f_r^t $ 减小,直至$\lambda =1.0$,$f_r^t =0$,即两向等压时,即使摩擦系数等于零,接触面上也不发生相对滑动.
3.2 衬砌和围岩各边界上切向应力的变化规律
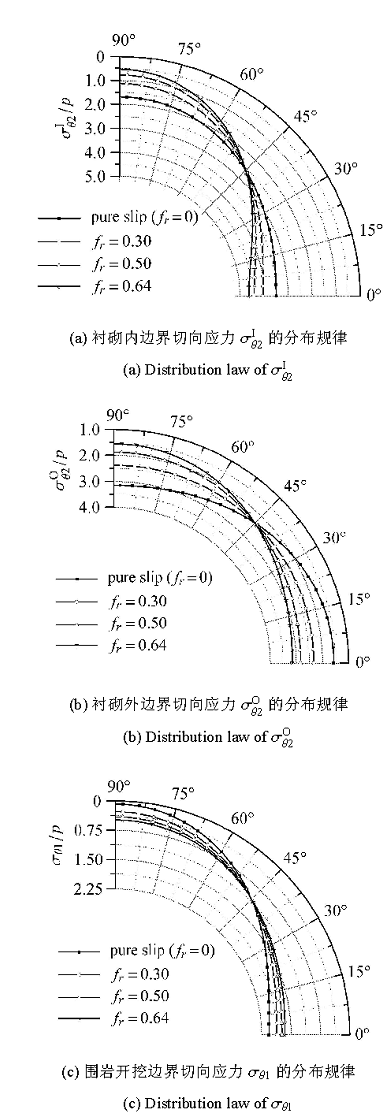
在隧洞的支护设计中,各边界上的切向应力变化规律十分重要,所以在这一节,我们取不同的摩擦系数$f_r$,分别分析它们的变化 对衬砌内外边界的切向应力 ($\sigma _{\theta2}^{\rm I} $ 和$\sigma _{\theta 2}^{\rm O} $)以及围岩开挖边界上切向应力 ($\sigma _{\theta 1} $) 的影响. 3.1节已经分析过当$\lambda = 0.5$,满足完全接触条件的阈值$f_r^t =0.64$,因此,在本节的讨论中,摩擦系数$f_r $的最大取值为0.64,其余参数不变化.
由图5 可以看出,当$\lambda =0.5$,不管摩擦系数如何改变,所有的切向应力都为压应力. 由图5 (a)和图5 (b) 可以看出,随着$f_r $的增大,衬砌内边界的切向应力$\sigma _{\theta 2}^{\rm I} $最大压应力增大,最小压应力减小,在$[0^\circ,90^\circ]$内,压应力随着角度的增大而减小, 其变化范围增大.在衬砌外边界上,随着$f_r $ 的增大,切向应力$\sigma _{\theta2}^{\rm O} $ 变化范围减小. 只是当$f_r $ 较小且趋于0时,从0$^\circ$到90$^\circ$,压应力随着角度的增大而增大,$\sigma _{\theta2}^{\rm O} $ 分别在0$^\circ$ 和90$^\circ$取得最小和最大压应力;当$f_r $ 较大时,结论恰好相反. 由图5 (c)可得,保持$\lambda = 0.5$ 不变,在$[0^\circ,90^\circ]$内,随着角度的增大,$\sigma _{\theta 1} $ 为压应力单调减小.随着$f_r $ 的增大,$\sigma _{\theta 1} $ 在90$^\circ$出现的最小压应力增大,在0$^\circ$ 出现的最大压应力减小.图 5 表明摩擦滑动接触条件下所得衬砌内外边界上的切向应力$\sigma_{\theta 2}^{\rm I} $, $\sigma _{\theta 2}^{\rm O} $以及围岩开挖边界上的切向应力$\sigma _{\theta 1} $都介于光滑接触和完全接触的结果之间.
图 5
图 5
各边界上切向应力随摩擦系数$f_r $ 变化的分布规律
Fig. 5
Distributions of the tangential stresses on the 3 boders for different $f_r $
4 结论
本文提出了更加符合实际情况的摩擦滑动接触条件来描述实际工程中围岩和衬砌之间的接触问题.以库仑摩擦模型模拟围岩衬砌之间的接触,当接触面上发生相对滑动之后,将接触面上产生最小滑移量的状态视为衬砌的真实工作状态,并以此为基础,利用最优化方法建立了摩擦滑动接触情形下新的解法.在利用混合罚函数法求解解析函数的系数时,减少了设计变量的个数,去掉了罚函数二次损失项中的$\sum_{j= 1}^8 {a_j^2 ({\pmb X} )} $,极大地简化了最优化解法的数学模型.
同时提出了能够精确获得满足完全接触条件的摩擦系数阈值的公式,并且得到了不同位移释放系数,不同衬砌厚度,不同水压力大小以及不同弹模比值情况下改变侧压力系数时所获得的阈值$f_r^t$,为判断围岩和衬砌接触方式提供了理论基础.摩擦滑动接触条件下所得的解都介于完全接触和光滑接触之间,并且能同时可以求解光滑接触和完全接触两种极限情况,具有一般性.特别地,在衬砌内边界上,摩擦滑动接触所得最大切向应力介于两种极限接触之间,且光滑接触所得最大切向应力最小,这说明在实际工程中,尽量减小衬砌和围岩之间的摩擦,可以增加衬砌的承载能力.
参考文献
View Option
[1]
张顶立 . 隧道及地下工程的基本问题及其研究进展
力学学报 , 2017 ,49 (1 ):3 -21
[本文引用: 1]
( Zhang Dingli . Essentialissues and their research progress in tunnel and underground engineering
Chinese Journal of Theoreticaland Applied Mechanics , 2017 ,49 (1 ):3 -21 (in Chinese))
[本文引用: 1]
[2]
张顶立 , 孙振宇 , 侯艳娟 . 隧道支护结构体系及其协同作用
力学学报 , 2019 ,51 (2 ):577 -593
[本文引用: 1]
( Zhang Dingli Sun Zhenyu Hou Yanjuan . Tunnel support structure system and its synergistic effect
Chinese Journal ofTheoretical and Applied Mechanics , 2019 ,51 (2 ):577 -593 (in Chinese))
[本文引用: 1]
[3]
Muskhelishvili NI . Some Basic Problems of the Mathematical Theory of Elasticity
Groningen:P. Noordhoff Ltd , 1953
[本文引用: 2]
[4]
施高萍 , 祝江鸿 , 李保海 等 . 矩形巷道孔边应力的弹性分析
岩土力学 , 2014 ,35 (9 ):2587 -2593
[本文引用: 1]
( Shi Gaoping Zhu Jianghong Li Baohai , et al . Elastic analysis of hole-edge stress of rectangular roadway
Rock and Soil Mechanics , 2014 ,35 (9 ):2587 -2593 (in Chinese))
[本文引用: 1]
[5]
Exadaktylos G Stavropoulou M . A closed-form elastic solution for stresses and displacements aroundtunnels
International Journal of Rock Mechanics and Mining Sciences , 2002 ,39 (7 ):905 -916
[本文引用: 1]
[6]
何川 , 齐春 , 封坤 等 . 基于 D-P 准则的盾构隧道围岩与衬砌结构相互作用分析
力学学报 , 2017 ,49 (1 ):31 -40
[本文引用: 1]
( He Chuan Qi Chun Feng Kun , et al . Theoretical analysis of interaction between surrounding rocks andlinging strcture of shield tunnel based on Drucker-Prager yield criteria
Chinese Journal of Theoreticaland Applied Mechanics , 2017 ,49 (1 ):31 -40 (in Chinese))
[本文引用: 1]
[7]
吴顺川 , 潘旦光 , 高永涛 . 深埋圆形巷道围岩和衬砌相互作用解析解
工程力学 , 2011 ,28 (3 ):136 -142
[本文引用: 1]
( WuShunchuan , Pan Danguang Gao Yongtao . Analytic solution for rock-liner interaction of deep circular tunnel
Engineering Mechanics , 2011 ,28 (3 ):136 -142 (in Chinese))
[本文引用: 1]
[8]
Hasanpour R Rostami J Özçelik Y . Impact of overcut on interaction between shield and groundin the tunneling with a double-shield TBM
Rock Mechanics & Rock Engineering , 2016 ,49 (5 ):2015 -2022
[本文引用: 1]
[9]
Ramoni M Anagnostou G . The interaction between shield, ground and tunnel support in tbm tunnellingthrough squeezing ground
Rock Mechanics & Rock Engineering , 2011 ,44 (1 ):37 -61
[本文引用: 1]
[10]
Son M . Adhesion strength at the shotcrete--rock contact in rock tunneling
Rock Mechanics & Rock Engineering , 2013 ,46 (5 ):1237 -1246 .
[本文引用: 1]
[11]
于学馥 , 郑颖人 , 刘怀恒 等 . 地下工程围岩稳定性分析 . 北京 : 煤炭工业出版社 , 1983 : 79 -90
[本文引用: 2]
( Yu Xuefu Zheng Yingren Liu Huaiheng , et al . Analysis on stability of ground of underground structure . Beijing : China CoalIndustry Publishing Housing , 1983 : 79 -90 (in Chinese))
[本文引用: 2]
[12]
Wang MB Li SC . A complex variable solution for stress and displacement field around a lined circulartunnel at great depth
International Journal for Numerical and Analytical Methods in Geomechanics , 2009 ,33 (7 ):939 -951
[本文引用: 2]
[13]
Lu AZ Zhang LQ Zhang N , Analytic stress solutions for a circular pressure tunnel at pressure andgreat depth including support delay
International Journal of Rock Mechanics & Mining Sciences , 2011 ,48 (3 ):514 -519
[本文引用: 7]
[14]
Lu AZ Zhang N , Analytic stress solutions for a circular pressure tunnel at great depth includingsupport delay and pure slip boundary condition
Rock Engineering and Rock Mechanics: Structures in and onRock Masses Alejano, Perucho, Olalla & Jiménez (Eds)© 2014 Taylor & Francis Group,London, 978-1-138-00149-7
[本文引用: 3]
[15]
Lu AZ Zhang N , Analytic solutions of stress and displacement for a non-circular tunnel at greatdepth including support delay
International Journal of Rock Mechanics & Mining Sciences , 2014 ,70 (9 ):69 -81
[本文引用: 2]
[16]
Lu AZ Zhang N Qin Y , Analytical solutions for the stress of a lined non-circular tunnel underfull-slip contact conditions
International Journal of Rock Mechanics & Mining Sciences , 2015 ,79 :183 -192
[本文引用: 2]
[17]
Bobet A . Lined circular tunnels in elastic transversely anisotropic rock at depth
RockMechanics & Rock Engineering , 2011 ,44 (2 ):149 -167
[本文引用: 2]
[18]
王少杰 , 吕爱钟 , 张晓莉 . 正交各向异性岩体中非圆形水工隧洞的解析解
岩土力学 , 2018 ,39 (12 ):149 -159,168
[本文引用: 2]
( Wang Shaojie Lü Aizhong Zhang Xiaoli . Analytical solution for the non-circular hydraulic tunnel buriedin the orthotropic rock mass
Rock and Soil Mechanics , 2018 ,39 (12 ):149 -159,168 (in Chinese))
[本文引用: 2]
[19]
Atkinson C Eftaxiopoulos DA . Numerical and analytical solutions for the problem of hydraulicfracturing from a cased and cemented wellbore
International Journal of Solids and Structures , 2002 ,39 (6 ):1621 -1650
[本文引用: 1]
[20]
高永涛 , 吴庆良 , 吕爱钟 . 一类非均布荷载作用下双层厚壁圆筒光滑接触时的应力解析解
工程力学 , 2013 ,30 (10 ):93 -99
[本文引用: 1]
( Gao Yongtao Wu Qingliang Lü Aizhong . Stress analytic solution of a double-layeredthick-walled cylinder with smooth contact interface subjected to a type of non-uniform distributed pressures
Engineering Mechanics , 2013 ,30 (10 ):93 -99 (in Chinese))
[本文引用: 1]
[21]
储昭飞 , 刘保国 , 刘开云 等 . 非静水应力场中圆形隧道衬砌与围岩间两种接触的黏弹性解析
岩土力学 , 2017 ,38 (11 ):142 -151
[本文引用: 1]
( Chu Zhaofei Liu Baoguo Liu Kaiyun , et al . Analytical viscoelastic solutions for linedcircular tunnels under two contact conditions in a non-hydrostatic stress field
Rock and SoilMechanics , 2017 ,38 (11 ):142 -151 (in Chinese))
[本文引用: 1]
[22]
王东 , 徐超杰 , 万强 等 . 连接结构接触界面非线性力学建模研究
力学学报 , 2018 ,50 (1 ):44 -57
[本文引用: 1]
( Wang Dong , XuChaojie, Wan Qiang, et al. Nonlinear mechanics modeling for joint interface of assembled structure
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (1 ):44 -57 (in Chinese))
[本文引用: 1]
[23]
Meschke G Ninić J Stascheit J , et al . Parallelized computational modeling of pile--soilinteractions in mechanized tunneling
Engineering Structures , 2013 ,47 (1 ):35 -44
[本文引用: 1]
[24]
Cavalieri FJ Cardona A . An augmented Lagrangian technique combined with a mortar algorithm formodelling mechanical contact problems
International Journal for Numerical Methods in Engineering , 2013 ,93 (4 ):420 -442
[本文引用: 1]
[25]
Cavalieri FJ Cardona A . Numerical solution of frictional contact problems based on a mortaralgorithm with an augmented Lagrangian technique
Multibody System Dynamics , 2015 ,35 (4 ):1 -23
[本文引用: 1]
[26]
苏宗贤 , 何川 . 盾构隧道管片衬砌内力分析的壳-弹簧-接触模型及其应用
工程力学 , 2007 ,24 (10 ):131 -136
[本文引用: 1]
( Su Zongxian He Chuan . Shell-spring-contact model for shield tunnel segmental lining analysis andits application
Engineering Mechanics , 2007 ,24 (10 ):131 -136 (in Chinese))
[本文引用: 1]
[27]
杨钊 , 潘晓明 , 余俊 . 盾构输水隧洞复合衬砌计算模型
中南大学学报(自然科学版) , 2010 ,41 (5 ):1945 -1952
[本文引用: 1]
( Yang Zhao Pan Xiaoming Yu Jun . Calculation model on double linings of water diversion shield tunnel
Journal of Central South University (Science and Technology) , 2010 ,41 (5 ):1945 -1952 (in Chinese))
[本文引用: 1]
[28]
Lu AZ Yin CL Zhang N . Analytic stress solutions for a lined circular tunnel under frictional slipcontact conditions.
European Journal of Mechanics-A/ Solids , 2019 ,75 :10 -20
[本文引用: 9]
[29]
Fletcher R . Practical Methods of Optimization, Volume 2. Constrained Optimization
New York:Chichelser , 1981
[本文引用: 1]
[30]
万耀青 编. 最优化计算方法常用程序汇编 . 北京 : 工人出版社 , 1983
[本文引用: 1]
( Wan Yaoqing Common Programs forOptimization Calculation. Beijing : Workers' Press , 1983 (in Chinese))
[本文引用: 1]
隧道及地下工程的基本问题及其研究进展
1
2017
... 隧洞是广泛应用于水电、交通、矿山及军事工程领域的常用地下结构.近来,随着我国经济的持续发展及高新技术的不断应用,我国的隧洞工程得到了前所未有的迅速发展,支护-围岩相互作用,以及如何保证隧洞围岩的稳定性是我们要研究的基本问题[1 -2 ] . ...
隧道及地下工程的基本问题及其研究进展
1
2017
... 隧洞是广泛应用于水电、交通、矿山及军事工程领域的常用地下结构.近来,随着我国经济的持续发展及高新技术的不断应用,我国的隧洞工程得到了前所未有的迅速发展,支护-围岩相互作用,以及如何保证隧洞围岩的稳定性是我们要研究的基本问题[1 -2 ] . ...
隧道支护结构体系及其协同作用
1
2019
... 隧洞是广泛应用于水电、交通、矿山及军事工程领域的常用地下结构.近来,随着我国经济的持续发展及高新技术的不断应用,我国的隧洞工程得到了前所未有的迅速发展,支护-围岩相互作用,以及如何保证隧洞围岩的稳定性是我们要研究的基本问题[1 -2 ] . ...
隧道支护结构体系及其协同作用
1
2019
... 隧洞是广泛应用于水电、交通、矿山及军事工程领域的常用地下结构.近来,随着我国经济的持续发展及高新技术的不断应用,我国的隧洞工程得到了前所未有的迅速发展,支护-围岩相互作用,以及如何保证隧洞围岩的稳定性是我们要研究的基本问题[1 -2 ] . ...
Some Basic Problems of the Mathematical Theory of Elasticity
2
1953
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
... 对于圆形隧洞,其应力分量和位移分量极易求得[3 ] ...
矩形巷道孔边应力的弹性分析
1
2014
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
矩形巷道孔边应力的弹性分析
1
2014
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
A closed-form elastic solution for stresses and displacements aroundtunnels
1
2002
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
D-P 准则的盾构隧道围岩与衬砌结构相互作用分析
1
2017
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
D-P 准则的盾构隧道围岩与衬砌结构相互作用分析
1
2017
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
深埋圆形巷道围岩和衬砌相互作用解析解
1
2011
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
深埋圆形巷道围岩和衬砌相互作用解析解
1
2011
... 利用解析法求解隧洞工程问题是一种基本的分析方法. 而由Muskhelishvili[3 ] 提出的平面弹性复变函数方法是求解隧洞围岩和衬砌中应力以及位移的常用解析法,通过这种方法容易获得无支护隧洞的应力和位移解[4 -5 ] .而在实际工程中,常在隧洞内设置衬砌支护以保证隧洞的安全,因此研究支护-围岩的相互作用更是十分重要,何川等[6 ] 以及吴顺川等[7 ] 分别利用D-P准则和莫尔库伦屈服准则,获得了围岩和衬砌相互作用的弹塑性解析解. ...
Impact of overcut on interaction between shield and groundin the tunneling with a double-shield TBM
1
2016
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
The interaction between shield, ground and tunnel support in tbm tunnellingthrough squeezing ground
1
2011
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
Adhesion strength at the shotcrete--rock contact in rock tunneling
1
2013
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
2
1983
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
2
1983
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
A complex variable solution for stress and displacement field around a lined circulartunnel at great depth
2
2009
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
Analytic stress solutions for a circular pressure tunnel at pressure andgreat depth including support delay
7
2011
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
... 如图2 所示在隧洞开挖之后,假设没有支护,围岩会完成相应的位移.此时围岩内任一点的径向位移$u_r $ 和切向位移$u_\theta $可以表示为[13 ] ...
... 隧洞开挖后进行支护,围岩和衬砌相互作用.围岩对应的两个解析函数为[13 ] ...
... 衬砌中的应力可表示为[13 ] ...
... 围岩中的应力应由开挖前,开挖后,支护后三部分的应力进行迭加.迭加后的应力仍用$\sigma _{r1} $,$\sigma _{\theta 1} $,$\tau_{r\theta 1} $ 符号表示,可求得[13 ] ...
... 由前面的推导我们知道,本文作者提出的摩擦滑动接触可以计算光滑接触和完全接触两种极限的接触工况,并且这与摩擦系数$f_r$的取值相关. 取侧压力系数$\lambda = 0.5$,分析摩擦系数$f_r$取不同值时接触面上接触应力$\sigma _r $,$\tau _{r\theta }$和切向位移间断值$\left| {u_{\theta 1} - u_{\theta 2} } \right|$的变化规律,并将其与完全接触[13 ] 和光滑接触[14 ] 的结果进行对比. ...
Analytic stress solutions for a circular pressure tunnel at great depth includingsupport delay and pure slip boundary condition
3
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
... 由前面的推导我们知道,本文作者提出的摩擦滑动接触可以计算光滑接触和完全接触两种极限的接触工况,并且这与摩擦系数$f_r$的取值相关. 取侧压力系数$\lambda = 0.5$,分析摩擦系数$f_r$取不同值时接触面上接触应力$\sigma _r $,$\tau _{r\theta }$和切向位移间断值$\left| {u_{\theta 1} - u_{\theta 2} } \right|$的变化规律,并将其与完全接触[13 ] 和光滑接触[14 ] 的结果进行对比. ...
Analytic solutions of stress and displacement for a non-circular tunnel at greatdepth including support delay
2
2014
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
Analytical solutions for the stress of a lined non-circular tunnel underfull-slip contact conditions
2
2015
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
Lined circular tunnels in elastic transversely anisotropic rock at depth
2
2011
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
正交各向异性岩体中非圆形水工隧洞的解析解
2
2018
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
正交各向异性岩体中非圆形水工隧洞的解析解
2
2018
... Hasanpour 等[8 ] 、Ramoni 等[9 ] 以及Son[10 ] 都对支护和岩土材料之间的相互作用问题进行了研究.在求解有支护的深埋隧洞问题的解时,可以将其简化为平面应变无限域问题,于学馥等[11 ] 、Wang等[12 ] 以 及Lu 等[13 -14 ] 已经获得了各向同性弹性岩体中圆形隧洞衬砌和围岩相互作用的解析解.Lu等[15 -16 ] 考虑了更复杂的孔形,以直墙半圆拱形隧洞为例获得了非圆形隧洞的解析解.Bobet[17 ] 和王少杰等[18 ] 考虑了更复杂的岩体材料,分别视岩体为横观各向同性和正交各向异性的弹性体,获得了非圆形隧洞的应力和位移的解析解. ...
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
Numerical and analytical solutions for the problem of hydraulicfracturing from a cased and cemented wellbore
1
2002
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
一类非均布荷载作用下双层厚壁圆筒光滑接触时的应力解析解
1
2013
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
一类非均布荷载作用下双层厚壁圆筒光滑接触时的应力解析解
1
2013
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
非静水应力场中圆形隧道衬砌与围岩间两种接触的黏弹性解析
1
2017
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
非静水应力场中圆形隧道衬砌与围岩间两种接触的黏弹性解析
1
2017
... 隧洞在施加衬砌支护之后,围岩和衬砌接触并相互作用,在以往的解析研究中,大都考虑了完全接触和光滑接触两种理想的接触方式.文献[12 -13 , 15 , 17 -18 ] 都假定围岩与衬砌之间的接触为完全接触,即认为接触界面上法向的径向应力和径向位移及环向的剪切应力和切向位移都是连续的.这种接触假定围岩与衬砌之间非常粗糙,接触面可以承受很大的摩擦力,不允许围岩与衬砌之间产生相对滑动;而文献[11 , 14 , 16 ] 在求解过程中将围岩与衬砌之间的接触视为光滑接触,即认为接触界面上法向的径向应力和径向位移仍然是连续的,即围岩和衬砌在法线方向不能相互脱开,但假定接触面充分光滑,在接触面的切线方向不能承受摩擦力,即认为环向方向的剪切应力为零,这种接触允许围岩与衬砌之间产生相对滑动. Atkinson和Eftaxiopoulos[19 ] 在求解套管井和胶结井水力压裂问题的解析解时,在水泥和岩石的接触面上考虑了这种光滑接触条件. 高永涛等[20 ] 考虑双层厚壁圆筒之间的光滑接触并获得了非均布荷载作用下内外壁的应力解析解.储昭飞等[21 ] 在求解非静水应力场中圆形隧道黏弹性解析解时,其中也考虑了衬砌和围岩之间的光滑接触. ...
连接结构接触界面非线性力学建模研究
1
2018
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
连接结构接触界面非线性力学建模研究
1
2018
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
Parallelized computational modeling of pile--soilinteractions in mechanized tunneling
1
2013
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
An augmented Lagrangian technique combined with a mortar algorithm formodelling mechanical contact problems
1
2013
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
Numerical solution of frictional contact problems based on a mortaralgorithm with an augmented Lagrangian technique
1
2015
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
盾构隧道管片衬砌内力分析的壳-弹簧-接触模型及其应用
1
2007
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
盾构隧道管片衬砌内力分析的壳-弹簧-接触模型及其应用
1
2007
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
盾构输水隧洞复合衬砌计算模型
1
2010
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
盾构输水隧洞复合衬砌计算模型
1
2010
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
Analytic stress solutions for a lined circular tunnel under frictional slipcontact conditions.
9
2019
... 完全接触和光滑接触是人为假定的两种理想情形,实际上两种材料的接触很可能并非为这两种理想情形,例如,在建立连接结构接触界面的非线性力学模型时,王东等[22 ] 就将名义的光滑平面视作凹凸不平的粗糙面,考虑了微凸体的黏滑摩擦行为.围岩和衬砌接触时,它们之间并非完全光滑,也并非可以承受任意大的摩擦力,当围岩与衬砌之间的剪应力大于所能承受的最大静摩擦力后,将发生切向滑动. 库仑摩擦模型作为刚体的摩擦模型,因其简单和实用而被广泛应用于工程分析中.该模型认为切向摩擦力的数值不能超过法向压力和摩擦系数的乘积. Meschke 等[23 ] 建立计算模型以模拟桩土相互作用时隧道的机械化开挖,其中就利用了库仑摩擦模型来模拟桩-土的相互作用.Cavalieri 等[24 -25 ] 利用增广拉格朗日法求解涉及摩擦的接触问题时,也利用库仑摩擦定律建立了计算模型.苏宗贤等[26 ] 和杨钊等[27 ] 利用库仑摩擦模型分别模拟了管片和围岩以及复合衬砌中内外层衬砌之间的接触. 吕爱钟等[28 ] 在库仑摩擦模型的基础上利用复变函数方法和最优化方法获得了圆形隧洞围岩和衬砌摩擦滑动接触的解析解,并与有限元软件ANSYS 所得结果进行了对比,验证了其方法合理性. ...
... 本文同样将通过库仑摩擦模型模拟接触面上的切向力学行为,但不同于文献[28 ] ,本文在优化过程中减少了设计变量的个数,极大地简化了优化模型. 在弹性接触分析中,库仑摩擦模型可表述如下 ...
... 文献[28 ] 使用混合罚函数方法来进行优化计算[29 -30 ] ,其数学模型为 ...
... 按照文献[28 ] 的求解过程,其将式 (18)~式 (25) 组成的8 个方程作为优化模型中的等式约束函数$a_j ({X})$, 而将式 (33)组成的不等式组作为不等式约束条件,然后将等式约束函数$a_j ({X})$ 和不等式约束函数$b_j ({\pmb X})$分别构成惩罚项加到目标函数$F({\pmb X})$构成一个新的无约束的称为罚函数的目标函数$p(x,r)$,其中$r$称为罚因子. 这样,就把原目标函数$F({\pmb X})$的约束极小值问题转为求罚函数$p(x,r)$ 的无约束极小值问题.其罚函数的具体形式为 ...
... 可以看出,较之文献[28 ] 中的罚函数的具体形式,本文的罚函数形式没有二次损失项中的$\sum_{j = 1}^8 {a_j^2 ({\pmb X})}$,并且计算初始点${\pmb X}^{(0)}$ 仅有$h_1^0$,这极大地简化了优化的数学模型. 模型中只有$h_1 $为设计变量,改变$h_1 $ 的值,使式 (36) 达到最小值的$\hat{h}_1 $即为该优化问题的解,此时其他8个变量可以由解方程组得出且分别表示为$\hat{c}_1 $,$\hat {d}_1 $,$\hat {d}_3 $,$\hat {e}_1 $,$\hat {f}_1$,$\hat {f}_3 $,$\hat {g}_1 $,$\hat {g}_3 $.为了比较两种模型的精确程度,我们以摩擦滑动接触为例,利用新旧两种模型分别计算出不同摩擦系数$f_r$对应的目标函数的值,其对比如表1 所示. ...
... 从表1 可以看出,比较不同摩擦系数$f_r $计算出的目标函数值,本文提出的新优化模型所得结果更小,这是因为本文通过解方程的方法可以使式 (34) 中的$a_j ({\pmb X}) = 0$精确满足,较之文献[28 ] 中的优化模型,该方法更加精确. ...
... 我们已经确定利用摩擦滑动接触解法可以求解完全接触和光滑接触两种极限接触问题, 而且通过推导已知当$f_r$ 的值大于某个值时,总能满足完全接触的条件,称这个值为阈值$f_r^t$,确定阈值$f_r^t $ 对判断接触面上的接触方式很有帮助. 文献[28 ] 通过反复试算的方式讨论了不同弹性模量和侧压力系数所确定的阈值$f_r^t$,但是这种方法不够精确,本文尝试利用一种精确的方法来确定阈值$f_r^t$. ...
... 同时,为了同文献[28 ] 中所得结果进行比较,取$R_0 =2.5$ m,侧压力系数分别为0.2,0.5,0.8,1.0,在不同弹模比值下所得阈值如表6 所示. ...
... 表3表明增大位移释放系数,阈值$f_r^t $逐渐减小,说明越晚支护,接触面上越不容易发生相对滑动;从表4 可以看出, 在洞径不变的前提下,增大衬砌厚度可以使阈值$f_r^t $减小. 表5 则很清晰地表示随着内水压力的增大,阈值$f_r^t $逐渐减小. 表6 说明当$E_2 / E_1 \leqslant10$,随着弹模比值的增大,阈值$f_r^t $ 也增大,而当$E_2 / E_1 >10$,阈值$f_r^t $ 随着弹模比值的增大而减小,而文献[28 ] 中利用试算方法所得阈值随着弹模比值的增大而增大,这与此处所得结论不同,说明了试算方法的局限性;从表3 ~表6 可以看出,侧压力系数$\lambda $ 对阈值的影响最大,随着$\lambda$ 的增大,满足完全接触的阈值$f_r^t $ 减小,直至$\lambda =1.0$,$f_r^t =0$,即两向等压时,即使摩擦系数等于零,接触面上也不发生相对滑动. ...
Practical Methods of Optimization, Volume 2. Constrained Optimization
1
1981
... 文献[28 ] 使用混合罚函数方法来进行优化计算[29 -30 ] ,其数学模型为 ...
1
1983
... 文献[28 ] 使用混合罚函数方法来进行优化计算[29 -30 ] ,其数学模型为 ...
1
1983
... 文献[28 ] 使用混合罚函数方法来进行优化计算[29 -30 ] ,其数学模型为 ...