引言
超疏水减阻是近20年来海洋工程领域关注的一个研究热点[1-8]. Rothstein等[9]直接观测超疏水规则微结构表面气液界面上的流速分布, 得到约20 $\mu$m滑移量和40%减阻量. Ghaemi等[10]发现在湍流状态下气膜层会导致明显的壁面滑移,并引起近壁区雷诺剪应力和正应力下降约15%. 胡海豹等[11]通过在转子壁面构造润湿梯度, 实现连续气环的稳定维持, 在雷诺数660~1320内获得超过70%的稳定减阻量. 保持超疏水表面气膜层的稳定是实现其减阻效果的关键[12]. 但实际上高水压[13-15]、气体扩散[16-18]、压力脉动[19]等因素均会造成超疏水微结构内部气体流失, 减阻失效, 甚至增阻. 尤其在湍流状态下[20], 流动不稳定性和剪切应力的共同作用, 会加速超疏水表面气膜层的破坏, 是目前亟待解决的技术瓶颈.
上述研究说明, 超疏水沟槽表面气膜层比单纯超疏水表面更加稳定, 且在较低雷诺数时减阻效果可观但实际工程应用中, 往往需要表面气膜层和减阻功能能够长期有效. 为此, 本文进一步探索了在超疏水沟槽表面通过通气方式来实现气膜层长时间维持的可行性.
1 实验装置与方法
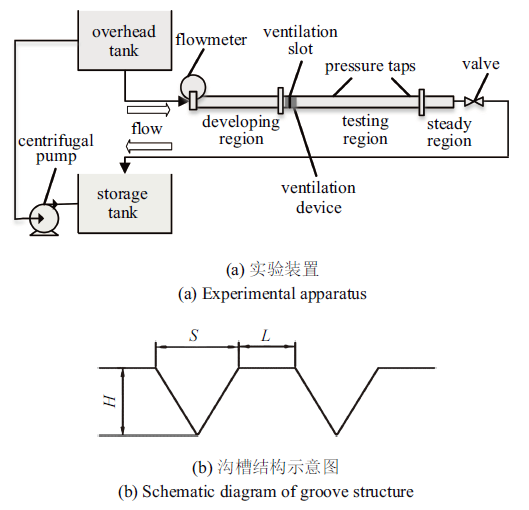
实验装置主要由上水箱、下水箱、离心泵、管道、流量计、测压和供气装置等组成(如图1). 其中, 上水箱尺寸为1170 mm $\times$ 1720 mm $\times$ 480 mm, 距地面高度3750 mm, 上下水箱通过离心泵和管路连接; 上水箱中水位保持不变, 依靠水的重力势能来驱动水流, 雷诺数调节范围为1.4 $\times$ 10$^{4}$$\sim $5.2 $\times$ 10$^{4}$(以管道水力直径为特征长度). 管道材质为无色亚克力(PMMA), 截面为60 mm $\times$ 20 mm的矩形; 实验平板有效尺寸770 mm $\times$ 60 mm $\times$ 20 mm, 装在管道上端面. 流量计测量范围0.8~15 m$^{3}$/h, 工作压力1.6 mPa; 压力变送器输出信号范围4~20 mA, 非线性误差$\pm $0.2%; 供气气缸直径160 mm、推程1 m, 由交流伺服电机和滚珠丝杠来精细驱动. 实验板表面沟槽高度$H$取1.2 mm, 1.6 mm和2.0 mm, 沟槽宽度取$S=H$, 槽间距取$L=2$ mm. 实验中, 为减小偶然误差, 每个数据重复采集100次.
图 1
图 1
实验装置及沟槽结构示意图
Fig. 1
Experimental apparatus and schematic diagram of groove structure
实验中采用进口商用超疏水涂层(ultra-ever dry)进行表面超疏水处理. 该涂层分底漆、面漆两层, 底漆能与试件表面牢固黏附, 面漆凝固后可形成微纳复合结构, 展现出优越的超疏水效果. 施工时, 采用气动喷枪分两轮进行底漆和面漆喷涂, 且时间间隔不小于30 min. 经测试, 水滴在该超疏水涂层表面接触角可达165$^\circ$, 滚动角小于2$^\circ$.
文中超疏水沟槽板减阻率
式中, $\Delta P_{1}$和$\Delta P_{2}$分别为光板和超疏水沟槽板对应的管道压降值.
为表征沟槽尺寸的影响, 参照沟槽减阻研究中的处理方法[35], 定义无量纲沟槽宽度$S^{+}$为
式中, $S$为槽宽, $\upsilon $为运动黏性系数, $V_\tau $则表示光板表面的壁面剪切速度, 其对应表达式为
其中, $\tau _0 $表示光板表面的壁面剪切应力, $V$为平均流速, $\rho $为流体密度, $D$为管道水力直径.
2 结果与分析
2.1 通气速率对减阻的影响
为研究通气对超疏水沟槽表面减阻的影响, 这里详细测试了三种典型尺寸沟槽在一系列不同通气速率($Q_{\rm a})$下的减阻情况. 图2(a)为沟槽宽度$S=1.2$ mm时超疏水沟槽表面压降随雷诺数($Re$)的变化曲线, 其中, "smooth''曲线为光板上的压降. 可以发现, 与光板类似, 超疏水沟槽表面压降与雷诺数呈二次方关系(如图中虚线), 且随$Q_{\rm a}$增大, 曲线整体下移, 减阻效果增强; 不过, 不通气状态下($Q_{\rm a} =0$), 超疏水沟槽表面压降曲线在光板之上, 表现为增阻效果, 说明这种大尺寸沟槽引起的粗糙增阻效应此时占主导作用. 对比图2(b)给出的三种通气速率下超疏水沟槽表面气膜形态可见, $Q_{\rm a}=0$时, 受水流剪切作用, 超疏水表面气膜逐渐流失, 仅在其微结构内部存留少量气体. 在未转变成完全浸润的Wenzel状态前,沟槽内部及槽间均处于Wenzel与Cassie之间的过渡状态, 此时气膜厚度小于表面粗糙颗粒高度; $Q_{\rm a}=2$ mL/s时部分沟槽内已被气体充满, 但槽间仍保持与无通气条件下的状态一致, 说明沟槽对气体有导向和稳定的作用; $Q_{\rm a}=10$ mL/s时超疏水沟槽均被完整的亚毫米级气膜层包覆. 上述不同通气速率下表面气膜形态的变化规律, 正好解释了图2(a)超疏水沟槽表面增阻作用和减阻效果差异的形成原因.
图 2
2.2 沟槽尺寸对减阻的影响
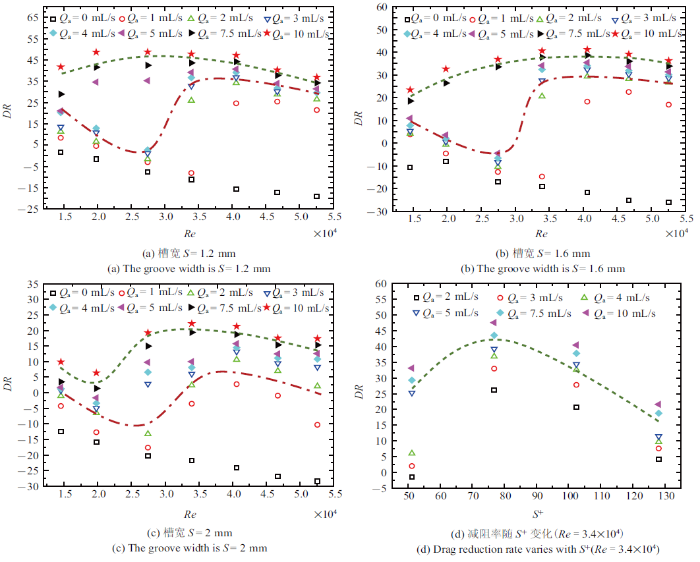
图3为超疏水沟槽表面减阻率随雷诺数及沟槽无量纲宽度$S^{+}$的变化曲线. 从图3(a)和图3(b)可以看出, 恒定通气速率下, 超疏水沟槽表面减阻率随雷诺数的变化表现为两种规律. 在槽宽$S=1.2$ mm的超疏水沟槽表面上(图3(a)), $Q_{\rm a}=1$ mL/s, 2 mL/s, 3 mL/s及4 mL/s时, 随雷诺数增大, 减阻率表现为先减再增后继续减小的规律(规律I); 当增大$Q_{\rm a}$至5 mL/s, 7.5 mL/s及10 mL/s时, 减阻率则表现为先增后减的规律(规律II). 在$S=1.6$ mm的超疏水沟槽表面(图3(b))也存在上述两种规律, 但$Q_{\rm a}=5$ mL/s时与图3(a)不同, 表现为规律I; 当$S$进一步增至2 mm时(图3(c)), 所有$Q_{\rm a}$下均表现为规律I. 可见, 随$S$增大, 规律I对应的通气速率范围扩大. 规律I与规律II产生和转变的原因将在下节详细解释. 同时还发现, 不通气时3种超疏水沟槽表面均表现为增阻效果, 且随沟槽尺寸增大阻力变大, 即大尺寸沟槽引起更大的粗糙增阻作用.
图 3
图 3
超疏水沟槽表面减阻率随雷诺数及$S^{+}$变化(线条表示趋势线)
Fig. 3
The variation of drag reduction rate with Reynolds number and$ S^{+}$(Lines indicate trend lines)
2.3 气膜铺展状态分析
这里以$S=1.2$ mm的超疏水沟槽表面气膜铺展状态为对象对上节减阻规律I和II进行分析. 图4(a) ~图4(c)分别为$Q_{\rm a}=10$ mL/s, $Re=1.4\times 10^{4}$, $Re=3.4\times 10^{4}$和$Re=5.2\times 10^{4}$时气膜状态(从图3(a)知对应于规律II), 其中反光部分为气膜层. 图4(a)中, $Re=1.4\times 10^{4}$时超疏水沟槽表面上气膜完整铺展, 且有少量富裕气体以形状不一的气泡形式分布在其表面, 这可能导致少量的额外阻力.图4(b)中, $Re$增大到$3.4\times 10^{4}$时, 因高水速带走更多的气体, 使得超疏水沟槽表面气膜铺展更趋均匀、平整, 此时减阻更佳. 但继续增大$Re$至$5.2\times 10^{4}$时(图4(c)), 均匀铺展的气膜层会在高速水流冲刷作用下产生局部破损, 导致气液面积比有所减小, 减阻率降低.
图4(d) ~图4(f)分别表示$Q_{\rm a}=4$ mL/s, $Re=2.7\times 10^{4}$, $Re=3.4\times 10^{4}$和$Re=4.0\times 10^{4}$时表面气膜铺展状态(对应于规律I). 观察图4(d)发现, $Re=2.7\times10^{4}$时沟槽结构引起的展向能垒[36-37]和水流冲刷的共同作用下, 使得通入气体仅在少数沟槽内沿流向铺展和移动, 未实现大面积展向铺展. 此时少数沟槽表面气膜减阻作用与多数无气膜覆盖沟槽引起的粗糙增阻效应同时存在,致使减阻率低.$Re$增大到$3.4\times 10^{4}$时(图4(e)), 管道内增强的湍流横向脉动和剪切作用致使少数沟槽表面气膜克服了展向能垒, 发生部分展向铺展, 气膜层覆盖的沟槽条数明显增加, 减阻率上升. 继续增大$Re$至$4.0\times 10^{4}$时(图4(f))发现, 此时在强横向扰动的作用下, 气膜已均匀展向铺展到整个超疏水沟槽表面, 表现出最佳的减阻效果. 当进一步增大$Re$时, 则会出现类似图4(c)的现象, 因高水速带来的大气量流失, 使得均匀铺展的气膜层受到破坏, 减阻率降低.
图 4
图 4
超疏水沟槽板表面气膜铺展状态
Fig. 4
The spreading state of gas film on superhydrophobic groove surfaces
2.4 与单纯超疏水表面通气减阻的对比
上述研究结果说明超疏水沟槽表面通气确实有利于表面气膜稳定, 但这种大尺寸沟槽会造成额外的增阻作用. 为更全面评价其减阻效果, 图5进一步给出了典型通气速率下单纯超疏水表面(SHS)与超疏水沟槽表面减阻率的对比. 从图5可以发现, 与超疏水沟槽表面展现的减阻规律I、规律II不同, 单纯超疏水表面减阻率均呈现单调降低趋势; 值得注意的是, 单纯超疏水表面仅在较低雷诺数时有减阻优势, 但较高雷诺数下超疏水沟槽表面具有更优异的减阻性能; 通气速率$Q_{\rm a}=1$ mL/s, 7.5 mL/s时, 超疏水沟槽表面分别在雷诺数大于$4.0\times 10^{4}$, $2.7\times 10^{4}$时展现大于超疏水表面的减阻效果, 这说明随$Q_{\rm a}$增大, 超疏水沟槽表面上有减阻优势的雷诺数范围扩大. 由此可见, 超疏水表面与沟槽的复合既有利于气膜稳定, 还能增强减阻.
图 5
图 5
通气时超疏水和超疏水沟槽表面减阻对比(线条为趋势线)
Fig. 5
Comparison of drag reduction rate between superhydrophobic and superhydrophobic groove surface under ventilation state(lines are trend lines)
图 5
图 5
通气时超疏水和超疏水沟槽表面减阻对比(线条为趋势线) (续)
Fig. 5
Comparison of drag reduction rate between superhydrophobic and superhydrophobic groove surface under ventilation state(Lines are trend lines) (continued)
3 结论
通过开展超疏水沟槽表面通气减阻实验, 分析其减阻规律以及气膜铺展状态, 发现:
(1)通气是长期维持超疏水沟槽表面气膜层和减阻性能的一种有效方式, 且在固定流动条件下存在减阻效果最佳的通气速率.
(2)与单纯沟槽减阻类似, 随沟槽尺寸扩大, 超疏水沟槽表面减阻率先增后减, 最优无量纲沟槽宽度$S^{+}\approx 76$.
(3)与单纯超疏水表面通气不同, 高雷诺数下超疏水沟槽表面既有利于气膜稳定束缚, 还可以增强减阻效果, 是一种潜在的新型稳定减阻手段.
另外, 受实验装置的限制, 论文未测试出超疏水沟槽表面通气状态下气液界面形态与边界层流场, 相关研究仍有待进一步深入.
参考文献
Natural and biomimetic artificial surfaces for superhydrophobicity, self-cleaning, low adhesion, and drag reduction
超疏水材料表面液-气界面的稳定性及演化规律
Stability and evolution of liquid-gas interfaces on superhydrophobic surfaces
Experimental drag reduction study of superhydrophobic surface with dual-scale structures
A porous superhydrophobic surface with active air plastron control for drag reduction and fluid impalement resistance
超疏水表面对湍流边界层相干结构影响的TRPIV实验研究
TRPIV experimental study of the effect of superhydrophobic surface on the coherent structure of turbulent boundary layer
Drag reductions and the air-water interface stability of superhydrophobic surfaces in rectangular channel flow
用于固液界面减阻无氟超疏水表面制备新方法
A new method for fluorine-free superhydrophobic surface used for drag-reduction at solid-liquid interface
微纳结构超疏水表面的浸润性分析及设计
Wettability analysis and design of micro-nanostructured superhydrophobic surface
Direct velocity measurements of the flow past drag-reducing ultrahydrophobic surfaces
Turbulent flow over wetted and non-wetted superhydrophobic counterparts with random structure
Significant and stable drag reduction with air rings confined by alternated superhydrophobic and hydrophilic strips
Drag reduction in turbulent flows over superhydrophobic surfaces
Cassie-Wenzel and Wenzel-Cassie transitions on immersed superhydrophobic surfaces under hydrostatic pressure
Sustainability of superhydrophobicity under pressure
Predicting shape and stability of air-water interface on superhydrophobic surfaces with randomly distributed, dissimilar posts
Ultimate stable underwater superhydrophobic state
Infinite lifetime of underwater superhydrophobic states
Plastron properties of a superhydrophobic surface
Two-dimensional analysis of air-water interface on superhydrophobic grooves under fluctuating water pressure
Experimental study of skin friction drag reduction on superhydrophobic flat plates in high Reynolds number boundary layer flow
Marine drag reduction of shark skin inspired riblet surfaces
Modeling and optimization of shark-inspired riblet geometries for low drag applications
Material selection and manufacturing of riblets for drag reduction: An updated review.
沟槽面湍流边界层减阻的TRPIV测量
TRPIV Measurement of drag Reduction in the turbulent boundary layer over riblets plate
沟槽方向对湍流边界层流动结构影响的实验研究
Flow structure in the turbulent boundary layer over directional riblets surfaces
正弦波沟槽对湍流边界层相干结构影响的TR-PIV实验研究
Influence of sinusoidal riblets on the coherent structures in turbulent boundary layer studied by time-resolved particle image velocimetry
Drag characteristics of V-groove and transverse curvature riblets
Experiments on drag-reducing surfaces and their optimization with an adjustable geometry
Turbulent boundary-layer modification by surface riblets
Active turbulence control for drag reduction in wall-bounded flows
沟槽对湍流边界层中展向涡影响的实验研究
An experimental study on riblet-induced spanwise vortices in turbulent boundary layers
Investigation of retention of gases in transverse hydrophobic microgrooved surfaces for drag reduction
Turbulent channel flow over riblets with superhydrophobic coating
Experimental study on the friction drag reduction of superhydrophobic surfaces in closed channel flow
Fluid drag reduction with shark-skin riblet inspired microstructured surfaces
矩形疏水沟槽表面水滴振荡特性
Characteristic of droplet oscillation on the surface of rectangular hydrophobic grooves
Motion of a droplet on an anisotropic microgrooved surface