引言
当海流绕过海洋立管时, 在立管下游会产生尾流和漩涡, 周期发放的漩涡对立管产生垂直于来流向的涡激升力, 引起立管的涡激振动(vortex-induced vibration, VIV). 立管涡激振动即立管尾流涡脱落的频率与结构频率接近时发生的自激振动, 一直以来是立管结构疲劳破坏的一个主要因素[1 -4 ] , 由于海流速度沿水深变化的非均匀性及流固耦合的复杂性, 涡激振动长期以来是海洋工程中颇具挑战性的问题之一, 涡激振动的准确预报是一个巨大的难题[5 ] .
海洋热塑性增强管(reinforced thermoplastic pipe, RTP)是一种复合材料管道, 可用作立管, 具有可盘卷(近百米一卷)、海陆施工快捷、质量小、耐疲劳、保温性能好, 以及高耐腐蚀等性能[6 -10 ] . 使用RTP作为立管可以减小海洋平台的体积, 减少海洋平台锚张力、减少立管顶张力, 显著降低开采成本. 同时, 使用复合材料立管操作成本低, 对系统其他构件的影响相对较小, 相比传统的钢制立管有更多的优越性[11 -12 ] . RTP在海上优势突出, 虽然要求高, 投资大, 但发展迅猛, 海洋用RTP市场可能超过陆用市场. 我国海洋油气资源丰富, 过去油气开采限制于100 m深以内的浅海, 近年向更深海域拓展, 满足深海要求的RTP成关键. 国内对复合材料立管的研究起步较晚, 关于完全非金属的复合材料RTP立管涡激振动的研究更少. 能够适用于工程上快速评估复合材料立管涡激振动性能的方法未见报道. RTP产品的种类繁多, 本文仅以如图1 所示的复合材料预制增强带RTP立管作为研究对象, 探索适合工程的复合材料立管的建模方法, 以及研究其涡激振动行为, 为工程上类似的复合材料立管快速建模和涡激振动快速分析提供参考.
1 海洋立管系统动力学模型
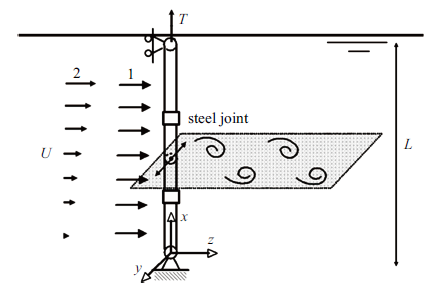
如果水深小于500 m, 一般采用传统的固定式平台或塔式平台. 假设本文研究的立管长度在50~ 150 m之间, 因此采用塔式平台, 即固定式平台. 针对密度与水接近的RTP立管, 忽略立管重力, 考虑均匀来流和剪切流引起的涡激升力、立管顶部的顶张力、连接管道的刚性接头, 简化后的RTP立管模型示意如图2 所示, 立管下端铰接在位于海底的万向节上, 上端铰接于固定平台上. 图中$T$为顶张力, 数字1表示均匀来流, 数字2表示剪切流. 本文研究所用到的立管参数如表1 所示. 忽略平台的振动, 立管边界条件可视为两端简支, 另外做如下假设:
图 1
图 1
RTP结构示意图
Fig. 1
Structural diagram of RTP
(2)立管内部流体为油, 视为附加质量, 不考虑内流速度对立管振动的影响;
(3)忽略立管本身的结构阻尼, 仅考虑立管振动引起的水动力阻尼;
RTP管道一般由内管、增强层和外管组成. 如表1 所示, 本文研究的RTP立管的材料包括高密度聚乙烯(HDPE)、中密度聚乙烯(MDPE)和芳纶纤维. 立管参数见表2 .
图 2
图 2
立管模型示意图
Fig. 2
Riser model
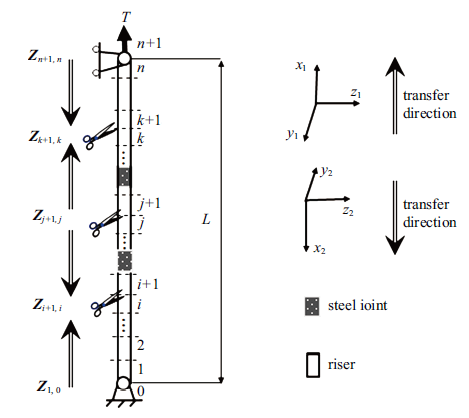
考虑柔性立管刚性接头等结构细节, 基于多体系统传递矩阵法计算其振动特性. 铰-铰约束的带有顶张力的立管的欧拉梁模型如图3 所示. 本文采取将梁分段的方法来建立柔性立管的力学模型. 为了便于考虑立管中刚性接头对振动特性的影响, 以刚性接头的长度为参考长度, 将RTP立管分为$n$段, 那么刚性接头的长度为$L/n$ (本节针对150 m长RTP立管计算时, 取$n=80$). 这样计算中可以任意选取刚性接头的个数, 只需将对应的梁元件的材料改为刚材料即可.
图 3
图 3
包括状态矢量和传递方向的立管模型
Fig. 3
Riser model including state vector and transfer direction
2 RTP立管动力学特性建模
文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为
(1) $ \begin{eqnarray} \label{eq1} {U}={B}(l){B}^{-1}(0) \end{eqnarray}$
(2) $ \begin{eqnarray} \label{eq2} {B}(x)=\left[\begin{array}{*{20}c} {\cos \beta x} & 0 & 0 & 0 & {\sin \beta x} & 0 \\ 0 & {\cosh (\lambda _1 x)} & {\sinh (\lambda _1 x)} & {\sinh (\lambda _1 x)} & 0 & {\sin (\lambda _2 x)} \\ 0 & {\lambda _1 \sinh (\lambda _1 x)} & {\lambda _1 \cosh (\lambda _1 x)} & {-\lambda _2 \sin (\lambda _2 x)} & 0 & {\lambda _2 \cos (\lambda _2 x)} \\ 0 & {EI\lambda _1 ^2\cosh (\lambda _1 x)} & {EI\lambda _1 ^2\sinh (\lambda _1 x)} & {-EI\lambda _2 ^2\cos (\lambda _2 x)} & 0 & {-EI\lambda _2 ^2\sin (\lambda _2 x)} \\ {\beta EA\sin \beta x} & 0 & 0 & 0 & {-\beta EA\cos \beta x} & 0 \\ 0 & {(EI\lambda _1 ^3+T\lambda _1 )\sinh (\lambda _1 x)} & {(EI\lambda _1 ^3+T\lambda _1 )\cosh (\lambda _1 x)} & {(EI\lambda _2 ^3-T\lambda _2 )\sin (\lambda _2 x)} & 0 & {(T\lambda _2 -EI\lambda _2 ^3)\cos (\lambda _2 x)} \end{array} \right] \end{eqnarray} $
由于柔性立管非常细长, 将立管分成四部分, 并使用图3 所示的传递方向, 以减小同一方向传递过程中由于过多矩阵相乘引起的高阶振型的数值误差. 柔性立管的传递方程为
(3) $ \begin{eqnarray} \label{eq3} \left.\begin{array}{l} {Z}_{i+1,i{\rm up}} ={U}^{\rm part1}{Z}_{1,0{\rm up}} \\ {Z}_{i+1,i{\rm down}} ={U}^{\rm part2}{Z}_{j+1,j{\rm down}} \\ {Z}_{k+1,k{\rm up}} ={U}^{\rm part3}{Z}_{j+1,j{\rm up}} \\ {Z}_{k,k+1{\rm down}} ={U}^{\rm part4}{Z}_{n+1,n{\rm down}} \\ {CZ}_{i+1,i{\rm down}} ={Z}_{i+1,i{\rm up}} \\ {CZ}_{k+1,k{\rm down}} ={Z}_{k+1,k{\rm up}} \\ {CZ}_{1,0{\rm down}} ={Z}_{1,0{\rm up}} \\ {CZ}_{n+1,n{\rm down}} ={Z}_{n+1,n{\rm up}} \\ \end{array}\right\} \end{eqnarray} $
式(3)中, 状态矢量的下标up和down分别表示联接点处的上方和下方对应的状态矢量. 另外, 由图3 中的坐标系和传递方向, 以及MSTMM书中的符号约定可知, 式(3)中[16 ]
(4) $ \begin{eqnarray} \label{eq4} {C}=\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c@{\ \ }c} {-1} & 0 & 0 & 0 & 0 & 0 \\ 0 & {-1} & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & {-1} & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array} }} \right] \end{eqnarray} $
(5) $ \begin{eqnarray} \label{eq5} {U}_{\rm all} {Z}_{\rm all} ={\bf0} \end{eqnarray} $
(6) $ \begin{eqnarray} \label{eq6} &&{U}_{\rm all} =\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c} {{U}^{\rm part1}} & {-{CU}^{\rm part2}} & {{0}_{6\times 6} } & {{0}_{6\times 6} } \\ {{0}_{6\times 6} } & {{0}_{6\times 6} } & {{U}^{\rm part3}} & {-{CU}^{\rm part4}} \\ {{0}_{6\times 6} } & {C} & {-{I}} & {{0}_{6\times 6} } \\ \end{array} }} \right] \end{eqnarray} $
(7) $ \begin{eqnarray} \label{eq7} Z_{\rm all}^{\rm T} =\left[ {{\begin{array}{c@{\ \ }c@{\ \ }c@{\ \ }c} {Z_{1,0{\rm up}}^{\rm T} } & {Z_{j+1,j{\rm down}}^{\rm T} } & {Z_{j+1,j{\rm up}}^{\rm T} } & {Z_{n+1,n{\rm down}}^{\rm T} } \\ \end{array} }} \right]^{\rm T} \end{eqnarray} $
式中, ${U}^{\rm part1}={U}_i \cdots {U}_3 {U}_2 {U}_1 $, ${U}^{\rm part2}={U}_{i+1} \cdots {U}_{j-1} {U}_j $, ${U}^{\rm part3}={U}_k \cdots {U}_{j+2} {U}_{j+1} $, ${U}^{\rm part4}={U}_{k+1} \cdots {U}_n {U}_{n+1,n}$. ${U}_1 ,{U}_2 \cdots {U}_n $分别代表柔性立管每一段传递矩阵, 可以充分考虑柔性立管具体的结构细节. 对于铰-铰连接的柔性立管的边界条件为
(8) $ \begin{eqnarray} \label{eq8} \left.\begin{array}{l} {Z}_{1,0{\rm up}} =[0,\ \ 0,\ \ \varTheta _z ,\ \ 0,\ \ Q_x ,\ \ Q_y ]^{\rm T} \\ {Z}_{j+1,j{\rm down}} =[X,\ \ Y,\ \ \varTheta _z ,\ \ M_z ,\ \ Q_x ,\ \ Q_y ]^{\rm T} \\ {Z}_{j+1,j{\rm up}} =[X,\ \ Y,\ \ \varTheta _z ,\ \ M_z ,\ \ Q_x ,\ \ Q_y ]^{\rm T} \\ {Z}_{n+1,n{\rm down}} =[X,\ \ 0,\ \ \varTheta _z ,\ \ 0,\ \ 0,\ \ Q_y ]^{\rm T} \\ \end{array}\right\} \end{eqnarray} $
(9) $ \begin{eqnarray} \label{eq9} \bar{{U}}_{\rm all} \bar{{Z}}_{\rm all} ={\bf0} \end{eqnarray} $
求解方程(9)即可得到系统的固有频率$\omega _k (k=1,2,\cdots )$, 然后求出系统边界点状态矢量$\bar{{Z}}_{\rm all} $和$Z_{\rm all} $, 进而通过元件传递方程得到对应于固有频率$\omega _k $的系统全部联接点的状态矢量, 得到RTP立管系统的振型.
3 RTP立管涡激振动动力学方程
基于MSTMM和Van der Pol尾流振子模型建立RTP立管涡激振动动力学方程为
(10) $ \begin{eqnarray} \label{eq10} {Mv}_{tt} +{Kv}={f} \end{eqnarray} $
其中, ${M}$和${K}$分别为质量矩阵和刚度矩阵. 令${V}=[{\begin{array}{*{20}c} {{V}^{\rm 1}} & {{V}^{\rm 2}} & \cdots & {{V}^n} \\ \end{array} }]$, ${q}=[{\begin{array}{*{20}c} {{q}^1} & {{q}^2} & \cdots & {{q}^n} \\ \end{array} }]^{\rm T}$, $n$表示立管系统模态叠加所用的模态阶数, 本节对于立管的涡激振动计算取前10阶模态, 即$n=10$. ${v}={Vq}$, 可以将式(10)转化到模态坐标系中, 则有
(11) $ \begin{eqnarray} \label{eq11} {MV\ddot{{q}}}+{KVq}={f} \end{eqnarray} $
(12) $ \begin{eqnarray} \label{eq12} &&MV\ddot{{q}}+{KVq}=\left(-\frac{1}{2}C_D \rho DU\right)V\dot{{q}}+\\&&\qquad\left(\frac{1}{4}C_{L_0 } \rho DU^2\right){q}_v \end{eqnarray} $
(13) $ \begin{eqnarray} \label{eq13} \ddot{{q}}_v +\varepsilon \varOmega _f ({q}_v^2 -1) \dot{{q}}_v +\varOmega _f^2 {q}_v =\frac{A}{D}{V\ddot{{q}}} \end{eqnarray} $
利用增广特征矢量的正交性, 在式(12)两边同时乘以${V}^{\rm T}$, 即
(14) $ \begin{eqnarray} \label{eq14} &&{V}^{\rm T}{MV\ddot{{q}}}+{V}^{\rm T}{KVq}={V}^{\rm T}\left[\left(-\frac{1}{2}C_D \rho DU\right)V\dot{{q}}+\right.\\&&\left.\qquad\left(\frac{1}{4}C_{L_0 } \rho DU^2\right){q}_v \right] \end{eqnarray} $
令${\bar{{M}}}={V}^{\rm T}{MV}$, ${\bar{{K}}}={V}^{\rm T}{KV}$,
(15) $ \begin{eqnarray} \label{eq15} &&{\bar{{M}}\ddot{{q}}}+{\bar{{K}}q}={V}^{\rm T}\left[\left(-\frac{1}{2}C_D \rho DU\right)V\dot{{q}}+\right.\\&&\left.\qquad\left(\frac{1}{4}C_{L_0 } \rho DU^2\right){q}_v \right] \end{eqnarray} $
(16) $ \begin{eqnarray} \label{eq16} {\ddot{{q}}}_v +\varepsilon \varOmega _f ({q}_v^2 -1)\dot{{q}}{ }_v+\varOmega _f^2 {q}_v =\frac{A}{D}{V\ddot{{q}}} \end{eqnarray} $
将式(15)、式(16)写成状态空间的形式, 令${x}_{\rm 1} ={q},{x}_{\rm 2} =\dot{{q}},{x}_{\rm 3} ={q}_v ,{x}_{\rm 4} =\dot{{q}}_v $, 则
(17) $ \begin{eqnarray} \label{eq17} \left.\begin{array}{l} {\dot{{x}}_1 ={x}_2 } \\ \dot{x}_2 =\dfrac{V^{\rm T}}{\bar{M}}\left[\left(-\dfrac{1}{2}C_D \rho DU\right){Vx}_2 + \\ \right.\qquad\left.\left(\dfrac{1}{4}C_{L_0 } \rho DU^2\right){x}_3 \right]-{\omega}^2{x}_1 \\ \dot{{x}}_3 ={x}_4 \\ \dot{{x}}_4 =\dfrac{A}{D}V\dot{{x}}_2 -\varepsilon \varOmega _f ({x}_3^2 -1){x}_4 -\varOmega _f^2 {x}_3 \\ \end{array} \right\} \end{eqnarray} $
采用龙格库塔法求解式(17), 其初始条件${q}=\dot{{q}}={0}_{1\times 10} ,{q}_v ={0.2}_{1\times 80} $, $\dot{{q}}_v ={0}_{1\times 80} $,时间步长大小一般取参考长度与来流速度比值的0.1$\sim $0.01倍, 此处取0.01 s.
4 模型验证及参数获取
4.1 振动特性及涡激振动模型验证
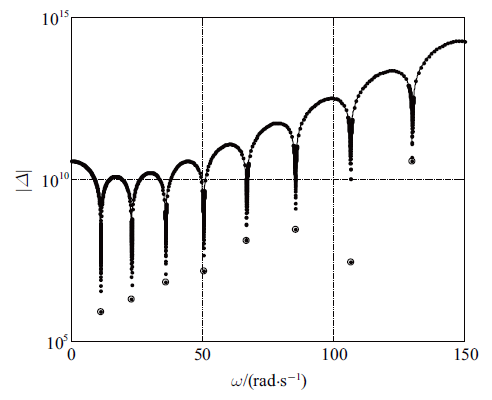
以文献[20 ] 中的立管参数为例, 采用MSTMM计算了细长立管的振动特性. 图4 为采用MSTMM计算顶张力为817 N的立管的干模态(不考虑周围流体的影响下的模态, 这种模态可以称为"干模态'', 即不受流体影响的模态)前8阶圆频率计算结果, 与文献[20 ] 中的理论分析解对比结果如表3 所示, 误差小于0.12%, 因此验证了基于MSTMM立管动力学特性计算模型的准确性.
图 4
图 4
干模态前8阶圆频率
Fig. 4
First eight circular frequencies of dry modal
在海流作用下, 立管上各点由漩涡脱落引起的振动可视为立管各模态振动的叠加(一般为前几阶湿模态, 湿模态即考虑周围流体影响下的模态, 工程上湿模态计算一般将立管外径对应的圆柱排开的流体质量作为附加质量考虑), 且一般存在主导振动模态. 以文献[20 ] 中的立管为例, 基于MSTMM和Van der Pol尾流振子模型, 通过式(17)采用模态叠加法计算带有顶张力的立管的涡激振动响应.
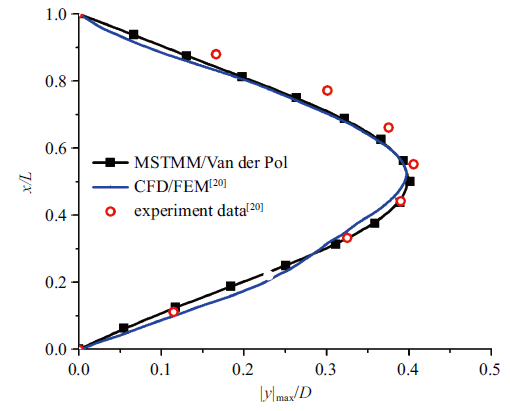
文献[20 ] 中, 均匀来流速度为0.2 m/s, 直径为0.02 m, 所以$Re=3988$, 根据$St$和$Re$的关系图[3 ] , $St$取0.23. Van der Pol尾流振子模型的计算精度一定程度上取决于经验系数的选取, 本文选取$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] . 如图5 所示, 仿真得到沿立管轴向的涡激振动最大振幅分布. 通过与文献[20 ] 的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性.
图 5
图 5
沿立管轴向的涡激振动振幅分布
Fig. 5
Amplitude of vortex induced vibration along the axis of riser
4.2 RTP立管等效刚度计算
(18) $ \begin{eqnarray} \label{eq18} f_n =\left(\frac{n^2\pi }{2L^2}\right)\sqrt {\frac{EI}{M}} \sqrt {1+\frac{TL^2}{n^2\pi ^2EI}},\quad n=1,2,3,... \end{eqnarray} $
式中, $T$为顶张力, $M$为单位长度的RTP管质量, $L$为立管长度, $E$为立管的弹性模量, $I$为立管的截面惯性矩.
在作者前期工作中[6 ] , 采用ANSYS软件的shell 181单元对RTP立管进行了复合材料建模, 并验证了建模方法的准确性. 本文为了获取RTP立管的等效刚度参数, 采用ANSYS软件计算一小段两端铰接的RTP短立管(此处取10 m长,直径为365 mm的短管进行有限元复合材料铺层并进行模态计算, 顶张力为1 N)的第一阶频率, 即可以利用式(18)反推出立管的等效刚度$EI$. 然后采用MSTMM就可以方便的计算出不同长度、不同顶张力的RTP立管的振动特性.
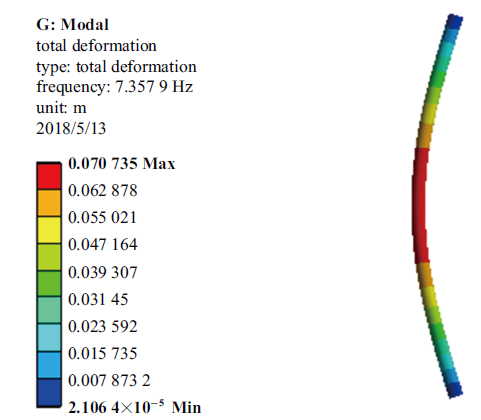
如图6 所示, 为短立管的第一阶模态分析的结果, 计算出短立管的第一阶频率为7.357 9 hz, 立管的单位质量为40.081 kg/m. 令式(18)中$n=1$, 因此可以反推出
(19) $ \begin{eqnarray} \label{eq19} EI=8 793 500\mbox{N}\cdot \mbox{m}^2 \end{eqnarray} $
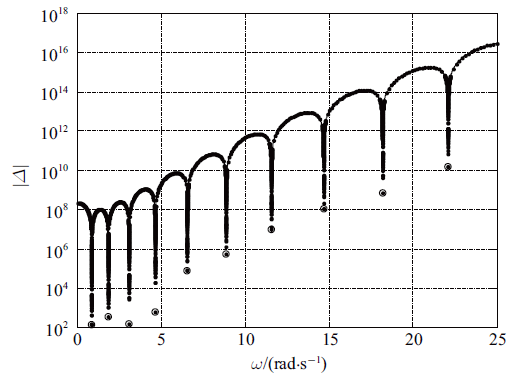
为了验证所获得的立管弯曲刚度参数的准确性, 采用MSTMM计算150 m长, 直径$D=365$ mm的复合材料RTP立管的前10阶频率和振型, 并与ANSYS有限元软件计算结果对比分析. 图7 为采用MSTMM计算得到的顶张力$T=60 000$ N情况下的RTP立管前10阶圆频率.
表4 为MSTMM与ANSYS有限元软件计算结果的对比, 两种方法计算结果相差较小, 说明采用短立管获取细长复合材料立管等效刚度的方法可行.
图 6
图 6
短立管模态分析
Fig. 6
Modal analysis of short riser
图 7
图 7
基于MSTMM的RTP立管前10阶圆频率
Fig. 7
The first ten circular frequencies of RTP riser based on MSTMM
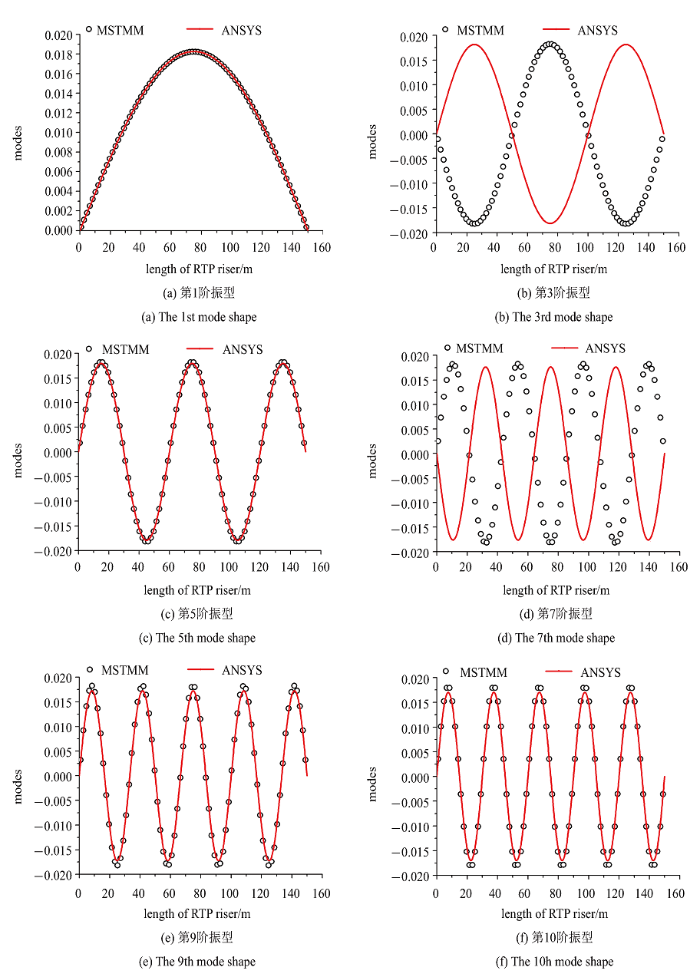
将MSTMM计算出的前10阶振型进行质量归一化, 然后与ANSYS计算出的振型进行对比. 如图 8 所示, 可以看出MSTMM计算出的振型与ANSYS软件计算出的复合材料立管的振型一致.
图 8
图 8
RTP立管的1, 3, 5, 7, 9, 10阶振型
Fig. 8
Modes 1, 3, 5, 7, 9 and 10 of RTP riser
5 仿真结果
5.1 RTP立管涡激振动特性分析
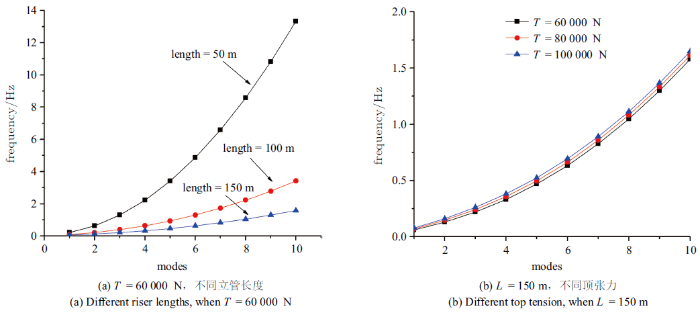
采用本文的方法省去了每改变一次参数就要对立管进行重新建模、复合材料铺层等繁琐步骤, 也无需划分大量网格单元, 计算量小, 且矩阵阶次低, 计算效率高. 直接采用MSTMM可以快速计算出RTP立管不同参数情况下的湿模态频率. 如图9 (a)所示, 计算了顶张力为60 000 N情况下, 不同长度RTP立管的湿模态频率. 随着立管长度的增大, 立管的高阶湿模态频率增长越缓慢, 且立管长度越大, 频率越小. 说明立管长度越大, 立管整体刚度越小. 立管的顶张力大小一般取立管重量的1$\sim $2倍之间. 150 m长立管的重量为60 000 N. 如图9 (b)所示, 分别计算了150 m长立管顶张力为60 000, 80 000, 100 000 N情况下的湿模态频率. 从图中可以看出, 顶张力对立管的湿模态频率影响不大, 随着顶张力的增大, RTP立管湿模态频率微弱增大.
图 9
图 9
RTP立管湿模态频率
Fig. 9
RTP riser wet modal frequency
5.2 RTP立管涡激振动特性分析
一般表层海流的水平流速从0.01 m/s到0.3 m/s, 深处的水平流速则在0.01 m/s以下. 基于MSTMM和Van der Pol尾流振子模型, 利用式(11) ~式(17)求解立管的涡激振动响应, 取Van der Pol 尾流振子模型中系数$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] , $St$取0.2.
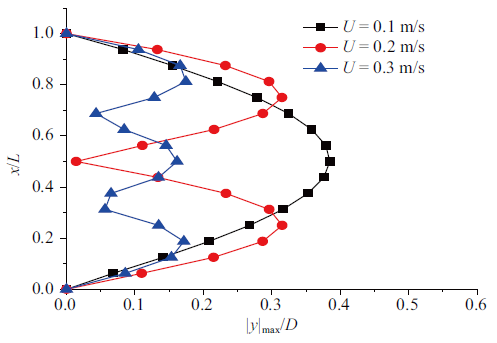
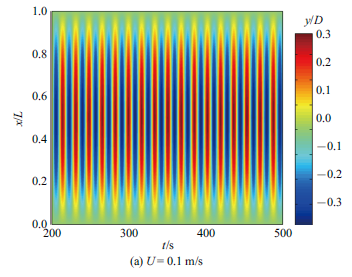
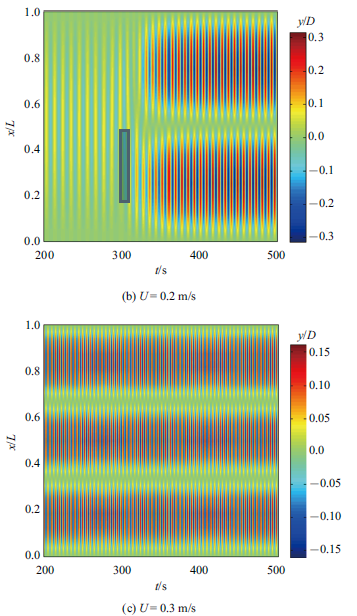
立管参数确定以后, 立管的固有频率就可确定, 但涡激升力的频率会随流速的增大而增大, 这就导致不同流速下立管涡激振动激发的模态不同. 从图10 可以看出, 150 m长, 顶张力为60 000 N的立管, 流速越大, 立管涡激振动激发模态越高, 但沿着立管轴向的最大振幅略有减小, 说明立管涡激振动位移主要受低阶模态控制. 这是由于150 m长立管相对于50 m长立管刚度大幅度减小, 容易激发出高阶模态为主导的振动响应. 图11 (a)、图11 (b)、图11 (c)分别是$L=150$ m, $T=60 000$ N的立管在$U=0.1$, 0.2, 0.3 m/s时的$y / D$历时云图. 图中水平坐标表示时间, 垂向坐标表示立管长度方向位置, 颜色代表的是不同的$y / D$的值. 从图11 (a)可以看出, 立管主要是以第1阶模态为主导的振动, 图11 (b)可以看出立管在来流速度为0.2 m/s时, 发生第1阶和第2阶模态切换现象. 这是由于柔性立管各阶振型对应的频率比较相近造成的. 图11 (c)为立管在来流速度为0.3 m/s时, 发生以第3阶模态为主导的振动历时云图.
图 10
图 10
沿RTP立管轴向的涡激振动振幅分布
Fig. 10
Amplitude of vortex induced vibration along the axis of RTP riser
图 11
图 11
沿RTP立管轴向的涡激振动响应历时云图
Fig. 11
Contour of vortex induced vibration response along the axis of RTP riser
图 11
图 11
沿RTP立管轴向的涡激振动响应历时云图(续)
Fig. 11
Contour of vortex induced vibration response along the axis of RTP riser (continued)
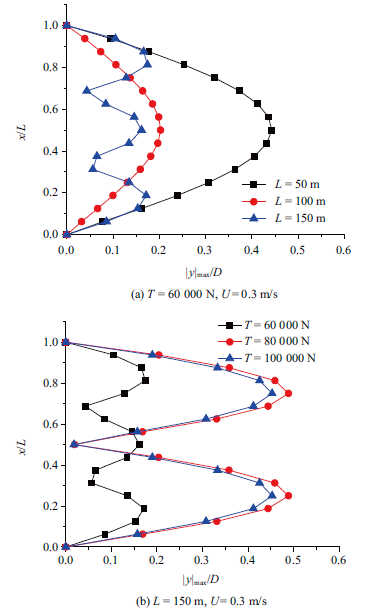
同样的, 计算立管不同长度, 不同顶张力情况下的涡激振动响应, 并绘出沿着立管轴向的涡激振动振幅分布图. 图12 (a)为来流速度为0.3 m/s情况下, 不同长度立管的涡激振动振幅沿着立管轴向分布图, 对照图10 、图11 可以看出, 立管长度为50 m和100 m时主要以第1阶模态为主导的振动, 立管长度为150 m时主要以第3阶模态为主导的振动. 如图12 (b)所示, 顶张力为80 000 N和100 000 N激发出以立管第2阶模态为主导的振动; 顶张力为60 000 N时, 激发出以立管第3阶模态为主导的振动. 随着顶张力增大, 立管振动位移略有增大. 这是由于顶张力增大, 立管弯曲刚度增大, 立管湿模态频率升高, 在同等流速下由于涡激频率不变, 导致立管激起模态降低, 从而使立管振动位移增大.
图 12
图 12
沿RTP立管轴向的涡激振动振幅分布
Fig. 12
Amplitude of vortex induced vibration along the axis of RTP riser
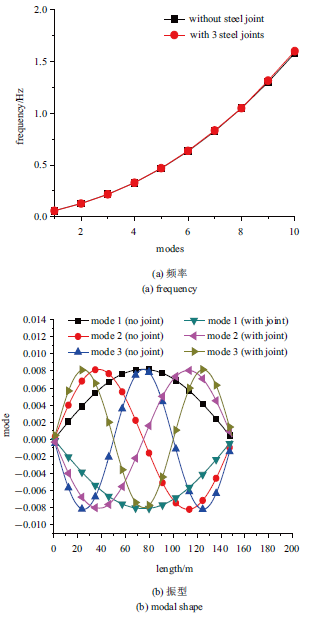
基于MSTMM快速建模的优点, 考虑150 m长立管中间包括多个刚性接头对涡激振动响应的影响, 只需将传递矩阵中的刚性接头部分的RTP的参数换成刚性接头的参数($EI=9.5734\times 10^7$ N$\cdot$m$^2$, $\bar{{m}}=284.70$ kg/m), 即可快速求解出立管振动特性及动力响应. 从图13 (a)可以看出, 均匀添加了3个刚性接头对RTP立管的频率影响较小. 这是由于添加了刚性接头, 同时微弱的增大了立管的质量和刚度, 因此立管的湿模态频率变化微弱. 从图13 (b)可以看出, 增加了刚性接头后, 对立管的振型也只是产生微弱的影响. 同理, 均匀添加了2个刚性接头对RTP立管的频率和振型几乎没有影响. 但是, 在立管中均匀添加2个或3个刚性接头会对涡激振动的振幅分布产生一定影响.
图 13
图 13
包含3个刚性接头情况下沿RTP的湿模态
Fig. 13
Wet mode along RTP with three rigid joints
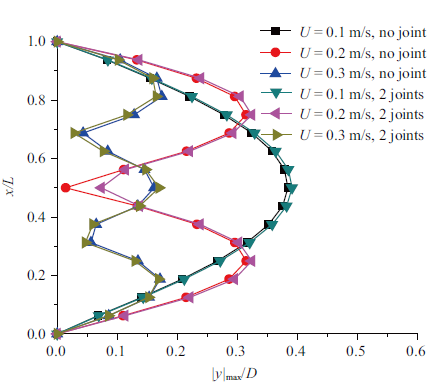
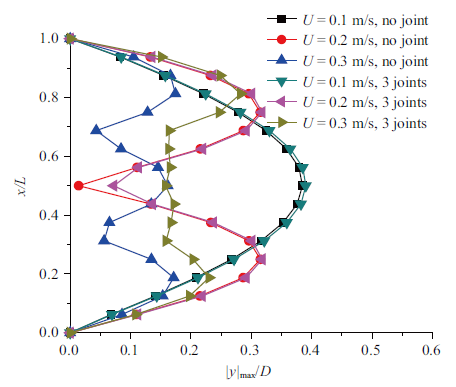
从图14 可以看出, 均匀添加了2个刚性接头后, 2个刚性接头对RTP立管的涡激振动振幅分布影响较小. 从图15 中可以看出, 在立管中添加3个刚性接头后, 沿着RTP立管的涡激振动振幅却有明显变化. 均匀分布的3个刚性接头对立管的低流速激发出以第1阶模态为主导的涡激振动振幅分布影响较小, 对立管中部0.2 m/s流速激发出以第2阶模态为主导的涡激振动振幅响应影响稍大. 当来流速度为0.3 m/s时, 刚性接头对涡激振动振幅分布的影响比较显著.这说明添加了3个刚性接头后, 随着流速的增大, 激发出的模态越高, 对涡激振动的振幅分布影响越大.
图 14
图 14
包含两个刚性接头情况下沿RTP立管轴向的涡激振动振幅分布
Fig. 14
Amplitude of vortex induced vibration along the axis of RTP riser with two rigid joints
图 15
图 15
包含3个刚性接头情况下沿RTP立管轴向的涡激振动振幅分布
Fig. 15
Amplitude of vortex induced vibration along the axis of RTP riser with three rigid joints
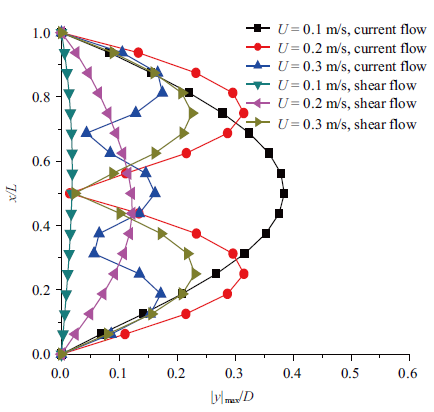
实际海洋环境中, 水流条件复杂多变, 立管不仅存在均匀流的作用, 更多实际情况下还受到倾斜流、剪切流、阶梯流等作用. 如图16 所示, 来流为线性剪切流, 靠近立管底部流体速度都为0, 靠近海平面的三种来流速度情况分别是0.1, 0.2, 0.3 m/s. 从图中可以看出, 剪切流顶端来流速度为0.1和0.2 m/s主要激发出了以第1阶模态为主导的振动. 剪切流顶端来流速度为0.3 m/s主要激发出以第2阶模态为主导的振动. 相对于均匀来流速度情况下的沿着立管轴向的涡激振动振幅分布有较大不同. 剪切流顶端来流速度为0.1和0.2 m/s时引起的涡激振动振幅都比均匀来流情况下引起的涡激振动振幅要小, 这主要是剪切流的能量相对于均匀流的能量过小的原因造成的. 而当剪切流顶端来流速度为0.3 m/s时, 涡激振动引起的振幅相比0.3 m/s的均匀来流情况下的振幅稍大. 这是由于, 剪切流顶端来流速度为0.3 m/s时激起的立管模态降低, 使得立管振动位移增大.
图 16
图 16
剪切流情况下沿RTP立管轴向的涡激振动振幅分布
Fig. 16
Amplitude of vortex induced vibration along the axial direction of RTP riser in shear flow
6 结论
(1)基于MSTMM和Van der Pol尾流振子模型建立了可以快速预测复合材料立管振动特性和涡激振动响应的动力学模型.
(2)流速越大, RTP立管涡激振动激发出的模态越高; 立管涡激振动位移主要受低阶模态控制; RTP立管的刚性接头对立管的湿模态频率和振型影响较小, 但是对较高阶模态为主所激发出的涡激振动振幅分布影响较大.
(3)剪切流对沿RTP立管轴向的涡激振动振幅分布影响较大, 低流速能量小所引起的涡激振动幅值较小, 但是当剪切流流速达到能激发出较高阶模态时, 相比同等流速的均匀流所引起的涡激振动振幅要大.
参考文献
View Option
[1]
Mathelin L Langre ED . Vortex-induced vibrations and waves under shear flow with a wake oscillator model
European Journal of Mechanics-B/Fluids , 2005 ,24 (4 ):478 -490
[本文引用: 2]
[2]
Mukundan H Modarres-Sadeghi Y Dahl JM , et al . Monitoring VIV fatigue damage on marine risers
Journal of Fluids & Structures , 2009 ,25 (4 ):617 -628
[3]
张杰 . 深海立管参激-涡激联合振动与疲劳特性研究. [博士论文]
天津: 天津大学 , 2014
[本文引用: 3]
( Zhang Jie . Vortex-induced vibration and fatigue analysis of deepwater risers considering parametric excitations. [PhD Thesis]
Tianjin: Tianjin University , 2014 (in Chinese))
[本文引用: 3]
[4]
Lie H Kaasen KE . Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow
Journal of Fluids & Structures , 2006 ,22 (4 ):557 -575
[本文引用: 1]
[5]
Srinil N . Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents
Applied Ocean Research , 2011 ,33 (1 ):41 -53
[本文引用: 1]
[6]
陈东阳 , Abbas LK 王国平 , 等 . 复合材料立管涡激振动数值计算
上海交通大学学报 , 2017 ,51 (4 ):495 -503
[本文引用: 2]
( Chen Dongyang Abbas LK Wang Guoping , et al . Numerical calculation of vortex-induced vibration of composite riser
Journal of Shanghai Jiaotong University , 2017 ,51 (4 ):495 -503 (in Chinese))
[本文引用: 2]
[7]
Kruijer MP Warnet LL Akkerman R . Analysis of the mechanical properties of a reinforced thermoplastic pipe (RTP)
Composites Part A Applied Science & Manufacturing , 2005 ,36 (2 ):291 -300
[8]
Bai Y Ruan W Cheng P , et al . Buckling of reinforced thermoplastic pipe (RTP) under combined bending and tension
Ships & Offshore Structures , 2014 ,9 (5 ):525 -539
[9]
Bai Y Tang J Xu W , et al . Collapse of reinforced thermoplastic pipe (RTP) under combined external pressure and bending moment
Ocean Engineering , 2015 ,94 :10 -18
[10]
Bai Y Liu T Cheng P , et al . Buckling stability of steel strip reinforced thermoplastic pipe subjected to external pressure
Composite Structures , 2016 ,152 :528 -537
[本文引用: 1]
[11]
Sun XS Tan VBC Chen Y , et al . An efficient analytical failure analysis approach for multilayered composite offshore production risers
Materials Science Forum , 2015 ,813 :3 -9
[本文引用: 1]
[12]
Post NL Case SW Lesko JJ . Modeling the variable amplitude fatigue of composite materials: A review and evaluation of the state of the art for spectrum loading
International Journal of Fatigue , 2008 ,30 (12 ):2064 -2086
[本文引用: 1]
[13]
Chen G Rui X Yang F , et al . Study on the natural vibration characteristics of flexible missile with thrust by using Riccati transfer matrix method
Journal of Applied Mechanics , 2016 ,83 (3 ):031006
[本文引用: 2]
[14]
Abbas LK Li MJ Rui XT . Transfer matrix method for the determination of the natural vibration characteristics of realistic thrusting launch vehicle-part I
Mathematical Problems in Engineering , 2013 ,2013 (2 ):388 -400
[本文引用: 2]
[15]
Li MJ Rui XT Abbas LK . Elastic dynamic effects on the trajectory of a flexible launch vehicle
Journal of Spacecraft & Rockets , 2015 ,52 (6 ):1 -17
[本文引用: 2]
[16]
芮筱亭 . 多体系统传递矩阵法 . 北京 : 科学出版社 , 2008
[本文引用: 2]
( Rui Xiaoting Transfer Matrix Method of Multibody System and Its Application. Beijing : Science Press , 2008 (in Chinese))
[本文引用: 2]
[17]
Rui X Wang G Lu Y , et al . Transfer matrix method for linear multibody system
Multibody System Dynamics , 2008 ,19 (3 ):179 -207
[18]
Rui XT Zhang JS Zhou QB . Automatic deduction theorem of overall transfer equation of multibody system
Advances in Mechanical Engineering , 2014 (2 ):1 -12
[本文引用: 1]
[19]
Dai HL Wang L Qian Q , et al . Vortex-induced vibrations of pipes conveying fluid in the subcritical and supercritical regimes
Journal of Fluids & Structures , 2013 ,39 (5 ):322 -334
[本文引用: 1]
[20]
Wang E Xiao Q . Numerical simulation of vortex-induced vibration of a vertical riser in uniform and linearly sheared currents
Ocean Engineering , 2016 ,121 :492 -515
[本文引用: 5]
Vortex-induced vibrations and waves under shear flow with a wake oscillator model
2
2005
... 当海流绕过海洋立管时, 在立管下游会产生尾流和漩涡, 周期发放的漩涡对立管产生垂直于来流向的涡激升力, 引起立管的涡激振动(vortex-induced vibration, VIV). 立管涡激振动即立管尾流涡脱落的频率与结构频率接近时发生的自激振动, 一直以来是立管结构疲劳破坏的一个主要因素[1 -4 ] , 由于海流速度沿水深变化的非均匀性及流固耦合的复杂性, 涡激振动长期以来是海洋工程中颇具挑战性的问题之一, 涡激振动的准确预报是一个巨大的难题[5 ] . ...
... 根据文献[1 , 19 ] 可得 ...
Monitoring VIV fatigue damage on marine risers
2009
深海立管参激-涡激联合振动与疲劳特性研究. [博士论文]
3
2014
... 文献[20 ] 中, 均匀来流速度为0.2 m/s, 直径为0.02 m, 所以$Re=3988$, 根据$St$和$Re$的关系图[3 ] , $St$取0.23. Van der Pol尾流振子模型的计算精度一定程度上取决于经验系数的选取, 本文选取$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] . 如图5 所示, 仿真得到沿立管轴向的涡激振动最大振幅分布. 通过与文献[20 ] 的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性. ...
... [3 ]. 如图5 所示, 仿真得到沿立管轴向的涡激振动最大振幅分布. 通过与文献[20 ] 的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性. ...
... 一般表层海流的水平流速从0.01 m/s到0.3 m/s, 深处的水平流速则在0.01 m/s以下. 基于MSTMM和Van der Pol尾流振子模型, 利用式(11) ~式(17)求解立管的涡激振动响应, 取Van der Pol 尾流振子模型中系数$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] , $St$取0.2. ...
深海立管参激-涡激联合振动与疲劳特性研究. [博士论文]
3
2014
... 文献[20 ] 中, 均匀来流速度为0.2 m/s, 直径为0.02 m, 所以$Re=3988$, 根据$St$和$Re$的关系图[3 ] , $St$取0.23. Van der Pol尾流振子模型的计算精度一定程度上取决于经验系数的选取, 本文选取$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] . 如图5 所示, 仿真得到沿立管轴向的涡激振动最大振幅分布. 通过与文献[20 ] 的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性. ...
... [3 ]. 如图5 所示, 仿真得到沿立管轴向的涡激振动最大振幅分布. 通过与文献[20 ] 的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性. ...
... 一般表层海流的水平流速从0.01 m/s到0.3 m/s, 深处的水平流速则在0.01 m/s以下. 基于MSTMM和Van der Pol尾流振子模型, 利用式(11) ~式(17)求解立管的涡激振动响应, 取Van der Pol 尾流振子模型中系数$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] , $St$取0.2. ...
Modal analysis of measurements from a large-scale VIV model test of a riser in linearly sheared flow
1
2006
... 当海流绕过海洋立管时, 在立管下游会产生尾流和漩涡, 周期发放的漩涡对立管产生垂直于来流向的涡激升力, 引起立管的涡激振动(vortex-induced vibration, VIV). 立管涡激振动即立管尾流涡脱落的频率与结构频率接近时发生的自激振动, 一直以来是立管结构疲劳破坏的一个主要因素[1 -4 ] , 由于海流速度沿水深变化的非均匀性及流固耦合的复杂性, 涡激振动长期以来是海洋工程中颇具挑战性的问题之一, 涡激振动的准确预报是一个巨大的难题[5 ] . ...
Analysis and prediction of vortex-induced vibrations of variable-tension vertical risers in linearly sheared currents
1
2011
... 当海流绕过海洋立管时, 在立管下游会产生尾流和漩涡, 周期发放的漩涡对立管产生垂直于来流向的涡激升力, 引起立管的涡激振动(vortex-induced vibration, VIV). 立管涡激振动即立管尾流涡脱落的频率与结构频率接近时发生的自激振动, 一直以来是立管结构疲劳破坏的一个主要因素[1 -4 ] , 由于海流速度沿水深变化的非均匀性及流固耦合的复杂性, 涡激振动长期以来是海洋工程中颇具挑战性的问题之一, 涡激振动的准确预报是一个巨大的难题[5 ] . ...
复合材料立管涡激振动数值计算
2
2017
... 海洋热塑性增强管(reinforced thermoplastic pipe, RTP)是一种复合材料管道, 可用作立管, 具有可盘卷(近百米一卷)、海陆施工快捷、质量小、耐疲劳、保温性能好, 以及高耐腐蚀等性能[6 -10 ] . 使用RTP作为立管可以减小海洋平台的体积, 减少海洋平台锚张力、减少立管顶张力, 显著降低开采成本. 同时, 使用复合材料立管操作成本低, 对系统其他构件的影响相对较小, 相比传统的钢制立管有更多的优越性[11 -12 ] . RTP在海上优势突出, 虽然要求高, 投资大, 但发展迅猛, 海洋用RTP市场可能超过陆用市场. 我国海洋油气资源丰富, 过去油气开采限制于100 m深以内的浅海, 近年向更深海域拓展, 满足深海要求的RTP成关键. 国内对复合材料立管的研究起步较晚, 关于完全非金属的复合材料RTP立管涡激振动的研究更少. 能够适用于工程上快速评估复合材料立管涡激振动性能的方法未见报道. RTP产品的种类繁多, 本文仅以如图1 所示的复合材料预制增强带RTP立管作为研究对象, 探索适合工程的复合材料立管的建模方法, 以及研究其涡激振动行为, 为工程上类似的复合材料立管快速建模和涡激振动快速分析提供参考. ...
... 在作者前期工作中[6 ] , 采用ANSYS软件的shell 181单元对RTP立管进行了复合材料建模, 并验证了建模方法的准确性. 本文为了获取RTP立管的等效刚度参数, 采用ANSYS软件计算一小段两端铰接的RTP短立管(此处取10 m长,直径为365 mm的短管进行有限元复合材料铺层并进行模态计算, 顶张力为1 N)的第一阶频率, 即可以利用式(18)反推出立管的等效刚度$EI$. 然后采用MSTMM就可以方便的计算出不同长度、不同顶张力的RTP立管的振动特性. ...
复合材料立管涡激振动数值计算
2
2017
... 海洋热塑性增强管(reinforced thermoplastic pipe, RTP)是一种复合材料管道, 可用作立管, 具有可盘卷(近百米一卷)、海陆施工快捷、质量小、耐疲劳、保温性能好, 以及高耐腐蚀等性能[6 -10 ] . 使用RTP作为立管可以减小海洋平台的体积, 减少海洋平台锚张力、减少立管顶张力, 显著降低开采成本. 同时, 使用复合材料立管操作成本低, 对系统其他构件的影响相对较小, 相比传统的钢制立管有更多的优越性[11 -12 ] . RTP在海上优势突出, 虽然要求高, 投资大, 但发展迅猛, 海洋用RTP市场可能超过陆用市场. 我国海洋油气资源丰富, 过去油气开采限制于100 m深以内的浅海, 近年向更深海域拓展, 满足深海要求的RTP成关键. 国内对复合材料立管的研究起步较晚, 关于完全非金属的复合材料RTP立管涡激振动的研究更少. 能够适用于工程上快速评估复合材料立管涡激振动性能的方法未见报道. RTP产品的种类繁多, 本文仅以如图1 所示的复合材料预制增强带RTP立管作为研究对象, 探索适合工程的复合材料立管的建模方法, 以及研究其涡激振动行为, 为工程上类似的复合材料立管快速建模和涡激振动快速分析提供参考. ...
... 在作者前期工作中[6 ] , 采用ANSYS软件的shell 181单元对RTP立管进行了复合材料建模, 并验证了建模方法的准确性. 本文为了获取RTP立管的等效刚度参数, 采用ANSYS软件计算一小段两端铰接的RTP短立管(此处取10 m长,直径为365 mm的短管进行有限元复合材料铺层并进行模态计算, 顶张力为1 N)的第一阶频率, 即可以利用式(18)反推出立管的等效刚度$EI$. 然后采用MSTMM就可以方便的计算出不同长度、不同顶张力的RTP立管的振动特性. ...
Analysis of the mechanical properties of a reinforced thermoplastic pipe (RTP)
2005
Buckling of reinforced thermoplastic pipe (RTP) under combined bending and tension
2014
Collapse of reinforced thermoplastic pipe (RTP) under combined external pressure and bending moment
2015
Buckling stability of steel strip reinforced thermoplastic pipe subjected to external pressure
1
2016
... 海洋热塑性增强管(reinforced thermoplastic pipe, RTP)是一种复合材料管道, 可用作立管, 具有可盘卷(近百米一卷)、海陆施工快捷、质量小、耐疲劳、保温性能好, 以及高耐腐蚀等性能[6 -10 ] . 使用RTP作为立管可以减小海洋平台的体积, 减少海洋平台锚张力、减少立管顶张力, 显著降低开采成本. 同时, 使用复合材料立管操作成本低, 对系统其他构件的影响相对较小, 相比传统的钢制立管有更多的优越性[11 -12 ] . RTP在海上优势突出, 虽然要求高, 投资大, 但发展迅猛, 海洋用RTP市场可能超过陆用市场. 我国海洋油气资源丰富, 过去油气开采限制于100 m深以内的浅海, 近年向更深海域拓展, 满足深海要求的RTP成关键. 国内对复合材料立管的研究起步较晚, 关于完全非金属的复合材料RTP立管涡激振动的研究更少. 能够适用于工程上快速评估复合材料立管涡激振动性能的方法未见报道. RTP产品的种类繁多, 本文仅以如图1 所示的复合材料预制增强带RTP立管作为研究对象, 探索适合工程的复合材料立管的建模方法, 以及研究其涡激振动行为, 为工程上类似的复合材料立管快速建模和涡激振动快速分析提供参考. ...
An efficient analytical failure analysis approach for multilayered composite offshore production risers
1
2015
... 海洋热塑性增强管(reinforced thermoplastic pipe, RTP)是一种复合材料管道, 可用作立管, 具有可盘卷(近百米一卷)、海陆施工快捷、质量小、耐疲劳、保温性能好, 以及高耐腐蚀等性能[6 -10 ] . 使用RTP作为立管可以减小海洋平台的体积, 减少海洋平台锚张力、减少立管顶张力, 显著降低开采成本. 同时, 使用复合材料立管操作成本低, 对系统其他构件的影响相对较小, 相比传统的钢制立管有更多的优越性[11 -12 ] . RTP在海上优势突出, 虽然要求高, 投资大, 但发展迅猛, 海洋用RTP市场可能超过陆用市场. 我国海洋油气资源丰富, 过去油气开采限制于100 m深以内的浅海, 近年向更深海域拓展, 满足深海要求的RTP成关键. 国内对复合材料立管的研究起步较晚, 关于完全非金属的复合材料RTP立管涡激振动的研究更少. 能够适用于工程上快速评估复合材料立管涡激振动性能的方法未见报道. RTP产品的种类繁多, 本文仅以如图1 所示的复合材料预制增强带RTP立管作为研究对象, 探索适合工程的复合材料立管的建模方法, 以及研究其涡激振动行为, 为工程上类似的复合材料立管快速建模和涡激振动快速分析提供参考. ...
Modeling the variable amplitude fatigue of composite materials: A review and evaluation of the state of the art for spectrum loading
1
2008
... 海洋热塑性增强管(reinforced thermoplastic pipe, RTP)是一种复合材料管道, 可用作立管, 具有可盘卷(近百米一卷)、海陆施工快捷、质量小、耐疲劳、保温性能好, 以及高耐腐蚀等性能[6 -10 ] . 使用RTP作为立管可以减小海洋平台的体积, 减少海洋平台锚张力、减少立管顶张力, 显著降低开采成本. 同时, 使用复合材料立管操作成本低, 对系统其他构件的影响相对较小, 相比传统的钢制立管有更多的优越性[11 -12 ] . RTP在海上优势突出, 虽然要求高, 投资大, 但发展迅猛, 海洋用RTP市场可能超过陆用市场. 我国海洋油气资源丰富, 过去油气开采限制于100 m深以内的浅海, 近年向更深海域拓展, 满足深海要求的RTP成关键. 国内对复合材料立管的研究起步较晚, 关于完全非金属的复合材料RTP立管涡激振动的研究更少. 能够适用于工程上快速评估复合材料立管涡激振动性能的方法未见报道. RTP产品的种类繁多, 本文仅以如图1 所示的复合材料预制增强带RTP立管作为研究对象, 探索适合工程的复合材料立管的建模方法, 以及研究其涡激振动行为, 为工程上类似的复合材料立管快速建模和涡激振动快速分析提供参考. ...
Study on the natural vibration characteristics of flexible missile with thrust by using Riccati transfer matrix method
2
2016
... 文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
... [13 ,14 ,15 ]所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
Transfer matrix method for the determination of the natural vibration characteristics of realistic thrusting launch vehicle-part I
2
2013
... 文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
... ,14 ,15 ]所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
Elastic dynamic effects on the trajectory of a flexible launch vehicle
2
2015
... 文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
... ,15 ]所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
2
2008
... 文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
... 式(3)中, 状态矢量的下标up和down分别表示联接点处的上方和下方对应的状态矢量. 另外, 由图3 中的坐标系和传递方向, 以及MSTMM书中的符号约定可知, 式(3)中[16 ] ...
2
2008
... 文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
... 式(3)中, 状态矢量的下标up和down分别表示联接点处的上方和下方对应的状态矢量. 另外, 由图3 中的坐标系和传递方向, 以及MSTMM书中的符号约定可知, 式(3)中[16 ] ...
Transfer matrix method for linear multibody system
2008
Automatic deduction theorem of overall transfer equation of multibody system
1
2014
... 文献[13 ,14 ,15 ] 基于多体系统传递矩阵法[16 -18 ] , 均推导了带有预应力的欧拉-伯努利梁的传递矩阵. 本文的立管模型也采用该梁模型, 但立管所受的定张力方向向上, 与文献[13 ,14 ,15 ] 所推导的传递矩阵存在正负号差别. 限于篇幅, 此处不作重新推导. 所得的该可以考虑横向和轴向振动的预应力欧拉-伯努利梁的传递矩阵为 ...
Vortex-induced vibrations of pipes conveying fluid in the subcritical and supercritical regimes
1
2013
Numerical simulation of vortex-induced vibration of a vertical riser in uniform and linearly sheared currents
5
2016
... 以文献[20 ] 中的立管参数为例, 采用MSTMM计算了细长立管的振动特性. 图4 为采用MSTMM计算顶张力为817 N的立管的干模态(不考虑周围流体的影响下的模态, 这种模态可以称为"干模态'', 即不受流体影响的模态)前8阶圆频率计算结果, 与文献[20 ] 中的理论分析解对比结果如表3 所示, 误差小于0.12%, 因此验证了基于MSTMM立管动力学特性计算模型的准确性. ...
... [20 ]中的理论分析解对比结果如表3 所示, 误差小于0.12%, 因此验证了基于MSTMM立管动力学特性计算模型的准确性. ...
... 在海流作用下, 立管上各点由漩涡脱落引起的振动可视为立管各模态振动的叠加(一般为前几阶湿模态, 湿模态即考虑周围流体影响下的模态, 工程上湿模态计算一般将立管外径对应的圆柱排开的流体质量作为附加质量考虑), 且一般存在主导振动模态. 以文献[20 ] 中的立管为例, 基于MSTMM和Van der Pol尾流振子模型, 通过式(17)采用模态叠加法计算带有顶张力的立管的涡激振动响应. ...
... 文献[20 ] 中, 均匀来流速度为0.2 m/s, 直径为0.02 m, 所以$Re=3988$, 根据$St$和$Re$的关系图[3 ] , $St$取0.23. Van der Pol尾流振子模型的计算精度一定程度上取决于经验系数的选取, 本文选取$A=12$和$\varepsilon =0.3$, $C_{L0} =0.25$, $C_D =1.2$[3 ] . 如图5 所示, 仿真得到沿立管轴向的涡激振动最大振幅分布. 通过与文献[20 ] 的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性. ...
... [20 ]的实验数据及CFD仿真数据对比, 误差较小, 验证了本文方法的可行性. ...