引言
在高寒高海拔地区修建隧道, 隧址区原有的热力平衡被打破, 隧道的通风对流使冷空气在隧道内部的流动, 造成了隧道内部温度的下降, 从而创造了隧道围岩形成季节冻土或多年冻土的条件. 当围岩温度过低围岩中的裂隙、孔隙水冻结时会发生体积膨胀,在这种体积膨胀受到隧道衬砌和未冻岩体的约束时, 冻结围岩便会对隧道衬砌产生冻胀力. 20世纪70~80年代, 日本对东北寒冷地区隧道的调查分析结果表明, 冻胀力是造成寒区隧道变形破坏主要因素. 由于我国经济的高速发展, 高速铁路、公路建设迎来了高速发展时期, 不可避免地需要在高寒高海拔地区修建隧道. 隧道常常发生冻害, 对隧道的维修养护造成了极大困难, 更是对隧道结构和运营安全构成了严重威胁. 为保证隧道结构和运营安全, 降低维修养护成本, 各国学者从不同方向、不同领域对寒区隧道冻胀力进行了研究.
Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论.
在以上寒区隧道研究中所涉及应用弹性、弹塑性理论计算寒区隧道冻胀力解析解时均采用圆形隧道模型, 并未采用与实际隧道断面相似的隧道模型进行计算. 由于计算模型的差异, 这些研究成果与实际结果存在一定的差异, 不能直接应用于非圆形寒区隧道问题中.
当考虑支护为圆形的条件时, 寒区隧道冻胀力和位移的弹性解析解通过连续性条件易于给出. 而当隧道断面形状为马蹄形、直墙拱形等非圆形状并且考虑隧道支护时, 由于考虑了隧道支护, 使问题由单连通域问题变为多连通域问题, 不能直接应用经典的复变函数理论求解非圆形隧道应力和位移. 所以, 还鲜有学者给出考虑衬砌因素的非圆形寒区隧道冻胀力和冻胀位移的弹性解析解. 综上所述, 为得到考虑衬砌的非圆形寒区隧道冻胀力弹性解析解, 应用经典复变函数理论幂级数解法, 结合连续性条件, 在文献[17 -18 ] 的基础上, 推导了考虑衬砌的非圆形寒区隧道冻胀力的弹性解析解. 为下一步非圆形寒区隧道冻胀力的弹塑性分析奠定了基础.
1 问题描述
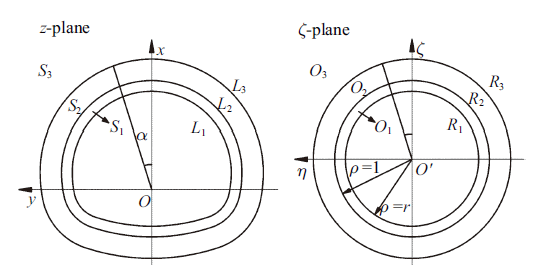
根据弹性理论, 寒区隧道在深埋条件下, 由于隧道开挖尺寸与埋深相比很小, 隧道开挖问题可视为在无限平面内的孔洞问题, 不受边界效应影响, 地应力变化梯度可忽略不计. 当考虑冻胀圈和支护结构时, 无限平面内的孔洞问题由单连通域孔洞问题变为多连通域问题, 无限平面被分割为3个区域. 图1 给出了无限平面内考虑冻胀圈的隧道孔洞模型. 其中在$Z$平面中衬砌、冻胀圈和未冻围岩分别表示为$S_{1}$, $S_{2}$和$S_{3}$区域, 所对应的边界$L_{1}$为衬砌与大气接触面, 它为自由边界, 受到的面力为零; $L_{2}$为衬砌与冻胀圈接触面, 它满足连续边界条件; $L_{3}$为冻胀圈与未冻围岩接触面, 它满足连续边界条件; 围岩的远场应力由隧道埋深边界条件确定. 为了进行计算,必须将$Z$平面上的非圆形衬砌、冻胀圈结构通过保角变换映射到$\zeta $平面上, 使得在$Z$平面上的非圆形结构变换为$\zeta $平面上的圆环结构. 这时$Z$平面上的区域$S_{3}$映射为$\zeta $平面行的区域$O_{3}$;区域$S_{2}$映射为$\zeta $平面行的区域$O_{2}$; 衬砌区域$S_{1}$映射为圆环区域$O_{1}$; 边界$L_{1}$, $L_{2}$及$L_{3}$分别映射为圆环$R_{1}$, $R_{2}$与$R_{3}$. 其中最一般的映射函数可写成洛朗级数的形式, 即
(1) $ \begin{eqnarray} w\left( \zeta \right) = R\left( {\zeta + \sum\limits_{k = 0}^\infty {C_k \zeta ^{ - k}} } \right) \end{eqnarray} $
图 1
图 1
$Z$平面保角变换为$\zeta$平面示意图
Fig. 1
Conformal mapping of tunnel in $z$-plane in to two concentric circles in $\zeta$-plane
其中, $R$是一个实常数, 它的大小反映了隧道孔洞的大小; $C_{k} $一般为复常数, 其中$k = 1,2,3, \cdots $, $C_{k} $反映了隧道断面形状, 在一般情况下$C_{k} $取前几项时, 映射函数的精度已经可以满足工程要求[19 ] . $\zeta$为$Z$平面上的点映射到$\zeta $平面上的正交曲线坐标, 通常可由角度$\theta$与半径$\rho$表示.
2 复变函数解法公式推导及求解
根据Kargar等[20 -22 ] 和陈子荫[23 ] 提出的方法, $\zeta $面上未冻围岩$O_{3}$区域内的应力函数可表示为
(2) $ \begin{eqnarray} &&\varphi _1 \left( \zeta \right) = \varGamma w\left( \zeta \right) + \varphi _0 \left( \zeta \right) \end{eqnarray} $
(3) $ \begin{eqnarray} &&\psi _1 \left( \zeta \right) = \varGamma' w\left( \zeta \right) + \psi _0 \left( \zeta \right) \end{eqnarray} $
(4) $ \begin{eqnarray} &&\varphi _0 \left( \zeta \right) = \mathop \sum \limits_{k = 0}^{\infty } h_{k} \zeta ^{ - {k}} \end{eqnarray} $
(5) $ \begin{eqnarray} &&\psi _0 \left( \zeta \right) = \mathop \sum \limits_{k = 0}^{\infty } m_{k} \zeta ^{ - {k}} \end{eqnarray} $
式中, $h_{k}$和$m_{k}$为所求复常数,它们均由边界条件确定; $\varphi _0 \left( \zeta \right)$和$\psi _0 \left( \zeta \right)$满足$\varphi _0 \left( \infty \right) = 0$和$\psi _0 \left( \infty \right) = 0$; Lu等[21 -22 ] 提出$\varGamma $和${\varGamma }'$可由无穷远处应力边界条件定出, 即
(6) $ \begin{eqnarray} &&{\varGamma }'=-(1-K)\gamma H \end{eqnarray} $
(7) $ \begin{eqnarray} &&{\varGamma }'=-(1-K)\gamma H \end{eqnarray} $
在方程(6)和(7)中$K$为侧压力系数, $\gamma$和$H$分别表征围岩重度与隧道埋深.
$\zeta$平面上冻胀圈$O_{2}$区域的应力函数$\varphi _2 \left( \zeta \right)$和$\psi _2 \left( \zeta \right)$可表示为
(8) $ \begin{eqnarray} &&\varphi _2 \left( \zeta \right) = \sum\limits_{{k} = 0}^\infty {a_{k} \zeta ^{k}} +\sum\limits_{{k} = 1}^\infty {b_{k} \zeta ^{{-k}}} \end{eqnarray} $
(9) $ \begin{eqnarray} &&\psi _2 \left( \zeta \right) = \mathop \sum \limits_{{k} = 0}^\infty c_{k} \zeta ^{k} + \mathop \sum \limits_{k = 1}^\infty d_{k} \zeta ^{ - {k}} \end{eqnarray} $
其中, $a_{k} $, $b_{k} $, $c_{k} $和$d_{k} $为所求复常数, 它们均由边界条件确定.
$\zeta$平面上衬砌$O_{1}$区域应力函数$\varphi _3 \left( \zeta \right)$和$\psi _3 \left( \zeta \right)$可表示为
(10) $ \begin{eqnarray} &&\varphi _3 \left( \zeta \right) = \mathop \sum \limits_{{k} = 0}^{\infty } A_{k} \zeta ^{k} + \mathop \sum \limits_{{k} = 1}^{\infty } B_{k} \zeta ^{ - {k}} \end{eqnarray} $
(11) $ \begin{eqnarray} &&\psi _3 \left( \zeta \right) = \mathop \sum \limits_{{k} = 0}^{\infty } C_{k} \zeta ^{k} + \mathop \sum \limits_{k = 1}^\infty D_{k} \zeta ^{ - {k}} \end{eqnarray} $
其中, $A_{k} $, $B_{k} $, $C_{k} $和$D_{k}$为所求复常数,它们均由边界条件确定.
在复变函数解中[24 -26 ] 应力均可以用两个应力函数$\varphi$和$\psi $表达, 衬砌、冻胀圈和未冻围岩上应力均可表示为
(12) $ \begin{eqnarray} &&\sigma _{\theta } + \sigma _{\rho } = 4{\rm Re}\left[ {\frac{{\varphi }'\left( \zeta \right)}{{w}'\left( \zeta \right)}} \right] \end{eqnarray} $
(13) $ \begin{eqnarray} &&\sigma _{\theta } - \sigma _{\rho } + 2{\rm i}\tau _{\rho \theta } = \frac{2\zeta ^2}{\rho^2}\frac{1}{\overline {{w}'\left( \zeta \right)} } \\&&\qquad \left[ {\overline {w\left( \zeta \right)} \frac{{\varphi }''\left( \zeta \right){w}'\left( \zeta \right) - {\varphi }'\left( \zeta \right){w}''\left( \zeta \right)}{{w}'\left( \zeta \right){w}'\left( \zeta \right)} + {\psi }'\left( \zeta \right)} \right] \end{eqnarray} $
其中, $\sigma _\rho $, $\sigma _{\theta } $和$\tau _{\rho \theta } $分别为正交曲线坐标下的法向应力、环向应力和剪应力.
假设寒区隧道衬砌$S_{1}$和未冻围岩$S_{3}$区域体积不受围岩温度变化影响, 相应$\zeta $平面上映射区域$O_{1}$和$O_{3}$位移满足复变函数[24 -26 ] 应力函数表达, 衬砌和未冻围岩上位移可表示为
(14) $ \begin{eqnarray} &&2G\left( u_{\rho} + {\rm i}u_{\theta} \right) = \frac{\zeta}{\rho}\frac{\overline{w'\left( \zeta \right)} }{\left| w\left( \zeta \right) \right|}\\&&\qquad\left[\kappa \varphi \left( \zeta \right) - \frac{w\left( \zeta \right)}{\overline{w' (\zeta)}}\overline{\varphi'\left( \zeta \right)} - \overline{\psi \left( \zeta \right)}\right] \end{eqnarray} $
其中, $u_{\rho } $和$u_{\theta }$分别表示法向位移与环向位移, $G$是切变模量, $\kappa $由泊松比确定, $\kappa= 3 - 4\upsilon $和$\kappa = \left( {3 - \upsilon } \right) / \left( {1 + \upsilon }\right)$分别为平面应变与平面应力状态下$\kappa $的取值, $\upsilon $为泊松比, 因隧道纵向长度与断面最大直径相比很大, 故问题可视为平面应变问题, $\kappa $取$3 - 4\upsilon $.
由于冻胀圈$S_{2}$区域内体积受温度变化影响, 故相应在$\zeta $平面上$O_{2}$区域内位移无法满足复变函数[24 -26 ] 应力函数表达, 需要重新推导(推导过程详见附录1), 经推导冻胀圈上位移可表示为
(15) $ \begin{eqnarray} && 2G\left(u_{\rho} + {\rm i}u_{\theta} \right) = \frac{\overline{\zeta}}{\rho}\frac{\overline{w'\left( \zeta \right)}}{\left| w\left( \zeta \right) \right|}\left[\kappa \varphi \left( \zeta \right) - \frac{w\left( \zeta \right)}{\overline{w' (\zeta)} }\overline{\varphi '\left( \zeta \right)} - \overline{\psi \left( \zeta \right)} \right] +\\&&\qquad 2G\frac{\overline{\zeta}}{\rho }\frac{\overline{w'\left( \zeta \right)}}{\left| w\left( \zeta \right) \right|}w\left( \zeta \right)\varepsilon \end{eqnarray} $
其中$\varepsilon $为冻胀圈线膨胀系数, 可由冻胀区单位冻胀体积变化定出, 即
\begin{eqnarray*} \varepsilon = \frac{1}{3}\Delta V \end{eqnarray*}
其中$\Delta V$是冻胀区单位冻胀体积变化.
应力函数$\varphi _1 \left( \zeta \right)$, $\psi _1 \left( \zeta \right)$, $\varphi _2 \left( \zeta \right)$和$\psi _2 \left( \zeta \right)$, $\varphi _3 \left( \zeta \right)$和$\psi _3 \left( \zeta \right)$必须分别在$R_{2}$和$R_{3}$上满足连续边界条件, 在$R_{1}$上满足应力边界条件. 在衬砌与大气接触面上力的边界条件可表示为
(16) $ \begin{eqnarray} \varphi _3 \left( {t_1 } \right) + \frac{w\left( {t_1 } \right)}{\overline{w' (t_1)}}\overline{\varphi'_3 (t_1)}+\overline{\psi_3 (t_1)}=0 \end{eqnarray} $
在计算非圆形隧道围岩应力时, 为能更好地反应实际隧洞变形位移, Lu等[20 -22 ] 在连续性位移条件中引入了开挖卸荷因子. 为了能更直观反映冻胀力对非圆形隧道衬砌的影响, 在位移连续边界条件中并未考虑开挖卸荷因子, 如需考虑开挖卸荷效应, 只需在位移边界条件中添加符合实际工况的开挖卸荷因子即可. 根据推导的位移公式, 在冻胀圈与衬砌接触面上位移连续边界条件可表示为
(17) $ \begin{eqnarray} &&\frac{\kappa_2}{2G_2}\varphi _2 \left(t_2\right)-\frac{1}{2G_2}\left(\frac{w\left( t_2 \right)}{\overline{w' (t_2)}}\overline{\varphi'_2\left( t_2 \right)} +\overline{\psi _2 \left( t_2 \right)}\right) +w\left( \zeta \right)\varepsilon =\\&&\qquad\frac{\kappa_3}{2G_3}\varphi_3 \left( t_2 \right)-\frac{1}{2G_3} \left(\frac{w\left( t_2 \right)}{\overline{w'(t_2)}} \overline{\varphi'_3\left( t_2 \right)} +\overline{\psi_3 \left( t_2 \right)}\right) \end{eqnarray} $
(18) $ \begin{eqnarray} &&\varphi _2 \left( {t_2} \right)+\frac{w\left( {t_2 } \right)}{\overline{w'( t_2)}}\overline{\varphi'_2\left( t_2 \right)} +\overline{\psi _2 \left( t_2 \right)}=\\&&\qquad \varphi _3 \left( {t_2} \right)+\frac{w\left( {t_2 } \right)}{\overline{w'( t_2)}}\overline{\varphi'_2\left( t_3 \right)} +\overline{\psi _3 \left( t_2 \right)} \end{eqnarray} $
在未冻围岩与冻胀圈接触面上, 根据推导的考虑冻胀作用的位移公式(附录1), 位移连续边界条件可表示为
(19) $ \begin{eqnarray} && \frac{\kappa_1}{2G_1 }\varphi _0 \left( t_3 \right)-\frac{1}{2G_1}\left(\frac{w\left( t_3 \right)}{\overline{w' (t_3)}} \overline{\varphi' _0 \left( t_3 \right)} +\overline{\psi _0 \left( t_3 \right)}\right)=\\ && \frac{\kappa_2}{2G_2 }\varphi _2 \left( t_3 \right)-\frac{1}{2G_2}\left(\frac{w\left( t_3 \right)}{\overline{w' (t_3)}} \overline{\varphi' _2 \left( t_3 \right)} +\overline{\psi _2 \left( t_3 \right)}\right) + w\left( \zeta \right)\varepsilon \end{eqnarray} $
在未冻围岩与冻胀圈接触面上力的连续边界条件可表示为
(20) $ \begin{eqnarray} &&\varphi _1 \left( {t_3} \right)+\frac{w\left( {t_3 } \right)}{\overline{w'( t_3)}}\overline{\varphi'_1\left( t_3 \right)} +\overline{\psi _1 \left( t_3 \right)}=\\&&\qquad \varphi _2 \left( {t_3} \right)+\frac{w\left( {t_3 } \right)}{\overline{w'( t_3)}}\overline{\varphi'_2\left( t_3 \right)} +\overline{\psi _2 \left( t_3 \right)} \end{eqnarray} $
其中, $t_1 $, $t_2 $和$t_3 $分别表示$\zeta$平面上$R_{1}$, $R_{2}$和$R_{3}$边界上的点.
方程(2)和(3)中的表达式$\varGamma w\left( \zeta \right)$和$\varGamma' w\left( \zeta \right)$表示围岩的初始地应力和初始位移的分量, 所以在方程(19)中计算由于开挖引起的位移时应将其去除[27 ] ; 方程(17)~(20)在计算过程中假设接触面之间无滑动.
应用于李岩松等[17 -18 ] 幂级数解法, 方程(16)可分别展开为正幂次方程组(21)和负幂次方程组(22)
(21) $ \begin{eqnarray} &&\mathop \sum \limits_{k=0}^\infty A_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-\mathop \sum \limits_{k=1}^\infty B_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+ \mathop \sum \limits_{k=1}^\infty \overline {A_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v-\\&&\qquad\mathop \sum \limits_{k=1}^\infty \overline {B_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v- \mathop \sum \limits_{k=0}^\infty \overline {C_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\mathop \sum \limits_{k=1}^\infty \overline {D_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v=0,\\&&\qquad v=1,2,3,\cdots \end{eqnarray} $
(22) $ \begin{eqnarray}&& \mathop \sum \limits_{k=0}^\infty A_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}-\mathop \sum \limits_{k=1}^\infty B_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty \overline {A_k } \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}- \\ &&\qquad\mathop \sum \limits_{k=1}^\infty \overline {B_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}- \mathop \sum \limits_{k=0}^\infty \overline {C_k } \rho^v\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty \overline {D_k } \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}=0,\\&&\qquad v=1,2,3,\cdots \end{eqnarray} $
其中, $L_v$可由方程(1)中$R$和$C_k$计算得出, $\zeta$为$Z$平面上的点映射到$\zeta $平面上的正交曲线坐标, 可表示为$\zeta =\rho\sigma $, 这里$\sigma =\exp\left( {\rm i}\theta \right)$; $\zeta$的共轭可表示为$\overline{\zeta}=\rho\sigma^{-1}$. 为便于计算, 方程(1)可写为
(23) $ \begin{eqnarray} w\left( \zeta \right)=\mathop \sum \limits_{v=-\infty }^{+\infty } L_v \zeta ^{-v} \end{eqnarray} $
方程(17)可分别展开为正幂次方程组(24)和负幂次方程组(25); 方程(18)可分别展开为正幂次方程组(26)和负幂次方程组(27); 方程(19)可分别展开为正幂次方程组(28)和负幂次方程组(29), 方程(24)~(29)表达式如下
(24) $ \begin{eqnarray} &&\frac{\kappa _2 }{G_2 }\mathop \sum \limits_{k=0}^\infty a_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-\frac{\kappa _2 }{G_2 }\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v+\\&&\qquad\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v+ \frac{1}{G_2 }\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-\\&&\qquad\frac{\kappa _3 }{G_3 }\mathop \sum \limits_{k=0}^\infty A_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v+\frac{\kappa _3 }{G_3 }\mathop \sum \limits_{k=1}^\infty B_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+ \frac{1}{G_3 }\mathop \sum \limits_{k=1}^\infty \overline {A_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v-\\&&\qquad\frac{1}{G_3 }\mathop \sum \limits_{k=1}^\infty \overline {B_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v-\frac{1}{G_3 }\mathop \sum \limits_{k=0}^\infty \overline {C_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\frac{1}{G_3 }\mathop \sum \limits_{k=1}^\infty \overline {D_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v=\\&&\qquad -\varepsilon \mathop \sum \limits_{k=0}^\infty L_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v+\varepsilon \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v, \quad v=1, 2, 3, \cdots \end{eqnarray} $
(25) $ \begin{eqnarray} && \frac{\kappa_2 }{G_2 }\mathop \sum \limits_{k=0}^\infty a_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}-\frac{k_2 }{G_2 }\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}- \frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}+\\&&\qquad\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}+ \frac{1}{G_2 }\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^v\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}- \\&&\qquad\frac{\kappa_3 }{G_3 }\mathop \sum \limits_{k=0}^\infty A_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}+\frac{k_3 }{G_3 }\mathop \sum \limits_{k=1}^\infty B_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}+ \frac{1}{G_3 }\mathop \sum \limits_{k=1}^\infty \overline {A_k } \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}-\\&&\qquad\frac{1}{G_3 }\mathop \sum \limits_{k=1}^\infty \overline {B_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}-\frac{1}{G_3 }\mathop \sum \limits_{k=0}^\infty \overline {C_k } \rho^v\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}+\frac{1}{G_3 }\mathop \sum \limits_{k=1}^\infty \overline {D_k } \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}= \\&&\qquad -\varepsilon \mathop \sum \limits_{k=0}^\infty L_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}+\varepsilon \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v},\quad v=0,1,2,3, \cdots \end{eqnarray} $
(26) $ \begin{eqnarray}&& \mathop \sum \limits_{k=0}^\infty a_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v- \\&&\qquad \mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v-\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v- \\&&\qquad \mathop \sum \limits_{k=0}^\infty A_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v+\mathop \sum \limits_{k=1}^\infty B_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\mathop \sum \limits_{k=1}^\infty \overline {A_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v+ \\&&\qquad \mathop \sum \limits_{k=1}^\infty \overline {B_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v+\mathop \sum \limits_{k=0}^\infty \overline {C_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\mathop \sum \limits_{k=1}^\infty \overline {D_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v=0, \\&&\qquad v=0,1,2,3, \cdots \end{eqnarray} $
(27) $ \begin{eqnarray} && \mathop \sum \limits_{k=0}^\infty a_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}-\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}-\\&&\qquad \mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}-\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^v\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}-\\&&\qquad \mathop \sum \limits_{k=0}^\infty A_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty B_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}-\mathop \sum \limits_{k=1}^\infty \overline {A_k } \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}+ \\&&\qquad \mathop \sum \limits_{k=1}^\infty \overline {B_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}+\mathop \sum \limits_{k=0}^\infty \overline {C_k } \rho^v\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}-\mathop \sum \limits_{k=1}^\infty \overline {D_k } \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}=0,\\&&\qquad v=0,1,2,3, \cdots \end{eqnarray} $
(28) $ \begin{eqnarray} && \frac{\kappa_2 }{G_2 }\mathop \sum \limits_{k=0}^\infty a_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-\frac{k_2 }{G_2 }\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v+ \\&&\qquad \frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v+\frac{1}{G_2 }\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v+ \\&&\qquad \frac{\kappa_1 }{G_1 }\mathop \sum \limits_{k=0}^\infty h_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\frac{1}{G_1 }\mathop \sum \limits_{k=0}^\infty \overline {h_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v+\frac{1}{G_1 }\mathop \sum \limits_{k=0}^\infty m_k \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v= \\&&\qquad -\varepsilon \mathop \sum \limits_{k=0}^\infty L_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v+\varepsilon \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v, \quad v=0,1,2,3, \cdots \end{eqnarray} $
(29) $ \begin{eqnarray} &&\frac{\kappa_2 }{G_2 }\mathop \sum \limits_{k=0}^\infty a_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}-\frac{\kappa _2 }{G_2 }\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}+ \\&&\qquad \frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}+\frac{1}{G_2 }\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^v\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}-\frac{1}{G_2 }\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}+ \\&&\qquad \frac{\kappa_1 }{G_1 }\mathop \sum \limits_{k=0}^\infty h_k \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}-\frac{1}{G_1 }\mathop \sum \limits_{k=0}^\infty \overline {h_k } \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}+\frac{1}{G_1 }\mathop \sum \limits_{k=0}^\infty m_k \rho^v\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}= \\&&\qquad -\varepsilon \mathop \sum \limits_{k=0}^\infty L_k \rho^{2k+v}\left( {k+v+1} \right)L_{k+v+1} \sigma ^{-v}+\varepsilon \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-2k+v}\left( {k-v-1} \right)L_{-k+v+1} \sigma ^{-v}, \quad v=0,1,2,3, \cdots \end{eqnarray} $
最后将方程(20)分别展开为正幂次方程组(30)和负幂次方程组(31). 应当注意的是: 由于边界条件不同, 方程(21)和(22)中的极半径$\rho $与方程(24)~(27)以及方程(28)~(31)中的极半径$\rho $在数值上分别等于$r_{1}$, 1和$r_{2}$.
结合行列式(21)、式(22)以及行列式(24) ~式(31), 可以得到无穷线性方程组[17 -18 ] , 求解无穷线性方程组得到应力函数(方程(2)和(3), 方程(8)和(9), 方程(10)和(11))中各项系数. 由得到的应力函数计算方程(12)和(13)得到非圆形寒区隧道应力解析解;由方程(14)计算衬砌和未冻围岩位移解析解; 最后由方程(15)计算冻胀圈位移解析解.
(30) $ \begin{eqnarray} &&\mathop \sum \limits_{k=0}^\infty a_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\mathop \sum \limits_{k=1}^\infty \overline {a_k } \rho^{2k+v-2}kL_{k+v-1} \sigma ^v-\\&&\qquad \mathop \sum \limits_{k=1}^\infty \overline {b_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v-\mathop \sum \limits_{k=0}^\infty \overline {c_k } \rho^{-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\mathop \sum \limits_{k=1}^\infty \overline {d_k } \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v+ \\&&\qquad \mathop \sum \limits_{k=0}^\infty h_k \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\mathop \sum \limits_{k=0}^\infty \overline {h_k } \rho^{-2k+v-2}kL_{-k+v-1} \sigma ^v-\mathop \sum \limits_{k=0}^\infty m_k \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v= \\&&\qquad 2\varGamma \mathop \sum \limits_{k=0}^\infty L_k \rho^{2k-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v-2\varGamma \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-2k-v}\left( {k+v-1} \right)L_{-k-v+1} \sigma ^v-\\&&\qquad \varGamma' \mathop \sum \limits_{k=0}^\infty L_k \rho^{-v} \left( {k+v-1} \right)L_{-k-v+1} \sigma ^v+\varGamma' \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-v}\left( {k-v+1} \right)L_{k-v+1} \sigma ^v,\quad v=0,1,2,3, \cdots \end{eqnarray} $
(31) $ \begin{eqnarray} &&\mathop \sum \limits_{k=0}^\infty a_k \rho^{2k+v}\left( k+v+1 \right)L_{k+v+1} \sigma ^{-v}-\mathop \sum \limits_{k=1}^\infty b_k \rho^{-2k+v}\left( k-v-1 \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty \overline{a_k} \rho^{2k-v-2}kL_{k-v-1} \sigma ^{-v}- \\&&\qquad \mathop \sum \limits_{k=1}^\infty \overline {b_k} \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}-\mathop \sum \limits_{k=0}^\infty \overline{c_k} \rho^v\left( k-v-1 \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=1}^\infty \overline{d_k} \rho^v\left( k+v+1 \right)L_{k+v+1} \sigma ^{-v}+\\&&\qquad \mathop \sum \limits_{k=0}^\infty h_k \rho^{-2k+v}\left( k-v-1 \right)L_{-k+v+1} \sigma ^{-v}+\mathop \sum \limits_{k=0}^\infty \overline {h_k} \rho^{-2k-v-2}kL_{-k-v-1} \sigma ^{-v}-\mathop \sum \limits_{k=0}^\infty m_k \rho^v\left( k+v+1 \right)L_{k+v+1} \sigma ^{-v}= \\&&\qquad 2\varGamma \mathop \sum \limits_{k=0}^\infty L_k \rho^{2k+v}\left(k+v+1 \right)L_{k+v+1} \sigma ^{-v}-2\varGamma \mathop \sum \limits_{k=1}^\infty L_{-k} \rho^{-2k+v}\left( k-v-1 \right)L_{-k+v+1} \sigma ^{-v}- \\&&\qquad \varGamma'\mathop \sum \limits_ {k=0}^\infty L_k \rho^v\left( k-v-1 \right)L_{-k+v+1} \sigma ^{-v}+\varGamma'\mathop \sum \limits_ {k=1}^\infty L_{-k} \rho^v\left(k+v+1 \right)L_{k+v+1} \sigma ^{-v},\quad v=0,1,2,3, \cdots \end{eqnarray} $
3 工程案例应用分析
以新建汶川至马尔康公路鹧鸪山特长隧道洞口段为研究对象, 利用上节解析方法, 对非圆形寒区隧道应力和变形进行求解, 并用Flac有限差分软件进行进行校核, 验证解析解的准确性.
根据现场大气、围岩实测温度、围岩及结构热力学试验, 估算围岩冻结深度.可知当原岩温度为10℃时, 冻结深度约为2 m[28 ] . 据此确定围岩冻胀圈和未冻围岩.
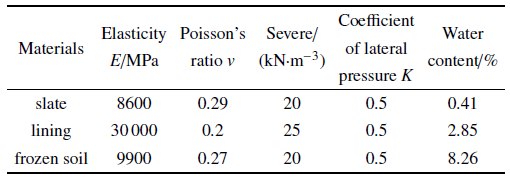
结合鹧鸪山隧道地质报告、室内岩石试验和点荷载试验数据[28 ] . 围岩、结构材料物理力学参数见表1 .
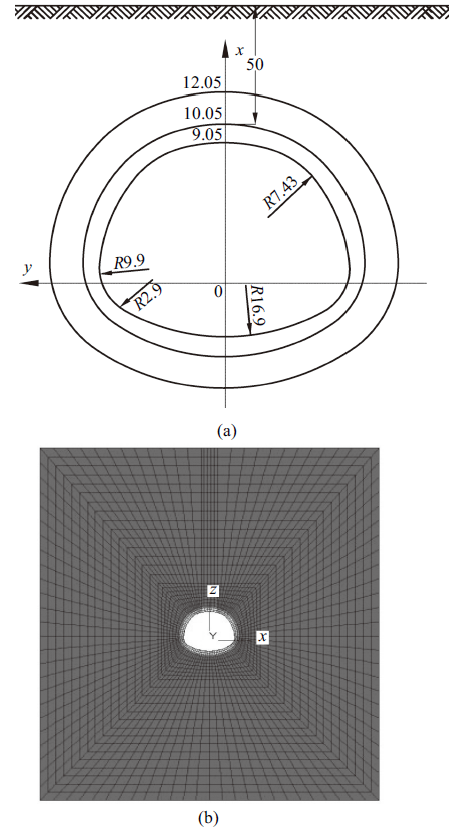
图2 (a)为鹧鸪山隧道K188 + 480 m处断面计算简图. 图2 (b)为Flac有限差分软件计算模型图, 共划分网格3916个, 用于模拟深埋非圆形寒区隧道开挖后衬砌、冻胀圈和围岩的应力及变形状态.隧道采用全断面开挖, 开挖后立即支护; 假定模型为弹性模型; 衬砌与冻胀圈, 冻胀圈与围岩之间只受法向力; 隧道冻胀系数采用等效热胀系数进行模拟; 假设冻胀圈温度恒定, 无温差; 隧道冻胀力和冻胀变形通过控制热力模型和结构模型交替开关进行计算; 衬砌与冻胀圈, 冻胀圈与围岩之间无滑动. 根据式(15)中对线胀系数的说明、水冻结为冰体积增大约9%及冻胀圈含水量计算得冻胀圈线膨胀系数$\varepsilon \approx 0.002 5$.
根据吕爱钟等[19 ] 提出的最优化法求解映射函数的思路, 编写相应MATLAB计算程序, 通过计算, 得到映射函数
(32) $ \begin{eqnarray} && w(\zeta)=8.033 9(\zeta +0.312 1-0.069 7\zeta^{-1}+\\&&\qquad0.033 8\zeta ^{-2}-0.008 7\zeta^{-3}-0.006 8\zeta ^{-4}) \end{eqnarray} $
在工程计算中方程(1)取前几项就可满足工程精度要求[19 ] , 所以为提高计算效率, 式(37)取映射函数(方程(1))的前四项; 式(37)中$\zeta=\rho \sigma $, 其中当$\rho=1.225$时, 表示映射函数所对应未冻围岩与冻胀圈接触面的边界条件; 当$\rho=1$时, 表示映射函数所对应冻胀圈与衬砌接触面的边界条件; 当$\rho =0.863 3$时, 表示映射函数所对应衬砌与大气接触面的边界条件.
图 2
图 2
(a)隧道计算简图(单位: m); (b)隧道计算模型
Fig. 2
(a) Tunnel calculation diagram (Unit: m) and (b) Finite mesh calculation mode
根据边界条件(方程(16)~(20))编写MATLAB计算程序, 求得寒区非圆形隧道冻胀应力及冻胀位移解析解, 并将其与Flac有限差分软件所求的数值解进行比较, 比较结果如下所示.
由于Flac有限差分软件计算应力为隧道衬砌及冻胀圈的竖向和水平向应力, 这与解析解所求法向、环向应力坐标系统不统一, 无法进行比较, 故将Flac有限差分软件所求应力结果进行坐标转换后再进行对比.
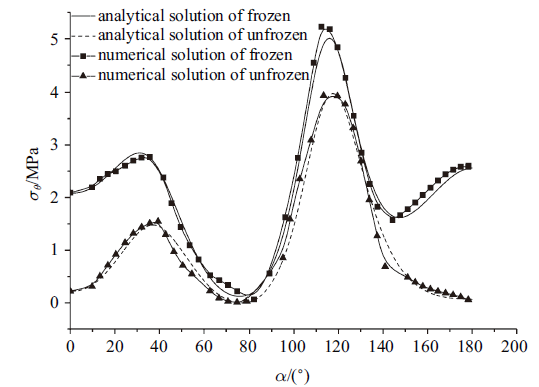
图3 是衬砌内边界环向应力, 由图中可看到, 数值解与解析解吻合得较好; 由于冻胀作用的影响衬砌内边界环向应力显著增大, 在拱顶($\alpha=0^{\circ}$)到拱肩($\alpha =40^{\circ}$)这一扇形区域衬砌所受的环向应力明显增大; 在拱脚($\alpha=120^{\circ}$)处, 环向应力集中明显, 拱脚处环向应力较未冻结时增大约25.9%; 在拱底($\alpha=180^{\circ}$)附近$30^{\circ}$的扇形区域范围内衬砌所受环向应力增长显著.
图 3
图 3
衬砌内边界环向应力
Fig. 3
Circumferential stress along the inner lining periphery
图4 为衬砌与冻胀圈接触面上法向应力, 由图4 可以看出: 衬砌法向应力较未受冻胀力时有明显波动. 由于冻胀作用, 衬砌在$\alpha=60^{\circ}$附近法向应力较未受冻胀力时增大约107.5%; 在$\alpha=110^{\circ}$附近冻胀后衬砌与未冻胀衬砌相比法向应力减小约82.4%; 在$\alpha=140^{\circ}$附近受冻胀力影响法向应力较未冻胀法向应力增大约21.4%; 在衬砌与冻胀圈接触面上, 数值模拟所求法向应力与解析法所求法向应力吻合得较好, 只是在部分路径上有一定的偏差.
图 4
图 4
衬砌与冻胀圈接触面上法向应力
Fig. 4
Normal stress along frost heaving ring-lining interface
由图5 可见, 冻胀作用对衬砌影响明显, 尤其在衬砌拱顶、拱脚、拱底处.由于冻胀力影响, 拱顶环向应力由2.01 mPa增大至4.55 mPa; 拱脚处环向应力较未冻胀环向应力增大约38.8%; 拱底环向应力由0.5 mPa增大至2.5 mPa; 在衬砌外边界上, 数值模拟所求环向应力与解析法所求环向应力吻合得较好, 只是在$\alpha=100^{\circ}$应力峰值附近有一定的偏差.
图 5
图 5
衬砌外边界环向应力
Fig. 5
Circumferential stress along outer lining periphery
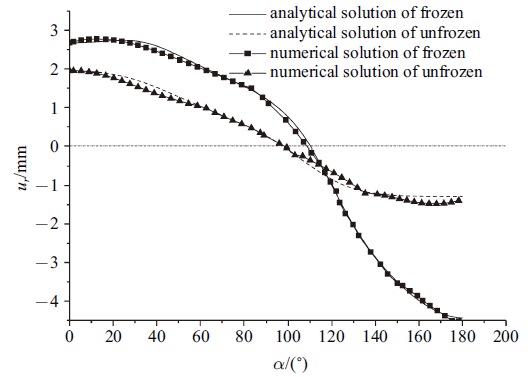
图6 为衬砌与冻胀圈接触面上的法向位移, 从图中可以看到: 数值法向位移解与解析法向位移解吻合得较好; 衬砌受到冻胀力, 产生了明显的冻胀变形.衬砌拱顶下沉较未受冻胀力时增大约37.4%.拱底隆起明显, 与未受冻胀力时相比增大约3 mm. 但是, 总的来说计算所得未冻胀和冻胀法向位移均较实测值偏小[28 ] , 这可能与未考虑开挖卸荷因子和塑性变形有关.
图 6
图 6
衬砌内边界上法向位移
Fig. 6
Radial displacement along the inner lining periphery
4 结论
根据复变函数理论, 首次提出了考虑衬砌的非圆形寒区隧道冻胀力和变形方法, 并将其应用于鹧鸪山隧道洞口段研究中, 得出了以下几点结论:
(1) 推导了衬砌-冻胀圈-围岩体系的非圆形隧道冻胀力弹性解析公式, 然后将复变函数解法得到的解析解与数值分析结果进行对比分析, 评价考虑围岩冻胀作用的非圆形隧道应力及位移解析解的合理性和准确性.
(2) 解析解与数值解吻合得较好, 围岩冻胀力对衬砌影响明显, 在拱顶、拱脚、拱底处因冻胀造成的环向附加应力显著增大; 在拱脚及两侧拱肩处受到较大的法向附加应力; 围岩冻胀力造成衬砌受力不均, 对隧道的结构安全构成了威胁.
(3) 以新建汶川至马尔康高速公路鹧鸪山特长隧道洞口段为研究对象, 结合工程实际, 利用MATLAB计算软件编写计算程序求解, 得到鹧鸪山隧道洞口段冻胀应力和冻胀位移解析解, 并将所得结果作为其数值计算和安全运行的参考依据.
(4) 由于衬砌几何结构的原因造成了隧道冻胀变形的不均匀, 进而造成冻胀力分布不均, 这较以往将围岩冻胀圈考虑为单一圆环的围岩冻胀力研究更符合实际.较以往所得解析解更能反映实际工况.
(5) 复变函数理论为寒区非圆形隧道冻胀力研究提出了一种除数值模拟、现场试验外新的计算方法.新方法为下一步寒区非圆形隧道冻胀力的弹塑性分析奠定了基础.
附录1
冻胀圈$S_{2}$区域内位移公式(15)推导过程如下.
将温度应变引入广义胡可定律得到考虑温度的广义胡可定律, 方程(A1)
(A1) $ \begin{eqnarray} \left. \begin{array}{l} \varepsilon _x -\varepsilon _1 =\dfrac{1}{E}\left[ {\sigma _x -\upsilon \left( {\sigma _y +\sigma _z } \right)} \right] \gamma _{xy} =\dfrac{\tau _{xy} }{G}\\ \varepsilon _y -\varepsilon _2 =\dfrac{1}{E}\left[ {\sigma _y -\upsilon \left( {\sigma _x +\sigma _z } \right)} \right] \gamma _{yz} =\dfrac{\tau _{yz} }{G}\\ \varepsilon _z -\varepsilon _3 =\dfrac{1}{E}\left[ {\sigma _z -\upsilon \left( {\sigma _x +\sigma _y } \right)} \right] \gamma _{xz} =\dfrac{\tau _{xz} }{G}\\ \end{array} \right\} \end{eqnarray} $
其中$\varepsilon_1$, $\varepsilon _2$, $\varepsilon _3$分别是冻胀围岩在$x$, $y$, $z$方向上的线胀系数, 假定冻胀围岩均匀冻胀, 则
(A2) $ \begin{eqnarray} \varepsilon _1 =\varepsilon _2 =\varepsilon _3 =\varepsilon =\dfrac{1}{3}\Delta V \end{eqnarray} $
(A3) $ \begin{eqnarray} \sigma _z =0\ \ \ \ \tau _{yz} =\tau _{xz} =0 \end{eqnarray} $
将式(A3)代入式(A1), 则式(A1)可改写为
(A4) $ \begin{eqnarray} \left. \begin{array}{l} \varepsilon _x =\dfrac{\partial u}{\partial x}=\dfrac{1}{E}\left( {\sigma _x -\upsilon \sigma _y } \right)+\varepsilon \\ \varepsilon _y =\dfrac{\partial v}{\partial y}=\dfrac{1}{E}\left( {\sigma _y -\upsilon \sigma _x } \right)+\varepsilon \\ \gamma _{xy} =\dfrac{\partial u}{\partial x}+\dfrac{\partial v}{\partial y}=\dfrac{\tau _{xy} }{G} \\ \end{array} \right\} \end{eqnarray} $
(A5) $ \begin{eqnarray} \left. \begin{array}{l} \sigma _x =\dfrac{{\partial }''U}{\partial {y}''} \\ \sigma _y =\dfrac{{\partial }''U}{\partial {x}''} \\ \tau _{xy} =-\dfrac{{\partial }''U}{\partial x\partial y} \\ \end{array} \right\} \end{eqnarray} $
(A6) $ \begin{eqnarray} &&\dfrac{\partial u}{\partial x}=\dfrac{1}{E}\left( {\dfrac{{\partial }''U}{\partial {y}''}-\upsilon \dfrac{{\partial }''U}{\partial {x}''}} \right)+\varepsilon = \\ &&\qquad\dfrac{1}{E}\left[ {\nabla ^2U-\left( {1+\upsilon } \right)\dfrac{{\partial }''U}{\partial {x}''}} \right]+\varepsilon = \\ &&\qquad\dfrac{1}{E}\left[ {P-\left( {1+\upsilon } \right)\dfrac{{\partial }''V}{\partial {x}''}} \right]+\varepsilon \end{eqnarray} $
(A7) $ \begin{eqnarray} &&\dfrac{\partial v}{\partial y}=\dfrac{1}{E}\left( {\dfrac{{\partial }''U}{\partial {x}''}-\upsilon \dfrac{{\partial }''U}{\partial {y}''}} \right)+\varepsilon = \\ &&\qquad\dfrac{1}{E}\left[ {P-\left( {1+\upsilon } \right)\dfrac{{\partial }''U}{\partial {y}''}} \right]+\varepsilon \end{eqnarray} $
(A8) $ \begin{eqnarray} P=4\dfrac{\partial p}{\partial x}=4\dfrac{\partial q}{\partial y} \end{eqnarray} $
将$2G={E}/({1+\upsilon})$代入式(A7)得
(A9) $ \begin{eqnarray} \left. \begin{array}{l} 2G\dfrac{\partial u}{\partial x}=\dfrac{P}{1+\upsilon }-\dfrac{{\partial }''U}{\partial {x}''}+2G\varepsilon \\ 2G\dfrac{\partial v}{\partial y}=\dfrac{P}{1+\upsilon }-\dfrac{{\partial }''U}{\partial {y}''}+2G\varepsilon \\ \end{array} \right\} \end{eqnarray} $
将式(A8)代入式(A9), 然后, 分别对$x$, $y$求导
(A10) $ \begin{eqnarray} \left. \begin{array}{l} 2G\dfrac{\partial u}{\partial x}=-\dfrac{{\partial }''U}{\partial {x}''}+\dfrac{4}{1+\upsilon }\cdot \dfrac{\partial p}{\partial x}+2G\varepsilon \\ 2G\dfrac{\partial v}{\partial y}=-\dfrac{{\partial }''U}{\partial {y}''}+\dfrac{4}{1+\upsilon }\cdot \dfrac{\partial q}{\partial y}+2G\varepsilon \\ \end{array} \right\} \end{eqnarray} $
对式(A10)第一式求$x$的积分, 对第二式求$y$的积分得
(A11) $ \begin{eqnarray} \left. \begin{array}{l} 2Gu=-\dfrac{\partial U}{\partial x}+\dfrac{4p}{1+\upsilon }+2G\varepsilon x+g_1 (y) \\ 2Gv=-\dfrac{\partial U}{\partial y}+\dfrac{4q}{1+\upsilon }+2G\varepsilon y+g_2 (x) \\ \end{array} \right\} \end{eqnarray} $
其中, $g_1 (y)$和$g_2(x)$为任意函数, 为确定其具体形式, 将式(A11)求偏导后代入式(A4)中第三式得
(A12) $ \begin{eqnarray} &&\gamma _{xy} =\dfrac{\partial u}{\partial x}+\dfrac{\partial v}{\partial y} = \\ &&\qquad \dfrac{1}{2G}\cdot \dfrac{\partial }{\partial y}\left[ {-\dfrac{\partial U}{\partial x}+\dfrac{4p}{1+\upsilon }+2G\varepsilon x+g_1 (y)} \right]+ \\ &&\qquad \dfrac{1}{2G}\cdot \dfrac{\partial }{\partial x}\left[ {-\dfrac{\partial U}{\partial y}+\dfrac{4q}{1+\upsilon }+2G\varepsilon y+g_2 (x)} \right]= \\ &&\qquad \dfrac{\tau _{xy} }{G}=-\dfrac{1}{G}\cdot \dfrac{{\partial }''U}{\partial x\partial y} \end{eqnarray} $
(A13) $ \begin{eqnarray} &&\gamma _{xy} =-\dfrac{{\partial }''U}{\partial x\partial y}+\dfrac{4}{1+\upsilon }\cdot \dfrac{\partial p}{\partial y}+{g}'_1 (y) - \\ &&\qquad \dfrac{{\partial }''U}{\partial x\partial y}+\dfrac{4}{1+\upsilon }\cdot \dfrac{\partial q}{\partial x}+{g}'_2 (x) = \\ &&\qquad -2\dfrac{{\partial }''U}{\partial x\partial y} \end{eqnarray} $
(A14) $ \begin{eqnarray} \dfrac{4}{1+\upsilon }\left( {\dfrac{\partial p}{\partial y}+\dfrac{\partial q}{\partial x}} \right)+{g}'_1 (y)+{g}'_2 (x)=0 \end{eqnarray} $
因${\partial p}/({\partial y})=-{\partial q}/({\partial x})$为柯西-黎曼条件, 即
(A15) $ \begin{eqnarray} {g}'_1 (y)+{g}'_2 (x)=0 \end{eqnarray} $
(A16) $ \begin{eqnarray} {g}'_1 (y)=A\ \ \ \ {g}'_2 (x)=-A \end{eqnarray} $
(A17) $ \begin{eqnarray} \left. \begin{array}{l} g_1 (y)=Ay+A_1 \\ g_2 (x)=-Ax+A_2 \\ \end{array} \right\} \end{eqnarray} $
由式(A17)可知$g_1 (y)$和$g_2(x)$为刚体位移[23 ] , 不影响应力与应变, 故将其略去.式(A11)可改写为
(A18) $ \begin{eqnarray} \left. \begin{array}{l} 2Gu=-\dfrac{\partial U}{\partial x}+\dfrac{4p}{1+\upsilon }+2G\varepsilon x \\ 2Gv=-\dfrac{\partial U}{\partial y}+\dfrac{4q}{1+\upsilon }+2G\varepsilon y \\ \end{array} \right\} \end{eqnarray} $
(A19) $ \begin{eqnarray} &&2G\left( {u+{\rm i}v} \right)=-\left( {\dfrac{\partial U}{\partial x}+{\rm i}\dfrac{\partial U}{\partial y}} \right)+ \\ &&\qquad \dfrac{4}{1+\upsilon }\left( {p+{\rm i}q} \right)+2G\varepsilon \left( {x+{\rm i}y} \right)= \\ &&\qquad -\left( {\dfrac{\partial U}{\partial x}+{\rm i}\dfrac{\partial U}{\partial y}} \right)+\dfrac{4}{1+\upsilon }\left( {p+iq} \right)+2G\varepsilon z\qquad \end{eqnarray} $
将应力函数$U=\left[ {\overline z \varphi _1 (z)+z\overline {{\varphi }'_1 \left( z \right)} +\theta _1 \left( z \right)} \right]\Big/2$对$x$求偏导, 由
\begin{eqnarray*} \dfrac{\partial \overline z }{\partial \overline x }=1,\ \ \ \dfrac{\partial \varphi _1 (z)}{\partial x}=\dfrac{\partial \varphi _1 (z)}{\partial z}\dfrac{\partial z}{\partial x}+\dfrac{\partial \varphi _1 (z)}{\partial \overline z }\dfrac{\partial \overline z }{\partial x}={\varphi }'_1 (z) \end{eqnarray*}
\begin{eqnarray*} \dfrac{\partial \overline {\varphi _1 (z)} }{\partial x}=\left({\dfrac{\partial \overline {\varphi _1 } }{\partial x}} \right)=\overline {{\varphi }'_1 (z)} \end{eqnarray*}
(A20) $ \begin{eqnarray} &&\dfrac{\partial U}{\partial x}=\dfrac{1}{2}\Big[ \varphi _1 (z)+\overline z {\varphi }'_1 \left( z \right)+\overline {\varphi _1 \left( z \right)} + \\ &&\qquad z\overline {{\varphi }'_1 \left( z \right)} +\theta _1 ^\prime \left( z \right)+\overline {\theta _1 ^\prime \left( z \right)} \Big] \end{eqnarray} $
(A21) $ \begin{eqnarray} &&\dfrac{\partial U}{\partial y}=\dfrac{\rm i}{2}\Big[ -\varphi _1 (z)+\overline z {\varphi }'_1 \left( z \right)+\overline {\varphi _1 \left( z \right)} - \\ &&\qquad z\overline {{\varphi }'_1 \left( z \right)} +\theta _1 ^\prime \left( z \right)-\overline {\theta _1 ^\prime \left( z \right)} \Big] \end{eqnarray} $
这里用$\psi _1 ^\prime \left( z \right)$表示$\theta _1 ^\prime \left( z\right)$, 即
(A22) $ \begin{eqnarray} &&2G\left( {u+{\rm i}v} \right)=-\varphi _1 (z)-z\overline {{\varphi }'_1 \left( z \right)} -\overline {\psi _1 \left( z \right)} + \\ &&\qquad\dfrac{4}{1+\upsilon }\varphi _1 (z) +2G\varepsilon z=\dfrac{3-\upsilon }{1+\upsilon }\varphi _1 (z)- \\ &&\qquad z\overline {{\varphi }'_1 \left( z \right)} -\overline {\psi _1 \left( z \right)} +2G\varepsilon z \end{eqnarray} $
以上是考虑冻胀位移的平面应力问题位移表示式, 对于平面应变问题, 把$\upsilon$改为${\upsilon}/({1-\upsilon })$, 所以平面问题位移表示式可以统一表示为
(A23) $ \begin{eqnarray} 2G\left( {u+{\rm i}v} \right)=\kappa \varphi _1 (z) -z\overline {{\varphi }'_1 \left( z \right)} -\overline {\psi _1 \left( z \right)} +2G\varepsilon z \end{eqnarray} $
(A24) $ \begin{eqnarray} \kappa =\left\{\begin{array}{l@{\ \ \ }l} 3-4\upsilon,& {\rm plane\ strain}\\ \dfrac{3-\upsilon }{1+\upsilon }, &{\rm plane\ stress} \\ \end{array} \right. \end{eqnarray} $
最后, 将直角坐标系下的位移解通过保角变换为正交曲线坐标系下的位移解, 得到方程(15), 即
(A25) $ \begin{eqnarray} &&2G\left( u_\rho +{\rm i}u_\theta \right)=2G{\rm e}^{-{\rm i}\alpha} \left( u+{\rm i}v \right)=\\ &&\qquad\dfrac{\overline{\zeta}}{\rho}\dfrac{\overline{w'\left( \zeta \right)}}{\left|w\left( \zeta \right) \right|} \left[ \kappa \varphi \left( \zeta \right)-\dfrac{w\left( \zeta \right)}{\overline{w' (\zeta )}}\overline{\varphi '\left( \zeta \right)} -\overline{\psi \left( \zeta \right)} \right] +\\ &&\qquad 2G\dfrac{\overline{\zeta}}{\rho}\dfrac{\overline{w'\left( \zeta \right)}}{\left| w\left( \zeta \right) \right|}w\left( \zeta \right)\varepsilon \end{eqnarray} $
(A26) $ \begin{eqnarray} \left. \begin{array}{l} \varphi_1 (z)=\varphi _1 (w(\zeta ))\to\varphi (\zeta ) \\ \psi _1 (z)=\psi _1 (w(\zeta ))\to\psi (\zeta ) \end{array} \right\} \end{eqnarray} $
参考文献
View Option
[1]
Lai YM Liu SY Wu ZW , et al . Approximate analytical solution for temperature fields in cold regions circular tunnels
Cold Reg. Sci. Technol , 2002 ,34 :43 -49
[本文引用: 1]
[2]
Zhang XF Lai YM Yu WB , et al . Non-linear analysis for the freezing--thawing situation of the rock surrounding the tunnel in cold regions under the conditions of different construction seasons, initial temperatures and insulations
Tunnelling Underground Space Technol , 2002 ,17 :315 -325
[3]
Zhang SJ Lai YM Zhang XF , et al . Study on the damage propagation of surrounding rock from a cold-region tunnel under freeze--thaw cycle condition
Tunnelling Underground Space Technol , 2004 ,19 :295 -302
[4]
Lai YM Wu H Wu ZW , et al . Analytical viscoelastic solution for frost force in cold-region tunnels
Cold Reg. Sci. Technol. , 2000 ,31 :227 -234
[本文引用: 1]
[5]
Gao GY Chen QS Zhang QS , et al . Analytical elasto-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels
Cold Reg. Sci. Technol. , 2012 ,72 :50 -57
[本文引用: 1]
[6]
Feng Q Zhang BS Qiang JG , et al . Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels
Cold Reg. Sci. Technol. , 2014 ,108 :59 -68
[本文引用: 1]
[7]
夏才初 , 黄继辉 , 卞跃威 等 . 融化作用下多年冻土隧道围岩的弹塑性解及其与支护的相互作用分析
岩土力学 , 2013 ,34 (7 ):1987 -1994
[本文引用: 1]
( Xia Caichu Huang Jihui Bian Yuewei , et al . Elastoplastic analysis of surrounding rock of permafrost tunnel with thawing effect and its interaction with support
Rock and Soil Mechanics , 2013 ,34 (7 ):1987 -1994 (in Chinese))
[本文引用: 1]
[8]
张常光 , 徐飞 , 张庆贺 等 . 岩石隧道塑性位移新解
岩石力学与工程学报 , 2011 ,30 (增2 ):3551 -3556
[本文引用: 1]
( Zhang Changguang Xu Fei Zhang Qinghe , et al . New plastic solution for displacement of rock tunnles
Chinese Journal of Rock Mechanics and Engineering , 2011 ,30 (supp.2 ):3551 -3556 (in Chinese))
[本文引用: 1]
[9]
谭贤君 . 高海拔寒区隧道冻胀机理及其保温技术研究. [博士论文]
武汉: 中国科学院武汉岩土力学研究所 , 2010
[本文引用: 1]
( Tan Xianjun . Study on the meehanism of frost heave of tunnel in cold region with high altitude and related insulation technology. [PhD Thesis]
Wuhan: Institute of Rock and Soil Mechanics, Chinese Academy of Sciences , 2010 (in Chinese))
[本文引用: 1]
[10]
杨罡 . 兰新高铁祁连山隧道围岩温度场及冻胀力研究. [硕士论文]
西安: 西安科技大学 , 2017
[本文引用: 1]
( Yang Gang . Study on surrounding rock temperature field and frost heave force of Qilian mountain tunnel of Lanxin railway. [Master Thesis].
Xi'An: Xi'an University of Science and Technology , 2017 (in Chinese))
[本文引用: 1]
[11]
黄继辉 , 夏才初 , 韩常领 等 . 寒区公路隧道冻胀力荷载的分布形式和简化计算方法
现代隧道技术 , 2016 ,53 (5 ):63 -70
[本文引用: 1]
( Huang Jihui Xia Caichu Han Changling , et al . The distribution form and simplified calculation method of frost heaving force load in highway tunnels in cold regions
Modern Tunneling Technology , 2016 ,53 (5 ):63 -70 (in Chinese))
[本文引用: 1]
[12]
黄继辉 , 夏才初 , 韩常领 等 . 考虑围岩不均匀冻胀的寒区隧道冻胀力解析解
岩石力学与工程学报 , 2015 ,34 (增2 ):3766 -3774
[本文引用: 1]
( Huang Jihui Xia Caichu Han Changling , et al . Analytical solution of frost heave force acting on cold-region tunnel liner considering anisotropy frost heave of surrounding rock
Chinese Journal of Rock Mechanics and Engineering , 2015 ,34 (supp.2 ):3766 -3774 (in Chinese))
[本文引用: 1]
[13]
苏林军 . 寒区隧道冻害预测与对策研究. [硕士论文]
成都: 西南交通大学 , 2007
[本文引用: 1]
( Su Linjun . Study on forcasting of frost damage and antifreezing strategies of tunnel in cold area. [Master Thesis]
Chengdu: Southwest Jiaotong University , 2007 (in Chinese))
[本文引用: 1]
[14]
吴剑 . 随道冻害机理及冻胀力计算方法的研究. [硕士论文]
成都: 西南交通大学 , 2004
[本文引用: 1]
( Wu Jian . Study on principle of tunnel freeze injure and calculation method of frost force. [Master Thesis]
Chengdu: Southwest Jiaotong University , 2004 (in Chinese))
[本文引用: 1]
[15]
Zheng H Shunji KN Niu FJ , et al . Three-dimensional frost heave evaluation based on practical Takashi's equation
Cold Regious Science & Technology , 2015 ,118 :30 -37
[本文引用: 1]
[16]
Tan XJ Chen WZ Wu GJ , et al . Numerical simulations of heat transfer with ice-water phase change occurring in porous media and application to a cold-region tunnel
Tunnelling Underground Space Technol. , 2013 ,38 :170 -179
[本文引用: 1]
[17]
李岩松 , 陈寿根 . 基于复变函数理论的非圆形隧道解析解
西南交通大学学报 , 2019 , DOI: 10.3969/j.issn.0258-2724.20180243
[本文引用: 3]
( Li Yansong Chen Shougen . Stress and deformation study of lining and surrounding rock in a non-circular tunnel based on the complex variable method Seepage
Journal of Southwest Jiaotong University , 2019 , DOI: 10.3969/j.issn.0258-2724.20180243 (in Chinese))
[本文引用: 3]
[18]
李岩松 , 陈寿根 . 考虑注浆加固作用下非圆形隧道应力和变形解析解
中国公路学报 , 2018 ,31 (10 ):255 -265
[本文引用: 3]
( Li Yansong Chen Shougen . Analytic solution on stress and deformation of non-circular tunnel considering grouting circle
China Journal of Highway and Transport , 2018 ,31 (10 ):255 -265 (in Chinese))
[本文引用: 3]
[19]
吕爱钟 , 张路青 . 地下隧洞力学分析的复变函数方法 . 北京 : 科学出版社 , 2007
[本文引用: 3]
( Lü Aizhong Zhang Luqing Complex Function Method for Mechanical Analysis of Underground Tunnel. Beijing : Science Press , 2007 (in Chinese))
[本文引用: 3]
[20]
Kargar AR Rahmannejad R Hajabasi MA . A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method
International Journal of Solids and Structures , 2014 ,51 :1475 -1482
[本文引用: 2]
[21]
Lu AZ Zhang N Kuang L . Analytic solutions of stress and displacement for a non-circular tunnel at great depth including support delay
International Journal of Rock Mechanics & Mining Sciences , 2014 ,70 :69 -81
[本文引用: 1]
[22]
Lu AZ Zhang N Qin Y . Analytical solutions for the stress of a lined non-circular tunnel under full-slip contact conditions
International Journal of Rock Mechanics & Mining Sciences , 2015 ,79 :183 -192
[本文引用: 3]
[23]
陈子荫 . 围岩力学分析中的解析方法 . 北京 : 煤炭工业出版社 , 1994
[本文引用: 2]
( Chen Ziyin Analytical Method in Mechanical Analysis of Surrounding Rock. Beijing : China Coal Industry Publishing House , 1994 (in Chinese))
[本文引用: 2]
[24]
张治国 , 杨轩 , 宫剑飞 等 . 复变函数法分析盾构隧道开挖引起的土体位移和衬砌变形
岩土工程学报 , 2017 ,39 (9 ):1626 -1635
[本文引用: 3]
( Zhang Zhiguo Yang Xuan Gong Jianfei , et al . A complex variable analysis of soil displacement and liner deformation induced by shield excavation
Chinese Journal of Geotechnical Engineering , 2017 ,39 (9 ):1626 -1635 (in Chinese))
[本文引用: 3]
[25]
Li YS Chen SG . A complex variable solution for lining stress and deformation in a non-circular deep tunnel II practical application and verification
Mathematical and Computational Applications , 2018 ,23 , 43 , doi: 10.3390/mca23030043
[26]
覃爱民 , 骆汉宾 . 基于Mohr-Coulomb准则寒区隧道围岩应力弹塑性解析
地下空间与工程学报 , 2018 ,14 (2 ):395 -402
[本文引用: 3]
( Tan Aimin Luo Hanbin . Elastoplastic analysis of stress in tunnel surrounding rock in cold region based on mohr-coulomb criterion
Chinese Journal of Underground Space and Engineering , 2018 ,14 (2 ):395 -402 (in Chinese))
[本文引用: 3]
[27]
Kargar AR Rahmannejad R Hajabasi MA . A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method
International Journal of Solids and Structures , 2014 ,51 :1475 -1482
[本文引用: 1]
[28]
赵玉报 . 高原高寒隧道围岩冻胀行为及施工对策研究. [博士论文]
成都: 西南交通大学 , 2011
[本文引用: 3]
( Zhao Yubao . Study on the frost heaving behavior and construction countermeasure for plateau tunnel in cold region after earthquake. [PhD Thesis]
Chengdu: Southwest Jiaotong University , 2011 (in Chinese))
[本文引用: 3]
[29]
黄诗冰 , 刘泉声 , 刘艳章 等 . 低温热力耦合下岩体椭圆孔(裂)隙中冻胀力与冻胀开裂特征研究
岩土工程学报 , 2018 ,40 (3 ):459 -467
( Huang Shibing Liu Quansheng Liu Yanzhang , et al . Frost heaving pressure and characteristics of frost cracking in elliptical cavity (crack) of rock mass under coupled thermal-mechanical condition at low temperature
Chinese Journal of Geotechnical Engineering , 2018 ,40 (3 ):459 -467 (in Chinese))
[30]
夏明 . 寒区隧道温度场数值分析研究. [硕士论文]
淮南: 安徽理工大学 , 2018
( Xia Ming . Numerical analysis of tunnel temperature field in cold area. [Master Thesis]
Huainan: Anhui University of Science & Technology , 2018 (in Chinese))
[31]
夏才初 , 刘宇鹏 , 吴福宝 等 . 基于西原模型的圆形隧道黏弹-黏塑性解析解
岩土力学 , 2019 ,40 (5 ):1638 -1648
( Xia Caichu Liu Yupeng Wu Fubao , et al . Viscoelasto-viscoplastic solutions for circular tunnel based on Nishihara model
Rock and Soil Mechanics , 2019 ,40 (5 ):1638 -1648 (in Chinese))
[32]
郭健 . 基于变形稳定的隧道结构可靠度分析. [博士论文]
兰州: 兰州交通大学 , 2018
( Guo Jian . Reliability analysis of tunnel structure based on deformation stability. [PhD Thesis]
Lanzhou: Lanzhou Jiaotong University , 2018 (in Chinese))
[33]
崔芳 , 王利 , 王云飞 . 非轴对称荷载下圆形隧道弹性围岩应力解析解
地下空间与工程学报 , 2017 ,13 (3 ):637 -642
( Cui Fang Wang Li Wang Yunfei . Analytical solution of stress in elastic surrounding rock of circular tunnel under non-axisymmetric load
Chinese Journal of Underground Space and Engineering , 2017 ,13 (3 ):637 -642 (in Chinese))
Approximate analytical solution for temperature fields in cold regions circular tunnels
1
2002
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
Non-linear analysis for the freezing--thawing situation of the rock surrounding the tunnel in cold regions under the conditions of different construction seasons, initial temperatures and insulations
2002
Study on the damage propagation of surrounding rock from a cold-region tunnel under freeze--thaw cycle condition
2004
Analytical viscoelastic solution for frost force in cold-region tunnels
1
2000
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
Analytical elasto-plastic solution for stress and plastic zone of surrounding rock in cold region tunnels
1
2012
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
Analytical elasto-plastic solution for stress and deformation of surrounding rock in cold region tunnels
1
2014
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
融化作用下多年冻土隧道围岩的弹塑性解及其与支护的相互作用分析
1
2013
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
融化作用下多年冻土隧道围岩的弹塑性解及其与支护的相互作用分析
1
2013
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
岩石隧道塑性位移新解
1
2011
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
岩石隧道塑性位移新解
1
2011
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
高海拔寒区隧道冻胀机理及其保温技术研究. [博士论文]
1
2010
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
高海拔寒区隧道冻胀机理及其保温技术研究. [博士论文]
1
2010
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
兰新高铁祁连山隧道围岩温度场及冻胀力研究. [硕士论文]
1
2017
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
兰新高铁祁连山隧道围岩温度场及冻胀力研究. [硕士论文]
1
2017
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
寒区公路隧道冻胀力荷载的分布形式和简化计算方法
1
2016
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
寒区公路隧道冻胀力荷载的分布形式和简化计算方法
1
2016
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
考虑围岩不均匀冻胀的寒区隧道冻胀力解析解
1
2015
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
考虑围岩不均匀冻胀的寒区隧道冻胀力解析解
1
2015
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
寒区隧道冻害预测与对策研究. [硕士论文]
1
2007
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
寒区隧道冻害预测与对策研究. [硕士论文]
1
2007
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
随道冻害机理及冻胀力计算方法的研究. [硕士论文]
1
2004
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
随道冻害机理及冻胀力计算方法的研究. [硕士论文]
1
2004
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
Three-dimensional frost heave evaluation based on practical Takashi's equation
1
2015
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
Numerical simulations of heat transfer with ice-water phase change occurring in porous media and application to a cold-region tunnel
1
2013
... Lai等[1 -4 ] 应用无量纲微扰法、Galerkin法、黏弹性理论以及CT技术分别对寒区隧道进行多项研究并取得了显著成果. 为寒区隧道施工、运营、维护提供了有力的参考依据; Gao等[5 ] 应用经典弹塑性理论得到了圆形寒区隧道围岩应力和塑性区,发现冻胀力会导致围岩塑性区显著膨胀并在屈服后出现塑性硬化现象; Feng等[6 ] 应用弹塑性理论得到了圆形寒区隧道围岩应力及位移的弹塑性解析解, 并且通过参数分析, 得出相关参数对冻结圆周内、外边缘塑性半径和围岩应力的影响结果;夏才初等[7 ] 考虑施工过程中机械产生的热量对多年冻土的融化影响, 分析了多年冻土融化范围, 建立并求解融化作用下多年冻土隧道围岩弹塑性模型, 确定了相应控制融化作用的关键因素; 张常光等[8 ] 在弹性模量变化、中间主应力效应、围岩应变软化和剪胀条件下, 基于统一强度理论推导了深埋圆形隧道塑性位移新解; 谭贤君[9 ] 、杨罡[10 ] 、黄继辉等[11 -12 ] 、苏林军[13 ] 应用有限元软件对冻土隧道冻胀力进行模拟,得到了一系列令人满意的结果; 吴剑[14 ] 通过模型试验结果与数值模拟结果对比, 详细研究冻土隧道冻胀力, 得出了不同冻胀条件下隧道衬砌变形特征曲线以及冻胀力分布规律; 根据Takashi方程Hao等[15 ] 得到了圆柱形冻土试块的冻胀力以及温度分布规律, 论证了该方法在三维空间中的适用性; Tan等[16 ] 应用数值模拟建立模型, 计算了寒区隧道在多孔介质中冻融循环的温度扩散问题, 通过数值模拟得到隧道衬砌表面的建筑保温材料会极大地改变衬砌和围岩温度的结论. ...
基于复变函数理论的非圆形隧道解析解
3
2019
... 当考虑支护为圆形的条件时, 寒区隧道冻胀力和位移的弹性解析解通过连续性条件易于给出. 而当隧道断面形状为马蹄形、直墙拱形等非圆形状并且考虑隧道支护时, 由于考虑了隧道支护, 使问题由单连通域问题变为多连通域问题, 不能直接应用经典的复变函数理论求解非圆形隧道应力和位移. 所以, 还鲜有学者给出考虑衬砌因素的非圆形寒区隧道冻胀力和冻胀位移的弹性解析解. 综上所述, 为得到考虑衬砌的非圆形寒区隧道冻胀力弹性解析解, 应用经典复变函数理论幂级数解法, 结合连续性条件, 在文献[17 -18 ] 的基础上, 推导了考虑衬砌的非圆形寒区隧道冻胀力的弹性解析解. 为下一步非圆形寒区隧道冻胀力的弹塑性分析奠定了基础. ...
... 应用于李岩松等[17 -18 ] 幂级数解法, 方程(16)可分别展开为正幂次方程组(21)和负幂次方程组(22) ...
... 结合行列式(21)、式(22)以及行列式(24) ~式(31), 可以得到无穷线性方程组[17 -18 ] , 求解无穷线性方程组得到应力函数(方程(2)和(3), 方程(8)和(9), 方程(10)和(11))中各项系数. 由得到的应力函数计算方程(12)和(13)得到非圆形寒区隧道应力解析解;由方程(14)计算衬砌和未冻围岩位移解析解; 最后由方程(15)计算冻胀圈位移解析解. ...
基于复变函数理论的非圆形隧道解析解
3
2019
... 当考虑支护为圆形的条件时, 寒区隧道冻胀力和位移的弹性解析解通过连续性条件易于给出. 而当隧道断面形状为马蹄形、直墙拱形等非圆形状并且考虑隧道支护时, 由于考虑了隧道支护, 使问题由单连通域问题变为多连通域问题, 不能直接应用经典的复变函数理论求解非圆形隧道应力和位移. 所以, 还鲜有学者给出考虑衬砌因素的非圆形寒区隧道冻胀力和冻胀位移的弹性解析解. 综上所述, 为得到考虑衬砌的非圆形寒区隧道冻胀力弹性解析解, 应用经典复变函数理论幂级数解法, 结合连续性条件, 在文献[17 -18 ] 的基础上, 推导了考虑衬砌的非圆形寒区隧道冻胀力的弹性解析解. 为下一步非圆形寒区隧道冻胀力的弹塑性分析奠定了基础. ...
... 应用于李岩松等[17 -18 ] 幂级数解法, 方程(16)可分别展开为正幂次方程组(21)和负幂次方程组(22) ...
... 结合行列式(21)、式(22)以及行列式(24) ~式(31), 可以得到无穷线性方程组[17 -18 ] , 求解无穷线性方程组得到应力函数(方程(2)和(3), 方程(8)和(9), 方程(10)和(11))中各项系数. 由得到的应力函数计算方程(12)和(13)得到非圆形寒区隧道应力解析解;由方程(14)计算衬砌和未冻围岩位移解析解; 最后由方程(15)计算冻胀圈位移解析解. ...
考虑注浆加固作用下非圆形隧道应力和变形解析解
3
2018
... 当考虑支护为圆形的条件时, 寒区隧道冻胀力和位移的弹性解析解通过连续性条件易于给出. 而当隧道断面形状为马蹄形、直墙拱形等非圆形状并且考虑隧道支护时, 由于考虑了隧道支护, 使问题由单连通域问题变为多连通域问题, 不能直接应用经典的复变函数理论求解非圆形隧道应力和位移. 所以, 还鲜有学者给出考虑衬砌因素的非圆形寒区隧道冻胀力和冻胀位移的弹性解析解. 综上所述, 为得到考虑衬砌的非圆形寒区隧道冻胀力弹性解析解, 应用经典复变函数理论幂级数解法, 结合连续性条件, 在文献[17 -18 ] 的基础上, 推导了考虑衬砌的非圆形寒区隧道冻胀力的弹性解析解. 为下一步非圆形寒区隧道冻胀力的弹塑性分析奠定了基础. ...
... 应用于李岩松等[17 -18 ] 幂级数解法, 方程(16)可分别展开为正幂次方程组(21)和负幂次方程组(22) ...
... 结合行列式(21)、式(22)以及行列式(24) ~式(31), 可以得到无穷线性方程组[17 -18 ] , 求解无穷线性方程组得到应力函数(方程(2)和(3), 方程(8)和(9), 方程(10)和(11))中各项系数. 由得到的应力函数计算方程(12)和(13)得到非圆形寒区隧道应力解析解;由方程(14)计算衬砌和未冻围岩位移解析解; 最后由方程(15)计算冻胀圈位移解析解. ...
考虑注浆加固作用下非圆形隧道应力和变形解析解
3
2018
... 当考虑支护为圆形的条件时, 寒区隧道冻胀力和位移的弹性解析解通过连续性条件易于给出. 而当隧道断面形状为马蹄形、直墙拱形等非圆形状并且考虑隧道支护时, 由于考虑了隧道支护, 使问题由单连通域问题变为多连通域问题, 不能直接应用经典的复变函数理论求解非圆形隧道应力和位移. 所以, 还鲜有学者给出考虑衬砌因素的非圆形寒区隧道冻胀力和冻胀位移的弹性解析解. 综上所述, 为得到考虑衬砌的非圆形寒区隧道冻胀力弹性解析解, 应用经典复变函数理论幂级数解法, 结合连续性条件, 在文献[17 -18 ] 的基础上, 推导了考虑衬砌的非圆形寒区隧道冻胀力的弹性解析解. 为下一步非圆形寒区隧道冻胀力的弹塑性分析奠定了基础. ...
... 应用于李岩松等[17 -18 ] 幂级数解法, 方程(16)可分别展开为正幂次方程组(21)和负幂次方程组(22) ...
... 结合行列式(21)、式(22)以及行列式(24) ~式(31), 可以得到无穷线性方程组[17 -18 ] , 求解无穷线性方程组得到应力函数(方程(2)和(3), 方程(8)和(9), 方程(10)和(11))中各项系数. 由得到的应力函数计算方程(12)和(13)得到非圆形寒区隧道应力解析解;由方程(14)计算衬砌和未冻围岩位移解析解; 最后由方程(15)计算冻胀圈位移解析解. ...
3
2007
... 其中, $R$是一个实常数, 它的大小反映了隧道孔洞的大小; $C_{k} $一般为复常数, 其中$k = 1,2,3, \cdots $, $C_{k} $反映了隧道断面形状, 在一般情况下$C_{k} $取前几项时, 映射函数的精度已经可以满足工程要求[19 ] . $\zeta$为$Z$平面上的点映射到$\zeta $平面上的正交曲线坐标, 通常可由角度$\theta$与半径$\rho$表示. ...
... 根据吕爱钟等[19 ] 提出的最优化法求解映射函数的思路, 编写相应MATLAB计算程序, 通过计算, 得到映射函数 ...
... 在工程计算中方程(1)取前几项就可满足工程精度要求[19 ] , 所以为提高计算效率, 式(37)取映射函数(方程(1))的前四项; 式(37)中$\zeta=\rho \sigma $, 其中当$\rho=1.225$时, 表示映射函数所对应未冻围岩与冻胀圈接触面的边界条件; 当$\rho=1$时, 表示映射函数所对应冻胀圈与衬砌接触面的边界条件; 当$\rho =0.863 3$时, 表示映射函数所对应衬砌与大气接触面的边界条件. ...
3
2007
... 其中, $R$是一个实常数, 它的大小反映了隧道孔洞的大小; $C_{k} $一般为复常数, 其中$k = 1,2,3, \cdots $, $C_{k} $反映了隧道断面形状, 在一般情况下$C_{k} $取前几项时, 映射函数的精度已经可以满足工程要求[19 ] . $\zeta$为$Z$平面上的点映射到$\zeta $平面上的正交曲线坐标, 通常可由角度$\theta$与半径$\rho$表示. ...
... 根据吕爱钟等[19 ] 提出的最优化法求解映射函数的思路, 编写相应MATLAB计算程序, 通过计算, 得到映射函数 ...
... 在工程计算中方程(1)取前几项就可满足工程精度要求[19 ] , 所以为提高计算效率, 式(37)取映射函数(方程(1))的前四项; 式(37)中$\zeta=\rho \sigma $, 其中当$\rho=1.225$时, 表示映射函数所对应未冻围岩与冻胀圈接触面的边界条件; 当$\rho=1$时, 表示映射函数所对应冻胀圈与衬砌接触面的边界条件; 当$\rho =0.863 3$时, 表示映射函数所对应衬砌与大气接触面的边界条件. ...
A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method
2
2014
... 根据Kargar等[20 -22 ] 和陈子荫[23 ] 提出的方法, $\zeta $面上未冻围岩$O_{3}$区域内的应力函数可表示为 ...
... 在计算非圆形隧道围岩应力时, 为能更好地反应实际隧洞变形位移, Lu等[20 -22 ] 在连续性位移条件中引入了开挖卸荷因子. 为了能更直观反映冻胀力对非圆形隧道衬砌的影响, 在位移连续边界条件中并未考虑开挖卸荷因子, 如需考虑开挖卸荷效应, 只需在位移边界条件中添加符合实际工况的开挖卸荷因子即可. 根据推导的位移公式, 在冻胀圈与衬砌接触面上位移连续边界条件可表示为 ...
Analytic solutions of stress and displacement for a non-circular tunnel at great depth including support delay
1
2014
... 式中, $h_{k}$和$m_{k}$为所求复常数,它们均由边界条件确定; $\varphi _0 \left( \zeta \right)$和$\psi _0 \left( \zeta \right)$满足$\varphi _0 \left( \infty \right) = 0$和$\psi _0 \left( \infty \right) = 0$; Lu等[21 -22 ] 提出$\varGamma $和${\varGamma }'$可由无穷远处应力边界条件定出, 即 ...
Analytical solutions for the stress of a lined non-circular tunnel under full-slip contact conditions
3
2015
... 根据Kargar等[20 -22 ] 和陈子荫[23 ] 提出的方法, $\zeta $面上未冻围岩$O_{3}$区域内的应力函数可表示为 ...
... 式中, $h_{k}$和$m_{k}$为所求复常数,它们均由边界条件确定; $\varphi _0 \left( \zeta \right)$和$\psi _0 \left( \zeta \right)$满足$\varphi _0 \left( \infty \right) = 0$和$\psi _0 \left( \infty \right) = 0$; Lu等[21 -22 ] 提出$\varGamma $和${\varGamma }'$可由无穷远处应力边界条件定出, 即 ...
... 在计算非圆形隧道围岩应力时, 为能更好地反应实际隧洞变形位移, Lu等[20 -22 ] 在连续性位移条件中引入了开挖卸荷因子. 为了能更直观反映冻胀力对非圆形隧道衬砌的影响, 在位移连续边界条件中并未考虑开挖卸荷因子, 如需考虑开挖卸荷效应, 只需在位移边界条件中添加符合实际工况的开挖卸荷因子即可. 根据推导的位移公式, 在冻胀圈与衬砌接触面上位移连续边界条件可表示为 ...
2
1994
... 根据Kargar等[20 -22 ] 和陈子荫[23 ] 提出的方法, $\zeta $面上未冻围岩$O_{3}$区域内的应力函数可表示为 ...
... 由式(A17)可知$g_1 (y)$和$g_2(x)$为刚体位移[23 ] , 不影响应力与应变, 故将其略去.式(A11)可改写为 ...
2
1994
... 根据Kargar等[20 -22 ] 和陈子荫[23 ] 提出的方法, $\zeta $面上未冻围岩$O_{3}$区域内的应力函数可表示为 ...
... 由式(A17)可知$g_1 (y)$和$g_2(x)$为刚体位移[23 ] , 不影响应力与应变, 故将其略去.式(A11)可改写为 ...
复变函数法分析盾构隧道开挖引起的土体位移和衬砌变形
3
2017
... 在复变函数解中[24 -26 ] 应力均可以用两个应力函数$\varphi$和$\psi $表达, 衬砌、冻胀圈和未冻围岩上应力均可表示为 ...
... 假设寒区隧道衬砌$S_{1}$和未冻围岩$S_{3}$区域体积不受围岩温度变化影响, 相应$\zeta $平面上映射区域$O_{1}$和$O_{3}$位移满足复变函数[24 -26 ] 应力函数表达, 衬砌和未冻围岩上位移可表示为 ...
... 由于冻胀圈$S_{2}$区域内体积受温度变化影响, 故相应在$\zeta $平面上$O_{2}$区域内位移无法满足复变函数[24 -26 ] 应力函数表达, 需要重新推导(推导过程详见附录1), 经推导冻胀圈上位移可表示为 ...
复变函数法分析盾构隧道开挖引起的土体位移和衬砌变形
3
2017
... 在复变函数解中[24 -26 ] 应力均可以用两个应力函数$\varphi$和$\psi $表达, 衬砌、冻胀圈和未冻围岩上应力均可表示为 ...
... 假设寒区隧道衬砌$S_{1}$和未冻围岩$S_{3}$区域体积不受围岩温度变化影响, 相应$\zeta $平面上映射区域$O_{1}$和$O_{3}$位移满足复变函数[24 -26 ] 应力函数表达, 衬砌和未冻围岩上位移可表示为 ...
... 由于冻胀圈$S_{2}$区域内体积受温度变化影响, 故相应在$\zeta $平面上$O_{2}$区域内位移无法满足复变函数[24 -26 ] 应力函数表达, 需要重新推导(推导过程详见附录1), 经推导冻胀圈上位移可表示为 ...
A complex variable solution for lining stress and deformation in a non-circular deep tunnel II practical application and verification
2018
基于Mohr-Coulomb准则寒区隧道围岩应力弹塑性解析
3
2018
... 在复变函数解中[24 -26 ] 应力均可以用两个应力函数$\varphi$和$\psi $表达, 衬砌、冻胀圈和未冻围岩上应力均可表示为 ...
... 假设寒区隧道衬砌$S_{1}$和未冻围岩$S_{3}$区域体积不受围岩温度变化影响, 相应$\zeta $平面上映射区域$O_{1}$和$O_{3}$位移满足复变函数[24 -26 ] 应力函数表达, 衬砌和未冻围岩上位移可表示为 ...
... 由于冻胀圈$S_{2}$区域内体积受温度变化影响, 故相应在$\zeta $平面上$O_{2}$区域内位移无法满足复变函数[24 -26 ] 应力函数表达, 需要重新推导(推导过程详见附录1), 经推导冻胀圈上位移可表示为 ...
基于Mohr-Coulomb准则寒区隧道围岩应力弹塑性解析
3
2018
... 在复变函数解中[24 -26 ] 应力均可以用两个应力函数$\varphi$和$\psi $表达, 衬砌、冻胀圈和未冻围岩上应力均可表示为 ...
... 假设寒区隧道衬砌$S_{1}$和未冻围岩$S_{3}$区域体积不受围岩温度变化影响, 相应$\zeta $平面上映射区域$O_{1}$和$O_{3}$位移满足复变函数[24 -26 ] 应力函数表达, 衬砌和未冻围岩上位移可表示为 ...
... 由于冻胀圈$S_{2}$区域内体积受温度变化影响, 故相应在$\zeta $平面上$O_{2}$区域内位移无法满足复变函数[24 -26 ] 应力函数表达, 需要重新推导(推导过程详见附录1), 经推导冻胀圈上位移可表示为 ...
A semi-analytical elastic solution for stress field of lined non-circular tunnels at great depth using complex variable method
1
2014
... 方程(2)和(3)中的表达式$\varGamma w\left( \zeta \right)$和$\varGamma' w\left( \zeta \right)$表示围岩的初始地应力和初始位移的分量, 所以在方程(19)中计算由于开挖引起的位移时应将其去除[27 ] ; 方程(17)~(20)在计算过程中假设接触面之间无滑动. ...
高原高寒隧道围岩冻胀行为及施工对策研究. [博士论文]
3
2011
... 根据现场大气、围岩实测温度、围岩及结构热力学试验, 估算围岩冻结深度.可知当原岩温度为10℃时, 冻结深度约为2 m[28 ] . 据此确定围岩冻胀圈和未冻围岩. ...
... 结合鹧鸪山隧道地质报告、室内岩石试验和点荷载试验数据[28 ] . 围岩、结构材料物理力学参数见表1 . ...
... 图6 为衬砌与冻胀圈接触面上的法向位移, 从图中可以看到: 数值法向位移解与解析法向位移解吻合得较好; 衬砌受到冻胀力, 产生了明显的冻胀变形.衬砌拱顶下沉较未受冻胀力时增大约37.4%.拱底隆起明显, 与未受冻胀力时相比增大约3 mm. 但是, 总的来说计算所得未冻胀和冻胀法向位移均较实测值偏小[28 ] , 这可能与未考虑开挖卸荷因子和塑性变形有关. ...
高原高寒隧道围岩冻胀行为及施工对策研究. [博士论文]
3
2011
... 根据现场大气、围岩实测温度、围岩及结构热力学试验, 估算围岩冻结深度.可知当原岩温度为10℃时, 冻结深度约为2 m[28 ] . 据此确定围岩冻胀圈和未冻围岩. ...
... 结合鹧鸪山隧道地质报告、室内岩石试验和点荷载试验数据[28 ] . 围岩、结构材料物理力学参数见表1 . ...
... 图6 为衬砌与冻胀圈接触面上的法向位移, 从图中可以看到: 数值法向位移解与解析法向位移解吻合得较好; 衬砌受到冻胀力, 产生了明显的冻胀变形.衬砌拱顶下沉较未受冻胀力时增大约37.4%.拱底隆起明显, 与未受冻胀力时相比增大约3 mm. 但是, 总的来说计算所得未冻胀和冻胀法向位移均较实测值偏小[28 ] , 这可能与未考虑开挖卸荷因子和塑性变形有关. ...
低温热力耦合下岩体椭圆孔(裂)隙中冻胀力与冻胀开裂特征研究
2018
低温热力耦合下岩体椭圆孔(裂)隙中冻胀力与冻胀开裂特征研究
2018
寒区隧道温度场数值分析研究. [硕士论文]
2018
寒区隧道温度场数值分析研究. [硕士论文]
2018
基于西原模型的圆形隧道黏弹-黏塑性解析解
2019
基于西原模型的圆形隧道黏弹-黏塑性解析解
2019
基于变形稳定的隧道结构可靠度分析. [博士论文]
2018
基于变形稳定的隧道结构可靠度分析. [博士论文]
2018
非轴对称荷载下圆形隧道弹性围岩应力解析解
2017
非轴对称荷载下圆形隧道弹性围岩应力解析解
2017