引言
气动弹性力学主要研究空气动力、弹性力和惯性力相互耦合作用下的动力学问题, 研究重点是弹性结构在气流中的颤振稳定性[1 -3 ] . 实现对飞行器结构颤振边界尤其是跨音速飞行条件下的颤振边界的精确预计, 需要建立精确的气动弹性数学模型. 传统的线性化气动力模型难以准确计算跨音速飞行时的非线性空气动力, 进而导致对飞行器结构跨音速气动弹性力学行为的预测产生误差.
计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] .
本工作采用非线性状态空间辨识方法, 推导出跨音速气动弹性系统的非线性降阶模型, 为了验证该非线性ROM在预测跨声速气动弹性问题的精确性, 给出了ROM的辨识过程并分别进行了气动力预测和气动弹性分析, 以期为建立适用于跨声速气动弹性系统的非线性降阶模型提供参考依据.
1 非线性状态空间模型降阶方法
不同于单自由度系统, 基于CFD的跨声速空气动力学系统是高维、非线性系统, 而且结构多模态运动和广义气动力输出是典型的非线性多输入/多输出动力学系统. 为了高效、高精度地预测跨音速非定常气动力、跨音速颤振边界以及极限环振荡(limit-cycle
oscillations, LCO)现象, 本节基于非线性状态空间法建立多输入/多输出的跨声速气动力降阶模型, 模型降阶过程分为线性状态空间模型辨识和非线性参数优化两部分.
1.1 线性状态空间模型的辨识
线性系统的辨识方法有很多种, 其中常见的有子空间辨识方法、ARMA方法以及基于特征系统实现算法的辨识方法等. 子空间辨识方法和ARMA模型对训练信号的设计要求较高(需要设定带宽和幅值), 且带宽和幅值的选择对结果影响较大. 特征系统实现算法只需要非定常气动力的单位脉冲响应数据, 过程简单且精度较高, 因此本文采用基于特征系统实现算法的辨识方法来辨识线性状态空间模型.
(1) $ \begin{eqnarray} \label{eq1} \left.\begin{array}{l} x_{\rm a} ( k+1)=A_{\rm a} x_{\rm a} (k)+B_{\rm a} u(k) \\ y_{\rm a} (k)=C_{\rm a} x_{\rm a} (k)+D_{\rm a} u(k)\\ \end{array}\right\} \end{eqnarray}$
其中, $x_{\rm a} \in {\bf R}^n$是状态向量, $u\in {\bf R}^m$是输入向量, $y_{\rm a} \in {\bf R}^l$是输出向量, $n$, $m$, $l$分别是状态变量、输入变量、输出变量的维数, 状态空间参数$(A_{\rm a} , B_{\rm a} , C_{\rm a} , D_{\rm a} )$是待辨识的变量. 基于ERA方法的状态空间系统辨识的过程如下:
(2) $ \begin{eqnarray} \label{eq2} \dot{{x}}=\lambda x \end{eqnarray}$
(3) $ \begin{eqnarray} \label{eq3} H=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {e^{\lambda \Delta t}} & {e^{2\lambda \Delta t}} & \cdots & {e^{m\lambda \Delta t}} \\ {e^{2\lambda \Delta t}} & {e^{3\lambda \Delta t}} & \cdots & {e^{\left( {m+1} \right)\lambda \Delta t}} \\ \vdots & \vdots & \ddots & \vdots \\ {e^{s\lambda \Delta t}} & {e^{\left( {s+1} \right)\lambda \Delta t}} & \cdots & {e^{\left( {s+m-1} \right)\lambda \Delta t}} \\ \end{array} }} \right] \end{eqnarray}$
由于矩阵的每一行都与第一行线性相关(如第二行是第一行的$e^{\lambda \Delta t}$倍), 该矩阵的秩$r=1$. 类似地, 矩阵的每一列都与第一列线性相关. 在这种情况下, 在延迟坐标中增广状态空间不会增大Hankel矩阵的秩, ROM将始终只含有一阶模态.
对于形式如公式(1)所示的线性状态空间模型, 其结构运动的离散时间脉冲响应如下式给出
(4) $ \begin{eqnarray} \label{eq4} u(k)=\left\{ \begin{array}{l@{\quad }l} I, & \mbox{for}\ k=0 \\ {\bf0}, &\mbox{for}\ k\in {\bf Z}^+ \\ \end{array} \right. \end{eqnarray}$
(5) $ \begin{eqnarray} \label{eq5} y_{\rm a}(k)=\left\{\begin{array}{l@{\quad }l} D, & \mbox{for}\ k=0 \\ CA^{k-1}B, & \mbox{for}\ k\in \bf{Z}^{+}\\ \end{array}\right. \end{eqnarray}$
由空气动力输出可分别建立如下形式的Hankel矩阵$H$和${H}'$
(6) $ \begin{eqnarray} \label{eq6} &&H=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {CB} & {CAB} & \cdots & {CA}^{m-s-1}{B} \\ {CAB} & {CA}^2B & \cdots & {CA}^{m-s}B \\ \vdots & \vdots & \ddots & \vdots \\ {CA}^{s-1}B & {CA}^s B & \cdots & {CA}^{m-2} B \\ \end{array} }} \right] \end{eqnarray}$
(7) $ \begin{eqnarray} \label{eq7} {H}'=\left[ {{\begin{array}{c@{\quad }c@{\quad }c@{\quad }c} {CAB} & {CA}^2B & \cdots & {CA}^{m-s}B \\ {CA}^2 B & {CA}^3B & \cdots & {CA}^{m-s+1}B \\ \vdots & \vdots & \ddots & \vdots \\ {CA}^sB & {CA}^{s+1}B & \cdots & {CA}^{m-1}B \\ \end{array} }} \right] \end{eqnarray}$
式中, $s$和$m$分别是Hankel矩阵的行数和Hankel矩阵中测量值的数目. 通过对$H$进行奇异值分解(singular value decomposition, SVD), 可以得到脉冲响应时间序列的主导时间模式
(8) $ \begin{eqnarray} \label{eq8} H=U\varSigma V^{\rm T}\approx U_r \varSigma _r V_r ^{\rm T} \end{eqnarray}$
其中, $r$表示对矩阵做秩为$r$的截断, $U$和$V$的列是特征时间序列, 能够描述跨越不同时间尺度的脉冲响应. 通过对Hankel矩阵$H$和$H'$进行SVD, 就可以得到$A$, $B$, $C$, $D$的低维近似
(9) $ \begin{eqnarray} \label{eq9} \left.\begin{array}{l} A_{\rm a} =\varSigma _r^{-1/2} U_r^{\rm T} H'V_r \varSigma _r^{-1/2} \\ B_{\rm a} =\varSigma _r^{1/2} V_r^{\rm T} \left[ \begin{array}{c} I_p \\ {\bf0}\\ \end{array}\right] \\ C_{\rm a} =\left[I_q \ \ {\bf0}\right]U_r \varSigma _r^{1/2} \\ D_{\rm a} =y\left( 0 \right) \\ \end{array}\right\} \end{eqnarray}$
1.2 非线性部分的优化
通过引入状态变量和输入变量的非线性函数, 可得到如下形式的非线性状态空间模型
(10) $ \begin{eqnarray} \label{eq10} \left.\begin{array}{l} x_{\rm a} \left( {k+1} \right)=A_{\rm a} x_{\rm a} (k)+B_{\rm a} u(k)+ E_{\rm a} \varPhi \left( {x_{\rm a} (k)} \right)+\\\qquad G_{\rm a}\varPhi \left( {u(k)} \right) \\ y(k)=C_{\rm a} x_{\rm a} (k)+D_{\rm a} u(k)+ F_{\rm a} \varPhi \left( {x_{\rm a} (k)} \right)+\\\qquad H_{\rm a} \varPhi \left( {u(k)} \right)\\ \end{array} \right\} \end{eqnarray}$
式中, $\varPhi \left( {x_{\rm a} (k)} \right)$和$\varPhi \left( {u(k)} \right)$分别是状态变量和输入变量的非线性函数, 非线性部分的系数$(E_{\rm a} , F_{\rm a} , G_{\rm a} , H_{\rm a} )$是待辨识的变量, 可通过广义优化[25 ] (Levenberg-Marquardt, LM)算法来确定非线性部分的系数. 本文选用神经网络辨识过程中最常见的双曲正切函数$\tanh \left( \cdot \right)$来表征上述非线性函数, 该函数被认为是一种能在线性和非线性行为间建立平衡的严格单调递增函数. 需要说明的是, 本文提出的非线性模型与Mannarino和Dowell提出的非线性降阶模型法相似[26 ] . 但在他们的研究中, 只考虑了与状态矢量有关的非线性贡献, 当空气动力非线性较强时, 该方法必须通过增加状态空间的阶数来提高辨识精度, 进而导致降阶模型的维数过高且可能出现过拟合问题. 在本文的研究中, 通过增加输入变量的非线性函数, 可在不增加状态空间维数的前提下显著提高空气动力的辨识精度.
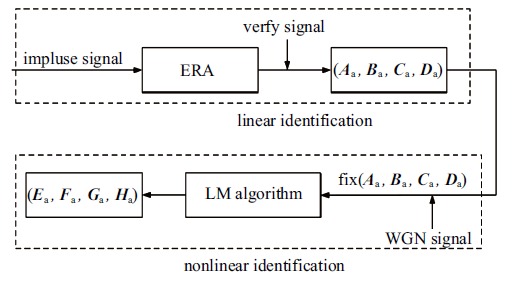
图1 所示是非线性状态空间模型的辨识过程. 首先, 以单位脉冲响应数据为训练样本, 通过ERA方法辨识线性状态空间参数. 其次, 以白噪声激励下的气动力输出数据为样本, 通过LM算法对非线性状态空间中的非线性参数进行优化, 进而获得最终的非线性降阶模型.
图 1
图 1
空气动力系统非线性ROM的辨识过程
Fig. 1
Identification process of nonlinear ROM for aerodynamic systems
1.3 基于非线性气动力降阶模型的气动弹性建模
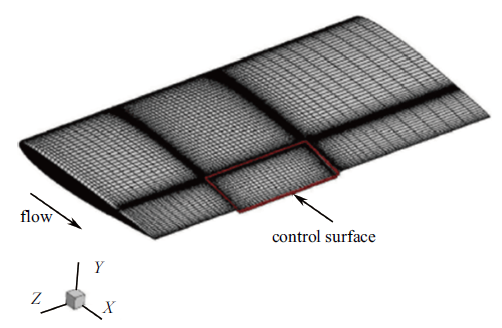
本节以BACT (benchmark active control technology)机翼为研究对象, 给出基于非线性气动力降阶模型的气动弹性建模过程. 该机翼为矩形机翼, 采用NACA 0012翼型[27 ] , 其风洞模型装配了后缘控制面以及上下表面扰流板. 本文研究中仅考虑后缘控制面作为气动伺服弹性输入.
图2 所示是BACT机翼的表面气动网格, 其结构动力学参数如表1 所示. 表中$M$, $S_\alpha$, $S_\beta$, $I_\alpha$, $S_{\alpha \beta }$, $K_h$, $K_\alpha$的定义见参考文献[28 ] .
图 2
图 2
BACT机翼模型
Fig. 2
BACT wing model
采用Lagrange方程方法和虚功原理, 建立如下气动弹性运动方程
(11) $ \begin{eqnarray} \label{eq11} && \left[ {{\begin{array}{*{20}c} M & {S_\alpha } \\ {S_\alpha } & {I_\alpha } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {\ddot{{h}}} \\ {\ddot{{\alpha }}} \\ \end{array} }} \right\}+\left[ {{\begin{array}{*{20}c} {2M\zeta _h \omega _h } & 0 \\ 0 & {2I_\alpha \zeta _\alpha \omega _\alpha } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {\dot{{h}}} \\ {\dot{{\alpha }}} \\ \end{array} }} \right\} +\\&&\left[ {{\begin{array}{*{20}c} {K_h } & 0 \\ 0 & {K_\alpha } \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} h \\ \alpha \\ \end{array} }} \right\}=-\left\{ {{\begin{array}{*{20}c} {S_\beta } \\ {S_{\alpha \beta } } \\ \end{array} }} \right\}\ddot{{\beta }}+q_\infty \left\{ {{\begin{array}{*{20}c} {Q_h } \\ {Q_\alpha } \\ \end{array} }} \right\} \end{eqnarray}$
其中, $h$和$\alpha $分别是BACT机翼的沉浮位移和俯仰角, $\beta $是控制面偏转角, $q_\infty $是飞行动压. 由于本文提出的非线性气动力降阶模型可用于预测考虑控制面输入的非线性气动力, 因此$\beta $是作为输入量. 非定常空气动力$Q_h $, $Q_\alpha $可通过下式计算
(12) $ \begin{eqnarray} \label{eq12} \left\{ {{\begin{array}{*{20}c} {Q_h } \\ {Q_\alpha } \\ \end{array} }} \right\}=\left\{ {{\begin{array}{*{20}c} {C_p \left( {x,y} \right){\rm d}x{\rm d}y} \\ {C_p \left( {x,y} \right)\left( {x_{\rm ae} -x} \right){\rm d}x{\rm d}y} \\ \end{array} }} \right\} \end{eqnarray}$
式中, $x_{\rm ae} $是弹性轴的位置. 基于模态坐标变换, 可将式(11)所示的气动弹性运动方程转化为以广义坐标表示的气动弹性运动方程
(13) $ \begin{eqnarray} \label{eq13} && M_{\xi \xi } \left\{ {{\begin{array}{*{20}c} {\ddot{{\xi }}_1 } \\ {\ddot{{\xi }}_2 } \\ \end{array} }} \right\}+C_{\xi \xi } \left\{ {{\begin{array}{*{20}c} {\dot{{\xi }}_1 } \\ {\dot{{\xi }}_2 } \\ \end{array} }} \right\}+K_{\xi \xi } \left\{ {{\begin{array}{*{20}c} {\xi _1 } \\ {\xi _2 } \\ \end{array} }} \right\}=\\&& -\varphi ^{\rm T}\left\{ {{\begin{array}{*{20}c} {S_\beta } \\ {S_{\alpha \beta } } \\ \end{array} }} \right\}\ddot{{\beta }}+q_\infty \varphi ^{\rm T}\left\{ {{\begin{array}{*{20}c} {Q_h } \\ {Q_\alpha } \\ \end{array} }} \right\} \end{eqnarray}$
式中, $\varphi $是振型矩阵, $M_{\xi \xi } $, $C_{\xi \xi } $, $K_{\xi \xi }$分别是广义质量矩阵、广义阻尼矩阵和广义刚度矩阵. 由于控制面的刚度不是无穷大, 不能认为控制面在控制输入下会立即做出响应. 在指定的控制输入下, 控制面的运动可认为是一种有阻尼单自由度系统的受迫振动, 其运动微分方程的数学表达式如下
(14) $ \begin{eqnarray} \label{eq14} \ddot{{\beta }}+2\omega _\beta \zeta _\beta \dot{{\beta }}+\omega _\beta ^2 \beta =k_\beta \omega _\beta ^2 \beta _c \end{eqnarray}$
其中, $k_\beta $, $\zeta _\beta $, $\omega _\beta $, $\beta _c $分别是增益、阻尼比、固有频率和控制指令, 参数值见文献[28 ] . 式(13)表达的气动弹性模型在包含了后缘控制面执行机构后可改写为
(15) $ \begin{eqnarray} \label{eq15} \dot{{x}}_s =A_s x_s +B_c \beta _c +q_\infty B_q Q_{\xi \xi } \left( {\xi _1 ,\xi _2 ,\beta } \right) \end{eqnarray}$
状态变量$x_s =\left[ {{\begin{array}{*{20}c} {\xi _1 } \ \ & {\xi _2 } \ \ & \beta \ \ & {\dot{{\xi }}_1 } \ \ & {\dot{{\xi }}_2 } \ \ & {\dot{{\beta }}} \\ \end{array} }} \right]^{\rm T}$, 矩阵$A_s $, $B_c $, $B_q $的定义如式(16)所示
(16) $ \begin{eqnarray} \label{eq16} \left.\begin{array}{l} A_s =\left[ \begin{array}{c@{\quad }c} {\bf 0}_{3\times3} & I_3 \\ -M^{-1}K & -M^{-1}C\\ \end{array}\right], \ B_c =\left[ \begin{array}{c} {\bf 0}_{3\times 1}\\ -M^{-1}\tilde{{B}}\\ \end{array}\right]\\ B_q =\left[ \begin{array}{c} {\bf 0}_{3\times 2}\\ -M^{-1}\left[I_2; {\bf 0}_{1\times 2} \right]\\ \end{array}\right]\\ \end{array}\right\} \end{eqnarray}$
如式(15)所示, 广义空气动力$Q_{\xi \xi } \left( {\xi _1 ,\xi _2 ,\beta }\right)$是以沉浮模态$\xi _1 $、俯仰模态$\xi _2 $和偏转角$\beta $为自变量的非线性函数, 因此本文的气动力降阶模型中状态变量包括沉浮模态、俯仰模态和控制面偏转模态. 而在气动弹性仿真中, 将$\beta $角度置零. 基于本文所提出的非线性ROM可高效计算广义气动力.
2 算例验证
本节通过识别基于CFD的空气动力系统来研究非线性ROM在给定马赫数下对线性和非线性气动弹性行为预测的精确性. 非定常空气动力训练样本由基于雷诺平均Navier-Stokes方程的开源CFD求解器求出. CFD求解器使用源代码求解, 当马赫数$M=0.71$时, 正弦激励信号幅值为0.05, 频率为21.11 hz, 流体的无量纲时间步长$\Delta \tau =5.0$, 转化为物理时间步长为$9.769 4\times 10^{-4}$ s.
2.1 非线性降阶模型的辨识
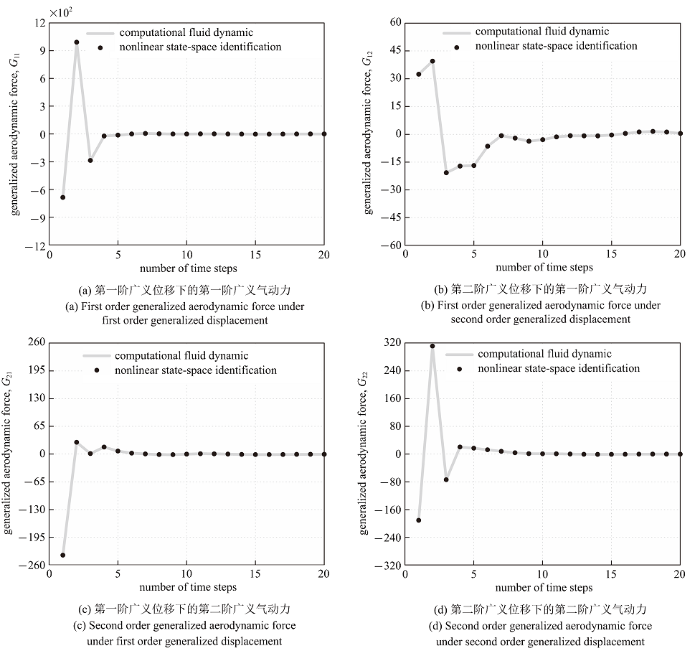
首先, 基于CFD产生的非定常空气动力的单位脉冲响应数据, 采用特征系统实现算法对非线性状态空间模型的线性动力学参数进行系统辨识. 图3 (a) ~图3 (d)分别给出了由状态空间辨识方法和CFD得到的空气动力单位脉冲响应, 图中$G_{ij}$代表对应第$j$个模态输入对第$i$个广义气动力输出的影响.
如前文所述, 建立该非线性ROM的关键在于对线性动力学部分的辨识. 在辨识过程中线性部分的系统阶数的选择对模型的精度具有较大影响. 为了保证仿真中降阶模型的收敛性并获得线性部分的最优状态空间方程, 需要通过ERA算法在较大的阶数范围(最大可达20阶)内进行相应的参数估计, 识别每个ERA模型的动力学线性部分, 并计算这些已辨识的线性部分的相对误差. 真实信号和预估信号的百分比误差如式(17)定义, 选择百分比误差的最小值所对应的系统阶数来确定系统的最优阶数, 最后确定状态空间方程. 通过对动力学系统线性部分的辨识, 得到模型的最优阶数$r=10$.
(17) $ \begin{eqnarray} \label{eq17} {\rm ERA_error}_{k+1} ={\rm ERA_error}_k +\sum {\left( {\frac{y_{\rm ROM} -y_{\rm CFD} }{\max \left( {y_{\rm CFD} } \right)}} \right)} ^2 \end{eqnarray}$
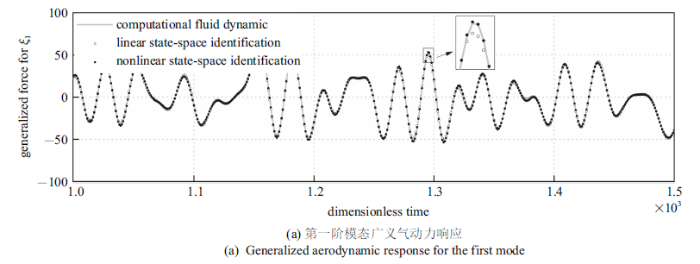
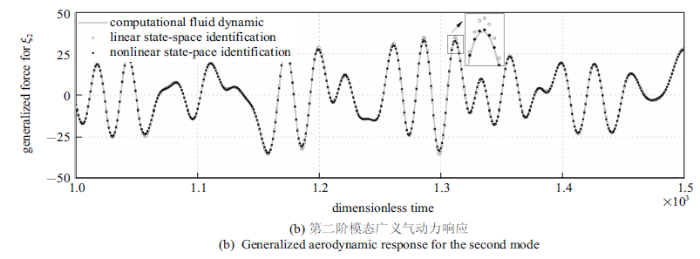
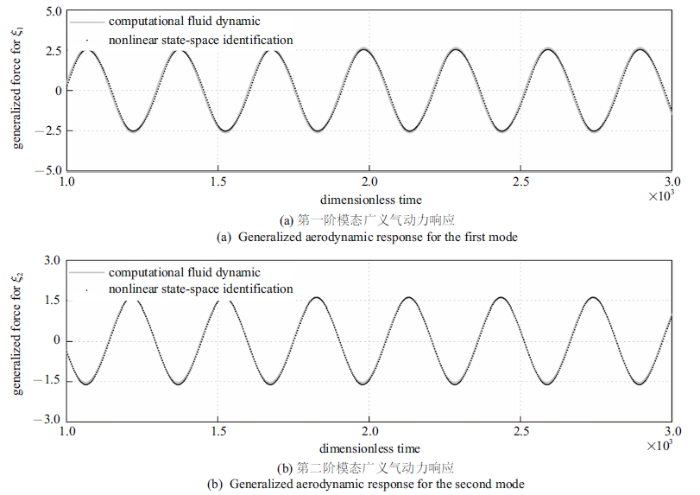
实现该方法的另一个关键问题是激励函数的选择. 已有研究表明, 滤波高斯白噪声(filtered Gaussian white noise, FWGN)函数是这类应用中的最优函数[14 ] . 本文的非线性ROM辨识是基于CFD空气动力系统在FWGN激励下所产生的非定常训练数据.当马赫数为0.71时, BACT机翼受非定常模态激励(如图4 所示的白噪声激励)时会产生激波振荡. 因此, 非线性来源于激波运动产生的非线性空气动力. 图4 给出了线性/非线性ROM预测的沉浮和俯仰模态所对应的广义空气动力, 并与直接CFD方法进行了对比. 如图所示, 线性状态空间辨识方法虽然能够较好的表达沉浮和俯仰模态受FWGN激励时的空气动力相位特征, 但在广义气动力较大峰值处的辨识精度要低于本文提出的非线性降阶模型. 为了验证非线性ROM预测结构模态受其他激励下的空气动力学特征,本文研究了在$M_\infty =0.71$时沉浮和俯仰模态受正弦激励的广义空气动力输出响应. 如图5 所示, 广义空气动力的对比表明了该非线性状态空间辨识方法能够与直接CFD计算结果相吻合.
图 3
图 3
脉冲激励下的空气动力比较
Fig. 3
Comparison of aerodynamic forces under the impulse excitation
图 4
图 4
FWGN激励下直接CFD模型输出和非线性ROM输出对比
Fig. 4
Direct CFD model outputs vs nonlinear ROM outputs under the FWGN excitation
图 4
图 4
FWGN激励下直接CFD模型输出和非线性ROM输出对比(续)
Fig. 4
Direct CFD model outputs vs nonlinear ROM outputs under the FWGN excitation (continued)
为了将线性与非线性方法预测能力进行对比, 引入CFD结果与ROM结果的方差(variance accounted for, VAF), 其定义式如下
(18) $ \begin{eqnarray} \label{eq18} v=\max \left( {1-\frac{{\rm var}\left( {y_{\rm CFD} -y_{\rm ROM} } \right)}{{\rm var}\left( {y_{\rm CFD} } \right)},0} \right)\times 100\% \end{eqnarray}$
若两种信号相同, 则VAF为100%; 若两种信号不同, 则VAF会变低. 线性与非线性方法的VAF值如表2 所示. 由表可知, 非线性方法能够提高辨识精度.
图 5
图 5
正弦激励下直接CFD模型输出和非线性ROM输出对比
Fig. 5
Direct CFD model outputs vs nonlinear ROM outputs under the sinusoidal excitation
为了说明非线性降阶模型模型的计算效率, 本文给出了白噪声作为训练信号时, 对非线性ROM和CFD方法计算气动弹性响应所需的时间进行了比较, 马赫数为0.71时,采用CFD、线性ROM和非线性ROM方法的气动弹性响应时间分别为187 h, 39 s和373 s. 说明气动弹性降阶模型可在较为精确预测气动弹性响应的前提下, 大幅度缩短计算所需时间. 由于Mannarino和Dowell提出的方法中, 同样分为线性状态空间模型的辨识和非线性部分的优化两步, 计算时间是两者的叠加, 因此计算效率与文中的ROM方法是相当的.
2.2 NACA0012翼型非定常气动力验证
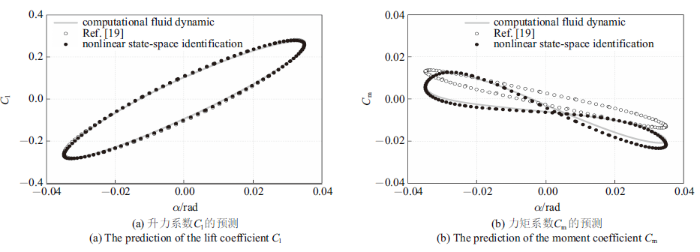
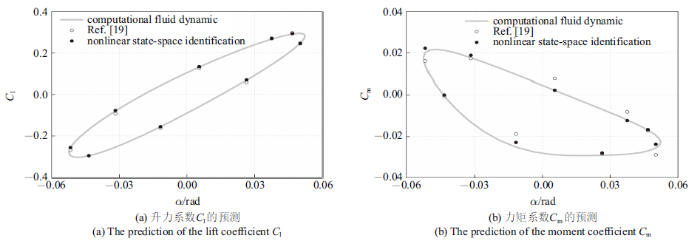
为了验证ROM预测非定常气动力的精度, 本文以NACA0012翼型的非定常气动力计算为例, 分别计算了折合频率$k_{\rm rf} =0.08$和$k_{\rm rf} =0.2$的两种谐波激励下的升力系数和力矩系数, 并与直接CFD方法和Mannarino等提出的方法进行对比. 折合频率$k_{\rm rf} $的定义式为
(19) $ \begin{eqnarray} \label{eq19} k_{\rm rf} =\frac{\omega \cdot c}{2V_\infty } \end{eqnarray}$
式中$\omega $, $c$, $V_\infty $分别是俯仰角频率、翼型弦长和来流速度. 如图6 和图7 所示, 由非线性ROM计算得到的升力系数$C_{\rm l} $和力矩系数$C_{\rm m} $与Mannarino等[19 ] 提出的方法相比, 本文提出的方法与CFD结果的吻合度更高, 尤其是在力矩系数$C_{\rm m} $的预测方面.
图 6
图 6
$k_{\rm rf} =0.08$时谐波激励下NACA 0012翼型的ROM验证
Fig. 6
The ROM validation of an NACA 0012 airfoil under harmonic excitation with $k_{\rm rf} =0.08$
图 7
图 7
$k_{\rm rf} =0.2$时谐波激励下NACA 0012翼型的ROM验证
Fig. 7
The ROM validation of an NACA 0012 airfoil under harmonic excitation with $k_{\rm rf} =0.2$
2.3 BACT机翼跨音速颤振分析
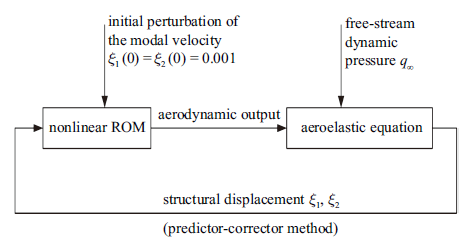
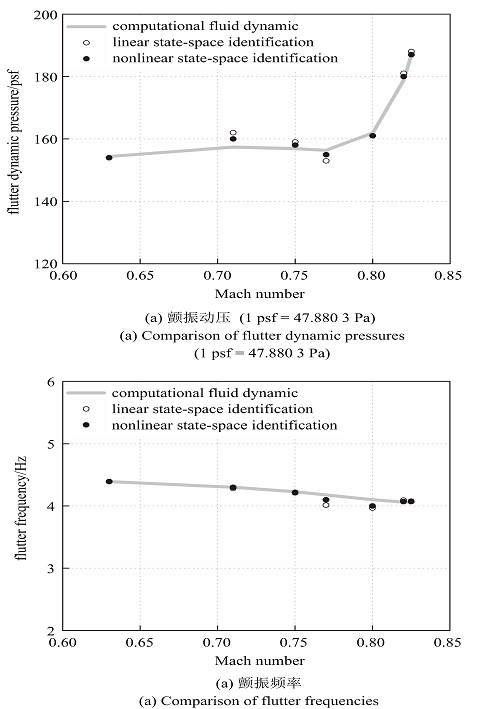
为了研究非线性ROM对BACT机翼颤振边界的预测精度, 在不同马赫数下($M_\infty = 0.63$, 0.71, 0.75, 0.77, 0.80, 0.82, 0.825)分别进行了基于非线性状态空间方法的系统辨识, 建立了不同的降阶模型, 并计算了颤振边界. 颤振计算方法为时域计算, 求解过程框图如图8 所示, 首先给定模态速度的初始扰动$\dot{{\xi}}_1( 0)=\dot{{\xi }}_2(0)=0.001$,代入到非线性ROM方程(10)中求出气动力输出, 然后将来流动压$q_\infty $和气动力输出代入到气动弹性方程(15), 用预估-校正法进行流固耦合计算, 得到结构位移$\xi _1 ,\xi _2 $, 再将其代入非线性ROM方程中进行迭代计算, 最终得到收敛且稳定的结构位移矩阵. 其中预估-校正法分为预估步和校正步, 首先由预估步计算出模态解$\tilde{{x}}^{n+1}$, 将预估步的解作用于结构表面, 在时间步为$n$+1时, 流场收敛于该解, 能够计算出新的广义力$\bar{{Q}}^{n+1}$, 然后由校正步计算出$x^{n+1}$. 为了验证提出的ROM法的有效性, 将非线性ROM的颤振结果与CFD结果以及线性ROM结果进行了比较, 其中线性ROM由相同的空气动力学系统训练数据的输入和输出来辨识. 图9 表示通过直接CFD模型、线性状态空间辨识和非线性状态空间辨识计算出的BACT机翼颤振动压和颤振频率的对比. 如图所示, 通过非线性状态空间辨识计算得到的颤振边界与直接CFD法计算得到的结果吻合较好. 而与非线性状态空间辨识相比, 由线性状态空间辨识确定的颤振边界精度略低. 从图中还可以得到颤振动压和颤振频率的相对误差, 相对误差$e$定义式为[15 ,29 ]
(20) $ \begin{eqnarray} \label{eq20} e=\frac{\left| {q_{\rm CFD} -q_{\rm ROM} } \right|}{q_{\rm CFD} } \end{eqnarray}$
图 8
图 8
颤振计算方法框图
Fig. 8
Flutter calculation method block diagram
式中$q_{\rm CFD} $, $q_{\rm ROM} $分别是通过直接CFD法和线性/非线性状态空间辨识计算出的颤振动压. 图9 表明了通过非线性状态空间辨识计算出的颤振动压和颤振频率的相对误差始终低于2%, 线性状态空间辨识计算结果的相对误差始终低于3%. 该结果说明非线性状态空间辨识比线性状态空间辨识更能准确地表征BACT模型的气动弹性行为.
图 9
图 9
BACT机翼颤振边界对比
Fig. 9
Comparison of the flutter boundaries of the BACT wing
2.4 极限环振荡分析
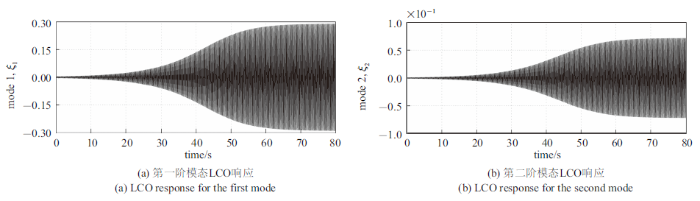
极限环振荡是另一种非常重要的非线性气动弹性现象[30 -33 ] , 其非线性来源于气动力的非线性. 由图9 可知, 当马赫数为0.71时, BACT机翼的颤振动压为160 psf. 因此, 当飞行动压高于颤振临界动压(即分叉点)时, 系统会发生极限环振荡. 当前的非线性ROM具有预测这一非线性气动弹性现象的能力, 可将其应用到BACT机翼极限环振荡现象的研究中. 图10 给出了在$M_\infty =0.825$, $q_\infty =190$ psf下结构两阶模态的LCO响应. 使用的模态速度的初始扰动$\dot{{\xi }}_1 \left( 0 \right)=\dot{{\xi }}_2 \left( 0 \right)=0.001$. 由图可见, 受空气动力非线性的影响, 当来流动压为190 psf时, BACT机翼发生极限环振荡.
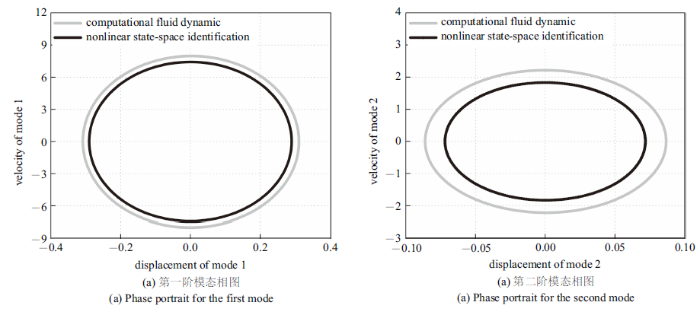
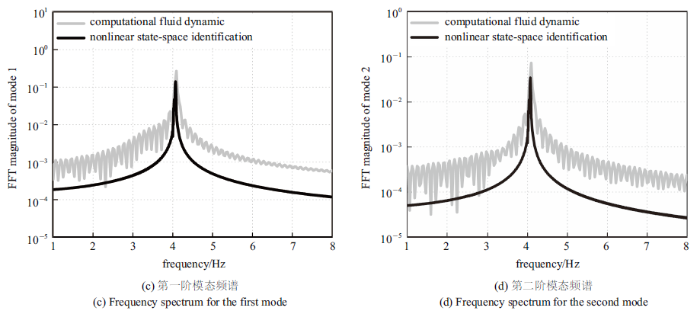
为进一步验证该非线性ROM在预测BACT机翼LCO现象时的精度, 将非线性ROM计算出的LCO相图和频谱同直接CFD方法计算出的结果进行了对比. 由图11 可知, 由非线性ROM与CFD方法计算出的两阶结构模态LCO频率的相对误差几乎为零. 而由两阶结构模态相图可以看出, 与CFD结果相比, 两阶结构模态的LCO幅值相对误差分别为19.0%和25.3%. 极限环振荡的幅值相对误差较大的原因在于, 在非线性状态空间辨识的过程中, 并未刻意设计训练信号的幅值和带宽以提高其在预测LCO现象时的精度.
图 10
图 10
非线性ROM法的LCO响应
Fig. 10
LCO response via the nonlinear ROM method
图 11
图 11
极限环振荡的幅值和频率比较
Fig. 11
Comparison of the amplitude and frequency of the limit-cycle oscillation
图 11
图 11
极限环振荡的幅值和频率比较(续)
Fig. 11
Comparison of the amplitude and frequency of the limit-cycle oscillation (continued)
3 结论
本文提出了一种基于非线性状态空间辨识的气动弹性模型降阶方法, 实现跨音速气动弹性行为的高效预测. 为了验证该降阶模型在预测跨音速气动 弹性力学行为的精确性, 本文以三维机翼为研究对象, 分别从基于非线性降阶模型的气动力辨识、跨声速颤振边界计算和极限环振荡预测三方面进行了算例验证. 对比ROM和CFD在$M_\infty = 0.63$, 0.71, 0.75, 0.77, 0.80, 0.82, 0.825时的颤振边界, 并比较了非线性ROM和直接CFD计算出的LCO响应. 结果表明, 该ROM能够与CFD方法得到的空气动力学响应相吻合, 通过非线性ROM计算出颤振动压和颤振频率的相对误差始终低于2%. 在误差允许范围内, 该ROM能够得到与传统CFD方法计算气动弹性问题相一致的结果, 从而降低计算成本. 在后续的工作中, 需要进一步提高极限环振荡幅值的精度, 计算在不同来流动压条件下极限环的变化趋势, 并考虑变马赫数的影响, 研究具有马赫数自适应的非线性降阶模型.
参考文献
View Option
[1]
杨超 . 飞行器气动弹性原理 . 北京 : 北京航空航天大学出版社 , 2016 : 1 -10
[本文引用: 1]
( Yang Chao Principles of Aeroelasticity for Aircraft. Beijing : Beihang University Press , 2016 : 1 -10 (in Chinese))
[本文引用: 1]
[2]
叶柳青 , 叶正寅 . 激波主导流动下壁板的热气动弹性稳定性理论分析
力学学报 , 2018 ,50 (2 ):222 -226
( Ye Liuqing Ye Zhengyin . Aeroelastic stability analysis of heated flexible panel in shock-dominated flows
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (2 ):222 -226 (in Chinese))
[3]
刘楚源 , 刘泽森 , 宋汉文 . 基于主动控制策略的机翼颤振特性模拟
力学学报 , 2019 ,51 (2 ):334 -335
[本文引用: 1]
( Liu Chuyuan Liu Zesen Song Hanwen . The simulation of airfoil flutter characteristic based on active control strategy
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,51 (2 ):334 -335 (in Chinese))
[本文引用: 1]
[4]
Hall KC Thomas JP Dowell EH . Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows
AIAA Journal , 2000 ,38 (10 ):1853 -1862
[本文引用: 1]
[5]
Falkiewicz NJ Cesnik CES Crowell AR , et al . Reduced-order aerothermoelastic framework for hypersonic vehicle control simulation
AIAA Journal , 2011 ,49 (8 ):1625 -1646
[6]
Xie D Xu M Dowell EH . Proper orthogonal decomposition reduced-order model for nonlinear aeroelastic oscillations
AIAA Journal , 2014 ,52 (2 ):229 -241
[7]
Zhou Q Li DF Ronch AD , et al . Computational fluid dynamic-based transonic flutter suppression with control delay
Journal of Fluids and Structures , 2016 ,66 :183 -206
[本文引用: 1]
[8]
Silva WA Bartels RE . Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3D v6.0 code
Journal of Fluids and Structures , 2004 ,19 (6 ):729 -745
[本文引用: 2]
[9]
Hall KC Thomas JP Clark WS . Computation of unsteady nonlinear flows in cascades using a harmonic balance technique
AIAA Journal , 2002 ,40 (5 ):879 -886
[本文引用: 1]
[10]
Yao W Marques S . Prediction of transonic limit-cycle oscillations using an aeroelastic harmonic balance method
AIAA Journal , 2015 ,53 (7 ):2040 -2051
[本文引用: 1]
[11]
Winter M Breitsamter C . Neurofuzzy-model-based unsteady aerodynamic computations across varying freestream conditions
AIAA Journal , 2016 ,54 (9 ):2705 -2720
[本文引用: 1]
[12]
Balajewicz M Nitzsche F Feszty D . Application of multi-input volterra theory to nonlinear multi-degree-of-freedom aerodynamic systems
AIAA Journal , 2010 ,48 (1 ):56 -62
[本文引用: 1]
[13]
Silva WA . Identification of nonlinear aeroelastic systems based on the volterra theory: Progress and opportunities
Nonlinear Dynamics , 2005 ,39 (1-2 ):25 -62
[本文引用: 1]
[14]
Huang R Hu HY Zhao YH . Nonlinear reduced-order modeling for multiple-input/multiple-output aerodynamic systems
AIAA Journal , 2014 ,52 (6 ):1219 -1231
[本文引用: 2]
[15]
Huang R Li HK Hu HY , et al . Open/closed-loop aeroservoelastic predictions via nonlinear, reduced-order aerodynamic models
AIAA Journal , 2015 ,53 (7 ):1812 -1824
[本文引用: 2]
[16]
Glaz B Friedmann PP Liu L , et al . Reduced-order nonlinear unsteady aerodynamic modeling using a surrogate-based recurrence framework
AIAA Journal , 2010 ,48 (10 ):2418 -2429
[本文引用: 1]
[17]
Liu H Hu HY Zhao YH , et al . Efficient reduced order modeling of unsteady aerodynamics robust to flight parameter variations
Journal of Fluids and Structures , 2014 ,49 :728 -741
[18]
Kim T . Parametric model reduction for aeroelastic systems. Invariant aeroelastic modes
Journal of Fluids and Structures , 2016 ,65 :196 -216
[本文引用: 1]
[19]
Kou JQ Zhang WW . A hybrid reduced-order framework for complex aeroelastic simulations
Aerospace Science and Technology , 2019 ,84 :880 -881
[本文引用: 2]
[20]
Li K Kou JQ Zhang WW . Deep neural network for unsteady aerodynamic and aeroelasitc modeling across multiple Mach numbers
Nonlinear Dynamics , 2019 ,96 :2157 -2159
[本文引用: 1]
[21]
Silva WA . Application of nonlinear systems theory to transonic unsteady aerodynamic responses
Journal of Aircraft , 1993 ,30 (5 ):660 -668
[本文引用: 1]
[22]
Balajewicz M Dowell EH . Reduced-order modeling of flutter and limit-cycle oscillations using the sparse volterra series
Journal of Aircraft , 2012 ,49 (6 ):1803 -1812
[本文引用: 1]
[23]
郑保敬 , 梁钰 , 高效伟 等 . 功能梯度材料动力学问题的POD模型降阶分析
力学学报 , 2018 ,50 (4 ):788 -794
[本文引用: 1]
( Zheng Baojing Liang Yu Gao Xiaowei , et al . Analysis for dynamic response of functionally graded materials using POD based reduced order model
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (4 ):788 -794 (in Chinese))
[本文引用: 1]
[24]
Huang R Liu HJ Yang ZJ , et al . Nonlinear reduced-order models for transonic aeroelastic and aeroservoelastic problems
AIAA Journal , 2018 ,56 (9 ):3719
[本文引用: 1]
[25]
Moré JJ . The Levenberg-marquardt algorithm: Implementation and theory
Numerical Analysis , 1978 : 105 -116
[本文引用: 1]
[26]
Mannarino A Dowell EH . Reduced-order models for computational-fluid-dynamics-based nonlinear aeroelastic problems
AIAA Journal , 2015 ,53 (9 ):2671 -2685
[本文引用: 1]
[27]
胡海岩 , 赵永辉 , 黄锐 . 飞机结构气动弹性分析与控制研究
力学学报 , 2016 ,48 (1 ):9 -14
[本文引用: 1]
( Hu Haiyan Zhao Yonghui Huang Rui . Studies on aeroelastic analysis and control of aircraft structures
Chinese Journal of Theoretical and Applied Mechanics , 2016 ,48 (1 ):9 -14 (in Chinese))
[本文引用: 1]
[28]
Waszak MR . Modeling the benchmark active control technology wind-tunnel model for application to flutter suppression
// 21st Atmospheric Flight Mechanics Conference , 1996 : 1996 -3437
[本文引用: 2]
[29]
黄锐 . 亚/跨音速飞机结构气动弹性控制及其实验研究. [博士论文]
南京: 南京航空航天大学 , 2014 : 108 -111
[本文引用: 1]
( Huang Rui . Aeroelastic control of aircraft structure in subsonic/transonic flows and its testification. [PhD Thesis]
Nanjing: Nanjing University of Aeronautics and Astronautics , 2014 : 108 -111 (in Chinese))
[本文引用: 1]
[30]
Walter AS . Simultaneous excitation of multiple-input/multiple-output CFD-based unsteady aerodynamic systems
Journal of Aircraft , 2008 ,45 (4 ):1267 -1269
[本文引用: 1]
[31]
Brent AM Jack JM . Efficient fluid thermal structural time marching with computational fluid dynamics
AIAA Journal , 2018 ,56 (9 ):3610 -3611
[32]
Tomer R Peretz PF . Multifidelity coKriging for high-dimensional output functions with application to hypersonic airloads computation
AIAA Journal , 2018 ,56 (8 ):3060 -3061
[33]
Ryan JK Carlos ESC . Nonlinear thermal reduced-order modeling for hypersonic vehicles
AIAA Journal , 2017 ,55 (7 ):2358 -2359
[本文引用: 1]
1
2016
... 气动弹性力学主要研究空气动力、弹性力和惯性力相互耦合作用下的动力学问题, 研究重点是弹性结构在气流中的颤振稳定性[1 -3 ] . 实现对飞行器结构颤振边界尤其是跨音速飞行条件下的颤振边界的精确预计, 需要建立精确的气动弹性数学模型. 传统的线性化气动力模型难以准确计算跨音速飞行时的非线性空气动力, 进而导致对飞行器结构跨音速气动弹性力学行为的预测产生误差. ...
1
2016
... 气动弹性力学主要研究空气动力、弹性力和惯性力相互耦合作用下的动力学问题, 研究重点是弹性结构在气流中的颤振稳定性[1 -3 ] . 实现对飞行器结构颤振边界尤其是跨音速飞行条件下的颤振边界的精确预计, 需要建立精确的气动弹性数学模型. 传统的线性化气动力模型难以准确计算跨音速飞行时的非线性空气动力, 进而导致对飞行器结构跨音速气动弹性力学行为的预测产生误差. ...
激波主导流动下壁板的热气动弹性稳定性理论分析
2018
激波主导流动下壁板的热气动弹性稳定性理论分析
2018
基于主动控制策略的机翼颤振特性模拟
1
2018
... 气动弹性力学主要研究空气动力、弹性力和惯性力相互耦合作用下的动力学问题, 研究重点是弹性结构在气流中的颤振稳定性[1 -3 ] . 实现对飞行器结构颤振边界尤其是跨音速飞行条件下的颤振边界的精确预计, 需要建立精确的气动弹性数学模型. 传统的线性化气动力模型难以准确计算跨音速飞行时的非线性空气动力, 进而导致对飞行器结构跨音速气动弹性力学行为的预测产生误差. ...
基于主动控制策略的机翼颤振特性模拟
1
2018
... 气动弹性力学主要研究空气动力、弹性力和惯性力相互耦合作用下的动力学问题, 研究重点是弹性结构在气流中的颤振稳定性[1 -3 ] . 实现对飞行器结构颤振边界尤其是跨音速飞行条件下的颤振边界的精确预计, 需要建立精确的气动弹性数学模型. 传统的线性化气动力模型难以准确计算跨音速飞行时的非线性空气动力, 进而导致对飞行器结构跨音速气动弹性力学行为的预测产生误差. ...
Proper orthogonal decomposition technique for transonic unsteady aerodynamic flows
1
2000
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Reduced-order aerothermoelastic framework for hypersonic vehicle control simulation
2011
Proper orthogonal decomposition reduced-order model for nonlinear aeroelastic oscillations
2014
Computational fluid dynamic-based transonic flutter suppression with control delay
1
2016
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Development of reduced-order models for aeroelastic analysis and flutter prediction using the CFL3D v6.0 code
2
2004
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
... [8 ](eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Computation of unsteady nonlinear flows in cascades using a harmonic balance technique
1
2002
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Prediction of transonic limit-cycle oscillations using an aeroelastic harmonic balance method
1
2015
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Neurofuzzy-model-based unsteady aerodynamic computations across varying freestream conditions
1
2016
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Application of multi-input volterra theory to nonlinear multi-degree-of-freedom aerodynamic systems
1
2010
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Identification of nonlinear aeroelastic systems based on the volterra theory: Progress and opportunities
1
2005
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Nonlinear reduced-order modeling for multiple-input/multiple-output aerodynamic systems
2
2014
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
... 实现该方法的另一个关键问题是激励函数的选择. 已有研究表明, 滤波高斯白噪声(filtered Gaussian white noise, FWGN)函数是这类应用中的最优函数[14 ] . 本文的非线性ROM辨识是基于CFD空气动力系统在FWGN激励下所产生的非定常训练数据.当马赫数为0.71时, BACT机翼受非定常模态激励(如图4 所示的白噪声激励)时会产生激波振荡. 因此, 非线性来源于激波运动产生的非线性空气动力. 图4 给出了线性/非线性ROM预测的沉浮和俯仰模态所对应的广义空气动力, 并与直接CFD方法进行了对比. 如图所示, 线性状态空间辨识方法虽然能够较好的表达沉浮和俯仰模态受FWGN激励时的空气动力相位特征, 但在广义气动力较大峰值处的辨识精度要低于本文提出的非线性降阶模型. 为了验证非线性ROM预测结构模态受其他激励下的空气动力学特征,本文研究了在$M_\infty =0.71$时沉浮和俯仰模态受正弦激励的广义空气动力输出响应. 如图5 所示, 广义空气动力的对比表明了该非线性状态空间辨识方法能够与直接CFD计算结果相吻合. ...
Open/closed-loop aeroservoelastic predictions via nonlinear, reduced-order aerodynamic models
2
2015
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
... 为了研究非线性ROM对BACT机翼颤振边界的预测精度, 在不同马赫数下($M_\infty = 0.63$, 0.71, 0.75, 0.77, 0.80, 0.82, 0.825)分别进行了基于非线性状态空间方法的系统辨识, 建立了不同的降阶模型, 并计算了颤振边界. 颤振计算方法为时域计算, 求解过程框图如图8 所示, 首先给定模态速度的初始扰动$\dot{{\xi}}_1( 0)=\dot{{\xi }}_2(0)=0.001$,代入到非线性ROM方程(10)中求出气动力输出, 然后将来流动压$q_\infty $和气动力输出代入到气动弹性方程(15), 用预估-校正法进行流固耦合计算, 得到结构位移$\xi _1 ,\xi _2 $, 再将其代入非线性ROM方程中进行迭代计算, 最终得到收敛且稳定的结构位移矩阵. 其中预估-校正法分为预估步和校正步, 首先由预估步计算出模态解$\tilde{{x}}^{n+1}$, 将预估步的解作用于结构表面, 在时间步为$n$+1时, 流场收敛于该解, 能够计算出新的广义力$\bar{{Q}}^{n+1}$, 然后由校正步计算出$x^{n+1}$. 为了验证提出的ROM法的有效性, 将非线性ROM的颤振结果与CFD结果以及线性ROM结果进行了比较, 其中线性ROM由相同的空气动力学系统训练数据的输入和输出来辨识. 图9 表示通过直接CFD模型、线性状态空间辨识和非线性状态空间辨识计算出的BACT机翼颤振动压和颤振频率的对比. 如图所示, 通过非线性状态空间辨识计算得到的颤振边界与直接CFD法计算得到的结果吻合较好. 而与非线性状态空间辨识相比, 由线性状态空间辨识确定的颤振边界精度略低. 从图中还可以得到颤振动压和颤振频率的相对误差, 相对误差$e$定义式为[15 ,29 ] ...
Reduced-order nonlinear unsteady aerodynamic modeling using a surrogate-based recurrence framework
1
2010
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Efficient reduced order modeling of unsteady aerodynamics robust to flight parameter variations
2014
Parametric model reduction for aeroelastic systems. Invariant aeroelastic modes
1
2016
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
A hybrid reduced-order framework for complex aeroelastic simulations
2
2019
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
... 式中$\omega $, $c$, $V_\infty $分别是俯仰角频率、翼型弦长和来流速度. 如图6 和图7 所示, 由非线性ROM计算得到的升力系数$C_{\rm l} $和力矩系数$C_{\rm m} $与Mannarino等[19 ] 提出的方法相比, 本文提出的方法与CFD结果的吻合度更高, 尤其是在力矩系数$C_{\rm m} $的预测方面. ...
Deep neural network for unsteady aerodynamic and aeroelasitc modeling across multiple Mach numbers
1
2019
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Application of nonlinear systems theory to transonic unsteady aerodynamic responses
1
1993
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Reduced-order modeling of flutter and limit-cycle oscillations using the sparse volterra series
1
2012
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
功能梯度材料动力学问题的POD模型降阶分析
1
2018
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
功能梯度材料动力学问题的POD模型降阶分析
1
2018
... 计算流体力学(computational fluid dynamics, CFD)方法为精确模拟跨音速气动弹性行为提供了高保真分析手段. 然而, 要获得精确的仿真结果, 基于CFD技术的跨音速气动弹性分析需要消耗大量的计算资源且难以用于控制律设计, 使得该方法的应用受到了限制. 为了应对这项挑战, 近年来国内外学者围绕如何建立高效且高精度的跨声速气动弹性降阶模型(reduced-order model, ROM)开展研究, 目的是发展低维、精确的气动力降阶模型来进行跨音速气动弹性分析, 从而在数量级上减少计算成本. 当前的气动力降阶模型研究可分为如下两类: 一类是基于流场特征分析方法(如本征正交分解法[4 -7 ] 、均衡实现算法[8 ] 、谐波平衡法[9 -10 ] ); 另一类是基于系统辨识方法(如递归局部线性神经模糊模型[11 ] 、Volterra 级数法[12 -13 ] 、Wiener模型法[14 -15 ] 、Kriging代理法[16 -18 ] 、特征系统实现算法[8 ] (eigensystem realization algorithm, ERA)). 相对于基于流场特征分析方法, 基于系统辨识方法受到了更为广泛的关注. 例如, 西北工业大学张伟伟等[19 ] 提出了一种混合降阶模型, 该模型基于完全耦合的子系统, 非线性输出反馈到线性和非线性系统中, 从而能够更精确地拟合非定常流中的物理现象. 该团队还提出了一种基于长短时记忆网络的非定常空气动力ROM, 该模型能够处理大量的训练样本, 且能够预测马赫数在较大范围内的气动载荷[20 ] . NASA兰利研究中心Silva[21 ] 首次将Volterra级数应用到非线性空气动力系统的ROM研究中, 实现了一种基于系统对脉冲输入响应的直接核识别方法. 为了把Volterra级数拓展应用到多输入/多输出(multiple-input/multiple-output, MIMO)的情况, Balajewicz等[22 ] 利用多输入Volterra级数, 提出了一种适用于两自由度气动弹性系统的非线性ROM. 尽管如此, MIMO系统的Volterra核的辨识过程仍非常复杂且辨识效率较低. 为了解决上述问题, 本文提出了一种基于非线性状态空间辨识的非线性ROM方法, 用来计算任意模态运动下的非定常空气动力响应. 同基于Volterra级数的ROM辨识方法相比, 该辨识算法更为简单, 也能够应用到MIMO空气动力系统的辨识. 同时, 由于该非线性ROM方法是基于二级训练, 可较为精确地预测跨音速线性和非线性气动弹性现象, 进而达到简化物理模型、节省计算时间和计算负荷的目的[23 ] . ...
Nonlinear reduced-order models for transonic aeroelastic and aeroservoelastic problems
1
2018
The Levenberg-marquardt algorithm: Implementation and theory
1
1978
... 式中, $\varPhi \left( {x_{\rm a} (k)} \right)$和$\varPhi \left( {u(k)} \right)$分别是状态变量和输入变量的非线性函数, 非线性部分的系数$(E_{\rm a} , F_{\rm a} , G_{\rm a} , H_{\rm a} )$是待辨识的变量, 可通过广义优化[25 ] (Levenberg-Marquardt, LM)算法来确定非线性部分的系数. 本文选用神经网络辨识过程中最常见的双曲正切函数$\tanh \left( \cdot \right)$来表征上述非线性函数, 该函数被认为是一种能在线性和非线性行为间建立平衡的严格单调递增函数. 需要说明的是, 本文提出的非线性模型与Mannarino和Dowell提出的非线性降阶模型法相似[26 ] . 但在他们的研究中, 只考虑了与状态矢量有关的非线性贡献, 当空气动力非线性较强时, 该方法必须通过增加状态空间的阶数来提高辨识精度, 进而导致降阶模型的维数过高且可能出现过拟合问题. 在本文的研究中, 通过增加输入变量的非线性函数, 可在不增加状态空间维数的前提下显著提高空气动力的辨识精度. ...
Reduced-order models for computational-fluid-dynamics-based nonlinear aeroelastic problems
1
2015
... 式中, $\varPhi \left( {x_{\rm a} (k)} \right)$和$\varPhi \left( {u(k)} \right)$分别是状态变量和输入变量的非线性函数, 非线性部分的系数$(E_{\rm a} , F_{\rm a} , G_{\rm a} , H_{\rm a} )$是待辨识的变量, 可通过广义优化[25 ] (Levenberg-Marquardt, LM)算法来确定非线性部分的系数. 本文选用神经网络辨识过程中最常见的双曲正切函数$\tanh \left( \cdot \right)$来表征上述非线性函数, 该函数被认为是一种能在线性和非线性行为间建立平衡的严格单调递增函数. 需要说明的是, 本文提出的非线性模型与Mannarino和Dowell提出的非线性降阶模型法相似[26 ] . 但在他们的研究中, 只考虑了与状态矢量有关的非线性贡献, 当空气动力非线性较强时, 该方法必须通过增加状态空间的阶数来提高辨识精度, 进而导致降阶模型的维数过高且可能出现过拟合问题. 在本文的研究中, 通过增加输入变量的非线性函数, 可在不增加状态空间维数的前提下显著提高空气动力的辨识精度. ...
飞机结构气动弹性分析与控制研究
1
2016
... 本节以BACT (benchmark active control technology)机翼为研究对象, 给出基于非线性气动力降阶模型的气动弹性建模过程. 该机翼为矩形机翼, 采用NACA 0012翼型[27 ] , 其风洞模型装配了后缘控制面以及上下表面扰流板. 本文研究中仅考虑后缘控制面作为气动伺服弹性输入. ...
飞机结构气动弹性分析与控制研究
1
2016
... 本节以BACT (benchmark active control technology)机翼为研究对象, 给出基于非线性气动力降阶模型的气动弹性建模过程. 该机翼为矩形机翼, 采用NACA 0012翼型[27 ] , 其风洞模型装配了后缘控制面以及上下表面扰流板. 本文研究中仅考虑后缘控制面作为气动伺服弹性输入. ...
Modeling the benchmark active control technology wind-tunnel model for application to flutter suppression
2
1996
... 图2 所示是BACT机翼的表面气动网格, 其结构动力学参数如表1 所示. 表中$M$, $S_\alpha$, $S_\beta$, $I_\alpha$, $S_{\alpha \beta }$, $K_h$, $K_\alpha$的定义见参考文献[28 ] . ...
... 其中, $k_\beta $, $\zeta _\beta $, $\omega _\beta $, $\beta _c $分别是增益、阻尼比、固有频率和控制指令, 参数值见文献[28 ] . 式(13)表达的气动弹性模型在包含了后缘控制面执行机构后可改写为 ...
亚/跨音速飞机结构气动弹性控制及其实验研究. [博士论文]
1
2014
... 为了研究非线性ROM对BACT机翼颤振边界的预测精度, 在不同马赫数下($M_\infty = 0.63$, 0.71, 0.75, 0.77, 0.80, 0.82, 0.825)分别进行了基于非线性状态空间方法的系统辨识, 建立了不同的降阶模型, 并计算了颤振边界. 颤振计算方法为时域计算, 求解过程框图如图8 所示, 首先给定模态速度的初始扰动$\dot{{\xi}}_1( 0)=\dot{{\xi }}_2(0)=0.001$,代入到非线性ROM方程(10)中求出气动力输出, 然后将来流动压$q_\infty $和气动力输出代入到气动弹性方程(15), 用预估-校正法进行流固耦合计算, 得到结构位移$\xi _1 ,\xi _2 $, 再将其代入非线性ROM方程中进行迭代计算, 最终得到收敛且稳定的结构位移矩阵. 其中预估-校正法分为预估步和校正步, 首先由预估步计算出模态解$\tilde{{x}}^{n+1}$, 将预估步的解作用于结构表面, 在时间步为$n$+1时, 流场收敛于该解, 能够计算出新的广义力$\bar{{Q}}^{n+1}$, 然后由校正步计算出$x^{n+1}$. 为了验证提出的ROM法的有效性, 将非线性ROM的颤振结果与CFD结果以及线性ROM结果进行了比较, 其中线性ROM由相同的空气动力学系统训练数据的输入和输出来辨识. 图9 表示通过直接CFD模型、线性状态空间辨识和非线性状态空间辨识计算出的BACT机翼颤振动压和颤振频率的对比. 如图所示, 通过非线性状态空间辨识计算得到的颤振边界与直接CFD法计算得到的结果吻合较好. 而与非线性状态空间辨识相比, 由线性状态空间辨识确定的颤振边界精度略低. 从图中还可以得到颤振动压和颤振频率的相对误差, 相对误差$e$定义式为[15 ,29 ] ...
亚/跨音速飞机结构气动弹性控制及其实验研究. [博士论文]
1
2014
... 为了研究非线性ROM对BACT机翼颤振边界的预测精度, 在不同马赫数下($M_\infty = 0.63$, 0.71, 0.75, 0.77, 0.80, 0.82, 0.825)分别进行了基于非线性状态空间方法的系统辨识, 建立了不同的降阶模型, 并计算了颤振边界. 颤振计算方法为时域计算, 求解过程框图如图8 所示, 首先给定模态速度的初始扰动$\dot{{\xi}}_1( 0)=\dot{{\xi }}_2(0)=0.001$,代入到非线性ROM方程(10)中求出气动力输出, 然后将来流动压$q_\infty $和气动力输出代入到气动弹性方程(15), 用预估-校正法进行流固耦合计算, 得到结构位移$\xi _1 ,\xi _2 $, 再将其代入非线性ROM方程中进行迭代计算, 最终得到收敛且稳定的结构位移矩阵. 其中预估-校正法分为预估步和校正步, 首先由预估步计算出模态解$\tilde{{x}}^{n+1}$, 将预估步的解作用于结构表面, 在时间步为$n$+1时, 流场收敛于该解, 能够计算出新的广义力$\bar{{Q}}^{n+1}$, 然后由校正步计算出$x^{n+1}$. 为了验证提出的ROM法的有效性, 将非线性ROM的颤振结果与CFD结果以及线性ROM结果进行了比较, 其中线性ROM由相同的空气动力学系统训练数据的输入和输出来辨识. 图9 表示通过直接CFD模型、线性状态空间辨识和非线性状态空间辨识计算出的BACT机翼颤振动压和颤振频率的对比. 如图所示, 通过非线性状态空间辨识计算得到的颤振边界与直接CFD法计算得到的结果吻合较好. 而与非线性状态空间辨识相比, 由线性状态空间辨识确定的颤振边界精度略低. 从图中还可以得到颤振动压和颤振频率的相对误差, 相对误差$e$定义式为[15 ,29 ] ...
Simultaneous excitation of multiple-input/multiple-output CFD-based unsteady aerodynamic systems
1
2008
... 极限环振荡是另一种非常重要的非线性气动弹性现象[30 -33 ] , 其非线性来源于气动力的非线性. 由图9 可知, 当马赫数为0.71时, BACT机翼的颤振动压为160 psf. 因此, 当飞行动压高于颤振临界动压(即分叉点)时, 系统会发生极限环振荡. 当前的非线性ROM具有预测这一非线性气动弹性现象的能力, 可将其应用到BACT机翼极限环振荡现象的研究中. 图10 给出了在$M_\infty =0.825$, $q_\infty =190$ psf下结构两阶模态的LCO响应. 使用的模态速度的初始扰动$\dot{{\xi }}_1 \left( 0 \right)=\dot{{\xi }}_2 \left( 0 \right)=0.001$. 由图可见, 受空气动力非线性的影响, 当来流动压为190 psf时, BACT机翼发生极限环振荡. ...
Efficient fluid thermal structural time marching with computational fluid dynamics
2018
Multifidelity coKriging for high-dimensional output functions with application to hypersonic airloads computation
2018
Nonlinear thermal reduced-order modeling for hypersonic vehicles
1
2017
... 极限环振荡是另一种非常重要的非线性气动弹性现象[30 -33 ] , 其非线性来源于气动力的非线性. 由图9 可知, 当马赫数为0.71时, BACT机翼的颤振动压为160 psf. 因此, 当飞行动压高于颤振临界动压(即分叉点)时, 系统会发生极限环振荡. 当前的非线性ROM具有预测这一非线性气动弹性现象的能力, 可将其应用到BACT机翼极限环振荡现象的研究中. 图10 给出了在$M_\infty =0.825$, $q_\infty =190$ psf下结构两阶模态的LCO响应. 使用的模态速度的初始扰动$\dot{{\xi }}_1 \left( 0 \right)=\dot{{\xi }}_2 \left( 0 \right)=0.001$. 由图可见, 受空气动力非线性的影响, 当来流动压为190 psf时, BACT机翼发生极限环振荡. ...