引言
梁是分析和设计工程结构时常用的简化模型,其结构动力学分析已有数百年历史,相对比较成熟.近年来,人们日益关注梁的动 力学设计.例如,提出变截面梁的"声学黑洞''概念并利用其进行减振设计[1 -2 ] ;对梁的截面和边界进行结构优化来获得期望的动力学特性[3 -4 ] . 在这些研究中,通常给定梁的动特性,求解梁的截面变化和边界条件.对于这类结构动力学反问题,其提法是否正确、求解能否成功,往往取决于对结构动力学的理论认知.
以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系?
20世纪60年代,Karnopp[9 ] 基于对偶变分原理研究变截面梁的固有振动问题,将不同边界条件下具有相同固有频率的梁称为对偶.此后,Ram和Elhay[10 ] 将变截面梁的微分方程进行有限差分,通过代数方法研究了梁的固有振动对偶问题.Wang等[11 ] 将材料力学中的共轭梁概念引入结构动力学,研究了梁在静定约束和静不定约束下的类比问题,重点讨论梁的振型节点规律.在结构动力学研究中,人们还引入多种对偶概念并开展相关研究,包括弹性结构与黏弹性结构之间的对偶问题[12 ] 、基于辛对偶的结构振动分析[13 ] ,但并未系统解决梁在固有振动中的对偶问题.
本文针对由线弹性均质材料制成的Euler-Bernoulli直梁 (以下简称为梁),将两种梁具有相同固有频率作为对偶,系统研究各种对偶关系.第1节给定梁的截面变化和齐次边界条件,确定其对偶梁的截面变化规律和齐次边界条件.第2节限定对偶梁具有相同的截面变化,确定梁的截面变化规律和齐次边界条件.第3节讨论等截面梁的对偶问题,指出等截面梁会产生新的对偶.
1 不同截面变化梁的对偶
本节给定某种梁的截面变化和齐次边界条件,寻求另一种具有不同截面变化的梁和对应的齐次边界条件,使两种梁具有相同固有频率,成为对偶. 按照齐次边界条件,对变截面梁的上述对偶进行分类,并指出梁的镜像、相似与上述对偶的关系.
1.1 位移描述与弯矩描述
首先,考察图1 所示的变截面梁$a$. 以梁的左端为原点,建立沿梁轴线的位置坐标$x \in [0,L]$,其中$L >0$为梁的长度. 采用梁截面中线的横向位移 (以下简称位移)$v(x,t)$ 描述梁的自由振动,则有
(1) $ \rho A(x)\dfrac{\partial ^2v(x,t)}{\partial t^2} + \dfrac{\partial ^2}{\partial x^2}\Bigg [EI(x)\dfrac{\partial ^2v(x,t)}{\partial x^2}\Bigg ] = 0$
其中,$\rho > 0$为梁的材料密度,$E > 0$为梁的材料弹性模量,$A(x) > 0$和$I(x)>0$为梁的截面积函数和截面惯性矩函数,它们均关于$x \in [0,L]$ 二阶连续可微.
图1
图1
变截面梁示意图
Fig. 1
A non-uniform beam
注意到式 (1)中的方括号项是梁$a$在动态变形过程中产生的弯矩,将其记为
(2) $ M(x,t) \equiv EI(x)\dfrac{\partial ^2v(x,t)}{\partial x^2}$
(3) $ \dfrac{\partial ^2v(x,t)}{\partial t^2} = - \dfrac{1}{\rho A(x)}\dfrac{\partial ^2M(x,t)}{\partial x^2}$
将式 (2)两端对时间$t$求两次偏导数并交换偏导数顺序,利用式 (3)得到
(4) $ \dfrac{\partial^2 M(x,t)}{\partial t^2} = EI(x)\dfrac{\partial ^2}{\partial x^2}\Bigg [\dfrac{\partial ^2v(x,t)}{\partial t^2}\Bigg] =\\ \qquad - EI(x)\dfrac{\partial ^2}{\partial x^2}\Bigg [\dfrac{1}{\rho A(x)}\dfrac{\partial ^2M(x,t)}{\partial x^2}\Bigg]$
上式可改写为由弯矩$M(x,t)$描述的梁$a$的动力学方程
(5) $ \left.\begin{array}{l} \rho \tilde {A}(x)\dfrac{\partial ^2M(x,t)}{\partial t^2} + \dfrac{\partial ^2}{\partial x^2}\Bigg [E\tilde {I}(x)\dfrac{\partial ^2M(x,t)}{\partial x^2}\Bigg] = 0 \\ \tilde {A}(x) \equiv \dfrac{1}{\rho EI(x)} ,\quad \tilde {I}(x) \equiv \dfrac{1}{\rho EA(x)} \end{array} \!\! \right \}$
式 (5)与式 (1)的形式相同,但类比截面积函数所定义的$\tilde {A}(x)$具有量纲 (s$^{2}$/kg$^{2}$),类比截面惯性矩函数定义的$\tilde {I}(x)$ 具有量纲 (m$^2\cdot $s$^2$/kg$^{2}$).
其次,考虑相同材料的变截面梁$b$,其长度也为$L > 0$,截面积函数为$\tilde {B}(x)> 0$,截面惯性矩函数为$\tilde {J}(x) > 0$,它们也关于$x \in[0,L]$二阶连续可微. 采用位移$\tilde {v}(x,t)$ 描述梁$b$的自由振动,则有
(6) $ \rho \tilde {B}(x)\dfrac{\partial ^2\tilde {v}(x,t)}{\partial t^2} + \dfrac{\partial ^2}{\partial x^2}\Bigg [E\tilde {J}(x)\dfrac{\partial ^2\tilde {v}(x,t)}{\partial x^2}\Bigg] = 0$
(7) $ \tilde {M}(x,t) \equiv E\tilde {J}(x)\dfrac{\partial ^2\tilde {v}(x,t)}{\partial x^2}$
类比于对梁$a$的分析过程,可得到由弯矩$\tilde {M}(x,t)$描述的梁$b$的动力学方程
(8) $ \left. \!\!\begin{array}{l} \rho B(x)\dfrac{\partial ^2\tilde {M}(x,t)}{\partial t^2} + \dfrac{\partial ^2}{\partial x^2}\Bigg [EJ(x)\dfrac{\partial ^2\tilde {M}(x,t)}{\partial x^2}\Bigg ] = 0 \\ B(x) \equiv \dfrac{1}{\rho E\tilde {J}(x)} ,\quad J(x) \equiv \dfrac{1}{\rho E\tilde {B}(x)} \end{array} \!\! \right \}$
(9) $ \left.\!\!\begin{array}{l} \tilde {B}(x) = \gamma \tilde {A}(x) = \dfrac{\gamma }{\rho EI(x)} \\ \tilde {J}(x) = \gamma \tilde {I}(x) = \dfrac{\gamma }{\rho EA(x)} ,\quad \gamma \equiv 1 \ ({\rm m}^2 \cdot {\rm kg}^2 /{\rm s}^{2}) \end{array} \!\! \right \}$
将式 (9)代入式 (6)和式 (8),则式 (6)与式 (5)中的偏微分方程形式完全相同,式 (8)与式 (1)也如此.本文 称满足式 (9)的梁$a$和梁$b$具有异截面对偶 (a dual of different cross-sections)的动力学方程;即梁$a$的位移动力学方程与梁$b$的弯矩动力学方程相同,梁$b$的位移动力学方程与梁$a$的弯矩动力学方程相同.
上述梁$a$和梁$b$是否具有相同固有频率,还取决于它们的边界条件是否对偶.现考察梁的齐次边界条件,这包括常见的固支边界、铰支边界、自由边界,以及图1 梁右端的滑支边界.该滑支边界限定梁端部的转角和剪力均为零,而其自身可在水平面上自由滑动,释放梁弯曲变形引起的轴向变形和轴向力,也属于齐次边界条件[9 ,11 ] .记$x_B \in \{0,L\}$为梁的端点坐标,考察基于位移和基于弯矩描述的4种齐次边界,其结果如表1 所示.将表1 中由位 移描述的边界条件$v(x_B ,t) = 0$和$v_x (x_B ,t) =0$转化为由弯矩描述时,用到动力学方程 (3),其推理如下
(10) $ \begin{array} v(x_B ,t) = 0\quad \Rightarrow \quad \dfrac{\partial ^2v(x_B ,t)}{\partial t^2} = 0 \\ \qquad \Rightarrow \quad \left. { \Bigg [\dfrac{1}{\rho A(x)}\dfrac{\partial ^2M(x,t)}{\partial x^2} \Bigg ]} \right|_{x = x_B } = 0 \\ \qquad \Rightarrow \quad M_{xx} (x_B ,t) = 0 \end{array}$
(11) $ \begin{array} v_x (x_B ,t) = 0\quad \Rightarrow \quad \dfrac{\partial ^2v_x (x_B ,t)}{\partial t^2} = 0 \\ \qquad \Rightarrow \quad \left. {\dfrac{\partial }{\partial x}\Bigg [\dfrac{1}{\rho A(x)}\dfrac{\partial^2M(x,t)}{\partial x^2}\Bigg]} \right|_{x = x_B } = 0 \\ \qquad \Rightarrow \quad [E\tilde {I}(x_B )M_{xx} (x_B ,t)]_x = 0 \end{array}$
其中,将$1 / \rho A(x_B )$代换为$E\tilde {I}(x_B )$ 是为了得到与位移描述中剪力为零相对称的表达式.
将表1 中的第2列和第3列作对比可见,由位移描述的自由边界等价于由弯矩描述的固支边界,由位移描述的滑支边界等价于由弯矩描述的滑支边界,由位移描述的铰支边界等价于由弯矩描述的铰支边界,由位移描述的固支边界等价于由弯矩描述的自由边界.本文称具有上述等价关系的一对边界为对偶边界 (a dual of boundaries).
1.2 异截面对偶梁及其分类
如果长度相同的梁$a$和梁$b$具有异截面对偶动力学方程,且满足对偶边界条件,则两者的动力学方程边值问题具有相同形式,故它们具有相同固有频率,本文称其为异截面对偶梁. 将表1 的4种边界条件进行组合,得到表2 所示的16种边界条件.根据上述异截面对偶梁概念,可得到如下结论:
(1) 表2 的异截面对偶梁分为7类,其中第2类、第3类和第4类还可细分为子类$A$和子类$B$.但若梁$a$和梁$b$的截面积函数、截面惯性矩函数关于截面$x = L /2$对称(以下简称为彼此镜像),则上述子类$A$和子类$B$属于彼此镜像,可不必区分.
(2) 对于上述7类异截面对偶梁,第1类至第3类中的对偶梁具有不同边界,第4类至第6类中的对偶梁具有相同边界,第7类中对偶梁具有彼此镜像边界,分别用黑色、蓝色和红色字体来区别.
(3)在上述7类异截面对偶梁中,每类包括两种固有频率完全相同的梁;它们彼此的位移振型与弯矩振型相同,进而可简化计算. 例如,若已知梁$a$的第$r$阶位移振型$v_r (x)$,由式 (2)得到其弯矩振型$M_r (x) =EI(x)\partial ^2v_r (x) / \partial x^2$,则梁$b$的第$r$阶位移振型可 取为$\tilde {v}_r (x)\!=\!M_r (x)$;反之,若已知梁$b$的第$r$阶位移振型$\tilde {v}_r(x)$,由式 (7)得到其弯矩振型$\tilde {M}_r (x) \!=\! E\tilde {J}(x)\partial ^2\tilde {v}_r (x) /\partial x^2$,则梁$a$的第$r$阶位移振型可取为$v_r (x) = \tilde {M}_r (x)$.
1.3 平凡与非平凡对偶
除了上述异截面对偶,梁$a$和梁$b$在如下两种情况下也具有相同固有频率.
(1) 镜像:即梁$a$及其边界条件与梁$b$及其边界条件关于截面$x = L /2$对称.显然,两镜像梁的固有频率相同,而它们的位移振型彼此为镜像.
(2) 相似:即梁$a$具有截面积函数$A(x)$和截面惯性矩函数$I(x)$,梁$b$具有与梁$a$相同的边界,且具有截面积函数$\beta A(x)$和截面惯性矩函数$\beta I(x)$,其中$\beta > 0$使梁$b$仍保持为Euler-Bernoulli梁.根据变截面梁的位移动力学方程,系数$\beta >0$不影响梁的固有振动,即两相似梁具有相同的固有频率和位移振型.在对偶研究中,将它们视为同一根梁.镜像和相似具有如下特点:一是它们属于平凡情况,无需对偶分析即获得梁的上述固有振动行为;二是两根梁彼此镜像或相似时,具有相同固有频率,属于引言所界定的对偶;三是根据1.2节中异截面对偶梁的位移振型与弯矩振型关系,它们不属于异截面对偶;四是对于两根彼此镜像或相似的梁,若其中之一与另一根梁构成异截面对偶,则它们均与该梁构成异截面对偶,即镜像或相似可传递对偶信息.基于上述特点,本文将镜像和相似作为平凡对偶 (trivial dual),而将异截面对偶作为非平凡对偶 (non-trivial dual).
1.4 案例:截面积四次变化的梁
现通过案例展示如何基于异截面对偶条件分析梁的固有振动.考察变截面固支-固支梁$a$,其截面积函数为$A(x) = A_0 (1 + \alpha x)^4$,$A_0 > 0$,$\alpha > - 1 / L$,截面惯性矩函数为$I(x) = A_0 r_g^2 (1 + \alpha x)^4$,$r_g > 0$为截面回转半径. 根据式 (1)得到梁的位移动力学方程边值问题
(12) $ \left.\!\!\begin{array}{l} \rho (1 + \alpha x)^4\dfrac{\partial ^2v(x,t)}{\partial t^2} + Er_g^2 \dfrac{\partial ^2}{\partial x^2}\Bigg [(1 + \alpha x)^4\dfrac{\partial v^2(x,t)}{\partial x}\Bigg ] = 0 \\ v(0,t) = 0 , \ \ v_x (0,t) = 0 , \ \ v(L,t) = 0 , \ \ v_x (L,t) = 0 \end{array}\!\!\right \}$
引入新的函数$w(x,t) \equiv (1 + \alpha x)^2v(x,t)$,可将式 (12)转化为[14 ]
(13) $ \left.\!\!\begin{array}{l} \dfrac{\partial ^2w(x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^4w(x,t)}{\partial x^4} = 0 , \ \ c_L \equiv \sqrt {\dfrac{E}{\rho }} \\ w(0,t) = 0 , \ \ w_x (0,t) = 0 , \ \ w(L,t) = 0 , \ \ w_x (L,t) = 0 \end{array} \!\!\right \}$
这是常见的等截面固支-固支梁的动力学方程边值问题,其固有频率和位移振型为[6 -8 ]
(14a) $ \left.\!\!\begin{array}{l} \omega _r = \kappa _r^2 c_L r_g , \ \ \kappa _1 \approx \dfrac{4.730}{L} , \ \ \kappa _2 \approx \dfrac{7.853}{L} \\ \kappa _3 \approx \dfrac{10.996}{L} , \ \ \kappa _r \approx \dfrac{(2r + 1) {\pi }}{2L} , \ \ r \geqslant 4 \end{array}\!\!\right \} $
(14b) $ \left.\!\!\begin{array}{l} w_r (x) = a_r [\cos (\kappa _r x) - \cosh (\kappa _r x) + \\ \qquad d_r \sinh (\kappa _r x) - d_r \sin (\kappa _r x)] \\ d_r \equiv \dfrac{\cos (\kappa _r L) - \cosh (\kappa _r L)}{\sin (\kappa _r L) - \sinh (\kappa _r L)} , \ \ r = 1,2,\cdots \end{array}\!\!\right \} $
变截面固支-固支梁$a$具有式 (14a)给出的固有频率,而其位移振型为
(15) $ v_r (x) = \dfrac{w_r (x,t)}{(1 + \alpha x)^2} = \dfrac{a_r }{(1 + \alpha x)^2}\Big[\cos (\kappa _r x) - \cosh (\kappa _r x) + \\ d_r \sinh (\kappa _r x) - d_r \sin (\kappa _r x)\Big] , \ \ r =1,2,\cdots $
取变截面自由-自由梁$b$的截面积函数和截面惯性矩函数分别为
(16) $ \left.\!\!\begin{array}{l} \tilde {B}(x) = \dfrac{\gamma }{\rho EI(x)} = \dfrac{\gamma }{\rho EA_0 r_0^2(1 + \alpha x)^4} \\ \tilde {J}(x) = \dfrac{\gamma }{\rho EA(x)} = \dfrac{\gamma }{\rho EA_0 (1 + \alpha x)^4} \end{array} \!\! \right \}$
根据异截面对偶关系,自由-自由梁$b$具有与固支-固支梁$a$相同的固有频率,其位移振型可取为
(17) $ \tilde {v}_r (x) = EI(x)\dfrac{\partial ^2v_r (x)}{\partial x^2} = a_r EA_0r_0^2 (1 + ax)^4 \Bigg \{\dfrac{\kappa _r^2 [d_r \sin (\kappa _r x) + d_r \sinh (\kappa _r x) - \cos (\kappa _r x) - \cosh (\kappa _r x)]}{(1 + \alpha x)^2}+ \\ \qquad \dfrac{4\alpha \kappa _r [\sin (\kappa _r x) + \sinh (\kappa _r x) + d_r \cos (\kappa _r x) - d_r \cosh (\kappa _r x)]}{(1 + \alpha x)^3} + \dfrac{6\alpha ^2[\cos (\kappa _r x) - \cosh (\kappa _r x) + d_r \sinh (\kappa _r x) - d_r \sin (\kappa _r x)]}{(1 + \alpha x)^4}\Bigg \} \qquad r = 1, 2, \cdots$
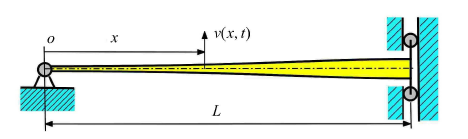
该结果的正确性可通过将式 (17)代入变截面自由-自由梁$b$的动力学边值问题得以验证.图2 是$\alpha = 2 /L$时异截面对偶梁的前三阶位移振型,此时梁$a$的截面积左小右大,故位移振型的幅值左高右低;而梁$b$的截面积变化相反,故位移振型的幅值左低右高.
图2
图2
$\alpha = 2 / L$时异截面对偶梁的最大位移归一化振型(第一阶:黑色,第二阶:红色,第三阶:蓝色)
Fig. 2
The normalized displacement mode shapes of a dual of beams of different cross-sections for $\alpha= 2 / L$ (the 1st order: black, the 2nd order: red, the 3rd order: blue)
2 相同截面变化梁的对偶
本节限定两种变截面梁具有相同的截面变化,研究它们在什么条件下具有相同固有频率. 为直观起见,先讨论一个案例,再研究一般情况.
2.1 案例:截面积指数变化的梁
考察固支-固支梁$a$,设其具有高度不变、宽度随指数变化的矩形截面,记截面积 函数为$A(x) =A_0 \exp (\alpha x)$,$A_0 > 0$,截面惯性矩函数 为$I(x) = A_0 r_g^2 \exp (\alpha x)$, 其中$r_g > 0$为截面回转半径.
再考察自由-自由梁$b$,取其截面积函数和截面惯性矩函数为
(18) $ \left.\begin{array}{l} \tilde {B}(x) = \dfrac{\gamma }{\rho EI(x)} = \dfrac{\gamma }{\rho EA_0 r_g^2 }\exp ( - \alpha x) \\ \tilde {J}(x) = \dfrac{\gamma }{\rho EA(x)} = \dfrac{\gamma }{\rho EA_0 }\exp ( - \alpha x) \end{array} \!\! \right \}$
因此,自由-自由梁$b$与固支-固支梁$a$构成异截面对偶梁.将梁$b$的镜像记为梁$c$,梁$c$可传递梁$b$携带的对偶信息,故自由-自由梁$c$与固支-固支梁$a$构成异截面对偶梁.注意到梁$c$的截面积和截面惯性矩分别为
(19) $ \left.\begin{array}{l} \hat {B}(x) = \dfrac{\gamma }{\rho EA_0 r_g^2 }\exp [\alpha (x - L)] = \dfrac{A(x)}{\beta } \\ \hat {J}(x) = \dfrac{\gamma }{\rho EA_0 }\exp [\alpha (x - L)] = \dfrac{I(x)}{\beta } \\ \beta \equiv \dfrac{\rho EA_0 A(L)r_g^2 }{\gamma } \end{array} \!\! \right \}$
再将自由-自由梁$c$的截面积$\hat {B}(x)$和截面惯性矩$\hat {J}(x)$ 乘以$\beta$,得到与梁$c$相似的自由-自由梁$d$,梁$d$与梁$c$具有相同固有频率. 从逻辑上看,固支-固支梁$a$与自由-自由梁$d$构成异截面对偶梁,具有相同的固有频率,两者的位移振型是对偶的弯矩振型.然而,梁$d$与梁$a$具有相同的截面积和截面惯性矩.由于这是相同截面变化的梁在不同边界条件下的对偶,故称其为同截面对偶 (dual of identical cross-sections).在后续研究中,可不再区分梁$a$和梁$d$.
为了进一步理解梁的同截面对偶,求解变截面固支-固支梁$a$的固有振动,再通过同截面对偶获得其在自由-自由边界条件下的固有振动.将梁$a$的截面积函数和截面惯性矩函数代入式 (1),消去$A_0 \exp (\alpha x) >0$,得到线性常系数偏微分方程
(20) $ \left.\!\! \begin{array}\dfrac{\partial ^2v(x,t)}{\partial t^2} + c_L^2 r_g^2 \Bigg [\dfrac{\partial ^4v(x,t)}{\partial x^4} + 2\alpha \dfrac{\partial ^3v(x,t)}{\partial x^3} + \\ \qquad \alpha ^2\dfrac{\partial ^2v(x,t)}{\partial x^2}\Bigg ] = 0 , \ \ c_L \equiv \sqrt {\dfrac{E}{\rho }} \end{array}\!\!\right\}$
其中$c_L $为等截面梁的纵波波速. 将分离变量解$v(x,t) = v(x)\sin (\omega t)$ 代入式 (20),得到常微分方程
(21) $ \left.\!\! \begin{array}\dfrac{d^4v(x)}{dx^4} + 2\alpha \dfrac{d^3v(x)}{dx^3} + \alpha ^2\dfrac{d^2v(x)}{dx^2} - \kappa ^{4}v(x) = 0 \\ \kappa \equiv \sqrt {\dfrac{\omega }{c_L r_g }} \end{array}\!\!\right\}$
(22) $ \lambda ^4 + 2\alpha \lambda ^3 + \alpha ^2\lambda ^2 - \kappa ^{4} =0$
由于求解式 (22)的解析解比较复杂,现研究$\alpha$为小参数时的情况,将式 (22)的解近似表示为$\lambda \approx \eta _0 + \eta _1 \alpha $. 将该表达式代入式 (22),比较$\alpha $的同次幂,得到$\eta _0 \in \{\pm {\rm i}\kappa ,\pm \kappa \}$,$\eta _1 = - 1 /2$,进而得到近似特征值
(23) $ \lambda _{1,2} \approx - \dfrac{\alpha }{2}\pm {\rm i}\kappa , \lambda _{3,4} \approx - \dfrac{\alpha }{2}\pm \kappa$
(24) $ \begin{array} v(x) = \exp \Big( - \dfrac{\alpha x}{2} \Big )\Big [c_1 \cos (\kappa x) + c_2 \sin (\kappa x) + \\ \qquad c_3 \cosh (\kappa x) + c_4 \sinh (\kappa x)\Big ] \end{array}$
对于固支-固支边界梁$a$,将式 (24)代入其边界条件,得到
(25) $ \left.\!\!\begin{array}{l} c_1 [\cos (\kappa L) - \cosh (\kappa L)] + c_2 [\sin (\kappa L) - \sinh (\kappa L)] = 0 \\ c_1 \Big \{\dfrac{\alpha }{2}[\cosh (\kappa L) - \cos (\kappa L)] - \kappa [\sin (\kappa L) + \sinh (\kappa L)] \Big \} + \\ \qquad c_2 \Big \{\dfrac{\alpha }{2}[\sinh (\kappa L) - \sin (\kappa L)] + \kappa [\cos (\kappa L) - \\ \qquad \cosh (\kappa L)] \Big \} = 0 \end{array} \!\! \right \}$
根据式 (25)有非零解的充分必要条件,可得到与等截面固支-固支梁相同的特征方程. 因此,变截面固支-固支梁$a$具有式 (14a)给出的固有频率,而根据式 (24)可得到其位移振型
(26) $ \left.\!\!\begin{array}{l} v_r (x) = c_1 \exp \Big ( - \dfrac{\alpha x}{2} \Big )\Big [\cos (\kappa _r x) - \cosh (\kappa _r x) + \\ \qquad d_r \sinh (\kappa _r x) - d_r \sin (\kappa _r x)\Big ] \\ d_r \equiv \dfrac{\cos (\kappa _r L) - \cosh (\kappa _r L)}{\sin (\kappa _r L) - \sinh (\kappa _r L)} \end{array} \!\! \right \}$
再考察与梁$a$对偶的自由-自由梁$b$,它满足式 (18).此时,梁$b$的固有频率与梁$a$完全相同,而其位移振型等同于梁$a$的弯矩振型,可取为
(27) $ \left.\!\!\begin{array}{l} \tilde {v}_r (x) = EI(x)\dfrac{\partial ^2v_r (x)}{\partial x^2} = \\ \qquad b_r \exp \Big(\dfrac{\alpha x}{2} \Big) \Big[(\alpha ^2 - 4\alpha d_r \kappa _r - 4\kappa _r^2 )\cos (\kappa _r x) + \\ \qquad (4\alpha \kappa _r - \alpha ^2d_r + 4d_r \kappa _r^2 )\sin (\kappa _r x) - \\ \qquad (\alpha ^2 + 4\alpha d_r \kappa _r + 4\kappa _r^2 )\cosh (\kappa _r x) + \\ \qquad (\alpha ^2d_r + 4\alpha \kappa _r + 4d_r \kappa _r^2 )\sinh (\kappa _r x) \Big] \\ b_r \equiv \dfrac{c_1 EA_0 r_g^2 }{4} \end{array} \!\! \right \}$
将式 (27)中的位置坐标$x$代换为$L - x$或改变$\alpha $的正负号,可得到梁$c$的位移振型$\hat {v}_r (x)$,也就是梁$d$和梁$a$在自由-自由边界条件下的位移振型.
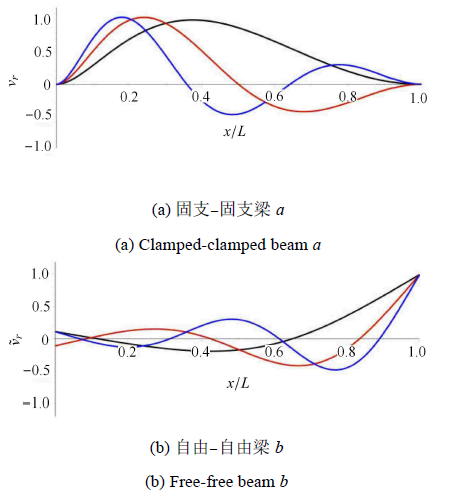
图3 给出$\alpha = 1 / 2L$时固支-固支梁和自由-自由梁的前三阶位移振型. 由于$\alpha > 0$,梁的截面积函数和截面惯性矩函数均随位置坐标$x$递增,故图3 中梁的右端位移小于左端位移.
图3
图3
$\alpha = 1 / 2L$时同截面对偶梁前三阶最大位移归一化振型(第一阶:黑色,第二阶:红色,第三阶:蓝色)
Fig. 3
The normalized displacement mode shapes of a dual of beams with identical cross-sections (the 1st order: black, the 2nd order: red, the 3rd order: blue)
2.2 同截面对偶条件
现将第2.1节的分析思路进行推广,得到梁的同截面对偶条件如下:存在常数$\beta >0$,使其截面积函数$A(x)$和惯性矩函数$I(x)$满足
(28) $ \left.\!\!\begin{array}{l} A(x) = \beta \hat {B}(x) = \dfrac{\beta \gamma }{\rho EI(L - x)} \\ I(x) = \beta \hat {J}(x) = \dfrac{\beta \gamma }{\rho EA(L - x)} \end{array} \!\! \right \}$
通过变量代换可知,式 (28)中的两个条件等价.现选择第一个条件进行研究,将其改写为
(29) $ \dfrac{A(x)}{\beta }\dfrac{I(L - x)}{\gamma / \rho E} = 1$
(30) $ \ln \Big [\dfrac{A(x)}{\beta }\Big] + \ln \Big [\dfrac{I(L - x)}{\gamma / \rho E}\Big] = 0$
(31) $ \left.\!\!\begin{array}{l} y \equiv x - \dfrac{L}{2} \in \Big [ - \dfrac{L}{2},\dfrac{L}{2}\Big] \\ f(y) \equiv \ln \Big [\dfrac{A(L / 2 + y)}{\beta }\Big] \\ g( - y) \equiv \ln \Big [\dfrac{I(L / 2 - y)}{\gamma / \rho E}\Big] \end{array} \!\! \right \}$
(32) $ f(y) + g( - y) = 0$
(33) $ \left.\begin{array}{l} A(x) = \beta \exp \Big [f(x - \dfrac{L}{2})\Big] \\ I(x) = \dfrac{\gamma }{\rho E}\exp \Big [ - f\Big (\dfrac{L}{2} - x\Big) \Big] \end{array} \right \}$
因此,选择光滑函数$f(y),y \in [ - L / 2,L /2]$,即可由式 (33)得到满足式 (28)的截面积函数$A(x)$ 和截面惯性矩函数$I(x)$. 虽然式 (33)限定了梁的截面变化,但因光滑函数$f(y)$ 的任意性,同截面对偶梁的设计空间非常大. 以下讨论两种典型情况.
(1) $f(y)$为奇函数:此时,$A(x)$和$I(x)$均关于$x = L / 2$反对称,且
(34) $ I(x) = \dfrac{\gamma }{\beta \rho E}A(x) = r_g^2 A(x) ,\quad \beta =\dfrac{\gamma }{\rho Er_g^2 }$
此时,截面回转半径$r_g $为常数.不难验证,第2.1节案例中梁的截面积函数和截面惯性矩函数满足式 (33)和式 (34),故该案例构成同截面对偶.
现以更复杂的奇函数$f(y) = - \alpha \sin ( \pi y / L)$,$\alpha > 0$为例,讨论同截面对偶关系.由式 (33)得到
(35) $ \left.\begin{array}{l} A(x) = A_0 \exp \Big [\alpha \cos \Big (\dfrac{ \pi x}{L} \Big) \Big] ,\ \ A_0 \equiv \beta \\ I(x) = I_0 \exp \Big [\alpha \cos \Big (\dfrac{ \pi x}{L} \Big) \Big] , \ \ I_0 \equiv A_0 r_g^2 \end{array} \right \}$
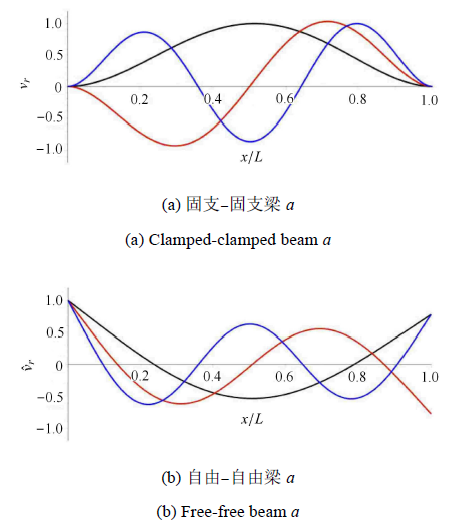
容易验证,式 (35)满足式 (28).设固支-固支梁$a$具有式 (35)所给出的截面积函数和截面惯性矩函数,图4 依次给出固支-固支梁$a$,与梁$a$异截面对偶的自由-自由梁$b$,以及梁$b$的镜像梁$c$的截面积对比.此时,梁$c$的截面积为$\hat {B}(x) = A(x) / \beta $,截面惯性矩为$\hat {J}(x) = I(x) / \beta $.将它们乘以$\beta $,得到与梁$c$相似的自由-自由梁$d$.由于梁$d$的截面积和截面惯性矩正是$A(x)$和$I(x)$,故梁$d$与梁$a$是同截面对偶.换言之,将梁$a$的固支-固支边界改为自由-自由边界后,两者具有相同固有频率.
图4
图4
固支-固支梁$a$,对偶的自由-自由梁$b$,梁$b$的镜像梁$c$的截面积对比
Fig. 4
A comparison of cross-sectional areas among clamped-clamed beam $a$, free-free beam $b$ in a dual, and beam $c$ mirrored from beam $b$
(2) $f(y)$为偶函数:此时,$A(x)$和$I(x)$均关于$x = L /2$对称,而截面回转半径随$x$变化
(36) $ r_g^2 = \dfrac{I(x)}{A(x)} = \dfrac{\gamma }{\beta \rho E}\exp \Big [ - 2f\Big (x - \dfrac{L}{2}\Big)\Big]$
以偶函数$f(y) = \alpha y^2 ,\alpha > 0$为例,由式 (33)得到
(37) $ \left.\begin{array}{l} A(x) = A_0 \exp\Big [\alpha \Big (x - \dfrac{L}{2}\Big)^2\Big] , \ \ A_0 \equiv \beta \\ I(x) = I_0 \exp\Big [ - \alpha\Big (x - \dfrac{L}{2}\Big)^2\Big] , \ \ I_0 \equiv \dfrac{\gamma }{\rho E} \end{array} \right \}$
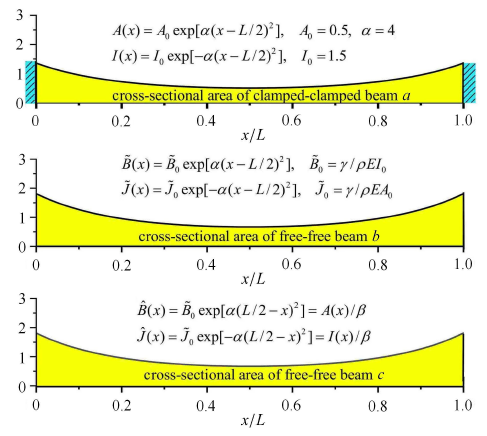
不难验证,式 (37)满足式 (28).设固支-固支梁$a$具有式 (37)所给出的截面积函数和截面惯性矩函数,图5 依次给出固支-固支梁$a$,与梁$a$异截面对偶的自由-自由梁$b$,以及梁$b$的镜像梁$c$的截面积对比.引入与梁$c$相似的自由-自由梁$d$,即得到固支-固支梁$a$的同截面对偶.
图5
图5
固支-固支梁$a$,对偶的自由-自由梁$b$,梁$b$的镜像梁$c$的截面积对比
Fig. 5
A comparison of cross-sectional areas among clamped-clamed beam $a$, free-free beam $b$ in a dual, and beam $c$ mirrored from beam $b$
2.3 同截面对偶梁的分类
对于满足式 (28)的变截面梁,现根据表2 考察形成同截面对偶梁的边界条件.第2.2节已分析了自由-自由梁与固支-固支梁的同截面对偶.类比第2.2节讨论梁$a$、异截面对偶梁$b$及其镜像梁$c$、与梁$c$相似的梁$d$之间的关系,可证明表2 中的第2类至第4类梁也属于同截面对偶.以第2A类的滑支-自由梁$a$为例,其异截面对偶是滑支-固支梁$b$,梁$b$的镜像是固支-滑支梁$c$,而与梁$c$相似的固支-滑支梁$d$具有与梁$a$相同的截面积和截面惯性矩;因此,第2A类的滑支-自由梁与第2B类的固支-滑支梁属于同截面对偶.采用相同方法可证明,第2A类的滑支-固支梁与第2B类的自由-滑支梁属于同截面对偶;第3A类的铰支-自由梁与第3B类的固支-铰支梁属于同截面对偶;第3A类的铰支-固支梁与第3B类的自由-铰支梁属于同截面对偶;第4A类的铰支-滑支梁与第4B类的滑支-铰支梁属于同截面对偶.
2.4 同截面非对偶梁
由于同截面对偶梁要满足比异截面对偶梁更苛刻的截面条件,故表2 中同截面对偶梁类别比异截面对偶梁类别要少. 以第7类梁为例,考察固支-自由梁$a$,其异截面对偶是自由-固支梁$b$,而梁$b$的镜像是固支-自由梁$c$,它与梁$a$具有相同截面变化和相同边界条件.根据第1.3节的讨论,梁$a$与梁$c$相似,可视为同一根梁,属于平凡对偶.换言之,固支-自由梁只能与其自身同截面对偶,其同类中的自由-固支梁也如此.此外,上述固支-自由梁$a$与自由-固支梁$b$的截面变化、边界条件均满足镜像条件,故两梁彼此镜像,属于平凡对偶.不难证明,表2 中的第5类梁和第6类梁均只能与自身同截面对偶,也属于平凡对偶.
2.5 非同截面对偶梁
不满足式 (28)的变截面梁比比皆是.以第1.4节中截面积四次变化梁$a$为例,其截面惯性矩为$I(x) = r_g^2A(x)$,但截面积函数$A(x)$不具有式 (33)的形式,故该梁不具有同截面对偶.已有研究表明[14 ] ,截面积四次变化梁在固支-固支边界和自由-自由边界下具有不同固有频率.
3 等截面梁的对偶
3.1 变截面梁的退化结果
对于满足$A(x) \equiv A_0 > 0$和$I(x) \equiv A_0 r_g^2 >0$的等截面梁$a$,记其纵波波速$c_L \equiv \sqrt {E / \rho }$,根据式 (1)和式 (5),可将梁的位移动力学方程边值问题和弯矩动力学方程边值问题分别简化为
(38) $ \left.\!\!\begin{array}{l} \dfrac{\partial ^2v(x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^4v(x,t)}{\partial x^4} = 0 \ v(x_B ,t) = 0 , \\ \ v_x (x_B ,t) = 0 \ v_{xx} (x_B ,t) = 0 \\ \ v_{xxx} (x_B ,t) = 0 , \ \ x_B \in \{0,L\} \end{array} \!\! \right \}$
(39) $ \left.\!\!\begin{array}{l} \dfrac{\partial^2 M(x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^2M(x,t)}{\partial x^2} = 0 \\ M_{xx} (x_B ,t) = 0 , \ \ M_{xxx} (x_B ,t) = 0 \ M(x_B ,t) = 0 , \\ \ M_x (x_B ,t) = 0 , \ \ x_B \in \{0,L\} \end{array} \!\! \right \}$
上述两式列出了所有可能边界条件的集合,对具体问题应根据表1 进行组合.根据式 (9)选择梁$b$,可类似地得到其位移动力学方程边值问题和弯矩动力学方程边值问题
(40) $ \left.\!\!\begin{array}{l} \dfrac{\partial^2 \tilde {v}(x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^2\tilde {v}(x,t)}{\partial x^2} = 0 \\ \tilde {v}_{xx} (x_B ,t) = 0 , \ \ \tilde {v}_{xxx} (x_B ,t) = 0 \\ \tilde {v}(x_B ,t) = 0 , \ \ \tilde {v}_x (x_B ,t) = 0 , \ \ x_B \in \{0,L\} \end{array} \!\! \right \}$
(41) $ \left. \!\! \begin{array}{l} \dfrac{\partial^2 \tilde {M}(x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^2\tilde {M}(x,t)}{\partial x^2} = 0 \\ \tilde {M}(x_B ,t) = 0 , \ \ \tilde {M}_x (x_B ,t) = 0 \\ \tilde {M}_{xx} (x_B ,t) = 0 , \ \ \tilde {M}_{xxx} (x_B ,t) = 0 , \ \ x_B \in \{0,L\} \end{array} \!\! \right \}$
由于上述方程中不出现截面积函数和截面惯性矩函数,可认为梁$a$和梁$b$是完全相同的梁,只能通过不同的齐次边界条件构成同截面对偶.注意到式 (38)与式 (41)的边界条件形式相同,式 (39)和式 (40)的边界条件形式相同.因此,在位移描述和弯矩描述对偶的前提下,有如下结论:
(1)表2 中的前3类等截面梁保持同截面对偶:第1类是自由-自由梁与固支-固支梁对偶;第2类是滑支-自由梁与固支-滑支梁对偶,或该对偶的镜像;第3类是铰支-自由梁与固支-铰支梁对偶,或该对偶的镜像.这3类对偶各有两种梁,一种梁具有静定约束,而另一种梁具有静不定约束.
(2)对于等截面梁,表2 中第4类的两种梁、第7类的两种梁均属于彼此镜像,第5类和第6类的梁则各属于一根梁;它们均属于平凡对偶.
3.2 等截面梁的对偶拓展
在位移描述和弯矩描述下,滑支-滑支梁、铰支-铰支梁各属于平凡对偶,彼此无对偶关系.但值得注意的是,铰支-铰支梁具有静定约束,而滑支-滑支梁具有静不定约束,这恰好是3.1节中前3类等截面梁对偶共有的基本特征.由此可猜想,在等截面前提下,这两种梁可否在其他描述下构成对偶?
根据式 (38),等截面滑支-滑支梁的位移动力学方程边值问题为
(42) $ \left.\begin{array}{l} \dfrac{\partial ^2v(x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^4v(x,t)}{\partial x^4} = 0 \\ v_x (0,t) = 0 , \ \ v_{xxx} (0,t) = 0 \\ v_x (L,t) = 0 , \ \ v_{xxx} (L,t) = 0 \end{array} \!\! \right \}$
将式 (42)中的偏微分方程两端对位置坐标$x$求一次偏导数,并将结果替换为梁的转角描述$\theta (x,t) \equiv v_x (x,t)$,得到等截面梁的转角动力学方程边值问题
(43) $ \left.\begin{array}{l} \dfrac{\partial ^2\theta (x,t)}{\partial t^2} + c_L^2 r_g^2 \dfrac{\partial ^4\theta (x,t)}{\partial x^4} = 0 \\ \theta (0,t) = 0 , \ \ \theta _{xx} (0,t) = 0 \\ \theta (L,t) = 0 , \ \ \theta _{xx} (L,t) = 0 \end{array} \right \}$
注意到式 (43)与位移描述的等截面铰支-铰支梁动力学方程边值问题具有相同形式,故等截面滑支-滑支梁的转角动力学与等截面铰支-铰支梁的位移动力学之间可形成同截面对偶. 若不计滑支-滑支梁垂直于轴线的刚体运动,这两种梁的第$r$阶固有振动频率均为
(44) $ \omega _r = \kappa _r^2 c_L r_g , \ \ \kappa _r = \dfrac{r {\pi }}{L} , \ \ r = 1,2,\cdots$
根据等截面铰支-铰支梁的位移振型,可取等截面滑支-滑支梁的转角振型为
(45) $ \theta _r (x) = a_r \sin (\kappa _r x) , \ \ r = 1,2,\cdots$
将上式对$x$积分,得到不计刚体运动时的等截面滑支-滑支梁的位移振型
(46) $ v_r (x) = b_r \cos (\kappa _r x) , \ \ b_r \equiv - \dfrac{a_r }{\kappa _r} , \ \ r = 1,2,\cdots$
3.3 刚体运动
最后以等截面梁为例,证明在非平凡对偶的两种梁中,必有一种梁具有刚体运动.考察对偶中含静定约束的梁,记其振动波数为$\kappa > 0$.考察对偶梁的转角和曲率,将其写为分离变量形式
(47a) $\tilde {v}_x (x,t) = \Big [c_1 \cos (\kappa x) + c_2 \sin (\kappa x)+ \\ \qquad c_3 \cosh (\kappa x) + c_4 \sinh (\kappa x)\Big ]q(t)$
(47b) $ \tilde {v}_{xx} (x,t) \equiv \dfrac{\tilde {M}(x)}{EI} = \Big [d_1 \cos (\kappa x) + d_2 \sin (\kappa x) + \\ \qquad d_3 \cosh (\kappa x) + d_4 \sinh (\kappa x)\Big ]q(t) $
将式 (47a)和 (47b)分别关于位置坐标$x$积分一次和两次,得到
(48a) $ v(x,t) = c_5 (t) + \dfrac{1}{\kappa }\Big [c_4 \cosh (\kappa x) + c_3 \sinh (\kappa x) - \\ \qquad c_2 \cos (\kappa x) + c_1 \sin (\kappa x)\Big ]q(t) $
(48b) $ v(x,t) = d_6 (t) + xd_5 (t) + \dfrac{1}{\kappa ^2EI}\Big [d_4 \sinh (\kappa x) + \\ \qquad d_3 \cosh (\kappa x) - d_2 \sin (\kappa x) - d_1 \cos (\kappa x)\Big ]q(t) $
其中$c_5 (t)$,$d_5 (t)$和$d_6 (t)$是与刚体运动相关的时间函数.式(48a)对应滑支-滑支梁、滑支-自由梁的位移动力学,$c_5(t)$是垂直于梁轴线的刚体运动;式 (48b)对应自由-自由梁的位移动力学,$d_6 (t) + xd_5(t)$是平面内的刚体运动;若式 (48b)中的$d_6 (t) = 0$,则对应铰支-自由梁的位移动力学,$xd_5(t)$是绕梁左端铰的刚体转动. 这些梁缺少足够的约束消除$c_5 (t)$,$d_5 (t)$和$d_6 (t)$,故必有刚体运动.
上述过程先获得梁在平衡位置附近的弹性振动,再积分获得刚体运动,形成两者的线性叠加.因此,式 (48)仅适用于描述在平衡位置附近作直线刚体运动的滑支-滑支梁、滑支-自由梁,以及在平衡位置附近呈现低速刚体转动的铰支-自由梁、自由-自由梁. 当铰支-自由梁、自由-自由梁的刚体转动速度较高时,则必须采用柔体动力学方法,计入梁的刚体转动与弹性振动的非线性耦合.
4 结论
(1)对于具有齐次边界条件的变截面梁,引入与位移描述对偶的弯矩描述,可获得不同截面变化下具有相同固有频率的对偶梁,本文称之为异截面对偶.研究表明,上述变截面梁可划分为以下7类异截面对偶,一是自由-自由梁与固支-固支梁,二是滑支-自由梁与滑支-固支梁(及其镜像),三是铰支-自由梁与铰支-固支梁(及其镜像),四是铰支-滑支梁与铰支-滑支梁(及其镜像),五是滑支-滑支梁与滑支-滑支梁,六是铰支-铰支梁与铰支-铰支梁,七是固支-自由梁与自由-固支梁.
(2) 若上述对偶中的两种梁具有相同截面变化,本文称其为同截面对偶.研究表明,同截面对偶梁具有特定指数函数形式的截面积函数和截面惯性矩函数.在此条件下,上述前4类对偶梁成为同截面对偶;而后3类对偶梁只能与其自身或镜像构成同截面对偶,属于平凡对偶.
(3)若进一步限定梁具有等截面,则前3类对偶梁保持同截面对偶关系,第4类对偶梁退化为彼此镜像. 此时,通过引入与位移描述对偶的转角描述,可发现等截面梁的一种新对偶,即滑支-滑支梁与铰支-铰支梁对偶.等截面梁的这4种对偶均具有如下特征,即一种梁具有静定约束,而另一种梁具有静不定约束.
表3 给出上述结论的完整归纳,在满足表中第一行的对偶条件前提下,不同齐次边界条件给出不同的对偶结果.其中,符号$ \Leftrightarrow $代表非平凡对偶;符号$ \rightleftarrows $代表平凡对偶;采用表2 的约定,以黑色字体表示对偶梁具有不同边界,蓝色字体表示对偶梁有相同边界,红色字体表示对偶梁有镜像边界.
上述结论不仅可提升对梁的固有振动特性认知水平,而且可为梁的动力学设计提供截面变化规律和边界条件选择的理论依据.
致谢
感谢哈尔滨工业大学深圳校区陈立群教授、北京理工大学罗凯助理教授、南京航空航天大学王怀磊副教授在撰稿过程中提供的建议.
参考文献
View Option
[1]
Krylov VV Tilman FJBS . Acoustic 'black holes' for flexural waves as effective vibration dampers
Journal of Sound and Vibration , 2004 ,274 :605 -619
[本文引用: 1]
[2]
Gao NS Wei ZY Zhang RH , et al . Low-frequency elastic wave attenuation in a composite acoustic black hole beam
Applied Acoustics , 2019 ,154 :68 -76
[本文引用: 1]
[3]
Zargham S Ward TA Ramli R , et al . Topology optimization: a review for structural designs under vibration problems
Structural and Multidisciplinary Optimization , 2016 ,53 :1157 -1177
[本文引用: 1]
[4]
Sun JL Tian Q Hu HY , et al . Topology optimization for eigenfrequencies of a rotating thin plate via moving morphable components
Journal of Sound and Vibration , 2019 ,448 :83 -108
[本文引用: 1]
[5]
胡海昌 . 多自由度结构固有振动理论 . 北京 : 科学出版社 , 1987 : 39 -81
[本文引用: 1]
( Hu Haichang Natural Vibration Theory of Structures of Multiple Degrees of Freedom. Beijing : Science Press , 1987 : 39 -81 (in Chinese))
[本文引用: 1]
[6]
胡海岩 . 机械振动与冲击 . 北京 : 航空工业出版社 , 1998 : 159 -160
[本文引用: 2]
( Hu Haiyan Mechanical Vibrations and Shocks. Beijing : Press of Aeronautical Industry , 1998 : 159 -160 (in Chinese))
[本文引用: 2]
[7]
Rao SS . Mechanical Vibrations, Fourth Edition
New Jersey: Pearson Prentice Hall , 2004 : 609 -613
[本文引用: 1]
[8]
Rao SS . Vibration of Continuous Systems
New York: John Wiley & Sons , 2007 : 317 -341
[本文引用: 2]
[9]
Karnoppe BH . Duality relations in the analysis of beam oscillations
Zeitschrift für Angewandte Mathematik und Physik ZAMP , 1967 ,18 :575 -580
[本文引用: 2]
[10]
Ram YM Elhay S . Dualities in vibrating rods and beams: continuous and discrete models
Journal of Sound and Vibration , 1995 ,184 :648 -655
[本文引用: 1]
[11]
Wang DJ Wang QC He BC . Qualitative Theory of Structural Mechanics
Singapore: Springer Nature , 2019 : 129 -132
[本文引用: 2]
[12]
Chen Q Zhu DM . Vibrational analysis theory and applications to elastic-viscoelastic composite structure
Computers and Structures , 1990 ,37 :585 -595
[本文引用: 1]
[13]
Li XJ Xu FY Zhang Z . Symplectic method for natural modes of beams resting on elastic foundations
ASCE Journal of Engineering Mechanics , 2018 ,144 :04018009
[本文引用: 1]
[14]
Abrate S . Vibration of non-uniform rods and beams
Journal of Sound and Vibration , 1995 ,185 :703 -716
[本文引用: 2]
Acoustic 'black holes' for flexural waves as effective vibration dampers
1
2004
... 梁是分析和设计工程结构时常用的简化模型,其结构动力学分析已有数百年历史,相对比较成熟.近年来,人们日益关注梁的动 力学设计.例如,提出变截面梁的"声学黑洞''概念并利用其进行减振设计[1 -2 ] ;对梁的截面和边界进行结构优化来获得期望的动力学特性[3 -4 ] . 在这些研究中,通常给定梁的动特性,求解梁的截面变化和边界条件.对于这类结构动力学反问题,其提法是否正确、求解能否成功,往往取决于对结构动力学的理论认知. ...
Low-frequency elastic wave attenuation in a composite acoustic black hole beam
1
2019
... 梁是分析和设计工程结构时常用的简化模型,其结构动力学分析已有数百年历史,相对比较成熟.近年来,人们日益关注梁的动 力学设计.例如,提出变截面梁的"声学黑洞''概念并利用其进行减振设计[1 -2 ] ;对梁的截面和边界进行结构优化来获得期望的动力学特性[3 -4 ] . 在这些研究中,通常给定梁的动特性,求解梁的截面变化和边界条件.对于这类结构动力学反问题,其提法是否正确、求解能否成功,往往取决于对结构动力学的理论认知. ...
Topology optimization: a review for structural designs under vibration problems
1
2016
... 梁是分析和设计工程结构时常用的简化模型,其结构动力学分析已有数百年历史,相对比较成熟.近年来,人们日益关注梁的动 力学设计.例如,提出变截面梁的"声学黑洞''概念并利用其进行减振设计[1 -2 ] ;对梁的截面和边界进行结构优化来获得期望的动力学特性[3 -4 ] . 在这些研究中,通常给定梁的动特性,求解梁的截面变化和边界条件.对于这类结构动力学反问题,其提法是否正确、求解能否成功,往往取决于对结构动力学的理论认知. ...
Topology optimization for eigenfrequencies of a rotating thin plate via moving morphable components
1
2019
... 梁是分析和设计工程结构时常用的简化模型,其结构动力学分析已有数百年历史,相对比较成熟.近年来,人们日益关注梁的动 力学设计.例如,提出变截面梁的"声学黑洞''概念并利用其进行减振设计[1 -2 ] ;对梁的截面和边界进行结构优化来获得期望的动力学特性[3 -4 ] . 在这些研究中,通常给定梁的动特性,求解梁的截面变化和边界条件.对于这类结构动力学反问题,其提法是否正确、求解能否成功,往往取决于对结构动力学的理论认知. ...
1
1987
... 以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系? ...
1
1987
... 以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系? ...
2
1998
... 以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系? ...
... 这是常见的等截面固支-固支梁的动力学方程边值问题,其固有频率和位移振型为[6 -8 ] ...
2
1998
... 以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系? ...
... 这是常见的等截面固支-固支梁的动力学方程边值问题,其固有频率和位移振型为[6 -8 ] ...
Mechanical Vibrations, Fourth Edition
1
2004
... 以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系? ...
Vibration of Continuous Systems
2
2007
... 以约束设计为例,结构动力学理论指出,对结构施加约束将提升 (至少不降低)其各阶固有频率,而结构施加约束前后的固有频率彼此相间[5 ] .对于含静不定约束的结构动力学问题,工程界主要关注其弹性振动,通常认为施加约束后的静定结构固有频率提升.多年前,笔者曾在教材中指出等截面梁的一类固有振动现象,即略去刚体运动后,自由-自由梁与固支-固支梁的固有频率相同,而铰支-自由梁与铰支-固支梁的固有频率相同[6 ] .21世纪以来,若干著作和教材也提及上述现象[7 -8 ] .虽然这些现象不违背上述结构动力学的约束理论,但人们诧异为何将梁的自由边界完全约束后不改变任何弹性振动的固有频率.这是某种巧合,还是这些梁之间具有某种内在联系?如果是内在联系,变截面梁之间是否也存在这种联系? ...
... 这是常见的等截面固支-固支梁的动力学方程边值问题,其固有频率和位移振型为[6 -8 ] ...
Duality relations in the analysis of beam oscillations
2
1967
... 20世纪60年代,Karnopp[9 ] 基于对偶变分原理研究变截面梁的固有振动问题,将不同边界条件下具有相同固有频率的梁称为对偶.此后,Ram和Elhay[10 ] 将变截面梁的微分方程进行有限差分,通过代数方法研究了梁的固有振动对偶问题.Wang等[11 ] 将材料力学中的共轭梁概念引入结构动力学,研究了梁在静定约束和静不定约束下的类比问题,重点讨论梁的振型节点规律.在结构动力学研究中,人们还引入多种对偶概念并开展相关研究,包括弹性结构与黏弹性结构之间的对偶问题[12 ] 、基于辛对偶的结构振动分析[13 ] ,但并未系统解决梁在固有振动中的对偶问题. ...
... 上述梁$a$和梁$b$是否具有相同固有频率,还取决于它们的边界条件是否对偶.现考察梁的齐次边界条件,这包括常见的固支边界、铰支边界、自由边界,以及图1 梁右端的滑支边界.该滑支边界限定梁端部的转角和剪力均为零,而其自身可在水平面上自由滑动,释放梁弯曲变形引起的轴向变形和轴向力,也属于齐次边界条件[9 ,11 ] .记$x_B \in \{0,L\}$为梁的端点坐标,考察基于位移和基于弯矩描述的4种齐次边界,其结果如表1 所示.将表1 中由位 移描述的边界条件$v(x_B ,t) = 0$和$v_x (x_B ,t) =0$转化为由弯矩描述时,用到动力学方程 (3),其推理如下 ...
Dualities in vibrating rods and beams: continuous and discrete models
1
1995
... 20世纪60年代,Karnopp[9 ] 基于对偶变分原理研究变截面梁的固有振动问题,将不同边界条件下具有相同固有频率的梁称为对偶.此后,Ram和Elhay[10 ] 将变截面梁的微分方程进行有限差分,通过代数方法研究了梁的固有振动对偶问题.Wang等[11 ] 将材料力学中的共轭梁概念引入结构动力学,研究了梁在静定约束和静不定约束下的类比问题,重点讨论梁的振型节点规律.在结构动力学研究中,人们还引入多种对偶概念并开展相关研究,包括弹性结构与黏弹性结构之间的对偶问题[12 ] 、基于辛对偶的结构振动分析[13 ] ,但并未系统解决梁在固有振动中的对偶问题. ...
Qualitative Theory of Structural Mechanics
2
2019
... 20世纪60年代,Karnopp[9 ] 基于对偶变分原理研究变截面梁的固有振动问题,将不同边界条件下具有相同固有频率的梁称为对偶.此后,Ram和Elhay[10 ] 将变截面梁的微分方程进行有限差分,通过代数方法研究了梁的固有振动对偶问题.Wang等[11 ] 将材料力学中的共轭梁概念引入结构动力学,研究了梁在静定约束和静不定约束下的类比问题,重点讨论梁的振型节点规律.在结构动力学研究中,人们还引入多种对偶概念并开展相关研究,包括弹性结构与黏弹性结构之间的对偶问题[12 ] 、基于辛对偶的结构振动分析[13 ] ,但并未系统解决梁在固有振动中的对偶问题. ...
... 上述梁$a$和梁$b$是否具有相同固有频率,还取决于它们的边界条件是否对偶.现考察梁的齐次边界条件,这包括常见的固支边界、铰支边界、自由边界,以及图1 梁右端的滑支边界.该滑支边界限定梁端部的转角和剪力均为零,而其自身可在水平面上自由滑动,释放梁弯曲变形引起的轴向变形和轴向力,也属于齐次边界条件[9 ,11 ] .记$x_B \in \{0,L\}$为梁的端点坐标,考察基于位移和基于弯矩描述的4种齐次边界,其结果如表1 所示.将表1 中由位 移描述的边界条件$v(x_B ,t) = 0$和$v_x (x_B ,t) =0$转化为由弯矩描述时,用到动力学方程 (3),其推理如下 ...
Vibrational analysis theory and applications to elastic-viscoelastic composite structure
1
1990
... 20世纪60年代,Karnopp[9 ] 基于对偶变分原理研究变截面梁的固有振动问题,将不同边界条件下具有相同固有频率的梁称为对偶.此后,Ram和Elhay[10 ] 将变截面梁的微分方程进行有限差分,通过代数方法研究了梁的固有振动对偶问题.Wang等[11 ] 将材料力学中的共轭梁概念引入结构动力学,研究了梁在静定约束和静不定约束下的类比问题,重点讨论梁的振型节点规律.在结构动力学研究中,人们还引入多种对偶概念并开展相关研究,包括弹性结构与黏弹性结构之间的对偶问题[12 ] 、基于辛对偶的结构振动分析[13 ] ,但并未系统解决梁在固有振动中的对偶问题. ...
Symplectic method for natural modes of beams resting on elastic foundations
1
2018
... 20世纪60年代,Karnopp[9 ] 基于对偶变分原理研究变截面梁的固有振动问题,将不同边界条件下具有相同固有频率的梁称为对偶.此后,Ram和Elhay[10 ] 将变截面梁的微分方程进行有限差分,通过代数方法研究了梁的固有振动对偶问题.Wang等[11 ] 将材料力学中的共轭梁概念引入结构动力学,研究了梁在静定约束和静不定约束下的类比问题,重点讨论梁的振型节点规律.在结构动力学研究中,人们还引入多种对偶概念并开展相关研究,包括弹性结构与黏弹性结构之间的对偶问题[12 ] 、基于辛对偶的结构振动分析[13 ] ,但并未系统解决梁在固有振动中的对偶问题. ...
Vibration of non-uniform rods and beams
2
1995
... 引入新的函数$w(x,t) \equiv (1 + \alpha x)^2v(x,t)$,可将式 (12)转化为[14 ] ...
... 不满足式 (28)的变截面梁比比皆是.以第1.4节中截面积四次变化梁$a$为例,其截面惯性矩为$I(x) = r_g^2A(x)$,但截面积函数$A(x)$不具有式 (33)的形式,故该梁不具有同截面对偶.已有研究表明[14 ] ,截面积四次变化梁在固支-固支边界和自由-自由边界下具有不同固有频率. ...