引言
瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径.
POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性.
虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显.
在前期的研究中[31 ] , 我们发现可以采用瞬态线性热传导分析中得到的POD模态对相同求解域的瞬态非线性热传导问题建立降阶模型进行近似计算, 这虽然简化并加快了降阶模型的构建, 但并未涉及到如何解决非线性降阶模型计算耗时的关键问题. 本文对此展开了深入系统的高效算法研究, 结构安排如下:第二部分给出瞬态非线性热传导问题的有限元全阶模型及其计算方法; 第三部分先采用POD方法建立瞬态非线性热传导问题的降阶模型, 并简要介绍其常规计算方法, 然后重点阐述新型计算方法的基本理论; 第四部分通过二维和三维算例验证本文提出的瞬态非线性热传导降阶模型新型计算方法的准确性和高效性;最后进行总结.
1 瞬态非线性热传导方程的有限元法
1.1 瞬态非线性热传导问题的控制方程
考虑材料的导热系数随温度变化形成的非线性热传导问题, 在求解域$\varOmega $内其非稳态、无内热源时的控制方程可表示为
(1) $ \begin{eqnarray} \label{eq1} \rho c\frac{\partial T\left(x,t \right)}{\partial t}=\frac{\partial }{\partial x_i }\left( {k\left( T \right)\frac{\partial T\left( {{x},t} \right)}{\partial x_i }} \right),\ \ t\geqslant t_0 ,\ \ {x}\in \varOmega \end{eqnarray}$
式中, $\rho $为材料的密度(kg/m$^{3})$, $c$为材料的比质量热容(J/(kg$\cdot$K)), $T\left( {{x},t} \right)$表示$t$时刻空间坐标$x$处的温度(K), $k\left( T \right)$表示材料随温度$T$变化的导热系数(W/(m$\cdot $K)), $t_0 $为初始时刻(s).
方程(1)是一类抛物型偏微分方程, 其定解条件包括初值条件
(2) $ \begin{eqnarray} \label{eq2} T\left( {{x},t} \right)|_{t=t_0 } =T_0 \left( {x} \right) \end{eqnarray}$
(3a) $ \begin{eqnarray} && \left. {T\left( {{x},t} \right)} \right|_{{x}=\varGamma _1 } =\bar{{T}} \end{eqnarray} $
(3b) $ \begin{eqnarray} \left. {k\left( T \right)\frac{\partial T\left( {{x},t} \right)}{\partial x_i }n_i } \right|_{{x}=\varGamma _2 } =\bar{{q}} \end{eqnarray} $
(3c) $ \begin{eqnarray} \left. {k\left( T \right)\frac{\partial T\left( {{x},t} \right)}{\partial x_i }n_i } \right|_{{x}=\varGamma _3 } =\bar{{h}}\left( {T_{\rm a} -T} \right) \end{eqnarray} $
式中, $T_0 $为初始时刻的温度场, $\varGamma =\varGamma _1 +\varGamma _2 +\varGamma _3 $为求解域$\varOmega $的边界, 其中$\varGamma_{1}$是第一类边界(Dirichlet条件), $\bar{{T}}=\bar{{T}}\left( {{x},t} \right)$是在边界$\varGamma _{1}$上给定的温度, $\varGamma _{2}$是第二类边界(Neumann条件), $\bar{{q}}=\bar{{q}}\left( {{x},t} \right)$是在边界$\varGamma_{2}$上给定的热流密度(W/m$^{2})$, $\varGamma _{3}$是第三类边界(Robin条件), $\bar{{h}}=\bar{{h}}\left({{x},t} \right)$是在边界$\varGamma_{3}$上给定的对流换热系数(W/(m$^{2}\cdot $K)), $T_{\rm a}$为环境温度, $n_i\left( {i=1,2,3} \right)$是边界$\varGamma $外法线的方向余弦. 当$\bar{{T}}$, $\bar{{q}}$和$\bar{{h}}$不随时间变化时称为定常边界条件,否则称为时变边界条件.
这里需要说明的是, 由于本文提出的模型降阶快速分析方法目前仅适用于解决第二类和第三类边界条件的瞬态非线性热传导问题,因此本文暂时不涉及第一类边界条件的相关问题.
1.2 瞬态非线性热传导方程的有限元离散格式
应用有限元法求解上述瞬态非线性热传导问题, 方程(1)及其定解条件(2)和(3)的弱解形式为
(4) $ \begin{eqnarray} \label{eq4} &&\int_\varOmega {N\rho c\frac{\partial T}{\partial t}{\rm d}V} +\int_\varOmega {k\left(T \right)\nabla N\cdot \nabla T{\rm d}V} =\\&& \int_{\varGamma _2 } {N\bar{{q}}{\rm d}S} + \int_{\varGamma _3 } {N\bar{{h}}\left( {T-T_{\rm a} } \right){\rm d}S} \end{eqnarray}$
式中, $N$为权函数. 由于所构造的权函数需要满足正交的特性, 这在整个求解域内是难以实现的. 为此有限元法通过将求解域离散成若干个微元子域(即网格单元),在各子域内构造相应的权函数以求得其温度场的近似解
(5) $ \begin{eqnarray} \label{eq5} T^e\left( t \right)=\sum\limits_{i=1}^n {N_i^e T_i^e \left( t \right)} ={N}^{e^{\rm T}}{T}^e\left( t \right),\ e=1,2,\cdots ,n_{\rm elem} \end{eqnarray}$
式中, $T^e\left( t \right)$为单元$e$的近似温度, $n$为单元$e$所含的节点数量, $N_i^e $和$T_i^e \left( t \right)$分别为单元$e$内节点$i$的权函数和温度, ${N}^e$和${T}^e\left( t\right)$分别为单元$e$内各节点的权函数向量和温度向量, $n_{\rm elem} $为求解域$\varOmega $的离散单元数量. 通过Galerkin投影可以得到单元$e$的非线性代数方程组
(6) $ \begin{eqnarray} \label{eq6} {C}^e{\dot{{T}}}^e\left( t \right)+{K}^e\left( {{T}^e} \right){T}^e\left( t \right)={F}^e\left( t \right) \end{eqnarray}$
式中, ${C}^e$, ${K}^e$和${F}^e$分别是单元$e$的热容矩阵、热传导矩阵和温度载荷向量, 其计算式如下
(7a) $ \begin{eqnarray} {C}^e=\int_{\varOmega _e } {\rho c{N}^e{N}^{e^{\rm T}}{\rm d}V} \end{eqnarray} $
(7b) $ \begin{eqnarray} {K}^e=\int_{\varOmega _e } {k\frac{\partial {N}^e}{\partial {x}}\left( {\frac{\partial {N}^e}{\partial {x}}} \right)^{\rm T}{\rm d}V} +\int_{\varGamma _3^e } {\bar{{h}}{N}^e{N}^{e^{\rm T}}{\rm d}S} \end{eqnarray} $
(7c) $ \begin{eqnarray} {F}^e=\int_{\varGamma _2^e } {\bar{{q}}{N}^e{\rm d}S} +\int_{\varGamma _3^e } {\bar{{h}}T_{\rm a} {N}^e{\rm d}S} \end{eqnarray} $
显然, ${C}^e$和${K}^e$都是$n \times n$方阵, 而${F}^e$是$n \times 1$列阵.
于是, 上述瞬态非线性热传导问题的有限元离散格式可由形如式(6)的求解域$\varOmega$内各单元的非线性代数方程组组集而成, 即
(8) $ \begin{eqnarray} \label{eq8} {C\dot{{T}}}\left( t \right)+{K}\left( {T} \right){T}\left( t \right)={F}\left( t \right) \end{eqnarray}$
式中, ${T}\left( t \right)$为$t$时刻的节点温度向量
(9) $ \begin{eqnarray} \label{eq9} {T}\left( t \right)=\left[ {{\begin{array}{*{20}c} {T_1 \left( t \right)} \ \ & {T_2 \left( t \right)} \ \ & \cdots \ \ & {T_{n_{\rm node} } \left( t \right)}\\ \end{array} }} \right]^{\rm T} \end{eqnarray}$
其中, $n_{\rm node} $为求解域$\varOmega $内的节点总量, 而${C}$, ${K}$和${F}$分别是热传导系统的总体热容矩阵、总体热传导矩阵和总体温度载荷向量
(10a) $ \begin{eqnarray}{C}=\sum\limits_{e=1}^{n_{\rm elem} } {{C}^e} \end{eqnarray} $
(10b) $ \begin{eqnarray} {K}=\sum\limits_{e=1}^{n_{\rm elem} } {{K}^e} \end{eqnarray} $
(10c) $ \begin{eqnarray} {F}=\sum\limits_{e=1}^{n_{\rm elem} } {{F}^e} \end{eqnarray} $
其中, ${C}$和${K}$都是$n_{\rm node}\times n_{\rm node}$方阵, 而${F}$是$n_{\rm node}\times 1$列阵.
由式(8)可以解得求解域$\varOmega $的温度场. 由于瞬态非线性热传导控制方程(1)的有限元模型的方程数量等于节点总量(即自由度数量), 当求解域$\varOmega $的规模较大、形状复杂时其内部须划分数量庞大的网格单元, 导致求解需要很大的存储资源并耗费大量的计算时间.
1.3 瞬态非线性热传导有限元模型的计算方法
式(8)中总体热传导矩阵${K}$是与温度${T}\left( t \right)$相关的, 因此该式是一个非线性微分方程组. 本文采用无条件稳定的Euler隐式格式
(11) $ \begin{eqnarray} \label{eq11} {C}\frac{{T}_{n+1} -{T}_n }{\Delta t}+{K}_{n+1} {T}_{n+1} ={F}_{n+1} \end{eqnarray}$
将其转化为非线性代数方程组, 并应用N-R方法进行迭代求解.
已知时刻$t_{n}$的温度场${T}_n $, 第$i$次迭代后的残值可表示成
(12) $ \begin{eqnarray} \label{eq12} R \left( {{T}_{n+1}^i } \right)={C}\left( {{T}_{n+1}^i -{T}_n } \right)+\Delta t\left( {{K}_{n+1}^i {T}_{n+1}^i -{F}_{n+1}^i } \right) \end{eqnarray}$
将残值$R $应用泰勒展开, 令$R \left( {{T}_{n+1}^{i+1} } \right)=0$, 有
(13) $ \begin{eqnarray} \label{eq13} \Delta {T}_{n+1}^{i+1} =-{K}_{\rm T}^{-1} R \left( {{T}_{n+1}^i } \right) \end{eqnarray}$
式中, ${K}_{\rm T} $为切向刚度矩阵, ${K}_{\rm T} ={\partial R }/({\partial {T}})$, 于是
(14) $ \begin{eqnarray} \label{eq14} {T}_{n+1}^{i+1} ={T}_{n+1}^i +\Delta {T}_{n+1}^{i+1} \end{eqnarray}$
当修正温度$\Delta {T}$或残值$R $达到收敛标准时, 时刻$t_{n+1}$的温度场为${T}_{n+1} ={T}_{n+1}^{i+1} $.
2 瞬态非线性热传导方程的模型降阶法
2.1 瞬态非线性热传导问题的降阶模型
对于需要实时控制或快速计算的工程领域, 有限元等常规的数值方法不能满足要求. 因为实际问题的自由度数量高达上千万甚至更多, 求解这种超大规模的非线性方程组需要很长的时间. 为此需要建立降阶模型以减小计算量, 从而达到实时控制或快速计算的目标. 根据本课题组前期的研究[31 ] , 基于特征正交分解方法建立的降阶模型能够对瞬态非线性热传导过程进行准确预测, 但是由于非线性问题的特殊性, 降阶模型在计算效率的提升方面不够显著, 本文致力于解决这一问题. 为保持文章的完整性, 下面简要介绍针对瞬态非线性热传导问题建立的降阶模型, 而关于特征正交分解方法的详细内容可参阅文献[32 ] .
首先, 通过实验测量、数值模拟等方法获得瞬态非线性热传导问题在若干个时刻点上的温度场, 通常称其为瞬像, 将所有瞬像按照时间顺序排列成瞬像矩阵${A}=\left[{{T}\left( {t_1 } \right)} \ \ {{T}\left( {t_2 } \right)}\ \ \cdots \ \ {{T}\left( {t_l } \right)} \right]_{n_{\rm node} \times l} $.
其次, 对瞬像矩阵${A}$进行特征正交分解, 获得一组正交基矢量, 通常称其为POD模态, 截取前$r$阶能够捕捉绝大部分能量的模态构成模态矩阵${\varPhi}=\left[ {\phi _1 } \ \ {\phi _2 } \ \ \cdots \ \ {\phi _r } \right]_{n_{\rm node} \times r} $.
最后, 利用模态矩阵${\varPhi }$可以将任意时刻的温度场${T}\left( t \right)$表示成
(15) $ \begin{eqnarray} \label{eq15} {T}\left( t \right)=\hat{{T}}_1 \left( t \right)\phi _1 +\hat{{T}}_2 \left( t \right)\phi _2 +\cdots +\hat{{T}}_r \left( t \right)\phi _r ={\varPhi \hat{{T}}}\left( t \right)\ \ \end{eqnarray}$
式中, $\hat{{T}}_i \left( t \right)$是第$i$个POD模态的系数. 将该式代入有限元离散方程式(8), 可得瞬态非线性热传导问题的降阶模型如下
(16) $ \begin{eqnarray} \label{eq16} {\hat{{C}}}\frac{\partial {\hat{{T}}}\left( t \right)}{\partial t}+{\hat{{K}}}\left( {T} \right){\hat{{T}}}\left( t \right)={\hat{{F}}}\left( t \right) \end{eqnarray}$
(17a) $ \begin{eqnarray} {\hat{{C}}}={\varPhi }^{\rm T}{C\varPhi }\end{eqnarray} $
(17b) $ \begin{eqnarray} {\hat{{K}}}\left( {T} \right)={\varPhi }^{\rm T}{K}\left( {T} \right){\varPhi } \end{eqnarray} $
(17c) $ \begin{eqnarray} {\hat{{F}}}\left( t \right)={\varPhi }^{\rm T}{F}\left( t \right) \end{eqnarray} $
显然, ${\hat{{C}}}$和${\hat{{K}}}$都是$r\times r$方阵, 而${\hat{{F}}}$是$r\times 1$列阵. 一般, $r$远小于$n_{\rm node}$.于是瞬态非线性热传导降阶模型是一个仅包含$r$个方程的非线性微分方程组,其计算量远低于原有限元全阶模型, 因而有利于提高计算效率.
2.2 瞬态非线性热传导问题降阶模型的常规计算方法
采用隐式时间推进方法建立的瞬态非线性热传导降阶模型的离散格式可表示成
(18) $ \begin{eqnarray} \label{eq18} {\hat{{C}}}\frac{{\hat{{T}}}_{n+1} -{\hat{{T}}}_n }{\Delta t}+{\hat{{K}}}_{n+1} {\hat{{T}}}_{n+1} ={\hat{{F}}}_{n+1} \end{eqnarray}$
这是关于${\hat{{T}}}_{n+1} $的非线性代数方程组,可以用与1.3小节相同的计算方法进行求解, 这里不再赘述.
然而需要强调的是, 由式(16)可见此降阶模型是不完备的, 即${\hat{{K}}}$仍然取决于原物理空间中的高维温度向量${T}_{n+1} $,而不能直接通过当前时刻得到的低维向量${\hat{{T}}}_{n+1} $来计算,使得在式(18)的计算过程当中每个迭代步都要出现下列额外的计算环节:
(1)将低维向量${\hat{{T}}}_{n+1} $利用关系式(15)变换回高维温度向量${T}_{n+1} $, 即
(19) $ \begin{eqnarray} \label{eq19} {T}_{n+1} ={\varPhi \hat{{T}}}_{n+1} \end{eqnarray}$
(2)根据新的温度场更新导热系数, 利用式(7b)和式(10b)重新计算各单元的热传导矩阵并组集成非线性热传导系统的总体热传导矩阵${K}_{n+1} $.
(3)通过式(17b)的矩阵运算将${K}_{n+1} $转换成非线性热传导降阶模型的系数矩阵${\hat{{K}}}_{n+1} $.
由于有限元全阶模型的自由度数量较大,这些额外的数据转换、矩阵组集和矩阵运算将耗费不少的计算时间,使得降低模型的小规模非线性代数方程组的求解带来的时间收益被抵消.在后面的算例验证部分我们可以看到, 在有限元全阶模型的规模不太大时,采用常规方法求解降阶模型对计算效率的提升效果并不理想.
2.3 瞬态非线性热传导问题降阶模型的新型计算方法
本小节将介绍瞬态非线性热传导降阶模型的一种新型高效计算方法, 它是直接通过对上述常规计算方法中两个耗时环节的技术处理以达到提升计算效率的目的: 一方面, 采用单元预转换方法(element pre-conversation method, EPM)压缩降阶模型系数矩阵${\hat{{K}}}$的计算时间; 另一方面, 采用多级线性化方法(multi-level linearization method, MLM)消除非线性方程组的迭代计算过程. 这种新方法解决了导热系数随温度变化情况下EPM和MLM的结合问题, 以及如何对换热边界单元的热传导矩阵进行相应计算. 下面对此作详细阐述.
EPM的主要思想是区分非线性热传导降阶模型的系数矩阵${\hat{{K}}}$中有限元全阶模型各个单元的贡献大小${\hat{{K}}}^e$, 可以表示成
(20) $ \begin{eqnarray} \label{eq20} {\hat{{K}}}=\sum\limits_{e=1}^{n_{\rm elem} } {{\hat{{K}}}^e} \end{eqnarray}$
这要求在有限元全阶模型的单元层面就预先将单元热传导矩阵${K}^e$进行转换, 其计算式为
(21) $ \begin{eqnarray} \label{eq21} {\hat{{K}}}^e={\varPhi }^{e^{\rm T}}{K}^e{\varPhi }^e \end{eqnarray}$
式中, ${\varPhi }^e$是模态矩阵${\varPhi }$中单元$e$的对应部分, ${\varPhi }^e$是$n\times r$矩阵. 显然, ${\hat{{K}}}^e$与${\hat{{K}}}$一样, 也是$r\times r$方阵.
(22) $ \begin{eqnarray} \label{eq22} {K}^e=\int_{\varOmega _e } {k\frac{\partial {N}^e}{\partial {x}}\left( {\frac{\partial {N}^e}{\partial {x}}} \right)^{\rm T}{\rm d}V} +{K}_h^e \end{eqnarray}$
式中, ${K}_h^e =\int_{\varGamma _3^e } {\bar{{h}}{N}^e{N}^{e^{\rm T}}{\rm d}S} $.
(23) $ \begin{eqnarray} \label{eq23} {K}_k^e =\int_{\varOmega _e } {k\frac{\partial {N}^e}{\partial {x}}\left( {\frac{\partial {N}^e}{\partial {x}}} \right)^{\rm T}{\rm d}V} \end{eqnarray}$
在计算${K}_k^e $时, 理论上应取各高斯积分点上的导热系数值$k$, 但由于网格单元的尺寸通常很小, 实际上一般取单元的平均导热系数$\bar{{k}}^e\left( {T} \right)$进行计算而不会引起大的偏差, 即
(24) $ \begin{eqnarray} \label{eq24} {K}_k^e =\bar{{k}}^e\left( {T} \right)\int_{\varOmega _e } {\frac{\partial {N}^e}{\partial {x}}\left( {\frac{\partial {N}^e}{\partial {x}}} \right)^{\rm T}{\rm d}V} \end{eqnarray}$
式(24)将${K}_k^e $分成了与解相关的$\bar{{k}}^e\left( {T} \right)$和与解无关的矩阵两个部分, 后者仅由单元形状决定, 方便起见, 定义其为
(25) $ \begin{eqnarray} \label{eq25} {K}_g^e =\int_{\varOmega _e } {\frac{\partial {N}^e}{\partial {x}}\left( {\frac{\partial {N}^e}{\partial {x}}} \right)^{\rm T}{\rm d}V} \end{eqnarray}$
(26) $ \begin{eqnarray} \label{eq26} {K}^e=\bar{{k}}^e\left( {T} \right){K}_g^e +{K}_h^e \end{eqnarray}$
(27) $ \begin{eqnarray} \label{eq27} {\hat{{K}}}=\sum\limits_{e=1}^{n_{\rm elem} } {\left( {\bar{{k}}^e\left( {T} \right){\hat{{K}}}_g^e +{\hat{{K}}}_h^e } \right)} \end{eqnarray}$
式中, ${\hat{{K}}}_g^e $和${\hat{{K}}}_h^e $均为$r\times r$方阵.
当瞬态非线性热传导问题的有限元全阶模型和对流换热边界确定后, ${\hat{{K}}}_g^e $和${\hat{{K}}}_h^e $都可以预先计算并存储备用.在迭代过程中, 采用式(27)计算降阶模型的系数矩阵${\hat{{K}}}$时, 只需要根据新的温度场计算出各个单元的平均导热系数即可. 因此, 与2.2节的常规计算方法相比, EPM能够有效压缩${\hat{{K}}}$的计算时间, 进而提高降阶模型的计算效率.
MLM的主要思想是通过插值技术取代非线性热传导系统的非线性项, 得到其近似的线性方程组, 从而利用前面若干级时刻点上已知的温度场直接计算出当前时刻的温度场. 方便起见, 将式(8)表示的瞬态非线性热传导问题的有限元全阶模型改写成
(28) $ \begin{eqnarray} \label{eq28} {\dot{{T}}}\left( t \right)+{WT}\left( t \right)={f} \end{eqnarray}$
式中, 系数阵${W}={C}\backslash{K}\left( {T} \right)$,载荷向量${f}={C}\backslash{F}\left( t \right)$.
本文采用无条件稳定的Dupont II多级线性化格式来求解式(28), 此格式为[33 ]
(29) $ \begin{eqnarray} \label{eq29} &&\left[ {{I}+\Delta t{W}_\ast } \right]{T}_{n+2} =\left[ {{I}+0.5\Delta t{W}_\ast } \right]{T}_{n+1} -\\&&0.5\Delta t{W}_\ast {T}_n +\Delta t{f}_\ast \end{eqnarray}$
式中, ${W}_\ast $表示插值温度${T}_\ast $下的系数矩阵${W}$, ${f}_\ast $表示插值时间$t_\ast $时的载荷向量${f}$, ${T}_\ast$和$t_\ast $按下式计算
(30a) $ \begin{eqnarray} {T}_\ast =1.5{T}_{n+1} -0.5{T}_n \end{eqnarray} $
(30b) $ \begin{eqnarray} t_\ast =t_{n+1.5} \end{eqnarray} $
将式(15)代入式(29), 然后方程两边同乘${\varPhi}^{\rm T}$就可以得到瞬态非线性热传导降阶模型的多级线性化格式
(31) $ \begin{eqnarray} \label{eq31} &&\left[ {{I}_r +\Delta t{\hat{{W}}}_\ast } \right]{\hat{{T}}}_{n+2} =\left[ {{I}_r +0.5\Delta t{\hat{{W}}}_\ast } \right]{\hat{{T}}}_{n+1} -\\&&0.5\Delta t{\hat{{W}}}_\ast {\hat{{T}}}_n +\Delta t{\hat{{f}}}_\ast \end{eqnarray}$
式中, ${I}_r $为$r$阶单位矩阵, 而${\hat{{W}}}_\ast $和${\hat{{f}}}_\ast $分别为
(32a) $ \begin{eqnarray} {\hat{{W}}}_\ast ={\varPhi }^{\rm T}{W}_\ast {\varPhi } \end{eqnarray} $
(32b) $ \begin{eqnarray} {\hat{{f}}}_\ast ={\varPhi }^{\rm T}{f}_\ast \end{eqnarray} $
由此降阶模型的多级线性化格式可见, 在前两个时刻$t_{n}$和$t_{n+1}$的${\hat{{T}}}$已知时, 可先利用式(15)计算原物理空间的温度场${T}_n $和${T}_{n+1} $, 然后根据式(30)计算插值温度${T}_\ast $和插值时间$t_\ast $, 继而求出${W}_\ast $和${f}_\ast $, 并利用式(32)将它们转换为${\hat{{W}}}_\ast $和${\hat{{f}}}_\ast $, 就可以通过式(31)直接计算时刻$t_{n+2}$的${\hat{{T}}}$, 得到其温度场${T}_{n+2} $.
实际计算时, 初始时刻$t_{0}$的温度场是已知的, 而第二个时刻$t_{1}$的温度场未知, 需要通过2.2节的常规方法或者基于前面EPM方法改进的常规方法求出, 此后各个时刻的温度场均可由多级线性化格式直接计算得到, 消除了耗时的迭代过程, 因而有利于提高降阶模型的计算效率.
鉴于EPM和MLM分别是针对常规方法中两个不同环节做出的改进, 这就为两者结合以获得降阶模型更高的计算效率提供了可能. 然而, 其结合的困难在于对MLM方法中式(32)的处理, 将${W}_\ast $和${f}_\ast$代入其中可见
(33a) $ \begin{eqnarray} {\hat{{W}}}_\ast ={\varPhi }^{\rm T}\left( {{C}\backslash{K}\left( {{T}_\ast } \right)} \right){\varPhi } \end{eqnarray} $
(33b) $ \begin{eqnarray} {\hat{{f}}}_\ast ={\varPhi }^{\rm T}\left( {{C}\backslash{F}\left( {t_\ast } \right)} \right) \end{eqnarray} $
该式要求进行总体热容矩阵的求逆和总体矩阵及其与模态矩阵之间的多重乘法运算, 这与EPM方法从单元层面的预处理方式是不协调的.
本文针对材料的比热容为常数、导热系数随温度变化这一类型的瞬态非线性热传导问题, 提出有限元全阶模型中的各个单元对降价模型系数矩阵${\hat{{W}}}_\ast $亦有其相应的贡献, 贡献大小用${\hat{{W}}}_\ast ^e $表示, 即
(34) $ \begin{eqnarray} \label{eq34} {\hat{{W}}}_\ast =\sum\limits_{e=1}^{n_{\rm elem} } {{\hat{{W}}}_\ast ^e} \end{eqnarray}$
这与EPM方法中处理${\hat{{K}}}$的思想是相同的, 式中${\hat{{W}}}_\ast^e $可与式(21)类似得到
(35) $ \begin{eqnarray} \label{eq35} {\hat{{W}}}_\ast ^e ={\varPhi }^{e^{\rm T}}{W}_\ast ^e {\varPhi }^e \end{eqnarray}$
由式(7a)得到的单元热容矩阵${C}^e$为协调质量热容矩阵, 为了计算式(35)中的单元矩阵${W}_\ast ^e $, 须将其转化为集中质量热容矩阵,这样由式(10a)得到的总体热容矩阵${C}$为对角矩阵, 可写为
(36) $ \begin{eqnarray} \label{eq36} {C}=\left[ {{\begin{array}{*{20}c} {c_{11} } & & & \\ & {c_{22} } & & \\ & & \ddots & \\ & & & {c_{n_{\rm node} n_{\rm node} } } \\ \end{array} }} \right] \end{eqnarray}$
由于比热容为常数, 于是${C}$是不随温度变化的恒常矩阵, 其逆矩阵亦为对角矩阵, 此时${W}_\ast ^e $可由下式进行计算
(37) $ \begin{eqnarray} \label{eq37} {W}^e _{\ast ij} =\frac{{K}^e _{\ast ij}}{{C}_{mm} }\ \ ( i,j=1,2,\cdots ,n; m=1,2,\cdots ,n_{\rm node})\ \ \end{eqnarray}$
式中, ${K}_\ast ^e $表示插值温度${T}_\ast $下的单元热传导矩阵, 下标$m$表示单元内第$i$个节点对应的总体节点号.
将式(24)代入式(37), 并补充单元处于对流换热边界上时存在的单元热传导矩阵修正项${K}_h^e $, 可得
(38) $ \begin{eqnarray} \label{eq38} {W}^e_{\ast ij} =\frac{\bar{{k}}^e\left( {{T}_\ast } \right)}{{C}_{mm} }\int_{\varOmega _e } {\frac{\partial N_i }{\partial {x}_p }\frac{\partial N_j }{\partial {x}_p }{\rm d}V} +\frac{\bar{{h}}}{{C}_{mm} }\int_{\varGamma _3^e } {N_i N_j {\rm d}S} \end{eqnarray}$
式中, 重复指标$p$表示执行爱因斯坦求和约定, 对二维问题和三维问题$p$分别取2和3.
(39) $ \begin{eqnarray} \label{eq39} {W}_h^e =\frac{\bar{{h}}}{{C}_{mm} }\int_{\varGamma _3^e } {N_i N_j {\rm d}S} \end{eqnarray}$
并观察式(38)右端第一项, 与EPM方法中的${K}_k^e $ (式(24))相仿, 我们也可将其分成两部分: $\bar{{k}}^e\left( {{T}_\ast } \right)$是插值温度${T}_\ast $下的单元平均导热系数, 它是随降阶模型的解而变化的部分; 其余部分则是由单元形状及其比热容的大小所决定, 是与降阶模型的解无关的恒常矩阵. 方便起见, 将前者简记为$\bar{{k}}_\ast ^e $, 而后者用符号${W}_g^e $表示, 于是式(38)可改写成
(40) $ \begin{eqnarray} \label{eq40} {W}_\ast ^e =\bar{{k}}_\ast ^e {W}_g^e +{W}_h^e \end{eqnarray}$
(41) $ \begin{eqnarray} \label{eq41} {\hat{{W}}}_\ast =\sum\limits_{e=1}^{n_{\rm elem} } {\left( {\bar{{k}}_\ast ^e {\hat{{W}}}_g^e +{\hat{{W}}}_h^e } \right)} \end{eqnarray}$
式中, ${\hat{{W}}}_g^e $和${\hat{{W}}}_h^e $均为$r\times r$方阵.
与EPM方法中的${\hat{{K}}}_g^e $和${\hat{{K}}}_h^e $一样, ${\hat{{W}}}_g^e $和${\hat{{W}}}_h^e $在瞬态非线性热传导问题的有限元全阶模型和对流换热边界确定时也是可以预先计算好的.
对于式(33b)中的${\hat{{f}}}_\ast $, 可仿照上述${\hat{{W}}}_\ast $的方式进行计算, 这里不再赘述.
这样, 就将EPM和MLM结合起来了. 在用式(31)降阶模型多级线性化格式进行计算时, 只需要根据前两个时刻已经得到的温度场计算出插值温度和插值时间即可,其余步骤和过程是与EPM完全相同的. 由此可见, 这种针对瞬态非线性热传导降阶模型发展的新型EPM-MLM复合方法, 与EPM具有良好的一致性, 其区别仅在于将${\hat{{K}}}_g^e $和${\hat{{K}}}_h^e $替换成了${\hat{{W}}}_g^e $和${\hat{{W}}}_h^e $, 简单易行, 便于编制规范统一的程序和软件.
3 算例分析
本部分通过二维和三维瞬态非线性热传导算例的计算和分析, 验证本文所提出的降阶模型新型计算方法的可行性、准确性和高效性. 为方便对比说明,下面将瞬态非线性热传导降阶模型的常规计算方法和新型计算方法分别命名为POD1和POD2.
3.1 算例1: 方板的瞬态非线性热传导问题
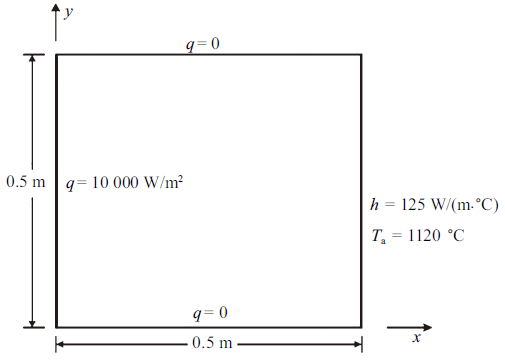
考虑如图1 所示边长为0.5 m的二维方板, 板材的密度$\rho =7850$ kg/m$^{3}$、比热容$c=460$ J/(kg$\cdot{^\circ}$C), 其导热系数随温度线性变化, $k=65$-0.05$T$ W/(m$\cdot{^\circ}$C). 方板的初始温度为20℃, 其右侧为对流换热边界, 换热系数125 W/(m$^{2}\cdot{^\circ}$C)、环境温度1120℃; 左侧为放热边界, 热流密度10 000 W/m$^{2}$; 上、下侧均为绝热边界.
图 1
图 1
方板的几何模型及热边界条件
Fig. 1
Geometric model and thermal boundary conditions of the square plate
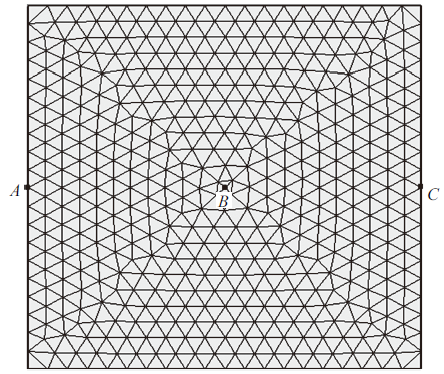
方板的有限元模型如图2 所示. 计算域采用线性三角形单元进行离散, 各侧边均布21个节点, 总计888个单元、485个节点. 为便于后处理分析, 取方板的左侧中点A、中心点B和右侧中点C等三个点作为参考点.
为建立方板瞬态非线性热传导问题的降阶模型, 本文采取数值模拟的方法构造瞬像矩阵: 时间步长取为50 s, 通过有限元法计算0$\sim $20 000 s时间范围内方板在上述定常热边界条件下温度场的变化, 选取$t=1000$, $2000$, $\cdots$, 20 000 s共计20个时刻点上方板的温度场构成瞬像矩阵${A}$. 对${A}$进行特征正交分解分析, 截取前4个特征值(即$r=4$)对应的POD模态构造模态矩阵${\varPhi }$. 利用式(15)可以得到仅包含4个非线性方程的降阶模型, 相比于原来由485个非线性方程组成的有限元全阶模型, 方程组的规模显著减小.
图 2
图 2
方板的有限元模型
Fig. 2
Finite element model of the square plate
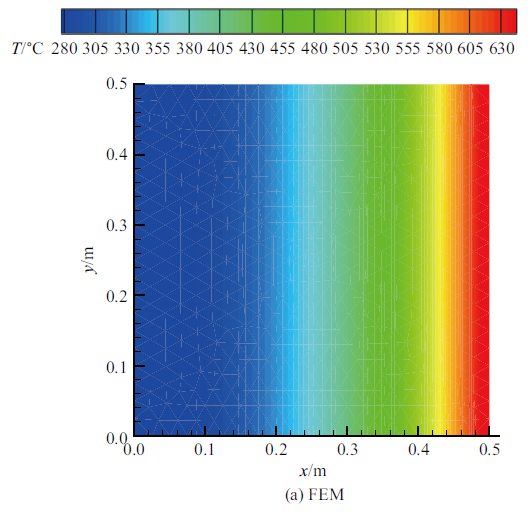
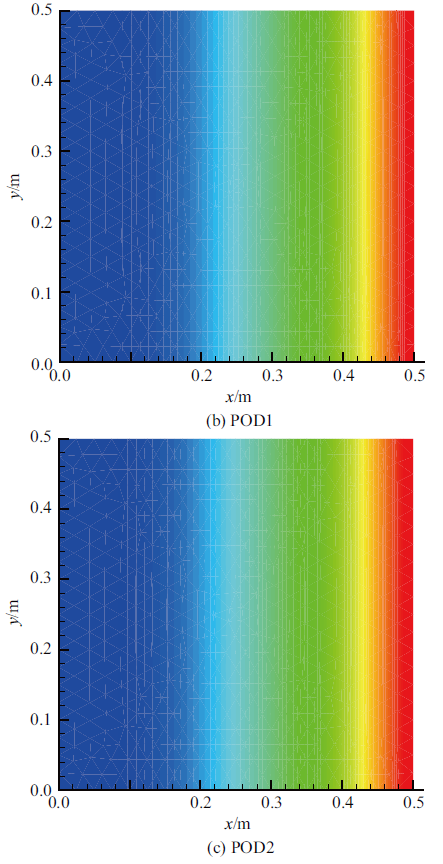
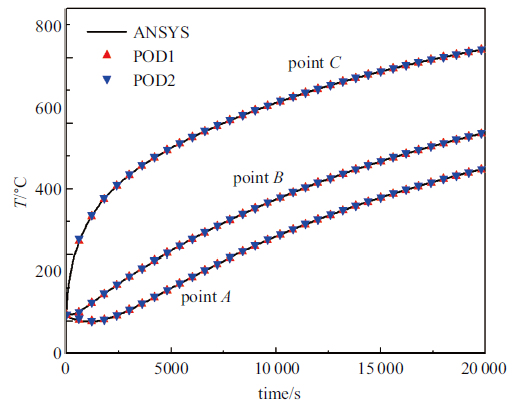
图3 给出了有限元全阶分析、常规降阶分析和新型降阶分析三种方法得到的方板在10 000 s时刻的温度场对比, 可以看到三者是高度一致的.图4 给出了方板上3个参考点的温度时变曲线, 它将常规降阶分析和新型降阶分析两种方法的计算结果与商业有限元软件ANSYS对此全阶模型的计算结果(图中以实线表示)进行比较,可见新型降阶算法POD2与常规的降阶算法POD1一样,在所研究的整个时间范围内能够得到与有限元方法吻合的结果. 因此,这些研究结果表明基于POD的模型降阶方法能够用于瞬态非线性热传导问题的分析并得出与有限元方法相同的结果,而所提出的新型算法POD2也可以得到正确的结果.
图 3
图 3
三种算法10 000 s时刻方板的温度场对比
Fig. 3
Comparison of temperature distributions in the square plate at $t=10 000$ s using different algorithms
图 3
图 3
三种算法10 000 s时刻方板的温度场对比(续)
Fig. 3
Comparison of temperature distributions in the square plate at $t=10 000$ s using different algorithms (continued)
图 4
图 4
参考点处温度随时间的变化曲线
Fig. 4
Temperature evolutions at reference points
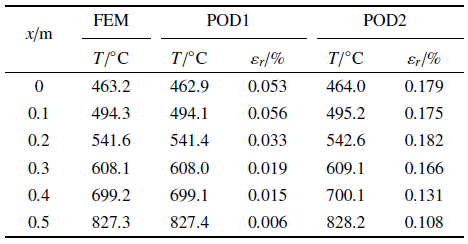
下面进一步对降阶模型新型算法的计算精度进行定量分析. 首先, 在方板的上边线上取等间距的6个点, 将其10 000 s时刻的计算温度和相对误差列于表1 .相对误差是以有限元全阶模型的计算结果为基准的误差, 其计算式为
(42) $ \begin{eqnarray} \label{eq42} \varepsilon _r =\frac{\left| {T_{\rm POD} -T_{\rm FEM} } \right|}{T_{\rm FEM} }\times 100\% \end{eqnarray}$
可见, 该时刻下POD2算法的相对误差相比于POD1算法略微增加, 这是因为POD2算法不仅包含POD1算法的模态截断误差, 还附加了线性化误差. 但是POD2算法的相对误差不超过0.2%, 仍然保持了比较高的精度, 因而这种新型算法的计算结果是准确的.
其次, 考虑所研究时间范围内各个时刻的方板整体温度的降阶模型计算误差, 采用均方根误差(root mean square error, RMSE)这一指标来衡量其大小
(43) $ \begin{eqnarray} \label{eq43} &&{\rm RMSE}\left( t \right)=\frac{\left\| {{T}_{\rm POD} \left( t \right)-{T}_{\rm FEM} \left( t \right)} \right\|_2 }{\left\| {{T}_{\rm FEM} \left( t \right)} \right\|_2 }\times\\&&\frac{1}{\sqrt {n_{\rm node} } }\times 100\% \end{eqnarray}$
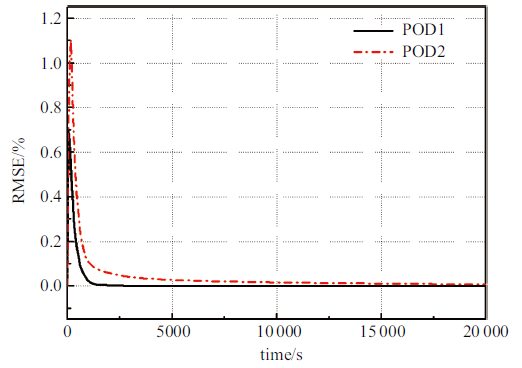
图5 给出了RMSE的时变曲线, 可见降阶模型的计算误差在经过起始很短时间的脉动后迅速趋近于零, 其峰值仅为1.1%. 图中也显示出新型算法POD2的误差略大于常规算法POD1, 其原因如前所述.
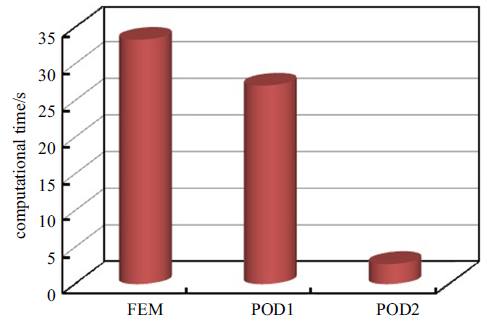
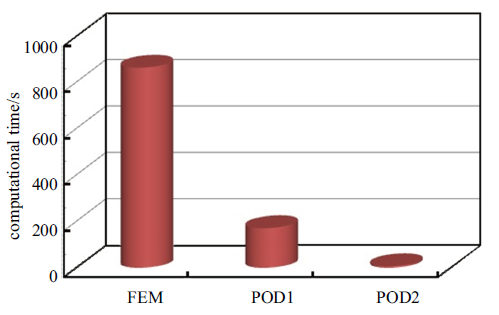
图6 对有限元全阶分析、常规降阶分析和新型降阶分析3种方法花费的计算时间进行了比较, 可以直观看到POD1用的计算时间较FEM略有减少, 而POD2用的计算时间则大幅减少, 这表明采用常规算法分析瞬态非线性热传导降阶模型时的计算效率并不比有限元全阶分析有明显改进, 而采用新型算法对降阶分析计算效率的提高是非常显著的.
图 5
图 5
方板温度的均方根误差随时间的变化曲线
Fig. 5
Temporal variation of the RMSE for Example 1
图 6
图 6
各种算法所用计算时间的比较
Fig. 6
Comparison of computational times cost by various algorithms for Example 1
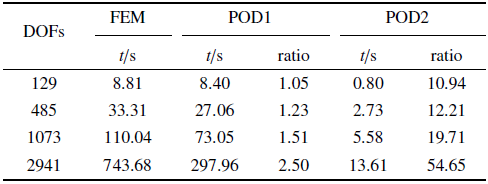
下面改变方板计算域的节点密度, 使有限元全阶模型的自由度数量从129逐渐增加到2941, 分析这个因素对降阶模型POD1和POD2两种算法计算效率的影响. 表2 中列出了不同自由度下各种算法所花费的计算时间, 同时给出了POD1和POD2的倍率数值. 倍率是有限元全阶分析与POD降阶分析所用计算时间的比值, 其大小可以衡量降阶分析对计算效率提升效果的强弱. 由表可见, 常规算法POD1的计算效率提高得不多, 尤其是在自由度数量较小时, 降阶分析所用的计算时间几乎与全阶分析的相近. 与之相比, 新型算法POD2的计算效率则提高了2个数量级, 而且在自由度数量较小时, 降阶分析所用的计算时间也是大幅减少. 此外, 随着自由度数量的增大, 新型算法POD2对计算效率的增幅愈加显著.
最后, 考虑到非线性热传导问题的有限元全阶分析往往要花费较长的计算时间, 而且实际工程上面对着各种复杂的热边界条件, 测试也比较的困难, 导致获取相应问题的模态矩阵建立其降阶模型既耗时又不易. 如果能够用简单的定常热边界条件下建立的降阶模型对相同计算域在复杂时变热边界条件下的瞬态非线性热传导过程进行分析和预测, 将是非常有意义和应用价值的. 为此, 下面采用图1 中定常热边界条件下建立的方板瞬态非线性热传导降阶模型来分析其在新的时变热边界条件下的热传导过程, 以检验这种方法的可行性.
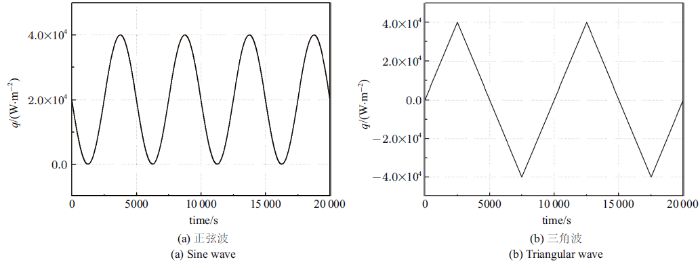
保持方板右侧对流换热条件和上、下侧绝热条件不变, 将其左侧改为时变的放热热流边界, 如图7 所示, 有二种情况:
$ \begin{eqnarray*} q=2\times 10^4\times\left[ {1-\sin \left( {\frac{\pi }{2500}t} \right)} \right]~{\rm W/m}^2 \end{eqnarray*} $
的形式光滑连续变化, 在0$\sim $20 000 s的时间范围内周期性变化4次.
(b)时变边界2: 热流密度按三角波的形式非光滑连续变化, 波动幅度增大为时变边界1的两倍, 而在0$\sim $20 000 s的时间范围内周期性变化次数则减少到两次.
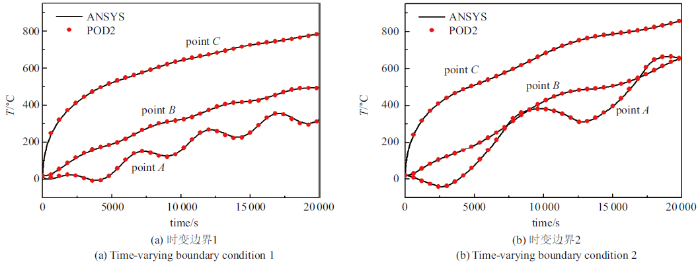
采用新型算法POD2对前面定常热边界条件下建立的方板瞬态非线性热传导降阶模型进行计算, 得到两种新的时变边界条件下方板的温度场, 图8 所示为3个参考点上的温度变化. 由图可见, 点A处的温度明显呈现出波动状升温的过程, 因为该点就处于左侧时变热边界上, 甚至在时变边界2的条件下,处于方板右侧边界上的点C也由于左侧大幅度变化的热流边界而使其温度呈现出轻微的波动. 为验证该降阶模型计算结果的准确性, 图中同时以曲线形式给出了ANSYS对相应边界条件下方板温度场的模拟结果, 可见两者是完全吻合的, 因此用定常热边界条件下建立的瞬态非线性热传导降阶模型能够准确有效的对相同计算域在各种复杂的时变热边界条件下的热传导过程进行分析与预测.
图 7
图 7
方板左侧施加的时变热流
Fig. 7
Time-varying heat flux on the left side of the square plate
图 8
图 8
时变边界下参考点处温度的时变曲线
Fig. 8
Temperature evolutions at reference points under time-varying boundary conditions
3.2 算例2: 散热器的瞬态非线性热传导问题
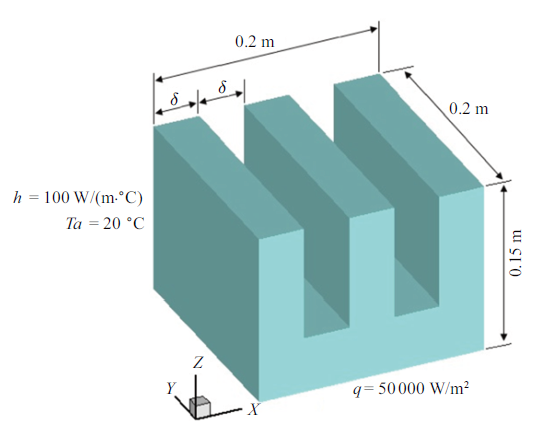
考虑一个三维结构的散热器, 如图9 所示, 其底面为边长0.2 m的方形, 高为0.15 m. 3个翅片的厚度及其间距均为$\delta$, $\delta =0.04$ m, 翅片高为0.1 m. 材料的密度$\rho =7800$ kg/m$^{3}$、比热容$c=400$ J/(kg$\cdot {^\circ}$C)、导热系数随温度线性变化, $k=60+0.05T$ W/(m$\cdot {^\circ}$C). 散热器的初始温度为20℃, 其底面是与发热体接触的加热面, 热流密度50 000 W/m$^{2}$; 翅片与环境气体间进行对流换热, 换热系数100 W/(m$^{2}\cdot{^\circ}$C)、环境温度20℃; 其余表面均为绝热面.散热器的有限元模型如图10 所示. 计算域采用六面体单元进行离散, 总计4400个单元、5796个节点. 为便于后处理, 取中部翅片的角点$A$和$B$作为参考点, 以及边线$CD$进行温度分析.
图 9
图 9
散热器的几何模型及热边界条件
Fig. 9
Geometric model and thermal boundary conditions of the radiator
图 10
图 10
散热器的有限元模型
Fig. 10
Finite element model of the radiator
与算例1一样, 为建立散热器的瞬态非线性热传导降阶模型, 采取数值模拟的方法构造瞬像矩阵: 时间步长取5 s, 通过有限元法计算0$\sim $500 s时间范围内散热器温度场的变化, 选取$t=25$, 50, $\cdots$, 500 s共计20个时刻点上的温度场构成瞬像矩阵${A}$. 对${A}$进行特征正交分解分析, 截取前5个特征值 (即$r=5$)对应的POD模态构造模态矩阵${\varPhi }$. 利用式(15)可以得到仅包含5个非线性方程的降阶模型, 相比于由5796个非线性方程组成的有限元全阶模型, 方程组的规模急剧减小.
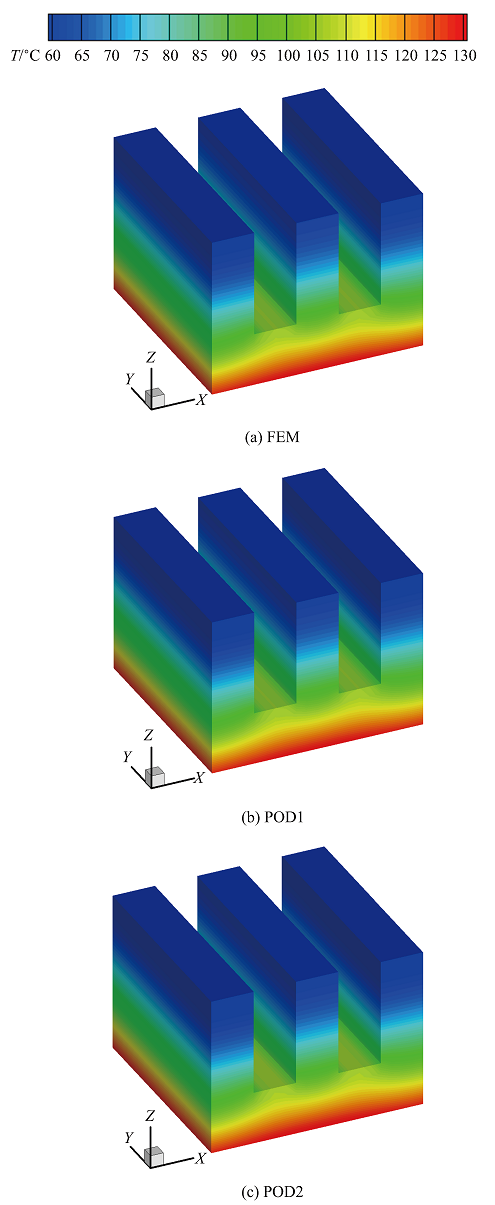
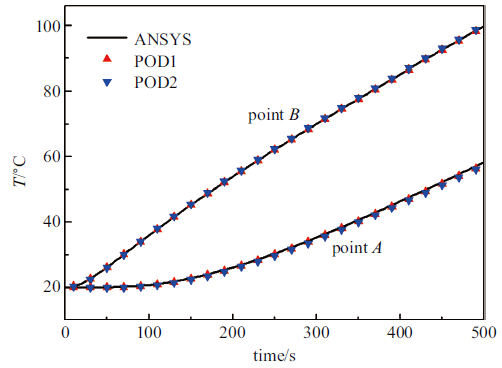
图11 给出了有限元全阶分析、常规降阶分析和新型降阶分析3种方法得到的散热器在末时刻500 s时的温度场对比, 可以看到三者基本上是相同的. 图12 给出了散热器上$A$, $B$二个参考点的温度时变曲线, 图中将POD1和POD2两种降阶模型算法的计算结果与商业有限元软件ANSYS对全阶模型的计算结果进行了比较, 同样可以看到新型算法POD2与常规算法POD1一样能够得到与有限元方法吻合的结果. 因此本文提出的新型算法POD2可以对瞬态非线性热传导问题进行准确的分析.
图 11
图 11
三种算法500 s时刻散热器的温度场对比
Fig. 11
Comparison of temperature distributions in the radiator at $t$=500 s using different algorithms
图 12
图 12
参考点处温度随时间的变化曲线
Fig. 12
Temperature evolutions at reference points
在散热器的边线CD上取等间距的6个点, 将其500 s时刻的计算温度和相对误差列于表3 中. 由表可见, 与算例1类似, 该时刻下POD2算法的相对误差相比于POD1算法略微增大. 常规算法POD1的最大相对误差约为1.12%, 而新型算法POD2的最大相对误差约为1.81%,因而这种新型算法仍然保持了比较高的精度, 其计算结果是准确的.
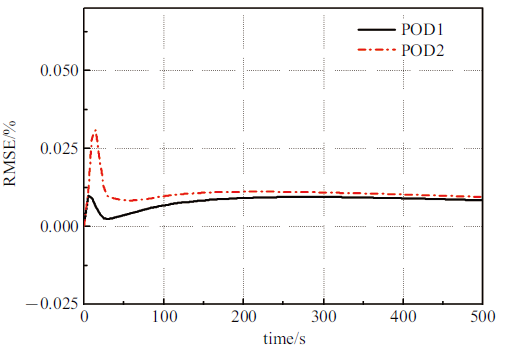
图13 给出了用POD1和POD2两种降阶模型算法计算得到的散热器整体温度的均方根误差RMSE的时变曲线, 可以看到降阶模型的计算误差经过起始时间的脉动, 在约200 s后缓慢稳定下降. POD1和POD2的脉动峰值分别为0.01%和0.03%. 降阶模型的计算误差在稳定段基本小于0.01%, 新型算法POD2的误差略大于常规算法POD1.
图14 对散热器算例采用有限元全阶分析、常规降阶分析和新型降阶分析3种方法花费的计算时间进行了比较. 由图可见, 由于该算例的自由度数量比较大, 有限元全阶分析需花费长达约862 s的计算时间, 此时常规降阶分析和新型降阶分析花费的计算时间均有不同程度减少, 尤其是后者, 用时仅为7 s, 计算效率提高了将近123倍.
图 13
图 13
散热器温度的均方根误差随时间的变化曲线
Fig. 13
Temporal variation of the RMSE for Example 2
图 14
图 14
各种算法所用计算时间的比较
Fig. 14
Comparison of computational times cost by various algorithms for Example 2
3.3 新型算法的特性分析
通过前面两个算例的计算分析, 验证了本文提出的降阶模型新型算法是准确有效的, 特别是在计算效率方面, 较常规算法有大幅度的提升.
与近年来发展的针对瞬态非线性热传导问题的其它一些降阶算法相比, 本文的新型算法也具有更高的计算效率. 表4 中列有IGA-IC[30 ] 、TLD-MS[28 ] 和CA[29 ] 等一些方法对自由度数量与本文算例尽量接近的算例所用的计算时间, 二维问题和三维问题分栏给出. 须说明的是, CA方法的计算时间文献中未直接给出, 是从其图上提取的, 故标为约数. 考虑到各个研究者所用计算机性能的不同,对计算时间是有影响的, 故表中同时给出了倍率值(全阶与降阶计算时间的比值), 以更客观的评价各种方法对降阶模型计算效率的提升效果. 由表可见, 本文的POD2方法在计算效率上较其它方法是占优的, 特别是三维问题. 而二维问题中TLD-MS方法的计算效率虽然接近POD2方法, 但该方法需要建立疏、密两套网格, 算法繁杂, 既存在网格匹配的要求, 又会因不同网格间的插值造成精度损失, 不利于通用软件的编制和实际工程的应用.
4 结论
本文针对导热系数随温度变化的一类瞬态非线性热传导问题, 发展并提出了一种基于POD模型降阶技术的新型高效快速分析方法. 通过单元预转换方法和多级线性化方法的有效结合解决了非线性降阶模型的常规计算方法在系数矩阵更新和迭代等计算环节的费时问题, 从而能够获得很高的计算效率.
通过二维和三维算例分析, 演示了瞬态非线性热传导降阶模型新型计算方法的应用细节, 通过与全阶模型有限元法计算结果的比较, 验证了该新型算法的准确性, 并通过与降阶模型常规计算方法以及近年来发展出的其他新方法在计算时间上的比较, 验证了该新型算法的高效性.
研究结果表明, 该新型算法具有良好的特性: 其一, 计算稳定性好, 算法基于的隐式时间推进格式和多级线性化格式均为无条件稳定; 其二, 计算速度快, 常规算法在全阶模型自由度数量较小时计算时间没有明显减少, 而新型算法无论自由度数量是大是小都能够加快计算速度, 并且自由度数量越多计算效率的提升效果越好, 在本文自由度数量不超过6000的小规模计算中其计算效率能提高2$\sim $3个数量级; 其三, 计算通用性好, 便于编制规范、统一的程序和软件, 有利于实际应用.
此外, 采用常数热边界条件下得到的POD模态建立的瞬态非线性热传导降阶模型可以对相同计算域在各种复杂的光滑/非光滑时变热边界条件下的非线性热传导过程进行快速、准确的分析和预测,
这进一步拓展了本文所提降阶模型新型算法在工程应用中的价值.
参考文献
View Option
[1]
Shih TM Sung CH Yang B . A numerical method for solving nonlinear heat transfer equations.
Numerical Heat Transfer, Part B: Fundamentals , 2008 ,54 (4 ):338 -353
[本文引用: 1]
[2]
李艾伦 , 傅卓佳 , 李柏纬 等 . 含肿瘤皮肤组织传热分析的广义有限差分法
力学学报 , 2018 ,50 (5 ):1198 -1205
[本文引用: 1]
( Li Ailun Fu Zhuojia Li Powei , et al . Generalized finite difference method for bioheat transfer analysis on skin tissue with tumors
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (5 ):1198 -1205 (in Chinese))
[本文引用: 1]
[3]
Li E Zhang ZP He ZC , et al . Smoothed finite element method with exact solutions in heat transfer problems
International Journal of Heat and Mass Transfer , 2014 ,78 :1219 -1231
[本文引用: 1]
[4]
Zhang J Chauhan S . Fast explicit dynamics finite element algorithm for transient heat transfer
International Journal of Thermal Science , 2019 ,139 :160 -175
[5]
刘硕 , 方国东 , 王兵 等 . 近场动力学与有限元方法耦合求解热传导问题
力学学报 , 2018 ,50 (2 ):339 -348
[本文引用: 1]
( Liu Shuo Fang Guodong Wang Bing , et al . Study of thermal conduction problem using coupled peridynamics and finite element method
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (2 ):339 -348 (in Chinese))
[本文引用: 1]
[6]
Copur M Eruslu MN . Finite volume modeling of the solidification of an axial steel cast impeller
Metalurgija , 2014 ,53 (2 ):149 -154
[本文引用: 1]
[7]
顾元宪 , 陈飚松 , 张洪武 等 . 非线性瞬态热传导的精细积分方法
大连理工大学学报 , 2000 ,40 (S1 ):24 -28
[本文引用: 1]
( Gu Yuanxian Chen Biaosong Zhang Hongwu , et al . Precise time integration method for solution of nonlinear transient heat conduction
Journal of Dalian University of Technology , 2000 ,40 (S1 ):24 -28 (in Chinese))
[本文引用: 1]
[8]
Tang JN Huang M Zhao YY , et al . A new procedure for solving steady-state and transient-state nonlinear radial conduction problems of nuclear fuel rods
Annaual Nuclear Energy , 2017 ,110 :492 -500
[本文引用: 1]
[9]
Yang K Peng HF Wang J , et al . Radial integration BEM for solving transient nonlinear heat conduction with temperature-dependent conductivity
International Journal of Heat and Mass Transfer , 2017 ,108 :1551 -1559
[本文引用: 1]
[10]
Cui M Xu BB Lv J , et al . Numerical solution of multi-dimensional transient nonlinear heat conduction problems with heat sources by an extended element differential method
International Journal of Heat and Mass Transfer , 2018 ,126 :1111 -1119
[本文引用: 1]
[11]
Gao XW Huang SZ Cui M , et al . Element differential method for solving general heat conduction problems
International Journal of Heat and Mass Transfer , 2017 ,115 :882 -894
[本文引用: 1]
[12]
Kunisch K Volkwein S . Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics
SIAM Journal of Numerical Analyze , 2002 ,40 (2 ):492 -515
[本文引用: 1]
[13]
段焰辉 , 吴文华 , 范召林 等 . 基于本征正交分解的气动优化设计外形数据挖掘
物理学报 , 2017 ,66 (22 ):220203
[本文引用: 1]
( Duan Yanhui Wu Wenhua Fan Zhaolin , et al . Proper orthogonal decomposition-based data mining aerodynamic shape for design optimization
Acta Physica Sinica , 2017 ,66 (22 ):220203 (in Chinese))
[本文引用: 1]
[14]
Krysl P Lall S Marsden JE . Dimensional model reduction in nonlinear finite element dynamics of solids and structures
International Journal of Numerical Methods in Engineering , 2001 ,51 (4 ):479 -504
[本文引用: 1]
[15]
郑保敬 , 梁钰 , 高效伟 等 . 功能梯度材料动力学问题的POD模型降阶分析
力学学报 , 2018 ,50 (4 ):787 -797
( Zheng Baojing Liang Yu Gao Xiaowei , et al . Analysis for dynamic response of functionally graded materials using POD based reduced order model
Chinese Journal of Theoretical and Applied Mechanics , 2018 ,50 (4 ):787 -797 (in Chinese))
[16]
芮珍梅 , 陈建兵 . 加性非平稳激励下结构速度响应的FPK方程降维
力学学报 , 2019 ,51 (3 ):922 -931
[本文引用: 1]
( Rui Zhenmei Chen Jianbing . Dimension reduction of FPK equation for velocity response analysis of structures subjected to additive nonstationary excitations
Chinese Journal of Theoretical and Applied Mechanics , 2019 ,51 (3 ):922 -931 (in Chinese))
[本文引用: 1]
[17]
Ravindran SS . A reduced-order approach for optimal control of fluids using proper orthogonal decomposition
International Journal of Numerical Methods in Fluids , 2000 ,34 (5 ):425 -448
[本文引用: 1]
[18]
Leibfritz F Volkwein S . Reduced order output feedback control design for PDE systems using proper orthogonal decomposition and nonlinear semi-definite programming
Linear Algebra Application , 2006 ,415 (2-3 ):542 -575
[本文引用: 1]
[19]
Biaecki RA Kassab AJ Fic A . Proper orthogonal decomposition and modal analysis for acceleration of transient FEM thermal analysis
International Journal of Numerical Methods in Engineering , 2005 ,62 (2 ):774 -797
[本文引用: 1]
[20]
Zhang XH Xiang H . A fast meshless method based on proper orthogonal decomposition for the transient heat conduction problems
International Journal of Heat and Mass Transfer , 2015 ,84 :729 -739
[本文引用: 1]
[21]
Gao XW Hu JX Huang SZ . A proper orthogonal decomposition analysis method for multimedia heat conduction problems
ASME Journal of Heat Transfer , 2016 ,138 (7 ):071301
[本文引用: 1]
[22]
胡金秀 , 高效伟 . 变系数瞬态热传导问题边界元格式的特征正交分解降阶方法
物理学报 , 2016 ,65 (1 ):014701
[本文引用: 1]
( Hu Jinxiu Gao Xiaowei . Reduced order model analysis method via proper orthogonal decomposition for variable coefficient of transient heat conduction based on boundary element method
Acta Physica Sinica , 2016 ,65 (1 ):014701 (in Chinese))
[本文引用: 1]
[23]
冯俞楷 , 杜小泽 , 杨立军 . 非稳态导热基于温度梯度的本征正交分解降维方法
中国科学: 技术科学 , 2018 ,48 (1 ):39 -47
[本文引用: 1]
( Feng Yukai Du Xiaoze Yang Lijun . Extrapolating POD reduced-order model based on temperature gradient for unsteady heat conduction
Scientia Sinica Technologica , 2018 ,48 (1 ):39 -47 (in Chinese))
[本文引用: 1]
[24]
Kerschen G Golinval JC Vakakis AF , et al . The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: An overview
Nonlinear Dynamical , 2005 ,41 (1-3 ):147 -169
[本文引用: 1]
[25]
Binion D Chen XL . A Krylov enhanced proper orthogonal decomposition method for efficient nonlinear model reduction
Finite Elements Analyze and Design , 2011 ,47 (7 ):728 -738
[本文引用: 1]
[26]
Fic A Biaecki RA Kassab AJ . Solving transient nonlinear heat conduction problems by proper orthogonal decomposition and the finite-element method.
Numerical Heat Transfer, Part B: Fundamentals , 2005 ,48 (2 ):103 -124
[本文引用: 1]
[27]
Han DX Yu B Zhang XY . Study on a BFC-Based POD-Galerkin reduced-order model for the unsteady-state variable-property heat transfer problem.
Numerical Heat Transfer, Part B: Fundamentals , 2014 ,65 (3 ):256 -281
[本文引用: 1]
[28]
Gaonkar AK Kulkarni SS . Application of multilevel scheme and two level discretization for POD based model order reduction of nonlinear transient heat transfer problems
Computational Mechanics , 2015 ,55 (1 ):179 -191
[本文引用: 2]
[29]
Feng SZ Cui XY Li AM . Fast and efficient analysis of transient nonlinear heat conduction problems using combined approximations (CA) method
International Journal of Heat and Mass Transfer , 2016 ,97 :638 -644
[本文引用: 2]
[30]
Ding CS Cui XY Deokar RR , et al . An isogeometric independent coefficients (IGA-IC) reduced order method for accurate and efficient transient nonlinear heat conduction analysis.
Numerical Heat Transfer, Part A: Applications , 2018 ,73 (10 ):667 -684
[本文引用: 2]
[31]
梁钰 , 郑保敬 , 高效伟 等 . 基于POD模型降阶法的非线性瞬态热传导分析
中国科学: 物理学力学天文学 , 2018 ,48 (12 ):124603
[本文引用: 2]
( Liang Yu Zheng Baojing Gao Xiaowei , et al . Reduced order model analysis method via proper orthogonal decomposition for nonlinear transient heat conduction problems.
Scientia Sinica Physica, Mechanica & Astronomica , 2018 ,48 (12 ):124603 (in Chinese))
[本文引用: 2]
[32]
Liang YC Lee HP Lim SP , et al . Proper orthogonal decomposition and its applications-Part I: Theory
Journal of Sound and Vibration , 2002 ,252 (3 ):527 -544
[本文引用: 1]
[33]
Hogge MA . A comparison of two- and three-level integration schemes for non-linear heat conduction//Lewis RW, Morgan K, Zienkiewics eds. Numerical Methods in Heat Transfer.
Chichester, UK: Wiley , 1981 : 75 -90
[本文引用: 1]
A numerical method for solving nonlinear heat transfer equations.
1
2008
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
含肿瘤皮肤组织传热分析的广义有限差分法
1
2018
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
含肿瘤皮肤组织传热分析的广义有限差分法
1
2018
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Smoothed finite element method with exact solutions in heat transfer problems
1
2014
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Fast explicit dynamics finite element algorithm for transient heat transfer
2019
近场动力学与有限元方法耦合求解热传导问题
1
2018
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
近场动力学与有限元方法耦合求解热传导问题
1
2018
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Finite volume modeling of the solidification of an axial steel cast impeller
1
2014
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
非线性瞬态热传导的精细积分方法
1
2000
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
非线性瞬态热传导的精细积分方法
1
2000
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
A new procedure for solving steady-state and transient-state nonlinear radial conduction problems of nuclear fuel rods
1
2017
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Radial integration BEM for solving transient nonlinear heat conduction with temperature-dependent conductivity
1
2017
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Numerical solution of multi-dimensional transient nonlinear heat conduction problems with heat sources by an extended element differential method
1
2018
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Element differential method for solving general heat conduction problems
1
2017
... 瞬态非线性热传导问题在实际工程中普遍存在, 这是因为材料的热物性参数通常是随温度变化的. 由于这类问题的复杂性, 很难得到其解析解, 一般采用有限差分法[1 -2 ] 、有限元法[3 -5 ] 、有限体积法[6 ] 等传统的数值方法得到其近似解. 鉴于这类问题的重要性, 研究者仍不断致力于发展新的求解手段. 比如, 顾元宪等[7 ] 采用精细积分法求解瞬态非线性热传导问题, 推导了热传导方程精细积分的具体列式; Tang等[8 ] 采用半边界法(half-boundary method, HBM)求解核燃料棒的一维瞬态非线性热传导问题; Yang等[9 ] 采用径向积分边界元法(radial integration boundary element method, RIBEM)求解导热系数随温度变化形成的瞬态非线性热传导问题; Cui等[10 ] 采用Gao等[11 ] 近年提出的单元微分法(element differential method, EDM)求解多维瞬态非线性热传导问题. 然而, 这些数值方法在对工程中的大型、复杂系统进行求解时, 得到的离散方程规模巨大, 其自由度数量可达数百万甚至千万, 这一方面对计算机的性能和存储容量提出了极高的要求, 另一方面需要耗费大量的计算时间, 无法满足一些需要对温度进行实时控制或快速预测的领域的要求. 为此,特征正交分解(proper orthogonal decomposition, POD)作为一种有效的模型降阶方法, 能够将高维系统转变为低维系统, 从而大大缩短计算所需要的时间, 因此是解决这个问题的重要途径. ...
Galerkin proper orthogonal decomposition methods for a general equation in fluid dynamics
1
2002
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
基于本征正交分解的气动优化设计外形数据挖掘
1
2017
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
基于本征正交分解的气动优化设计外形数据挖掘
1
2017
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
Dimensional model reduction in nonlinear finite element dynamics of solids and structures
1
2001
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
功能梯度材料动力学问题的POD模型降阶分析
2018
功能梯度材料动力学问题的POD模型降阶分析
2018
加性非平稳激励下结构速度响应的FPK方程降维
1
2019
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
加性非平稳激励下结构速度响应的FPK方程降维
1
2019
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
A reduced-order approach for optimal control of fluids using proper orthogonal decomposition
1
2000
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
Reduced order output feedback control design for PDE systems using proper orthogonal decomposition and nonlinear semi-definite programming
1
2006
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
Proper orthogonal decomposition and modal analysis for acceleration of transient FEM thermal analysis
1
2005
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
A fast meshless method based on proper orthogonal decomposition for the transient heat conduction problems
1
2015
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
A proper orthogonal decomposition analysis method for multimedia heat conduction problems
1
2016
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
变系数瞬态热传导问题边界元格式的特征正交分解降阶方法
1
2016
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
变系数瞬态热传导问题边界元格式的特征正交分解降阶方法
1
2016
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
非稳态导热基于温度梯度的本征正交分解降维方法
1
2018
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
非稳态导热基于温度梯度的本征正交分解降维方法
1
2018
... POD方法又被称为主成分分析(principal component analysis, PCA)或奇异值分解(singular value decomposition, SVD), 在流体力学[12 -13 ] 、结构动力学[14 -16 ] 、最优控制[17 -18 ] 等诸多领域都得到广泛应用. 在传热学领域, Biaecki等[19 ] 采用POD方法对瞬态线性热传导问题的有限元模型进行降阶, 使计算效率得到显著提高; Zhang和Xiang[20 ] 将POD方法和无网格法结合建立了瞬态线性热传导问题的降阶模型, 在保持计算精度的同时使计算时间大为减少;Gao等[21 ] 提出了一种多域POD方法, 能够对由多种常物性材料组成的复杂求解域的瞬态热传导过程进行快速分析; 胡金秀和高效伟[22 ] 建立了变系数瞬态热传导问题边界元格式的POD降阶模型, 解决了边界元法计算速度慢、算法稳定性差的问题; 冯俞楷等[23 ] 提出从温度场的梯度提取POD模态建立瞬态线性热传导问题的降阶模型, 不仅提高了计算效率, 还具有更强的外推能力. 这些研究展示出基于POD的模型降阶方法在处理线性热传导问题时的高效性及其与各种数值方法结合的广泛适用性. ...
The method of proper orthogonal decomposition for dynamical characterization and order reduction of mechanical systems: An overview
1
2005
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
A Krylov enhanced proper orthogonal decomposition method for efficient nonlinear model reduction
1
2011
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
Solving transient nonlinear heat conduction problems by proper orthogonal decomposition and the finite-element method.
1
2005
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
Study on a BFC-Based POD-Galerkin reduced-order model for the unsteady-state variable-property heat transfer problem.
1
2014
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
Application of multilevel scheme and two level discretization for POD based model order reduction of nonlinear transient heat transfer problems
2
2015
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
... 与近年来发展的针对瞬态非线性热传导问题的其它一些降阶算法相比, 本文的新型算法也具有更高的计算效率. 表4 中列有IGA-IC[30 ] 、TLD-MS[28 ] 和CA[29 ] 等一些方法对自由度数量与本文算例尽量接近的算例所用的计算时间, 二维问题和三维问题分栏给出. 须说明的是, CA方法的计算时间文献中未直接给出, 是从其图上提取的, 故标为约数. 考虑到各个研究者所用计算机性能的不同,对计算时间是有影响的, 故表中同时给出了倍率值(全阶与降阶计算时间的比值), 以更客观的评价各种方法对降阶模型计算效率的提升效果. 由表可见, 本文的POD2方法在计算效率上较其它方法是占优的, 特别是三维问题. 而二维问题中TLD-MS方法的计算效率虽然接近POD2方法, 但该方法需要建立疏、密两套网格, 算法繁杂, 既存在网格匹配的要求, 又会因不同网格间的插值造成精度损失, 不利于通用软件的编制和实际工程的应用. ...
Fast and efficient analysis of transient nonlinear heat conduction problems using combined approximations (CA) method
2
2016
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
... 与近年来发展的针对瞬态非线性热传导问题的其它一些降阶算法相比, 本文的新型算法也具有更高的计算效率. 表4 中列有IGA-IC[30 ] 、TLD-MS[28 ] 和CA[29 ] 等一些方法对自由度数量与本文算例尽量接近的算例所用的计算时间, 二维问题和三维问题分栏给出. 须说明的是, CA方法的计算时间文献中未直接给出, 是从其图上提取的, 故标为约数. 考虑到各个研究者所用计算机性能的不同,对计算时间是有影响的, 故表中同时给出了倍率值(全阶与降阶计算时间的比值), 以更客观的评价各种方法对降阶模型计算效率的提升效果. 由表可见, 本文的POD2方法在计算效率上较其它方法是占优的, 特别是三维问题. 而二维问题中TLD-MS方法的计算效率虽然接近POD2方法, 但该方法需要建立疏、密两套网格, 算法繁杂, 既存在网格匹配的要求, 又会因不同网格间的插值造成精度损失, 不利于通用软件的编制和实际工程的应用. ...
An isogeometric independent coefficients (IGA-IC) reduced order method for accurate and efficient transient nonlinear heat conduction analysis.
2
2018
... 虽然POD是依赖信号来重构系统的一种线性处理方法, 但研究表明它对于非线性系统也有一定的应用价值[24 -25 ] . 目前国内外对瞬态非线性热传导问题的模型降阶研究尚非常缺乏. Fic等[26 ] 初步研究了对瞬态非线性热传导问题采用POD方法建立其降阶模型的可行性,发现无需重新计算POD模态; Han等[27 ] 针对瞬态变物性热传导问题发展了基于适体坐标(body-fitted coordinate, BFC)和有限体积法的POD降阶模型. 尽管降阶分析能够准确地预测非线性热传导过程, 但是对计算效率的提升效果却远不及其对线性热传导问题的那样显著, 通常要小1$\sim $2个数量级. 其原因是在瞬态非线性热传导问题的迭代计算过程中, 每个迭代步都必须更新降阶模型的系数矩阵, 其关联计算会耗费大量时间. 于是POD降阶模型的计算效率成为制约其在瞬态非线性热传导问题中应用的关键, 也成为了近年来的研究热点. Gaonkar和Kulkarni[28 ] 采用两级离散和多级格式相结合的方法(two leveldiscretization - multilevel scheme, TLD-MS)有效提高了瞬态非线性热传导问题的POD降阶模型计算效率, 但该方法局限于结构化网格且存在网格匹配性要求以及插值引起额外的精度损失; Feng等[29 ] 采用组合近似方法(combined approximations, CA),而Ding等[30 ] 则采用等几何分析和独立系数相结合的方法(isogeometric analysis - independent coefficients, IGA-IC), 分别建立了瞬态非线性热传导问题的非POD降阶模型, 虽然提高了计算效率, 但在全阶模型的自由度数量较少时效果亦不明显. ...
... 与近年来发展的针对瞬态非线性热传导问题的其它一些降阶算法相比, 本文的新型算法也具有更高的计算效率. 表4 中列有IGA-IC[30 ] 、TLD-MS[28 ] 和CA[29 ] 等一些方法对自由度数量与本文算例尽量接近的算例所用的计算时间, 二维问题和三维问题分栏给出. 须说明的是, CA方法的计算时间文献中未直接给出, 是从其图上提取的, 故标为约数. 考虑到各个研究者所用计算机性能的不同,对计算时间是有影响的, 故表中同时给出了倍率值(全阶与降阶计算时间的比值), 以更客观的评价各种方法对降阶模型计算效率的提升效果. 由表可见, 本文的POD2方法在计算效率上较其它方法是占优的, 特别是三维问题. 而二维问题中TLD-MS方法的计算效率虽然接近POD2方法, 但该方法需要建立疏、密两套网格, 算法繁杂, 既存在网格匹配的要求, 又会因不同网格间的插值造成精度损失, 不利于通用软件的编制和实际工程的应用. ...
基于POD模型降阶法的非线性瞬态热传导分析
2
2018
... 在前期的研究中[31 ] , 我们发现可以采用瞬态线性热传导分析中得到的POD模态对相同求解域的瞬态非线性热传导问题建立降阶模型进行近似计算, 这虽然简化并加快了降阶模型的构建, 但并未涉及到如何解决非线性降阶模型计算耗时的关键问题. 本文对此展开了深入系统的高效算法研究, 结构安排如下:第二部分给出瞬态非线性热传导问题的有限元全阶模型及其计算方法; 第三部分先采用POD方法建立瞬态非线性热传导问题的降阶模型, 并简要介绍其常规计算方法, 然后重点阐述新型计算方法的基本理论; 第四部分通过二维和三维算例验证本文提出的瞬态非线性热传导降阶模型新型计算方法的准确性和高效性;最后进行总结. ...
... 对于需要实时控制或快速计算的工程领域, 有限元等常规的数值方法不能满足要求. 因为实际问题的自由度数量高达上千万甚至更多, 求解这种超大规模的非线性方程组需要很长的时间. 为此需要建立降阶模型以减小计算量, 从而达到实时控制或快速计算的目标. 根据本课题组前期的研究[31 ] , 基于特征正交分解方法建立的降阶模型能够对瞬态非线性热传导过程进行准确预测, 但是由于非线性问题的特殊性, 降阶模型在计算效率的提升方面不够显著, 本文致力于解决这一问题. 为保持文章的完整性, 下面简要介绍针对瞬态非线性热传导问题建立的降阶模型, 而关于特征正交分解方法的详细内容可参阅文献[32 ] . ...
基于POD模型降阶法的非线性瞬态热传导分析
2
2018
... 在前期的研究中[31 ] , 我们发现可以采用瞬态线性热传导分析中得到的POD模态对相同求解域的瞬态非线性热传导问题建立降阶模型进行近似计算, 这虽然简化并加快了降阶模型的构建, 但并未涉及到如何解决非线性降阶模型计算耗时的关键问题. 本文对此展开了深入系统的高效算法研究, 结构安排如下:第二部分给出瞬态非线性热传导问题的有限元全阶模型及其计算方法; 第三部分先采用POD方法建立瞬态非线性热传导问题的降阶模型, 并简要介绍其常规计算方法, 然后重点阐述新型计算方法的基本理论; 第四部分通过二维和三维算例验证本文提出的瞬态非线性热传导降阶模型新型计算方法的准确性和高效性;最后进行总结. ...
... 对于需要实时控制或快速计算的工程领域, 有限元等常规的数值方法不能满足要求. 因为实际问题的自由度数量高达上千万甚至更多, 求解这种超大规模的非线性方程组需要很长的时间. 为此需要建立降阶模型以减小计算量, 从而达到实时控制或快速计算的目标. 根据本课题组前期的研究[31 ] , 基于特征正交分解方法建立的降阶模型能够对瞬态非线性热传导过程进行准确预测, 但是由于非线性问题的特殊性, 降阶模型在计算效率的提升方面不够显著, 本文致力于解决这一问题. 为保持文章的完整性, 下面简要介绍针对瞬态非线性热传导问题建立的降阶模型, 而关于特征正交分解方法的详细内容可参阅文献[32 ] . ...
Proper orthogonal decomposition and its applications-Part I: Theory
1
2002
... 对于需要实时控制或快速计算的工程领域, 有限元等常规的数值方法不能满足要求. 因为实际问题的自由度数量高达上千万甚至更多, 求解这种超大规模的非线性方程组需要很长的时间. 为此需要建立降阶模型以减小计算量, 从而达到实时控制或快速计算的目标. 根据本课题组前期的研究[31 ] , 基于特征正交分解方法建立的降阶模型能够对瞬态非线性热传导过程进行准确预测, 但是由于非线性问题的特殊性, 降阶模型在计算效率的提升方面不够显著, 本文致力于解决这一问题. 为保持文章的完整性, 下面简要介绍针对瞬态非线性热传导问题建立的降阶模型, 而关于特征正交分解方法的详细内容可参阅文献[32 ] . ...
A comparison of two- and three-level integration schemes for non-linear heat conduction//Lewis RW, Morgan K, Zienkiewics eds. Numerical Methods in Heat Transfer.
1
1981
... 本文采用无条件稳定的Dupont II多级线性化格式来求解式(28), 此格式为[33 ] ...