射流对绕水翼云空化流动抑制机理研究 1)

doi:10.6052/0459-1879-19-282

射流对绕水翼云空化流动抑制机理研究 ¹⁾

王巍^,²⁾, 张庆典, 唐滔, 安昭阳, 佟天浩, 王晓放

大连理工大学能源与动力学院,海洋能源利用与节能教育部重点实验室,辽宁大连 116024

MECHANISM INVESTIGATION OF WATER INJECTION ON SUPPRESSING HYDROFOIL CLOUD CAVITATION FLOW ¹⁾

Wang Wei^,²⁾, Zhang Qingdian, Tang Tao, An Zhaoyang, Tong Tianhao, Wang Xiaofang

School of Energy and Power Engineering,Key Laboratory of Ocean Energy Utilization and Energy Conservation of Ministry of Education,Dalian University of Technology, Dalian 116024,Liaoning,China

通讯作者: 2) 王巍,副教授,主要研究方向：先进动力装置及流体机械设计和优化. E-mail:wangw@dlut.edu.cn

收稿日期: 2019-10-14 接受日期: 2019-12-8 网络出版日期: 2020-01-18

基金资助:

1) 国家自然科学基金. 51876022
国家重点基础研究发展计划. 2015CB057301

Received: 2019-10-14 Accepted: 2019-12-8 Online: 2020-01-18

作者简介 About authors

摘要

为理解绕水翼云空化流动的发展机理和探究水翼吸力面开孔射流的影响,采用密度修正的RNG $k$-$\varepsilon $湍流模型和Schnerr-Sauer空化模型对原始NACA66(mod) 水翼和采用射流后的水翼的云空化非定常过程进行模拟和对比分析;采用在水翼吸力面近壁区设立监测线的方法对近壁区的流场进行监测,得到近壁区汽相体积分数、回射流速度、压力及压力梯度的时空分布云图;开展了云空化流场特性的涡动力学分析,进而分析水翼云空化的发生机理和射流抑制空化的抑制机理. 结果表明：游离型空泡在下游溃灭时产生强烈的局部高压,其向上游传播导致前缘空穴的一次回缩,而空穴的二次回缩受回射流的影响. 回射流的发展区域受限于较高的压力梯度,高的压力梯度一直存在,但回射流在一个周期内的首次出现需要时间的积累. 在水翼吸力面射流使得射流孔附近压力升高,弥补了由于空化和绕流造成的压降,压力梯度增大,抗逆压能力增强,对回射流起到阻挡作用;另一方面,射流使得回射流区域面积和回射流的强度也有所减小,从而对云空化的发展起到抑制的效果. $Q$准则的涡结构云图相比于汽相体积分数云图能显示复杂的流动结构,前缘附着型空穴和尾缘游离型空穴内存在旋涡,回射流对空穴存在剪切作用造成空穴脱落. 而射流对空穴和回射流的剪切和阻挡使云空化发展得到抑制.

关键词： 空化抑制 ; 水翼 ; 回射流 ; 云空化 ; 涡结构

Abstract

In order to understand the development mechanism of cloud cavitation and investigate the influence of jet flow on the suction surface of hydrofoil, the unsteady evolution process of cloud cavitation of the original NACA66(mod) hydrofoil and the hydrofoil with jet flow is simulated and compared by using density modified RNG $k$-$\varepsilon $ turbulence model and Schnerr-Sauer cavitation model. Monitoring lines of the hydrofoil suction surface are adopted and then spatiotemporal evolution of the vapor phase volume fraction, re-entrant jet flow, pressure and pressure gradient near the hydrofoil wall is obtained. The flow field characteristics of the cloud cavitation are analyzed by vortex dynamic. The suppression mechanism of active jet is analyzed. The results show that the first retraction of the attached cavity is caused by the strong local high pressure when the dissociated cavity collapse downstream, and the second retraction is affected by the re-entrant jet. The re-entrant jet zone is limited to higher pressure gradient. High pressure gradient always exists, but the initial occurrence of re-entrant jet in a time period needs the accumulation of time. Jet flow on the suction surface of hydrofoil can reduce cloud cavitation. The suppression mechanism is that injected jet makes the pressure rise near jet holes, making up for the pressure drop caused by cavitation and circumfluence, so as to increase the pressure gradient and enhance the anti-pressure ability. On the other hand, the re-entrant jet strength is decreased. The vortex structure contour of Q criterion shows complex flow structure compared to the vapor phase volume fraction contour. Vortex cores are existed in the front attached cavity and dissociated cavity, while shear may be present in re-entrant jet zone. The shear function of the injected jet suppresses the development of cavitation and re-entrant jet.

Keywords： cavitation suppression ; hydrofoil ; re-entrant jet ; cloud cavitation ; vortex structure

PDF (28189KB) 元数据多维度评价相关文章导出 EndNote| Ris| Bibtex 收藏本文

本文引用格式

王巍, 张庆典, 唐滔, 安昭阳, 佟天浩, 王晓放. 射流对绕水翼云空化流动抑制机理研究 ¹⁾. 力学学报[J], 2020, 52(1): 12-23 DOI:10.6052/0459-1879-19-282

Wang Wei, Zhang Qingdian, Tang Tao, An Zhaoyang, Tong Tianhao, Wang Xiaofang. MECHANISM INVESTIGATION OF WATER INJECTION ON SUPPRESSING HYDROFOIL CLOUD CAVITATION FLOW ¹⁾. Chinese Journal of Theoretical and Applied Mechanics[J], 2020, 52(1): 12-23 DOI:10.6052/0459-1879-19-282

引言

空化存在于水力机械过流部件的低压区域,是一种复杂的水动力学现象,涉及湍流、相变、可压缩、非定常等复杂的流体力学问题^[1-3]. 空化的发生常伴随振动和噪声^[4],尤其是云空化发生时的非定常准周期性溃灭过程还会对船舶推进器^[5] 以及水利水电设备^[6]、液压机械^[7] 等过流部件造成持续性的冲击和疲劳损伤. 空化是造成流场流动不稳定的主要来源之一,为了确保水力机械高效、可靠和安全地运行,就必须要对流场流动的不稳定性进行主动控制和管理,至少避免和部分消除与系统过流部件发生共振现象的可能性. 这就需要研究者们深入研究流场不稳定的原因,系统产生低频压力脉动的原因,进而分析空化发生的机制和演变过程,揭示空化的抑制策略和抑制机理,寻找更高效和更有针对性的抑制方法.

近年来,国内外学者对流场流动不稳定的原因进行深入研究并将其分为两类：水力系统的不稳定性和固有不稳定性^[8].系统的不稳定性受系统不同过流部件的结构设计所影响而较少的被研究.固有不稳定性由空泡本身产生,在压力脉动频谱上表现出比前者更高的脉动频率,因而产生的危害更大,受到广大学者的重视.例如研究较为成熟的回射流机制^[9-10] 和近年来通过试验发现的激波机制^[11-14] 就属于固有不稳定性.在不同的工况下,回射流机制和激波机制各占主导地位,造成片空化失稳和片空化向云空化的演变.

水力机械云空化的控制目的在于减小因空化非定常特性造成的压力脉动,从而减小水力机械受到的应力.Tsujimoto等^[15-17]对水翼流动模型进行一维简化和分析,发现空化流动中的低频压力脉动与空穴积对时间的二阶导数成正比,揭示了空化流场中低频压力脉动产生的根源,将空化激振力与空化状态的关系进行了定量描述.在空化状态和发展的控制策略上,一般采取被动控制和主动控制的方法.被动控制是通过某种方式改变壁面特性来实现的,不需要向流场提供能量,因而容易实现,可操作性强.但很难实现对不同工况的交互精准调节^[18-20].主动控制通过采取注入气体、聚合物和水等的方法,实现对流场的控制.Timoshevskiy等^[21-22]和王巍等^[23]分别采用在水翼吸力面布置切向射流水槽和不同角度的射流水孔进行射流的方法,都实现了对水翼云空化的抑制.

先前的研究者通过实验和模拟等手段对云空化的发展过程进行了详细的研究,揭示了空化的演变过程和回射流与空穴间的相互作用. 但先前的研究更侧重于对云空化准周期过程选取若干个特征时刻,对这些特征时刻的流场进行研究从而来概括流场的整个非定常演变过程.本文设想既然人们更关注于空化对水翼叶型吸力面或其他过流部件造成的影响,则吸力面附近(吸力线)是研究的重点.另一方面,空化流动的涡动力特性逐渐成为空化研究的热点. Ji等^[24] 研究者综合Gopalan^[25]的实验结果,得出相比于气体体积分数云图,$Q$准则涡量图更能准确地反应流场中复杂的流场结构.因此,本文采用对数值模拟的瞬态结果一维简化的的方法,再增加时间维度重构二维的时空分布云图,用于研究云空化的非定常周期性演变过程和射流抑制空化的抑制机制.对流场的非定常空化形态与涡结构的相互关系进行研究,旨在研究射流抑制空化的深层次抑制机理.

1 数值模拟方法

1.1 控制方程

基于均相流模型的控制方程. 假定汽液两相为均质平衡流,两相间无滑移速度,则汽液两相的连续性方程和动量方程为^[26]

(1) $ \dfrac{\partial \rho _{\rm m} }{\partial t} + \dfrac{\partial \left( {\rho _{\rm m} u_j } \right)}{\partial x_j } = 0$

(2) $ \dfrac{\partial \rho _{\rm m} \mu _i }{\partial t} + \dfrac{\partial (\rho _{\rm m} \mu _i \mu _j )}{\partial x_j } = - \dfrac{\partial p}{\partial x_i } + \dfrac{\partial }{\partial x_j }\left[ {(\mu _{\rm m} + \mu _{\rm t} )(\dfrac{\partial \mu _i }{\partial x_j } + \dfrac{\partial \mu _j }{\partial x_i } - \dfrac{2}{3}\dfrac{\mu }{\partial x_j }\delta _{ij} )} \right]$

混合相密度和黏度为

(3) $ \rho _{\rm m} = \rho _{\rm l} \alpha _{\rm l} + \rho _{\rm v} \alpha _{\rm v}$

(4) $ \mu _{\rm m} = \mu _{\rm l} \alpha _{\rm l} + \mu _{\rm v} \alpha _{\rm v}$

式中,下标$i$和$j$代表坐标方向,$u$和$p$分别为混合相速度和压力, $\rho_{\rm m}$,$\mu_{\rm m}$和$\mu_{\rm t}$分别是混合相密度和混合相层流/湍流黏性系数, $\alpha$代表体积分数,下标l和v分别表示液相和汽相. 由于引入了新的未知量$\rho_{\rm l}$和$\rho_{\rm v}$,在求解空化流场时,除了需要对湍流进行封闭外,还需要求解汽液相密度,因此需要寻求混合相密度与其他量的关系,或引入空化模型进行求解. 本文的研究过程采用引入质量输运模型即空化模型进行方程封闭求解.

1.2 空化模型

空化模型是描述汽液两相相间转化关系的数学模型. 本文采用Schnerr-Sauer空化模型对汽液相密度进行求解. Schnerr-Sauer模型基于汽液均相流的假设,由Rayleigh-Plesset方程推导而来^[27]. 蒸汽体积分数具有如下的一般表达形式

(5) $ \dfrac{\partial }{\partial {\rm t}}(a_{\rm v} \rho _{\rm v} ) + \nabla (a_{\rm v} \rho _{\rm v} {\pmb v} ) = R_{\rm e} + R_{\rm c}$

这里,静质量源项的表达式为

(6) $ R_{\rm e} + R_{\rm c} = \dfrac{\rho _{\rm v} \rho _{\rm l} }{\rho _{\rm m} }\dfrac{{\rm D}\alpha _{\rm v} }{{\rm D}t}$

式中,$R_{\rm e}$为气泡的蒸发速率,$R_{\rm c}$为气泡的冷凝速率.

与其他主流空化模型不同,Schnerr和Sauer将蒸汽体积分数和单位体积的液体中的气泡数量进行联系,有

(7) $ \alpha _{\rm v} = \dfrac{4n_{\rm b} \pi R_{\rm B}^3/3 }{1 + 4n_{\rm b} \pi R_{\rm B}^{\rm 3}/3 }$

式中,$R_{\rm B}$为气泡直径. 因此,经过整理后的Schnerr-Sauer空化模型为

(8) $ \left. \begin{array}R_{\rm e} = \dfrac{\rho _{\rm v} \rho _{\rm l} a_{\rm v} \left( {1 - a_{\rm v} } \right)}{\rho _{\rm m} }\dfrac{3}{R_{\rm B} }\sqrt {\dfrac{2\max (p_{\rm v} - p,0)}{3\rho _l }} \\ R_{\rm c} = - \dfrac{\rho _{\rm v} \rho _{\rm l} a_{\rm v} \left( {1 - a_{\rm v} } \right)}{\rho _{\rm m} }\dfrac{3}{R_{\rm B} }\sqrt {\dfrac{2\max (p - p_{\rm v} ,0)}{3\rho _{\rm l} }} \end{array}\!\!\right\}$

1.3 湍流模型

本文采用密度修正的的RNG $k$-$\varepsilon $湍流模型来对雷诺方程进行封闭. 该模型在传统的RNG$k$-$\varepsilon $模型上考虑了汽液两相密度变化对湍流黏度的影响^[28]. 在标准RNG $k$-$\varepsilon$模型中,湍流黏度为

(9) $ \mu _{\rm t} = \rho c_\mu \dfrac{k^2}{\varepsilon }$

修正的RNG $k$-$\varepsilon$湍流模型考虑了汽液两相密度变化对湍流黏度的影响,修正后的湍流模型采用以下两式计算湍流黏度

(10) $ \mu _t = f\left( \rho \right)c_\mu \dfrac{k^2}{\varepsilon }$

(11) $ f\left( \rho \right) = \rho _{\rm v} + \left( {1 - \alpha _{\rm v} } \right)^n\left({\rho _{\rm l} - \rho _{\rm v} } \right)$

式中, $\varepsilon $为湍动能耗散率;$c_{\mu}$为模型常数,取0.085;通过密度修正指数$n$来对湍流黏度进行修正,本文中取$n =3$.

1.4 计算网格与模型验证

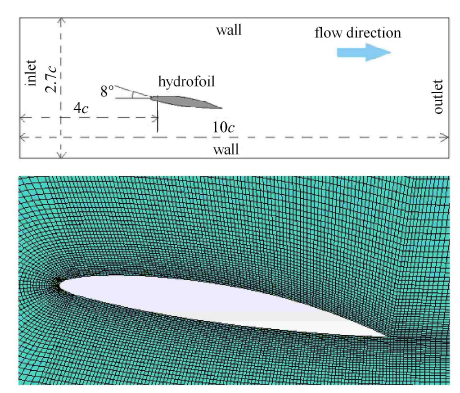
本文基于数值计算方法开展绕NACA66(mod) 水翼的空化流动分析.计算的几何模型,计算域的尺寸和工况条件的设置均与实验条件保持一致. 水洞试验段的来流速度$U_{\infty}$为7.832 m/s,来流攻角为8$^\circ$,流场温度为290 K,饱和蒸汽压1940 Pa,动力黏度$\mu=1.08$ g/(m$\cdot$s),空化数$\sigma=0.99$,雷诺数$Re=5.1 \times 10^{5}$.计算区域划分如图1,水翼表面进行加密处理,最终网格数约为73 000. 文献^[29]已对本文选用的网格和时间步长的选择进行了无关性验证,此处不再赘述. 非定常计算的时间步长选择为$\Delta t=5.0 \times10^{-4}$.

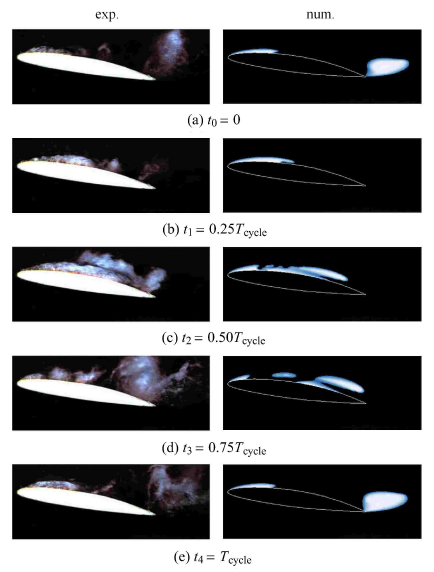
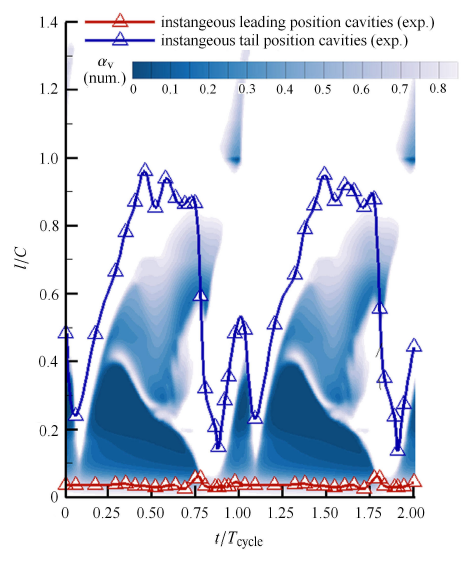
为了验证所采用数值方法的可行性,将数值模拟结果与实验结果进行对比. 实验设备及条件如文献^[30]所述. 在实验中采用高速全流场相机对瞬时空化流场形态进行捕捉.瞬时空化形态如图2所示,对比原始水翼空化流动的实验测试结果,发现采用数值分析方法较好地预测出空泡准周期的生长、发展、脱落和溃灭的过程. 周期为 $T_{\rm cycle} = 66$ ms,频率为$f =15.15$ Hz, 则基于水翼弦长的斯特劳哈尔数为$St = f c/U=0.135 0$,相比较该工况下实验所得的斯特劳哈尔数$St =0.137 3$,误差仅为1.7%,说明所选用的数值分析模型和模拟结果能够较好地预测云状空化流场的周期性.但是,在对水翼尾缘脱落空穴的捕捉相比于实验有一定的缩短或者厚度变薄,但周期性和变化趋势基本一致,如图3所示.

图1

新窗口打开| 下载原图ZIP| 生成PPT

图1 计算区域与近壁网格划分

Fig. 1 Computational domain and near foil meshing

图2

新窗口打开| 下载原图ZIP| 生成PPT

图2 一个周期内特征时刻空穴形态对比图($\sigma =0.99$,$Re=5.1\times 10^{5}$

Fig. 2 Instantaneous outline of cavities of experiment and simulation in a time period

图3

新窗口打开| 下载原图ZIP| 生成PPT

图3 二个周期内空穴无量纲长度对比

Fig. 3 Instantaneous length of cavities of experiment and simulation in two time periods

2 结果分析

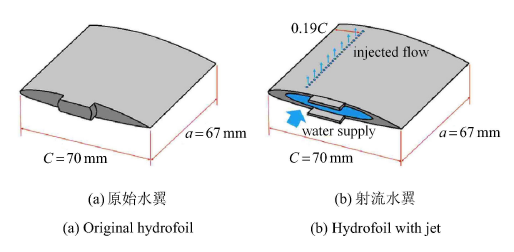
本文首先对原始水翼模型,即表面无射流孔的NACA66(mod) 水翼模型进行数值模拟,模拟工况为$\sigma=0.99$,研究其发生云空化时的非定常周期特性,其次对含有射流孔水翼的数值分析结果进行对比研究. 原始水翼和射流水翼结构如图4所示. 先前的研究表明对应安装攻角下的水翼吸力面最高点附近的流场速度最高,且往往存在流动分离和损失. 在最高点处布置射流水孔,有利于阻挡回射流,降低损失^[29]. 因此,本研究中将射流水翼的射流位置布置于该安装攻角下的吸力面最高点(即距水翼前缘0.19倍水翼弦长位置).

图4

新窗口打开| 下载原图ZIP| 生成PPT

图4 水翼结构示意图

Fig. 4 Schematic diagram of hydrofoil

2.1 绕流原始水翼的云空化流动特性分析

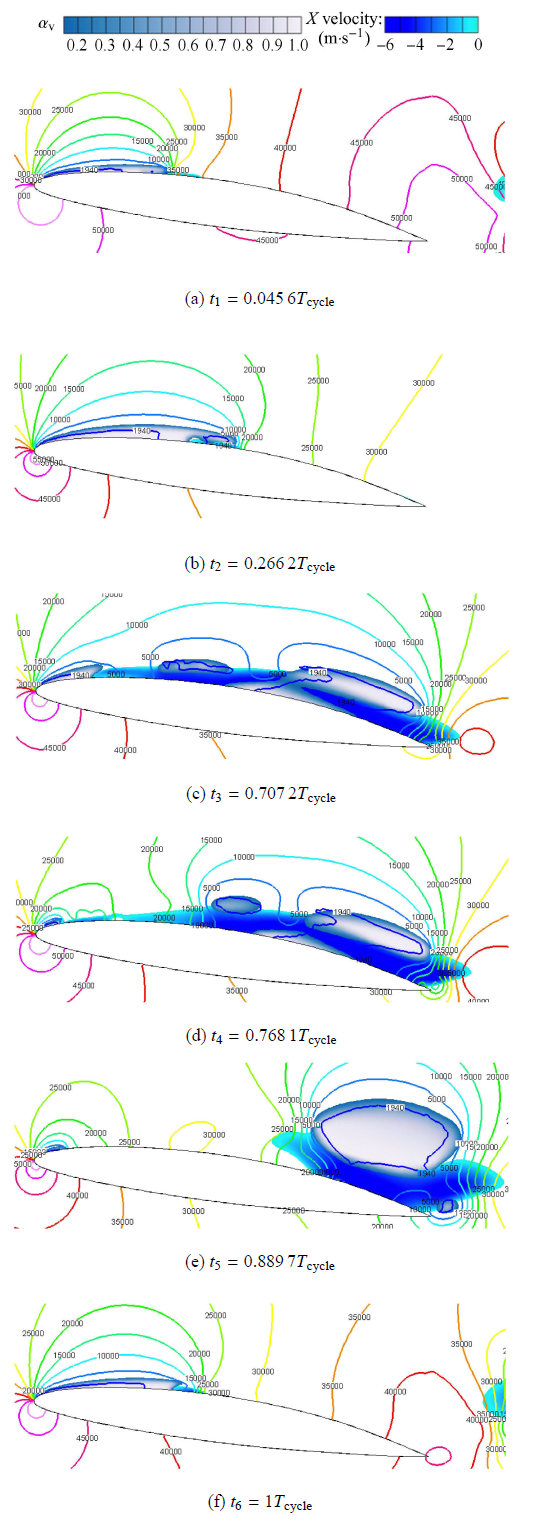
图5给出了绕原始水翼空穴在特征时刻的瞬时形态变化.为了研究回射流区和空化区的相互作用,除了空穴的瞬时形态变化,图上还分别显示了压力瞬时分布(等值线,单位Pa)和回射流区的瞬时形态变化.从图中可以看出,模拟的结果较好地显示了云空化发生时空穴的生长、回缩、发展和溃灭的准周期过程.在$t_1$时刻,游离型空穴在水翼尾缘的下游处溃灭,其溃灭的瞬间出现局部的高压,在从水翼尾缘到水翼前缘的压力梯度的作用下着向水翼前缘传播,并导致了水翼前缘附着型空穴的一次回缩.从$t_1$到$t_2$为附着型空穴的生长过程, $t_2$时刻在空穴的尾缘第一次出现了回射流.回射流出现后空穴继续发展,在$t_3$时刻空穴充分发展,而回射流也在这个过程中推进到最靠近水翼前缘的位置,并几乎遍布满整个水翼的吸力面,回射流和空穴存在强烈的相互作用.$t_4$时刻水翼表面的附着型空穴几乎完全消失,出现了附着型空穴的二次回缩过程.脱落的空穴在回射流的作用下被抬起,脱离水翼表面.$t_5$时刻几乎完全消失的附着型空穴开始再次出现,而在水翼的尾缘附近,游离型空穴逐渐远离水翼壁面.值得一提的是,游离型空穴在此过程体积有所增大,呈现膨胀的形态. $t_5$和$t_6$水翼前缘的附着型空穴继续生长,而在尾缘附近的游离型空穴体积最大,相应于$t_6$时刻,在水翼下游溃灭,局部高压区再次出现,云空化的非定常准周期性发展进入下一周期.

图5

新窗口打开| 下载原图ZIP| 生成PPT

图5 绕NACA66水翼非定常云状空穴结构演化过程 (空穴含汽率$\alpha_{\rm v} >0.15$,周期$T_{\rm cycle} = 66$ ms)

Fig. 5 The numerically predicted vapor fraction ($\alpha _{\rm v} >0.15$) of cavitation pattern around a NACA66 hydrofoil ($T_{\rm cycle} = 66$ ms)

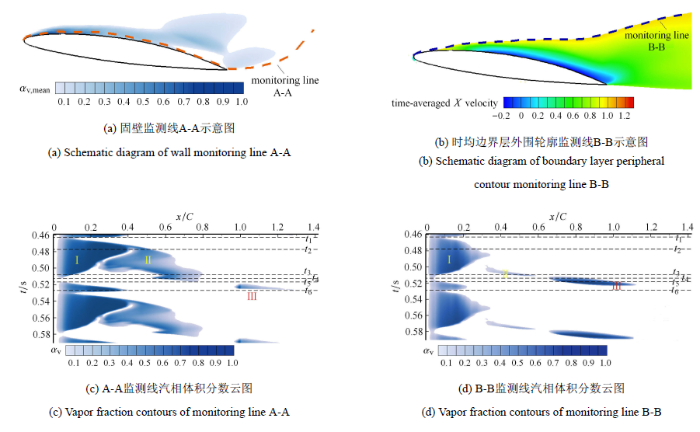
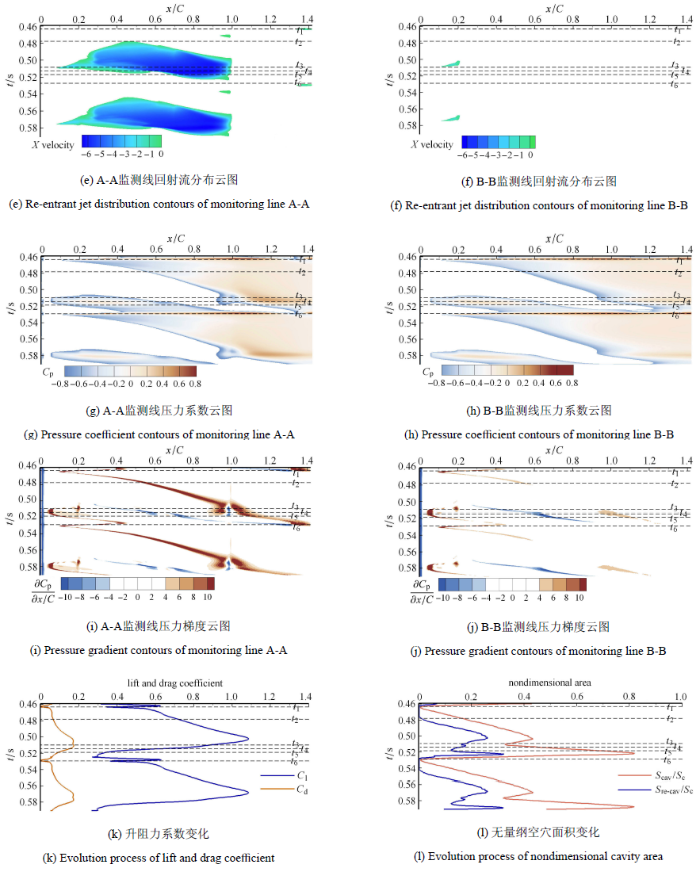
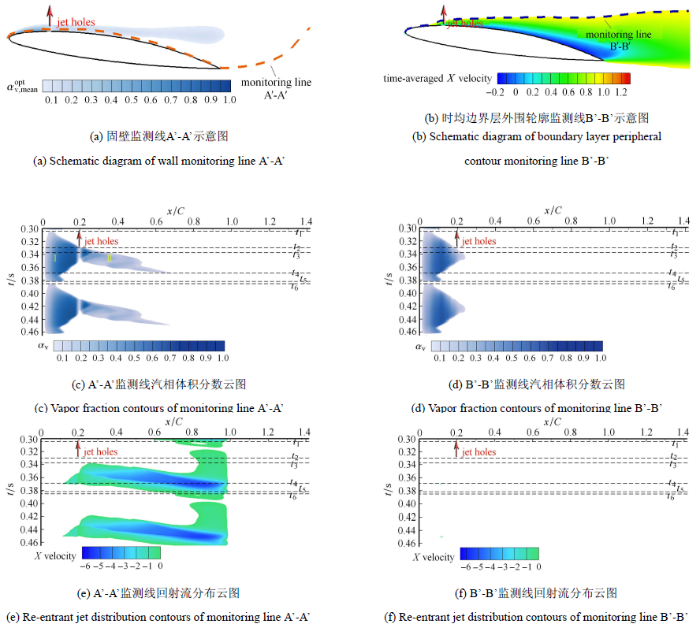
为进一步深入地研究绕流水翼云空化发展过程和影响因素,本文在水翼吸力面近壁区设立一条监测线 (monitoring lineA-A),对水翼吸力面近壁区的流场特征参数进行监测,如图6(a)所示.同时,为了研究边界层空化流场特性,在时均空化流场的边界层$(U_{\rm BL,mean} <0.99U_{\infty})$的外部轮廓线 (monitoring line B-B) 上设立同步监测线,如图6(b)所示.开展上述两条监测线上空化流动特征参数的对比分析.由于云空化非定常准周期性,本文对一维的瞬时空化流场增加时间维度,获得水翼吸力面近壁区和边界层处的汽相体积分数、回射流速度、压力系数等特征参数的时空分布云图.进而分析绕流水翼云空化的发展和射流抑制空化机理,如图6所示.

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 绕NACA66水翼非定常云状空化流场的时空分布云图(空穴含汽率$\alpha_{\rm v}>0.15$)

Fig. 6 Spatiotemporal distribution of unsteady cloud cavitation flow around NACA66 hydrofoil

图6

新窗口打开| 下载原图ZIP| 生成PPT

图6 绕NACA66水翼非定常云状空化流场的时空分布云图(空穴含汽率$\alpha _{v}>0.15$) (续)

Fig. 6 Spatiotemporal distribution of unsteady cloud cavitation flow around NACA66 hydrofoil (continued)

定义当地压力系数和无量纲压力梯度

(12) $ C_{\rm p} = \dfrac{2(p - p_\infty) }{\rho _{\rm l} U_\infty ^2}$

(13) $ {\rm grad}C_{\rm p} = \dfrac{\partial C_{\rm p} }{\partial (x/C)}$

式中,$p$为当地压力,而$p_{\infty }$为来流压力.而压力梯度值的正负代表着方向,正值代表着逆压梯度,是造成回射流的主要原因之一;负值代表着从前缘到尾缘的顺压梯度. 为了便于分析,压力梯度云图只显示了压力梯度的较高值 ( 即$ | {\rm grad} C_{\rm p} | >4$).图 6中的$t_1 \sim t_6$时刻线均与图5相对应.

汽相体积分数的时空分布如图6(c)和图6(d)所示.图6(c)清晰地反映了云空化非定常周期性过程,吸力面附近的空穴在整个周期内可以被分为3个部分：当地含汽率大于0.7的附着型空化区、小于0.7的附着型空化Ⅱ区(汽液混合区)和位于翼型尾缘附近的游离型空穴区(空化Ⅲ区);图6(d)的边界层外部轮廓线监测结果显示了空穴的发展厚度与边界层的关系：在水翼前部边界层监测线之外仍然存在汽相体积分数较大的Ⅰ区域,水翼中部的Ⅱ空穴区域基本被包含在边界层内部,而脱落的游离型空穴在$t_4 ~_6$时刻内已经被抬起到边界层附近,不断的向下游发展并最终溃灭.

回射流的时空分布云图6(e)和图6(f)所示,在$t_2$时刻初现的回射流位于该瞬时附着型空穴的尾部 ($t[s]=t_2$,$x/C=0.4$).之后回射流的存在区域不断扩大,并向水翼前缘推进造成空化Ⅰ区的回缩;随着空穴的发展,回射流存在区域向水翼尾缘扩张并与空化Ⅱ区相掺混,造成当地含汽率的下降,说明回射流不断被空穴汽化^[31].图 6(f)可以发现在时均边界层轮廓线上,几乎没有回射流的存在,主要原因是回射流起源于空穴尾部,并在水翼吸力面和空穴之间流动.另一方面说明了沿壁面法线方向,边界层内部速度由负到正,存在很大的速度梯度.

压力系数和压力梯度的云图如图6(g)~图6(i)所示,可以发现在游离型空穴溃灭的瞬时 ($t_1$时刻),产生了局部高压^[32],压力系数可以达0.8左右,且维持时间较短,产生了向水翼前缘的压力梯度,造成了附着型空穴的一次回缩. 此外,由图6(g) 和图6(c)的对比可以发现,空化区位于流场的低压区域中 ($C_{\rm p}<-0.8$).由图6(i)和图6(e)的对比可以发现,回射流区的发展受限于较高的压力梯度 ($ | {\rm grad} C_{\rm p} |>4$).

图6(l)显示整个周期空穴无量纲面积变化,其中$S_{\rm cav}$为空穴面积,$S_{\rm c}$表示水翼端部截面积,而$S_{\rm re - cav}$为空穴与回射流的相互掺混部分的面积.可以发现空穴对回射流的汽化作用和回射流对空穴体的冲击作用在回射流初现的时刻 ($t_2$时刻)就开始发生,直至周期结束 ($t_6$时刻). 其中$t_5\sim t_6$时间内面积的变化显示了空穴的充分发展,然后迅速溃灭的过程.

综合汽相体积分数、回射流区域、压力系数分布、压力梯度分布的时空云图可以得出以下结论：游离型空穴溃灭时产生的局部高压导致附着型空穴的一次回缩,同时升力系数也有所下降( 如图6(k)所示). 回射流出现于附着型空穴的尾部,并与空穴相互作用,其向水翼前缘推进,对附着型空穴产生冲击作用;一部分随空穴向下游发展被汽化,造成当地含汽率的下降. 空化区存在于流场的低压区域中 ($C_{\rm p}<-0.8$),回射流的区域也受限于较高的压力梯度. 高的压力梯度一直存在,但回射流的首次出现需要时间积累. 游离型空穴在回射流的作用下脱落和抬升、远离固壁,导致升力系数的第二次急剧下降. 在游离型空穴抬升和溃灭的同时$(t_3\sim t_5)$,水翼尾缘处出现正负交接的压力梯度,推测有涡的出现.

2.2 主动射流控制空化流动的特性分析

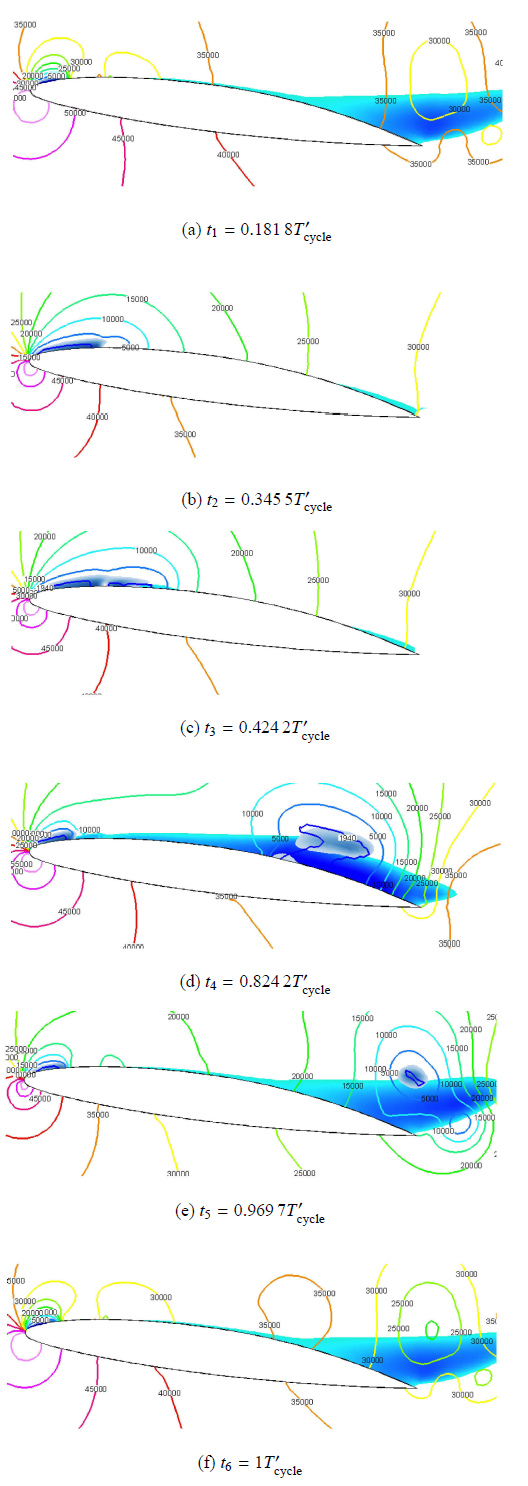
基于上述原始水翼的空化条件,开展了表面开孔射流这一主动控制策略对绕流水翼空化流场的影响研究,射流孔位于距水翼前缘0.19倍弦长位置.图 7显示了射流水翼云空化发展的非定常周期性过程.$t_1$时刻依然为游离型空穴溃灭产生局部高压的瞬时.此后前缘的附着型空穴开始慢慢发展,$t_2$时刻为附着型空穴发展到射流孔位置处,由于存在主动射流,此时空穴和射流开始相互接触并掺混.而回射流在$t_3=0.424 2 T'_{\rm cycle}$时刻在空穴尾端才首次出现,与原始水翼的回射流初现时刻相比,推迟了15.8%.回射流初现后不断的发展 ($t_3\sim t_4$时间内),之后回射流、射流和空穴三者间相互作用.在$t_4$时刻回射流推进到最靠近水翼前缘点位置处,同时水翼尾缘处的空穴被托起,开始远离壁面,脱落型空穴的面积不断缩小,并最终在$t_6$时刻溃灭.相比原始水翼的空穴发展周期66 ms,射流水翼明显增加,达到82.5 ms,空穴脱落频率降低了20%.

图7

新窗口打开| 下载原图ZIP| 生成PPT

图7 绕NACA66射流水翼非定常云状空穴结构演化过程 (空穴含汽率$\alpha _{\rm v} >0.15$,$T'_{\rm cycle} = 82.5$ ms)

Fig. 7 The numerically predicted vapor fraction ($\alpha _{\rm v} >0.15$) of cavitation pattern around a NACA66 hydrofoil with jet flow ($T'_{\rm cycle} = 82.5$ ms)

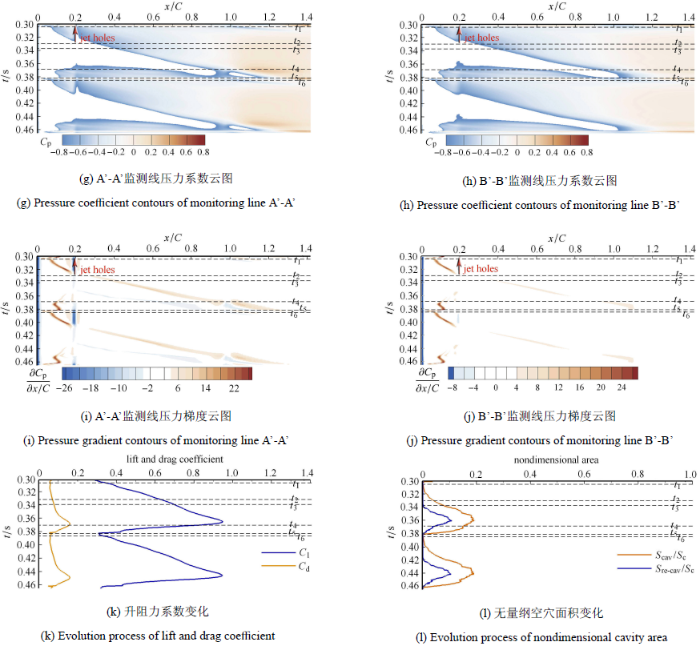
射流水翼的时空分布云图则更能清晰地反映射流、回射流和空穴三者间的相互作用过程,进而分析射流抑制空化的机理,如图8所示. 图中的$t_1\sim t_6$时刻线均与图7相对应.图 8(c)汽相体积分数的时空分布云图反映了射流水翼云空化的周期性发展过程. 与原始水翼不同,射流水翼前缘的附着型空穴发展较晚,在$t_1$时刻产生的局部高压也较小 ($C_{\rm p}=0.2$),并没有监测到附着型空穴的回缩现象;在$t_2$时刻附着型空穴发展到射流孔位置处;在$t_2~_4$过程中,附着型空化区被射流切分为Ⅰ和Ⅱ两个部分,射流孔及其附近含汽率较小.此外,图7的瞬时云图显示了该工况下依旧存在空穴的脱落,而在图8(d)水翼尾缘边界层外轮廓线附近并没有监测到脱落的的游离型空穴. 这说明射流水翼的空穴脱落和溃灭在刚离开固壁就已经发生,整个过程位于时均边界层内部. 相比于原始水翼,图8(e)和图8(f)显示采用射流使得回射流强度减弱,回射流区域减小. 这也可从图8(i)和图8(j)看出,在射流孔位置处出现较高的顺压梯度,该顺压梯度与造成回射流的逆压梯度的分布相隔断,对回射流强度和范围起到了消减的作用. 射流减弱了回射流对空穴的冲击作用,空化发展受到抑制.

相比于图6(l)无量纲空穴面积分析结果,采用主动射流后,绕流射流水翼的无量纲空穴面积有大幅度的减少,如图8(l)所示,证明了该工况下射流抑制空化的有效性.

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 绕NACA66射流水翼非定常云状空化流场的时空分布云图 (空穴含汽率$\alpha_{\rm v} >0.15$)

Fig. 8 Spatiotemporal distribution of unsteady cloud cavitation flow around NACA66 hydrofoil with jet flow

图8

新窗口打开| 下载原图ZIP| 生成PPT

图8 绕NACA66射流水翼非定常云状空化流场的时空分布云图 (空穴含汽率$\alpha_{\rm v} >0.15$) (续)

Fig. 8 Spatiotemporal distribution of unsteady cloud cavitation flow around NACA66 hydrofoil with jet flow (continued)

2.3 空化流动控制的涡旋特性分析

$Q$是在伽利略变换下的速度梯度张量第二不变量,近年来,研究者认为以$Q$显示的涡流能够更清晰的反应流场内的涡旋结构,且空化与旋涡间存在交互作用^[33-35].为了深入研究空化及射流抑制空化机理,本文利用$Q$判据对空化流场进行分析. 对于三维流场,$Q$定义如下

(14) $ { Q} = \dfrac{\partial U}{\partial x}\dfrac{\partial V}{\partial y} - \dfrac{\partial V}{\partial x}\dfrac{\partial U}{\partial y} + \\ \qquad \dfrac{\partial V}{\partial y}\dfrac{\partial W}{\partial z} - \dfrac{\partial W}{\partial y}\dfrac{\partial V}{\partial z} + \dfrac{\partial U}{\partial x}\dfrac{\partial W}{\partial z} - \dfrac{\partial W}{\partial x}\dfrac{\partial U}{\partial z} $

对于二维的流场研究,上式可以简化成

(15) $ Q = \dfrac{\partial U}{\partial x}\dfrac{\partial V}{\partial y} - \dfrac{\partial V}{\partial x}\dfrac{\partial U}{\partial y}$

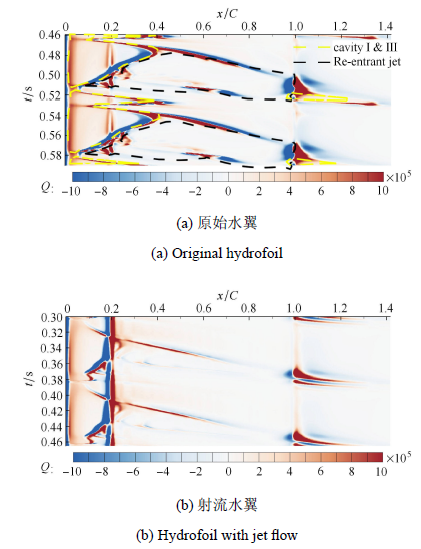
图 9显示了原始水翼的固壁监测线 (monitoring lineA-A)和射流水翼的固壁监测线 (monitoring line A'-A')的$Q$值时空分布云图.$Q$的局部最大正值可以用来识别涡核,而负值则表示可能存在剪切但没有旋涡运动的流动区域.图 9(a)原始水翼的$Q$值时空分布云图显示,在某一瞬时沿弦长方向壁面监测线上的$Q$值正负交错,在水翼非定常发展过程中,$Q$值也发生变化. 对比分析$Q$值和图6中的汽相体积分数、回射流的时空分布云图,可以发现,$Q$值分布云图中的正值与附着型空化I区和游离型空化区 (III)相契合,如图中黄色显示区域;负值与回射流的区域外轮廓线相契合,如图中黑色虚线包围的区域,而在正值与负值相互围绕的中间区域则与汽液混合区(附着型空化II区)相契合.这说明了在水翼前缘的含汽率较高的附着型空化I区和水翼尾缘的游离型空穴内,存在着旋涡运动;回射流对周围的空穴存在着剪切作用;而在水翼弦长靠中间位置,即存在着旋涡又存在着回射流的剪切作用,为含汽率相对较低的汽液混合物.图 (b)为在0.19倍弦长位置上开设射流后的$Q$时空分布云图,可以看出$Q$值的强度和范围都得到了减小,且在射流孔的位置左右出现了正负值相互对立的隔断面,这说明射流也存在着剪切作用,但该剪切作用能对前缘的附着型空穴向后发展和回射流向水翼前缘的推进形成阻挡,从而对云空化起到抑制作用.

图9

新窗口打开| 下载原图ZIP| 生成PPT

图9 水翼壁面监测线的$Q$值时空分布云图

Fig. 9 Spatiotemporal distribution contours of $Q$-criterion around NACA66 hydrofoil

3 结论

本文采用数值分析方法,对NACA66(mod)原始水翼和射流水翼的云空化非定常过程开展研究,通过采用设置水翼固壁监测线的方法对流场一维简化并加入时间维度,得到时空分布云图,引入$Q$判据对时空流场中的涡旋特性进行研究,分析空化和空化抑制的机理. 得到的主要结论如下：

(1) 水翼尾缘游离型空穴溃灭时存在瞬间高压,并向水翼前缘传播;而采用主动射流后,该瞬间高压得到显著消减.

(2) 回射流区域的发展受限于较高的压力梯度. 采用射流后,水翼吸力面压力梯度减小,射流孔附近压力增高,回射流初生的时间延迟,回射流的强度降低,有效抑制了空化的脱落发展.

(3) 水翼空化的发展和流场中的涡结构有着紧密的联系. $Q$正值分布与水翼前缘附着型空穴和尾缘的游离型空穴形状相契合;$Q$负值分布与回射流的外部轮廓相契合. 说明前缘和尾缘空穴内部存在旋涡作用,而回射流对空穴也存在剪切作用.

(4) 射流对前缘附着型空穴和回射流具有剪切作用,抑制了回射流向前缘的推进和前缘附着型空穴的向后发展.

参考文献

原文顺序

文献年度倒序

文中引用次数倒序

被引期刊影响因子

[1]

潘森森, 彭晓星 . 空化机理. 北京: 国防工业出版社, 2013