引言
求解包含间断的复杂流场, 需采用高分辨率的激波捕捉格式,要求格式既能锐利地捕捉间断而不产生数值振荡, 又能清晰分辨光滑区域的细微结构.加权基本无振荡(weighted essentially on-oscillatory,WENO)格式在间断附近保持基本无振荡(essentially non-oscillatory, ENO)特性,并在光滑区域达到高阶精度, 是求解复杂流场较为理想的选择.其受到研究者们的广泛关注, 已被成功应用于求解磁流体流动[1]、多组分流动[2]、两相流[3]、超音速湍流燃烧混合层流动[4]、可压缩湍流[5-7]、气动声学问题[8]以及其他不同领域的模型方程[9-12].
作为对高阶ENO格式[13]的改进, WENO格式最早由Liu等[14]提出.ENO格式采用自适应模板, 在几个候选模板中总是选择最光滑的那一个来重构数值通量;WENO格式则是将所有候选模板上的数值通量加权平均.格式中的非线性加权机制能自动识别间断, 为包含间断的子模板分配趋近于0的权重值,从而保证格式的ENO特性; 并在光滑区域逼近理想权重, 从而提高格式的精度. 随后,Jiang等[15]构造了新的光滑度量因子, 将WENO格式的精度提高到了最优阶.这一格式被命名为WENO-JS.针对WENO-JS格式耗散过大及在极值点附近精度降低的缺点, 学者们提出了一系列改进.Henrick等[16]使用映射函数修正WENO-JS格式的权重, 得到五阶WENO-M格式,克服了在极值点附近精度降低的问题. 但其所采用的权重算子过于复杂, 计算量大.为此, Borges等[17]提出了形式更为简单的WENO-Z格式. 其特点是使用子模板上的低阶光滑度量因子进行线性组合,构造高阶全局光滑度量因子,以与WENO-JS格式近乎相同的计算代价获得了同WENO-M格式基本一样的精度. 此后,研究者们又提出了一系列新的光滑度量因子来改进WENO-Z格式的数值性能[18-26].
本文细致分析了WENO-Z$+\!$格式中$\lambda$取值方式的缺陷,并根据其权重的特点重新设计$\lambda$的计算公式, 对WENO-Z$+\!$格式做出了改进.
1 控制方程及其离散
1.1 Euler方程组
无黏、可压缩流动由Euler方程组描述. 以一维Euler方程组为例
其中
式中, $\rho $, $u$和$p$分别表示流体的密度、速度和压强, $E$为单位体积流体的总能量, $\gamma $是绝热指数, 通常取$\gamma = 1.4$.
1.2 数值离散
在对Euler方程组进行数值离散时, 首先使用通量分裂技术(本文采用全局Lax-Friedrichs分裂[15]将方程组的通量项分裂成正负两部分
然后使用高阶迎风格式分别重构半节点上的正负数值通量$\bar{ F}_{i +{1}/{2}}^\pm $. 通量分裂和重构都是在特征空间中进行的, 再将得到的结果投影回物理空间.由此得到方程组(1)的半离散化形式
最后使用适宜的时间推进方法求解上述半离散方程组. 本文采用三阶总变差不增(total variation diminishing, TVD)的 Runge-Kutta格式[15]
下面我们将详细论述数值通量的WENO重构方法. 我们只给出正通量的重构方法;负通量的重构方法根据对称性容易获得, 在此省略.
2 数值格式
定义1: 若${f}'(x_{\rm c} ) = \cdots = f^{(n_{{\rm cp}} )}(x_{\rm c} ) = 0$且$f^{(n_{{\rm cp}} +1)}(x_{\rm c} ) \ne 0$, $n_{{\rm cp}} > 0$, 称$x=x_{\rm c}$是$f(x)$的$n_{{\rm cp}} $阶极值点. 若$n_{{\rm cp}} = 0$, 则$x=x_{\rm c}$不是极值点.
定义2: 对于任意表达式$g(\Delta x)$, 符号$\theta (g)$表示$g$的阶数. $\theta _n (g)$表示$g$在$n$阶极值点处的阶数. 特别的, $\theta _0 (g)$表示$g$在非极值点处的阶数.
定义3: $g = \varOmega (\Delta x^n)$表示$\theta (g) \leqslant n$; $g = O(\Delta x^n)$表示$\theta (g) \geqslant n$; $g = \varTheta (\Delta x^n)$表示$\theta (g) = n$.
2.1 WENO格式
一般地, 将$r$阶ENO格式的全部(共$r$个)数值通量加权平均, 可得到$R = 2r - 1$阶WENO格式. 五阶($r = 3$)WENO格式用到3个子模板及相应的3种低阶重构方式
由当地流场数据计算每个子模板上的权重值$\omega _k(k = 0,1,2$), WENO格式的数值通量是上述3种重构方式的加权平均
在间断处, 含间断子模板上的权重趋近于零, 确保格式的ENO性质; 在光滑区域,非线性权重逼近理想权重, 使格式达到最优阶精度. 在模板给定的情况下,非线性权重的数学性质决定了WENO格式的数值性能. 因此,合理设计非线性权重是改进WENO格式的关键.
2.2 WENO-JS格式
Jiang和Shu[15]提出的WENO-JS权重形式如下
$(d_0 ,d_1 ,d_2 ) = ({1}/{10},{6}/{10},{3}/{10})$是理想权重.小参数$\varepsilon > 0$原本被设置用来避免分母为零,为了不影响非线性权重的激波捕捉性能,被取为极小的值(如取$\varepsilon = 10^{ - 40}$). 但后来的研究[27-28]发现, $\varepsilon $的形式对WENO格式的收敛精度有重要影响: 若$\varepsilon = \varOmega (\Delta x^2)$, WENO-JS格式能在整个流场光滑区域保持最优阶精度; 否则,格式的收敛精度会在极值点处降低. $\beta _k $是光滑度量因子, 具体形式如下
2.3 WENO-Z格式
Borges等[17]提出的WENO-Z权重形式如下
式中, $\tau _5$称为全局光滑度量因子. $p \geqslant 1$能调控格式的数值耗散,通常取$p = 2$.与WENO-JS格式相似, $\varepsilon $的形式影响WENO-Z格式的收敛精度: 若$\varepsilon = \varOmega (\Delta x^4)$, $p = 2$的五阶WENO-Z格式能在整个流场光滑区域保持最优阶精度; 否则,格式的收敛精度在二阶以上的极值点处降低. 详见文献[28].由于WENO-Z格式相比于WENO-JS格式增大了欠光滑子模板上的权重,因而其数值耗散更低、分辨率更高.
2.4 WENO-Z$+\!$格式
为了进一步增大欠光滑子模板上的权重, Acker[29]在WENO-Z格式的权重公式中新增一项, 得到WENO-Z$+\!$格式. 其权重形式如下
$\xi _k$是WENO-Z权重中原有的项, 其作用是使含间断子模板上的权重趋近于零,并在光滑区域减小欠光滑子模板上的权重、增大数值耗散. 新增项${1}/{\xi _k }$的作用则刚好相反, 能增大欠光滑子模板上的权重、减小数值耗散. 同时,由于该项与全局光滑度量因子$\tau _5 $成反比, 因而其作用在间断处十分微弱, 这就保证了格式的ENO性质.我们希望充分发挥该项的作用,在光滑区域尽可能增大欠光滑子模板上的权重、减小数值耗散. 但若该项作用过大,又会影响格式的稳定性. 为此, 系数$\lambda $被设置用来调控其作用.
2.5 对WENO-Z$+\!$格式的分析
(1)因为在Titarev-Toro问题中更容易发生对高频波的虚假放大,最终就以Titarev-Toro问题的数值结果为准确定了$\lambda$的值. 但很明显,在Shu-Osher问题中, $\lambda$可取更大的值而不产生负耗散. 例如, 当$\lambda = \Delta x^{{1}/{2}}$时, 在Titarev-Toro问题中出现了对高频波的虚假放大;在Shu-Osher问题中则未出现这一情况, 反而进一步改善了数值结果[29]. 因此, 这种取值方式无视流动状态的差异, 对所有的流动条件采用同样的取值,无法充分发挥WENO-Z$+\!$格式的潜力.
(2)虽然当$\lambda = \Delta x^{{2}/{3}}$时, 格式能在Titarev-Toro问题中保持稳定,但这并不能确保格式在其他问题中也能同样保持稳定. 就像$\lambda = \Delta x^{{1}/{2}}$确实能使格式在Shu-Osher问题中保持稳定, 却在Titarev-Toro问题中造成了负耗散.
基于上述分析, 本文将重新设计的计算公式.
2.6 对WENO-Z$+\!$格式的改进
上文已经提及, 针对不同的流动条件, $\lambda$可取不同的值. 进一步推论,$\lambda$的值应当随当地流场数据而变化, 方能充分发挥WENO-Z$+\!$格式的潜力.由于WENO-Z$+\!$格式是在WENO-Z格式的基础上进一步增大欠光滑子模板上的权重,因此在WENO-Z权重已足够接近理想权重的地方, 新增项的作用容易过度量,应分配较小的$\lambda$值; 而在WENO-Z权重偏离理想权重的地方,新增项的作用有充足的发挥空间, 应分配较大的$\lambda$值. 于是,我们就有了$\lambda$公式的设计 策略.
考虑在欠光滑子模板(子模板中光滑度量因子最大的那一个)上WENO-Z权重($p = 1$)与理想权重之间的比值
式中, $d_k $和$\xi _k $的含义同式(12). $0 < z \leqslant 1$, 可以用来衡量WENO-Z权重偏离理想权重的程度. $z$越接近零, $\lambda $应当越大; $z$越接近1, $\lambda $应当越小. 因此, 本文给出$\lambda $的计算公式
常数$a$, $q > 0$需以某种方式确定取值. 本文将采用上述$\lambda $公式的新格式命名为WENO-Z++.
文献[29]在选取$\lambda $的值时仅参考了两个标准算例(对应于两种波动频率)的数值结果,这样确定的$\lambda $值无法保证适用于所有情况. 本文在确定参数$a$和$q$的值时依据格式的近似色散关系(approximate dispersion relation, ADR)[32]. ADR方法求解模型方程, 对给定网格上的全部Fourier模式进行求解,揭示格式在整个频域内的数值行为. 因此依据ADR来确定参数值比依据有限几个数值算例(对应于有限几种波动频率)要可靠得多.对于波数为$w$的正弦波, 从数值结果换算得到修正波数${w}'$. ${w}'$通常为复数, 其实部Re$({w}')$正比于数值解的相速度, 反映格式的色散误差; 虚部Im$({w}')$决定振幅的衰减速率, 反映格式的耗散误差. 当Im$({w}') < 0$时, 格式具有正耗散; 而当Im$({w}') > 0$时, 格式具有负耗散, 这是应当避免的 情况.
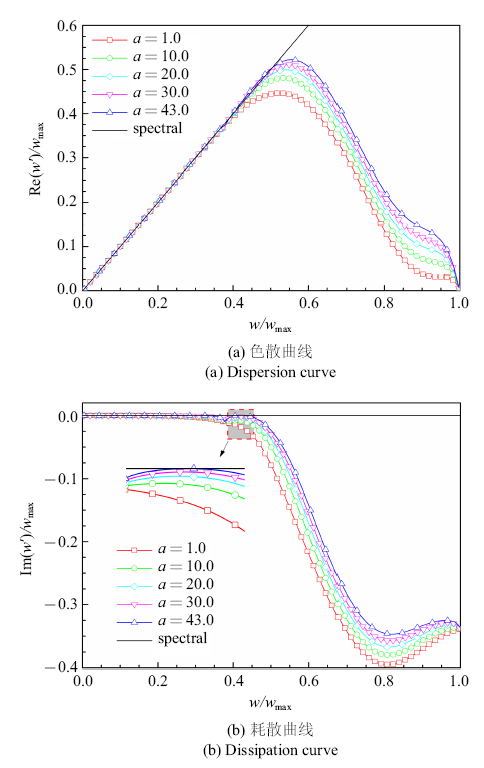
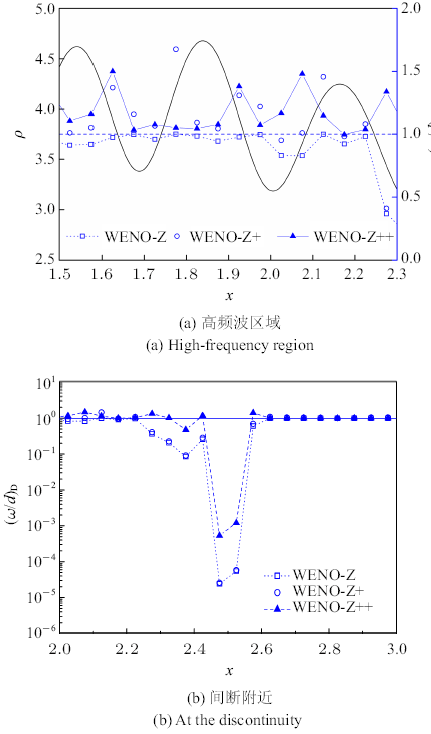
本文取$q = 2$. 图1给出当$q = 2$时WENO-Z++格式的ADR随$a$值的变化. 观察到, 当$a$增大时, 数值解的相速度增大,同时格式的数值耗散减小. 增大$a$的值是增大新增项的作用,也就是增大了欠光滑子模板上的权重,可见欠光滑子模板上的权重影响WENO的频谱特性. 更具体的,增大欠光滑子模板上的权重能提高数值解的相速度, 减小格式的数值耗散,这对于提升WENO格式的分辨率都是有益的. 然而, 当$a$值的增大超过了一定限度,会首先在某一波数范围内出现负耗散,这意味着格式对这一波数范围内的波动造成了虚假放大. 基于ADR的数值实验表明,当$q = 2$时, $a$的值最大可取到43而不出现负耗散.
图1
图1
当$a$取不同值时WENO-Z++格式的ADR
Fig.1
The ADR of the WENO-Z++ scheme when parameter $a$ takes different values
当然, $q$也可以取其他的值, 例如取$q = 1$或3, 并按照上述相同的过程确定相应的$a$值. 但是当$q = 1$时, 相应的$a$值较小, 格式的提升受限; 而当$q = 3$时, 格式的分辨率损失较大. 因此本文最终取$q = 2$, $a = 43$.
2.7 WENO-Z++格式的ENO特性
2.8 WENO-Z++格式的频谱特性
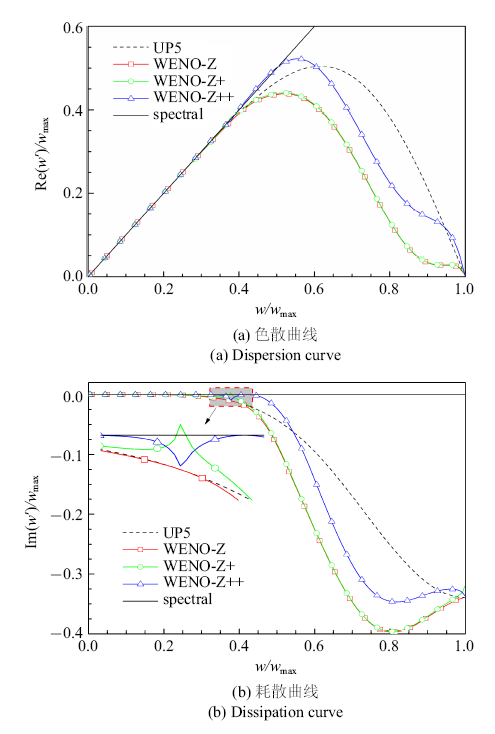
图2
另一个值得注意的事实是,WENO-Z++格式的频谱特性甚至要显著优于对应的线性迎风格式. 事实上,WENO-Z$+\!$格式的频谱特性也在一定的波数范围内优于线性迎风格式,只是不如WENO-Z++格式明显. 这与以往的WENO格式不同. 在以往的WENO格式中,欠光滑子模板上的权重总是小于理想权重,因而其频谱特性总是劣于对应的线性迎风格式.WENO-Z+和WENO-Z++格式可在光滑区域为欠光滑子模板分配大于理想权重的权重值,这使得其频谱特性有可能超过对应的线性格式.这一现象将在另一篇文章中得到更为细致的研究.
2.9 WENO-Z++格式的精度
由于WENO-Z++格式只是改进了$\lambda $的计算公式, 其权重形式仍与WENO-Z$+\!$格式相同, 因而可直接对其使用文献[29]的结论: 若在权重公式(12)中为$\tau _5 $和$\beta _k $搭配不同的参数$\varepsilon $, 即
WENO-Z++格式在整个流场光滑区域都能达到最优阶精度的一个充分条件是
式中$r$是子模板上数值通量的收敛精度, 对于五阶WENO格式, $r = 3$. 根据文献[17], 在光滑区域($n_{{\rm cp}} $阶极值点处)
代入式(14)有
$\varepsilon$应尽可能小,因而取$\varepsilon _\beta = \Delta x^2$,从而有
条件$\theta (\varepsilon _\tau ) \geqslant n > 0$意味着只需要将$\varepsilon _\tau $的值取得足够小(比如$\varepsilon _\tau = 10^{ - 40}$), 因此关键在于$\theta (\tau )$的条件. 根据文献[17]
当$n_{\rm cp} \geqslant 1$时, $\theta (\tau )$的条件显然满足, 意味着WENO-Z++格式可在任意阶极值点附近保持五阶的最优精度.而当$n_{\rm cp} = 0$时(即在非极值点处), $\theta (\tau _5 ) = 5$, 不能满足$\theta (\tau ) > 5.75$的条件. 但需要注意的是, 式(16)所给出的只是一个充分而非必要条件. 同时,下文中的精度测试将表明: 当取$\varepsilon _\beta = \Delta x^2$, $\varepsilon_\tau = 10^{ - 40}$时, 虽然$\theta \left( {\tau _5 } \right) > 5.75$的条件不能满足, WENO-Z++格式仍在非极值点处具有五阶精度.于是可得到一组能够使五阶WENO-Z++格式在整个流场光滑区域保持最优阶精度的参数设置
这也意味着若取$\varepsilon _\beta = \varepsilon _\tau = 10^{ - 40}$, 格式的收敛精度有可能会在极值点处降低.
3 数值试验和结果分析
接下来的数值试验将进一步表明本文所提出新格式的优越性. 为了便于比较,本文为所有WENO格式取$p = 2$, $\varepsilon = 10^{ - 40}$.
3.1 精度测试
$g_n (x)$, $n \geqslant 1$在区间$x \in [ - 1,1 ]$内有且仅有一个极值点,位于$x = 0$处,阶数为$n$; $g_0 (x)$没有极值点.这一特性使得该函数族适合用来测试差分格式在高阶极值点处的收敛精度. 在测试时,我们使用差分格式在不同规格的网格上计算函数$g_n (x)$ ($n=0$, 1, 2)的导数值, 并考察计算误差. 在测试中,对WENO-Z++格式使用两组不同的参数设置, 以验证2.9节的结论
参数设置I: $\varepsilon _\beta = \varepsilon _\tau = 10^{ - 40}$
参数设置II: $\varepsilon _\beta = \Delta x^2$, $\varepsilon _\tau = 10^{-40}$
将使用以上两组参数的WENO-Z++格式分别标识为WENO-Z++1和WENO-Z++2,并与WENO-Z和WENO-Z$+\!$格式进行比较.
表1给出在本测试中4种WENO格式的$L^{1}$误差和收敛精度. 在没有极值点的情况下,表中列出的所有格式都能达到五阶精度. 在一阶极值点处, WENO-Z$+\!$格式降为四阶,WENO-Z++格式仍能保持五阶精度. 在二阶极值点处, WENO-Z++1降为三阶,只有WENO-Z++2仍能保持五阶精度, 这就验证了2.9节的结论. 在所有情况下,WENO-Z++2的误差最小, WENO-Z++1次之, 这表明本文所提出的新格式具有更高的精度.
表1 在计算由式(22)所定义的函数的导数值时,4种WENO格式(WENO-Z, WENO-Z+, WENO-Z++1和 WENO-Z++2)的$L^1$误差和收敛精度
Table 1
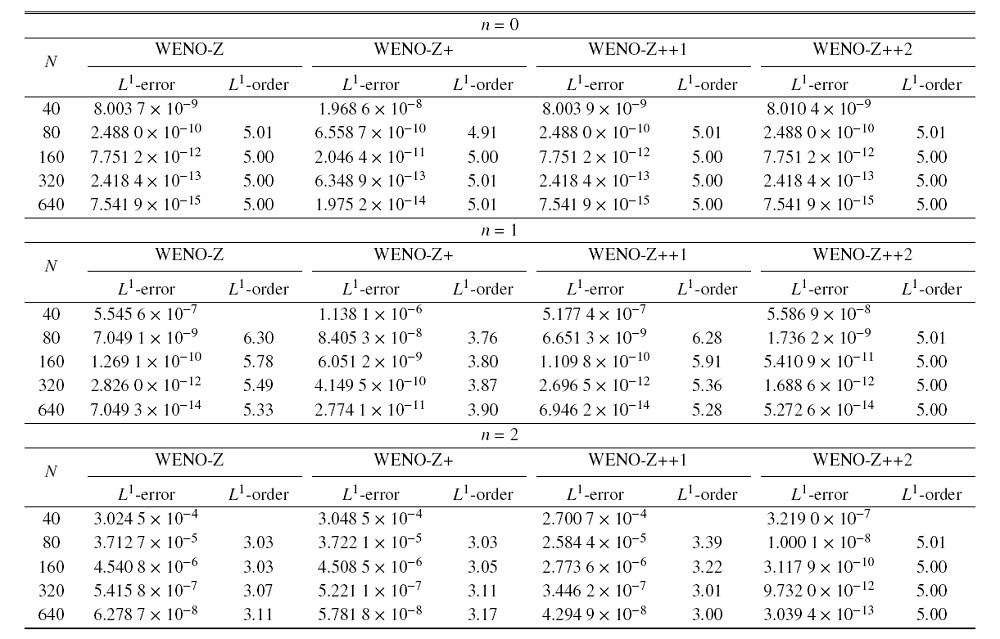 |
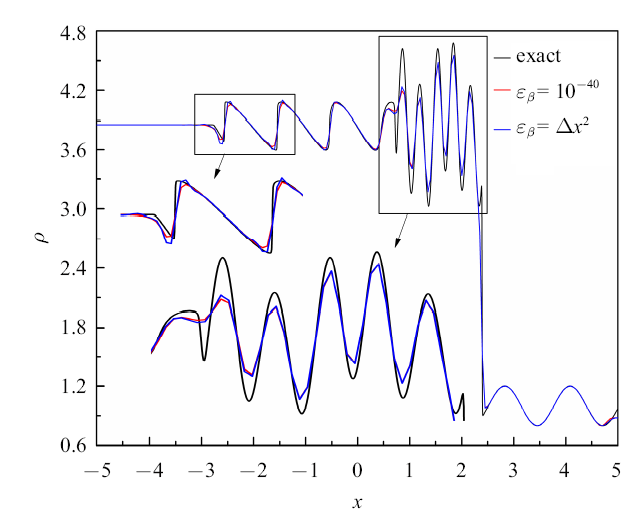
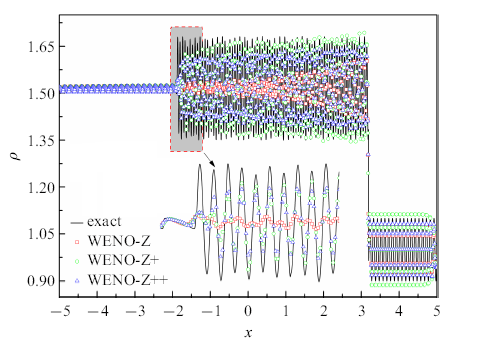
图3比较了使用两组参数设置的WENO-Z++格式对Osher-Shu问题的计算结果. 观察到,使用参数设置II并未对高频熵波的计算结果带来明显改善,反而在声波区域产生了更多的数值振荡.这说明: 使用参数设置II虽能提高格式在极值点处的精度,却不能明显改善格式的分辨率, 反而会降低格式的稳定性. 因此,在接下来的数值试验中, 我们仍对WENO-Z++格式使用参数设置I.
图3
图3
当WENO-Z++格式中参数$\varepsilon _\beta $取不同值时Osher-Shu问题的数值解
Fig.3
Numerical solutions of the Osher-Shu problem when the parameter $\varepsilon _\beta $ in WENO-Z++ scheme takes different values
3.2 Osher-Shu问题
该问题描述一道马赫数3的右行激波与一系列熵波之间的相互作用[33].在激波通过的地方, 熵波被压缩和放大, 同时产生一系列向下游传播的声波.该算例可用来测试格式的激波捕捉能力、数值稳定性、耗散性和高频波分辨率.
在区间$[ - 5,5 ]$上求解一维Euler方程, 初始条 件为
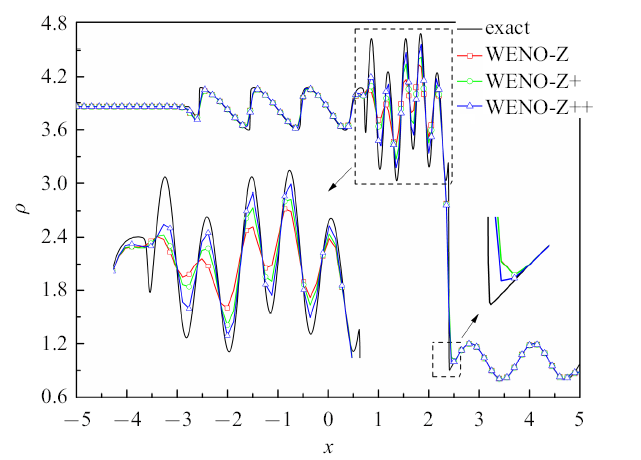
式中, $\rho$, $u$, $p$分别表示无量纲的密度, 速度和压强.网格数量$N = 200$, $CFL = 0.5$,计算终止时间为$t = 1.8$(无量纲). 图4给出3种WENO格式的计算结果, 并与$N = 2000$时WENO-Z格式的计算结果(标识为``exact'')进行对比.
图4
图4
Osher-Shu问题的密度分布曲线及其局部放大图
Fig.4
Density distribution curves of the Osher-Shu problem and its partial enlarged detail
观察图4, WENO-Z$+\!$格式相对于WENO-Z格式的提升主要体现在高频波区域; 而在间断处,两者的计算结果几乎完全一样. 相比之下, WENO-Z++格式不仅进一步提升了对高频波的分辨率,其在间断处的结果也有明显的改善.
图5给出3种WENO格式在欠光滑子模板上(用下标``D''来标识)非线性权重$\omega $与理想权重$d$之间比值的分布. $\omega $的值使用密度值$\rho $计算得到. 图5(a)和图5(b)分别给出的是在高频波区域和在间断附近的结果.观察图5(a), WENO-Z$+\!$格式相比于WENO-Z格式大幅度提高了欠光滑子模板上的权重,因而显著提升了对高频波的分辨率. 总体而言,WENO-Z++格式在欠光滑子模板上的权重相比WENO-Z$+\!$格式进一步增大,因而其对高频波的分辨率得到了进一步的提升. 注意, 在所有网格界面上,WENO-Z++格式为欠光滑子模板所分配的权重都要大于理想权重,这说明: 在光滑区域使欠光滑子模板上的权重大于理想权重对于提升WENO格式的分辨率是有益的,只要这种增大不超过一定限度而出现负耗散.
图5
图5
在Osher-Shu问题中几种WENO格式在欠光滑子模板上的权重的分布
Fig.5
The distributions of the weights of less-smooth substencils for different WENO schemes in the Osher-Shu problem
观察图5(b), WENO-Z$+\!$格式和WENO-Z格式在间断处的权重分布几乎完全一样,因而其在间断处的数值结果也基本没有差异. 相比之下,WENO-Z++ 格式显著增大了含间断子模板的权重, 因而其数值耗散更低,捕捉到的激波更为干脆; 同时, 这一权重值仍然足够小,从而WENO-Z++格式仍能保持ENO特性. 这就验证了2.7节的分析结果.
3.3 Titarev-Toro问题
Titarev-Toro问题[34]是Osher-Shu问题的变种, 其激波马赫数为1.1;其熵波频率要比Osher-Shu问题高得多; 计算终止时间也更长, 为$t = 5$. 初始条 件为
网格数量$N = 1000$; $CFL = 0.5$. 图6给出3种WENO格式的计算结果, 同时与$N = 8000$时WENO-Z格式的计算结果(标识为``exact'')进行对比.
图6
图6
Titarev-Toro问题的密度分布曲线及其局部放大图
Fig.6
Density distribution curves of the Titarev-Toro problem and its partial enlarged detail
图6显示, 在穿过激波后, WENO-Z格式计算的高频波迅速衰减, 最终完全失真;WENO-Z$+\!$格式和WENO-Z++格式则都能比较准确地反映高频波.其中WENO-Z$+\!$格式得到的峰值更高,但在激波前和激波后附近的区域都存在对高频波的虚假放大,这就验证了2.8节的分析结果: WENO-Z$+\!$格式未能完全消除负耗散;WENO-Z++格式则有效地避免了对高频波的虚假放大.
在这一算例中, WENO-Z$+\!$格式对高频波的分辨率似乎要优于WENO-Z++格式.这是因为: WENO-Z$+\!$格式放宽了对稳定性的要求, 允许负耗散的存在, 从而$\lambda $可取较大的值; 若要彻底消除负耗散, $\lambda $的值需进一步减小, 这样WENO-Z$+\!$格式所得到的峰值也将相应地降低,在其他算例中的分辨率也要进一步折损. 或者, WENO-Z++格式也放宽对稳定性的要求,为式(14)中的取更大的值, 这样其得到的峰值也会进一步提高.
3.4 Lax问题
一维Riemann问题是测试数值格式激波捕捉能力的经典算例,其流场中同时包含有激波、接触间断、膨胀波和平滑区域. 对于Lax问题[35], 在区间$[ - 5,5]$上求解一维Euler方程, 初始条件为
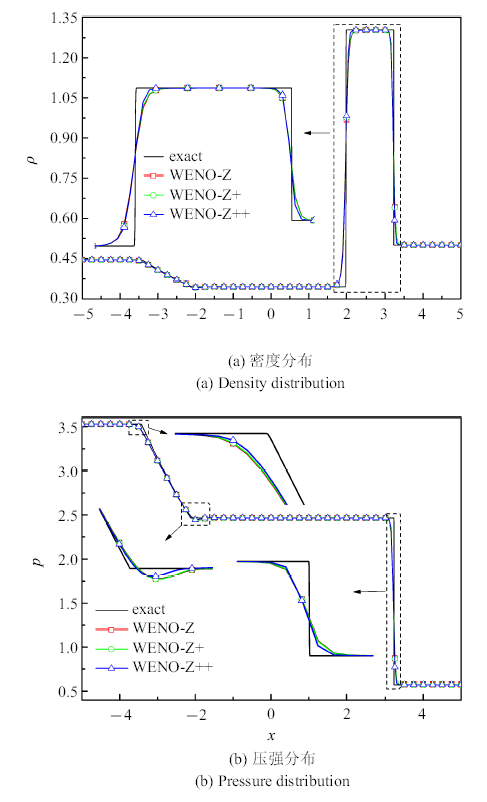
网格数量为$N = 200$; $CFL = 0.5$; 计算终止时间为$t = 1.3$. 图7给出3种WENO格式的计算结果, 并与精确解(标记为`exact')进行对比.
图7
图7
Lax问题的密度(a)和压强(b)分布曲线及其局部放大图
Fig.7
Density (a) and pressure (b) distribution curves of the Lax problem and the partial enlarged details
观察图7, WENO-Z$+\!$格式的计算结果相比WENO-Z格式并没有明显的改善;WENO-Z++格式则显著改善了对激波、接触间断和膨胀波计算结果.这就验证了新格式的ENO特性和更优异的对间断的分辨率.
3.5 二维Riemann问题
相比一维Riemann问题, 二维问题包含多尺度的流场结构,可测试数值格式的多尺度分辨率[36]. 在正方形区域$[0,1]\times [0,1]$内求解二维Euler方程, 初始条件为
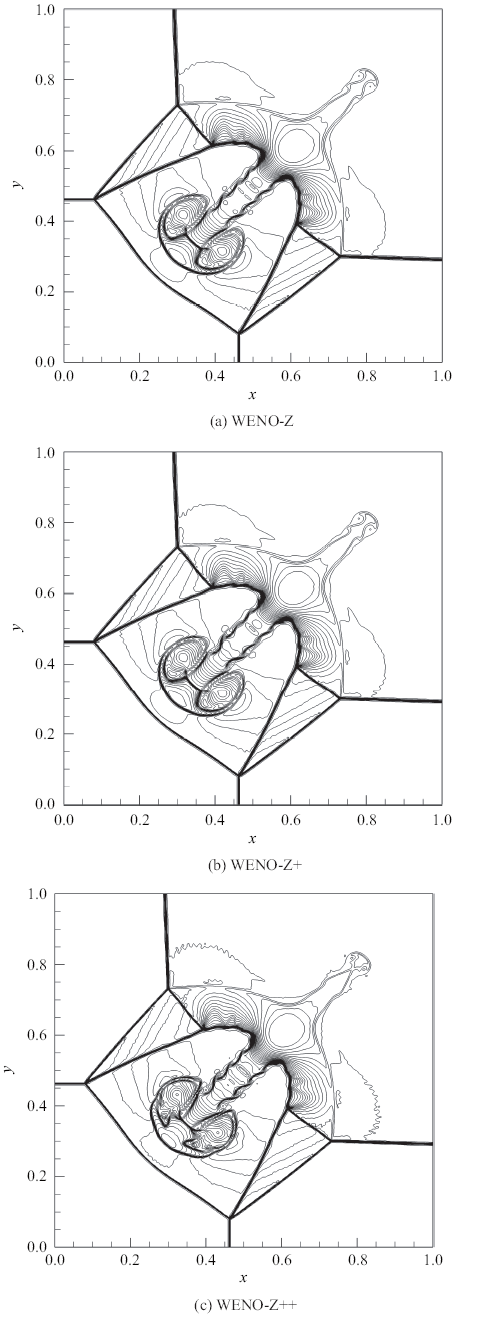
其中, $\rho$, $u$, $v$, $p$分别为无量纲的密度, $x$方向和$y$方向上的速度以及压强.网格数量为$400\times 400$; $CFL = 0.5$;计算终止时间为$t = 0.8$.图8给出3种WENO格式的计算结果. 密度等值线是从0.14到1.7之间等间距的40条.
图8
图8
二维Riemann问题的密度等值线图
Fig.8
Density contours of the two-dimensional Riemann problem
观察图8, WENO-Z$+\!$格式的数值结果与WENO-Z格式的相比差别不大.WENO-Z++格式的数值结果则有显著的提升.这表明: 虽然WENO-Z$+\!$格式在仅涉及单一波动成分的算例(例如Osher-Shu 问题和Titarev-Toro问题)中取得了显著改善的结果,其多尺度的分辨率并没有明显提升; 相比之下,WENO-Z++格式则显著提升了多尺度的分辨率.这与2.8节的分析结果一致: WENO-Z$+\!$格式的频谱特性只在非常小的波数范围内有所提升;WENO-Z++格式则在全部波数范围内都有显著提升.
3.6 双马赫反射
在双马赫反射问题[37]中, 一道马赫数10的斜激波撞击无黏壁面,所产生的流场中包含极其复杂的激波反射和丰富的旋涡结构,可用来测试数值格式的激波捕捉能力、数值稳定性、耗散性和分辨率.
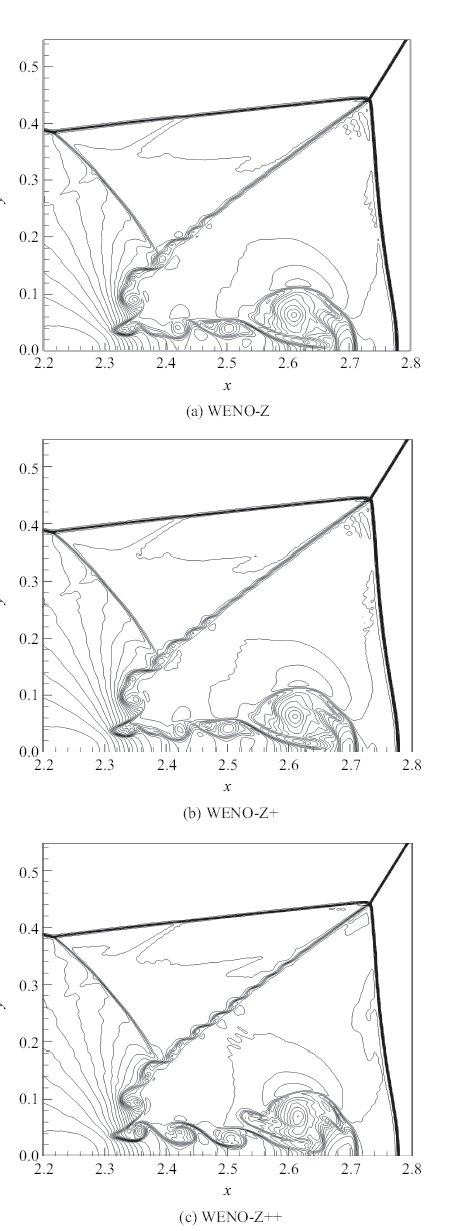
该问题的计算区域为$[0,4]\times [0,1]$, 初始条件为一道与$x$轴成$60^{\circ}$, $Ma = 10$的斜激波在$x = {1}/{6}$处与底部壁面边界相遇. 激波上游参数为$(\rho ,u,v,p) = (1.4,0,0,1)$; 下游参数由激波关系式得出. 计算域的上边界为激波传播的精确解; 左边界及底部$x\leqslant {1}/{6}$的部分为入流边界条件; 右边界为出流边界条件; 底部$x > {1}/{6}$的部分为壁面边界条件. 计算终止时间(无量纲)为$t = 0.2$; $CFL = 0.5$; 网格数量为$1920\times 480$. 由于该算例中流场的复杂结构主要集中在$x \in [2.2,2.8]$之间、双马赫杆附近的区域, 图9给出这一区域的密度等值线图, 等值线为2到22之间的40等份.
图9
观察图9, WENO-Z$+\!$格式的计算结果与WENO-Z格式相比没有明显的差异. 相比之下,WENO-Z++格式的计算结果有显著的提升, 其捕捉到的激波更为干脆,旋涡结构更为清晰和丰富. 这表明新格式具有更低的数值耗散和更高的分辨率.
3.7 Rayleigh-Tayler不稳定性问题
在Rayleigh-Tayler不稳定性问题[38]中,两种密度不同的流体分别位于上下两层, 重力方向由重流体指向轻流体.沿此方向给与一个速度扰动, 流场开始演化. 在流场演化的后期,轻流体的空泡和重流体的``尖钉''相互侵入, 形成非常复杂的"蘑菇头"形状.实际的流动由Navier-Stokes方程控制, 物理黏性决定流场的形态.而当求解Euler方程时, 数值结果就能反映出格式的数值耗散.
在计算域$[0,0.25]\times [0,1]$内给定初始条件
在本算例中, 绝热指数为$\gamma = {5}/{3}$. 左右边界为无黏壁面; 上下边界的流场数据固定. 计算终止时间为$t = 1.95$; $CFL = 0.5$; 网格数量为$120\times 480$.
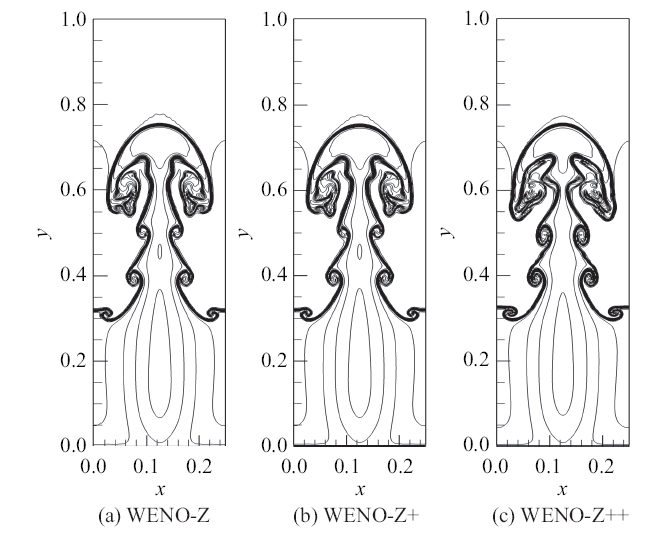
图10给出3种WENO格式的计算结果. 密度等值线是0.952 269到2.145 89之间的15等份.WENO-Z格式和WENO-Z$+\!$格式的计算结果基本没有差异.WENO-Z++格式则捕捉到了更多的流场细节, 表明其更低的数值耗散和更高的分辨率.
图10
图10
Rayleigh-Tayler不稳定性问题的密度等值线图
Fig.10
Density contours of the two-dimensional Rayleigh-Taylor instability problem
4 结论
在WENO-Z$+\!$格式中, 新增项的系数$\lambda $对格式的数值性能具有至关重要的影响. 本文分析表明,文献[29]所采用的$\lambda $取值方法既不能充分发挥格式的潜力, 也未完全消除负耗散.本文根据WENO-Z$+\!$格式的权重特性重新设计了$\lambda $的计算公式. 该公式利用当地流场数据来计算$\lambda $的值, 因此能自适应地调控新增项的作用. 一系列数值试验表明,这一改进方法不仅有效消除了负耗散,还进一步提升了格式的精度、激波捕捉能力和对光滑细微结构的分辨率.新格式被命名为WENO-Z++.
在极值点处收敛精度降低是WENO格式的通病,因此本文推导了能够使WENO-Z++格式在极值点处保持最优阶精度的参数设置.但使用该参数设置并未实质性地改善数值结果, 反而导致了更多的数值振荡.这一事实再次验证了文献[29]的结论: 在通常的应用中,极值点处的精度并不是影响WENO格式数值结果的最主要因素,欠光滑子模板上的权重才是更为重要的因素.
本文还发现, 欠光滑子模板上的权重影响WENO格式的频谱特性. 具体而言,增大欠光滑子模板上的权重能提高数值解的相速度并减小格式的数值耗散.甚至可使欠光滑子模板上的权重大于理想权重,从而使WENO格式的频谱特性优于对应的线性迎风格式.只需要将这种增大控制在一定限度内以避免负耗散. 这一现象应得到更为细致的研究,以期对WENO格式的改进和应用提供新的思路.
参考文献
High-order low-dissipation targeted ENO schemes for ideal magnetohydrodynamics
Characteristic finite-difference WENO scheme for multicomponent compressible fluid analysis: Overestimated quasi-conservative formulation maintaining equilibriums of velocity, pressure, and temperature
A mixed upwind/central WENO scheme for incompressible two-phase flows
Numerical study of combustion effects on the development of supersonic turbulent mixing layer flows with WENO schemes
激波与转捩边界层干扰非定常特性数值分析
激波与边界层干扰的非定常问题是高速飞行器气动设计中基础研究内容之一.以往研究主要针对层流和湍流干扰,在分离激波低频振荡及其内在机理方面存在着上游机制和下游机制两类截然不同的理论解释.分析激波与转捩边界层干扰下非定常运动现象有助于进一步加深理解边界层状态以及分离泡结构对低频振荡特性的影响规律,为揭示其产生机理指出新的方向.采用直接数值模拟方法对来流马赫数2.9,24°压缩拐角内激波与转捩边界层干扰下激波的非定常运动特性进行了数值分析.通过在拐角上游平板特定的流向位置添加吹吸扰动激发流动转捩,使得进入拐角的边界层处于转捩初期阶段.在验证了计算程序可靠性的基础上,详细分析了转捩干扰下激波运动的间歇性和振荡特征,着重研究了分离泡展向三维结构对激波振荡特性的影响规律,最后还初步探索了转捩干扰下激波低频振荡产生的物理机制.研究结果表明:分离激波的非定常运动仍存在强间歇性和低频振荡特征,其时间尺度约为上游无干扰区内脉动信号特征尺度的10倍量级;分离泡展向三维结构不会对分离激波的低频振荡特征产生实质影响.依据瞬态脉动流场的低通滤波结果,转捩干扰下激波低频振荡的诱因来源于拐角干扰区下游,与流场中分离泡的收缩/膨胀运动存在一定的关联.
Numerical analysis of unsteady motion in shock wave/transitional boundary layer interaction
激波与边界层干扰的非定常问题是高速飞行器气动设计中基础研究内容之一.以往研究主要针对层流和湍流干扰,在分离激波低频振荡及其内在机理方面存在着上游机制和下游机制两类截然不同的理论解释.分析激波与转捩边界层干扰下非定常运动现象有助于进一步加深理解边界层状态以及分离泡结构对低频振荡特性的影响规律,为揭示其产生机理指出新的方向.采用直接数值模拟方法对来流马赫数2.9,24°压缩拐角内激波与转捩边界层干扰下激波的非定常运动特性进行了数值分析.通过在拐角上游平板特定的流向位置添加吹吸扰动激发流动转捩,使得进入拐角的边界层处于转捩初期阶段.在验证了计算程序可靠性的基础上,详细分析了转捩干扰下激波运动的间歇性和振荡特征,着重研究了分离泡展向三维结构对激波振荡特性的影响规律,最后还初步探索了转捩干扰下激波低频振荡产生的物理机制.研究结果表明:分离激波的非定常运动仍存在强间歇性和低频振荡特征,其时间尺度约为上游无干扰区内脉动信号特征尺度的10倍量级;分离泡展向三维结构不会对分离激波的低频振荡特征产生实质影响.依据瞬态脉动流场的低通滤波结果,转捩干扰下激波低频振荡的诱因来源于拐角干扰区下游,与流场中分离泡的收缩/膨胀运动存在一定的关联.
高超声速激波湍流边界层干扰直接数值模拟研究
Direct numerical simulation of hypersonic shock wave and turbulent boundary layer interactions
各向同性湍流通过正激波的演化特征研究
Study on evolution characteristics of isotropic turbulence passing through a normal shock wave
Interface flux reconstruction method based on optimized weight essentially non-oscillatory scheme
A truly forward semi-Lagrangian WENO scheme for the Vlasov-Poisson system
A WENO finite-difference scheme for a new class of Hamilton-Jacobi equations in nonlinear solid mechanics
High order WENO finite volume approximation for population density neuron model
High-order Lax-Friedrichs WENO fast sweeping methods for the $S_{N}$ neutron transport equation
Uniformly high order accurate essentially non-oscillatory schemes, III
Weighted essentially non-oscillatory schemes
Stratocumulus clouds are the most common type of boundary layer cloud; their radiative effects strongly modulate climate. Large eddy simulations (LES) of stratocumulus clouds often struggle to maintain fidelity to observations because of the sharp gradients occurring at the entrainment interfacial layer at the cloud top. The challenge posed to LES by stratocumulus clouds is evident in the wide range of solutions found in the LES intercomparison based on the DYCOMS-II field campaign, where simulated liquid water paths for identical initial and boundary conditions varied by a factor of nearly 12. Here we revisit the DYCOMS-II RF01 case and show that the wide range of previous LES results can be realized in a single LES code by varying only the numerical treatment of the equations of motion and the nature of subgrid-scale (SGS) closures. The simulations that maintain the greatest fidelity to DYCOMS-II observations are identified. The results show that using weighted essentially non-oscillatory (WENO) numerics for all resolved advective terms and no explicit SGS closure consistently produces the highest-fidelity simulations. This suggests that the numerical dissipation inherent in WENO schemes functions as a high-quality, implicit SGS closure for this stratocumulus case. Conversely, using oscillatory centered difference numerical schemes for momentum advection, WENO numerics for scalars, and explicitly modeled SGS fluxes consistently produces the lowest-fidelity simulations. We attribute this to the production of anomalously large SGS fluxes near the cloud tops through the interaction of numerical error in the momentum field with the scalar SGS model.
Efficient implementation of weighted ENO schemes
Mapped weighted essentially non-oscillatory schemes: Achieving optimal order near critical points
An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws
An improved weighted essentially non-oscillatory scheme with a new smoothness indicator
In this paper, we present a new smoothness indicator that evaluates the local smoothness of a function inside of a stencil. The corresponding weighted essentially non-oscillatory (WENO) finite difference scheme can provide the fifth convergence order in smooth regions, especially at critical points where the first derivative vanishes (but the second derivatives are non-zero). We provide a detailed analysis to verify the fifth-order accuracy. Some numerical experiments are presented to demonstrate the performance of the proposed scheme. We see that the proposed WENO scheme provides at least the same or improved behavior over the fifth-order WENO-JS scheme [10] and other fifth-order WENO schemes called as WENO-M [9] and WENO-Z [2], but its advantage seems more salient in two dimensional problems. (C) 2012 Elsevier Inc.
Modified non-linear weights for fifth-order weighted essentially non-oscillatory schemes
A new smoothness indicator for improving the weighted essentially non-oscillatory scheme
In this work, a new smoothness indicator that measures the local smoothness of a function in a stencil is introduced. The new local smoothness indicator is defined based on the Lagrangian interpolation polynomial and has a more succinct form compared with the classical one proposed by Jiang and Shu [12]. Furthermore, several global smoothness indicators with truncation errors of up to 8th-order are devised. With the new local and global smoothness indicators, the corresponding weighted essentially non-oscillatory (WENO) scheme can present the fifth order convergence in smooth regions, especially at critical points where the first and second derivatives vanish (but the third derivatives are not zero). Also the use of higher order global smoothness indicators incurs less dissipation near the discontinuities of the solution. Numerical experiments are conducted to demonstrate the performance of the proposed scheme. (C) 2014 Elsevier Inc.
New nonlinear weights for improving accuracy and resolution of weighted compact nonlinear scheme
Third-order energy stable WENO scheme
A systematic methodology for constructing high-order energy stable WENO schemes
On the efficient computation of smoothness indicators for a class of WENO reconstructions
An efficient hybrid WENO scheme with a problem independent discontinuity locator
A brief review on the convergence to steady state solutions of Euler equations with high-order WENO schemes
Analysis of WENO schemes for full and global accuracy
Liu, Osher, and Chan introduced weighted essentially nonoscillatory (WENO) reconstructions in [X.-D. Liu, S. Osher, and T. Chan, J. Comput. Phys., 115 (1994), pp. 200-212] to improve the order of accuracy of essentially nonoscillatory (ENO) reconstructions [A. Harten et al., J. Comput. Phys., 71 (1987), pp. 231-303]. In [G.-S. Jiang and C.-W. Shu, J. Comput. Phys., 126 (1996), pp. 202-228], the authors proposed smoothness indicators to obtain a WENO fifth order reconstruction from third order ENO reconstructions. With these smoothness indicators, Balsara and Shu [J. Comput. Phys., 160 (2000), pp. 405-452] and, later, [G. A. Gerolymos, D. Senechal, and I. Vallet, J. Comput. Phys., 228 (2009), pp. 8481-8524] obtained (2r - 1)th order WENO reconstructions from rth order ENO reconstructions for 4 <= r <= 6, resp., 7 <= r <= 9. In [A. K. Henrick, T. D. Aslam, and J. M. Powers, J. Comput. Phys., 207 (2005), pp. 542-567], the authors noticed that these reconstructions do not attain the optimal order 2r - 1 at extrema and they proposed a fix for the problem. Other authors [R. Borges et al., J. Comput. Phys., 227 (2008), pp. 3191-3211; N. K. Yamaleev and M. H. Carpenter, J. Comput. Phys., 228 (2009), pp. 4248-4272] have addressed this problem with different weight designs for Jiang-Shu smoothness indicators. In this paper we exploit the special structure of Jiang-Shu smoothness indicators and analyze the role of a parameter appearing in the weight definition to avoid division by zero to obtain for any r >= 2, by standard approximation properties of Lagrange interpolation, that the order of the WENO reconstruction is 2r - 1 at smooth regions, regardless of neighboring extrema, whilst this order is r, as ENO reconstructions have, when the function has a discontinuity in the stencil of 2r - 1 points but it is smooth in at least one of the substencils of r points. The optimal weights are also obtained in closed form.
Accuracy of the weighted essentially non-oscillatory conservative finite difference schemes
In the reconstruction step of (2r - 1) order weighted essentially non-oscillatory conservative finite difference schemes (WENO) for solving hyperbolic conservation laws, nonlinear weights alpha(k) and omega(k), such as the WENO-JS weights by Jiang et al. and the WENO-Z weights by Borges et al., are designed to recover the formal (2r - 1) order (optimal order) of the upwinded central finite difference scheme when the solution is sufficiently smooth. The smoothness of the solution is determined by the lower order local smoothness indicators beta(k) in each substencil. These nonlinear weight formulations share two important free parameters in common: the power p, which controls the amount of numerical dissipation, and the sensitivity epsilon, which is added to beta(k) to avoid a division by zero in the denominator of alpha(k). However, epsilon also plays a role affecting the order of accuracy of WENO schemes, especially in the presence of critical points. It was recently shown that, for any design order (2r - 1), epsilon should be of Omega(Delta x(2)) (Omega(Delta x(m)) means that epsilon >= C Delta x(m) for some C independent of Delta x, as Delta x -> 0) for the WENO-JS scheme to achieve the optimal order, regardless of critical points. In this paper, we derive an alternative proof of the sufficient condition using special properties of beta(k). Moreover, it is unknown if the WENO-Z scheme should obey the same condition on epsilon. Here, using same special properties of beta(k), we prove that in fact the optimal order of the WENO-Z scheme can be guaranteed with a much weaker condition epsilon = Omega(Delta x(m)), where m(r,p) >= 2 is the optimal sensitivity order, regardless of critical points. Both theoretical results are confirmed numerically on smooth functions with arbitrary order of critical points. This is a highly desirable feature, as illustrated with the Lax problem and the Mach 3 shock-density wave interaction of one dimensional Euler equations, for a smaller e allows a better essentially non-oscillatory shock capturing as it does not over-dominate over the size of beta(k). We also show that numerical oscillations can be further attenuated by increasing the power parameter 2 <= p <= r 1, at the cost of increased numerical dissipation. Compact formulas of beta(k) for WENO schemes are also presented. (C) 2013 Elsevier Inc.
An improved WENO-Z scheme
The rapid progress of high-throughput DNA sequencing techniques has dramatically reduced the costs of whole genome sequencing, which leads to revolutionary advances in gene industry. The explosively increasing volume of raw data outpaces the decreasing disk cost and the storage of huge sequencing data has become a bottleneck of downstream analyses. Data compression is considered as a solution to reduce the dependency on storage. Efficient sequencing data compression methods are highly demanded.
Recent results on the improved WENO-Z+ scheme
// Bittencourt ML eds.
An improved third-order WENO-Z scheme
The modification of the algebraic-diagrammatic construction (ADC) scheme for the polarization propagator using ground-state coupled-cluster (CC) instead of Møller-Plesset (MP) amplitudes, referred to as CC-ADC, is extended to the calculation of molecular properties, in particular, dipole polarizabilities. Furthermore, in addition to CC with double excitations (CCD), CC with single and double excitations (CCSD) amplitudes can be used, also in the second-order transition moments of the ADC(3/2) method. In the second-order CC-ADC(2) variants, the MP correlation coefficients occurring in ADC are replaced by either CCD or CCSD amplitudes, while in the F/CC-ADC(2) and F/CC-ADC(3/2) variants, they are replaced only in the second-order modified transition moments. These newly implemented variants are used to calculate the static dipole polarizability of several small- to medium-sized molecules, and the results are compared to the ones obtained by full configuration interaction or experiment. It is shown that the results are consistently improved by the use of CC amplitudes, in particular, for aromatic systems such as benzene or pyridine, which have proven to be difficult cases for standard ADC approaches. In this case, the second-order CC-ADC(2) and F/CC-ADC(2) variants yield significantly better results than the standard third-order ADC(3/2) method, at a computational cost amounting to only about 1% of the latter.
On the spectral properties of shock-capturing schemes
Efficient implementation of essentially non-oscillatory shock-capturing schemes, II
Finite-volume WENO schemes for three-dimensional conservation laws
Weak solutions of nonlinear hyperbolic equations and their numerical computation
Solution of two-dimensional Riemann problems of gas dynamics by positive schemes
The numerical simulation of two-dimensional fluid flow with strong shocks
Resolution of high order WENO schemes for complicated flow structures
A quantitative study is carried out in this paper to investigate the size of numerical viscosities and the resolution power of high-order weighted essentially nonoscillatory (WENO) schemes for solving one- and two-dimensional Navier-Stokes equations for compressible gas dynamics with high Reynolds numbers. A one-dimensional shock tube problem, a one-dimensional example with parameters motivated by supernova and laser experiments, and a two-dimensional Rayleigh-Taylor instability problem are used as numerical test problems. For the two-dimensional Rayleigh-Taylor instability problem, or similar problems with small-scale structures, the details of the small structures are determined by the physical viscosity (therefore, the Reynolds number) in the Navier-Stokes equations. Thus, to obtain faithful resolution to these small-scale structures, the numerical viscosity inherent in the scheme must be small enough so that the physical viscosity dominates. A careful mesh refinement study is performed to capture the threshold mesh for full resolution, for specific Reynolds numbers, when WENO schemes of different orders of accuracy are used. It is demonstrated that high-order WENO schemes are more CPU time efficient to reach the same resolution, both for the one-dimensional and two-dimensional test problems.