引言
航空发动机系统中涡轮转子叶片的工作性能对飞行安全有着十分重要的影响,在动力学研究中涡轮转子叶片的结构通常简化为旋转中心刚体-柔性梁模型,其在高温环境下高速旋转时,会受到热应力、大范围旋转刚体运动与柔性梁弹性变形耦合作用等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温的能力.功能梯度材料因能在极限环境下反复地正常工作而被应用于发动机叶片的设计和分析中[1 ] .同时高温引起的热力载荷、内冷通道的冷却[2 -12 ] 和截面尺寸变化等也是涡轮转子叶片系统动力学建模中需考虑的因素.
自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性.
然而, 上述研究分析的动力学模型虽然完善, 并且考虑了温度场的影响,但同时考虑高温环境影响下内冷通道的冷却和截面尺寸变化的中心刚体-FGM柔性梁的动力学研究还尚少.本文对旋转中心刚 体-FGM梁刚柔热耦合动力学特性进行研究,首先考虑柔性梁的横向弯曲变形和轴向拉伸变形,并计入横向弯曲变形引起的纵向缩短, 即非线性耦合变形量,其次考虑了叶片实际存在的内冷通道和截面尺寸变化, 其中外部高温、内冷通道冷却,即外部到内冷通道温度场呈非线性分布,运用一维热稳态传导方程求解得到FGM梁沿厚度方向分布的温度场,进而在本构关系中计入热应变, 利用虚功原理求解温度载荷的影响量,接着采用假设模态法和第二类拉格朗日方程推导得到系统的刚柔热耦合动力学方程,并编制动力学仿真软件. 最后基于动力学仿真软件, 对系统在不同温度环境,不同旋转速度以及不同功能梯度指数下的动力学特性进行研究.
1 旋转中心刚体柔性梁动力学模型
1.1 系统的物理模型
如图1 所示, 空心柔性梁与中心刚体固接在一起, 中心刚体绕$Z$轴转动, 半径为$R$, 其中$O$-$XYZ$为系统的惯性坐标系. 外部施加的驱动力矩为$\tau $, 梁的长度为$l$, 梁的外部厚度为$h_{\rm e} (x)$, 宽度为$b_{\rm e} (x)$, 内冷通道的厚度为$h_{\rm i} (x)$, 宽度为$b_{\rm i} (x)$.
图1
图1
含内冷通道的中心刚体-FGM梁物理模型
Fig.1
Physical model of the hub-FGM beam with internal cooling passage
FGM梁材料分布是两侧耐高温的陶瓷(ceramics)材料按幂律变化至中间金属(metal)材料的形式.
(1) $\begin{eqnarray}Q(y) = (Q_{\rm c} - Q_{\rm m} )\left| {\frac{2y}{h}} \right|^N + Q_{\rm m}\end{eqnarray}$
其中, $Q$代表材料的物理属性参数, 包括弹性模量$E$, 密度$\rho $, 热传导系数$K$以及热膨胀系数$\alpha $. $N$为材料功能梯度指数, $h$为梁的厚度, 在仿真计算中为相应截面厚度$h_{\rm e}(x)$, 即任意截面均满足式(1)规律, 下标c, m分别代表陶瓷和金属. 具体参数为$E_{\rm c} = 1.51\times 10^{11}$~Pa, $\rho _{\rm c} = 3.0\times 10^3$ kg/m$^3$, $K_{\rm c} = 2.09$, $\alpha _{\rm c} = 1.0\times 10^{ - 5}$; $E_{\rm m} = 7.0\times 10^{11}$~Pa, $\rho _{\rm m} = 2.707\times 10^3$ kg/m$^{3}$, $K_{\rm m} = 204$, $\alpha _{\rm m} = 2.3\times 10^{ - 5}$.
梁近刚体端外部厚度为$h_{\rm e} $, 宽度为$b_{\rm e} $, 内冷通道厚度为$h_{\rm i} $, 宽度为$b_{\rm i}$; 远刚体端外部厚度为${h}'_{\rm e} $, 宽度为${b}'_{\rm e} $, 内冷通道为$h_{\rm i} ^\prime $, 宽度为$b_{\rm i} ^\prime $; 则
(2) $\begin{eqnarray}&&h_{\rm e} (x) = h_{\rm e} - \frac{x}{l}(h_{\rm e} - {h}'_{\rm e} ) =h_{\rm e} \left( {1 - \frac{x}{l}g_{\rm 1} } \right)\end{eqnarray}$
(3) $\begin{eqnarray}\\&&b_{\rm e} (x) = b_{\rm e} - \frac{x}{l}(b_{\rm e} - {b}'_{\rm e} ) =b_{\rm e} \left( {1 - \frac{x}{l}g_{\rm 2} } \right)\end{eqnarray}$
(4) $\begin{eqnarray}\\&&h_{\rm i} (x) = h_{\rm i} - \frac{x}{l}(h_{\rm i} - h_{\rm i} ^\prime)=h_{\rm i} \left( {1 - \frac{x}{l}g_{\rm 3} } \right)\end{eqnarray}$
(5) $\begin{eqnarray}\\&&b_{\rm i} (x) = b_{\rm i} - \frac{x}{l}(b_{\rm i} - b_{\rm i} ^\prime ) =b_{\rm i} \left( {1 - \frac{x}{l}g_{\rm 4} } \right)\end{eqnarray}$
$$\begin{eqnarray*}&&g_{\rm 1} =1 - \frac{{h}'_{\rm e} }{h_{\rm e} },\ \ g_{\rm 2} =1 -\frac{{b}'_{\rm e} }{b_{\rm e} }\\&&g_{\rm 3} =1 - \frac{h_{\rm i} ^\prime }{h_{\rm i}},\ \ g_{\rm 4} = 1 - \frac{b_{\rm i} ^\prime}{b_{\rm i} }\end{eqnarray*}$$
1.2 热传导方程
本文考虑的是叶片在稳态热环境下的动力学响应, 此时认为上下热源$T_1 $和内部冷却温度$T_0 $为定值, 梁材料的热传导方程为
(6) $\begin{eqnarray}\frac{\rm d}{{\rm d}y}\left[ {K\left( y \right)\frac{{\rm d}T(y)}{{\rm d}y}} \right] = 0\end{eqnarray}$
实心部分边界条件为(两侧实心处, 假设处于对称面处的温度为$T_0 $)
(7) $\begin{eqnarray}\left. \begin{array}{ll} T = T_1,\ \ & y = \pm \dfrac{h_{\rm e} (x)}{2} \\ T = T_0, &y = 0 \\\end{array} \right\} \end{eqnarray}$
将式(7)代入式(6)得实心部分温度场$T_{\rm a} (y)$的函数为
(8) $\begin{eqnarray}T_{\rm a} (y) = T_0 + \frac{\Delta T}{c_1}\int_0^{|y|}{1}\Bigg/\lt(K_{{\rm cm}} \left| {\frac{2y}{h_{\rm e} }} \right|^N + K_{\rm m}) {\rm d}y \end{eqnarray}$
其中 $c_{\rm 1} = \displaystyle\int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {1}\Bigg/\lt(K_{{\rm cm}} \left| {\frac{2y}{h_{\rm e} }} \right|^N + K_{\rm m}) {\rm d}y$, $K_{{\rm cm}} = K_{\rm c} - K_{\rm m} $, $\Delta T = T_1 - T_0 $.
将$T_{\rm a} (y)$根据泰勒展开并参照文献[34 ,35 ] 可取其前七项作为解
(9) $\begin{eqnarray}&&T_{\rm a} (y) = T_0 + \frac{\Delta T}{c_1 }\Bigg[\left| {\frac{2y}{h_{\rm e} }} \right| - \frac{K_{{\rm cm}} }{(N + 1)K_{\rm m} }\left| {\frac{2y}{h_{\rm e} }} \right|^{N + 1} +\\&&\qquad \frac{K_{{\rm cm}}^2 }{(2N + 1)K_{\rm m}^2 }\left| {\frac{2y}{h_{\rm e} }} \right|^{2N + 1} - \frac{K_{{\rm cm}}^3 }{(3N + 1)K_{\rm m}^3 }\left| {\frac{2y}{h_{\rm e} }} \right|^{3N + 1} +\\&&\qquad \frac{K_{{\rm cm}}^4 }{(4N + 1)K_{\rm m}^4 }\left| {\frac{2y}{h_{\rm e} }} \right|^{4N + 1} - \frac{K_{{\rm cm}}^5 }{(5N + 1)K_{\rm m}^5 }\left| {\frac{2y}{h_{\rm e} }} \right|^{5N + 1}\Bigg] \end{eqnarray}$
(10) $\begin{eqnarray}&&c_1 = \Bigg[1 - \frac{K_{{\rm cm}} }{(N + 1)K_{\rm m} } + \frac{K_{{\rm cm}}^2 }{(2N + 1)K_{\rm m}^2 } - \frac{K_{{\rm cm}}^3}{(3N + 1)K_{\rm m}^3 } +\\&&\qquad \frac{K_{{\rm cm}}^4 }{(4N + 1)K_{\rm m}^4 } - \frac{K_{{\rm cm}}^5}{(5N + 1)K_{\rm m}^5 }\Bigg] \end{eqnarray}$
(11) $\begin{eqnarray}\left. {{\begin{array}{*{20}c} {T = T_1 ,y = \pm \dfrac{h_{\rm e} (x)}{2}} \\\\{T = T_0 ,y = \pm \dfrac{h_{\rm i} (x)}{2}}\\\end{array} }} \right\}\end{eqnarray}$
将式(11)代入式(6)解得中空处壁厚温度场的函数$T_{\rm b} (y)$为
(12) $\begin{eqnarray}T_{\rm b} (y) = T_0 + \frac{\Delta T}{c_2 }\int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| y \right|} {1}\Bigg/\Bigg({K_{{\rm cm}} \left| {\frac{2y}{h_{\rm e} }} \right|^N + K_{\rm m}}\Bigg){\rm d}y \end{eqnarray}$
其中, $c_{\rm 2} = \displaystyle\int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|}{1}\Bigg/\Bigg({K_{{\rm cm}} \left| {\frac{2y}{h_{\rm e} }} \right|^N + K_{\rm m}}\Bigg){\rm d}y$, 同理可得
(13) $\begin{eqnarray} &&T_{\rm b} (y) = T_0 + \frac{T}{c_2 }\Bigg\{\left| {\frac{2y}{h_e }} \right| - \left( {\frac{h_{\rm i} }{h_e }} \right) -\\&&\qquad \frac{K_{{\rm cm}} }{(N + 1)K_{\rm m} }\Bigg[\left| {\frac{2y}{h_{\rm e} }} \right|^{N + 1} - \left( {\frac{h_{\rm i} }{h_e }} \right)^{N + 1}\Bigg] +\\&&\qquad \frac{K_{{\rm cm}}^2 }{(2N + 1)K_{\rm m}^2 }\Bigg[\left| {\frac{2y}{h_{\rm e} }} \right|^{2N + 1} - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{2N + 1}\Bigg] -\\&&\qquad \frac{K_{{\rm cm}}^3 }{(3N + 1)K_{\rm m}^3 }\Bigg[\left| {\frac{2y}{h_{\rm e} }} \right|^{3N + 1} - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{3N + 1}\Bigg] +\\&&\qquad \frac{K_{{\rm cm}}^4 }{(4N + 1)K_{\rm m}^4 }\Bigg[\left| {\frac{2y}{h_{\rm e} }} \right|^{4N + 1} - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{4N + 1}\Bigg] -\\&&\qquad \frac{K_{{\rm cm}}^5 }{(5N + 1)K_{\rm m}^5 }\Bigg[\left| {\frac{2y}{h_{\rm e} }} \right|^{5N + 1} - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{5N + 1}\Bigg]\Bigg\} \end{eqnarray}$
(14) $\begin{eqnarray} \label{eq14} && c_2 = 1 - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right) - \frac{K_{{\rm cm}} }{(N + 1)K_{\rm m} }\Bigg[1 - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{N + 1}\Bigg] +\\&&\qquad \frac{K_{{\rm cm}}^2 }{(2N + 1)K_{_{\rm m} }^{\rm 2} }\Bigg[1 - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{2N + 1}\Bigg] -\\&&\qquad \frac{K_{{\rm cm}}^3 }{(3N + 1)K_{_{\rm m} }^{\rm 3} }\Bigg[1 - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{3N + 1}\Bigg] +\\&&\qquad \frac{K_{{\rm cm}}^4 }{(4N + 1)K_{_{\rm m} }^{\rm 4} }\Bigg[1 - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{4N + 1}\Bigg] -\\&&\qquad \frac{K_{{\rm cm}}^5 }{(5N + 1)K_{_{\rm m} }^{\rm 5} }\Bigg[1 - \left( {\frac{h_{\rm i} }{h_{\rm e} }} \right)^{5N + 1}\Bigg] \end{eqnarray}$
1.3 系统的动力学方程
如图2 所示, 在柔性梁上建立的浮动坐标系${o}'xyz$, $\theta $是浮动坐标系${o}'x$轴与惯性系$OX$轴的夹角, 与传统均质梁不同, 本文研究的FGM梁材料属性沿厚度方向呈幂律变化,因此梁的弹性模量$E(y)$, 密度$\rho \left( y \right)$, 热膨胀系数$\alpha \left( y \right)$和热传导系数$K\left( y \right)$均是$y$的函数.
图2
图2
梁变形示意图
Fig.2
The schematic diagram of flexible beam deformation
如图2 所示, 在浮动坐标系中柔性梁上任一点$p$在变形后的矢径可表示为
(15) $\begin{eqnarray} r = r_{\rm 0} + \rho _0 + u \end{eqnarray}$
其中, $ r_0 $为刚体中心$O$到浮动系坐标原点${o}'$的矢径, $ \rho _0 $为未变形前$p$点于浮动系的矢径, $ u$为变形位移矢量, 具体为
(16) $\begin{eqnarray} \label{eq16} \left. {{\begin{array}{l} {u_x \left( {x,t} \right) = w_1 + w_{\rm c} } \\ {u_y \left( {x,t} \right) = w_2 } \\ {w_{\rm c} \left( {x,t} \right) = - \dfrac{1}{2}\displaystyle\int_0^x {\left( {\dfrac{\partial w_2 }{\partial \zeta }} \right)^2{\rm d}\zeta } } \\ \end{array} }} \right\} \end{eqnarray}$
其中, $w_1 $和$w_2 $分别为梁轴向伸长量和横向弯曲变形量, $w_{\rm c} $则横向弯曲变形引起的纵向缩短量.
设$\varTheta = \left( {{\begin{array}{c@{\ \ }c} {\cos \theta } & { - \sin \theta } \\ {\sin \theta } & {\cos \theta } \\\end{array} }} \right)$为浮动坐标系相对于惯性坐标系的方向余弦矩阵, 则在惯性系下$p$的矢径可表示为
(17) $\begin{eqnarray} \label{eq17} && r = \varTheta \left( { r_0 + \rho _0 + u} \right) =\\&&\qquad \left( {{\begin{array}{*{20}c} {\cos \theta } & { - \sin \theta } \\ {\sin \theta } & {\cos \theta } \\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} {R + x + w_1 + w_{\rm c} } \\ {w_2 } \\ \end{array} }} \right) \end{eqnarray}$
将上式对时间求导, 可得$p$点的速度, 则系统的动能可表示为
(18) $\begin{eqnarray} T_k =\frac{1}{2}J_{\rm oh} \dot{\theta }^2 + \frac{1}{2}\int_V {\rho \left( y \right)} \dot{ r}^{\rm T}\dot{ r}{\rm d}V \end{eqnarray}$
(19) $\begin{eqnarray}U=\frac12\int_V {E(y)\varepsilon _x^2 {\rm d}V}\end{eqnarray}$
$\varepsilon _x$为梁上任意点的轴向应变
(20) $\begin{eqnarray}\varepsilon _x = \frac{\partial w_1 }{\partial x} - y\frac{\partial ^2w_2}{\partial x^2}\end{eqnarray}$
(21) $\begin{eqnarray} \sigma = E(y)(\varepsilon _x - \alpha (y)\Delta T) \end{eqnarray}$
(22) $\begin{eqnarray} \left. {{\begin{array}{*{20}c} {w_1 (x,t) = \varPhi _x (x) A(t)} \\ {w_2 (x,t) = \varPhi _y (x) B(t)} \\ \end{array} }} \right\} \end{eqnarray}$
其中, $ \varPhi _x (x) \in R^{1\times Nx}$, $ \varPhi _y (x) \in R^{1\times Ny}$分别为梁的轴向与横向振动的模态函数行矢量, $ A(t) \in R^{Nx\times 1}$, $ B(t) \in R^{Ny\times 1}$分别为轴向振动和横向振动的坐标矢量, 则非线性耦合项$w_{\rm c} $为
(23) $\begin{eqnarray} w_{\rm c} = - \frac{1}{2} B^{\rm T} H(x) B \end{eqnarray}$
其中$ H(x) = \int_0^x {{ \varPhi'}_y^{\rm T} (\xi ){ \varPhi'}_y (\xi )} {\rm d}\xi $, ${ \varPhi'}_y (\xi ) = {\partial \varPhi _y (\xi )}/{\partial \xi }$. 取广义坐标$q = (\theta\ \ A^{\rm T} \ \ B^{\rm T})^{\rm T}$, 则变温度场对柔性梁所做的虚功为
(24) $\begin{eqnarray} && \delta W_{\rm T} = \int_V {\delta \varepsilon _x \sigma _{\rm T} } =\\&&\qquad \int_V {\delta \varepsilon _x } E(y)( - \alpha (y)\Delta T){\rm d}V = \delta Q_{\rm T}^{\rm T} \delta q \end{eqnarray}$
式中$\sigma _{\rm T} = - \alpha (y)\Delta T$为热应力, $ Q_{\rm T}$为由温度载荷影响所产生的广义列向量,其由中空处的壁厚温度载荷影响$ Q_{{\rm Ta}} $和两侧实心处的温度载荷影响$ Q_{{\rm Tb}} $组成, $ Q_{{\rm Ta}} $和$ Q_{{\rm Tb}} $具体表达式为
(25) $\begin{eqnarray} && Q_{{\rm Ta}} = \Bigg[0,\int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)b_{\rm e} (x)\alpha (y)} \Delta T{\rm d}y\int_0^l {{\varphi }'_x {\rm d}x} , - \\&&\qquad \int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {yE(y)b_{\rm e} (x)\alpha (y)} \Delta T{\rm d}y\int_0^l {{\varphi }''_y {\rm d}x} \Bigg]^{\rm T}\end{eqnarray}$
(26) $\begin{eqnarray} && Q_{{\rm Tb}} = \Bigg[0,\int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)b_{\rm i} (x)\alpha (y)} \Delta T{\rm d}y\int_0^l {{\varphi }'_x {\rm d}x} , -\\&&\qquad \int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {yE(y)b_{\rm i} (x)\alpha (y)}\Delta T{\rm d}y\int_0^l {{\varphi }''_y {\rm d}x} \Bigg]^{\rm T} \end{eqnarray}$
(27) $\begin{eqnarray} \frac{\rm d}{{\rm d}t}\left( {\frac{\partial T_k }{\partial \dot{q}}} \right) - \frac{\partial T_k }{\partial q} = - \frac{\partial U}{\partial q} + Q_{\rm T} + F_q \end{eqnarray}$
式中, $F_{\rm q} = (\tau\ \ {\rm {\bf 0}}\ \ {\rm {\bf 0}})$为外主动力, $\tau $为外部施加的驱动力矩. 将式(18)、式(19)、式(25)、式(26)代入式(27),可得系统的动力学方程
(28) $\begin{eqnarray} \left( {{\begin{array}{*{20}c} {M_{11} } & { M_{12} } & { M_{13} } \\ { M_{21} } & { M_{22} } & { M_{23} } \\ { M_{31} } & { M_{32} } & { M_{33} } \\ \end{array} }} \right)\left( {{\begin{array}{*{20}c} \ddot{\theta } \\ \ddot{ A} \\ \ddot{ B} \\ \end{array} }} \right) = \left[ {{\begin{array}{*{20}c} {Q_{\rm \theta } } \\ { Q_{\rm A} } \\ { Q_{\rm B} } \\ \end{array} }} \right] \end{eqnarray}$
(29) $\begin{eqnarray}&& M_{11} = J_{{\rm oh}} + J_{{\rm ob}} + 2 S_x A + A^{\rm T} M_x A + \\&&\qquad B^{\rm T} M_y B - B^{\rm T} C B + \\&&\qquad \frac{1}{4}\Bigg(\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)(\underline{ B^{\rm T} H B B^{\rm T} H B})} {\rm d}x- \\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)(\underline{ B^{\rm T} H B B^{\rm T} H B})} {\rm d}x\Bigg) -\\&&\qquad \Bigg(\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)(\underline{ A^{\rm T} \varPhi_x^{\rm T} B^{\rm T} H B})} {\rm d}x -\\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)(\underline{ A^{\rm T} \varPhi _x^{\rm T} B^{\rm T} H B})} {\rm d}x\Bigg)\\\end{eqnarray}$
(30) $\begin{eqnarray} && M_{22}= M_{x}\end{eqnarray}$
(31) $\begin{eqnarray} && M_{33} = M_y + \int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)(\underline{ H B B^{\rm T} H})} {\rm d}x -\\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)(\underline{ H B B^{\rm T} H})} {\rm d}x \\ \end{eqnarray}$
(32) $\begin{eqnarray}&& M_{21} = M_{12}^{\rm T} = - M_{xy} B \end{eqnarray}$
(33) $\begin{eqnarray} && M_{31} = M_{13}^{\rm T} = S_y^{\rm T} + M_{{xy} }^{\rm T} A + \\&&\qquad \int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)\underline{ H B \varPhi _y B^{\rm T}}} {\rm d}x -\\&&\qquad \frac{1}{2}\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)\underline{ H \varPhi _{_y }^{\rm T} B^{\rm T} H B}} {\rm d}x -\\&&\qquad \Bigg(\int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)\underline{ H B \varPhi _y B^{\rm T}}} {\rm d}x -\\&&\qquad \frac{1}{2}\int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)\underline{ H \varPhi _{_y }^{\rm T} B^{\rm T} H B}} {\rm d}x\Bigg) \\ \end{eqnarray}$
(34) $\begin{eqnarray} && M_{32} = M_{{23}}^{\rm T} = - \Bigg(\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)\underline{ H B \varPhi _x }} {\rm d}x-\\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)\underline{ H B \varPhi _x }} {\rm d}x\Bigg)\\ \end{eqnarray}$
(35) $\begin{eqnarray}&& Q_ \theta=\tau-2\dot{\theta}[ S_x\dot{ A}+ A^{\rm T} M_x\dot{ A}+ B^{\rm T} M_y\dot{ B}- B^{\rm T} \underline{ C}\dot{ B}] -\\&&\qquad \Bigg[\int_0^l \rho b_{\rm e} (x)h_{\rm e} (x) \underline{ B^{\rm T} \varPhi _y^{\rm T} \dot{ B}^{\rm T} H\dot{ B}}{\rm d}x - \\&&\qquad \int_0^l \rho b_{\rm i} (x)h_{\rm i} (x) \underline{ B^{\rm T} \varPhi_y^{\rm T} \dot{ B}^{\rm T} H\dot{ B}}{\rm d}x\Bigg] +\\&&\qquad \dot{\theta }\Bigg[\int_0^l \rho b_{\rm e} (x)h_{\rm e} (x) \underline{\dot{ A}^{\rm T} \varPhi _x^{\rm T} B^{\rm T} H B}{\rm d}x -\\&&\qquad \int_0^l \rho b_{\rm i} (x)h_{\rm i} (x) \underline{\dot{ A}^{\rm T} \varPhi _x^{\rm T} B^{\rm T} H B}{\rm d}x\Bigg] + \\&&\qquad \dot{\theta }\int_0^l \rho b_{\rm e} (x)h_{\rm e} (x) (\underline{2 A^{\rm T} \varPhi _x^{\rm T} B^{\rm T} H\dot{ B}}){\rm d}x -\\&&\qquad \dot{\theta}\int_0^l \rho b_{\rm e} (x)h_{\rm e} (x) (\underline{ B^{\rm T} H B B^{\rm T} H\dot{ B}}){\rm d}x -\\&&\qquad \dot{\theta }\Bigg[\int_0^l \rho b_{\rm i} (x)h_{\rm i} (x) (\underline{2 A^{\rm T} \varPhi _x^{\rm T} B^{\rm T} H\dot{ B}}){\rm d}x -\\&&\qquad \int_0^l \rho b_{\rm i} (x)h_{\rm i} (x) (\underline{ B^{\rm T} H B B^{\rm T} H\dot{ B}}){\rm d}x\Bigg]\\ \end{eqnarray}$
(36) $\begin{eqnarray} && Q_A = \dot{\theta }^2( S_x^{\rm T} + M_x A) + 2\dot{\theta } M_{xy} \dot{ B} - K_1 A + K_2 B - \\&&\qquad\frac{1}{2}\dot{\theta }^2\Bigg[\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)(\underline{ \varPhi _x^{\rm T} B^{\rm T} H B})} {\rm d}x -\\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)(\underline{ \varPhi _x^{\rm T} B^{\rm T} H B})} {\rm d}x\Bigg] +\\&&\qquad \int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)(\underline{ \varPhi _x^{\rm T} \dot{ B}^{\rm T} H\dot{ B}})} {\rm d}x -\\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)(\underline{ \varPhi _x^{\rm T} \dot{ B}^{\rm T} H\dot{ B}})} {\rm d}x - K_4 \\ \end{eqnarray}$
(37) $\begin{eqnarray}&& Q_B = \dot{\theta }^2(\underline{ M_y - C}) B - 2\dot{\theta } M_{xy} \dot{ A} - K_3 B + K_2^{\rm T} A + \\&&\qquad\dot{\theta }^2\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)\Bigg(\underline{\frac{1}{2} H B B^{\rm T} H B - H B\varPhi _x A}\Bigg)} {\rm d}x -\\&&\qquad \dot{\theta }^2\int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)\Bigg(\underline{\frac{1}{2} H B B^{\rm T} H B - H B \varPhi _x A}\Bigg)} {\rm d}x -\\&&\qquad 2\dot{\theta }\Bigg[\int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)(\underline{ H B \varPhi _y \dot{ B} - \varPhi _y^{\rm T} B^{\rm T} H\dot{ B}})} {\rm d}x -\\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)(\underline{ H B \varPhi _y \dot{ B} - \varPhi _y^{\rm T} B^{\rm T} H\dot{ B}})} {\rm d}x\Bigg] -\\&&\qquad \int_0^l \rho \lt[b_{\rm e} (x)h_{\rm e} (x) - b_{\rm i} (x)h_{\rm i} (x)]\cdot\\&&\qquad(\underline{ H B\dot{ B}^{\rm T} H\dot{ B}}) {\rm d}x + K_5 \end{eqnarray}$
(38) $\begin{eqnarray}&&\rho = 2\int_{\frac{h_{\rm i} }{2}}^{\frac{h_{\rm e} }{2}} {\rho (y)}{\rm d}y\end{eqnarray}$
(39) $\begin{eqnarray} \\&&J_{\rm ob}=\int_0^l\rho[b_{\rm e}(x)h_{\rm e}(x)-b_{\rm i}(x)h_{\rm i}(x)](R+x)^2{\rm d}x\end{eqnarray}$
(40) $\begin{eqnarray}\\&& S_x = \int_0^l \rho [b_{\rm e} (x)h_{\rm e} (x) - b_{\rm i} (x)h_{\rm i} (x)]\cdot\\&&\qquad(R + x)\varPhi _x (x) {\rm d}x \end{eqnarray}$
(41) $\begin{eqnarray}\\&& S_y = \int_0^l \rho [b_{\rm e} (x)h_{\rm e} (x) - b_{\rm i} (x)h_{\rm i} (x)]\cdot\\&&\qquad(R + x)\varPhi _y (x) {\rm d}x \end{eqnarray}$
(42) $\begin{eqnarray}\\&& M_x = \int_0^l \rho [b_{\rm e} (x)h_{\rm e} (x) - b_{\rm i} (x)h_{\rm i} (x)]\cdot\\&&\qquad\varPhi _x^{\rm T} (x)\varPhi _x (x){\rm d}x\end{eqnarray}$
(43) $\begin{eqnarray}\\&& M_y = \int_0^l {\rho b_{\rm e} (x)h_{\rm e} (x)\varPhi _y^{\rm T} (x)\varPhi _y } (x){\rm d}x - \\&&\qquad \int_0^l {\rho b_{\rm i} (x)h_{\rm i} (x)\varPhi _y^{\rm T} (x)\varPhi _y } (x){\rm d}x \end{eqnarray}$
(44) $\begin{eqnarray}\\&& M_{xy} = \int_0^l \rho [b_{\rm e} (x)h_{\rm e} (x) - b_{\rm i} (x)h_{\rm i} (x)]\cdot\\&&\qquad\varPhi _x^{\rm T} (x)\varPhi _y (x){\rm d}x\end{eqnarray}$
(45) $\begin{eqnarray}\\&& C = \int_0^l \rho [b_{\rm e} (x)h_{\rm e} (x) - b_{\rm i} (x)h_{\rm i} (x)]\cdot\\&&\qquad(R + x) H(x){\rm d}x\end{eqnarray}$
(46) $\begin{eqnarray}\\&& K_{\rm 1} = \int_0^l {E_{\rm 1} {\varPhi'}_x^{\rm T} (x)} {\varPhi'}_x {\rm d}x\end{eqnarray}$
(47) $\begin{eqnarray}\\&& K_{\rm 2} = \int_0^l {E_2 {\varPhi'}_x (x)} {{\varPhi''}}_y (x){\rm d}x\end{eqnarray}$
(48) $\begin{eqnarray}\\&& K_{\rm 3} = \int_0^l {E_3 {\varPhi''}_y^{\rm T} (x){\varPhi''}_y (x)} {\rm d}x\end{eqnarray}$
(49) $\begin{eqnarray}\\&& K_4 = \int_0^l {E_4 } {\varPhi'}_x {\rm d}x\end{eqnarray}$
(50) $\begin{eqnarray}\\&& K_5 = \int_0^l {E_5 } {\varPhi''}_y {\rm d}x\end{eqnarray}$
(51) $\begin{eqnarray}\\&& E_{\rm 1} = \int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)(} b_{\rm e} - b_{\rm i} ){\rm d}x + \int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)b_{\rm i} } {\rm d}x\end{eqnarray}$
(52) $\begin{eqnarray}\\&&E_{\rm 2} = \int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)y(} b_{\rm e} - b_{\rm i} ){\rm d}x + \int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)yb_{\rm i} } {\rm d}x\end{eqnarray}$
(53) $\begin{eqnarray}\\&&E_{\rm 3} = \int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)y^2(} b_{\rm e} - b_{\rm i} ){\rm d}x + \int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)y^2b_{\rm i} } {\rm d}x\end{eqnarray}$
(54) $\begin{eqnarray}\\&& E_4 = \underline{\underline {\int_{\left| {\frac{h_i }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y){b}_{\rm e} (x)\alpha } (y)(T_{\rm a} (y) - T_0 ){\rm d}y}} + \\&&\qquad\underline{\underline{\underline {\int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)[b_{\rm e} (x) - b_{\rm i} (x)]\alpha (y)} (T_{\rm b} (y) - T_0 ){\rm d}y}} }\end{eqnarray}$
(55) $\begin{eqnarray}\\&& E_5 = \underline{\underline {\int_{\left| {\frac{h_{\rm i} }{2}} \right|}^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y){b}_{\rm e} (x)\alpha } (y)[T_{\rm a} (y) - T_0 ]y{\rm d}y}} +\\&&\qquad \underline{\underline{\underline {\int_0^{\left| {\frac{h_{\rm e} }{2}} \right|} {E(y)[b_{\rm e} (x) - b_{\rm i} (x)]\alpha (y)} (T_b (y) - T_0 )y{\rm d}y}} }\\&& \end{eqnarray}$
式中单下划线的为考虑了二次耦合变形量而产生的附加耦合项,即为一次耦合(FOAC)模型. $ K_4 $, $ K_5 $为温度引起的载荷项. 双下划线为中空壁厚处热载荷的影响;三下划线为实体处热载荷的影响.若去掉这些带下划线的项则上述方程退化为传统的零次模型(ZOAC).
2 动力学仿真
2.1 大范围运动已知的动力学仿真
涡轮机叶片在工作时往往是由加速转动阶段和匀速转动两部分组成,为探究其过程首先对已知速度变化情况下的系统动力学响应进行研究.大范围运动已知的角速度变化规律如下所示
(56) $\begin{eqnarray}\dot{\theta} = \left\{\begin{array}{l@{\quad} l} \dfrac{\omega _0 }{T_{\rm t} }t - \dfrac{\omega _0 }{2{\pi}}\sin \left( \dfrac{2\pi}{T_{\rm t}}t \right), & 0 \leqslant t \leqslant T_{\rm t} \\ \omega _0, & t > T_{\rm t}\\ \end{array}\right. \end{eqnarray}$
式中, $T_{\rm t} = 15$ s, $\omega _0 = 4$ rad/s, 即梁在15 s时旋转角速度达到4 rad/s, 随后以恒定角速度旋转.
考虑3种不同叶片的简化模型: 等截面实心梁(equal section solid beam,ESSB)、等截面空心梁(equal section hollow beam, ESHB)和变截面空心梁(tapered hollow beam, THB), 并比较该3种物理模型不同的动力学响应情况.
具体模型尺寸如下: (1) 等截面实心梁$L = 8$ m, $b_1 = 1.985\,9$ mm, $h_1 = 3.675\,9$ cm; (2) 变截面实心梁 $L = 8$ m, $b_{\rm e} = 2.808\,5$ mm, $h_{\rm e} = 5.198\,5$ cm, $b_{\rm i} = 1.985\,9$ mm, $h_{\rm i} = 3.675\,9$ cm; $g_{\rm i} = 0.293$; (3) 变截面空心梁$L = 8$ m, $b_{\rm e} = 3.439\,7$ mm, $h_{\rm e} = 6.366\,8$ cm, $b_{\rm i} = 1.985\,9$ mm, $h_{\rm i} = 3.675\,9$ cm; $g_{\rm i} = 0.634$.
令$N=0$, $\Delta T = 0$此时功能梯度材料退化为单一的陶瓷材料, 且不受热的状态.为了验证本文建模理论的正确性, 令$Q_{\rm c} = Q_{\rm m} $, 仿真结果如图3 所示, 由图可知本文仿真结果与文献[17 ] 一致.
图3
图3
文献对比验证
Fig.3
Contrast verification
图4 表示$\omega_{0} = 0.5$ rad/s和$\omega _{0} = 3$ rad/s时柔性梁一次耦合模型和传统零次模型末端横向弯曲变形图. 由图4 (a)可知,当$\omega_{0}$较小时, 一次耦合模型和传统零次模型结果基本相同, 且收敛. 当$\omega _{0}$增大时,一次耦合模型仍然保持收敛, 但零次模型则发散了,因此在动力学建模中横向弯曲变形引起的纵向缩短不可忽略.
图4
图4
一次耦合模型和传统零次模型对比
Fig.4
Comparison of a FOAC model and a ZOAC model
图5 表示大范围运动已知时3种模型柔性梁末端变形图, 等截面实心梁用黑实线表示,变截面实心梁用划线表示, 变截面空心梁用点线表示. 从图5 (a)可知,等截面实心梁变形最大, 变截面实心梁其次, 而更符合实际建模的变截面空心梁最小.图5 (b)表示大范围旋转角速度恒定时柔性梁横向弯曲变形, 从图5 (b)可知,柔性梁作周期性振动, 其中变截面空心梁振幅最小、频率最大,等截面实心梁振幅最大, 频率最小. 从图5 分析可知,柔性梁的实际结构对动力学响应影响较大,因此符合实际工程的建模对于此类结构动力学特性分析至关重要.
图5
图5
三种模型柔性梁末端的横向弯曲变形
Fig.5
Comparison of tip deformation of flexible beam in three different models
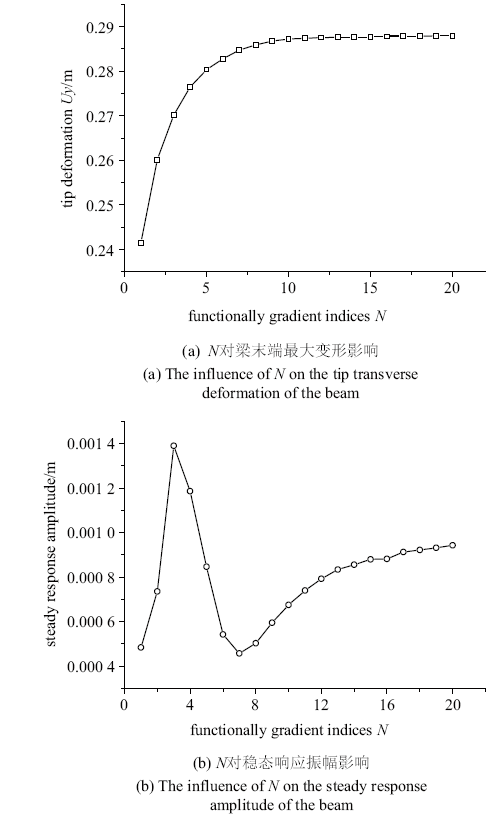
图6 表示大范围运动已知时不同热冲击载荷下柔性梁末端响应图, 从图6 (a)可知,随着内外部温差逐渐增大, 柔性梁的末端变形反而随之减小.高温处的陶瓷热膨胀系数小, 低温处的金属热膨胀系数大,同时功能梯度梁的材料为对称分布形式, 梁的横向弯曲变形被抑制,并且这种抑制作用随着温度的升高得到不断增强, 呈现出与温度变化相反的变化趋势.从图6 (b)可知, 大范围运动恒定时随着柔性梁内外温差增大, 热冲击的影响效应增强,柔性梁振动周期变短, 频率增大, 与此同时柔性梁呈现高频振荡,且随着抑制作用的增大, 振荡越来越剧烈.
图6
图6
不同热冲击载荷下梁的末端变形
Fig.6
Tip deformation of flexible beam under the influence of the different thermal shock load
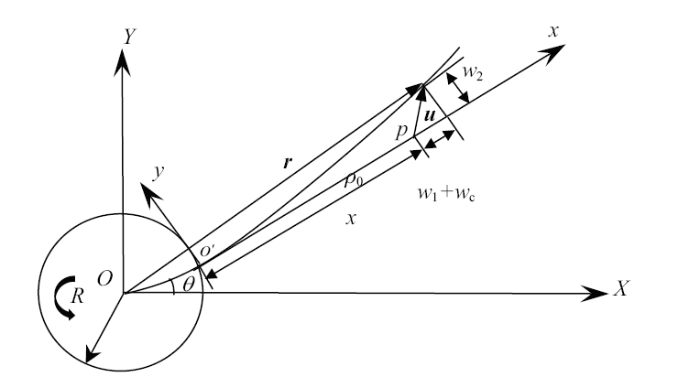
图7 表示温度差$\Delta T = 300$ K时, 功能梯度指数$N$对变截面空心梁末端最大横向弯曲响应以及稳态响应振幅的影响. 由图7 (a)可知,随着功能梯度指数的增大, 柔性梁的末端变形也随之增大, 并且在$N < 10$时, 影响较为显著, 随着$N$的进一步增大, 对柔性梁的变形影响效果开始减弱.由图7 (b)可知,稳态响应阶段的振幅则不是一个连续变化的阶段, 其振幅的大小随着$N$的增大先增大, 再减小然后继续增大, 在$N = 3$时达到最大值, $N = 7$时继续增大, 并逐渐趋于平稳.
图7
图7
$N$对梁端最大横向弯曲响应以及稳态响应振幅的影响
Fig.7
Tip deformation and steady response amplitude of the beam under the influence of the different $N$
2.2 大范围运动未知情况下的动力学仿真
涡轮机叶片的转动是在外力矩驱动下实现的,因此接下来对已知外力矩的情况进行动力学研究, 外力矩随时间的变化函数如下
(57) $\begin{eqnarray} \tau (t) = \left\{\begin{array}{ll} \tau _0 \sin \left( {\dfrac{2{\pi }}{T_{\rm t} }t} \right), \ \ & 0 \leqslant t \leqslant T_{\rm t} \\ 0, & t > T_{\rm t} \\ \end{array} \right. \end{eqnarray}$
其中, $T_{\rm t}=10$ s, $\tau _0 = 1$ N$\cdot$m.
图8 是大范围运动未知的情况下不考虑热冲击情况下3种模型柔性梁末端横向弯曲变形图,其中实心线表示等截面实心梁, 划线表示变截面实心梁, 点线表示的是变截面空心梁.由图8 (a)可知, 3种梁的变形量的大小差异与大范围运动已知是一致的,等截面实心梁变形最大, 变截面空心梁变形最小. 由图8 (b)可知在撤去外力后,梁进入稳定的周期振动阶段, 其中等截面实心梁的振幅最大、频率最小,变截面空心梁的振幅最小、频率最大.
图8
图8
三种模型柔性梁末端的横向弯曲变形
Fig.8
Comparison of tip deformation of flexible beam in three different models
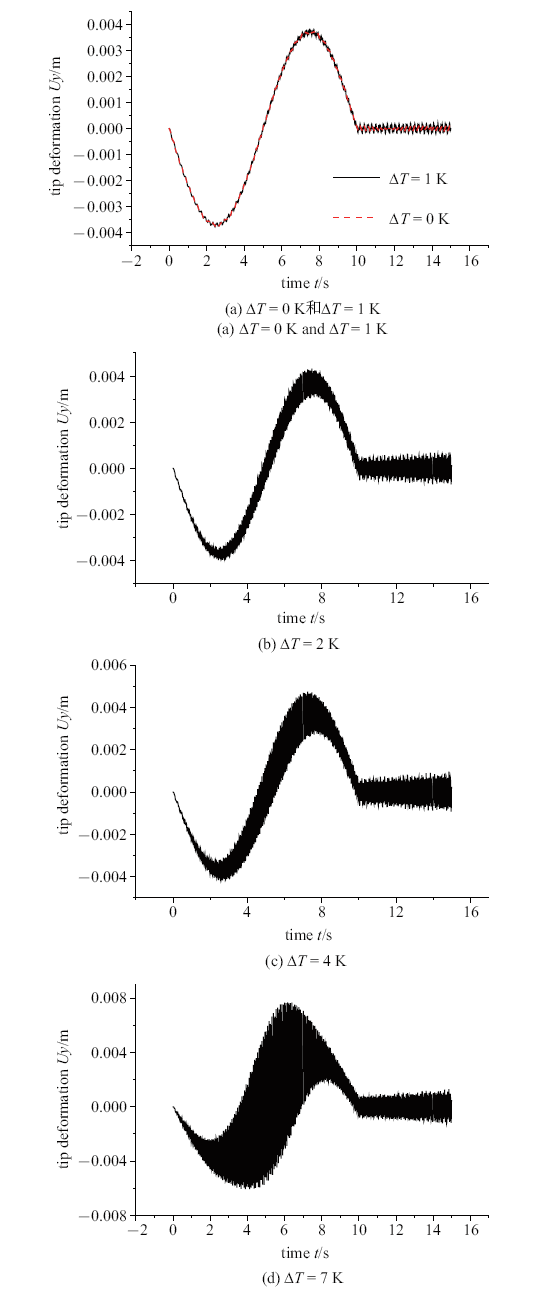
图9 为大范围运动未知时不同热冲击下柔性梁末端横向弯曲变形响应图,与大范围运动已知不同, 大范围运动未知是由较小的外力矩驱动的,导致热效应产生的作用相对于外力矩的作用不可忽略, 且相互耦合在一起,导致柔性梁末端变形增大. 比较图9 可进一步发现在温度场的作用下,梁的变形呈现出高频振荡, 并且随着温度的升高振荡越剧烈.图9 (a)为考虑热冲击与不考虑热冲击的对比, 由图可知在温度载荷的作用下,梁的变形已经开始出现高频振荡. 在撤去外加的力矩后,由图8 可知不考虑热冲击载荷末端变形处于稳定的周期性变化,并且振动幅值可视为一定值, 而当施加热冲击载荷后, 这种周期 indent 变化的平衡被打破,如图9 可知, 随着时间的推移, 变形随着热冲击作用的叠加也越来越大.
图9
图9
不同热冲击载荷下柔性梁末端横向弯曲变形为了进一步探究
Fig.9
Tip deformation of flexible beam under the influence of the different thermal shock load
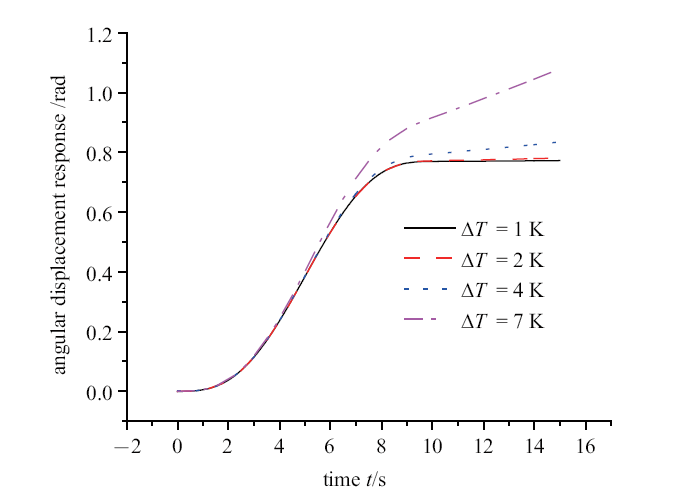
图9 中稳定平衡被打破的原因, 给出图10 不同热冲击载荷下,中心刚体大范围运动的角位移时程, 由图可知当内外温差升高后,撤去外力后中心刚体的角位移增长的幅度增大, 这就导致图9 中$T_{\rm t}>10$ s时的运动响应不再稳定, 随着时间的延长而增大. 大范围运动未知是由外力矩驱动,此时热冲击和外力矩产生热力耦合效应, 由于热力耦合的作用,在运动的初期就呈现高频振荡, 随着外力的撤销,柔性梁在热冲击载荷作用下继续高频振荡, 且振幅增大,随之带动中心刚体继续转动,呈现刚柔热耦合效应.
图10
图10
不同温度下中心刚体大范围运动角位移
Fig.10
Angular displacement response of the hub under the influence of the temperature
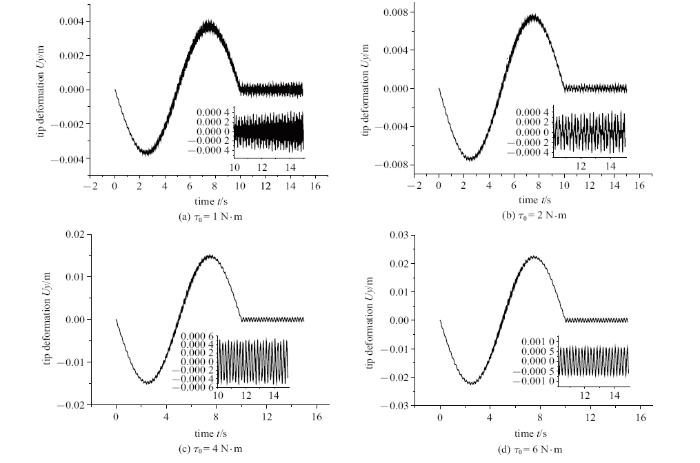
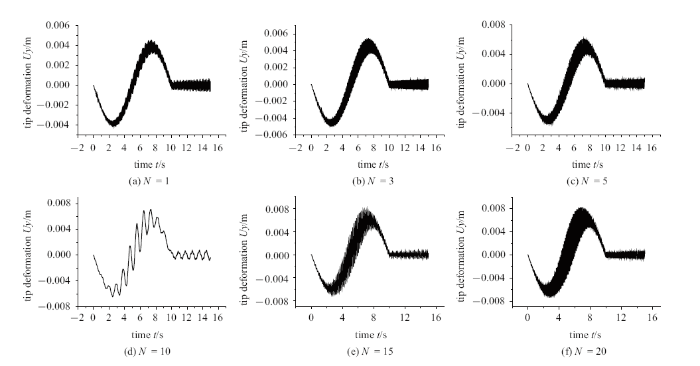
图11 表示$\Delta T = 2$ K时随着外力矩$\tau _{\rm 0} $的增大变截面空心梁末端横向弯曲变形. 如图可知, 随着外力矩$\tau _{\rm 0}$的增大, 热效应产生的振荡效应减弱, 当$T_{\rm t}> 10$ s时大范围运动恒定时振荡也开始趋于平稳, 说明随着外力矩增大,热冲击效应相对于外力矩作用的影响变小. 图12 表示$\Delta T = 2$ K时不同功能梯度指数下柔性梁的末端横向弯曲变形图,由图可知功能梯度指数对梁末端变形有较大影响, 随着$N$的增大, 柔性梁的末端变形也随之增大.高频振荡是由于弹性变形与热冲击耦合而产生的, 功能梯度指数$N$的变化主要改变梁的结构组成, 进一步改变梁的固有频率和振型, 如图12 可知, 当$N = 10$时, 外部激励对柔性梁振荡影响较小.
图11
图11
不同$\tau _{\rm 0} $下柔性梁的末端变形
Fig.11
Tip deformation of flexible beam under the influence of the different $\tau _{\rm 0} $
图12
图12
不同功能梯度指数柔性梁的末端变形
Fig.12
Tip deformation of flexible beam under the influence of the different $N$
3 结论
(1)不同的结构形式对于柔性梁的动力学响应有较大影响,通过对比发现等截面实心梁和变截面空心梁两种简化模型差异较大,在进行分析计算时不能简单的等效.
(2)大范围运动已知时柔性梁在热冲击载荷作用下, 由于高温处陶瓷热膨胀系数小,低温处金属热膨胀系数大, 同时功能梯度梁的材料为对称分布形式,梁的横向弯曲变形被抑制, 且抑制作用随温度增大而增强;而大范围运动恒定时随着柔性梁内外温差增大, 热冲击的作用进一步叠加,进而产生高频振荡.
(3)当柔性梁由外力矩驱动和热冲击载荷作用时, 大范围运动未知是由较小的外力矩驱动,此时热冲击和外力矩产生热力耦合效应, 由于热力耦合的作用,在运动的初期就呈现高频振荡, 即柔性梁弹性变形和热冲击载荷产生耦合效应;随着外力矩的撤销, 柔性梁在热冲击载荷作用下继续高频振荡, 且振幅增大,随之带动中心刚体继续转动,即说明柔性梁弹性变形、热冲击载荷产生的热效应和中心刚体大范围旋转运动产生了刚柔热耦合作用.
(4)功能梯度指数$N$对两种运动的影响效果也不尽相同, 对于大范围运动已知主要在$N$较小时对其变形的大小产生作用, $N$过大对变形的影响已经不再明显; 对于大范围运动未知时, 合适的$N$将有效减小外部激励对柔性梁振荡的影响.
参考文献
View Option
[1]
Koizumi M FGM activities in Japan
Composites Part B: Engineering 1997 ,28 (1-2 ):1 -4
DOI
URL
[本文引用: 1]
[2]
贾广森 , 张丽 , 卢聪明 等 . 内冷通道横流条件下气膜冷却特性
航空动力学报 , 2015 ,30 (4 ):823 -830
[本文引用: 1]
( Jia Guangseng Zhang Li Lu Congming et al . Film cooling performance with internal coolant channel crossflow
Journal of Aerospace Power 2015 ,30 (4 ):823 -830 (in Chinese))
[本文引用: 1]
[3]
李广超 , 莫唯书 , 张魏 等 . 涡轮导向叶片综合冷却特性实验研究
推进技术 , 2018 ,39 (12 ):2772 -2778
( Li Guangchao Mo Weishu Zhang Wei et al . Experimental investigation on integrated colling performance of nozzle guide vane
Journal of Propulsion Technology 2018 ,39 (12 ):2772 -2778 (in Chinese))
[4]
史晓军 , 税琳棋 , 高建民 等 . 汽雾两相流强化冷却燃气轮机叶片内冷通道
航空动力学报 , 2015 ,30 (11 ):2561 -2567
( Shi Xiaojun Shui Linqi Gao Jianmin et al . Internal cooling passage of mist/steam two-phase flow enhanced cooling gas turbine blade
Journal of Aerospace Power 2015 ,30 (11 ):2561 -2567 (in Chinese))
[5]
Chowdhury NHK Qureshi SA Zhang M et al . Influence of turbine blade leading edge shape on film cooling with cylindrical holes
International Journal of Heat and Mass Transfer 2017 ,115 :895 -908
DOI
URL
[6]
Fan X Li L Zou J et al . Local heat transfer of vortex cooling with multiple tangential nozzles in a gas turbine blade leading edge cooling passage
International Journal of Heat and Mass Transfer 2018 ,126 :377 -389
DOI
URL
[7]
李彦霖 , 饶宇 , 王德强 . 涡轮叶片冷却通道高性能微小肋湍流传热的数值研究
工程热物理学报 , 2018 ,39 (10 ):161 -169
( Li Yanlin Rao Yu Wang Deqiang Numerical study on turbulent heat transfer of miniature ribs in turbine blade internal passage
Journal of Aerospace Power 2018 ,39 (10 ):161 -169 (in Chinese))
[8]
邱庆刚 , 沈胜强 . 肋片几何形状对仿螺旋肋片内冷通道流动与换热的影响
航空动力学报 , 2006 ,21 (1 ):71 -76
( Qiu Qinggang Shen Shengqiang Effect of Helix-Alike fin surface shape on flow and heat transfer in the internal cooling passage
Journal of Aerospace Power 2006 ,21 (1 ):71 -76 (in Chinese))
[9]
邱庆刚 , 王海鹏 , 赵亮 等 . 楔形肋片内冷通道传热与流动阻力特性
航空动力学报 , 2011 ,26 (12 ):2648 -2654
( Qiu Qinggang Wang Haipeng Zhao Liang et al . Heat transfer and friction behavior in internal cooling duct with cuniform-fins
Journal of Aerospace Power 2011 ,26 (12 ):2648 -2654 (in Chinese))
[10]
朱兴丹 , 张靖周 , 谭晓茗 . 旋转对涡轮叶片异型孔气膜冷却的影响
推进技术 , 2016 ,37 (9 ):1713 -1719
( Zhu Xingdan Zhang JinZhou Tan Xiaoming Effects of rotation on shaped-hole film cooling on a turbine blade
Journal of Propulsion Technology 2016 ,37 (9 ):1713 -1719 (in Chinese))
[11]
朱兴丹 , 张靖周 , 谭晓茗 . 旋转状态下涡轮叶片复合冷却结构
航空动力学报 , 2017 (3 ):584 -591
DOI
URL
( Zhu Xingdan Zhang Jinzhou Tan Xiaoming Composite cooling structure on rotating turbine blade
Journal of Aerospace Power 2017 (3 ):584 -591 (in Chinese))
DOI
URL
[12]
韩枫 , 李海旺 , 马薏文 等 . 旋转对弯扭涡轮叶片前缘气膜冷却的影响
航空动力学报 , 2019 ,34 (6 ):1352 -1363
[本文引用: 1]
( Han Feng Li Haiwang Ma Yiwen et al . Effect of rotation on the leading-sdge region film cooling of a twisted turbine blade
Journal of Aerospace Power 2019 ,34 (6 ):1352 -1363 (in Chinese))
[本文引用: 1]
[13]
Kane TR Ryan R Banerjee AK Dynamics of a cantilever beam attached to a moving base
Journal of Guidance, Control, and Dynamics 1987 ,10 (2 ):139 -151
DOI
URL
[本文引用: 1]
[14]
黎亮 , 章定国 , 洪嘉振 . 中心刚体-功能梯度材料梁系统的动力学特性
机械工程学报 , 2013 ,49 (13 ):77 -84
[本文引用: 2]
( Li Liang Zhang Dingguo Hong Jiazhen Dynamics of hub-functionally graded material beam systems
Journal of Mechanical Engineering 2013 ,49 (13 ):77 -84 (in Chinese))
[本文引用: 2]
[15]
黎亮 , 章定国 , 洪嘉振 . 作大范围运动 FGM 矩形薄板的动力学特性研究
动力学与控制学报 , 2013 ,11 (4 ):329 -335
[本文引用: 1]
( Li Liang Zhang Dingguo Hong Jiazhen Dynamics of rectangular functionally graded thin plates undergoing overall motion
Journal of Dynamics and Control 2013 ,11 (4 ):329 -335 (in Chinese))
[本文引用: 1]
[16]
方建士 , 章定国 . 旋转悬臂梁的刚柔耦合动力学建模与频率分析
计算力学学报 , 2012 ,29 (3 ):333 -339
[本文引用: 1]
( Fang Jianshi Zhang Dingguo Rigid-flexible couping and frequency analysis of a rotating cantilever beam
Chinese Journal of Computational Mechanics 2012 ,29 (3 ):333 -339 (in Chinese))
[本文引用: 1]
[17]
杜超凡 , 章定国 . 基于无网格点插值法的旋转悬臂梁的动力学分析
物理学报 , 2015 ,64 (3 ):396 -405
[本文引用: 2]
( Du Chaofan Zhang Dingguo A meshfree method based on point interpolation for dynamic analysis of rotating cantilever beams.
Acta Phys. Sin 2015 ,64 (3 ):396 -405 (in Chinese))
[本文引用: 2]
[18]
范纪华 , 章定国 , 洪嘉振 . 基于Bezier插值方法的作大范围旋转运动锥形悬臂梁动力学研究
动力学与控制学报 , 2012 ,10 (4 ):347 -354
[本文引用: 1]
( Fan Jihua Zhang Dingguo Hong Jiazhen Dynamic analysis of a rotating tapered cantilever beam based on Bezier curve interpolation
Journal of Dynamics and Control 2012 ,10 (4 ):347 -354 (in Chinese))
[本文引用: 1]
[19]
范纪华 , 章定国 . 基于变形场不同离散方法的柔性机器人动力学建模与仿真
力学学报 , 2016 ,48 (4 ):843 -856
DOI
URL
[本文引用: 1]
研究了基于变形场不同离散方法的柔性机器人动力学建模和仿真问题. 针对多杆空间链式柔性机器人系统,采用假设模态法、有限元法、Bezier 插值方法和B 样条插值方法对柔性杆变形场进行描述,构造统一形式,运用Lagrange 方法,结合4×4 齐次变换矩阵,在计入柔性杆横向弯曲变形引起的纵向缩短的情况下,推导得到多杆空间柔性机器人动力学方程,并编制基于4 种变形场不同离散方法的多杆空间链式柔性机器人仿真软件.通过仿真算例对柔性机器人系统的动力学问题进行研究. 仿真结果表明:有限元法的计算效率较低;假设模态法在处理较大变形问题时其精度低于Bezier 插值方法和B 样条插值方法的精度;作为新的变形体离散方法,Bezier 插值方法和B 样条插值方法可以有效地描述柔性杆的变形场,并能运用到多杆空间柔性机器人动力学建模中.
( Fan Jihua Zhang Dingguo Dynamic modeling and simulation of flexible robots based on different discretization methods
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (4 ):843 -856 (in Chinese))
DOI
URL
[本文引用: 1]
研究了基于变形场不同离散方法的柔性机器人动力学建模和仿真问题. 针对多杆空间链式柔性机器人系统,采用假设模态法、有限元法、Bezier 插值方法和B 样条插值方法对柔性杆变形场进行描述,构造统一形式,运用Lagrange 方法,结合4×4 齐次变换矩阵,在计入柔性杆横向弯曲变形引起的纵向缩短的情况下,推导得到多杆空间柔性机器人动力学方程,并编制基于4 种变形场不同离散方法的多杆空间链式柔性机器人仿真软件.通过仿真算例对柔性机器人系统的动力学问题进行研究. 仿真结果表明:有限元法的计算效率较低;假设模态法在处理较大变形问题时其精度低于Bezier 插值方法和B 样条插值方法的精度;作为新的变形体离散方法,Bezier 插值方法和B 样条插值方法可以有效地描述柔性杆的变形场,并能运用到多杆空间柔性机器人动力学建模中.
[20]
范纪华 , 章定国 . 旋转柔性悬臂梁动力学的Bezier插值离散方法研究
物理学报 , 2014 ,63 (15 ):154501 -154501
DOI
URL
[本文引用: 1]
在旋转柔性梁变形场描述中,引入Bezier插值离散方法. 首先构建旋转运动悬臂梁物理模型,接着采用第二类Lagrange动力学方程和Bezier插值离散方法,在计入柔性梁横向弯曲变形引起的纵向缩短的情况下,推导了旋转柔性梁的刚柔耦合动力学方程,并编制旋转柔性梁的动力学仿真软件,然后通过仿真算例对系统的动力学问题进行研究. 最后将仿真结果与有限元法、假设模态法进行分析比较,验证了提出的Bezier插值离散方法的正确性,并得出Bezier插值离散法的计算效率较高;计算精度符合工程实际需要,高速时计算精度大于假设模态法;Bezier插值离散方法在处理大柔性问题时比假设模态法合理. 因此在多体系统动力学领域具有优良性能和应用价值的Bezier插值离散方法将具有推广价值.
( Fan Jihua Zhang Dingguo Bezier interpolation method for the dynamics of rotating flexible cantilever beam
Acta Phys. Sin 2014 ,63 (15 ):154501 -154501 (in Chinese))
DOI
URL
[本文引用: 1]
在旋转柔性梁变形场描述中,引入Bezier插值离散方法. 首先构建旋转运动悬臂梁物理模型,接着采用第二类Lagrange动力学方程和Bezier插值离散方法,在计入柔性梁横向弯曲变形引起的纵向缩短的情况下,推导了旋转柔性梁的刚柔耦合动力学方程,并编制旋转柔性梁的动力学仿真软件,然后通过仿真算例对系统的动力学问题进行研究. 最后将仿真结果与有限元法、假设模态法进行分析比较,验证了提出的Bezier插值离散方法的正确性,并得出Bezier插值离散法的计算效率较高;计算精度符合工程实际需要,高速时计算精度大于假设模态法;Bezier插值离散方法在处理大柔性问题时比假设模态法合理. 因此在多体系统动力学领域具有优良性能和应用价值的Bezier插值离散方法将具有推广价值.
[21]
范纪华 , 章定国 . 旋转悬臂梁动力学的B样条插值方法
机械工程学报 , 2012 ,48 (23 ):59 -64
[本文引用: 1]
( Fan Jihua Zhang Dingguo B-spline interpolation method for the dynamics of rotating cantilever beam
Journal of Mechanical Engineering 2012 ,48 (23 ):59 -64 (in Chinese))
[本文引用: 1]
[22]
韩广才 , 吴艳红 , 王寅超 等 . 旋转叶片刚柔耦合系统动力学分析
哈尔滨工程大学学报 , 2011 (6 ):736 -741
[本文引用: 1]
( Han Guangcai Wu Yanhong Wang Yanchao et al . Dynamic analysis of a rotating blade with a rigid-flexible coupling, pre-twisted angle, and variable cross-section
Journal of Harbin Engineering University 2011 (6 ):736 -741 (in Chinese))
[本文引用: 1]
[23]
陈思佳 , 章定国 . 中心刚体-变截面梁系统的动力学特性研究
力学学报 , 2011 ,43 (4 ):790 -794
URL
[本文引用: 1]
对在平面内做大范围转动的中心刚体-变截面梁系统的动力学进行了研究.考虑柔性梁横向弯曲变形和纵向伸长变形, 且在纵向位移中计及由于横向变形而引起的纵向缩短项, 即非线性耦合变形项. 采用假设模态法描述变形, 运用第二类Lagrange方程推导得到系统刚柔耦合动力学方程. 在此基础上对做大范围旋转运动的中心刚体-楔形梁以及中心刚体-梯形梁模型的动力学进行了详细研究. 研究表明: 梁宽比、梁高比以及梯形梁变截面位置都对系统的动力学特性有很大影响.
( Chen Sijia Zhang Dingguo Dynamics od hub-varable section beam systems
Chinese Journal of Theoretical and Applied Mechanics 2011 ,43 (4 ):790 -794 (in Chinese))
URL
[本文引用: 1]
对在平面内做大范围转动的中心刚体-变截面梁系统的动力学进行了研究.考虑柔性梁横向弯曲变形和纵向伸长变形, 且在纵向位移中计及由于横向变形而引起的纵向缩短项, 即非线性耦合变形项. 采用假设模态法描述变形, 运用第二类Lagrange方程推导得到系统刚柔耦合动力学方程. 在此基础上对做大范围旋转运动的中心刚体-楔形梁以及中心刚体-梯形梁模型的动力学进行了详细研究. 研究表明: 梁宽比、梁高比以及梯形梁变截面位置都对系统的动力学特性有很大影响.
[24]
高晨彤 , 黎亮 , 章定国 等 . 考虑剪切效应的旋转FGM楔形梁刚柔耦合动力学建模与仿真
力学学报 , 2018 ,50 (3 ):210 -222
[本文引用: 1]
( Gao Chentong Li Liang Zhang Dingguo et al . Dynamci modeling and simulation of rotating FGM tapered beams with shear effect
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (3 ):210 -222 (in Chinese))
[本文引用: 1]
[25]
Oh SY Librescu L Song O Vibration of turbomachinery rotating blades made-up of functionally graded materials and operating in a high temperature field
Acta Mechanica 2003 ,166 (1-4 ):69 -87
DOI
URL
[本文引用: 1]
[26]
万云博 , 马戎 , 王年华 等 . 基于混合网格多维梯度重构的热流预测方法研究
力学学报 , 2018 ,50 (5 ):1003 -1012
[本文引用: 1]
( Wan Yunbo Ma Rong Wang Nianhua et al . Accurate aero-heating predictions based on multi-dimensional gradient reconstruction on hybrid unstructured grids
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (5 ):1003 -1012 (in Chinese))
[本文引用: 1]
[27]
许新 , 李世荣 . 功能梯度材料微梁的热弹性阻尼研究
力学学报 , 2017 ,49 (2 ):308 -316
[本文引用: 1]
( Xu Xin Li Shirong Analysis of thermoelastic damping for functionally graded material micro-beam
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (2 ):308 -316 (in Chinese))
[本文引用: 1]
[28]
曹蕾蕾 , 裴建中 , 张学敏 等 . 功能梯度材料热传导问题的仿真
计算机仿真 , 2012 ,29 (8 ):387 -390
[本文引用: 1]
( Cao Leilei Pei Jianzhong Zhang Xuemin et al . Simulation method of steady-state heat conduction in functionally graded material
Computer Simulation 2012 ,29 (8 ):387 -390 (in Chinese))
[本文引用: 1]
[29]
刘锦阳 , 袁瑞 , 洪嘉振 . 考虑热效应的柔性板的刚-柔耦合动力学特性
上海交通大学学报 , 2008 ,42 (8 ):1226 -1232
[本文引用: 1]
( Liu Jinyang Yuan Rui Hong Jiazhen The on ridig-flexible coupling dynamicperformance for a rectangular plate considering thermal effect
Journal of Shanghai Jiaotong University 2008 ,42 (8 ):387 -390 (in Chinese))
[本文引用: 1]
[30]
Cui YQ Yu ZQ Lan P A novel method of thermo-mechanical coupled analysis based on the unified description
Mechanism and Machine Theory 2019 ,134 :376 -392
DOI
URL
[本文引用: 1]
[31]
Cepon G Starc B Zupancic B et al . Coupled thermo-structural analysis of a bimetallic strip using the absolute nodal coordinate formulation
Multibody System Dynamics 2017 ,41 (4 ):391 -402
DOI
URL
[本文引用: 1]
[32]
李世荣 , 苏厚德 , 程昌钧 . 热环境中粘贴压电层功能梯度材料梁的自由振动
应用数学和力学 , 2009 ,30 (8 ):907 -918
URL
[本文引用: 1]
研究了上下表面粘贴压电层的功能梯度材料Euler-Bernoulli梁在升温及电场作用下的屈曲和自由振动行为.在精确考虑轴线伸长基础上,建立了压电功能梯度材料层合梁在热-电-机载荷作用下的几何非线性动力学控制方程.其中,假设功能梯度材料性质沿厚度方向按照幂函数连续变化,上下压电层为各向同性均匀材料.在小振幅和谐振动假设下,上述非线性偏微分方程组被转化为两套相互耦合的常微分方程组,即过屈曲问题的控制方程和过屈曲构形附近的线性振动控制方程.采用打靶法数值求解上述两个耦合的常微分方程边值问题,获得了在均匀电场和横向非均匀升温场作用下两端固定压电-功能梯度材料层合梁在屈曲前和过屈曲构型附近的自由振动响应.绘出了梁的过屈曲平衡路径以及前3阶固有频率随热、电载荷及材料梯度参数变化的特性曲线.结果表明,梁的前3阶频率在屈曲前随着温度升高而减小,在进入过屈曲后它们却随着温度升高而增加.通过施加电压在压电层产生拉应力可有效地提高粱的热屈曲临界载荷,从而提高其固有频率.
( Li Shirong Su Houde Cheng Changjun Free vibration of functionally Graded material beams with surface-bonded piezeoelectric layers in thermal environment
Applied Mathematics and Mechanics 2009 ,30 (8 ):907 -918 (in Chinese))
URL
[本文引用: 1]
研究了上下表面粘贴压电层的功能梯度材料Euler-Bernoulli梁在升温及电场作用下的屈曲和自由振动行为.在精确考虑轴线伸长基础上,建立了压电功能梯度材料层合梁在热-电-机载荷作用下的几何非线性动力学控制方程.其中,假设功能梯度材料性质沿厚度方向按照幂函数连续变化,上下压电层为各向同性均匀材料.在小振幅和谐振动假设下,上述非线性偏微分方程组被转化为两套相互耦合的常微分方程组,即过屈曲问题的控制方程和过屈曲构形附近的线性振动控制方程.采用打靶法数值求解上述两个耦合的常微分方程边值问题,获得了在均匀电场和横向非均匀升温场作用下两端固定压电-功能梯度材料层合梁在屈曲前和过屈曲构型附近的自由振动响应.绘出了梁的过屈曲平衡路径以及前3阶固有频率随热、电载荷及材料梯度参数变化的特性曲线.结果表明,梁的前3阶频率在屈曲前随着温度升高而减小,在进入过屈曲后它们却随着温度升高而增加.通过施加电压在压电层产生拉应力可有效地提高粱的热屈曲临界载荷,从而提高其固有频率.
[33]
黎亮 , 章定国 , 郭永彬 . 变温度场中刚柔耦合功能梯度梁系统的动力学特性研究
振动工程学报 , 2017 ,30 (1 ):9 -19
[本文引用: 1]
( Li Liang Zhang Dingguo Guo Yongbin Dynamics of rigid--flexible coupling Fgm beam systems in variable temperature fields
Journal of Vibration Engineering 2017 ,30 (1 ):9 -19 (in Chinese))
[本文引用: 1]
[34]
Javaheri R Eslami MR Thermal buckling of functionally graded plates based on higher order theory
Journal of Thermal Stresses 2002 ,25 (7 ):603 -625
DOI
URL
[本文引用: 1]
[35]
Chen Y Jin G Zhang C et al . Thermal vibration of FGM beams with general boundary conditions using a higher-order shear deformation theory
Composites Part B: Engineering 2018 ,153 :376 -386
DOI
URL
[本文引用: 1]
FGM activities in Japan
1
1997
... 航空发动机系统中涡轮转子叶片的工作性能对飞行安全有着十分重要的影响,在动力学研究中涡轮转子叶片的结构通常简化为旋转中心刚体-柔性梁模型,其在高温环境下高速旋转时,会受到热应力、大范围旋转刚体运动与柔性梁弹性变形耦合作用等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温的能力.功能梯度材料因能在极限环境下反复地正常工作而被应用于发动机叶片的设计和分析中[1 ] .同时高温引起的热力载荷、内冷通道的冷却[2 -12 ] 和截面尺寸变化等也是涡轮转子叶片系统动力学建模中需考虑的因素. ...
内冷通道横流条件下气膜冷却特性
1
2015
... 航空发动机系统中涡轮转子叶片的工作性能对飞行安全有着十分重要的影响,在动力学研究中涡轮转子叶片的结构通常简化为旋转中心刚体-柔性梁模型,其在高温环境下高速旋转时,会受到热应力、大范围旋转刚体运动与柔性梁弹性变形耦合作用等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温的能力.功能梯度材料因能在极限环境下反复地正常工作而被应用于发动机叶片的设计和分析中[1 ] .同时高温引起的热力载荷、内冷通道的冷却[2 -12 ] 和截面尺寸变化等也是涡轮转子叶片系统动力学建模中需考虑的因素. ...
内冷通道横流条件下气膜冷却特性
1
2015
... 航空发动机系统中涡轮转子叶片的工作性能对飞行安全有着十分重要的影响,在动力学研究中涡轮转子叶片的结构通常简化为旋转中心刚体-柔性梁模型,其在高温环境下高速旋转时,会受到热应力、大范围旋转刚体运动与柔性梁弹性变形耦合作用等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温的能力.功能梯度材料因能在极限环境下反复地正常工作而被应用于发动机叶片的设计和分析中[1 ] .同时高温引起的热力载荷、内冷通道的冷却[2 -12 ] 和截面尺寸变化等也是涡轮转子叶片系统动力学建模中需考虑的因素. ...
Influence of turbine blade leading edge shape on film cooling with cylindrical holes
2017
Local heat transfer of vortex cooling with multiple tangential nozzles in a gas turbine blade leading edge cooling passage
2018
涡轮叶片冷却通道高性能微小肋湍流传热的数值研究
2018
涡轮叶片冷却通道高性能微小肋湍流传热的数值研究
2018
肋片几何形状对仿螺旋肋片内冷通道流动与换热的影响
2006
肋片几何形状对仿螺旋肋片内冷通道流动与换热的影响
2006
旋转对弯扭涡轮叶片前缘气膜冷却的影响
1
2019
... 航空发动机系统中涡轮转子叶片的工作性能对飞行安全有着十分重要的影响,在动力学研究中涡轮转子叶片的结构通常简化为旋转中心刚体-柔性梁模型,其在高温环境下高速旋转时,会受到热应力、大范围旋转刚体运动与柔性梁弹性变形耦合作用等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温的能力.功能梯度材料因能在极限环境下反复地正常工作而被应用于发动机叶片的设计和分析中[1 ] .同时高温引起的热力载荷、内冷通道的冷却[2 -12 ] 和截面尺寸变化等也是涡轮转子叶片系统动力学建模中需考虑的因素. ...
旋转对弯扭涡轮叶片前缘气膜冷却的影响
1
2019
... 航空发动机系统中涡轮转子叶片的工作性能对飞行安全有着十分重要的影响,在动力学研究中涡轮转子叶片的结构通常简化为旋转中心刚体-柔性梁模型,其在高温环境下高速旋转时,会受到热应力、大范围旋转刚体运动与柔性梁弹性变形耦合作用等因素的影响,这就要求发动机叶片具有较高的可靠性以及承受高温的能力.功能梯度材料因能在极限环境下反复地正常工作而被应用于发动机叶片的设计和分析中[1 ] .同时高温引起的热力载荷、内冷通道的冷却[2 -12 ] 和截面尺寸变化等也是涡轮转子叶片系统动力学建模中需考虑的因素. ...
Dynamics of a cantilever beam attached to a moving base
1
1987
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
中心刚体-功能梯度材料梁系统的动力学特性
2
2013
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
... 梯度分布规律如下[14 ] ...
中心刚体-功能梯度材料梁系统的动力学特性
2
2013
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
... 梯度分布规律如下[14 ] ...
作大范围运动 FGM 矩形薄板的动力学特性研究
1
2013
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
作大范围运动 FGM 矩形薄板的动力学特性研究
1
2013
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转悬臂梁的刚柔耦合动力学建模与频率分析
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转悬臂梁的刚柔耦合动力学建模与频率分析
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
基于无网格点插值法的旋转悬臂梁的动力学分析
2
2015
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
... 令$N=0$, $\Delta T = 0$此时功能梯度材料退化为单一的陶瓷材料, 且不受热的状态.为了验证本文建模理论的正确性, 令$Q_{\rm c} = Q_{\rm m} $, 仿真结果如图3 所示, 由图可知本文仿真结果与文献[17 ] 一致. ...
基于无网格点插值法的旋转悬臂梁的动力学分析
2
2015
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
... 令$N=0$, $\Delta T = 0$此时功能梯度材料退化为单一的陶瓷材料, 且不受热的状态.为了验证本文建模理论的正确性, 令$Q_{\rm c} = Q_{\rm m} $, 仿真结果如图3 所示, 由图可知本文仿真结果与文献[17 ] 一致. ...
基于Bezier插值方法的作大范围旋转运动锥形悬臂梁动力学研究
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
基于Bezier插值方法的作大范围旋转运动锥形悬臂梁动力学研究
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
基于变形场不同离散方法的柔性机器人动力学建模与仿真
1
2016
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
基于变形场不同离散方法的柔性机器人动力学建模与仿真
1
2016
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转柔性悬臂梁动力学的Bezier插值离散方法研究
1
2014
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转柔性悬臂梁动力学的Bezier插值离散方法研究
1
2014
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转悬臂梁动力学的B样条插值方法
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转悬臂梁动力学的B样条插值方法
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转叶片刚柔耦合系统动力学分析
1
2011
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
旋转叶片刚柔耦合系统动力学分析
1
2011
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
中心刚体-变截面梁系统的动力学特性研究
1
2011
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
中心刚体-变截面梁系统的动力学特性研究
1
2011
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
考虑剪切效应的旋转FGM楔形梁刚柔耦合动力学建模与仿真
1
2018
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
考虑剪切效应的旋转FGM楔形梁刚柔耦合动力学建模与仿真
1
2018
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
Vibration of turbomachinery rotating blades made-up of functionally graded materials and operating in a high temperature field
1
2003
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
基于混合网格多维梯度重构的热流预测方法研究
1
2018
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
基于混合网格多维梯度重构的热流预测方法研究
1
2018
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
功能梯度材料微梁的热弹性阻尼研究
1
2017
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
功能梯度材料微梁的热弹性阻尼研究
1
2017
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
功能梯度材料热传导问题的仿真
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
功能梯度材料热传导问题的仿真
1
2012
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
考虑热效应的柔性板的刚-柔耦合动力学特性
1
2008
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
考虑热效应的柔性板的刚-柔耦合动力学特性
1
2008
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
A novel method of thermo-mechanical coupled analysis based on the unified description
1
2019
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
Coupled thermo-structural analysis of a bimetallic strip using the absolute nodal coordinate formulation
1
2017
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
热环境中粘贴压电层功能梯度材料梁的自由振动
1
2009
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
热环境中粘贴压电层功能梯度材料梁的自由振动
1
2009
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
变温度场中刚柔耦合功能梯度梁系统的动力学特性研究
1
2017
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
变温度场中刚柔耦合功能梯度梁系统的动力学特性研究
1
2017
... 自从Kane等[13 ] 揭示了``动力刚化''现象以来,国内外的学者对此进行了诸多探索, 并取得了丰硕的成果.黎亮等[14 ] 对考虑了两种不同功能梯度指数分布规律的功能梯度悬臂梁进行对比分析,探究了不同功能梯度指数和分布规律对作大范围旋转运动柔性梁动力学特性的影响,接着进一步分析了大范围旋转运动功能梯度矩形薄板的动力学特性[15 ] ,并与传统零次模型进行对比验证了在大转速下一次近似耦合模型能够更好的描述系统的动力学特性.方建士等[16 ] 利用Hamilton变分原理和假设模态法,建立考虑二阶耦合量的一次近似耦合模型, 并对悬臂梁的频率特性进行研究.杜超凡等[17 ] 基于无网格点插值法对柔性梁的变形场进行离散,并与有限元法对比, 该方法不仅正确还有前处理简单的优点.文献[18 ,19 ,20 ,21 ] 将B样条和Bezier插值法应用于柔性梁的变形场离散,并对旋转中心刚体-柔性梁系统以及柔性机器人系统进行动力学仿真,进而丰富了柔性梁变形场理论.韩广才等[22 ] 考虑了叶片的剪切效应和截面变化并利用Hamilton原理与有限元法建立了叶片的动力学方程.陈思佳等[23 ] 建立了中心刚体-变截面梁高次耦合动力学模型,研究了截面变化对末端响应的影响. 高晨彤等[24 ] 通过研究进一步指出,实际的工程应用中变截面梁更为常见, 并对以往非剪切模型进行了完善.Oh等[25 ] 对高温作用下的旋转FGM叶片的动力学特性进行了研究.万云博等[26 ] 发展了基于常规的非结构/混合网格的高精度热流计算方法.许新等[27 ] 基于Euler-Bernoulli梁理论和单项耦合的热传导理论,研究了功能梯度材料微梁的热弹性阻尼.曹蕾蕾等[28 ] 利用无网格数值算法对功能梯度材料的热传导问题进行了研究.刘锦阳等[29 ] 建立了柔性板的动力学与热传导耦合方程,研究温度变化对刚柔耦合系统动力学特性的影响.Cui等[30 ] 提出一种基于统一描述的热力耦合分析的新方法,将传热学与连续介质力学进行了很好的结合. $\check{C}$epon等[31 ] 在分析暴露在高温下的不同热膨胀系数的双金属条时提出了一种新的基于绝对坐标形式的热-结构耦合分析的双金属带材模型,对其大范围运动响应进行了分析, 并与有限元软件进行对比,验证了所提出理论的正确性.李世荣等[32 ] 对粘贴压电层的功能梯度梁建立了热-电-机载荷作用下的非线性动力学方程,探究了温度影响下的自由振动问题.黎亮等[33 ] 建立了基于热力学和刚柔耦合动力学理论的旋转中心刚体-FGM梁热刚柔耦合动力学模型,研究了不同温度场环境下两种FGM梁做大范围旋转运动的动力学特性. ...
Thermal buckling of functionally graded plates based on higher order theory
1
2002
... 将$T_{\rm a} (y)$根据泰勒展开并参照文献[34 ,35 ] 可取其前七项作为解 ...
Thermal vibration of FGM beams with general boundary conditions using a higher-order shear deformation theory
1
2018
... 将$T_{\rm a} (y)$根据泰勒展开并参照文献[34 ,35 ] 可取其前七项作为解 ...