引言
在过去的几十年中, 陶瓷基复合材料(ceramic matrix composite, CMC)因能在高温、氧化、疲劳和蠕变等状况下保持良好的力学性能而备受关注, 超高速飞行器的热防护系统、涡轮发动机的火焰筒、涡轮导向叶片、涡轮外环、隔热屏和火焰稳定器 等关键热端静止部件都可应用CMC[1 -3 ] . 国外的诸如综合高性能涡轮发动机技术(integrated high performance turbine engine technology, IHPTET)计划、超高效发动机技术(ultra efficient engine technologies, UEET)和高马赫数涡轮发动机/涡轮基组合循环发动机(high Mach turbine engine/turbine based combined cycle engine, HMTE)等均将CMC作为研究重点[4 ] . 我国的航空发动机及燃气轮机重大专项基础研究项目中也将CMC的本征性能与环境性能相关性等研究列为研究重点.
基于材料成型与制造工艺的发展, 具有较高环境稳定性的氧化物/氧化物CMC和非氧化物CMC已经成为主要的研究对象. 非氧化物CMC, 如SiC/SiC CMC, 虽然在1200$\sim$1350${^\circ}$C的高温环境中具有优越的力学性能, 但是在700$\sim$800${^\circ}$C温度环境中抗氧化性较差, 尤其在水氧环境中极易发生氧化反应, 进而造成其力学性能急剧下降. 尽管已经开发了许多抗氧化涂层系统, 但其高温氧化问题远未得到有效解决[5 -6 ] . 与非氧化物CMC相比, 氧化物/氧化物CMC在1000$\sim$1300${^\circ}$C的高温环境中具有更好的稳定性和抗氧化性能, 因此成为未来航空发动机热端部件的理想候选材料[7 ] .
陶瓷基复合材料的优化设计与工程有效应用需要深入了解材料的损伤机理与演化规律, 并对材料的失效进行准确预测. 因此, CMC损伤本构模型的建立与讨论在材料结构设计与性能评估中起着重要的作用. 为了阐述损伤导致的材料全局非线性应力-应变行为, 文献中所提出的各种方法大致可分为(a)基 于宏观唯象的连续损伤力学模型(continuum damage mechanics, CDM)和(b)基于微观力学的损伤模型(micromechanics damage models, MDM).
CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据.
MDM方法通过代表性体积元素(representative volume element, RVE)对复合材料各组分在各个加载阶段进行定义与建模, 可区分纤维, 基体以及界面的损伤, 并且对于复合材料中每个组分的损伤萌生与演化均需要建立不同的准则[17 ] . 大量文献中所提的MDM方法之间的差异主要在于RVE的表述以及组分损伤对全局应变影响的表示. Evans等[18 ] 系统地梳理了单向纤维增强CMC的微观结构和力学性能之间的关系, 提出由界面的微观性能来控制材料的韧性, 并在微观力学计算和实验的基础上, 讨论了界面脱粘和滑移阻力等问题. Hsueh[19 ] 分析了单向CMC中纤维/基体界面处的粘结性能, 纤维的泊松效应以及残余应力, 进一步澄清了基体裂纹张开位移与由界面脱粘而产生的位移之间的差异, 并推导了它们与纤维桥接应力的解析表达式. 姚寅和陈少华[20 ] 提出了改进的剪切滞后理论模型, 以研究碳纤维增强复合材料的界面特性和纤维拔出性能, 获得了碳纤维应力的闭式解和界面剪切强度(inter-facial shear strength, IFSS). 然而, 基于剪切滞后的微观力学模型中的一些物理假设与实验所测试的结果还存在一定的偏差, 比如在拉伸试验中观察到基体微裂纹密度随着所施加载荷的增大而增大, 裂纹平行于纤维/基体界面[21 ] . 此外, 如何在涉及多轴应力状态的情况下使用基于剪切滞后微观力学模型尚不清楚.
另外, CMC在热机械载荷作用下不可避免地产生了热机械损伤, 关于这种含热机械预损伤材料结构在机械载荷下的力学行为和损伤特性的描述和研究还未见文献报道[22 -24 ] .
本工作采用连续介质损伤力学方法, 在平面应力状态下, 推导含预损伤氧化物/氧化物CMC的损伤本构关系, 研究含循环热冲击预损伤氧化物/氧化物CMC在单调拉伸载荷作用下的损伤演化规律, 以期为氧化物/氧化物CMC在循环热冲击/机械载荷耦合作用下的力学行为评估提供参考.
1 含预损伤氧化物/氧化物CMC损伤实验
1.1 实验材料
本文所用材料Nextel$^{\rm TM}$ 610纤维(99% $\alpha$-Al$_{2}$O$_{3})$编织于Al$_{2}$O$_{3}$-ZrO$_{2}$-SiO$_{2}$基体中的氧化物/氧化物CMC. 原材料板材由八条缎纹编织(8HSW)布用精细Al$_{2}$O$_{3}$基体浸渍, 然后, 将8层单独的预浸布以 [0/90]$_{\rm 2S}$彼此堆叠烧结而成, 板厚为2.8 mm. 材料密度约为2.71~g/mm$^{3}$, 纤维体积分数约为44%, 基体的组成成分为氧化铝(质量分数为85\%)和3 mol/mol 氧化钇(质量分数为15\%)稳定氧化锆(3 mol/mol Yttria-stabilized monoclinic and tetragonal ZrO$_{2}$, 3YSZ), 属于典型的多孔基体CMC[24 -25 ] .
1.2 循环热冲击试验
由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式.
基于上述考虑, 本文先对CMC进行循环热冲击实验,对循环热冲击引起的热机械损伤进行定量的描述,然后再对含有循环热冲击预损伤的材料进行单调拉伸损伤实验.
热冲击试验过程为: 将马弗炉加热到预定温度, 然后将试件置于炉中并保温10 min,以使试件的温度均匀化, 并与炉膛充分建立热平衡; 然后将试件迅速取出,放入有25${^\circ}$C蒸馏水的恒温水浴炉中,同时不断搅拌以避免蒸气层的积聚(试件表面在与蒸馏水沸腾换热中产生的气泡),使试件能与蒸馏水进行充分的热交换. 将试件在水浴中冷却到室温,
取出并在空气中干燥, 对每个试件进行编号.通过重复上述过程以研究循环热冲击的影响, 即热机械疲劳.根据材料使用的最高温度范围, 将热冲击温度$T_{\rm shock}$设定为1100${^\circ}$C.
1.3 单调拉伸载荷下CMC的应力应变曲线
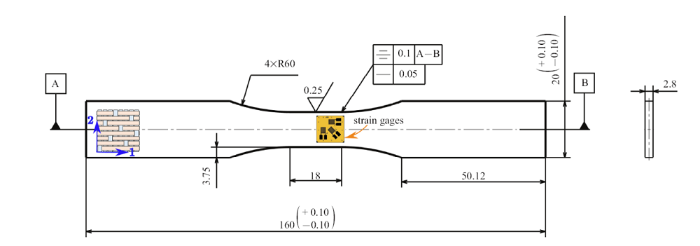
为深入了解含循环热冲击预损伤的氧化物/氧化物CMC在单调拉伸载荷下的力学行为和损伤特性,在室温下对含循环热冲击预损伤的氧化物/氧化物CMC开展损伤实验.根据笔者课题组的前期研究[20 ] ,氧化物/氧化物CMC在经历累积8次循环热冲击($T_{\rm shock}=1100~{^\circ}$C)后,由循环热冲击引起的热机械损伤接近饱和. 因此,本工作选定经历了8次循环热冲击的氧化物/氧化物CMC作为研究对象.在MTS809液压伺服拉扭疲劳试验机上进行单调拉伸损伤实验,拉伸试验使用的试件尺寸如图1 所示.在试件标距段内沿试件轴线方向粘贴应变花以同时测量试件在轴向应力$\sigma _x $作用下$x$--$y$全局坐标系下的正应变($\varepsilon _x $和$\varepsilon _y $). 采用位移控制加载方式, 加-卸载过程的应变速率均设定为10$^{ - 4}$ s$^{-1}$, 以保证准静态加载条件. 拉伸载荷由MTS试验机的测试系统实时测得, 同时采用动态信号测试分析系统(DH5922D)以10~Hz的采样频率同步采集试件的应变.使用三维全场变形检测仪(digital image correlation, DIC)对应变测量进行校核.为获得可靠的试验结果, 需要特别注意试件的对中. 对于所有的拉伸试验,如果试件在标距段内断裂, 则认为测试结果有效.
图1
图1
氧化物/氧化物CMC单调拉伸试件几何尺寸
Fig.1
Monotonic tension specimen geometry of the oxide/oxide CMC
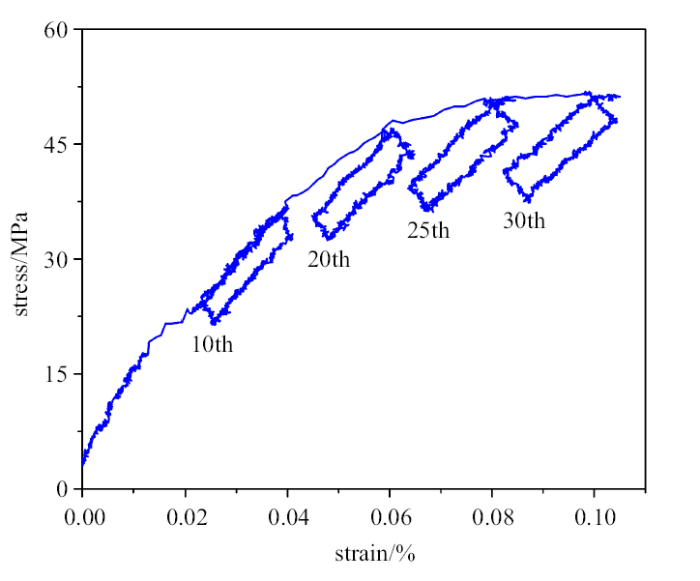
根据经历了循环热冲击的氧化物/氧化物CMC的单拉试验确定的应力-应变关系,确定损伤试验中的位移增量, 以获取一定数目不同应变水平下的加载-卸载循环.每次再加载都施加相同的应变增量, 与第一次加载相比,每次再加载的损伤增长通常非常小.在弹性卸载段测量弹性模量(弹性模量等于弹性卸载曲线的斜率), 如图2 所示.
图2
图2
在单轴拉伸试验中用于确定损伤演变的加载-卸载曲线
Fig.2
Loading--unloading curves for determining damage tension tests
由于卸载-再加载过程被控制在一个很小的应变范围内且循环次数少,故忽略整个加载历程中的疲劳损伤效应[31 -32 ] . 需要注意的是,在卸载和再加载路径上的有效弹性特性仅取决于材料当前的损伤状态. 实验证实,卸载阶段测量的弹性模量在数值上与再加载阶段相同,说明测量所得的弹性模量值是可靠的.
从图2 中可看到, 含循环热冲击预损伤的氧化物/氧化物CMC在初始加载阶段保持线弹性,随着所施加的应变不断增大, 加-卸载曲线的卸载模量不断减小,且卸载后材料产生了非弹性应变, 在卸载-再加载的过程中形成迟滞环,这可能是由于(i)基体/纤维界面接触摩擦导致的能量耗散,和(ii)基体裂纹渐进开裂或者纤维脱粘过程中形成新的自由表面,这两个不可逆的过程都吸收了一定的应变能. 随着拉伸应力持续增大,迟滞环的宽度和卸载后的非弹性应变值也在逐渐增大. 由此推断,含循环热冲击预损伤的氧化物/氧化物CMC的应力-应变曲线呈现非线性特征的主要原因是其弹性模量的不断降低和非弹性应变的不断累积.
除了${0^ \circ }/{90^ \circ }$正轴向试件的损伤试验, 还开展了$\pm 45^ \circ $偏轴试件的损伤试验, 并根据ASTM 3518测试标准, 得到材料面内剪切模量$G_{12} $. 对于$\pm 45^ \circ $偏轴试件, 剪切模量$G_{12} $可通过轴向应变$\varepsilon _x $和横向应变$\varepsilon _y $得到[24 ,33 ]
(1) $\begin{eqnarray} \label{eq1} G_{12} = \frac{\sigma _x }{2\left( {\varepsilon _x - \varepsilon _y } \right)} \end{eqnarray}$
式中, $\sigma _x $为轴向拉伸应力, $\sigma _x = {F}/{A}$ ($A$为材料在拉伸方向的横截面积), $\sigma _y $, $\tau _{xy} = 0$.
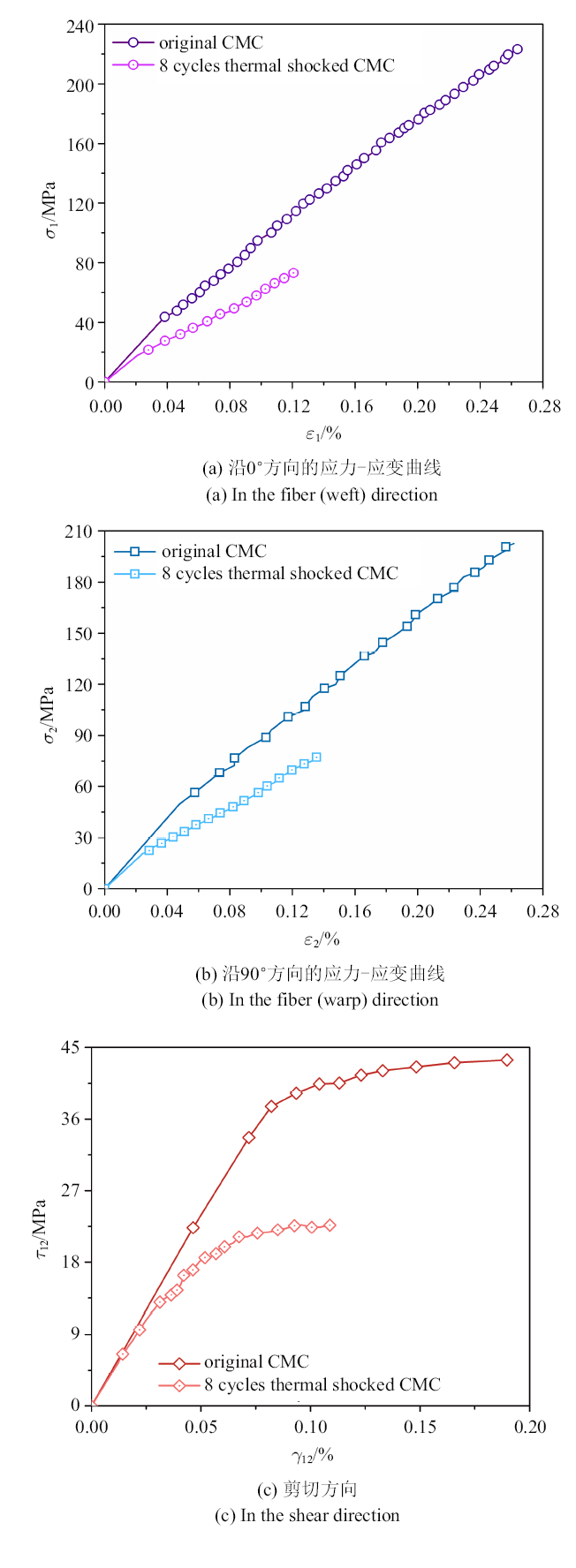
原始的和含循环热冲击预损伤的氧化物/氧化物CMC的应力-应变曲线如图3 所示.
图3
图3
原始的和含循环热冲击预损伤的CMC的单调加载应力-应变曲线从
Fig.3
Stress--strain curve of original CMC and thermal shocked CMC under tensile loading
图3 中看出, 在单调拉伸载荷下,原始的氧化物/氧化物CMC与含循环热冲击预损伤的氧化物/氧化物CMC在纤维方向表现出弹脆性行为,即材料在失效前基本保持为线弹性,但是含循环热冲击预损伤的氧化物/氧化物CMC的弹性模量、抗拉强度和断裂应变均降低.从剪切应力-剪切应变曲线(图3 (c))中可以观察到明显的非线性现象,这种非线性力学响应可以归因于随着剪切应力的增大, 纤维束之间的基体开裂,纤维/基体脱粘和滑动等导致损伤增长率不断增大.
根据Lemaitre的连续介质损伤力学理论[34 ] , 材料损伤$D$用材料弹性模量的降低来定义
(2) $\begin{eqnarray} \label{eq2} D = 1 - \frac{\tilde {E}}{E_0 },\ \ D = 1 - \frac{\tilde {G}}{G_0 } \end{eqnarray}$
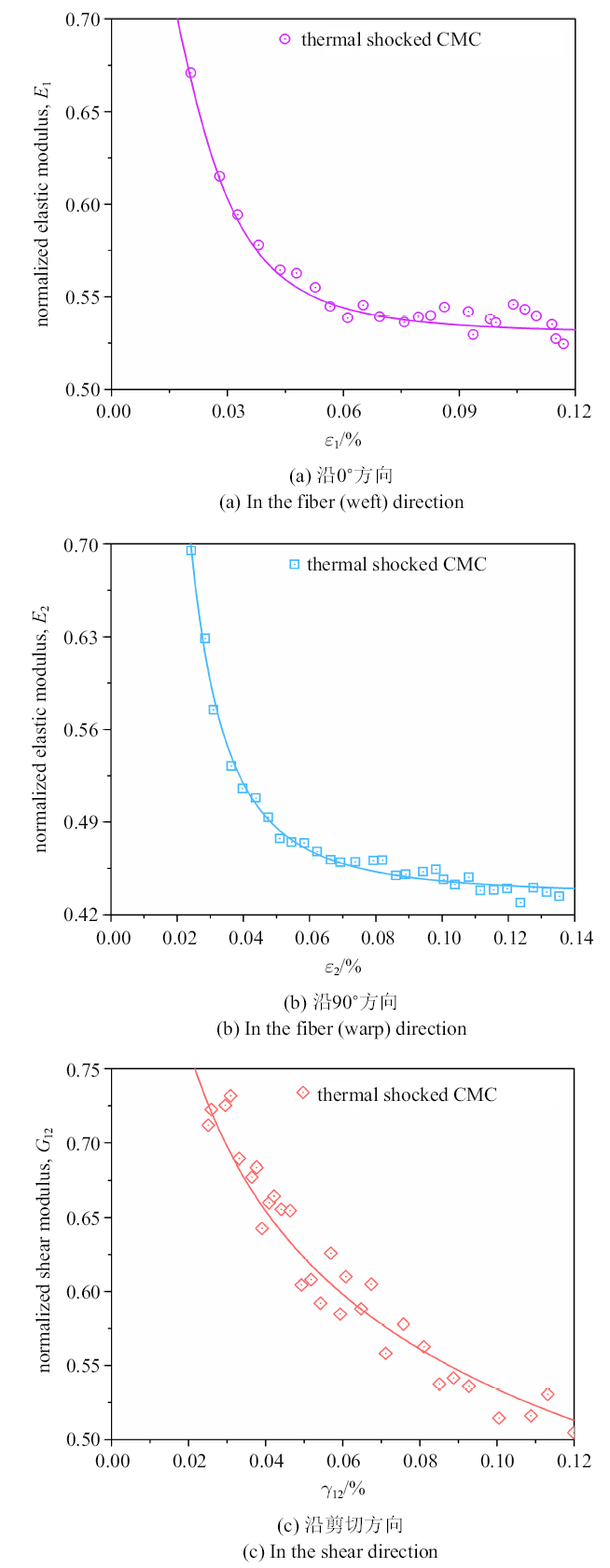
式中, $\tilde {E}$和$\tilde {G}$分别表示当前材料的弹性模量和剪切模量,$E_{0}$和$G_{0}$分别表示原始材料的弹性模量和剪切模量. 在单轴加载情况下,含循环热冲击预损伤的氧化物/氧化物CMC损伤试验中模量随应变水平的增加的演化情况如图4 所示.
图4
图4
含循环热冲击预损伤的氧化物/氧化物CMC弹性模量和剪切模量随应变的演化曲线
Fig.4
Elastic modulus and shear modulus evolution with applied strain of thermal shocked CMC
从图4 中看到, 含循环热冲击预损伤的氧化物/氧化物CMC的归一化弹性模量和剪切模量并没有从起始点1开始下降,这是因为材料本身已经含有由循环热冲击导致的预损伤.在相对较小的应变水平下, 材料的弹性模量就开始快速下降,说明损伤在弹性阶段就已经萌生, 且随着应变的增大而不断累积,表明损伤演化似乎受应变控制, 损伤的累积与应变的增加直接相关,即应变是复合材料中损伤演化的主要因素, 且在轴向$0^ \circ $和$90^ \circ $方向以及剪切方向均有着类似的演化趋势.
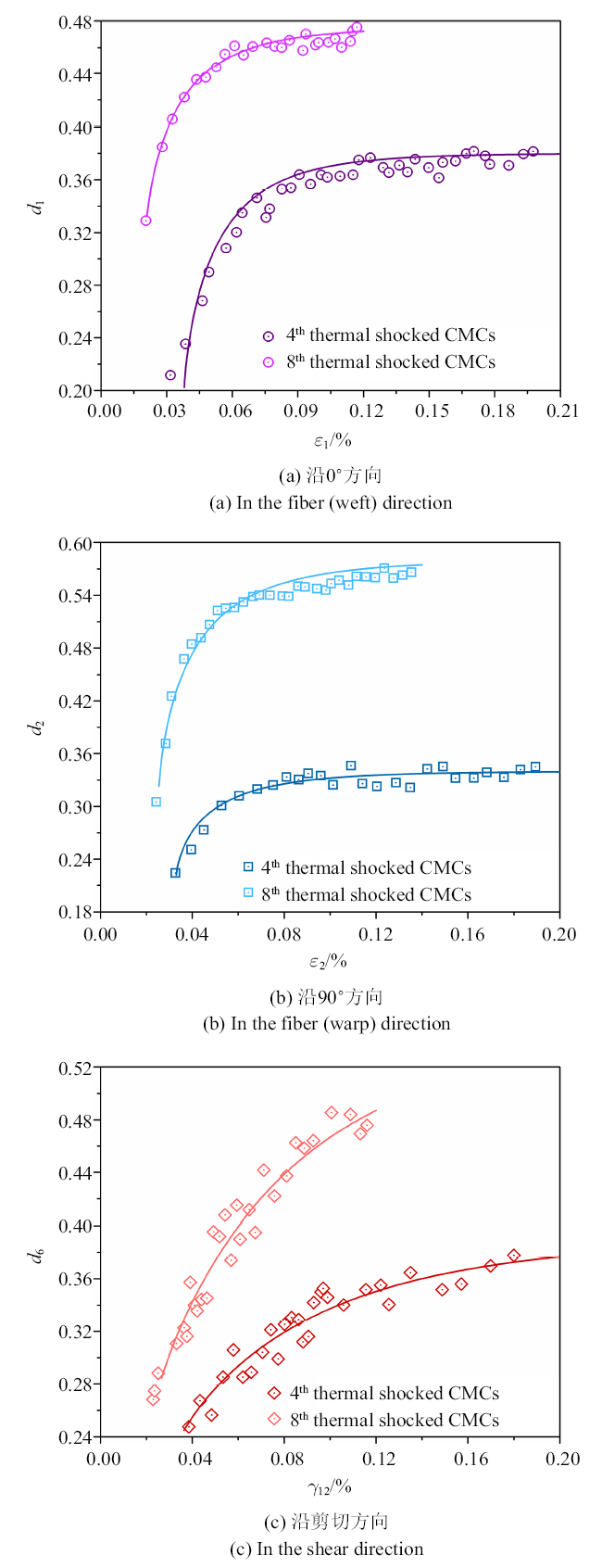
通过测量在加载-卸载-再加载循环期间的弹性模量(轴向拉伸试验)和剪切模量($45^\circ $离轴拉伸试验)来计算材料的损伤.在平行于方向1的载荷下进行的拉伸损伤试验确定了损伤变量$d_1 $的演化规律(图4 (a)); 在平行于方向2的载荷下进行的拉伸损伤试验,定了损伤变量$d_2 $的演化规律(图4 (b)); 同理, 通过$45^ \circ $离轴拉伸损伤试验, 换算得到材料面内剪切模量$G_{12} $的演化规律, 从而给出了损伤变量$d_6 $的演化过程(图4 (c)). 从图4 中看到, 正轴向拉伸的损伤变量$d_1 $和$d_2 $演化规律与面内剪切的损伤变量$d_6 $的演化规律基本一致, 说明材料在拉伸和剪切过程中的损伤机制可能一致. 特别地,对于轴向$0^ \circ $拉伸试件, 从总体应变的角度来看, 可以确定以下4个不同的区域.
(1)对于$\varepsilon \in \left( {0,0.018\% } \right)$, 含循环热冲击预损伤的氧化物/氧化物CMC处于弹性范围内, 没有除预损伤之外的损伤, 在该应变范围内测量的初始弹性模量几乎恒定.
(2)当$\varepsilon \in \left( {0.018\% ,0.05\% } \right)$, 材料开始产生损伤且弹性模量开始发生变化, 随着应变持续增大, 损伤也迅速增加,这是氧化物/氧化物CMC呈弹脆性损伤的典型特征.
(3)当$\varepsilon \in \left( {0.05\% ,0.12\% } \right)$时, 损伤基本处于饱和稳定状态.
(4)当$\varepsilon > 0.12\% $, 材料发生断裂失效, 断裂应变约为0.12%.
对于正轴向$90^ \circ $拉伸损伤变量$d_2 $和面内剪切损伤变量$d_6$也同样存在类似上述机械损伤演化过程. 由此, 对于弹脆性材料,其机械损伤和所施加应变之间存在幂律演化律, 其损伤可简单表达为[35 ]
(3) $\begin{eqnarray} \label{eq3} d_i = \kappa \left( {\frac{\varepsilon _i }{\varepsilon _{{\rm f},i} }} \right)^b,\ \ i = 1,2,6 \end{eqnarray}$
式中, $\kappa $和$b$是材料常数, $\varepsilon _{\rm f} $是材料在单调拉伸载荷下的断裂应变. 根据式(3)的幂律演化律,可给出含循环热冲击预损伤的氧化物/氧化物CMC机械损伤$d_i $与应变$\varepsilon $之间的关系, 式(3)表明可以通过幂律演化对CMC的损伤与应变关系进行描述,但其并不能反映材料的损伤机制. 为了完全表征机械损伤,有必要进一步确定能全局描述材料损伤机制的损伤演化律.
1.4 损伤与失效机制分析
在单调拉伸载荷作用下,含循环热冲击预损伤的氧化物/氧化物CMC在不同尺度上表现出多种损伤机制.通过SEM观察从试验件上切割下的碎片,证明了材料内部产生了基体开裂、纤维基体剥离、界面脱粘、纤维断裂和拔出和分层等多种损伤模式.含循环热冲击预损伤的氧化物/氧化物CMC的单拉损伤断口形貌如图5 所示.
图5
图5
含循环热冲击预损伤的氧化物/氧化物CMC典型损伤模式
Fig.5
SEM micrographs showing typical damage mode under tensile loading
在拉伸试验期间主要产生3种类型损伤: (1)纤维内微裂纹, 在轴向拉伸试验中, 其产生于两个相互垂直的纤维丝束之间; (2)基体开裂与纤维断裂,CMC力学性能受材料在成型和加工过程中产生的基体微裂纹和热残余应力的影响,由于基体内的热残余应力和拉伸应力相互叠加, 导致脆性基体开裂;在基体微裂纹扩展时, 由于裂纹尖端场的应力集中, 导致纤维断裂[36 ] ;(3)界面滑移, 由于循环热冲击导致局部基体/纤维界面分层,基体微裂纹在界面处发生偏转, 使得纤维和基体在加-卸载作用下, 发生界面滑移.预先存在的基体裂纹和分层等损伤在拉伸载荷作用下产生滑动摩擦,从而导致能量耗散并导致材料最终失效.
2 含循环热冲击预损伤的CMC本构方程
通常, CMC表现出弹脆性行为, 材料在没有明显的塑性变形时就已经产生损伤, 因此,不考虑材料的塑性以及热残余应力对损伤演化的滞后效应的影响,构建含热机械预损伤的CMC的损伤本构方程.
2.1 含循环热冲击预损伤的CMC本构模型
对于编织CMC, 损伤取决于载荷作用的方向, 假设在机械加载的过程中, 材料满足(1)在层内1, 2方向是平面应力状态; (2) 材料呈现正交各向异性特征; (3)材料刚度矩阵中的非对角线项保持不变, 即${\upsilon _{21} }/{E_1 } = {\rm const}$, 式中, $\upsilon _{21} $ 是泊松比, $E_1 $是1方向的弹性模量. 那么,由一组可观察的内部状态变量来表征含预损伤的CMC的当前应力-应变状态,将损伤演化方程定义为弹性应变张量$\varepsilon _{ij} $的函数
(4) $\begin{eqnarray} \label{eq4} \dot{d}_{ij} = f\left( {\dot{\varepsilon }_{ij} } \right) \end{eqnarray}$
其中, 损伤率$\dot{d}_{ij} $是关于应变张量率$\dot{\varepsilon }_{ij} $的函数. 式(4)表明需要确定损伤变量和施加应变之间的关系.下面分别就正轴向拉伸损伤变量($d_1 $和$d_2 $)和面内剪切损伤变量($d_6 $), 建立能一定程度反映材料损伤演化机制的损伤演化方程.
为表征含循环热冲击预损伤的CMC在机械载荷作用下的损伤状态,忽略加-卸载过程中迟滞效应的影响, 在材料的局部坐标系下,定义一组标量型损伤变量$d_i \left( {i = 1,2,6} \right)$
(5) $\begin{eqnarray} \label{eq5} d_1=1-\frac{E_1}{E_1^0},\ \ d_2=1-\frac{E_2}{E_2^0},\ \ d_6=1-\frac{G_{12}}{G_{12}^0} \end{eqnarray}$
式中, $E_1 $, $E_2 $和$G_{12} $表示含循环热冲击预损伤的CMC在机械载荷下的弹性模量和剪切模量,上标0表示CMC的初始状态. 从原始材料的角度看,含循环热冲击预损伤的CMC的初始损伤为循环热冲击导致的热机械损伤.
根据CDM原理, 将含热机械损伤材料的弹性应变能$\rho \varPhi $写为
(6) $\begin{eqnarray} \label{eq6} &&\rho \varPhi = \frac{1}{2}\frac{\sigma _1^2 }{E_1^0 \left( {1 - d_1 } \right)} - \frac{\nu _{12}^0 \sigma _1 \sigma _2 }{E_1^0 } + \frac{1}{2}\frac{\sigma _2^2 }{E_2^0 \left( {1 - d_2 } \right)} +\\&&\qquad \frac{1}{2}\frac{\sigma _6^2 }{G_{12}^0 \left( {1 - d_6 } \right)} \end{eqnarray}$
式中, $\sigma _1 $, $\sigma _2 $和$\sigma _6 $是Cauchy应力张量$\sigma $的分量, $\nu _{12}^0 $是不含损伤材料的主平面面内的泊松比, 这样材料的状态律可写为
(7) $\begin{eqnarray} \label{eq7} \varepsilon^{\rm e} = \rho \frac{\partial \varPhi }{\partial \sigma } \end{eqnarray}$
式中, $\varepsilon^{\rm e}$为弹性应变张量.
为建立合理的含预损伤的CMC损伤模型, 有必要考虑弹性应变$\varepsilon^{\rm e}$和损伤变量$d_i $之间的耦合关系, 弹性应变可以表示为
(8) $\left. \begin{array}{l@{\quad}l} \varepsilon _{11}^{\rm e} = \dfrac{\sigma _{11} }{E_1^0 \left( {1 - d_1 } \right)} - \dfrac{v_{12}^0 }{E_1^0 }\sigma _{22} \\ \varepsilon _{22}^{\rm e} = \dfrac{\sigma _{22} }{E_2^0 \left( {1 - d_2 } \right)} - \dfrac{v_{12}^0 }{E_1^0 }\sigma _{11} \\ \gamma _{12}^{\rm e} = \dfrac{\sigma _{12} }{G_{12}^0 \left( {1 - d_6 } \right)} \end{array} \right\}$
2.2 机械损伤演化方程
在单轴拉伸载荷下, 纤维在承载中占主导地位,基体裂纹诱发的材料缺陷随机分布在基体和纤维中,而且基体裂纹和纤维断裂失效也呈随机脆性失效特征,其断裂概率受应力-应变状态影响显著. 文献表明[37 -38 ] ,基于断裂统计理论的Weibull脆性断裂方法适用于弹脆性材料在单轴应力状态下的损伤本构建模.
假设纤维断裂概率服从Weibull统计分布,包含有纤维的代表性体积单元的尺寸既大到包含足够多的微观孔隙、裂纹,也充分小到可以用连续介质力学中质点的概念来考虑,那么包含有纤维的代表性体积单元的失效概率$P_{{\rm FL}} $可以表示为
(9) $\begin{eqnarray} \label{eq9} P_{\rm FL}=1-\exp[(\frac{\sigma_{\rm u}}{\sigma_{\rm w}})^m] \end{eqnarray}$
式中, $\sigma_{\rm u} $为材料在拉伸载荷下的断裂应力, $\sigma_{\rm w} $为尺寸参数, $m$是Weibull模量.
Lamon等[38 -39 ] 将单个纤维的失效概率推广到编织CMC结构中,对于纤维数量为$n$的编织纤维CMC结构, 设断裂失效的纤维数量为$nb = nP_{{\rm FL}} $, 那么未断裂失效的纤维数量为$n - nb = n\left( {1 - P_{{\rm FL}} } \right)$. 假设编织CMC结构中包含有纤维的代表性体积单元的弹性模量为$E_0 $, 施加在试件上的载荷为$F=\sum_{i}\sigma_iA_0$. 由于断裂失效的纤维不承载, 则$\sigma _i = 0$, 而未断裂失效的纤维承担的载荷为$\sigma _i = \varepsilon E_0 $, 那么对于整个含损伤的材料, 其承担载荷为
(10) $\begin{eqnarray} \label{eq10} F=E_0\varepsilon A_0(1-P_{\rm FL})n=E_0\varepsilon A(1-P_{\rm FL}) \end{eqnarray}$
式中, $A$为试件的承载面积. 根据真实应力$\bar{\sigma}$的定义
(11) $\begin{eqnarray} \label{eq11} \bar{\sigma}=\frac{F}{A}=E_0\varepsilon (1-P_{\rm FL}) \end{eqnarray}$
根据CDM理论, 将材料的损伤变量定义为包含有纤维的代表性体积单元的失效概率,即$d = P_{{\rm FL}} $. 联立式(9)可得单调拉伸载荷下材料的损伤表达式
(12) $\begin{eqnarray} \label{eq12} d=1-\exp[(\frac{E_0\varepsilon}{\sigma_w})^m] \end{eqnarray}$
由式(12)可知, CMC的机械损伤是关于所施加应变的单调函数,即每个应变水平对应唯一的损伤状态,直接反映了CMC基体裂纹和纤维断裂随机脆性失效的微观损伤机制. 然而,式(12)并不能完全反映含预损伤材料的损伤特性: (1)氧化物/氧化物CMC的机械损伤发生在一定的应变水平下,即该应变水平使得材料发生基体开裂; (2)材料的损伤状态受初始损伤$d^0$和材料断裂失效时的临界损伤$d^{{\rm cr}}$控制. 鉴于此, 引入初始损伤$d^0$, 考虑临界断裂失效损伤$d^{{\rm cr}}$和应变阈值$\varepsilon _{{\rm th}} $[40 ] , 将CMC的损伤表达式(12)写为
(13) $v\begin{eqnarray} \label{eq13} d=d^0+(d^{\rm cr}-d_0)\{1-\exp[(\frac{E\langle\varepsilon-\varepsilon_{\rm th}\rangle}{\sigma_w})^{m}]\} \end{eqnarray}$
式中, $\langle\,\cdot\,\rangle$是Macauley括号, 当$x \geqslant 0$, $\left\langle x \right\rangle = x$. 当轴向应变小于$\varepsilon _{{\rm th}} $时, 材料处于纯线弹性变形阶段, 不产生损伤. 因此,损伤对应状态下材料的应变范围为$\left[ {\varepsilon _{{\rm th}} ,\varepsilon_{\rm f} } \right]$, 其中$\varepsilon _{\rm f} $为材料在单调拉伸载荷下的断裂应变.式(13)给出了材料从初始状态或者含预损伤状态$\left( {d^0} \right)$到断裂失效状态$\left( {d^{{\rm cr}}} \right)$之间的损伤演化规律. 那么, 对于正轴向($0^ \circ $和$90^ \circ $方向)和剪切方向的损伤$d_i \left( {i = 1,2,6} \right)$演化方程可写为
(14) $\begin{eqnarray}\label{eq14}d_i = d_i^0 + \left( {d_i^{{\rm cr}} - d_i^0 } \right)\left\{ {1 - \exp\left[ { - \left( {\frac{E_i^0 \left\langle {\varepsilon _i - \varepsilon_{{\rm th},i} } \right\rangle }{\sigma _{{\rm w},i} }} \right)^{m_i }}\right]} \right\}\end{eqnarray}$
式(14)表明, 材料的损伤本质上与应变相关, 即应变是CMC中损伤演化的决定性因素.更为重要的是, 如果损伤机制不变, 材料在$\left( {d^0,d^{{\rm cr}}} \right)$间的损伤演化对实验应力-应变的响应并不敏感, 由此可将此模型推广到疲劳载荷.含循环热冲击预损伤的CMC损伤演化方程由材料初始损伤值$d^0$、应变阈值$\varepsilon _{{\rm th}} $、断裂失效临界值$d^{{\rm cr}}$、损伤指数$m$和尺寸参数$\sigma_{\rm w} $五个参数共同作用控制, 其参数辨识如下.
(1)初始损伤$d^0$. 由于原始材料中的初始损伤量很难测量, 通常假设$d^0 = 0$. 然而, 本课题所研究的是含循环热冲击预损伤的氧化物/氧化物CMC, 那么,材料的初始损伤即为材料经历循环热冲击作用而产生的热机械损伤, 具体热机械损伤的量化模型在先前研究中已经做了详细的论述[22 ] .
(2)应变阈值$\varepsilon _{{\rm th}} $. 氧化物/氧化物CMC的机械损伤出现在一定的应变水平下, 基体发生开裂.而低于此应变水平, 材料微观结构为连续体.由于氧化物/氧化物CMC的基体/纤维的界面较弱,那么阈值应变可能与基体弹性应变的数量级相同, 式(14)中的应变阈值$\varepsilon_{{\rm th}} $的精确测定是相当困难的.
(3)断裂失效临界值$d^{{\rm cr}}$. 当损伤变量$d$接近其断裂失效临界值$d^{{\rm cr}}$时, 基体微裂纹与基体/纤维剥离之间的相互作用减少了材料的有效抵抗面积.这种损伤机制的贡献难以准确量化, 一般通过用均匀化理论进行估算.假设材料断裂失效前,基体孔隙或基体微裂纹聚结过程和纤维脆性断裂将材料承载区迅速推向断裂状态.因此, $d^{{\rm cr}}$为单调拉伸试验中材料的断裂应变所对应的临界损伤量. 理论上,当材料发生断裂失效时, 临界损伤变量$d^{{\rm cr}}$应该等于1. 但实验观察与分析表明, 材料在$d^{{\rm cr}} < 1$时就发生了断裂失效.
(4)损伤指数$m$. 所提出的非线性损伤模型中损伤指数$m$蕴含关于损伤演化动力学形状的信息, 表征了损伤演化的非线性程度,可通过材料的单调拉伸试验确定. 指数$m$为实验损伤值拟合线的斜率
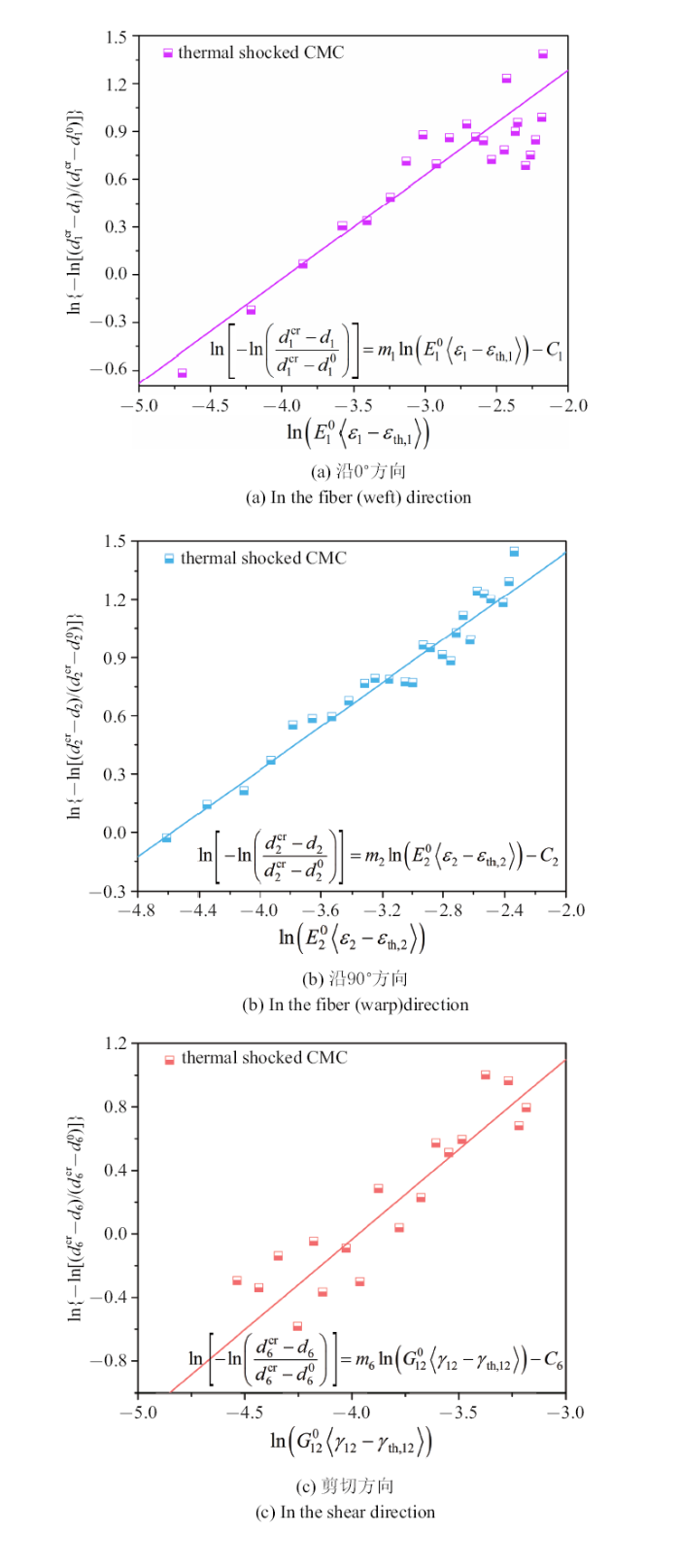
(15) $\begin{eqnarray} \label{eq15} \ln\lt[-\ln\lt(\frac{d^{\rm cr}_i-d_i}{d^{\rm cr}_i-d_i^0})]=m_i\ln[E^0_i(\varepsilon_i-\varepsilon_{{\rm th},i})]-C_i \end{eqnarray}$
式中, $C_i = m_i \ln \left( {\sigma _{\mbox{w},i} } \right)$. 将实验结果与用于损伤参数识别的实验曲线进行比较, 如图6 所示,发现所获得的损伤参数与实验数据吻合得较好, 从而证实了模型参数的有效性.
图6
图6
含循环热冲击预损伤CMC损伤模型参数辨识
Fig.6
Parameter identification of damage model for thermal shocked CMC
(5)尺寸参数$\sigma_{\rm w} $. 同样表征了损伤演化的非线性程度, 通过实验数据拟合得到.
通过上述参数辨识方法得到含循环热冲击预损伤的CMC的损伤模型参数.
图7 给出了含循环热冲击预损伤的氧化物/氧化物CMC损伤随着所施加应变的增大而不断演化的情况.从图7 中看出, 当所施加的应变小于应变阈值$\varepsilon _{{\rm th}} $时, 材料处于纯线弹性阶段, 没有机械损伤.
图7
图7
含循环热冲击预损伤的CMC在单调拉伸载荷下的机械损伤曲线
Fig.7
Damage evolution of thermal shocked CMC under monotonic tensile loading
当累积应变超过$\varepsilon _{{\rm th}} $时, 损伤开始出现并不断增大, 随着应变的持续增大,材料达到临界损伤状态而出现断裂失效. 需要说明的是,由于材料含有循环热冲击的热机械损伤, 损伤并没有从零开始,图中损伤的起点是材料经历循环热冲击后的热机械损伤值,关于热机械损伤的确定在作者的前期论文中有详细论述[22 ] ; 另外,为了验证所提模型的适用性,图7 给出了含4次循环热冲击预损伤的CMC在机械载荷下的损伤演化曲线,结果表明所提模型可以很好地描述含不同预损伤的CMC在机械载荷下的力学行为.
需要指出的是, 在开发损伤模型时, 重点在于对相关损伤机制进行建模,而不是使构建模型的过程变得相当复杂,以至于在实际工程中设计和使用陶瓷基复合材料部件变得不切合实际.
3 非弹性应变累积描述
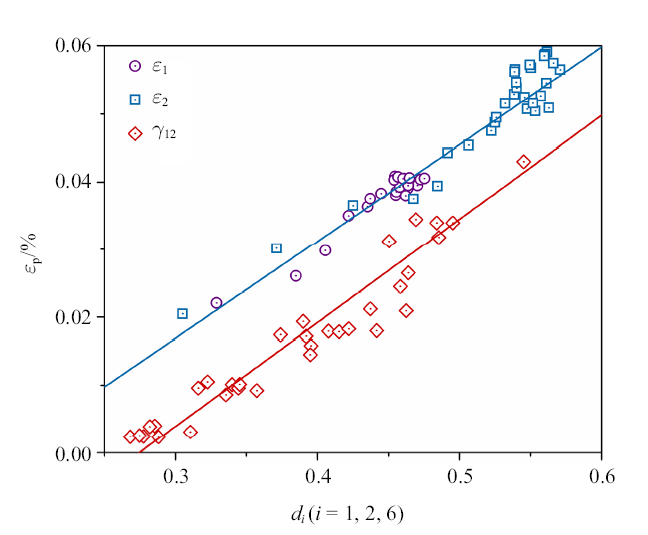
用经典塑性理论来描述CMC的非弹性应变.含循环热冲击预损伤的氧化物/氧化物CMC在卸载-再加载的过程中形成迟滞环,表明材料在卸载过程由于基体开裂、界面脱粘等微结构损伤而产生了非弹性应变.显然, CMC的非弹性应变涉及界面摩擦与滑动, 并且可能与损伤有关.不同于金属材料中由经典塑性引起的非弹性应变现象,含循环热冲击预损伤的氧化物/氧化物CMC损伤-非弹性应变耦合情况如图8 所示,说明材料的非弹性应变会随着损伤共同演化.
图8
图8
含循环热冲击预损伤的氧化物/氧化物CMC损伤与非弹性应变之间的关系
Fig. 8
Inelastic strain evolution with the damage in thermal shocked oxide/oxide CMC
在含损伤的材料中,内力是由材料中的微缺陷以及缺陷之间的相互作用而减少的有效抵抗截面积承受的.又考虑到非弹性变形发生在含损伤的材料的未损伤区域内, 因此,根据Ladevèze等 [10 ,41 ] 的非弹性应变模型,在塑性力学框架下构建非弹性应变累积模型, 引入有效应力张量$\bar { \sigma }$
(16) $\begin{eqnarray} \label{eq16} \bar{ \sigma }=\left[\begin{array}{cc} \dfrac{\sigma_1}{1-d_1}&\dfrac{\sigma_{12}}{1-d_6}\\ \dfrac{\sigma_{12}}{1-d_6}&\dfrac{\sigma_2}{1-d_2} \end{array}\right] \end{eqnarray}$
和与塑性耗散能(塑性功)$W_{\rm p} $相关的有效非弹性应变率张量[42 ]
(17) $\begin{eqnarray} \label{eq17} \dot{\tilde{ \varepsilon}}^{\rm p}=\left[\begin{array}{c@{\ \ }c} \dot{\varepsilon}_p^1(1-d_1)&\dot{\varepsilon}_p^{12}(1-d_6)\\ \dot{\varepsilon}_p^{12}(1-d_6)&\dot{\varepsilon}_p^2(1-d_2) \end{array}\right] \end{eqnarray}$
单位体积内的塑性功$W_{\rm p} $可以由等效塑性应变率来表示
(18) $\begin{eqnarray} \label{eq18} \dot{W}_p=\bar { \sigma }:\dot{ \varepsilon}^{\rm p}=\tilde{\sigma}\dot{\tilde{\varepsilon}}^{\rm p} \end{eqnarray}$
为简化起见, 假设材料在加载过程中屈服面满足各向同性强化法则.基于有效应力空间的概念, 将塑性屈服准则$F(\bar { \sigma }, \tilde{\varepsilon}^{\rm p})$表示为有效应力张量$\bar { \sigma }$的函数
(19) $\begin{eqnarray} \label{eq19} F(\bar { \sigma }, \tilde{\varepsilon}^{\rm p})=F^{\rm p}(\bar { \sigma })-\kappa(\tilde{\varepsilon}^{\rm p})=0 \end{eqnarray}$
式中, $F^{\rm p}$为塑性势, $\kappa \left( {\tilde {\varepsilon }^{\rm p}} \right)$是以等效非弹性应变$\tilde {\varepsilon }^{\rm p}$为变量的各向同性强化函数, 用于描述屈服面的大小, 其表达式如下
(20) $\begin{eqnarray} \label{eq20} \kappa(\tilde{\varepsilon}^{\rm p})=\tilde{\sigma}(\tilde{\varepsilon}^{\rm p})=R_0+\beta(\tilde{\varepsilon}^{\rm p})^{n_{\rm p}} \end{eqnarray}$
式中, $R_0 $为非弹性应变的初始阈值应力, $\tilde {\sigma }\left( {\tilde {\varepsilon}^{\rm p}} \right)$代表了各向同性强化法则, $\beta $和$n_{\rm p} $是强化曲线的系数, 可通过材料的单调拉伸试验确定, $\tilde {\sigma }$是相对于等效非弹性应变$\tilde { \varepsilon }^{\rm p}$的等效应力.
为简单起见,本研究采用平面应力条件下单参数塑性势的等效形式来描述复合材料在拉伸载荷作用下的不可逆应变.结合式(19), 塑性屈服函数可\lb 写为
(21) $\begin{eqnarray} \label{eq21} F(\bar{ \sigma},\tilde{\varepsilon}^{\rm p})=(\bar{\sigma}_1+\bar{\sigma}_2+n^2\bar{\sigma}_{12}^2)^{\frac12} -\kappa(\tilde{\varepsilon}^{\rm p})=0 \end{eqnarray}$
式中, $n$为材料参数, 它与单轴拉伸载荷和剪切载荷作用下产生的非弹性应变的比值成正比;
$\bar {\sigma }_{12} $是面内有效剪切应力. 等效应力用$\bar {\sigma }_1 $, $\bar {\sigma }_2 $和$\bar {\sigma }_{12} $表示如下
(22) $\begin{eqnarray} \label{eq22} \tilde{\sigma}=[\bar{\sigma}_1+\bar{\sigma}_2+n^2\bar{\sigma}_{12}^2]^{\frac12} \end{eqnarray}$
考虑到复合材料的塑性流动的方向和屈服面的法向成正比, 即关联塑性流动法则,非弹性应变率$\varepsilon^{\rm p}$由下式给出
(23) $\begin{eqnarray} \label{eq23} \dot{\varepsilon}^{\rm p}=\dot{\lambda}^{\rm p}\frac{\partial F}{\partial\bar{ \sigma}} \end{eqnarray}$
式中, $\dot{\lambda }^{\rm p} \geqslant 0$是一个非负塑性一致性参数. 将方程(21)代入方程(23),得到非弹性应变率的显式形式为
(24) $\begin{eqnarray} \label{eq24} \left[\begin{array}{c}\dot{\varepsilon}_1^{\rm p}\\ \dot{\varepsilon}_2^{\rm p}\\ \dot{\varepsilon}_{12}^{\rm p}\end{array}\right] =\dot{\lambda}^{\rm p}\frac{\partial F}{\partial\bar{ \sigma}} =\left[\begin{array}{c} \dfrac{\bar{\sigma}_1}{\tilde{\sigma}}\\[2mm] \dfrac{\bar{\sigma}_2}{\tilde{\sigma}}\\[2mm] \dfrac{n^2\bar{\sigma}_{12}}{\tilde{\sigma}}\\ \end{array}\right] \end{eqnarray}$
(25) $\begin{eqnarray} \label{eq25} \dot{\tilde{\varepsilon}}^{\rm p}=\dot{\lambda}^{\rm p} \end{eqnarray}$
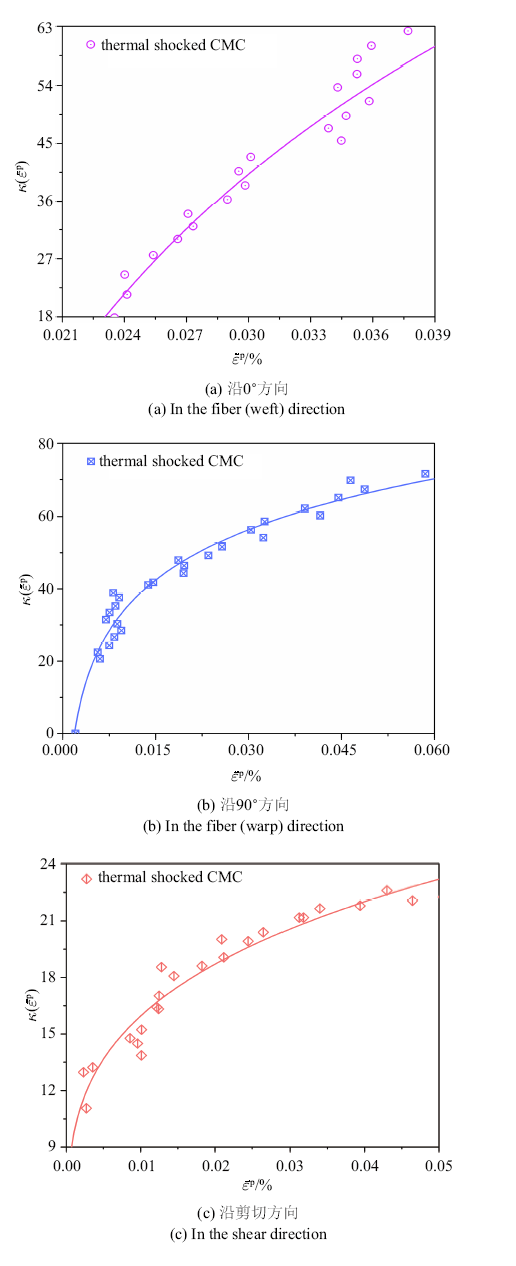
由式(24)可知, 材料的非弹性应变演化可完全由$\dot{\lambda }^{\rm p}$和$\bar {\sigma }$确定. 从图9 可以看出, 所提出的各向同性强化函数关于非弹性应变的表达式与实验数据吻合得\lb 较好.
图9
图9
含预损伤CMC非弹性应变演化与非弹性应变之间的关系
Fig.9
$\kappa $ evolution with inelastic strain in thermal shocked CMC
4 结论
本文主要开展了含循环热冲击预损伤的氧化物/氧化物CMC的单调拉伸损伤实验,描述了含循环热冲击预损伤的氧化物/氧化物CMC在轴向拉伸载荷下的非线性应力-应变行为,将所施加的应变作为机械损伤的函数, 在此基础上,提出了含循环热冲击预损伤的氧化物/氧化物CMC的非线性损伤演化模型,得到如下主要结论:
(1)单调拉伸损伤实验证实, 含循环热冲击预损伤的氧化物/氧化物CMC弹性模量的降低与所施加的应变直接相关,当所施加应变超过应变阈值$\varepsilon _{{\rm th}} $, 损伤发生并累积, 直到施加应变达到失效应变$\varepsilon ^{{\rm cr}}$, 试件断裂失效, 推断出应变是氧化物/氧化物CMC中机械损伤演化的决定性因素,由此建立了基于应变的氧化物/氧化物CMC损伤分析模型.
(2)由一组标量损伤变量表示含循环热冲击预损伤的氧化物/氧化物CMC在单调拉伸载荷下的损伤行为,包括根据正轴向$0^ \circ $和$90^ \circ $方向的单调拉伸实验得到主方向1和主方向2上的损伤行为, 由偏轴$\pm 45^ \circ $方向单调拉伸实验换算得到剪切方向的损伤行为, 基于Lamon的CMC的损伤模型,提出由弹性应变阈值$\varepsilon _{{\rm th}} $和断裂失效临界值$d^{{\rm cr}}$以及初始损伤值$d^0$来构建含预损伤的CMC在单调拉伸载荷下的损伤演化方程.
(3)在塑性力学理论框架下, 在有效应力空间上建立屈服函数,使用各向同性硬化函数和关联流动法则描述了氧化物/氧化物CMC中由基体损伤引起的非弹性应变演化过程,该工作弥补了含预损伤的CMC在机械加载下损伤演化模型在理论及实验研究方面的不足.
参考文献
View Option
[1]
Rajan VP Shaw JH Rossol MN et al . An elastic--plastic constitutive model for ceramic composite laminates
Composites Part A$:$ Applied Science and Manufacturing 2014 ,66 :44 -57
[本文引用: 1]
[2]
Chateau C Gelebart L Bornert M et al . Modeling of damage in unidirectional ceramic matrix composites and multi-scale experimental validation on third generation SiC/SiC minicomposites
Journal of the Mechanics and Physics of Solids 2014 ,63 :298 -319
DOI
URL
The purpose of this paper is to experimentally validate a ID probabilistic model of damage evolution in unidirectional SiC/SiC composites. The key point of this approach lies in the identification and validation at both local and macroscopic scales. Thus, in addition to macroscopic tensile tests, the evolution of microscopic damage mechanisms - in the form of matrix cracks and fiber breaks - is experimentally analyzed and quantified through in-situ scanning electron microscope and computed tomography tensile tests. A complete model, including both matrix cracking and fiber breaking, is proposed on the basis of existing modeling tools separately addressing these mechanisms. It is based on matrix and fiber failure probability laws and a stress redistribution assumption in the vicinity of matrix cracks or fiber breaks. The identification of interfacial parameters is conducted to fit the experimental characterization, and shows that conventional assumptions of 1D probabilistic models can adequately describe matrix cracking at both macro- and microscopic scales. However, it is necessary to enrich them to get a proper prediction of ultimate failure and fiber break density for Hi-Nicalon type S fiber-reinforced SiC/SiC minicomposites. (C) 2013 Elsevier Ltd.
[3]
Gowayed Y Abouzeida E Smyth I et al . The role of oxidation in time-dependent response of ceramic--matrix composites
Composites Part B$:$ Engineering 2015 ,76 :20 -30
[本文引用: 1]
[4]
Askarinejad S Rahbar N Sabelkin V et al . Mechanical behavior of a notched oxide/oxide ceramic matrix composite in combustion environment: Experiments and simulations
Composite Structures 2015 ,127 :77 -86
DOI
URL
[本文引用: 1]
[5]
Xu W Zok FW McMeeking RM . Model of Oxidation-Induced Fiber Fracture in SiC/SiC Composites
Journal of the American Ceramic Society 2014 . 97 (11 ): 3676 -3683
DOI
URL
[本文引用: 2]
Stress rupture of SiC/SiC composites at intermediate temperatures in oxidizing environments is the result of a series of internal chemical and thermomechanical processes that lead to premature, localized fiber fracture. This article presents analytical models for two potentially critical steps in this process. The first involves the generation of tensile stresses in the fibers due to SiO2 scale formation (following removal of fiber coatings) and the associated reduction in the applied stress required for fiber fracture. The second occurs once the gaps produced by coating removal are filled with oxide and subsequent oxidation occurs subject to the constraints imposed by the matrix crack faces. In this domain, the failure model is couched in terms of the stress intensification within the fibers caused by constrained oxidation. The models incorporate the combined kinetic effects of oxide growth and viscous flow. The competing effects of increased oxidation rate and accelerated stress relaxation with increasing temperature on fiber stress feature prominently in the results. The results suggest that, in dry air environments, the highest risk of fiber fracture occurs at temperatures in the range 840 degrees C-940 degrees C. In this range, the oxide scales grow at appreciable rates yet the resulting growth stresses cannot be mitigated sufficiently rapidly by viscous flow.
[6]
Lamon J Review: Creep of fibre-reinforced ceramic matrix composites
International Materials Reviews 2019 : 1 -35
[本文引用: 1]
[7]
Ben Ramdane C Julian-Jankowiak A Valle R et al . Microstructure and mechanical behavior of a Nextel TM 610/alumina weak matrix composite subjected to tensile and compressive loadings
Journal of the European Ceramic Society 2017 ,37 (8 ): 2919 -2932
DOI
URL
[本文引用: 1]
[8]
Shojaei A Li GQ Fish J et al . Multi-scale constitutive modeling of ceramic matrix composites by continuum damage mechanics
International Journal of Solids and Structures 2014 . 51 (23-24 ):4068 -4081
DOI
URL
[本文引用: 1]
The microscale damage mechanisms in brittle ceramics are investigated in detail and a Continuum Damage Mechanics (CDM) model is developed in this work to study two common failure modes in Ceramic Matrix Composites (CMC), i.e. matrix/interphase fracture and fiber sliding. In order to empower the developed framework for performing crashworthiness studies, the effect of the dynamic energy density content on the microscale fracture modes of CMCs is also considered. The CDM model is developed within a physically consistent framework that includes basic fracture mechanics of CMCs. Also the CDM model is developed in such a way that most of the material parameters are directly obtainable form the experimental data rather than cumbersome and time consuming numerical curve fitting techniques. In order to construct a computationally effective multiscale analysis platform for CMCs, this work aims to provide an asymptotic solution for a microscale representative volume element (RVE) which represents the fiber, interphase and matrix interactions. The developed asymptotic solution can capture the non-linear response of CMCs through CDM model; and it considerably reduces the computational cost of hierarchical multiscale analysis in comparison to the numerical methods, e.g. numerical models that simulate the real microstructure. The CDM model and the RVE asymptotic solution are utilized to study the microscale damage mechanisms in CMC systems. It is shown that the developed scheme performs quite well in capturing available experiments in the literature and provides a comprehensive description of microscale damage mechanisms in CMCs. The developed framework can be utilized in the future developments of the hierarchical multiscale analysis of CMC systems. (C) 2014 Elsevier Ltd.
[9]
Talreja R Continuum modeling of damage in ceramic matrix composites
Mechanics of Materials 1991 ,12 (2 ): 165 -80
DOI
URL
[本文引用: 1]
[10]
Ladeveze P Gasser A Allix O Damage mechanisms modeling for ceramic composites
Journal of Engineering Materials and Technology 1994 ,116 (3 ): 331
DOI
URL
PMID
[本文引用: 2]
Advanced engineering and functional ceramics are sensitive to damage cracks, which delay the wide applications of these materials in various fields. Ceramic composites with enhanced fracture toughness may trigger a paradigm for design and application of the brittle components. This paper reviews the toughening mechanisms for the nanolayered MAX phase ceramics. The main toughening mechanisms for these ternary compounds were controlled by particle toughening, phase-transformation toughening and fiber-reinforced toughening, as well as texture toughening. Based on the various toughening mechanisms in MAX phase, models of SiC particles and fibers toughening Ti₃SiC₂ are established to predict and explain the toughening mechanisms. The modeling work provides insights and guidance to fabricate MAX phase-related composites with optimized microstructures in order to achieve the desired mechanical properties required for harsh application environments.
[11]
Chaboche JL Maire JF New progress in micromechanics-based CDM models and their application to CMCs
Composites Science and Technology 2001 ,61 (15 ): 2239 -46
DOI
URL
[本文引用: 1]
Abstract A previously developed continuum-damage theory for modeling ceramic-matrix composites is modified relative to the deactivation rule. The new deactivation is directly based on mechanics of microcrack behaviour, considering both closure effects and the corresponding elastic energy storage. The model uses two sets of damage state variables, scalar ones corresponding to microcracks oriented by reinforcements and a second rank tensor that evolves with the maximum principal strain directions. The model is applied to uniaxial and multiaxial monotonic and cyclic tests on a SiC/SiC composite.
[12]
Chaboche JL Maire JF A new micromechanics based CDM model and its application to CMC's
Aerospace Science and Technology 2002 ,6 (2 ): 131 -145
DOI
URL
[本文引用: 1]
Abstract A CDM theory is further developed in order to better model the non linear and dissipative behavior of Ceramic Matrix Composites. A new damage deactivation rule is developed, directly based on mechanics of microcrack behavior, considering both closure effects and the corresponding elastic energy storage. The complete model uses two sets of damage state variables, the scalar ones correspond to microcracks oriented by reinforcements and a second order tensor that evolves with the maximum principal strain directions. The model is applied to uniaxial and multiaxial monotonic and cyclic tests on a SiC/SiC composite. In addition, the new version of the damage deactivation rule allows a progressive effect and a better description of the residual strain.
[13]
Camus G Modelling of the mechanical behavior and damage processes of fibrous ceramic matrix composites: Application to a 2-D SiC/SiC
International Journal of Solids and Structures 2000 ,37 (6 ): 919 -942 .
DOI
URL
[本文引用: 1]
[14]
Li J Jiao GQ Wang B et al . Damage characteristics and constitutive modeling of the 2D C/SiC composite: Part I - Experiment and analysis
Chinese Journal of Aeronautics 2014 ,27 (6 ): 1586 -1597
DOI
URL
[本文引用: 1]
This paper reports an experimental investigation on the macroscopic mechanical behaviors and damage mechanisms of the plain-woven (2D) C/SiC composite under in-plane on-and off-axis loading conditions. Specimens with 15 degrees, 30 degrees, and 45 degrees off-axis angles were prepared and tested under monotonic and incremental cyclic tension and compression loads. The obtained results were compared with those of uniaxial tension, compression, and shear specimens. The relationships between the damage modes and the stress state were analyzed based on scanning electronic microscopy (SEM) observations and acoustic emission (AE) data. The test results reveal the remarkable axial anisotropy and unilateral behavior of the material. The off-axis tension test results show that the material is fiber-dominant and the evolution rate of damage and inelastic strain is accelerated under the corresponding combined biaxial tension and shear loads. Due to the damage impediment effect of compression stress, compression specimens show higher mechanical properties and lower damage evolution rates than tension specimens with the same off-axis angle. Under cyclic tension-compression loadings, both on-axis and off-axis specimens exhibit progressive damage deactivation behaviors in the compression range, but with different deactivation rates. (C) 2014 Production and hosting by Elsevier Ltd. on behalf of CSAA & BUAA.
[15]
Li J Jiao GQ Wang B et al . Damage characteristics and constitutive modeling of the 2D C/SiC composite: Part II -- Material model and numerical implementation
Chinese Journal of Aeronautics 2015 ,28 (1 ): 314 -326
DOI
URL
[本文引用: 1]
In this work, a macroscopic non-linear constitutive model accounting for damage, inelastic strain and unilateral behavior is proposed for the 2D plain-woven C/SiC composite. A set of scalar damage variables and a new thermodynamic potential expression are introduced in the framework of continuum damage mechanics. In the deduced constitutive equations, the material's progressive damage deactivation behavior during the compression loading is described by a continuous function, and different deactivation rates under uniaxial and biaxial compression loadings are also considered. In damage evolution laws, the coupling effect among the damage modes and impediment effect of compression stress on the development of shear damage in different plane stress states are taken into account. Besides, the general plasticity theory is applied to describing the evolution of inelastic strain in tension and/or shear stress state. The Tsai-Wu failure criterion is adopted for strength analysis. Additionally, the material model is implemented as a user-defined material subroutine (UMAT) and linked to the ABAQUS finite element software, and its performance is demonstrated through several numerical examples.
[16]
Xie JB Fang GD Chen Z et al . An anisotropic elastoplastic damage constitutive model for 3D needled C/C-SiC composites
Composite Structures 2017 ,176 :164 -177
DOI
URL
[本文引用: 1]
[17]
Pineda EJ Bednarcyk BA Arnold SM Validated progressive damage analysis of simple polymer matrix composite laminates exhibiting matrix microdamage: Comparing macromechanics and micromechanics
Composites Science and Technology 2016 ,133 :184 -191
DOI
URL
[本文引用: 1]
[18]
Evans AG Marshall DB The mechanical behavior of ceramic matrix composites//Proceedings of The 7th International Conference On Fracture(ICF7)
1989 , Pergamon: Oxford , 3593 -3641
[本文引用: 1]
[19]
Hsueh CH Matrix cracking with frictional bridging fibres in continuous fibre ceramic composites
Journal of Materials Science 1995 ,30 (7 ): 1781 -1789
DOI
URL
[本文引用: 1]
[20]
Yao Y Chen SH Effects of the longitudinal surface roughness on fiber pull-out behavior in carbon fiber-reinforced epoxy resin composites
Journal of Applied Mechanics 2013 ,80 (2 ): 1 -13
[本文引用: 2]
[21]
Santhosh U Ahmad J Ojard G et al . Deformation and damage modeling of ceramic matrix composites under multiaxial stresses
Composites Part B-Engineering 2016 ,90 :97 -106
DOI
URL
[本文引用: 1]
[22]
Yang ZM Yuan H Liu H Evolution and characterization of cyclic thermal shock-induced thermomechanical damage in oxide/oxide ceramics matrix composites
International Journal of Fatigue 2019 ,120 :150 -161
DOI
URL
[本文引用: 3]
[23]
Yang ZM Yuan H Markert B Representation of micro-structural evolution and thermo-mechanical damage in thermal shocked oxide/oxide ceramic matrix composites
International Journal of Fatigue 2019 ,126 :122 -129
DOI
URL
[24]
Yang ZM Liu H Yuan H Micro-porosity as damage indicator for characterizing cyclic thermal shock-induced anisotropic damage in oxide/oxide ceramic matrix composites
Engineering Fracture Mechanics 2019 ,220 :106669
DOI
URL
[本文引用: 3]
[25]
Wilson DM Visser LR High performance oxide fibers for metal and ceramic composites
Composites Part A-Applied Science and Manufacturing 2001 ,32 (8 ): 1143 -1153
DOI
URL
[本文引用: 1]
Abstract A family of oxide fibers, Nextel™ 610 Ceramic Oxide Fiber, Nextel™ 720 Ceramic Oxide Fiber and a new fiber, Nextel™ 650 Ceramic Oxide Fiber, has been developed specifically for the reinforcement of metal and ceramic matrix composites. This paper summarizes room and high temperature properties for these fibers. The strength of both single filaments and multi-filament rovings of Nextel 610, 650 and 720 fibers was determined between 25 and 250 mm gauge length. Weibull analysis was used to compare the statistical fracture distribution and gauge length dependence of strength. Fiber fracture statistics were in accord with Weibull theory; the effect of diameter variability on the statistical analysis was found to be small. Fractographic analysis on Nextel 610 fiber was used to identify primary fracture-causing defects; defect size was correlated with Griffith fracture predictions.
High temperature single filament strength measurements were performed on Nextel 610, 650 and 720 fibers between 800 and 1400°C. High temperature strength varied inversely with strain rate. In combination with tensile creep tests at 1100 and 1200°C, these were used to compare the elevated temperature capability of each fiber and determine maximum use temperatures. The development of crystalline yttrium aluminum garnet fibers that demonstrate further improvements in creep performance relative to Nextel 720 fibers is also discussed.
[26]
Moser B Rossoll A Weber L et al . Damage evolution of Nextel 610TM alumina fibre reinforced aluminium
Acta Materialia 2004 ,52 (3 ): 573 -581
DOI
URL
[27]
Mall S Nye AR Jefferson G Tension--tension fatigue behavior of Nextel TM 720/Alumina under combustion environment
International Journal of Applied Ceramic Technology 2012 ,9 (1 ): 159 -71
DOI
URL
[本文引用: 1]
Fatigue behavior of Nextel720 (TM)/alumina was investigated under combustion environment, which was then compared with that in laboratory environment. Fatigue strength for 90,000 cycles was equal to 150 MPa under combustion condition, while 170 MPa in laboratory environment. However, normalized fatigue strength (ratio of fatigue strength and ultimate tensile strength) was equal in combustion and laboratory environments. The difference in fatigue strength was due to thermal stresses from impingement of combustion flame on one side of specimen. Fractographic analysis showed that combustion had little effect on fiber/matrix bonding in only flame impingement region. Combustion environment was not thus damaging to Nextel720 (TM)/alumina.
[28]
Arai Y Aoki Y Kagawa Y Effect of cristobalite formation on the delamination resistance of an oxide/Si/(SiC/SiC) environmental barrier coating system after cyclic high temperature thermal exposure
Scripta Materialia 2017 ,139 :58 -62
DOI
URL
[本文引用: 1]
[29]
Yang ZM Liu H Effects of thermal aging on the cyclic thermal shock behavior of oxide/oxide ceramic matrix composites
Materials Science and Engineering$:$ A 2020 ,769 :138494
[本文引用: 1]
[30]
李伟 , 方国东 , 李玮洁 等 . 碳纤维增强复合材料微观烧蚀行为数值模拟
力学学报 , 2019 ,51 (3 ):835 -844
[本文引用: 1]
( Li Wei Fang Guodong Li Weijie et al . Numerical simulation of micro-ablation behavior for carbon fiber reinforced composites
Chinese Journal of Theoretical and Applied Mechanics 2019 ,51 (3 ): 835 -844 (in Chinese))
[本文引用: 1]
[31]
李龙彪 . 纤维增强陶瓷基复合材料疲劳迟滞回线模型研究
力学学报 , 2014 ,46 (5 ): 710 -29
DOI
URL
[本文引用: 1]
纤维增强陶瓷基复合材料初始加载到疲劳峰值应力时, 基体出现裂纹, 纤维/基体界面发生脱粘. 在疲劳载荷作用下, 纤维相对基体在界面脱粘区往复滑移使得陶瓷基复合材料出现疲劳迟滞现象. 建立了纤维陶瓷基复合材料疲劳迟滞回线细观力学模型, 采用断裂力学方法确定了初始加载纤维/基体界面脱粘长度、卸载界面反向滑移长度与重新加载新界面滑移长度, 分析了4种不同界面滑移情况的疲劳迟滞回线. 假设正交铺设与编织陶瓷基复合材料疲劳迟滞回线主要受0°铺层、轴向纱线内纤维/基体界面滑移的影响, 预测了单向、正交铺设与编织陶瓷基复合材料在不同峰值应力与不同循环的疲劳迟滞回线, 与试验结果吻合.
( Li Longbiao Investigation on fatigue hysteresis loops models of fibre-reinforced ceramic-matrix composites
Chinese Journal of Theoretical and Applied Mechanics 2014 ,46 (5 ): 710 -729 (in Chinese))
DOI
URL
[本文引用: 1]
纤维增强陶瓷基复合材料初始加载到疲劳峰值应力时, 基体出现裂纹, 纤维/基体界面发生脱粘. 在疲劳载荷作用下, 纤维相对基体在界面脱粘区往复滑移使得陶瓷基复合材料出现疲劳迟滞现象. 建立了纤维陶瓷基复合材料疲劳迟滞回线细观力学模型, 采用断裂力学方法确定了初始加载纤维/基体界面脱粘长度、卸载界面反向滑移长度与重新加载新界面滑移长度, 分析了4种不同界面滑移情况的疲劳迟滞回线. 假设正交铺设与编织陶瓷基复合材料疲劳迟滞回线主要受0°铺层、轴向纱线内纤维/基体界面滑移的影响, 预测了单向、正交铺设与编织陶瓷基复合材料在不同峰值应力与不同循环的疲劳迟滞回线, 与试验结果吻合.
[32]
王奇志 , 林慧星 , 许赟泉 . 二维编织陶瓷基复合材料偏轴拉伸力学性能预测
复合材料学报 , 2018 ,35 (12 ): 3423 -3432
[本文引用: 1]
( Wang Qizhi Lin Huixing Xu yunquan Mechanical properties prediction of 2D braided ceramic matrix composites under off-axial tension
Acta Materiae Compositae Sinica 2018 ,35 (12 ): 3423 -3432 (in Chinese))
[本文引用: 1]
[33]
Gowayed Y Pierce J Buchanan D et al . Effect of microstructural features and properties of constituents on the thermo-elastic properties of ceramic matrix composites
Composites Part B: Engineering 2018 ,135 :155 -65
DOI
URL
[本文引用: 1]
[34]
Lemaitre J Desmorat R . Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures. Berlin, Heidelberg: Springer-
Verlag Berlin Heidelberg , 2005 : 1 -76
[本文引用: 1]
[35]
Bonora N Newaz G Modeling damage evolution in a hybrid ceramic matrix composite under static tensile load
Journal of Engineering Materials and Technology 1997 ,119 (4 ): 401 -407
DOI
URL
[本文引用: 1]
[36]
郭洪宝 , 王波 , 贾普荣 等 . 平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
力学学报 , 2016 ,48 (2 ):361 -368
DOI
URL
[本文引用: 1]
采用约西佩斯库(Iosipescu)纯剪切试件,研究了平纹编织SiC/SiC和C/SiC复合材料的面内剪切应力-应变行为和细观损伤特性.通过试验获得了材料不同方向上的单调和迟滞应力-应变行为,对比分析了两种材料的剪切损伤特性,结果表明材料的剪切损伤演化规律受热残余应力水平影响严重.由试件断口电镜扫描结果发现剪切加载状态下桥连纤维承受显著的弯曲载荷和变形,据此提出了纤维弯曲承载机制,并结合裂纹闭合效应分阶段阐释了材料的剪切迟滞环形状.基于材料的剪切细观损伤机制,通过两个损伤变量表征了材料的剪切损伤演化进程,得到了材料的面内剪切细观损伤演化模型.对比发现2D-C/SiC复合材料45°方向基体裂纹的起裂应力明显小于2D-SiC/SiC复合材料,而两者0°/90°方向裂纹的起裂应力基本相同.
( Guo Hongbao Wang Bo Jia Purong et al . Mesoscopic damage behaviors of plain woven ceramic composite under in-plane shear loading
Chinese Journal of Theoretical and Applied Mechanics 2016 ,48 (2 ): 361 -368 (in Chinese))
DOI
URL
[本文引用: 1]
采用约西佩斯库(Iosipescu)纯剪切试件,研究了平纹编织SiC/SiC和C/SiC复合材料的面内剪切应力-应变行为和细观损伤特性.通过试验获得了材料不同方向上的单调和迟滞应力-应变行为,对比分析了两种材料的剪切损伤特性,结果表明材料的剪切损伤演化规律受热残余应力水平影响严重.由试件断口电镜扫描结果发现剪切加载状态下桥连纤维承受显著的弯曲载荷和变形,据此提出了纤维弯曲承载机制,并结合裂纹闭合效应分阶段阐释了材料的剪切迟滞环形状.基于材料的剪切细观损伤机制,通过两个损伤变量表征了材料的剪切损伤演化进程,得到了材料的面内剪切细观损伤演化模型.对比发现2D-C/SiC复合材料45°方向基体裂纹的起裂应力明显小于2D-SiC/SiC复合材料,而两者0°/90°方向裂纹的起裂应力基本相同.
[37]
Jagannathan N Gururaja S Manjunatha CM Probabilistic strength based matrix crack evolution in multi-directional composite laminates
Composites Part B$:$ Engineering 2016 ,87 :263 -73
[本文引用: 1]
[38]
Lamon J Thommeret B Percevault C Probabilistic-statistical approach to matrix damage and stress--Strain behavior of 2-D woven SiC/SiC ceramic matrix composites
Journal of the European Ceramic Society 1998 ,18 (13 ): 1797 -808
DOI
URL
[本文引用: 2]
[39]
Lamon J Fiber reinforced ceramic matrix composites: A probabilistic micromechanics-based approach
// Handbook of Mechanics of Materials, S. Schmauder et al ., Editors. 2018 , Springer Singapore: Singapore , 1 -32
[本文引用: 1]
[40]
Bonora N Labarbera A Marchetti M et al . Experimental verification and theoretical simulation of fracture behaviors of composite-materials
Composite Structures 1993 ,23 (2 ): 87 -97
DOI
URL
[本文引用: 1]
[41]
Siron O Pailhes J Lamon J Modelling of the stress/strain behaviour of a carbon/carbon composite with a 2.5 dimensional fiber architecture under tensile and shear loads at room temperature
Composite Science Technology 1999 ,59 (1 ): 1 -12
DOI
URL
[本文引用: 1]
[42]
Mahboob Z Chemisky Y Meraghni F et al . Mesoscale modelling of tensile response and damage evolution in natural fibre reinforced laminates
Composites Part B: Engineering 2017 ,119 :168 -183
DOI
URL
[本文引用: 1]
An elastic--plastic constitutive model for ceramic composite laminates
1
2014
... 在过去的几十年中, 陶瓷基复合材料(ceramic matrix composite, CMC)因能在高温、氧化、疲劳和蠕变等状况下保持良好的力学性能而备受关注, 超高速飞行器的热防护系统、涡轮发动机的火焰筒、涡轮导向叶片、涡轮外环、隔热屏和火焰稳定器 等关键热端静止部件都可应用CMC[1 -3 ] . 国外的诸如综合高性能涡轮发动机技术(integrated high performance turbine engine technology, IHPTET)计划、超高效发动机技术(ultra efficient engine technologies, UEET)和高马赫数涡轮发动机/涡轮基组合循环发动机(high Mach turbine engine/turbine based combined cycle engine, HMTE)等均将CMC作为研究重点[4 ] . 我国的航空发动机及燃气轮机重大专项基础研究项目中也将CMC的本征性能与环境性能相关性等研究列为研究重点. ...
Modeling of damage in unidirectional ceramic matrix composites and multi-scale experimental validation on third generation SiC/SiC minicomposites
2014
The role of oxidation in time-dependent response of ceramic--matrix composites
1
2015
... 在过去的几十年中, 陶瓷基复合材料(ceramic matrix composite, CMC)因能在高温、氧化、疲劳和蠕变等状况下保持良好的力学性能而备受关注, 超高速飞行器的热防护系统、涡轮发动机的火焰筒、涡轮导向叶片、涡轮外环、隔热屏和火焰稳定器 等关键热端静止部件都可应用CMC[1 -3 ] . 国外的诸如综合高性能涡轮发动机技术(integrated high performance turbine engine technology, IHPTET)计划、超高效发动机技术(ultra efficient engine technologies, UEET)和高马赫数涡轮发动机/涡轮基组合循环发动机(high Mach turbine engine/turbine based combined cycle engine, HMTE)等均将CMC作为研究重点[4 ] . 我国的航空发动机及燃气轮机重大专项基础研究项目中也将CMC的本征性能与环境性能相关性等研究列为研究重点. ...
Mechanical behavior of a notched oxide/oxide ceramic matrix composite in combustion environment: Experiments and simulations
1
2015
... 在过去的几十年中, 陶瓷基复合材料(ceramic matrix composite, CMC)因能在高温、氧化、疲劳和蠕变等状况下保持良好的力学性能而备受关注, 超高速飞行器的热防护系统、涡轮发动机的火焰筒、涡轮导向叶片、涡轮外环、隔热屏和火焰稳定器 等关键热端静止部件都可应用CMC[1 -3 ] . 国外的诸如综合高性能涡轮发动机技术(integrated high performance turbine engine technology, IHPTET)计划、超高效发动机技术(ultra efficient engine technologies, UEET)和高马赫数涡轮发动机/涡轮基组合循环发动机(high Mach turbine engine/turbine based combined cycle engine, HMTE)等均将CMC作为研究重点[4 ] . 我国的航空发动机及燃气轮机重大专项基础研究项目中也将CMC的本征性能与环境性能相关性等研究列为研究重点. ...
Model of Oxidation-Induced Fiber Fracture in SiC/SiC Composites
2
2014
... 基于材料成型与制造工艺的发展, 具有较高环境稳定性的氧化物/氧化物CMC和非氧化物CMC已经成为主要的研究对象. 非氧化物CMC, 如SiC/SiC CMC, 虽然在1200$\sim$1350${^\circ}$C的高温环境中具有优越的力学性能, 但是在700$\sim$800${^\circ}$C温度环境中抗氧化性较差, 尤其在水氧环境中极易发生氧化反应, 进而造成其力学性能急剧下降. 尽管已经开发了许多抗氧化涂层系统, 但其高温氧化问题远未得到有效解决[5 -6 ] . 与非氧化物CMC相比, 氧化物/氧化物CMC在1000$\sim$1300${^\circ}$C的高温环境中具有更好的稳定性和抗氧化性能, 因此成为未来航空发动机热端部件的理想候选材料[7 ] . ...
... 由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式. ...
Review: Creep of fibre-reinforced ceramic matrix composites
1
2019
... 基于材料成型与制造工艺的发展, 具有较高环境稳定性的氧化物/氧化物CMC和非氧化物CMC已经成为主要的研究对象. 非氧化物CMC, 如SiC/SiC CMC, 虽然在1200$\sim$1350${^\circ}$C的高温环境中具有优越的力学性能, 但是在700$\sim$800${^\circ}$C温度环境中抗氧化性较差, 尤其在水氧环境中极易发生氧化反应, 进而造成其力学性能急剧下降. 尽管已经开发了许多抗氧化涂层系统, 但其高温氧化问题远未得到有效解决[5 -6 ] . 与非氧化物CMC相比, 氧化物/氧化物CMC在1000$\sim$1300${^\circ}$C的高温环境中具有更好的稳定性和抗氧化性能, 因此成为未来航空发动机热端部件的理想候选材料[7 ] . ...
Microstructure and mechanical behavior of a Nextel TM 610/alumina weak matrix composite subjected to tensile and compressive loadings
1
2017
... 基于材料成型与制造工艺的发展, 具有较高环境稳定性的氧化物/氧化物CMC和非氧化物CMC已经成为主要的研究对象. 非氧化物CMC, 如SiC/SiC CMC, 虽然在1200$\sim$1350${^\circ}$C的高温环境中具有优越的力学性能, 但是在700$\sim$800${^\circ}$C温度环境中抗氧化性较差, 尤其在水氧环境中极易发生氧化反应, 进而造成其力学性能急剧下降. 尽管已经开发了许多抗氧化涂层系统, 但其高温氧化问题远未得到有效解决[5 -6 ] . 与非氧化物CMC相比, 氧化物/氧化物CMC在1000$\sim$1300${^\circ}$C的高温环境中具有更好的稳定性和抗氧化性能, 因此成为未来航空发动机热端部件的理想候选材料[7 ] . ...
Multi-scale constitutive modeling of ceramic matrix composites by continuum damage mechanics
1
2014
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
Continuum modeling of damage in ceramic matrix composites
1
1991
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
Damage mechanisms modeling for ceramic composites
2
1994
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
... 在含损伤的材料中,内力是由材料中的微缺陷以及缺陷之间的相互作用而减少的有效抵抗截面积承受的.又考虑到非弹性变形发生在含损伤的材料的未损伤区域内, 因此,根据Ladevèze等 [10 ,41 ] 的非弹性应变模型,在塑性力学框架下构建非弹性应变累积模型, 引入有效应力张量$\bar { \sigma }$ ...
New progress in micromechanics-based CDM models and their application to CMCs
1
2001
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
A new micromechanics based CDM model and its application to CMC's
1
2002
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
Modelling of the mechanical behavior and damage processes of fibrous ceramic matrix composites: Application to a 2-D SiC/SiC
1
2000
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
Damage characteristics and constitutive modeling of the 2D C/SiC composite: Part I - Experiment and analysis
1
2014
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
Damage characteristics and constitutive modeling of the 2D C/SiC composite: Part II -- Material model and numerical implementation
1
2015
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
An anisotropic elastoplastic damage constitutive model for 3D needled C/C-SiC composites
1
2017
... CDM方法计算效率很高, 对材料结构的渐进损伤分析极为有用[8 ] . 在Talreja[9 ] 提出了描述CMC力学行为的连续介质损伤力学模型, 并且考虑了基体失效, 纤维/基体界面滑移和纤维/基体剥离等损伤机制. Ladev\`{e}ze等[10 ] 提出了描述复合材料损伤机制和本构模型的一般损伤力学方法, 建立了表征材料内部损伤状态的方法并预测了复合材料的应力/应变行为. Chaboche和Maire[11 -12 ] 在热力学框架下, 提出了基于CDM的一般损伤模型, 以描述CMC的非线性与能量耗散行为. 该模型忽略了所有局部的微观特征, 引入最大主应变方向的二阶张量, 通过全局本构和物理方程对材料力学性能进行预测, 并且以SiC/SiC复合材料为研究对象, 进行了单轴/多轴实验, 证实所提模型与实验结果吻合良好. Camus[13 ] 对多轴载荷作用下的二维机织SiC$_{\rm f}$/SiC复合材料力学性能进行了分析, 通过定义基于现象学的内部损伤变量, 建立了损伤本构模型, 该模型可以很好地描述材料在复杂多轴载荷下的非线性力学行为. 李俊等[14 -15 ] 对二维编织C/SiC复合材料在平面应力状态下的损伤和非弹性应变的演化特性以及损伤和失效模式进行了较为系统的试验研究, 并在CDM和塑性力学的理论框架下, 以材料弹性模量的退化程度作为损伤变量, 建立了宏观弹塑性损伤本构模型. 谢军波等[16 ] 建立了一种塑性-损伤相结合的宏观非线性本构模型以对三维针刺C/C-SiC复合材料的非线性力学行为进行描述, 并通过塑性和损伤理论对复合材料的非弹性变形和刚度退化进行了表征. 上述研究工作均是在CDM理论和热力学框架下建立了CMC的本构模型. 然而, 该方法并不能区分纤维/基体以及界面等组分中损伤的发生与演化, 且损伤张量的建立是基于大量的实验数据. ...
Validated progressive damage analysis of simple polymer matrix composite laminates exhibiting matrix microdamage: Comparing macromechanics and micromechanics
1
2016
... MDM方法通过代表性体积元素(representative volume element, RVE)对复合材料各组分在各个加载阶段进行定义与建模, 可区分纤维, 基体以及界面的损伤, 并且对于复合材料中每个组分的损伤萌生与演化均需要建立不同的准则[17 ] . 大量文献中所提的MDM方法之间的差异主要在于RVE的表述以及组分损伤对全局应变影响的表示. Evans等[18 ] 系统地梳理了单向纤维增强CMC的微观结构和力学性能之间的关系, 提出由界面的微观性能来控制材料的韧性, 并在微观力学计算和实验的基础上, 讨论了界面脱粘和滑移阻力等问题. Hsueh[19 ] 分析了单向CMC中纤维/基体界面处的粘结性能, 纤维的泊松效应以及残余应力, 进一步澄清了基体裂纹张开位移与由界面脱粘而产生的位移之间的差异, 并推导了它们与纤维桥接应力的解析表达式. 姚寅和陈少华[20 ] 提出了改进的剪切滞后理论模型, 以研究碳纤维增强复合材料的界面特性和纤维拔出性能, 获得了碳纤维应力的闭式解和界面剪切强度(inter-facial shear strength, IFSS). 然而, 基于剪切滞后的微观力学模型中的一些物理假设与实验所测试的结果还存在一定的偏差, 比如在拉伸试验中观察到基体微裂纹密度随着所施加载荷的增大而增大, 裂纹平行于纤维/基体界面[21 ] . 此外, 如何在涉及多轴应力状态的情况下使用基于剪切滞后微观力学模型尚不清楚. ...
The mechanical behavior of ceramic matrix composites//Proceedings of The 7th International Conference On Fracture(ICF7)
1
1989
... MDM方法通过代表性体积元素(representative volume element, RVE)对复合材料各组分在各个加载阶段进行定义与建模, 可区分纤维, 基体以及界面的损伤, 并且对于复合材料中每个组分的损伤萌生与演化均需要建立不同的准则[17 ] . 大量文献中所提的MDM方法之间的差异主要在于RVE的表述以及组分损伤对全局应变影响的表示. Evans等[18 ] 系统地梳理了单向纤维增强CMC的微观结构和力学性能之间的关系, 提出由界面的微观性能来控制材料的韧性, 并在微观力学计算和实验的基础上, 讨论了界面脱粘和滑移阻力等问题. Hsueh[19 ] 分析了单向CMC中纤维/基体界面处的粘结性能, 纤维的泊松效应以及残余应力, 进一步澄清了基体裂纹张开位移与由界面脱粘而产生的位移之间的差异, 并推导了它们与纤维桥接应力的解析表达式. 姚寅和陈少华[20 ] 提出了改进的剪切滞后理论模型, 以研究碳纤维增强复合材料的界面特性和纤维拔出性能, 获得了碳纤维应力的闭式解和界面剪切强度(inter-facial shear strength, IFSS). 然而, 基于剪切滞后的微观力学模型中的一些物理假设与实验所测试的结果还存在一定的偏差, 比如在拉伸试验中观察到基体微裂纹密度随着所施加载荷的增大而增大, 裂纹平行于纤维/基体界面[21 ] . 此外, 如何在涉及多轴应力状态的情况下使用基于剪切滞后微观力学模型尚不清楚. ...
Matrix cracking with frictional bridging fibres in continuous fibre ceramic composites
1
1995
... MDM方法通过代表性体积元素(representative volume element, RVE)对复合材料各组分在各个加载阶段进行定义与建模, 可区分纤维, 基体以及界面的损伤, 并且对于复合材料中每个组分的损伤萌生与演化均需要建立不同的准则[17 ] . 大量文献中所提的MDM方法之间的差异主要在于RVE的表述以及组分损伤对全局应变影响的表示. Evans等[18 ] 系统地梳理了单向纤维增强CMC的微观结构和力学性能之间的关系, 提出由界面的微观性能来控制材料的韧性, 并在微观力学计算和实验的基础上, 讨论了界面脱粘和滑移阻力等问题. Hsueh[19 ] 分析了单向CMC中纤维/基体界面处的粘结性能, 纤维的泊松效应以及残余应力, 进一步澄清了基体裂纹张开位移与由界面脱粘而产生的位移之间的差异, 并推导了它们与纤维桥接应力的解析表达式. 姚寅和陈少华[20 ] 提出了改进的剪切滞后理论模型, 以研究碳纤维增强复合材料的界面特性和纤维拔出性能, 获得了碳纤维应力的闭式解和界面剪切强度(inter-facial shear strength, IFSS). 然而, 基于剪切滞后的微观力学模型中的一些物理假设与实验所测试的结果还存在一定的偏差, 比如在拉伸试验中观察到基体微裂纹密度随着所施加载荷的增大而增大, 裂纹平行于纤维/基体界面[21 ] . 此外, 如何在涉及多轴应力状态的情况下使用基于剪切滞后微观力学模型尚不清楚. ...
Effects of the longitudinal surface roughness on fiber pull-out behavior in carbon fiber-reinforced epoxy resin composites
2
2013
... MDM方法通过代表性体积元素(representative volume element, RVE)对复合材料各组分在各个加载阶段进行定义与建模, 可区分纤维, 基体以及界面的损伤, 并且对于复合材料中每个组分的损伤萌生与演化均需要建立不同的准则[17 ] . 大量文献中所提的MDM方法之间的差异主要在于RVE的表述以及组分损伤对全局应变影响的表示. Evans等[18 ] 系统地梳理了单向纤维增强CMC的微观结构和力学性能之间的关系, 提出由界面的微观性能来控制材料的韧性, 并在微观力学计算和实验的基础上, 讨论了界面脱粘和滑移阻力等问题. Hsueh[19 ] 分析了单向CMC中纤维/基体界面处的粘结性能, 纤维的泊松效应以及残余应力, 进一步澄清了基体裂纹张开位移与由界面脱粘而产生的位移之间的差异, 并推导了它们与纤维桥接应力的解析表达式. 姚寅和陈少华[20 ] 提出了改进的剪切滞后理论模型, 以研究碳纤维增强复合材料的界面特性和纤维拔出性能, 获得了碳纤维应力的闭式解和界面剪切强度(inter-facial shear strength, IFSS). 然而, 基于剪切滞后的微观力学模型中的一些物理假设与实验所测试的结果还存在一定的偏差, 比如在拉伸试验中观察到基体微裂纹密度随着所施加载荷的增大而增大, 裂纹平行于纤维/基体界面[21 ] . 此外, 如何在涉及多轴应力状态的情况下使用基于剪切滞后微观力学模型尚不清楚. ...
... 为深入了解含循环热冲击预损伤的氧化物/氧化物CMC在单调拉伸载荷下的力学行为和损伤特性,在室温下对含循环热冲击预损伤的氧化物/氧化物CMC开展损伤实验.根据笔者课题组的前期研究[20 ] ,氧化物/氧化物CMC在经历累积8次循环热冲击($T_{\rm shock}=1100~{^\circ}$C)后,由循环热冲击引起的热机械损伤接近饱和. 因此,本工作选定经历了8次循环热冲击的氧化物/氧化物CMC作为研究对象.在MTS809液压伺服拉扭疲劳试验机上进行单调拉伸损伤实验,拉伸试验使用的试件尺寸如图1 所示.在试件标距段内沿试件轴线方向粘贴应变花以同时测量试件在轴向应力$\sigma _x $作用下$x$--$y$全局坐标系下的正应变($\varepsilon _x $和$\varepsilon _y $). 采用位移控制加载方式, 加-卸载过程的应变速率均设定为10$^{ - 4}$ s$^{-1}$, 以保证准静态加载条件. 拉伸载荷由MTS试验机的测试系统实时测得, 同时采用动态信号测试分析系统(DH5922D)以10~Hz的采样频率同步采集试件的应变.使用三维全场变形检测仪(digital image correlation, DIC)对应变测量进行校核.为获得可靠的试验结果, 需要特别注意试件的对中. 对于所有的拉伸试验,如果试件在标距段内断裂, 则认为测试结果有效. ...
Deformation and damage modeling of ceramic matrix composites under multiaxial stresses
1
2016
... MDM方法通过代表性体积元素(representative volume element, RVE)对复合材料各组分在各个加载阶段进行定义与建模, 可区分纤维, 基体以及界面的损伤, 并且对于复合材料中每个组分的损伤萌生与演化均需要建立不同的准则[17 ] . 大量文献中所提的MDM方法之间的差异主要在于RVE的表述以及组分损伤对全局应变影响的表示. Evans等[18 ] 系统地梳理了单向纤维增强CMC的微观结构和力学性能之间的关系, 提出由界面的微观性能来控制材料的韧性, 并在微观力学计算和实验的基础上, 讨论了界面脱粘和滑移阻力等问题. Hsueh[19 ] 分析了单向CMC中纤维/基体界面处的粘结性能, 纤维的泊松效应以及残余应力, 进一步澄清了基体裂纹张开位移与由界面脱粘而产生的位移之间的差异, 并推导了它们与纤维桥接应力的解析表达式. 姚寅和陈少华[20 ] 提出了改进的剪切滞后理论模型, 以研究碳纤维增强复合材料的界面特性和纤维拔出性能, 获得了碳纤维应力的闭式解和界面剪切强度(inter-facial shear strength, IFSS). 然而, 基于剪切滞后的微观力学模型中的一些物理假设与实验所测试的结果还存在一定的偏差, 比如在拉伸试验中观察到基体微裂纹密度随着所施加载荷的增大而增大, 裂纹平行于纤维/基体界面[21 ] . 此外, 如何在涉及多轴应力状态的情况下使用基于剪切滞后微观力学模型尚不清楚. ...
Evolution and characterization of cyclic thermal shock-induced thermomechanical damage in oxide/oxide ceramics matrix composites
3
2019
... 另外, CMC在热机械载荷作用下不可避免地产生了热机械损伤, 关于这种含热机械预损伤材料结构在机械载荷下的力学行为和损伤特性的描述和研究还未见文献报道[22 -24 ] . ...
... (1)初始损伤$d^0$. 由于原始材料中的初始损伤量很难测量, 通常假设$d^0 = 0$. 然而, 本课题所研究的是含循环热冲击预损伤的氧化物/氧化物CMC, 那么,材料的初始损伤即为材料经历循环热冲击作用而产生的热机械损伤, 具体热机械损伤的量化模型在先前研究中已经做了详细的论述[22 ] . ...
... 当累积应变超过$\varepsilon _{{\rm th}} $时, 损伤开始出现并不断增大, 随着应变的持续增大,材料达到临界损伤状态而出现断裂失效. 需要说明的是,由于材料含有循环热冲击的热机械损伤, 损伤并没有从零开始,图中损伤的起点是材料经历循环热冲击后的热机械损伤值,关于热机械损伤的确定在作者的前期论文中有详细论述[22 ] ; 另外,为了验证所提模型的适用性,图7 给出了含4次循环热冲击预损伤的CMC在机械载荷下的损伤演化曲线,结果表明所提模型可以很好地描述含不同预损伤的CMC在机械载荷下的力学行为. ...
Representation of micro-structural evolution and thermo-mechanical damage in thermal shocked oxide/oxide ceramic matrix composites
2019
Micro-porosity as damage indicator for characterizing cyclic thermal shock-induced anisotropic damage in oxide/oxide ceramic matrix composites
3
2019
... 另外, CMC在热机械载荷作用下不可避免地产生了热机械损伤, 关于这种含热机械预损伤材料结构在机械载荷下的力学行为和损伤特性的描述和研究还未见文献报道[22 -24 ] . ...
... 本文所用材料Nextel$^{\rm TM}$ 610纤维(99% $\alpha$-Al$_{2}$O$_{3})$编织于Al$_{2}$O$_{3}$-ZrO$_{2}$-SiO$_{2}$基体中的氧化物/氧化物CMC. 原材料板材由八条缎纹编织(8HSW)布用精细Al$_{2}$O$_{3}$基体浸渍, 然后, 将8层单独的预浸布以 [0/90]$_{\rm 2S}$彼此堆叠烧结而成, 板厚为2.8 mm. 材料密度约为2.71~g/mm$^{3}$, 纤维体积分数约为44%, 基体的组成成分为氧化铝(质量分数为85\%)和3 mol/mol 氧化钇(质量分数为15\%)稳定氧化锆(3 mol/mol Yttria-stabilized monoclinic and tetragonal ZrO$_{2}$, 3YSZ), 属于典型的多孔基体CMC[24 -25 ] . ...
... 除了${0^ \circ }/{90^ \circ }$正轴向试件的损伤试验, 还开展了$\pm 45^ \circ $偏轴试件的损伤试验, 并根据ASTM 3518测试标准, 得到材料面内剪切模量$G_{12} $. 对于$\pm 45^ \circ $偏轴试件, 剪切模量$G_{12} $可通过轴向应变$\varepsilon _x $和横向应变$\varepsilon _y $得到[24 ,33 ] ...
High performance oxide fibers for metal and ceramic composites
1
2001
... 本文所用材料Nextel$^{\rm TM}$ 610纤维(99% $\alpha$-Al$_{2}$O$_{3})$编织于Al$_{2}$O$_{3}$-ZrO$_{2}$-SiO$_{2}$基体中的氧化物/氧化物CMC. 原材料板材由八条缎纹编织(8HSW)布用精细Al$_{2}$O$_{3}$基体浸渍, 然后, 将8层单独的预浸布以 [0/90]$_{\rm 2S}$彼此堆叠烧结而成, 板厚为2.8 mm. 材料密度约为2.71~g/mm$^{3}$, 纤维体积分数约为44%, 基体的组成成分为氧化铝(质量分数为85\%)和3 mol/mol 氧化钇(质量分数为15\%)稳定氧化锆(3 mol/mol Yttria-stabilized monoclinic and tetragonal ZrO$_{2}$, 3YSZ), 属于典型的多孔基体CMC[24 -25 ] . ...
Damage evolution of Nextel 610TM alumina fibre reinforced aluminium
2004
Tension--tension fatigue behavior of Nextel TM 720/Alumina under combustion environment
1
2012
... 由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式. ...
Effect of cristobalite formation on the delamination resistance of an oxide/Si/(SiC/SiC) environmental barrier coating system after cyclic high temperature thermal exposure
1
2017
... 由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式. ...
Effects of thermal aging on the cyclic thermal shock behavior of oxide/oxide ceramic matrix composites
1
2020
... 由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式. ...
碳纤维增强复合材料微观烧蚀行为数值模拟
1
2019
... 由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式. ...
碳纤维增强复合材料微观烧蚀行为数值模拟
1
2019
... 由于高温力学性能测试技术等的限制, 实现循环热冲击实验与材料单调拉伸损伤实验同步进行极为困难. 目前已有文献报道使用机械加载耦合燃气环境试验台来评估CMC力学性能以及CMC结构件的环境耐久性与适用性[27 -28 ] . 然而, 这样的评估与考核实验成本极其昂贵, 并且也不利于对机械加载耦合燃气环境中造成材料损伤的众多因素的各自贡献进行准确评估. 另一方面, 在燃烧火焰的灼烧下, 试件的迎火焰面(正面)产生了压缩应力, 而背面产生了拉伸应力, 与此同时局部热应力梯度降低了材料基体裂纹的萌生与扩展的应力阈值, 从而加剧了材料力学性能退化. 尤其需要注意的是, 对于非氧化物CMC, 过早的基体开裂为氧的扩散提供了通道, 从而加快了材料的损伤与失效[5 ,29 -30 ] , 因此, 机械加载耦合燃气环境试验台并不是CMC材料级力学性能评价的最佳方式. ...
纤维增强陶瓷基复合材料疲劳迟滞回线模型研究
1
2014
... 由于卸载-再加载过程被控制在一个很小的应变范围内且循环次数少,故忽略整个加载历程中的疲劳损伤效应[31 -32 ] . 需要注意的是,在卸载和再加载路径上的有效弹性特性仅取决于材料当前的损伤状态. 实验证实,卸载阶段测量的弹性模量在数值上与再加载阶段相同,说明测量所得的弹性模量值是可靠的. ...
纤维增强陶瓷基复合材料疲劳迟滞回线模型研究
1
2014
... 由于卸载-再加载过程被控制在一个很小的应变范围内且循环次数少,故忽略整个加载历程中的疲劳损伤效应[31 -32 ] . 需要注意的是,在卸载和再加载路径上的有效弹性特性仅取决于材料当前的损伤状态. 实验证实,卸载阶段测量的弹性模量在数值上与再加载阶段相同,说明测量所得的弹性模量值是可靠的. ...
二维编织陶瓷基复合材料偏轴拉伸力学性能预测
1
2018
... 由于卸载-再加载过程被控制在一个很小的应变范围内且循环次数少,故忽略整个加载历程中的疲劳损伤效应[31 -32 ] . 需要注意的是,在卸载和再加载路径上的有效弹性特性仅取决于材料当前的损伤状态. 实验证实,卸载阶段测量的弹性模量在数值上与再加载阶段相同,说明测量所得的弹性模量值是可靠的. ...
二维编织陶瓷基复合材料偏轴拉伸力学性能预测
1
2018
... 由于卸载-再加载过程被控制在一个很小的应变范围内且循环次数少,故忽略整个加载历程中的疲劳损伤效应[31 -32 ] . 需要注意的是,在卸载和再加载路径上的有效弹性特性仅取决于材料当前的损伤状态. 实验证实,卸载阶段测量的弹性模量在数值上与再加载阶段相同,说明测量所得的弹性模量值是可靠的. ...
Effect of microstructural features and properties of constituents on the thermo-elastic properties of ceramic matrix composites
1
2018
... 除了${0^ \circ }/{90^ \circ }$正轴向试件的损伤试验, 还开展了$\pm 45^ \circ $偏轴试件的损伤试验, 并根据ASTM 3518测试标准, 得到材料面内剪切模量$G_{12} $. 对于$\pm 45^ \circ $偏轴试件, 剪切模量$G_{12} $可通过轴向应变$\varepsilon _x $和横向应变$\varepsilon _y $得到[24 ,33 ] ...
Engineering Damage Mechanics: Ductile, Creep, Fatigue and Brittle Failures. Berlin, Heidelberg: Springer-
1
2005
... 根据Lemaitre的连续介质损伤力学理论[34 ] , 材料损伤$D$用材料弹性模量的降低来定义 ...
Modeling damage evolution in a hybrid ceramic matrix composite under static tensile load
1
1997
... 对于正轴向$90^ \circ $拉伸损伤变量$d_2 $和面内剪切损伤变量$d_6$也同样存在类似上述机械损伤演化过程. 由此, 对于弹脆性材料,其机械损伤和所施加应变之间存在幂律演化律, 其损伤可简单表达为[35 ] ...
平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
1
2016
... 在拉伸试验期间主要产生3种类型损伤: (1)纤维内微裂纹, 在轴向拉伸试验中, 其产生于两个相互垂直的纤维丝束之间; (2)基体开裂与纤维断裂,CMC力学性能受材料在成型和加工过程中产生的基体微裂纹和热残余应力的影响,由于基体内的热残余应力和拉伸应力相互叠加, 导致脆性基体开裂;在基体微裂纹扩展时, 由于裂纹尖端场的应力集中, 导致纤维断裂[36 ] ;(3)界面滑移, 由于循环热冲击导致局部基体/纤维界面分层,基体微裂纹在界面处发生偏转, 使得纤维和基体在加-卸载作用下, 发生界面滑移.预先存在的基体裂纹和分层等损伤在拉伸载荷作用下产生滑动摩擦,从而导致能量耗散并导致材料最终失效. ...
平纹编织陶瓷基复合材料面内剪切细观损伤行为研究
1
2016
... 在拉伸试验期间主要产生3种类型损伤: (1)纤维内微裂纹, 在轴向拉伸试验中, 其产生于两个相互垂直的纤维丝束之间; (2)基体开裂与纤维断裂,CMC力学性能受材料在成型和加工过程中产生的基体微裂纹和热残余应力的影响,由于基体内的热残余应力和拉伸应力相互叠加, 导致脆性基体开裂;在基体微裂纹扩展时, 由于裂纹尖端场的应力集中, 导致纤维断裂[36 ] ;(3)界面滑移, 由于循环热冲击导致局部基体/纤维界面分层,基体微裂纹在界面处发生偏转, 使得纤维和基体在加-卸载作用下, 发生界面滑移.预先存在的基体裂纹和分层等损伤在拉伸载荷作用下产生滑动摩擦,从而导致能量耗散并导致材料最终失效. ...
Probabilistic strength based matrix crack evolution in multi-directional composite laminates
1
2016
... 在单轴拉伸载荷下, 纤维在承载中占主导地位,基体裂纹诱发的材料缺陷随机分布在基体和纤维中,而且基体裂纹和纤维断裂失效也呈随机脆性失效特征,其断裂概率受应力-应变状态影响显著. 文献表明[37 -38 ] ,基于断裂统计理论的Weibull脆性断裂方法适用于弹脆性材料在单轴应力状态下的损伤本构建模. ...
Probabilistic-statistical approach to matrix damage and stress--Strain behavior of 2-D woven SiC/SiC ceramic matrix composites
2
1998
... 在单轴拉伸载荷下, 纤维在承载中占主导地位,基体裂纹诱发的材料缺陷随机分布在基体和纤维中,而且基体裂纹和纤维断裂失效也呈随机脆性失效特征,其断裂概率受应力-应变状态影响显著. 文献表明[37 -38 ] ,基于断裂统计理论的Weibull脆性断裂方法适用于弹脆性材料在单轴应力状态下的损伤本构建模. ...
... Lamon等[38 -39 ] 将单个纤维的失效概率推广到编织CMC结构中,对于纤维数量为$n$的编织纤维CMC结构, 设断裂失效的纤维数量为$nb = nP_{{\rm FL}} $, 那么未断裂失效的纤维数量为$n - nb = n\left( {1 - P_{{\rm FL}} } \right)$. 假设编织CMC结构中包含有纤维的代表性体积单元的弹性模量为$E_0 $, 施加在试件上的载荷为$F=\sum_{i}\sigma_iA_0$. 由于断裂失效的纤维不承载, 则$\sigma _i = 0$, 而未断裂失效的纤维承担的载荷为$\sigma _i = \varepsilon E_0 $, 那么对于整个含损伤的材料, 其承担载荷为 ...
Fiber reinforced ceramic matrix composites: A probabilistic micromechanics-based approach
1
2018
... Lamon等[38 -39 ] 将单个纤维的失效概率推广到编织CMC结构中,对于纤维数量为$n$的编织纤维CMC结构, 设断裂失效的纤维数量为$nb = nP_{{\rm FL}} $, 那么未断裂失效的纤维数量为$n - nb = n\left( {1 - P_{{\rm FL}} } \right)$. 假设编织CMC结构中包含有纤维的代表性体积单元的弹性模量为$E_0 $, 施加在试件上的载荷为$F=\sum_{i}\sigma_iA_0$. 由于断裂失效的纤维不承载, 则$\sigma _i = 0$, 而未断裂失效的纤维承担的载荷为$\sigma _i = \varepsilon E_0 $, 那么对于整个含损伤的材料, 其承担载荷为 ...
Experimental verification and theoretical simulation of fracture behaviors of composite-materials
1
1993
... 由式(12)可知, CMC的机械损伤是关于所施加应变的单调函数,即每个应变水平对应唯一的损伤状态,直接反映了CMC基体裂纹和纤维断裂随机脆性失效的微观损伤机制. 然而,式(12)并不能完全反映含预损伤材料的损伤特性: (1)氧化物/氧化物CMC的机械损伤发生在一定的应变水平下,即该应变水平使得材料发生基体开裂; (2)材料的损伤状态受初始损伤$d^0$和材料断裂失效时的临界损伤$d^{{\rm cr}}$控制. 鉴于此, 引入初始损伤$d^0$, 考虑临界断裂失效损伤$d^{{\rm cr}}$和应变阈值$\varepsilon _{{\rm th}} $[40 ] , 将CMC的损伤表达式(12)写为 ...
Modelling of the stress/strain behaviour of a carbon/carbon composite with a 2.5 dimensional fiber architecture under tensile and shear loads at room temperature
1
1999
... 在含损伤的材料中,内力是由材料中的微缺陷以及缺陷之间的相互作用而减少的有效抵抗截面积承受的.又考虑到非弹性变形发生在含损伤的材料的未损伤区域内, 因此,根据Ladevèze等 [10 ,41 ] 的非弹性应变模型,在塑性力学框架下构建非弹性应变累积模型, 引入有效应力张量$\bar { \sigma }$ ...
Mesoscale modelling of tensile response and damage evolution in natural fibre reinforced laminates
1
2017
... 和与塑性耗散能(塑性功)$W_{\rm p} $相关的有效非弹性应变率张量[42 ] ...