引 言
在当前世界能源格局中, 天然气的重要地位日渐凸显[1 ] . 中国南海海域就蕴藏着丰富的天然气资源[2 -3 ] . 南海许多气田位于深海海域, 勘探和开发难度很大. 利用浮式液化天然气(floating liquified natural gas, FLNG)平台进行深海气田开发是一种可行的方案. FLNG平台多采用船形设计, 在运行期间会长期漂浮在气田上方海面, 并利用体内若干巨型液舱来储存液化后的天然气.
为保证FLNG平台的海上作业安全, 在设计阶段必须对两个重要的水动力问题进行分析: 一是浮式结构物与波浪之间的相互作用问题, 二是各液舱内晃荡液体与浮式结构物的相互作用问题. 实际上, 这两个问题会借由浮体运动进一步耦合起来. 具体而言, 外部波浪会激发浮体运动, 浮体运动会引起各液舱内液体的晃荡; 与此同时, 液体晃荡力会瞬间反作用于浮体而影响其运动, 进而影响外部波浪场. 因此, 浮式结构物与外部波浪场以及各个液舱内的晃荡液体组成了一个耦合的力学系统, 系统各部分的运动是瞬间相互决定的. 如何对多液舱浮式结构物的运动进行准确的数值预报, 是FLNG平台设计阶段的一个重要问题.
第一类是频域方法. 代表性工作包括Molin等[4 ] , Malenica等[5 ] 和Newman[6 ] , 后两者也分别被水动力学软件HYDROSTAR和WAMIT所采用. 频域方法主要在线性势流理论的框架下考虑浮体运动和液舱晃荡问题, 通常能对非共振工况给出有效的预报结果. 但受限于稳态假设, 频域方法对共振工况的预报结果往往需要校准, 该局限性已在实验中显现[7 ] . Malenica等[5 ] 在数值模型中引入人工阻尼项来校准计算结果, 但阻尼系数的选取仍依赖物理模型实验.
第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统.
针对多液舱浮式结构物的运动模拟问题, 本文将引入一种有效的时域解耦算法[25 ] . 该方法以模态分解法为基础, 通过对浮式结构物所受外场水动力和各液舱内非线性晃荡力进行模态分解, 形成时域解耦运动方程, 无需迭代过程即可显式计算浮式结构物的瞬时加速度. 该方法可以避免迭代过程在迭代次数、截断误差和收敛特性等方面的限制, 并大大减少解决耦合效应的时间消耗. 本文将基于边界元数值方法, 对单液舱浮式结构物和多液舱浮式结构物的分别开展运动模拟, 验证该算法的有效性, 并对带液舱浮式结构物的运动特性进行分析.
1 数学公式
1.1 问题描述
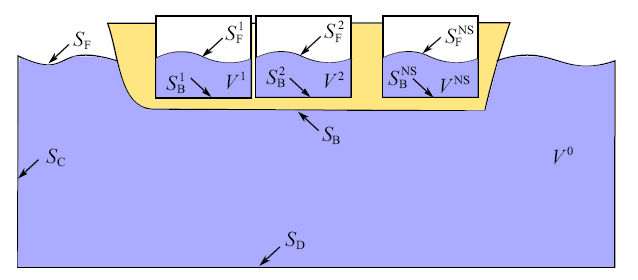
如图1 所示, 考虑一个带有$N_{\rm s} $个液舱的浮体, 该模型共包含$\left( {N_{\rm s} + 1} \right)$个计算流域. 外场流域$V^0$的边界为: 自由水面$S_{\rm F}^0 $, 浮体湿表面$S_{\rm B}^0 $, 水底$S_{\rm D} $和远场边界$S_{\rm C} $. 在第$k$个液舱, 流域、自由表面和液舱湿表面分别用$V^k$, $S_{\rm F}^k $和$S_{\rm B}^k $表示. 后文用上标$k$标记各个流域. 定义大地坐标系$O_o$-$x_o y_o z_o $和运动坐标系$O$-$xyz$, 其中原点$O$位于浮体质心位置. 初始时刻浮体保持静止, 两个坐标系彼此重合, $x$轴从FLNG平台艏部指向尾部, $z$轴垂直向上.
图1
图1
多液舱浮式结构物的流域示意图
Fig.1
Sketch of floating vessel with liquid tanks
浮体和液舱壁均是刚性的. 浮体可进行6个自由度(degree of freedom, DOF)的运动, 其平移和旋转运动可以分别由$O_o$-$x_o y_o z_o $下的牛顿方程和$O$-$xyz$下的欧拉方程确定, 即
(1) $\left. \begin{array}{l@{\quad}l} \bar{M}a + \left\{\begin{array}{*{20}c} 0\\ 0\\ 0\\ \varOmega \times (\bar{I}\varOmega)\\ \end{array}\right\} = \left\{\begin{array}{l} F_{\rm d} \\ M_{\rm d} \\ \end{array} \right\} + \left\{ \begin{array}{l} F_{\rm s} \\ M_{\rm s} \\ \end{array} \right\} + \left\{ \begin{array}{l} F_{\rm e} \\ M_{\rm e} \\ \end{array} \right\} \\\bar{M} = \left[\begin{array}{*{20}c} m & & & & & \\ & m & & & 0 & \\ & & m & & & \\ & & & {I_{{\rm xx}} } & {I_{{\rm xy}} } & {I_{{\rm xz}} } \\ & 0 & & {I_{{\rm yx}} } & {I_{{\rm yy}} } & {I_{{\rm yz}} } \\ & & & {I_{{\rm zx}} } & {I_{{\rm zy}} } & {I_{{\rm zz}} } \\ \end{array} \right]\\ \bar{I} = \left[ \begin{array}{*{20}c} {I_{{\rm xx}} } \hfill & {I_{{\rm xy}} } \hfill & {I_{{\rm xz}} } \hfill \\ {I_{{\rm yx}} } \hfill & {I_{{\rm yy}} } \hfill & {I_{{\rm yz}} } \hfill \\ {I_{{\rm zx}} } \hfill & {I_{{\rm zy}} } \hfill & {I_{{\rm zz}} } \hfill \\ \end{array} \right]\\ a = \left\{ {\dot{v}_{\rm c} ,\dot{\varOmega }} \right\}^{\rm T} \end{array} \right\}$
其中, $m$是船体质量, $I_{{\rm xx}} $到$I_{{\rm zz}} $是转动惯量, $\dot{ v}_{\rm c} = \left\{ {a_1 ,a_2 ,a_3 } \right\} = \left\{ {\dot{v}_1 ,\dot{v}_2 ,\dot{v}_3 } \right\} = \left\{ {\ddot {x}_1 ,\ddot {x}_2 ,\ddot {x}_3 } \right\}$是浮体质心的加速度, $\dot{\varOmega } = \left\{ {a_4 ,a_5 ,a_6 } \right\} = \left\{ {\dot{v}_4 ,\dot{v}_5 ,\dot{v}_6 } \right\}$是浮体角加速度, $\left\{ { F_{\rm d} , M_{\rm d} } \right\} = \left\{ {F_1 ,F_2 ,F_3 ,F_4 ,F_5 ,F_6 } \right\}$代表$V^0$中的水动力/力矩, $\left\{ { F_{\rm s} , M_{\rm s} } \right\}$是液体晃荡产生的力/力矩, $\left\{ { F_{\rm e} , M_{\rm e} }\right\}$表示由重力、系泊系统等外部因素引起的力/力矩. 下标1$\sim$3表示$O_o$-$x_o y_o z_o $下的平移运动相关量, 下标4$\sim$6表示$O$-$xyz$下的旋转运动相关量.
通过在浮体湿表面$S_{\rm B}^0 $上进行压力积分可以得到$\left\{ { F_{\rm d} , M_{\rm d} } \right\}$. 假定流体无黏、不可压缩且运动无旋, 压力可由势流理论下的伯努利方程得到. $\left\{ { F_{\rm d} , M_{\rm d} } \right\}$的表达式为
(2) $\begin{eqnarray} \label{eq2} &&\left\{ {\begin{array}{l} F_{\rm d} \\ M_{\rm d} \\ \end{array}} \right\} = - \rho ^0\displaystyle\iint\limits_{S_{\rm B}^0 } \left( {\frac{\partial \varphi }{\partial t} + \frac{1}{2}\nabla _o \varphi \nabla _o \varphi + gz_o } \right)\cdot \\&&\qquad\left\{ {\begin{array}{c} n \\ r\times n \\ \end{array}} \right\}{\rm d}S \end{eqnarray}$
其中, $\rho ^0$为水体密度, $\varphi \left( {x,y,z,t} \right)$是速度势标量, 其梯度是流体速度, $ r = \left\{ {x,y,z} \right\}$是位置向量, $ n = \left\{ {n_1 ,n_2 ,n_3 } \right\}$表示边界上指向流域外侧的单位法向量, $ r\times n = \left\{ {n_4 ,n_5 ,n_6 } \right\}$. 速度势$\varphi $由下面边值问题确定
(3) $\begin{eqnarray} &&\nabla _o^2 \varphi = 0,\ \mbox{in}\ V^0 \end{eqnarray}$
(4) $\begin{eqnarray} \frac{\partial \varphi }{\partial n} = v_{\rm c} \cdot n + \varOmega \cdot \left( {r\times n} \right) = \sum\limits_{i = 1}^6 {v_i n_i } ,\ \mbox{on}\ S_{\rm B}^0 \end{eqnarray}$
(5) $\begin{eqnarray} \frac{\partial \eta _o }{\partial t} = \frac{\partial \varphi }{\partial z_o } - \frac{\partial \varphi }{\partial x_o }\frac{\partial \eta _o }{\partial x_o } - \frac{\partial \varphi }{\partial y_o }\frac{\partial \eta _o }{\partial y_o },\ \mbox{on}\ S_{\rm F}^0 \end{eqnarray}$
(6) $\begin{eqnarray} \frac{\partial \varphi }{\partial t} = - g\eta _o - \frac{1}{2}\nabla _o \varphi \cdot \nabla _o \varphi ,\ \mbox{on}\ S_{\rm F}^0 \end{eqnarray}$
(7) $\begin{eqnarray} \frac{\partial \varphi }{\partial n} = \frac{\partial \varphi _{\rm I} }{\partial n},\ \mbox{on}\ S_{\rm C} \end{eqnarray}$
(8) $\begin{eqnarray} \frac{\partial \varphi }{\partial n} = 0,\ \mbox{on}\ S_{\rm D} \end{eqnarray}$
其中, $\eta _o \left( {x_o ,y_o ,t} \right)$表示自由表面升高, 下标$\mbox{I}$表示与入射波的相关量. 采用式(7)时, 须在靠近$S_{\rm C}$处的自由面条件中添加阻尼区以耗散外传波浪. 求解该边值问题可以得到式(2)的速度势及其梯度值. 式(2)的时间导数项${\partial \varphi }/{\partial t}$或$\varphi _t $, 可由下列边值问题求得
(9) $\begin{eqnarray} &&\nabla _o^2 \varphi _t = 0,\ \mbox{in}\ V^0 \end{eqnarray}$
(10) $\begin{eqnarray} \varphi _t = - gz_o - \frac{1}{2}\nabla _o \varphi \nabla _o \varphi ,\ \mbox{on}\ S_{\rm F}^0 \end{eqnarray}$
(11) $\begin{eqnarray} \frac{\partial \varphi _t }{\partial n} = \sum\limits_{i = 1}^6 {a_i n_i } - v_{\rm c} \cdot \frac{\partial \nabla _o \varphi }{\partial n} +\\ \varOmega \cdot \frac{\partial }{\partial n}\left[ {r\times \left( {v_{\rm c} - \nabla _o \varphi } \right)} \right],\ \mbox{on}\ S_{\rm B}^0 \end{eqnarray}$
(12) $\begin{eqnarray} \frac{\partial \varphi _t }{\partial n} = \frac{\partial ^2\varphi _{\rm I} }{\partial n\partial t},\ \mbox{on}\ S_{\rm C} \end{eqnarray}$
(13) $\begin{eqnarray} \frac{\partial \varphi _t }{\partial n} = 0,\ \mbox{on}\ S_{\rm D} \end{eqnarray}$
在液舱湿表面$S_{\rm B}^k $上进行压力积分可得到$\left\{ {F_{\rm s} ,M_{\rm s} } \right\}$. 对于液舱$k$, 可在运动坐标系下将速度势的边值问题表示为
(14) $\begin{eqnarray} \nabla ^2\varphi = 0,\ \mbox{in}\ V^k \end{eqnarray}$
(15) $\begin{eqnarray} \dfrac{\partial \eta }{\partial t} + \left( {v_{\rm c} + \varOmega \times r} \right) \cdot \left\{ { - \dfrac{\partial \eta }{\partial x}, - \dfrac{\partial \eta }{\partial y},1} \right\} + \dfrac{\partial \varphi }{\partial x}\dfrac{\partial \eta }{\partial x} +\\ \qquad \dfrac{\partial \varphi }{\partial y}\dfrac{\partial \eta }{\partial y} - \dfrac{\partial \varphi }{\partial z} = 0,\ \mbox{on}\ S_{\rm F}^k \end{eqnarray}$
(16) $\begin{eqnarray} \dfrac{\partial \varphi }{\partial t} - \left( {v_{\rm c} + \varOmega \times r} \right) \cdot \nabla \varphi + \dfrac{1}{2}\nabla \varphi \cdot \nabla \varphi + gz_{\rm c} +\\ \qquad g\left( {T_{31} x + T_{32} y + T_{33} \eta } \right) = 0 ,\ \mbox{on}\ S_{\rm F}^k \end{eqnarray}$
(17) $\begin{eqnarray} \dfrac{\partial \varphi }{\partial n} = \sum\limits_{i = 1}^6 {v_i n_i },\ \mbox{on}\ S_{\rm B}^k \end{eqnarray}$
其中, $\eta \left( {x,y,t} \right)$表示在运动坐标系下的自由表面升高, $T_{31} = - \cos \alpha _1 \sin \alpha _2 \cos \alpha _3 + \sin \alpha _1 \sin \alpha _3 $, $T_{32} = \cos \alpha _1 \sin \alpha _2 \sin \alpha _3 + \sin \alpha _1 \cos \alpha _3 $, $T_{33} = \cos \alpha _1 \cos \alpha _2 $, $\alpha _1 $, $\alpha _2 $和$\alpha _3 $为表征浮体姿态的欧拉角. 各液舱中$\varphi _t $的边界值问题与式(9)$\sim\!$式(11)相同, 只需将$V^0$, $S_{\rm F}^0 $和$S_{\rm B}^0 $替换为$V^k$, $S_{\rm F}^k $和$S_{\rm B}^k $.
由式(11)可见, $\varphi_t$的边界条件包含未知的浮体瞬时加速度$a_i $, 如何处理$\varphi _t $是对多液舱浮式结构物进行运动解耦的关键.
1.2 无液舱浮体运动模拟的时域解耦方法
第一种是迭代法[26 -27 ] . 迭代过程首先预估浮体加速度或所受水动力, 求解浮体运动方程后更新浮体加速度或水动力. 反复进行该过程, 当加速度或水动力收敛至稳定值时, 终止迭代过程. 该方法思路简单, 但有引言所述缺点.
第二种是隐式边界条件法[28 -29 ] . 该方法核心思想是将浮体加速度$a = \bar{M}^{ - 1}\left( {F_{\rm d} + F_{\rm e} } \right)$代入$\varphi _t $的边界条件, 形成关于$\varphi _t $的显式边值问题, 求解可得流域边界上的$\varphi _t $值, 进而计算当前时刻浮体所受水动力和浮体加速度. 该方法避免了迭代过程, 但需要为$\varphi _t $与$\varphi $分别构建具有不同系数矩阵的线性方程组, 系数矩阵元素表达式复杂. 当引入多个液舱时, 这种不便性将更加突出.
第三种是模态分解方法[30 -32 ] . 该方法首先将$\varphi _t$中各加速度项显式分离出来, 形成多模态求和的形式
(18) $\begin{eqnarray}\varphi _t = \sum\limits_{i = 1}^6 {\varPsi_i a_i } + \overline{\varphi _t } \end{eqnarray}$
(19) $\begin{eqnarray} \nabla _o^2 \varPsi _i = 0,\ \mbox{in}\ V^0 \end{eqnarray}$
(20) $\begin{eqnarray} \varPsi _i = 0,\ \mbox{on}\ S_{\rm F}^0 \end{eqnarray}$
(21) $\begin{eqnarray} \frac{\partial \varPsi _i }{\partial n} = n_i ,\ \mbox{on}\ S_{\rm B}^0 \end{eqnarray}$
(22) $\begin{eqnarray} \frac{\partial \varPsi _i }{\partial n} = 0,\ \mbox{on}\ S_{\rm C} \ \mbox{and}\ S_{\rm D} \end{eqnarray}$
根据$\varphi _t $的边值问题, 可相应得到$\overline {\varphi _t } $的边值问题
(23) $\begin{eqnarray} \nabla _o^2 \overline {\varphi _t } = 0,\ \mbox{in}\ V^0 \end{eqnarray}$
(24) $\begin{eqnarray} \overline {\varphi _t } = - gz_o - \frac{1}{2}\nabla _o \varphi \nabla _o \varphi ,\ \mbox{on}\ S_{\rm F}^0 \end{eqnarray}$
(25) $\begin{eqnarray} \frac{\partial \overline {\varphi _t } }{\partial n} = - v_{\rm c} \cdot \frac{\partial \nabla _o \varphi }{\partial n} + \\ \qquad \varOmega \cdot \frac{\partial }{\partial n}\left[ {r\times \left( {v_{\rm c} - \nabla _o \varphi } \right)} \right],\ \mbox{on}\ S_{\rm B}^0 \end{eqnarray}$
(26) $\begin{eqnarray} \frac{\partial \overline {\varphi _t } }{\partial n} = \frac{\partial ^2\varphi _{\rm I} }{\partial n\partial t},\ \mbox{on}\ S_{\rm C} \end{eqnarray}$
(27) $\begin{eqnarray} \frac{\partial \overline {\varphi _t } }{\partial n} = 0,\ \mbox{on}\ S_{\rm D} \end{eqnarray}$
(28a) $\begin{eqnarray} && \left\{ {\begin{array}{l} F_{\rm d} \\ M_{\rm d} \\ \end{array}} \right\} = - \rho ^0\bar{A}^0 a - \rho ^0 U^0\\ \end{eqnarray}$
(28b) $\begin{eqnarray} U^0 = \left\{ {U_1^0 ,U_2^0 ,U_3^0 ,U_4^0 ,U_5^0 ,U_6^0 } \right\}^{\rm T} \\ \end{eqnarray}$
(28c) $\begin{eqnarray} \bar{A}^0 = \left[ {{\begin{array}{*{20}c} {A_{11}^0 } & {A_{12}^0 } & \cdots & {A_{16}^0 } \\ {A_{21}^0 } & {A_{22}^0 } & \cdots & {A_{26}^0 } \\ \vdots & \vdots & & \vdots \\ {A_{61}^0 } & {A_{62}^0 } & \cdots & {A_{66}^0 } \\ \end{array} }} \right] \\ \end{eqnarray}$
(28d) $\begin{eqnarray} \bar{A}^0 = \left[ {{\begin{array}{*{20}c} {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _1 } n_1 \mbox{d}S} & {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _2 } n_1 \mbox{d}S} & \cdots & {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _6 } n_1 \mbox{d}S} \\ {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _1 } n_2 \mbox{d}S} & {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _2 } n_2 \mbox{d}S} & \cdots & {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _6 } n_2 \mbox{d}S} \\ \vdots & \vdots & & \vdots \\ {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _1 } n_6 \mbox{d}S} & {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _2 } n_6 \mbox{d}S} & \cdots & {\displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _6 } n_6 \mbox{d}S} \\ \end{array} }} \right] \\ \end{eqnarray}$
其中, $A_{ij}^0 = \displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _j n_i \mbox{d}S} $, $U_i^0 = \displaystyle\iint\limits_{S_{\rm B}^0 } {\overline {\varphi _t } n_i \mbox{d}S} + \displaystyle\iint\limits_{S_{\rm B}^0 } {\left( {\dfrac{1}{2}\nabla _o \varphi \nabla _o \varphi + gz_o } \right)n_i \mbox{d}S} $. 根据格林公式
(29) $\begin{eqnarray} \displaystyle\iint\limits_{S_{\rm B}^0 + S_{\rm F}^0 + S_{\rm C} + S_{\rm D} } {\left( {\varPsi _i \frac{\partial \varPsi _j }{\partial n} - \frac{\partial \varPsi _i }{\partial n}\varPsi _j } \right)\mbox{d}S} = 0 \end{eqnarray}$
(30) $\begin{eqnarray} \displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _j n_i \mbox{d}S} = \displaystyle\iint\limits_{S_{\rm B}^0 } {\varPsi _j \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} = \\ \qquad \displaystyle\iint\limits_{S_{\rm B}^0 + S_{\rm F}^0 + S_{\rm C} + S_{\rm D} } {\varPsi _j \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} - \displaystyle\iint\limits_{S_{\rm F}^0 } {\varPsi _j \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} = \\ \qquad \displaystyle\iint\limits_{S_{\rm B}^0 + S_{\rm F}^0 + S_{\rm C} + S_{\rm D} } {\frac{\partial \varPsi _j }{\partial n}\varPsi _i \mbox{d}S} - \displaystyle\iint\limits_{S_{\rm F}^0 } {\varPsi _j \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} = \\ \qquad \displaystyle\iint\limits_{S_{\rm B}^0 } {\frac{\partial \varPsi _j }{\partial n}\varPsi _i \mbox{d}S} = \displaystyle\iint\limits_{S_{\rm B}^0 } {n_j \varPsi _i \mbox{d}S} \end{eqnarray}$
(31) $\begin{eqnarray} \label{eq34} \left( {\bar{M} + \rho ^0\bar{A}^0} \right) a = - \left\{ {{\begin{array}{c} 0 \\ 0 \\ 0 \\ {\varOmega \times \left( {\bar{ I}\varOmega } \right)} \\ \end{array} }} \right\} - \rho ^0 U^0 + \left\{ {\begin{array}{c} F_{\rm e} \\ M_{\rm e} \\ \end{array}} \right\} \end{eqnarray}$
由此可以显式计算浮体瞬时加速度. 如果采用边界元方法求解各个边值问题, 则该方法尤其有效, 因为$\varPsi _i $和$\overline {\varphi _t } $线性方程组的系数矩阵和$\varphi $的系数矩阵是相同的. 此外, 由于$\varPsi _i $和$\overline {\varphi _t } $的边界值问题求解是彼此独立的, 可将线性方程组右侧设为多列形式, 通过一次求解同时获得$\varPsi _i $和$\overline {\varphi _t } $.
第四种是辅助函数法[33 -34 ] . 该方法可看作模态分解法的变种. 由于$\varPsi _i $和$\overline {\varphi _t } $均满足Laplace方程, 可根据格林公式得到
(32) $\begin{eqnarray} \label{eq35} \displaystyle\iint\limits_{S_{\rm B}^0 + S_{\rm F}^0 + S_{\rm C} + S_{\rm D} } {\left( {\overline {\varphi _t } \frac{\partial \varPsi _i }{\partial n} - \frac{\partial \overline {\varphi _t } }{\partial n}\varPsi _i } \right)\mbox{d}S} = 0 \end{eqnarray}$
(33) $\begin{eqnarray} \displaystyle\iint\limits_{S_{\rm B}^0 } {\overline {\varphi _t } n_i \mbox{d}S} = \displaystyle\iint\limits_{S_{\rm B}^0 } {\overline {\varphi _t } \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} = \\ \qquad \displaystyle\iint\limits_{S_{\rm B}^0 + S_{\rm F}^0 + S_{\rm C} + S_{\rm D} } {\overline {\varphi _t } \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} - \displaystyle\iint\limits_{S_{\rm F}^0 } {\overline {\varphi _t } \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} = \\ \qquad \displaystyle\iint\limits_{S_{\rm B}^0 + S_{\rm F}^0 + S_{\rm C} + S_{\rm D} } {\frac{\partial \overline {\varphi _t } }{\partial n}\varPsi _i \mbox{d}S} - \displaystyle\iint\limits_{S_{\rm F}^0 } {\overline {\varphi _t } \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} = \\ \qquad \displaystyle\iint\limits_{S_{\rm B}^0 } {\frac{\partial \overline {\varphi _t } }{\partial n}\varPsi _i \mbox{d}S} - \displaystyle\iint\limits_{S_{\rm F}^0 } {\overline {\varphi _t } \frac{\partial \varPsi _i }{\partial n}\mbox{d}S} \end{eqnarray}$
(34) $\begin{eqnarray} \left( {\bar{ M} + \rho ^0\bar{ A}^0} \right) a = - \left\{ {{\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ { \varOmega \times \left( {\bar{ I} \varOmega } \right)} \hfill \\ \end{array} }} \right\} - \\ \qquad \rho ^0\displaystyle\iint\limits_{S_{\rm B}^0 } {\frac{\partial \overline {\varphi _t } }{\partial n}\left\{ {{\begin{array}{*{20}c} {\varPsi _1 } \\ {\varPsi _2 } \\ \vdots \\ {\varPsi _6 } \\ \end{array} }} \right\}{\rm d}S} + \rho^0\displaystyle\iint\limits_{S_{\rm F}^{\rm 0} } {\overline {\varphi _t } \left\{ {{\begin{array}{*{20}c} {{\partial \varPsi _1 }/{\partial n}} \\ {{\partial \varPsi _2 }/{\partial n}} \\ \vdots \\ {{\partial \varPsi _6 }/{\partial n}} \\ \end{array} }} \right\}{\rm d}S} - \\ \qquad \rho ^0\displaystyle\iint\limits_{S_{\rm B}^{\rm 0} }\left( {\frac{1}{2}\nabla _o \varphi \nabla _o \varphi + gz_o } \right)\left\{ {\begin{array}{c} n \\ r\times n \\ \end{array}} \right\}{\rm d}S + \left\{ {\begin{array}{c} F_{\rm e} \\ M_{\rm e} \\ \end{array}} \right\} \\ \end{eqnarray}$
注意, 文献[33 ] 在式(32)中采用了$\varphi _t $而非$\overline \varphi _t $, 本质上与本文推导等同. 该方法无需求解$\overline \varphi _t $, 但也不能直接获得浮体表面的压力. 如需计算压力, 可在求得浮体加速度后进一步求解关于$\varphi _t $的边界值问题.
1.3 多液舱浮体运动模拟的时域解耦方法
本文将进一步考虑多液舱浮体的情况. 采用模态分解法分析各液舱中液体晃荡引发的力$F_{\rm s} =F^1 + F^2+ \cdots + F^{{N}_{\rm s} }$和力矩$M_{\rm s} = M^1 + M^2+ \cdots + M^{{N}_{\rm s} }$. 在液舱$k$中, 晃荡作用力/力矩通过在液舱湿表面上的进行压力积分获得
(35) $\begin{eqnarray} F_i^k = - \rho ^k\displaystyle\iint\limits_{S_{\rm B}^k } {\left( {\frac{\partial \varphi ^k}{\partial t} + \frac{1}{2}\nabla _o \varphi ^k\nabla _o \varphi ^k + gz_o } \right)n_i \mbox{d}S} \end{eqnarray}$
其中$k = 1,2, \cdots ,{N}_{\rm s} $和$i = 1,2, \cdots ,6$. 将$\varphi _t^k $分解为
(36) $\begin{eqnarray} \varphi _t^k = \sum\limits_{i = 1}^6 {\varPsi _i^k a_i } + \overline {\varphi _t^k } \end{eqnarray}$
其中, $\varPsi _i^k $满足边界值问题
(37) $\begin{eqnarray} \nabla _o^2 \varPsi _i^k = 0,\ \mbox{in}\ V^k \end{eqnarray}$
(38) $\begin{eqnarray} \varPsi _i^k = 0,\ \mbox{on}\ S_{\rm F}^k \end{eqnarray}$
(39) $\begin{eqnarray} \frac{\partial \varPsi _i^k }{\partial n} = n_i ,\ \mbox{on}\ S_{\rm B}^k \end{eqnarray}$
且$\overline {\varphi _t^k } $满足边界值问题
(40) $\begin{eqnarray} \nabla _o^2 \overline {\varphi _t^k } = 0,\ \mbox{in}\ V^k \end{eqnarray}$
(41) $\begin{eqnarray} \overline {\varphi _t^k } = - gz_o - \frac{1}{2}\nabla _o \varphi ^k\nabla _o \varphi ^k,\ \mbox{on}\ S_{\rm F}^k \end{eqnarray}$
(42) $\begin{eqnarray} \frac{\partial \overline {\varphi _t^k } }{\partial n} = - v_{\rm c} \cdot \frac{\partial \nabla _o \varphi ^k}{\partial n} +\\ \qquad \varOmega \cdot \frac{\partial }{\partial n}\left[ {r\times \left( {v_{\rm c} - \nabla _o \varphi ^k} \right)} \right],\ \mbox{on}\ S_{\rm B}^k \end{eqnarray}$
(43) $\begin{eqnarray} F_{{\rm s}i} = \sum\limits_{k = 1}^{{\rm Ns}} {F_i^k } = - \sum\limits_{k = 1}^{{\rm Ns}} \rho ^k\lt( \sum\limits_{j = 1}^{\ \ 6} {A_{ij}^k a_j } + U_i^k ) \end{eqnarray}$
其中, $U_i^k = \displaystyle\iint\limits_{S_{\rm B}^k } {\overline {\varphi _t^k } n_i {\rm d}S} + \displaystyle\iint\limits_{S_{\rm B}^k } {\left( {\frac{1}{2}\nabla _o \varphi ^k\nabla _o \varphi ^k + gz_o } \right)n_i \mbox{d}S} $, $A_{ij}^k = \displaystyle\iint\limits_{S_{\rm B}^k } {\varPsi _j^k n_i {\rm d}S} $. 由此得到多液舱浮式结构物的运动方程
(44a) $\begin{eqnarray} \left( {\bar{M} + \sum\limits_{k = 0}^{{\rm Ns}} {\rho ^k\bar{A}^k} } \right)a = - \sum\limits_{k = 0}^{{\rm Ns}} {\rho ^kU^k} - \\ \qquad \left\{ {{\begin{array}{*{20}c} 0 \\ 0 \\ 0 \\ {\varOmega \times \left( {\bar{I}\varOmega } \right)} \\ \end{array} }} \right\} + \left\{ {\begin{array}{l} F_{\rm e} \\ M_{\rm e} \\ \end{array}} \right\} \end{eqnarray}$
(44b) $\begin{eqnarray} {A^k} = \left[ {{\begin{array}{*{20}c} {A_{11}^k } & {A_{12}^k } & \cdots & {A_{16}^k } \\ {A_{21}^k } & {A_{22}^k } & \cdots & {A_{26}^k } \\ \vdots & \vdots & & \vdots \\ {A_{61}^k } & {A_{62}^k } & \cdots & {A_{66}^k } \\ \end{array} }} \right] \end{eqnarray}$
(44c) $\begin{eqnarray} U^k = \left\{ {U_1^k ,U_2^k ,U_3^k ,U_4^k ,U_5^k ,U_6^k } \right\}^{\rm T} \end{eqnarray}$
注意到式(43)中包含二阶微分项${\partial \nabla _o \varphi ^k}/{\partial n}$和${\partial \left[ { r\times \left( { v_{\rm c} - \nabla _o \varphi ^k} \right)} \right]}/{\partial n}$, 难以直接计算. 利用下列关系
(45) $\begin{eqnarray} \frac{\partial }{\partial n}\left( {\overline {\varphi _t^k } } \right) = - \frac{\partial }{\partial n}\left( {v_{\rm c} \cdot \nabla _o \varphi ^k} \right) + \\ \qquad \frac{\partial }{\partial n}\left[ {\varOmega \cdot \left( {r\times v_{\rm c} } \right) - \varOmega \cdot \left( {r\times \nabla _o \varphi ^k} \right)} \right] \end{eqnarray}$
可引入辅助函数$\chi ^k$来间接求解[35 ] . 辅助函数形式为
(46) $\begin{eqnarray} \chi ^k = \overline {\varphi _t^k } + v_{\rm c} \cdot \nabla _o \varphi ^k + \nabla _o \varphi ^k \cdot \left( {\varOmega \times r} \right) - v_{\rm c} \cdot \left( {\varOmega \times r} \right)\quad \end{eqnarray}$
(47) $\begin{eqnarray} \frac{\partial \chi ^k}{\partial n} = \frac{\partial \overline {\varphi _t ^k} }{\partial n} + \frac{\partial }{\partial n}\left( { v_{\rm c} \cdot \nabla _o \varphi ^k} \right) + \frac{\partial }{\partial n}\left[ {\nabla _o \varphi ^k \cdot \left( {\varOmega \times r} \right)} \right] - \\ \qquad \frac{\partial }{\partial n}\left[ {v_{\rm c} \cdot \left( {\varOmega \times r} \right)} \right] \end{eqnarray}$
由于$\chi ^k$的各项均满足Laplace方程, 因此式(40)$\sim\!$式(42)可以转换为关于$\chi ^k$的边值问题. 求得$\chi ^k$后便可根据式(46)得到$\overline {\varphi _t^k } $.
1.4 脉冲响应函数方法
上述方法可用于全非线性外场波浪、全非线性液体晃荡和浮体大幅运动的情形. 如果浮体运动幅值和外场波高相对于浮体特征尺寸和水深均为小量, 可进一步对外场波浪与浮体的相互作用问题进行线性化处理, 以简化计算.
假设$S_{\rm F}^0 $和$S_{\rm B}^0 $分别围绕平均位置$\overline S _{\rm F} $和$\overline S _{\rm B} $振动, 可以将式(3)$\sim\!$式(8)的边值问题线性化处理. 忽略高阶项后, $V^0$中的水动力/力矩可表示为
(48) $\begin{eqnarray} F_i ^{\left( 0 \right)} + F_i ^{\left( 1 \right)} = - \rho ^0\displaystyle\iint\limits_{\overline S _{\rm B}^0 } {\varphi _t^{\left( 1 \right)} n_i \mbox{d}S} + F_{{\rm B}i} = F_i^{\rm l} + F_{{\rm B}i} \end{eqnarray}$
其中, $F_{{\rm B}i} $是恢复力, $F_i^{\rm l} $是$i$方向的波浪力. 上标$\left( 0 \right)$和$\left( 1 \right)$分别对应于定常量和线性量. $F_{{\rm B}i} $由浮体的水下几何形状和浮体重心确定[25 ]
(49) $\begin{eqnarray} \label{eq54} &&\left\{ {\begin{array}{c} F_{\rm B} \\ M_{\rm B} \\ \end{array}} \right\} = \left\{ {{\begin{array}{*{20}c} {F_{{\rm B1}} } \\ {F_{{\rm B2}} } \\ {F_{{\rm B3}} } \\ {F_{{\rm B4}} } \\ {F_{{\rm B5}} } \\ {F_{{\rm B6}} } \\ \end{array} }} \right\} \approx \left[ {{\begin{array}{*{20}c} 0 & 0 & & & & 0 \\ 0 & 0 & & & & \\ & & {C_{33} } & {C_{34} } & {C_{35} } & \\ & & {C_{43} } & {C_{44} } & {C_{45} } & \\ & & {C_{53} } & {C_{54} } & {C_{55} } & \\ 0 & & & & & 0 \\ \end{array} }} \right]\left\{ {{\begin{array}{*{20}c} {x_1 } \\ {x_2 } \\ {x_3 } \\ {x_4 } \\ {x_5 } \\ {x_6 } \\ \end{array} }} \right\} \end{eqnarray}$
(50) $\left. \begin{array} \\ C_{33} = - \rho ^0g\displaystyle\iint\limits_{\overline S _{\rm F} } {\mbox{d}S}\\C_{34} = C_{43} = - \rho ^0g\displaystyle\iint\limits_{\overline S _{\rm F} } {y\mbox{d}S} \\ C_{35} = C_{53} = \rho ^0g\displaystyle\iint\limits_{\overline S _{\rm F} } {x\mbox{d}S} \\C_{44} = - \rho ^0g\displaystyle\iint\limits_{\overline S _{\rm F} } {y^2\mbox{d}S} - \rho ^0g\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\over {V}} z_{\rm b} \\ C_{55} = - \rho ^0g\displaystyle\iint\limits_{\overline S _{\rm F} } {x^2\mbox{d}S} - \rho ^0g\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\over {V}} z_{\rm b}\\C_{45} = C_{54} = \rho ^0g\displaystyle\iint\limits_{\overline S _{\rm F} } {xy\mbox{d}S} \\ \end{array} \right\}$
其中, $\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\frown$}}\over {V}} $是排水体积, $z_{\rm b} $是浮心垂向坐标, $\left\{ {x_4 ,x_5 ,x_6 } \right\}$是线性化的欧拉角. 波浪力$F_i ^l$可以进一步分解为Froude-Krylov(FK)力$F_{{\rm I}i} $、由于物体存在扰动入射波而产生的绕射力$F_{{\rm D}i} $和无入射波情况下由浮体运动引起的辐射力$F_{{\rm R}i1}$$\sim$$F_{{\rm I}i6} $, 即
(51) $\left. \begin{array} F_i ^{\rm l} = F_{{\rm I}i} + F_{{\rm D}i} + \displaystyle\sum\limits_{j = 1}^6 {F_{{\rm R}ij} } \\ \mbox{ or } F^{\rm l} = F_{{\rm I}1} + F_{{\rm D1}} + \displaystyle\sum\limits_{j = 1}^6 {F_{{\rm R}j} } \end{array} \right\}$
下标$\mbox{R}1$到$\mbox{R}6$分别对应浮体运动模态1至6, 即纵荡、横荡、垂荡、横摇、纵摇和艏摇. 相应地, 速度势可以分解为
(52) $\begin{eqnarray} \varphi ^{\left( 1 \right)} = \varphi _{\rm I} + \varphi _{\rm D} + \sum\limits_{j = 1}^6 {\varphi _{{\rm R}j} } \end{eqnarray}$
可用脉冲响应函数方法[36 ] 表示浮体的辐射势. 在$t$时刻, 辐射势可以写成
(53) $\begin{eqnarray} \varphi _{{\rm R}i} \left( {x,y,z,t} \right) = \varPsi _i \left( {x,y,z} \right)v_i \left( t \right) + \\ \qquad \displaystyle\int_{ - \infty }^t {\chi _i \left( {x,y,z,t - \tau } \right)} v_i \left( \tau \right)\mbox{d}\tau \end{eqnarray}$
其中, $\varPsi _i $为当前瞬间由单位速度(即一个“脉冲”)引起的速度势, 时间卷积项表示在$t$时刻之前各个时刻浮体单位速度运动引起的波浪场对当前时刻速度势的影响, $\chi _i $可被认为是脉冲响应函数. 由此, 辐射力$F_{{\rm R}ij} $可以被写为
(54) $\begin{eqnarray} F_{{\rm R}ij} = - \rho ^0\displaystyle\iint\limits_{\overline S _{\rm B}^0 } {\left( {\frac{\partial \varphi _{{\rm R}j} }{\partial t}} \right)n_i } \mbox{d}S = \\ \qquad \rho ^0\dot{v}_j \left( t \right)\underbrace {\left( { - \displaystyle\iint\limits_{\overline S _{\rm B}^0 } {\varPsi _j \left( {x,y,z} \right)n_i \mbox{d}S} } \right)}_{A_{{\rm R}ij} } + \\ \qquad \rho ^0\displaystyle\int_{ - \infty }^t {v_j \left( \tau \right)\underbrace {\left( { - \displaystyle\iint\limits_{\overline S _{\rm B}^0 } {\frac{\partial \chi _j \left( {x,y,z,t - \tau } \right)}{\partial t}n_i \mbox{d}S} } \right)}_{B_{{\rm R}ij} }} \mbox{d}\tau = \\ \qquad \rho ^0A_{{\rm R}ij} \dot{v}_j \left( t \right) + \rho ^0\displaystyle\int_{ - \infty }^t {B_{{\rm R}ij} \left( {t - \tau } \right)v_j \left( \tau \right)} \mbox{d}\tau \end{eqnarray}$
其中, $B_{{\rm R}ij} $为延迟函数, 表示在$t$时刻之前某时刻由浮体单位速度运动引起的波浪场扰动, 持续到当前时刻后作用于浮体的力. 将$\tau $替换为$t$$-$$\tau $, 可得到一种更方便的积分形式
(55) $\begin{eqnarray} \displaystyle\int_{ - \infty }^t {B_{{\rm R}ij} \left( {t - \tau } \right)v_j \left( \tau \right)} \mbox{d}\tau = \\ \qquad \displaystyle\int_0^{ + \infty } {B_{{\rm R}ij} \left( \tau \right)v_j \left( {t - \tau } \right)} \mbox{d}\tau \end{eqnarray}$
将晃荡力、恢复力、FK力、辐射力和绕射力代入运动方程可得到
(56) $\begin{eqnarray} \sum\limits_{j = 1}^6 [\left( {M_{ij} - \rho ^0A_{{\rm R}ij} + \sum\limits_{k = 1}^{{Ns}} {\rho ^kA_{ij}^k } } \right)\ddot {x}_j - \\ \qquad \rho ^0\displaystyle\int_0^{ + \infty } {B_{{\rm R}ij} \left( \tau \right)\dot{x}_j \left( {t - \tau } \right)} \mbox{d}\tau - C_{ij} x_j] = \\ \qquad - \sum\limits_{k = 1}^{{Ns}} {\rho ^kU_i^k } + F_{{\rm D}i} + F_{{\rm I}i} + F_{{\rm e}i} \end{eqnarray}$
其中$i = 1,2, \cdots ,6$, $M_{ij} $代表矩阵$\bar{ M}$中的各个元素.
利用Ogilvie[36 ] 方法, 可求得系数$A_{{\rm R}ij} $和$B_{{\rm R}ij} $. 在频域中, 浮体运动和辐射势可以表示为
(57) $\begin{eqnarray} x_i = {\rm Re}\left[ {\tilde{x}_i {\rm e}^{-{\rm i}\omega t}} \right] \end{eqnarray}$
(58) $\begin{eqnarray} \varphi _{{\rm R}i} \left( {x_o ,y_o ,z_o ,t} \right) = {\rm Re}\left[ {\tilde{\varphi }_{{\rm R}i} \left( {x_o ,y_o ,z_o } \right){\rm e}^{-{\rm i}\omega t}} \right] \end{eqnarray}$
其中, $\tilde{x}_i $和$\tilde{\varphi }_{{\rm R}i} $为复变量, ${\rm Re}\left[ \right]$和Im$\left[ \right]$分别表示复变量的实部和虚部. 考虑$\overline S _{\rm B} $上的边界条件, $\tilde{\varphi }_{{\rm R}i} $可表示为$\tilde{\varphi }_{{\rm R}i} \left( {x_o ,y_o ,z_o } \right) = - {\rm i}\omega \tilde{x}_i \tilde{\varphi }_{{\rm R}i}’ \left( {x_o ,y_o ,z_o } \right)$. 于是得到辐射力的表示形式
(59) $\begin{eqnarray} F_{{\rm R}ij} =\rho ^0a_j \left( { - \displaystyle\iint\limits_{\overline S _{\rm B}^0 } {{\rm Re}\left[ {\tilde{\varphi }_{{\rm R}j}’ } \right]n_i } \mbox{d}S} \right) + \\ \qquad \rho ^0v_j \left( { - \omega \displaystyle\iint\limits_{\overline S _{\rm B}^0 } {{\rm Im}\left[ {\tilde{\varphi }_{{\rm R}j}’ } \right]n_i } \mbox{d}S} \right) = \\ \qquad \rho ^0\tilde{A}_{{\rm R}ij} \left( \omega \right)a_j + \rho ^0\tilde{B}_{{\rm R}ij} \left( \omega \right)v_j \end{eqnarray}$
其中, $\tilde{A}_{{\rm R}ij} $是附加质量, $\tilde{B}_{{\rm R}ij} $是辐射阻尼. 换言之, 辐射力由分别与加速度和速度同相位的两个分量组成. 系数$A_{Rij} $和$B_{Rij} $可由下列关系式求得
(60) $\begin{eqnarray} A_{{\rm R}ij} = \tilde{A}_{{\rm R}ij} \left( \omega \right) + \frac{1}{\omega }\displaystyle\int_0^{ + \infty } {B_{{\rm R}ij} \left( \tau \right)\sin \left( {\omega \tau } \right)} \mbox{d}\tau \end{eqnarray}$
(61) $\begin{eqnarray} \displaystyle\int_0^{ + \infty } {B_{{\rm R}ij} \left( \tau \right)\cos \left( {\omega \tau } \right)} \mbox{d}\tau = \tilde{B}_{{\rm R}ij} \left( \omega \right) \end{eqnarray}$
通过傅里叶逆变换可以获得$B_{{\rm R}ij} \left( \tau \right)$的显式表达式
(62) $\begin{eqnarray} B_{{\rm R}ij} \left( \tau \right) = \frac{2}{\pi }\displaystyle\int_0^{ + \infty } {\tilde{B}_{{\rm R}ij} \left( \omega \right)\cos \left( {\omega \tau } \right)} \mbox{d}\omega \end{eqnarray}$
2 数值算法
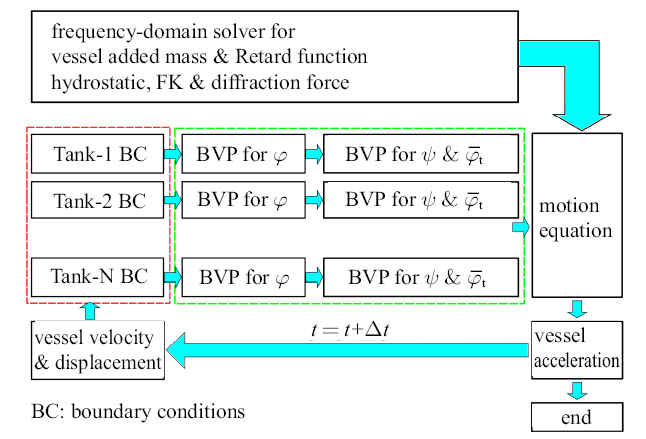
图2 给出了时域解耦算法的实现流程. 首先是参数准备阶段. 计算式(50)中的恢复力系数$C_{ij} $, 利用频域求解器生成频率相关系数(包括$\tilde{A}_{{\rm R}ij} $和$\tilde{B}_{{\rm R}ij} )$和绕射力,并由式(60)和式(62)求得到脉冲响应函数方法的系数$A_{{\rm R}ij}$和$B_{{\rm R}ij}$(本文采用开源软件Nemoh[37 ] 在频域中求解速度势的边值问题得到系数$\tilde{A}_{{\rm R}ij} $和$\tilde{B}_{{\rm R}ij} )$. 然后是时间步进阶段. 在各时刻计算开始前, 浮体的位移和速度是已知的. 先求解各液舱的速度势$\varphi $, 再求解各液舱中的$\varPsi _i^k $和$\overline{\varphi _t^k } $的边值问题, 之后计算系数$A_{ij}^k $和$U_i^k $, 进一步利用式(56)计算浮体瞬时加速度. 已知浮体瞬时加速度后, 可以通过时间步进得到下一时间步浮体的速度和位移, 以及各流域的边界条件, 并进行下一时间步的计算. 应该指出的是, 作为示意, 图2 为欧拉时间步进方法, 本文采用了更高精度的时间步进方法. 本文首先采用了四阶Runge-Katta方法进行前十步时间步进运算, 然后采用四阶Adams-Bashforth方法进行后续时间步进.
图2
图2
时域解耦算法的数值实现流程
Fig.2
Workflows of time-domain decoupling algorithm
采用边界元方法求解各流域关于$\varphi $, $\varPsi _i^k $和$\overline {\varphi _t^k } $的边界值问题. 以求解$\varphi $为例. 基于Green第三定理, 将Laplace方程转换为在流体边界上表示的边界积分方程
(63) $\begin{eqnarray} \left( { x_{\rm p} } \right)\varphi \left( { x_{\rm p} } \right) = \\ \qquad \displaystyle\iint\limits_S {\left[ {G\left( { x_{\rm p} , x} \right)\frac{\partial \varphi \left( x \right)}{\partial n} - \varphi \left( x \right)\frac{\partial G\left( { x_{\rm p} , x} \right)}{\partial n}} \right]} \mbox{d}S\quad \end{eqnarray}$
$\begin{eqnarray*} G\left( { x_{\rm p} ,x} \right) = {1}\bigg/{\left[ {\left( {x - x_{\rm p} } \right)^2 + \left( {y - y_{\rm p} } \right)^2 + \left( {z - z_{\rm p} } \right)^2} \right]^{{1}/{2}}}, \end{eqnarray*}$
$x_{\rm p} = \left\{ {x_{\rm p} ,y_{\rm p} ,z_{\rm p} } \right\}$表示配置点, $x = \left\{ {x,y,z} \right\}$表示$S$上一点, $c\left(x_{\rm p} \right)$是固角系数, $G\left( x_{\rm p} , x \right)$是Green函数.
将边界$S$离散为相邻却不重叠的单元. 每个单元上的节点坐标、速度势及其法向导数分布, 由下式表示
(64) $\left. \begin{array} \\ x\left( \xi ,\varsigma \right) = \sum^K_{k = 1}N_k \left( \xi ,\varsigma \right)x_k \\[1mm] y\left( \xi ,\varsigma \right) = \sum^K_{k = 1}N_k \left( \xi ,\varsigma \right)y_k \\[1mm] z\left( \xi ,\varsigma \right) = \sum^K_{k = 1}N_k \left( \xi ,\varsigma \right)z_k \\[1mm] \varphi \left( \xi ,\varsigma \right) = \sum^K_{k = 1}N_k \left( \xi ,\varsigma \right)\varphi _k \\[1mm] \dfrac{\partial \varphi \left( \xi ,\varsigma \right)}{\partial n} = \sum^K_{k = 1}N_k \left( \xi ,\varsigma \right)\left( \dfrac{\partial \varphi }{\partial n} \right)_k \\ \end{array} \right\}$
(65) $\left. \begin{array}{l@{\quad}l} \left. {\begin{array}{l} N_1 \left( {\xi ,\varsigma } \right) = 1 - \xi - \varsigma \\ N_2 \left( {\xi ,\varsigma } \right) = \xi \\ N_3 \left( {\xi ,\varsigma } \right) = \varsigma \\ \end{array}} \right\},\ \ \mbox{for}\ K = 3 \\ \left. {\begin{array}{l} N_1 \left( {\xi ,\varsigma } \right) = 0.25\left( {1 - \xi } \right)\left( {1 - \varsigma } \right) \\ N_2 \left( {\xi ,\varsigma } \right) = 0.25\left( {1 + \xi } \right)\left( {1 - \varsigma } \right) \\ N_3 \left( {\xi ,\varsigma } \right) = 0.25\left( {1 + \xi } \right)\left( {1 + \varsigma } \right) \\ N_4 \left( {\xi ,\varsigma } \right) = 0.25\left( {1 - \xi } \right)\left( {1 + \varsigma } \right) \\ \end{array}} \right\},\ \ \mbox{for}\ K = 4 \end{array} \right\}$
其中, 下标$k$表示单元第$k$个节点处的变量, $N_k \left( {\xi ,\varsigma } \right)$是形状函数, $K$是各单元上的节点总数. 设$N_{\rm e} $为单元数量, $N_{\rm p} $为边界上的节点数量, $S_e $为第$e$个单位, $\varepsilon \left( {e,k} \right)$是第$e$个单元的第$k$个节点的全局编号. 由此可将边界积分方程离散为边界元方程
(67) $\begin{eqnarray} \sum^{N_{\rm p}}_{j=1}H_{ij}\varphi_j=\sum^{N_{\rm p}}_{j=1}G_{ij}\lt(\frac{\partial \varphi}{\partial n})_j, \ \ {\rm for }\ \ i=1,2,\cdots, N_{\rm p}\\ \end{eqnarray}$
(68) $\begin{eqnarray} G_{ij}=\sum^{N_{\rm e}}_{e=1}\sum^{K}_{k=1}\lt[\displaystyle\iint\limits_{N’_{\rm e}}N_k(\xi, \varsigma)G(\xi, \varsigma)| J(\xi, \varsigma)|{\rm d}\xi{\rm d}\varsigma]\cdot \\ \qquad\delta_{\varepsilon(e,k)}^j\\ H_{ij} = c_i \delta _j^i + \sum^{N_{\rm e}}_{e = 1}\sum^{K}_{k = 1} \lt[ \displaystyle\iint\limits_{S’_{\rm e}}N_k \left(\xi,\varsigma \right)\frac{\partial G\left( \xi ,\varsigma \right)}{\partial n}\cdot \\ \vert J\left( \xi ,\varsigma \right)\vert \mbox{d}\xi \mbox{d}\varsigma ]\delta _{\varepsilon \left( e,k \right)}^j \end{eqnarray}$
其中$i$是配点$x_{\rm p} $的全局索引, $J$是Jacobi矩阵, $S_e’$是二维平面$\xi$-$\varsigma$上的区域$S_e$的映射区域, $\delta _j^i = \left\{ {1,i = j;0,i \ne j} \right\}$是Kronecker delta函数.
为了计算自由表面节点$ x_0 $上的$\varphi $的切向导数, 可在垂直于法向量的平面$\xi$-$\varsigma $上将$\varphi $可以表示为(参考文献[25 ] )
(69) $\begin{eqnarray} \varphi^{\rm h}\left(x,x_0 \right) = \sum^m_{j=1}p_j(x_0)a_j(x_0) \end{eqnarray}$
其中, $\varphi ^{\rm h}\left( {x,x_0 } \right)$是拟合函数, $p_j \left( {x_0 } \right)$基函数, $a_j \left( {x_0 } \right)$是系数. $p_j \left( {x_0 } \right)$可以被选择为多项式函数. 本文在$m = 3$时选择$\left\{ {p_1 ,p_2 ,p_3 } \right\} = \left\{ {1,\xi ,\varsigma } \right\}$, 在$m = 6$时选择$\left\{ {p_1 ,p_2 , \cdots ,p_6 } \right\} = \left\{ {1,\xi ,\varsigma ,\xi ^2,\xi \varsigma ,\varsigma ^2} \right\}$. 通过在相邻节点中使用加权最小二乘法计算系数$a_j \left( {x_0 } \right)$, 进而求得空间导数${\partial \varphi ^h}/{\partial \xi }$和${\partial \varphi ^h}/{\partial \varsigma }$.
3 结果与讨论
3.1 单液舱浮式结构物的运动模拟
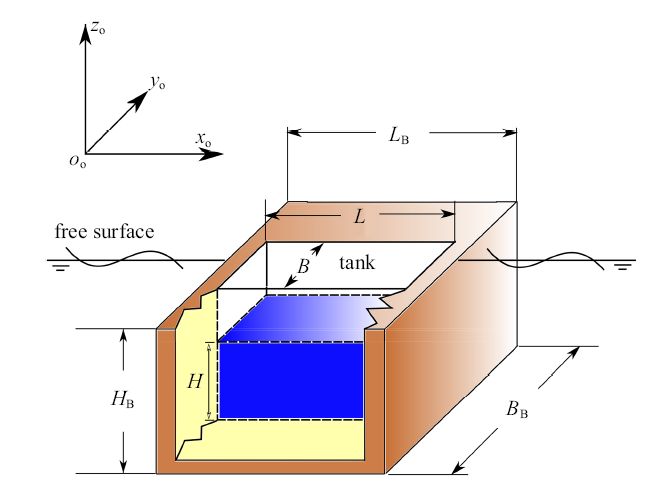
本节考虑带有单个晃荡液舱的浮体. 首先采用本文数值方法重现物理模型实验[7 ] . 如图3 所示, 在水深1.03 m的波浪水槽中, 放置一个矩形浮体, 浮体长$L_{\rm B} = 0.4$ m、宽$B_{\rm B} = 0.596$ m、吃水$H_{\rm B} = 0.2$ m, 浮体内安置一只矩形水箱. 包括舱内液体在内, 浮体总质量为$\rho _{\rm 0} L_{\rm B} B_{\rm B} H_{\rm B} $. 通过配重来调整浮体吃水. 入射波沿着浮体长度方向传播, 浮体可以沿着两个低摩擦轨道在波浪方向上自由移动. 为了防止浮体漂移, 在浮体上安装刚度系数为30.9 N/m的弹簧, 弹簧固有频率远低于入射波的频率.
图3
图3
带液舱的浮体剖面图
Fig.3
Sketch of vessel with liquid tank
为避免瞬时效应的影响, 本文用缓冲函数$\gamma _{{\rm ramp}} $乘以入射波波幅, 使入射波的波幅缓慢增大
(70) $\begin{eqnarray} \gamma _{{\rm ramp}} (t) = \left\{ \begin{array}{l@{\ \ \ }l} \left[1 - \cos\left(\pi t/T_{\rm ramp}\right)\right]\Big/2,&\mbox{for}\ t < T_{\rm ramp}\\ 1,&\mbox{for}\ t \geqslant T_{\rm ramp}\\ \end{array}\right. \end{eqnarray}$
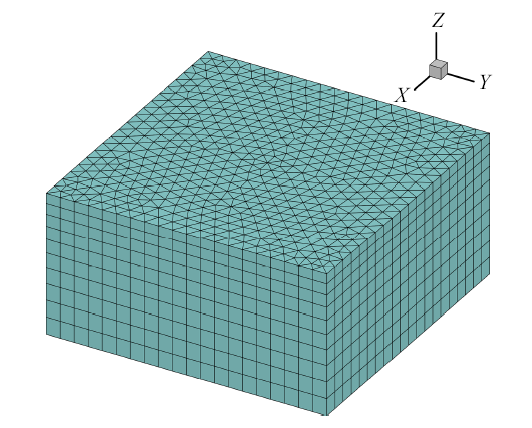
其中$T_{{\rm ramp}} $为缓冲时间. 本节数值模拟将缓冲时间设置为5个入射波周期. 采用长$L$、宽$B$和初始液深$H$的矩形液舱. 如图4 所示, 在本文的边界元计算中, 自由表面边界被离散为三角形单元, 舱底和舱壁边界被离散为四边形单元. 在每个时间步, 自由面单元节点位置和边界条件实时更新, 舱壁节点在自由面和舱底之间相应拉伸, 舱壁单元节点从自由面到舱底分布为
(71) $\begin{eqnarray} z_i = \eta - (H + \eta )\frac{(\gamma + 1) - (\gamma - 1)\left( \dfrac{\gamma + 1}{\gamma - 1}\right)^{1 - i / m}}{\left(\dfrac{\gamma + 1}{\gamma - 1} \right)^{1 - i / m} + 1}, \\ \qquad\mbox{for }i = 0,1, \cdots ,m \end{eqnarray}$
图4
图4
液舱流域边界的单元分布
Fig.4
Mesh model of liquid domain in sloshing tank
其中, $m$是垂向节点数, $z_i $是各节点的垂直坐标, 常数$\gamma (\gamma > 1)$表示垂向节点分布的均匀性. 本文在液舱侧壁和水底面分别设置20$\times$10和20$\times$20的四边形单元, 在自由面上利用根据Delaunay三角化方法生成三角形单元, 选取$\gamma =1.5$. 单元划分收敛性验证参见文献[25 ] .
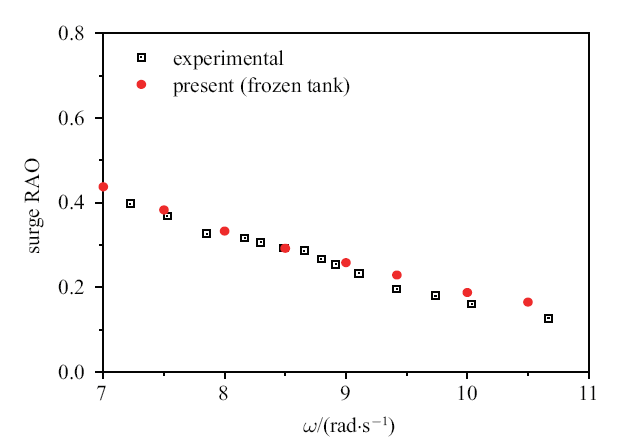
首先, 考虑无液舱的情况. 用等效质量的固体代替液体, 可认为舱内液体被冷冻为固体. 入射波波幅$A=0.015$ m, 入射波圆频率为$\omega _{\rm a} $. 图5 对比了通过数值计算与模型实验得到的浮体纵荡幅值响应算子(response amplitude operator, RAO), 两者吻合良好, 验证了本数值方法模拟浮体与波浪相互作用问题的准确性.
图5
图5
无液舱浮体的纵荡RAO
Fig.5
Surge RAO of vessel with frozen tank
进一步考虑舱内有液体自由晃荡的情况. 液舱长$L=0.376$ m、宽$B=0.15$ m和水深$H=0.184$ m. 此时液舱的最小自然晃荡频率为$\omega_{10}=8.64$ rad/s(此处下标10中第一个数字1标记了标识码度方向的第一个自然晃荡频率).
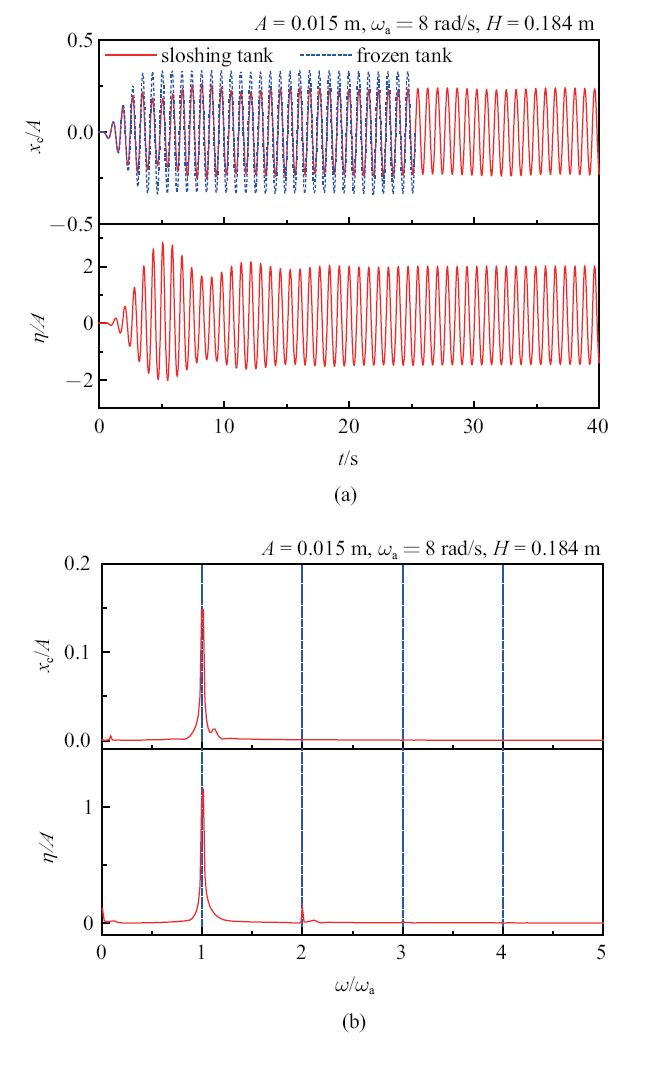
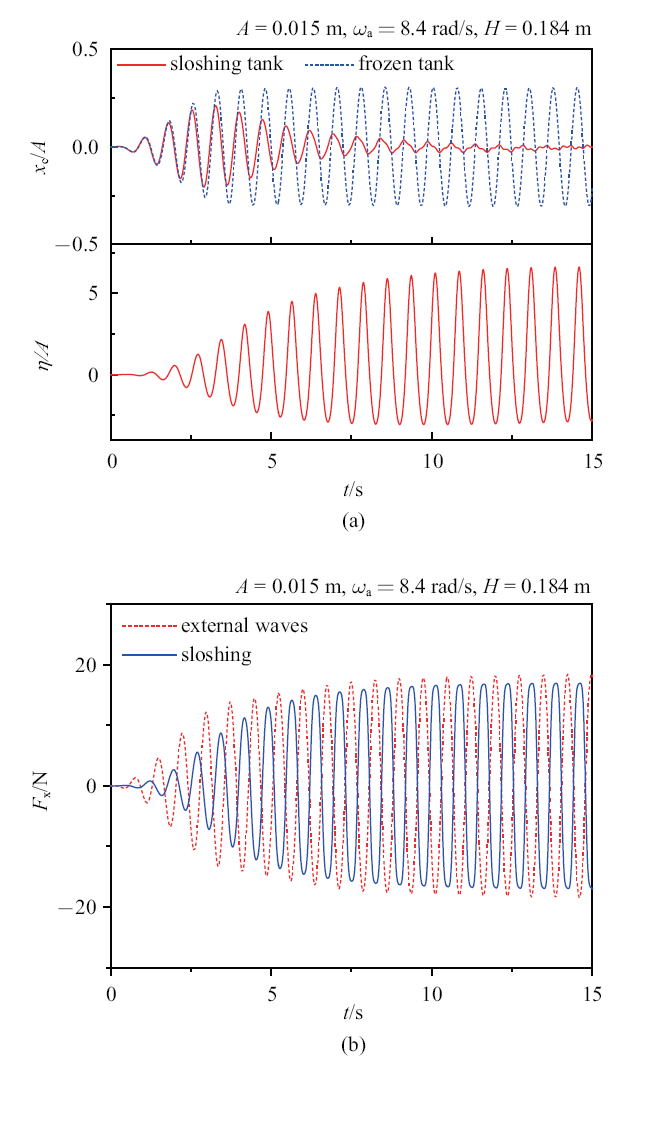
第一种情况, 设置入射波波幅$A=0.015$ m和频率$\omega _{\rm a}=8$ rad/s(注意此时$\omega _{\rm a} <\omega _{10}$). 图6 (a)分别给出了浮体纵荡位移和自由液面升高沿液舱右壁的时间历程曲线. 在大约10 s的瞬态响应之后, 浮体运动和液舱晃荡逐渐进入具有恒定振幅和频率的稳定阶段. 图6 (b)的FFT分析显示, 浮体运动和液体晃荡都只包含波浪激励频率的成分. 理论上, 对于没有阻尼的液舱晃荡问题, 液体晃荡也应该包含自然晃荡频率的成分. 然而, 在本算例中, 由于外部流体域包含了波浪阻尼效应, 导致液舱中液体晃荡的能量可以通过浮体的自由运动传递转到外部波浪场而耗散. 在有足够阻尼的条件下, 舱内液体最终在波浪激励频率下做强迫晃荡. 图6 (b)下面出现了入射波倍频的二阶成分, 显示出液舱晃荡的非线性特性. 图6 (a)也对比了相同波浪环境中, 冰冻液舱与晃荡液舱浮体的位移时间历程曲线. 在该情况下, 晃荡液舱的存在减小了浮体运动幅度. 图7 对比了外部波浪和晃荡液体作用在浮体上的力的时间历程. 结果显示, 在稳定阶段, 液体晃荡和外部波浪产生了相反相位的力作用在浮体上. 换言之, 晃荡液体产生的力抵消了一部分外部波浪力. 晃荡液舱产生了与船舶上常见的被动减摇水舱类似的效果.
图6
图6
$\omega _{\rm a}=8$ rad/s工况下, (a) 浮体位移和舱壁右侧自由面升高的时间历程曲线; (b) FFT分析
Fig.6
(a) History of vessel displacement and wave elevation along the right tank wall; and (b) Corresponding FFT analyses, for $\omega _{\rm a}=8$ rad/s
图7
图7
$\omega _{\rm a} =8$ rad/s工况下, 作用在浮体上的力的时间历程曲线
Fig.7
History of forces acting on the vessel for $\omega _{\rm a} =8$ rad/s
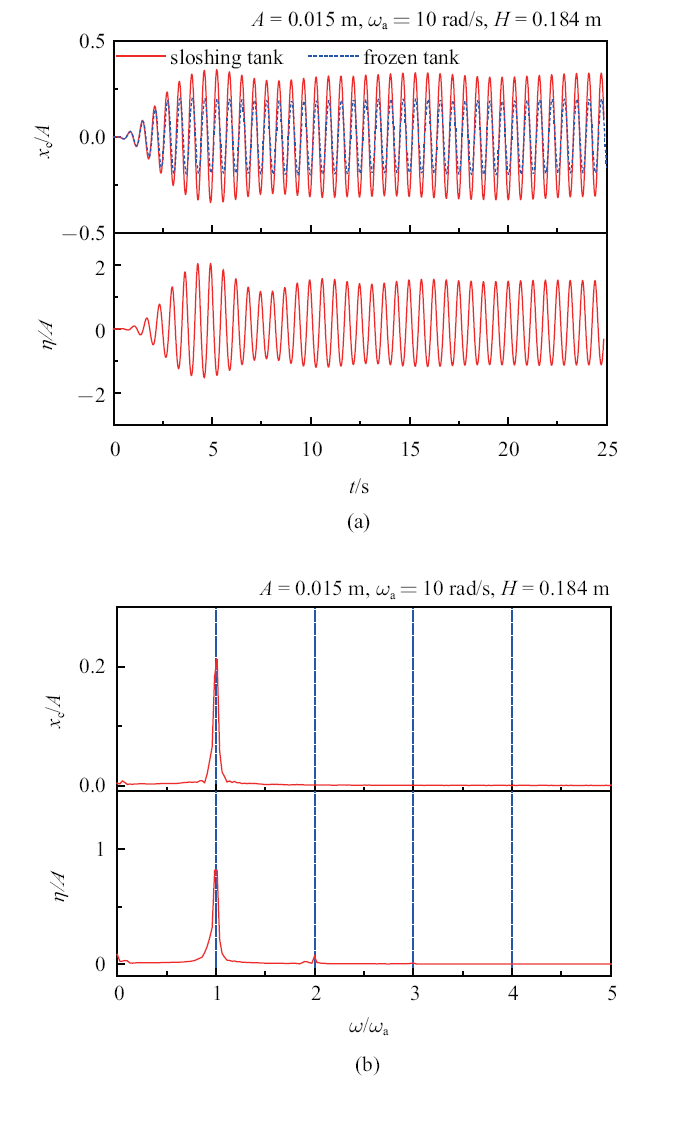
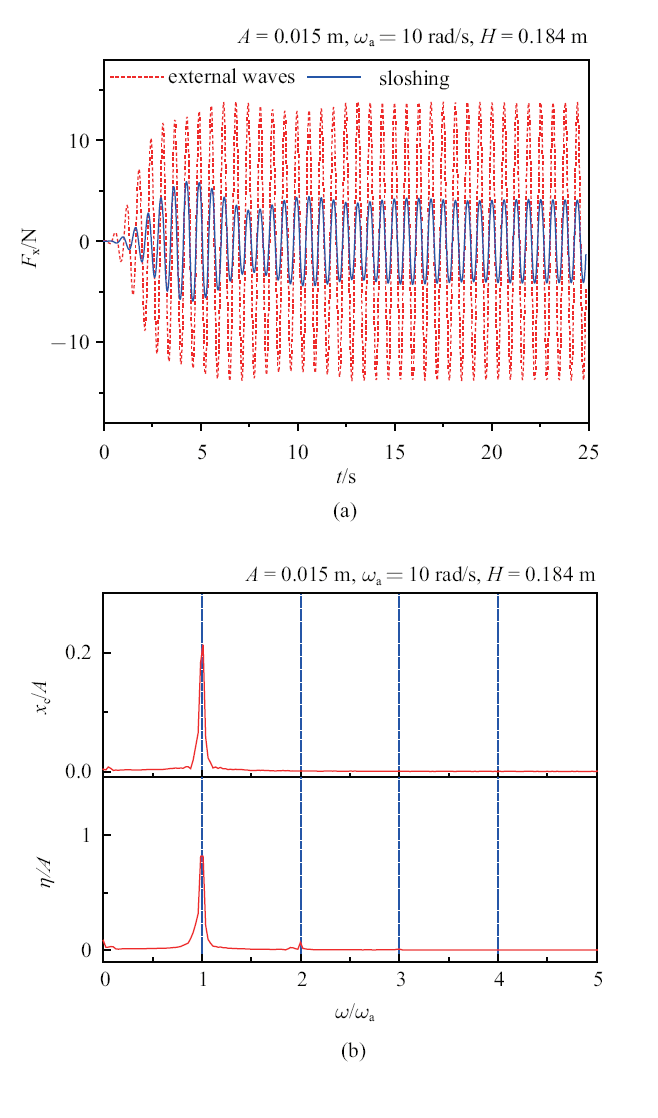
第二种情况, 考虑波浪激励频率$\omega _{\rm a}=10$ rad/s高于$\omega _{10}$的情况. 图8 (a)给出浮体纵荡位移和沿舱壁右侧的自由液面升高的时间历程曲线. 随着时间步进, 两条时间历程曲线均逐渐进入稳定阶段. 图8 (b)的FFT分析显示, 液舱内液体晃荡的主要频率也是外部波浪频率. 然而, 与$\omega _{\rm a}=8$ rad/s情况不同的是, 晃荡液舱浮体比冰冻液舱浮体有更大的位移幅值. 图9 比较外部波浪力和液舱晃荡力的时间历程曲线, 可以发现该工况下液舱引发的晃荡力与外部波浪力具有相同相位.
图8
图8
$\omega _{\rm a}=10$ rad/s工况下, (a) 浮体位移和舱壁右侧自由面升高的时间历程曲线; (b) FFT分析
Fig.8
(a) History of vessel displacement and wave elevation along the right tank wall; and (b) Corresponding FFT analyses, for $\omega _{\rm a}=10$ rad/s
图9
图9
$\omega _{\rm a}=10$ rad/s工况下, 作用在浮体上的力的时间历程曲线
Fig.9
History of forces acting on the vessel for $\omega _{\rm a}=10$ rad/s
从$\omega _{\rm a}=8$ rad/s到$\omega _{\rm a}=10$ rad/s, 由于液体晃荡力和外部波浪力之间的相位差, 液体晃荡可以减弱或加剧浮体运动幅值. 本文进一步在$\omega _{\rm a}=8.2$, 8.3, 8.4, 8.5, 8.64, 8.7, 8.8, 9.0和9.5 rad/s频率下进行了模拟, 以研究晃荡力和波浪力的相位差随频率是如何变化的.
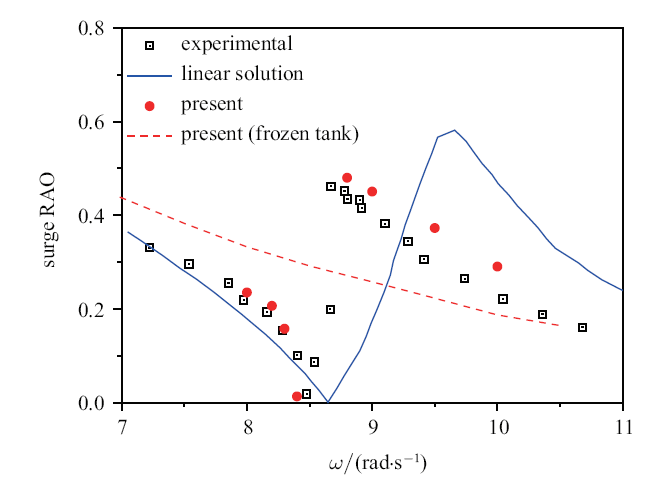
对于$\omega _{\rm a}=8$$\sim$8.3 rad/s和$\omega _{\rm a}=8.8$$\sim$10 rad/s的情况, 可以在浮体位移的时间历程曲线中观察到稳定阶段. 图10 给出了这些频率下的浮体纵荡RAO, 计算结果与实验测量结果吻合良好. 值得注意的是, 在频率高于$\omega _{\rm a}=9$ rad/s的情况下, RAO数值结果略高于实验数据. 这是因为通常在较高频率条件下流体的黏性效应更明显, 但这种微弱的偏差并未影响RAO随频率变化的整体趋势. 图中也标出具有相同总质量的冰冻液舱浮体的纵荡RAO. 通过比较可以发现, 晃荡液舱可以对浮体运动产生明显影响. 图10 也标出了文献[7 ] 的线性解析解, 线性解析解可以粗略地预测实验数据的总体趋势, 但在较宽的频率范围内无法提供令人满意的RAO预报值, 这体现了采用非线性模型进行运动预报的必要性.
图10
图10
带液舱浮体的纵荡RAO
Fig.10
Surge RAO of vessel with sloshing tank
从图10 中可以看出, 从$\omega _{\rm a}=8$ rad/s到$\omega _{\rm a}=8.4$ rad/s, 晃荡液舱浮体的运动幅值小于冰冻液舱浮体的运动幅值, 这是由于晃荡力和外场波浪力具有相反相位. 而且, 随着入射波频率逐渐增大至接近液舱自然晃荡频率, 晃荡力逐渐增大, 导致浮体纵荡RAO的幅值减小. 当$\omega _{\rm a}=8.4$ rad/s时, 浮体纵荡RAO达到最小值. 图11 (a)给出了浮体位移和液舱自由面升高的时间历程曲线. 可以看出, 在瞬态阶段之后, 浮体的位移幅度逐渐减小到一个非常小的值, 而液舱自由面升高的幅值逐渐增大直至进入稳定阶段. 图11 (b)比较了此时作用在浮体的晃荡力和外场波浪力, 发现此时两个力具有相似的幅值但相反的相位, 这导致作用在浮体上的两个力的合力非常小. 而从$\omega _{\rm a}=8.8$ rad/s到$\omega _{\rm a}=10$ rad/s, 晃荡引起的力与外场波浪力几乎同相位, 这导致晃荡液舱浮体的纵荡RAO大于冰冻液舱浮体的纵荡RAO. 随着$\omega _{\rm a} $进一步增大, 晃荡力逐渐减小, 晃荡液舱对浮体运动影响减弱.
图11
图11
$\omega _{\rm a}=8.4$ rad/s工况下的时间历程曲线, (a) 浮体位移和沿舱壁右侧的波浪高度; (b) 作用于浮体上的力
Fig.11
Time history of (a) Vessel displacement and wave elevation along the right tank wall; and (b) Forces acting on the vessel, for $\omega _{\rm a}=8.4$ rad/s
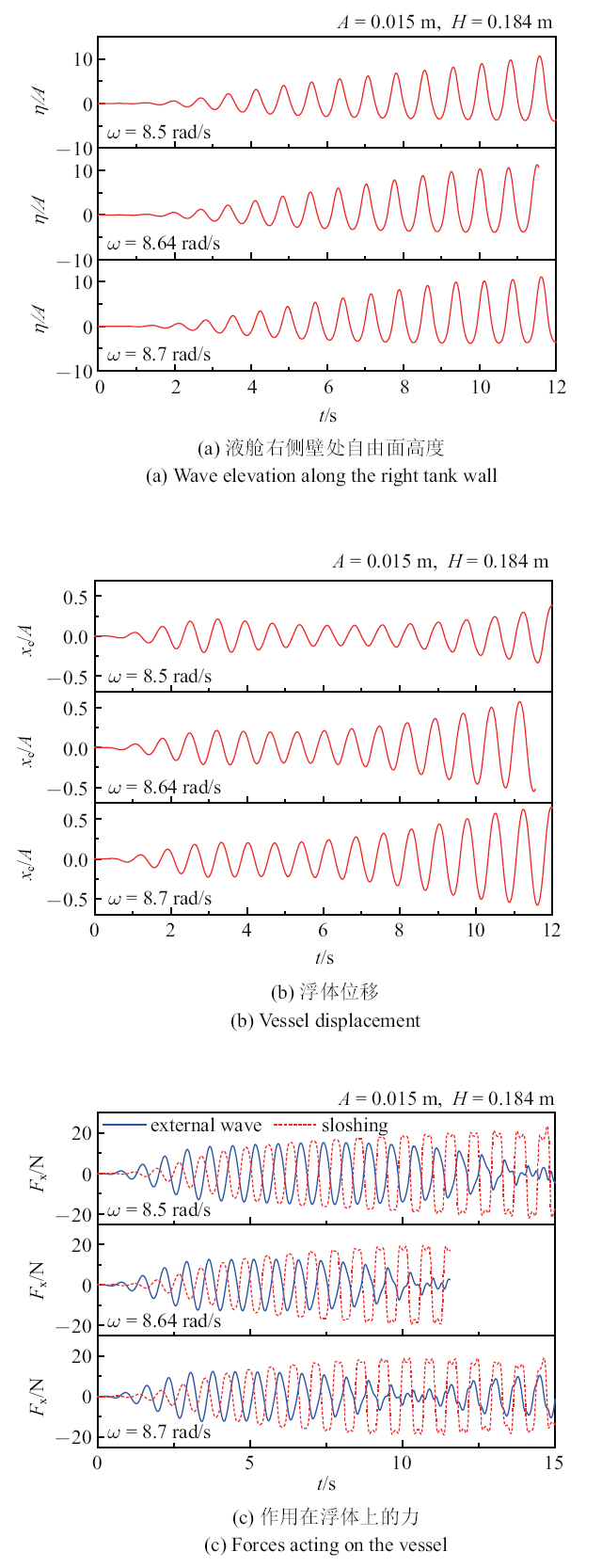
从图10 可以看出, 在自然晃荡频率$\omega _{10}$ (在$\omega _{\rm a}=8.4$ rad/s和$\omega _{\rm a} =8.7$ rad/s之间)附近的频率范围内存在RAO跳跃. 图12 给出了$\omega _{\rm a}=8.5$, 8.64和 8.7 rad/s三种工况下液舱自由面升高、浮体位移和浮体受力的时间历程曲线. 从图12 (a)液舱自由面升高的时间历程曲线中可以看出, 液体运动幅度随着计算持续增加, 直到计算中断, 这是近共振情况. 同样在图12 (b)中, 随着时间的推移, 浮体位移幅度显示出增加的趋势. 图12 (c)比较了作用在浮体上的晃荡力和外场波浪力, 显示两个力的相位差在$0^{\circ}$和$180^{\circ}$之间, 这与图7 和图9 的情况不同. 换句话说, 在该频率范围内晃荡力和外场波浪力之间存在不确定的相位差, 这使得在时域结果中难以观察到稳态结果. 另外, 在初始瞬态阶段之后, 晃荡力的幅度总是大于外场波浪力的幅度. 事实上, 由于液舱内没有任何阻尼, 晃荡液体的动能仅在通过浮体运动传递到外部波浪场之后才能被消减. 而在液体晃荡加剧至近共振状态时, 外部波浪场的阻尼可能不足以完全耗散液舱晃荡的能量. 这导致舱中液体的机械能被连续累积, 形成不稳定状态.
图12
图12
时间历程曲线
Fig.12
Time history
3.2 多液舱浮式结构物的运动模拟
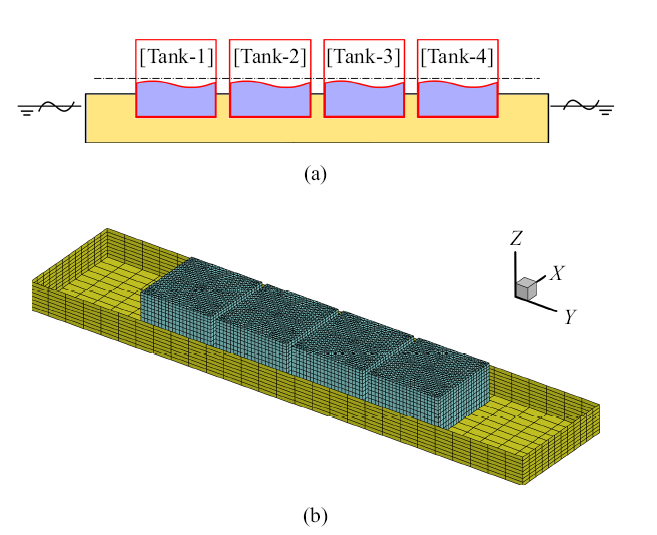
本节将考虑一个简化的FLNG平台模型. FLNG平台连接在转塔式系泊系统上. 该平台能够像风向标一样旋转, 使其能够顺应入射波的方向. 此时, FLNG平台主要进行纵荡、垂荡和纵摇运动. 本节参考文献[38 ] 采用如图13 (a)的简化模型. 该平台具有驳船形状, 长280 m, 宽60 m和吃水15 m. 浮体上沿长度方向均匀分布4个边长为40 m的立方体液舱. 各液舱舱底位于浮体龙骨线以上3 m位置处. 相邻液舱之间有3 m距离. 各液舱装有LNG, 其密度约为水密度的0.46倍. 每个液舱内液体深度是20 m. 设定浮体质量为$m$, 各工况下浮体吃水保持不变. 固定坐标系$O$ $\!-\!$ $xyz$的原点$O$位于浮体重心处, $Ox$ 轴指向船尾. 重心距离浮体底部15 m. 浮体的惯性回转半径$\sqrt {{I_{{\rm xx}}}/{m}}$, $\sqrt {{I_{{\rm yy}} }/{m}} $和$\sqrt {{I_{{\rm zz}} }/{m}} $分别为20 m, 80 m和80 m. 另外, 沿水平方向施加刚度系数为$6.5\times10^5$ N/m的系泊系统. 外部波浪的入射角为0度, 且波幅为2 m. 边界单元分布如图13 (b)所示. 浮体表面和液舱流域边界上分别有976和2218个单元. 各液舱的水平合力可以超过来自外场波浪的水平力, 而外部波浪的力矩总是大于晃荡引起的力矩. 随着时间的推移, 晃荡引起的力/力矩逐渐接近与外场波浪力/力矩同相位, 导致浮体运动幅度增大.
图13
图13
(a)FLNG平台示意图;(b)流域单元分布
Fig.13
(a) Sketch of FLNG; (b) boundary discretization of fluid domains
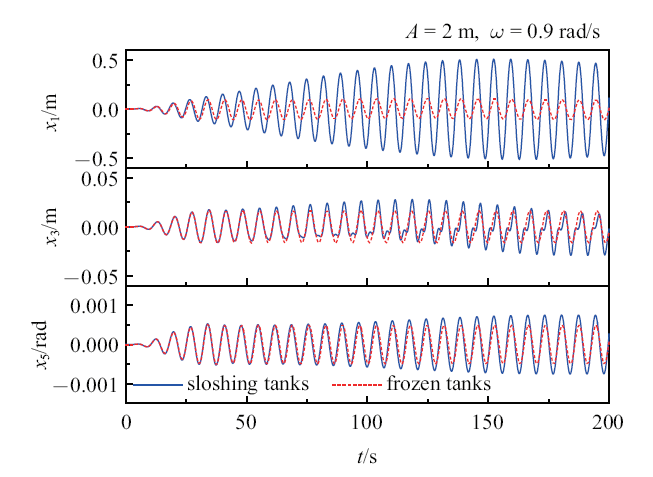
由计算可知, 各液舱的自然晃荡频率为$\omega _{10}=0.84$ rad/s. 首先考虑$\omega _{\rm a}=0.9$ rad/s的具体情况. 浮体的纵荡、垂荡和纵摇的时间历程如图14 所示. 与冰冻液舱的情况相比, 晃荡液舱的存在使浮体的最大纵荡幅值增大了近4倍, 最大纵摇幅值增加了近1.5倍. 图15 进一步比较了外场波浪力和晃荡液舱的合力.
图14
图14
在$\omega _{\rm a}=0.9$ rad/s浮体的纵荡、垂荡和纵摇时间历程曲线
Fig.14
History of vessel surge, heave and pitch for $\omega _{\rm a}=0.9$ rad/s
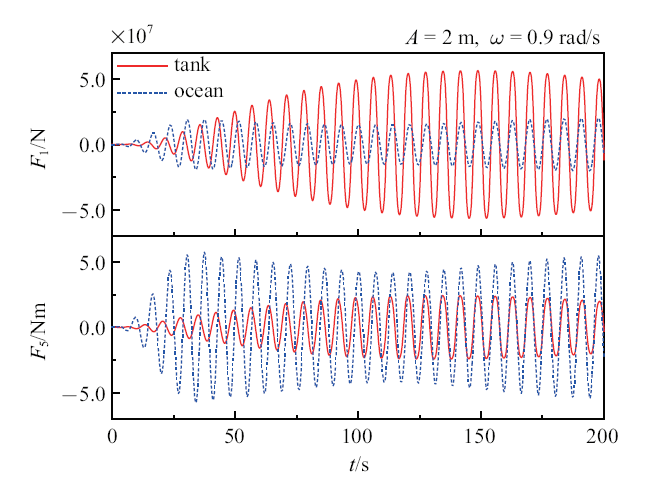
图15
图15
在$\omega _{\rm a}=0.9$ rad/s作用在浮体上的力和力矩的时间历程曲线(图例Tank表示液舱内晃荡力/力矩, 图例Ocean表示浮体外域的波浪力/力矩)
Fig.15
History of force and moment acting on the vessel for $\omega _{\rm a}=0.9$ rad/s (Legends ‘Tank’ and ‘Ocean’ denote forces/moments from the liquid tank and external fluid domain, respectively)
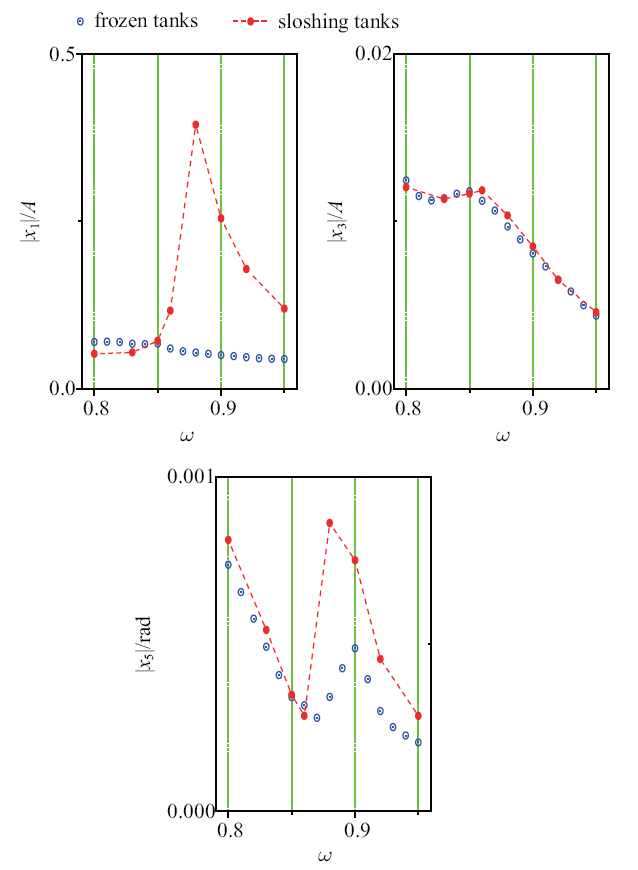
进一步考虑更多入射波频率的情况. 图16 对比了浮体的纵荡、垂荡和纵摇的最大幅值. 与冰冻液舱的情况相比, 晃荡液舱的存在明显影响了浮体的最大纵荡幅值. 在$\omega >0.85$ rad/s, 晃荡液舱对浮体纵荡幅值的影响最大的情况发生在$\omega=0.88$ rad/s. 随着$\omega $从0.88 rad/s增大到1.0 rad/s, 液舱晃荡对最大纵荡幅值的影响逐渐减弱. 对于垂荡运动, 晃荡液舱在所测试频率范围内没有明显改变浮体垂荡运动幅值. 对于纵摇运动, 存在临界频率$\omega _{\rm c} > \omega _{10} $. 低于$\omega _{\rm c} $ 时, 晃荡液舱不会对纵摇幅度产生太大影响; 高于$\omega _{\rm c} $时, 液体晃荡可使最大纵摇幅值增大1倍.
图16
图16
有晃荡液舱浮体的纵荡, 垂荡和纵摇的最大幅度
Fig.16
Maximum surge, heave and pitch amplitude of vessel with sloshing tanks
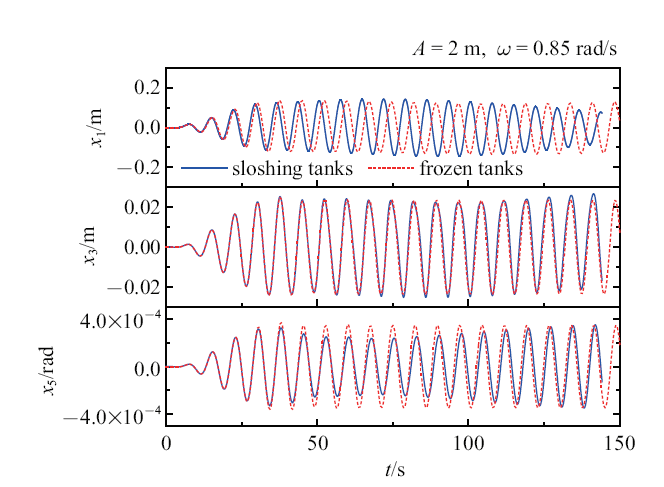
从图16 中可见, 在$\omega _{\rm a}=0.85$ rad/s的情况下, 晃荡液舱对浮体纵荡、垂荡和纵摇的最大幅值都不产生明显影响. 图17 给出了该条件下浮体运动的时间历程曲线. 对于垂荡和纵摇运动, 晃荡液舱没有对浮体运动的时间历程产生太大影响. 而对于纵摇运动, 尽管晃荡对浮体纵荡的最大幅值影响有限, 但对其相位产生一定影响.
图17
图17
在$\omega _{\rm a}=0.85$ rad/s下的浮体纵荡、垂荡和纵摇的时间历程曲线
Fig.17
History of vessel surge, heave and pitch for $\omega _{\rm a}=0.85$ rad/s
4 结 论
本文针对多液舱浮式结构物的运动模拟问题, 引入一种有效的时域解耦算法. 该方法以模态分解法为基础, 通过对浮式结构物所受外域水动力和各液舱内非线性晃荡力进行模态分解, 最终形成时域解耦运动方程, 无需迭代过程即可显式计算浮式结构物的瞬时加速度. 该方法可避免传统迭代方法在迭代次数、截断误差和收敛特性等方面的限制, 减少解耦过程的计算耗时.
本文进一步结合边界元数值方法, 分别对单液舱浮式结构物和多液舱浮式结构物的开展运动模拟. 对于单液舱浮式结构物, 计算得到的纵荡RAO与实验测量值吻合良好, 验证了该解耦方法的有效性. 详细分析了晃荡力对浮体运动的影响, 发现在自然晃荡频率附近存在一个频率区间(共振影响区间). 如果外场波浪频率在该区间内, 则可能无法在时域结果中观察到稳定状态; 在该区间之外, 则浮体运动可以达到稳定状态. 在比共振影响区间更低频的波况下, 液舱内部晃荡力与外场波浪力相位相反, 晃荡液舱的存在可以减弱浮体运动, 液舱内晃荡力和外场波浪力甚至可能相互抵消, 导致极小的浮体位移. 在比共振影响区间更高频的波况下, 液舱内晃荡力与外场波浪力具有相同相位, 晃荡液舱的存在会加剧浮体的运动. 本文进一步以FLNG平台的简化模型为例, 模拟了多液舱浮式结构物的运动, 考虑了四液舱浮体发生自由纵荡、垂荡和纵摇运动的情况. 发现液舱晃荡可明显影响浮体的最大纵荡和纵摇幅值, 但对浮体的垂荡运动影响很小.
应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ).
参考文献
View Option
[1]
BP . BP Energy Outlook (2019 edition)
London: BP PLC , 2019
[本文引用: 1]
[2]
Schenk CJ Brownfield ME Charpentier RR , et al . Assessment of undiscovered oil and gas resources of southeast Asia
U.S. Geological Survey Fact Sheet 2010-3015 , 2010
DOI
URL
PMID
[本文引用: 1]
Among the greatest uncertainties in future energy supply and a subject of considerable environmental concern is the amount of oil and gas yet to be found in the Arctic. By using a probabilistic geology-based methodology, the United States Geological Survey has assessed the area north of the Arctic Circle and concluded that about 30% of the world's undiscovered gas and 13% of the world's undiscovered oil may be found there, mostly offshore under less than 500 meters of water. Undiscovered natural gas is three times more abundant than oil in the Arctic and is largely concentrated in Russia. Oil resources, although important to the interests of Arctic countries, are probably not sufficient to substantially shift the current geographic pattern of world oil production.
[3]
潘建纲 . 南海油气资源及其开发展望
海洋论坛 , 2002 ,3 :39 -49
[本文引用: 1]
( Pan Jiangang . Hydrocarbon resources and its development prospect in the South China sea
Marine Forum 2002 ,3 :39 -49 (in Chinese))
[本文引用: 1]
[4]
Molin B Remy F Rigaud S , et al . LNG-FPSO’s: Frequency domain, coupled analysis of support and liquid cargo motion
//IMAM Conference, Rethymnon, Greece , 2002
[本文引用: 2]
[5]
Malenica S Zalar M Chen XB . Dynamic coupling of seakeeping and sloshing
//Proceedings of 13th ISOPE, Honolulu, Hawaii, USA , 2003
[本文引用: 2]
[6]
Newman JN . Wave effects on vessels with internal tanks
//20th IWWWFB, Longyearbyen, Norway , 2005
[本文引用: 1]
[7]
Rognebakke OF Faltinsen OM . Effect of sloshing on ship motions
//16th IWWWFB, Hiroshima, Japan , 2001
[本文引用: 3]
[8]
Kim Y . A numerical study on sloshing flows coupled with ship motion: The anti-rolling tank problem
Journal of Ship Research 2002 ,46 :52 -62
[本文引用: 2]
[9]
Nam BW Kim Y Kim DW . Nonlinear effects of sloshing flows on ship motion
//21th IWWWFB , 2006
[10]
Kim Y Nam BW Kim DW , et al . Study on coupling effects of ship motion and sloshing
Ocean Engineering 2007 ,34 :2176 -2187
DOI
URL
Abstract This study considers the coupling effects of ship motion and sloshing. The linear ship motion is solved using an impulse-response-function (IRF) method, while the nonlinear sloshing flow is simulated using a finite-difference method. The IRF method requires the frequency-domain solution prior to conversion to time domain, but the computational effort is much less than that of direct time-domain approaches. The developed scheme is verified by comparing the motion RAOs between the frequency-domain solution and the solution obtained by the IRF method. Furthermore, a soft-spring concept and linear roll damping are implemented to predict more realistic motions of surge, sway, yaw, and roll. For the simulation of sloshing flow in liquid tanks, a physics-based numerical approach adopted by Kim [2001. Numerical simulation of sloshing flows with impact load. Applied Ocean Research 23, 53–62] and Kim et al. [2004. Numerical study on slosh-induced impact pressures on three-dimensional prismatic tanks. Applied Ocean Research 26, 213–226] is applied. In particular, the present method focuses on the simulation of the global motion of sloshing flow, ignoring some local phenomena. The sloshing-induced forces and moments are added to wave-excitation forces and moments, and then the corresponding body motion is obtained. The developed schemes are applied for two problems: the sway motion of a box-type barge with rectangular tanks and the roll motion of a modified S175 hull with rectangular anti-rolling tank. Motion RAOs are compared with existing results, showing fair agreement. It is found that the nonlinearity of sloshing flow is very important in coupling analysis. Due to the nonlinearity of sloshing flow, ship motion shows a strong sensitivity to wave slope.
[11]
Lee SJ Kim HM Lee DH , et al . The effects of LNG-tank sloshing on the global motions of LNG carriers
Ocean Engineering 2007 ,34 (1 ):10 -20
DOI
URL
Abstract The coupling and interactions between ship motion and inner-tank sloshing are investigated by a time-domain simulation scheme. For the time-domain simulation, the hydrodynamic coefficients and wave forces are obtained by a potential-thoery-based three-dimensional (3D) diffraction/radiation panel program in frequency domain. Then, the corresponding simulations of motions in time domain are carried out using convolution integral. The liquid sloshing in a tank is simulated in time domain by a Navier–Stokes solver. A finite difference method with SURF scheme is applied for the direct simulation of liquid sloshing. The computed sloshing force and moment are then applied as external excitations to the ship motion. The calculated ship motion is in turn inputted as the excitation for liquid sloshing, which is repeated for the ensuing time steps. For comparison, we independently developed a coupling scheme in the frequency domain using a sloshing code based on the linear potential theory. The hydrodynamic coefficients of the inner tanks are also obtained by a 3D panel program. The developed schemes are applied to a barge-type FPSO hull equipped with two partially filled tanks. The time-domain simulation results show similar trend when compared with MARIN's experimental results. The most pronounced coupling effects are the shift or split of peak-motion frequencies. It is also found that the pattern of coupling effects between vessel motion and liquid sloshing appreciably changes with filling level. The independent frequency-domain coupled analysis also shows the observed phenomena.
[12]
Lee SJ . The effects of LNG-sloshing on the global responses of LNG-carriers
[PhD Thesis]. Texas: Texas A&M University , 2008
DOI
URL
PMID
The introduction of the electronic health record (EHR) has had a significant impact on provider-patient interactions, particularly revolving around patient-centeredness. More research is needed to understand the provider perspective of this interaction.
[13]
Wang X Arai M . Research on computational method of coupled ship motions and sloshing
Journal of the Japan Society of Naval Architects and Ocean Engineers 2011 ,14 :97 -104
DOI
URL
[本文引用: 1]
[14]
Hashimoto H Sueyoshi M . Numerical simulation method for a coupling motion of ship and tank fluid
//25th IWWWFB, Harbin, China
[本文引用: 1]
[15]
Li Y Zhu R Miao G . et al . Simulation of tank sloshing based on OpenFOAM and coupling with ship motions in time domain
Journal of Hydrodynamics 2012 ,24 (3 ):450 -457
DOI
URL
[本文引用: 1]
Tank sloshing in ship cargo is excited by ship motions, which induces impact load on tank wall and then affects the ship motion. Wave forces acting on ship hull and the retardation function are solved by using three-dimensional frequency domain theory and an impulse response function method based on the potential flow theory, and global ship motion is examined coupling with nonlinear tank sloshing which is simulated by viscous flow theory. Based on the open source Computational Fluid Dynamics (CFD) development platform Open Field Operation and Manipulation (OpenFOAM), numerical calculation of ship motion coupled with tank sloshing is achieved and the corresponding numerical simulation and validation are carried out. With this method, the interactions of wave, ship body and tank sloshing are completely taken into consideration. This method has quite high efficiency for it takes advantage of potential flow theory for outer flow field and viscous flow theory for inside tank sloshing respectively. The numerical and experimental results of the ship motion agree well with each other.
[16]
Jiang S Teng B Bai W , et al . Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action
Ocean Engineering 2015 ,108 :140 -154
DOI
URL
[本文引用: 1]
[17]
Mitra S Wang CZ Reddy JN , et al . A 3D fully coupled analysis of nonlinear sloshing and ship motion
Ocean Engineering 2012 ,39 :1 -13
DOI
URL
[本文引用: 1]
This study investigates the coupling effects of six degrees of freedom in ship motion with fluid oscillation inside a three-dimensional rectangular container using a novel time domain simulation scheme. During the time marching, the tank-sloshing algorithm is coupled with the vessel-motion algorithm so that the influence of tank sloshing on vessel motions and vice versa can be assessed. Several factors influencing the dynamic behavior of tank-liquid system due to moving ship are also investigated. These factors include container parameters, environmental settings such as the significant wave height, current velocity as well as the direction of wind, wave and flow current acting on the ship. The nonlinear sloshing is studied using a finite element model whereas nonlinear ship motion is simulated using a hybrid marine control system. Computed roll response is compared with the existing results, showing fair agreement. Although the two hull forms and the sea states are not identical, the numerical result shows the same trend of the roll motion when the anti-rolling tanks are considered. Thus, the numerical approach presented in this paper is expected to be very useful and realistic in evaluating the coupling effects of nonlinear sloshing and 6-DOF ship motion. (C) 2011 Elsevier Ltd.
[18]
Huang S Duan W Zhang H . A coupled analysis of nonlinear sloshing and ship motion
Journal of Marine Science and Application 2012 ,11 (4 ):427 -436
DOI
URL
[本文引用: 2]
[19]
Zhao W Yang J Hu Z , et al . Coupled analysis of nonlinear sloshing and ship motions
Applied Ocean Research 2014 ,47 :85 -97
DOI
URL
[本文引用: 2]
A coupled numerical model considering nonlinear sloshing flows and the linear ship motions has been developed based on a boundary element method. Hydrodynamic performances of a tank containing internal fluid under regular wave excitations in sway are investigated by the present time-domain simulation model and comparative model tests. The numerical model features well the hydrodynamic performance of a tank and its internal sloshing flows obtained from the experiments. In particular, the numerical simulations of the strong nonlinear sloshing flows at the natural frequency have been validated. The influence of the excitation wave height and wave frequency on ship motions and internal sloshing has been investigated. The magnitude of the internal sloshing increases nonlinearly as the wave excitation increases. It is observed that the asymmetry of the internal sloshing relative to still water surface becomes more pronounced at higher wave excitation. The internal sloshing-induced wave elevation is found to be amplitude-modulated. The frequency of the amplitude modulation envelope is determined by the difference between the incident wave frequency and the natural frequency of the internal sloshing. Furthermore, the coupling mechanism between ship motions and internal sloshing is discussed. (C) 2014 Elsevier Ltd.
[20]
Zhang C . Analysis of liquid sloshing in LNG carrier with wedge-shaped tanks
Ocean Engineering 2015 ,105 :304 -317
DOI
URL
[21]
Zhang C Li Y Meng Q . Fully nonlinear analysis of second-order sloshing resonance in a three-dimensional tank
Computers & Fluids 2015 ,116 :88 -104
DOI
URL
PMID
Active development of quantum informational components such as quantum computers and quantum key distribution systems requires parameter characterization of single photon detectors. A key property of the single photon detectors is detection efficiency. One of the methods of the detection efficiency measurement, as listed in the international standard ETSI, is the reference-free twin-photon-based Klyshko method. The signal-to-noise ratio (SNR) of this method depends on the combination of the pump wavelength, the nonlinear crystal's axis angle, and the type of detector's sensitive element. When the combination is difficult, one has to deal with the low SNR of the detector counts measurement. To gain the high SNR, one has to average the long record complicated with the &quot;random telegraph signal&quot; noise. This type of noise exhibits high spectral density at a zero frequency, where simple averaging works. The heterodyne based method we have proposed is to perform averaging at the higher frequency of the modulation introduced to the standard Klyshko measurement scheme. The method was numerically simulated and experimentally tested. The 14 times improvement in SNR for the proposed method relative to the simple averaging was demonstrated by the numerical simulation and confirmed experimentally.
[22]
Zhang C Ning D Teng B . Secondary resonance of liquid sloshing in square-base tanks undergoing the circular orbit motion
European Journal of Mechanics / B Fluids 2018 ,72 :235 -250
[本文引用: 1]
[23]
Yang C Lohner R Lu H . An unstructured-grid based volume-of-fluid method for extreme wave and freely-floating structure interactions
//Conference of Global Chinese Scholars on Hydrodynamics , 2006
[本文引用: 1]
[24]
Celebi MS Akyildiz H . Nonlinear modeling of liquid sloshing in a moving rectangular tank
Ocean Engineering 2002 ,29 :1527 -1553
DOI
URL
[本文引用: 1]
[25]
Zhang C . Numerical study of nonlinear sloshing and its coupling with vessel motions
[PhD Thesis]. London: University College London , 2016
[本文引用: 4]
[26]
Cao Y Beck RF Schultz WW . Nonlinear computation of wave loads and motions of floating bodies in incident waves
//9th IWWWFB , 1994
[本文引用: 1]
[27]
Ma QW Yan S . QALE-FEM for numerical modelling of non-linear interaction between 3D moored floating bodies and steep waves
International Journal for Numerical Methods in Engineering 2008 ,78 (6 ):713 -756
DOI
URL
[本文引用: 1]
[28]
Van Daalen E . Numerical and theoretical studies of water waves and floating bodies
[PhD Thesis]. Netherlands: University of Twente , 1993
[本文引用: 1]
[29]
Tanizawa K . A nonlinear simulation method of 3-D body motions in waves
Journal of the Japan Society of Naval Architects and Ocean Engineers 1995 ,178 :179 -191
[本文引用: 1]
[30]
Vinji T Brevig P . Numerical simulation of breaking wave
//3rd International Conference on Finite Elements in Water Resources , 1981
DOI
URL
PMID
[本文引用: 1]
The main objectives of this study are to investigate the interference of multiple bottom reflected waves in the surface wave transmission (SWT) measurements in a plate and to propose a practical guide to source-and-receiver locations to obtain reliable and consistent SWT measurements in a plate. For these purposes, a series of numerical simulations, such as finite element modelling (FEM), are performed to investigate the variation of transmission coefficient of surface waves across a surface-breaking crack in various source-to-receiver configurations in plates. Main variables in this study include the crack depths (0, 10, 20, 30, 40 and 50 mm), plate thicknesses (150, 200, 300, 400 and 800 mm), source-to-crack distances (100, 150, 200, 250 and 300 mm) and receiver-to-crack distances. The validity of numerical simulation results was verified by comparison with results from experiments using Plexiglas specimens using two types of noncontact sensors (laser vibrometer and air-coupled sensor) in the laboratory. Based on simulation and experimental results in this study, practical guidelines for sensor-to-receiver locations are proposed to reduce the effects of the interference of bottom reflected waves on the SWT measurements across a surface-breaking crack in a plate. The findings in this study will help obtain reliable and consistent SWT measurements across a surface-breaking crack in plate-like structures.
[31]
Cointe R Geyer P King B , et al . Nonlinear and linear motions of a rectangular barge in a perfect fluid
//18th Symposium on Naval Hydrodynamics , 1990
[32]
Koo W Kim M . Freely floating-body simulation by a 2D fully nonlinear numerical wave tank
Ocean Engineering 2004 ,31 (16 ):2011 -2046
DOI
URL
[本文引用: 1]
Abstract Nonlinear interactions between large waves and freely floating bodies are investigated by a 2D fully nonlinear numerical wave tank (NWT). The fully nonlinear 2D NWT is developed based on the potential theory, MEL/material-node time-marching approach, and boundary element method (BEM). A robust and stable 4th-order Runge–Kutta fully updated time-integration scheme is used with regriding (every time step) and smoothing (every five steps). A special φn -η type numerical beach on the free surface is developed to minimize wave reflection from end-wall and wave maker. The acceleration-potential formulation and direct mode-decomposition method are used for calculating the time derivative of velocity potential. The indirect mode-decomposition method is also independently developed for cross-checking. The present fully nonlinear simulations for a 2D freely floating barge are compared with the corresponding linear results, Nojiri and Murayama’s (Trans. West-Jpn. Soc. Nav. Archit. 51 (1975)) experimental results, and Tanizawa and Minami’s (Abstract for the 6th Symposium on Nonlinear and Free-surface Flow, 1998) fully nonlinear simulation results. It is shown that the fully nonlinear results converge to the corresponding linear results as incident wave heights decrease. A noticeable discrepancy between linear and fully nonlinear simulations is observed near the resonance area, where the second and third harmonic sway forces are even bigger than the first harmonic component causing highly nonlinear features in sway time series. The surprisingly large second harmonic heave forces in short waves are also successfully reproduced. The fully updated time-marching scheme is found to be much more robust than the frozen-coefficient method in fully nonlinear simulations with floating bodies. To compare the role of free-surface and body-surface nonlinearities, the body-nonlinear-only case with linearized free-surface condition was separately developed and simulated.
[33]
Wu G Eatock Taylor R . Transient motion of a floating body in steep water waves
//11th IWWWFB , 1996
[本文引用: 2]
[34]
Kashiwagi M Momoda T Inada M . A time-domain nonlinear simulation method for wave-induced motions of a floating body
Journal of the Japan Society of Naval Architects and Ocean Engineers 1998 ,184 :139 -148
[本文引用: 1]
[35]
Wu G Hu Z . Simulation of nonlinear interactions between waves and floating bodies through a finite-element-based numerical tank
Proceedings of the Royal Society A 2004 ,460 :2797 -2817
DOI
URL
[本文引用: 1]
[36]
Ogilvie T . Recent progress toward the understanding and prediction of ship motions
//5th Symposium on Naval Hydrodynamics , 1964
[本文引用: 2]
[37]
Babarit A . NEMOH BEM documentation
Technical Report, Ecole Centrale de Nantes , 2014
[本文引用: 1]
[38]
Lee SJ Kim MH . The effects of inner-liquid motion on LNG vessel responses
Journal of Offshore Mechanics and Arctic Engineering 2010 ,132 (2 ):021101 -8
DOI
URL
[本文引用: 1]
[39]
朱跃 , 姜胜耀 , 杨星团 等 . 粒子法中压力振荡的机理研究
力学学报 , 2018 ,50 (3 ):688 -698
[本文引用: 1]
( Zhu Yue Jiang Shengyao Yang Xingtuan , et al . Mechanism analysis of pressure oscillation in particle method
Chinese Journal of Theoretical and Applied Mechanics 2018 ,50 (3 ):688 -698 (in Chinese))
[本文引用: 1]
[40]
李翔 , 张崇伟 , 宁德志 等 . 非周期波浪与直墙作用的非线性数值研究
力学学报 , 2017 ,49 (5 ):1042 -1049
[本文引用: 1]
( Li Xiang Zhang Chongwei Ning Dezhi , et al . Nonlinear numerical study of non-periodic waves acting on a vertical cliff
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (5 ):1042 -1049 (in Chinese))
[本文引用: 1]
[41]
Zhang C Duan W . Numerical study on a hybrid water wave radiation condition by a 3D boundary element method
Wave Motion 2012 ,49 :525 -543
DOI
URL
[本文引用: 1]
Based on the constant boundary element method in a 3D numerical wave tank, a hybrid radiation condition which is the composition of the multi-transmitting formula (MTF) method and the damping zone is studied. Numerical solutions show excellent agreements with the analytical ones, which verify the effectiveness of the hybrid method. This method can be considered as a trimming of the MTF condition, or an extension of the damping zone method, and has good ability of simulating irregular waves with relatively large frequency span. (C) 2012 Elsevier B.V.
[42]
刘晶波 , 宝鑫 , 谭辉 等 . 波动问题中流体介质的动力人工边界
力学学报 , 2017 ,49 (6 ):1418 -1427
[本文引用: 1]
( Liu Jingbo Bao Xin Tan Hui , et al . Dynamical artificial boundary for fluid medium in wave motion problems
Chinese Journal of Theoretical and Applied Mechanics 2017 ,49 (6 ):1418 -1427 (in Chinese))
[本文引用: 1]
BP Energy Outlook (2019 edition)
1
2019
... 在当前世界能源格局中, 天然气的重要地位日渐凸显[1 ] . 中国南海海域就蕴藏着丰富的天然气资源[2 -3 ] . 南海许多气田位于深海海域, 勘探和开发难度很大. 利用浮式液化天然气(floating liquified natural gas, FLNG)平台进行深海气田开发是一种可行的方案. FLNG平台多采用船形设计, 在运行期间会长期漂浮在气田上方海面, 并利用体内若干巨型液舱来储存液化后的天然气. ...
Assessment of undiscovered oil and gas resources of southeast Asia
1
2010
... 在当前世界能源格局中, 天然气的重要地位日渐凸显[1 ] . 中国南海海域就蕴藏着丰富的天然气资源[2 -3 ] . 南海许多气田位于深海海域, 勘探和开发难度很大. 利用浮式液化天然气(floating liquified natural gas, FLNG)平台进行深海气田开发是一种可行的方案. FLNG平台多采用船形设计, 在运行期间会长期漂浮在气田上方海面, 并利用体内若干巨型液舱来储存液化后的天然气. ...
南海油气资源及其开发展望
1
2002
... 在当前世界能源格局中, 天然气的重要地位日渐凸显[1 ] . 中国南海海域就蕴藏着丰富的天然气资源[2 -3 ] . 南海许多气田位于深海海域, 勘探和开发难度很大. 利用浮式液化天然气(floating liquified natural gas, FLNG)平台进行深海气田开发是一种可行的方案. FLNG平台多采用船形设计, 在运行期间会长期漂浮在气田上方海面, 并利用体内若干巨型液舱来储存液化后的天然气. ...
南海油气资源及其开发展望
1
2002
... 在当前世界能源格局中, 天然气的重要地位日渐凸显[1 ] . 中国南海海域就蕴藏着丰富的天然气资源[2 -3 ] . 南海许多气田位于深海海域, 勘探和开发难度很大. 利用浮式液化天然气(floating liquified natural gas, FLNG)平台进行深海气田开发是一种可行的方案. FLNG平台多采用船形设计, 在运行期间会长期漂浮在气田上方海面, 并利用体内若干巨型液舱来储存液化后的天然气. ...
LNG-FPSO’s: Frequency domain, coupled analysis of support and liquid cargo motion
2
2002
... 第一类是频域方法. 代表性工作包括Molin等[4 ] , Malenica等[5 ] 和Newman[6 ] , 后两者也分别被水动力学软件HYDROSTAR和WAMIT所采用. 频域方法主要在线性势流理论的框架下考虑浮体运动和液舱晃荡问题, 通常能对非共振工况给出有效的预报结果. 但受限于稳态假设, 频域方法对共振工况的预报结果往往需要校准, 该局限性已在实验中显现[7 ] . Malenica等[5 ] 在数值模型中引入人工阻尼项来校准计算结果, 但阻尼系数的选取仍依赖物理模型实验. ...
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Dynamic coupling of seakeeping and sloshing
2
2003
... 第一类是频域方法. 代表性工作包括Molin等[4 ] , Malenica等[5 ] 和Newman[6 ] , 后两者也分别被水动力学软件HYDROSTAR和WAMIT所采用. 频域方法主要在线性势流理论的框架下考虑浮体运动和液舱晃荡问题, 通常能对非共振工况给出有效的预报结果. 但受限于稳态假设, 频域方法对共振工况的预报结果往往需要校准, 该局限性已在实验中显现[7 ] . Malenica等[5 ] 在数值模型中引入人工阻尼项来校准计算结果, 但阻尼系数的选取仍依赖物理模型实验. ...
... [5 ]在数值模型中引入人工阻尼项来校准计算结果, 但阻尼系数的选取仍依赖物理模型实验. ...
Wave effects on vessels with internal tanks
1
2005
... 第一类是频域方法. 代表性工作包括Molin等[4 ] , Malenica等[5 ] 和Newman[6 ] , 后两者也分别被水动力学软件HYDROSTAR和WAMIT所采用. 频域方法主要在线性势流理论的框架下考虑浮体运动和液舱晃荡问题, 通常能对非共振工况给出有效的预报结果. 但受限于稳态假设, 频域方法对共振工况的预报结果往往需要校准, 该局限性已在实验中显现[7 ] . Malenica等[5 ] 在数值模型中引入人工阻尼项来校准计算结果, 但阻尼系数的选取仍依赖物理模型实验. ...
Effect of sloshing on ship motions
3
2001
... 第一类是频域方法. 代表性工作包括Molin等[4 ] , Malenica等[5 ] 和Newman[6 ] , 后两者也分别被水动力学软件HYDROSTAR和WAMIT所采用. 频域方法主要在线性势流理论的框架下考虑浮体运动和液舱晃荡问题, 通常能对非共振工况给出有效的预报结果. 但受限于稳态假设, 频域方法对共振工况的预报结果往往需要校准, 该局限性已在实验中显现[7 ] . Malenica等[5 ] 在数值模型中引入人工阻尼项来校准计算结果, 但阻尼系数的选取仍依赖物理模型实验. ...
... 本节考虑带有单个晃荡液舱的浮体. 首先采用本文数值方法重现物理模型实验[7 ] . 如图3 所示, 在水深1.03 m的波浪水槽中, 放置一个矩形浮体, 浮体长$L_{\rm B} = 0.4$ m、宽$B_{\rm B} = 0.596$ m、吃水$H_{\rm B} = 0.2$ m, 浮体内安置一只矩形水箱. 包括舱内液体在内, 浮体总质量为$\rho _{\rm 0} L_{\rm B} B_{\rm B} H_{\rm B} $. 通过配重来调整浮体吃水. 入射波沿着浮体长度方向传播, 浮体可以沿着两个低摩擦轨道在波浪方向上自由移动. 为了防止浮体漂移, 在浮体上安装刚度系数为30.9 N/m的弹簧, 弹簧固有频率远低于入射波的频率. ...
... 对于$\omega _{\rm a}=8$$\sim$8.3 rad/s和$\omega _{\rm a}=8.8$$\sim$10 rad/s的情况, 可以在浮体位移的时间历程曲线中观察到稳定阶段. 图10 给出了这些频率下的浮体纵荡RAO, 计算结果与实验测量结果吻合良好. 值得注意的是, 在频率高于$\omega _{\rm a}=9$ rad/s的情况下, RAO数值结果略高于实验数据. 这是因为通常在较高频率条件下流体的黏性效应更明显, 但这种微弱的偏差并未影响RAO随频率变化的整体趋势. 图中也标出具有相同总质量的冰冻液舱浮体的纵荡RAO. 通过比较可以发现, 晃荡液舱可以对浮体运动产生明显影响. 图10 也标出了文献[7 ] 的线性解析解, 线性解析解可以粗略地预测实验数据的总体趋势, 但在较宽的频率范围内无法提供令人满意的RAO预报值, 这体现了采用非线性模型进行运动预报的必要性. ...
A numerical study on sloshing flows coupled with ship motion: The anti-rolling tank problem
2
2002
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
... [8 ]、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Nonlinear effects of sloshing flows on ship motion
2006
Study on coupling effects of ship motion and sloshing
2007
The effects of LNG-tank sloshing on the global motions of LNG carriers
2007
The effects of LNG-sloshing on the global responses of LNG-carriers
2008
Research on computational method of coupled ship motions and sloshing
1
2011
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Numerical simulation method for a coupling motion of ship and tank fluid
1
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Simulation of tank sloshing based on OpenFOAM and coupling with ship motions in time domain
1
2012
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Numerical simulation of coupling effect between ship motion and liquid sloshing under wave action
1
2015
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
A 3D fully coupled analysis of nonlinear sloshing and ship motion
1
2012
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
A coupled analysis of nonlinear sloshing and ship motion
2
2012
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
... [18 ]、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Coupled analysis of nonlinear sloshing and ship motions
2
2014
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
... [19 , 24 ]); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Analysis of liquid sloshing in LNG carrier with wedge-shaped tanks
2015
Fully nonlinear analysis of second-order sloshing resonance in a three-dimensional tank
2015
Secondary resonance of liquid sloshing in square-base tanks undergoing the circular orbit motion
1
2018
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
An unstructured-grid based volume-of-fluid method for extreme wave and freely-floating structure interactions
1
2006
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Nonlinear modeling of liquid sloshing in a moving rectangular tank
1
2002
... 第二类是时域方法. 通常将液舱浮式结构物的运动模拟分为两部分进行处理. 一是液体晃荡部分. 可以采用多种数值方法进行模拟, 如有限差分法[8 -13 ] 、MPS粒子方法[14 ] 、基于OpenFOAM的有限体积法[15 -16 ] 、标识码开法[4 ] 、基于势流理论的有限元法[17 ] 和边界元法[18 -22 ] . 上述方法均可以考虑液体晃荡的非线性效应, 同时也需要消耗更多计算时间. 二是波浪与浮体相互作用部分. 可以采用时域Rankine元法[8 ] 、瞬态Green函数法[18 ] 、脉冲响应函数法[19 ] 、或Navier-Stokes标识码解器[23 ] 进行模拟. 为简化计算, 上述研究多将浮体水动力问题线性化后再进行数值求解. 而从严格意义上讲, 上述两部分计算是耦合在一起需要同时求解的. 具体而言, 求解液体晃荡和外部波浪对浮体的瞬时水动力, 需已知浮体的瞬时加速度(如文献[19 , 24 ] ); 而浮体的瞬时加速度是未知的, 需根据牛顿第二定律计算, 即加速度的计算反过来又取决于瞬时晃荡力和波浪力. 在实际计算中, 可以通过迭代过程来解决力和运动的相互依赖关系. 例如, 可以先给定一个近似的瞬时加速度, 初步计算液体晃荡和外场波浪对浮体的作用力, 得到一个新的浮体加速度; 然后更新浮体瞬时加速度, 继续上述过程, 直至计算所得浮体加速度迭代至收敛. 然而, 迭代方法也具有明显的局限性: (1)迭代次数多时计算会非常耗时; (2)实现收敛的迭代次数在各时间步具有不确定性; (3)如果迭代次数超过了预设的最大值, 会存在截断误差; (4)无法保证迭代过程一定收敛, 特别是对于多液舱浮式结构物的这一多因素系统. ...
Numerical study of nonlinear sloshing and its coupling with vessel motions
4
2016
... 针对多液舱浮式结构物的运动模拟问题, 本文将引入一种有效的时域解耦算法[25 ] . 该方法以模态分解法为基础, 通过对浮式结构物所受外场水动力和各液舱内非线性晃荡力进行模态分解, 形成时域解耦运动方程, 无需迭代过程即可显式计算浮式结构物的瞬时加速度. 该方法可以避免迭代过程在迭代次数、截断误差和收敛特性等方面的限制, 并大大减少解决耦合效应的时间消耗. 本文将基于边界元数值方法, 对单液舱浮式结构物和多液舱浮式结构物的分别开展运动模拟, 验证该算法的有效性, 并对带液舱浮式结构物的运动特性进行分析. ...
... 其中, $F_{{\rm B}i} $是恢复力, $F_i^{\rm l} $是$i$方向的波浪力. 上标$\left( 0 \right)$和$\left( 1 \right)$分别对应于定常量和线性量. $F_{{\rm B}i} $由浮体的水下几何形状和浮体重心确定[25 ] ...
... 为了计算自由表面节点$ x_0 $上的$\varphi $的切向导数, 可在垂直于法向量的平面$\xi$-$\varsigma $上将$\varphi $可以表示为(参考文献[25 ] ) ...
... 其中, $m$是垂向节点数, $z_i $是各节点的垂直坐标, 常数$\gamma (\gamma > 1)$表示垂向节点分布的均匀性. 本文在液舱侧壁和水底面分别设置20$\times$10和20$\times$20的四边形单元, 在自由面上利用根据Delaunay三角化方法生成三角形单元, 选取$\gamma =1.5$. 单元划分收敛性验证参见文献[25 ] . ...
Nonlinear computation of wave loads and motions of floating bodies in incident waves
1
1994
... 第一种是迭代法[26 -27 ] . 迭代过程首先预估浮体加速度或所受水动力, 求解浮体运动方程后更新浮体加速度或水动力. 反复进行该过程, 当加速度或水动力收敛至稳定值时, 终止迭代过程. 该方法思路简单, 但有引言所述缺点. ...
QALE-FEM for numerical modelling of non-linear interaction between 3D moored floating bodies and steep waves
1
2008
... 第一种是迭代法[26 -27 ] . 迭代过程首先预估浮体加速度或所受水动力, 求解浮体运动方程后更新浮体加速度或水动力. 反复进行该过程, 当加速度或水动力收敛至稳定值时, 终止迭代过程. 该方法思路简单, 但有引言所述缺点. ...
Numerical and theoretical studies of water waves and floating bodies
1
1993
... 第二种是隐式边界条件法[28 -29 ] . 该方法核心思想是将浮体加速度$a = \bar{M}^{ - 1}\left( {F_{\rm d} + F_{\rm e} } \right)$代入$\varphi _t $的边界条件, 形成关于$\varphi _t $的显式边值问题, 求解可得流域边界上的$\varphi _t $值, 进而计算当前时刻浮体所受水动力和浮体加速度. 该方法避免了迭代过程, 但需要为$\varphi _t $与$\varphi $分别构建具有不同系数矩阵的线性方程组, 系数矩阵元素表达式复杂. 当引入多个液舱时, 这种不便性将更加突出. ...
A nonlinear simulation method of 3-D body motions in waves
1
1995
... 第二种是隐式边界条件法[28 -29 ] . 该方法核心思想是将浮体加速度$a = \bar{M}^{ - 1}\left( {F_{\rm d} + F_{\rm e} } \right)$代入$\varphi _t $的边界条件, 形成关于$\varphi _t $的显式边值问题, 求解可得流域边界上的$\varphi _t $值, 进而计算当前时刻浮体所受水动力和浮体加速度. 该方法避免了迭代过程, 但需要为$\varphi _t $与$\varphi $分别构建具有不同系数矩阵的线性方程组, 系数矩阵元素表达式复杂. 当引入多个液舱时, 这种不便性将更加突出. ...
Numerical simulation of breaking wave
1
1981
... 第三种是模态分解方法[30 -32 ] . 该方法首先将$\varphi _t$中各加速度项显式分离出来, 形成多模态求和的形式 ...
Nonlinear and linear motions of a rectangular barge in a perfect fluid
1990
Freely floating-body simulation by a 2D fully nonlinear numerical wave tank
1
2004
... 第三种是模态分解方法[30 -32 ] . 该方法首先将$\varphi _t$中各加速度项显式分离出来, 形成多模态求和的形式 ...
Transient motion of a floating body in steep water waves
2
1996
... 第四种是辅助函数法[33 -34 ] . 该方法可看作模态分解法的变种. 由于$\varPsi _i $和$\overline {\varphi _t } $均满足Laplace方程, 可根据格林公式得到 ...
... 注意, 文献[33 ] 在式(32)中采用了$\varphi _t $而非$\overline \varphi _t $, 本质上与本文推导等同. 该方法无需求解$\overline \varphi _t $, 但也不能直接获得浮体表面的压力. 如需计算压力, 可在求得浮体加速度后进一步求解关于$\varphi _t $的边界值问题. ...
A time-domain nonlinear simulation method for wave-induced motions of a floating body
1
1998
... 第四种是辅助函数法[33 -34 ] . 该方法可看作模态分解法的变种. 由于$\varPsi _i $和$\overline {\varphi _t } $均满足Laplace方程, 可根据格林公式得到 ...
Simulation of nonlinear interactions between waves and floating bodies through a finite-element-based numerical tank
1
2004
... 可引入辅助函数$\chi ^k$来间接求解[35 ] . 辅助函数形式为 ...
Recent progress toward the understanding and prediction of ship motions
2
1964
... 可用脉冲响应函数方法[36 ] 表示浮体的辐射势. 在$t$时刻, 辐射势可以写成 ...
... 利用Ogilvie[36 ] 方法, 可求得系数$A_{{\rm R}ij} $和$B_{{\rm R}ij} $. 在频域中, 浮体运动和辐射势可以表示为 ...
NEMOH BEM documentation
1
2014
... 图2 给出了时域解耦算法的实现流程. 首先是参数准备阶段. 计算式(50)中的恢复力系数$C_{ij} $, 利用频域求解器生成频率相关系数(包括$\tilde{A}_{{\rm R}ij} $和$\tilde{B}_{{\rm R}ij} )$和绕射力,并由式(60)和式(62)求得到脉冲响应函数方法的系数$A_{{\rm R}ij}$和$B_{{\rm R}ij}$(本文采用开源软件Nemoh[37 ] 在频域中求解速度势的边值问题得到系数$\tilde{A}_{{\rm R}ij} $和$\tilde{B}_{{\rm R}ij} )$. 然后是时间步进阶段. 在各时刻计算开始前, 浮体的位移和速度是已知的. 先求解各液舱的速度势$\varphi $, 再求解各液舱中的$\varPsi _i^k $和$\overline{\varphi _t^k } $的边值问题, 之后计算系数$A_{ij}^k $和$U_i^k $, 进一步利用式(56)计算浮体瞬时加速度. 已知浮体瞬时加速度后, 可以通过时间步进得到下一时间步浮体的速度和位移, 以及各流域的边界条件, 并进行下一时间步的计算. 应该指出的是, 作为示意, 图2 为欧拉时间步进方法, 本文采用了更高精度的时间步进方法. 本文首先采用了四阶Runge-Katta方法进行前十步时间步进运算, 然后采用四阶Adams-Bashforth方法进行后续时间步进. ...
The effects of inner-liquid motion on LNG vessel responses
1
2010
... 本节将考虑一个简化的FLNG平台模型. FLNG平台连接在转塔式系泊系统上. 该平台能够像风向标一样旋转, 使其能够顺应入射波的方向. 此时, FLNG平台主要进行纵荡、垂荡和纵摇运动. 本节参考文献[38 ] 采用如图13 (a)的简化模型. 该平台具有驳船形状, 长280 m, 宽60 m和吃水15 m. 浮体上沿长度方向均匀分布4个边长为40 m的立方体液舱. 各液舱舱底位于浮体龙骨线以上3 m位置处. 相邻液舱之间有3 m距离. 各液舱装有LNG, 其密度约为水密度的0.46倍. 每个液舱内液体深度是20 m. 设定浮体质量为$m$, 各工况下浮体吃水保持不变. 固定坐标系$O$ $\!-\!$ $xyz$的原点$O$位于浮体重心处, $Ox$ 轴指向船尾. 重心距离浮体底部15 m. 浮体的惯性回转半径$\sqrt {{I_{{\rm xx}}}/{m}}$, $\sqrt {{I_{{\rm yy}} }/{m}} $和$\sqrt {{I_{{\rm zz}} }/{m}} $分别为20 m, 80 m和80 m. 另外, 沿水平方向施加刚度系数为$6.5\times10^5$ N/m的系泊系统. 外部波浪的入射角为0度, 且波幅为2 m. 边界单元分布如图13 (b)所示. 浮体表面和液舱流域边界上分别有976和2218个单元. 各液舱的水平合力可以超过来自外场波浪的水平力, 而外部波浪的力矩总是大于晃荡引起的力矩. 随着时间的推移, 晃荡引起的力/力矩逐渐接近与外场波浪力/力矩同相位, 导致浮体运动幅度增大. ...
粒子法中压力振荡的机理研究
1
2018
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...
粒子法中压力振荡的机理研究
1
2018
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...
非周期波浪与直墙作用的非线性数值研究
1
2017
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...
非周期波浪与直墙作用的非线性数值研究
1
2017
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...
Numerical study on a hybrid water wave radiation condition by a 3D boundary element method
1
2012
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...
波动问题中流体介质的动力人工边界
1
2017
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...
波动问题中流体介质的动力人工边界
1
2017
... 应该说明的是, 本文基于势流理论开展计算, 尚未考虑流体黏性和湍流等因素的影响, 特别是对于涉及大幅波浪翻卷破碎的极端情况, 须采用黏性流体力学计算模型(如文献[39 ] ). 浮体外域可采用全非线性势流理论方法求解(如文献[40 ] ). 除了自由面阻尼区方法外, 也可以在外域截断边界处采用其他形式的人工边界条件(如文献[41 ,42 ] ). ...