引 言
由于多刚体系统动力学已发展的比较成熟和完善,本文主要关注多柔体系统动力学. 过去,人们对多柔体系统的部件动力学设计通常采用试错法. 这种设计方法不仅耗时,而且无法保证得到最优结果. 人们也常将系统中某个重要部件进行单独静力学优化,根据经验来假定部件所受的载荷,不考虑系统运行环境对部件优化的影响. 这类优化设计适用于比较刚性的多体系统,无法处理具有大范围运动与大变形耦合的多柔体系统. 事实上,部件柔性对多柔体系统的动力学行为影响很大,直接影响到优化结果. 因此,不论是航空、航天等科技领域,还是机械领域,均需要发展基于多柔体系统动力学的柔性部件优化设计方法[4].
传统的结构优化设计包括尺寸优化、形状优化和拓扑优化等,已非常成熟[5]. 然而,多柔体系统优化设计仍处于发展阶段. 多柔体系统动力学优化设计的目的是寻找安全、经济的多柔体系统形式或多柔 体系统中某些部件的结构形式. 多柔体系统形式包括系统中运动副的数量、位置和类型,柔性部件的布局等;而部件的结构形式包括部件尺寸、形状和拓扑等信息. 为了能够设计出超越设计者经验的多柔体系统构型和部件构型,拓扑优化是非常有效的工具. 多柔体系统动力学优化设计是集多柔体系统动力学、有限单元法、数学规划法、数值计算方法、程序设计等诸多学科的产物. 其主要思想是:在满足工程系统各种性能要求的约束条件下,建立多柔体系统动力学优化数学模型,将多柔体系统动力学分析 和优化算法相结合,对多柔体系统中柔性部件的尺寸、形状和拓扑等进行优化设计. 多柔体系统动力学优化设计使得多柔体系统动力学的研究任务由被动的数值仿真和分析预测上升为主动的设计与优化. 因此,多柔体系统动力学优化具有重要的应用价值,同时具有更大的难度和挑战.
根据 Web of Science 数据库检索(截至 2019 年 10 月 17 日),以“multibody dynamics” 为主题的 SCI 检索期刊论文共 4019篇,在这些结果中再以 “optimization of multibody dynamics” 为主题进行检索,得到 SCI 检索期刊论文 502 篇. 在这 502 篇文章中,中国学者发表的论文占 103 篇,位居第一;位居第二的是美国学者,共发表95篇. 这表明,在多体系统动力学研究中,对动力学优化的研究比重还不高;而在研究动力学优化的学者中,以中国学者和美国学者为主. 此外,在这 502 篇期刊论文中,尚没有 ESI 高被引论文,表明该领域的学术影响力尚待提高.
在 Web of Science 数据库中,以 “optimization of multibody dynamics” 为主题的 SCI 期刊论文来源数量位居前八名的期刊分别是:《Multibody System Dynamics》《Vehicle System Dynamics》《Journal of Computational and Nonlinear Dynamics》《Mechanism and Machine Theory》《Structural and Multidisciplinary Optimization》《Nonlinear Dynamics》《International Journal for Numerical Methods in Engineering》和《Mechanics based Design of Structures and Machines》. 其中《Structural and Multidisciplinary Optimization》创刊于 1989 年,是结构优化研究领域的专业期刊,也是国际结构与多学科优化学会 (International Society of Structural and Multidisciplinary Optimization,ISSMO) 的官方期刊. ISSMO隔年举办系列国际会议——世界结构与多学科优化大会 (World Congress of Structural and Multidisciplinary Optimization,WCSMO). 最新一届大会 (The 13th WCSMO) 于 2019 年 5 月 20—24 日在北京召开,北京理工大学胡海岩教授作大会唯一特邀报告“Deployable Space Structures: Challenges to Computational Dynamics”,报告系统介绍了其学术团队在多柔体系统动力学建模、分析及优化方面的研究进展. 另外,北京理工大学田强教授和美国 Shabana 教授在 2018 年 6 月召开的第18届美国理论与应用力学大会[6] (18th U.S. National Congress of Theoretical and Applied Mechanics,USNCTAM2018) 上联合组织了多体系统动力学分论坛,并作了 “Structural and Topology Optimization of Flexible Multibody Systems” 的报告[7],获得多位国际著名学者的高度评价. 下面,本文从多柔体系统动力学建模、动力学优化和部件优化等方面对国内外相关研究成果和最新进展进行回顾, 并梳理值得关注的若干问题,为相关的研究者提供参考.
1 多柔体系统动力学建模研究
对多柔体系统动力学开展优化设计,首先要建立多柔体系统的动力学模型,然后根据系统动力学响应或动力学特性的设计目标, 通过优化设计方法寻优求解得到优化结果. 因此,动力学模型是进行多柔体系统优化设计的基础与前提.
目前,对于具有小变形、小转动或低转速的多柔体系统,其动力学建模已比较成熟[2],采用商用软件 ADAMS[8] 即可完成任务. 但对于具有大范围运动和大变形耦合的多柔体系统,尤其是含变长度柔性部件的多柔体系统动力学建模问题,其动力学建模仍具有不少挑战. 本节综述 3 种多柔体系统动力学建模方法,即浮动坐标方法 (floating frame of reference formulation,FFRF),几何精确方法 (geometrically exact formulation,GEF) 和绝对节点坐标方法 (absolute nodal coordinate formulation,ANCF),并在每种方法中总结了含变长度柔性部件的多柔体系统动力学建模进展.
1.1 浮动坐标方法
针对浮动坐标法的不足,学者们已提出若干解决方案. 例如,对于高度非线性的惯性力项,Lugrís 等[14]提出两种计算惯性力的高效方法. 一种方法是通过变量映射矩阵 将有限元质量矩阵映射到广义坐标上,另一种方法是在预处理阶段进行惯性形状积分计算. Orzechowski等[15]提供了一种在浮动坐标法中计算惯性力项的可靠且通用方法. 对于经典浮动坐标法只能描述柔性部件小变形问题,Nada 等[16] 研究了采用浮动坐标法描述具有大范围运动与大变形的 多柔体系统,并进行了实验验证. Das 等[17] 采用拉格朗日描述的协同转动法来描述柔性部件的大变形. Wu 和 Tiso[18] 采用模态导数法研究了具有大变形的多柔体系统的降阶模型. 但上述努力并未从根本上解决问题. 主要原因是尚未提出一种能够同时克服浮动坐标法所有不足的改进方案,也没有提出能够描述高速转动的浮动坐标方法.
1.2 几何精确方法
几何精确方法一般包含几何精确梁方法 (geometrically exact beam formulation,GEBF) 和几何精确板/壳等方法[21-27],其中几何精确梁方法诞生于 20 世纪 80 年代[28-29], 能够高效并精确地处理梁的大转动与大变形耦合问题. 在一些文献中,该方法又被称为大转动矢量方法[30] (large rotation vector formulation,LRVF) 或几何精确非线性有限元方法[4, 31]. Shabana 在综述论文[32]中介绍了大转动矢量方法的特点及其不足之处. 例如,大转动矢量方法采用位移与转角相互独立的节点坐标表达梁的截面转动,这种分别插值不仅会导致坐标冗余, 还会导致几何描述的巨大差异. 对于某些细长结构,还会产生奇异问题和不真实的剪切力[33]. 此外,矢量的加法运算并不适用于有限转动矢量,比如采用 3 个欧拉角描述的转动矢量[34],而在大转动矢量 方法中的转动矢量插值涉及到矢量加法,这与刚体运动学的基本原理是相违背的[30]. 这些不足限制了大转动矢量方法在多柔体系统建模中的广泛应用[32]. Shabana[35] 还指出大转动矢量方法对位移场和转角场分别插值会导致空间曲线的两种不同几何形状以及不同的刚体位移. 例如,对位移场线性插值在单元内部不会产生曲率,而对转角场线性插值则会在单元内部产生高度非线性的曲率,从而导 致多柔体系统运动学描述的不唯一性问题. Ding 等[34, 36] 也指出上述问题,同时还指出转角插值会降低应变能和惯性力计算的精度,尤其是大变形问题.
为了解决大转动矢量方法的上述局限性,不少学者做出了努力. 例如,Jeleni$\acute{c}$ 和 Crisfield[37] 提出了三维梁转角的两种插值形式,可保证转角的客观性和兼容性. Betsch 等[38]针对壳单元大转角提出了一种无奇异的插值形式. Ghosh 和 Roy[39] 研究了四元数插值的几何精确梁模型,将传统的大转动矢量转变为四元数,从而使插值更加高效. Ghosh 和 Roy[40] 还提出了一种相对转动矢量插值方式和转动矢量更新形式,可得到旋转不变性和路径无关性的结果. Bauchau 和 Han 系统地研究了位移场和转角场的插值方式,提出的插值方式能够保证旋转张量不变性以及精度[41], 并引入辛矩阵,采用哈密尔顿力学对梁进行建模[42]. M$\ddot{a}$kinen[43] 通过改变旋转流形上的参数,消除几何精确梁大转动时的奇异性. Zupan等[44] 提出了一种基于四元数的三维几何精确梁理论,可满足相容条件. Zhang 和 Zhong[45-46] 在完全拉格朗日格式 (total Lagrangian formulation) 下推导了二维和三维几何精确梁单元,并采用四元数法来描述梁单元的大转动,可有效避免奇异性,并且减少广义坐标的个数. Fan 和 Zhu[47] 提出了一种无奇异的 Euler--Bernoulli 几何精确曲梁,采用欧拉参数来描述梁截面的转角. 此后,Fan和Zhu[48-49] 还提出了无闭锁问题的三维剪变梁单元. Shabana[30] 提出了一种一致旋转方法 (consistent rotation-based formulation,CRBF),采用绝对节点坐标方法的运动学描述,只定义一个转角场、采用一种插值方式,进而能描述剪切变形, 避免坐标冗余问题.
近年来,基于李群描述的多柔体系统动力学建模研究引起众多学者关注. Brüls等[50-51]借助李群和李代数基本理论,在特殊欧氏群 ${SE}$(3) 中描述物体的运动, 并定义适当的局部标架,对角速度进行插值,可有效避免转角的参数化问题,因此,该方法也被称为局部标架法 (local frame formulation). 其优点是能够统一处理节点转动与平动,使得运动方程更加紧凑、约束方程简单等. 此外,基于李群描述的多柔体系统动力学优化与控制等研究也引起广泛关注. 例如,空间多刚体系统动力学建模研究[52]、李群描述的几何精确梁单元研究[53]、多体系统灵敏度 分析[54]、多柔体系统部件优化设计[55]、无穷维力学系统的 Hamel 形式[56] 和球形移动机器人最优控制[57] 等. 这表明,李群理论已成为多柔体系统动力学研究的重要工具.
由于有限转动的不可交换性,经典的几何精确方法或大转动矢量方法通常借助共旋坐标法 (corotational frame formulation) 来实现,关于共旋坐标法的详细介绍可参考综述文章[58-59] 和博士论文[60]. 基于李群描述的局部标架法与共旋坐标法看似相似,但有着本质的区别. 第一,局部标架法的局部标架定义在节点上,例如一个二节点的几何精确梁单元有两个局部标架,而共旋坐标法的共 旋标架定义在单元上,即每个单元对应一个共旋标架;第二,由于局部标架定义在节点上,故可轻易地进行有限元组装, 而共旋坐标定义在单元内部,无法进行组装;第三,局部标架法得到的动力学方程定义在局部标架中,而共旋坐标法得到的动 力学方程定义在全局坐标系中,共旋标架只起到中间连接的作用.
对于含变长度柔性部件的多柔体系统,近年来,学者们提出了基于任意拉格朗日-欧拉 (arbitrary Lagrangian--Eulerian,ALE) 描述的几何精确梁方法[61],但该方法研究仍处于起步阶段.
1.3 绝对节点坐标方法
20 世纪 90 年代中期,Shabana 提出绝对节点坐标方法[62-63]. 该方法的理论基础是连续介质力学和有限单元法,推动了多柔体系统动力学与有限元方法的紧密结合. 该方法是多柔体系统动力学研究史上的里程碑,也是多柔体系统动力学的研究热点之 一[2]. 该方法在全局坐标系下考察柔性部件的动态构型,选择单元节点的位置矢量坐标和斜率矢量坐标作为广义坐标,有效避 开了有限转动的参数化问题. 基于该方法建模的优点是系统动力学方程具有常质量矩阵,不存在科氏力和离心力项,约束方程描述简单、无需进行坐标转换等. 此外,在惯性坐标系下,可采用统一的插值函数描述柔体的大范围转动与大变形,能精确地反映柔性部件动力学中的几何非线性. 当然,绝对节点坐标方法也有其局限性. 例如,该方法通常导致系统动力学方程具有很高维数和众多约束,计算效率偏低. 对于线性位移应变关系,采用绝对节点坐标方法得到的刚度矩阵具有非线性,对于非线性位移应变关系,其刚度矩阵将会更复杂[64]. 此外,绝对节点坐标描述的单元通常还会遇到泊松闭锁[65] 和剪切闭锁[66] 等问题,学者们也提出了相应的解决方案[66 -68].
目前,根据不同的研究背景与目的,学者们已提出了多种基于绝对节点坐标描述的梁单元和板壳单元. 例如,田强等[3]系统综 述了 2010 年之前绝对节点坐标法的单元研究进展. Gerstmayr 等[69] 系统地综述了2013年之前基于绝对节点坐标描述的梁、板单元的研究进展. Nachbagauer[70] 详细综述了绝对节点坐标法在单元构造、高效计算格式构建与工程应用方面进展情况. 王庆涛[71] 和常汉江[64] 也综述了基于绝对节点坐标描述的各种梁单元和板壳单元,包括缩减单元和全 参数单元、黏弹性单元、超弹性单元以及单元的闭锁问题与解决方案等. Hu等[72] 对绝对节点坐标法在软机器动力学建模与仿真中研究进行了综述. 因此,本文不再赘述基于绝对节点坐标描述的梁单元和板壳单元,而是总结基于绝对节点坐标描述的实体单元,因为实体 单元是多柔体系统中三维部件优化设计的建模基础.
近年来,基于绝对节点坐标描述的三维实体单元得到广泛关注与应用. Olshevskiy 等[73]最早提出了基于绝对节点坐标描述的八节点六面体实体单元;随后又提出了基于绝对节点坐标描 述的四面体实体单元[74]. 但 Olshevskiy 等[73-74] 并没有推导单元非线性弹性力的计算公式,也没有给出应用算例. Wei 等[75]提出两种基于绝对节点坐标描述的八节点六面体实体单元,并研究了完全拉格朗日描述下的液体晃动模型. Wei 等[75]提出的第一种八节点六面体实体单元与 Olshevskiy 等[73] 提出的单元一致,采用不完全的多项式表达, 只取 8 个节点的位置矢量和3个方向的斜率矢量作为广义坐标,单元的广义坐标数为 96. Wei 等[75]提出的第二种八节点六面体实体单元则采用完全多项式表达,节点广义坐标除了位置矢量和3个方向的斜率 矢量外,还包含3个二阶梯度项和一个三阶梯度项,故单元的广义坐标数为 192. Pappalardo 等[76]也提出了基于绝对节点坐标描述的四面体实体单元,并给出了两种参数定义方法. 他们采用节点位置矢量和 3 个斜率矢量作为单元广义节点坐标. 与 Olshevskiy 等[74] 不同的是,Pappalardo 等[76] 给出了基于绝对节点坐标描述的四面体实体单元的具体细节. Pappalardo 等[76] 还指出,由于传统六面体单元和四面体单元不含斜率项,无法保证节点处斜率的连续性和转动场的连续性, 而基于绝对节点坐标描述的三维实体单元可以解决该问题.
2011 年,清华大学任革学教授等提出 ALE--ANCF 变长度索、梁单元[77-79]. Tang 等[79] 结合拉格朗日描述和欧拉描述,提出了绝对节点坐标的变长度索单元,并研究了绳系卫星的展开动力学仿真. 但Tang 等[79] 提出的变长度索单元需事先定义边界单元故只能描述简单边界情况. Hong 和 Ren[78]、Hong 等[77] 通过引入两个物质坐标,提出了 ALE--ANCF 变长度梁单元. 该单元可处理复杂边界情况,比如柔性绳索上的滑动铰. 此外,根据单元弹性力定义,该单元既可描述变长度细长梁和绳索,又可描述不可压流体. 然而,Hong 和 Ren[78]、Hong 等[77] 并没有考虑变长度梁单元的扭转. Du 等[80] 提出了一种仅采用节点位置矢量作为广义坐标的变长度索单元,不计单元弯曲和扭转变形,研究了绳索驱动的并联机器人. Escalona[81] 提出了一种变长度索单元,通过引入一个转角坐标考虑单元扭转变形,并研究了经典的滑轮绳索系统动力学. 在该研究中,Escalona[81] 采用两个节点的位置矢量、两个物质坐标和两个扭转角作为广义坐标,没有采用节点斜率坐标. 因此,根据 Shabana[63] 关于绝对节点坐标法的定义,Du 等[80] 和 Escalona[81] 所提出的变长度 索单元并不属于绝对节点坐标单元. Yang等[82]对上述变长度的索、梁单元进行综合,提出一种新的ALE--ANCF变长度梁单元. 该单元采用两个节点的位置矢量、斜率矢量、两个物质坐标和两个截面扭转角作为广义坐标,从而可描述变长度梁结构的扭转变形.
2 多柔体系统动力学优化研究
根据优化设计的目的,多柔体系统动力学优化设计可分为多柔体系统动力学响应优化和多柔体系统动力学特性优化. 本节分别对这两类优化问题以及多柔体动力学灵敏度分析进行综述.
2.1 动力学响应优化
对具有大范围运动的机械系统开展动力学响应优化设计可追溯到 20 世纪 70 年代. 例如,Erdman 等[86] 采用经典有限元描述柔性连杆的变形,并根据试错法来更新设计变量. Imam 和 Sandor[87]、Oral 和 Kemal Ider[88] 根据最坏情况法将与时间相关的约束转化为逐点约束. Imam 和 Sandor[89] 通过两步法研究了高速机械系统的设计,先将连杆看作刚体进行运动学分析,再根据弹性动力平 衡条件设计连杆的截面面积. Khan 等[90]和 Thornton 等[91]采用优化准则法优化了柔性连杆的质量. Cleghorn 等[92]、Zhang 和 Grandin[93]提出一种改进的 Khan 方法,可减少优化迭代的步数. 这种改进的Khan方法就是通过两次 Khan 方法分别找到设计变量的初始值和最优值. Sohoni 和 Haug[94]采用状态空间法优化机械系统,可以处理一般的目标函数和约束函数. Etman 和 Van Campen[95] 采用连续近似概念优化多体系统,根据有限差分法计算设计变量的灵敏度信息,并折中选取设计变量值以提高近似精度. Kim 和 Choi[96] 提出一种机械系统动力学响应优化设计的全局收敛算法,采用近似增广拉格朗日进行线性搜 索,并采用精确的增广拉格朗日找到搜索方向.
在早期的机械系统动力学响应优化设计中,通常采用试错法. 该方法不仅耗时,而且无法保证得到最优结果. 此外,人们一般仅对系统中某个部件单独进行优化,不考虑系统运行环境对部件优化的影响. 此时,部件所受载荷只能根据设计人员的经验来假设,并通过引入动载荷因子来保障设计安全性. 这类优化过 程可用于较为刚硬的机械系统,但不适用于柔体系统,因为部件柔性对系统动力学的响应影响非常大.
近年来,随着多柔体系统动力学建模方法的发展,多柔体系统动力学响应优化设计引起很多学者关注. 基于精确的多柔体系统动 力学模型,可真实地描述柔性部件的大范围运动和大变形耦合,得到准确的动力学响应,从而得到更加合理的优化结果. 本文第1节已综述了多柔体系统动力学的主要建模方法,以下概述基于浮动坐标方法、几何精确方法、绝对节点坐标法方法的 多柔体系统动力学优化研究进展.
还有的学者基于绝对节点坐标法,开展了多柔体系统动力学优化设计研究. 例如,Vohar 等[107]最早采用绝对节点坐标梁单元研究了柔性机械臂的动力学响应尺寸优化设计. 但他们在优化时并没有根据绝对节点坐标法建立的模型进行优化,而是采用映射方法,将绝对节点坐标梁单元映射到传统有限元上进行优化. 孙加亮等[108]采用绝对节点坐标缩减梁单元和三维全参数梁单元分别研究细长柔性连杆和星载机械臂的动力学响应尺寸优化设计, 并考虑了应力约束问题. 随后,孙加亮等采用绝对节点坐标薄板单元和三维实体单元,研究了二维[109]和三维[110]多柔体系统结构拓扑优化设计问题. Kim和Cho[111]采用绝对节点坐标梁单元研究了平面多柔体系统优化设计问题,提出了一种等效模型,可在单元层次高效地求解单元 刚度矩阵,提高优化计算效率. 孙加亮等基于 ALE--ANCF 变长度薄板单元和三维实体单元,分别研究了含变长度柔性部件的二维多柔体系统结构拓扑优化设计[84]和 空间三维伸展臂的尺寸与拓扑优化设计[112].
在上述这些研究中,多柔体系统动力学响应优化设计方法可分为两类[4]:一是基于强耦合模型的优化设计,二是基于弱耦合模型的 优化设计. 现对这两种优化模型分别进行综述.
(1)强耦合优化模型
多柔体系统动力学响应的强耦合优化模型源自对一类系统动力学响应优化问题. 以绝对节点坐标建模方法为例,其优化方程可表示为
式中,${\pmb b}$ 为设计变量列阵,$N_b $ 为设计变量的个数,设计变量可以是待优化部件的几何参数或材料参数;$f({\pmb b}, {\pmb q}_D (t))$ 为目标函数,一般为部件的质量、体积、应力等;对于动力学响应优化问题,目标函数不仅与设计变量 ${\pmb b}$ 相关,还与时间 $t$ 相关.
在式 (1) 的约束方程中,前两个方程是一般的多柔体系统动力学方程,通常为指标 3 的微分-$\!$-代数方程组 (differential-algebraic equations,DAEs). 其中,${\pmb M}$ 为系统质量矩阵,${\pmb q}_D $ 为系统广义坐标列阵,${\pmb \lambda }$ 为拉氏乘子列阵,${\pmb \varPhi }$ 为多柔体系统运动学约束列阵,${\pmb \varPhi }_{,{q}_D } $ 表示 ${\partial {\pmb \varPhi }} / {\partial {\pmb q}_D }$;${\pmb \varPhi }_{,{q}_D }^{\rm T} {\pmb \lambda }$ 表示系统的约束力列阵,${\pmb Q}({\pmb b}, {\pmb q}_D , \dot{\pmb q}_D )$ 表示系统的广义力列阵,可表示为
式中,${\pmb F}_{\rm f} ({\pmb b}, {\pmb q}_D , \dot {\pmb q}_D )$ 为广义外力列阵,包括重力、接触力、空气阻力等,${\pmb F}_{\rm e} ({\pmb b}, {\pmb q}_D )$ 为广义弹性力列阵.
在式(1)的约束方程中,第3个方程是不等式约束方程,其中,$g_j ({\pmb b},{\pmb q}_D (t)) \ (j = 1, 2, \cdots , N_r )$ 表示系统的$N_r $个动力学响应,可以是跟踪误差响应、应力响应等,$G_j \ (j = 1, 2, \cdots , N_r )$ 表示这些动力学响应方程的允许最大值. 值得注意的是,式 (1) 只包含不等式约束方程,因为在理论上任何一个等式约束都可等效为两个不等式约束. 在式 (1) 的约束方程中,第4个方程表示设计变量所属的设计空间,即 $\mathcal{U}_{b} $ 包含每个设计变量的上限和下限.
优化求解式 (1) 时,在每个迭代步上都需要进行多柔体系统动力学分析与灵敏度分析,并处理与时间相关的约束. 因此, 多柔体系统动力学响应强耦合优化模型具有求解耗时、效率低[113],并且实现复杂等[114-117]难点. Kang 等[118]综述了 2006 年之前机械系统动力学响应优化设计. 近期,Tromme 等[4] 详细综述了基于多柔体系统动力学响应的结构优化设计模型与方法进展. Pereira 和 Dias[119] 基于强耦合优化模型,研究了防碰撞性动力学优化设计. Brüls等[120]采用进化数值算法,研究了多柔体系统中柔性部件的拓扑优化设计. 此外,Wang、Dong、Held 和 Tromme 等[121-124] 研究了强耦合优化模型在多柔体系统动力学响应优化上的应用.
(2)弱耦合优化模型
多柔体系统动力学响应的弱耦合优化模型源自另一类系统动力学响应优化问题. 此时,可将动力学响应优化设计问题通过等效静载荷转化为静力学响应优化设计问题,根据部件的静力学响应进行优化设计. 以绝对节点坐标建模方法为例,其优化方程可表示为
式中,$t_i $ 为第 $i$ 个时间步,$N_t $ 为总的时间步的个数,${\pmb F}_{\rm e} $ 为系统弹性力列阵,${\pmb F}_{\rm eq} $ 为系统等效静载荷列阵. 值得注意的是,式 (3) 中的 ${\pmb q}_S $ 也表示系统广义坐标列阵. 与式 (1) 中的 ${\pmb q}_D $ 不同,计算 ${\pmb q}_D $ 要求解系统动力学方程,而计算 ${\pmb q}_S $ 只要求解等效静平衡方程.
对于这类模型的优化求解,可分两步进行[97]:
第一步,进行多柔体系统动力学分析,得到所优化部件在各个时间步的等效静载荷集. 基于绝对节点坐标方法建模,系统中单个部件的等效静载荷集定义为:在任意一个时间步上,根据多柔体系统动力学分析与等效静力学分析得到该部件相同变形场的载荷集[108],其表达式如下
式中,上标 $c$ 表示第 $c$ 个部件,系统中待优化的总部件数为 $N_m $,${\pmb q}_R $ 表示多柔体系统对应刚性运动的广义坐标. 这样,${\pmb F}_{\rm eq}^{ c} $, $ {\pmb K}^{ c}$, ${\pmb q}_D^{ c} $ 和 ${\pmb q}_R^{ c} $ 分别表示第 $c$ 个部件的等效静载荷集、刚度矩阵、广义坐标、刚性运动广义坐标. $ {\pmb q}_D^{ c} (t_i ) - {\pmb q}_R^{ c} (t_i )$ 表示该部件在不同时间步的变形场. 从式 (4) 的定义可见,在计算等效静载荷时,已将部件的刚体运动 ${\pmb q}_R^c $ 从其大范围运动 ${\pmb q}_D^{ c} $ 中去除. 这样处理的原因如下:一是部件刚体运动不 产生应变能,故从大范围运动 ${\pmb q}_D^{ c} $中分离出的变形场 ${\pmb q}_D^{ c} - {\pmb q}_R^{ c} $ 与 $ {\pmb q}_D^{ c} $ 具有相同应变能;二是采用变形场而不是位移场 来定义等效静载荷,可避免在静平衡分析时的奇异性.
第二步,根据等效静力学响应优化柔性部件的结构,完成如下静响应优化设计问题
此外,为了消除动力学系统与等效静力学系统的差异,以上两步优化过程需要不断循环进行. 例如,H$\ddot{a}$ussler 等[125-126] 在进行多柔体系统动力学分析时,考虑了运动副和边界条件的约束反力,并 将这些力代入静力学优化中. Ilzhöfer 等[127] 和 Albers 和 H$\ddot{a}$ussler[128] 基于等效静载荷方法,研究了寿命预测设计和耐久性设计. Kang等[4]基于浮动坐标方法,首次提出了多柔体系统中柔性部件的等效静载荷定义. 随后,学者们还给出了基于不同非线性有限元描述的多柔体系统中柔性部件的等效静载荷的定义[105, 108, 129],并用于多柔体系统动力学响应优化设计[84, 98, 109-112, 130-133].
2.2 动力学特性优化
结构动力学特性优化设计主要关注结构的固有频率、振型、阻尼、刚度与质量分布等,其中研究最早、成果最多的是 以结构固有频率为目标或约束的优化设计[134]. 林家浩[135]、Grandhi[136] 和陈建军 等[134] 分别对 1983 年、1993 年和 2001 年之前的结构动力学特性优化设计研究进展作了综述, Zargham 等[137] 则对截至2016年的结构动力学特性拓扑优化设计研究进展进行了综述. 目前,结构动力学特性优化设计已发展的比较成熟. 然而,对多柔体系统动力学特性优化设计还鲜有文献报道. 一方面,由于多柔体系统经历大范围运动,尤其是高速运动与大变形耦合,如何描述其动力学特性就是开放的问题. 另一方面,当多柔体系统的柔性部件转速增大时,其动力学特性会变得非常复杂,不同阶次的共振频率与转速间 曲线呈现交叉等现象,增加了动力学特性优化设计的难度.
在航天科技领域,许多小型航天器的动力学模型是自旋中心刚体和柔性薄板组合而成的系统,其动力学设计引起人们关注. 自 20 世纪 70 年代以来,很多学者[138-146] 研究了绕定轴旋转板的动力学建模与动力学特性分析. Zhao 等[146] 指出,传统的旋转板动力学模型[138, 143-145] 在经历大范围运动与大变形耦合时,会遇到采用无穷小转角作为广义坐标导致的数值计算问题. Zhao 等[146] 采用绝对节点坐标方法,建立了旋转矩形薄板的动力学模型,分析了不同转速下旋转矩形薄板的动力学特性. Zhao 等[146] 指出,在转速较低、薄板变形较小时,绝对节点坐标模型与传统模型的差异很小;但当转速较高、薄板变 形较大时,两种模型具有显著差异. Zhang 等[147] 基于绝对节点坐标模型研究了旋转梁的动力学特性分析, 也发现当旋转结构的纵向变形较大时,绝对节点坐标模型与传统模型结果相差较大. 造成此差异的原因是,Zhao 等[146] 和 Zhang 等[147]在旋转坐标系下建立结构动力学模型时,忽略了科式力项. 已有研究表明,科氏力效应可能在某些情况下产生了重要的影响[148-149].
近年来,人们开始关注对旋转的柔性结构动力学特性进行优化设计. 例如,Liu 等[150] 利用拓扑优化方法对旋转梁的横截面进行拓扑优化. 他们的研究考虑两种目标函数,一是最大化旋转梁的第一阶共振频率,二是最大化任意相邻两阶共振频率的间隙. 其中,最 大化第一阶共振频率的优化方程可以表示为如下的边界形式
式中,$\lambda _n $ 为第 $n$ 阶共轭特征值,第 $n$ 阶共振频率 $\omega _n $ 可表示为 $\lambda _n $ 的虚部,${\pmb Z}_n $ 为第 $n$ 阶特征向量,$N_d $ 为系统的自由度数;一般取 $N_u (N_u < N_d )$ 足够大,以确保所有大于或等于第一阶的共振频率不小于 $C_1 $. 第 2 个约束方程为广义特征值方程,其中 ${\pmb M}$ 为质量矩阵,${\pmb C}$ 为由科氏力引起的陀螺力矩阵,${\pmb K}$ 为由离心力和弹性力引起的刚度矩阵;$\mathcal{U}_{b} $ 为设计变量 ${\pmb b}$ 的设计空间.
同样的,对于最大化旋转结构第 $k$ 阶和第 $k +1$ 阶共振频率间隙问题,其优化方程可表示为如下的双边界形式
式中,$N_u $ 和 $N_l $ 均取得足够大,以确保所有大于或等于第 $k +1$ 阶的特征值不小于 $C_1 $,并且所有小于或等于第 $k$ 阶的特征值不大于 $C_2 $.
为对旋转梁横截面进行拓扑优化,Liu 等[150] 采用 Giavotto 梁理论与 Hamilton 原理,建立了任意截面 形状旋转梁的动力学模型,并考虑了陀螺力的影响. 在进行拓扑优化时,Liu 等[150] 采用密度法进行优化,并基于 Kreisselmeier-Steinhauser 函数推导了共振频率 灵敏度的近似计算公式. 由于旋转梁横截面的拓扑优化设计不存在局部模态问题,Liu 等[150] 并没有考虑拓扑优化时局部模态的消除. Liu 等[150] 指出,转动角速度对旋转梁横截面拓扑优化的结果影响很大,并研究了直升机旋翼翼型的频率拓扑优化设计. 上述研究可适用于长宽比较大的旋转矩形薄板,但不适用于长宽比较小的旋转矩形薄板.
对薄板结构(包括旋转薄板结构)进行频率拓扑优化设计时,在结构的低密度区会出现局部模态问题[151]. 这是由于在低密度区,结构非常柔软,容易产生低频优势模态. 然而,结构优化中的低密度区通常是去除材料的区域,故上述局部模态是一种虚假模态. 为了消除这类局部模态,学者们提出了很多方法[151-154]. 这些方法的本质都是改变质量矩阵和刚度矩阵的惩罚函数比,或者惩罚低密度区的质量矩阵,以提高低密度区域局部模态的阶次. 对于旋转薄板,随着转速增加,其各阶共振频率值也随之增大. 因此,传统的消除局部模态方法[151-154]可能在薄板转速较高时失效,故需要特别处理. 孙加亮等提出了一种适用于不同转速下旋转薄板低密度区域局部模态消除方法[155].
2.3 动力学灵敏度分析
基于多柔体系统动力学的灵敏度分析不仅能够提供系统状态变量、目标函数等对设计变量的依赖关系,也是联系多柔体系统 动力学分析与最优化设计的桥梁[156].
对于多柔体系统动力学的响应优化问题,计算一般动力学响应函数的灵敏度主要有以下4种方 法[157]:即有限差分法、直接微分法、伴随变量法和自动微分法. 其中,有限差分法[158]是一种数值方法,包括向前、向后和中间差分方法,该方法通过对设计变量取扰动量,并取前 后动响应函数差值与扰动量之商作为动响应函数的灵敏度值,具有实现简单的优点;但由于计算精度和效率不高,基本不被采用. 直接微分法[159]作为一种解析方法,首先直接将系统动力学方程对设计变量求导,然后通过求解灵敏度方程组得到状 态变量的灵敏度,最后将其代入动响应函数灵敏度表达式得到其灵敏度值,其优点是采用隐式积分法可有效控制时间积分误差; 但是当设计变量较多时,需大量求解灵敏度方程组,计算效率较低. 伴随变量法[160]也是一种解析方法,通过引入一组伴随变量并适当取值,可避免求解复杂的状态变量灵敏度,故对于设计 变量较多的情况无需大量求解微分-代数方程组,求解效率可大幅提高;但是其分析推导过程复杂,计算所需资源也较多. 自动微分法[161-162]可以自动计算动响应函数对设计变量的灵敏度,目前在多柔体系统动力学灵敏度分析中应用较 少,其计算效率与上述3种方法相比尚不明确[163].
在上述4种方法中,最常见的方法是直接微分法[164-182]和伴随变量法[100, 169, 178, 183-195]. 例如,Ding 等[196-197] 推导了多体系统动力学的二阶灵敏度. Pi 等[198] 推导了基于绝对节点坐标描述的多柔体系统的一阶灵敏度. Tromme 等[104]采用直接微分法,开展了强耦合优化模型的灵敏度分析. Banerjee 和 Mcphee[199] 推导了基于图论描述的多体系统动力学灵敏度. Held等[100]采用伴随变量法推导了基于浮动坐标法描述的多柔体系统动力学灵敏度分析. Li和Wang[179]采用直接微分法推导了基于自然坐标描述的多体系统动力学灵敏度. Sonneville 和 Brüls[54] 同时采用直接微分法和伴随变量法推导了基于李群描述的多体系统动力学灵敏度. Tu等[177]采用直接微分法,推导了基于转移矩阵描述的多体系统动力学灵敏度. Dopico等[181]采用直接微分法推导了含完整约束与非完整约束的多体系统动力学灵敏度.
对于多柔体系统动力学特性优化问题,一般需要计算特征频率,尤其是多重特征频率的灵敏度信息. 对此,学者们提出了多种 特征频率灵敏度分析方法. 现有方法可分为两类,一是通过计算特征值的灵敏度来分析特征频率的灵敏度[200-202],二是通过近似函数来 直接求解特征频率的灵敏度[150, 203-205]. 此外,还需要计算特征向量的灵敏度[206-207]. 由于计算效率和存储量需求的原因,经典的特征向量灵敏度计算方法[206]无法适用于高维系统. 为此,学者们提出很多改进和加速方法. 例如,改进的近似法[208]、加速的子空间迭代法[209]、最小二乘法[210]和改进的Nelson方法[211]等.
3 多柔体系统部件优化研究概况
对于结构优化,可按照设计变量类型分为尺寸优化、形状优化和拓扑优化3个层次,其分别对应产品设计中 3 个不同的阶段, 即详细设计、基本设计以及概念设计[5]. 对于多柔体系统部件优化,主要研究多柔体系统的动力学响应或动力学特性,进而指导设计系统中单个或多个部件的尺 寸、形状或拓扑,使其在满足动力学性能要求的前提下质量最小,或在给定质量前提下动力学性能最优. 在优化设计时,考虑的动力学响应包括位移响应、变形响应、应变能响应、约束力响应和应力响应等;考虑的动力学特 性目标函数包括使结构各阶共振频率都远离外激励频率、或使其某两阶共振频率之间的间隙达到最大、使得其某一阶共 振振型满足一定的形状要求、或使得结构发生内共振的可能性最小等.
3.1 尺寸优化
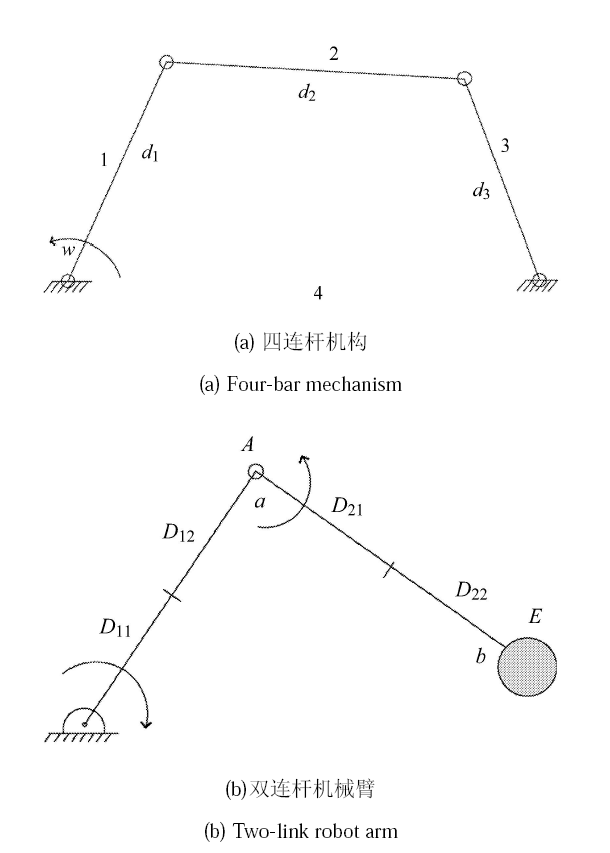
结构尺寸优化是指在保持结构拓扑和形状不变的情况下,寻求结构组件最佳界面尺寸,优化杆的横截面尺寸,或者选择 板厚以使结构性能得到优化,其特点是变量少,求解容易. 多柔体系统部件尺寸优化发展最早,也最为成熟,其研究可追溯到 20 世纪 70 年代早期[86]. 对于多柔体系统部件尺寸的优化,经典算例包括四连杆机构[55, 86-87, 89, 92-95, 97, 105-106] 和双连杆机械 臂[55, 88, 97, 103, 105-108, 111]. 如图1 所示,取连杆的横截面尺寸为设计变量. 例如,Imam 和 Sandor[89]研究了高速四连杆机构的连杆横截面尺寸优化,并考虑应力约束和位移约束. Oral 和 Kemal Ider[88] 研究了双连杆机械臂的连杆横截面尺寸优化,并根据最坏情况法处理了与时间相关的应力约束和挠度约束. Kang 等[97]基于浮动坐标描述,研究了四连杆机构和双连杆机械臂的尺寸优化,并与经典方法对比,发现效率有所提高. 孙加亮等[108]基于绝对节点坐标描述,优化了双连杆机械臂的横截面尺寸,并成功地应用到空间刚-柔抓 取机械臂应力约束下的尺寸优化. Tromme 等[106]基于几何精确非线性有限元描述,对比研究了弱耦合优化模型和强耦合优化模型在四连杆机构和双连杆机 械臂尺寸优化上的性能,发现弱耦合模型的效率高,但强耦合模型适用性更强. Tromme 等[55]还基于局部标架法,即李群描述的非线性有限元法,推导了系统等效静载荷,并采用经典的四连杆机构和双 连杆机械臂尺寸优化进行验证.
图1
在多柔体系统部件尺寸优化过程中,由于设计变量选取较为简单,故其重点主要集中在优化算法和灵敏度分析上. 虽然尺寸优化是结构优化的最低层次,但却为验证多种多柔体系统部件优化方法提供了宝贵的经验.
3.2 形状优化
结构形状优化则是保持结构拓扑不变,寻求结构最理想的结构边界和几何形状,设计变量通常取为杆系结构的节点坐标或表示结构外形的变量.
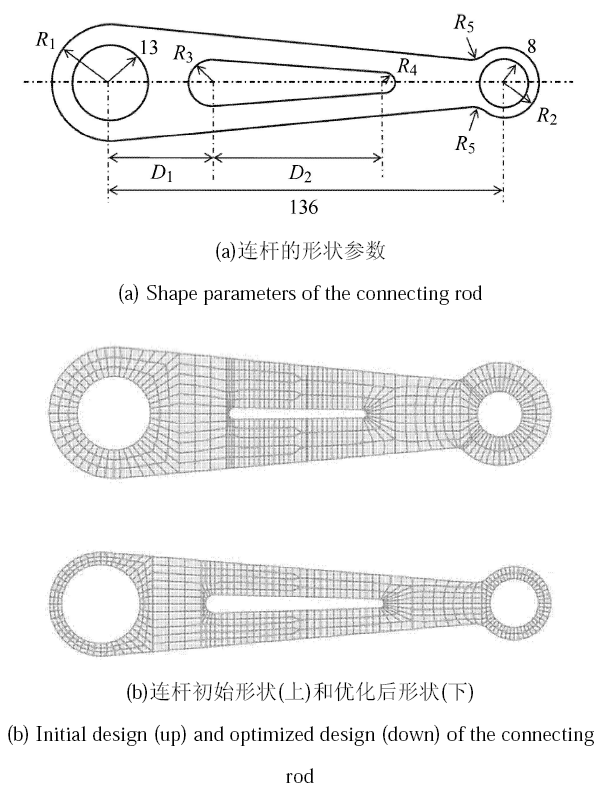
相对于多柔体系统的部件尺寸优化,多柔体系统部件形状优化起步较晚,研究成果也较少. 例如,H$\ddot{a}$ussler 和 Albers[212]基于耐久性分析,优化了多体系统中柔性部件的形状,提高其在动载荷作用下的抗疲劳能力. Vohar 等[107] 采用设计元法,在总能量消耗约束下优化了机械臂的骨架形状,证明该方法可有效减少形状优化的设计变量. Hong 等[98]首先采用拓扑优化方法来优化仿人机器人的骨盆,然后基于拓扑优化结果,进行应力约束下的形状优化,得到更加 精细的结构. Tromme 等[103]取 7 个形状参数作为设计变量,优化了曲柄滑块机构中柔性连杆的形状,使其在伸长率的约束下质量最轻,其形 状参数定义与优化结果如图2 所示. Chaudhary 和 Chaudhary[213]采用B样条曲线描述四连杆机构的连杆形状,优化每根柔性连杆的形状,使其达到动平衡目的.
分析多柔体系统部件形状优化研究成果相对较少的原因,主要有以下两点[214]:一是结构形状的描述困难, 因为在优化过程中分析模型不断变化,为了计算动响应信息,需要不断变更有限元网格,既耗时又有挑战;二是形状敏度 的分析,其难度与计算量也比尺寸优化大得多.
图2
3.3 拓扑优化
结构拓扑优化则是在满足应力、位移等约束条件下,在特定的设计域内寻求使结构某种性态达到最优的材料分布方式. 结构拓扑优化是结构优化领域最难,也是最富有挑战性的研究方向.
自从 1988年Bends$\phi$e 和 Kikuchi[215] 采用均匀化方法 (homogenization method) 提出结构拓扑优化概念以来,结构拓扑优化的理论与方法已有了长足进展. Hassani 和 Hinton[216-218] 详细综述了 1998 年之前均匀化方法的理论和研究进展. Rozvany[219]综述了截至2009年的结构拓扑优化方法研究进展,尤其是已应用于商业软件中的拓扑优化方法, 主要包括 SIMP (simplified isotropic material with penalization) 方法和渐进结构优化方法 (evolutionary structural optimization,ESO). Deaton 和 Grandhi[220]综述了 2000 年至 2012 年期间的结构拓扑优化方法理论和应用研究进展,主要回顾了 4 种方法: (1) 密度法 (density method),包括应用最为广泛的 SIMP 方法; (2) 硬杀法(hard-kill method),包括渐进结构优化方法;(3) 边界变异法 (boundary variation method),包括水平集方法 (level set method,LSM) 和相场方法 (phase field method);(4) 基于细胞分裂的生物启发方法. Sigmund 和 Maute[221]详细综述了 2013 年之前多种结构拓扑优化方法的优点、缺点、相似点和不同点,主要包括:(1) 密度法; (2) 拓扑导数法 (topological derivatives method),又称冒泡法 (bubble method);(3) 水平集方法;(4) 相场方法;(5) 渐进结构优化方法和双向渐进结构优化方法 (bi-directional evolutionary structural optimization,BESO). Sigmund和Maute[221]指出,ESO 和 BESO 方法可以归类到离散的密度法中. 此外,针对某类结构拓扑优化方法,也有不少学者对其进行综述研究. 比如,van Dijk 等[222]详细综述了 2013 年之前不同水平集方法的研究进展,其分类可根据水平集函数的参数化形式、几何映射、物 理模型、更新形式以及正则化方式等. Xia 等[223]详细综述了自1993年渐进结构优化方法的提出以来和自 2007 年双向渐进结构优化方法的提出以来,这两种方 法的理论和应用研究进展.
图3
图4
图5
(1)密度法
密度法以每个单元的相对密度作为设计变量,设计变量的个数与单元个数相等. 当单元的相对密度为 1 时,表示材料域;当单元的相对密度为 0 时,表示空域;而当单元的相对密 度在 0 和 1 之间时,表示中间密度材料.对于中间密度材料单元的物理属性,一般需要进行插值或者惩罚,主要有以下 3 种模型. 20 世纪 80 年代末和 90 年代初, Bends$\phi$e[226], Zhou和 Rozvany[227]以及 Mlejnek[228] 提出了密度法的SIMP模型. 随后,Bends$\phi$e 和 Sigmund[229]证明了SIMP 模型的物理意义. 后来,Stolpe 和 Svanberg[230]提出了密度法的 RAMP (rational approximation of material properties) 模型. Pedersen 和 Pedersen[231] 提出了密度法的 NLPI (non linear penalization or interpolation) 模型. 无论对于 SIMP 模型、RAMP 模型还是 NLPI 模型,上述学者都假设单元材料的物理属性(如弹性模量、许用应力等)和单元的 密度有某种对应关系,可表示为单元密度的连续、显式函数. 他们指出,这 3 种模型的差异体现在上述对应关系的表达式上,并给出了具体插值函数表达式及其特点[231].
密度法的特点是能将结构拓扑优化问题转化为连续、可微的优化问题,从而可采用基于梯度的数学规划法进行求解,并且还可 以直接处理全局约束问题[221]. 但对于应力约束等参数化问题,密度法求解时可能遇到困难,优化结果还可能出现网格依赖性和棋盘格式等问题.
(2)水平集方法
水平集方法采用高一维水平集函数的零等值线(或面)来描述低一维的曲线(或曲面),通过水平集函数值的变化来实现结构拓扑边界的演化. 当结构中某一点的水平集函数值大于零时,表示材料域;当水平集函数值小于零时,表示空域;当水平集函数值等于零时,表示结构边界. 2000 年,Sethian 和 Wiegmann[232] 首次将水平集方法引入到结构拓扑优化中,并进行等应力结构的设计. 此后,Osher 和 Santosa[233] 采用水平集方法研究了鼓膜的频率拓扑优化设计. Wang 等[234]和 Allaire 等[235]将形状导数引入到水平集拓扑优化方法中,通过结构边界的法向移动 速度建立了 Hamilton--Jacobi 偏微分方程 (partial differential equation,PDE) 同形状导数的关系,并采用逆风格式求解水平集方程. Luo 等[236]指出,传统的水平集方法[234-235]有一些缺点,比如优化结果的初值依赖性、求解偏微分方程步长很小、收敛速度慢、需要耗时的周期性初始化以及 难以处理多约束问题、难以与数学规划法相结合等. 因此,Luo 等[236] 提出采用一种半隐式的加性分裂算子[236] (additive operator splitting,AOS) 差分格式求解 Hamilton--Jacobi 偏微分方程. 该格式不受积分步长大小的影响,求解效率高,优化收敛快;此外,该方法可在结构优化中自由生成新孔,以防止 优化结构收敛到局部最优解,并且不需要进行周期性的初始化.
水平集方法的特点是在优化过程中能够精确描述曲线(或曲面)的拓扑变化,利用有限差分法可在离散网格上方便地进行数值近似求解, 同时可利用空间导数很好地进行近似函数梯度,还可方便计算曲线(或曲面)的几何特征,如单位法矢和其对应的曲率等[236]. 但 Sigmund 和 Maute[221]指出,水平集方法在采用有限元求解和实现时,会遇到和密度法相同的中间密度区域,并且目标函数和 约束函数的演化都定义在结构边界上,会导致优化问题很复杂. 尽管近年来将水平集方法和数学规划法相结合的研究受到广泛关注,但还没有学者详细比较过传统水平集方法和基于数学规划法的水平集方法. 因此,基于数学规划法的水平集拓扑优化方法仍是一个开放的问题.
(3)移动可变形组件方法
Guo 等[237]提出了移动可变形组件方法,采用可变形的移动结构组件来显式描述结构的拓扑,通过结构组件的移动、 变形、交叉、重叠等机制实现结构拓扑的变化. 该方法采用结构组件的位置、尺寸和方向等参数作为设计变量,可显著减少拓扑优化设计变量的个数,尤其是三维结构的 拓扑优化问题. 此外,采用显式的几何参数描述结构的拓扑,其优化结果可直接借助计算机辅助设计 (compute aided design,CAD) 软件建立模型,并且非常方便地控制结构的最小尺寸. 在移动可变形组件方法中,结构组件所在的位置表示材料域,没有结构组件的位置表示空域,而结构组件的边界表示结构拓扑边界.
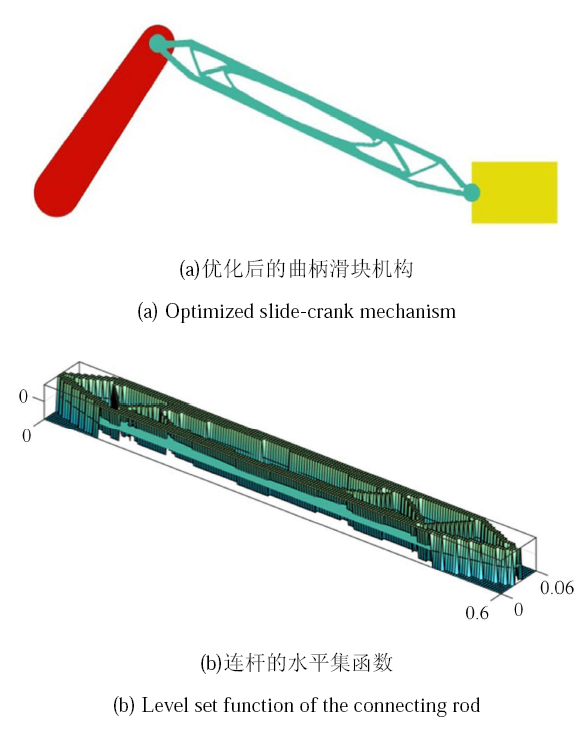
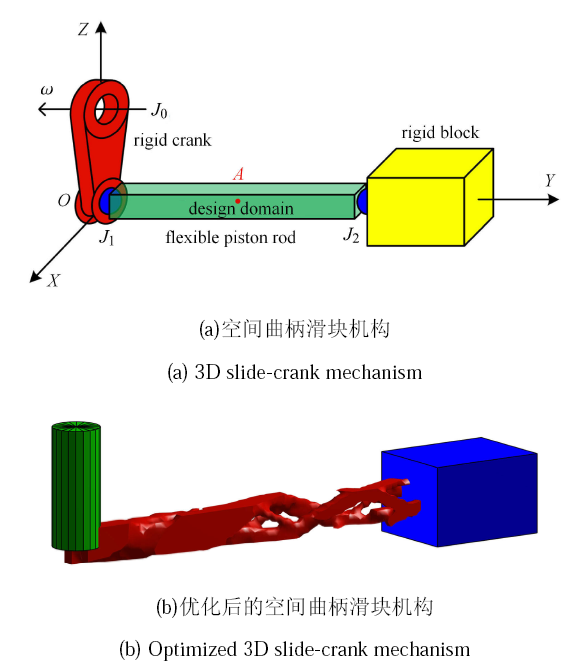
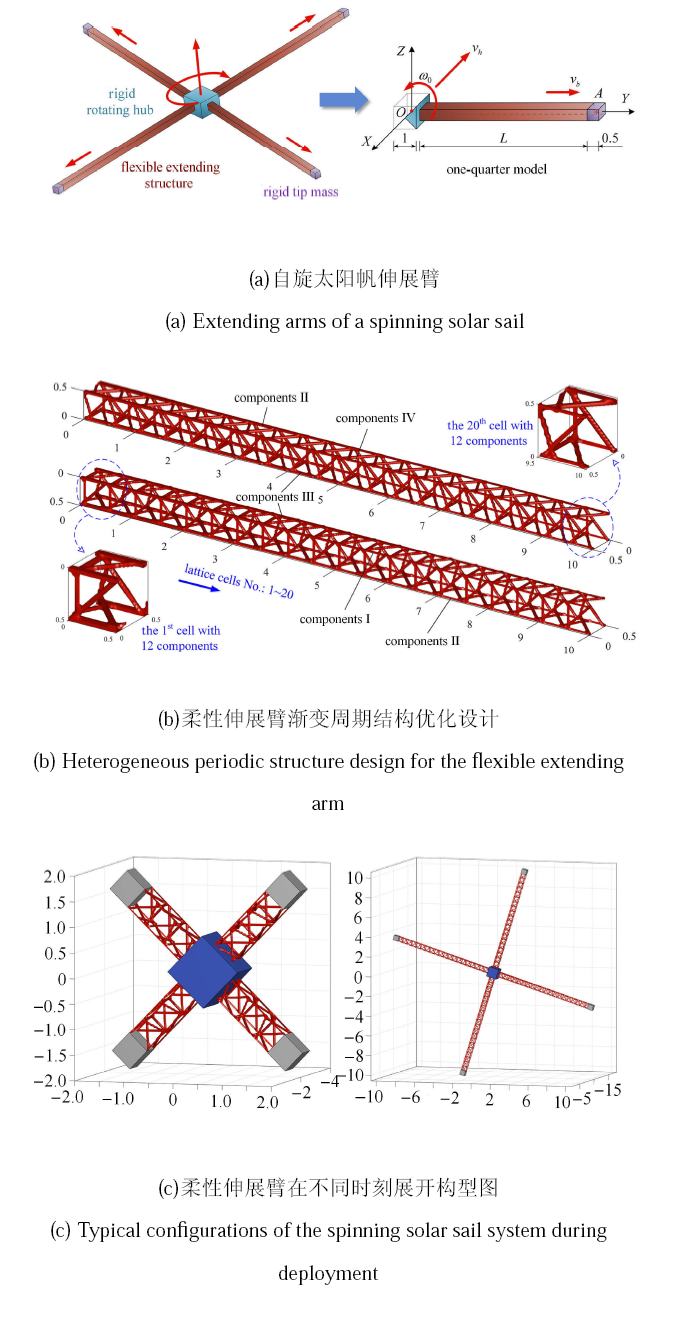
随着 3D 打印等增材制造方法的提出和发展,基于显式几何描述的结构拓扑优化设计方法也迅速发展. 移动可变形组件方法作 为一种新兴的显式结构拓扑优化方法,已被成功应用于多个领域,例如图6 所示的自旋太阳帆的柔性伸展臂拓扑优化[112], 图7 所示的旋转薄板的共振频率优化设计[155]. 在图6 所示自旋太阳帆展开的第一阶段,4根柔性伸展臂从一个刚性轮毂中伸出;与此同时,刚性轮毂保持自旋并向面外方向移动. 优化设计目标是:在给定量的材料下,优化柔性伸展臂的拓扑结构,并设计为渐变周期结构,使之在展开过程中动态柔顺度 (或应变能) 最小. 这是一个具有变长度柔性部件的多柔体系统动力学优化问题,难度很大. 孙加亮等将多柔体系统动力学与移动可变形组件法结合,成功解决了这类难题[112].
图6
图7
值得指出,移动可变形组件方法仍有若干研究难题,比如对初值依赖性问题[110]、孤立组件的闭锁问题、以及整个结 构的拓扑描述函数不可微问题等.
4 若干值得关注的问题
通过以上综述可见,多柔体系统动力学优化仍处于发展之中,还有许多问题需要进一步研究. 以下是值得关注的若干问题:
(1) 对于复杂的多柔体系统动力学优化设计,研究高效的动力学灵敏度分析与计算技术,包括非光滑多柔体系统灵敏度分析、 含变长度柔性部件的多柔体系统灵敏度分析等.
(2) 针对复杂变长度结构,研究其动力学建模与优化设计. 例如,建立变长度的薄壳单元,进而可对航天工程中具有重要应用前景的卷簧类部件展开动力学进行优化设计,提高其在可展 开空间结构中的应用成效.
(3) 针对工程中的复杂约束,研究多柔体系统动力学优化设计. 例如,在旋转薄膜结构的去皱褶优化设计中,需要考虑应力约束;在高速运动连杆的优化设计中,需要考虑屈曲约束等.
(4) 针对接触/碰撞,研究非光滑多柔体系统动力学建模与优化设计. 例如,对具有广泛应用前景的软抓取、软对接等软机器进行动力学设计,包括由介电弹性体等软材料构成的多柔体系统进行动力学优化.
(5) 针对工程中的不确定性因素,研究多柔体系统动力学优化设计. 例如,研究基于可靠性的优化设计 (reliability-based optimization) 和鲁棒优化设计 (robust design optimization).
(6) 针对工程中的布局设计需求,研究多柔体系统动力学布局优化,即对多柔体系统的刚/柔性部件和运动副开展一体化设计. 在一体化设计中,可进行多材料分布优化设计,甚至可同时优化运动副的布局和类型,以获得全新、最优的多柔体系统.
5 结 语
近年来,多柔体系统动力学优化引起了广泛关注,其理论与应用研究也取得长足的发展. 一方面,多柔体系统动力学与结构优化相结合,极大丰富了学科内涵,突显了学科交叉属性和应用属性;另一方面,借助多 柔体系统动力学模型进行结构优化,可以解决一批过去无法解决的问题,使得结构优化设计与工程实际结合得更加紧密.
本文对多柔体系统动力学建模、动力学优化以及部件优化等研究进行总结. 根据动力学建模方法不同,分别介绍了浮动坐标方法、几何精确方法和绝对节点坐标方法的研究成果;根据动力学优化目的的 不同,分别介绍了多柔体系统动力学响应优化、动力学特性优化和动力学灵敏度分析等方面的研究成果;根据优化设计变量的不同, 分别介绍了多柔体系统部件尺寸优化、形状优化和拓扑优化等方面的研究成果. 虽然本文已有非常宽的覆盖面,但仍存在挂一漏万的可能性.
本文指出该领域值得关注的若干问题. 在未来研究中,应将结构优化设计的理论属性和多柔体系统动力学的应用属性更加完美的结合,推动学科发展的同时,实现若 干重要的工程设计.
致谢
感谢丹麦技术大学(Technical University of Denmark)Niels L. Pedersen教授在相关研究过程中提供的建议和帮助.
参考文献
柔性多体系统刚-柔耦合动力学
首先指出大量复杂系统动力学与控制性态分析与优化等工程问题对柔性多体系统动力学领域的进一步需求,在回顾柔性多体系统动力学研究的若干阶段与当前的研究现状后指出:柔性多体系统刚- 柔耦合动力学的研究是多体系统动力学的一个新的阶段.文末提出了刚- 柔耦合动力学的研究任务。
Flexible multibody dynamics with coupled rigid and deformation motions
首先指出大量复杂系统动力学与控制性态分析与优化等工程问题对柔性多体系统动力学领域的进一步需求,在回顾柔性多体系统动力学研究的若干阶段与当前的研究现状后指出:柔性多体系统刚- 柔耦合动力学的研究是多体系统动力学的一个新的阶段.文末提出了刚- 柔耦合动力学的研究任务。
多柔体系统动力学研究进展与挑战
Advances and challenges in dynamics of flexible multibody systems
柔性多体系统动力学绝对节点坐标方法研究进展
阐述了多体系统动力学理论的研究背景,指出了多种传统的柔性多体系统动力学研究方法的不足.系统地从4个方面回顾了柔性多体系统动力学绝对节点坐标方法诞生十几年以来的研究进展,即:单元研究进展、系统动力学方程求解数值算法研究进展、非线性材料多体系统动力学研究进展以及相关的应用研究进展.最后提出了值得进一步研究的问题.
Advances in the absolute nodal coordinate method for the flexible multibody dynamics
阐述了多体系统动力学理论的研究背景,指出了多种传统的柔性多体系统动力学研究方法的不足.系统地从4个方面回顾了柔性多体系统动力学绝对节点坐标方法诞生十几年以来的研究进展,即:单元研究进展、系统动力学方程求解数值算法研究进展、非线性材料多体系统动力学研究进展以及相关的应用研究进展.最后提出了值得进一步研究的问题.
System-based approaches for structural optimization of flexible mechanisms
Recent development in structural design and optimization
With the fast development of computational mechanics and thecapacity as well as the speed of modern computers, simulationbased structural optimization has become an indispensable tool inthe design process of competitive products. This paper presents abrief description of the current status of structural optimizationby reviewing some significant progress made in the last decades.Potential research topics are also discussed. The entireliteratures of the field are not covered due to the limitation ofthe length of paper. The scope of this review is limited andclosely related to the authors' own research interests.
第十八届美国理论与应用力学大会总结
18th U.S. National Congress of Theoretical and Applied Mechanics
Structural and topology optimization of flexible multibody systems
//
Multibody systems history of ADAMS
Dynamics of large scale flexible mechanical systems
[PhD Thesis].Understanding the molecular-scale behavior of fluids confined and sheared between solid surfaces is important for many applications, particularly tribology where this often governs the macroscopic frictional response. In this study, nonequilibrium molecular dynamics simulations are performed to investigate the effects of fluid and surface properties on the spatially resolved temperature and flow profiles, as well as friction. The severe pressure and shear rate conditions studied are representative of the elastohydrodynamic lubrication regime. In agreement with tribology experiments, flexible lubricant molecules give low friction, which increases linearly with logarithmic shear rate, while bulky traction fluids show higher friction, but a weaker shear rate dependence. Compared to lubricants, traction fluids show more significant shear heating and stronger shear localization. Models developed for macroscopic systems can be used to describe both the spatially resolved temperature profile shape and the mean film temperature rise. The thermal conductivity of the fluids increases with pressure and is significantly higher for lubricants compared to traction fluids, in agreement with experimental results. In a subset of simulations, the efficiency of the thermostat in one of the surfaces is reduced to represent surfaces with lower thermal conductivity. For these unsymmetrical systems, the flow and the temperature profiles become strongly asymmetric and some thermal slip can occur at the solid-fluid interface, despite the absence of velocity slip. The larger temperature rises and steeper velocity gradients in these cases lead to large reductions in friction, particularly at high pressure and shear rate.
Variable degree of freedom component mode analysis of inertia-variant flexible mechanical systems
Finite element appendage equations for hybrid coordinate dynamcis analysis
The use of coagulants and flocculants in the water and wastewater industry is predicted to increase further in the coming years. Alum is the most widely used coagulant, however, the use of ferric chloride (FeCl3) is gaining popularity. Drinking water production that uses FeCl3 as coagulant produces waste sludge rich in iron. We hypothesised that the iron-rich drinking water sludge (DWS) can potentially be used in the urban wastewater system to reduce dissolved sulfide in sewer systems, aid phosphate removal in wastewater treatment and reduce hydrogen sulfide in the anaerobic digester biogas. This hypothesis was investigated using two laboratory-scale urban wastewater systems, one as an experimental system and the other as a control, each comprising sewer reactors, a sequencing batch reactor (SBR) for wastewater treatment, sludge thickeners and anaerobic digestion reactors. Both were fed with domestic wastewater. The experimental system received in-sewer DWS-dosing at 10 mgFe L-1 while the control had none. The sulfide concentration in the experimental sewer effluent decreased by 3.5 ± 0.2 mgS L-1 as compared with the control, while the phosphate concentration decreased by 3.6 ± 0.3 mgP L-1 after biological wastewater treatment in the experimental SBR. The dissolved sulfide concentration in the experimental anaerobic digester also decreased by 15.9 ± 0.9 mgS L-1 following the DWS-dosing to the sewer reactors. The DWS-doing also enhanced the settleability of the mixed liquor suspended sludge (MLSS) (SVI decreased from 193.2 ± 22.2 to 108.0 ± 7.7 ml g-1), and the dewaterability of the anaerobically digested sludge (the cake solids concentration increased from 15.7 ± 0.3% to 19.1 ± 1.8%). The introduction of DWS into the experimental system significantly increased the COD and TSS concentrations in the wastewater, and consequently the MLSS concentration in the SBR, however, this did not affect normal operation. The results demonstrated that iron-rich waste sludge from drinking water production can be used in the urban wastewater system achieving multiple benefits. Therefore, an integrated approach to urban water and wastewater management should be considered to maximise the benefits of iron use in the system.
The dynamics of flexible bodies
Code biology uses protein synthesis to pursue how living systems fabricate themselves. Weight falls on intermediary systems or adaptors that enable translated DNA to function within a cellular apparatus. Specifically, code intermediaries bridge between independent worlds (e.g. those of RNAs and proteins) to grant functional lee-way to the resulting products. Using this Organic Code (OC) model, the paper draws parallels with how people use artificial codes. As illustrated by Tetris and Morse, human players/signallers manage code functionality by using bodies as (or like) adaptors. They act as coding intermediaries who use lee-way alongside &quot;a small set of arbitrary rules selected from a potentially unlimited number in order to ensure a specific correspondence between two independent worlds&quot; (Barbieri, 2015). As with deep learning, networked bodily systems mesh inputs from a coded past with current inputs. Received models reduce 'use' of codes to a run-time or program like process. They overlook how molecular memory is extended by living apparatuses that link codes with functioning adaptors. In applying the OC model to humans, the paper connects Turing's (1937) view of thinking to Wilson's (2004) appeal to wide cognition. The approach opens up a new view of Kirsh and Maglio's (1994) seminal studies on Tetris. As players use an interface that actualizes a code or program, their goal-directed (i.e. 'pragmatic') actions co-occur with adaptor-like 'filling in' (i.e. 'epistemic' moves). In terms of the OC model, flexible functions derive from, not actions, but epistemic dynamics that arise in the human-interface-computer system. Second, I pursue how a Morse radio operator uses dibs and dabs that enable the workings of an artificial code. While using knowledge ('the rules') to resemiotize by tapping on a transmission key, bodily dynamics are controlled by adaptor-like resources. Finally, turning to language, I sketch how the model applies to writing and reading. Like Morse operators, writers resemiotize a code-like domain of alphabets, spelling-systems etc. by acting as (or like) bodily adaptors. Further, in attending to a text-interface (symbolizations), a reader relies on filling-in that is (or feels) epistemic. Given that humans enact or mimic adaptor functions, it is likely that the OC model also applies to multi-modal language.
Efficient calculation of the inertia terms in floating frame of reference formulations for flexible multibody dynamics
Inertia forces and shape integrals in the floating frame of reference formulation
Use of the floating frame of reference formulation in large deformation analysis: Experimental and numerical validation
Analysis of multibody systems experiencing large elastic deformations
Nonlinear model order reduction for flexible multibody dynamics: A modal derivatives approach
Numerical approach for flexible body motion with large displacement and time-varying length
//
Numerical approach in the analysis of flexible body motion with time-varying length and large displacement using multiple time scales
//
On a stress resultant geometrically exact shell model. Part VII: Shell intersections with 56-DOF finite element formulations
On a stress resultant geometrically exact shell model. Part V. Nonlinear plasticity: Formulation and integration algorithms
On a stress resultant geometrically exact shell model. Part III: Computational aspects of the nonlinear theory
On a stress resultant geometrically exact shell model. Part IV: Variable thickness shells with through-the-thickness stretching
On a stress resultant geometrically exact shell model. Part I: Formulation and optimal parametrization
On a stress resultant geometrically exact shell model. Part II: The linear theory; Computational aspects
A geometrically-exact rod model incorporating shear and torsion-warping deformation
On the dynamics of flexible beams under large overall motions - the plane case, part I and II
A finite strain beam formulation. The three-dimensional dynamic problem. Part I
ANCF consistent rotation-based finite element formulation
Flexible Multibody Dynamics: A Finite Element Approach
General personality dimensions are associated with clinical severity and treatment response in individuals with depression and many anxiety disorders, but little is known about these relationships in individuals with obsessive-compulsive disorder (OCD). Individuals in the current study included 705 adults with OCD who had participated in family and genetic studies of the disorder. Participants self-completed the Neuroticism, Extraversion, Openness Personality Inventory or Neuroticism, Extraversion, Openness Five-Factor Inventory-3. Relationships between personality scores, and subjective impairment and OCD treatment response, were evaluated. The odds of subjective impairment increased with (unit increase in) the neuroticism score (odds ratio, OR = 1.03; 95% CI = 1.01-1.04; p &lt; 0.01) and decreased with extraversion scores (OR = 0.98; 95% CI = 0.96-0.99; p &lt; 0.01). The odds of reporting a good response to serotonin/selective serotonin reuptake inhibitors (OR = 1.02; 95% CI = 1.01-1.04; p &lt; 0.01) or cognitive behavioural therapy (OR = 1.03; 95% CI = 1.01-1.05; p &lt; 0.01) increased with the extraversion score. The magnitude of these relationships did not change appreciably after adjusting for other clinical features related to one or more of the personality dimensions. The findings suggest that neuroticism and extraversion are associated with subjective impairment, and that extraversion is associated with self-reported treatment response, in individuals with OCD. © 2019 John Wiley &amp; Sons, Ltd.
Flexible multibody dynamics: review of past and recent developments
An accurate and robust geometrically exact curved beam formulation for multibody dynamic analysis
Use of independent rotation field in the large displacement analysis of beams
This paper examines the effect of using independent finite rotation field in the large displacement analysis of flexible bodies. This finite rotation description is at the core of the large rotation vector formulation (LRVF), which has been used in the dynamic analysis of bodies experiencing large rotation and deformation. The LRVF employs two independently interpolated meshes for describing the flexible body dynamics: the position mesh and the rotation mesh. The use of these two geometrically independent meshes can lead to coordinate and geometric invariant redundancy that can be the source of fundamental problems in the analysis of large deformations. It is demonstrated in this paper that the two geometry meshes can define different space curves, which can differ by arbitrary rigid-body displacements. The material points of the two meshes occupy different positions in the deformed configuration, and as a consequence, the geometries of the two meshes can differ significantly. The paper also discusses other issues including the inextensibility of the rotation mesh. Simple examples are presented in order to shed light on these fundamental issues.
Uniqueness of the geometric representation in large rotation finite element formulations
On the issue of redundancy in the large rotation vector formulation//ASME 2014 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Buffalo, New York, USA, 201437 Jeleni$\acute{c}$ G, Crisfield MA. Interpolation of rotational variables in nonlinear dynamics of 3D beams
On the parametrization of finite rotations in computational mechanics: A classification of concepts with application to smooth shells
Consistent quaternion interpolation for objective finite element approximation of geometrically exact beam
A frame-invariant scheme for the geometrically exact beam using rotation vector parametrization
While frame-invariant solutions for arbitrarily large rotational deformations have been reported through the orthogonal matrix parametrization, derivation of such solutions purely through a rotation vector parametrization, which uses only three parameters and provides a parsimonious storage of rotations, is novel and constitutes the subject of this paper. In particular, we employ interpolations of relative rotations and a new rotation vector update for a strain-objective finite element formulation in the material framework. We show that the update provides either the desired rotation vector or its complement. This rules out an additive interpolation of total rotation vectors at the nodes. Hence, interpolations of relative rotation vectors are used. Through numerical examples, we show that combining the proposed update with interpolations of relative rotations yields frame-invariant and path-independent numerical solutions. Advantages of the present approach vis-a-vis the updated Lagrangian formulation are also analyzed.
Interpolation of rotation and motion
In Cosserat solids such as shear deformable beams and shells, the displacement and rotation fields are independent. The finite element implementation of these structural components within the framework of flexible multibody dynamics requires the interpolation of rotation and motion fields. In general, the interpolation process does not preserve fundamental properties of the interpolated field. For instance, interpolation of an orthogonal rotation tensor does not yield an orthogonal tensor, and furthermore, does not preserve the tensorial nature of the rotation field. Consequently, many researchers have been reluctant to apply the classical interpolation tools used in finite element procedures to interpolate these fields. This paper presents a systematic study of interpolation algorithms for rotation and motion. All the algorithms presented here preserve the fundamental properties of the interpolated rotation and motion fields, and furthermore, preserve their tensorial nature. It is also shown that the interpolation of rotation and motion is as accurate as the interpolation of displacement, a widely accepted tool in the finite element method. The algorithms presented in this paper provide interpolation tools for rotation and motion that are accurate, easy to implement, and physically meaningful.
Three-dimensional beam theory for flexible multibody dynamics
Total Lagrangian Reissner's geometrically exact beam element without singularities
The quaternion-based three-dimensional beam theory
Weak form quadrature element analysis of spatial geometrically exact shear-rigid beams
In this paper a total Lagrangian weak form quadrature element formulation of spatial shear-rigid beams undergoing large displacements and rotations is presented. A geometrically exact beam model with zero transverse shear deformation is adopted. Quaternion representation of finite rotations of spatial beams is used to avoid possible singularity in parameterization of rotation. The formulation reduces the number of degrees of freedom within the element as well as satisfies the demand of strain-objectivity. Several numerical examples are presented to illustrate the feasibility of the formulation. (C) 2014 Elsevier B.V.
Weak form quadrature element analysis of planar slender beams based on geometrically exact beam theory
This paper is devoted to the modeling of planar slender beams undergoing large displacements and finite rotations. Transverse shear deformation of beams that is trivial for most slender beams is neglected in the present model, though within the framework of the geometrically exact beam theory proposed by Reissner. A weak form quadrature element formulation is proposed which is characterized by highly efficient numerical integration and differentiation, thus minimizing the number of elements as well as the total degrees-of-freedom. Several typical examples are presented to demonstrate the effectiveness of the beam model and the weak form quadrature element formulation.
An accurate singularity-free formulation of a three-dimensional curved Euler-Bernoulli beam for flexible multibody dynamic analysis
An accurate singularity-free and locking-free formulation of a three-dimensional shear-deformable beam using Euler parameters
A new locking-free formulation of a three-dimensional shear-deformable beam
Lie group generalized-$\alpha $ time integration of constrained flexible multibody systems
This paper studies a Lie group extension of the generalized-alpha time integration method for the simulation of flexible multibody systems. The equations of motion are formulated as an index-3 differential-algebraic equation (DAE) on a Lie group, with the advantage that rotation variables can be taken into account without the need of introducing any parameterization. The proposed integrator is designed to solve this equation directly on the Lie group without index reduction. The convergence of the method for DAEs is studied in detail and global second-order accuracy is proven for all solution components, i.e. for nodal translations, rotations and Lagrange multipliers. The convergence properties are confirmed by three benchmarks of rigid and flexible systems with large rotation amplitudes. The Lie group method is compared with a more classical updated Lagrangian method which is also formulated in a Lie group setting. The remarkable simplicity of the new algorithm opens interesting perspectives for real-time applications, model-based control and optimization of multibody systems. (C) 2011 Elsevier Ltd.
On the use of Lie group time integrators in multibody dynamics
A formulation on the special Euclidean group for dynamic analysis of multibody systems
Geometrically exact beam finite element formulated on the special Euclidean group
This paper describes a dynamic formulation of a straight beam finite element in the setting of the special Euclidean group SE(3). First, the static and dynamic equilibrium equations are derived in this framework from variational principles. Then, a non-linear interpolation formula using the exponential map is introduced. It is shown that this framework leads to a natural coupling in the interpolation of the position and rotation variables. Next, the discretized internal and inertia forces are developed. The semi-discrete equations of motion take the form of a second-order ordinary differential equation on a Lie group, which is solved using a Lie group time integration scheme. It is remarkable that no parameterization of the nodal variables needs to be introduced and that the proposed Lie group framework leads to a compact and easy-to-implement formulation. Some important numerical and theoretical aspects leading to a computationally efficient strategy are highlighted and discussed. For instance, the formulation leads to invariant tangent stiffness and mass matrices under rigid body motions and a locking free element. The proposed formulation is successfully tested in several numerical static and dynamic examples. (C) 2013 Elsevier B.V.
Sensitivity analysis for multibody systems formulated on a lie group
A direct differentiation method and an adjoint variable method are proposed for the efficient semi-analytical evaluation of the sensitivities of multibody systems formulated in a matrix Lie group framework. These methods rely on the linearization of the equations of motion and/or of the time integration procedure. The simpler structure of the equations of motion in the Lie group formalism appears as an advantage for that purpose. Lie bracket contributions and the non-linearity of the exponential map need to be taken into account in the sensitivity algorithms. Nevertheless, essential characteristics of formulations of the direct differentiation method and the adjoint variable method on linear spaces are recovered. Some implementation issues are discussed and two relevant examples illustrate the properties of these methods.
System-wise equivalent static loads for the design of flexible mechanisms
Hamel's formalism for infinite-dimensional mechanical systems
Optimal control of a mobile robot on sphere
Computational strategies for flexible multibody systems
Movement in biology is an essential aspect of survival for many organisms, animals and plants. Implementing movement efficiently to meet specific needs is a key attribute of natural living systems, and can provide ideas for man-made developments. If we had to find a subtitle able to essentially convey the aim of this special section, it could read as follows: 'taking inspiration from nature for new materials, actuators, structures and controls for systems that move'. Our world is characterized by a huge variety of technical, engineering systems that move. They surround us in countless products that integrate actuators for different kinds of purposes. Basically, any kind of mechatronic system, such as those used for consumer products, machines, vehicles, industrial systems, robots, etc, is based on one or more devices that move, according to different implementations and motion ranges, often in response to external and internal stimuli. Despite this, technical solutions to develop systems that move do not evolve very quickly as they rely on traditional and well consolidated actuation technologies, which are implemented according to known architectures and with established materials. This fact limits our capability to overcome challenges related to the needs continuously raised by new fields of application, either at small or at large scales. Biomimetics-based approaches may provide innovative thinking and technologies in the field, taking inspiration from nature for smart and effective solutions. In an effort to disseminate current advances in this field, this special section collects some papers that cover different topics. A brief synopsis of the content of each contribution is presented below. The first paper, by Lienhard et al [1], deals with bioinspiration for the realization of structural parts in systems that passively move. It presents a bioinspired hingeless flapping mechanism, considered as a solution to the kinematics of deployable systems for architectural structures. The approach relies on structural elasticity to replace the need for local hinges. To this end, the authors have used fibre-reinforced polymers combining high tensile strength with low bending stiffness. The solution favours lower structural complexity as well as higher design versatility. Bioinspiration from the elastic kinetics of plants is a central pillar of the paper, which highlights the interrelation of form, actuation and kinematics in those natural systems. The second paper, by Nakata et al [2], deals with bioinspired systems that actively move, and, more specifically, fly. The paper is about the aerodynamics of a bio-inspired flexible flapping-wing micro air vehicle conceived to fly in a Reynolds number regime used by most natural flyers, including insects, bats and birds. The paper presents a study of the flexible wing aerodynamics of the flapping vehicle by combining an in-house computational fluid dynamic model with wind tunnel experiments. In particular, the developed model is shown to be able to predict unsteady aerodynamics in terms of vortex and wake structures and their relationship with aerodynamic force generation. Simulations are validated by wind tunnel experiments, confirming the effectiveness of the adopted design solutions, as well as the importance of wing flexibility in designing small flapping-wing vehicles. The third paper, by Annunziata et al [3], deals with bioinspired control strategies for systems that move. In particular, the paper describes approaches to increase the stiffness variability in multi-muscle driven joints. Different strategies for simultaneous control of torque and stiffness in a hinge joint actuated by two antagonistic muscle pairs are presented. The proposed strategies combine torque and stiffness control by co-activation with approaches based on activation overflow and inverse modelling. Extensive simulations are performed and described to assess the control efficacy. In the fourth paper, Merker et al [4] present a study on stable walking with asymmetric legs. The authors are concerned with the need to clarify to what extent differences in the leg function of contralateral limbs can be tolerated during walking or running. A bipedal spring-mass model simulating walking with compliant legs is used to show that even remarkable differences between contralateral legs can not only be tolerated, but may also introduce advantages to the robustness of the system dynamics. This study might contribute to shedding light on the stability of asymmetric leg walking, including the potential benefits of asymmetry, with possible implications for design of prosthetic or orthotic systems. The last two papers of this special section deal with active bioinspired systems driven by new actuators made of smart materials. In particular, the paper authored by Rossi et al [5] presents an underwater fish-like robot based on bending structures driven by shape memory alloys. These kinds of actuators are used to bend the backbone of the fish, which in turn causes a change in the curvature of the fish body. The paper describes the mechanisms by which standard swimming patterns can be reproduced with the proposed design, and show characterizations in terms of the actuation speed and position accuracy of prototype systems. The last paper, by Carpi et al [6], presents an overview on ionic- and electronic-type electromechanically active polymer actuators as artificial muscles for bioinspired applications. The electrical responsiveness and numerous functional and structural properties that these materials and actuators have in common with natural muscles are shown to be the key motivation by which they are studied as artificial muscles for a huge variety of possible uses. The authors describe the fundamental aspects of relevant technologies and emphasize how after several years of basic research, electromechanically active polymer actuators are today facing their important initial transition from academia into commercialization. In conclusion, we hope that the selection of papers in this special section might help to provide readers with a balanced overview, through examples on the relevant fundamental aspects, materials, actuators, structures, controls and on their effective integration, in order to develop approaches which will be successful in 'taking inspiration from nature for systems that move'. References [1] Lienhard J, Schleicher S, Poppinga S, Masselter T, Milwich M, Speck T and Knippers J 2011 Flectofin: a hingeless flapping mechanism inspired by nature Bioinsp. Biomim. 6 045001 [2] Nakata T, Liu H, Tanaka Y, Nishihashi N, Wang X and Sato A 2011 Aerodynamics of a bio-inspired flexible flapping-wing micro air vehicle Bioinsp. Biomim. 6 045002 [3] Annunziata S, Paskarbeit J and Schneider A 2011 Novel bioinspired control approaches to increase the stiffness variability in multi-muscle driven joints Bioinsp. Biomim. 6 045003 [4] Merker A, Rummel J and Seyfarth A 2011 Stable walking with asymmetric legs Bioinsp. Biomim. 6 045004 [5] Rossi C, Colorado J, Coral W and Barrientos A 2011 Bending continuous structures with SMAs: a novel robotic fish design Bioinsp. Biomim. 6 045005 [6] Carpi F, Kornbluh R, Sommer-Larsen P and Alici G 2011 Electroactive polymer actuators as artificial muscles: are they ready for bioinspired applications? Bioinsp. Biomim. 6 045006.
柔性多体动力学的共旋坐标法
The co-rotational formulation for flexible multibody dynamics
刚-柔耦合系统动力学建模理论与仿真技术研究
[博士论文].
Study on modeling theory and simulation technique for rigid-flexible coupling systems dynamics
[PhD Thesis].
An arbitrary Lagrangian-Eulerian formulation of a geometrically exact Timoshenko beam running through a tube
An absolute nodal coordinates formulation for the large rotation and deformation analysis of flexible bodies. [Technical Report]. Report No. MBS96-1-UIC
Definition of ANCF finite elements
空间结构展开动力学的等几何有限元建模方法
[博士论文].
Finite element modeling of deployment dynamics of space structures via isogeometric analysis
[PhD Thesis].
Description of elastic forces in absolute nodal coordinate formulation
The objective of this paper is to investigate the accuracy of the elastic force models that can be used in the absolute nodal coordinate finite element formulation. This study focuses on the description of the elastic forces in three-dimensional beams. The elastic forces of the absolute nodal coordinate formulation can be derived using a continuum mechanics approach. This study investigates the accuracy and usability of such an approach for a three-dimensional absolute nodal coordinate beam element. This study also presents an improvement proposal for the use of a continuum mechanics approach in deriving the expression of the elastic forces in the beam element. The improvement proposal is verified using several numerical examples that show that the proposed elastic force model of the beam element agrees with the analytical results as well as with the solutions obtained using existing finite element formulation. In the beam element under investigation, global displacements and slopes are used as the nodal coordinates, which resulted in a large number of nodal degrees of freedom. This study provides a physical interpretation of the nodal coordinates used in the absolute nodal coordinate beam element. It is shown that a beam element based on the absolute nodal coordinate formulation relaxes the assumption of a rigid cross-section and is capable of representing a distortional deformation of the cross-section. The numerical results also imply that the beam element does not suffer from the phenomenon called shear locking.
A new locking-free shear deformable finite element based on absolute nodal coordinates
The absolute nodal coordinate formulation has been recently extended to shear deformable beam or plate elements. This has been accomplished, in practice, by parameterizing the complete volume of the elements instead of a line or surface in the element kinematics description. In the absolute nodal coordinate formulation, the position of any point of the element volume is defined employing independent slope coordinates. The use of a large number of slope coordinates leads to unusual kinematic features that must be accounted for in order to avoid the element locking. This study demonstrates that the shear deformable element based on the absolute nodal coordinate formulation suffers from curvature thickness locking and shear locking in addition to the previously reported Poisson’s locking. Due to the tendency of locking, the use of the absolute nodal coordinate formulation can lead to elements with weak performance. In order to eliminate locking problems, this study introduces a new absolute nodal coordinate-based finite element. The introduced element uses redefined polynomial expansion together with a reduced integration procedure. The performance of the introduced element is studied by means of certain dynamic problems. The element exhibits a competent convergence rate and it does not suffer from the previously mentioned locking effects.
A curved beam element in the analysis of flexible multi-body systems using the absolute nodal coordinates
Analysis of thin beams and cables using the absolute nodal co-ordinate formulation
The purpose of this paper is to present formulations for beam elements based on the absolute nodal co-ordinate formulation that can be effectively and efficiently used in the case of thin structural applications. The numerically stiff behaviour resulting from shear terms in existing absolute nodal co-ordinate formulation beam elements that employ the continuum mechanics approach to formulate the elastic forces and the resulting locking phenomenon make these elements less attractive for slender stiff structures. In this investigation, additional shape functions are introduced for an existing spatial absolute nodal co-ordinate formulation beam element in order to obtain higher accuracy when the continuum mechanics approach is used to formulate the elastic forces. For thin structures where bending stiffness can be important in some applications, a lower order cable element is introduced and the performance of this cable element is evaluated by comparing it with existing formulations using several examples. Cables that experience low tension or catenary systems where bending stiffness has an effect on the wave propagation are examples in which the low order cable element can be used. The cable element, which does not have torsional stiffness, can be effectively used in many problems such as in the formulation of the sliding joints in applications such as the spatial pantograph/catenary systems. The numerical study presented in this paper shows that the use of existing implicit time integration methods enables the simulation of multibody systems with a moderate number of thin and stiff finite elements in reasonable CPU time.
Review on the absolute nodal coordinate formulation for large deformation analysis of multibody systems
State of the art of ANCF elements regarding geometric description, interpolation strategies, definition of elastic forces, validation and the locking phenomenon in comparison with proposed beam finite elements
The focus of the present article lies on new enhanced beam finite element formulations in the absolute nodal coordinate formulation (ANCF) and its embedding in the available formulations in the literature. The ANCF has been developed in the past for the modeling of large deformations in multibody dynamics problems. In contrast to the classical nonlinear beam finite elements in literature, the ANCF does not use rotational degrees of freedom, but slope vectors for the parameterization of the orientation of the cross section. This leads to several advantages compared to the classical formulations, e.g. ANCF elements do not necessarily suffer from singularities emerging from the parameterization of rotations. In the classical large rotation vector formulation, the mass matrix is not constant with respect to the generalized coordinates. In the case of ANCF elements, a constant mass matrix follows, which is advantageous in dynamic analysis. In the standard geometrically exact formulation, the parameterization of rotations leads to a nonlinear term containing quadratic velocities. The so-called quadratic velocity vector vanishes for ANCF elements which is advantageous in dynamic applications. In the present article, existing beam finite element formulations are analyzed and improved to derive formulations which are able to solve industrial applications with high performance, efficiency and accuracy. The interest lies especially on finite element formulations for multibody dynamics systems that are capable of large deformations in order to derive accurate solutions of nonlinear engineering and research problems. Existing shear deformable ANCF beam finite elements show an overly stiff behavior caused by the locking phenomenon. Existing locking problems are discussed in this article and avoided in the proposed elements in order to gain accurate solutions. The state of the art of ANCF elements in literature is reviewed including the basic description of the kinematics, interpolation strategies and definition of elastic forces, but also problems and known disadvantages arising in the existing elements, as e.g. the locking phenomenon. Regarding the description of the elastic forces, the present article shows the two standard approaches in literature as well as new enhanced formulations to avoid locking: a continuum mechanics based formulation for the elastic forces with elimination of Poisson and shear locking, and an extended hybrid structural mechanics based formulation for the elastic forces including a term for penalizing shear and cross section deformation. The definition of the element kinematics and interpolation strategies in existing elements are discussed and compared to the according descriptions of the proposed elements. A comparison of the solution of the proposed finite elements to analytical solutions in the literature and to the solution retrieved from commercial finite element software have shown high accuracy and high order of convergence. The speed of convergence is evaluated regarding different interpolation strategies and different formulations for the elastic forces. The investigations show that the proposed elements have high potential for simulation of geometrically nonlinear problems arising from real-life multibody applications and therefore are highly competitive with existing elements in commercial finite element codes. It has to be mentioned here that most of the studies on nonlinear elements based on the ANCF in literature use linear constitutive laws.
Regarding many applications in which geometric and material nonlinearities arise, elastic material models are not sufficient to represent the real problem accurately. For this reason, an extension of the material model is necessary in order to fulfill the requirements of current but also of future materials arising in engineering or research. An overview of existing nonlinear material models in literature can be found in the "Appendix".
经历大范围运动和大变形的细梁接触动力学
[博士论文].
Contact dynamics of thin beams subject to overall motions and large deformations
[PhD Thesis].
Soft machines: Challenges to computational dynamics
Three-dimensional solid brick element using slopes in the absolute nodal coordinate formulation
Absolute nodal coordinate formulation of tetrahedral solid element
A total lagrangian ANCF liquid sloshing approach for multibody system applications
Development of ANCF tetrahedral finite elements for the nonlinear dynamics of flexible structures
Dynamic modeling of mass-flowing linear medium with large amplitude displacement and rotation
In this paper, a dynamic model of a linear medium with mass flow, such as traveling strings, cables, belts, beams or pipes conveying fluids, is proposed, in the framework of Arbitrary-Lagrange-Euler (ALE) description. The material coordinate is introduced to characterize the mass-flow of the medium, and the Absolute Nodal Coordinate Formulation (ANCF) is employed to capture geometric nonlinearity of the linear media under large displacement and rotation. The governing equations are derived in terms of d'Alembert's principle. When using an ALE description, complex mass-flowing boundary conditions can be easily enforced. Numerical examples are presented to validate the proposed method by comparison with analytical results of simplified models. The computed critical fluid velocity for the stability of a cantilevered pipe conveying fluid is correlated with the available theory in literature. The large amplitude limit-cycle oscillations of flexible pipes conveying fluid are presented, and the effect of the velocity of the fluid on the static equilibrium of the pipe under gravity is investigated. (C) 2011 Elsevier Ltd.
A modeling of sliding joint on one-dimensional flexible medium
The dynamic modeling of a sliding joint on a one-dimensional medium, such as a cable or a beam, is studied in this paper. The sliding joint is implemented by positioning it at a moving node on the one-dimensional medium, which is realized by variable-length elements at either side of the joint. The variable-length element is established with an absolute nodal coordinate formulation (ANCF) in the framework of the Arbitrary Lagrange-Euler (ALE) description. The sliding of the joint is described by the increasing of the length on one side of the one-dimensional medium and a corresponding decreasing of the other side. In order to capture the discontinuity of the slopes at the position of the sliding joint, the moving node has two slopes as generalized coordinates which are equal to each other in the case of a beam but not in the case of a cable, and in order to avoid the addition-deletion constraint, the node adjacent to the moving node is added or deleted if the element is too long or too short. The governing equations for the coupled system are derived in terms of D'Alembert's principle and the resulting equations of motion are formulated in the standard form of differential algebraic equations of multibody systems. Numerical examples are presented to validate the method proposed by comparing with analytical results which are available or are made possible by simplifying the model.
Dynamics of variable-length tethers with application to tethered satellite deployment
The dynamics of variable-length tethers are studied using a flexible multibody dynamics method. The governing equations of the tethers are derived using a new, hybrid Eulerian and Lagrangian framework, by which the mass flow at a boundary of a tether and the length variation of a tether element are accounted for. The variable-length tether element based on the absolute nodal coordinate formulation is developed to simulate the deployment of satellite tethers. The coupled dynamic equations of tethers and satellites are obtained using the Lagrangian multiplier method. Several tethered satellite systems involving large displacements, rotations, and deformations are numerically simulated, where the tethers are released from several meters to about 1 km. A control strategy is proposed to avoid slackness of the tethers during deployment. The accuracy of the modeling and solution procedures was validated on an elevator model. (C) 2010 Elsevier B.V.
Dynamic analysis of cable-driven parallel manipulators using a variable length finite element
An arbitrary Lagrangian-Eulerian discretization method for modeling and simulation of reeving systems in multibody dynamics
A variable-length beam element incorporating the effect of spinning
A thin plate element based on the combined arbitrary Lagrange-Euler and absolute nodal coordinate formulations
Topology optimization of a flexible multibody system with variable-length bodies described by ALE-ANCF
Axially variable-length solid element of absolute nodal coordinate formulation
A general method for kineto-elastodynamic analysis and synthesis of mechanisms
This paper summarizes the scientific discussion on the issue of public-private partnership in healthcare sector. The main purpose of research is to analyze the public-private partnership as the progressive form of innovative and investment mechanism in Ukrainian healthcare sector, taking into the consideration international experience in this sphere. The key methods used in the conducted research are data analysis, summarization and comparison. The data synthesis and analysis are the basic value-added elements of this research, which could help to find out the main prospective of PPP-model use in Ukrainian healthcare sector. The object of research is the group of countries such as USA, UK, Canada, and BRIC countries, because namely they are the most progressive in public-private partnership in health care. Practical importance of the scientific research results lies in defining the general principles of public-private partnerships and a set of criterion for its efficiency estimation. Also, the worldwide experience was analyzed in this research and main challenges for its implementation in Ukrainian healthcare practice were considered. It is important for the further development of the healthcare sphere, and improvement of the healthcare facilities' activity in Ukraine. Further research directions are aimed at study of the specific issue of public-private partnership, such as circumstances for creating alliances between private and public actors from a strategy perspective, explore the impact of incentive mechanisms and risk management procedures on health service performance throughout the extended project life-cycle, and to create conducive environments to foster inter-project learning.
A general method of kineto-elastodynamic design of high speed mechanisms
The mechanisms of skull impact loading may change following surgical interventions such as the removal of bone lesions, but little is known about the consequences in the event of subsequent head trauma. We, therefore, prepared acrylonitrile butadiene styrene human skull models based on clinical computed tomography skull data using a three-dimensional printer. Six replicate physical skull models were tested, three with bone excisions and three without. A drop tower was used to simulate the impact sustained by falling backwards onto the occipital lobe region. The impacts were recorded with a high-speed camera, and the occipital strain response was determined by digital image correlation. Although the hole affected neither the magnitude nor the sequence of the fracture pattern, the digital image correlation analysis highlighted an increase in strain around the excised area (0.45%-16.4% of the principal strain). Our approach provides a novel method that could improve the quality of life for patients on many fronts, including protection against trauma, surgical advice, post-operative care, advice in litigation cases, as well as facilitating general biomechanical research in the area of trauma injuries.
Optimum design of high-speed flexible robotic arms with dynamic behavior constraints
Active development of quantum informational components such as quantum computers and quantum key distribution systems requires parameter characterization of single photon detectors. A key property of the single photon detectors is detection efficiency. One of the methods of the detection efficiency measurement, as listed in the international standard ETSI, is the reference-free twin-photon-based Klyshko method. The signal-to-noise ratio (SNR) of this method depends on the combination of the pump wavelength, the nonlinear crystal's axis angle, and the type of detector's sensitive element. When the combination is difficult, one has to deal with the low SNR of the detector counts measurement. To gain the high SNR, one has to average the long record complicated with the &quot;random telegraph signal&quot; noise. This type of noise exhibits high spectral density at a zero frequency, where simple averaging works. The heterodyne based method we have proposed is to perform averaging at the higher frequency of the modulation introduced to the standard Klyshko measurement scheme. The method was numerically simulated and experimentally tested. The 14 times improvement in SNR for the proposed method relative to the simple averaging was demonstrated by the numerical simulation and confirmed experimentally.
High-speed mechanism design——a general analytical approach
Optimality criterion techniques applied to mechanical design
Mechanism optimization via optimality criterion techniques
Optimum design of high speed flexible mechanisms
Optimum design of flexible mechanisms
We discuss here a unique flexible non-carbonaceous layered host, namely, metal titanium niobates (M-Ti-niobate, M: Al3+ , Pb2+ , Sb3+ , Ba2+ , Mg2+ ), which can synergistically store both lithium ions and sodium ions via a simultaneous intercalation and alloying mechanisms. M-Ti-niobate is formed by ion exchange of the K+ ions, which are specifically located inside galleries between the layers formed by edge and corner sharing TiO6 and NbO6 octahedral units in the sol-gel synthesized potassium titanium niobate (KTiNbO5 ). Drastic volume changes (approximately 300-400 %) typically associated with an alloying mechanism of storage are completely tackled chemically by the unique chemical composition and structure of the M-Ti-niobates. The free space between the adjustable Ti/Nb octahedral layers easily accommodates the volume changes. Due to the presence of an optimum amount of multivalent alloying metal ions (50-75 % of total K+ ) in the M-Ti-niobate, an efficient alloying reaction takes place directly with ions and completely eliminates any form of mechanical degradation of the electroactive particles. The M-Ti-niobate can be cycled over a wide voltage range (as low as 0.01 V) and displays remarkably stable Li+ and Na+ ion cyclability (>2 Li+ /Na+ per formula unit) for widely varying current densities over few hundreds to thousands of successive cycles. The simultaneous intercalation and alloying storage mechanisms is also studied within the density functional theory (DFT) framework. DFT expectedly shows a very small variation in the volume of Al-titanium niobate following lithium alloying. Moreover, the theoretical investigations also conclusively support the occurrence of the alloying process of Li ions with the Al ions along with the intercalation process during discharge. The M-Ti-niobates studied here demonstrate a paradigm shift in chemical design of electrodes and will pave the way for the development of a multitude of improved electrodes for different battery chemistries.
A state space technique for optimal design of mechanisms
Design optimization of multibody systems by sequential approximation
Min-max dynamic response optimization of mechanical systems using approximate augmented Lagrangian
Optimization of flexible multibody dynamic systems using the equivalent static load method
Optimization of flexible components of multibody systems via equivalent static loads
An optimization methodology that iteratively links the results of multibody dynamics and structural analysis software to an optimization method is presented to design flexible multibody systems under dynamic loading conditions. In particular, rigid multibody dynamic analysis is utilized to calculate dynamic loads of a multibody system and a structural optimization algorithm using equivalent static loads transformed from the dynamic loads are used to design the flexible components in the multibody dynamic system. The equivalent static loads, which are derived from equations of motion, are used as multiple loading conditions of linear structural optimization. A simple example is solved to verify the proposed methodology and the pelvis part of the biped humanoid, a complex multibody system which consists of many bodies and joints, is redesigned using the proposed methodology.
On the influence of model reduction techniques in topology optimization of flexible multibody systems using the floating frame of reference approach
Structural sensitivity analysis of flexible multibody systems modeled with the floating frame of reference approach using the adjoint variable method
Modeling of revolute joints in topology optimization of flexible multibody systems
Topology optimization of members of flexible multibody systems under dominant inertia loading
Discussion on the optimization problem formulation of flexible components in multibody systems
Structural optimization of multibody system components described using level set techniques
On the equivalent static load method for flexible multibody systems described with a nonlinear finite element formalism
Weakly and fully coupled methods for structural optimization of flexible mechanisms
Implementation of an ANCF beam finite element for dynamic response optimization of elastic manipulators
Structural optimization of flexible components in a flexible multibody system modeled via ANCF
Topology optimization based on level set for a flexible multibody system modeled via ANCF
Topology optimization of a three-dimensional flexible multibody system via moving morphable components
Design of a planar multibody dynamic system with ANCF beam elements based on an element-wise stiffness evaluation procedure
Simultaneous topology and size optimization of a 3D variable-length structure described by the ALE-ANCF
Analytic Methods for Design Practice
There is a concern that the apparent effectiveness of interventions tested in clinical trials may not be an accurate reflection of their actual effectiveness in usual practice. Pragmatic randomized controlled trials (RCTs) are designed with the intent of addressing this discrepancy. While pragmatic RCTs may increase the relevance of research findings to practice they may also raise new ethical concerns (even while reducing others). To explore this question, we interviewed key stakeholders with the aim of identifying potential ethical challenges in the design and conduct of pragmatic RCTs with a view to developing future guidance on these issues.
Determination of the crash pulse and optimization of the crash components using the response surface approximate optimization
Crashworthiness design optimization using successive response surface approxim
Finite Element (FE) method is among the most powerful tools for crash analysis and simulation. Crashworthiness design of structural members requires repetitive and iterative application of FE simulation. This paper presents a crashworthiness design optimization methodology based on efficient and effective integration of optimization methods, FE simulations, and approximation methods. Optimization methods, although effective in general in solving structural design problems, loose their power in crashworthiness design. Objective and constraint functions in crashworthiness optimization problems are often non-smooth and highly non-linear in terms of design variables and follow from a computationally costly (FE) simulation. In this paper, a sequential approximate optimization method is utilized to deal with both the high computational cost and the non-smooth character. Crashworthiness optimization problem is divided into a series of simpler sub-problems, which are generated using approximations of objective and constraint functions. Approximations are constructed by using statistical model building technique, Response Surface Methodology (RSM) and a Genetic algorithm. The approximate optimization method is applied to solve crashworthiness design problems. These include a cylinder, a simplified vehicle and New Jersey concrete barrier optimization. The results demonstrate that the method is efficient and effective in solving crashworthiness design optimization problems.
Design optimization of multi-body systems under impact loading by response surface methodology
Optimization of a car body component subjected to side impact
A review of optimization of structures subjected to transient loads
Various aspects of structural optimization techniques under transient loads are extensively reviewed. The main themes of the paper are treatment of time-dependent constraints, calculation of design sensitivity, and approximation. Each subject is reviewed with corresponding papers that have been published since the 1970s. The treatment of time-dependent constraints in both the direct method and the transformation method is discussed. Two ways of calculating design sensitivity of a structure under transient loads are discussed—direct differentiation method and adjoint variable method. The approximation concept mainly focuses on the response surface method in crashworthiness and local approximation with the intermediate variables. Especially, a method using the equivalent static load is discussed as an approximation method. It takes advantage of the well-established static response optimization. The structural optimization in flexible multibody dynamic systems is reviewed in the viewpoint of the above three themes.
Optimization of rigid and flexible multibody systems with application to vehicle dynamics and crashworthiness
//
Optimization of multibody systems and their structural components
Spectral computed tomography (CT) reconstructs the same scanned object from projections of multiple narrow energy windows, and it can be used for material identification and decomposition. However, the multi-energy projection dataset has a lower signal-noise-ratio (SNR), resulting in poor reconstructed image quality. To address this thorny problem, we develop a spectral CT reconstruction method, namely spatial-spectral cube matching frame (SSCMF). This method is inspired by the following three facts: i) human body usually consists of two or three basic materials implying that the reconstructed spectral images have a strong sparsity; ii) the same basic material component in a single channel image has similar intensity and structures in local regions. Different material components within the same energy channel share similar structural information; iii) multi-energy projection datasets are collected from the subject by using different narrow energy windows, which means images reconstructed from different energy-channels share similar structures. To explore those information, we first establish a tensor cube matching frame (CMF) for a BM4D denoising procedure. Then, as a new regularizer, the CMF is introduced into a basic spectral CT reconstruction model, generating the SSCMF method. Because the SSCMF model contains an L0-norm minimization of 4D transform coefficients, an effective strategy is employed for optimization. Both numerical simulations and realistic preclinical mouse studies are performed. The results show that the SSCMF method outperforms the state-of-the-art algorithms, including the simultaneous algebraic reconstruction technique, total variation minimization, total variation plus low rank, and tensor dictionary learning.
Structural optimization of flexible components within a multibody dynamics approach
[PhD Thesis].
On structural optimization of flexible multibody systems
[PhD Thesis].
Topology optimization for multi-functional components in multibody dynamics systems
[PhD Thesis].
A study of alternative formulations for optimization of structural and mechanical systems subjected to static and dynamic loads
[PhD Thesis].
Topology optimization of dynamically loaded parts in mechanical systems: Coupling of MBS, FEM and structural optimization: NAFEMS seminar analysis of multi-body systems using FEM and MBS
Automated topology optimization of flexible components in hybrid finite element multibody systems using ADAMS/Flex and MSC.Construct
//
Shape optimization based on parameters from lifetime prediction: Nafems Seminar: Fatigue Analysis
Topology optimization of dynamic loaded parts using multibody simulation and durability analysis
//
Gradient-based optimization of flexible multibody systems using the absolute nodal coordinate formulation
//
A topological optimization approach for structural design of a high-speed low-load mechanism using the equivalent static loads method
In high-speed low-load mechanisms, the principal loads are the inertial forces caused by the high accelerations and velocities. Hence, mechanical design should consider lightweight structures to minimize such loads. In this paper, a topological optimization method is presented on the basis of the equivalent static loads method. Finite element (FE) models of the mechanism in different positions are constructed, and the equivalent loads are obtained using flexible multibody dynamics simulation. Kinetic DOFs are used to simulate the motion joints, and a quasi-static analysis is performed to obtain the structural responses. The element sensitivity is calculated according to the static-load-equivalent equilibrium, in such a way that the influence on the inertial force is considered. A dimensionless component sensitivity factor (strain energy caused by unit load divided by kinetic energy from unit velocity) is used, which quantifies the significance of each element. Finally, the topological optimization approach is presented on the basis of the evolutionary structural optimization method, where the objective is to find the maximum ratio of strain energy to kinetic energy. In order to show the efficiency of the presented method, we presented two numerical cases. The results of these analyses show that the presented method is more efficient and can be easily implemented in commercial FE analysis software. Copyright (C) 2011 John Wiley & Sons, Ltd.
A topological optimization method for flexible multi-body dynamic system using epsilon algorithm
Efficient topology optimization of large dynamic finite element systems using fatigue
Efficient topology optimization for large and dynamically loaded FE models: IMAC-XXVII
//
结构动力优化设计述评与展望
结构动力优化设计是当前工程结构设计研究领域中的前沿性课题。文中着重从结构动力特性优化、结构动力响应设计、结构动力灵敏度分析和基于可靠性的结构动力优化设计等四个专题方面对结构动力优化设计研究的发展与现状进行了述评,并粗略地展望了结构动力优化研究未来的发展趋势。
A review on structural dynamic optimum design
结构动力优化设计是当前工程结构设计研究领域中的前沿性课题。文中着重从结构动力特性优化、结构动力响应设计、结构动力灵敏度分析和基于可靠性的结构动力优化设计等四个专题方面对结构动力优化设计研究的发展与现状进行了述评,并粗略地展望了结构动力优化研究未来的发展趋势。
结构动力优化设计发展综述
Review on the development in structural dynamic optimum design
Structural optimization with frequency constraints-a review
Topology optimization: A review for structural designs under vibration problems
Free vibration analysis of rotating thick plates
Modal characteristic of a rotating rectangular cantilever plate
Flapwise bending vibration of rotating plates
Modal analysis of rotating composite cantilever plates
Free vibration analysis of rotating cantilever plates
Finite element free vibration analysis of rotating laminated composite pretwisted cantilever plates
Natural frequencies of twisted rotating plates
Vibration analysis of rotating cantilever plates
In the past three decades, finite element (FE) modelling has provided considerable understanding to the area of musculoskeletal biomechanics. However, most of this understanding has been generated using generic, standardised or idealised models. Patient-specific modelling (PSM) is almost never used for making clinical decisions. Imaging technologies have made it possible to create patient-specific geometries and FE meshes for modelling. While these have brought us closer to PSM, several challenges associated with the definition of material properties, loads, boundary conditions and interaction between components still need to be overcome. This study reviews the current status of PSM with respect to defining material behaviour and prescribing boundary conditions and interactions. With regard to the constitutive modelling of bone, it is seen that imaging is being increasingly used to define elastic properties (isotropic as well as anisotropic). However, the post-elastic and time-dependent behaviour, important for several modelling situations, is mostly obtained from in vitro experiments. Strain-based plasticity, not commonly available in FE codes, appears to have the potential of reducing an element of patient-specificity in modelling the yielding behaviour of bone. PSM of real boundary conditions that include muscles and ligaments continues to remain a challenge; many clinically relevant questions can be, however, answered without their inclusion. Simulation techniques to undertake PSM of interactions between bone and uncemented implants are available. Interference fit employed in both joint replacement fracture treatments induces considerable preload whose inclusion in models is important for the prediction of interface behaviour.
Modal analysis of a rotating thin plate via absolute nodal coordinate formulation
Modal characteristics of a rotating flexible beam with a concentrated mass based on the absolute nodal coordinate formulation
Vibration analysis of a rotating Timoshenko beam
Dynamic analysis of a rotating planar Timoshenko beam using an accurate global spatial discretization method
Dynamic topology optimization design of rotating beam cross-section with gyroscopic effects
Maximization of eigenvalues using topology optimization
Topology optimization is used to optimize the eigenvalues of plates. The results are intended especially for MicroElectroMechanical Systems (MEMS) but can be seen as more general. The problem is not formulated as a case of reinforcement of an existing structure, so there is a problem related to localized modes in low density areas. The topology optimization problem is formulated using the SIMP method. Special attention is paid to a numerical method for removing localized eigenmodes in low density areas. The method is applied to numerical examples of maximizing the first eigenfrequency. One example is a practical MEMS application; a probe used in an Atomic Force Microscope (AFM). For the AFM probe the optimization is complicated by a constraint on the stiffness and constraints on higher order eigenvalues.
Topology optimization of resonating structures using SIMP method
Eigenvalue topology optimization via efficient multilevel solution of the frequency response
Buckling strength topology optimization of 2D periodic materials based on linearized bifurcation analysis
Topology optimization for eigenfrequencies of a rotating thin plate via moving morphable components
基于多体系统的灵敏度分析及动态优化设计
[博士论文].
Sensitivity analysis and design optimization of multibody systems
[PhD Thesis].
柔性多体系统动力学及其设计灵敏度分析
[博士论文].
Flexible multibody system dynamics and its design sensitivity analysis
[PhD Thesis].
Computational aspects of sensitivity calculations in transient structural analysis
Active development of quantum informational components such as quantum computers and quantum key distribution systems requires parameter characterization of single photon detectors. A key property of the single photon detectors is detection efficiency. One of the methods of the detection efficiency measurement, as listed in the international standard ETSI, is the reference-free twin-photon-based Klyshko method. The signal-to-noise ratio (SNR) of this method depends on the combination of the pump wavelength, the nonlinear crystal's axis angle, and the type of detector's sensitive element. When the combination is difficult, one has to deal with the low SNR of the detector counts measurement. To gain the high SNR, one has to average the long record complicated with the &quot;random telegraph signal&quot; noise. This type of noise exhibits high spectral density at a zero frequency, where simple averaging works. The heterodyne based method we have proposed is to perform averaging at the higher frequency of the modulation introduced to the standard Klyshko measurement scheme. The method was numerically simulated and experimentally tested. The 14 times improvement in SNR for the proposed method relative to the simple averaging was demonstrated by the numerical simulation and confirmed experimentally.
Optimal design of mechanical systems with constraint violation stabilization method
Design sensitivity analysis of elastic mechanical systems
Surface acoustic wave sensors have the advantage of fast response, low-cost, and wireless interfacing capability and they have been used in the medical analysis, material characterization, and other application fields that immerse the device under a liquid environment. The theoretical analysis of the single guided layer shear horizontal acoustic wave based on the perturbation theory has seen developments that span the past 20 years. However, multiple guided layer systems under a liquid environment have not been thoroughly analyzed by existing theoretical models. A dispersion equation previously derived from a system of three rigidly coupled elastic mass layers is extended and developed in this study with multiple guided layers to analyze how the liquid layer's properties affect the device's sensitivity. The combination of the multiple layers to optimize the sensitivity of an acoustic wave sensor is investigated in this study. The Maxwell model of viscoelasticity is applied to represent the liquid layer. A thorough analysis of the complex velocity due to the variations of the liquid layer's properties and thickness is derived and discussed to optimize multilayer Surface acoustic wave (SAW) sensor design. Numerical simulation of the sensitivity with a liquid layer on top of two guided layers is investigated in this study as well. The parametric investigation was conducted by varying the thicknesses for the liquid layer and the guided layers. The effect of the liquid layer viscosity on the sensitivity of the design is also presented in this study. The two guided layer device can achieve higher sensitivity than the single guided layer counterpart in a liquid environment by optimizing the second guided layer thickness. This perturbation analysis is valuable for Love wave sensor optimization to detect the liquid biological samples and analytes.
ADIFOR 2.0: Automatic differentiation of Fortran 77 programs
ADIFOR-generating derivative codes from Fortran programs
On the calculation of Jacobian matrices by the Markowitz rule
No. ANL/CP-75176; CONF-910189-4.
A divide-and-conquer direct differentiation approach for multibody system sensitivity analysis
In the design and analysis of multibody dynamics systems, sensitivity analysis is a critical tool for good design decisions. Unless efficient algorithms are used, sensitivity analysis can be computationally expensive, and hence, limited in its efficacy. Traditional direct differentiation methods can be computationally expensive with complexity as large as O(n 4+n 2 m 2+nm 3), where n is the number of generalized coordinates in the system and m is the number of algebraic constraints. In this paper, a direct differentiation divide-and-conquer approach is presented for efficient sensitivity analysis of multibody systems with general topologies. This approach uses a binary tree structure to traverse the topology of the system and recursively generate the sensitivity data in linear and logarithmic complexities for serial and parallel implementations, respectively. This method works concurrently with the forward dynamics problem, and hence, requires minimal data storage. The differentiation required in this algorithm is minimum as compared to traditional methods, and is generated locally on each body as a preprocessing step. The method provides sensitivity values accurately up to integration tolerance and is insensitive to perturbations in design parameter values. This approach is a good alternative to existing methodologies, as it is fairly simple to implement for general topologies and is computationally efficient.
Implicit numerical integration for design sensitivity analysis of rigid multibody systems
Recursive sensitivity analysis for constrained multi-rigid-body dynamic systems design optimization
Analytical fully-recursive sensitivity analysis for multibody dynamic chain systems
This paper presents a novel fully recursive method, a direct differentiation based approach, which facilitates first-order sensitivityanalysis in optimal design problems involving multibody dynamic systems. A state space O(n) dynamic analysis algorithm based on avelocity space projection method, as promoted by Kane [18], forms the foundation of the underlying formulation. This algorithm cansignificantly reduce the massive number of mathematical and associated computational operations involved in explicitly generatingand solving the sensitivity equations. This benefit is particularly evident for systems involving a combination of many state variablesand design parameters. The development presented in this paper focuses on chain systems to illustrate the recursive nature of thealgorithm. The computational efficiency and solution accuracy of the presented algorithm are investigated through the proceduresapplication to the simulation and design sensitivity determination of spatial chain systems involving 2, 4, 6, ..., 24 degrees offreedom, as well as a simple planar double pendulum.
Kinematic and kinetic derivatives in multibody system analysis
Sensitivity analysis of rigid-flexible multibody systems
Optimization of multibody dynamics using object oriented programming and a mixed numerical-symbolic penalty formulation
Multibody dynamic response optimization with ALM and approximate line search
Analysis and optimal design of spatial mechanical systems
Acquisition of high-quality x-ray images using low patient exposures requires detectors with high detective quantum efficiency (DQE). We describe a novel apodized-aperture pixel (AAP) design that increases high-frequency modulation transfer function (MTF) and DQE values. The AAP design makes a separation of physical sensor elements from image pixels by using very small sensor elements (e.g., 0.010-0.025 mm) to synthesize desired larger image pixels (e.g., 0.1-0.2 mm).
Sensitivity analysis of flexible multibody systems using composite materials components
多体系统动力学设计灵敏度分析直接微分法
Direct differentiation method for design sensitivity analysis of multibody system dynamics
多体系统动力学设计灵敏度分析的直接微分方法
The direct differentiation method for sensitivity analysis of multibody system dynamics
Direct sensitivity analysis of multibody systems: A vehicle dynamics benchmark
Direct differentiation method for sensitivity analysis based on transfer matrix method for multibody systems
Direct and adjoint sensitivity analysis of ordinary differential equation multibody formulations
Sensitivity analysis approach to multibody systems described by natural coordinates
The classical natural coordinate modeling method which removes the Euler angles and Euler parameters from the governing equations is particularly suitable for the sensitivity analysis and optimization of multibody systems. However, the formulation has so many principles in choosing the generalized coordinates that it hinders the implementation of modeling automation. A first order direct sensitivity analysis approach to multibody systems formulated with novel natural coordinates is presented. Firstly, a new selection method for natural coordinate is developed. The method introduces 12 coordinates to describe the position and orientation of a spatial object. On the basis of the proposed natural coordinates, rigid constraint conditions, the basic constraint elements as well as the initial conditions for the governing equations are derived. Considering the characteristics of the governing equations, the newly proposed generalized-a integration method is used and the corresponding algorithm flowchart is discussed. The objective function, the detailed analysis process of first order direct sensitivity analysis and related solving strategy are provided based on the previous modeling system. Finally, in order to verify the validity and accuracy of the method presented, the sensitivity analysis of a planar spinner-slider mechanism and a spatial crank-slider mechanism are conducted. The test results agree well with that of the finite difference method, and the maximum absolute deviation of the results is less than 3%. The proposed approach is not only convenient for automatic modeling, but also helpful for the reduction of the complexity of sensitivity analysis, which provides a practical and effective way to obtain sensitivity for the optimization problems of multibody systems.
An efficient direct differentiation approach for sensitivity analysis of flexible multibody systems
Direct sensitivity analysis of multibody systems with holonomic and nonholonomic constraints via an index-3 augmented Lagrangian formulation with projections
Identification and identifiability of unknown parameters in multibody dynamic systems
Assessing design changes in mechanical systems from simulationresults requires both accurate dynamic models and accurate values forparameters in the models. Model parameters are often unavailable ordifficult to measure. This study details an identification procedure fordetermining optimal values for unknown or estimated model parametersfrom experimental test data. The resulting optimization problem issolved by Levenberg–Marquardt methods. Partial derivative matricesneeded for the optimization are computed through sensitivity analysis.The sensitivity equations to be solved are generated analytically.Unfortunately, not all parameters can be uniquely determined using anidentification procedure. An issue of parameter identifiability remains.Since a global identifiability test is impractical for even the simplestmodels, a local identifiability test is developed. Two examples areprovided. The first example highlights the test for parameteridentifiability, while the second shows the usefulness of parameteridentification by determining vehicle suspension parameters fromexperimentally measured data.
基于微分/代数方程的多体系统动力学设计灵敏度分析的伴随变量方法
基于多体系统动力学微分/代数方程数学模型和通用积分形式的目标函数,建立了多体系统动力学设计灵敏度分析的伴随变量方法,避免了复杂的设计灵敏度计算,对于设计变量较多的多体系统灵敏度分析具有较高的计算效率.文中给出了通用公式以及具体的计算过程和验证方法,并将目标函数及其导数积分形式的计算转化为微分方程的初值问题,进一步提高了计算效率和精度.文末通过一曲柄-滑块机构算例对算法的有效性进行了验证.
Adjiont variable method for sensitivity analysis of multibody system dynamics described by differential/algebraic equations
基于多体系统动力学微分/代数方程数学模型和通用积分形式的目标函数,建立了多体系统动力学设计灵敏度分析的伴随变量方法,避免了复杂的设计灵敏度计算,对于设计变量较多的多体系统灵敏度分析具有较高的计算效率.文中给出了通用公式以及具体的计算过程和验证方法,并将目标函数及其导数积分形式的计算转化为微分方程的初值问题,进一步提高了计算效率和精度.文末通过一曲柄-滑块机构算例对算法的有效性进行了验证.
基于二阶常微分方程的多体系统动力学设计灵敏度分析的伴随变量方法
针对二阶常微分方程描述的多体动力学模型和通用积分形式的目标函数,通过引入伴随变量,系统地推导了多体系统动力学设计灵敏度分析计算公式,避免了直接微分方法中广义坐标及其各阶导数对设计参数偏微分的计算,在设计参数较多的情况下提高了计算效率。又将目标函数及其导数积分形式的计算转化为微分方程的初值问题,进一步提高了计算效率和精度。文末给出一个平面机械臂模型算例。
Adjoint variable method for design sensitivity analysis of multibody system dynamics described by ordinary differential equations
针对二阶常微分方程描述的多体动力学模型和通用积分形式的目标函数,通过引入伴随变量,系统地推导了多体系统动力学设计灵敏度分析计算公式,避免了直接微分方法中广义坐标及其各阶导数对设计参数偏微分的计算,在设计参数较多的情况下提高了计算效率。又将目标函数及其导数积分形式的计算转化为微分方程的初值问题,进一步提高了计算效率和精度。文末给出一个平面机械臂模型算例。
Adjoint sensitivity analysis for differential-algebraic equations: Algorithms and software
Sensitivity analysis of differential-algebraic equations: A comparison of methods on a special problem
Design optimization of multibody systems by sequential approximation
Sensitivity analysis of constrained flexible multibody systems with stability considerations
Sensitivity analysis of constrained multibody systems
Design sensitivity analysis of large-scale constrained dynamic mechanical systems. Journal of Mechanisms, Transmissions,
Second-order design sensitivity analysis of mechanical system dynamics
Noninvasive measurement of tissue viscoelastic properties is gaining more attention for screening and diagnostic purposes. Recently, measuring dynamic response of tissue under a constant force has been studied for estimation of tissue viscoelastic properties in terms of retardation times. The essential part of such a test is an instrument that is capable of creating a controlled axial force and is suitable for clinical applications. Such a device should be lightweight, portable, and easy to use for patient studies to capture tissue dynamics under external stress. In this paper, we present the design of an automated compression device for studying the creep response of materials with tissue-like behaviors. The device can be used to apply a ramp-and-hold force excitation for a predetermined duration of time and it houses an ultrasound probe for monitoring the creep response of the underlying tissue. To validate the performance of the device, several creep tests were performed on tissue-mimicking phantoms, and the results were compared against those from a commercial mechanical testing instrument. Using a second-order Kelvin-Voigt model and surface measurement of the forces and displacements, retardation times T1 and T2 were estimated from each test. These tests showed strong agreement between our automated compression device and the commercial mechanical testing system, with an average relative error of 2.9% and 12.4%, for T1 and T2, respectively. Also, we present the application of compression device to measure local retardation times for four different phantoms with different size and stiffness.
Design sensitivity analysis of planar mechanism and machine dynamics
Discrete adjoint method for the sensitivity analysis of flexible multibody systems
Dynamic response optimization of complex multibody systems in a penalty formulation using adjoint sensitivity
Adjoint sensitivity analysis for differential-algebraic equations: The adjoint DAE system and its numerical solution
Second-order sensitivity analysis of multibody systems described by differential/algebraic equations: Adjoint variable approach
Second order adjoint sensitivity analysis of multibody systems described by differential-algebraic equations
First order sensitivity analysis of flexible multibody systems using absolute nodal coordinate formulation
Design sensitivity analysis of flexible multibody systems is important in optimizing the performance of mechanical systems. The choice of coordinates to describe the motion of multibody systems has a great influence on the efficiency and accuracy of both the dynamic and sensitivity analysis. In the flexible multibody system dynamics, both the floating frame of reference formulation (FFRF) and absolute nodal coordinate formulation (ANCF) are frequently utilized to describe flexibility, however, only the former has been used in design sensitivity analysis. In this article, ANCF, which has been recently developed and focuses on modeling of beams and plates in large deformation problems, is extended into design sensitivity analysis of flexible multibody systems. The Motion equations of a constrained flexible multibody system are expressed as a set of index-3 differential algebraic equations (DAEs), in which the element elastic forces are defined using nonlinear strain-displacement relations. Both the direct differentiation method and adjoint variable method are performed to do sensitivity analysis and the related dynamic and sensitivity equations are integrated with HHT-I3 algorithm. In this paper, a new method to deduce system sensitivity equations is proposed. With this approach, the system sensitivity equations are constructed by assembling the element sensitivity equations with the help of invariant matrices, which results in the advantage that the complex symbolic differentiation of the dynamic equations is avoided when the flexible multibody system model is changed. Besides that, the dynamic and sensitivity equations formed with the proposed method can be efficiently integrated using HHT-I3 method, which makes the efficiency of the direct differentiation method comparable to that of the adjoint variable method when the number of design variables is not extremely large. All these improvements greatly enhance the application value of the direct differentiation method in the engineering optimization of the ANCF-based flexible multibody systems.
Graph-theoretic sensitivity analysis of multibody systems
On maximal eigenfrequency separation in two-material structures: The 1D and 2D scalar cases
On topology optimization of plates with prestress
Multiple eigenvalues in structural optimization problems
Structural optimization considering smallest magnitude eigenvalues: A smooth approximation
On the sensitivities of multiple eigenvalues
We consider the generalized symmetric eigenvalue problem where matrices depend smoothly on a parameter. It is well known that in general individual eigenvalues, when sorted in accordance with the usual ordering on the real line, do not depend smoothly on the parameter. Nevertheless, symmetric polynomials of a number of eigenvalues, regardless of their multiplicity, which are known to be isolated from the rest depend smoothly on the parameter. We present explicit readily computable expressions for their first derivatives. Finally, we demonstrate the utility of our approach on a problem of finding a shape of a vibrating membrane with a smallest perimeter and with prescribed four lowest eigenvalues, only two of which have algebraic multiplicity one.
Smooth convex approximation to the maximum eigenvalue function
Simplified calculation of eigenvector derivatives
Design of cantilever probes for Atomic Force Microscopy (AFM)
Microfluidic atomic force microscopy (AFM) cantilever probes have all the functionalities of a standard AFM cantilever along with fluid pipetting. They have a channel inside the cantilever and an aperture at the tip. Such probes are useful for precise fluid manipulation at a desired location, for example near or inside cells. They are typically made by complex microfabrication process steps, resulting in expensive probes. Here, we used two different 3D additive manufacturing techniques, stereolithography and two-photon polymerization, to directly print ready-to-use microfluidic AFM cantilever probes. This approach has considerably reduced the fabrication time and increased the design freedom. One of the probes, 564 μm long, 30 μm wide, 30 μm high, with a 25 μm diameter channel and 2.5 μm wall thickness had a spring constant of 3.7 N m-1 and the polymer fabrication material had an elastic modulus of 4.2 GPa. Using these 3D printed probes, AFM imaging of a surface, puncturing of the cell membrane, and aspiration at the single cell level have been demonstrated.
Improved approximate methods for computing eigenvector derivatives in structural dynamics
Accelerated subspace iteration for eigenvector derivatives
Venckunas, T, Snieckus, A, Trinkunas, E, Baranauskiene, N, Solianik, R, Juodsnukis, A, Streckis, V, and Kamandulis, S. Interval running training improves cognitive flexibility and aerobic power of young healthy adults. J Strength Cond Res 30(8): 2114-2121, 2016-The benefits of regular physical exercise may well extend beyond the reduction of chronic diseases risk and augmentation of working capacity, to many other aspects of human well-being, including improved cognitive functioning. Although the effects of moderate intensity continuous training on cognitive performance are relatively well studied, the benefits of interval training have not been investigated in this respect so far. The aim of the current study was to assess whether 7 weeks of interval running training is effective at improving both aerobic fitness and cognitive performance. For this purpose, 8 young dinghy sailors (6 boys and 2 girls) completed the interval running program with 200 m and 2,000 m running performance, cycling maximal oxygen uptake, and cognitive function was measured before and after the intervention. The control group consisted of healthy age-matched subjects (8 boys and 2 girls) who continued their active lifestyle and were tested in the same way as the experimental group, but did not complete any regular training. In the experimental group, 200 m and 2,000 m running performance and cycling maximal oxygen uptake increased together with improved results on cognitive flexibility tasks. No changes in the results of short-term and working memory tasks were observed in the experimental group, and no changes in any of the measured indices were evident in the controls. In conclusion, 7 weeks of interval running training improved running performance and cycling aerobic power, and were sufficient to improve the ability to adjust behavior to changing demands in young active individuals.
Iterative least-squares calculation for modal eigenvector sensitivity
Improved Nelson's method for computing eigenvector derivatives with distinct and repeated eigenvalues
Shape optimization of structural parts in dynamic mechanical systems based on fatigue calculations
In this paper a new method for an automated shape optimization of dynamically loaded components in mechanical systems is presented. The optimization is carried out by means of the results of a durability analysis based on finite elements. Load time histories, which are necessary for durability analyses, are derived from a multibody simulation. The whole optimization loop, which is an iterative procedure, incorporates all these gradual analysis steps and is implemented by the authors in a straightforward, batch-oriented manner using well-known standard software. Since the whole process involves several different analysis types, such as multibody system simulation and durability analysis, the resulting setup is rather complex. Furthermore, the reader may not be familiar with all the terms arising within the context of every single analysis domain. Therefore, some essential aspects of each of the stages involved in the process are explained to provide the reader with the necessary background. In the following, the required software setup as well as the implementation are described. Finally, an academic example is discussed to illustrate and clearly outline the potential of this method.
Shape optimization of dynamically balanced planar four-bar mechanism
工程结构优化设计发展综述
Survey of the developing in engineering structural optimization design
Generating optimal topologies in structural design using a homogenization method
A review of homogenization and topology optimization I--Homogenization theory for media with periodic structure
A review of homogenization and topology opimization II--Analytical and numerical solution of homogenization equations
A review of homogenization and topology optimization III--Topology optimization using optimality criteria
A critical review of established methods of structural topology optimization
A survey of structural and multidisciplinary continuum topology optimization: Post 2000
Topology optimization approaches: a comparative review
No details on P2X receptor architecture had been known at the atomic resolution level. Using comparative homology-based molecular modelling and threading, it was attempted to predict the three-dimensional structure of P2X receptors. This prediction could not be carried out, however, because important properties of the P2X family differ considerably from that of the potential template proteins. This paper reviews an alternative approach consisting of three research fields: bioinformatics, structural modelling, and a variety of the results of biological experiments.
Level-set methods for structural topology optimization: A review
This review paper provides an overview of different level-set methods for structural topology optimization. Level-set methods can be categorized with respect to the level-set-function parameterization, the geometry mapping, the physical/mechanical model, the information and the procedure to update the design and the applied regularization. Different approaches for each of these interlinked components are outlined and compared. Based on this categorization, the convergence behavior of the optimization process is discussed, as well as control over the slope and smoothness of the level-set function, hole nucleation and the relation of level-set methods to other topology optimization methods. The importance of numerical consistency for understanding and studying the behavior of proposed methods is highlighted. This review concludes with recommendations for future research.
Bi-directional evolutionary structural optimization on advanced structures and materials: A comprehensive review
Topology optimization of members of elastic multibody systems
Structural topology optimization of multibody systems
Optimal shape design as a material distribution problem
Cancer is the major public health problem in developing countries. The treatment of cancer requires a multimodal approach and chemotherapy is one of them. Chemotherapeutic drug is administered to cancer patients in the form of a formulation which is prepared by mixing an active ingredient (drug) with the excipient. The role of excipient in a formulation is to regulate the release, bio-distribution, and selectivity of drug within the body.
The COC algorithm, part II: topological, geometry and generalized shape optimization
Some aspects of the genesis of structures
Along with supernumerary bones, sesamoids, defined as any organized intratendinous/intraligamentous structure, including those composed of fibrocartilage, adjacent to an articulation or joint, have been frequently considered as enigmatic structures associated with the joints of the skeletal system of vertebrates. This review allows us to propose a dynamic model to account for part of skeletal phenotypic diversity: during evolution, sesamoids can become displaced, attaching to and detaching from the long bone epiphyses and diaphysis. Epiphyses, apophyses and detached sesamoids are able to transform into each other, contributing to the phenotypic variability of the tetrapod skeleton. This dynamic model is a new paradigm to delineate the contribution of sesamoids to skeletal diversity. Herein, we first present a historical approach to the study of sesamoids, discussing the genetic versus epigenetic theories of their genesis and growth. Second, we construct a dynamic model. Third, we present a summary of literature on sesamoids of the main groups of tetrapods, including veterinary and human clinical contributions, which are the best-studied aspects of sesamoids in recent decades. Finally, we discuss the identity of certain structures that have been labelled as sesamoids despite insufficient formal testing of homology. We also propose a new definition to help the identification of sesamoids in general. This review is particularly timely, given the recent increasing interest and research activity into the developmental biology and mechanics of sesamoids. With this updated and integrative discussion, we hope to pave the way to improve the understanding of sesamoid biology and evolution.
Material interpolation schemes in topology optimization
An alternative interpolation scheme for minimum compliance optimization
Interpolation/penalization applied for strength design of 3D thermoelastic structures
With design independent loads and only a constrained volume (no local bounds), the same optimal design leads simultaneously to minimum compliance and maximum strength. However, for thermoelastic structures this is not the case and a maximum volume may not be an active constraint for minimum compliance. This is proved for thermoelastic structures by sensitivity analysis of compliance that facilitates localized determination of sensitivities, and the compliance is not identical to the total elastic energy (twice strain energy). An explicit formula for the difference is derived and numerically illustrated with examples. In compliance minimization for thermoelastic structures it may be advantageous to decrease the total volume, but for strength maximization it is argued to keep the total permissible volume. Linear interpolation (no penalization) may to a certain extent be argued for 2D thickness optimized designs, but for 3D design problems interpolation must be included and not only from the penalization point of view to obtain 0–1 designs. Three interpolation types are presented in a uniform manner, including the well known one parameter penalizations, named SIMP and RAMP. An alternative two parameter interpolation in explicit form is preferred, and the influence of interpolation on compliance sensitivity analysis is included. For direct strength maximization the sensitivity analysis of local von Mises stresses is demanding. An applied recursive procedure to obtain uniform energy density is presented in details, and it is shown by examples that the obtained designs are close to fulfilling also strength maximization. Explicit formulas for equivalent thermoelastic loads in 2D and 3D finite element analysis are derived and applied, including the sensitivity analysis.
Structural boundary design via level set and immersed interface methods
Level set methods for optimization problems involving geometry and constrains I. Frequencies of a two-density inhomogeneous drum
A level set method for structural topology optimization
We review various mathematical and computational techniques for drug discovery exemplifying some recent works pertinent to group theory of nested structures of relevance to phylogeny, topological, computational and combinatorial methods for drug discovery for multiple viral infections. We have reviewed techniques from topology, combinatorics, graph theory and knot theory that facilitate topological and mathematical characterizations of protein-protein interactions, molecular-target interactions, proteomics, genomics and statistical data reduction procedures for a large set of starting chemicals in drug discovery. We have provided an overview of group theoretical techniques pertinent to phylogeny, protein dynamics especially in intrinsically disordered proteins, DNA base permutations and related algorithms. We consider computational techniques derived from high level quantum chemical computations such as QM/MM ONIOM methods, quantum chemical optimization of geometries complexes, and molecular dynamics methods for providing insights into protein-drug interactions. We have considered complexes pertinent to Hepatitis Virus C non-structural protein 5B polymerase receptor binding of C5-Arylidebne rhodanines, complexes of synthetic potential vaccine molecules with dengue virus (DENV) and HIV-1 virus as examples of various simulation studies that exemplify the utility of computational tools. It is demonstrated that these combinatorial and computational techniques in conjunction with experiments can provide promising new insights into drug discovery. These techniques also demonstrate the need to consider a new multiple site or allosteric binding approach to drug discovery, as these studies reveal the existence of multiple binding sites.
Structural optimization using sensitivity analysis and a level-set method
A semi-implicit level set method for structural shape and topology optimization
Doing topology optimization explicitly and geometrically--A new moving morphable components based framework
Explicit three dimensional topology optimization via moving morphable void (MMV) approach
Explicit isogeometric topology optimization using moving morphable components