引言
自然界的天然材料可用作工程材料的主要有岩石、土壤、木材,由于是天然材料,因而材料的力学性质一般都比较复杂.通过试验以及不断的工程实践,土壤材料是一种典型的摩擦型材料,主要是源于材料的强度特点所决定的.而岩石材料则相对于土壤材料具有一定的抗拉强度,因而具备相当程度的凝聚性特点.对于人工材料金属而言,由于是典型的凝聚型材料,因而偏差应力是造成金属晶体破坏的主因.由于是对应的偏差应力,因而根据金属破坏性质,首先给出的是偏平面上对应正六边形的Tresca准则[1],以及广义Von-Mises准则[2]等等. 而与之不同的是,岩土材料,则是由应力比来决定破坏与否.如著名的摩尔$\!$-$\!$-$\!$库伦准则[3],Lade-Duncan准则[4]以及Matsuoka和Nakai所提出的SMP准则[5].
三维强度以及屈服准则是描述主应力空间中的破坏特性的主要手段. 目前,针对岩土材料提出了众多的破坏与屈服准则.从准则表达式本身是否具备一定的物理意义来区分,则从大类上分为两大类,一大类是物理概念型准则,另一大类则是统计实用型准则.前者包含很多准则,如俞茂宏等[6-9]所提的双剪应力强度准则、SMP准则、三剪应力准则[10]、广义非线性强度准则[11-15].而后者也存在大量的准则表达式,如Lade-Duncan准则,适用于岩石材料的Hoek-Brown准则[16],适用于混凝土的四参数准则[17-18].还有通过形状函数来表达偏平面上破坏形态的拟合参数准则,如Zienkiewicz[19],郑颖人等[20]提出的准则,能够描述破坏时应力状态,但这种静水压力效应造成的形状影响无法得到合理反映.此外,针对影响 岩土强度性质的一系列因素的分析研究也得以展开,如各向异性因素[21-26]、黏土胶结结构性因 素[27-29]、非饱和土的基质吸力因素[30-32]、冻土的温度影响因素[33-34]等等,也都取得了一定的进展.
分析广义Von-Mises准则以及Lade-Duncan,SMP准则采用应力不变量表达形式,借鉴Mortara[35]对SMP和LD准则采用幂参数插值的做法.在幂参数上分别引入两个参量$m$和$n$,将上述3种准则扩展为一个统一准则中,新准则除了能够退化为上述3个强度准则之外,还能广泛的描述在偏平面上开口形状为曲边三角形到完全圆形的广阔破坏形态.在子午面上,为了能反映静水压力效应带来的破坏应力非线性特点,采用广义非线性准则中的幂函数表达形式来反映子午面上的非线性强度特性.为了反映岩土材料的压剪耦合性质,采用水滴型屈服面作为屈服准则.新准则具有参数较少,且物理意义明确,表达形式简单等特点.
1 偏平面上VML强度准则公式
1.1 MNLD准则简介
意大利学者Mortara在分析SMP准则以及Lade准则由主应力不变量表述形式的相似性后提出了MNLD准则,其通过巧妙的在幂次上设置了一个参数$n$,便在偏平面上得到了一个非线性的广义强度准则. 该准则表述如下
式中,$I_{1}$为第一应力张量不变量,而$I_{3}$为第三应力张量不变量, $n$为参数, $d$为 常数. 显然,当$n =1$时,则式(1)退化为SMP准则公式,当$n = 3$时,则式(1)退化为Lade准则公式.
当MNLD准则退化为上述两种常用的强度准则公式时,常数$d$可由三轴压缩状态下的内摩擦角 $\varphi $来表达. 显然式(1)中的常数$d$不仅与内摩擦角 $\varphi $有关,而且还与参数$n$有关,因此通过常规三轴压缩应力路径的强度值关系,可得到如下表达式
由于参数$n$可用于调整偏平面上破坏曲线的形状,故参数$n$可通过如下两式来联合确定
其中,$M_{c}$表示常规三轴压缩下的应力比值, $\beta $表示常规三轴伸长与压缩偏应力强度值之比.
式(1)中的等式右端为常数,表示其不受静水压力$p$的影响,然而有充分的试验证据表明,岩土材料具有典型的静水压力效应,即偏应力强度受到球应力的影响. 为了能反映静水压力带来的强度值影响性质,可将式(1)扩展为
观察式(5)可发现,在子午面上的强度曲线为曲线形态,表明随着球应力$p$的增大,偏应力强度值不再按照线性规律变化,而是按照曲线形态变化,且随着参数$c_{1}$的增大,偏应力强度曲线的斜率逐渐减小,表明增加速率在减小.
1.2 VML准则
根据适用于金属材料的广义Von-Mises准则,以及适用于岩土材料的SMP准则、Lade-Duncan准则表达式,可用主应力变量表达的不变量形式依次表达为如下形式.
(1)对于广义Von-Mises准则,可表达为
(2)对于SMP准则,可表达为
(3)对于Lade-Duncan准则,可表达为
其中,$I_{1}$,$I_{2}$,$I_{3}$分别是主应力变量表达的应力第一、二、三不变量,而 $\varphi $则是对应三轴压缩路径下的内摩擦角,等式最右端的$c_{1}$,$c_{2}$,$c_{3}$都为常数.
观察上述3种准则的表达式形式,可以利用两个参数$m$和$n$将其在幂次位置上进行插值,从而可以得到一个非线性强度准则表达式,表达式形式可以统一写为
显然,当$m$= 1时,则式(4)退化为
当$n = 1$时,则式(10)退化为式(6),表示为反映金属材料的广义Von-Mises准则表达式.
当$n \ne 1$时,则式(10)表示为与$I_{3}$无关的非线性准则.
当$m = 0$时,则式(9)退化为
式(11)退化为Mortara所提出的MNLD准则. 该准则为SMP准则与Lade-Duncan准则的幂次参数插值非线性准则.
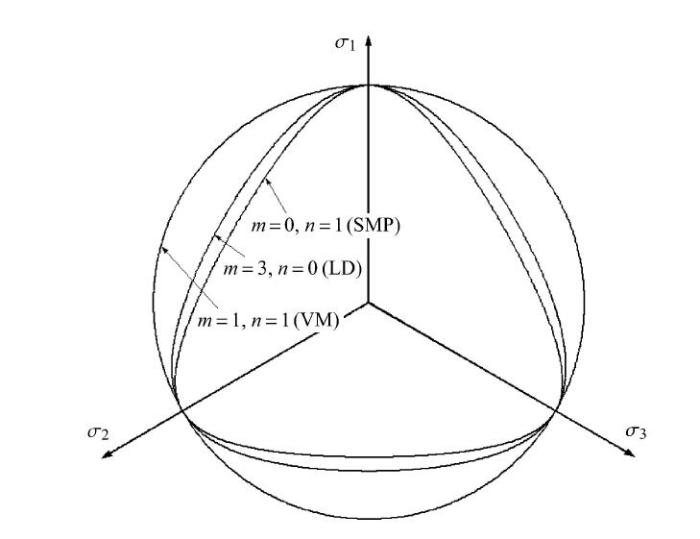
显然,在$m = 0$前提下,当$n = 1$时,则式(11)退化为式(7),表示为SMP准则. 而当$n =3$时,则式(11)退化为式(8),表示为Lade-Duncan准则.3种典型的强度曲线分别如图1所示,显然当参数$m$与$n$的组合满足图中所示情形,则所提的VML准则分别退化为SMP,Lade-Duncan以及广义Von-Mises 准则.
图1
图1
内摩擦角为30$^\circ$下偏平面上3种典型准则曲线
Fig. 1
Three typical criterion curves in deviatoric plane with $\varphi =30^\circ$
将式(9)整理,可得到关于球应力以及三轴压缩对应的内摩擦角的函数,可表示为
对于子午面上的广义偏应力强度,令
其中,$p_{\rm r}$表示使球应力无量纲化的参量,通常可取为一个大气压. $\sigma_{0}$则是一个参数,表示材 料的拉伸强度. $t$则是反映静水压力效应的幂参数参量. 当$t =1$时,则随着静水压力的增大,则偏应力强度值不受影响,而当$t <1$时,则偏应力强度随着静水压力的增大而出现增长缓慢现象,表现出静水压力对强度值的影响效应.
对于三轴压缩的广义偏应力强度,可表示为如下形式
其中,$\bar {q}_{\rm c} $为对应三轴压缩下的广义偏应力强度.
显然,当参数$s > 1$时,则式(16)退化为
显然,当参数$s < 1$或者$s = 1$时,则式(16)退化为
对于一般应力,式(12)可表达为
若利用$p$,$q$, $\theta $为变量的形式,则式(13)可表达为
当对于三轴压缩所对应的破坏点时,显然,式(21)可化简为
显然,联立式(13)、式(16)、式(20),则上述三式即为VML强度与屈服准则表达式.
应力罗德角示意图如图2所示,除了球应力$p$,偏应力$q$,还有应力罗德角$\theta $能够联合表示由3个主应力表达的强度准则. 当$\sigma _{0}=0$,$n =1$时,则 式(19)可表示为如下形式
图2
根据应力比表达式$q/p=\eta $,则式(22)可化为
对于式(23),当 $\theta = 90^\circ$时,沿$y$轴的破坏点所对应的是三轴压缩路径破坏点,而当 $\theta =150^\circ$时, 所对应的是三轴伸长路径破坏点,当 $\theta $取易于上述两种应力路径时,破坏点所对应的是真三轴压缩路径破坏点.
三轴压缩与伸长路径下所对应的破坏应力比分别为$M_{\rm c}$, $M_{\rm e}$,则经过变换可得到如下公式
$\left( {1-m} \right)\ln \left( {\dfrac{2M_{\rm c}^3 }{27^2}-\dfrac{M_{\rm c}^2}{81} + \dfrac{1}{27}} \right) + \ln c_4 =$
$\left( {1-m} \right)\ln \left( {-\dfrac{2M_{\rm e}^3 }{27^2}-\dfrac{M_{\rm e}^2}{81} + \dfrac{1}{27}} \right) + \ln c_4 =$
利用岩土材料具有临界状态这一特性,则当岩土体进入临界状态时,显然,屈服面所对应的塑性体积应变保持恒定,此时塑性体变增量为零,应力增量为零. 则可假设以式(22)为屈服面表达式,此时,假设材料服从理想弹塑性特性,服从相关联流动法则,则由屈服面方程可得到
根据条件可知
由于塑性因子 $\lambda $不为零,因此可将式(28)转化为如下方程
显然,联立式(24)、式(25)、式(29),最终可求取出参数$m$, $n$, $c_{4}$,即可确定出所需的强度参数$m$和$n$的值.
2 偏平面上参量${\pmb m}/{\pmb n}$对破坏曲线形状影响
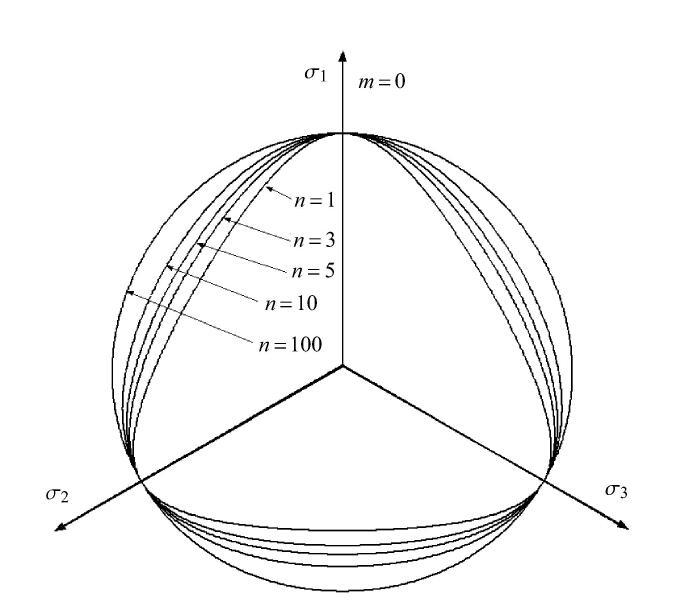
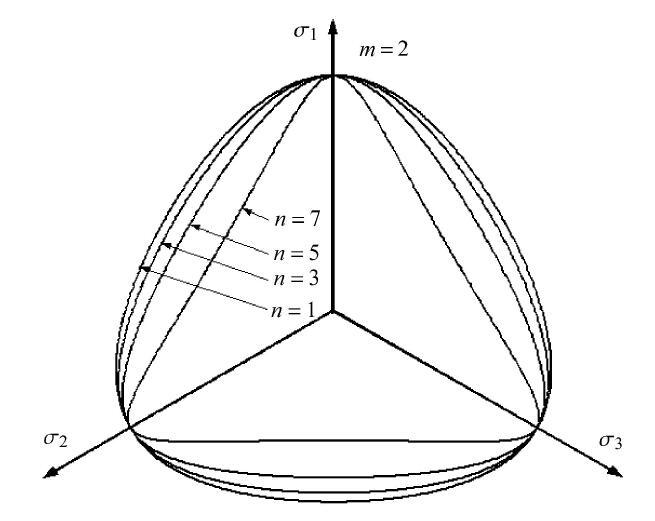
为了考察参量$m/n$对于偏平面上破坏曲面开口形状的影响规律,分别先选用$m =0$,1,2,5为常量情况下,变动参量$n$以探究$n$值不同所带来的偏平面上形状变化. 由图3所示,当$m =0$且内摩擦角为30$^\circ$下,则$n = 1$以及$n =3$时,则新准则分别退化为SMP与LD准则,随着$n$值的增大,则应力罗德角对于广义偏应力强度的影响越来越小. 当$n =100$时,则开口形状趋近于圆形. 当$m =1$时,由于准则表达式中缺乏了$I_{3}$项,$n$值的变化对于曲线开口形状影响几乎可以忽略,除了$n =1$是严格的圆形外,其他都是准圆形(见图4). 当$m = 2$时,$n$值的增大,则开口形状的变化与$m = 0$完全相反的规律.当$n$值越大,则开口形状由外凸逐渐变为内凹,当$n = 7$时,则偏平面上强度曲线由凸曲线变为凹曲线(见图5).
图3
图3
$m = 0$情形内摩擦角为30$^\circ$下偏平面上准则曲线分布
Fig. 3
Criterion curves in deviatoric plane with $\varphi =30^\circ$when $m = 0$
图4
图4
$m = 1$情形内摩擦角为30$^\circ$下偏平面上准则曲线分布
Fig. 4
Criterion curves in deviatoric plane with $\varphi =30^\circ$ when $m = 1$
图5
图5
$m = 2$情形内摩擦角为30$^\circ$下偏平面上准则曲线分布
Fig. 5
Criterion curves in deviatoric plane with $\varphi =30^\circ$ when $m = 2$
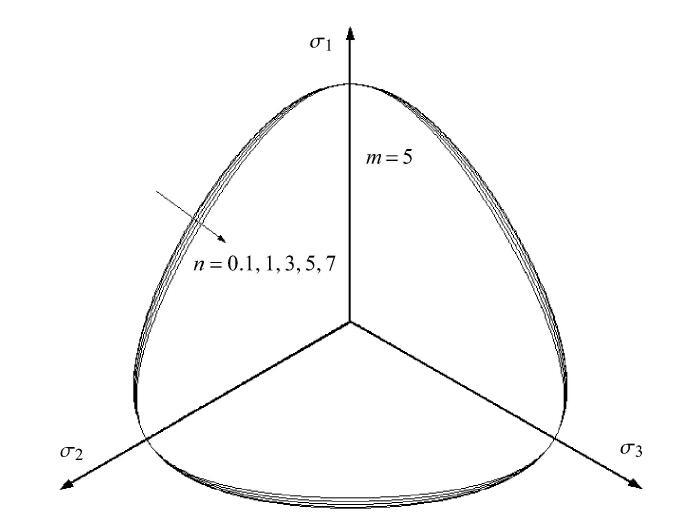
当$m = 5$时,则随着$n$值的增大,虽然偏平面上对于广义偏应力强度仍然从外向内变化,即由外凸逐渐向内凹变化(见图6),但由于$m$值的幂次过大,造成了 式(22)中分母项的过大,因而$n$值的变化影响很小. 分析$m$值从0$\sim$5的变化过程,可见,$m = 1$是分水岭,当$0 < m <1$时,则随着$n$值的增大,偏平面开口形态越来越趋近于圆形,表明凝聚性越大,而摩擦性越小. 而当$m =1$时,则由于缺失了$I_{3}$项,因此$n$值的变化不影响开口形状,都是圆形曲线. 而当$m >1$时,出现两点变化:(1)随着$n$值的增大,曲线开口由外向内逐渐由圆向三角形形状变化;(2)随着$m$值的增大, 由于幂次过大,因而出现了$n$值对于曲线性状差异影响越来越小的趋势.
图6
图6
$m = 5$情形内摩擦角为30$^\circ$下偏平面上准则曲线分布
Fig. 6
Criterion curves in deviatoric plane with $\varphi =30^\circ$when $m = 5$
3 偏平面上强度准则广义偏应力强度值有效根的选取
为了考察新强度准则下$m$和$n$参数取值对于广义偏应力强度$q$的影响,考察式(14)的根$q$的分布规律. 取 $\sigma _{0 }= 0$, $\theta = 90^\circ$,$t = 1$, $\varphi = 30^\circ$,$I_{1 }= 300$,kPa,$m = 0$,1,2,5,在每个$m$值下分别取$n =1$,2,3,5,10,分别考察三维空间下根的分布规律. 式(27)可化为
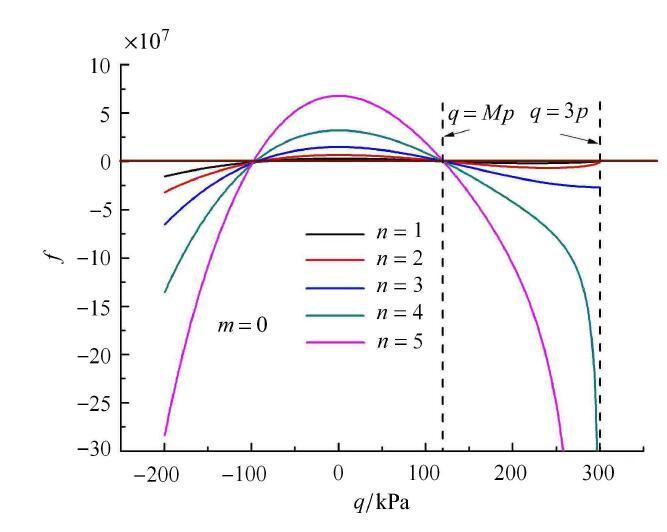
如图7所示,当$m = 0$时,分别选取$n = 1 \sim 5$,则函数式(30)的曲线分别为图中曲线. 图中黑色水平直线为$f =0$所对应的常数函数,而其他曲线与水平直线的交点显然就是式(30)的根. 5条曲线有两个公共根,一正一负,正根对应的是${Mp}$值,也是曲线准则所对应的三轴压缩的广义偏应力强度值. 而对于无侧限抗压强度值$3 p$,则$n =1$所对应SMP准则也同样取到该值. 而$n = 2/3$则略过该值. 对于$n = 4/5$,则曲线表现出了不同的形态,不同于$n =1 \sim 3$的倒"S"形态,$n = 4/5$表现为类似于准抛物型形态曲线,且$3 p$为其右侧曲线的渐近线.
图7
图7
$m = 0$情况下方程(24)的根的分布曲线
Fig. 7
Distribution curves of roots for Eq.(24) with $m = 0$
对于当$m = 1$情况下,显然式(30)中,左端第一项化为$c_{4}$,最终可求解出关于$p$的一正一负两个根.正根 具有唯一性. 对应于图4中的圆形曲线上的广义偏应力强度值.
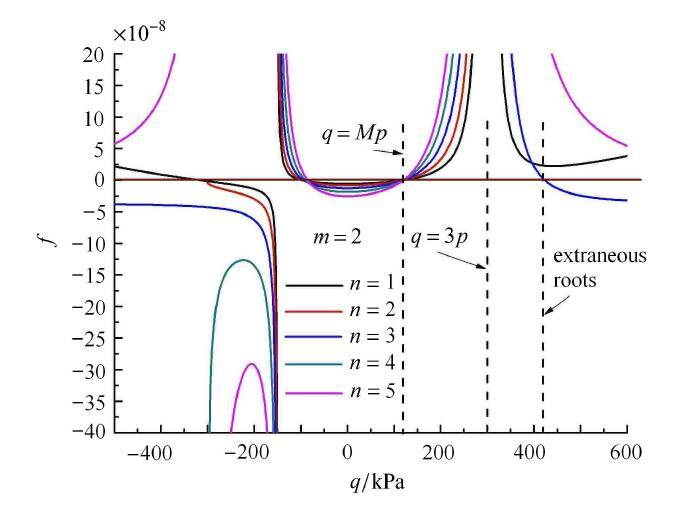
对于当$m = 2$情况下,由图8可见,则$n = 1 \sim 5$所对应的5条曲线在靠近原点附近存在一个开口的类抛物线曲线,且具有公共的一正一负两个根,而正根对应的是$Mp$值, $3 p$对应的是5条曲线的一条渐近线.
图8
图8
$m = 2$情况下方程(24)的根的分布曲线
Fig. 8
Distribution curves of roots for Eq.(24) with $m = 2$
由图9可见,在当$m = 3$情况下,上述5条曲线表现出了与$m = 2$情况相类似的分布规律特点. 与$m =2$相比较,可发现类抛物线曲线开口更小,且不同$n$值曲线的间距更小,表明曲线受$n$值影响越来越小,曲线趋近于渐近线更为迅速.
图9
图9
$m = 3$情况下方程(24)的根的分布曲线
Fig. 9
Distribution curves of roots for Eq.(24) with $m = 3$
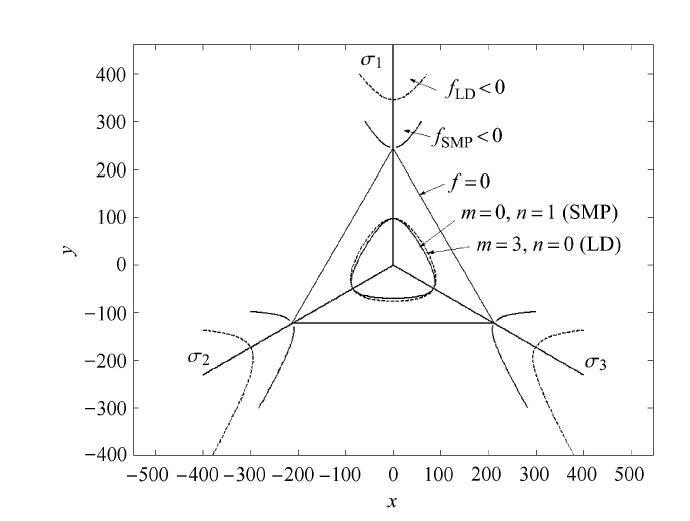
图10是偏平面上根的分布特点,当$m =0$时,图中黑色实线以及曲线分别表示SMP准则与LD准则的根,而正三角形则表示SMP准则的外凸边界形状. 表示的是对应3$p$的根的分布情况.
图10
图10
偏平面上$m = 0$情况下方程(24)的根的分布曲线
Fig. 10
Distribution curves of roots for Eq.(24) with $m = 0 $in deviatoric plane
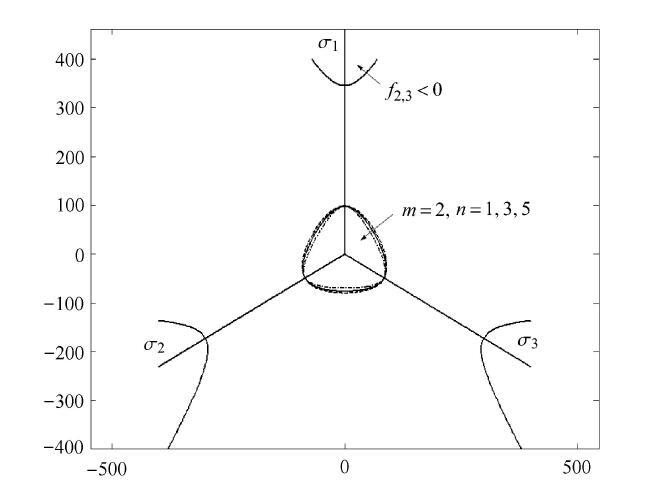
图11
图11
偏平面上$m = 2$情况下方程(24)的根的分布曲线
Fig. 11
Distribution curves of roots for Eq.(24) with $m = 2$in deviatoric plane
4 偏平面上$\theta $角对曲面凹凸性影响
为了考察偏平面上参数$m/n$对于破坏曲线凹凸性的影响,主要考察应力罗德角 $\theta $在变化时对于曲面凹凸性的影响. 这里设定参数 $\sigma_{0} = 0$, $\theta = 90^\circ$,$t = 1$, $\varphi = 30^\circ$,$I_{1 } = 300$,kPa,先固定每个$m$值,然后考察$n$与 $\theta $变动时曲面凹凸性的大小. 这里为了便于分析判断凹凸性,对凹凸性的大小进行定量化考量.
对于图10,由极坐标可知,强度曲线上的点的极半径可表示为广义偏应力$q$的函数.
罗德角 $\theta $也可表示为
由此,式(27)可表达为含有${xy}$的隐函数,因而,凹凸性参数$F$可表达为
式中,$f_{x}$,$f_{y}$,$f_{xx}$,$f_{yy}$,$f_{xy}$分别是隐函数f对于$x, y$的一阶以及二阶偏导数
图12
图12
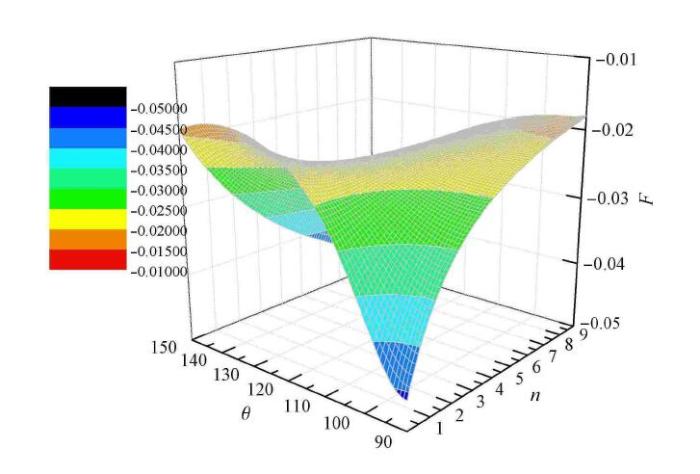
$m = 0$情况下应力罗德角$\theta $对偏平面上曲线的凹凸性的影响
Fig. 12
Effect of stress Lode angle on the concavity and convexity of curve with $m = 0$
图13
图13
$m = 2$情况下应力罗德角$\theta $对偏平面上曲线的凹凸性的影响
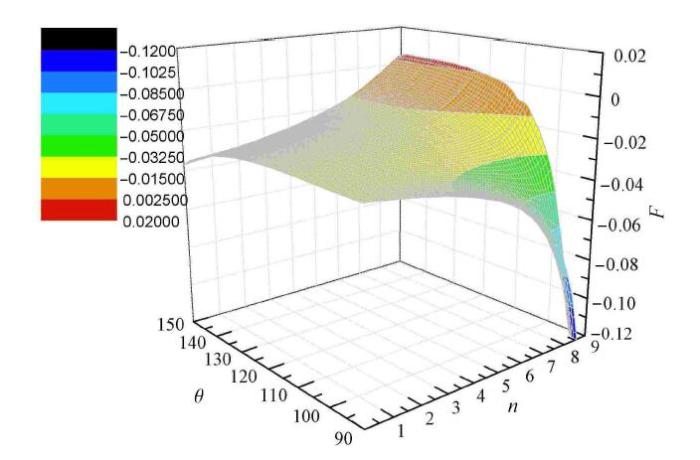
Fig. 13
Effect of stress Lode angle on the concavity and convexity of curve with $m = 2$
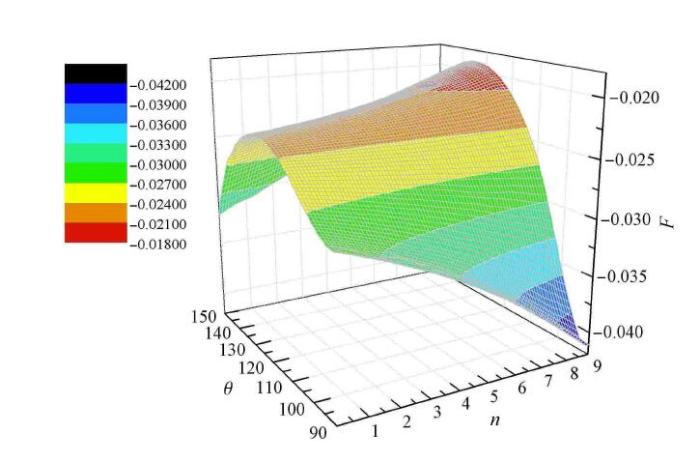
当$m = 5$时,由图14可观察出,所对应的所有曲线都满足$F <0$,也就是所有曲线都满足外凸性条件. 对于三轴压缩所对应的90$^\circ$附近的外凸性,随着$n$值的增大,$F$呈现出单调减小规律,表明$n$值越大,则曲线越凸. 且曲线最"凹"的位置由原来的150$^\circ$附近转移到130$^\circ$左右,且随着$n$值的增大,而逐渐趋向于150$^\circ$位置. 说明,当$m =5$时,随着$n$值的增大,开口曲线的形态外凸性整体位置分布以及外凸性大小都产生了变化.
图14
图14
$m = 5$情况下应力罗德角$\theta $对偏平面上曲线的凹凸性的影响
Fig. 14
Effect of stress Lode angle on the concavity and convexity of curve with $m = 5$
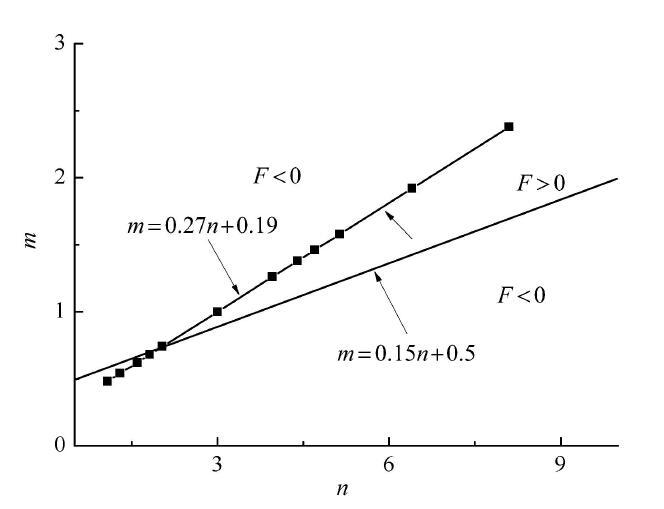
图15
图15
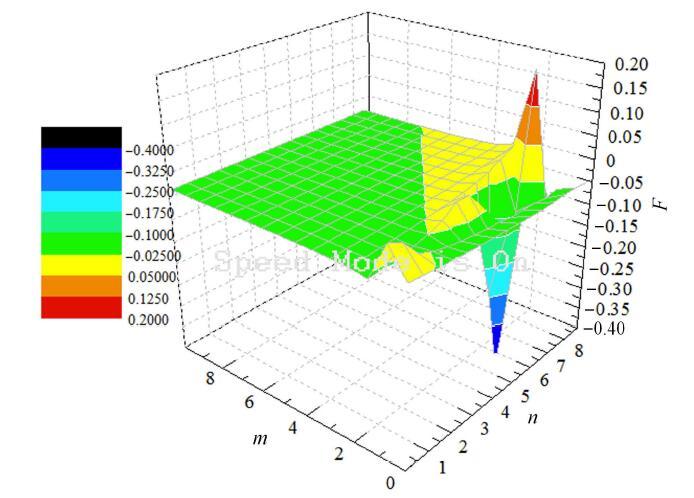
$\theta =150^\circ$情况下应力$m-n$空间中曲线的凹凸性的影响
Fig. 15
The concavity and convexity of curve with $\theta = 150^\circ$\\ in $m-n$space
图16
图16
$\theta =150^\circ$情况下应力$m-n$空间中凹凸分界线
Fig. 16
The boundary of concave and convex in $m-n$space with $\theta = 150^\circ$
5 子午面上屈服面的凹凸性
对于子午面上的屈服面,判断其凹凸性,可通过参数$s$来进行分析.
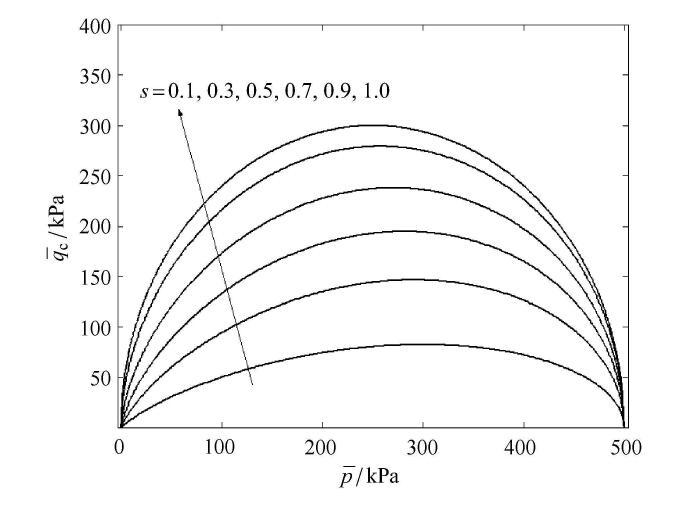
由图17可见,当参数$s$介于$0 \sim 1$之间时,则屈服面形状为介于直线与椭圆之间的水滴型屈服面.
图17
图17
三轴压缩情况下屈服面形状受参数$s$的影响分布规律
Fig. 17
Distribution law of the shape of yield surfaces affected by the parameter $s$under triaxial compression condition
由于屈服面外凸性可由下述二阶偏导数来判定.
将式(42)代入式(41),可得到
由于
观察式(44)中,并无含有$\bar {p}$的分项,因此可得
式(43)可化简为
由于
因此,屈服面凹凸性可由$\dfrac{\partial ^2\bar {q}_{\rm c} }{\partial \bar {p}^2}$的正负性质来判断.而根据图17可知,图中所有曲线都满足上凸条件,即满足$\dfrac{\partial ^2\bar {q}_{\rm c} }{\partial \bar {p}^2}< 0$,因而,在在当参数$0 < s < 1$时,则屈服面恒满足外凸条件.
6 强度及屈服准则预测及变换应力法验证
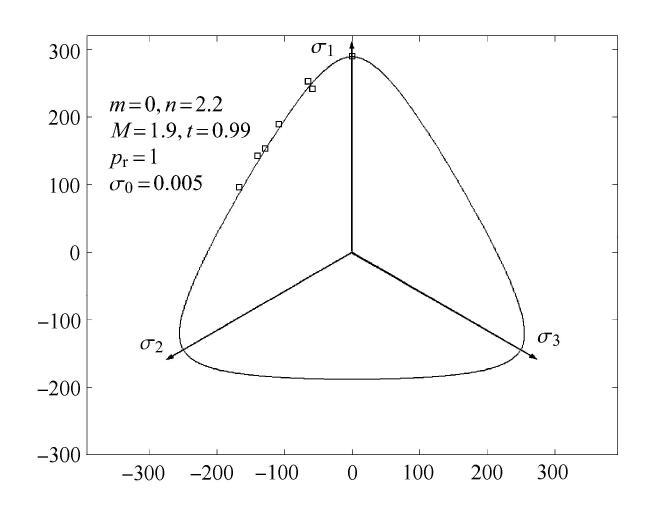
图18
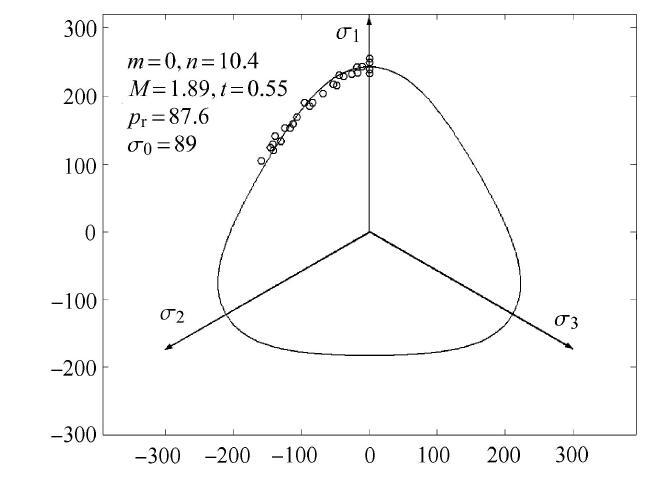
图18
利用VML准则对Toyoura砂土在偏平面上破坏数据的预测对比
Fig. 18
Prediction comparison of failure data of Toyoura sand on deviatoric plane using VML criterion
4.1 强度准则验证及预测对比
图19
图19
利用VML准则对粗面岩在偏平面上破坏数据的预测对比
Fig. 19
Prediction comparison of failure data of trachyte in deviatoric plane by VML criterion
图20
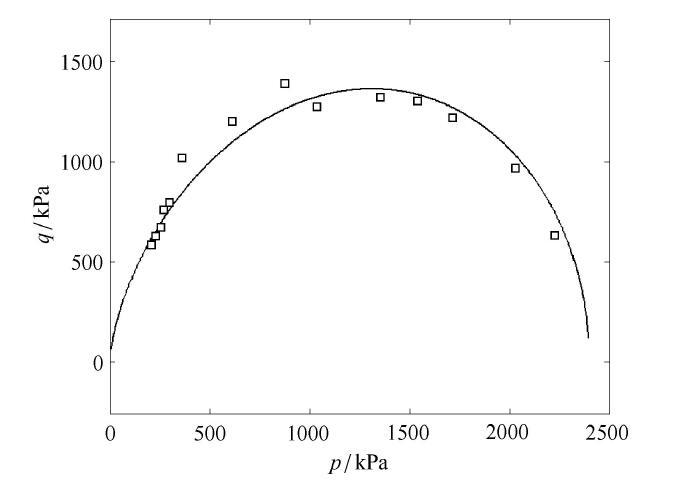
图20
利用VML准则对灰屑岩在$p-q$空间中屈服数据的预测对比
Fig. 20
Prediction comparison of yield data of calcarenite in $p-q $space by VML criterion
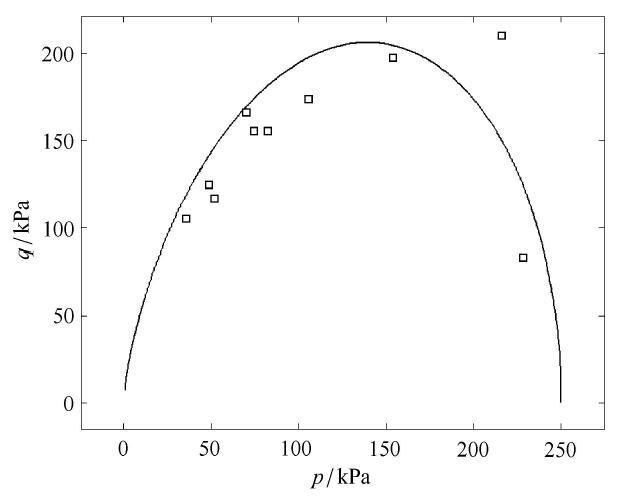
图21
图21
利用VML准则对Leda黏土在$p-q$空间中屈服数据的预测对比
Fig. 21
Prediction comparison of yield data of Leda clay in $p-q$space by VML criterion
7 结论
通过分析广义Von-Mises, SMP,LD准则的主应力不变量$I_{1}$,$I_{2}$,$I_{3}$的表达形式,由上述三者的表达方式,提出了一种广义的非线性强度与屈服准则,该准则可通过适当的变形分别退化为上述3种典型强度准则.在子午面上,则利用广义非线性的幂函数来作为反映静水压力效应带来的破坏曲线非线性表达式,对于压剪耦合特性,采用了水滴型函数作为屈服面表达式.并基于该新准则探讨了新准则参数$m$/$n$对于偏平面上开口形状的影响规律. 基于上述分析,得到了如下几点结论:
(1)在3种典型强度准则基础上,利用幂参数$m$/$n$外插表达式,得到了一种新的适用于岩土、金属等多种材料的非线性强度准则.
(2)在子午面上,利用幂函数曲线型作为强度准则表达式,而岩土材料具有压剪耦合特性,基于体积压缩所导致的屈服特性,提出了一并考虑剪切破坏屈服与压缩体积屈服相耦合的破坏准则关系式.
(3)基于上述所提的VML强度准则,分析了$m$和$n$对于偏平米破坏曲线的形状影响规律. 结果表明,当$m$为较小的正数以及$n$在较小正数范围内,准则满足强度以及屈服曲面的外凸性质. 且便于用作岩土类材料的破坏与屈服准则.
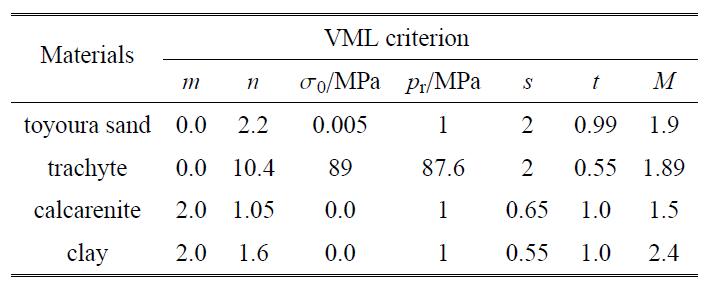
采用所提的VML准则对于砂土、岩石以及黏土的强度以及屈服性质进行预测,对比结果表明,所提的VML准则可简单准确地应用到岩土材料的模拟中,具有很强的适用性以及实用性.
参考文献
Relationship arnong Tresca, Mises, Mohr Coulomb and Matsuoka-Naka failure criteria
The Cam-clay models revised by the SMP criterion
Deformation and strength characteristics of soft Bangkok clay. Journal of Geotechnical Engineering Division,
Three-dimensional behavior of remolded clay. Journal of Geotechnical and Geoenvironmental Engineering, Division,
On the significance of the spatial mobilized plane
广义双剪应力强度理论及其推广
Twin shear stress theory and its generalization. Science in China,
岩土类材料的统一强度理论及其应用
Unified strength theory for geomaterials and its applications
线性和非线性的统一强度理论
Linear and nonlinear unified strength theory
岩石广义非线性统一强度理论
Generalized nonlinear unified strength theory of rock
三剪应力统一强度理论研究
Study of three-shear stress unified strength theory
广义非线性强度理论及其变换应力空间
Generalized non-linear strength theory and transformed stress space. Science in China:Ser
广义非线性强度理论在岩石材料中的应用
Applications of generalized non-linear strength theory to rock materials
岩土材料的变换应力空间及其应用
Transformed stress space for geomaterials and its application
混凝土材料非线性多轴动态强度准则
Nonlinear multiaxial dynamic strength criterion for concrete material. Science in China:Ser
一种简便的岩石三维Hoek-Brown强度准则
A simple convenient three-dimnesional Hoek-Brown criterion for rocks
A plastic-fracture model for concrete
Plastic model for concrete in plane stress state. II: Numerical validation
Some useful forms of isotropic yieldsurface for soil and rock mechanics//Pande GW. Finite Elements in Geomechnaics
塑性力学中的分量理论------广义塑性力学
Componental plastic mechanics---Generalized plastic mechanics
砂土的各向异性强度准则:原生各向异性
Anisotropic strength criteria of sand: inherent anisotropy
横观各向同性砂土的强度准则
New strength criterion for sand with cross-anisotropy
横观各向同性土的三维强度准则
Three-dimensional strength criterion for transverse isotropic geomaterials
Characterization of failure in cross-anisotropic soils. J. Eng. Mech
Anisotropic three-dimensional behavior of a normally consolidated Clay. Can. Geotech
A novel transversely isotropic strength criterion for soils based on a mobilised plane approach
A destructuration theory and its application to SANICLAY model
An elstoplastic description of two distinct volume change mechanisms of soils
An elasto-plastic model for unsaturated soil in three-dimensional stresses
Modelling the effect of initial density on soil-water characteristic curves
Modelling the variation of degree of saturation in a deformable unsaturated soil
Permafrost studies in the Qinghai-Tibet plateau for road construction
Seismic response of seasonally frozen ground
A new yield and failure criterion for geomaterials
Shear behaviors of sand and clay under three-dimensional stress condition
Fracture and flow of rocks under high triaxial compression
An experimental and theoretical study of the behaviour of a calcarenite in triaxial compression
Un concept de rupture unifié pour les matériaux rocheux derises et poreux. [PhD Thesis]
An elasto-plastic model for unsaturated soil in three-dimensional %stresses