海底地震动模拟中, 需要考虑震声(seismoacoustic)散射,若不适当计入流固边界条件, 将导致沿界面的面波误差较大. Nakamura等^[1]通过有限差分方法, 考虑海底地形和海水层的影响,模拟了2009年Suruga Bay地震的地震波传播; 为了满足流固界面条件,在界面附近的方程采用二阶近似, 其余部分采用四阶近似,两者精度不一致. Okamoto和Takenaka^[2]采用反射/透射矩阵方法,考虑流固界面条件,模拟了P-SV波入射情形二维不规则流固界面情形的震声散射,但该方法仅适用于坡度较缓地形, 对于陡峭地形, 容易导致计算失稳. Qian和Yamanaka^[3]利用边界元法适于陡峭地形的特点,以及全局矩阵传播子在模拟多层介质中波动对内存需求较少的特点,对全局矩阵传播子进行扩展, 考虑流固界面条件,将边界元法与全局矩阵传播子方法结合,模拟了P-SV波入射情形二维不规则流固界面情形的震声散射.Komatitsch等^[4]考虑海水与基岩界面法向速度连续和应力连续,建立平衡方程的耦合弱积分形式, 通过谱元离散和显式Newmark时间积分,得到海底地震波的谱元模拟方法.

海洋声学中, 也需考虑海底地形对声波传播的影响^[5-6],一般采用抛物方程(PE)方法, 该方法可快速建立远距离声场,在海洋声学领域得到广泛应用, 但考虑海底不规则复杂地形时, 较为困难.Murphy等^[7]采用有限元方法模拟海洋声场, 相比于抛物方程法,可以计算全波场及海底复杂地形的影响, 但效率较低,文中忽略了海底弹性介质的剪切效应.

在海洋物理勘探中, 对于含油气的页岩, 需要考虑为多孔介质.海洋工程结构地基液化失效问题,也需要考虑海床为多孔介质^[8-11].李伟华等^[11]考虑理想流体和饱和土层的界面连续条件,建立了水与饱和场地耦合的显式有限元动力分析方法.

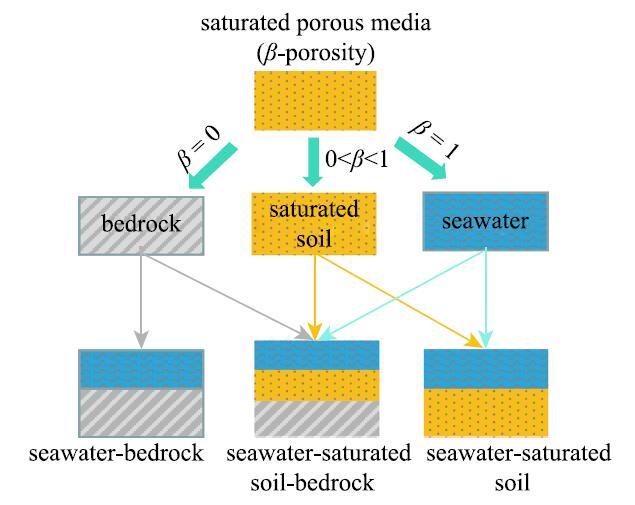
以上研究中, 海水、基岩、饱和多孔介质分别采用不同波动方程进行描述,再通过界面条件进行耦合求解, 十分不便^[12-21]. 理论上,固体和流体介质均为饱和多孔介质的特殊情形, 孔隙率分别为0和1,上述耦合均可在饱和多孔介质理论体系进行描述, 如图1所示. 基于此,可从饱和多孔介质的一般情形出发,考虑不同孔隙率的饱和多孔介质之间的耦合,从而将上述所有耦合统一在同一计算框架, 避免不同模块之间的交互.在文献^[22]中考虑了海域水平成层场地情形.本文将考虑不规则海底地形情形, 需要考虑界面的法向方向导数,若按文献^[22]中的方法, 变得较为困难.这里采用求解法向和切向界面力的方法, 可较为方便地解决此问题.

采用有限元法进行海底地震动和海洋声场的模拟,需要采用人工边界模拟无限域的影响,一般采用透射边界^[23-25]和黏弹性边界^[26-27],并分别以自由场^[28]和等效力^[29]作为输入.本文采用集中质量显式有限元方法结合透射边界条件,可避免求解大型线性方程组, 效率较高, 且易于实现并行计算,有望用于大型海底地震波以及海洋声场的模拟中. 通过两凹陷地形的算例,验证了本文统一计算框架的有效性.

饱和多孔介质的固相平衡方程^[30]

(1)\begin{equation} \label{eq1} {\bf L}_{\rm s}^{\rm T} \boldsymbol \sigma'-(1- \beta ){\bf L}_{\rm w}^{\rm T} P + b(\dot{\boldsymbol U}- \dot{\boldsymbol u}) = (1-\beta )\rho _{\rm s} \ddot{\boldsymbol u} \end{equation}

液相平衡方程

(2)\begin{equation} \label{eq2} -\beta {\bf L}_{\rm w}^{\rm T} P + b(\dot{\boldsymbol u}-\dot{\boldsymbol U}) = \beta \rho _{\rm w} \ddot{\boldsymbol U} \end{equation}

相容方程(考虑初始孔压和初始体应变为零时)

(3)$$\tau =-\beta P = E_{\rm w} [\beta e^{\rm w} + (1-\beta )e^{\rm s}] $$

其中, ${\bf L}_{\rm s}$和${\bf L}_{\rm w} $为微分算子矩阵

(4a)$${\bf L}_{\rm s} = \left[ {{\begin{array}{*{20}c} \partial/\partial x_1 & 0 & 0 \\ 0 & \partial/\partial x_2 & 0 \\ 0 & 0 & \partial/\partial x_3\\ \partial/\partial x_2 & \partial/\partial x_1 & 0 \\ 0 & \partial/\partial x_3 & \partial/\partial x_2 \\ \partial/\partial x_3 & 0 & \partial/\partial x_1\\ \end{array} }} \right] $$

(4b)$${\bf L}_{\rm w} = \left(\partial/\partial x_1,\partial/x_2, \partial/\partial x_3\right) $$

式中, $\boldsymbol \sigma'$为有效应力矢量, $\tau $为平均孔压,以拉为正; $P$为孔隙水压, 以压为正; $\boldsymbol U$, $\boldsymbol u$分别为液相和固相的位移矢量, $\dot{\boldsymbol U}$,$\dot{\boldsymbol u}$为速度, $\ddot{\boldsymbol U}$,$\ddot{\boldsymbol u}$为加速度; $\rho _{\rm s}$, $\rho _{\rm w}$分别为固相和液相的密度, $\beta $为孔隙率, $b = \beta ^2\mu_0/k_0 $, $k_0 $为流体渗透系数, $\mu _0 $为动黏度系数; $E_{\rm w}$为流体的体变模量, $e^{\rm s}$, $e^{\rm w}$分别为固相和液相的体 应变.Dirichlet边界条件

(5a)$$\boldsymbol u-\bar{\boldsymbol u} = 0 $$

(5b)$$\boldsymbol U-\bar{\boldsymbol U} = 0 $$

Neumann边界条件

(5c)$$\hat{\boldsymbol n}\boldsymbol \sigma-\bar{\boldsymbol \sigma} = 0$$

(5d)$$(P-\bar{P})\boldsymbol n = 0 $$

其中, $\bar{\boldsymbol u}$, $\bar{\boldsymbol U}$分别为在边界上给定的固相和液相位移. $\bar{\boldsymbol \sigma}$,$\bar{P}$分别为边界上固相平均应力和真实孔压的给定值; $\boldsymbol n$为沿边界外法线的方向矢量, $\hat{\boldsymbol n}$为由方向导数组成的矩阵, 其形式如下

(6a)$$\boldsymbol n = \left( n_x, n_y, n_z\right)^{\rm T} $$

(6b)$$\hat{\boldsymbol n} = \left[ {{\begin{array}{*{20}c} {n_x } & 0 & 0 & {n_y } & 0 & {n_z } \\ 0 & {n_y } & 0 & {n_x } & {n_z } & 0 \\ 0 & 0 & {n_z } & 0 & {n_y } & {n_x } \\ \end{array} }} \right] $$

对方程(1)和(2)采用伽辽金方法离散, 考虑边界条件,可得任一结点$i$的解耦运动平衡方程为^[28]

(7)$\ddot{\boldsymbol u}_i \boldsymbol M_{{\rm s}i} + \boldsymbol F_i^{\rm s} + \boldsymbol T_i^{\rm s}-\boldsymbol S_i^{\rm s} = 0$

(8)\end{equation} \begin{equation} \label{eq6} \ddot{\boldsymbol U}_i \boldsymbol M_{{\rm w}i} + \boldsymbol F_i^{\rm w} + \boldsymbol T_i^{\rm w}-\boldsymbol S_i^{\rm w} = 0 \end{equation}

其中, $\boldsymbol M_{{\rm s}i}$, $\boldsymbol M_{{\rm w}i} $分别为集中在$i$结点上的固相质量和液相质量; $\boldsymbol F_i^{\rm s} $, $\boldsymbol F_i^{\rm w} $分别为集中在节点$i$的固、液相本构力; $\boldsymbol T_i^{\rm s} $,$\boldsymbol T_i^{\rm w} $分别为集中在节点$i$的固、液相黏性阻力; $\boldsymbol S_i^{\rm s} $, $\boldsymbol S_i^{\rm w}$分别作用在节点$i$的固、液相边界力. 在同一介质内,由于所有位移和应力都连续,通过单元界面作用在它们之上的应力大小相等、方向相反,在单元组装的过程中, 内部节点的$\boldsymbol S_i^{\rm s} $和$\boldsymbol S_i^{\rm w}$均为零.

(9a)$$\boldsymbol M_{{\rm s}i} = \sum\limits_e \sum\limits_{j = 1}^J \int_{\varOmega^e} \boldsymbol N_i^{\rm T}(1-\beta )\rho _{\rm s} \boldsymbol N_j {\rm d}V $$

(9b)$$\boldsymbol M_{{\rm w}i} = \sum\limits_e \sum\limits_{j = 1}^J \int_{\varOmega ^e} \boldsymbol N_i^{\rm T} \beta \rho _{\rm w} \boldsymbol N_j {\rm d}V $$

(9c)$$\boldsymbol F_i^{\rm s} = \sum\limits_e { f}_i^{\rm se} = \sum\limits_e \int_{\varOmega ^e} (\boldsymbol L_{\rm s} \boldsymbol N_i )^{\rm T} \boldsymbol \sigma{\rm d}V $$

(9d)$$\boldsymbol F_i^{\rm w} = \sum\limits_e { f}_i^{\rm we} = \sum\limits_e \int_{\varOmega^e} (\boldsymbol L_{\rm w} \boldsymbol N_i )^{\rm T} \beta P {\rm d}V $$

(9e)$$\boldsymbol T_i^{\rm s} = \sum\limits_e \int_{\varOmega ^e} \boldsymbol N_i^{\rm T}b\boldsymbol N_j (\dot{\boldsymbol u}_j- \dot{\boldsymbol U}_j) {\rm d}V $$

(9f)$$\boldsymbol T_i^{\rm w} =-\boldsymbol T_i^{\rm s} $$

(9g)$$\boldsymbol S_i^{\rm s} = \sum\limits_e \int_{S^e} \boldsymbol N_i ^{\rm T} \hat{\boldsymbol n}\boldsymbol \sigma{\rm d}S $$

(9h)$$\boldsymbol S_i^{\rm w} = \sum\limits_e \int_{S^e} \boldsymbol N_i^{\rm T} \boldsymbol n\beta P{\rm d}S $$

若节点$i$为内部节点(非界面点), $\boldsymbol S_i^{\rm s}$和$\boldsymbol S_i^{\rm w} $均为零, 给定本构关系,可对式(7)、式(8)采用时步积分求解^[30].这里讨论节点$i$为两种不同介质的界面点情形, 如图2所示.采用隔离体概念, 则介质一中界面点$i$的动力方程由式(7)、式(8)描述,介质二中界面点$k$的动力方程表示如下(除微分算子和形函数外,其他物理量均带上划线, 以区别于介质一)

(10)$$\ddot{\overline{\boldsymbol u}}_k \bar{\boldsymbol M}_{{\rm s}k} + \bar{\boldsymbol F}_k^{\rm s} + \bar{\boldsymbol T}_k^{\rm s}- \bar{\boldsymbol S}_k^{\rm s} = 0 $$

(11)$$\ddot{\overline{\boldsymbol U}}_k \bar{\boldsymbol M}_{{\rm w}k} + \bar{\boldsymbol F}_k^{\rm w} + \bar{\boldsymbol T}_k^{\rm w}- \bar{\boldsymbol S}_k^{\rm w} = 0 $$

其中

(12a)$$\bar{\boldsymbol M}_{{\rm s}k} = \sum\limits_e \sum\limits_{j = 1}^J \int_{\varOmega ^e} \boldsymbol N_k^{\rm T} (1-\bar{\beta })\bar{\rho}_{\rm s} \boldsymbol N_j {\rm d}V $$

(12b)$$\bar{\boldsymbol M}_{{\rm w}k} = \sum\limits_e \sum\limits_{j = 1}^J \int_{\varOmega ^e} \boldsymbol N_k^{\rm T} \bar{\beta }\bar {\rho}_{\rm w}\boldsymbol N_j {\rm d}V $$

(12c)$$\bar{\boldsymbol F}_k^{\rm s} = \sum\limits_e \bar{\boldsymbol f}_k^{{\rm s}e} = \sum\limits_e \int_{\varOmega ^e} (\boldsymbol L_{\rm s} \boldsymbol N_k )^{\rm T} \bar{\boldsymbol \sigma}{\rm d}V $$

(12d)$$\bar{\boldsymbol F}_k^{\rm w} = \sum\limits_e \bar{\boldsymbol f}_k^{{\rm w}e} = \sum\limits_e \int_{\varOmega ^e} (\boldsymbol L_{\rm w} \boldsymbol N_k )^{\rm T}\bar{\beta}\bar {P} {\rm d}V $$

(12e)$$\bar{\boldsymbol T}_k^{\rm s} = \sum\limits_e \int_{\varOmega ^e} \boldsymbol N_k^{\rm T}\bar {b}\boldsymbol N_j (\dot{\overline{\boldsymbol u}}_j-\dot{\overline{\boldsymbol U}}_j ) {\rm d}V $$

(12f)$$\bar{\boldsymbol T}_k^{\rm w} =-\bar{\boldsymbol T}_k^{\rm s} $$

(12g)$$\bar{\boldsymbol S}_k^{\rm s} = \sum\limits_e \int_{S^e} \boldsymbol N_k ^{\rm T} \hat{\overline{\boldsymbol n}}\bar{\boldsymbol \sigma}{\rm d}S $$

(12h)$$\bar{\boldsymbol S}_k^{\rm w} = \sum\limits_e \int_{S^e} \boldsymbol N_k ^{\rm T} \bar{\boldsymbol n}\bar{\beta}\bar{P}{\rm d}S $$

此时, $\boldsymbol S_i^s $和$\boldsymbol S_i^w$为介质二作用在界面点$i$上的界面力, $\bar{\boldsymbol S}_k^s$和$\bar{\boldsymbol S}_k^w $为介质一作用在界面点$k$上的界面力,它们之间的关系由如下界面连续条件^[31]确定

(13a)$$\boldsymbol \sigma_{\rm N} + \boldsymbol \tau = \bar{\boldsymbol \sigma}_{\rm N} + \bar{\boldsymbol \tau} $$

(13b)$$\boldsymbol \sigma_{\rm T} = \bar{\boldsymbol \sigma}_{\rm T} $$

(13c)$$P-\bar {P} = 0 $$

(13d)$$\boldsymbol u_{\rm N} = \bar{\boldsymbol u}_{\rm N},\quad \boldsymbol u_{\rm T} = \bar{\boldsymbol u}_{\rm T} $$

(13e)$$\beta (\boldsymbol U_{\rm N}-\boldsymbol u_{\rm N} ) = \bar {\beta }(\bar{\boldsymbol U}_{\rm N}-\bar{u}_{\rm N} ) $$

其中, 下标N表示矢量的法向分量, 下标T表示矢量得切向分量.在文献^[22]中, 已讨论水平界面情形, 即水平成层海域场地情形.对于非水平成层情形, 采用文献^[22]中的方法, 将变得十分繁琐.本文采用求解界面力的方法.

采用如下显式积分格式

(14)$$\ddot{U}^p = \frac{1}{\Delta t^2}(U^{(p + 1)}-2U^p + U^{(p-1)}) $$

(15)$$\dot {U}^p = \frac{1}{\Delta t}(U^p-U^{(p-1)}) $$

其中, 上标$p$表示$t = p\Delta t$时刻, 下同.

对式(7)、式(8)~$p$时刻的平衡方程进行时步积分得

(16)$$\boldsymbol u_i^{(p + 1)} = \hat{\boldsymbol u}_i^{(p + 1)} +\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} + \Delta \boldsymbol u_{{\rm T}i}^{(p + 1)} $$

(17)$$\boldsymbol U_i^{(p + 1)} = \hat{\boldsymbol U}_i^{(p + 1)} +\Delta \boldsymbol U_{{\rm N}i}^{(p + 1)} + \Delta \boldsymbol U_{{\rm T}i}^{(p + 1)} $$

其中

(18a)$$\hat{\boldsymbol u}_i^{(p + 1)} = 2\boldsymbol u_i^p- \boldsymbol u_i^{(p-1)}-\frac{(\Delta t)^2}{m_i^{\rm s} }(\boldsymbol F_i^{{\rm s}p} + \boldsymbol T_i^{{\rm s}p} ) $$

(18b)$$\hat{\boldsymbol U}_i^{(p + 1)} = 2 \hat{\boldsymbol U}_i^p- \hat{\boldsymbol U}_i^{(p-1)}-\frac{(\Delta t)^2}{m_i^w }(\boldsymbol F_i^{{\rm w}p} + \boldsymbol T_i^{{\rm w}p} ) $$

(18c)$$\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} = \frac{(\Delta t)^2}{m_i^s }\boldsymbol S_{{\rm N}i}^{{\rm s}p} $$

(18d)$$\Delta \boldsymbol u_{{\rm T}i}^{(p + 1)} = \frac{(\Delta t)^2}{m_i^s }\boldsymbol S_{{\rm T}i}^{{\rm s}p} $$

(18e)$$\Delta \boldsymbol U_{{\rm N}i}^{(p + 1)} = \frac{(\Delta t)^2}{m_i^w }\boldsymbol S_{{\rm N}i}^{{\rm w}p} $$

(18f)$$\Delta \boldsymbol U_{{\rm T}i}^{(p + 1)} = \frac{(\Delta t)^2}{m_i^w }\boldsymbol S_{{\rm T}i}^{{\rm w}p} $$

其中, $\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)}$是由法向界面力$\boldsymbol S_{{\rm N}i}^{{\rm s}p}$引起的固相位移, $\Delta\boldsymbol u_{{\rm T}i}^{(p + 1)}$是由切向界面力$\boldsymbol S_{{\rm T}i}^{{\rm s}p}$引起的固相位移, $\Delta \boldsymbol U_{{\rm N}i}^{(p + 1)}$是由法向界面力$\boldsymbol S_{{\rm N}i}^{{\rm w}p}$引起的液相位移, $\Delta \boldsymbol U_{{\rm T}i}^{(p + 1)}$是由切向界面力$\boldsymbol S_{{\rm T}i}^{{\rm w}p}$引起的液相位移.

同样可得

(19)$$\bar{\boldsymbol u}_k^{(p + 1)} = \hat{\overline{\boldsymbol u}}_k^{(p + 1)} + \Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)} + \Delta \bar{\boldsymbol u}_{{\rm T}k}^{(p + 1)} $$

(20)$$\bar{\boldsymbol U}_k^{(p + 1)} = \hat{\overline{\boldsymbol U}}_k^{(p + 1)} + \Delta \bar{\boldsymbol U}_{{\rm N}k}^{(p + 1)} + \Delta \bar{\boldsymbol U}_{{\rm T}k}^{(p + 1)} $$

右端各项如同式(18).

由界面连续条件可知(其中式(21c)利用了式(13c)、式(9h)、式(12h))

(21a)$$\boldsymbol S_{{\rm N}i}^{\rm s} + \boldsymbol S_{{\rm N}i}^{\rm w} =-(\bar{\boldsymbol S}_{{\rm N}k}^{\rm s} + \bar{\boldsymbol S}_{{\rm N}k}^{\rm w}) $$

(21b)$$\boldsymbol S_{{\rm T}i}^{\rm s} =-\bar{\boldsymbol S}_{{\rm T}k}^{\rm s} $$

(21c)$$\bar{\beta }\boldsymbol S_{{\rm N}i}^{\rm w} =-\beta \bar{\boldsymbol S}_{{\rm N}k}^{\rm w} $$

(21d)$$\boldsymbol S_{{\rm T}i}^{\rm w} = \bar{\boldsymbol S}_{{\rm T}k}^{\rm w} = 0 $$

(21e)$$\boldsymbol u_{{\rm N}i} = \bar{\boldsymbol u}_{{\rm N}k} $$

(21f)$$\boldsymbol u_{{\rm T}i} = \bar{\boldsymbol u}_{{\rm T}k} $$

(21g)$$\beta \boldsymbol U_{{\rm N}i} = \bar {\beta }(\bar{\boldsymbol U}_{{\rm N}k}-\bar{\boldsymbol u}_{{\rm N}k} ) + \beta \bar{\boldsymbol u}_{{\rm N}k} $$

将式(16)、式(19)代入界面处固相法向位移连续条件式(21e),可得

(22)\begin{equation} \label{eq47} \boldsymbol n_i \left( \boldsymbol n_i \cdot \hat{\boldsymbol u}_i^{(p + 1)} \right) + \Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} = \boldsymbol n_i \left( \boldsymbol n_i \cdot \hat{\overline{\boldsymbol u}}_k^{(p + 1)} \right) + \Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)} \end{equation}

利用式(18c)、式(21a)、式(21c), 得

(23)$$\boldsymbol n_i \left( \boldsymbol n_i \cdot \hat{\boldsymbol u}_i^{(p + 1)} \right) + \frac{(\Delta t)^2}{m_i^{\rm s} }\boldsymbol S_{{\rm N}i}^{{\rm s}p} = \boldsymbol n_i \left( {\boldsymbol n_i \cdot \hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right)+ \\ \frac{(\Delta t)^2}{m_k^{\rm s}}\left[-\boldsymbol S_{{\rm N}i}^{{\rm s}p}-\boldsymbol S_{{\rm N}i}^{{\rm w}p} + (\bar{\beta}/\beta )\boldsymbol S_{{\rm N}i}^{{\rm w}p} \right] $$

由界面处法向连续条件(21g), 考虑到式(16)、式(19)、式(20)、式(21a)、式(21c), 可得

(24)$$\boldsymbol n_i \left( {\beta \boldsymbol n_i \cdot \hat{\boldsymbol U}_i^{(p + 1)} } \right) + \beta \left( {\frac{(\Delta t)^2}{m_i^{\rm w}}\boldsymbol S_{{\rm N}i}^{{\rm w}p} } \right) = \\ \boldsymbol n_i \left\{ {\boldsymbol n_i \cdot \left[ {\bar {\beta }\left( {\hat{\overline{\boldsymbol U}}_k^{(p + 1)}- \hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right) + \beta \hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right]} \right\} + \bar {\beta }\cdot\\ \bigg[-\left( {\bar {\beta }/\beta } \right)\frac{(\Delta t)^2}{m_k^{\rm w}}\boldsymbol S_{{\rm N}i}^{{\rm w}p}-\frac{(\Delta t)^2}{m_k^{\rm s}}\Big( - \boldsymbol S_{{\rm N}i}^{{\rm s}p}-\boldsymbol S_{{\rm N}i}^{{\rm w}p} + \\ \left( {\bar {\beta }/\beta } \right)\boldsymbol S_{{\rm N}i}^{{\rm w}p} \Big) \bigg]+ \beta \left[ {\frac{(\Delta t)^2}{m_k^{\rm s} }\left( {- \boldsymbol S_{{\rm N}i}^{{\rm s}p}-\boldsymbol S_{{\rm N}i}^{{\rm w}p} + \left( {\bar {\beta }/\beta } \right)\boldsymbol S_{{\rm N}i}^{{\rm w}p} } \right)} \right] $$

由式(23)和式(24), 可解得

(25)$$\boldsymbol S_{{\rm N}i}^{{\rm s}p} = \frac{A_{22} B_1-A_{12} B_2 }{A_{22} A_{11}-A_{12} A_{21} } $$

(26)$$\boldsymbol S_{{\rm N}i}^{{\rm w}p} = \frac{A_{21} B_1-A_{11} B_2 }{A_{21} A_{12}-A_{11} A_{22} } $$

其中

(27a)$$A_{11} = (\Delta t)^2\left( {\frac{1}{m_i^{\rm s}} + \frac{1}{m_k^{\rm s}}} \right) $$

(27b)$$A_{12} = \left( {1-\frac{\bar {\beta }}{\beta }} \right)\frac{(\Delta t)^2}{m_k^{\rm s}} $$

(27c)$$B_1 = \boldsymbol n_i \left[ {\boldsymbol n_i \cdot \left( {\hat{\overline{\boldsymbol u}}_k^{(p + 1)}-\hat{\boldsymbol u}_i^{(p + 1)} } \right)} \right] $$

(27d)$$A_{21} = (\Delta t)^2\left( {-\frac{\bar {\beta }}{m_k^{\rm s} } + \frac{\beta }{m_k^{\rm s}}} \right) $$

(27e)$$A_{22} = (\Delta t)^2\left[ {\frac{\beta }{m_i^{\rm w}} + \frac{\bar {\beta }^2}{\beta m_k^{\rm w}} + \frac{\left( {\bar {\beta }-\beta } \right)\left( {\bar {\beta }-\beta } \right)}{\beta m_k^{\rm s}}} \right] $$

(27f)$$B_2 = \boldsymbol n_i \left\{ {\boldsymbol n_i \cdot \left[ {\bar {\beta }\left( {\hat{\overline{\boldsymbol U}}_k^{(p + 1)}- \hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right)-\beta \left( {\hat{\boldsymbol U}_i^{(p + 1)}-\hat{\boldsymbol u}_k^{(p + 1)} } \right)} \right]} \right\} $$

由式(25)、式(26)求得$\boldsymbol S_{{\rm N}i}^{{\rm s}p}$和$\boldsymbol S_{{\rm N}i}^{{\rm w}p} $后,可进一步由式(21a)、式(21c)解得$\bar{\boldsymbol S}_{{\rm N}k}^{{\rm s}p} $和$\bar{\boldsymbol S}_{{\rm N}k}^{{\rm w}p} $.

切向方向导数不确定, 所以固相切向位移连续条件不能直接用.由于界面处固相法向和切向位移连续, 因此界面处固相位移连续

(28)\begin{equation} \label{eq58} \hat{\boldsymbol u}_i^{(p + 1)} + \Delta \boldsymbol u_{Ni}^{(p + 1)} + \Delta \boldsymbol u_{Ti}^{(p + 1)} = \hat{\overline{\boldsymbol u}}_k^{(p + 1)} + \Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)} + \Delta \bar{\boldsymbol u}_{{\rm T}k}^{(p + 1)} \end{equation}

将式(18d)、式(21b)代入式(28), 整理得

(29)$$\left( {\frac{(\Delta t)^2}{m_i^{\rm s}} + \frac{(\Delta t)^2}{m_k^{\rm s}}} \right)\boldsymbol S_{{\rm T}i}^{{\rm s}p} = \\ \left( {\hat{\overline{\boldsymbol u}}_k^{(p + 1)} + \Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)}-\hat{\boldsymbol u}_i^{(p + 1)}-\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} } \right) $$

由此可解得

(30)\begin{equation} \label{eq60} \boldsymbol S_{{\rm T}i}^{{\rm s}p} = \frac{\left( {\hat{\overline{\boldsymbol u}}_k^{(p + 1)} + \Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)}-\hat{\boldsymbol u}_i^{(p + 1)}-\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} } \right)m_i^{\rm s} m_k^{\rm s} }{(\Delta t)^2(m_i^{\rm s} + m_k^{\rm s} )} \end{equation}

式中, $\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} $可由式(18c)求得,同样可求得$\Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)} $.求得$\boldsymbol S_{{\rm T}i}^{{\rm s}p} $后,由式(21b)可得$\boldsymbol S_{{\rm T}k}^{{\rm s}p} $. 有了界面力,由式(16)、式(17)可求得$\boldsymbol u_i^{(p + 1)} $, $\boldsymbol U_i^{(p + 1)} $. 同样, 由式(19)、式(20)可得$\bar{\boldsymbol u}_k^{(p + 1)} $, $\bar{\boldsymbol U}_k^{(p + 1)} $.

(1)流体--饱和土情形

考虑饱和土上覆流体情形. 此时, 图2中介质二为饱和多孔介质,介质一为流体, 则$\beta = 1$, $\boldsymbol M_{{\rm s}i} = 0$.考虑无黏的理想流体, 动黏度系数为零, 则$b = 0$, $\boldsymbol T_i^{\rm s} = 0$, $\boldsymbol T_i^{\rm w} = 0$;不存在固相, 固相骨架模量可取为零, 则$\boldsymbol F_i^{\rm s} = 0$, $\boldsymbol S_i^{\rm s} = 0$; 由此, 式(7)自动满足,式(8)退化为如下理想流体方程

(31)\begin{equation}\label{eq61} \ddot{\boldsymbol U}_i \boldsymbol M_{{\rm w}i} +\boldsymbol F_i^{\rm w}-\boldsymbol S_i^{\rm w} = 0 \end{equation}

因此, 饱和多孔介质方程可以用来分析理想流体的动力响应.

流体--饱和土界面连续条件为^[32]

(32a)$$\boldsymbol S_{{\rm N}i}^{\rm w} =-(\bar{\boldsymbol S}_{{\rm N}k}^{\rm s} + \bar{\boldsymbol S}_{{\rm N}k}^{\rm w}) $$

(32b)$$\bar {\beta }\boldsymbol S_{{\rm N}i}^{\rm w} =-\bar{\bf S}_{{\rm N}k}^{\rm w} $$

(32c)$$\boldsymbol U_{{\rm N}i} = \bar {\beta }(\bar{\boldsymbol U}_{{\rm N}k}-\bar{\boldsymbol u}_{{\rm N}k} ) + \bar{\boldsymbol u}_{{\rm N}k} $$

由动力方程(10)、(11)和(31)以及界面连续条件式(32), 按2.1节的方法,可得界面点的运动方程如下

(33a)$$\boldsymbol n_i \left( {\boldsymbol n_i \cdot \hat{\boldsymbol U}_i^{(p + 1)} } \right) + \frac{(\Delta t)^2}{m_i^{\rm w}}\boldsymbol S_{{\rm N}i}^{{\rm w}p} = \boldsymbol n_i \\ \left[ {\boldsymbol n_i \cdot \left( {\bar {\beta }\hat{\overline{\boldsymbol U}}_k^{(p + 1)} + \left( {1-\bar {\beta }} \right)\hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right)} \right] + \\ \left( {-\frac{(\Delta t)^2}{m_k^{\rm w}}\bar {\beta }^2\boldsymbol S_{{\rm N}i}^{{\rm w}p}-\frac{(\Delta t)^2}{m_k^{\rm s} }\left( {\bar {\beta }-1} \right)^2\boldsymbol S_{{\rm N}i}^{{\rm w}p} } \right) $$

由式(33a)可解得

(33b)$$\label{eq66} \boldsymbol S_{{\rm N}i}^{{\rm w}p} = \frac{ B_2 }{A_{22} } $$

其中

(33c)$$A_{22} = (\Delta t)^2\left( {\frac{1}{m_i^{\rm w} } + \frac{\bar {\beta }^2}{m_k^{\rm w}} + \frac{\left( {\bar {\beta }-1} \right)^2}{m_k^{\rm s} }} \right) $$

(33d)$$B_2 = \boldsymbol n_i \left\{ {\boldsymbol n_i \cdot \left[ {\left( {\bar {\beta }\hat{\overline{\boldsymbol U}}_k^{(p + 1)} + \left( {1-\bar {\beta }} \right)\hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right)-\hat{\boldsymbol U}_i^{(p + 1)} } \right]} \right\}\qquad\quad $$

求得$\boldsymbol S_{{\rm N}i}^{{\rm w}p} $后,可由式(32a)和式(32b)可得$\bar{\boldsymbol S}_{{\rm N}k}^{{\rm s}p}$和$\bar{\boldsymbol S}_{{\rm N}k}^{{\rm w}p} $.

由于流体为无黏理想流体, 切向界面力为零. 有了界面力,则可由式(17)、式(19)、式(20)求得位移及其他响应.

(2)饱和土--干基岩情形

图2中的介质二若为不透水的基岩, 不存在液相, 则$\bar {\beta } = 0$,$\bar{\boldsymbol M}_{{\rm w}k} = 0$;液相体积模量和固液之间的黏性力取为零, 则$\bar{\boldsymbol F}_k^{\rm w} = 0$, $\bar{\boldsymbol T}_k^{\rm w} = 0$,$\bar{\boldsymbol T}_k^{\rm s} = 0$, $\bar{\boldsymbol S}_k^{\rm w} = 0$, 方程(11)自动满足,式(10)退化为如下干基岩方程

(34)\begin{equation} \label{eq69} \ddot{\overline{\boldsymbol u}}_k \bar{\boldsymbol M}_{{\rm s}k} + \bar{\boldsymbol F}_k^{\rm s}-\bar{\boldsymbol S}_k^{\rm s} = \boldsymbol 0 \end{equation}

因此, 饱和多孔介质方程可以用来分析干基岩的动力响应.

饱和土--干基岩界面条件为^[31]

(35a)$$\boldsymbol S_{{\rm N}i}^{\rm s} + \boldsymbol S_{{\rm N}i}^{\rm w} =-\bar{\boldsymbol S}_{{\rm N}k}^{\rm s} $$

(35b)$$\boldsymbol S_{{\rm T}i}^{\rm s} =-\bar{\boldsymbol S}_{{\rm T}k}^{\rm s} $$

(35c)$$\boldsymbol u_{{\rm N}i} = \bar{\bf u}_{{\rm N}k} $$

(35d)$$\boldsymbol u_{{\rm T}i} = \bar{\boldsymbol u}_{{\rm T}k} $$

(35e)$$\beta (\boldsymbol U_{{\rm N}i}-\boldsymbol u_{{\rm N}i} ) = 0 $$

由界面处固相法向位移连续,将式(16)、式(19)代入式(35c)可得

(36)$$\boldsymbol n_i \left( {\boldsymbol n_i \cdot \hat{\boldsymbol u}_i^{(p + 1)} } \right) + \Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} = \boldsymbol n_i \left( {\boldsymbol n_i \cdot \hat{\bar{\boldsymbol u}}_k^{(p + 1)} } \right) + \Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)} $$

整理得

(37a)$$\bar {u}_{ky}^{(p + 1)} = 2\bar {u}_{ky}^p-\bar {u}_{ky}^{(p- 1)}- \frac{\Delta t^2}{(m_{{\rm s}i} + \bar {m}_{{\rm s}k} )} \cdot \\ (F_{iy}^{{\rm s}p} + \bar {F}_{ky}^{{\rm s}p} + T_{iy}^{{\rm s}p} ) $$

(37b)$$\boldsymbol n_i \left( {\boldsymbol n_i \cdot \hat{\boldsymbol u}_i^{(p + 1)} } \right) + \frac{(\Delta t)^2}{m_i^{\rm s} }\boldsymbol S_{{\rm N}i}^{{\rm s}p} = \boldsymbol n_i \left( {\boldsymbol n_i \cdot \hat{\bar{\boldsymbol u}}_k^{(p + 1)} } \right)+ \\ \frac{(\Delta t)^2}{m_k^{\rm s}}\left( {-\boldsymbol S_{{\rm N}i}^{{\rm s}p}-\boldsymbol S_{{\rm N}i}^{{\rm w}p} } \right) $$

由界面处法向连续条件(35e), 并将式(16)、式(17)代入可得

(38)$$\boldsymbol n_i \left[ {\beta \boldsymbol n_i \cdot \left( {\hat{\boldsymbol U}_i^{(p + 1)}-\hat{\boldsymbol u}_i^{(p + 1)} } \right)} \right] + \\ \beta (\Delta \boldsymbol U_{{\rm N}i}^{(p + 1)}-\Delta \boldsymbol u_{{\rm N}i}^{(p + 1)} ) = 0 $$

整理得

(39)$$\boldsymbol n_i \left[ {\beta \boldsymbol n_i \cdot \left( {\hat{\boldsymbol U}_i^{(p + 1)}-\hat{\boldsymbol u}_i^{(p + 1)} } \right)} \right] + \\ \beta \left( {\frac{(\Delta t)^2}{m_i^{\rm w}}\boldsymbol S_{{\rm N}i}^{{\rm w}p}-\frac{(\Delta t)^2}{m_i^{\rm s}}\boldsymbol S_{{\rm N}i}^{{\rm s}p} } \right) = 0 $$

由式(37)和式(39), 可解得

(40a)$$\boldsymbol S_{{\rm N}i}^{{\rm s}p} = \frac{A_{22} B_1- A_{12} B_2 }{A_{22} A_{11}-A_{12} A_{21} } $$

(40b)$$\boldsymbol S_{{\rm N}i}^{{\rm w}p} = \frac{A_{21} B_1- A_{11} B_2 }{A_{21} A_{12}-A_{11} A_{22} } $$

其中

(41a)$$A_{11} = (\Delta t)^2\left( {\frac{1}{m_i^{\rm s}} + \frac{1}{m_k^{\rm s}}} \right) $$

(41b)$$A_{12} = \frac{(\Delta t)^2}{m_k^{\rm s}} $$

(41c)$$B_1 = \boldsymbol n_i \left[ {\boldsymbol n_i \cdot \left( {\hat{\overline{\boldsymbol u}}_k^{(p + 1)}-\hat{\boldsymbol u}_i^{(p + 1)} } \right)} \right] $$

(41d)$$A_{21} = \frac{-\beta (\Delta t)^2}{m_i^{\rm s}} $$

(41e)$$A_{22} = \frac{(\Delta t)^2\beta }{m_i^{\rm w}} $$

(41f)$$B_2 = \boldsymbol n_i \left\{ {\boldsymbol n_i \cdot \left[ {\beta \left( {\hat{\boldsymbol u}_i^{(p + 1)}-\hat{\boldsymbol U}_i^{(p + 1)} } \right)} \right]} \right\} $$

由式(35a)可求得$\bar{\boldsymbol S}_{{\rm N}k}^{{\rm s}p} $.与1.1节中相同, 可求得$\boldsymbol S_{{\rm T}i}^{{\rm s}p}$和$\bar{\boldsymbol S}_{{\rm T}k}^{{\rm s}p} $,进而可求得界面点的位移响应.

(3)流体--干基岩情形

此时, 图2中介质一为理想流体, 介质二为干基岩. 按前述参数取值,运动方程分别退化为式(31)、式(34).流体--干基岩界面连续条件为(不透水)

(42a)$$\boldsymbol S_{{\rm N}i}^{\rm w} =-\bar{\boldsymbol S}_{{\rm N}k}^{\rm s} $$

(42b)$$\boldsymbol U_{{\rm N}i} = \bar{\boldsymbol u}_{{\rm N}k} $$

将式(17)、式(19)代入式(42b), 可得

(42c)$$\label{eq89} \boldsymbol n_i \left[ {\boldsymbol n_i \cdot \left( {\hat{\boldsymbol U}_i^{(p + 1)}-\hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right)} \right] + {\Delta \boldsymbol U_{{\rm N}i}^{(p + 1)}-\Delta \bar{\boldsymbol u}_{{\rm N}k}^{(p + 1)} } = 0 $$

利用式(18), 整理得

(43a)$$\boldsymbol n_i \left[ {\boldsymbol n_i \cdot \left( {\hat{\boldsymbol U}_i^{(p + 1)}-\hat{\overline{\boldsymbol u}}_k^{(p + 1)} } \right)} \right] + \\ \left( {\frac{(\Delta t)^2}{m_i^{\rm w} }\boldsymbol S_{{\rm N}i}^{{\rm w}p} + \frac{(\Delta t)^2}{m_k^{\rm s}}\boldsymbol S_{{\rm N}i}^{{\rm w}p} } \right)= 0 $$

可解得

(43b)$$\label{eq91} \boldsymbol S_{{\rm N}i}^{{\rm w}p} = \frac{\boldsymbol B_2 }{A_{22} } $$

其中

(43c)$$A_{22} = (\Delta t)^2\left( {\frac{1}{m_i^{\rm w}} + \frac{1}{m_k^{\rm s}}} \right) $$

(43d)$$\boldsymbol B_2 = \boldsymbol n_i \left[ {\boldsymbol n_i \cdot \left( {\hat{\overline{\boldsymbol u}}_k^{(p + 1)}- \hat{\boldsymbol U}_i^{(p + 1)} } \right)} \right] $$

由式(42a)可得$\bar{\boldsymbol S}_{{\rm N}k}^{{\rm s}p} $,切向界面力为零, 进而可得界面点的位移响应.

综上可知,流体、固体、饱和多孔介质之间的耦合均可统一在饱和多孔介质理论框架进行分析.

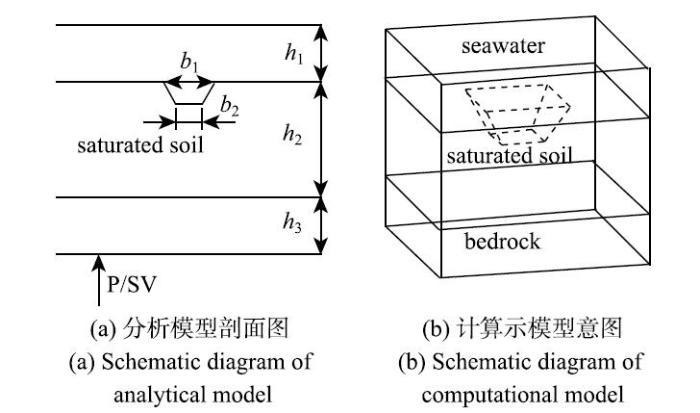
以图3所示的模型为例,考虑饱和海床表面一凹陷地形情形的海水--饱和海床--基岩非水平成层体系,在平面P波垂直入射时的反应.

对于该复杂地形, 需要通过有限元等数值方法进行求解.因此对图3(a)所示的问题采用本文提出的方法求解, 计算模型如图3(b),在侧面和底面采用多次透射人工边界^[23-24],用于模拟无限域.在人工边界上采用传递矩阵方法得到的自由场^[35]作为波动输入.海水--饱和海床--基岩体系中,内部点(除人工边界点和界面点外的其余节点)及界面点的响应计算,均采用统一的饱和多孔介质方程和界面点的计算方法,即1.1节和1.2节中的理论方法; 人工边界点的响应通过多次透射公式计算.基于此, 编制了相应的三维有限元计算程序, 以实现本文方法.

采用如下线弹性本构

(44a)$$\sigma '_{ij}-(1-\alpha )\delta _{ij} P = 2\mu e_{ij} +\delta _{ij} \lambda e $$

(44b)$$P =-\alpha Me + M\zeta $$

其中, 根据文献^[33,34], $\lambda $和$\mu$为固相骨架在排水情形时的拉梅常数, $\alpha$和$M$则为表征饱和多孔介质压缩性的常数, 以压缩模量表示时, 为

(45)$$\alpha = 1-\frac{E_{\rm b}}{E_{\rm u}} $$

(46)$$M = \frac{E_u^2 }{E_{\rm u} \left[n\left(\dfrac{E_{\rm u}}{E_{\rm w}}-1\right) + 1\right]-E_{\rm b}} $$

其中, $E_{\rm u}$和$E_{\rm b}$分别为不排水和排水时饱和多孔介质的压缩模量, $E_{\rm w}$为孔隙流体的压缩模量, $k_0 $为渗透系数.

下面所有算例模型, $x$和$y$方向尺寸均为40 m,$z$方向的尺寸如模型图所示. 将计算域划分为八节点六面体单元,单元尺寸为1 m $\times$1 m $\times$1 m. 输入图4所示的单位脉冲,时间步距为$\Delta t = 0.000~1$s. 单元尺寸$\varDelta \le \lambda_{\min } / 10$, 满足精度要求, 其中$\lambda _{\min }$为所需模拟的最小波长. 所有材料参数见表1.

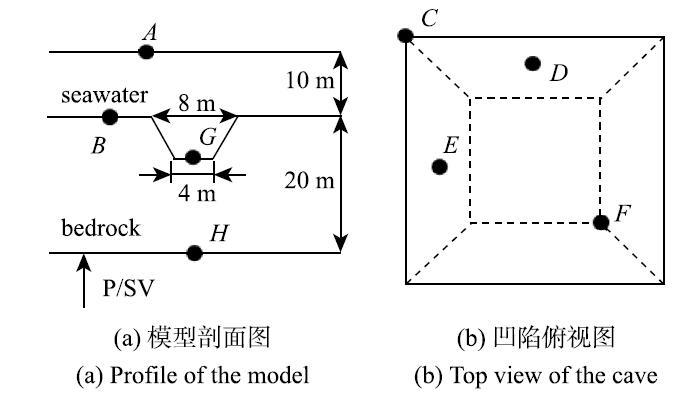
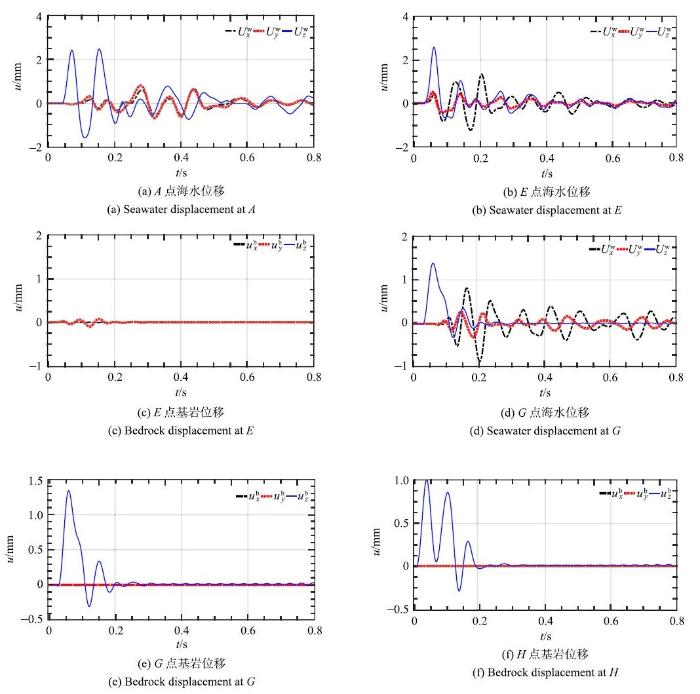
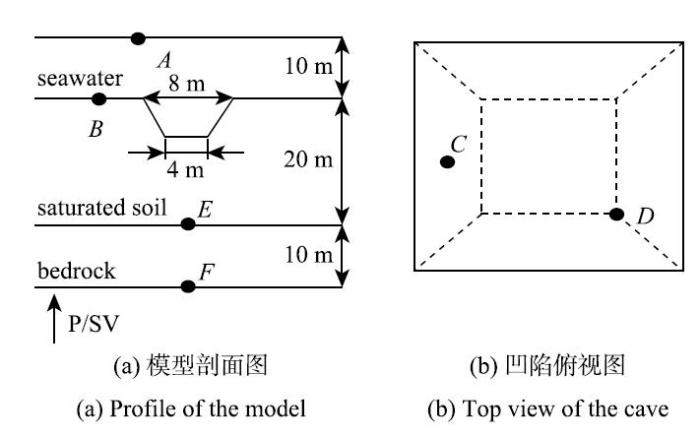
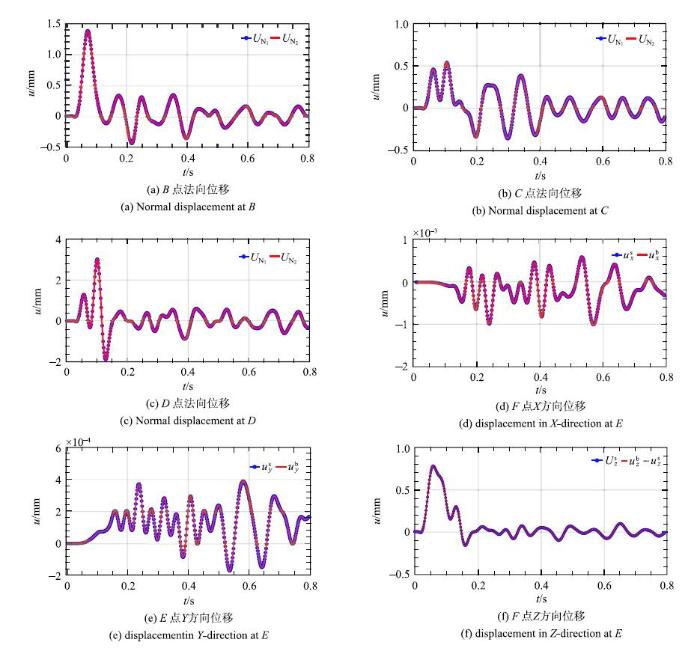
考虑基岩海床表面一三维凹陷(如图5(b))地形的海水--基岩非水平成层模型,其剖面如图5(a)所示. 图6为P波垂直入射时各点的响应, 图例中,位移$U$的下标表示方向, 上标w表示海水, 上标b表示基岩,上标s表示饱和土, 如$u_x^{\rm b}$为基岩固相$x$方向的位移, $U_{{\rm N}}^{\rm w}$为界面处海水法向位移. 由图中可以看出, 由于凹陷的存在,即使P波垂直入射时, 也会引起海水层水平方向的响应. $G$点由于对称性,其水平向位移为零. 由于三维海域非水平成层的波动散射问题较为复杂,目前还没有相关解析解. 因此, 图7给出界面点法向方向海水和基岩的位移,检查其是否满足界面连续条件(42b). 从图中可以看出,界面上海水与基岩法向位移完全吻合, 满足海水--干基岩界面连续条件.

海水--饱和海床--基岩模型如图8所示. 图9为P波垂直入射时的响应.

同样, 由于凹陷地形的存在, 即使P波垂直入射时也会引起海水$A$,$B$点处的水平位移.

界面点$B$的海水位移和饱和土固、液相位移在法向(该点处为$z$方向)满足位移连续(式32(c)),因此该点处海水$z$方向位移与固相$z$方向的位移接近,与液相$z$方向位移差异较大, 但满足(式32(c))的连续条件(如图10(a));

切向位移不连续(此处为$x$, $y$方向),因此该点处海水水平方向位移与饱和土水平向位移差异较大. 界面点$C$,界面为倾斜面, 位移仅在法向满足连续条件(式32(c)), 在$x$, $y$,$z$方向不连续,因此该点处饱和土位移和海水位移差异较大(图9(e)$\sim$图9(g)),但满足法向位移连续(如图10(b)). $D$点为角点, 其法向方向不存在,具体实施计算时, 取周围界面在该点处的单位法向矢量叠加,再归一化为单位矢量, 作为该点的单位法向导数; 同样,该点处饱和土位移和海水位移差异较大(图9(h)$\sim$图9(i)),但满足法向位移连续(如图10(b)).

$E$和$F$分别为饱和土与基岩界面点和基岩底 面点.

图10为P波入射时的法向位移. 从图中可以看出,海水与饱和土海床接触面上同一位置点的$\boldsymbol U_{{\rm N}1} $,$\boldsymbol U_{{\rm N}2} $完全吻合($\boldsymbol U_{{\rm N}1} $,$\boldsymbol U_{{\rm N}2} $如式(47)),满足海水--饱和土海床界面连续条件,且饱和土与基岩接触面也满足界面连续条件.

(47a)$$\boldsymbol U_{{\rm N}1} = \beta \boldsymbol U_{{\rm N}i} $$

(47b)$$\boldsymbol U_{{\rm N}2} = \bar {\beta }(\bar{\boldsymbol U}_{{\rm N}k}-\bar{\boldsymbol u}_{{\rm N}k} ) + \beta \bar{\boldsymbol u}_{{\rm N}k} $$

通过上述两个算列验证了本文非水平成层海域场地有限元方法的有效性.

本文考虑海底不规则地形,将理想流体、固体、饱和多孔介质之间的耦合分析纳入到饱和多孔介质统一计算框架,建立了集中质量显式有限元求解方法, 并编制了相应的三维并行分析程序.通过分析半无限海水--弹性基岩、海水--饱和海床--弹性基岩体系凹陷地形模型在P波垂直入射时的动力响应,验证了该统一计算框架的有效性以及并行计算的可行性.

本文采用集中质量显式有限元方法结合透射边界条件,可避免求解大型线性方程组, 效率较高, 且易于实现并行计算,有望用于大型海底地震波以及海洋声场的模拟中.