引言
折叠翼、舵模型可分为二元模型和三元模型[4].二元模型是一种理想模型,假设翼展方向等截面,弦向不发生弯曲变形,结构的运动仅由机翼刚心的沉浮、绕刚心的俯仰及控制面的偏转来描述,可以模拟机翼的弯曲和扭转振动.虽然有别于真实舵面,但其模型简单,通常用于各种非线性气动弹性问题的理论研究[5-10].Tang和Dowell[5]研究了受突风激励的非零攻角典型翼面在亚声速气流中的气弹响应,并发现极限环振荡幅值对初始俯仰角很敏感.贾尚帅和丁千[6]建立了高超声速含间隙二元机翼的气动弹性方程,并研究了弹体扰动对颤振的影响.刘芳和丁千[7]利用平均法解析地研究了俯仰和沉浮均具有间隙的二元舵面的主共振响应.He等[8]利用描述函数法研究了具有控制面间隙的二元翼在跨音速流中的颤振嗡鸣现象,并观察到了双极限环现象.Sazesh和Shams[9]利用随机方法研究了含间隙二元翼的颤振问题.王人凤等[10]考虑了三维响应,对经典二元舵的运动方程进行了修正.二元模型可以定性地研究间隙对气动弹性的影响,但只能在一个位置存在非线性.
三元模型考虑了结构的弹性变形,并且可以在多个位置存在非线性,与实际工程更加贴合,但自由度数更多,求解更为复杂.有学者通过欧拉$\!$-$\!$-$\!$伯努利梁理论[11]和利兹+罚函数方法[12]半解析地建立了折叠机构的运动微分方程,但国内外学者在结构存在间隙时大多采用有限元方法进行数值仿真研究. 间隙非线性问题计算量巨大,如何缩减模型是一个新的问题.Karpel和Raveh[13]提出的虚拟质量法是简化模型的一个途径.该方法在刚度发生改变的自由度施加惯性极大的虚拟质量,得到了可以表示不同非线性子域物理坐标的同一系列模态,从而将非线性问题转化到模态空间进行求解.Bae等[14]利用该方法对具有控制面间隙的机翼进行了非线性气动弹性分析,并在飞行速度低于线性颤振速度时观察到了极限环和混沌现象. Lee和Chen[15]又将该方法应用到铰链具有间隙非线性的折叠翼中. 但Yang等[16]指出虚拟质量的参数只能在一个建议的范围内选择,而且非线性刚度不能直接表示在非线性方程中. Yang[16-17]等利用动态子结构法建立了折叠舵面的气动弹性方程,并分别在时域和频域给出了求解方法.该方法首先建立内、外舵面的子结构模型,接着利用非线性弹簧进行连接,模型的缩减通过在第一次坐标变换中选取不完备的主模态集来完成.Wu等[18]又进一步对折叠舵面的时域仿真数据做希尔伯特变换,辨识得到了铰接处的非线性刚度模型.在带集中非线性系统的气动弹性研究中,主要有三种非线性类型:间隙非线性、立方非线性和迟滞非线性[4].除此之外,也有学者提出带预载的双线性型非线性[17]和双曲切线型非线性[19].其中,大部分学者均利用刚度为分段线性的非线性弹簧来模拟铰链处的间隙和接触.该建模方法较为简单,但在利用传统的数值积分算法处理这种非光滑型非线性刚度时,因为很难精确地找到切换点,会存在误差[4].同时,该类非线性刚度也很难描述内、外舵面铰接处的实际弹性碰撞.
已有很多学者通过风洞实验对含间隙舵面的气动弹性响应进行研究[20-23].风洞实验花销巨大且实施困难,大部分航 空航天结构在进行吹风之前都需要通过地面振动实验来获取结构的动力学特性.为了得到更加精确的数学模型,一些学者对舵面的间隙模型展开了实验辨识.Lee和Tron[24]利用从CF-18舰载机地面测试中获得的铰链力矩$\!$-$\!$-$\!$折叠翼转角曲线通过描述函数法获得了铰链的等效刚度.Wu 等[25]对全动舵面进行了地面振动实验,并且利用反向路径法获得了舵轴处的转动间隙.Kim等[26-27]利用恢复力曲面法对可展开导弹舵面的铰链进行了实验辨识,但是在计算铰链处的相对转角时内、外舵面均被假设为刚体.在此基础上,Shin等[28]又通过正弦扫频实验获得了舵面的含间隙传动装置的动刚度,并将平均值代入到气动弹性的计算中.Fuellekrug和Goege[29]研究了大型飞机受非线性影响严重的副翼模态,首先在小量级激励下通过相位共振法和相位分离法获得线性模态参数,接着提高量级并利用恢复力曲面法和共振衰减法进行非线性参数辨识.通过地面振动实验研究间隙对折叠舵面动力学特性影响的文献还不充分,还需要进行间隙可调折叠舵面的基础激励实验研究.
本工作对现有文献关于有间隙折叠舵面在实验和仿真方面的研究不足进行了补充.实验方面,分别利用锤击法和振动台基础激励对无间隙和有间隙折叠舵面进行了地面振动实验,研究了间隙对其动力学特性的影响.仿真方面,提出了一种适用于具有集中非线性的折叠机构的模型缩减方法,并对舵面有限元模型进行了缩减.根据Hertz接触理论建立具有非线性组合刚度的扭转弹簧来模拟间隙和接触.建立了折叠舵面在基础激励下非线性振动响应的求解流程. 以期为折叠舵面气动弹性分析的结构建模提供参考.
1 实验
首先利用锤击法对无间隙折叠舵面进行模态实验,得到线性结构的模态参数. 接着利用振动台进行基础激励,研究间隙引起的非线性现象,从而定性分析非线性类型,为后续的有限元建模提供基础.
1.1 实验装置
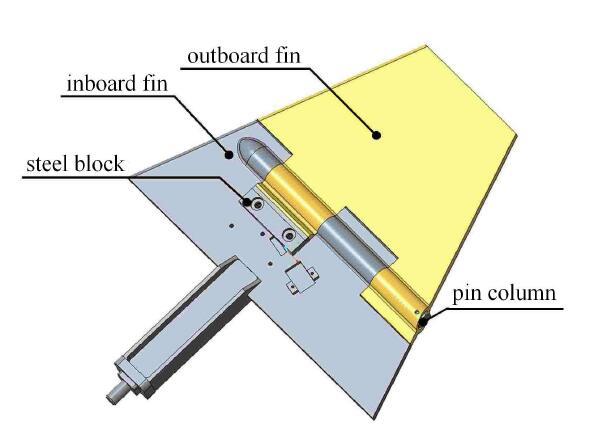
折叠舵面如图1所示,舵面由内舵面、外舵面、圆销柱和限位挡块(钢块)组成. 内、外舵面通过圆销柱相连,弯矩通过外舵面与内舵面上的限位挡块的接触面传递. 间隙可以通过改变限位挡块的位置来调节.内舵面的根部舵轴通过螺栓固定在夹具上. 舵面主体结构的材质为2A12铝,限位挡块的材质为45号钢.
图1
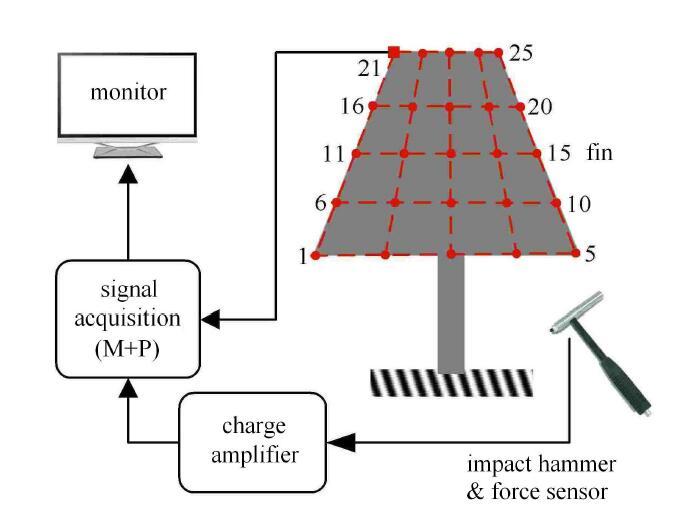
1.2 锤击法模态实验
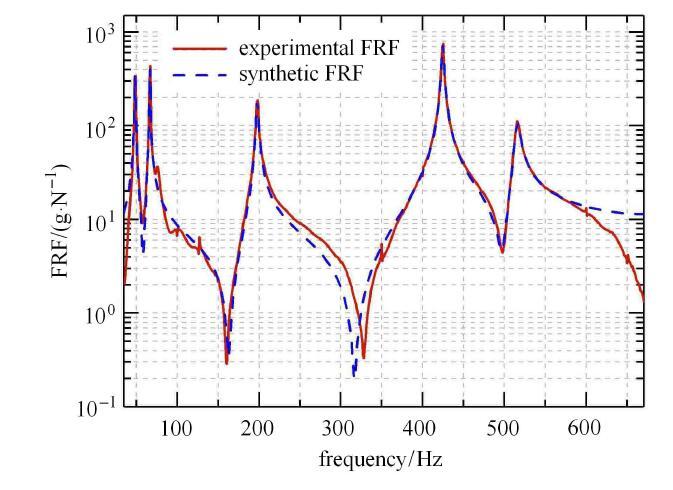
图2
图3
1.3 振动台激励实验
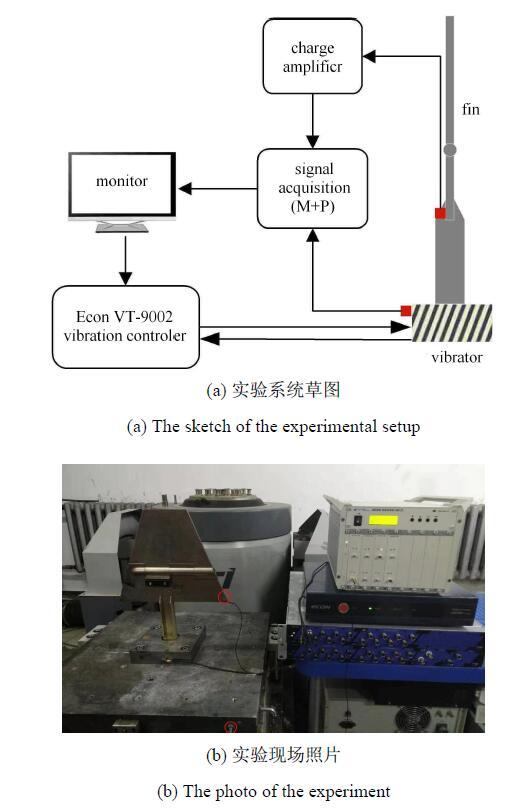
打开间隙,折叠舵面为非线性结构.非线性结构的响应对激励量级很敏感,而锤击法很难控制锤击力度,所以不宜采用锤击法进 行非线性结构的振动实验.采用振动台进行基础激励,实验系统如图4所示.为了得到舵面振动的传递函数(这里的传递函数采用$H_{1}$估计方法通过MATLAB自带函数tfestimate对激励和响应时域信号做变换获得),需要在基础和舵面上各粘贴一传感器,传感器粘贴位置如图4(b)的红圈所示,其中舵面上的传感器型号为联能CA-YD-125,基础上的传感器型号为PCB 333B32,前者为电荷型传感器,所以需要通过电荷放大器将信号转变为电压信号.振动台选择定加速度幅值正弦扫频激励,这时激励信号的速度幅值和位移幅值会随着激励频率的变化而变化.扫频范围为10$\sim $80,Hz(包含前两阶频率),扫频速度为40,Hz/min.扫频实验的整个时间历程包括先正向扫描和后反向扫描两部分,时长总计210,s.
图4
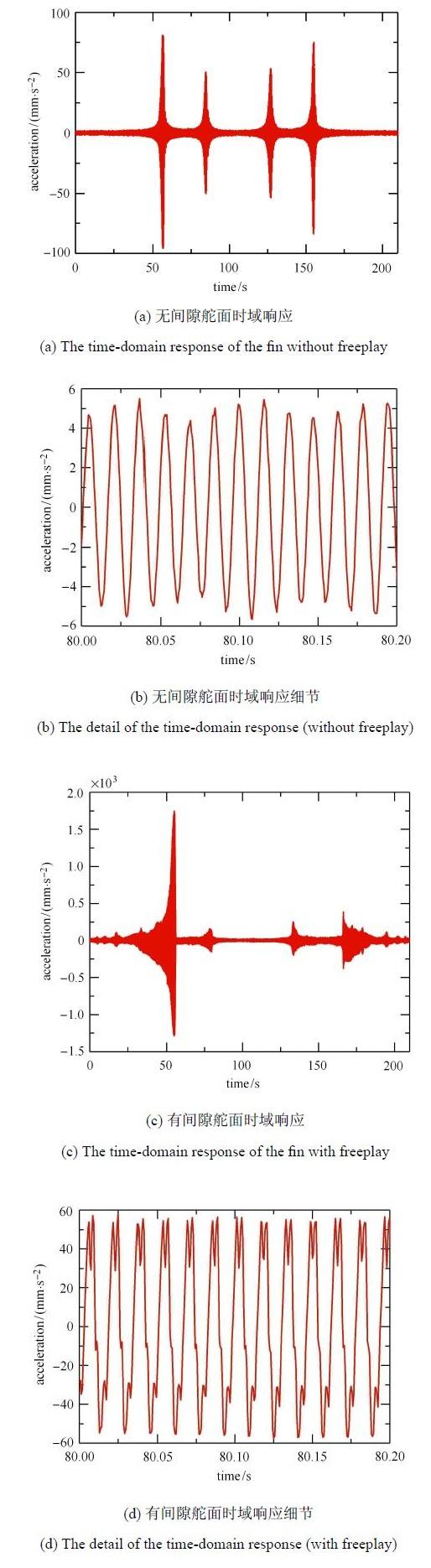
首先在时域比较了无间隙和有间隙折叠舵面的加速度响应,如图5所示(无间隙情况激励量级为0.1,g;有间隙情况间隙为0.03,mm,激励量级为1.5,g). 可知,间隙的存在会使时域曲线畸变并产生毛刺, 这些毛刺可以解释为激励频率的高次谐波.有间隙舵面的时域曲线在55,s和165,s左右发生跳跃,这时的激励频率接近舵面的第一阶频率.
图5
图5
无间隙与有间隙舵面扫频时域曲线
Fig. 5
The time-domain sweep response of the fin without and with freeplay
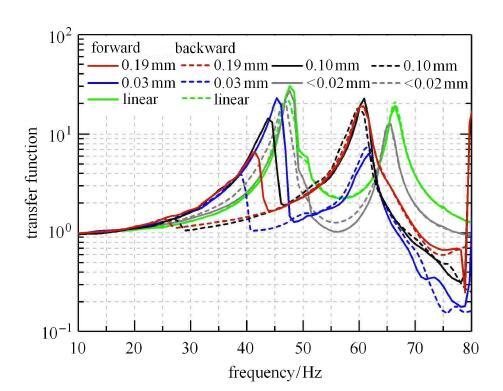
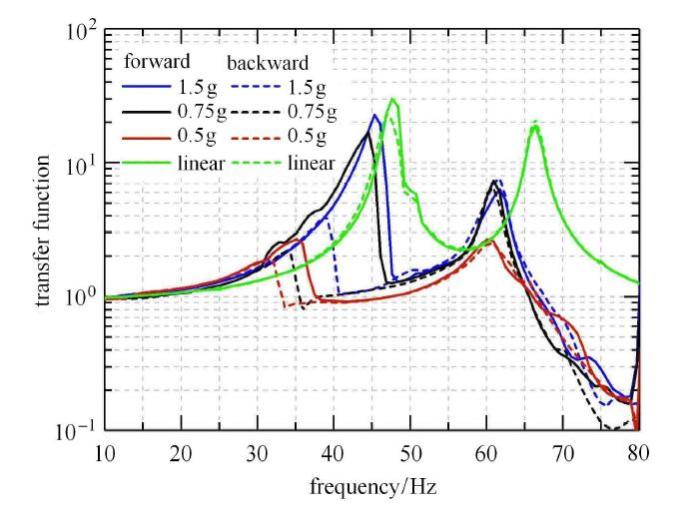
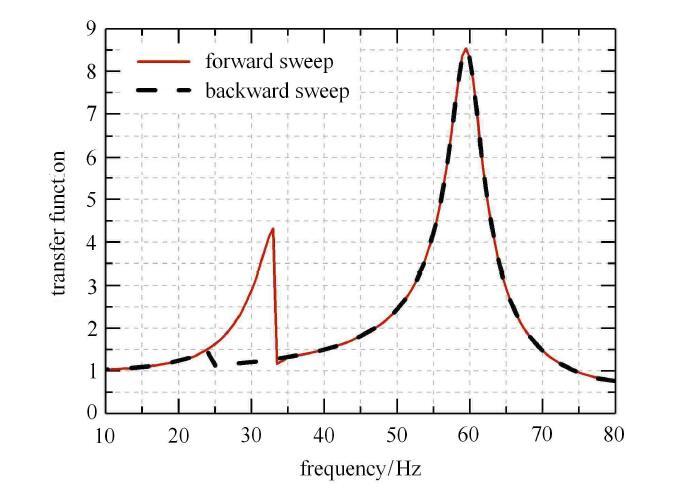
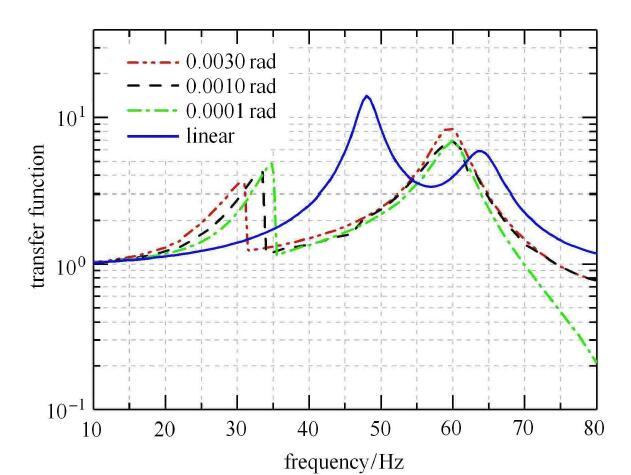
以上非线性现象在频域中更加明显. 分别改变折叠舵面的间隙和激励量级,得到的传递函数如图6和图7所示(实线为正向扫描、 虚线为反向扫描;图6中的激励量级为1.5,g,图7中的间隙为0.03,mm).可知,有间隙舵面的传递函数在第一阶频率处发生跳跃现象,这与时域现象相符;正向扫描和反向扫描的结果不同,正向扫描得到的第一阶频率比反向扫描高,但第二阶频率基本不受扫描方向的影响;间隙的减小会使第一阶频率和峰值增大,且逐渐接近无间隙舵面的结果,第二阶频率在间隙大于0.03,mm时受间隙影响较小,频率的变化幅度与第一阶相比很小.虽然峰值有所下降,但是在间隙进一步减小至0.02,mm以下时峰值回升并接近线性结果;激励量级的增大同样会使第一阶频率和峰值增大,且逐渐接近无间隙舵面的结果,对第二阶频率的影响与第一阶相比较小,峰值在量级从0.5,g变化到0.75,g时呈上升趋势.图6和图7中传递函数的跳跃发生在峰值点的右侧,这说明系统具有硬刚度的特征,类似杜芬振子.
图6
图6
不同间隙的传递函数比较
Fig. 6
The comparison of the transfer functions under different freeplays
图7
图7
不同量级的传递函数比较
Fig. 7
The comparison of the transfer functions under different excitation magnitudes
2 建模
本节首先建立折叠舵面的限元模型,并利用提出的模型缩减方法进行缩减,接着建立铰接处的间隙与接触模型,最后建立了基础激励下折叠舵面非线性振动响应的求解流程.
2.1 有限元模型
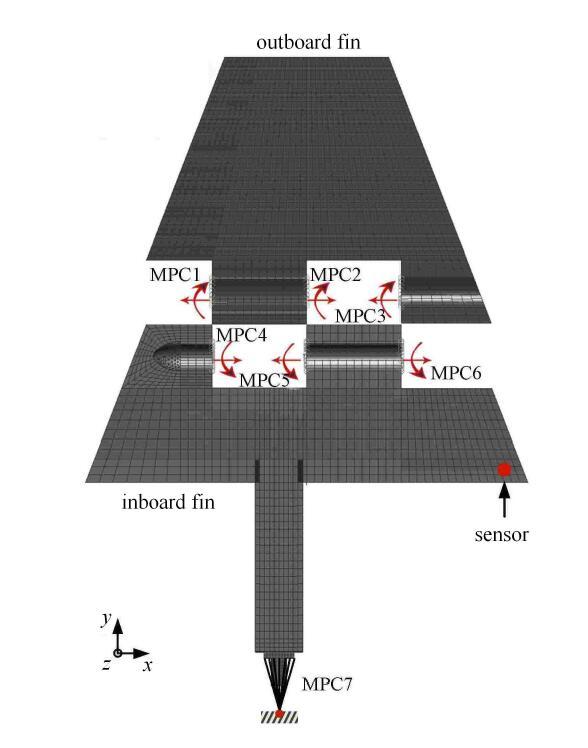
折叠舵面采用商用有限元软件MSC. Patran/Nastran建模,模型如图8所示.颤振分析对质量和质心的要求很高,所以该结构采用体单元建模. 外舵面的圆锥体采用Tet4单元,其他部分采用Hex8单元,加速度传感器用Point质量单元模拟.连接内、外舵面的销柱没有单独建模,而是将内、外舵面插入销柱的圆孔填实.这样,整个折叠舵面的有限元模型仅由内、外舵面两部分组成,它们之间的弯矩传递用3个$R_{x}$方向的扭转弹簧模拟.按照这样的建模方法,非线性仅存在于内、外舵面的连接部分.如果弹簧为线性,则整个模型为线性模型,可以利用传统的模态叠加方法计算结构的固有频率和振型;如果弹簧为非线性,则模型为非线性模型,传统的模态叠加方法不再适用,而需要利用非线性数值算法来进行动力学响应求解.将内舵面的舵轴根部与基础相接触的表面上的所有节点通过MPC (多点约束)刚性连接到舵轴中心线上的一个节点,通过固支该节点来模拟固支约束. 在进行基础激励动响应计算时,需要释放掉该节点$z$方向自由度的约束,并在此方向施加强迫运动.
图8
2.2 适用于折叠机构的模型缩减方法
折叠舵面有限元模型有10,122个节点.在进行线性模型的模态计算时耗时较短,但如果直接利用此有限元模型进行动响应求解,尤其是非线性动响应,计算效率很低而且存在的高阶虚假模态会使计算结果出现较大误差,所以有必要进行模型缩减.
折叠舵面结构由内、外舵面两部分组成,可以利用Craig-Bampton子结构法[30](也即固定界面模态综合法)建立该结构的振动控制方程. 固定界面模态综合法是一种传统子结构法,适用于线性结构.杨等[17]将该方法扩展到非线性结构,并对弦向多个自由度具有非线性刚度的折叠翼进行了非线性气动弹性分析.这两种方法的核心都是两次坐标变换,在对子结构的第一次坐标变换中可以选取不完备的主模态集来构造坐标变换矩阵,从而达到对子结构进行模态缩减的目的. 第二次坐标变换用于子结构的连接,文献[17]的方法会保留全部的界面自由度.按照该方法建立的有限元模型的内、外舵面会各存在三个界面节点,每一个点有6个自由度($x$, $y$, $z$, $R_{x}$,$R_{y}$, $R_{z})$. 在两子结构连接的过程中每一个点有5个自由度($x$, $y$, $z$, $R_{y}$,$R_{z})$是需要刚接的,剩下的1个自由度($R_{x})$需要施加扭转弹簧作为弹性连接.这样,将子结构连接后共剩下了21个界面自由度(连接前6个界面节点共有36个自由度,每两个相邻节点有5个自由度因为刚接而消失,所以最后剩下$36-3 \times 5=21$个自由度).这其中只有弹性连接的自由度才与非线性有关,其他的刚接自由度与非线性无关,但却往往比保留的模态数目还要多.针对文献[17]的方法会保留全部界面自由度的问题,本文提出了一种可以缩减界面处的刚接自由度,而只保留弹性连接自由度的模型缩减方法.该方法借鉴了文献[17]两次坐标变换的核心思想,但不需要分别对子结构进行建模,而是进行整体建模,并且特别适用于具有集中非线性的折叠机构.第一次坐标变换直接作用于去掉弹性连接自由度但包含刚性连接自由度的线性整体模型,从而进行缩减,第二次坐标变换是对弹性自由度进行连接.该方法可以将折叠机构的线性主体部分直接缩减,而只把非线性连接的相关自由度当作物理坐标保留下来单独处理,这样可以将线性模态和非线性自由度分开,从而进一步简化了有限元模型. 具体思路如下.
(1) 第一次坐标变换
将整体结构的振动方程按照非保留内部坐标${\pmb u}_{i}$和保留物理坐标${\pmb u}_{j}$分块. 对于折叠舵面这种折叠机构,在每个铰接点处只有绕转轴旋转的转动自由度需要保留,该点的其他自由度均作为非保留内部坐标进行模态缩减,这个过程可以表示为
式中,${\pmb f}_{j}$为转动自由度内力,${\pmb u}_{j}$包括激励点、响应测点和铰接处的转动自由度.
令${\pmb\varPhi}_{\rm N} = \left[ {\pmb\varPhi}_{{ii}}^{\rm T} {\bf 0} \right]^{\rm T}$为结构的主模态集,它表示保留物理坐标完全被约束后的结构模态, 其中${\pmb\varPhi}_{{ii}} = \left[{\pmb\varphi}_1 {\pmb\varphi}_2 \cdots {\pmb\varphi}_{ n}\right]$为结构的正则化模态($n$为保留的模态数).主模态集通常是不完备的,即将高阶模态截断的低阶模态集,从而达到缩减的目的.
令${\pmb\varPhi}_{\rm C} = \left[ {\pmb\varPhi}_{{ij}}^{\rm T} {\pmb I} \right]^{\rm T}$为结构的约束模态集,它相当于保留物理坐标完全被约束住后,逐个释放保留自由度并使之产生单位位移得到的静变形,其中${\pmb\varPhi} _{{ij}} =-{\pmb K}_{{ii}}^{-1} {\pmb K}_{{ij}} $.
定义第一次坐标变换为
式中
其中,$\lambda _{\rm r} $为保留物理坐标完全被约束后的结构的圆频率,$r =1,2, \cdots, n$.
(2) 第二次坐标变换
下面在内、外舵面的铰接处添加弹簧. 式(2)中的保留自由度${\pmb p}_{ j}$包括:激励位置和测点响应$z$方向的自由度${\pmb p}_{\rm f} $,铰接点与外舵面相连的转动自由度${\pmb\theta}_{\rm \alpha } $,铰接点与内舵面相连的转动自由度${\pmb\theta} _{\rm \beta } $. 将坐标${p}$重新排序,令${\pmb p} = \left[ {\pmb p}_{\rm f} {\pmb p}_{ i} {\pmb\theta }_{\rm \alpha } {\pmb\theta }_{\rm \beta } \right]^{\rm T}$. 内、外舵面铰接处的位移协调不同于固连结构的连接条件,对接位移不相等. 假设相对转角为 ${\pmb\gamma }$,则连接条件可以写为
令${\pmb q} = \left[ {\pmb p}_{\rm f} {\pmb p}_{ i} {\pmb\theta} _{\rm \alpha } {\pmb\gamma } \right]^{\rm T}$,从而建立广义自由度${\pmb q}$与非独立坐标${\pmb p}$之间的变换关系为
利用坐标变换矩阵式(6),可以得到系统的运动方程
其中,广义力为
其中,${\pmb f}_{{\rm \theta }_{\rm \beta } } =-{\pmb f} ({\pmb\gamma })$为连接内力,当连接为线性弹簧时,有${\pmb f}({\pmb\gamma }) ={\pmb k}{\pmb\gamma }$;当为非线性弹簧时,具体表达形式见2.3节.
阻尼模型采用比例阻尼,令$\tilde {\pmb C} = \alpha _1 \tilde{\pmb M} + \alpha _2\tilde{\pmb K}$. 因此,系统的运动方程可以写为
2.3 间隙与接触模型
图9
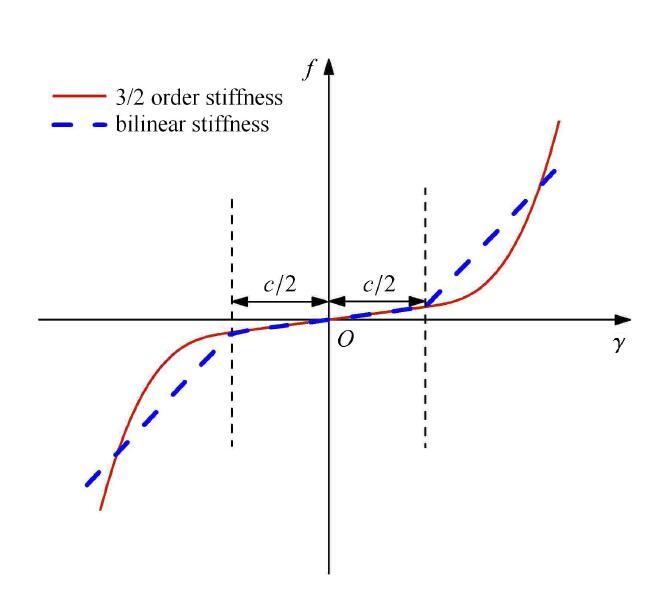
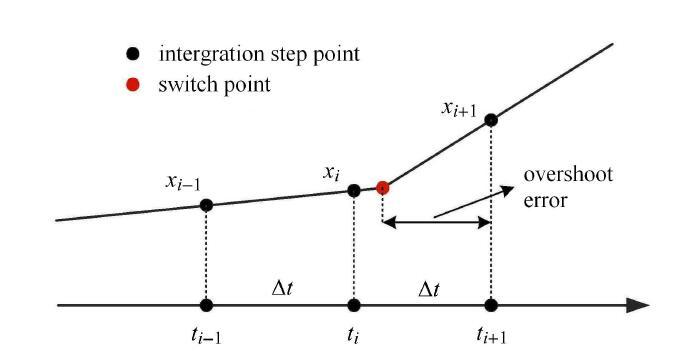
由文献[4]可知,数值积分方法具有计算精度高,收敛速度快等优点,但该类方法只能处理连续型非线性动力学系统. 传统的数值积分算法大多基于泰勒级数展开,这就要求方程具有较好的光滑性.在处理式(10)这种非光滑型非线性刚度时,如图10所示,因为很难精确地找到刚度切换点,就会存在一阶导数间断点位于一个积分步长内的情况,这时得到的下一时刻的响应就会存在误差[31].胡海岩[32]指出非光滑恢复力会产生非持久跳跃现象,若仍想采用传统的数值积分算法,如四阶龙格库塔(RK4),就需要缩小步长,这会增加机时消耗,替代方法是利用曲线拟合将间隙刚度变为光滑的刚度函数. 其他文献[33,34,35]也指出了传统数值积分算法在进行双线性刚度求解时会产生误差.文献[31]进一步指出,RK4在进行具有间隙非线性刚度的二元机翼气动弹性计算时会出现多个相邻很近的极限环,而利用可以精确识别切换点的数值积分算法则只会出现一个稳定的极限环,而且RK4方法不能得到瞬时混沌响应.因此,本文采用光滑的非线性刚度函数. 同时,双线性刚度也很难描述内、外舵面的实际弹性碰撞.Vasconcellos等[19]利用三次多项式和双曲切线表示接触刚度,但却不能体现间隙特征.因此,本文根据Hertz接触理论[36-41],采用3/2次刚度来模拟碰撞时产生的作用力.同时为了体现间隙,只有在内、外舵面铰接处的相对转角超过间隙大小的一半时才会发生接触.该非线性刚度是一种光滑的非线性刚度,如图9中红色实线所示,表达式如下
图10
2.4 基础激励
将结构的瞬态动力学方程按照约束节点集(基础激励中对该点施加强迫振动)和自由节点集分块,可以表示为
其中,$p_{\rm f}$为约束节点集,${\pmb p}_{\rm s}$为自由节点集;${\pmb f}_{\rm N} ({\pmb p}_{\rm s})$为非线性力;$F_{\rm f}$为约束节点外力,在这里可以理解为振动台施加给该约束节点的作用力,${\pmb F}_{\rm s}$为自由节点受到的外力.
如果没有基础激励,即$p_{\rm f} = \dot {p}_{\rm f} = \ddot {p}_{\rm f} =0$,则自由振动的运动方程可以化简为
如需计算结构的模态,如频率和振型,只需令式(13)中的非线性力${\pmb f}_{\rm N}({\pmb p}_{\rm s})$为零并按照特征值问题处理即可.
基础激励时,$p_{\rm f} ,\dot {p}_{\rm f} ,\ddot {p}_{\rm f} \ne0$,式(12)的第2行可以写为
假设基础激励为定加速度幅值($A)$,激励圆频率为$\omega $,则约束节点的加速度、速度和位移分别为
3 结果与讨论
3.1 线性模型验证
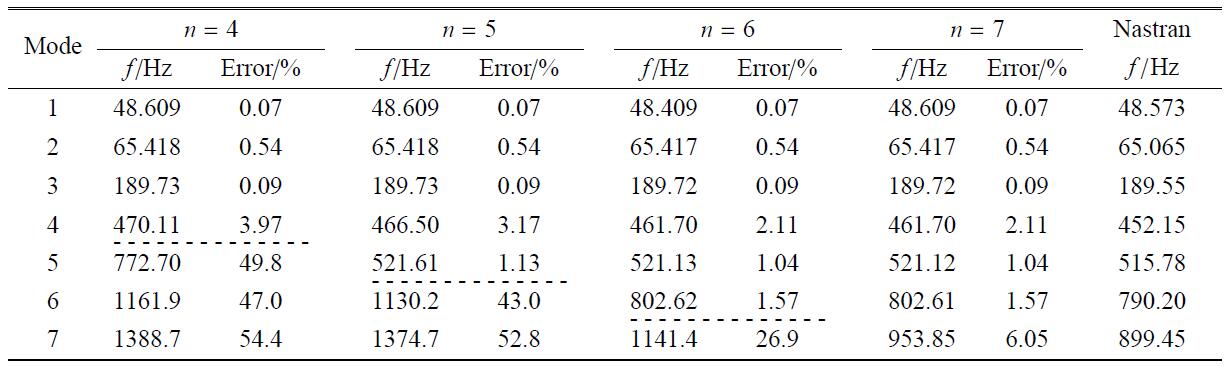
首先利用无间隙线性模型验证本文提出的适用于折叠机构的模型缩减方法的准确性. 这时,模型中的弹簧为线性弹簧.选取不同的模态截断数目$(n)$,将本文方法与Nastran的计算结果进行比较,这里假设三个线性扭转弹簧刚度相同,均为10$^{9}$,kg$\cdot$mm$^{2}\cdot $s$^{-2}\cdot $rad$^{-1}$.如表2所示,该方法有较好的计算精度,且保留的模态数目越多,该方法可以准确估计的频率阶次越高(虚线上方的频率),所以在后续的计算中,选取$n= 7$.
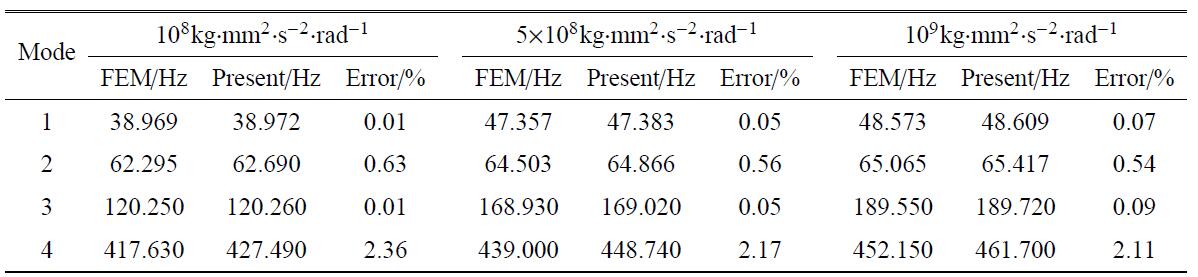
接着利用该方法计算不同铰接刚度下折叠舵面的前四阶固有频率,如表3所示. 结果表明, 3种不同的刚度下,该方法均可以得到准确的 频率结果,且铰接刚度越大,前四阶频率越大.
表3 不同弹簧刚度的前四阶频率
Table 3
 |
最后根据实验得到的模态参数,利用基于优化的模型修正方法辨识铰接处的3个弹簧刚度. 采用遗传算法获取全局范围内的最优解,优化变量为3个弹簧刚度,优化函数如式(18)
其中,$f_{ i}^{{\rm exp}} $表示实验得到的第$i$阶频率,$f_{ i}^{{\rm simu}}(k)$表示数值计算得到第$i$阶频率,它是3个弹簧刚度的函数. \ 优化得到的弹簧刚度为(保留3位有效数字)
表4 实验与仿真前四阶模态参数比较
Table 4
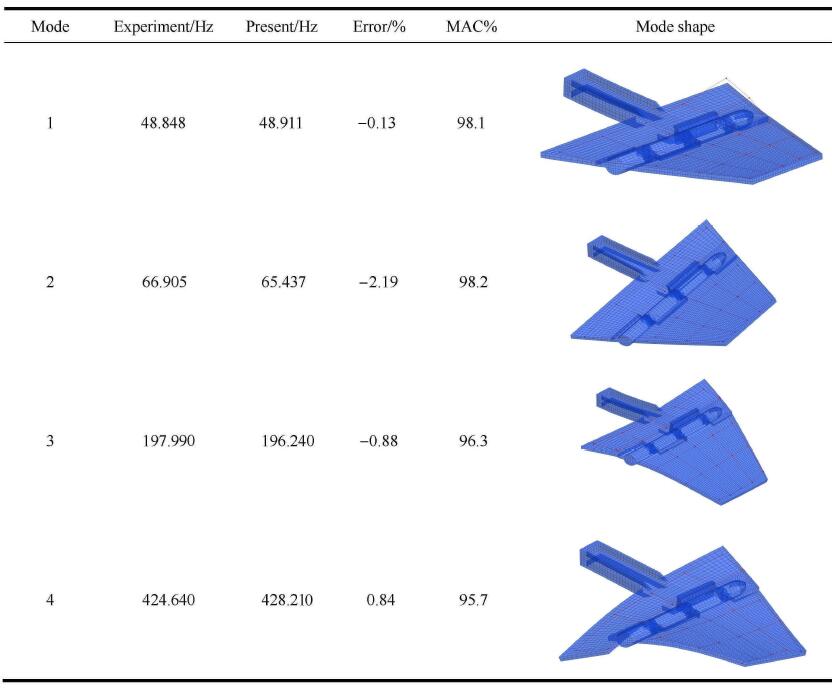 |
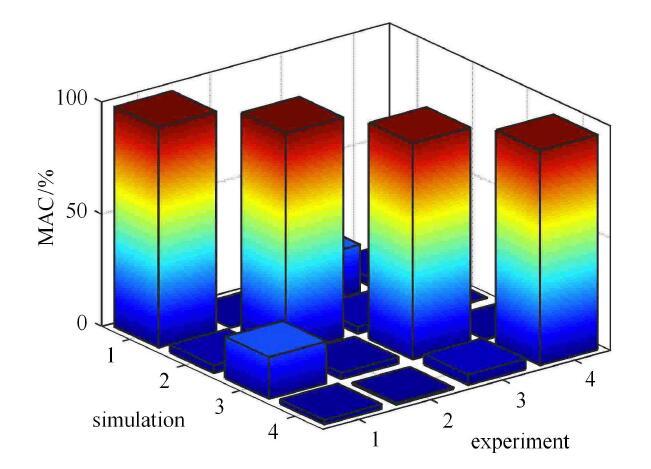
图11
图11
实验与仿真振型的MAC值
Fig. 11
MAC of mode shapes obtained by experiments and simulations
3.2 非线性模型基础激励响应
3.1节验证了线性模型的准确性,本节在内、外舵面的铰接处施加非线性扭转弹簧,研究基础激励下的振动响应.采用式(11)的间隙与接触模型. 需要注意的是,该模型中的间隙为扭转间隙,单位是弧度(rad).实验中的间隙是通过塞尺测量得到的,所以单位为长度(mm).在进行非线性参数辨识时,需要根据舵面的实际结构建立两者之间的几何关系.本文的重点在于非线性建模的正问题方面,所以没有列出该几何关系.
令式(11)中的3个扭转弹簧具有相同的非线性参数,如式(20)
文献[42]指出,在算法中引入数值耗散可以对有限单元离散产生的虚假高频起到滤波的作用.本节采用具有可控耗散的、低频精度更 高的Bathe两子步隐式复合算法$^{ [43 \hbox{-}44]}$进行非线性动力学计算.传递函数的计算方法为:首先得到结构在定频激励下的时域响应,一段时间后响应幅值保持稳定,通过读取记录时间内最后1秒的峰值来获取稳态响应幅值. 改变频率,从而得到结构的幅频响应. 将幅频响应除以激励量级得到结构的传递函数.与实验相同,响应和激励的量纲均为加速度量纲,所以传递函数的量纲为1.
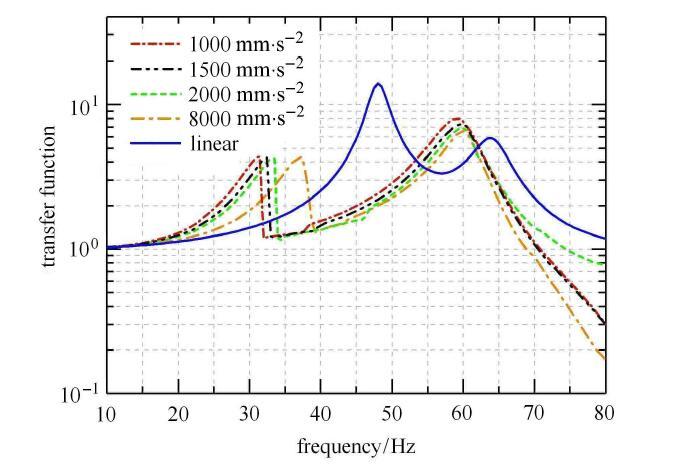
由图14可知,激励量级越大,第一阶频率越高,第二阶频率的变化较小.
图12
图12
正、反扫传递函数比较
Fig. 12
The comparison of transfer functions under forward sweep and backward sweep
图13
图13
不同间隙的传递函数比较
Fig. 13
The comparison of transfer functions under different freeplays
图14
图14
不同激励量级的传递函数比较
Fig. 14
The comparison of transfer functions under different excitation magnitudes
4 结论
本文从实验和仿真两方面对间隙可调折叠舵面的地面振动响应及建模方法进行了研究.建立了有间隙折叠舵面在基础激励下非线性 振动响应的求解流程.舵面的线性结构利用本文提出的适用于折叠机构的模型缩减方法进行了缩减,连接处的间隙和接触采用具有线性和3/2次刚度组合形式的非线性扭转弹簧来模拟.通过实验与仿真结果的对比和分析,可以得到以下结论:
(1)间隙的存在会使响应产生多谐波、正反向扫描差异、跳跃及频移等非线性现象,而且主要体现在弯曲模态对应的第一阶频率上.
(2)随着间隙的减小,第一阶频率和峰值均逐渐增大并趋近于线性结果,第二阶频率在间隙大于0.03,mm时受间隙的影响较小,峰值有所下降. 但在间隙进一步减小时,峰值回升并接近线性结果.
(3)随着激励量级的增大,第一阶频率和峰值均逐渐增大并趋近于线性结果,第二阶频率变化较小,当量级从0.5,g增大到0.75,g时峰值呈上升趋势.
(4)提出的模型缩减方法与固定界面模态综合法相比可以对连接处的非弹性连接自由度进行缩减,且计算结果有较高精度.
(5)根据Hertz接触理论提出的间隙处的非线性建模方法可以很好地描述实验中所观察到的频率变化特征.
本文按照正问题的研究思路对折叠舵面铰接处的数学模型进行了探讨,定性地揭示了实验中存在的非线性现象,但是该模型还不能在数值上与实验结果取得一致. 这还需要进行反问题研究,即还需要通过非线性模型修正或系统辨识来识别含参接触刚度模型的非线性参数,从而得到更加接近真实结构的数学模型. 这一部分工作将在后续开展.
参考文献
局部非线性结构的动力学计算与试验辨识研究. [博士论文]
Calculation and identification of structures with localized nonlinearities. [PhD Thesis]
Limit cycle behavior of an airfoil with a control surface
The comparison of an airfoil to experimental limit cycle oscillation
带集中非线性的机翼气动弹性问题研究进展
Advance in the study on wing aeroelasticity with concentrated nonlinearity
Aeroelastic airfoil with free play at angle of attack with gust excitation
含间隙超音速二元弹翼非线性颤振与主动控制
Nonlinear flutter and active control of the supersonic two-dimensional missile wings with a freeplay. Sci Sin-
含间隙折叠舵面的主共振响应分析
Primary resonance response analysis on folding rudder with gaps.
Limit cycle oscillation behavior of transonic control surface buzz considering free-play nonlinearity
Nonlinear aeroelastic analysis of an airfoil with control surface free-play using stochastic approach
两自由度舵$\!$-$\!$-$\!$轴系统振动三维效应修正模型
A modified model for the vibrations of a two-degree-of-freedom hydrofoil-rod system considering 3D effect
Continuum aeroelastic model for a folding-wing configuration
Equivalent plate modeling for complex wing configurations
Fictitious mass element in structural dynamics
Linear and nonlinear aeroelastic analysis of fighter-type wing with control surface
Nonlinear aeroelastic studies on a folding wing configuration with freeplay hinge nonlinearity
Nonlinear flutter wind tunnel test and numerical analysis of folding fins with freeplay nonlinearities
折叠翼的结构非线性颤振分析
Flutter analysis of a folding wing with structural nonlinearity
Identification of nonlinear multi-degree-of freedom structures based on Hilbert transformation
Representation and analysis of control surface freeplay nonlinearity
Experimental aeroelastic models design and wind tunnel testing for correlation with new theory
Aeroelastic response and limit cycle oscillations for wing-flap-tab section with freeplay in tab
Experimental and numerical investigation of an autonomous flap for load alleviation
Two-domain and three-domain limit cycles in a typical aeroelastic system with freeplay in pitch
Effects of structural nonlinearities on flutter characteristics of the CF-18 aircraft
Identification of nonlinear structures by the conditioned reverse path method
Nonlinear Aeroelastic Analysis of a Deployable Missile Control Fin
Dynamic model establishment of a deployable missile control fin with nonlinear hinge
Nonlinear aeroelastic analysis for a control fin with an actuator
Identification of weak non-linearities within complex aerospace structures
Coupling of substructures for dynamic analyses
A comparison of classical Runge-Kutta and Henon's methods for capturing chaos and chaotic transients in an aeroelastic system with freeplay nonlinearity
分段线性系统动力学的非光滑性分析
Nonsmooth analysis of dynamics of a piecewise linear system,
Accurate numerical integration of state-space models for aeroelastic systems with free play
Analysis of piecewise linear aeroelastic systems using numerical continuation.
Non-linear aeroelastic analysis using the point transformation method, part 1: Freeplay model
机械结合面切向接触阻尼计算模型
A calculation model for tangential contact damping of machine joint interfaces
连接结构接触界面非线性力学建模研究
Nonlinear mechanics modelling for joint interface of assembled structure
考虑等效曲率的超二次曲面单元非线性接触模型
Non-linear contact model for super-quadric element considering the equivalent radius of curvature
Dynamic responses of aerothermoelastic functionally graded CNT reinforced composite panels in supersonic airflow subjected to low-velocity impact
接触非线性对声黑洞梁减振效果的影响
Effect of contact nonlinearity on acoustic black hole beam for vibration damping
Dynamic response analysis of the vertical elastic impact of the spherical rock on the metal plate
结构动力响应数值算法耗散和超调特性设计
Two time integral algorithms with numerical dissipation and without overshoot for structural dynamic
Insight into an implicit time integration scheme for structural dynamics
Further insights into an implicit time integration scheme for structural dynamics