引言
随着航天技术的飞速发展,以大跨度、低刚度、轻质、高速的柔性机械臂、卫星天线、太阳能帆板等为代表的柔性构件越来越多地出现在空间飞行器中.这类柔性构件在工作过程中往往会由构件本身的大位移运动引起自身的弹性变形,大位移运动和自身的弹性变形存在着非线性强耦合效应,而传统的多刚体系统模型已无法正确描述该类系统的动力学性态[1-2]. 在此背景下各国学者从不同的参考坐标系出发,建立了目前运用较广泛的有浮动坐标系 法[3-15]和绝对节点坐标法[16-38].浮动坐标系法起源于多刚体系统动力学,该方法将柔性体的运动分解为随浮动坐标系的大位移运动和相对于浮动坐标系的弹性变形运动,该建模方法有利于变形描述的线性化,通常对于柔性体的小变形问题具有较高的计算精度和效率,但其在动力学方程建立中必须经历复杂的坐标转换,同时在处理柔性体大变形或复杂变形问题时, 会显得力不从心;绝对节点坐标法基于连续介质力学理论和非线性有限元法[16-17],其将柔性体的大位移及其弹性变形都用相对于绝对坐标系的单元节点坐标表示,直接建立柔性体的应变--位移关系[18],该方法具有能有效避免坐标转换的繁琐过程,并具有程式化好、编程方便等优点, 不过其也具有计算效率较低的缺点,因此合理优化刚度矩阵是绝对节点坐标法在多体系统动力学研究中的重点以及难点之一.
Berzeri等[19]采用绝对节点坐标法对二维欧拉伯努利梁进行研究,并建立了简单精确的四种弹性力求解模型,其模型考虑了弯曲变形和轴向变形,以及弯曲变形和轴向变形的相互耦合作用. Omar等[20]采用有限元法和连续介质力学理论对二维铁木辛柯梁进行研究,并通过非线性应变位移关系来求解弹性力,该文献中对于形函数的定义和刚度矩阵的求解存在一些错误.Dufva等[21]采用绝对节点坐标法对二维铁木辛柯梁进行研究,并将仿真结果与Ansys软件仿真结果进行对比.随后Shabana和 Yakoub[22-23]对三维梁模型的建模理论、仿真应用进行了研究,通过非线性的格林--拉格朗日应变张量和连续介质力学理论对三维梁弹性力进行求解.田强等[24-25]利用绝对节点坐标法建立了含间隙铰关节、曲梁和圆柱壳单元的动力学模型,对绝对节点坐标法的单元模型进行了补充和拓展.随后文献[26,27]将绝对节点坐标法应用到含芯拧绞绳非线性弯曲动力学特性分析和车辆钢板弹簧模型动力学建模中.郑彤等[28]对三维大变形柔性梁系统的动力学建模与仿真进行研究,将仿真结果和ADAMS软件计算的结果进行对比,指出ADAMS在计算大变形物体动力学时具有局限性.赵春璋等[29]对复杂变截面柔性梁结构进行研究,提出在不影响梁刚度的情况可通过改变截面参数有效降低梁的质量.文献[30]将传热与连续介质力学相结合,提出了对位移和温度场的统一描述,构建了一个热集成的绝对节点坐标公式全参数化梁单元,同时航天器中刚柔热耦合效应被重点关注[31-32]. 为了优化刚度矩阵, 提升绝对节点坐标法计算效率,Garcia-Vallejo等[33]对三维梁模型弹性力的求解进行简化,提出不变矩阵法.章孝顺等[34]运用拉格朗日恒等式给出了柔性梁横向弯曲变形能新的表达式,通过新的变形能表达式得到新的弹性力模型,进而提高计算效率.陈渊钊等[35]为了消除或减弱传统ANCF中缩减单元的"失真现象",提出了柔性梁基于无网格径向基点插值的ANCF法[36], 其将有效提高计算精度和计算效率.文献[37]在ANCF低阶单元上开发了一种数学分析方法,进而提高计算效率.文献[38]提出了一种基于正交分解和Galerkin投影的模型阶数约简的系统方法来提高计算效率,并通过刚性和柔性多体系统仿真实例验证方法的有效性.由上述研究可知,计算效率仍然是绝对节点坐标法目前急需解决的难点之一.
本文采用有限元法对三维梁单元位移场进行离散,通过求解梁单元常数质量阵、广义刚度阵、广义力阵,进而建立单元的动力学方程, 通过转换矩阵得到三维梁的动力学方程.接着重点给出求解弹性力的两种方法:连续介质力学方法与弹性线方法,并从理论上对这两种方法进行分析比较. 最后,基于上述理论对绝对节点坐标法下柔性单摆的动力学问题进行研究,并将连续介质力学方法和弹性线方法用于履带式车辆动力学模型中,进而通过仿真实例说明弹性线方法在计算效率上的突出提升.
1 三维梁单元位移场离散
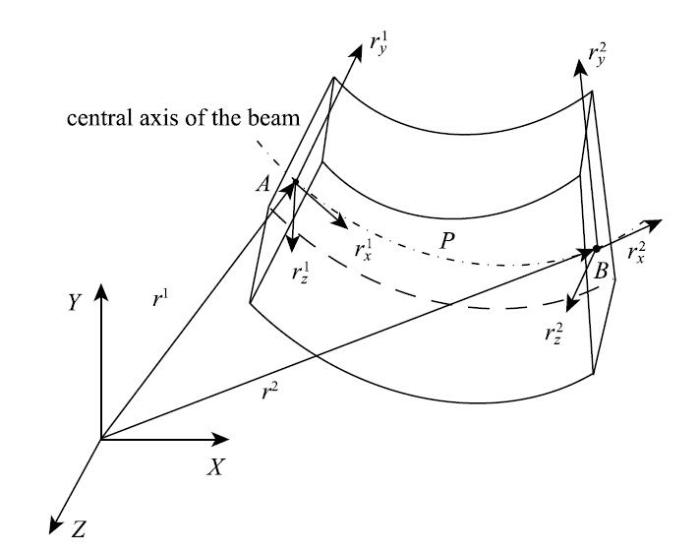
如图1所示三维梁单元, 其上任意一点$P$的全局位移矢量$r$可表示为
图1
其中, $S$是单元形函数, $x$为沿着轴线的单元局部坐标,取值范围为$\left[ {0, l} \right]$. $l$为单元的初始长度, $e$为单元节点坐标的广义坐标矢量
式中, 上标$k = 1,2$代表单元的节点编号,单元节点广义坐标矢量在节点$k$包括节点的三个全局位移以及九个全局斜率,具体形式如下
通过单元函数表达式和单元始端、末端的函数值进行推导,可以得到单元形函数$S$的表达式为
其中, $I_3 $为3$\times $3单位矩阵, 形函数$s_i = s_i (\xi ,\eta,\zeta ),~ i = 1,2, \cdots, 8$形式为
其中, $\xi = x / l$, $\eta = y / l$, $\zeta = z / l$,$x$的取值范围为$\left[ {0,l} \right]$, $y$的取值范围为$\left[ {-b / 2, b / 2} \right]$, $z$的取值范围为$\left[ {-h / 2, h / 2}\right]$, $l$代表单元的长度, $b$代表单元的宽度,$h$代表单元的厚度.
2 绝对节点坐标下的动力学方程
采用有限元法对柔性梁位移场进行描述,柔性梁单元上任意点的位移可由广义坐标矢量$e$与单元形函数$S$表示,这样就使连续无限自由度的动力学模型转化为有限自由度的动力学模型,进而模型的动力学方程就可数值求解.绝对节点坐标下三维梁单元的动力学方程形式为
式中, $M$为单元常数质量阵; 弹性力${ Q}_k = K( e) e$, 其中$K( e)$为广义刚度阵, ${ Q}_e $为广义力阵.
2.1 常数质量阵
梁单元上任意点的全局位移矢量已经通过方程(1)得到,将方程对时间求导数, 可得到全局位移速度矢量
通过单元的全局节点速度矢量, 可得到单元的动能为
其中, $V$为梁单元的体积, $\rho $为梁的材料密度, 则$M$即为单元的广义质量阵, 上述方程的广义质量阵为常对称矩阵,通过方程(4)给出的形函数, 可以得到广义质量阵.
2.2 广义刚度阵
由非线性Green-Lagrange应力--位移关系计算任意质点的变形梯度为
其中, $\overline { X}$为单元坐标系, $\overline { X} =[x,y,z]$定义单元坐标系下的某个点的位置矢量.当梁的初始位置是任意的$J_0 $必须考虑, 而当梁初始位置是水平时,$J_0 $为单位矩阵.
通过变形梯度方程可得到应变张量为
其中, $r_\alpha = \dfrac{\partial r}{\partial \alpha },~\alpha = x,y,z$. 结合位移公式$r = S(x,y,z) e$, 则
则应变张量方程(11)的各个分量表达式
通过应变表示式以及应力应变关系式可得到单元应变能为
其中, $V$为单元的体积, $\lambda $和$G$为材料的模量常数,则应变能产生的弹性广义力矢量为
其中
则方程(15)转化为
对上述方程进一步简化得
其中
文献[33]提出不变矩阵法, 通过该方法将广义刚度矩阵$K( e)$分解为一常数刚度矩阵和一个非线性刚度矩阵,其将大大提高仿真的计算效率.
2.3 广义外力阵
采用虚功原理对广义外力矢量进行求解, 作用在单元上任意一点的外力$F$所做的虚功为
其中, $r$为外力作用点的位置矢量, $Q_e^{\rm T} = F^{\rm T} S$代表等效到该单元节点的等效广义力.考虑重力作用下的广义外力, 假设单元的截面面积在变形过程中恒为常数,梁单元材料为均匀材质, 即密度为常量.单元质心的全局位移矢量可参考文献[19]得到
其中, $I$为3$\times $3单位矩阵, $y$方向为重力加速度作用方向,则重力的虚功为
则可知单元上的重力为
考虑外力矩作用在梁截面上, 该外力矩绕$Z$轴旋转(如图1),则该外力矩的虚功为
其中, $\gamma $为单元梁截面绕$Z$轴的旋转角,则通过坐标旋转矩阵可得到
则可知$\sin \gamma , \cos \gamma $为
通过方程(25)和(26), 可以得到外力矩产生的虚拟旋转角$\gamma $为
若外力矩作用在图1中单元的节点$A$处, 则外力矩$M_z $产生的广义力矢量为
同理, 可以得到梁截面受到绕$Y$轴旋转的外力矩$M_y $产生的作用在图1中单元节点$A$处的广义力 矢量
3 弹性力求解的连续介质力学方法与弹性线方法
基于绝对节点坐标法的质量矩阵是常数, 这也增加了求解弹性力的繁琐性.本节详细介绍求解弹性力的两种方法:一般连续介质力学方法和弹性线方法,并从理论上分析比较两种方法的优缺点.
3.1 连续介质力学方法
非线性格林--拉格朗日应变张量如方程(11)所示, 使用虚功的原理,广义的弹性力的矢量$Q_k $被定义为
其中, $E$为弹性系数矩阵, $e$为单元节点坐标矢量, $Q_k $的具体求解方式详见2.2节.
3.2 弹性线方法
在弹性线方法中格林--拉格朗日应变张量被定义在中心线上,而采用曲率公式来定义弯曲应变, 转角公式来定义扭转应变.三维梁单元中心线上的位移梯度矢量表达式为
其中, 矢量$r_{0x} $位于中心线的切线方向, 而$r_y $和$r_z $定义在中心线任意点$x$处的横截面上.由于位移场被定义为空间坐标$y$和$z$的线性关系, 因此$r_y $和$r_z $不需要下标"0".三维梁单元的中心线的应变张量可以通过拉格朗日应变张量和曲率表示
其中, ${(}')$表示对空间坐标$x$求导, $\varepsilon _{011} ,\varepsilon _{22} ,\varepsilon _{33} $表示正应变, $\gamma _{012},\gamma _{013} ,\gamma _{23} $表示剪切应变, $\theta $表示扭曲转角,$\bar {\kappa }_{0y} ,\bar {\kappa }_{0z} $表示弯曲曲率.梁中心线的格林--拉格朗日应变张量可以代入方程(30),但是该方法求解的弹性力不包含梁单元的弯曲和扭转, 弯曲曲率$\bar{\kappa }_{0y} ,\bar {\kappa }_{0z} $用于求解弯曲应变能,而扭转转角$\theta $用于表达扭转应变能,弯曲应变能和扭转变形能的表达式为
则广义的弹性力的矢量$Q_k $为
其中, $\varepsilon _{0} $为弹性线方法中格林--拉格朗日应变张量,具体见式(32).
3.3 两种方法的比较
为了比较一般连续介质力学方法和弹性线的应变张量, 全局位移矢量$r$可写为
其中, $r_{0} $为中心线上任意一点的位移矢量, $\Delta r = y r_y + z r_z $表示梁中心线横截面上任意一点的位移矢量.则全局位移矢量对于空间坐标$x$的导数$r_x $为
采用如前所示的位移场和格林--拉格朗日应变张量,基于连续介质力学方法得到梁的应变分量为
应变张量可转化为
比较式(37)和式(38),可知采用一般连续介质力学方法和弹性线方法在描述变形上的差异有:
(1) 在一般连续介质力学方法中, 弯曲应变是通过$y r_{0x}^{\rm T} r_{yx} + z r_{0x}^{\rm T} r_{zx} $来定义的;而弹性线方法的弯曲应变是通过弯曲曲率$\bar {\kappa }_{0y} $和$\bar{\kappa }_{0z} $来定义的. 这两种定义方式是不一样的,并可能带来不同的刚度特性.
(2) 在弹性线理论方法中, 忽\vspace{1mm}略了对弯曲变形运动影响相对很小的高阶正应变分量$\dfrac{1}{2}(y r_{yx} + z r_{zx} )^{\rm T}\cdot$$(y r_{yx} + z r_{zx} )$.
(3) 在一般连续介质力学理论方法中, 扭转应变通过$y r_{yx}^{\rm T} r_y + z r_{zx}^{\rm T} r_y $和$y r_{yx}^{\rm T} r_z+ z r_{zx}^{\rm T} r_z $来定义表达;而弹性线方法通过转角表达式$\theta $来表达定义.这两种定义方式是不一样的, 并可能带来不同的刚度特性.
4 动力学仿真
4.1 柔性单摆动力学仿真
图2
图3
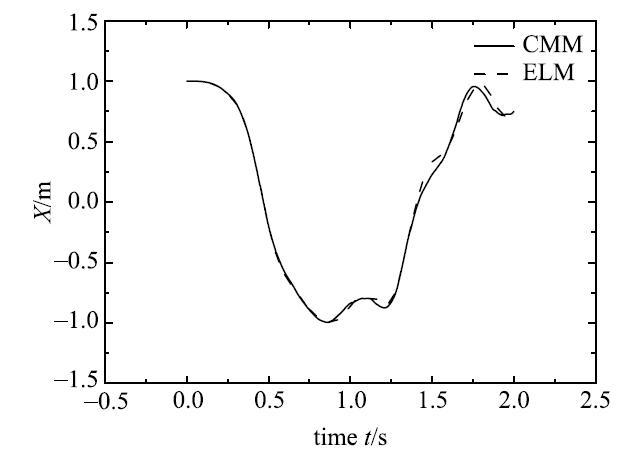
图3
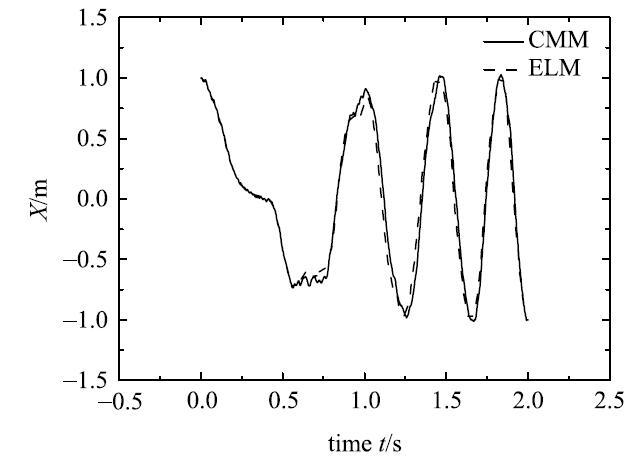
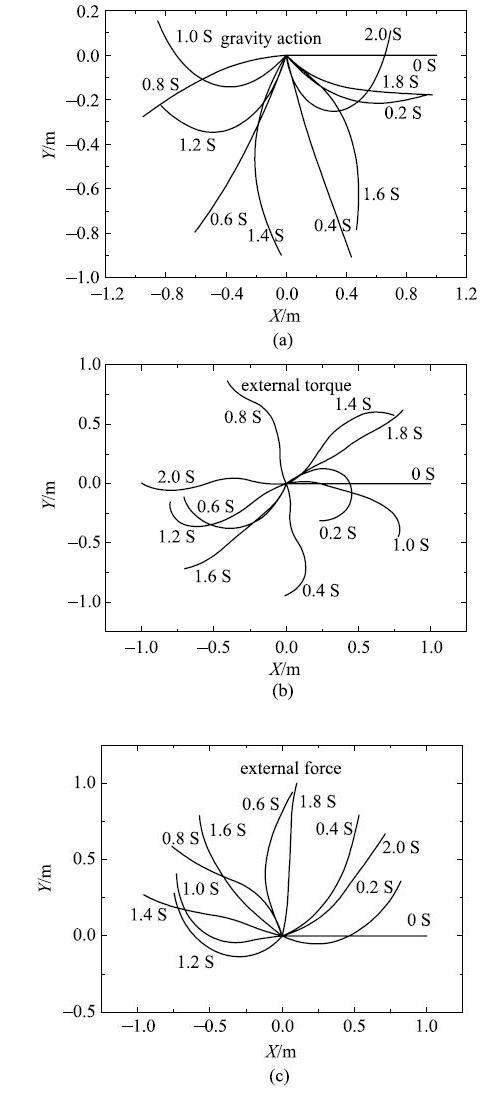
自由落体柔性单摆末端$B$点$X$方向的位移
Fig. 3
The displacement of the $X$direction at the end of the free-fall flexible pendulum
图4
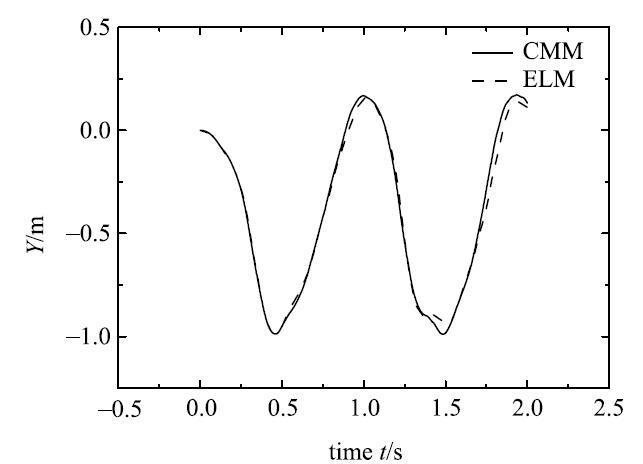
图4
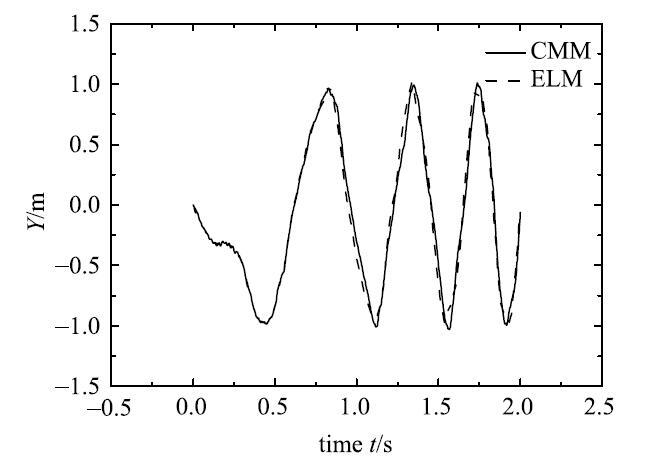
自由落体柔性单摆末端$B$点$Y$方向的位移
Fig. 4
The displacement of the $Y$direction at the end of the free-fall flexible pendulum
图5
图5
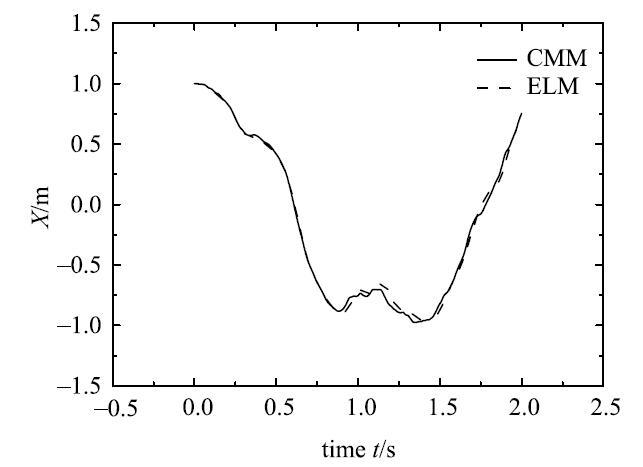
受外力矩作用柔性单摆末端$B$点$X$方向位移
Fig. 5
The displacement of the $X$direction at the end of the flexible pendulum which subject to external torque
图6
图6
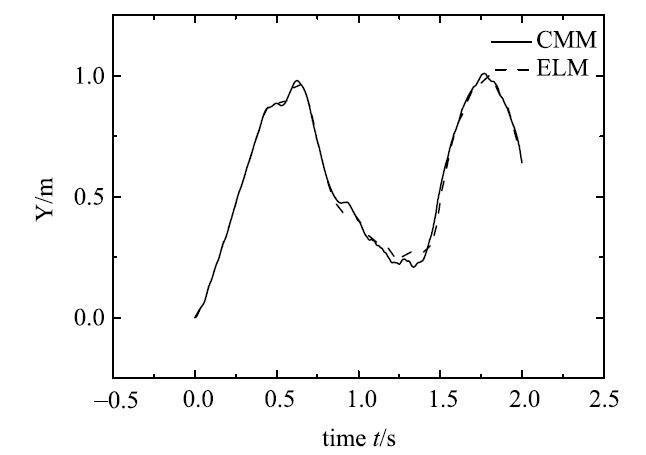
受外力矩作用柔性单摆末端$B$点$Y$方向位移
Fig. 6
The displacement of the $Y$direction at the end of the flexible pendulum which subject to external torque
图7
图7
受外力作用柔性单摆末端$B$点$X$方向位移
Fig. 7
The displacement of the $X$direction at the end of the flexible pendulum which subject to external force
图8
图8
受外力作用柔性单摆末端$B$点$Y$方向位移
Fig. 8
The displacement of the $X$direction at the end of the flexible pendulum which subject to external force
图9
4.2 履带式车辆动力学仿真
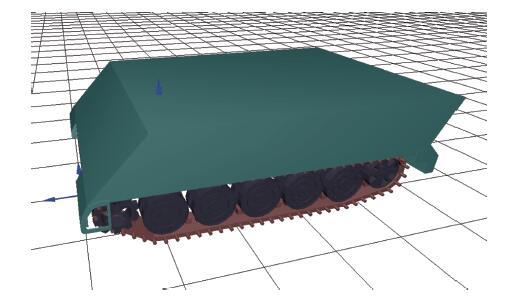
考虑如图10所示的履带式车辆,本仿真采用三维梁单元对该模型两条链条进行建模, 而其他结构设为刚体,链条的材料为不锈钢S15600, 其材料参数为:密度$\rho =15.6~\mbox{Mg/m}^{3}$, 弹性模量$E =200~\mbox{GPa}$, 泊松比$\mu =0.3$, 重力加速度$g = 9.81~\mbox{m/s}^{2}$.每条链条被分成64个三维梁单元, 由于链条首尾相连,即第一个节点亦为最后一个节点, 则每条链条的单元节点为64个,每个单元的长度$l = 0.151~624~\mbox{m}$, 单元宽度$b =0.381~\mbox{m}$, 厚度$h = 0.02~\mbox{m}$.全局坐标系为:履带式车辆的前进方向为$Y$轴, 沿地面向上为$Z$轴,则$X$轴沿图10向内. 地面为刚体, 链条与地面的接触采用Hertz接触.采用连续介质力学方法和弹性线方法对履带式车辆进行仿真,定义链轮的旋转角速度(单位: rad/s)为如下函数形式
图10
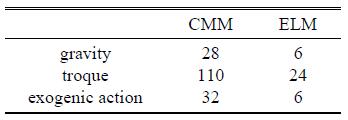
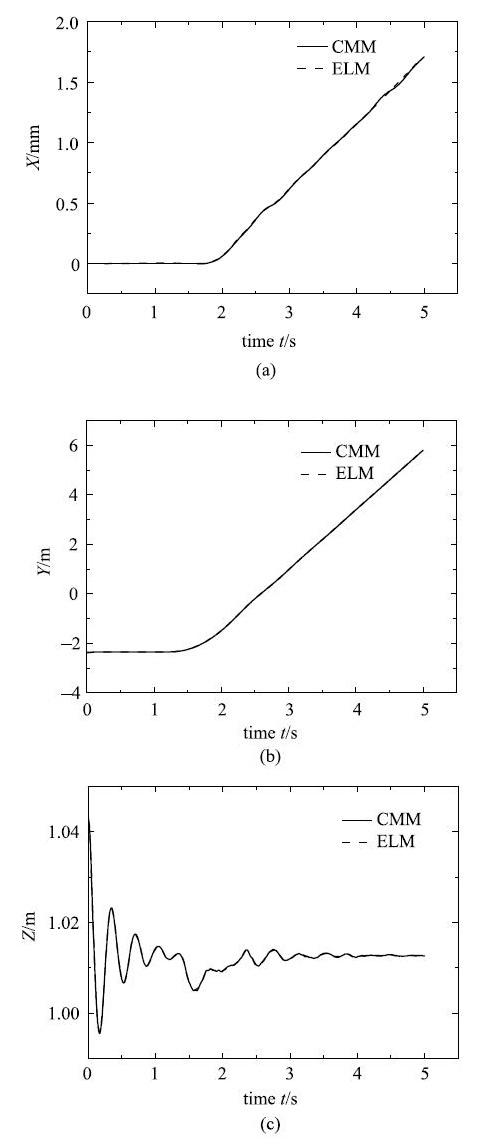
图11表示履带式车辆运动$X,Y$和$Z$方向的位移,Z方向有位移波动是因为履带式车辆在Z方向受到重力作用.图12表示履带式车辆前进方向的运动速度. 从图11和图12可知,弹性图11表示履带式车辆运动$X,Y$和$Z$方向的位移,Z方向有位移波动是因为履带式车辆在Z方向受到重力作用.图12表示履带式车辆前进方向的运动速度.从图11和图12可知, 弹性线方法的仿真结果与连续介质力学方法的基本一致,说明采用弹性线方法来求解弹性力的方法是可行且正确的.同时从计算时间上考虑,采用连续介质力学方法求解弹性力的履带式车辆的计算时间是采用弹性线方法的9倍.仿真结果表明:采用弹性线方法求解弹性力的履带式车辆仿真在保证计算精度的情况下,计算效率将远高于连续介质力学方法的.因此弹性线方法值得在绝对节点坐标法中重点研究,其将有效弥补绝对节点坐标法计算效率较低的缺点.
图11
图12
5 结论
(1)弹性线方法将弯曲变形和扭转应变通过曲率和转角来表示,将弹性力求解从三重体积分简化到沿梁长方向的一重积分,其大大节省仿真计算时间.
(2)通过柔性单摆的动力学仿真表明:弹性线的仿真结果与一般连续介质力学方法的一致,且仿真计算效率要优于一般连续介质力学方法的.
(3)采用弹性线方法能有效处理实际工程履带式车辆的动力学问题,并在保证精度的要求下提高计算效率.
参考文献
Dynamics, vibration and control of rotating composite beams and blades: A critical review
大型柔性航天器动力学与振动控制研究进展
Advances in dynamics and vibration control of large-scale flexible spacecraft
Geometric stiffening effect on rigid-flexible coupling dynamics of an elastic beam
考虑剪切效应的旋转 FGM 楔形梁刚柔耦合动力学建模与仿真
Dynamic modeling and simulation of rotating FGM tapered beams with shear effect
Dynamic analysis of a flexible hub-beam system with tip mass
平面柔性梁的刚--柔耦合动力学特性分析与仿真
Analysis and imitation of dynamic properties for rigid-flexible coupling systems of a planar flexible beam
大变形旋转柔性梁的一种高次刚柔耦合动力学模型
A high-order rigid-flexible coupling model of a rotating flexible beam under large deformation
旋转柔性悬臂梁动力学的Bezier 插值离散方法研究
Bezier interpolation method for the dynamics of rotating flexible cantilever beam
径向基点插值法在旋转柔性梁动力学中的应用
A meshfree method based on radial point interpolation method for the dynamic analysis of rotating flexible beams
基于变形场不同离散方法的柔性机器人动力学建模与仿真
Dynamic modeling and simulation of flexible robots based on different discretization methods
考虑曲率纵向变形效应的大变形柔性梁刚柔耦合动力学建模与仿真
Rigid-flexible coupling dynamic modeling and simulation with the longitudinal deformation induced curvature effect for a rotating flexible beam under large deformation
Coupling vibration analysis of rotating three-dimensional cantilever beam
Free vibration analysis of bidirectional-functionally graded and doubletapered rotating micro-beam in thermal environment using modified couple stress theory
Free vibration analysis of rotating functionally graded double-tapered beam including porosities
On size-dependent dynamic behavior of rotating functionally graded Kirchhoff microplates
On the dynamics in space of rods undergoing large motions the planar case: Part I-II. ASME Transactions,
Development of simple models for the elastic forces in the absolute nodal coordinate formulation
A two-dimensional shear deformable beam for large rotation and deformation problems
A two-dimensional shear deformation beam element based on the absolute nodal coordinate formulation
Three dimensional absolute nodal coordinate formulation for beam elements: Theory
Three dimensional absolute nodal coordinate formulation for beam elements: Implementation and applications
Simulation of planar flexible multibody systems with clearance and lubricated revolute joints
New spatial curved beam and cylindrical shell elements of gradient-deficient absolute nodal coordinate formulation
含芯拧绞绳非线性弯曲动力学特性分析与研究
Analysis of the cored stranded wire rope on the nonlinear bending dynamic characteristics
完备化ANCF 薄板单元及在钢板弹簧动力学建模中的应用
The completed form of elastic model for ANCF thin plate element and its application on dynamic modeling of the leaf spring
三维大变形梁系统的动力学建模与仿真
Dynamic modeling and simulation for three dimensional flexible beam systems with large deformations
基于绝对节点坐标法的变截面梁动力学建模与运动变形分析
Dynamic modeling and kinematic behavior of variable cross-section beam based on the absolute nodal coordinate formulation
A novel method of thermo-mechanical coupled analysis based on the unified description
Rigid-flexible-thermal coupling dynamic formulation for satellite and plate multibody system
Thermal shock induced dynamics of a spacecraft with a flexible deploying boom
Efficient evaluation of the elastic forces and the Jacobian in the absolute nodal coordinate formulation
基于绝对节点坐标法的大变形柔性梁几种动力学模型研究
Several dynamic models of a large deformation flexible beam based on the absolute nodal coordinate formulation
平面细长梁基于无网格径向基点插值的绝对节点坐标法
An absolute nodal coordinate formation based on radial point interpolation method for planar slender beams
Dynamic analysis of rotating curved beams by using absolute nodal coordinate formulation based on radial point interpolation method
Analytically derived matrix end-form elastic-forces equations for a low-order cable element using the absolute nodal coordinate formulation
Model order reduction for dynamic simulation of a flexible multibody system via absolute nodal coordinate formulation