引言
目前,国内外有一些学者致力于研究液体非线性晃动问题并且取得了一些研究成果.Moiseev [14]研究了一般形状贮箱中液体的非线性晃动,但是过程繁琐很难应用于实际工程. Hutton[15]利用泰勒级数对静液面附近液体自由液面的运动学和动力学边界条件进行展开,研究了受水平横向外激励作用的充液圆柱贮箱自由液面的非平面运动现象.Faltisen等[16-17]利用多维模态方法研究了矩形贮箱中液体在不同充液比、激励频率等工况下的非线性动力学特性,并结合实验证明了该方法的正确性. 在研究刚--液耦合问题时,Peterson等[18-19]将圆柱贮箱航天器刚--液耦合系统简化为一个弹簧--阻尼--质量系统模型,结合解析方法和实验方法研究了液体的非线性晃动动力学特性,并且论证了研究刚--液耦合系统时考虑液体非线性的重要性.尹立中等[20]研究了俯仰激励下的圆柱贮箱固--液耦合系统,观察到了零点漂移、分叉等非线性动力学现象. 岳宝增等[21]研究了微重力环境下刚--液耦合系统液体晃动的混沌现象,研究发现面内模态和外模态具有静止、周期运动、准周期运动和混沌运动等稳态动力学行为;而且改变外激励参数, 会对面内、外模态的稳态动力学行为产生影响.然而目前应用理论方法深入研究刚--液耦合系统非线性动力学特性的成果仍然较少,这对于深入分析耦合系统中液体晃动的非线性动力学现象是不利的.因而无论从工程需要还是科学研究的角度,应用理论方法研究刚--液耦合系统非线性动力学问题都具有十分重要的意义.
本文利用多维模态方法对由航天器主刚体和部分充液的圆柱贮箱构成的刚--液耦合系统建立动力学方程组,应用多尺度方法对耦合系统液体一阶主共振的非线性动力学特性进行解析分析,并结合数值方法深入分析和讨论液体稳态解的幅频响应特性,为深入研究充液航天器非线性动力学提供了理论参考.
1 航天器刚--液耦合动力学方程
1.1 耦合系统物理模型描述
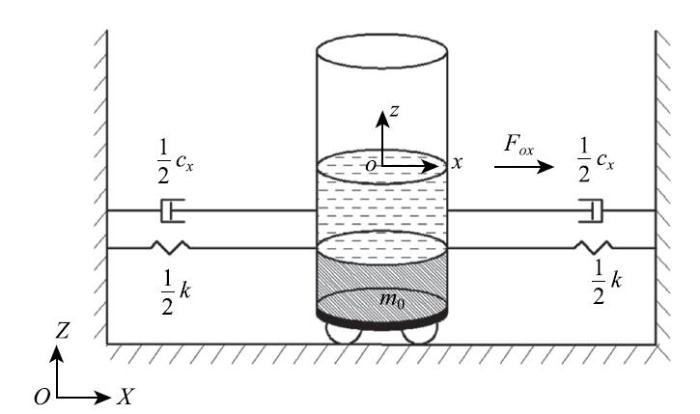
将携带圆柱贮箱的充液航天器系统简化为图1所示的刚--液耦合动力学模型. 假设贮箱为刚体贮箱,贮箱底部为固定质量块.充液圆柱贮箱、弹簧和阻尼器组成用于描述耦合系统平动的晃动模型.$\eta (x,y,t)$为自由液面波高函数, 假设未扰动自由液面为平面.坐标系$OXYZ$为惯性参考坐标系; 坐标系$oxyz$为贮箱固连坐标系,坐标系平面$oxy$与液体未扰动自由液面重合,坐标系原点$o$位于静液面中心.
图1
1.2 液体晃动模态方程
其中, $\varPhi (x,y,z,t)$表示绝对速度势函数, ${{ v}}_{ox}$为流体质点沿$x$轴方向的绝对速度, $Q(t)$表示液体运动区域,$S(t)$表示与液体接触的贮箱壁面, $\varSigma(t)$表示液体自由液面区域. ${{ n}}$为$Q(t)$区域的外法线方向,$U(x,y,z,t)$为重力势能函数.
将绝对速度势函数分解为牵连速度势函数和相对速度势函数$\varphi $.${{ r}}$为贮箱内流体质点相对于$o$点的位置向量
假设自由液面波高函数和相对速度势函数可按广义Fourier级数展开为如下形式
其中, $\eta _i (x,y)$, $\varphi _n (x,y,z)$分别称为面模态, 体模态,$\beta _i (t)$和$R_n (t)$为模态系数.
各系数表达式如下
$$A_n = \rho \int_{Q(t)} {\varphi _n } {\rm d}Q,\quad A_{nk} = \rho \int_{Q(t)} {\nabla \varphi _n \cdot \nabla \varphi _k } {\rm d}Q \\ \varphi _n = \eta _n \frac{\cosh \kappa _n (z + h)}{\cosh \kappa _n h},\quad \lambda _{i1} = \rho \int_\Sigma {r\eta _i \cos \theta } {\rm d}\Sigma$$
其中, $\rho,\beta_i,a$和$h$分别表示液体密度、第$i$阶模态系数、贮箱半径和充液深度. 受横向激励作用的刚--液耦合系统,液体运动方向与激励方向一致, 保留液体面内模态即可,然而若只考虑主模态则无法准确描述耦合系统动力学行为[18-19].因而选取面内主模态$\eta _1 = {\rm J}_1 (\kappa _{11} r)\cos \theta$, 轴对称模态$\eta _3 = {\rm J}_0 (\kappa _{01}r)$和面内次模态$\eta _4 = {\rm J}_2 (\kappa _{21} r)\cos 2\theta $来描述液体非线性晃动.其中$\kappa _{01} ,\kappa _{11} $和$\kappa _{21}$分别为贝塞尔函数${\rm J}'_1 (\kappa _{11} a) = 0,{\rm J}'_0(\kappa _{01} a) = 0$和${\rm J}'_2 (\kappa _{21} a) =0$的根:$\kappa _{11}=1.8412/a,\kappa _{01}=3.8317/a,\kappa_{21}=3.0542/a$. 将三阶模态代入至方程(8)和(9),并且假设主模态$\beta _1 $高于次模态$\beta _3 $和$\beta _4$一个量级,展开后得到描述圆柱贮箱内液体晃动的模态系数相互耦合的有限维模态方程组.
1.3 航天器动力学方程
忽略表面张力影响,液体晃动产生的横向晃动力由液体内动压强产生[26].通过推导可以得到
根据牛顿定理即可建立图1所示刚--液耦合系统的动力学方程组.其中$F_x$表示航天器沿$x$轴方向受到的非保守力, $m_0$表示航天器刚体质量, $c_x $表示阻尼系数, $k$表示弹簧刚度系数
方程(8)$\sim $(12)构成了平动航天器刚--液耦合系统的非线性方程组.
2 耦合系统动力学的多尺度方法
$$T_0 = t, \quad T_1 = \varepsilon t, \quad T_2 = \varepsilon ^2t$$
设航天器刚体受到沿$ox$轴的外力$F_O = f\sin \varOmega t$.为了更加符合工程实际, 引入液体模态阻尼系数$\zeta _{\beta _1 } $.假设阻尼为线性小阻尼, 此时很小的激励幅值就能激发出强烈的共振,为了使激励项与阻尼项出现在幅频响应方程中需引入变换:$f \to\varepsilon ^3f$, $\zeta _{\beta _1 } \to \varepsilon ^2\zeta_{\beta _1 } $. 将模态系数和刚体位移$x$分别在3个时间尺度上展开,表示为
将表达式(13)代入方程(8)$\sim $(12), 合并$\varepsilon$阶同次幂项的系数, 得到微分方程组
利用固有频率的特征方程, 计算得到耦合系统的固有频率
其中
$$\varLambda = [k + (G_1 + m_0 )\sigma _1^2 ]^2 - 4(G_1 + m_0 + W_1D_1 K_0 )k\sigma _1^2$$
方程组(14)的解可表示为
研究表明当外激励频率更容易与耦合系统的低阶频率接近时要容易,引发共振响应[1]. 由于$v_1 < v_2 $,所以需要重点研究激励频率接近频率$v_1 $时的动力学特性.引入解谐参数$\sigma $表示激励频率$\varOmega$与系统一阶固有频率$v_1 $的接近程度, 激励频率可表示为
设
将式(13)、式(15)$\sim $\!式(21)代入方程(8)、(9)和(12).合并方程组中$\varepsilon ^2$同阶次幂系数, 可以得到$\beta _{31},\beta _{41} $关于$\beta _{10} $和$x_0 $的表达式. 合并$\varepsilon^3$阶同次幂项的系数, 为消除久期项得到方程
稳态运动的定常解振幅$\alpha _1 $和相角$\theta _1 $不再随时间变化,分离式(22)中的实部和虚部, 利用三角函数的性质消除相角$\theta _1 $,得到耦合系统一阶主共振时稳态解的幅频响应方程
系数$m_F $, $P_{x1} $, $\zeta $的表达式较为复杂, 略.
3 数值分析与讨论
3.1 给定水平外力时定充液比稳态解分析
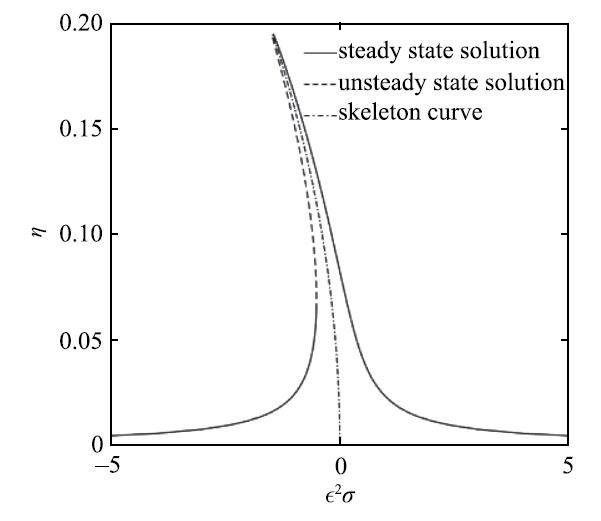
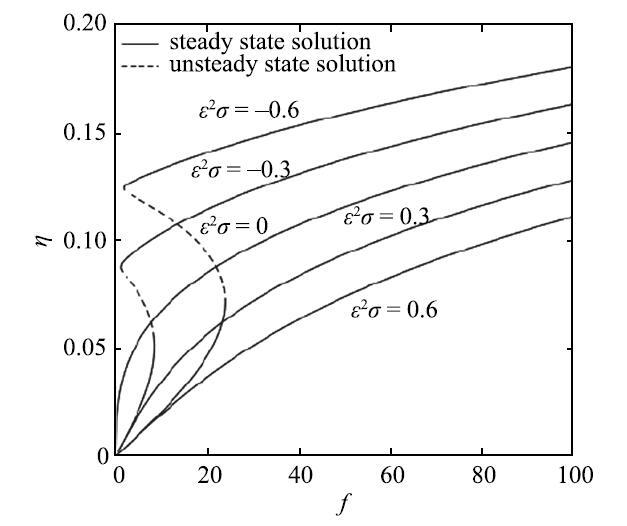
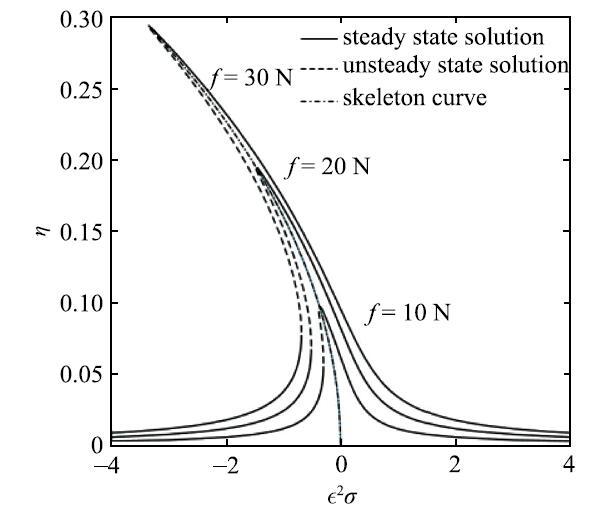
取系统参数$m_0 = 80$kg, $a = 0.15$m, $h = 0.1~\mbox{m}$, $g = 9.8~\mbox{m}/\mbox{s}^{ 2}$, $\rho =1000~\mbox{kg}/\mbox{m}^{ 3}$, $\zeta _{\beta _1 } = 0.08$, $c_x= 8~\mbox{kg}/\mbox{s}$, $\varepsilon = 0.1$, $f = 20~\mbox{N}$.$\bar {h} = h / a$表示系统充液比.图2和图3分别为液体一阶主共振时液体稳态解的幅频响应曲线和激励--幅值曲线.在激励频率远小于系统一阶固有频率时, 随激励频率增加, 幅值响应增大;当激励频率增加至某一值时幅值响应突然增大, 发生了跳跃现象. 此时,液体稳态解的幅频响应表现为软弹簧特性. 若反向扫频,发现当激励频率减小至某一值时幅值响应突然减小,而且正反扫频的跳跃点是不同的, 与Peterson[18]的结论是相吻合的. 结合定常解的稳定性分析, 当$\varOmega <v_1 $时, 激励--幅值响应存在多稳态解和跳跃现象; 当$\varOmega > v_1 $时,随激励幅值增大, 幅值响应单调增大.
图2
图2
$h = 0.1~\mbox{m}$时的幅频响应曲线
Fig. 2
Amplitude-frequency response as $h = 0.1~\mbox{m}$
图3
图3
$h = 0.1~\mbox{m}$时的激励--幅值曲线
Fig. 3
Excitation-amplitude response as $h = 0.1~\mbox{m}$
3.2 给定水平外力时变充液比稳态解分析
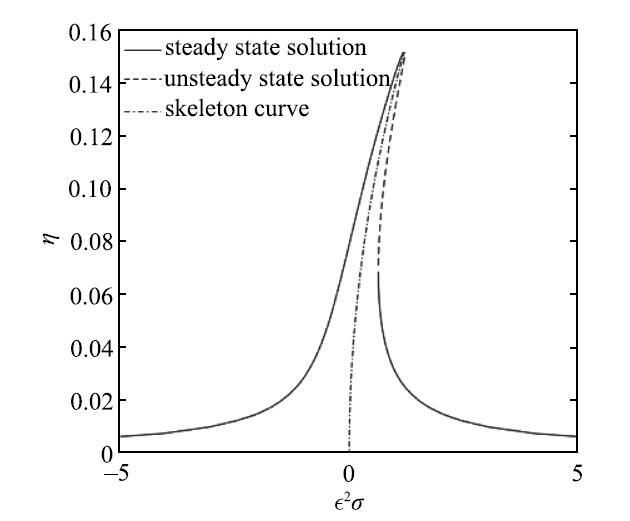
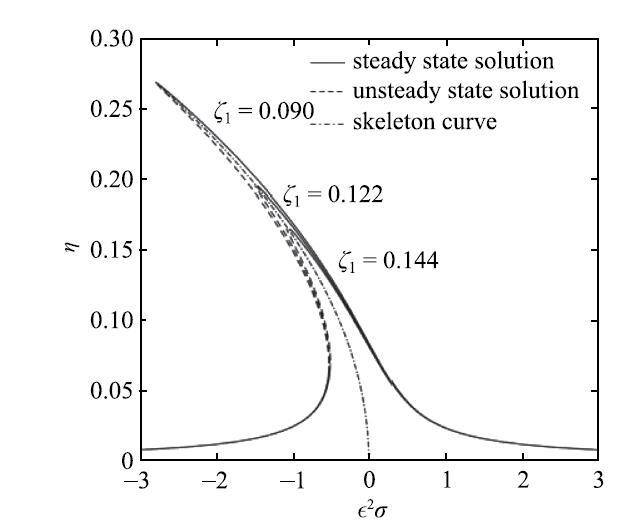
航天器机动时由于液体燃料的消耗充液比将发生变化,因而研究航天器不同充液比状态的动力学特性具有十分重要的工程意义.改变充液深度为$h = 0.07$m, 其他参数不变, 数值计算结果如图4所示.根据计算结果可知, 充液比较大时幅频响应表现为软弹簧特性;随着液体燃料消耗, 在充液比较小时,幅频曲线向右弯曲即表现为硬弹簧特性.软、硬弹簧转换点对应的充液比称为临界充液比,当液体深度经过此临界深度时, 液体的动力学特性将发生明显变化,因而有必要研究软、硬弹簧转换点与系统参数之间的关系.
图4
图4
$h = 0.07~\mbox{m}$时的幅频响应曲线
Fig. 4
Amplitude-frequency response as $h = 0.07~\mbox{m}$
图5
图5
外激励对幅频响应曲线的影响
Fig. 5
Amplitude-frequency response under different external excitation
图6
令方程(23)中$f = \zeta = 0$, 得到幅频响应的骨架曲线方程
图7
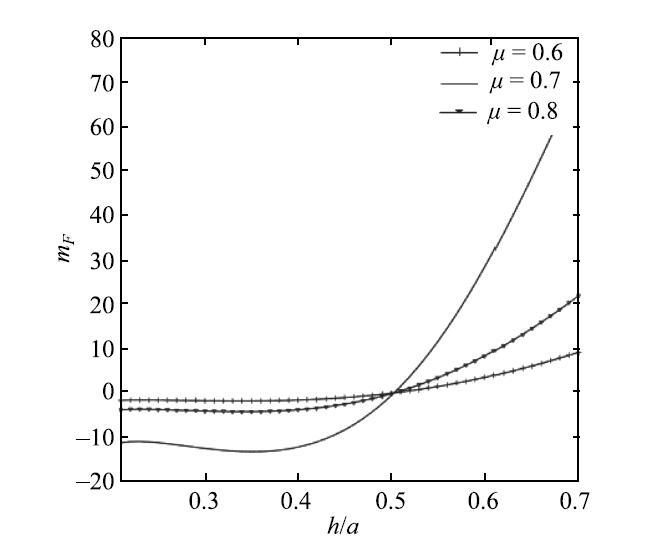
图7
不同干湿比$m_F - \bar {h}$曲线
Fig. 7
$m_F - \bar {h}$under different dry-wet ratios
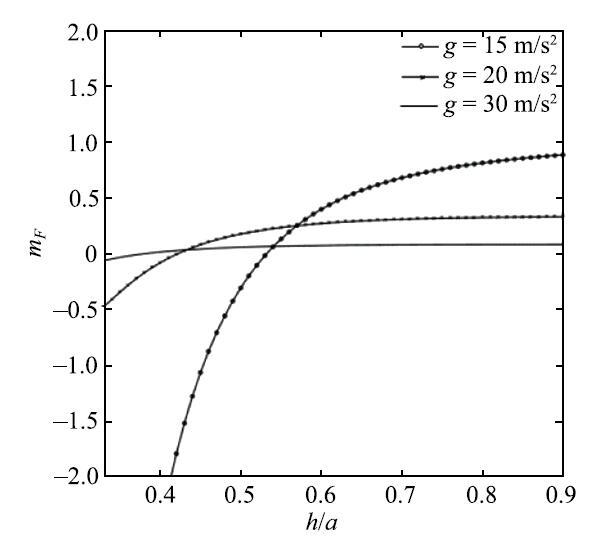
图8
图8
不同重力加速度$m_F - \bar {h}$曲线
Fig. 8
$m_F - \bar {h}$under different gravity accelerations
图9
图9
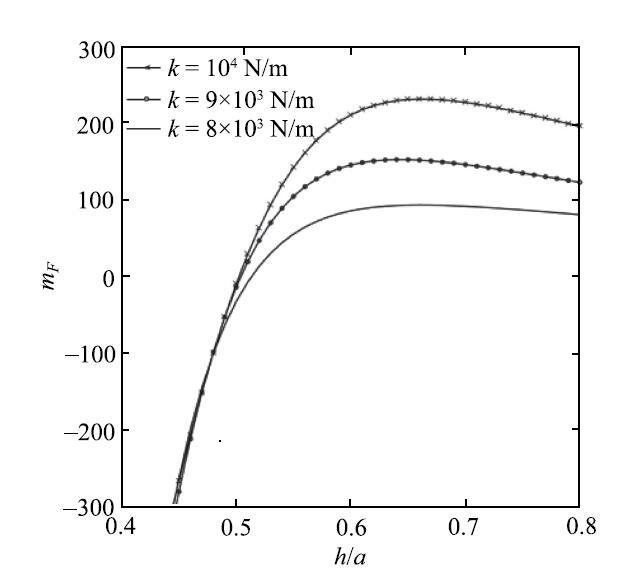
不同弹簧系数$m_F - \bar {h}$曲线
Fig. 9
$m_F - \bar {h}$under different spring coefficients
根据数值结果可知, 3种不同干湿比下的$m_{F1} - \bar{h}$曲线并不重合, 在充液比较小时$m_{F1} < 0$, 充液比较大时$m_{F1}> 0$, 但是$m_{F1} =0$时对应的充液比相同,所以耦合系统干湿比不影响幅频响应曲线的软、硬弹簧特性.模拟的3种重力加速度下$m_{F1} - \bar {h}$曲线不重合, 且$m_{F1} =0$时对应的充液比不相同, 随重力加速度增大对应的临界充液比减小,即重力加速$g$对系统的软、硬弹簧转换点有影响.根据不同弹簧刚度系数时的$m_{^{F1}} - \bar {h}$曲线可知,$k$对幅频特性的软、硬弹簧转换点有影响:随$k$增加,耦合系统的临界充液比减小.
4 结论
本文利用多尺度方法研究了圆柱贮箱航天器刚--液耦合系统平动时系统一阶主共振的非线性动力学特性.数值分析结果表明, 幅频响应曲线表现为软弹簧特性时,若激励频率小于耦合系统一阶线性固有频率,幅频响应和激励幅值响应的解存在多稳态解及跳跃现象;若激励频率大于耦合系统一阶线性固有频率,幅频响应和激励幅值响应对应唯一稳态解. 随液体燃料充液比变化,幅频曲线发生软、硬弹簧特性转换现象:充液比较大时,幅频响应表现为软弹簧特性; 充液比较小时, 幅频响应表现为硬弹簧特性.重力加速度和弹簧刚度系数对幅频响应曲线的软、硬弹簧特性转换点有影响.这些结果对进一步深入了解充液航天器非线性动力学特性有重要的参考价值.
参考文献
Dynamic analysis of the flexible spacecraft with liquid sloshing in axisymmetrical container
Nonlinear model and attitude dynamics of flexible spacecraft with large amplitude slosh
Attitude dynamics and control of spacecraft with a partially filled liquid tank and flexible panels
多储液腔航天器刚液耦合动力学与复合控制
Rigid and liquid coupling dynamics and hybrid control of spacecraft with multiple propellant tanks
大型柔性航天器动力学与振动控制研究进展
Advances in dynamics and vibration control of large-scale flexible spacecraft
微重力下圆柱形贮箱内液体晃动的分岔现象
Bifurcations of liquid sloshing in cylindrical containers in microgravity condition
球形贮箱中三维液体大幅晃动数值模拟
Numerical simulation of three dimensional large-amplitude liquid sloshing in spherical containers
液体大幅晃动类等效力学模型研究
Study on the equivalent mechanical model for large amplitude slosh
Nonlinear coupled dynamics of liquid-filled spherical container in microgravity
液体非线性晃动的同步Hopf分叉现象
Synchronous Hopf bifurcation of liquid nonlinear sloshing
Sloshing in a vertical circular cylindrical tank with an annular baffle. Part 2. Nonlinear resonant waves
On the theory of nonlinear vibrations of a liquid of finite volume
An investigation of resonant, nonlinear,nonplanar free surface oscillations of a fluid.
Multidimensional modal analysis of nonlinear sloshing in a rectangular tank with finite water depth
An adaptive multimodal approach to nonlinear sloshing in a rectangular tank
The nonlinear coupled dynamics of fluids and spacecraft in low gravity. [PhD Thesis]
Nonlinear fluid slosh coupled to the dynamics of a spacecraft
圆柱贮箱类液固耦合系统转动响应分析
Analysis on dynamic response of the liquid-solid coupling system with the liquid in a cylindrical container under pitching excitation
微重力环境下刚液耦合系统液体晃动混沌现象研究
Nonlinear coupled dynamics of liquid-fluid cylindrical container in microgravity
Multidimensional modal analysis of liquid nonlinear sloshing in right circular cylindrical tank
利用多维模态理论分析圆柱贮箱液体非线性晃动
Analyzing liquid nonlinear sloshing circular cylindrical tank by multidimensional modal theory
Resonant sloshing in an upright annular tank
平动矩形贮箱刚--液耦合非线性动力学研究
Study on nonlinear dynamics of rigid-liquid coupling rectangular tanks under horizontal excitation
具有曲率和惯性非线性以及材料内阻的旋转复合材料轴的主共振
Primary resonances of an internally damped rotating composite shaft with nonlinearities in curvature and inertia