引言
在实际工程中,结构中存在着大量不确定性参数,这些参数对几何非线性静力响应分析有着或多或少的影响.因此,为了分析参数不确定结构的几何非线性静力响应,国内外许多学者开展了积极的研究.例如,Bielewicz等[1]将Monte-Carlo模拟与有限元方法相结合,对具有几何缺陷的壳体结构进行了可靠度分析.Schenk等[2]采用Karhunen-Loeve级数展开表示几何缺陷,利用随机有限元法计算了临界载荷下壳体结构的响应.Capiez-Lernout等[3]针对具有几何非线性的不确定性弧形结构,建立了随机非线性降阶的计算模型.Impouonia等[4-5]先后提出一种响应面法和基于二阶泰勒展开的改进摄动随机有限元方法,获得了几何非线性桁架结构的位移响应的统计矩.程进[6]提出了将响应面法、有限元法和蒙特卡洛模拟法三者结合的集成化响应面方法对几何非线性桁架结构进行了概率响应分析.Contento等[7]推导出适用于平面框架的几何非线性问题的离散性摄动方程.文献[8]采用双迭代随机摄动有限元法对平面桁架进行了非线性分析.文献[9]利用多变量高阶摄动方法对随机杆系结构的几何非线性问题进行了求解等等.上述文献研究表明,摄动法是求解随机结构几何非线性问题的一种重要方法.然而,当结构随机参数的变异性增大时,采用低阶摄动甚至高阶摄动得到的结构随机响应的计算精度会下降,有时下降程度还比较大.这个现象和文献[10]描述的摄动法收敛特点也是吻合的,即摄动法的收敛域是由Taylor展开或摄动展开点邻域逐渐向周围扩大的,随摄动阶数的增大,收敛域扩张速度迅速降低.
在早期非线性结构的确定性分析中,为了提高摄动法的收敛范围和求解精度,谭国强等[11]、孙博华[12]先后在摄动法的基础上结合伽辽金法提出了摄动加权残数法、摄动权余法求解确定性薄板大挠度问题.赵琪等[13]提出了基于可变基函数的伽辽金方法.在文献[14]中,Noor结合摄动和伽辽金法分析了确定性非线性结构的稳定性问题.进一步,考虑结构参数的随机性,孟广伟等[15]将摄动法和局部正交无网格伽辽金法相结合,求解了结构随机响应问题.文献[16]提出了改进的递推随机有限元方法即混合摄动-伽辽金法,首次将多变量的混 合摄动-伽辽金法应用于随机结构的力学分析.这个方法已成功应用于线性随机结构的静力问题及静力可靠性问题的分析中[17-19].和已有的随机伽辽金法如混沌多项式方法(PC)、GPC相比[20-21],该方法具有如下优点:(1)试函数由摄动解的线性组合而成,求解非线性问题时,试函数的获取具有自适应性.(2)在处理具有不同分布的多随机变量问题时,其误差降低较快,有时呈指数型递减[22],而GPC法不是这样的.有意思的是,计算误差呈指数型递减的特点正是GPC在处理非高斯随机变量问题时优于PC法的地方[23],也是该方法得以被广泛应用的重要理论基础.(3)在处理大尺度模型问题时,PC或GPC法需要求解一个扩阶的高维非线性方程组,而本文方法只需要在摄动解基础上增加一个低维的非线性方程组求解,计算量大为减少,且求解更为容易.另外,和文献[24]中的随机减基法相比,混合摄动-伽辽金法可以处理载荷为随机的情况,而随机减基法不行,且不方便求解非线性问题. 另外,求解随机非线性问题还可尝试其他的方法[25-30].
针对随机桁架结构几何非线性问题,本文在文献[9]给出的多变量高阶摄动求解方法的基础上,首次将混合摄动-伽辽金法应用到该问题的求解.首先将含位移项的随机割线弹性模量以及随机响应量表示为幂多项式展开,运用高阶摄动方法确定随机结构几何非线性响应的幂多项式展开的各项系数.以摄动解为基础,确立伽辽金试函数的表达形式,进一步通过伽辽金投影得到试函数的未知系数,从而得到随机结构几何非线性响应的显式表达式.一个指数函数算例表明,混合摄动-伽辽金法可以较大地扩展摄动法的随机收敛范围.一个两变量的非线性随机函数例子表明,对于具有不同概率分布多随机变量问题,混合摄动-伽辽金法比同阶的GPC法精度要高.两杆桁架的几何非线性分析结果表明,在精度相当的情况下,本文方法比GPC法求解更方便,计算量更小.同时,两杆桁架和平面桁架拱的数值算例结果都表明,对于随机杆系结构的几何非线性问题,当随机参数涨落较大时,混合摄动-伽辽金法比高阶摄动法更逼近蒙特卡洛模拟的结果,说明了所提求解方法的有效性.
1 几何非线性随机平衡方程
对于具有$N$个自由度的确定性弹性桁架结构体系,考虑它的几何非线性,则它的任一单元的静力平衡方程可由下式表示
式中,${\pmb K}^{\rm e} ({\pmb u}^{\rm e})$为单元割线刚度矩阵,${\pmb u}^{\rm e}$为单元位移向量, ${\pmb F}^{\rm e}$为单元载荷向量. 采用Green应变表示应力与位移之间的关系,单元割线刚度矩阵可以表示为
式中,$\varOmega ^{\rm e}$为单元积分域,$E_{\rm s} $为割线弹性模量,${\pmb B}_{\rm L}$为Green应变线性部分,${\pmb B}_{{\rm L}1} $为Green应变非线性部分.
假定已知载荷作用下的单元位移向量为${\pmb u}^{\rm e}$,利用表达式(1)和式(2),将桁架各单元集成,可有
式中,$\varOmega $为积分域,${\pmb F}$为桁架系统的载荷向量.
若将桁架结构中杆件的弹性模量$E$,截面积$A$和载荷考虑为随机量,那么式(3)的割线弹性模量$E_s $和积分域$\varOmega $等也是随机的,此时的式(3)为含随机参数的桁架结构几何非线性平衡方程.
2 随机平衡方程的高阶摄动求解
2.1 随机量的表达
假设桁架结构的杆件弹性模量、截面积和载荷分别含有$n_1 $, $n_2 $和$n_3$个随机变量,那么随机弹模$E$、随机截面积$A$、随机积分域$\varOmega$和随机载荷${\pmb F}$可分别表示为
式中,$n=n_{1}+n_{2}+n_{3}$,$\gamma _i (i = 1, 2, \cdots, n)$为$n$个独立的随机变量;$E_0 $, $A_0 $, $\varOmega _0 $和${\pmb F}_0 $为已知的弹性模量、截面积、积分域和载荷等随机量的均值部分;$E_i $, $A_i$, $\varOmega _i $和${\pmb F}_i$分别为已知的弹性模量、截面积、积分域和载荷的随机部分的确定性量. 对于非杆系结构的连续体,可以采用Karhunen-Loeve展开将连续随机场用$n$个独立随机变量表示.
将具有$N$个自由度的结构位移响应向量${\pmb u}$表示为关于独立的随机变量$\gamma _i (i = 1, 2, \cdots, n)$的非正交幂多项式展开,如下所示
式中,${\pmb u}_0 $为随机变量取均值时的确定性结构的位移,${\pmb u}_i $,${\pmb u}_{ij} $和${\pmb u}_{ijk} $为待求的前三阶展开系数项;$\gamma _i $,$\gamma _i \gamma _j $,$\gamma _i\gamma _j \gamma _k $为非正交多项式基.
割线弹性模量随位移变化,也可用多变量幂多项式展开为
式中,$E_{{\rm s}0} $为割线弹性模量的确定性部分;$E_{{\rm s}i} $,$E_{{\rm s}ij} $,$E_{{\rm s}ijk} $为割线弹性模量对随机变量的各阶偏导,可通过对$E_{\rm s} $进行偏导求得.
2.2 随机的非线性几何关系
在式(2)中,应变线性部分${\pmb B}_{\rm L} $与随机量无关,而应变非线性部分${\pmb B}_{{\rm L}1} $与结构响应${\pmb u}$有关,可将其表达为
式中,${B}_{{\rm L}10} = {b u}_0 {\pmb \eta }^{\rm T}{\pmb J}^{\rm T}{\pmb J\pmb\eta }$,${B}_{{\rm L}1i} = {\pmb u}_i {\pmb \eta }^{\rm T}{\pmb J}^{\rm T}{\pmb J\pmb\eta }\gamma _i $,${B}_{{\rm L}1ij} = {\pmb u}_{ij} {\pmb \eta }^{\rm T}{\pmb J}^{\rm T}{pb J\eta }\gamma _i \gamma _j $,${B}_{{\rm L}1ijk} = {\pmb u}_{ijk} {\pmb \eta }^{\rm T}{\pmb J}^{\rm T}{\pmb J\pmb\eta }\gamma _i \gamma _j\gamma _k $,${\pmb \eta }$是局部坐标到整体坐标的转换矩阵,${\pmb J} = \left[ { - {I}_{3\times 3} ,{I}_{3\times 3} } \right] / L$,$L$为初始的桁架杆件长度.
2.3 高阶摄动求解
将结构位移${\pmb u}({\pmb \gamma })$,割线弹性模量$E_{ s}$,Green应变,随机积分域和随机载荷表达式代入方程(1),可得到以下平衡方程
式中
$${\pmb K}_0 = \int_{\varOmega _0 } {\pmb B}_{\rm L}^{\rm T} E_0 {\pmb B}_{\rm L} V + \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{\rm L}^{\rm T} E_0 {\pmb B}_{{\rm L}10} V + \\ \int_{\varOmega _0 } {\pmb B}_{{\rm L}10}^{\rm T} E_0 {\pmb B}_{\rm L} V + \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{{\rm L}10}^{\rm T} E_0 {\pmb B}_{{\rm L}10} V \\ {\pmb K}_i = \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{\rm L}^{\rm T} E_0 {\pmb B}_{{\rm L}1i} V + \int_{\varOmega _0 } {\pmb B}_{\rm L}^{\rm T} E_i {\pmb B}_{\rm L} V + \\ \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{\rm L}^{\rm T} E_i {\pmb B}_{{\rm L}10} V + \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{{\rm L}10}^{\rm T} E_0 {\pmb B}_{{\rm L}1i} V + \\ \int_{\varOmega _0 } {\pmb B}_{{\rm L}10}^{\rm T} E_i {\pmb B}_{\rm L} V + \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{{\rm L}10}^{\rm T} E_i {\pmb B}_{{\rm L}10} V + \\ \qquad \int_{\varOmega _0 } {\pmb B}_{{\rm L}1i}^{\rm T} E_0 {\pmb B}_{\rm L} V + \dfrac{1}{2}\int_{\varOmega _0 } {\pmb B}_{{\rm L}1i}^{\rm T} E_0 {\pmb B}_{{\rm L}10} V + \\ \int_{\varOmega _i } {\pmb B}_{\rm L}^{\rm T} E_0 {\pmb B}_{\rm L} V + \dfrac{1}{2}\int_{\varOmega _i } {\pmb B}_{\rm L}^{\rm T} E_0 {\pmb B}_{{\rm L}10} V + \\ \int_{\varOmega _i } {\pmb B}_{{\rm L}10}^{\rm T} E_0 {\pmb B}_{\rm L} V + \dfrac{1}{2}\int_{\varOmega _i } {\pmb B}_{{\rm L}10}^{\rm T} E_0 {\pmb B}_{{\rm L}10} V $$
考虑篇幅,${\pmb K}_{ij} $在这里不再展开. 当$i=1$, 2, $\cdots$, $n_{1}+n_{2}$, ${\pmb F}_i = 0$.
由于每个随机变量必须满足方程式(8),因此随机平衡方程两边同阶次的幂多项式展开系数之和必须为零,从而可分别建立一系列的确定性的递归方程. 因此,利用高阶摄动法,可以得到幂多项式展开的各阶系数,从而可得非线性位移的表达式,具体步骤可参考文献[9].
3 伽辽金法求解
3.1 伽辽金试函数的确定
为了提高随机结构几何非线性位移响应的幂多项式展开(5)的逼近精度,在上述高阶摄动法的基础上,利用伽辽金投影对结构位移响应的各阶系数进行修正. 首先,选择一组试函数,该试函数为一组$N\times 1$维基向量${\pmb \varPi }_i \ (i = 0,1, \cdots,m)$,$m$为试函数个数. 此时,随机位移响应向量可以重新表达为
式中,$\beta _i \ (i = 0, 1, 2, \cdots, m)$是试函数或坐标函数${\pmb \varPi }_i \ (i = 0, 1, 2, \cdots,m)$的待求系数,试函数${\pmb \varPi }_i $可表示为
式中,展开系数向量${\pmb u}_0 $,${\pmb u}_i $,${\pmb u}_{ij} $,${\pmb u}_{ijk}$等是通过对方程(8)进行高阶摄动求解获得. 于是,随机位移响应向量可重新写为
3.2 随机量的重新表达
随机割线弹性模量的幂多项式展开系数或各阶偏导将随位移响应向量${\pmb u}^m$变化,例如,割线弹性模量一阶偏导数将表示为
式中
$$\delta = 2E\left[ {\dfrac{1}{(\lambda + 1)^2} - \dfrac{1}{\lambda ^2}} \right]\dfrac{1}{\lambda }\left[ {\dfrac{1}{2}\beta _0 \beta _1 {\pmb u}_i^{\rm T} {\pmb \eta }^{\rm T}{\pmb J}^{\rm T}{\pmb J\pmb\eta \pmb u} + } \right. \\ \left. {\beta _0 {\pmb B}_L {\pmb \eta \pmb u}_i + \dfrac{1}{2}\beta _0 \beta _1 {\pmb u}^{\rm T}{\pmb \eta }^{\rm T}{\pmb J}^{\rm T}{\pmb J\pmb \eta \pmb u}_i } \right] $$
其中$\lambda$为杆件变形前后的长度比.
考虑到Green应变的非线性部分与结构位移向量${\pmb u}^m$的关系,可将其重新写为
将式(12)代入割线弹模表达式(6), 并和Green应变的非线性应变(13)一起代入表达式(2),可得新的割线刚度矩阵
3.3 随机伽辽金投影
利用式(8)、式(11)及式(14),可得新的随机桁架结构的几何非线性平衡方程为
式中,$\beta =[\beta _1 ,\beta _2 , \cdots ,\beta _m ]$. 将方程(14)在试函数基向量${\pmb \varPi }_i \ (i = 0,1,2, \cdots,m)$上进行伽辽金投影并求期望,可以得到
式中,${\pmb F} = {\pmb F}_0 + \sum_{i = 1}^n {\pmb F}_i \gamma _i $,$\langle ,\cdot ,\rangle $表示数学期望的运算符.
然后,运用Newton-Raphson方法求解非线性方程组(16),可以得到修正系数$\beta _i$,从而获得随机桁架结构几何非线性响应的最终显式表达式.
当不考虑割线刚度矩阵(14)中的应变非线性部分${\pmb B}_{L1}$时,它将退化为线弹性刚度矩阵,非线性方程组(16)将变为一个$(m+1)\times (m+1)$维线性方程组.在实际应用中,$m$取值较小. 也就是说,对于线性问题, 需要求解${NP}(NP = (n + m)! / (n!m!))$个$N\times N$维摄动方程和一个小的线性方程组. 而对于同一问题,PC或GPC法需要求解一个(${NP}\cdot N)\times ({NP}\cdot N)$维扩阶的确定性方程组. 显然,PC或GPC方法的计算量一般要远大于本文的方法[16].当考虑矩阵(14)中的应变非线性部分时,本文方法只需要求解一个$(m+1)\times (m+1)$维的非线性方程组.而对于PC或GPC法,需要求解一个$(NP\cdot N)\times (NP\cdot N)$维扩阶的非线性方程组,计算量巨大.特别是PC或GPC法 的初始解难于确定,而本文方法的初始值一般 取1即可.
关于方程(15)的解,有如下说明. 由于位移向量${\pmb u}^m$是方程(3)中位移向量${\pmb u}$的一个截断,这样方程(3)和方程(15)之间的随机误差向量可以写为
从而方程(16)可以写成
式(18)表明,随机误差向量${\pmb e}({\pmb \gamma })$与基向量${\pmb \varPi }_k $正交,从而使得随机误差向量${\pmb e}({\pmb \gamma})$取最小值. 随着幂多项式展开项的增加,方程(16)的解将会趋向收敛[18].
4 数值算例
算例1 考虑一个指数函数,它的自变量$\gamma$为随机变量,服从期望为零,方差为1的标准正态分布,其函数关系如式(19)所示
分别采用四阶泰勒展开(Taylor)或高阶摄动方法、混合摄动-伽辽金法(HPGM)和PC法对该指数函数进行逼近,得到指数函数的近似表达式如下
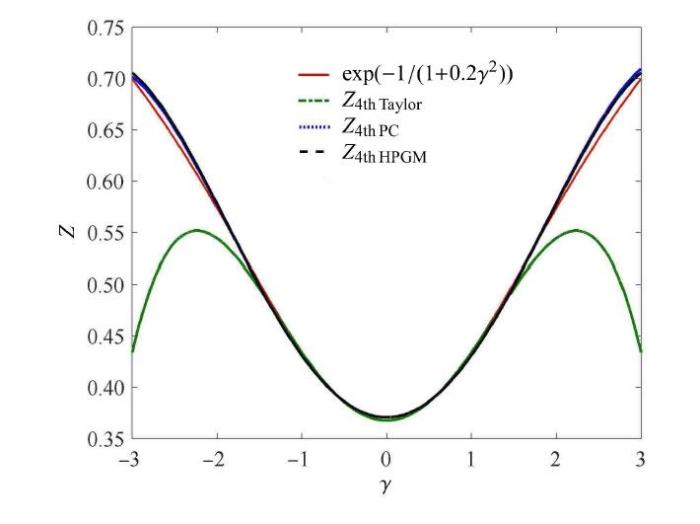
上述函数与自变量的关系如图1所示. 从图中可以看出,当自变量在范围[-3,3]内时,由混合摄动-伽辽金法和PC法得到的近似函数比同阶的高阶摄动法更能逼近指数函数(19).同时可以看出,在 处理单变量非线性函数关系时,混合摄动-伽辽金法的精度不弱于PC法.有趣的是,对于这个单变量函数,如果忽略PC法结果中的奇数项,PC法的多项式展开系数与混合摄动-伽辽金法很相近.
图1
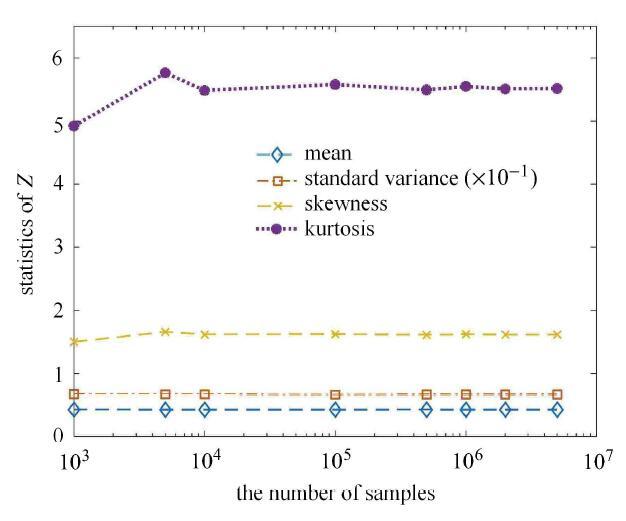
为了说明上述3个逼近函数的前四阶统计矩的计算精度,首先对蒙特卡洛方法所采用的样本数量进行了确认. 前四阶统计矩包括期望(mean)、均方差(standard variance)、偏度(skewness)和峰度(kurtosis). 图2给出了蒙特卡洛方法取不同数量样本时得到的$Z$的前四阶统计矩值,所取用的样本数量从1000逐渐增加到500万,可以看出当样本数量为10万时,$Z$的前四阶统计矩值已趋于收敛,故本算例中蒙特卡洛方法所采用的样本数量为10万.
图2
图2
采用不同样本数量蒙特卡洛方法计算的$Z$的前四阶统计矩
Fig. 2
First four order statistical moments of $Z$obtained by the Monte-Carlo simulation method with different amount of samples
算例2 一个非线性函数关系如式(23)所示
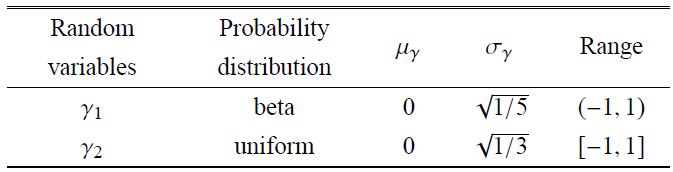
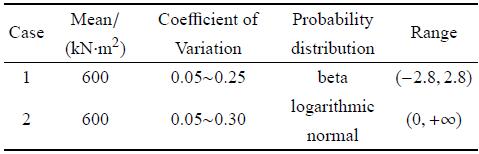
函数中的两个随机变量是相互独立的,表2给出了它们的均值$\mu _\gamma$、均方差$\sigma _\gamma $以及分布区间.
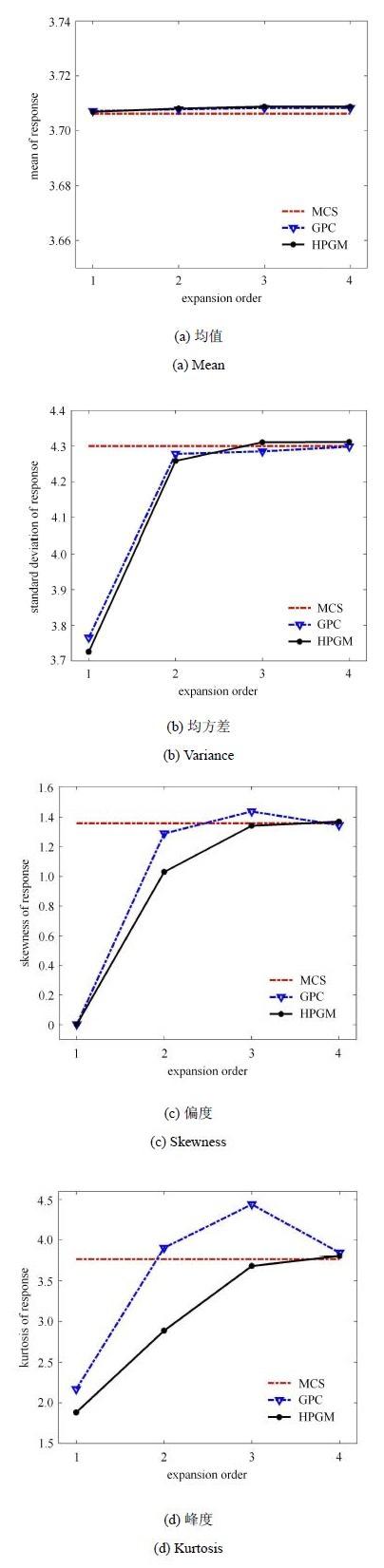
分别采用混合摄动-伽辽金法(HPGM)和GPC法来计算函数$Z_{1}$的前四阶统计矩. 注意运用GPC法时,为了保证多变量多项式基的正交性,必须先将两个随机变量的概率分布同一化,如将$\gamma _2$转化成贝塔分布的随机变量的正交多项式展开.首先,图3给出了不同展开阶次时本文方法和GPC法所求得的均值、均方差、偏度和峰度值,将采用10万样本的蒙特卡洛模拟法(MCS)的结果作为标准值.从图3中可以看到,对于均值和均方差,GPC法和本文方法在二阶展开时就可以得到比较稳定的结果;对于偏度和峰度,混合摄动-伽辽金法三阶展开的结果就已经趋于稳定,而GPC法四阶展开的结果才会接近于蒙特卡洛模拟法的结果.这些观察说明,对非线性函数(23)的逼近,GPC法计算结果的误差呈指数型递减的特征不再出现,而本文方法结果较GPC法收敛更快.究其原因,和处理非高斯分布随机问题的PC法是一样的,由于要将所有非高斯随机变量转换为具有同一高斯分布的随机变量的正交多项式展开,增加了误差的传递,从而导致结果的指数型收敛特征得不到保证[20].
图3
图3
GPC法和HPGM法计算的$Z_{1}$的前四阶统计矩与展开阶数的关系
Fig. 3
Relationship of the first four statistical moments of $Z_{1}$obtained by the GPC and HPGM with expansion order number
当采用四阶GPC方法时,将均匀分布随机变量$\gamma _2$转化为贝塔分布随机变量$\tau _2 $对应的雅可比正交多项式展开
式中,$\tau _2 $具有和$\gamma _1$相同的概率分布,但两者相互独立. 然后,以两变量的雅可比正交多项式基为基底,应用GPC法得到函数(23)的近似表达式如下
本文给出的四阶混合摄动-伽辽金法得到的近似表达式如下
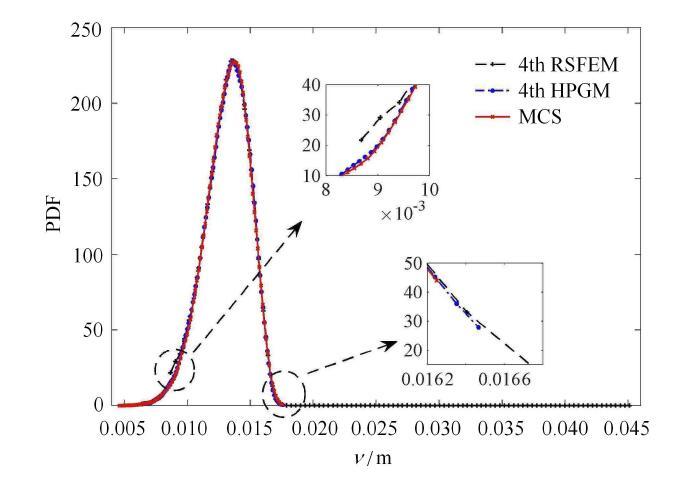
对比式(25)和式(26)的系数项,可以发现,两个多项式展开并不相同,这和单变量函数情况是不一样的. 根据上述得到的表达式绘制出概率密度函数图和蒙特卡洛(10万个样本)结果如图4所示.
图4
图4
函数$Z_{1}$的概率密度函数曲线
Fig. 4
Probability density function curve of function $Z_{1}$
从图4可以看出,在具有不同分布的多随机变量情况下,混合摄动-伽辽金在概率密度函数曲线的尾部和端部优于GPC方法,体现了混合摄动-伽辽金法求解的精确性.
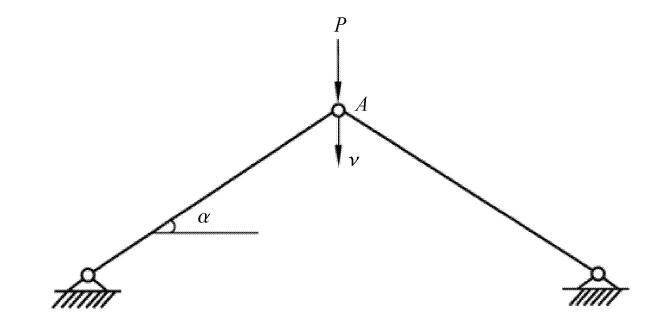
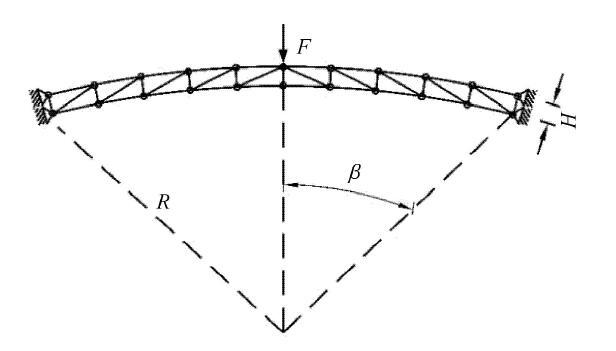
算例3 考虑一个弹性两杆桁架结构,如图5所示. 在该桁架顶铰处作用有载荷$P$,其大小为0.075,kN. 假设各杆件长度为1,m,杆件倾角$\alpha$为30$^\circ$,杆件截面积为0.02,m$^2$.
图5
假设杆件弹性模量为随机变量,分两种工况. 在工况1中,杆件的弹性模量为贝塔分布,在工况2中,其为对数正态分布.杆件弹性模量的统计特征如表3所示.然后,分两种工况分别利用高阶摄动法(RSFEM),GPC法,混合摄动-伽辽金法和蒙特卡洛模拟法(10万个样本)对两杆桁架结构中顶铰$A$点处的竖向位移$\upsilon $进行计算.
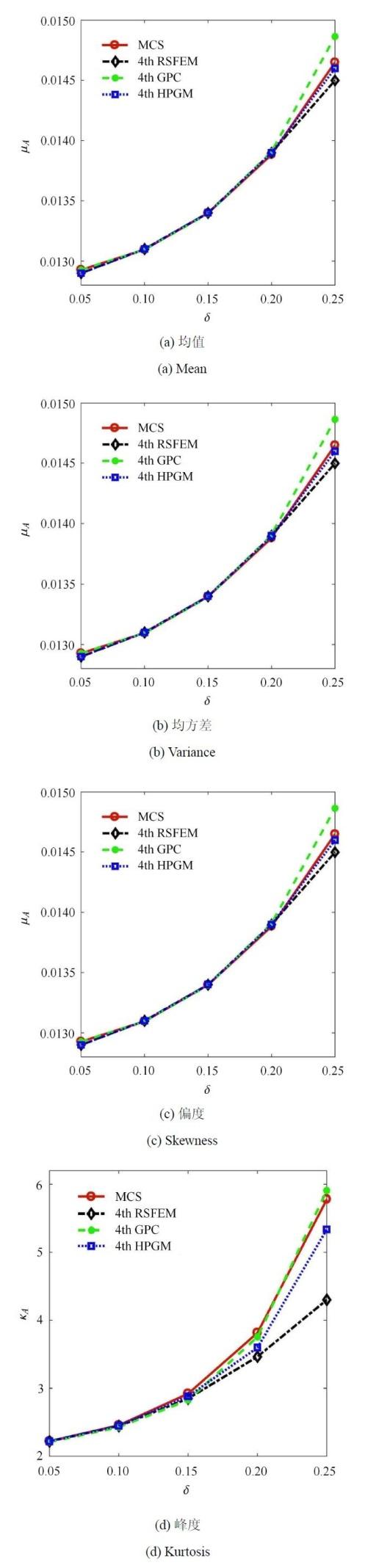
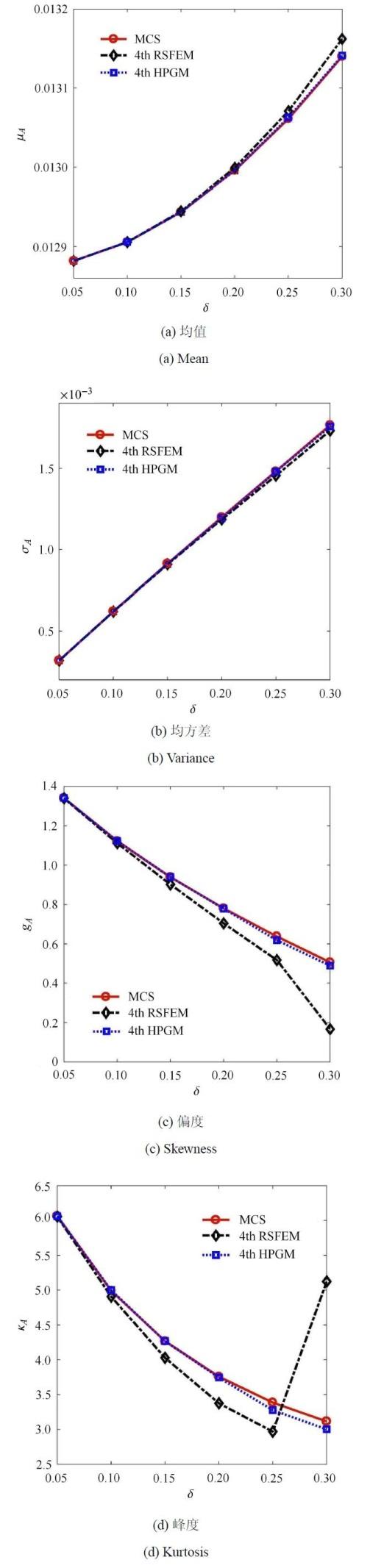
工况1:弹性模量服从贝塔分布,变异系数$\delta $的变化范围为0.05$\sim $0.25. 铰顶$A$点处竖向位移的均值($\mu _A)$、均方差($\sigma _A )$、偏度($g_A )$和峰度($k_A)$与弹性模量变异系数的关系分别如图6(a)、图6(b)、图6(c)和 图6(d)所示.从图6(a)和图6(b)中可以看出,当弹性模量的变异系数小于0.2时,混合摄动-伽辽金法,GPC法和高阶摄动法的前两阶统计值结果都很好;当$\delta$为0.25时,相对于蒙特卡洛结果,3个近似方法得到的均方差误差分别为2.12%,5.48%和8.76%,混合摄动-伽辽金法的精度明显好于高阶摄动法.
图6
图6
铰顶位移均值、均方差、偏度和峰度与弹性模量变异系数的关系
Fig. 6
The relationship between the mean value, variance, skewness and kurtosis of $\upsilon $and the coefficient of variation $\delta $of the elastic modulus
从图6(c)和图6(d)中可以看出,当弹性模量变异系数$\delta $小于0.15时,3个近似方法得到的偏度和峰度结果精度都不错.随着变异系数的增大,高阶摄动法的误差越来越大. 当$\delta$为0.25时,高阶摄动的位移偏度和峰度误差分别达到了18.08%和25.56%. 相应地,GPC法位移的偏度和峰度误差分别为12.44%和2.23%,而混合摄动-伽辽金法位移偏度和峰度误差分别为3.21%和7.66%. ,这个结果说明, 混合摄动-伽辽金法对随机桁架结构几何非线性问题的求解精度明显好于高阶摄动法,和GPC法精度相比,略好或基本相当. 这里需要注意,GPC法中求解扩阶的10$\times$10维非线性方程组时,初始解难于确定.目前采取的办法是,利用本文方法结果以及正交多项式展开与非正交多项式展开之间的关系矩阵[9],确定了对应竖向位移$\upsilon $的GPC法初始解. 由于本文只需要求取5$\times$5维的非线性方程组,故计算量比GPC法小,且修正系数的初始解直接取1即可.
图7
图7
铰顶位移均值、均方差、偏度和峰度与弹性模量变异系数的关系(工况2)
Fig. 7
The relationship between the mean value, variance, skewness and kurtosis of $\upsilon $and the coefficient of variation $\delta $of the elastic modulus (Case 2)
从图7(c)和图7(d)中可以发现,当弹性模量的变异系数$\delta $超过0.1时,两个近似方法的结果都会偏离精确值.当$\delta$为0.20时,高阶摄动位移偏度和峰度误差分别为9.77%和10.13%,而混合摄动-伽辽金法位移偏度和峰度,误差分别 为0.21%和0.33%. 当$\delta $为0.30时,高阶摄动位移偏度、峰度和蒙特卡洛模拟结果相比出现了明显的偏离,而相应的混合摄动-伽辽金法位移偏度和峰度误差分别为3.27%和3.61%.通过对不同概率分布工况的数值结果分析,再一次说明,当结构的随机参数涨落较大时,混合摄动-伽辽金法的精度要好于高阶摄动法,体现出本文方法的有效性.
图8
图8
铰顶处竖向位移$\upsilon $的概率密度函数图(变异系数为0.25)
Fig. 8
PDF curves of the displacement $\upsilon $(The coefficient of variation is 0.25)
图9
图10
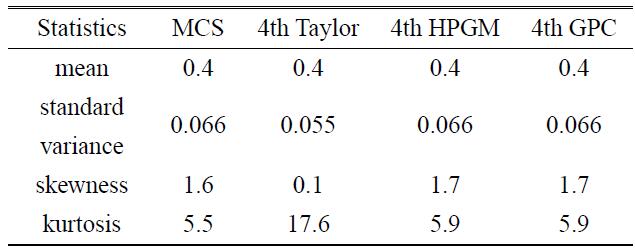
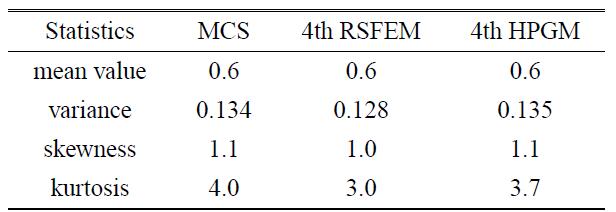
分别利用高阶摄动法(RSFEM),混合摄动-伽辽金法和蒙特卡洛模拟法(10万个样本)对桁架结构中顶铰处的竖向位移进行计算,给出了位移响应的各阶统计矩,如表6所示.
从表6的数据可以看出,混合摄动-伽辽金法的精度高于高阶摄动法,特别是偏度和峰度,高阶摄动法偏离蒙特卡洛结果较大,体现了混合摄动-伽辽金法求解非线性随机结构的优越性.
5 结论
(1)本文应用混合摄动-伽辽金法求解了随机桁架结构几何非线性问题.将含位移项的随机割线弹性模量以及随机响应量表示为幂多项式展开,将用摄动法得到的几何非线性响应向量的幂多项式展开式作为试函数,利用伽辽金投影对试函数的系数进行求解,获得了随机桁架结构几何非线性响应的显式表达式.
(2)两变量非线性函数算例表明,当多个随机变量概率分布不同时,本文方法比同阶的广义正交多项式方法(GPC)计算精度要高. 两杆桁架分析结果表明,在精度相当的情况下,本文方法比GPC法求解更方便,计算量更小. 当几何非线性随机桁架结构中随机参数的变异性较大时,混合-摄动伽辽金法结果的四阶统计量包括均值、均方差、偏度和峰度以及概率密度函数均好于高阶摄动法的结果,显示了混合摄动-伽辽金法对随机桁架结构几何非线性问题求解的有效性.
参考文献
Shells with random geometric imperfections simulation --- based approach. International Journal of
Buckling analysis of cylindrical shells with cutouts including random boundary and geometric imperfections
Computational stochastic statics of an uncertain curved structure with geometrical nonlinearity in three-dimensional elasticity
Static and dynamic analysis of non-linear uncertain structures
A response surface approach for the static analysis of stochastic structures with geometrical nonlinearities
基于响应面法的几何非线性结构概率响应分析
Probabilistic response analysis of geometrically nonlinear structure based on systematic response surface method
Static and dynamic consistent perturbation analysis for nonlinear inextensible planar frames
On the dual iterative stochastic perturbation-based finite element method in solid mechanics with Gaussian uncertainties
随机杆系结构几何非线性分析的递推求解
Geometrical nonlinear analysis of truss structures with random parameters utilizing recursive stochastic finite element method
摄动权余法及在薄板大挠度问题上的应用
Perturbation weighted residuals method and its application in large deflection problems of thin plates
Hybrid changeable basis galerkin technique for nonlinear analysis of structures
Recent advances in reduction methods for instability analysis of structures
摄动随机局部正交无网格伽辽金法
Perturbation stochastic local orthogonal element-free Galerkin method
Recursive approach for random response analysis using non-orthogonal polynomial expansion
随机结构有限元分析的递推求解方法的改进
Improvement on recursive stocha-stic finite element method
Reliability analysis of structure with random parameters based on multivariate power polynomial expansion
Hybrid perturbation-Galerkin methods for structural reliability analysis
Polynomial chaos in stochastic finite elements
The Wiener--Askey polynomial chaos for stochastic differential equations
基于混合摄动$\!$-$\!$-$\!$伽辽金法的结构可靠性分析. [博士论文]
Structural Reliability Analysis Based on Hybrid Perturbation-Galerkin Methods. [PhD Thesis]
Modeling uncertainty in steady state diffusion problems via generalized polynomial chaos
Multi-element stochastic reduced basis methods
基于最大熵方法的水下航行体结构动力响应概率建模
Probabilistic modelling of dynamic response of underwater vehicle structure via maximum entropy method
加性非平稳激励下结构速度响应的FPK方程降维
Dimension reduction of FPK equation for velocity response analysis of structures subjected to additive nonstationary excitations
概率密度演化方程TVD格式的自适应时间步长技术及其初值条件改进
Non-uniform time step TVD scheme for probability density evolution function with improvement of initial condition
A new homotopy-based approach for structural stochastic analysis
Robust stability analysis of structures with uncertain parameters using mathematical programming approach
Non-stationary random response analysis of structures with uncertain parameters