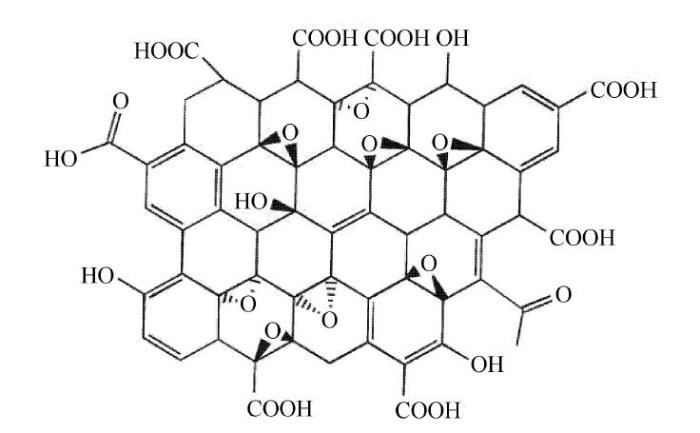
引言
图1
为此,Zheng等[21]利用分子力学和分子动力学方法研究了分子结构、官能团的分子量和功能化程度等对石墨烯片剪切模量、强度和临界起皱应变与化学功能化的关系,结果表明,杨氏模量与官能团的官能团化程度和分子结构密切相关,官能团分子量对杨氏模量的影响较小. 化学功能化还降低了剪切模量和临界起皱应变.官能团与石墨烯片之间的结合能是这些发现的主要原因.Pei等[22-23]基于分子动力学方法,分别研究了只含有氢官能团和甲基官能团时的力学性能,结果表明,功能化石墨烯的力学性能主要取决于甲基的位置、分布和覆盖范围,当甲基随机分布时,石墨烯弹性模量随甲基覆盖范围的增大而逐渐减小,而在低覆盖范围下强度和断裂应变均有明显下降.当甲基覆盖范围达到饱和时,弹性模量、强度和断裂应变分别下降18%,43%和47%.Gomez-Navarro等[24]利用原子力显微镜(AFM)对氧化石墨烯的杨氏模量进行了测试,结果表明,其杨氏模量约为250$\pm$150,GPa. Suk等[25]测试了氧化石墨烯的厚度和杨氏 模量,结果表明,其厚度为7 å,杨氏模量约为207.6$\pm$23.4,GPa. 此外,若选取氧化石墨烯厚度为7å时,则基于分子动力学数值模拟得到氧化石墨烯的杨氏模量约为325,GPa,极限强度约为31,GPa[26].
1 数值模拟方法
1.1 氧化石墨烯模型
分子模拟计算软件(materials studio,MS)具有较强的构建、显示和分析分子、固体及表面的结构模型的能力,在分子模拟领域具有广泛应用. 因此,本文利用MS软件创建羟基、羧基和环氧基随机分布的氧化石墨烯无序结构模型.根据文献[30]的研究结果,官能团的随机分布应满足以下条件:
(1)同一碳原子位只包含一个官能团;
(2)官能团的不恰当布置会引起石墨烯片层的应力和形变,因此,应分别于石墨烯片层两侧的近邻碳原子上成对添加官能团,并保持两侧官能团总数近似相等;
(3)为避免不饱和边界效应,边界碳原子上增加氢原子,由于C---C键长为1.42 å,C---H键长为1.14å,氢原子和连接氢原子的碳原子的电荷分别为$+0.1268$e 和$-0.1268$e,因此可保证整个模型为中性;
(4)对石墨烯某单个碳六元环而言,由于空间限域效应,理论上其一侧最多有6个碳原子连接官能团.但当某个碳六元环一侧的碳原子中有4个及其以上连接羟基时,必会出现在同一平面上有羟基两两相邻的情况,致使其相互作用生成气相水分子而脱附;而当一侧有超过5个碳原子连接环氧基时,将会使碳六元环局部出现较大曲率,从而造成体系稳定性变差.故所建模型中应保证每个碳六元环一侧有少于4个碳原子连接羟基或少于5个碳原子连接环氧基[30].
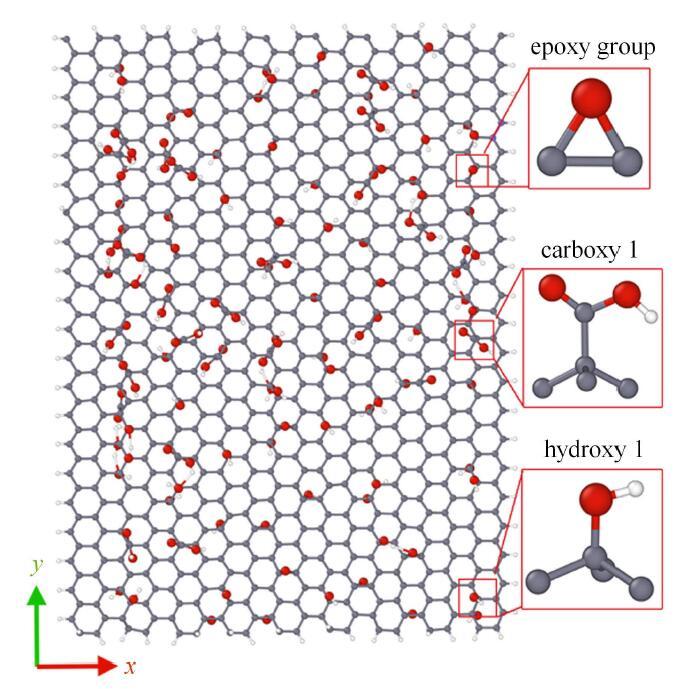
基于上述原则,即可创建包含有羟基、羧基和环氧基随机分布的氧化石墨烯无序结构模型,如 图2所示.
图 2
图 2
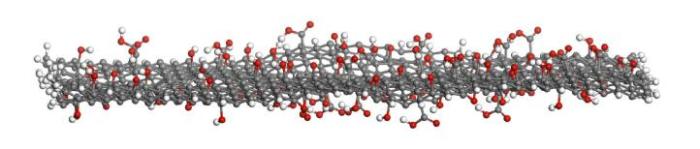
氧化石墨烯原子构型图(图中灰色粒子为碳原子,红色为氧原子,白色为氢原子)
Fig. 2
Atomic configuration diagram of graphene oxide(The grey particles are carbon atoms, red particles are oxygen atoms, and white particles are hydrogen atoms)
1.2 模拟方法
图 3
图 3
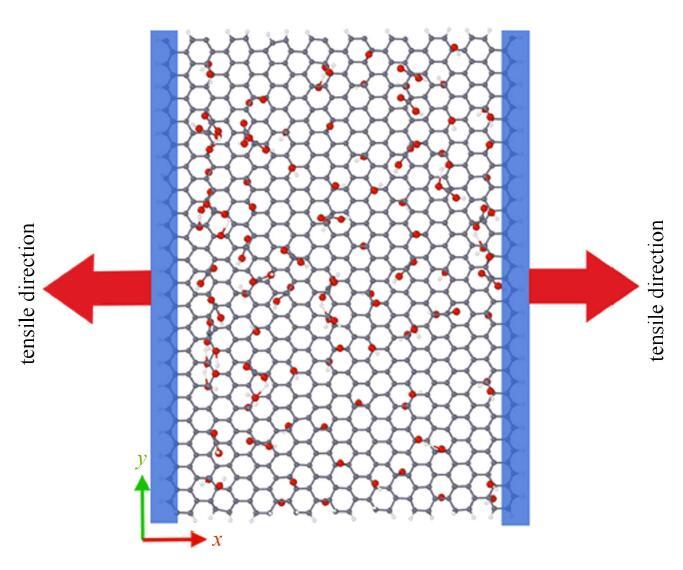
氧化石墨烯Armchair向拉伸模型(蓝色区域为拉伸加载端)
Fig. 3
GO tensile along Armchair direction (The blue area is the stretch loading end)
图 4
图 4
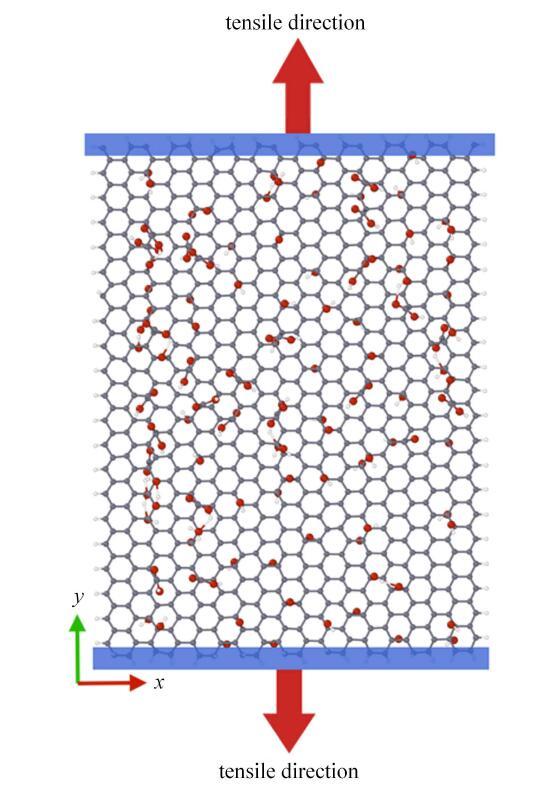
氧化石墨烯Zigzag向拉伸模型(蓝色区域为拉伸加载端)
Fig. 4
GO tensile along Zigzag direction (The blue area is the stretch loading end)
拉伸模拟时,首先将模型在温度为300,K 的NVT系综下弛豫25,ps.待弛豫完成后,固定一端,另一端沿拉伸方向施加位移载荷,每加载一次后弛豫1,ps,待体系达到平衡后继续重复上述过程直至 破坏.
1.3 模拟方法验证
完美石墨烯的拉伸力学性能已被大量的试验和数值模拟所研究,为验证上文所述方法的正确性,首先利用上述方法对完美石墨烯的拉伸力学性能进行模拟,并与已有结果进行对比,以此验证所述数值方法的正确性.
图5
图5
完美石墨烯沿不同方向拉伸示意图
Fig. 5
Schematic diagram of perfect graphene tesiled along different directions
图6
图6
完美石墨烯拉伸应力$\!$-$\!$-$\!$应变曲线
Fig. 6
Tensile stress-strain curves of graphene
根据图6所示应力$\!$-$\!$-$\!$应变曲线,通过对两个方向的拉伸初始阶段(拉伸应变0$\sim$0.04)的应力$\!$-$\!$-$\!$应变曲线进行线性拟合,并取两个方向的平均值即可得完美石墨烯的弹性模量约为1.052,TPa,该结果与通过纳米压痕测试的1.0,TPa以及通过第一性原理计算所得的1.05,TPa非常接近,从而验证了所述数值方法的正确性.
2 结果与讨论
2.1 弛豫行为分析
为获得稳定的氧化石墨烯模型,拉伸前首先应对模型进行充分地弛豫,使其体系能量最小化,图7即为体系能量随弛豫时间变化曲线图.
图7
由图可见,在开始阶段(0$\sim$2,ps),模型能量随弛豫步数快速递减,随后达到平衡状态,直至弛豫结束(25,ps),表明氧化石墨烯模型达到稳定状态.
弛豫后的氧化石墨烯原子构型呈现不规则褶皱状,如图8所示,分析认为,这是由于氧化石墨烯表面的官能团所引起的局部晶格畸变;且由于不同官能团在石墨烯表面的随机分布,致使晶格畸变的密度和程度不均匀,从而使氧化石墨烯呈现不规则的褶皱状.
图 8
图 8
弛豫后的氧化石墨烯原子构型
Fig. 8
Atomic configuration diagram of GO after energy minimization
2.2 拉伸断裂行为分析
2.2.1 拉伸断裂过程
根据上文所述模拟方法,对弛豫后氧化石墨烯分别沿armchair和zigzag方向进行拉伸模拟,可见拉伸过程中氧化石墨烯C---C键逐渐伸长,官能团出现不同程度的无序振动.
因此,对于石墨烯而言,其裂缝扩展路径基本相同,而氧化石墨烯裂缝扩展路径则主要取决于官能团的分布,即远离羟基和羧基 的环氧基的位置对裂缝的扩展具有明显的"诱导"作用.
图9
图9
氧化石墨烯沿airmchair方向拉伸破坏过程图
Fig. 9
The failure process under tension along armchair direction
2.2.2 拉伸断裂机理
根据以上所述,氧化石墨烯的断裂行为主要受到远离羟基和羧基且与环氧基相连的C---C键的影响,以下从化学成键、体系能量和应力分布3个方面对其断裂机理进行分析.
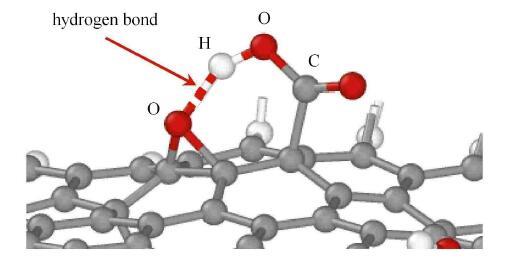
(1)化学成键方面. 分析认为,氧化石墨烯的裂缝启裂和扩展位置位于远离羟基和羧基的环氧基,是由于当与羟基或羧基相近时, 环氧基会与羟基或羧基形成氢键,从而使得结构体系稳定性增强,如图10所示;而当远离羟基和羧基时,环氧基无法与羟基或羧 基反应形成氢键,因此结构稳定性较差,在外力作用下,更易发生断裂,因此,远离羟基和羧基的环氧基对氧化石墨烯的开裂及 裂纹扩展表现出一定的"诱导"作用.
图10
图10
临近的环氧基和羧基形成氢键示意图
Fig. 10
Schematic diagram of adjacent epoxy and carboxyl groups forming hydrogen bonds
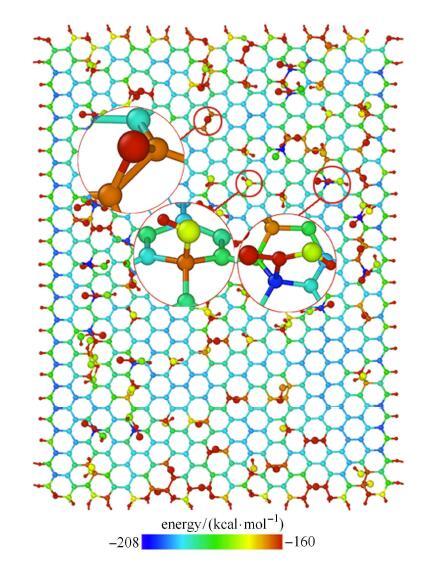
(2)体系能量方面. 原子结构体系的稳定与否取决于体系能量大小,能量越高,体系越不稳定. 为此,对弛豫后的氧化石墨烯上与不 同官能团相连的碳原子的能量进行对比,如图11所示.
图 11
由图可见,含有官能团的区域能量明显高于其他区域.且与环氧基和羟基官能团相连的氧化石墨烯碳原子所具有的能量明显高于与羧基官能团直接相连的氧化石墨烯碳原子能量,因此更易于失稳而发生断裂.
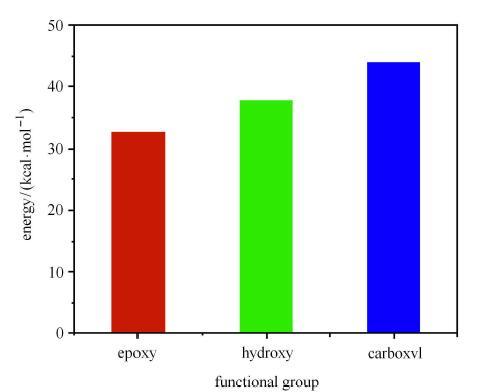
为进一步说明不同官能团对断裂的影响规律,分别比较断裂路径上与环氧基、羟基和羧基相连的C---C键在断裂时所需的能量,如图12所示.由图可见,连接环氧基的C---C键断裂时所需能量最小,羟基次之,羧基最高,说明在氧化石墨烯拉伸加载过程中,相较于羟基与羧基,环氧基官能团更易达到断键能量,在断键区域形成多元环缺陷,进而导致氧化石墨烯结构破坏.
图12
图12
官能团断键能量对比图
Fig. 12
Comparison diagram of bond breaking energy of functional groups
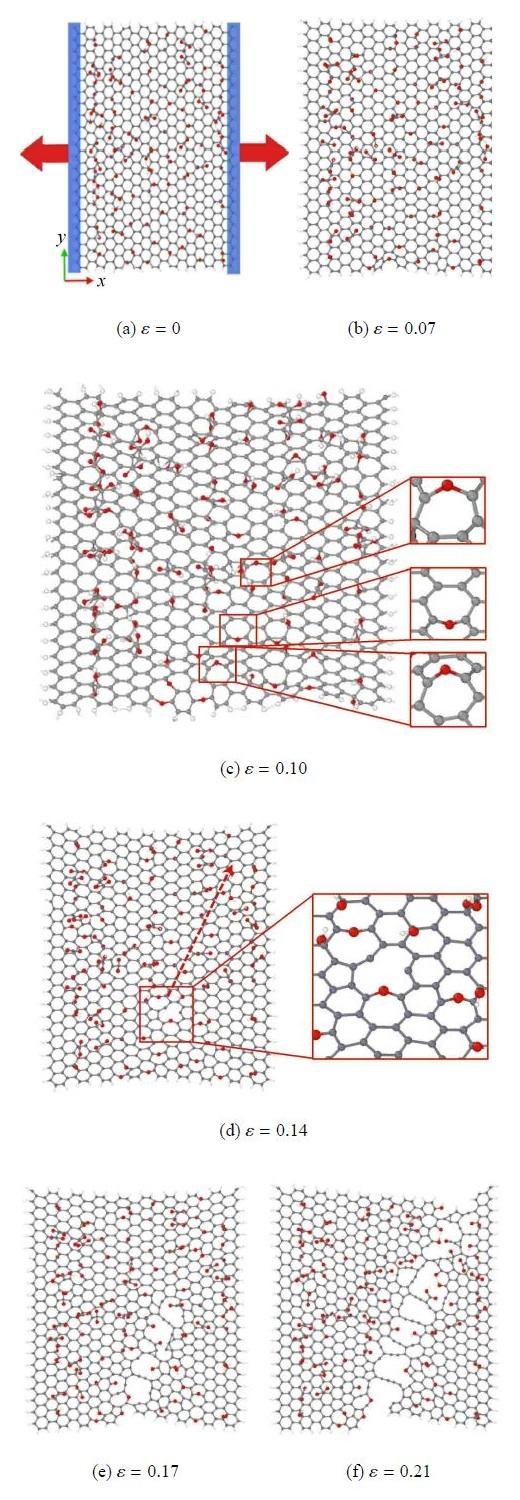
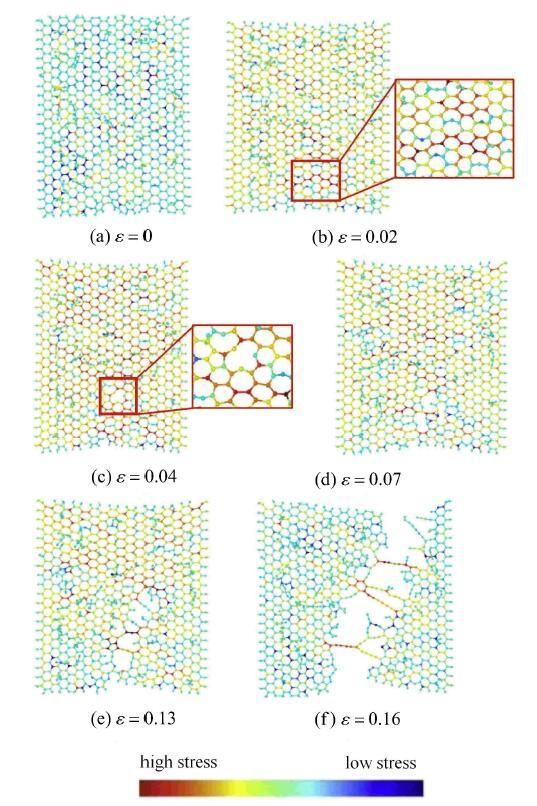
(3)应力分布方面. 图13为拉伸过程中氧化石墨烯的的原子应力分布构型图. 由图13(a)可见,拉伸初始状态时,整个体系应 力水平较低,且由于官能团的存在,使得连接官能团的原子处晶格失配,整个体系应力分布不均,而由于环氧基同时连接两个碳 原子,造成该区域应力分布更加不均匀. 随着不断加载,整个模型上的平均应力逐渐增大,当拉伸应变增至0.02时,连接环氧基 且远离羟基和羧基的部位由于应力较大,逐渐出现多元环缺陷,且应力明显高于其它部位,如图13(b) $\sim$图13(c)所示. 当载荷继续增大后,自然追踪至远离羟基和羧基的环氧基所连接的C---C环,如图13(d) $\sim$图13(e). 之后,随着拉伸 载荷的继续 增加,裂纹继续扩展直至贯通,导致石墨烯的最终断裂,整个体系能量重新降低至较低水平,如图13(f).
图13
图13
氧化石墨烯单向拉伸过程中原子应力分布图
Fig. 13
Stress distribution diagram of GO under uniaxial tensionfunctional groups
因此,远离羟基和羧基的环氧基由于同时连接两个碳原子,致使体系局部晶格失配程度较大,应力集中现象明显,极易在外力作用下发生破坏而出现断裂.
2.3 拉伸力学性能
2.3.1 应力$\!$-$\!$-$\!$应变曲线
应力$\!$-$\!$-$\!$应变曲线可以反映结构的极限强度、极限应变和弹性模量等力学基本参数,是表征材料力学性能的重要依据[28].
图 14
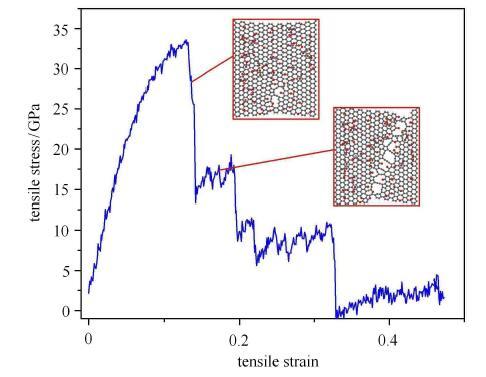
图 14
Armchair向拉伸应力$\!$-$\!$-$\!$应变曲线
Fig. 14
Stress-strain curve of GO tensiled along armchair direction
图 15
图 15
Zigzag向拉伸应力$\!$-$\!$-$\!$应变曲线
Fig. 15
Stress-strain curve of of GO tensiled along zigzag direction
由图可见,与图6所示的完美石墨烯的应力$\!$-$\!$-$\!$应变曲线具有较大的手性相关性不同,氧化石墨烯在两个方向的拉伸力学性能相近,没有明显的手性相关性.分析认为,这是由于氧化石墨烯的力学性能很大程度上取决于表面含氧官能团的分布情况,而所建模型上的官能团为随机分布,因此致使手性对力学性能的影响并不明显.
此外,与完美石墨烯相比,氧化石墨烯拉伸应力应变曲线显得"不光滑",分析认为,这主要是由于氧化石墨烯表面随机分布有大量羟基、羧基和环氧基等,这些含氧官能团的存在会加剧氧化石墨烯的局部晶格畸变程度,使得氧化石墨烯在稳定状态下呈现不规则的褶皱状(图8所示);同时在拉伸过程中各官能团的热振动使石墨烯片层表面局部晶格畸变程度进一步加剧,表面的褶皱不规则程度更大,导致在拉伸过程中,应力和应变间呈现不稳定的变化关系,从而使应力$\!$-$\!$-$\!$应变曲线呈现不光滑状.
此外,由图可见,应力与应变曲线在初始阶段(应变为0$\sim$0.04)呈现较强的非线性关系. 分析认为,这也是由于含氧官能团的无序分布使得弛豫后氧化石墨烯呈现不规则的褶皱状,即各部分褶皱的程度不同,从而使得各部分从褶皱至拉伸平展所需的时间和荷载存在一定差异,致使整体模型的应力和应变之间的呈现一定非线性.
达到极限强度后,应力$\!$-$\!$-$\!$应变曲线会呈震荡性衰减,分析认为,这是由于氧化石墨烯断裂后会由于吸附现象,不同原子间会重新成键,形成若干链状结构(如图中原子构形图可见),该结构仍可暂时性维持一定的抗拉能力. 随着拉伸的进一步进行,链状体系逐渐断裂,但由于其断裂的时间不同,因此应力$\!$-$\!$-$\!$应变曲线会出现不规则的震荡现象,直至完全断裂.
2.3.2 力学性能与官能团覆盖度关系
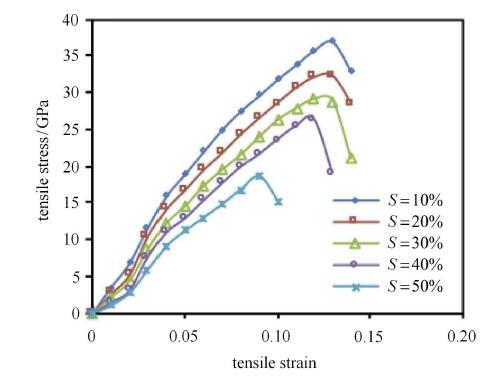
由上文可知,含氧官能团对氧化石墨烯的力学性能具有重要影响,为此,基于上文所述方法,创建官能团比例为O:OH:COOH=1:1:0.2,覆盖度分别为10%, 20%, 30%,40%和50%的氧化石墨烯数值模型,并分别进行拉伸模拟,可得不同覆盖度下的应力应变 曲线,如图16所示.其中,官能团覆盖度$S$ 的定义为: $S$=(连官能团C数/体系C总数)$\times $100%.
图16
图16
氧化石墨烯拉伸应力$\!$-$\!$-$\!$应变曲线与官能团覆盖度关系图
Fig. 16
Relationship between tensile stress-strain curve and functional group coverage of GO
图17
图17
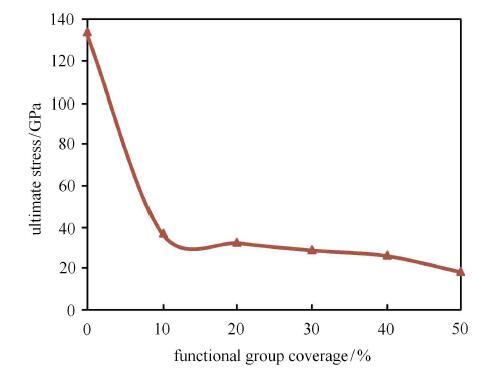
极限强度随官能团覆盖度变化曲线图
Fig. 17
Variation curve of ultimate strength with functional group coverage
图18
图18
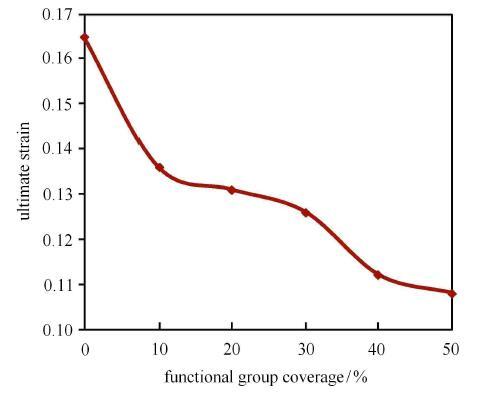
极限应变随官能团覆盖度变化曲线图
Fig. 18
Variation curve of ultimate strain with functional group coverage
由图17可见,随官能团覆盖度增大,拉伸强度逐渐减小.与石墨烯相比(官能团覆盖度为0),当氧化石墨烯的含氧官能团覆 盖度分别为10%, 20%, 30%,40%和50%时,其拉伸强度分别下降了72.39%, 75.90%, 78.28%, 80.37%和86.19%.
由图18可见,与石墨烯相比(官能团覆盖度为0),当氧化石墨烯的含氧官能团覆盖度为10%, 20%, 30%, 40%和50%时,其拉伸极限应变分别下降了17.58%, 20.61%, 23.64%, 32.12%和34.55%,表明羟基、羧基和环氧基等含氧官能团对氧化石墨烯的拉伸力学性能具有极大地削弱作用.
分析认为,含氧官能团对氧化石墨烯力学性能削弱的主要原因是官能团对氧化石墨烯电子结构的改变.首先,由于完美石墨烯 上碳六元环的C原子以 sp$^{2}$杂化轨道组成,所形成的$\pi$键具有强大的键合能,从而使得石墨烯具有优异的面内抗拉强 度.而羟基、羧基和环氧基等官能团会导致石墨烯碳环的C原子间作用由sp$^{2}$杂化转化为sp$^{3}$杂化形式,使得原来碳环C原子间的$\pi $键转变成较弱的$\sigma$键,使得键合能极度弱化;其次,氧化石墨烯表面的官能团对石墨烯表面的C原子会具有吸附力作用,从而致使C原子脱离石墨烯表面,造成局部碳原子键长的增大,进一步弱化原子间键合能. 而以上两方面的影响都会随着官能团覆盖度的增加而加剧,因此,致使力学性能随官能团覆盖度的增加而显著降低.
3 结论
本文利用分子动力学方法,创建了氧化石墨烯数值模型;研究了不同含氧官能团覆盖度下氧化石墨烯的应力$\!$-$\!$-$\!$应变曲线、极限强度和极限应变等变化规律,并对其机理进行了分析. 主要结论包括:
(1) 拉伸断裂行为结果表明,远离羟基和羧基的环氧基对断裂有"诱导"所用.分析认为,一方面是远离羟基和羧基时可避免氢 键的生成;另一方面连接环氧基的C---C键断裂时所需能量最小.
(2) 氧化石墨烯的应力$\!$-$\!$-$\!$应变曲线、极限强度和极限应变等拉伸力学性质与含氧官能团覆盖度具有很大相关性. 官能团覆盖度越大,应力$\!$-$\!$-$\!$应变曲线的初始阶段的非线性越强,且整体越不光滑. 而极限强度和极限应变均随着覆盖度的增大而呈减小趋势.
(3) 官能团对氧化石墨烯力学性能的影响机理主要是由于官能团的出现使得石墨烯碳环的C原子由面内sp$^{2}$杂化转化为面外sp$^{3}$杂化,使得C原子间键合能弱化,力学性能得到削弱.
参考文献
Spontaneous rolling-up and assembly of graphene designed by using defects
Molecular dynamics study on the anisotropic Poisson's ratio of the graphene
Negative Poisson's ratio in graphene oxide
The effect of Stone-Thrower-Wales defects on mechanical properties of graphene sheets-a molecular dynamics study
Synthesis, properties, and applications of graphene oxide/reduced graphene oxide and their nanocomposites
Precisely controlled growth of poly (ethyl acrylate) chains on graphene oxide and the formation of layered structure with improved mechanical properties
Graphene oxide: Preparation, functionalization, and electrochemical applications
A one-step strategy for thermal- and pH-responsive graphene oxide interpenetrating polymer hydrogel networks
Multifunctional graphene oxide-based triple stimuli-responsive nanotheranostics
Multi-stimuli responsive smart elastomeric hyperbranched polyurethane/reduced graphene oxide nanocomposites
Recent advances in graphene based polymer composites
A rapid and efficient self-healing thermo-reversible elastomer crosslinked with graphene oxide
Synergistic effects of fly ash and graphene oxide on workability,mechanical property of cement-based materials
Fast self-healing of graphene oxide-hectorite clay-Poly ($N$,$N$-dimethylacrylamide) hybrid hydrogels realized by near-infrared irradiation
Tough, stretchable, compressive novel polymer/graphene oxide nanocomposite hydrogels with excellent self-healing performance
A self-healable nanocomposite based on dual-crosslinked graphene oxide/polyurethane
Self-healing and self-mendable polymers
Amino functionalization of graphite nanoplatelet
Effects of functional group on the mechanical and wrinkling properties of graphene sheets
A molecular dynamics study of the mechanical properties of hydrogen functionalized graphene
Mechanical properties of methyl functionalized graphene: A molecular dynamics study
Elastic properties of chemically derived single graphene sheets
Mechanical properties of monolayer graphene oxide
Computational studies of the structure, behavior upon heating, and mechanical properties of graphite oxide
基于分子动力学$\!$-$\!$-$\!$格林函数法的微凸体接触数值分析
Numerical analysis of asperity contact model based on molecular dynamics Green's function method
双层金属纳米板界面能密度的尺寸效应
Size effect of the interface energy density in bi-nano-scaled-metallic plates
含氢原子缺陷晶界的剪切行为
Shear response of grain boundaries with hydrogen defects
弯曲碳纳米管和氧化石墨烯的原子尺度模拟. [博士论文]
Atomistic simulations of the curved carbon nanotubes and graphene oxide. [PhD Thesis]
ReaxFF reactive force field for molecular dynamics simulations of hydrocarbon oxidation
Hydrogen bond networks in graphene oxide composite paper: Structure and mechanical properties
A reactive molecular dynamics simulation study of methane oxidation assisted by platinum/graphene-based catalysts
Effect of lattice stacking orientation and local thickness variation on the mechanical behavior of few layer graphene oxide